Abstract
Geodesic vector fields and other distinguished vector fields on a Riemann manifold were used in the study of free motions on such a manifold, and we applied the geometric Hamilton–Jacobi theory for the search of geodesic vector fields from Hamilton–Jacobi vector fields and the same for closed vector fields. These properties were appropriately extended to the framework of Newtonian and generalised Newtonian systems, in particular systems defined by Lagrangians of the mechanical type and velocity-dependent forces. Conserved quantities and a generalised concept of symmetry were developed, particularly for Killing vector fields. Nonholonomic constrained Newtonian systems were also analysed from this perspective, as well as the relation among Newtonian vector fields and Hamilton–Jacobi equations for conformally related metrics.
Keywords:
geodesic vector fields; eikonal; geometric Hamilton-Jacobi; external forces in mechanical systems PACS:
02.40.Ky; 45.20.-d
MSC:
53C80; 58Z05; 70H33; 70G45
1. Introduction
The active interface between mathematics and theoretical physics during the last few years has been very useful for both disciplines. This interaction is very efficient, and in particular, the modern tools of differential geometry have been used to deal with old problems of classical and quantum mechanics, offering a new perspective to analyse conceptual problems, as, for instance, the existence and non-uniqueness of the solution of the inverse problem for a given system of second-order differential equations describing a time evolution. However, many physical theories have also motivated mathematicians, a good example being the theory of group representations, because of its usefulness in the symmetry theory of quantum mechanics.
Riemannian geometry is very relevant in the geometric reformulation of classical systems of a mechanical type, a Riemann metric allowing us the definition, in an intrinsic way, of kinetic energy. Free motions of holonomic constrained systems correspond to geodesic curves of their associated Levi-Civita connection, and the physical systems under the action of external forces can also be dealt with, the curves of motion corresponding to integral curves of an appropriately defined dynamical vector field. In this sense, the Riemannian approach is closer to the elementary and original ideas of Newton on the description of mechanical systems.
The importance of geodesics leads to the study of geodesic vector fields in a Riemann manifold, i.e., vector fields whose integral curves are geodesics. These vector fields are used in the study of Yamabe solitons (see, e.g., [1]) and are also useful in many other fields of physics, where they appear as solutions of the eikonal equation and even in medical imaging [2]. Unfortunately, these autoparallel vector fields have scarcely been studied in the literature, and we hope that the application of well-known ingredients of classical mechanics, as the Hamilton–Jacobi equation, conveniently reformulated in a geometric way, may shed some light on the characterisation and determination of such an interesting class of vector fields. This is the main aim of the first part of this paper.
Once the study of these notions on the geodesic flow is performed, it is natural to ask about their possible extension to more general second-order vector fields, in particular those coming from mechanical systems subjected to external forces. We developed this extension including the case of nonholonomic mechanical systems with nonholonomic constraints. Then, we studied not only the geodesic case, for which many results are known, but also the unknown case of mechanical and generalized mechanical systems, with external forces possibly depending on the velocity.
The structure of this article is as follows. In Section 2, we quickly review the theory of the Levi-Civita connection on a Riemann manifold, mainly to fix the notation to be used. A quick review of the geometric approach to Lagrangian and Hamiltonian systems is given, and the geodesic flow appears as the flow of a Hamiltonian vector field. In Section 3, we review the properties of some distinguished vector fields in Riemannian manifolds with a special emphasis on geodesic vector fields, which are our main aim. The geometric approach to the Hamilton–Jacobi theory, whose fundamental ideas were developed in a series of articles elaborated by the authors and their coworkers, is reviewed in Section 4, where the concept of the Hamilton–Jacobi vector field is also introduced. The search for Hamilton–Jacobi vector fields for the second-order geodesic vector field and their relations with autoparallel vector fields are studied in Section 5, and the relation between a geodesic vector field, its tangent lift, and the second-order geodesic vector field is studied in Section 6. General Newtonian dynamical systems, the existence of Noether conserved quantities, and Newtonian vector fields and their properties are studied in Section 7, and an application for studying some relations between two conformally related metrics is studied in Section 8. Conclusions and an outlook on future work are given in Section 9. Finally, in order for the paper to be self-contained, we added an Appendix A with some definitions and mathematical results on tensor fields along maps.
2. Notation, Basic Definitions, and Geometric Preliminaries
2.1. Riemannian Manifolds and Levi-Civita Connection
Let M be an n-dimensional differentiable manifold. A Riemannian metric on M is a two-times covariant symmetric tensor field g, which is positive definite, hence non-degenerate. The pair is called a Riemann manifold.
Non-degeneracy implies that the map from the tangent bundle, , to the cotangent bundle, , defined by , where , is a vector bundle isomorphism. As is a fibred map over the identity on M, it induces a natural map between the modules of sections of the tangent and cotangent bundles, denoted by the same letter : , i.e., .
Given a local chart on M, we can consider the coordinate basis of , usually denoted , and its dual basis for , . Then, any , with , is , and any is , with and being the usual velocities and momenta.
The local coordinate expression for the Riemannian metric g in the open set U is:
The arc-length of a curve , , between the points and is given by
i.e., the classical local expression for the arc-length is given by .
Recall (see, e.g., [3,4]) that a linear connection ∇ on a manifold M is a map , which is -linear on both inputs, -linear on the first one, and satisfies the rule , for and . It is easy to prove that depends only on X and Y on ; hence, in a local coordinate system , the connection symbols are defined by
while is given by
Recall that is known as the covariant derivative of the vector field Y with respect to the vector field X. Observe from the above local expression that the value of on a point only depends, with respect to X, on .
Moreover, each linear connection has associated a (1,2) tensor field , called the torsion tensor, which is skew-symmetric in the two subscripts, and it is defined as follows:
A connection ∇ on a Riemann manifold is metric when, given , we have that
where denotes Lie derivative with respect to the vector field X. This is equivalent to saying that . Recall that the operator , for , can be extended as a derivation that commutes with the tensor contractions, on all the tensor fields on M. In particular, is defined by the expression:
because g is non-degenerate. See, e.g., [3,4] for more details on the covariant derivative of tensor fields.
It is a fundamental result that every Riemann manifold is endowed with a uniquely determined torsionless metric connection ∇, called the Levi-Civita connection, which is given by the so-called Koszul formula:
for every . In terms of local coordinates on M, the Koszul formula gives
and, by the above definition of connection symbols (usually called second-class Christoffel symbols),
where . On the other hand, the vanishing of the torsion tensor is equivalent to the symmetry property of the Christoffel symbols: . As indicated above, these symbols locally determine for every pair of vector fields by making use of (4).
2.2. Geodesics: Definition and Second-Order Geodesic Vector Field
Let be a curve in the manifold M. For each , denotes the tangent vector to the curve at the point . This shows that we can define a curve on , , by . As , the curve defines a vector field along , i.e., . However, we remark that the curve on can also be considered as the lift to the tangent bundle of the curve . To distinguish both roles of , when necessary, we will denote such a lifted curve as instead of simply . Observe that
Let ∇ be a connection on a manifold M. It is a remarkable fact (see, e.g., [3,4] for details, or have a look at the expression (4) above) that the value of at a point , , only depends, with respect to X, on the value of X at such a point and, with respect to Y, on the value of Y along any segment of the curve representing the tangent vector .
Then, for each , we can define , where X is any vector field such that . Moreover, given a curve in M, if , we can define by , while when , is defined as . Similarly, if , we can define as the vector field along given by .
This allows us to introduce the concept of the parallelism of a vector field along a curve as follows: a vector field, , along the curve , is parallel along if , for all . Observe that this expression is correct by the comments in the previous paragraph.
In the particular case of , every curve such that its velocity vector field is parallel along the curve, that is for all , is called a geodesic.
Definition 1.
We call geodesics of the connection ∇ the curves γ in M whose velocity vector field is parallel along the curve, .
In the case of a Riemann manifold and its Levi-Civita connection ∇, the geodesic curves are uniquely defined by the Riemannian metric g, and they are local extrema of the distance function as defined in (2).
Recalling the expression (4), given a curve , , which we can assume to be parametrised by its arc-length s, that is for every s, we have
Then, the local equation of the geodesic lines, , is the second-order differential equation:
If we consider a reparametrisation of a solution of (10) with a generic parameter defined, as a given function of s, by
we have
and the corresponding differential Equation (10) for geodesics in such a generic parametrisation is
with
Hence, as if, and only if, , we can conclude that, as indicated in [5,6,7], a geodesic curve is parametrised by a parameter that is an affine function of its arc-length, , where , i.e., a geodesic is essentially parametrised by its arc-length s.
2.3. Lagrangian Dynamical Systems
A Lagrangian dynamical system is a pair , where M is a differentiable manifold, the configuration manifold, and is the Lagrangian function. The associated dynamical system is defined with the following elements (see [8,9] for details):
- 1.
- The Cartan Lagrangian one-form , with S being the vertical endomorphism on the tangent bundle .
- 2.
- The Cartan Lagrangian two-form .
- 3.
- The energy function , with the Liouville vector field on .
- 4.
- Assuming that is a symplectic form (see below), a unique vector field solution to the Hamilton dynamical equation is defined:
The vector field is called the Lagrangian dynamical vector field, and it is the Hamiltonian vector field, defined by the energy function , for the Hamiltonian system . Furthermore, is an SODE vector field in , that is its integral curves are canonical lifts to of curves , i.e., .
In local natural coordinates, , of , the expressions of the above elements are:
and the dynamical second-order vector field is:
The differential equations for the integral curves, , of are
giving , that is a second-order differential equation.
The condition for the Lagrangian two-form to be symplectic is related to the partial Hessian of L with respect to the velocities: is symplectic if, and only if, , which, in local coordinates, reads
As a consequence, the coefficients are univocally determined if is symplectic.
2.4. The Geodesic Flow as a Lagrangian Dynamical System
If is a geodesic curve in the Riemannian manifold , its lift to , , is an integral curve of a vector field (see, e.g., [5,10]); this is the Hamiltonian dynamical vector field defined by the Lagrangian , which gives the Lagrangian system , i.e., is the unique solution of the Hamiltonian equation , where the kinetic energy function, , is defined by
and the Cartan one-form is given by
the associated symplectic two-form on being .
The dynamical vector field corresponding to the Lagrangian system is the unique solution to the equation:
whose local expression is given by
The integral curves of are liftings of curves in M that are solutions of the system of differential equations for geodesic curves, , i.e., the system (10).
Observe that is such that, if , for a vector field and its complete lift to , then from the relation , we obtain that , and this is only possible when X is a Killing vector field, that is if, and only if, . Moreover, if , i.e., is closed, then is a closed semibasic one-form, and therefore basic, and this implies that , i.e., ; we have that if, and only if, X is a Killing vector field.
2.5. Hamiltonian Dynamical Systems
Going to , we know that there is a canonical symplectic structure coming from the symplectic form defined by , where is the Liouville one-form in . See [11,12] for details. Their local expressions in natural coordinate systems, , are:
Given a function, the Hamiltonian, , we can obtain a dynamical vector field defined univocally by the equation . Locally, the expression of the integral curves, , of this vector field is
which are known as Hamilton dynamical equations.
2.6. The Geodesic Flow as a Hamiltonian Dynamical System
We study in this paragraph the case of the geodesic flow corresponding to the Lagrangian system , where g is a Riemannian metric on M.
Associated with this system in , there is a Hamiltonian system in obtained through the Legendre map; see [11,12] for details.
Given the geodesic Lagrangian system on the Riemann manifold , the associated Hamiltonian system is , with Hamiltonian , where ; hence, is the corresponding matrix of the metric in the fibres of .
The Hamiltonian vector field for , , is given by
Thus, the Hamilton differential equations of a geodesic , , are
As , the second set of these equations can be reduced, by making use of the expression of the Christoffel symbols, to Equations (10).
3. Distinguished Vector Fields in a Riemann Manifold
The aim of this section is to review some known properties of Killing vector fields and obtain new ones related to geodesic, and other kinds, of vector fields.
3.1. Definitions and Initial Relations
There are distinguished classes of vector fields on a Riemann manifold . If ∇ denotes its associated Levi-Civita connection, then:
Definition 2.
(i) We say that a vector field is aconformal Killing vector fieldif there exists a function such that . A conformal Killing vector field ishomotheticwhen the function ψ is a constant.
(ii) We say that a vector field is aKilling vector fieldif X is such that , i.e., the local flow of the vector field X preserves g.
(iii) We say that a vector field is anautoparallel vector fieldif .
(iv) We say that a vector field is ageodesic vector fieldif each integral curve of X is a geodesic curve of the associated Levi-Civita connection.
It is well known that the set of conformal Killing vector fields is a Lie algebra called the conformal Lie algebra [13], which contains two Lie subalgebras, the homothetic Lie subalgebra and the Killing Lie algebra, because if and , then
In particular, when X and Y are homothetic, then .
As indicated in [5], one can see that a Killing vector field has constant length if, and only if, every integral curve of X is a geodesic, i.e., X is a geodesic vector field (see, e.g., Lemma 3 in [14]). We can also see that, as will be proven later on, if the vector field is autoparallel, then is constant along the integral curves of X, that is .
The condition for to be a Killing vector field, , can be rewritten, using only norms, as
because
For the local expression of Killing vector fields, let be the vector field with local expression in a local chart:
then the Lie derivative with respect to X of the metric tensor field g is
or using the symmetry property of the metric tensor field,
which shows that the condition for X to be a Killing vector field, i.e., , is written in local coordinates as
Thus, the local conditions for a vector field to be a Killing symmetry are:
We can show (see next subsection) that a vector field is a geodesic vector field if, and only if, it is an autoparallel vector field, i.e., if , because the vector field X is a geodesic vector field if, and only if, its integral curves are geodesics, i.e., they satisfy the condition (see, e.g., [1]).
It has also been remarked in [5] that, for each nonvanishing function , if is an autoparallel vector field, then satisfies . However, each integral curve of the vector field X coincides with one of , up to a reparametrisation, and therefore, the preceding property can be used to derive that each integral curve of a vector field X can be reparametrised to be a geodesic curve if, and only if, , where f is a nonvanishing function . Moreover, it was proven in [5] that all the integral curves of a vector field can be transformed by a Sundman transformation (see [5] and the references therein) into geodesic curves of the metric g if, and only if, X is a pregeodesic vector field, that is there exists a function such that . This leads to the following definition:
Definition 3.
We say that a vector field is ageneralised geodesic vector field, sometimes also-calledpregeodesic vector field, if there is a nonvanishing function such that .
Observe that an integral curve of such a vector field is such that its acceleration is proportional to its velocity. It was proven in [1] that a nonzero generalised geodesic vector field of constant length is a geodesic vector field.
Using that the metric g provides an identification of and , and as closed and exact one-forms are distinguished ones, we can correspondingly introduce the definition of closed and gradient vector fields [15] and some of their properties:
Definition 4.
We say that a vector field is aclosed vector fieldwhen its corresponding one-form is closed, . In the special case of exact one-forms, we say that the vector field X is agradient vector field: if , the vector field X is said to be the gradient of f.
As an immediate application of (6), we see the above-mentioned property: if a vector field is autoparallel, then is constant along the integral curves of X, that is
Having in mind also that we obtain from (6) and the torsionless condition for the Levi-Civita connection that
In particular, for , we have
Similarly,
and then, as the connection is metric,
and as the connection is torsionless, such an expression reduces to
which can also be rewritten as
therefore, when X is a closed vector field,
Some of these expressions will be used in the sequel.
3.2. Some Properties of Geodesic Vector Fields
For the sake of completeness, we give here a brief account of some known results on geodesic vector fields and references relating them to other specific classes of vector fields. The proofs we include are slightly different from the original ones in the given references (see, e.g., [5] and the references therein):
1. Our first remark is that a vector field is an autoparallel vector field if, and only if, its integral curves are geodesics, i.e., they satisfy the equation , and then, when lifted to the tangent bundle , are integral curves of , the second-order geodesic vector field.
In fact, suppose that , and let be an integral curve of X, that is . Then:
and therefore, is a geodesic curve in M. If, on the contrary, we suppose that every integral curve of X satisfies the equation and let and be the integral curve of X with initial condition p, we have
However, as this is true for every , we have .
Because of this property, the autoparallel vector fields are also-called geodesic vector fields [16]. In the definitions we introduced at the beginning of the section, for a vector field, it is the same to be geodesic as to be autoparallel. We remark that, for each real number a, if X is a geodesic vector field, then is geodesic also.
2. There are some relations between autoparallel and Killing vector fields, as the following ones.
It was proven in [14], Lemma 3, and it was used in [7,17] that a Killing vector field has constant length if, and only if, every integral curve of X is a geodesic, that is X is a geodesic vector field. We can give a little more general proof:
Proof.
(a) Using that the connection ∇ is metric and torsionless, we have, on the one hand, that, for arbitrary vector fields ,
because and, according to (5), . However, by making use of (7) with an interchange of the roles of X and Y,
and on the other hand,
Comparing both expressions, we have that, for arbitrary vector fields ,
(b) If , the expression (30) reduces to and this relation shows that if X is a geodesic vector field, , then , that is the norm of X is constant along the integral curves of X, in agreement with Property (22).
(c) Moreover, if X is a Killing vector field, we have that , and consequently, as Y is an arbitrary vector field, we see that, then, X is a geodesic vector field, i.e., , if, and only if, is a real constant, as we wanted. □
3. As far as the more general class of vector fields in a Riemannian manifold is concerned, that of the so-called generalised geodesic vector fields, usually also-called pregeodesic vector fields, which are those such that there exists a function f satisfying , a remarkable property was proven in [1]: a generalised geodesic vector field X of constant length on a Riemannian manifold is a geodesic vector field, because if is the function defined by , as , we have that
and equivalently, , which shows that as is constant, then ; therefore, X is a geodesic vector field.
3.3. Another Interesting Property of Killing Vector Fields
First of all, we establish a lemma whose result is to be used later on:
Lemma 1.
Let be a Riemannian manifold. The vector field is a Killing vector field if, and only if, we have that , for every vector field .
Proof.
Consider the following chain of identities for :
obtained by using the properties of the Levi-Civita connection. This shows that the condition , for every vector field , is equivalent to , for every vector field , and therefore, Condition (18) for a Killing vector field holds; this proves the result of the lemma. □
There is a kind of Noether theorem associated with a Killing vector field , to which we can associate a one-form . We recall that, given a one-form , we can define an associated, linear in the fibres, function , by . In particular, the one-form has associated the function . Therefore, the one-form has associated the function , and then, we can prove that if is a Killing vector field, the function is invariant along geodesics. More specifically, we have:
Proposition 1.
Let be a Riemannian manifold and a Killing vector field. If is a geodesic curve and , then the function is constant along the lifted to curve , that is
Proof.
We have:
and both summands on the right-hand side are null, the first one as a consequence of the preceding lemma and the second one because is a geodesic. □
In classical mechanics, the differential one-form is related to the so-called momentum form associated with the vector field X for geodesic motion. For instance, if with the usual metric, the infinitesimal generators of translations and rotations give rise to Killing vector fields whose associated momenta are the linear momentum form and the angular momentum form. More specifically, recall the important property (see, e.g., [18]) that, if X is a vector field on M, , and denotes its complete lift, , then
because, by using the definition of the Lie derivative of the function and that if is the flow of X and the flow of is , we have that, for all ,
Consequently, is a Killing vector field for the Riemann structure g if, and only if, is a symmetry for the corresponding kinetic energy function defined by g, and if we consider the symplectic manifold , when is a Killing vector field, then the vector field is a Hamiltonian vector field, because ; then, . Its Hamilton function is the linear in velocities function corresponding to the one-form , because implies that .
In order to clarify the meaning of the function , we remark that, if is given in a chart by (19), namely
then the coordinate expression of its complete lift is
and that of the one-form on M is
whose associated function is
We remark also that, as indicated above, the contraction of the complete lift vector field with the semibasic one-form:
is given by
and therefore, .
In this sense, the one-form corresponds to a function on that is the Hamiltonian function of the vector field , as shown by a comparison of (33) with (36).
For instance, in the particular case of endowed with the Euclidean metric, if X is the vector field:
the infinitesimal generator of rotations along the third axis, such a vector field is a Killing vector field, and we obtain the one-form , whose associated function is constant along a geodesic line, i.e., the corresponding constant of the motion is the third component of the angular momentum.
With our understanding of as the dynamical Lagrangian vector field of the Lagrangian system , the function is the Noether invariant corresponding to the symmetry of the Lagrangian . This is because , as we have shown above.
Note also that, as the coordinate expression of the vertical lift of the vector field given by (19) is
we have
3.4. Killing Vector Fields and the Geodesic Flow
In Equation (31) and the following paragraphs of Section 3.3, we proved that, if X is a Killing vector field on the Riemannian manifold , then its complete lift to , , is a symmetry of the kinetic energy function , and consequently we have that and . From these properties, we have the following:
Proposition 2.
Let be a Killing vector field on , its complete lift to , and the local flow of X. We have the following:
- (i)
- If is the second-order geodesic vector field, then .
- (ii)
- If is a geodesic curve, then is also a geodesic curve.
- (iii)
- If is a geodesic vector field, i.e., , then is a geodesic vector field, that is
Proof.
However, , by Equation (31). Hence, , and being a symplectic form, we have that .
(ii) If is a geodesic curve, then is an integral curve of . From (i), we have that ; hence, if is an integral curve of , then is an integral curve of .
We have then that is a geodesic because .
(iii) If is a geodesic vector field, then its integral curves are geodesics. However, the integral curves of are of the form , which, by Item (ii), are geodesics; hence, is a geodesic vector field by Item 1 in Section 3.2, because all its integral curves are geodesic curves. □
4. Hamilton–Jacobi Vector Fields
There are several methods to integrate systems of differential equations, and one of the most significant is to reduce the dimension of the manifold where the vector field corresponding to the system of differential equation is defined. Generically, this method allows us to obtain not all the solutions, but only a subset. As an instance with these ideas, a modern geometric approach to the Hamilton–Jacobi theory was developed in [19]. Even if such a theory is always developed in a Hamiltonian context, we can also consider the framework of the tangent bundle of the given Riemann manifold and extend the theory to a Lagrangian setting. In some cases, we can obtain what is called a complete solution to the Hamilton–Jacobi problem and, through it, all the solutions of the initial equation if the full set of reduced equations can be solved.
In the next subsections, we develop a quick survey of the general theory of Hamilton–Jacobi reduction and the particular cases of the Lagrangian and Hamiltonian formalism with their differences and relations.
4.1. Geometric Hamilton–Jacobi Theory
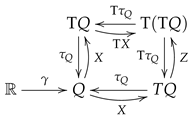
Let be a differentiable vector bundle and . We say that a pair , where denotes the set of sections of , i.e., the set of maps such that , is a Hamilton–Jacobi pair for the vector field Z if , that is is s-related with Z. Equivalently, .
Suppose that is a Hamilton–Jacobi pair for Z and is an integral curve of X, , then we have that
and then, the curve in E is an integral curve of Z. It is easy to see that the converse property is true: if Z and are such that every integral curve of X lifted to E by s is an integral curve of Z, then , which can be seen by using that, for every point , there is an integral curve of X with the initial condition at p.
We can summarize the situation in the following diagram:
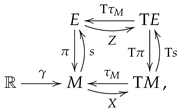 where the initial data are the vector field Z, the Hamilton–Jacobi pair is , and the diagram is commutative.
where the initial data are the vector field Z, the Hamilton–Jacobi pair is , and the diagram is commutative.

4.2. Lagrangian Theory
In the Lagrangian case, the initial bundle E is a tangent bundle , , , and ; hence, the section s is another vector field, , and we have that, if is a Hamilton–Jacobi pair, then , or equivalently, . The corresponding commutative diagram is
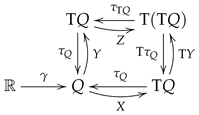 and therefore, if is an integral curve of X, then is an integral curve of Z.
and therefore, if is an integral curve of X, then is an integral curve of Z.

A particular case, very relevant in the Lagrangian framework, is when the vector field is an SODE, a second-order differential equation, vector field. Then, as indicated above, with and is a Hamilton–Jacobi pair if . However, if is an integral curve of X, i.e., , the relatedness condition shows that the curve in is an integral curve of the Z, but as Z is assumed to be a SODE vector field, its integral curves are canonical lifts of curves in Q; hence, we have that, necessarily, , because the curve in is an integral curve of Z, and this implies that , because is an arbitrary integral curve of X. Thus, in this case, given Z, we look for a vector field X such that , or equivalently, , and the relevant commutative diagram is
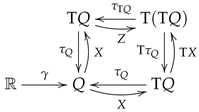

This is a specific characteristic of the Hamilton–Jacobi problem in the case of second-order differential equations: we have only one vector field, which plays a double role, first, as a vector field on Q and, second, as a section for , as solution of the Hamilton–Jacobi problem associated with a vector field Z.
4.3. Hamiltonian Theory
In this case, the initial bundle is the cotangent bundle , , and , i.e., the section s is a one-form on Q, ; we have that is a Hamilton–Jacobi par for Z if, and only if, , or equivalently, . The corresponding commutative diagram is
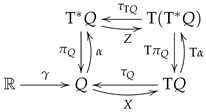

We can ask ourselves if there is any relation between the vector field X and the one-form . Actually, from the relation and as is a section of , we have that
Thus, we have that
In this case, we have two relevant specific situations. Recall first that a cotangent bundle , with , is endowed with a canonical one-form , called the Liouville one-form, such that , for each . Moreover, the two-form is a symplectic form. Then, the first relevant situation is when the one-form of the Hamilton–Jacobi pair is a closed (and therefore, locally exact) one-form, , where is a differentiable function. This is equivalent to saying that the image of is a Lagrangian submanifold of the natural symplectic manifold , because it is an n-dimensional submanifold such that, since , by the definition of the canonical one-form of , we see that, as is a closed one-form, we have , i.e., the image of is a Lagrangian submanifold of .
The second relevant situation is when the considered vector field is a Hamiltonian vector field, namely , with being a differentiable function, the Hamiltonian function associated with Z. In this case, we have the following result:
Proposition 3.
Suppose that is a Hamiltonian vector field, with Hamiltonian function H, i.e., , and that is a Hamilton–Jacobi pair for Z with α a closed one-form, . Then, .
Proof.
From , we have that . However, using that because a Hamilton–Jacobi pair for Z, the left-hand side of this relation is
because, for any vector field ,
We proved before that the closedness of the one-form implies that , and from the relation , we obtain that . □
Consequently, when Q is connected, locally, , and if, also locally, by the Poincaré lemma, then , that is
which is the classical Hamilton–Jacobi equation. Recall that, as indicated in (37), the vector field X can be recovered from the vector field Z and the one-form as .
5. Hamilton–Jacobi Vector Fields for the Second-Order Geodesic Vector Field
In this section, we fix our attention on the particular case of Hamilton–Jacobi vector fields for a second-order geodesic vector field according to the theory developed in [19], but not only in a Hamiltonian context, but also in the Lagrangian setting for systems of a mechanical type developed in the framework of the tangent bundle of the given Riemann manifold (see, e.g., [5]).
Recall that, as indicated in the preceding section, a Hamilton–Jacobi pair for a vector field in the tangent bundle reduces to only a vector field in Q playing a double role. More explicitly, we establish the following definition:
Definition 5.
Given an SODE vector field , a vector field is said to be a Hamilton–Jacobi vector field for Z if, for every integral curve of X, the curve is an integral curve of Z.
In [19,20,21,22], some useful properties of these Hamilton–Jacobi vector fields were studied. Recall that, alternatively, a vector field is a Hamilton–Jacobi vector field for an SODE vector field Z if, and only if, , i.e., X and Z are X-related vector fields, , or equivalently, if the following diagram is commutative:

Let now be an n-dimensional Riemann manifold and ∇ denote its associated Levi-Civita connection. The relation among autoparallel vector fields and Hamilton–Jacobi vector fields for the second-order geodesic vector fields is given in the following statement:
Proposition 4.
A vector field is an autoparallel vector field on a Riemann manifold , that is , if, and only if, it is a Hamilton–Jacobi vector field for the second-order geodesic vector field Γ of g, i.e., .
Proof.
Suppose that the vector field is autoparallel. If and is the integral curve of the vector field X, , with initial condition , then we know that the tangent lift of from M to is an integral curve of , and hence, as , is an integral curve of ; therefore, and X are X-related, i.e., X is a Hamilton–Jacobi vector field for .
Conversely, suppose that is the integral curve with initial condition of a vector field , i.e., . If X is a Hamilton–Jacobi vector field for , then is an integral curve of . Hence, is a geodesic curve, and then, , which implies that . However, as is arbitrary, we have , i.e., and X is autoparallel. □
Observe that, in that case, the curve is given in local coordinates as
Hence, the local condition for X to be geodesic is
for every integral curve of X. Equivalently:
As there are integral curves of X passing through every point in M, we have
as the set of local conditions for a vector field X in M to be a geodesic vector field.
Now, we go to the problem of how to find geodesic vector fields because Equation (41) is not easy to solve, nor is it even easy to know whether it has solutions. As far as closed Hamilton–Jacobi fields are concerned, we have the following:
Proposition 5.
(Hamilton–Jacobi equation)
Let be a closed vector field on a Riemann manifold , i.e., satisfying the condition . Then, X is an autoparallel vector field, , i.e., X is a geodesic vector field, if, and only if, the function on M satisfies , where is the kinetic energy function defined by (14).
Proof.
For each vector field , as , we have:
where use has been made of (7).
Now, taking into account (26), i.e., that
when the vector field X is closed and , we have
and then, (42) shows that . Therefore, as is an arbitrary vector field, we proved that, for closed vector fields X, i.e., such that ,
□
As indicated above, the closedness condition tells us that the image of the differential one-form on is a Lagrangian submanifold of endowed with its canonical symplectic structure. Of course, as each exact form is closed, the closedness condition is satisfied for the particular case of gradient vector fields.
According to the Poincaré lemma, condition is equivalent to saying that the function is locally constant, and this is the standard Hamilton–Jacobi equation. In fact, in local coordinates, it reads as
When X is a gradient vector field, , then , and as
the Hamilton–Jacobi equation is the standard one:
This last equation provides a method for finding Hamilton–Jacobi gradient vector fields for the second-order geodesic dynamical vector field of the metric g, by solving the preceding partial differential equation for the function U. This is, once again, another particular expression of the Hamilton–Jacobi equation.
From a complete solution of this PDE, we can obtain all the geodesics of the metric by integrating vector fields on M, that is systems of first-order ordinary differential equations.
Observe that, if X is a gradient vector field, then X is a geodesic vector field, , if, and only if, , because if X is a gradient, then it satisfies .
Therefore, by taking into account the three conditions for vector fields in a Riemann manifold:
we proved the following logical relations for vector fields:
In the case where X is a gradient, it satisfies and the corresponding logical relations.
Finally, we remark that, if , the length of X, the function , is constant along the integral curves of X, but this does not imply that must be a real constant. For example, in the ordinary Euclidean plane , the vector field is a geodesic vector field, but is not a constant.
6. Hamilton–Jacobi Vector Fields and Complete Lift of Vector Fields
In Section 4.2, we saw that, when looking for Hamilton–Jacobi vector fields for an SODE , we must take as the section appearing in a Hamilton–Jacobi pair , the same Hamilton–Jacobi vector field . Hence, the Hamilton–Jacobi pair is . We analyse a similar situation where this also happens.
Let be a vector field and denote its complete lift from M to . We can ask whether is a Hamilton–Jacobi pair for , i.e., whether .
Proposition 6.
If is a vector field on a Riemann manifold , then , and therefore, X is a Hamilton–Jacobi vector field for .
Proof.
In local coordinates for M and the induced ones for , respectively, the local expressions of X and its complete lift are
Hence,
which is equal to , as it can be easily computed. Consequently, , i.e., is a Hamilton–Jacobi pair. □
For a geodesic vector field X on a Riemann manifold , for which , we have that X is a Hamilton–Jacobi vector field for and for . The results of Proposition 4 and Proposition 6 are summarised as follows:
Proposition 7.
Let be a geodesic vector field on a Riemann manifold and the second-order geodesic vector field on . Then, , and X is a Hamilton–Jacobi vector field for and also for .
7. General Newtonian Dynamical Systems and Newtonian Vector Fields
Up to now, we have studied geodesic motions on Riemann manifolds; from the point of view of dynamical systems, they are called free systems. In the coming sections, we extend our study to motions under the action of external forces acting on the system, i.e., forced geodesic motions. We will define Newtonian systems and give the dynamical equations, the notion of symmetry, and a kind of Noether theorem. We will finish the section by introducing the idea of Newtonian vector fields and the Hamilton–Jacobi equation. We will follow the notation used in [5].
7.1. Newtonian Systems and Their Dynamical Equations
Let be an n-dimensional Riemann manifold, and consider a semibasic one-form F called the force form or work form. The dynamics is given by the SODE vector field solution of the dynamical equation:
instead of the corresponding one for the free case, . When the one-form F is basic, , the system is said to be Newtonian. In this last case, given the force form F, then , where is the second-order geodesic vector field defined by (16) and is the local expression of the vector field of force, which is the vertical lift to of the vector field on M such that , i.e., . The local expression of is , with .
Moreover, when F is exact, with , we say that F is a force of potential type, and then, if we introduce a Lagrange function on by , and therefore , the dynamical vector field is the solution of
When the one-form F can be written as a sum , if we define the Lagrangian function L as , the dynamical Equation (44) becomes
See [23] for a more detailed study on Lagrangian systems with external forces.
Going back to the above general case, as indicated in [5], the projections on M of the integral curves of the SODE vector field corresponding to Equation (44) satisfy the second-order differential equation:
and a curve is a solution of this system if, and only if, it satisfies the following condition:
as we can prove by expressing both members of the last equation in local coordinates. The trajectories of the mechanical system defined on we are studying are therefore solutions of the dynamical Equation (48), which only uses tensorial objects on the base manifold M
We denote this system by and collect this notion in the following:
Definition 6.
ANewtonian dynamical systemis given by , where is a Riemann manifold and F is a basic one-form on , and its dynamical equation is
where is the vector field such that . The solution curves to this equation are called trajectories of the system.
Observe that, when , then we obtain the equation of geodesic curves, . Recall that we say that is a simple mechanical-type system if F is an exact one-form, .
We are also interested in the relevant case in which the external force F is a semibasic one-form, which can also be seen as a one-form along the map , i.e., is such that . In this more general case of generalised Newtonian systems for which F may be strictly semibasic, we must use the formalism of tensor fields along maps, and a short summary of this theory is summarised in the Appendix A. Now, F is not a basic one-form on , but a semibasic one. The vector field solution of the dynamical Equation (44) when F is semibasic is said to be the second-order dynamical vector field associated with the given system , and it is given by
where is the vertical vector field of force whose local coordinate expression is
In order to recover in an intrinsic way such a vector field, observe first that there is one vector field along , , such that , where is the one-form on defined for by [24,25]
Remark that is semibasic because when Y is a vertical vector field, then, according to the definition (51), .
Then, the vector field is defined as the vertical lift to of the mentioned , a vector field along , that is:
where is the usual vertical lifting.
The local coordinate expressions of and F are, respectively,
where, now, are functions on . The vector field of force is as defined above, and its coordinate expression is
The trajectories of are the projections on M of the integral curves of and satisfy the system of second-order differential equations
This system corresponds to the SODE vector field:
A curve is a solution of the system (52) if, and only if, it satisfies the following condition:
as we can prove by expressing both members of the equation in local coordinates.
We remark first that, if , i.e., is such that , then is such that , and therefore, is a vector field along , that is . Consequently, both sides of the equality (54) are vector fields along the curve .
The trajectories of the mechanical system defined on we are studying are therefore solutions of the dynamical Equation (54).
As basic one-forms are also semibasic ones, the apparent difference between the dynamical Equations (48) and (54) may seem a surprise. Note, however, that, given a vector field as in (48), it has associated a by means of , and using such in (54), we see that , which shows the identity of the dynamical Equations (48) and (54) for basic force one-forms. More explicitly:
Definition 7.
A generalised Newtonian dynamical system is given by , where is a Riemann manifold and F is a semibasic one-form on , and its dynamical equation is
where is the vector field along defined by .
As we have shown in the previous comments, this definition includes as a particular case the case of Newtonian dynamical systems. From now on, we will study the generalised systems and only comment on the particular case when necessary. This situation corresponds to the case where the forces on a mechanical system depend not only on the positions, but also on the velocities.
7.2. Conserved Quantities and Dynamical Symmetries
The reduction processes of the integrability problem of a system make mainly use of infinitesimal symmetries and of constants of motion, and sometimes, there exist relations among these ingredients when a compatible geometric structure is known, using results similar to those of the well-known Noether’s theorem.
The concept of (infinitesimal) symmetry plays a relevant role. We have seen that, for free geodesic motions, the symmetries are given by the Killing vector fields, because if is a Killing vector field, then its complete lift preserves both the symplectic form and the free Lagrangian . Moreover, shows that the vector field is Hamiltonian with corresponding Hamiltonian function , which is, moreover, a conserved quantity for the second-order geodesic vector field , as we showed in Proposition 1 and the associated comments.
We can ask for the vector fields playing in the case of forced geodesic motions the role of Killing vector fields in the case of free geodesic flow, that is we look for a generalisation of Killing vector fields for this kind of Newtonian systems.
We devote the first part of this section to a kind of Noether theorem for these Newtonian, and even for generalised Newtonian, dynamical systems. According to Definition 7 and the previous comments, the Newtonian systems can be considered as a particular case of generalised Newtonian dynamical systems; hence, we develop our results for these vector fields and only comment on the particular case when there are some specific differences.
Given a vector field , consider the one-form on M and its associated function defined on as . We study under what conditions the function is constant along the lifts to of the trajectories of a generalised Newtonian system , that is . Then, if is a trajectory of the dynamical system on M defined by , i.e., it is the projection onto M of an integral curve of the associated dynamical SODE vector field , and thus, satisfies (55), we have that
Hence, if F is a semibasic one-form on M, and is the vector field along such that , then
We can change the expression of the second element of the right-hand side to a more suitable one with the following lemma:
Lemma 2.
Let be a Riemannian manifold and the associated kinetic energy. For any , we have that
Proof.
Using that and the torsionless property of the Levi-Civita connection, we have that
from which the result of the lemma follows. □
As a consequence, we have the following result:
Proposition 8.
Let be a generalised Newtonian dynamical system and and its complete lift. Then, the function is constant along the lifts to of the trajectories γ of the given system on M if, and only if,
Proof.
Particularly interesting cases are those corresponding to Killing vector fields , for which , and then, Condition (57) reduces to , or what is equivalent , that is, at every vector , the vector is orthogonal to . One says that the Killing vector field satisfying the condition is a Killing symmetry of the generalised Newtonian system and the function is the associated conserved quantity. Summing up, we obtained the following proposition:
Proposition 9.
Let be a generalised Newtonian dynamical system, such that , a Killing vector field, and its complete lift. Then, the function is constant along the lifts to of the trajectories γ of the given system if, and only if, the semibasic one-form F vanishes on , i.e., .
Comments:
- 1.
- Observe that ; hence, the condition in the above proposition is that and X are orthogonal.
- 2.
- If F is a basic one-form, that is is a Newtonian dynamical system, the result is the same.
- 3.
- In the case of the geodesic systems, , the condition is trivially satisfied, and we obtain the result of Proposition 1 as a particular case.
- 4.
- If the system is a conservative simple mechanical one and its potential function is , then and . In this situation, the condition is , that is the potential function V is invariant by the vector field X.
Now, we go to the dynamical symmetries of a Newtonian system.
Recall that a vector field is a dynamical symmetry for the dynamics if , i.e., the flow of the vector field Y preserves .
Definition 8.
A vector field is called aLie symmetryof the dynamics defined by the generalised Newtonian system , when is a dynamical symmetry of the associated dynamical vector field Γ, namely .
To characterise the dynamical symmetries of a generalised Newtonian system , we need to have an expression of the dynamical vector field . We know that the curves in M solutions to the dynamical Equation (55), when lifted to , are the integral curves of the SODE vector field , the uniquely defined solution to the equation:
then applying the exterior differential to both sides, we obtain that the SODE vector field satisfies
and therefore, is not a locally Hamiltonian vector field when F is not closed, but only when F is closed.
With this interpretation of the dynamical vector field, we can obtain Proposition 8 and Proposition 9 in this different approach for the generalised Newtonian system :
Proposition 10.
(i) Given a vector field , the function is a conserved quantity for the generalised Newtonian system if, and only if, .
(ii) If is a Killing vector field, then the function is a conserved quantity for the generalised Newtonian system if, and only if, .
Proof.
(i) The contraction with the complete lift of the vector field of both sides of Relation (58) leads to
The left-hand side can be rewritten as
and having in mind that
and that is a vertical vector field on which vanishes, the relation (60) becomes
and therefore, is a conserved quantity if, and only if, .
(ii) In the particular case of a Killing vector field, as , we have that is a conserved quantity if, and only if, . □
As far as the dynamical symmetries are concerned, we have the following:
Proposition 11.
Given a generalised Newtonian system , a Killing vector field is a Lie symmetry of the dynamical vector field solution of (58) if, and only if, .
Proof.
Using the relation:
we obtain
because, as X is a Killing vector, and . Since is nondegenerate, vanishes if, and only if, does, and then, the result of the proposition follows. □
Another approach to a similar result, but related to the case of conserved quantities, is the following property:
Proposition 12.
For a generalised Newtonian system , if a Killing vector field is such that , then X is a Lie symmetry of Γ if, and only if, .
Proof.
We first remark about an important relation that we can derive by making use of the relation , from which we see that
As the dynamical vector field satisfies (59), we can write
and from the expression (61) for , the preceding equation becomes
if is a Killing vector field, reduces the preceding relation to
This shows that, if and, therefore, , we have that if, and only if, . Recall that and imply that . □
Comments:
- 1.
- We remark about the difference between Proposition 9 and Proposition 12 for the characterisation of the vector field X as a generator of a conserved quantity or as a dynamical symmetry.
- 2.
- In the case of a conservative simple mechanical system, that is , if X is a Killing vector field, we have that:(a) If , then the quantity is conserved by the dynamics;(b) If , then the vector field is a dynamical symmetry of . This condition on V and X is equivalent to , which is a condition weaker than Condition (a).In fact, we have that Condition (a) implies Condition (b), then we can have a dynamical symmetry X such that is not a conserved quantity. In these circumstances, the vector fields X satisfying Condition (a) are usually called Noether symmetries. Obviously, a Noether symmetry is a dynamical symmetry, but not the contrary.
As we said above, see [23] for a comparison of the obtained results and used methods.
7.3. Newtonian Vector Fields
Similar to the definition of geodesic vector fields, we introduce the following definitions:
Definition 9.
(i) ANewtonian vector fieldfor the Newtonian system is a vector field satisfying the equation:
where the vector field is such that .
(ii) Ageneralised Newtonian vector fieldfor the generalised Newtonian system is a vector field such that
where is such that .
We remark that, when , we can replace on the right-hand side of (62) by , and this fact identifies (62) with (63), because the remark preceding Definition 7 leads to considering as equivalent both definitions (62) and (63), and hereafter, we only consider the generalised case and Condition (63).
These concepts play an interesting role when studying relations among geodesics for conformal metrics in the next section.
The first interesting property of this kind of vector fields is similar to the characterisation of the geodesic vector fields for the second-order geodesic vector field.
Proposition 13.
A vector field is a generalised Newtonian vector field for the generalised Newtonian system if, and only if, its integral curves satisfy the dynamical equation .
Proof.
Let , and suppose that its integral curves satisfy the dynamical Equation (54). If and is the integral curve of X with the initial condition , we have that and . Then,
However, the point is arbitrary; hence, .
Conversely, suppose that satisfies the equation , and let be an integral curve of X, that is . Then,
hence, as is arbitrary, . □
We can extend some results on geodesic vector fields contained in Proposition 2 to the case of generalised Newtonian vector fields. In fact, recall first that, according to Proposition 12, if is a Killing vector field of the Riemann manifold and denotes its complete lift, then the vector field X is a Lie symmetry of if, and only if, . Two important properties are then the following:
Proposition 14.
(i) Let be a Lie symmetry of the generalised Newtonian system and its local flow. If is a trajectory of the generalised Newtonian system , then is also a trajectory.
(ii) If is a generalised Newtonian vector field for , i.e., , then is also a generalised Newtonian vector field for the same system, that is
Proof.
(i) Let be a trajectory of the system , then is an integral curve of . As , we have that . Hence being an integral curve of , we have that is an integral curve of . Thus, is a trajectory of the system because .
(ii) Let be a generalised Newtonian vector field, then its integral curves are trajectories of the system. However, the integral curves of are of the form , which, by Item (i), are also trajectories; hence, is a Newtonian vector field by Proposition 13. □
The geodesic systems are characterized by , and then, all the results on geodesic vector fields appear as particular cases of Newtonian systems. Moreover, in these geodesic cases, the condition is equivalent to , that is X is a Killing vector field, and the above results correspond to those in Proposition 2.
In [23], several different situations with symmetries of a Lagrangian system with external forces were studied. We only work here with geodesic systems whose Lagrangian is and forced geodesic systems, where external forces depending on the velocities may appear, and we study them as generalised Newtonian systems. In the coming sections, we will try to generalise the ideas of geodesic vector fields and apply them to conformal metrics.
7.4. Hamilton–Jacobi Vector Fields for Generalised Newtonian Systems
This section is devoted to generalising to the framework of generalised Newtonian systems the results obtained in Section 5.
Consider a generalised Newtonian system as above, and let , with , the corresponding dynamical SODE vector field. We say that a vector field is a Hamilton–Jacobi vector field for the system if, for every integral curve of X, we have that is an integral curve of . As in the geodesic case, we have the following equivalence:
Proposition 15.
A vector field is a generalised Newtonian vector field for the generalised Newtonian system if, and only if, it is a Hamilton–Jacobi vector field for the same system.
Proof.
Suppose that is a Hamilton–Jacobi vector field for the generalised Newtonian system , and let be an integral curve of X. Then, is an integral curve of . Hence, satisfies the equation . By Proposition 13, we have that , because is arbitrary, and consequently, X is a generalised Newtonian vector field.
Conversely, if is a generalised Newtonian vector field, then, for any integral curve , we have that , and therefore, is an integral curve of . □
Apart from the definition, we have no explicit characterisation of the generalised Newtonian vector fields, but, using the preceding proposition, we can try to obtain a local equation for them.
Suppose that is a Hamilton–Jacobi vector field for the generalised Newtonian system , and let be an integral curve of X. Then, , that is . In local natural coordinates, we have:
for every integral curve of X. Equivalently:
However, as and there are integral curves through every point in M, we have
as the local condition for a vector field X in M to be a generalised Newtonian vector field. Observe that, if the external force vanishes, , hence , then we obtain the corresponding expression (41) for geodesic vector fields.
In parallel with Proposition 5, we have the following result for a generalised Newtonian system :
Proposition 16.
(Hamilton–Jacobi equation)
Let be a closed vector field, i.e., satisfying the condition , and a general Newtonian system. The following conditions are equivalent:
- (i)
- X is a generalised Newtonian vector field, .
- (ii)
- The function on M satisfies the condition , where is the kinetic energy function defined by (14).
Proof.
We know (see (42)) that, for each vector field , we have:
Now, as indicated in Section 5, taking into account that X is closed and using (26), we have that . Consequently, if X is a generalised Newtonian vector field, using (63), . However, is an arbitrary vector field, then for closed vector fields, i.e., such that , we have that
If, conversely, the vector field satisfies (65), then, from Equation (42), we obtain that , and using (43), because X is a closed vector field, this can be rewritten as . However, satisfies , then we obtain and as the vector field Y is arbitrary, this implies that , i.e., the vector field X is a generalised Newtonian vector field. □
The expression (65) is the Hamilton–Jacobi equation for a generalised Newtonian system for an associated closed generalised Newtonian vector field X, and as
we can rewrite such an equation as
which, in the case of F being an exact one-form, gives the usual expression of the Hamilton–Jacobi equation for simple mechanical systems.
In local coordinates Equation (66) gives
7.5. The Case of Nonholonomic Generalised Newtonian Systems
Consider now a generalised Newtonian system , with , and suppose the system is constrained to move on a submanifold , with . Then, we have a nonholonomic system, and the dynamical equation is obtained supposing there exists a constraint force , which forces the system to move on the submanifold C. Hence, the dynamical equation is
and by the application of the d’Alembert nonholonomic principle (see [10] for more details), we impose that the constraint force is such that its vertical lift is orthogonal to C: for every , we suppose that
Recall that .
Comment: For every , we used the notation to denote the subspace of such that its vertical lifting gives . As is a linear subspace of , the meaning of its orthogonal complement with respect to the metric g is clear.
One of the most-interesting cases is when the constraint submanifold C is defined by the annihilation of a family of functions , , independent with respect to the velocities, that is such that are linearly independent at every point of C (recall that , where S is the vertical endomorphism in ). Locally, this condition is equivalent to saying that, for a natural coordinate system on , , they satisfy that
at every point of C.
In this situation, in order to satisfy the d’Alembert nonholonomic principle, see [10], we have that there exist functions , called Lagrange multipliers, such that
where the vector fields along , , are defined by , and the dynamical equation is:
To solve this equation for the trajectory and the Lagrange multipliers , we need to add the equations , which are the constraint functions defining C. Observe that we also have the constraint form , defined by , whose expression is given by:
Going to conserved quantities, we can apply Propositions 8 and 9 to the dynamical Equation (67) and obtain, by direct application, the following results for a nonholonomic system defined by and the constraint submanifold C, with the above notations:
Proposition 17.
Let be and its complete lift. Then, the function is constant along the lifts to of the trajectories γ of the given system on M if, and only if,
Proposition 18.
Let be a Killing vector field and its complete lift. Then, the function is constant along the lifts to of the trajectories γ of the given system if, and only if, the semibasic one-form vanishes on , i.e., .
Proposition 19.
Let be a Killing vector field and its complete lift. Suppose that . Then, the function is constant along the lifts to of the trajectories γ of the given system if, and only if, the semibasic one-form F vanishes on , i.e., .
If the constraint submanifold C is , the condition can be reduced to
because are semibasic forms. Hence, in order to satisfy the condition , it is enough to satisfy , . This is equivalent to saying that at every point of C.
With respect to the Newtonian and Hamilton–Jacobi vector fields, we can extend to this case Propositions 13, 14, and 16 and Hamilton–Jacobi Equation (66) without change, but including the constraint force.
8. Application to Conformal Metrics
8.1. Conformal Metrics: Definitions and Geodesics
Definition 10.
Two metrics g and on the manifold M are conformally related if there exists a function such that .
This definition allows us to establish an equivalence relation in the set of metrics. A conformal structure is an equivalence class of metrics. The covariant derivatives with respect to both metrics g and are related by (see [5] for details):
In the case of , the above expression reduces to
The new Christoffel symbols of the second kind of the Levi-Civita connection are related to the previous ones by (see [5]):
where denotes the Kronecker delta symbol.
How related are the geodesic curves of conformally related Riemannian metrics? This is the question we will study now. Recall that, as we stated in Section 2, given a Riemann manifold , the geodesic curves are the curves in M whose velocity vector field is parallel along the curve, . They satisfy that is a constant function, and we can parametrise the curves with the arc parameter, then . Locally, the geodesics are the solutions to the system of second-order differential Equations (10).
where the functions are the Christoffel symbols corresponding to the Levi-Civita connection of the Riemannian metric g. This equation corresponds to an SODE vector field on the tangent bundle , the so-called second-order geodesic vector field, denoted by , whose local expression is given by
As indicated above is the only vector field on satisfying (16):
that is is the Hamiltonian dynamical vector field defined by the Lagrangian dynamical system, , where the kinetic energy function is defined in (14) and is the associated Cartan two-form.
Now, we go to the expression of the geodesic curves of the conformal metric .
As the Christoffel symbols corresponding to are given by (71), we have that
which gives
where
namely
We can rewrite it as , with
where is the identity map, seeing it as a vector field along , and
because , as we consider the geodesic curves parametrised by the parameter arc defined by .
We obtained in this way that the geodesic curves of the metric are the trajectories of a generalised Newtonian system , where with
As the one-form is exact, following the terminology of [23] and Expression (46), we can consider the system as the Lagrangian system on M with Lagrangian function and external force .
We remark that, in the expression of , appears as a vector field along . This corresponds to the classical evolution operator for functions defined on the configuration space M, that is, for ,
If is a trajectory of the system, that is is an integral curve of the SODE dynamical vector field , then
See [26] and the references therein for a detailed exposition on the evolution operator and its extension to functions defined on the phase space.
8.2. Newtonian Vector Fields and Hamilton–Jacobi Equation for Geodesics of the Metric
We know that the geodesic vector fields of the metric satisfy the equation
where denotes the Levi-Civita connection for the Riemann structure .
However, we proved that the geodesic curves of the metric are the trajectories of a generalised Newtonian system with
and then, according to (63), the associated Newtonian vector fields satisfy the equation
If we look for the corresponding Hamilton–Jacobi equation, corresponding to (65), we have
or equivalently,
which is the classical Hamilton–Jacobi equation for a simple mechanical system with external force given by . Compare with similar expressions in [27].
If we consider our system as the Lagrangian system defined on the Riemann manifold by the Lagrangian function and with an external force one-form , then Equation (74) can be written as
where is the Lagrangian energy corresponding to L. This last expression is the classical Hamilton–Jacobi equation in Lagrangian form for our Lagrangian system. See [19,27] for a comparison.
9. Conclusions and Future Work
We developed a detailed study from the perspective of the geometric mechanics of the properties of geodesic vector fields, i.e., autoparallel vector fields, on a Riemann manifold. Geodesic motion then corresponds to free motions of mechanical systems on a Riemann manifold, and therefore, the relevant tools in classical mechanics, as Hamilton–Jacobi theory, must shed light on the properties on geodesic motions and related vector fields. As the autoparallel vector fields are very helpful in such a study, one can try to introduce an analogous concept for classical systems of the mechanical type, also-called natural Lagrangian systems, or even for systems under the action of additional external forces, even in the case of velocity-dependent forces. We identified autoparallel vector fields on a Riemann manifold as Hamilton–Jacobi vector fields for the second-order geodesic vector field of the given metric g, and furthermore, we showed that closed vector fields are autoparallel vector fields and satisfy , the classical Hamilton–Jacobi equation. We also remarked that each vector field is a Hamilton–Jacobi vector field for its complete lift and that each geodesic vector field is a Hamilton–Jacobi vector field for both its complete lift and the second-order geodesic vector field of the given metric g.
These properties were appropriately extended to the framework of Newtonian and generalised Newtonian systems, in particular systems defined by Lagrangians of the mechanical type. Conserved quantities and a generalised concept of symmetry were developed, particularly for the case of Killing vector fields. The role of geodesic vector fields is now played by the so-called Newtonian vector fields, and their properties were studied, in particular the relation with Hamilton–Jacobi theory. The properties of generalised Newtonian systems subjected to nonholonomic constraints were also analysed from this perspective, and the relation among Newtonian vector fields and Hamilton–Jacobi equations for conformally related metrics was displayed. This last property is a consequence of the understanding of the geodesic flow of a conformal metric as a generalised mechanical system on the Riemann manifold of the initial metric.
There are other interesting systems to continue studying with the same methods. First is the particular case where the velocity-dependent forces come from a Rayleigh function and the study of the associated dissipated quantities. See [23] for another approach and [28,29] for several generalizations and nice examples.
Finally, there is another geometric way of dealing with dissipative systems, which comes from contact mechanics. We hope that the application of similar techniques to those of our approach may be interesting. Therefore, we will study one of the simplest mechanical contact systems, where the Lagrangian has, in addition to the kinetic energy coming from the metric, a velocity-dependent potential with an extra variable, usually called s, to describe the dissipation, that is . The variational principle is due to Herglotz /9see [30] and the references therein), and the dynamical equations contain another term coming from the potential, the gradient as in the usual situation, and a dissipation term. Furthermore, another dynamical equation for the dissipation variable is needed, . See [31,32] for other approaches. We also aim to use in the near future all the geometric machinery here developed to deal with these contact dissipative systems and complete the application to the study of conformal metrics, started in Section 8, together with the utilisation of the Sundman transformation; see [5,33].
Author Contributions
The two authors, J.F.C. and M.-C.M.-L., equally contributed to the paper and have approved the submitted version. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support came from the Spanish Ministerio de Ciencia, Innovación y Universidades Projects PID2021-125515NB-C21, PID2021-125515NB-C22, PGC2018-098265-B-C31 and PGC2018-098265-B-C33. The second author acknowledges the financial support of the GEOMVAP-UPC research group.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all individual participants included in the study.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the financial support from the Spanish Ministerio de Ciencia, Innovación y Universidades Projects PID2021-125515NB-C21, PID2021-125515NB-C22, PGC2018-098265-B-C31 and PGC2018-098265-B-C33. The second author acknowledges the financial support of the GEOMVAP-UPC research group.
Conflicts of Interest
The authors declare that they have no competing interests.
Appendix A. Sections along Maps and External Forces
Recall the concept of section along a map [24,25,34,35,36]. Let be a fibre bundle and a differentiable map. A section along is a map such that .
They are in a 1-1 correspondence with sections of the induced bundle
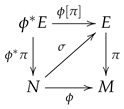 where
where

The set of sections along will be noted . When E is a vector bundle the set is endowed with a -module structure.
In particular we will be interested in the vector bundles , , for , and in these cases we will denote, respectively,
When and the set coincides with and the set reduces to .
As an example, if is a curve on M, the tangent vectors define a section of along . The restriction of on the curve , that is the composition , defines also a vector field along .
The generalisation of these examples is:
Let be a map from N to M. A vector field defines a vector field along by . Similarly, when the restriction of X on the image by is a vector field along . The above vector fields X and Y are said to be -related when and coincide along .
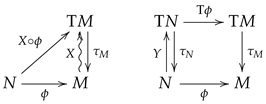
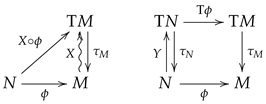
If is a p-form in M, the restriction of on the image of is a p-form along .
Given , is a p-form in N. The pull-back by of is obtained by iteration of both processes .
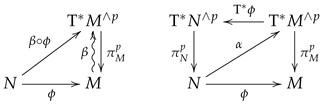
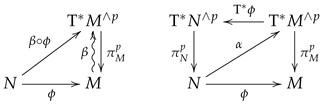
Local expressions:
When E is a vector bundle and is a local basis of , then is a local basis of , and can be written as
In the above case, taking local coordinates in N and in M we have
Observe that , and are functions in N.
When and is the projection the vector fields and forms along are written as
Vector fields along act on functions on M giving rise to functions on N. If and then is a tangent vector to M at the point which acts on a function by . The Leibniz rule for tangent vectors implies that
A map satisfying this property is called a -derivation (of degree 0).
Pidello and Tulczijev generalised in [37] the theory of Frölicher and Nijenhuis for these new derivations:
Definition A1.
Given a differentiable map , a -derivation of degree r of scalar on M is a -linear map satisfying
for and . It is said to be of type when .
For instance, given a vector field along , , a type -derivation of degree is defined by and if ,
where .
By a type -derivation of degree r we mean a -derivation such that . An example of such a type -derivation, , is defined by
where stands for the operator of exterior differentiation in M. This is of type , i.e.,
Note that when the -derivations and are but the contraction or inner product (or ) and the Lie derivative , respectively. For this reason, and will be called contraction and Lie derivative, respectively.
Appendix A.1. The Case of a Riemannian Manifold
We are especially interested in the case of vector fields and one-forms along the projection on a Riemann manifold . The metric induces natural isomorphisms between the -modules of vector fields and one-forms . They are given by the musical isomorphisms between the tangent and cotangent bundles
one inverse of the other, defined by
and extended by -linearity to the sections and . We use the same notation, ♭ and ♯, for the maps on the bundles and the sections, as usual.
These isomorphisms can be extended in the same way to the spaces of vector fields and one-forms along . In fact, given , , we have
for and .
For sections along in general, , and , we have:
and there is a duality relation between and given by
Appendix A.2. External Forces Depending on Velocities
The use we make of the above notions is the following: the elements of are the forms of force, or external forces, acting on a system in the case they depend not only on the positions but on the velocities also. Then the elements of are the vector forces depending on the positions and velocities. The musical isomorphisms give the way to pass from one to the other depending on the form of the equations we use.
For the Lagrangian formulation, in the phase space , we use expressions with , but for Riemannian expressions, in the configuration manifold M, is more suitable to use . Musical isomorphisms and the duality relation helps us to pass form one formulation to the other.
Observe that if is a curve, its tangent prolongation and , then is a vector field along , that is , because .
On the same way we have that if , then .
Appendix A.3. External Forces as Semibasic Forms on TM
Usually in the study of Lagrangian systems we say that an external force is a semibasic one-form on , that is such that for any vertical vector field on . The local expression of such kind of forces is
in a natural coordinate system of . In the case that the coordinates of do not depend on the velocities, , then the form is basic and there exists a one-form such that . The set of semibasic one-forms on is denoted by with the subindex indicating that the contraction with a vertical vector field is null.
Is there any relation between the sets , of semibasic one-forms and , the set of one-forms along the map ? Let see how it goes:
Let and . Then . We can consider that acts on as
Observe that this is well defined because is semibasic, hence if , then is vertical hence .
On the other side , hence we have defined a map which is an element of , that is, we have a map:
which is -linear. This map is an isomorphism with inverse given by the following map: if , and , then take
then, clearly, . That this last one is the inverse of the other is easy to prove.
Hence we have proven that both -modules are canonically isomorphic.
References
- Deshmukh, S.; Chen, B.Y. A note on Yamabe solitons. Balkan J. Geom. Appl. 2018, 23, 37–42. [Google Scholar]
- Mosayebi, P.; Cobzas, D.; Murtha, A.; Jagersand, M. Tumor invasion margin on the Riemannian space of brain fibers. Med. Image Anal. 2012, 16, 361–373. [Google Scholar] [CrossRef]
- Lee, J.M. Introduction to Riemannian Manifolds. In Graduate Texts in Mathematics; Springer: Berlin/Heidelberg, Germany, 2018; Volume 176. [Google Scholar]
- Conlon, L. Differentiable Manifolds; Modern Birkhäuser Classics, Birkhäuser: Boston, MA, USA, 2008. [Google Scholar]
- Cariñena, J.F.; Martínez, E.; Muñoz-Lecanda, M.C. Infinitesimal time reparametrisation and its applications. J. Nonl. Math. Phys. 2022, 29, 523–555. [Google Scholar] [CrossRef]
- Berestovski, V.N.; Nikonorov, Y.G. Killing vector fields of constant length on Riemannian manifolds. Sib. Math. J. 2008, 49, 395–407. [Google Scholar] [CrossRef]
- Nikonorov, Y.G. Spectral properties of Killing vector fields of constant length. J. Geom. Phys. 2019, 145, 103485. [Google Scholar] [CrossRef]
- Crampin, M. On the differential geometry of the Euler–Lagrange equations and the inverse problem in Lagrangian dynamics. J. Phys. A Math. Gen. 1981, 14, 2567–2575. [Google Scholar] [CrossRef]
- Crampin, M. Tangent bundle geometry for Lagrangian dynamics. J. Phys. A Math. Gen. 1983, 16, 3755–3772. [Google Scholar] [CrossRef]
- Muñoz-Lecanda, M.C. Newtonian mechanics in a Riemannian manifold. arXiv 2021, arXiv:2112.10171. [Google Scholar]
- Cariñena, J.F.; Ibort, A.; Marmo, G.; Morandi, G. Geometry from Dynamics: Classical and Quantum; Springer: Dordrecht, The Netherlands, 2015. [Google Scholar]
- Abraham, R.; Marsden, J.E. Foundations of Mechanics, 2nd ed.; Benjamin–Cummings: New York, NY, USA, 1978. [Google Scholar]
- Tsamparlis, M.; Paliathanasis, A.; Basialakos, S.; Capozziello, S. Conformally related metrics and Lagrangians and their physical interpretation in cosmology. Gen. Rel. Grav. 2013, 45, 2003–2022. [Google Scholar] [CrossRef]
- VBerestovskii, N.; Nikonorov, Y.G. Clifford-Wolf homogeneous Riemannian manifolds. J. Diff. Geom. 2009, 82, 467–500. [Google Scholar]
- Deshmukh, S. Geometry of conformal vector field. Arab. J. Math. Sci. 2014, 23, 44–73. [Google Scholar] [CrossRef]
- Deshmukh, S.; Peska, P.; Turki, N.B. Geodesic Vector Fields on a Riemannian Manifold. Mathematics 2020, 8, 137. [Google Scholar] [CrossRef]
- Nikonorov, Y.G. Killing vector fields of constant length on compact homogeneous Riemannian manifolds. Ann. Glob. Anal. Geom. 2015, 48, 305–330. [Google Scholar] [CrossRef]
- Cariñena, J.F.; Gheorghiu, I.; Martínez, E.; Santos, P. Conformal Killing vector fields and a virial theorem. J. Phys. A Math. Theor. 2014, 47, 465206. [Google Scholar] [CrossRef]
- Cariñena, J.F.; Gràcia, X.; Martínez, G.M.E.; noz–Lecanda, M.C.M.; Román-Roy, N. Geometric Hamilton–Jacobi theory. Int. J. Geom. Methods Mod. Phys. 2006, 3, 1417–1458. [Google Scholar] [CrossRef]
- Cariñena, J.F.; Gràcia, X.; Martínez, G.M.E.; noz–Lecanda, M.C.M.; Román-Roy, N. Geometric Hamilton–Jacobi theory for Nonholonomic Dynamical Systems. Int. J. Geom. Methods Mod. Phys. 2010, 7, 431–454. [Google Scholar] [CrossRef]
- Cariñena, J.F.; Gràcia, X.; Martínez, G.M.E.; Muñoz–Lecanda, M.C.; Román-Roy, N. Structural aspects of Hamilton–Jacobi theory. Int. J. Geom. Methods Mod. Phys. 2016, 13, 1650017. [Google Scholar] [CrossRef]
- Román-Roy, N. An Overview of the Hamilton–Jacobi Theory: The Classical and Geometrical Approaches and Some Extensions and Applications. Mathematics 2021, 9, 85. [Google Scholar] [CrossRef]
- de León, M.; Lainz, M.; López-Gordón, A. Symmetries, constants of the motion, and reduction of mechanical systems with external forces. J. Math. Phys. 2021, 62, 042901. [Google Scholar] [CrossRef]
- Cariñena, J.F.; López, C.; Martínez, E. A new approach to the converse of Noether’s theorem. J. Phys. A Math. Gen. 1989, 22, 4777–4786. [Google Scholar] [CrossRef]
- Cariñena, J.F. Sections along maps in Geometry and Physics. Rend. Sem. Mat. Univ. Pol. Torino 1996, 54, 245–256. [Google Scholar]
- Cariñena, J.F.; Gràcia, X.; Martínez, G.M.E.; Muñoz–Lecanda, M.C.; Román-Roy, N. Geometric Hamilton–Jacobi Theory and the Evolution Operator. In Mathematical Physics and Field Theory, Julio Abad in Memoriam; Manuel, A., Ed.; Prensas Universitarias de Zaragoza: Zaragoza, Spain, 2009; pp. 177–186. [Google Scholar]
- de León, M.; Lainz, M.; López-Gordón, A. Geometric Hamilton–Jacobi theory for systems with external forces. J. Math. Phys. 2022, 63, 022901. [Google Scholar] [CrossRef]
- Minguzzi, E. Rayleigh’s dissipation function at work. Eur. J. Phys. 2015, 36, 035014. [Google Scholar] [CrossRef]
- Lurie, A.I. Analytical Mechanics. In Foundations of Engineering Mechanics; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 978-3-540-45677-3. [Google Scholar]
- de León, M.; Lainz, M.; Muñoz-Lecanda, M.C. Optimal Control, Contact Dynamics and Herglotz Variational Problem. J. Nonlinear Sci. 2023, 33, 9. [Google Scholar] [CrossRef]
- Gaset, J.; Gràcia, X.; Muñoz-Lecanda, M.C.; Rivas, X.; Román-Roy, N. New contributions to the Hamiltonian and Lagrangian contact formalisms for dissipative mechanical systems and their symmetries. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050090. [Google Scholar] [CrossRef]
- Colombo, L.J.; de León, M.; López-Gordón, A. Contact Lagrangian systems subject to impulsive constraints. J. Phys. A Math. Theor. 2022, 55, 425203. [Google Scholar] [CrossRef]
- Cariñena, J.F.; Martínez, E.; Muñoz-Lecanda, M.C. Sundman transformation and alternative tangent structures. 2022; submitted for publication. [Google Scholar]
- Cariñena, J.F.; López, C.; Martínez, E. Sections along a map applied to higher-order Lagrangian Mechanics. Noether’s theorem. Acta Appl. Math. 1991, 25, 127–151. [Google Scholar] [CrossRef]
- Martínez, E.; Cariñena, J.F.; Sarlet, W. Derivations of differential forms along the tangent bundle projection. Diff. Geom. Appl. 1992, 2, 17–43. [Google Scholar] [CrossRef]
- Martínez, E.; Cariñena, J.F.; Sarlet, W. Derivations of differential forms along the tangent bundle projection II. Diff. Geom. Appl. 1993, 3, 1–29. [Google Scholar] [CrossRef]
- Pidello, G.; Tulczyjew, W.M. Derivations of differential forms on jet bundles. Ann. Math. Pura Appl. 1987, 147, 249–265. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).