On the Study of Rainbow Antimagic Connection Number of Comb Product of Friendship Graph and Tree

Abstract

Given a graph G with vertex set $V\left(G\right)$ and edge set $E\left(G\right)$, for the bijective function $f\left(V\right(G\left)\right)\to \{1,2,\cdots ,|V\left(G\right)\left|\right\}$, the associated weight of an edge $xy\in E\left(G\right)$ under f is $w\left(xy\right)=f\left(x\right)+f\left(y\right)$. If all edges have pairwise distinct weights, the function f is called an edge-antimagic vertex labeling. A path P in the vertex-labeled graph G is said to be a rainbow $x-y$ path if for every two edges $xy,x^{\prime }{y}^{\prime }\in E\left(P\right)$ it satisfies $w\left(xy\right)\ne w\left(x^{\prime }{y}^{\prime }\right)$. The function f is called a rainbow antimagic labeling of G if there exists a rainbow $x-y$ path for every two vertices $x,y\in V\left(G\right)$. We say that graph G admits a rainbow antimagic coloring when we assign each edge $xy$ with the color of the edge weight $w\left(xy\right)$. The smallest number of colors induced from all edge weights of antimagic labeling is the rainbow antimagic connection number of G, denoted by $rac\left(G\right)$. This paper is intended to investigate non-symmetrical phenomena in the comb product of graphs by considering antimagic labeling and optimizing rainbow connection, called rainbow antimagic coloring. In this paper, we show the exact value of the rainbow antimagic connection number of the comb product of graph ${\mathcal{F}}_n⊳T_m$, where ${\mathcal{F}}_n$ is a friendship graph with order $2n+1$ and $T_m\in \{P_m,S_m,B{r}_{m,p},S_{m,m}\}$, where $P_m$ is the path graph of order m, $S_m$ is the star graph of order $m+1$, $B{r}_{m,p}$ is the broom graph of order $m+p$ and $S_{m,m}$ is the double star graph of order $2m+2$.

1. Introduction

Let G and H be two connected graphs. Let v be a vertex of graph H. The comb product between graphs G and H, denoted by $G⊳H$, is a graph obtained by taking one copy of G and $\left|V\right(G\left)\right|$ copies of H and grafting the i-th copy of H at the vertex v to the i-th vertex of G. In this study, the graph definition used is based on Chartrand et al. [1].

The study of the graph in this research is focused on rainbow antimagic coloring, which is a combination of the concepts of antimagic labeling and rainbow coloring. Rainbow connection definitions can be found in [2,3]. Let G be a connected graph, the edge coloring of G with the function $f\left(E\right(G\left)\right)\to \{1,2,\cdots ,k\},k\in E\left(G\right)$ is k-coloring of graph G, where adjacent edges can be colored with the same color. Rainbow $u-v$ path is the path in G if no two edges are the same color. The graph G is a rainbow connection if every $u,v\in V\left(G\right)$ has a rainbow path. The edge coloring on G has a rainbow connection called rainbow coloring. The minimum colors to make G rainbow-connected is called the rainbow connection number of G and is denoted by $rc\left(G\right)$. Rainbow coloring is an interesting study and has found many results, including [4,5].

Rainbow vertex coloring and rainbow total coloring are other variants of rainbow coloring. Rainbow vertex coloring was introduced in [6] and rainbow vertex coloring results can be found in [7,8]. Total rainbow coloring results can be seen in [9,10]. Wallis et al. [11] introduced graph labeling. Hartsfield and Ringel [12] introduced antimagic labeling. The antimagic labeling of graph G is a bijective function of the edge set $E\left(G\right)$ to $\{1,2,\dots ,|E\left(G\right)\left|\right\}$ and $w\left(v\right)={\Sigma }_{e\in E\left(v\right)}f\left(e\right)$, and $E\left(v\right)$ is the set of edges incident with the vertex v for vertices $u,v\in V\left(G\right)$, $w\left(u\right)\ne w\left(v\right)$.

Antimagic labeling has had several results, including those of Baca et al. in [13,14,15,16]. Dafik et al. contributed to the antimagic labeling in [17]. In addition, antimagic labeling results can also be found in [18,19]. The concept of combining graph labeling and graph coloring was initiated by Arumugam et al. [20]. The bijective function from edge set $E\left(G\right)$ to $\{1,2,\dots |E\left(G\right)\left|\right\}$ is $w\left(v\right)={\Sigma }_{e\in E\left(v\right)}f\left(e\right)$, and $E\left(v\right)$ is the set of edges that are incident to vertices v, for every $v\in V\left(G\right)$ The bijective function f for two adjacent vertices $u,v\in V\left(G\right),w\left(u\right)\ne w\left(v\right)$ is called antimagic labeling. The coloring of the vertices on G with the vertices of v colored with $w\left(v\right)$ is the local antimagic label. If we consider the local antimagic labeling chromatic number, then it is called local antimagic coloring.

Motivated by the combination performed by Arumugam, in [21], Dafik et al. took the initiative to combine the concepts of antimagic labeling and rainbow coloring on graphs into a new concept, namely, rainbow antimagic coloring. Septory et al. determined the lower bound of rainbow antimagic connection number for any connected graph.

Lemma 1

([22]). Let G be any connected graph. Let $rc\left(G\right)$ and $\Delta \left(G\right)$ be the rainbow connection number of G and the maximum degree of G, respectively. $rac\left(G\right)\ge max\left\{rc\right(G),\Delta (G\left)\right\}$.

While Dafik et al., has two theorems about characterizing the existence of rainbow $u-v$ path of any graph of $diam\left(G\right)\le 2$, the result of rainbow antimagic connection number of friendship graph and any tree is shown in the following Theorem.

Theorem 1

([21]). Let G be a connected graph of diameter $diam\left(G\right)\le 2$. Let f be any bijective function from $V\left(G\right)$ to the set $\{1,2,\cdots ,|V\left(G\right)\left|\right\}$; there exists a rainbow $u-v$ path.

Theorem 2

([21]). For $n\ge 2$, $rac\left({\mathcal{F}}_n\right)=2n$.

Theorem 3

([21]). For $T_m$, being any tree of order $m\ge 3$, $rac\left(T_m\right)=m-1$.

Some other results about rainbow antimagic connection number can be found in [21,22,23,24]. In this paper, we will study the rainbow antimagic connection number of graph ${\mathcal{F}}_n⊳T_m$ where ${\mathcal{F}}_n$ is a friendship graph with order $2n+1$ and $T_m\in \{P_m,S_m,B{r}_{m,p},S_{m,m}\}$, where $P_m$ is the path graph of order m, $S_m$ is the star graph of order $m+1$, $B{r}_{m,p}$ is the broom graph of order $m+p$ and $S_{m,m}$ is the double star graph of order $2m+2$.

2. Results

In this section, we will show our new results about rainbow antimagic connection number on those above graphs stated in a lemma and theorem. Our strategy is firstly determined with the lower bound rainbow antimagic connection number of $rac({\mathcal{F}}_n⊳T_m)$. Finally, we show the exact values of $rac({\mathcal{F}}_n⊳P_m)$, $rac({\mathcal{F}}_n⊳S_m)$, $rac({\mathcal{F}}_n⊳B{r}_{m,p})$ and $rac({\mathcal{F}}_n⊳S_{m,m})$.

Lemma 2.

Let ${\mathcal{F}}_n⊳T_m$ be a comb product of friendship graph ${\mathcal{F}}_n$ and $T_m$ be any tree of order $m\ge 2$. The lower bound of $rac({\mathcal{F}}_n⊳T_m)\ge rac\left(T_m\right)\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)$.

Proof of Lemma 2.

Graph ${\mathcal{F}}_n⊳T_m$ is the comb product of two graphs ${\mathcal{F}}_n$ and $T_m$, and o is the vertex of $T_m$. Graph ${\mathcal{F}}_n⊳T_m$ is obtained by taking one copy of ${\mathcal{F}}_n$ and $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of $T_m$ and grafting o from the i-th copy of $T_m$ at the i-th vertex of ${\mathcal{F}}_n$. By this definition, it implies that graph ${\mathcal{F}}_n⊳T_m$ contains graph ${\mathcal{F}}_n$ and $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of graph $T_m$. We can determine $rac({\mathcal{F}}_n⊳T_m)$ by finding $rac\left({\mathcal{F}}_n\right)$ and $rac\left(T_m\right)$. Based on Theorem 2, we have $rac\left({\mathcal{F}}_n\right)=2n$. Based on Theorem 3, we have $rac\left(T_m\right)=E\left(T_m\right)=m-1$; so, every edge of all i-th copies of $T_m$ has a different color. Thus, $rac({\mathcal{F}}_n⊳T_m)\ge (rac\left(T_m\right)\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)$. □

Theorem 4.

For $n,m\ge 3$, $rac({\mathcal{F}}_n⊳P_m)=2nm+m-2n-1$.

Proof of Theorem 4.

Graph ${\mathcal{F}}_n⊳P_m$ is a connected graph with vertex set $V({\mathcal{F}}_n⊳P_m)=\left\{a\right\}\cup \{x_i,y_i,1\le i\le n\}\cup \{x_{ij},y_{ij},1\le i\le n,1\le j\le m-1\}\cup \{z_j,1\le j\le m-1\}$ and edge set $E({\mathcal{F}}_n⊳P_m)=\{a{x}_i,a{y}_i,x_i{y}_i,x_i{x}_1,y_i{y}_1,1\le i\le n\}\cup \left\{a{z}_1\right\}\cup \{z_j{z}_{j+1},1\le j\le m-2\}\cup \{x_{ij}{x}_{ij+1},y_{ij}{y}_{ij+1},1\le i\le n,1\le j\le m-2\}$. The cardinality of $\left|V\right({\mathcal{F}}_n⊳P_m\left)\right|=2nm+m-1$ and the cardinality of $\left|E\right({\mathcal{F}}_n⊳P_m\left)\right|=n+m+2nm$.

To prove the rainbow antimagic connection number of $rac({\mathcal{F}}_n⊳P_m)$, first, we have to show the lower bound of $rac({\mathcal{F}}_n⊳P_m)$. Based on Lemma 2, we have rac $({\mathcal{F}}_n⊳P_m)\ge rac\left(P_m\right)\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)$. Since $rac\left(P_m\right)=m-1$, $rac({\mathcal{F}}_n⊳P_m)\ge 2nm+m-2n-1$.

Secondly, we have to show the upper bound of $rac({\mathcal{F}}_n⊳P_m)$. Define the vertex labeling $f\left(V({\mathcal{F}}_n⊳P_m)\right)\to \{1,2,...,2nm+m-1\}$ as follows:

$$\begin{array}{cc}\hfill f\left(a\right)& =2n+1\hfill \\ \hfill f\left(x_i\right)& =2n+1-i,\mathrm{for}1\le i\le n\hfill \\ \hfill f\left(y_i\right)& =4n+2-i,\mathrm{for}1\le i\le n\hfill \\ \hfill f\left(z_j\right)& =2nj+2n+j+1,\mathrm{for}1\le j\le m-1\hfill \\ \hfill f\left(x_{ij}\right)& =\left\{\begin{array}{cc}2n-2i+1,\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2nj+j+i,\hfill & \mathrm{for}1\le i\le n,2\le j\le m-1\hfill \end{array}\right.\hfill \\ \hfill f\left(y_{ij}\right)& =\left\{\begin{array}{cc}2i,\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2nj+2n+j-i+1,\hfill & \mathrm{for}1\le i\le n,2\le j\le m-1\hfill \end{array}\right.\hfill \end{array}$$

The edge weights of the above vertex labeling f can be presented as

$$\begin{array}{cc}\hfill w\left(a{x}_i\right)& =4n+2+i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(a{y}_i\right)& =6n+3-i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(a{z}_1\right)& =6n+3\hfill \\ \hfill w\left(z_j{z}_{j+1}\right)& =6n+4nj+2j+3,\mathrm{for}1\le j\le m-2\hfill \\ \hfill w\left(x_i{x}_{i1}\right)& =4n+2-i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(y_i{y}_{i1}\right)& =4n+4-i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(x_{ij}{x}_{ij+1}\right)& =\left\{\begin{array}{cc}6n+3-i\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2n+4nj+2j+2i+1\hfill & \mathrm{for}1\le i\le n,2\le j\le m-2\hfill \end{array}\right.\hfill \\ \hfill w\left(y_{ij}{y}_{ij+1}\right)& =\left\{\begin{array}{cc}6n+i+3\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 6n+4nj+2j-2i+3\hfill & \mathrm{for}1\le i\le n,2\le j\le m-2\hfill \end{array}\right.\hfill \end{array}$$

It is easy to see that the above edge weight will induce a rainbow antimagic coloring of graph ${\mathcal{F}}_n⊳P_m$. Based on Theorem 3, $rac\left(P_m\right)=m-1$; since $E\left(P_m\right)=m-1$, the weight of each edge in graph $P_m$ is different. Therefore, the sum of the weights on $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of graph $P_m$ is $\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)\left(\right|E\left(P_m\right)\left|\right)=2nm+m-2n-1$. Based on the description above, we have that the distinct weight of graph $({\mathcal{F}}_n⊳P_m)$ is $2nm+m-2n-1$. It implies that the edge weights of $f\left(V({\mathcal{F}}_n⊳P_m)\right)\to \{1,2,...,2nm+m-1\}$ induce a rainbow antimagic coloring of $2nm+m-1$ colors. Thus, $rac({\mathcal{F}}_n⊳P_m)\le 2nm+m-2n-1$. Comparing the two bounds, we have the exact value of $rac({\mathcal{F}}_n⊳P_m)=2nm+m-2n-1$.

The next step is to evaluate to prove the existence of a rainbow $u-v$ path ${\mathcal{F}}_n⊳P_m$. Based on the definition of graph ${\mathcal{F}}_n⊳P_m$, graph ${\mathcal{F}}_n⊳P_m$ contains one graph ${\mathcal{F}}_n$ and $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of $P_m$; so, we can evaluate the rainbow $u-v$ path of graph ${\mathcal{F}}_n⊳P_m$ by evaluating the rainbow $u-v$ path on graph ${\mathcal{F}}_n$ and graph $P_m$. Since $diam\left({\mathcal{F}}_n\right)=2$, based on Theorem 1, there is a rainbow $u-v$ path for every $u,v\in V\left({\mathcal{F}}_n\right)$. Based on Theorem 3, $rac\left(P_m\right)=m-1$; since $P_m$ has $m-1$ edges, there is a rainbow $u-v$ path for every $u,v\in V\left(P_m\right)$. Therefore, according to the explanation, it can be seen that there is a rainbow $u-v$ path for every $u,v\in V({\mathcal{F}}_n⊳P_m)$. □

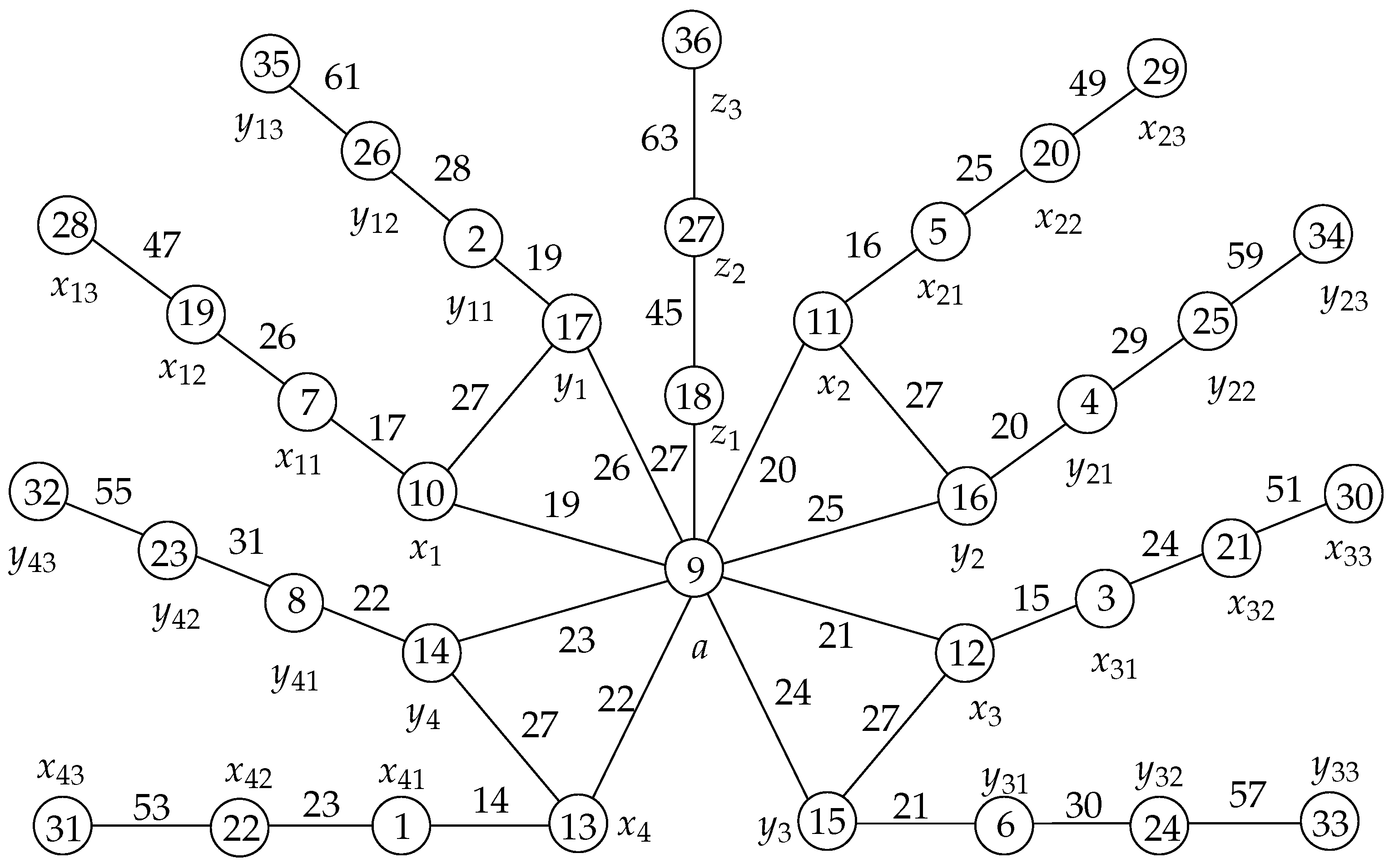
The illustration of a rainbow antimagic coloring of graph ${\mathcal{F}}_n⊳P_m$ can be seen in Figure 1.

Theorem 5.

For $n\ge 3,m=2n-1$, $rac({\mathcal{F}}_n⊳S_m)=2nm+m$.

Proof of Theorem 5.

Graph ${\mathcal{F}}_n⊳S_m$ is a connected graph with vertex set $V({\mathcal{F}}_n⊳S_m)=\left\{a\right\}\cup \{x_i,y_i,1\le i\le n\}\cup \{z_j,1\le j\le m\}\cup \{x_{ij},y_{ij},1\le i\le n,1\le j\le m\}$ and edge set $E({\mathcal{F}}_n⊳S_m)=\{a{x}_i,a{y}_i,x_i{y}_i,1\le i\le n\}\cup \{a{z}_j,1\le j\le m\}\cup \{x_i{x}_{ij}.y_i{y}_{ij},1\le i\le n,1\le j\le m\}$. The cardinality of $\left|V\right({\mathcal{F}}_n⊳S_m\left)\right|=2n+m+2nm+1$ and the cardinality of $\left|E\right({\mathcal{F}}_n⊳S_m\left)\right|=3n+m+2nm$.

To prove the rainbow antimagic connection number of $rac({\mathcal{F}}_n⊳S_m)$, first, we have to show the lower bound of $rac({\mathcal{F}}_n⊳S_m)$. Based on Lemma 2, we have rac $({\mathcal{F}}_n⊳S_m)\ge rac\left(S_m\right)\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)$. Since $rac\left(S_m\right)=m$, $rac({\mathcal{F}}_n⊳S_m)\ge 2nm+m$.

Secondly, we have to show the upper bound of $rac({\mathcal{F}}_n⊳S_m)$. Define the vertex labeling $f\left(V({\mathcal{F}}_n⊳S_m)\right)\to \{1,2,...,2n+m+2nm+1\}$ as follows:

$$\begin{array}{cc}\hfill f\left(a\right)& =2n+1\hfill \\ \hfill f\left(x_i\right)& =4n+i,\mathrm{for}1\le i\le n\hfill \\ \hfill f\left(y_i\right)& =6n+1-i,\mathrm{for}1\le i\le n\hfill \\ \hfill f\left(z_j\right)& =\left\{\begin{array}{cc}8n\hfill & \mathrm{for}j=1\hfill \\ 2j-1\hfill & \mathrm{for}2\le j\le \lceil \frac{m}{2}\rceil \hfill \\ 2j+1\hfill & \mathrm{for}\lceil \frac{m}{2}\rceil +1\le j\le m\hfill \end{array}\right.\hfill \\ \hfill f\left(x_{ij}\right)& =\left\{\begin{array}{cc}4n+2-2i\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 1\hfill & \mathrm{for}i=1,j=2\hfill \\ 6n+j-2\hfill & \mathrm{for}i=1,3\le j\le m\hfill \\ 6n+m+j-3\hfill & \mathrm{for}i=2,2\le j\le 3\hfill \\ 6n+m+j-2\hfill & \mathrm{for}i=2,4\le j\le m\hfill \\ 6n+im+j-m-i\hfill & \mathrm{for}3\le i\le n,2\le j\le m\hfill \end{array}\right.\hfill \\ \hfill f\left(y_{ij}\right)& =\left\{\begin{array}{cc}2i\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2nm+2n+m+i+j-im\hfill & \mathrm{for}1\le i\le n,2\le j\le m\hfill \end{array}\right.\hfill \end{array}$$

The edge weights of the above vertex labeling f can be presented as

$$\begin{array}{cc}\hfill w\left(a{x}_i\right)& =6n+1+i,\mathrm{for}1\le i\le n\hfill \end{array}$$

$$\begin{array}{cc}\hfill w\left(a{y}_i\right)& =8n+2-i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(a{z}_j\right)& =\left\{\begin{array}{cc}10n+1\hfill & \mathrm{for}j=1\hfill \\ 2n+2j\hfill & \mathrm{for}2\le j\le \lceil \frac{m}{2}\rceil \hfill \\ 2n+2j+2\hfill & \mathrm{for}\lceil \frac{m}{2}\rceil +1\le j\le m\hfill \end{array}\right.\hfill \\ \hfill w\left(x_i{x}_{ij}\right)& =\left\{\begin{array}{cc}8n+2-i\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 4n+2\hfill & \mathrm{for}i=1,j=2\hfill \\ 10n+j+i-2\hfill & \mathrm{for}i=1,3\le j\le m\hfill \\ 10n+m+j+i-3\hfill & \mathrm{for}i=2,2\le j\le 3\hfill \\ 10n+m+j+i-2\hfill & \mathrm{for}i=2,4\le j\le m\hfill \\ 10n+im+j-m\hfill & \mathrm{for}3\le i\le n,2\le j\le m\hfill \end{array}\right.\hfill \\ \hfill w\left(y_i{y}_{ij}\right)& =\left\{\begin{array}{cc}6n+1+i\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2nm+8n+m+j-im+1\hfill & \mathrm{for}1\le i\le n,2\le j\le m\hfill \end{array}\right.\hfill \end{array}$$

It is easy to see that the above edge weight will induce a rainbow antimagic coloring of graph ${\mathcal{F}}_n⊳S_m$. Based on Theorem 3, $rac\left(S_m\right)=m$; since $E\left(S_m\right)=m$, the weight of each edge in graph $S_m$ is different. Therefore, the sum of the weights on $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of graph $S_m$ is $\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)\left(\right|E\left(S_m\right)\left|\right)=2nm+m$. Based on the description above, we have that the distinct weight of graph $({\mathcal{F}}_n⊳S_m)$ is $2nm+m$. It implies that the edge weights of $f\left(V({\mathcal{F}}_n⊳S_m)\right)\to \{1,2,...,2n+m+2nm+1\}$ induce a rainbow antimagic coloring of $2nm+m$ colors. Thus, $rac({\mathcal{F}}_n⊳S_m)\le 2nm+m$. Comparing the two bounds, we have the exact value of $rac({\mathcal{F}}_n⊳S_m)=2nm+m$.

The next step is to evaluate to prove the existence of a rainbow $u-v$ path ${\mathcal{F}}_n⊳S_m$. Based on the definition of graph ${\mathcal{F}}_n⊳S_m$, graph ${\mathcal{F}}_n⊳S_m$ contains one graph ${\mathcal{F}}_n$ and $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of $S_m$; so, we can evaluate the rainbow $u-v$ path of graph ${\mathcal{F}}_n⊳S_m$ by evaluating the rainbow $u-v$ path on graph ${\mathcal{F}}_n$ and graph $S_m$. Since $diam\left({\mathcal{F}}_n\right)=2$, based on Theorem 1, there is a rainbow $u-v$ path for every $u,v\in V\left({\mathcal{F}}_n\right)$. Based on Theorem 3, $rac\left(S_m\right)=m$; since $S_m$ has m edges, there is a rainbow $u-v$ path for every $u,v\in V\left(S_m\right)$. Therefore, according to the explanation, it can be seen that there is a rainbow $u-v$ path for every $u,v\in V({\mathcal{F}}_n⊳S_m)$. □

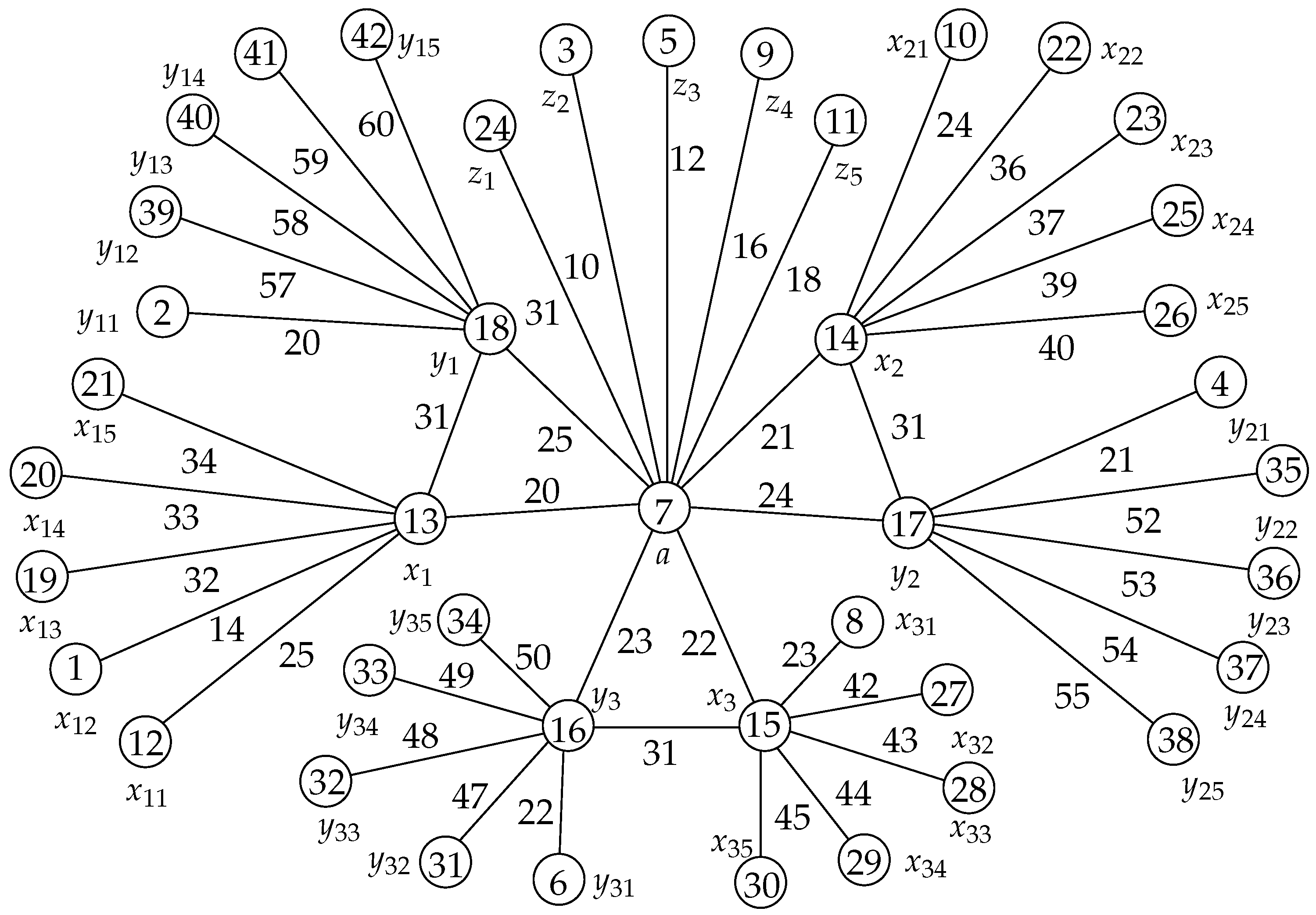
The illustration of a rainbow antimagic coloring of graph ${\mathcal{F}}_3⊳S_5$ can be seen in Figure 2.

Theorem 6.

For $n,m,p\ge 3$, $rac({\mathcal{F}}_n⊳B{r}_{m,p})=2nm+2np+m+p-2n-1$.

Proof of Theorem 6.

Graph ${\mathcal{F}}_n⊳B{r}_{m,p}$ is a connected graph with vertex set $V({\mathcal{F}}_n⊳B{r}_{m,p})=\left\{a\right\}\cup \{x_i,y_i,1\le i\le n\}\cup \{x_{ij},y_{ij},1\le i\le n,1\le j\le m-1\}\cup \{z_j,1\le j\le m-1\}\cup \{z_{mk},b_{jk},c_{jk},1\le j\le m-1,1\le k\le p\}$ and edge set $E({\mathcal{F}}_n⊳B{r}_{m,p})=\{a{x}_i,a{y}_i,x_i{x}_{i1},y_i{y}_{i1},x_i{y}_i,1\le i\le n\}\cup \left\{a{z}_1\right\}\cup \{z_j{z}_{j+1},1\le j\le m-2\}\cup \{x_{ij}{x}_{ij+1},y_{ij}{y}_{ij+1},1\le i\le n,1\le j\le m-2\}\cup \{z_m{z}_{mk},1\le k\le p\}\cup \{x_{im}{b}_{ik},y_{im}{c}_{ik},1\le i\le n,1\le k\le p\}$. The cardinality of $\left|V\right({\mathcal{F}}_n⊳B{r}_{m,p}\left)\right|=2nm+m+3mp-3p$ and the cardinality of $\left|E\right({\mathcal{F}}_n⊳B{r}_{m,p}\left)\right|=n+2nm+m-1+p+2np$.

To prove the rainbow antimagic connection number of $rac({\mathcal{F}}_n⊳B{r}_{m,p})$, first, we have to show the lower bound of $rac({\mathcal{F}}_n⊳B{r}_{m,p})$. Based on Lemma 2, we have $rac({\mathcal{F}}_n⊳B{r}_{m,p})\ge rac\left(B{r}_{m,p}\right)\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)$. Since $rac\left(B{r}_{m,p}\right)=m+p-1$, $rac({\mathcal{F}}_n⊳B{r}_{m,p})\ge 2nm+2np+m+p-2n-1$.

Secondly, we have to show the upper bound of $rac({\mathcal{F}}_n⊳B{r}_{m,p})$. Define the vertex labeling $f\left(V({\mathcal{F}}_n⊳B{r}_{m,p})\right)\to \{1,2,...,2nm+m+3mp-3p\}$ as follows:

$$\begin{array}{cc}\hfill f\left(a\right)& =2n+1\hfill \\ \hfill f\left(x_i\right)& =2n+1-i,\mathrm{for}1\le i\le n\hfill \\ \hfill f\left(y_i\right)& =4n+2-i,\mathrm{for}1\le i\le n\hfill \\ \hfill f\left(z_j\right)& =2nj+2n+j+1,\mathrm{for}1\le j\le m-1\hfill \\ \hfill f\left(x_{ij}\right)& =\left\{\begin{array}{cc}2n-2i+1,\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2nj+j+i,\hfill & \mathrm{for}1\le i\le n,2\le j\le m-1\hfill \end{array}\right.\hfill \\ \hfill f\left(y_{ij}\right)& =\left\{\begin{array}{cc}2i,\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2nj+2n+j-i+1,\hfill & \mathrm{for}1\le i\le n,2\le j\le m-1\hfill \end{array}\right.\hfill \\ \hfill f\left(z_{m-1k}\right)& =2nm+2np+m+k,\mathrm{for}1\le k\le p\hfill \\ \hfill f\left(b_{ik}\right)& =2nm+m+ip+k-p,\mathrm{for}1\le i\le n,1\le k\le p\hfill \\ \hfill f\left(c_{ik}\right)& =2nm+2np+m+k-ip,\mathrm{for}1\le i\le n,1\le k\le p\hfill \end{array}$$

The edge weights of the above vertex labeling f can be presented as

$$\begin{array}{cc}\hfill w\left(a{x}_i\right)& =4n+2+i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(a{y}_i\right)& =6n+3-i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(a{z}_1\right)& =6n+3\hfill \\ \hfill w\left(z_j{z}_{j+1}\right)& =6n+4nj+2j+3,\mathrm{for}1\le j\le m-2\hfill \\ \hfill w\left(x_i{x}_{i1}\right)& =4n+2-i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(y_i{y}_{i1}\right)& =4n+4-i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(x_{ij}{x}_{ij+1}\right)& =\left\{\begin{array}{cc}6n+3-i\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2n+4nj+2j+2i+1\hfill & \mathrm{for}1\le i\le n,2\le j\le m-3\hfill \end{array}\right.\hfill \\ \hfill w\left(y_{ij}{y}_{ij+1}\right)& =\left\{\begin{array}{cc}6n+i+3\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 6n+4nj+2j-2i+3\hfill & \mathrm{for}1\le i\le n,2\le j\le m-3\hfill \end{array}\right.\hfill \\ \hfill w\left(z_{m-1}{z}_{m-1k}\right)& =4nm+2np+2m+k,\mathrm{for}1\le k\le p\hfill \\ \hfill w\left(x_{im-1}{b}_{ik}\right)& =4nm+2m+i+ip+k-2n-p-1,\mathrm{for}1\le i\le n,1\le k\le p\hfill \\ \hfill w\left(y_{im-1}{c}_{ik}\right)& =4nm+2np+2m+k-i-ip,\mathrm{for}1\le i\le n,1\le k\le p\hfill \end{array}$$

It is easy to see that the above edge weight will induce a rainbow antimagic coloring of graph ${\mathcal{F}}_n⊳B{r}_{m,p}$. Based on Theorem 3, $rac\left(B{r}_{m,p}\right)=m+p-1$; since $E\left(B{r}_{m,p}\right)=m+p-1$, the weight of each edge in graph $B{r}_{m,p}$ is different. Therefore, the sum of the weights on $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of graph $B{r}_{m,p}$ is $\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)\left(\right|E\left(B{r}_{m,p}\right)\left|\right)=2nm+2np+m+p-2n-1$. Based on the description above, we have that the distinct weight of graph $({\mathcal{F}}_n⊳S_m)$ is $2nm+2np+m+p-2n-1$. It implies that the edge weights of $f\left(V({\mathcal{F}}_n⊳B{r}_{m,p})\right)\to \{1,2,...,2nm+3mp+m-3p\}$ induce a rainbow antimagic coloring of $2nm+2np+m+p-2n-1$ colors. Thus, $rac({\mathcal{F}}_n⊳B{r}_{m,p})\le 2nm+2np+m+p-2n-1$. Comparing the two bounds, we have the exact value of $rac({\mathcal{F}}_n⊳B{r}_{m,p})=2nm+2np+m+p-2n-1$.

The next step is to evaluate to prove the existence of a rainbow $u-v$ path ${\mathcal{F}}_n⊳B{r}_{m,p}$. Based on the definition of graph ${\mathcal{F}}_n⊳B{r}_{m,p}$, graph ${\mathcal{F}}_n⊳B{r}_{m,p}$ contains one graph ${\mathcal{F}}_n$ and $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of $B{r}_{m,p}$; so, we can evaluate the rainbow $u-v$ path of graph ${\mathcal{F}}_n⊳B{r}_{m,p}$ by evaluating the rainbow $u-v$ path on graph ${\mathcal{F}}_n$ and graph $B{r}_{m,p}$. Since $diam\left({\mathcal{F}}_n\right)=2$, based on Theorem 1, there is a rainbow $u-v$ path for every $u,v\in V\left({\mathcal{F}}_n\right)$. Based on Theorem 3$rac\left(B{r}_{m,p}\right)=m+p-1$, since $B{r}_{m,p}$ has $m+p-1$ edges, there is a rainbow $u-v$ path for every $u,v\in V\left(B{r}_{m,p}\right)$. Therefore, according to the explanation, it can be seen that there is a rainbow $u-v$ path for every $u,v\in V({\mathcal{F}}_n⊳B{r}_{m,p})$. □

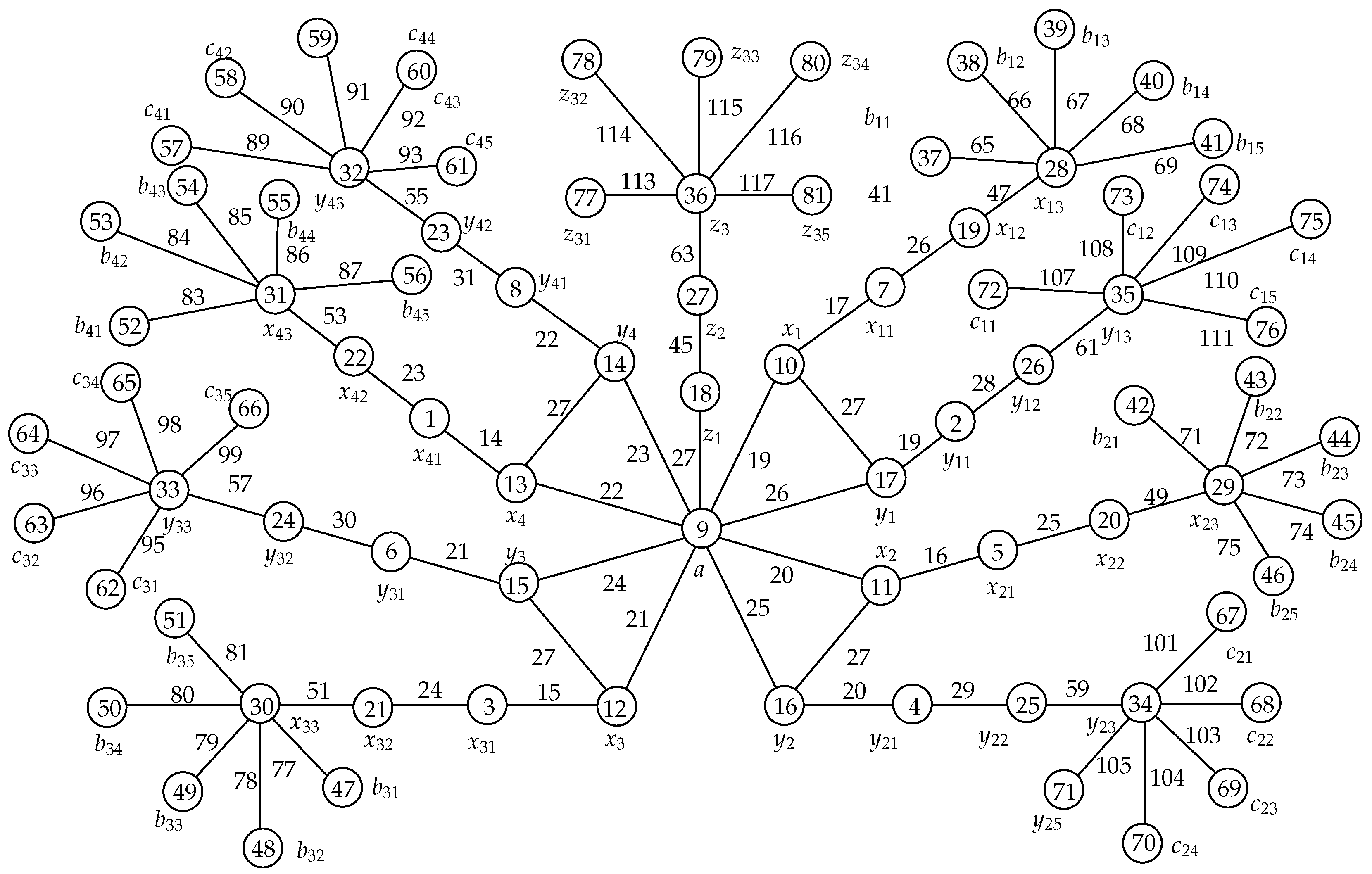
The illustration of a rainbow antimagic coloring of graph ${\mathcal{F}}_n⊳B{r}_{m,p}$ can be seen in Figure 3.

Theorem 7.

For $n\ge 3,m=2n-2$, $rac({\mathcal{F}}_n⊳S_{m,m})=4nm+2n+2m+1$.

Proof of Theorem 7.

Graph ${\mathcal{F}}_n⊳S_{m,m}$ is a connected graph with vertex set $V({\mathcal{F}}_n⊳S_{m,m})=\left\{a\right\}\cup \{x_i,y_i,1\le i\le n\}\cup \{z_j,1\le j\le m\}\cup \{x_{ij},y_{ij},1\le i\le n,1\le j\le m\}\cup \left\{a_0\right\}\cup \{a_k,1\le k\le m\}\cup \{b_i,c_i,1\le j\le n\}\cup \{b_{ik},c_{ik},1\le i\le n,1\le k\le m\}$ and edge set $E({\mathcal{F}}_n⊳S_{m,m})=\{a{x}_i,a{y}_i,x_i{y}_i,1\le i\le n\}\cup \{a{z}_j,1\le j\le m\}\cup \left\{a{a}_0\right\}\cup \{a_0{a}_k,1\le k\le m\}\cup \{x_i{x}_{ij},y_i{y}_{ij},1\le i\le n,1\le j\le m\}\cup \{x_i{b}_i,y_i{c}_i,1\le i\le n\}\cup \{b_i{b}_{i}k,c_i{c}_{ik},1\le i\le n,1\le k\le k\}$. The cardinality of $\left|V\right({\mathcal{F}}_n⊳S_{m,m}\left)\right|=4n+2m+4nm+2$ and the cardinality of $\left|E\right({\mathcal{F}}_n⊳S_{m,m}\left)\right|=5n+2m+4nm+1$. To prove the rainbow antimagic connection number of $rac({\mathcal{F}}_n⊳S_{m,m})$, first, we have to show the lower bound of $rac({\mathcal{F}}_n⊳S_{m,m})$. Based on Lemma 2, we have $rac({\mathcal{F}}_n⊳S_{m,m})\ge rac\left(S_{m,m}\right)\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)$. Since $rac\left(S_{m,m}\right)=2m+1$, $rac({\mathcal{F}}_n⊳S_{m,m})\ge 4nm+2n+2m+1$.

Secondly, we have to show the upper bound of $rac({\mathcal{F}}_n⊳S_{m,m})$. Define the vertex labeling $f\left(V({\mathcal{F}}_n⊳S_{m,m})\right)\to \{1,2,...,4n+2m+4nm+2\}$ as follows:

$$\begin{array}{cc}\hfill f\left(a\right)& =2n+1\hfill \\ \hfill f\left(x_i\right)& =4n+i,\mathrm{for}1\le i\le n\hfill \end{array}$$

$$\begin{array}{cc}\hfill f\left(y_i\right)& =6n+1-i,\mathrm{for}1\le i\le n\hfill \\ \hfill f\left(z_j\right)& =\left\{\begin{array}{cc}2j+1\hfill & \mathrm{for}1\le j\le \lfloor \frac{m}{2}\rfloor \hfill \\ 2j+3\hfill & \mathrm{for}\lceil \frac{m}{2}\rceil \le j\le m\hfill \end{array}\right.\hfill \\ \hfill f\left(x_{ij}\right)& =\left\{\begin{array}{cc}4n+2-2i\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 1\hfill & \mathrm{for}i=1,j=2\hfill \\ 6n+j-2\hfill & \mathrm{for}i=1,3\le j\le m\hfill \\ 6n+m+j-2\hfill & \mathrm{for}i=2,2\le j\le 3\hfill \\ 6n+m+j-1\hfill & \mathrm{for}i=2,4\le j\le m\hfill \\ 6n+im+j-m-i\hfill & \mathrm{for}3\le i\le n,2\le j\le m\hfill \end{array}\right.\hfill \\ \hfill f\left(y_{ij}\right)& =\left\{\begin{array}{cc}2i\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2nm+4n+m+j-im+1\hfill & \mathrm{for}1\le i\le n,2\le j\le m\hfill \end{array}\right.\hfill \\ \hfill f\left(a_0\right)& =8n\hfill \\ \hfill f\left(b_i\right)& =\left\{\begin{array}{cc}6n+m-1\hfill & \mathrm{for}i=1\hfill \\ 6n+im\hfill & \mathrm{for}2\le i\le n\hfill \end{array}\right.\hfill \\ \hfill f\left(c_i\right)& =2nm+4n+2m+2-im,\mathrm{for}1\le i\le n\hfill \\ \hfill f\left(a_k\right)& =2nm+4n+2m+2+k,\mathrm{for}1\le k\le m\hfill \\ \hfill f\left(b_{ik}\right)& =\left\{\begin{array}{cc}2nm+4n+m+2+k\hfill & \mathrm{for}i=1,1\le k\le m,\hfill \\ 2nm+4n+m+im+2+k\hfill & \mathrm{for}2\le i\le n,1\le k\le m\hfill \end{array}\right.\hfill \\ \hfill f\left(c_{ik}\right)& =4nm+4n+2m+k+2-im,\mathrm{for}1\le i\le n,1\le k\le m\hfill \end{array}$$

The edge weights of the above vertex labeling f can be presented as

$$\begin{array}{cc}\hfill w\left(a{x}_i\right)& =6n+i+1,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(a{y}_i\right)& =8n+1-i,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(x_i{y}_i\right)& =10n+1,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(a{z}_j\right)& =\left\{\begin{array}{cc}2n+2j+2\hfill & \mathrm{for}1\le j\le \lfloor \frac{m}{2}\rfloor \hfill \\ 2n+2j+4\hfill & \mathrm{for}\lceil \frac{m}{2}\rceil +1\le j\le m\hfill \end{array}\right.\hfill \\ \hfill w\left(x_i{x}_{ij}\right)& =\left\{\begin{array}{cc}8n+2-i\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 4n+2\hfill & \mathrm{for}i=1,j=2\hfill \\ 10n+j+i-2\hfill & \mathrm{for}i=1,3\le j\le m\hfill \\ 10n+m+j+i-2\hfill & \mathrm{for}i=2,2\le j\le 3\hfill \\ 10n+m+j+i-1\hfill & \mathrm{for}i=2,4\le j\le m\hfill \\ 10n+j+im+i-m-1\hfill & \mathrm{for}3\le i\le n,2\le j\le m\hfill \end{array}\right.\hfill \\ \hfill w\left(y_i{y}_{ij}\right)& =\left\{\begin{array}{cc}6n+i+1\hfill & \mathrm{for}1\le i\le n,j=1\hfill \\ 2nm+10n+m+j+2-i-im\hfill & \mathrm{for}1\le i\le n,2\le j\le m\hfill \end{array}\right.\hfill \\ \hfill w\left(a{a}_0\right)& =10n+1\hfill \\ \hfill w\left(x_i{b}_i\right)& =\left\{\begin{array}{cc}10n+m+i-1\hfill & \mathrm{for}i=1\hfill \\ 10n+im+i\hfill & \mathrm{for}2\le i\le n\hfill \end{array}\right.\hfill \\ \hfill w\left(y_i{c}_i\right)& =2nm+10n+2m+3-i-im,\mathrm{for}1\le i\le n\hfill \\ \hfill w\left(a_0{a}_k\right)& =2nm+12n+2m+2+k,\mathrm{for}1\le k\le m\hfill \\ \hfill w\left(b_i{b}_{ik}\right)& =\left\{\begin{array}{cc}2nm+10n+2m+1+k\hfill & \mathrm{for}i=1,1\le k\le m,\hfill \\ 2nm+10n+m+2im+2+k\hfill & \mathrm{for}2\le i\le n,1\le k\le m\hfill \end{array}\right.\hfill \\ \hfill w\left(c_i{c}_{ik}\right)& =6nm+8n+4m+k+4-2im,\mathrm{for}1\le i\le n,1\le k\le m\hfill \end{array}$$

It is easy to see that the above edge weight will induce a rainbow antimagic coloring of graph ${\mathcal{F}}_n⊳S_{m,m}$. Based on Theorem 3, $rac\left(S_{m,m}\right)=2m+1$; since $E\left(S_{m,m}\right)=2m+1$, the weight of each edge in graph $S_{m,m}$ is different. Therefore, the sum of the weights on $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of graph $S_{m,m}$ is $\left(\right|V\left({\mathcal{F}}_n\right)\left|\right)\left(\right|E\left(S_{m,m}\right)\left|\right)=4nm+2n+2m+1$. Based on the description above, we have that the distinct weight of graph $({\mathcal{F}}_n⊳S_{m,m})$ is $4nm+2n+2m+1$. It implies that the edge weights of $f\left(V({\mathcal{F}}_n⊳S_{m,m})\right)\to \{1,2,...,4n+2m+4nm+2\}$ induce a rainbow antimagic coloring of $4nm+2n+2m+1$ colors. Thus, $rac({\mathcal{F}}_n⊳S_{m,m})\le 4nm+2n+2m+1$. Comparing the two bounds, we have the exact value of $rac({\mathcal{F}}_n⊳S_{m,m})=4nm+2n+2m+1$.

The next step is to evaluate to prove the existence of a rainbow $u-v$ path ${\mathcal{F}}_n⊳S_{m,m}$. Based on the definition of graph ${\mathcal{F}}_n⊳S_{m,m}$, graph ${\mathcal{F}}_n⊳S_{m,m}$ contains one graph ${\mathcal{F}}_n$ and $\left|V\right({\mathcal{F}}_n\left)\right|$ copies of $S_{m,m}$; so, we can evaluate the rainbow $u-v$ path of graph ${\mathcal{F}}_n⊳S_{m,m}$ by evaluating the rainbow $u-v$ path on graph ${\mathcal{F}}_n$ and graph $S_{m,m}$. Since $diam\left({\mathcal{F}}_n\right)=2$, based on Theorem 1, there is a rainbow $u-v$ path for every $u,v\in V\left({\mathcal{F}}_n\right)$. Based on Theorem 3, $rac\left(S_{m,m}\right)=2m+1$; since $S_{m,m}$ has $2m+1$ edges, there is a rainbow $u-v$ path for every $u,v\in V\left(S_{m,m}\right)$. Therefore, according to the explanation, it can be seen that there is a rainbow $u-v$ path for every $u,v\in V({\mathcal{F}}_n⊳S_{m,m})$. □

3. Conclusions

We have studied the rainbow antimagic coloring of the comb product of a friendship graph with any tree graph. Based on the result, we have a new lower bound of rainbow antimagic connection number for the comb product of a friendship graph with any tree ${\mathcal{F}}_n⊳T_m$ and the exact value of the rainbow antimagic connection number of graph ${\mathcal{F}}_n⊳T_m$, where $T_m$ is path $P_m$, star $S_m$, broom $B{r}_{m,p}$ and double star $S_{m,m}$. However, if it is not a tree, it is still difficult to determine the exact value of the rainbow antimagic connection number. Therefore, this study raises an open problem:

Determine the exact value of the rainbow antimagic connection number of graph $G⊳H$ where H is not a tree.