An Offset-Boostable Chaotic Oscillator with Broken Symmetry

Abstract

A new 3D offset-boostable symmetric system is proposed by an absolute value function introduced. The system seems to be more fragile and easier to the state of broken symmetry. Coexisting symmetric pairs of attractors get closer and closer, and finally get emerged together. Basins of attraction show how these coexisting attractors are arranged in phase space. All these coexisting attractors can be easily offset boosted in phase space by a single constant when the initial condition is revised accordingly. PSpice simulations prove all the phenomena.

1. Introduction

In recent years, the study of nonlinear and chaotic dynamical systems has received particular attention due to the rapid development of computers and their potential applications in several fields of science and engineering, like this: sensors, reservoir computing, encryption, and secure communications [1,2,3]. Several types of research have been done based on some famous chaotic systems like the Lorenz system [4], Chen system [5], Lü system [6], and other three dimensional systems [7,8,9,10,11]. These system equations are divided into autonomous differential equations and non-autonomous differential equations. The attractors of these systems are classified into hidden attractors and self-excited attractors [12,13]. Later, extreme multistability, symmetry broken, or offset boosting were studied [14,15].

The size of chaotic signals can be changed, researchers can design different systems with the change of the scale and position of the chaotic attractor, namely amplitude control and offset boosting [16,17]. From the point of view of phase orbit, the amplitude is the size or dimension of phase orbit, and from the point of view of the signal is the amplitude of the signal; from the point of view of the phase orbit, the offset is the position of the phase orbit, and from the point of view of the signal is the DC component or average of the signal [18,19]. The combination of the two can represent the position and size of phase orbits in space, that is, geometric features [20,21]. From the point of view of dynamic equation, multistability is different solutions under different initial conditions, and from the point of view of system, it is multiple coexisting attractors at different positions in phase space such as self-reproducing [22], attractor doubling [23], conditional symmetry [24], or even repellor construction [25]. There are two main methods to achieve self-reproduction of attractors. One is to use parameter introduction and change parameter value to realize the boosting of attractors. Another approach is to introduce periodic or absolute value functions to extract attractor doubles with different offsets by changing initial conditions [26,27,28].

Chaotic system has been studied by many researchers because of its special characteristics [29,30]. Due to the sensitivity of chaotic systems to initial values, extreme multistability states related to initial values are studied [31,32,33,34]. Multistability refers to the possibility of multiple attractors when the initial values changed with the structure of the nonlinear dynamic system no change. The symmetry of the system is also a kind of multisteady state [35,36,37].

In addition to the multistability mentioned above, symmetric dynamical systems exhibit many interesting behaviors, such as spontaneous symmetry breaking, instantaneous chaos, attractor doubling, and merger crisis [38,39,40,41,42]. However, the interesting dynamic behavior of symmetry breaking is rarely studied in the literature [43,44,45,46]. Symmetry breaking attractors may exhibit an attractor merging crisis when bifurcation parameters in the system change. It is very rare that the system also has chaos before and after merging, so it is meaningful to construct the simplest chaotic system with such behavior [47,48]. In the debugging process of the circuit, the resistance used does not need to be very precise, so there is no use of field programmable gate arrays (FPGA) to program coefficient parameters. At the same time, it refers to many excellent simulation articles based on PSpice, and it is easy to implement [49,50]. Future research focuses on the hardware implementation of the system. Valencia-Ponce, M.A et.al. propose to use CMOS integrated circuit to design FOCOs, and use OTAS to realize the CMOS design of the cascaded fractional integrator of the first-order active filter module [51]. It will be an interesting and challenging topic for future research.

In this article, a new chaotic system is designed and its symmetry breaking, and offset boosting control are analyzed. In Section 2, the model of the chaotic system is given, and the dissipatedness and the stability are investigated with the change of the parameters. In Section 3, we study the problem of multiple topologies with the coexisting of broken symmetric attractors. In Section 4, we discuss the analysis of variable distribution based on the dynamical system equations, the geometric regulation of chaotic attractors in circuits is realized by dissociating nonbifurcation parameters in the dynamical system. In Section 5, the simulate circuit experiment verifies the consistency of theoretical analysis and numerical analysis. The last part gives some discussion and conclusion.

2. Symmetric Chaotic Model

A New Chaotic Model

A series of boostable (VB) chaotic systems were proposed in [52], VB17 was selected as the prototype for the construction of symmetry, based on the criterion that the system was indeed much simpler than all other known examples [53]. a new chaotic system is obtained.

$$\{\begin{array}{l}\stackrel{.}{x}=yz\\ \stackrel{.}{y}=a\left|z\right|-y-z^2\\ \stackrel{.}{z}=x-bz\end{array}$$

(1)

where x, y, z are system variables, a, b are bifurcation parameters of the system (1). When the parameters are set as a = 4.5, b = 1.6 with initial condition (1, 0, 1), we adopt the ODE45 algorithm through MATLAB software, and the integration step is 0.005 and the running time is 500. system (1) phase space or phase plane the projection is shown in Figure 1. Figure 1b shows the 2 Monge projections. The Lyapunov exponent spectrum was calculated by the Wolf method. The corresponding Lyapunov exponents are LE1 = 0.157742, LE2 = 0, LE3 = −2.710722, and Kaplan-Yorke dimension is 2.0582. The dissipativity of this system can be described by the following expression:

$$\nabla V=\frac{\partial \stackrel{.}{x}}{\partial x}+\frac{\partial \stackrel{.}{y}}{\partial y}+\frac{\partial \stackrel{.}{z}}{\partial z}=-1-b$$

(2)

when the parameters b = 1.6, the ∇V of this system is negative. It means the system is dissipative.

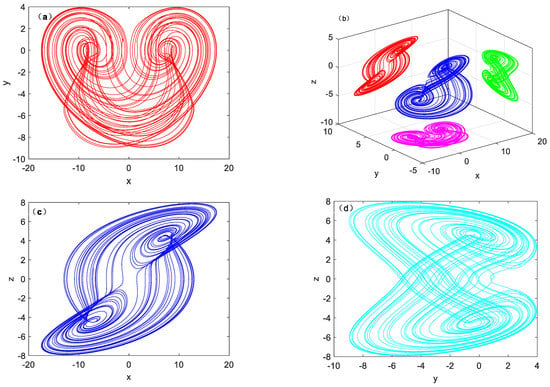
Figure 1. Phase portraits of system (1) with a = 4.5, b = 1.6 under initial condition [1, 0, 1]: (a) x-y plane, (b) x-y-z spatial graph, (c) x-z plane, (d) y-z plane.

3. Equilibrium Point and Bifurcation Analysis

3.1. Analysis of Equilibrium Points

The system (1) has three equilibrium points, when $\stackrel{.}{x}=\stackrel{.}{y}=\stackrel{.}{z}=0$, the specific calculation method is as follows:

$$\{\begin{array}{l}yz=0\\ a\left|z\right|-y-z^2=0\\ x-bz=0\end{array}$$

(3)

After calculation, Equation (3) has three equilibrium points (0, 0, 0), (ab, 0, a), (−ab, 0, −a), The linear Jacobian matrix J of system (1) can be expressed as follows:

$$J=\left[\begin{array}{lll}0& z& y\\ 0& -1& a\mathrm{sgn}z-2z\\ 1& 0& -b\end{array}\right]$$

(4)

System Equation (1) has a zero equilibrium point E0 and two non-zero equilibrium points E1, E2. Table 1 lists these three types under the change of parameters, the equilibrium point of system Equation (2) corresponds to eigenvalues and stability. E0 is the unstable saddle point and E1 and E2 is the unstable saddle-focus.

Table 1. Equilibrium points and eigenvalues of system (1) with a = 4.5, b = 1.6.

Equilibrium Points	Eigenvalues	Stability
E0 = (0, 0, 0)	(0, −1.6, −1)	unstable saddle points
E1 = (7.2, 0, 4.5)	(−2.1187, 0.6260 + 1.6715i, 0.6260 − 1.6715i)	unstable saddle-foci
E2 = (−7.2, 0, −4.5)	(−3.6685, 0.5343 + 2.2879i, 0.5343 − 2.2879i)	unstable saddle-foci

3.2. Bifurcation Analysis

The dynamical behaviors of the chaotic system (1) were further investigated with conventional dynamical analysis tools, such as Lyapunov exponent spectra and bifurcation diagram.

When parameter b changes from 0.6 to 2, with fixed parameter a = 4.5 and set the initial conditions as (1, 0, 1), The maximum value of state variable x is used to draw the bifurcation diagram. The bifurcation diagram and the corresponding Lyapunov spectra are presented in Figure 2. Figure 3 shows the typical topology phase diagram under different parameters b.

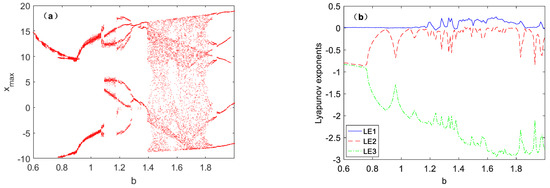
Figure 2. Bifurcation diagram and Lyapunov exponent spectra of system (1) with a = 4.5 under initial condition (1, 0, 1): (a) Bifurcation diagram, (b) Lyapunov exponent spectra.

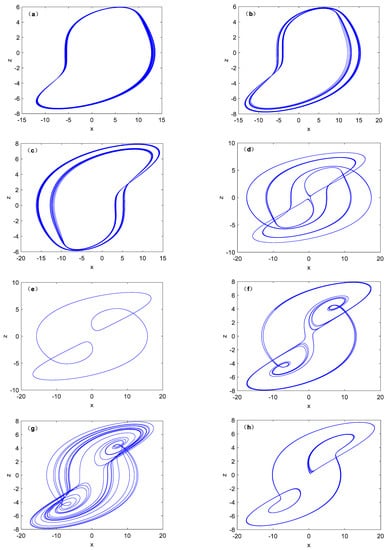
Figure 3. Various phase portraits with different b on the x-z plane. (a) b = 0.98, (b) b = 1.17, (c) b = 1.1, (d) b = 1.2, (e) b = 1.38, (f) b = 1.58, (g) b = 1.6, (h) b = 1.84.

As it is shown in Figure 2a, system (1) converges on the interval of b ∈ (0.6, 1.4), and it can be seen that all Lyapunov spectra in the corresponding region are negative. When the parameter changes to b = 1.4, the system enters a chaotic state and positive maximum Lyapunov spectra appear. When parameter b is in the interval of [1.41, 1.82], the system goes to a chaos state. Figure 3 depicts the phase trajectories of the x-z plane under different values of parameter b. In Figure 3a, when b is around 0.6, the system enters a narrow period window. The system is still periodic within b ∈ [0.6, 1.4]. The system is in period-1 cycle state for b = 0.68. The system is in period-2 cycle state for b = 1.17. The system is in period-2 cycle state for b = 1.1. It is not difficult to find that when parameter b is set to 1.17 and 1.1, Figure 3b,c are symmetric, as shown in Figure 4. In fact, it is the process of attractor aggregation, because of the symmetry breaking, so in the process of parameter bifurcation, it will be presented back and forth between the two broken attractors. Finally, nearby b = 1.84, The system is periodic. Therefore, a crisis of attractor breakage occurs after parameter change.

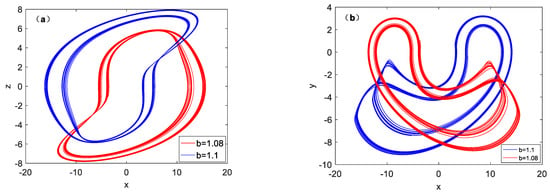
Figure 4. The change of broken attractor with different b, (a) x-z plane, (b) x-y plane.

3.3. Symmetry Analysis

Elementary symmetries are divided into inversion, rotation, and reflection associated with the equations with respect to changing the sign of three, two, and one variable, respectively. The solution of Equation (1) remains constant when it is transformed by (x, y, z) → (−x, y, −z), so the system can be considered as a rotationally symmetric system with respect to the y-axis. In general, a system with coexisting attractors is multi-stable. The system can generate different attractors under different initial conditions with fixed parameter values unchanged.

When the value of parameter b is fixed as 1.6 and the value of state variable x is 2.5~5, the coexistence bifurcation diagram is shown in Figure 5a, where the initial conditions of the red bifurcation track are set as (1, 0, 1), and blue bifurcation track set as (−1, 0, −1). The coexistence bifurcation diagram with two different initial conditions under the same parameter a is symmetric with respect to X_max = 0. Figure 5b shows the Lyapunov exponent spectra corresponding to the two initial conditions under parameter a. It can be seen that the Lyapunov exponential of the chaotic system under different initial conditions is not affected by the initial conditions.

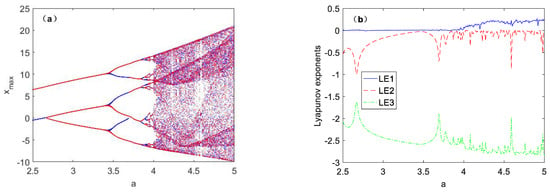
Figure 5. Dynamic behaviors under different initial conditions varying with parameter a: (a) Coexistence bifurcation diagram (red (1, 0, 1) and blue (−1, 0, −1)), (b) Corresponding Lyapunov exponent spectra.

The coexistence attractor phase trajectory is shown in Figure 6. When set the parameter a as 3.67 and parameter b = 1.6, and select two groups of initial conditions (1, 0, 1) and (−1, 0, −1) at the same time. The initial conditions are abbreviated as IC in the following figure. Figure 6a,b,d show that the red track starts from the initial condition(−1, 0, −1), and the blue track starts from the initial condition (1, 0, 1). Figure 6c show the 2 Monge projections. The coexistence attractor is axially symmetric in the y-z plane with respect to y = 0. The coexistence attractor is rotationally symmetric in the x-z plane. Therefore, it can be determined that symmetrically coexisting attractors will be present in the chaotic system under different initial conditions under certain conditions. This conclusion is confirmed by analyzing the symmetries of different topological structures produced by different parameters b and different initial conditions.

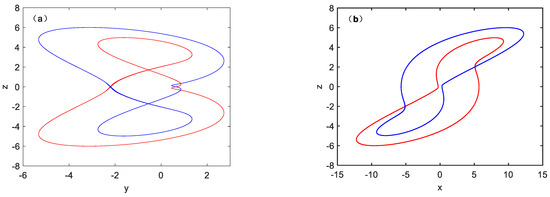
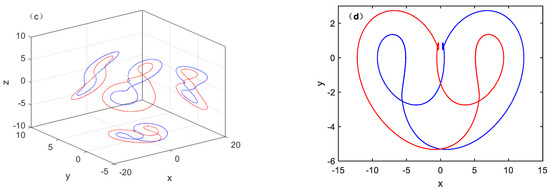
Figure 6. Coexisting symmetric chaotic attractors of system (1) with a = 3.67, b = 1.6 under IC1 = (−1, 0, −1) (red); IC2 = (1, 0, 1) (blue). (a) y-z plane; (b) x-z plane; (c) x-y-z spatial graph; (d) x-y plane.

When fixed parameter b as 1.6 and takes different parameter a, coexisting attractor pairs with initial conditions of (−1, 0, −1) and (1, 0, 1) can also be obtained, as shown in Figure 7, where the cyan orbit shows the initial conditions of (−1, 0, −1), and the initial conditions of (1, 0, 1) shows in magenta color. The two kinds of symmetric periodic orbits are shown in Figure 7a–c. Two symmetric double vortex single cycle attractors are shown in Figure 7d. Figure 7e,f shows two symmetric pairs of chaotic attractors. It is worth noting that the variation of parameter a affects the amplitude and frequency of the variable, and has a positive correlation. Figure 8 shows the phase diagram and time variation diagram of system (1).

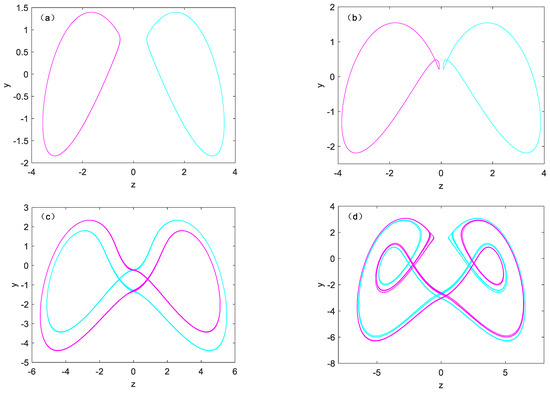
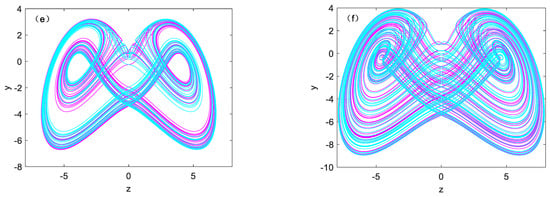
Figure 7. Typical attractors system (1) with b = 1.6: (a) a = 2.5, (b) a = 2.65, (c) a = 3.5, (d) a = 3.9, (e) a = 4, (f) a = 4.5, initial condition IC1 = (1, 0, 1) (cyan); IC2 = (−1, 1,−1) (magenta).

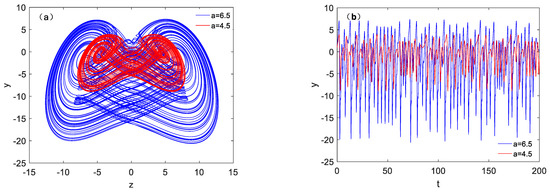
Figure 8. Phase diagram of amplitude control of system (1) with b = 1.6, under initial condition (−1, 0, −1): (a) Phase diagram in z-y plane, (b) Signal y(t).

3.4. Analysis of Multistability

When fixed the parameters as a = 4.4, b = 1.17, and the initial values fixed as $y(0)=0$, select $x(0)$ and $z(0)$ as two variables, then we analyzed the dynamic behaviors under initial condition $x(0)$ and $z(0)$ by using bifurcation diagram and Lyapunov exponent spectrum.

When the interval of the state variable $x(0)$ is [−2, 2], as can be seen from Figure 9, when the state variable $x(0)$ keeps changing, the system presents a symmetry period-2 phenomenon.

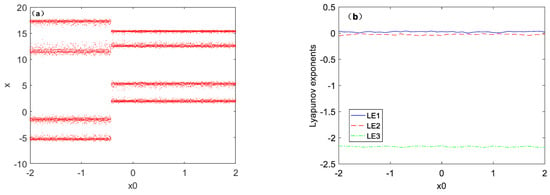
Figure 9. Dynamic behavior of system (1) with a = 4.4, b = 1.17 under initial condition [x(0), 0, 1], (a) Bifurcation diagram, (b) Lyapunov exponents spectrum.

When the interval of state variable $z(0)$ is [−2, 2], as can be seen from Figure 10, when the state variable $z(0)$ keeps changing, the change of the attractor is similar to the change of variable $x(0)$, but the value of the attractor switch is different.

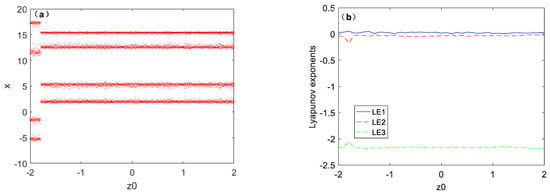
Figure 10. Dynamic behavior of system (1) with a = 4.4, b = 1.17 under initial condition [1, 0, z(0)], (a) Bifurcation diagram, (b) Lyapunov exponents spectrum.

When the system selects different initial conditions, the phase trajectory diagram of the system will run in different states, as shown in Figure 11. It can be seen from Figure 11 that the amplitude range of the state variable x is large, which is not convenient for the implementation of the circuit. The proportional uniform compression of variables can be considered in the circuit.

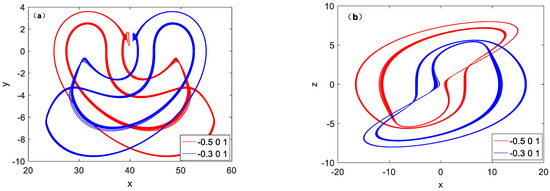
Figure 11. Coexisting phase portraits of system (1) with a = 4.4, b = 1.17, under initial conditions IC1 = (−0.5, 0, 1) (red); IC2 = (−0.3, 0, 1) (blue). (a) x-y plane; (b) x-z plane.

The basin of attraction has predictive symmetry and complex fractal structure. To further verify the multi-stability of system (1), Figure 12 shows the basin of attraction of this system. For the convenience of calculation, the coordinate range is (−50, 50), and the calculation unit of 200×200 is generated by taking 0.2 as the step. In the calculation of Figure 12a, the cross section is z = 0, and in the calculation of Figure 12b, the cross section is y = 0. For each point, the phase orbit is run out through the MATLAB program, and the center of gravity point of the phase orbit generated by the initial value point and the mean value of each signal are calculated through the code. When the difference between the calculated results of two different phase orbits exceeds the threshold, it is marked as another type of attractor. Finally, the basin of attraction is generated according to the results of all the calculated points [54,55]. The same color is used in the attractor pool to show similar chaotic attractors. It is clearly can be seen from Figure 12 that the two regions filled with different colors correspond exactly to different types of attractors.

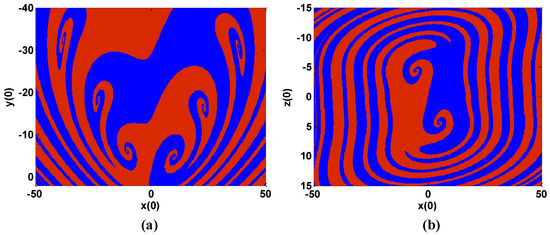
Figure 12. Basin of at traction between different state variables with a = 4.4, b = 1.17. (a) x-y plane; (b) x-z plane.

4. Offset Boosting

When x changes to x + m (m is a constant), the equation $\stackrel{.}{x}=f(y,z)$ remains no change without any revision, but only leaves an additional constant in the last equation:

$$\{\begin{array}{l}\stackrel{.}{x}=yz\\ \stackrel{.}{y}=a\left|z\right|-y-z^2\\ \stackrel{.}{z}=x+m-bz\end{array}$$

(5)

It can be seen from Equation (1) that variable x only appears in the third dimension, the kinetic equation obtained from replacing the original x with x + m is shown in Equation (2). This parameter m is only for bias control and does not contribute to other dynamic characteristics of system (1). This parameter m is usually supplied by the dc power supply of the circuit and can be interchangeable between polarities. When m is positive, the offset moves in the positive direction of the x-axis and negative m moves in the opposite direction. When a = 4.5, b = 1.6, the added constant m can easily change the signal x between unipolar and bipolar boosted, which is indicated by the different colors’ attractors in Figure 13.

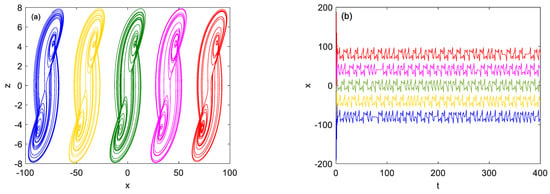
Figure 13. Multi-attractors coexist of system (2) with a = 4.5, b = 1.6, initial conditions IC1 = (−80, 0, 1) (blue); IC2 = (−40, 0, 1) (yellow); IC3 = (1, 0, 1) (green); IC4 = (40, 0, 1) (cyan); IC5 = (80, 0, 1) (red): (a) Phase graph in z-x plane, (b) Offset-boosting time signal x(t).

As shown in Figure 14a, the Lyapunov exponential spectrum does not change with the change of offset m. It can be seen from Figure 14b that when parameter m ∈ (−30, 30), the bifurcation diagram of variable x increases in an absolutely linear direction, because the variable x only exist in a third dimension and the third dimension only has a constant.

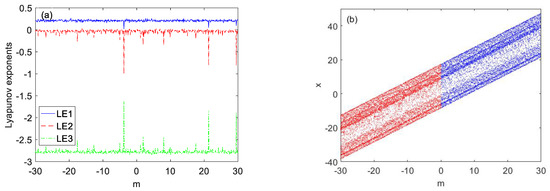
Figure 14. Dynamic evolution of system (2) with a = 4.5, b = 1.6 under initial condition (1, 0, 1): (a) Lyapunov exponents and (b) Bifurcation diagram.

5. Circuit Simulation

In order to verify the chaotic characteristics of the system. PSpice circuit simulation software is used to design the chaotic system circuit. The system described above is ideal for providing signals with the polarity required for signal processing. The simulation circuit is shown in Figure 15, from which the state equations can be obtained as follows:

$$\{\begin{array}{l}\stackrel{.}{x}=\frac{1}{R_1{C}_1}yz\\ \stackrel{.}{y}=\frac{1}{R_7{C}_2}\left|z\right|-\frac{1}{R_5{C}_2}y-\frac{1}{R_4{C}_2}{z}^2\\ \stackrel{.}{z}=\frac{1}{R_{19}{C}_3}x-\frac{1}{R_{20}{C}_3}z\end{array}$$

(6)

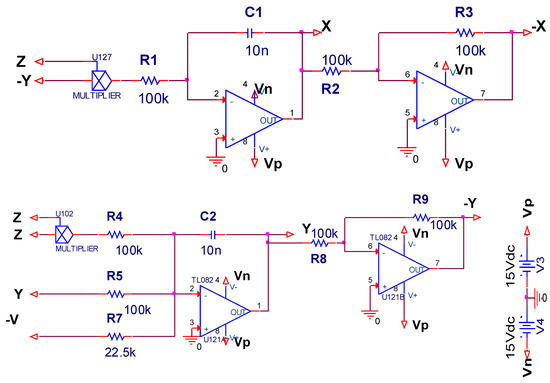
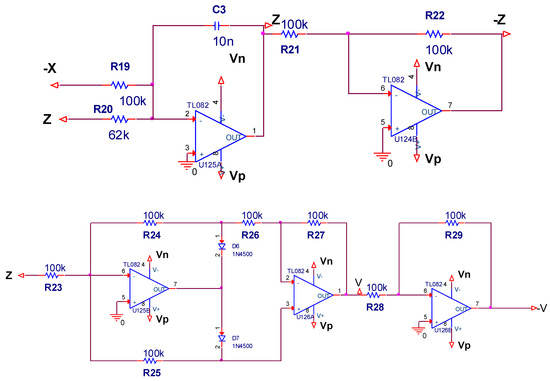
Figure 15. Circuit schematic of system (3).

The circuit of the whole system is composed of three channels, which respectively realize x, y, z integration, addition, and subtraction, including operational amplifier LM741, ideal multiplier AD633 for nonlinear product operations, resistors, capacitors, and absolute value function ($V=\left|z\right|$). State variables x, y, and z in system (1) correspond to the state voltages of the capacitors in three channels. The letter V represents the absolute value of the state variable z. The integration time constant was chosen to be 1 ms in our simulation experiments. In Figure 15, capacitance and resistance values are set as follows: C₁ = C₂ = C₃ = 10 nF, R₁₃ = R₁₄ = R₁₅ = R₁₆ = R₁₇ = 10 K, R₁ = R₂ = R₃ = R₄ = R₅ = R₈ = R₉ = R₁₀ = R₁₉ = R₂₁ = R₂₂ = R₂₃ = R₂₄ = R₂₅ = R₂₆ = R₂₇ = R₂₈ = R₂₉ = 100 K, R₇ = 22.5 K, R₂₀ = 62 K.

The phase diagram of circuit Equation (1) under certain parameters is shown in Figure 16. Limit cycle symmetric attractors with IC = (−1, 0, −1) with green and IC = (1, 0, 1) with blue under parameter b = 1.17 (R₂₀ = 85 K) are shown in Figure 17. Attractors of different topological structures of systems (1) with different (R₂₀) resistance values as shown in Figure 18. It can be seen that the results of MATLAB 2016a simulation and theoretical calculation are completely similar.

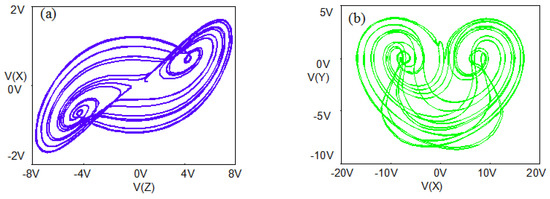
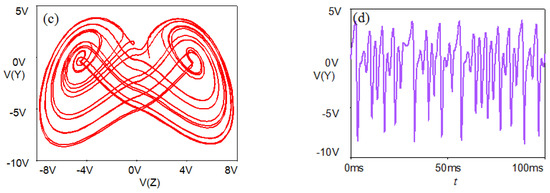
Figure 16. Circuit simulation of system (1) with a = 4.5, b = 1.6 under initial condition IC = (1, 0, 1): (a) x-z plane, (b) x-y plane, (c) y- z plane, (d) y-t.

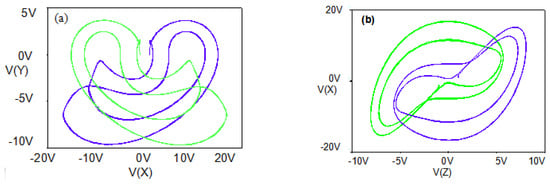
Figure 17. Symmetric attractors of Equation (6) with a = 4.5, b = 1.17 (R₂₀ = 85 K) under initial condition IC1 = (1, 0, 1) (blue), IC 2= (−1, 0, −1) (green), (a) x-y plane, (b) x-z plane.

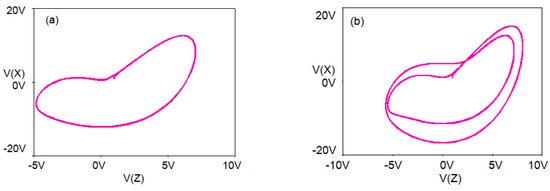
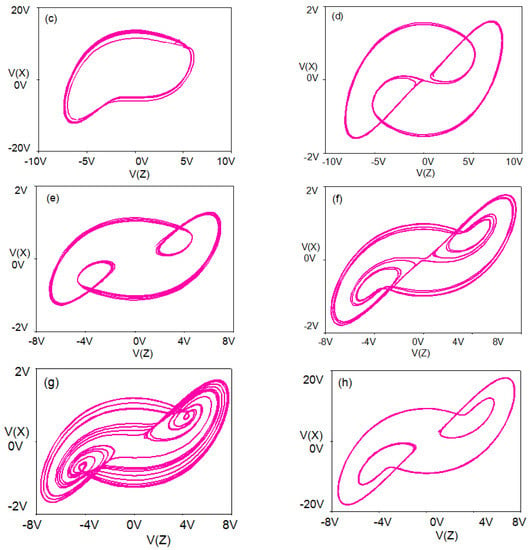
Figure 18. Various phase portraits with different b (R₂₀) on the x-z plane. (a) R₂₀ = 85 K, (b) R₂₀ = 85.6 K, (c) R₂₀ = 98 K, (d) R₂₀ = 75.5 K, (e) R₂₀ = 80 K, (f) R₂₀ = 55 K, (g) R₂₀ = 63.3 K, (h) R₂₀ = 53 K.

6. Concluding Remarks

It was shown that this paper has explored the dynamics of 3-D chaotic systems with symmetry breaking. In this paper, we propose a chaotic system with a symmetric structure, in which there exists an independent parameter which can be used to regulate the amplitude of the system variable. The boosting of attractors in phase space is realized by introducing additional constant terms. The process of attractor aggregation, because of the symmetry breaking, will be presented back and forth between the two broken attractors in the process of parameter bifurcation. In this paper, the complex dynamical phenomena such as attractor symmetry and coexistence bifurcation of the improved system under different parameters and different initial values have been proved. An appropriate electronic analog schematic diagram of the electronic simulation of the system was designed and simulated in PSpice. The simulation results of the circuit experiment are basically consistent with the numerical simulation results of MATLAB, which proves the independence of the observed chaotic behavior from the simulation method.