Image Encryption Based on Local Fractional Derivative Complex Logistic Map

Abstract

Local fractional calculus (fractal calculus) plays a crucial role in applications, especially in computer sciences and engineering. One of these applications appears in the theory of chaos. Therefore, this paper studies the dynamics of a fractal complex logistic map and then employs this map to generate chaotic sequences for a new symmetric image encryption algorithm. Firstly, we derive the fractional complex logistic map and investigate its dynamics by determining its equilibria, geometric properties, and chaotic behavior. Secondly, the fractional chaotic sequences of the proposed map are employed to scramble and alter image pixels to increase resistance to decryption attacks. The output findings indicate that the proposed algorithm based on fractional complex logistic maps could effectively encrypt various kinds of images. Furthermore, it has better security performance than several existing algorithms.

1. Introduction

Advancements in communications and computer technologies facilitate data transmission over internet networks. However, the main issues of data transmission over the internet are the safety of the information from unauthorized users. Recently, image encryption, which aims to keep information secret, has attracted researchers from various fields [1]. In the encryption and decryption processes, security keys are an integral part. The security keys are used to convert the data to nonsense data and vice versa; thus, security keys should be shared to recover the original image [2].

The process of image encryption and decryption is based on mathematical models, which are used to encrypt images using multi-secret keys [3]. Many encryption models have been proposed. The most known image encryption algorithms are based on chaotic encryption [4,5,6]. Over the years, chaos theory has been applied in science and engineering [7,8]. It especially received much attention in the area of image encryption.

T. Gopalakrishnan and S. Ramakrishnan [9] presented an image encryption method given by multiple chaotic maps. The method utilizes various keys for four-round encryption cycles. The method can be employed to encrypt grayscale images and color images. Y. Luo, et al. [10] demonstrated how a grouping of a Baker map and a logistic map can be used as a two-dimensional chaotic system that can encrypt images. Li et al. [11] designed an encryption system that uses key streams depending on the input image. The system employs a chaotic system and hash function to achieve its goals. Nestor Tsafack et al. [12] published a novel image encryption method that is formulated by a new chaotic map with dynamic analysis for the health internet of things.

Fractal calculus [13,14,15] (local fractional calculus) plays a major role in wide fields of science and engineering such as geology, economics, chemical physics, control theory, and fluid flow [16,17]. Fractal calculus has been utilized to generalize chaotic systems, chaotic maps, optimization, operation, and other theories of chaos [18,19,20,21,22]. Chaos is an extensive stimulating occurrence in nonlinear dynamical systems, which has been widely investigated through the recent period. Different researchers have proposed various new chaotic maps that have more security [23,24]. Additionally, cryptographic algorithms utilize common chaotic models such as logistic maps [25]. G. Zhang et al. [26] proposed a new chaotic logistic map called tent delay-sine cascade (TDSCL) for image encryption. The algorithm of this image encryption achieves confusion and diffusion. Y. Zhang et al. [27] proposed a new fractional-order logistic map based on S-boxes. The proposed fractional-order chaotic system provided a larger key space to make the image encryption more efficient against crypto-analytic attacks. The proposed S-boxes were used for the encryption confusion process.

Fractal calculus models are now widely used in image security due to their infinite boundaries property [28]. Sangavi and Thangavel [29] proposed an image encryption algorithm that employs fractal geometry of colored images. This proposed image encryption algorithm has a large key space with complex behavior to produce the confusion behavior. The confusion behavior of the proposed model helps to shuffle the image’s pixel positions to avoid correlation between image pixels.

This paper studies the dynamics of a new fractal complex logistic (FCL) map and then investigates its performance as an essential seed for image encryption algorithms. Firstly, the dynamical characteristics of the FCL, including the equilibrium point, the geometric properties, and chaotic behaviors, are discovered. Simulation analysis proves that the FCL generates wider chaotic regions and ensures the pseudo-randomness of this map. Secondly, to demonstrate the efficiency of the FCL map in real applications, we employ it in an image encryption algorithm. In this algorithm, the fractal complex sequences of the FCL are used to alter the image’s pixels to drastically increase the resistance to decryption attacks. The output findings indicate that our proposed algorithm could effectively encrypt various kinds of images with a high level of security performance.

The rest of this paper is organized as follows: Section 2 introduces the fractal complex logistic map and then defines its structure, fixed points, and geometric properties. Furthermore, this section proposes a new encryption algorithm to demonstrate the efficiency of the map. Section 3 analyzes the performance of the proposed encryption algorithm. Finally, the conclusions are presented in Section 4.

2. Materials and Methods

The proposed mathematical FCL map model that is used for the image encryption algorithm is given as follows [13,14,15]:

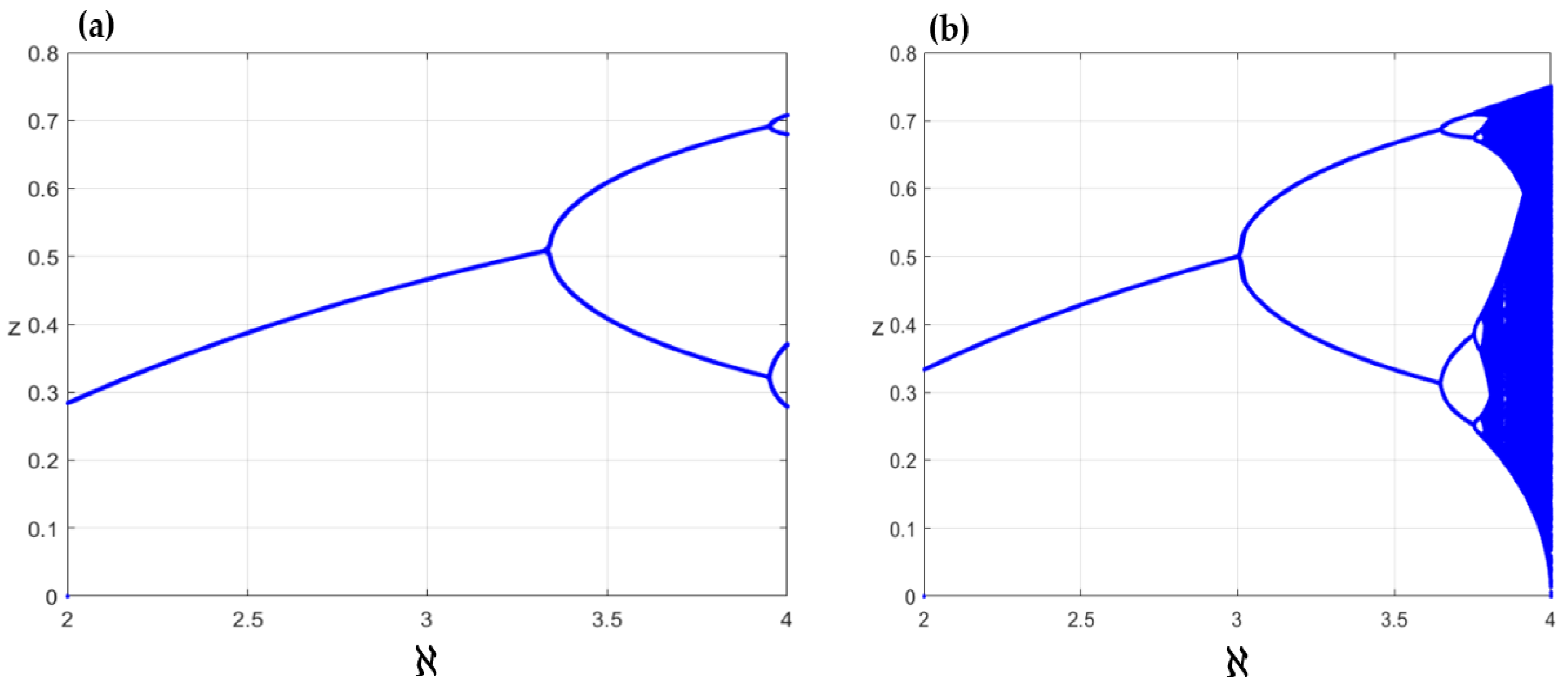
2.1. Fractal Complex Logistic (FCL) Map

Let $C_{\alpha }(a,b),\alpha \in (0,1]$ be a fractal set and let $f\in C_{\alpha }.$ For $ϵ>0$ and $|\chi -{\chi }_0|<\delta$; the limit

$$f^{\left(\alpha \right)}\left(\chi {}_0\right):={\Delta }^{\left(\alpha \right)}f\left(\chi {}_0\right)=li{m}_{\chi \to {\chi }_0}\frac{\mathsf{\Gamma }(\alpha +1)(f\left(\chi \right)-f\left({\chi }_0\right))}{{(\chi -{\chi }_0)}^{\alpha }}$$

(1)

is finite and exists. Here, the gamma function is defined as $\mathsf{\Gamma }\left(z\right)={\int }_0^{\infty }{x}^{(z-1)}{e}^{-x}dx$.

Note that

$${\Delta }^{\left(2\alpha \right)}f\left(\chi {}_0\right)={\Delta }^{\left(\alpha \right)}\left({\Delta }^{\left(\alpha \right)}f\left(\chi {}_0\right)\right),{\Delta }^{\left(3\alpha \right)}f\left(\chi {}_0\right)={\Delta }^{\left(\alpha \right)}\left({\Delta }^{\left(\alpha \right)}\left({\Delta }^{\left(\alpha \right)}f\left(\chi {}_0\right)\right)\right)\dots$$

The 2D-fractal derivative is suggested for a complex function $f\left(z\right)$, where $z=x+iy$ expressing on a fractal set of $C_{\alpha }\left(U\right),U\subset C$ (the complex plane), as follows [30]:

$${\Delta }^{\left(\alpha \right)}f\left(z_0\right)=li{m}_{z\to z_0}\frac{\mathsf{\Gamma }(\alpha +1)(f\left(z\right)-f\left(z_0\right))}{{(z-z_0)}^{\alpha }},z\in U,$$

(2)

where the difference operator is formulated by

$$D^{\alpha }f\left(z_0\right)=\mathsf{\Gamma }(\alpha +1)\left(f\left(z\right)-f\left(z_0\right)\right),z\in U.$$

(3)

For instance, $f\left(z^{\alpha }\right)=z^{\alpha n},$ has a fractal derivative

$${\Delta }^{\left(\alpha \right)}{z}^{n\alpha }=\frac{\mathsf{\Gamma }(\alpha n+1)}{\mathsf{\Gamma }\left(\alpha \right(n-1)+1)}{z}^{(n-1)\alpha }.$$

(4)

Hence, generally, for an analytic function f in a complex domain, we obtain the construction of a fractal derivative, as follows Theorem 9 [30]:

$${\Delta }^{\left(\alpha \right)}f\left(z\right)=\sum _{n=1}^{\infty }\frac{{\mathsf{\Phi }}_n(a,b)}{\mathsf{\Gamma }\left(\alpha \right(n-1)+1)}{z}^{(n-1)\alpha },$$

(5)

where f is located in some fractal set.

The fractal integral can be recognized by the discrete formula

$$J^{\left(\alpha \right)}f\left(z\right)=\frac{1}{\mathsf{\Gamma }(1+\alpha )}\sum _{n=1}^{k}f\left(z_n\right){\left(\delta z_n\right)}^{\alpha },$$

(6)

where $\delta z_n:=z_n-z_{n-1}.$

Proposition 1.

Consider the fractal equation

$${\Delta }^{\left(\alpha \right)}f\left(z\right)=F\left(z_n,f\left(z_n\right)\right).$$

(7)

Then, the solution becomes as follows

$$f\left(z\right)=f\left(z_0\right)+\frac{1}{\mathsf{\Gamma }(1+\alpha )}\sum _{n=1}^{k}F(z_n,f\left(z_n\right)){(z_n-z_{n-1})}^{\alpha }.$$

(8)

2.2. Structure of FCL Map

By using the difference fractal operator, we proceed to define the FCL map. A complex logistic map is given by the structure

$$z_{n+1}=\aleph z_n(1-z_n),z\in C,\aleph \in [0,4],$$

(9)

where ℵ is the control parameter. However, the above discrete complex logistic map can be converted to the continuous type, as follows:

$$z^{•}=\aleph z(1-z),z\in C,\aleph \in [0,4],$$

(10)

By considering, $z=\chi +i\mathsf{{\rm Y}},$ we have the system

$${\chi }^{•}=\aleph \chi -\aleph \left({\chi }^2-{\mathsf{{\rm Y}}}^2\right)$$

(11)

$${\mathsf{{\rm Y}}}^{•}=\aleph \mathsf{{\rm Y}}-2\aleph \chi \mathsf{{\rm Y}}.$$

(12)

By considering the discrete fractal operator, we have the following FCL map,

$$\mathsf{\Gamma }(\alpha +1)\left(z_{n+1}-z_n\right)=\mathsf{\Gamma }(\alpha +1)\left(\aleph z_n(1-z_n)-z_n\right).$$

(13)

Consequently, we obtain the FCL map

$$D^{\alpha }{z}_{n+1}=\mathsf{\Gamma }(\alpha +1)\left(\aleph z_n(1-z_n)-z_n\right),\alpha \in [0,1],$$

(14)

which corresponds to the dynamic system

$$D^{\alpha }\chi =\mathsf{\Gamma }\left(\alpha +1\right)\left(\left(\aleph -1\right)\chi -\aleph \left({\chi }^2-{\mathsf{{\rm Y}}}^2\right)\right)$$

(15)

$$D^{\alpha }\mathsf{{\rm Y}}=\mathsf{\Gamma }(\alpha +1)\left((\aleph -1)\mathsf{{\rm Y}}-2\aleph \chi \mathsf{{\rm Y}}\right).$$

(16)

It is clear that when $\alpha =0,$ System (16) reduces to System (12).

2.3. Properties of FCL Map

2.3.1. Equilibrium Points

Consider the following two equations

$$f_1:\mathsf{\Gamma }\left(\alpha +1\right)\left(\left(\aleph -1\right)\chi -\aleph \left({\chi }^2-{\mathsf{{\rm Y}}}^2\right)\right)=0$$

(17)

$$f_2:\mathsf{\Gamma }(\alpha +1)\left((\aleph -1)\mathsf{{\rm Y}}-2\aleph \chi \mathsf{{\rm Y}}\right)=0.$$

(18)

Now, we have the following set

$$\mathsf{\Xi }:=\left\{{\mathsf{\Sigma }}_0(0,0),{\mathsf{\Sigma }}_1(\frac{\aleph -1}{\aleph },0),{\mathsf{\Sigma }}_2(\frac{\aleph -1}{2\aleph },\frac{+i\left(\aleph -1\right)}{2\aleph }),{\mathsf{\Sigma }}_3\left(\frac{\aleph -1}{2\aleph },\frac{-i\left(\aleph -1\right)}{2\aleph }\right)\right\}.$$

(19)

The Jacobian matrix becomes

$$J_{\mathsf{\Sigma }\left(\chi ,\mathsf{{\rm Y}}\right)}=\left(\begin{array}{c}{\partial }_{\chi }\left(f_1\right){\partial }_{\mathsf{{\rm Y}}}\left(f_1\right)\hfill \\ {\partial }_{\chi }\left(f_2\right){\partial }_{\mathsf{{\rm Y}}}\left(f_2\right)\hfill \end{array}\right)$$

$=\left(\begin{array}{c}\mathsf{\Gamma }\left(\alpha +1\right)\left(\left(\aleph -1\right)-2\chi \right)2\aleph \mathsf{\Gamma }\left(\alpha +1\right)\mathsf{{\rm Y}}\hfill \\ -2\aleph \mathsf{\Gamma }\left(\alpha +1\right)\mathsf{{\rm Y}}\mathsf{\Gamma }\left(\alpha +1\right)(\aleph -1-2\aleph \chi )\hfill \end{array}\right).$

Note that

$$J_{\mathsf{\Sigma }(0,0)}=\left(\begin{array}{c}\mathsf{\Gamma }\left(\alpha +1\right)\left(\aleph -1\right)0\hfill \\ 0\mathsf{\Gamma }(\alpha +1)(\aleph -1)\hfill \end{array}\right),$$

which leads to two equal Eigenvalues ${\lambda }_{1,2}=\mathsf{\Gamma }(\alpha +1)(\aleph -1).$

Now, we obtain the equilibrium points of System (14) by resolving the next system

$$\chi =\mathsf{\Gamma }\left(\alpha +1\right)\left(\left(\aleph -1\right)\chi -\aleph \left({\chi }^2-{\mathsf{{\rm Y}}}^2\right)\right)$$

(20)

$$\mathsf{{\rm Y}}=\mathsf{\Gamma }(\alpha +1)\left((\aleph -1)\mathsf{{\rm Y}}-2\aleph \chi \mathsf{{\rm Y}}\right).$$

(21)

The set of solutions is formulated as follows:

$$\mathsf{\Theta }:=\left\{\left(\frac{-\left(-\aleph b+b+1\right)}{2\aleph },\frac{\sqrt{-\frac{{((\aleph -1)b-1)}^2}{\aleph }}}{2\sqrt{\aleph }}\right),\left(\frac{\left(\aleph -1\right)b-1}{\aleph },0\right),\left(0,0\right)\right\},$$

(22)

where $b:=\mathsf{\Gamma }(\alpha +1).$

2.3.2. Geometric Properties

Consider an FCL map that is defined on a fractal set of the open unit disk := $\{z\in C:|z|<1\}.$ To study the geometric properties of the FCL map, we need the following definition:

Definition 1.

Two analytic functions, $f,g$, are subordinated in U denoted by $f\prec g$ if they occur as the function $\omega \in U,\left|\omega \right|\le \left|z\right|$ satisfying $f\left(z\right)=g\left(\omega \right(z\left)\right)$. They are majorized $(f\ll g)$ if $f\left(z\right)=\omega \left(z\right)g\left(z\right)$, which is equivalent to $|a_n|\le |b_n|$ where $a_n$ and $b_n$ are the coefficients of f and g, respectively.

The following shows the geometric behavior of the logistic map and the FCL map in terms of the limacon map $L_{\wp }\left(z\right)={(1+\wp z)}^2$.

Proposition 2.

Consider the logistic map$F\left(z\right)=\aleph z(1-z)$and its fractal the FCL map$F_{\alpha }=\aleph \mathsf{\Gamma }(1+\alpha )z(1-z),$where$\aleph \ne 0.$

1.

If$|\aleph |\le 2{\wp }^2,0<\wp \le 1/2$then$F\left(z\right)\prec z{L}_{\wp }^{\prime }\left(z\right),0.1<\left|z\right|<0.3;$

2.

If$|\aleph |\le \frac{2{\wp }^2}{\mathsf{\Gamma }(1+\alpha )},0<\wp \le 1/2$then$F_{\alpha }\left(z\right)\prec z{L}_{\wp }^{\prime }\left(z\right),0.1<\left|z\right|<0.3;$

Proof. 

Clearly, we have

$$z{L}_{\wp }^{\prime }\left(z\right)=2\wp z(1+\wp z),z\in U,$$

(23)

which is the starlike analytic function in $U,$ whenever $\wp \in (0,1/2]$ (see [22]). Utilizing the first condition of the theorem, we obtain

$$F\left(z\right)\ll z{L}_{\wp }^{\prime }\left(z\right),\wp \in (0,1/2].$$

(24)

Similarly, the second condition implies that

$$F_{\alpha }\left(z\right)\ll z{L}_{\wp }^{\prime }\left(z\right),\wp \in (0,1/2].$$

(25)

Since $F^{\prime }\left(0\right)\ne 0$ in view of Corollary 2 [31], we obtain the first assertion

$$F\left(z\right)\prec z{L}_{\wp }^{\prime }\left(z\right),\wp \in (0,1/2],\aleph \ne 0.$$

(26)

In the same manner, we obtain the second inequality

$$F_{\alpha }\left(z\right)\prec z{L}_{\wp }^{{}^{\prime }}\left(z\right),\wp \in (0,\frac{1}{2}],\aleph \ne 0,\alpha \in <0,1>.$$

(27)

The geometry of the logistic map and the fractal logistic map is dominated by a starlike function in the open unit disk $U.$ Note that the analytic function $\varphi \left(z\right)$ is called starlike if and only if $R\left(\frac{z\varphi {}^{\prime }\left(z\right)}{\varphi \left(z\right)}\right)>0$. Proposition 2 yields a relation between the derivative of the logistic map (normal and fractal) and the second derivative of the limacon map, which represents to the convexity behavior the map following Theorem 3 [31]:

$$F^{\prime }\left(z\right)\ll {\left(z{L}_{\wp }^{\prime }\left(z\right)\right)}^{\prime },\left|z\right|<3-\sqrt{8};$$

(28)

and

$$F{{}^{\prime }}_{\alpha }\left(z\right)\ll {\left(z{L}_{\wp }^{\prime }\left(z\right)\right)}^{\prime },\left|z\right|<3-\sqrt{8}.$$

(29)

□

2.4. The FCL Map Algorithm

From Proposition 1, we use Equation (14) to obtain

$$J^{\left(\alpha \right)}\left(D^{\alpha }{z}_{n+1}\right)=J^{\left(\alpha \right)}\left(\mathsf{\Gamma }(\alpha +1)\left(\aleph z_n(1-z_n)-z_n\right)\right),$$

(30)

$$z_{n+1}=\left(z_0\right)+\frac{1}{\mathsf{\Gamma }(1+\alpha )}\sum _{n=0}^{k-1}\left(\mathsf{\Gamma }(\alpha +1)\left(\aleph z_n(1-z_n)-z_n\right)\right){(z_{n+1}-z_n)}^{\alpha }$$

(31)

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=z_0+\sum _{n=1}^k\left(\aleph z_{n-1}(1-z_{n-1})-z_{n-1}\right){(z_n-z_{n-1})}^{\alpha },$$

(32)

where $0\le \left|z_0\right|<\left|z_1\right|<\dots <\left|z_n\right|<1.$ It is clear that the map $z_{n+1}$ depends on the previous information, since there is a fractional kernel ${(z_n-z_{n-1})}^{\alpha }.$

Figure 1 illustrates the behavior of the proposed FCL map by depicting its bifurcation diagram. From the bifurcation diagram (Figure 1a), it is obvious that the system with $\alpha =0.5$ shows a period-doubling bifurcation with a complete absence of chaotic behavior for the range of $\aleph \in [2,4]$. Meanwhile, Figure 1b shows that the system with $\alpha =0.6$ enters into chaotic behavior by period-doubling bifurcation with a complete absence of periodic windows, mainly where $\aleph \in (3.7,4]$.

Furthermore, Figure 2 illustrates the randomness of chaotic sequences of the FCL map by using the statistical package NIST SP800-22, which contains 16 empirical tests. Here, a binary sequence has been taken from the FCL map with a length of 1,000,000 bits to employ as the testing input. The sequence can be considered as random when the obtained p-value is larger than 0.01. As can be seen in Figure 2a,b, the chaotic sequence generated by the FCL map can pass all the sub-tests. That means this map is suitable for image encryption algorithms.

2.5. The Encryption Method

The steps for symmetric image encryption by the proposed method are as follows:

1.

Read the input image (I), and convert the values to a 52-bit binary stream using IEEE 754 float standard; then, the digital numbers from 33rd to 40th in each binary stream are used;

2.

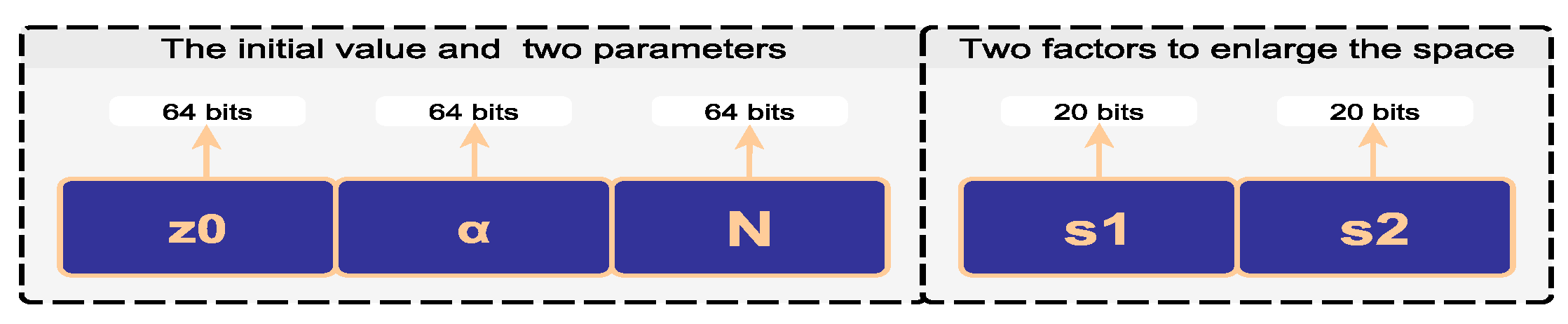
Set the secret key, which is mainly generated from the initial value and control parameters of the FCL map, as illustrated in Figure 3;

3.

Use proposed FCL to generate the chaotic sequences $Z=\{\left|z_1\right|,\left|z_2\right|,|z_3\left|,\dots \dots ,\right|z_n\left|\right\}$. Note that for all $n,0\le \left|z_n\right|<1$;

4.

Start the confusion of the input image by changing the position of pixels by using conditional shift, which stops the algorithm for any shifting cases to make the variable z outside the open unit disk;

5.

Convert the chaotic sequences to binary numbers using IEEE 754 float standard in which each chaotic output produces eight binary numbers;

6.

Start the diffusion of the confusing image to obtain the encrypted image by using the XOR operation between the binary input image and the binary form of chaotic sequence as: I${}_x$(i) = bitxor (Ib(i),(z(i));

7.

Convert I${}_x$ into a two-dimensional encrypted image (Ie);

8.

The previous steps are applied in reverse to decrypt the image.

The bifurcation diagram is used to illustrate the behavior of the proposed chaotic maps through the distribution of iterates z${}_n$ versus the control parameter ℵ. Essentially, the FCL map can be governed by two parameters (z${}_n$ and ℵ), and the map has a random behavior that is represented by an alteration in the values of either or both of the aforementioned parameters (z${}_n$ and ℵ). The key idea of applying the FCL map in image encryption is based on a repetition function in which the previous output value of z${}_{n-1}$ will influence the current value of z_n.

Figure 2. The NIST SP800-22 result: (a,b) represent the statistical sub-tests of the chaotic sequence generated by FCL map with the initial value $z_0=0.1$ and the parameters $\alpha$ = 0.6 and $\aleph =3.72$.

Figure 2. The NIST SP800-22 result: (a,b) represent the statistical sub-tests of the chaotic sequence generated by FCL map with the initial value $z_0=0.1$ and the parameters $\alpha$ = 0.6 and $\aleph =3.72$.

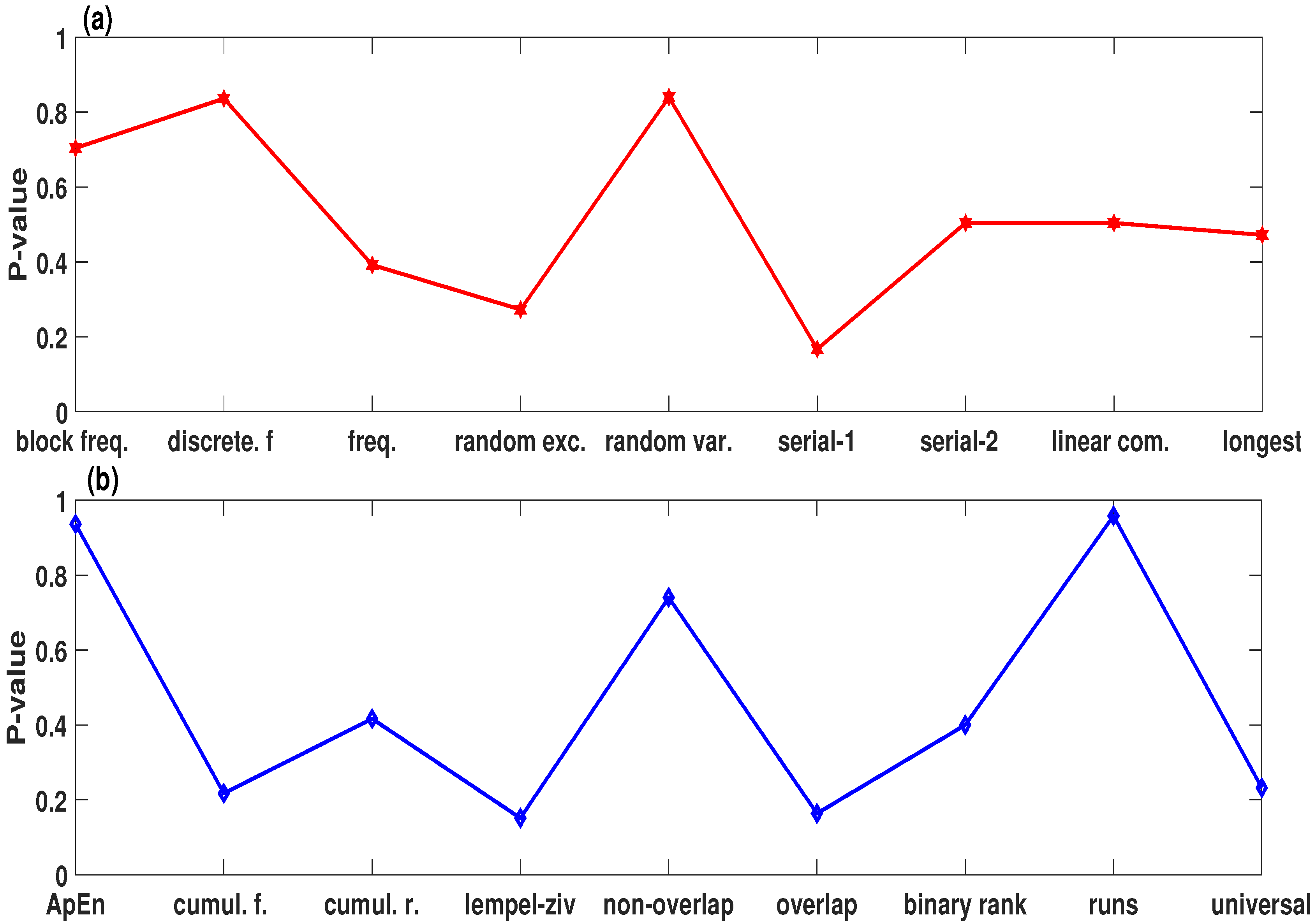
3. Results

Here, the performance of the proposed image encryption model with the initial value $z_0=0.1$ and the parameters $\alpha$ = 0.6 and $\aleph =3.72$ is demonstrated using standard test images, commonly known as Barbara, sketch, handwriting, and Lena, with the size $256\times 256$. We employed statistical analyses to assess the model’s performance. The experiments were undertaken using MATLAB R2021a with Windows 10, 8.00 GB RAM, Intel(R) Core (TM) i7-6700HQ CPU @2.60 GHz.

3.1. Encrypting Different Kinds of Images

To demonstrate the ability of the proposed symmetric image encryption algorithm for ciphering different types of images, Figure 4 depicts the encryption results with uniformly distributed histograms of various kinds of images. The first column depicts the animal sketches, handwriting, and Lena images. The second column plots the histograms of these images. Meanwhile, the third column plots the encryption of the animal sketches, the handwriting, and Lena images, respectively. Finally, the fourth column depicts histograms of the encrypted images. It can be seen from these results that the proposed encryption algorithm can effectively encrypt various kinds of images.

3.2. Information Entropy Analysis

The entropy measures the degree of n predictability of information. The information entropy is calculated for encrypted images to measure the degree of uncertainty; however, any certain degree of predictability will threaten the encryption security [32].

Table 1. Comparison of information entropy between plain and encrypted images.

Images	Plain	Encrypted
Barbara	7.8056	7.9785
Baboon	7.3583	7.9995
Boat	7.1901	7.9865
Lena	7.7481	7.9995
Average	7.5255	7.9910

is an assessment of the data entropy of the plaintext and the encrypted image for the suggested FCL map model.

Table 2. Comparison of data entropy of various encryption procedures utilizing Lena.

Encryption Algorithm	Entropy
Wang and Guo 2014 [33]	7.9977
Liu Lingfeng 2016 [34]	7.9995
Li, Tao 2020 [32]	7.9894
Zhang Fangfanf 2021 [35]	7.9994
Proposed FCL map model	7.9995

illustrates the comparison of information entropy of several algorithms using Lena as a test image. As can be seen, the encrypted image produced by our FCL map algorithm is close to the value of 8, which indicates that the chaotic sequences generated by the proposed FCL map model have complex dynamic behaviors.

3.3. Correlation Analysis

The aim of image encryption algorithms is to decrease the correlation among the image pixels in order to make the prediction of any given pixel from its neighbors more difficult. The correlation between two adjacent pixels can be calculated by Equation (33) [12]:

$$\varrho \left(S,T\right)=\frac{Corr(S,T)}{\sqrt{D\left(S\right)}\sqrt{D\left(T\right)}}$$

(33)

where S, T are pixel values of two adjacent pixel positions and n is the total number of adjacent pixels, where

$$Corr\left(S,T\right)=\frac{1}{n}\sum _{i=1}^n(S_i-E\left(S\right))(T_i-E\left(T\right))$$

(34)

$$D\left(S\right)=\frac{1}{n}\sum _{i=1}^n{(S_i-E\left(S\right))}^2$$

(35)

$$E\left(S\right)=\frac{1}{n}\sum _{i=1}^n{S}_i$$

(36)

Table 3. The correlation between plain and encrypted images. Horizontal (H), vertical (V), and diagonal (D) indicate the correlation directions.

Image		Plain	Encrypted
Barbara	H	0.8135	−0.0006
	V	0.8708	0.0025
	D	0.9294	−0.0315
Baboon	H	0.9371	0.0007
	V	0.9485	0.0006
	D	0.9325	−0.0459
Boat	H	0.9371	0.0045
	V	0.9324	0.0006
	D	0.9342	0.0218
Lena	H	0.9387	0.0045
	V	0.9812	0.0016
	D	0.97261	0.0017
Average	H	0.9066	0.0025
	V	0.93322	0.0013
	D	0.9421	−0.0134

demonstrates the correlation coefficients of the original and encrypted images. The calculated correlation coefficients illustrate that the correlation coefficients of the encrypted images are close to zero, which proves that the FCL map of the proposed model can effectively decrease the correlation among adjacent pixels of the original images.

Taking the average values for testing images as an experimental object, the comparison of correlation between different encryption algorithms in the horizontal (H), vertical (V), and diagonal (D) directions are illustrated in

Table 4. Comparison of the encryption time (second), and the correlation of different encryption algorithms using average values for testing images. Horizontal (H), vertical (V), and diagonal (D) indicate the correlation directions.

Algorithm	Encryption Time (s)		Encrypted
Hua et al. 2015 [36]	0.2338	H	0.0024
		V	−0.0086
		D	0.0402
Tong et al. 2015 [37]	0.1900	H	0.0038
		V	0.0058
		D	0.0133
Liu, Lingfeng 2016 [34]	0.0659	H	0.0021
		V	0.0046
		D	0.0033
Li, Tao 2020 [32]	0.4604	H	0.0033
		V	0.0011
		D	0.0008
Proposed FCL map model	0.0589	H	0.0025
		V	0.0013
		D	−0.0134

.

The encryption time is used to measure the efficiency of the encryption algorithm and it depends on certain parameters such as CPU cycles and memory usage. The image encryption time of the proposed algorithm is the time that it takes to encrypt the input image using proposed algorithm. In this study, the average encryption time of test images was measured using the stopwatch timer MATLAB functions, tic and toc.

The test results of the encryption speeds of different image encryption algorithms are also included in Table 4. Because the source codes of the encryption algorithms illustrated in Table 4 are not publicly available, all encryption times are reported in Table 4 according to what is given by these references. The proposed FCL map model has the fastest encryption speed with the lowest time complexity, so it can be used in real-time image applications such as video stream cyphering.

3.4. Key Sensitivity Analysis

The image encryption algorithm primarily depends on the key sensitivity. Even one bit change to the key combinations can produce a different encrypted image. The proposed FCL map model is proven to be highly sensitive to changes in the encryption key. As shown in Figure 5, the model is sensitive to changes as small as one bit. As a result, if the decryption key is slightly changed, the decryption algorithm will not be able to correctly decrypt the image.

3.5. Differential Attack Analysis

To check the ability of our encryption algorithm to resist differential attack, we use the two metrics: the NPCR and UACI, which are the abbreviations for (Number of Pixel Change Rate) and (Unified Average Changing Intensity), respectively. The NPCR indicates the changed pixel numbers in the cipher image for which only one pixel is changed in the plain image. Meanwhile, the UACI refers to the average value of difference between two cipher images. The NPCR and UACI are given by:

$$NPCR=\frac{{\sum }_{i,j}A(i,j)}{H}\times 100\%$$

(37)

$$UACI=\frac{1}{H}\left[\sum _{i,j}\frac{\left|G1(i,j)-G2(i,j)\right|}{255}\right]\times 100\%$$

(38)

where $A\left(j,j\right)=\left\{\begin{array}{c}1,\left(G1\left(i,j\right)\ne G2\left(i,j\right)\right)\hfill \\ 0,otherwise\hfill \end{array}\right.$, where G1 and G2 are two pixels with the same coordinates and H represents the image size.

Table 5. The NPCR and UACI of the proposed model for the given testing images.

Image	NPCR	UACI
Barbara	0.9967	0.3343
Baboon	0.9966	0.3396
Boat	0.9968	0.3358
Lena	0.99 68	0.3312

shows the NPCR and UACI for the proposed FCL map encryption algorithm. Furthermore, the comparisons of NPCR and UACI for the “Lena” image with other algorithms are presented in

Table 6. Comparison of the NPCR and UACI for the testing image “Lena”.

Algorithm	NPCR	UACI
Liu Lingfeng 2016 [34]	0.9949	0.3156
Li Tao [32]	0.9949	0.3156
Zhang Fangfang 2021 [35]	0.9960	0.3347
Proposed FCL map model	0.9968	0.3312

. From the results shown in Table 5 and Table 6, it is clear that our encryption algorithm has superior or competitive performance in defending from differential attacks (which are also called chosen-plaintext attacks).

3.6. Noise and Data Loss Analysis

Several types of noise and data lose can spoil the encrypted images. Therefore, image encryption algorithms should be able to resist these kinds of noise and data lose. The first and second columns of Figure 6 show the quality results of the recovered image when the encrypted image undergoes Gaussian noise with $5\%$ density, as well as salt and pepper noise with $12\%$ density. It can be observed that, although the encrypted images contain noise, the recovered images have most of the visual information of the original images.

4. Conclusions

This paper studied the dynamics of a new fractal complex logistic (FCL) map, including the equilibrium point, geometric properties, and chaotic behaviors. Furthermore, the randomness of the FCL map was examined by the statistical test NIST SP800-22, which revealed that the map is suitable for cryptographical applications. To further investigate the FCL map, we designed a simple symmetric image encryption algorithm that used the FCL map to generate chaotic sequences. Simulation results demonstrated the efficiency of the encryption algorithm for the encryption of various kinds of images. We also analyzed the information entropy, correlation coefficients between adjacent pixels, the sensitivity of the key, and the resistance to chosen-plaintext attack. The analysis results show that the proposed encryption algorithm has a high-security level and has superiority over several encryption algorithms. That indicates the effectiveness of the FCL map in such applications.