Study of a Viscous ΛWDM Model: Near-Equilibrium Condition, Entropy Production, and Cosmological Constraints
Abstract
1. Introduction
2. Exact Analytical Solution in Eckart’s Theory with CC
3. Near-Equilibrium Condition and Entropy Production
3.1. Near-Equilibrium Condition
3.2. Entropy Production
4. Study of the Exact Solution
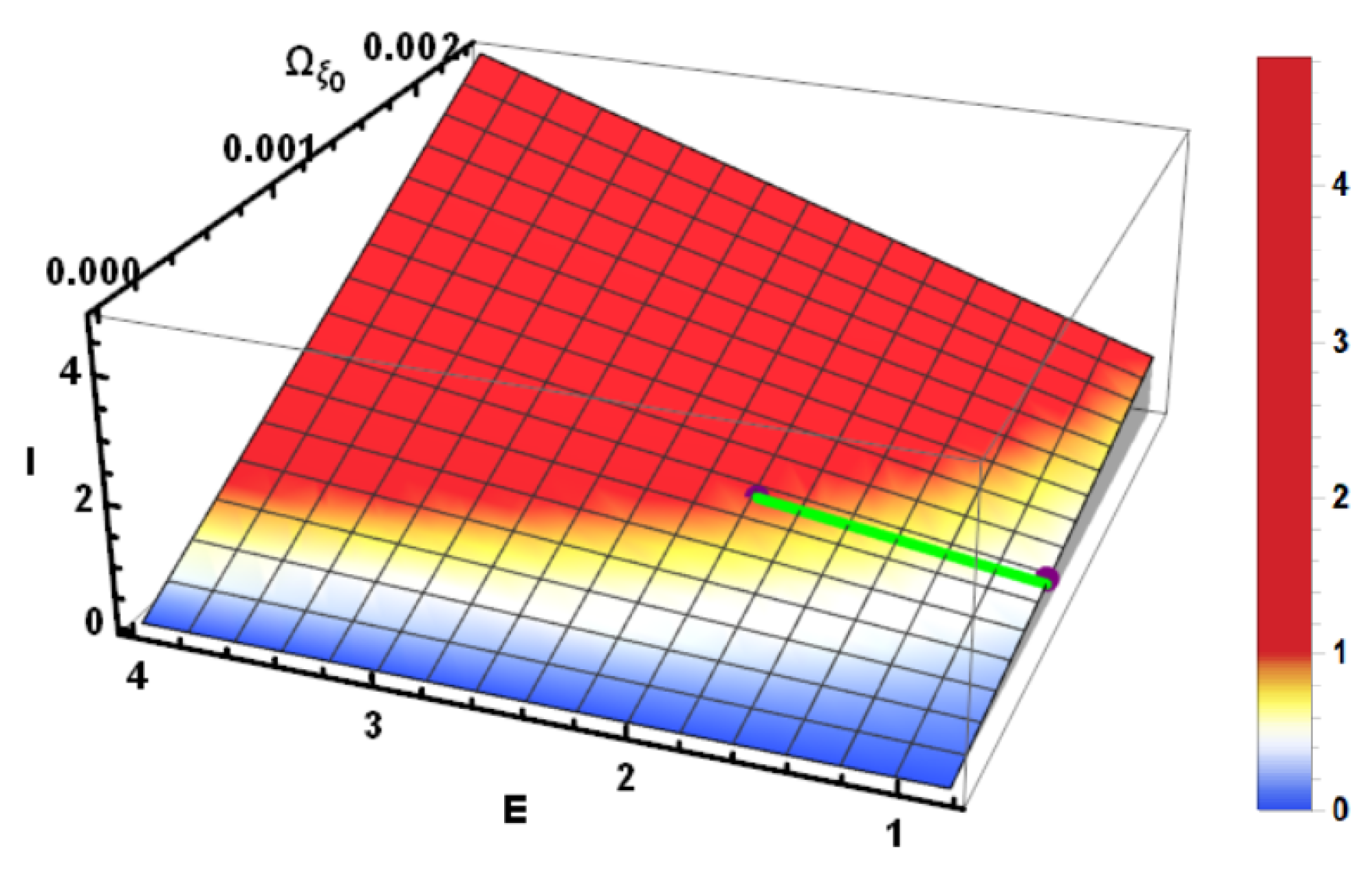
4.1. Near-Equilibrium Condition of the Exact Solution
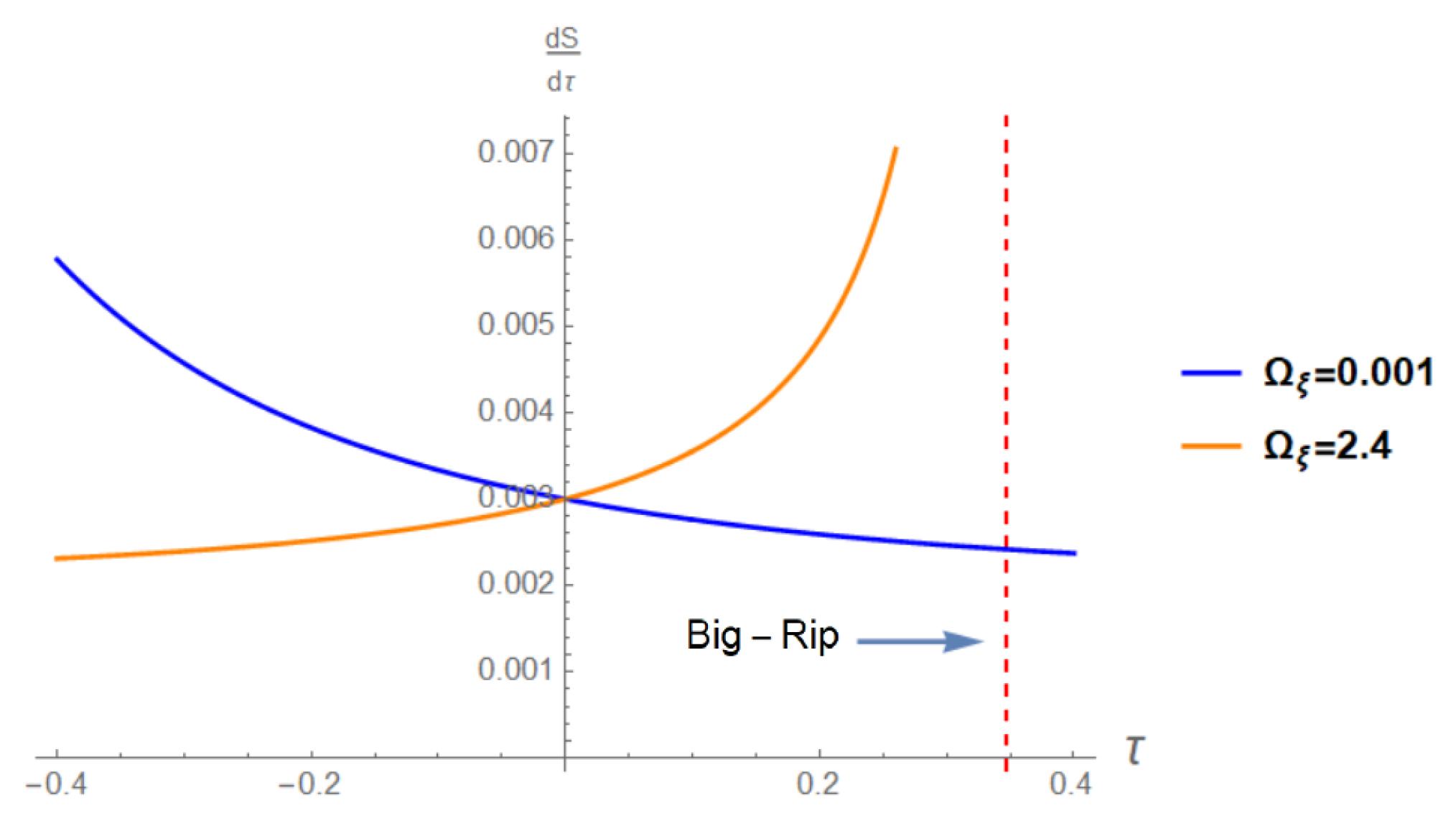
4.2. Entropy Production of the Exact Solution
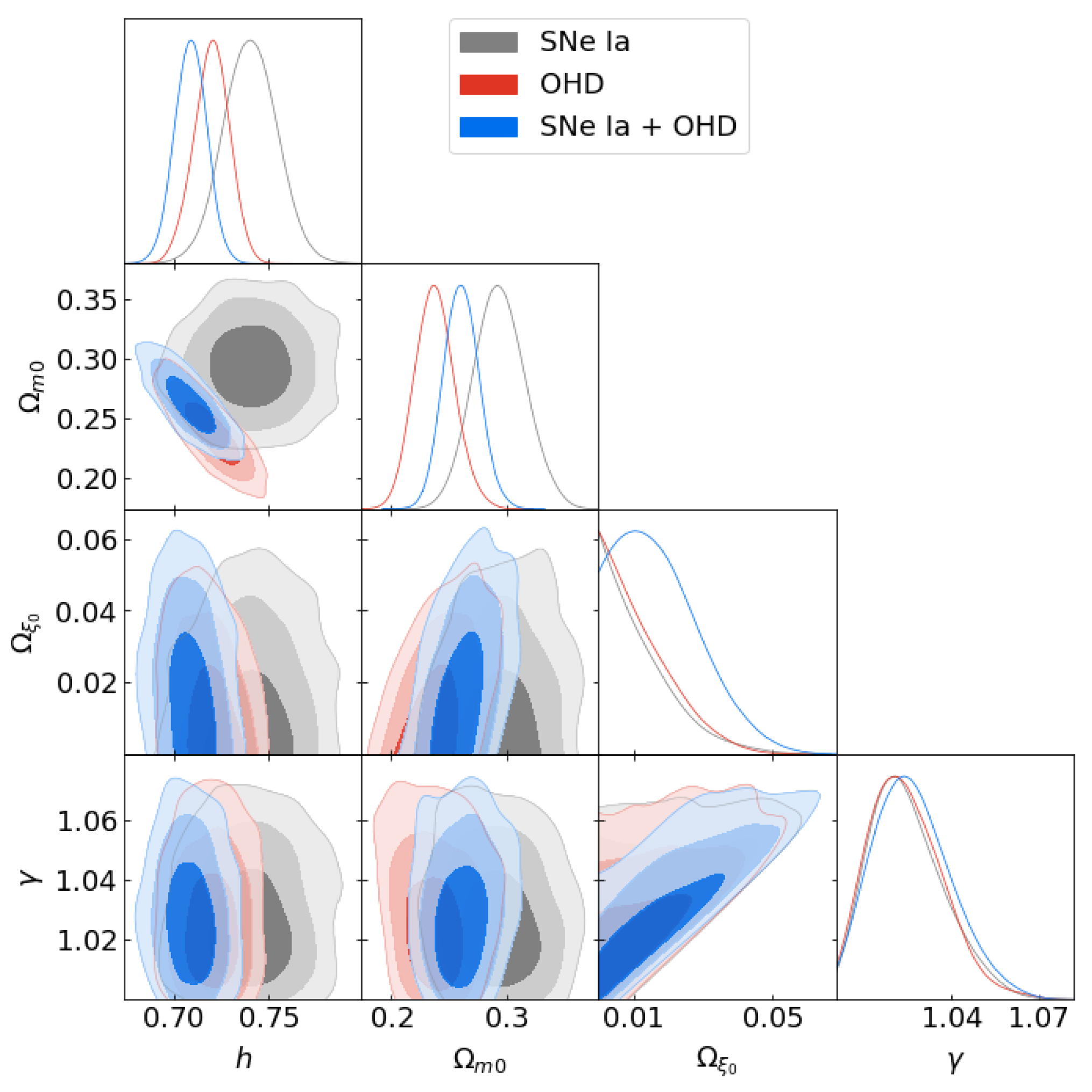
5. Cosmological Constraints
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DM | Dark matter |
| DE | Dark energy |
| CC | Cosmological constant |
| EoS | Equation of state |
References
- Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. arXiv 2020, arXiv:1807.06209. [Google Scholar]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. 2013, 208, 19. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H.; et al. The clustering of galaxies in the completed SDSS-III Baryon OscillationSpectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Cao, S.; Ryan, J.; Ratra, B. Using Pantheon and DES supernova, baryon acoustic oscillation, and Hubble parameter data to constrain the Hubble constant, dark energy dynamics, and spatial curvature. Mon. Not. R. Astron. Soc. 2021, 504, 300–310. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S.M.; Press, W.H.; Turner, E.L. The cosmological constant. Annu. Rev. Astron. Astrophys. 1992, 30, 499–542. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.; Steinhardt, P.J. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Anand, S.; Chaubal, P.; Mazumdar, A.; Mohanty, S. Cosmic viscosity as a remedy for tension between PLANCK and LSS data. J. Cosmol. Astropart. Phys. 2017, 11, 5. [Google Scholar] [CrossRef]
- Raveri, M. Are cosmological data sets consistent with each other within the Λ cold dark matter model? Phys. Rev. D 2016, 93, 043522. [Google Scholar] [CrossRef]
- Bowman, J.D.; Rogers, A.E.E.; Monsalve, R.A.; Mozdzen, T.J.; Mahesh, N. An absorption profile centred at 78 megahertz in the sky-averaged spectrum. Nature 2018, 555, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Cruz, M.; Cruz, N.; Lepe, S. Accelerated and decelerated expansion in a causal dissipative cosmology. Phys. Rev. D 2017, 96, 124020. [Google Scholar] [CrossRef]
- Fabris, J.C.; Goncalves, S.V.B.; de Sa Ribeiro, R. Bulk viscosity driving the acceleration of the Universe. Gen. Relativ. Gravit. 2006, 38, 495–506. [Google Scholar] [CrossRef]
- Li, B.; Barrow, J.D. Does Bulk Viscosity Create a Viable Unified Dark Matter Model? Phys. Rev. D 2009, 79, 103521. [Google Scholar] [CrossRef]
- Hipólito-Ricaldi, W.S.; Velten, H.E.S.; Zimdahl, W. Viscous dark fluid universe. Phys. Rev. D 2010, 82, 063507. [Google Scholar] [CrossRef]
- Avelino, A.; Nucamendi, U. Can a matter-dominated model with constant bulk viscosity drive the accelerated expansion of the universe? J. Cosmol. Astropart. Phys. 2009, 904, 6. [Google Scholar] [CrossRef]
- Avelino, A.; Nucamendi, U. Exploring a matter-dominated model with bulk viscosity to drive the accelerated expansion of the Universe. J. Cosmol. Astropart. Phys. 2010, 1008, 9. [Google Scholar] [CrossRef]
- Sasidharan, A.; Mathew, T.K. Bulk viscous matter and recent acceleration of the Universe. Eur. Phys. J. C 2015, 75, 348. [Google Scholar] [CrossRef]
- Sasidharan, A.; Mathew, T.K. Phase space analysis of bulk viscous matter dominated universe. J. High Energy Phys. 2016, 1606, 138. [Google Scholar] [CrossRef]
- Mohan, N.D.J.; Sasidharan, A.; Mathew, T.K. Bulk viscous matter and recent acceleration of the universe based on causal viscous theory. Eur. Phys. J. C 2017, 77, 849. [Google Scholar] [CrossRef]
- Cruz, N.; González, E.; Palma, G. Exact analytical solution for an Israel–Stewart cosmology. Gen. Relativ. Gravit. 2020, 52, 62. [Google Scholar] [CrossRef]
- Cruz, N.; González, E.; Palma, G. Testing dissipative dark matter in causal thermodynamics. Mod. Phys. Lett. A 2021, 36, 2150032. [Google Scholar] [CrossRef]
- Almada, A.H.; Aspeitia, M.A.G.; Rodríguez-Meza, M.A.; Motta, V. A hybrid model of viscous and Chaplygin gas to tackle the Universe acceleration. arXiv 2021, arXiv:2103.16733. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Inhomogeneous Equation of State of the Universe: Phantom Era, Future Singularity and Crossing the Phantom Barrier. Phys. Rev. D 2005, 72, 023003. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Elizalde, E.; Nojiri, S.; Odintsov, S.D. Observational constraints on dark energy with generalized equations of state. Phys. Rev. D 2006, 73, 043512. [Google Scholar] [CrossRef]
- Herrera-Zamorano, L.; Hernández-Almada, A.; García-Aspeitia, M.A. Constraints and cosmography of CDM in presence of viscosity. Eur. Phys. J. C 2020, 80, 637. [Google Scholar] [CrossRef]
- Elizalde, E.; Khurshudyan, M.; Odintsov, S.D.; Myrzakulov, R. An analysis of the H0 tension problem in a universe with a viscous dark fluid. Phys. Rev. D 2020, 102, 123501. [Google Scholar] [CrossRef]
- Normann, B.D.; Brevik, I.H. Could the Hubble tension be resolved by bulk viscosity? arXiv 2021, arXiv:2107.13533. [Google Scholar]
- Bhatt, J.R.; Mishra, A.K.; Nayak, A.C. Viscous dark matter and 21 cm cosmology. Phys. Rev. D 2019, 100, 063539. [Google Scholar] [CrossRef]
- Foot, R.; Vagnozzi, S. Dissipative hidden sector dark matter. Phys. Rev. D 2015, 91, 023512. [Google Scholar] [CrossRef]
- Foot, R.; Vagnozzi, S. Solving the small-scale structure puzzles with dissipative dark matter. J. Cosmol. Astropart. Phys. 2016, 2016, 13. [Google Scholar] [CrossRef]
- Hofmann, S.; Schwarz, D.J.; Stoecker, H. Damping scales of neutralino cold dark matter. Phys. Rev. D 2001, 64, 083507. [Google Scholar] [CrossRef]
- Schweizer, M.A. Transient and transport coefficients for radiative fluids. Astrophys. J. Part 1 1982, 258, 798–811. [Google Scholar] [CrossRef]
- Udey, N.; Israel, W. General relativistic radiative transfer: The 14-moment approximation. Mon. Not. R. Astron. Soc. 1982, 199, 1137–1147. [Google Scholar] [CrossRef]
- Zimdahl, W. ‘Understanding’ cosmological bulk viscosity. Mon. Not. R. Astron. Soc. 1996, 280, 1239. [Google Scholar] [CrossRef]
- Zimdahl, W.; Pavón, D. Cosmology with adiabatic matter creation. Int. J. Mod. Phys. D 1994, 3, 327–330. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Butterworth-Heinemann: Oxford, UK, 1959; Volume 6. [Google Scholar]
- Blas, D.; Floerchinger, S.; Garny, M.; Tetradis, N.; Wiedemann, U.A. Large scale structure from viscous dark matter. J. Cosmol. Astropart. Phys. 2015, 2015, 49. [Google Scholar] [CrossRef]
- Calogero, S.; Velten, H. Cosmology with matter diffusion. J. Cosmol. Astropart. Phys. 2013, 11, 25. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I. Interacting Diffusive Unified Dark Energy and Dark Matter from Scalar Fields. Eur. Phys. J. C 2017, 77, 396. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.; Haba, Z. Unification of dark energy and dark matter from diffusive cosmology. Phys. Rev. D 2019, 99, 123521, Erratum in: Phys. Rev. D 2020, 101, 049901. [Google Scholar] [CrossRef]
- Weinberg, S.; Dicke, R.H. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1972. [Google Scholar]
- Murphy, G.L. Big-Bang Model Without Singularities. Phys. Rev. D 1973, 8, 4231–4233. [Google Scholar] [CrossRef]
- Padmanabhan, T.; Chitre, S. Viscous universes. Phys. Lett. A 1987, 120, 433. [Google Scholar] [CrossRef]
- Brevik, I.; Gorbunova, O. Dark energy and viscous cosmology. Gen. Relativ. Gravit. 2005, 37, 2039–2045. [Google Scholar] [CrossRef]
- Cruz, N.; González, E.; Lepe, S.; Gómez, D.S.C. Analysing dissipative effects in the ΛCDM model. J. Cosmol. Astropart. Phys. 2018, 12, 17. [Google Scholar] [CrossRef]
- Normann, B.D.; Brevik, I. Characteristic Properties of Two Different Viscous Cosmology Models for the Future Universe. Mod. Phys. Lett. A 2017, 32, 1750026. [Google Scholar] [CrossRef]
- Normann, B.D.; Brevik, I. General Bulk-Viscous Solutions and Estimates of Bulk Viscosity in the Cosmic Fluid. Entropy 2016, 18, 215. [Google Scholar] [CrossRef]
- Brevik, I.; Grøn, Ø.; de Haro, J.; Odintsov, S.D.; Saridakis, E.N. Viscous Cosmology for Early- and Late-Time Universe. Int. J. Mod. Phys. D 2017, 26, 1730024. [Google Scholar] [CrossRef]
- Bode, P.; Ostriker, J.P. Halo formation in warm dark matter models. Astrophys. J. 2001, 556, 93–107. [Google Scholar] [CrossRef]
- de Vega, H.J.; Sanchez, N.G. Warm dark matter in the galaxies:theoretical and observational progresses. Highlights and conclusions of the chalonge meudon workshop 2011. arXiv 2011, arXiv:1109.3187. [Google Scholar]
- Klypin, A.; Kravtsov, A.V.; Valenzuela, O.; Prada, F. Where are the missing Galactic satellites? Astrophys. J. 1999, 522, 82–92. [Google Scholar] [CrossRef]
- Moore, B.; Ghigna, S.; Governato, F.; Lake, G.; Quinn, T.R.; Stadel, J.; Tozzi, P. Dark Matter Substructure within Galactic Halos. Astrophys. J. Lett. 1999, 524, L19–L22. [Google Scholar] [CrossRef]
- Newton, O.; Leo, M.; Cautun, M.; Jenkins, A.; Frenk, C.S. Constraints on the properties of warm dark matter using the satellite galaxies of the Milky Way. J. Cosmol. Astropart. Phys. 2021, 8, 62. [Google Scholar] [CrossRef]
- Viel, M.; Lesgourgues, J.; Haehnelt, M.G.; Matarrese, S.; Riotto, A. Constraining warm dark matter candidates including sterile neutrinos and light gravitinos with WMAP and the Lyman-alpha forest. Phys. Rev. D 2005, 71, 063534. [Google Scholar] [CrossRef]
- Boyarsky, A.; Lesgourgues, J.; Ruchayskiy, O.; Viel, M. Lyman-alpha constraints on warm and on warm-plus-cold dark matter models. J. Cosmol. Astropart. Phys. 2009, 5, 12. [Google Scholar] [CrossRef]
- Asaka, T.; Blanchet, S.; Shaposhnikov, M. The νmsm, dark matter and neutrino masses. Phys. Lett. 2005, B631, 151–156. [Google Scholar] [CrossRef]
- Asaka, T.; Shaposhnikov, M. The νMSM, dark matter and baryon asymmetry of the universe [rapid communication]. Phys. Lett. B 2005, 620, 17–26. [Google Scholar] [CrossRef]
- Dodelson, S.; Widrow, L.M. Sterile-neutrinos as dark matter. Phys. Rev. Lett. 1994, 72, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Fuller, G.M. A new dark matter candidate: Non-thermal sterile neutrinos. Phys. Rev. Lett. 1999, 82, 2832–2835. [Google Scholar] [CrossRef]
- Abazajian, K.; Fuller, G.M.; Patel, M. Sterile neutrino hot, warm, and cold dark matter. Phys. Rev. D 2001, 64, 023501. [Google Scholar] [CrossRef]
- Asaka, T.; Laine, M.; Shaposhnikov, M. Lightest sterile neutrino abundance within the numsm. J. High Energy Phys. 2007, 1, 91. [Google Scholar] [CrossRef]
- Laine, M.; Shaposhnikov, M. Sterile neutrino dark matter as a consequence of νMSM-induced lepton asymmetry. J. Cosmol. Astropart. Phys. 2008, 0806, 031. [Google Scholar] [CrossRef]
- Colombi, S.; Dodelson, S.; Widrow, L.M. Large scale structure tests of warm dark matter. Astrophys. J. 1996, 458, 1. [Google Scholar] [CrossRef]
- Eckart, C. The Thermodynamics of Irreversible Processes. III. Relativistic Theory of the Simple Fluid. Phys. Rev. 1940, 58, 919. [Google Scholar] [CrossRef]
- Israel, W. Nonstationary irreversible thermodynamics: A Causal relativistic theory. Ann. Phys. 1976, 100, 310–331. [Google Scholar] [CrossRef]
- Muller, I. Zum Paradoxon der Warmeleitungstheorie. Z. Phys. 1967, 198, 329–344. [Google Scholar] [CrossRef]
- Israel, W.; Stewart, J.M. Transient relativistic thermodynamics and kinetic theory. Ann. Phys. 1979, 118, 341–372. [Google Scholar] [CrossRef]
- Israel, W.; Stewart, J.M. On Transient Relativistic Thermodynamics and Kinetic Theory. II. R. Soc. Lond. A 1977, 357, 59–75. [Google Scholar]
- Maartens, R. Dissipative cosmology. Class. Quantum Gravity 1995, 12, 1455–1465. [Google Scholar] [CrossRef]
- Hernández-Almada, A. Cosmological test on viscous bulk models using Hubble Parameter measurements and type Ia Supernovae data. Eur. Phys. J. C 2019, 79, 751. [Google Scholar] [CrossRef]
- Wilson, J.R.; Mathews, G.J.; Fuller, G.M. Bulk Viscosity, Decaying Dark Matter, and the Cosmic Acceleration. Phys. Rev. D 2007, 75, 043521. [Google Scholar] [CrossRef]
- Hu, J.; Hu, H. Viscous universe with cosmological constant. Eur. Phys. J. Plus 2020, 135, 718. [Google Scholar] [CrossRef]
- Cataldo, M.; Cruz, N.; Lepe, S. Viscous dark energy and phantom evolution. Phys. Lett. B 2005, 619, 5–10. [Google Scholar] [CrossRef]
- Viel, M.; Becker, G.D.; Bolton, J.S.; Haehnelt, M.G. Warm dark matter as a solution to the small scale crisis: New constraints from high redshift Lyman-α forest data. Phys. Rev. D 2013, 88, 043502. [Google Scholar] [CrossRef]
- Asaka, T.; Shaposhnikov, M.; Kusenko, A. Opening a new window for warm dark matter. Phys. Lett. B 2006, 638, 401–406. [Google Scholar] [CrossRef]
- Avelino, A.; Cruz, N.; Nucamendi, U. Testing the EoS of dark matter with cosmological observations. arXiv 2012, arXiv:1211.4633. [Google Scholar]
- Tamayo, D. Thermodynamics of viscous dark energy. arXiv 2020, arXiv:2006.14153. [Google Scholar]
- Cornejo-Pérez, O.; Belinchón, J.A. Exact solutions of a flat full causal bulk viscous frw cosmological model through factorization. Int. J. Mod. Phys. D 2013, 22, 1350031. [Google Scholar] [CrossRef]
- Cruz, M.; Cruz, N.; Lepe, S. Phantom solution in a non-linear Israel–Stewart theory. Phys. Lett. B 2017, 769, 159. [Google Scholar] [CrossRef]
- Maartens, R. Causal Thermodynamics in Relativity. arXiv 1996, arXiv:astro-ph/9609119. [Google Scholar]
- Hiscock, W.A.; Salmonson, J. Dissipative Boltzmann-Robertson-Walker cosmologies. Phys. Rev. D 1991, 43, 3249–3258. [Google Scholar] [CrossRef]
- Cruz, M.; Lepe, S.; Odintsov, S.D. Thermodynamically allowed phantom cosmology with viscous fluid. Phys. Rev. D 2018, 98, 083515. [Google Scholar] [CrossRef]
- Mohan, N.J.; Krishna, P.; Sasidharan, A.; Mathew, T.K. Dynamical system analysis and thermal evolution of the causal dissipative model. arXiv 2018, arXiv:1807.04041. [Google Scholar]
- Mathew, T.K.; Aswathy, M.B.; Manoj, M. Cosmology and thermodynamics of FLRW universe with bulk viscous stiff fluid. Eur. Phys. J. C 2014, 74, 3188. [Google Scholar] [CrossRef]
- Brevik, I.; Timoshkin, A.V. Thermodynamic aspects of entropic cosmology with viscosity. Int. J. Mod. Phys. D 2021, 30, 2150008. [Google Scholar] [CrossRef]
- Jerin Mohan, N.D.; Mathew, T.K. On the feasibility of truncated Israel-Stewart model in the context of late acceleration. Class. Quantum Gravity 2021, 38, 145016. [Google Scholar] [CrossRef]
- Brevik, I. Viscosity-Induced Crossing of the Phantom Barrier. Entropy 2015, 17, 6318–6328. [Google Scholar] [CrossRef]
- Cruz, N.; González, E.; Jovel, J. Singularities and Soft-Big Bang in a viscous ΛCDM model. Phys. Rev. D 2022, 105, 024047. [Google Scholar] [CrossRef]
- Rebhan, E. ‘Soft bang’ instead of ‘big bang’: Model of an inflationary universe without singularities and with eternal physical past time. Astron. Astrophys. 2000, 353, 1–9. [Google Scholar]
- Novello, M.; Elbaz, E. Soft big bang model induced by nonminimal coupling. Nuovo C. B 1994, 109, 741–746. [Google Scholar] [CrossRef][Green Version]
- McInnes, B. The dS/CFT Correspondence and the Big Smash. J. High Energy Phys. 2002, 0208, 029. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Tsujikawa, S. Properties of singularities in (phantom) dark energy universe. Phys. Rev. D 2005, 71, 063004. [Google Scholar] [CrossRef]
- Bouhmadi-López, M.; Kiefer, C.; Martín-Moruno, P. Phantom singularities and their quantum fate: General relativity and beyond—A CANTATA COST action topic. Gen. Relativ. Gravit. 2019, 51, 135. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Magaña, J.; Amante, M.H.; Garcia-Aspeitia, M.A.; Motta, V. The Cardassian expansion revisited: Constraints from updated Hubble parameter measurements and type Ia supernova data. Mon. Not. R. Astron. Soc. 2018, 476, 1036. [Google Scholar] [CrossRef]
- Goodman, J.; Weare, J. Ensemble samplers with affine invariance. Commun. Appl. Math. Comput. Sci. 2010, 5, 65–80. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Conley, A.; Meierjurgen Farr, W.; Hogg, D.W.; Lang, D.; Marshall, P.; Price-Whelan, A.; Sanders, J.; Zuntz, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Tripp, R. A two-parameter luminosity correction for Type IA supernovae. Astron. Astrophys. 1998, 331, 815. [Google Scholar]
- Kessler, R.; Scolnic, D. Correcting Type Ia Supernova Distances for Selection Biases and Contamination in Photometrically Identified Samples. Astrophys. J. 2017, 836, 56. [Google Scholar] [CrossRef]
- Lazkoz, R.; Nesseris, S.; Perivolaropoulos, L. Exploring cosmological expansion parametrizations with the gold SnIa data set. J. Cosmol. Astropart. Phys. 2005, 2005, 10. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461. [Google Scholar] [CrossRef]
- Brevik, I. Temperature Variation in the Dark Cosmic Fluid in the Late Universe. Mod. Phys. Lett. A 2016, 31, 1650050. [Google Scholar] [CrossRef]
- Mueller, C.M. Cosmological bounds on the equation of state of dark matter. Phys. Rev. D 2005, 71, 047302. [Google Scholar] [CrossRef]
- Kumar, S.; Xu, L. Observational constraints on variable equation of state parameters of dark matter and dark energy after Planck. Phys. Lett. B 2014, 737, 244–247. [Google Scholar] [CrossRef]
- Boyanovsky, D. Sterile Neutrinos as Dark Matter: Alternative Production Mechanisms in the Early Universe. Universe 2021, 7, 264. [Google Scholar] [CrossRef]



| Data | Total Steps | MAF | ||||
|---|---|---|---|---|---|---|
| CDM Model | ||||||
| SNe Ia | 1050 | ⋯ | ⋯ | |||
| OHD | 1000 | ⋯ | ⋯ | |||
| SNe Ia+OHD | 800 | ⋯ | ⋯ | |||
| Viscous WDM Model | ||||||
| SNe Ia | 2700 | |||||
| OHD | 2450 | |||||
| SNe Ia+OHD | 2700 | |||||
| Data | Best-Fit Values | Goodness of Fit | ||||
|---|---|---|---|---|---|---|
| h | BIC | |||||
| CDM Model | ||||||
| SNe Ia | ⋯ | ⋯ | ||||
| OHD | ⋯ | ⋯ | ||||
| SNe Ia+OHD | ⋯ | ⋯ | ||||
| Viscous WDM Model | ||||||
| SNe Ia | ||||||
| OHD | ||||||
| SNe Ia+OHD | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz, N.; González, E.; Jovel, J. Study of a Viscous ΛWDM Model: Near-Equilibrium Condition, Entropy Production, and Cosmological Constraints. Symmetry 2022, 14, 1866. https://doi.org/10.3390/sym14091866
Cruz N, González E, Jovel J. Study of a Viscous ΛWDM Model: Near-Equilibrium Condition, Entropy Production, and Cosmological Constraints. Symmetry. 2022; 14(9):1866. https://doi.org/10.3390/sym14091866
Chicago/Turabian StyleCruz, Norman, Esteban González, and Jose Jovel. 2022. "Study of a Viscous ΛWDM Model: Near-Equilibrium Condition, Entropy Production, and Cosmological Constraints" Symmetry 14, no. 9: 1866. https://doi.org/10.3390/sym14091866
APA StyleCruz, N., González, E., & Jovel, J. (2022). Study of a Viscous ΛWDM Model: Near-Equilibrium Condition, Entropy Production, and Cosmological Constraints. Symmetry, 14(9), 1866. https://doi.org/10.3390/sym14091866







