Sampled-Data Control for a Class of Singular Takagi-Sugeno Fuzzy Systems with Application in Truck-Trailer System

Abstract

In order to solve the admissibility problem for a class of nonlinear singular systems with sampling, nonlinearity, and external disturbances, a sample-data control algorithm based on input delay methodology is proposed in this paper. Firstly, the system is converted to a time-delay system based on Takagi–Sugeno fuzzy models via an input delay approach, with many novel time-delay methods being used to deal with the sampled-data control problem. Secondly, both the upper and lower bounds of the sampling period are considered, which has a wider application scope. Thirdly, to obtain less conservative results, an appropriate Lyapunov–Krasovskii function, which involves several symmetric positive definite matrices, is established, and a relaxation variable is introduced by the method of reciprocally convex inequality. Then the conditions of admissibility are given, and the design method of the sampled-data controller is introduced. Finally, a truck-trailer example and two numerical examples are given to prove that the proposed approaches are valid and applicable.

1. Introduction

Recently, lots of valuable research results have been produced for many types of singular systems, such as uncertain singular time-delay systems [1], switched singular system [2,3], singular neutral system [4], fuzzy singular system [5,6,7], Markov singular system [8] and nonlinear discrete-time system [9], with several approaches being adopted in singular systems, such as the linear matrix inequality (LMI) approach [10], delta operator model [11], extended quadratic Lyapunov approach [12] and so on. For example, in [8], a stochastic integral SMC strategy for a Markov descriptor system with singular perturbations was developed, and an unavailable boundary of the matched perturbations was estimated by the proposed technique. In [11], by establishing the relationship between discrete and delta operator models, the admissibility problem for singular systems was discussed. Reference [12] gave a sufficient criterion for the admissibility of a fuzzy singular system with time delay by using a new integral inequality. The authors of [13] designed an integrated switching function to study the fault detection of a sliding mode controller for the fuzzy singular system. In [14], the problem of an adaptive event triggering the reachable set synthesis for a class of singular systems with time-varying delay was studied. Compared with the static event triggering mechanism, the adaptive event triggering mechanism saves communication resources effectively. In [15], the design of asynchronous fault detection filters for fuzzy singular systems is discussed. A mode-dependent dynamic event triggering scheme is adopted to reduce the communication load.

With the rapid development of digital technology, sampled-data control research has also been highly valued. This control method uses the system’s instantaneous sampling information, which greatly reduces the information transmission. Therefore, it can ensure better performance of the system and reduce the operation cost of the system. Now, the analysis of the control problem for a sampled-data system has received much attention, and considerable research results have been obtained from multi-agent systems [16,17], fuzzy systems [18,19], chaotic systems [20,21,22,23], neural network systems [24,25,26], and so on ([27,28,29,30,31,32,33,34]). For example, in [33], the fuzzy stabilization criterion for a time-delay system was studied by using the memory sampled-data strategy under the background of a cyclic function. It is assumed that the sampling period varies within one interval. In [34], several effective control schemes for complex memristor neural networks based on data quantization were proposed. By considering the limited communication resources and the disturbance of faults to the system, a state quantization controller was designed.

TS fuzzy models play a key role in approximating many complex nonlinear systems with a small error. With the development of fuzzy control theory, sampled-data control has been widely used in fuzzy systems using the TS fuzzy model ([35,36]). In reference [35], a desired sampling-state-feedback controller was designed through the Lyapunov method, which effectively improved the system’s performance. The authors of [36] studied the quantization problem of fuzzy sampled-data systems by an improved input delay method and Wirtinger integral inequality, with the design method of the corresponding quantization controller given. In reference [37], an input-delay method and the constructed Lyapunov–Krasovskii function was improved, with a new criterion given to guarantee the stabilization of a fuzzy system, and the conservatism of the system was also reduced. The authors of [38] further improved the delay-independent Lyapunov function, with the stability of fuzzy sampled-data systems also studied. By combining the interactive-convex-combination method and Wirtinger inequality, less conservative stability results can be obtained. In [39], the dissipative stability for fuzzy systems with sampled data control was studied. To improve the adaptability of the controller, internal and external factors of communication delay and aperiodic sampling modes were considered. In [40], a quantized sampled-data controller for a fuzzy system, under random network attacks, was studied, and a new delay product relaxation condition was introduced, which can obtain relaxation constraints for delayed information. In [41], the aperiodic sampled-data control problem for chaotic systems with TS fuzzy models was discussed. However, the references mentioned above are only applicable to the normal fuzzy system, although a singular system more excellently describes some physical systems (rather than normal systems). Few research findings have reported good handling of the sampled-data problem for nonlinear singular systems. In fact, the research gaps are:

(1)

How to deal with the obtained results to ensure that the system is not only stable but also regular and impulse-free;

(2)

How to construct LKF to obtain less conservative results by adding novel items or introducing new integral inequality;

(3)

How to design sampled-data controllers to ensure that the system is asymptotically admissible.

Therefore, these questions are the motivations of this paper.

In this paper, the sampled-data control problem of singular systems is studied based on TS fuzzy models. Through the input delay method, the system is converted to a time-delay system. Both the lower and upper bounds of the delay are considered. A suitable Lyapunov function is constructed, and the conditions of stability, non-impulsivity, and regularity are given. By introducing convex reciprocal inequality, the conservatism of the results is reduced. Finally, three examples are exploited to prove that the proposed results are effective.

The rest of the paper is organized as follows. The problem formulation is introduced in Section 2. Section 3 introduces the main results. Section 4 gives three examples to validate the effectiveness of the proposed algorithm.

2. Problem Formulation

Consider the nonlinear singular system with TS fuzzy models as follow:

Mode Rule i: IF ${\theta }_1(t)$ is ${\omega }_{i\mathrm{l}}$ and $\cdots$${\theta }_r(t)$ is ${\omega }_{ir}$, THEN

$$\{\begin{array}{l}E\dot{x}(t)=A_{i}x(t)+B_{i}u(t)+B_{wi}w(t),\hspace{1em}i=1,2,\dots r\\ y(t)=C_{i}x(t)\end{array}$$

(1)

where $x(t)\in {ℝ}^n$ is state, $u(t)\in {ℝ}^m$ is the control input, $y(t)\in {ℝ}^p$ is the control output, $w(t)\in L_2\left[0,\infty \right)$ is the disturbance, matrix $E$ is assumed to be singular and the $\mathrm{rank}(E)=r\le n$. $A_i,B_i,C_i,B_{wi}$ are known constant matrices. ${\theta }_1(t),{\theta }_2(t),\dots ,{\theta }_r(t)$ are premise variables, ${\omega }_{ir}$ are the fuzzy sets, and r denotes the number of rules. The overall fuzzy models are inferred as follows:

$$\{\begin{array}{l}E\dot{x}(t)={\displaystyle \sum _{i=1}^r{\mu }_i(\theta (t))\left[A_{i}x(t)+B_{i}u(t)++B_{wi}w(t)\right]}\\ y(t)={\displaystyle \sum _{i=1}^r{\mu }_i(\theta (t))C_{i}x(t)}\end{array}$$

(2)

where:

$$\begin{array}{l}{\mu }_i(\theta (t))=\frac{{\omega }_i(\theta (t))}{{\displaystyle \sum _{i=1}^r{\omega }_i(\theta (t))}}\ge 0\\ {\omega }_i(\theta (t))={\displaystyle \prod _{j=1}^q{\omega }_{ij}({\theta }_j(t))},\hspace{1em}{\displaystyle \sum _{i=1}^r{\mu }_i(\theta (t))}=1,\hspace{1em}{\displaystyle \sum _{i=1}^r{\dot{\mu }}_i(\theta (t))}=0,\\ \theta (t)=\left[{\theta }_1(t),{\theta }_2(t),\dots ,{\theta }_r(t)\right],\end{array}$$

(3)

${\omega }_{ij}({\theta }_j(t))$ represents the membership grade of ${\theta }_j(t)$ in ${\omega }_{ij}$.

The structure of the system is shown in Figure 1.

The state variables are assumed to be sampled at each sampling time

$0=t_0<t_1<\cdots <t_k<\cdots <\underset{k\to \infty }{\lim }{t}_k=+\infty$. Assume the sampling period is

$$d_1\le t_{k+1}-t_k\le d_2,\hspace{1em}\forall k\ge 0,d_2>d_1\ge 0,$$

(4)

where $d_1$ and $d_2$ are the lower and upper bounds of the sampling period, respectively.

According to parallel distributed compensation, the controller’s rules are designed such that:

Mode Rule i: IF ${\theta }_1(t)$ is ${\omega }_{i1}$ and $\cdots$${\theta }_r(t)$ is ${\omega }_{ir}$, THEN

$$u(t)=K_{i}x(t_k),\hspace{1em}{t}_k\le t<t_{k+1},$$

(5)

where K_i is the gain matrix. Then, the overall fuzzy controller is described such that:

$$u(t)={\displaystyle \sum _{j=1}^r{\mu }_j(\theta (t))K_{j}x(t_k)},\hspace{1em}{t}_k\le t<t_{k+1}$$

(6)

By substituting (6) into (2), then we obtain:

$$\{\begin{array}{l}E\dot{x}(t)={\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^r{\mu }_i(\theta (t)){\mu }_j(\theta (t_k))\left[A_{i}x(t)+B_i{K}_{j}x(t_k)+B_{wi}w(t)\right]}}\\ y(t)={\displaystyle \sum _{i=1}^r{\mu }_i(\theta (t))C_{i}x(t)}\end{array}$$

(7)

Remark 1. 

If E = I, then system (7) is simplified to a normal fuzzy system, and the sampled-data control problem is discussed in [42,43,44]. However, in [42], the lower bound of the sampling period is assumed to be zero, which limits its application range and leads to conservatism in the results. In [43], the constant sampling periods are considered, but the variable sampling periods are omitted. In [44], the admissible issue for a sampled-data singular system is discussed. However, this method is only suitable for linear-singular systems. In the paper, the sampled-data control issue for nonlinear-singular systems is discussed, and both the lower and upper bounds of the sampling period are considered. If $d_1=d_2=d$, then the sampling period will become a constant, as it is in [42,43,44]. Therefore, the proposed methods have a wider range of applications than these references.

To obtain the main results, the definitions are stated as follows:

Definition 1. [45]

1.1 

If there exists a constant$s\in ℂ$($ℂ$represents complex field) satisfying$\det \left(sE-A\right)\ne 0$, then the matrix pairs$\left(E,A\right)$are regular;

1.2 

If there exists a scalar function,$V(x)$, which satisfies$V(0)=0,\hspace{1em}V(x)>0$for any non-zero$x(t)$, then the system is stable;

1.3 

If$\mathrm{deg}\left(\det \left(sE-A\right)\right)=\mathrm{rank}(E)$, then the matrix pairs$\left(E,A\right)$are impulse free.

Definition 2. [46]

2.1 

If the pair (E, A) is regular and impulse-free, then the system:

$$E\dot{x}(t)=Ax(t)+Bu(t)$$

(8)

is said to be regular and impulse-free.

2.2 

System (8) is said to be asymptotically admissible if it is regular, impulse-free and asymptotically stable.

The object of this paper is to design the sampled-data controller to satisfy:

(1)

That system (7), with $w(t)=0$, is asymptotically admissible.

(2)

Under a zero condition, the output $y(t)$ satisfies $\left|\right|y(t)|{|}_2\le \gamma ||w(t)|{|}_2$ for all nonzero $w(t)\in L_2\left[0,\infty \right)$, where $\gamma >0$.

Via the input delay approach, we define:

$$\tau (t)=t-t_k,\hspace{1em}{t}_k\le t<t_{k+1}$$

(9)

where $\tau (t)$ is piecewise-linear, which satisfies:

$$\tau (t)\in \left[d_1,d_2\right),\dot{\tau }(t)=1,\hspace{1em}t\ne t_k$$

(10)

Combining (9) and (6) gives:

$$u(t)={\displaystyle \sum _{j=1}^r{\mu }_j(\theta (t))K_{j}x(t-(t-t_k))={\displaystyle \sum _{j=1}^r{\mu }_j(\theta (t))K_{j}x(t-\tau (t))}},\hspace{1em}{t}_k\le t<t_{k+1}$$

(11)

Substituting (11) into (8), system (7) is derived as:

$$\{\begin{array}{l}E\dot{x}(t)={\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^r{\mu }_i(\theta (t)){\mu }_j(\theta (t_k))\left[A_{i}x(t)+B_i{K}_{j}x(t-\tau (t))+B_{wi}w(t)\right]}}\\ y(t)={\displaystyle \sum _{i=1}^r{\mu }_i(\theta (t))C_{i}x(t)}\end{array}$$

(12)

The following lemma will be used.

Lemma 1.

([47]). Given a series of functions, $f_1,f_2,\dots ,f_N:{ℝ}^m\to ℝ$, which have a positive on the set of an open subinterval $D$, and the reciprocal convex combination of $f_i,(i=1,2,\dots ,N)$ on $D$, satisfies:

$$\underset{\{{\alpha }_i|{\alpha }_i>0,{\displaystyle \sum _i{\alpha }_i=1}\}}{\min }{\displaystyle \sum _i\frac{f_i(t)}{{\alpha }_i}={\displaystyle \sum _i{f}_i(t)+\underset{g_{ij}(t)}{\max }}}{\displaystyle \sum _{g_{ij}(t)}{g}_{ij}(t)},$$

(13)

where $g_{ij}(t)$is an arbitrary function and satisfies:

$$\left\{g_{ij}(t):{ℝ}^m\to ℝ,g_{ij}(t)=g_{ji}(t),\left[\begin{array}{cc}{f}_i(t)& g_{ij}(t)\\ g_{ji}(t)& f_i(t)\end{array}\right]\ge 0\right\}$$

3. Main Results

In this section, the admissibility condition for system (11) is given by introducing an appropriate LKF. Then the fuzzy sampled-data controller is designed.

Theorem 1.

For constant delay$d_1,d_2$, system (11) is asymptotically stable when$w(t)=0$if there exist symmetric positive definite matrices$P,R,Q_i,Z_i,i=1,2,3$, such that:

$$E^{T}P=P^{T}E\ge 0,$$

(14)

$$\left[\begin{array}{cc}{Z}_3& R\\ R^T& Z_3\end{array}\right]>0,$$

(15)

$${\Pi }_{ij}=\left[\begin{array}{ccccccc}{\Xi }_{11i}& E^T{Z}_{1}E& P^T{B}_i{K}_j& E^T{Z}_{2}E& d_1{A}_i^T{Z}_1& d_2{A}_i^T{Z}_2& d_{21}{A}_i^T{Z}_3\\ *& {\Xi }_{22}& {\Xi }_{23}& E^{T}RE& 0& 0& 0\\ *& *& {\Xi }_{33}& {\Xi }_{34}& d_1{K}_j^T{B}_i^T{Z}_1& d_1{K}_j^T{B}_i^T{Z}_2& d_{21}{K}_j^T{B}_i^T{Z}_3\\ *& *& *& {\Xi }_{44}& 0& 0& 0\\ *& *& *& *& -Z_1& 0& 0\\ *& *& *& *& *& -Z_2& 0\\ *& *& *& *& *& *& -Z_3\end{array}\right],$$

(16)

where:

$$\begin{array}{l}{\Xi }_{11i}=P^T{A}_i+A_i^{T}P+Q_1+Q_2+Q_3-E^T{Z}_{1}E-E^T{Z}_{2}E\\ {\Xi }_{22}=-Q_1-E^T{Z}_{1}E-E^T{Z}_{3}E\\ {\Xi }_{23}={\Xi }_{34}=E^T{Z}_{3}E-E^{T}RE\\ {\Xi }_{33}=-2E^T{Z}_{3}E+E^{T}RE+E^T{R}^{T}E\\ {\Xi }_{44}=-Q_3-E^T{Z}_{2}E-E^T{Z}_{3}E\\ d_{21}=d_2-d_1\end{array}$$

Proof. 

Firstly, system (11) is proved to be regular and impulse-free. According to (12), it follows that:

$$Q_1+Q_2+Q_3+A_i^{T}P+P^T{A}_i-E^T{Z}_{1}E-E^T{Z}_{2}E<0,$$

(17)

As $Q_1>0,Q_2>0,Q_3>0$, then

$$A_i^{T}P+P^T{A}_i-E^T{Z}_{1}E-E^T{Z}_{2}E<0,$$

(18)

Since $\mathrm{rank}(E)=r\le n$, there are invertible matrices $M\in {ℝ}^{n\times n}$ and $H\in {ℝ}^{n\times n}$, satisfying:

$$\overline{E}=MEH=\left[\begin{array}{cc}{I}_r& 0\\ 0& 0\end{array}\right]$$

(19)

and:

$${\overline{A}}_i=M{A}_{i}H=\left[\begin{array}{cc}{A}_{11i}& A_{12i}\\ A_{21i}& A_{22i}\end{array}\right],\hspace{1em}\overline{P}=M^{-T}PH=\left[\begin{array}{cc}{P}_{11}& P_{12}\\ P_{21}& P_{22}\end{array}\right]$$

(20)

which means:

$$\overline{P}=\left[\begin{array}{cc}{\overline{P}}_{11}& 0\\ {\overline{P}}_{21}& {\overline{P}}_{22}\end{array}\right],{\overline{P}}_{11}^T={\overline{P}}_{11}>0$$

(21)

pre-multiply and post-multiply $H^T$ and $H$ with ${\Xi }_{11i}<0$, to then give:

$$A_{22i}^T{P}_{22}+P_{22}^T{A}_{22i}<0$$

(22)

From (21), it implies that $A_{22i}$ is non-singular and the pair $\left(E,A_i\right)$ are regular and impulse-free. According to Definition 1, system (11) is regular and impulse-free.

Then, the asymptotical stability of system (11) is proved. Consider the following LKF:

$$V(t)=V_1(t)+V_2(t)+V_3(t)$$

(23)

$$\begin{array}{l}{V}_1(t)=x{(t)}^T{E}^{T}Px(t)\\ V_2(t)={\displaystyle {\int }_{t-d_1}^{t}x{(s)}^T{Q}_{1}x(s)ds}+{\displaystyle {\int }_{t-\tau (t)}^{t}x{(s)}^T{Q}_{2}x(s)ds}+{\displaystyle {\int }_{t-d_2}^{t}x{(s)}^T{Q}_{3}x(s)ds}\\ V_3(t)=d_1{\displaystyle {\int }_{-d_1}^0{\displaystyle {\int }_{t+\theta }^t{\dot{x}}^T(s)E^T{Z}_{1}E\dot{x}(s)dsd\theta }}+d_2{\displaystyle {\int }_{-d_2}^0{\displaystyle {\int }_{t+\theta }^t{\dot{x}}^T(s)E^T{Z}_{2}E\dot{x}(s)dsd\theta }}\\ \hspace{1em}\hspace{1em}+d_{21}{\displaystyle {\int }_{-d_2}^{-d_1}{\displaystyle {\int }_{t+\theta }^t{\dot{x}}^T(s)E^T{Z}_{3}E\dot{x}(s)dsd\theta }}\end{array}$$

Calculate the derivative of $V(t)$ to obtain:

$$\begin{array}{l}{\dot{V}}_1(t)=2x{(t)}^T{E}^{T}P\dot{x}(t)\\ {\dot{V}}_2(t)=x{(t)}^T{Q}_{1}x(t)-x{(t-d_1)}^T{Q}_{1}x(t-d_1)+x{(t)}^T{Q}_{2}x(t)\\ \hspace{1em}\hspace{1em}+x{(t)}^T{Q}_{3}x(t)-x{(t-d_2)}^T{Q}_{3}x(t-d_2)\\ {\dot{V}}_3(t)=d_1^2\dot{x}{(t)}^T{E}^T{Z}_{1}Ex(t)+d_2^2\dot{x}{(t)}^T{E}^T{Z}_{2}E\dot{x}(t)+d_{21}^2\dot{x}{(t)}^T{E}^T{Z}_{3}E\dot{x}(t)-\\ \hspace{1em}\hspace{1em}{d}_1{\displaystyle {\int }_{t-d_1}^t{\dot{x}}^T(s)E^T{Z}_{1}E\dot{x}(s)ds}-d_2{\displaystyle {\int }_{t-d_2}^t{\dot{x}}^T(s)E^T{Z}_{2}E\dot{x}(s)ds}\\ \hspace{1em}\hspace{1em}-d_{21}{\displaystyle {\int }_{t-d_2}^{t-d_1}{\dot{x}}^T(s)E^T{Z}_{3}E\dot{x}(s)ds}\end{array}$$

(24)

Using Jensen inequality, this yields:

$$\begin{array}{l}-d_1{\displaystyle {\int }_{t-d_1}^t{\dot{x}}^T(s)E^T{Z}_{1}E\dot{x}(s)ds}\le -{\left[x(t)-x(t-d_1)\right]}^T{E}^T{Z}_{1}E\left[x(t)-x(t-d_1)\right],\\ -d_2{\displaystyle {\int }_{t-d_2}^t{\dot{x}}^T(s)E^T{Z}_{2}E\dot{x}(s)ds}\le -{\left[x(t)-x(t-d_2)\right]}^T{E}^T{Z}_{2}E\left[x(t)-x(t-d_2)\right],\end{array}$$

(25)

and:

$$\begin{array}{l}-d_{21}{\displaystyle {\int }_{t-d_2}^{t-d_1}{\dot{x}}^T(s)E^T{Z}_{3}E\dot{x}(s)ds}\\ =-d_{21}{\displaystyle {\int }_{t-d_2}^{t-\tau (t)}{\dot{x}}^T(s)E^T{Z}_{3}E\dot{x}(s)ds}-d_{21}{\displaystyle {\int }_{t-\tau (t)}^{t-d_1}{\dot{x}}^T(s)E^T{Z}_{3}E\dot{x}(s)ds}\\ \le -\frac{d_{21}}{\tau (t)-d_1}{\left[x(t-d_1)-x(t-\tau (t))\right]}^T{E}^T{Z}_{3}E\left[x(t-d_1)-x(t-\tau (t))\right]\\ -\frac{d_{21}}{d_2-\tau (t)}{\left[x(t-\tau (t))-x(t-d_2)\right]}^T{E}^T{Z}_{3}E\left[x(t-\tau (t))-x(t-d_2)\right]\end{array}$$

(26)

From (15), one calculates:

$$\begin{array}{l}{\left[\begin{array}{c}\sqrt{\frac{d_2-d(t)}{\tau (t)-d_1}}\left(x(t-d_1)-x(t-\tau (t))\right)E\\ -\sqrt{\frac{d(t)-d_1}{d_2-\tau (t)}}\left(x(t-\tau (t))-x(t-d_2)\right)E\end{array}\right]}^T\left[\begin{array}{cc}{Z}_3& R\\ R^T& Z_3\end{array}\right]\\ \left[\begin{array}{c}\sqrt{\frac{d_2-\tau (t)}{\tau (t)-d_1}}\left(x(t-d_1)-x(t-\tau (t))\right)E\\ -\sqrt{\frac{\tau (t)-d_1}{d_2-\tau (t)}}\left(x(t-\tau (t))-x(t-d_2)\right)E\end{array}\right]\ge 0,\end{array}$$

(27)

By Lemma 1, it can be obtained from (26) and (27) that:

$$\begin{array}{l}-d_{21}{\displaystyle {\int }_{t-d_2}^{t-d_1}{\dot{x}}^T(s)E^T{Z}_{3}E\dot{x}(s)ds}\\ \le -{\left[\begin{array}{c}x(t-d_1)-x(t-\tau (t))\\ x(t-\tau (t))-x(t-d_2)\end{array}\right]}^T\left[\begin{array}{cc}{E}^T{Z}_{3}E& E^{T}RE\\ *& E^T{Z}_{3}E\end{array}\right]\left[\begin{array}{c}x(t-d_1)-x(t-\tau (t))\\ x(t-\tau (t))-x(t-d_2)\end{array}\right]\\ =-{\vartheta }^T(t)\left[\begin{array}{ccc}{E}^T{Z}_{3}E& -E^T{Z}_{3}E+E^{T}RE& -E^{T}RE\\ *& 2E^T{Z}_{3}E-E^T\left(R^T+R\right)E& -E^T{Z}_{3}E+E^{T}RE\\ *& *& E^T{Z}_{3}E\end{array}\right]\vartheta (t)\end{array}$$

(28)

where:

$$\vartheta (t)={\left[\begin{array}{ccc}{x}^T(t-d_1)& x^T(t-\tau (t))& x^T(t-d_2)\end{array}\right]}^T$$

Combining (28) with (24), such that:

$$\begin{array}{l}\dot{V}(t)\le {\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^r{\mu }_i(z(t)){\mu }_j(z(t)){\varsigma }^T(t)({\Phi }_{ij}+}}\\ {\left[\begin{array}{cccc}{A}_i& 0& B_i{K}_j& 0\end{array}\right]}^T\left(d_1^2{Z}_1+d_2^2{Z}_2+d_{21}^2{Z}_3\right)\left[\begin{array}{cccc}{A}_i& 0& B_i{K}_j& 0\end{array}\right])\varsigma (t)\end{array}$$

(29)

where:

$$\begin{array}{l}{\Phi }_{ij}=\left[\begin{array}{cccc}{\Xi }_{11i}& E^T{Z}_{1}E& P^T{B}_i{K}_j& E^T{Z}_{2}E\\ *& {\Xi }_{22}& {\Xi }_{23}& E^{T}RE\\ *& *& {\Xi }_{33}& {\Xi }_{34}\\ *& *& *& {\Xi }_{44}\end{array}\right],\\ \zeta (t)={\left[\begin{array}{cccc}{x}^T(t)& x^T(t-d_1)& x^T(t-\tau (t))& x^T(t-d_2)\end{array}\right]}^T.\end{array}$$

Following Schur complement, (27) guarantees that:

$${\Phi }_{ij}+{\left[\begin{array}{cccc}{A}_i& 0& B_i{K}_j& 0\end{array}\right]}^T\left(d_1^2{Z}_1+d_2^2{Z}_2+d_{21}^2{Z}_3\right)\left[\begin{array}{cccc}{A}_i& 0& B_i{K}_j& 0\end{array}\right]<0$$

(30)

which implies that $\dot{V}(t)<-\sigma {\Vert x(t)\Vert }^2$ when $x(t)\ne 0,\sigma >0$. Thus, system (11) is asymptotically stable with $w(t)=0$.

Then, according to Theorem 2, system (11) is proved to satisfy the $H_{\infty }$ performance under external disturbances. □

Theorem 2.

For constant delay$d_1,d_2,\gamma$, system (11) is asymptotically stable with$H_{\infty }$performance$\gamma$if there exists symmetric positive definite matrices$P,R,Q_i,Z_i,i=1,2,3$, such that:

$$E^{T}P=P^{T}E\ge 0,$$

(31)

$$\left[\begin{array}{cc}{Z}_3& R\\ R^T& Z_3\end{array}\right]>0,$$

(32)

$${\Pi }_{ij}=\left[\begin{array}{cccccccc}{\Xi }_{11i}& E^T{Z}_{1}E& P^T{B}_i{K}_j& E^T{Z}_{2}E& P^T{B}_{wi}& d_1{A}_i^T{Z}_1& d_2{A}_i^T{Z}_2& d_{21}{A}_i^T{Z}_3\\ *& {\Xi }_{22}& {\Xi }_{23}& E^{T}RE& 0& 0& 0& 0\\ *& *& {\Xi }_{33}& {\Xi }_{34}& 0& d_1{K}_j^T{B}_i^T{Z}_1& K_j^T{B}_i^T{Z}_2& K_j^T{B}_i^T{Z}_3\\ *& *& *& {\Xi }_{44}& 0& 0& 0& 0\\ *& *& *& *& -{\gamma }^{2}I& d_1{B}_{wi}^T{Z}_1& d_2{B}_{wi}^T{Z}_2& d_{21}{B}_{wi}^T{Z}_3\\ *& *& *& *& *& -Z_1& 0& 0\\ *& *& *& *& *& *& -Z_2& 0\\ *& *& *& *& *& *& *& -Z_3\end{array}\right]$$

(33)

where:

$$\begin{array}{l}{\Xi }_{11i}=P^T{A}_i+A_i^{T}P+Q_1+Q_2+Q_3-E^T{Z}_{1}E-E^T{Z}_{2}E+C_i^T{C}_i\\ {\Xi }_{22}=-Q_1-E^T{Z}_{1}E-E^T{Z}_{3}E\\ {\Xi }_{23}={\Xi }_{34}=E^T{Z}_{3}E-E^{T}RE\\ {\Xi }_{33}=-2E^T{Z}_{3}E+E^{T}RE+E^T{R}^{T}E\\ {\Xi }_{44}=-Q_3-E^T{Z}_{2}E-E^T{Z}_{3}E\\ d_{21}=d_2-d_1\end{array}$$

Proof. 

The following $H_{\infty }$ performance index is defined as:

$$J_{zw}={\displaystyle {\int }_0^{\infty }\left[y^T(s)y(s)-{\gamma }^2{w}^T(s)w(s)\right]ds},\hspace{1em}\gamma >0$$

(34)

then:

$$\begin{array}{l}{y}^T(t)y(t)-{\gamma }^2{w}^T(t)w(t)+\dot{V}(t)\\ \le {\displaystyle \sum _{i=1}^r{\displaystyle \sum _{j=1}^r{\mu }_i(z(t)){\mu }_j(z(t)){\zeta }^T(t)({\Theta }_{ij}+{\left[\begin{array}{ccccc}{C}_i& 0& 0& 0& 0\end{array}\right]}^T\left[\begin{array}{ccccc}{C}_i& 0& 0& 0& 0\end{array}\right]+}}\\ {\left[\begin{array}{ccccc}{A}_i& 0& B_i{K}_j& 0& B_{wi}\end{array}\right]}^T\left(d_1^2{Z}_1+d_2^2{Z}_2+d_{21}^2{Z}_3\right)\left[\begin{array}{ccccc}{A}_i& 0& B_i{K}_j& 0& B_{wi}\end{array}\right])\zeta (t)\end{array}$$

(35)

where:

$$\zeta (t)={\left[\begin{array}{ccccc}{x}^T(t)& x^T(t-d_1)& x^T(t-\tau (t))& x^T(t-d_2)& w^T(t)\end{array}\right]}^T$$

$${\Theta }_{ij}=\left[\begin{array}{ccccc}{\Xi }_{11i}& E^T{Z}_{1}E& P^T{B}_i{K}_j& E^T{Z}_{2}E& P{B}_{wi}\\ *& {\Xi }_{22}& {\Xi }_{23}& E^{T}RE& 0\\ *& *& {\Xi }_{33}& {\Xi }_{34}& 0\\ *& *& *& {\Xi }_{44}& 0\\ *& *& *& *& -{\gamma }^{2}I\end{array}\right]$$

(36)

By Schur complement, (33) guarantees that:

$$\begin{array}{l}{\Theta }_{ij}+{\left[\begin{array}{ccccc}{C}_i& 0& 0& 0& 0\end{array}\right]}^T\left[\begin{array}{ccccc}{C}_i& 0& 0& 0& 0\end{array}\right]+{\left[\begin{array}{ccccc}{A}_i& 0& B_i{K}_j& 0& B_{wi}\end{array}\right]}^T\\ \left(d_1^2{Z}_1+d_2^2{Z}_2+d_{21}^2{Z}_3\right)\left[\begin{array}{ccccc}{A}_i& 0& B_i{K}_j& 0& B_{wi}\end{array}\right]<0\end{array}$$

(37)

From (37), one obtains:

$$y^T(t)y(t)-{\gamma }^2{w}^T(t)w(t)+\dot{V}(t)<0$$

(38)

Under zero initial conditions, one obtains $V(0)=0$, $V(\infty )\ge 0$. From (34), it can be calculated that $\left|\right|y(t)|{|}_2\le \gamma ||w(t)|{|}_2$ for all non-zero $w(t)\in L_2\left[0,\infty \right)$. This completes the proof. □

Remark 2. 

Compared with [48,49], a relaxed defining technique is adopted to estimate cross-product terms like, $-d_{21}{\displaystyle {\int }_{t-d_2}^{t-d_1}{\dot{x}}^T\left(s\right)E^T{Z}_{3}E\dot{x}\left(s\right)ds}$which may lead to conservativeness in the results. In the paper, the convex combination techniques combined with Jensen inequality are used to handle the items. Moreover, a free matrix, R, is considered in (27) to handle the items:

$$\begin{array}{l}\frac{d_{21}}{d_2-\tau (t)}{\left(x(t-\tau (t))-x(t-d_2)\right)}^T{E}^T{Z}_{3}E\left(x(t-\tau (t))-x(t-d_2)\right),\\ \frac{d_{21}}{\tau (t)-d_1}{\left(x(t-d_1)-x(t-\tau (t)\right)}^T{E}^T{Z}_{3}E\left(x(t-d_1)-x(t-\tau (t)\right).\end{array}$$

which are ignored in [48,49]. Therefore, the conservatism of the system is further reduced.

Furthermore, the design methods of the fuzzy sampled-data controllers are introduced by the following theorem.

Theorem 3.

For scales$d_1,d_2,\gamma$, system (11) is asymptotically admissible with$H_{\infty }$performance$\gamma$if there exist symmetric positive definite matrices$P,R,Q_i,Z_i,i=1,2,3$satisfying:

$$E^{T}P=P^{T}E\ge 0,$$

(39)

$$\left[\begin{array}{cc}{\overline{Z}}_3& \overline{R}\\ {\overline{R}}^T& {\overline{Z}}_3\end{array}\right]>0,$$

(40)

$${\Pi }_{ij}=\left[\begin{array}{cccccccc}{\Xi }_{11i}& E^T{\overline{Z}}_{1}E& B_i{\overline{K}}_j& E^T{\overline{Z}}_{2}E& B_{wi}& d_1\overline{P}{A}_i^T{\overline{Z}}_1& d_2\overline{P}{A}_i^T{\overline{Z}}_2& d_{21}\overline{P}{A}_i^T{\overline{Z}}_3\\ *& {\Xi }_{22}& {\Xi }_{23}& E^T\overline{R}E& 0& 0& 0& 0\\ *& *& {\Xi }_{33}& {\Xi }_{34}& 0& d_1{\overline{K}}_j^T{\overline{B}}_i^T{\overline{Z}}_1& {\overline{K}}_j^T{\overline{B}}_i^T{\overline{Z}}_2& {\overline{K}}_j^T{\overline{B}}_i^T{\overline{Z}}_3\\ *& *& *& {\Xi }_{44}& 0& 0& 0& 0\\ *& *& *& *& -{\gamma }^{2}I& d_1\overline{P}{B}_{wi}^T{Z}_1& d_2\overline{P}{B}_{wi}^T{\overline{Z}}_2& d_{21}\overline{P}{B}_{wi}^T{\overline{Z}}_3\\ *& *& *& *& *& -{\overline{Z}}_1& 0& 0\\ *& *& *& *& *& *& -{\overline{Z}}_2& 0\\ *& *& *& *& *& *& *& -{\overline{Z}}_3\end{array}\right],$$

(41)

where:

$$\begin{array}{l}{\overline{\Xi }}_{11i}=A_i\overline{P}+\overline{P}{A}_i^T+{\overline{Q}}_1+{\overline{Q}}_2+{\overline{Q}}_3-E^T{\overline{Z}}_{1}E-E^T{\overline{Z}}_{2}E+C_i^T{C}_i\\ {\overline{\Xi }}_{22}=-{\overline{Q}}_1-E^T{\overline{Z}}_{1}E-E^T{\overline{Z}}_{3}E\\ {\overline{\Xi }}_{23}=E^T{\overline{Z}}_{3}E-E^T\overline{R}E\\ {\Xi }_{33}=-2E^T{\overline{Z}}_{3}E+E^T\overline{R}E+E^T{\overline{R}}^{T}E\\ {\overline{\Xi }}_{34}=E^T{\overline{Z}}_{3}E-E^T\overline{R}E\\ {\Xi }_{44}=-{\overline{Q}}_3-E^T{\overline{Z}}_{2}E-E^T{\overline{Z}}_{3}E\\ d_{21}=d_2-d_1\end{array}$$

The fuzzy controller is derived, such that:

$$K_j={\overline{K}}_j{\overline{P}}^{-1}$$

(42)

Proof. 

By noticing that $-\overline{P}{\overline{Z}}^{-1}\overline{P}\le \overline{Z}-2\overline{P}$, let $\eta =diag\left\{P^{-T},P^{-T},P^{-T},P^{-T},I,I,I,I\right\}$. Defining

$$\begin{array}{l}\overline{P}=P^{-1},\hspace{0.17em}{\overline{K}}_j=K_j{P}^{-1},\hspace{0.17em}\overline{Z}=P^{-T}Z{P}^{-1},\hspace{0.17em}\overline{R}=P^{-T}R{P}^{-1},\\ {\overline{Z}}_i=P^{-T}{Z}_i{P}^{-1},\hspace{0.17em}{\overline{Q}}_i=P^{-T}{Q}_i{P}^{-1},i=1,2,3\end{array}$$

Pre- and post-multiplying (33) by $\eta$ and ${\eta }^T$, respectively, (39) is obtained according to Schur complement. The proof is completed. □

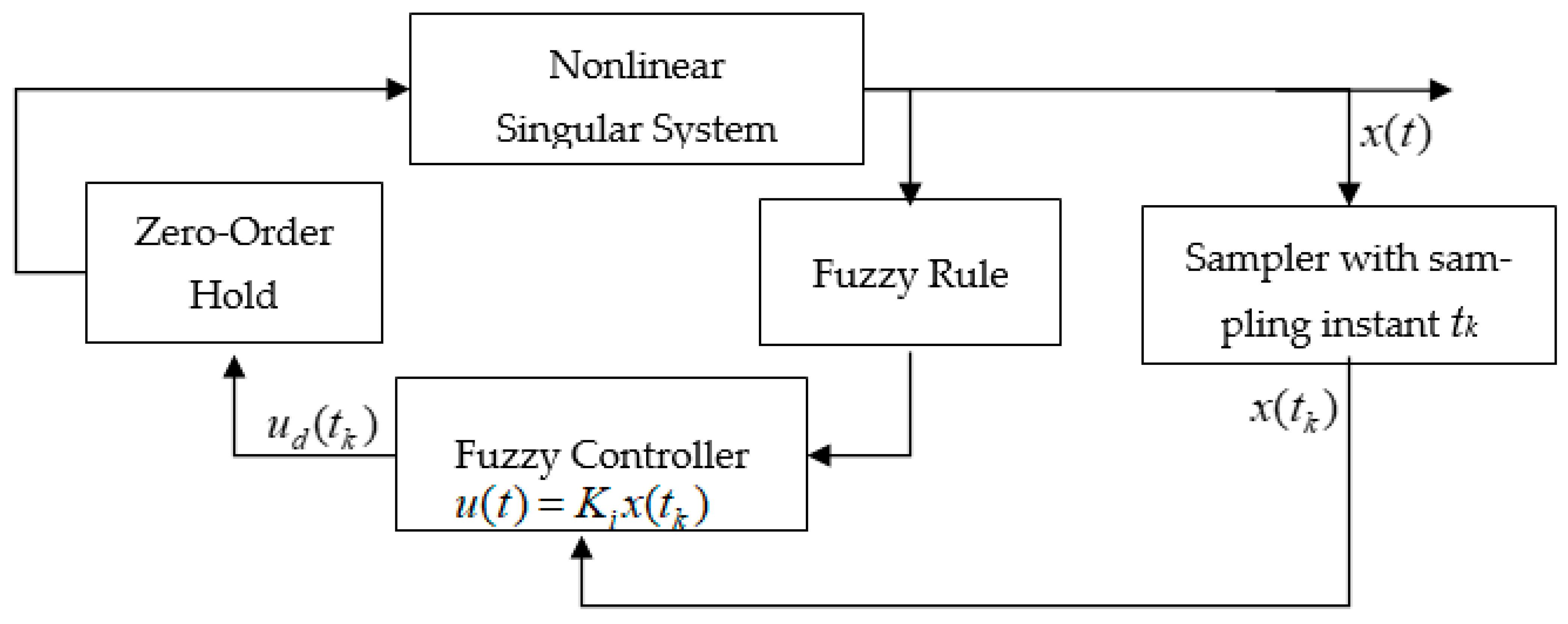
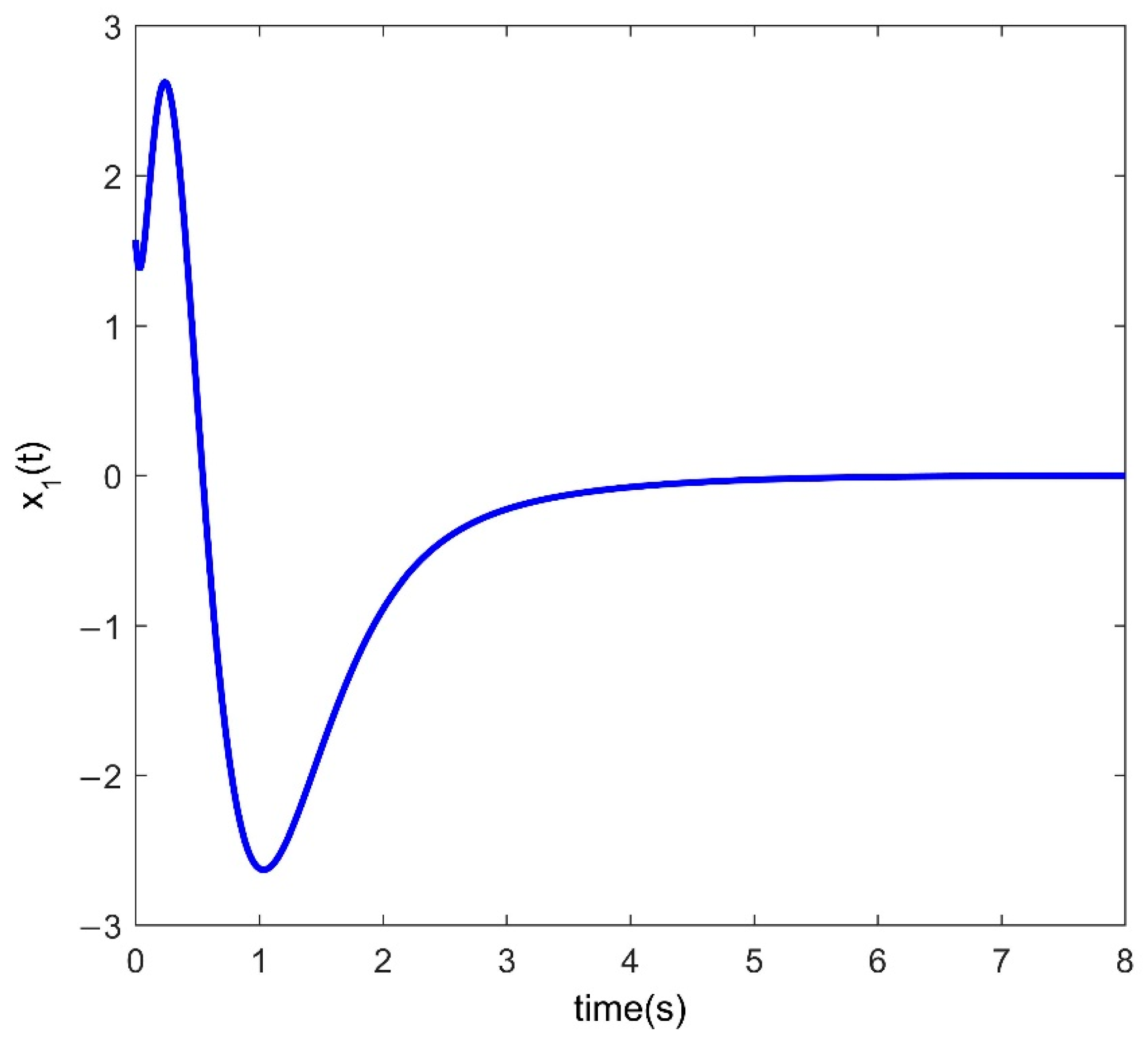
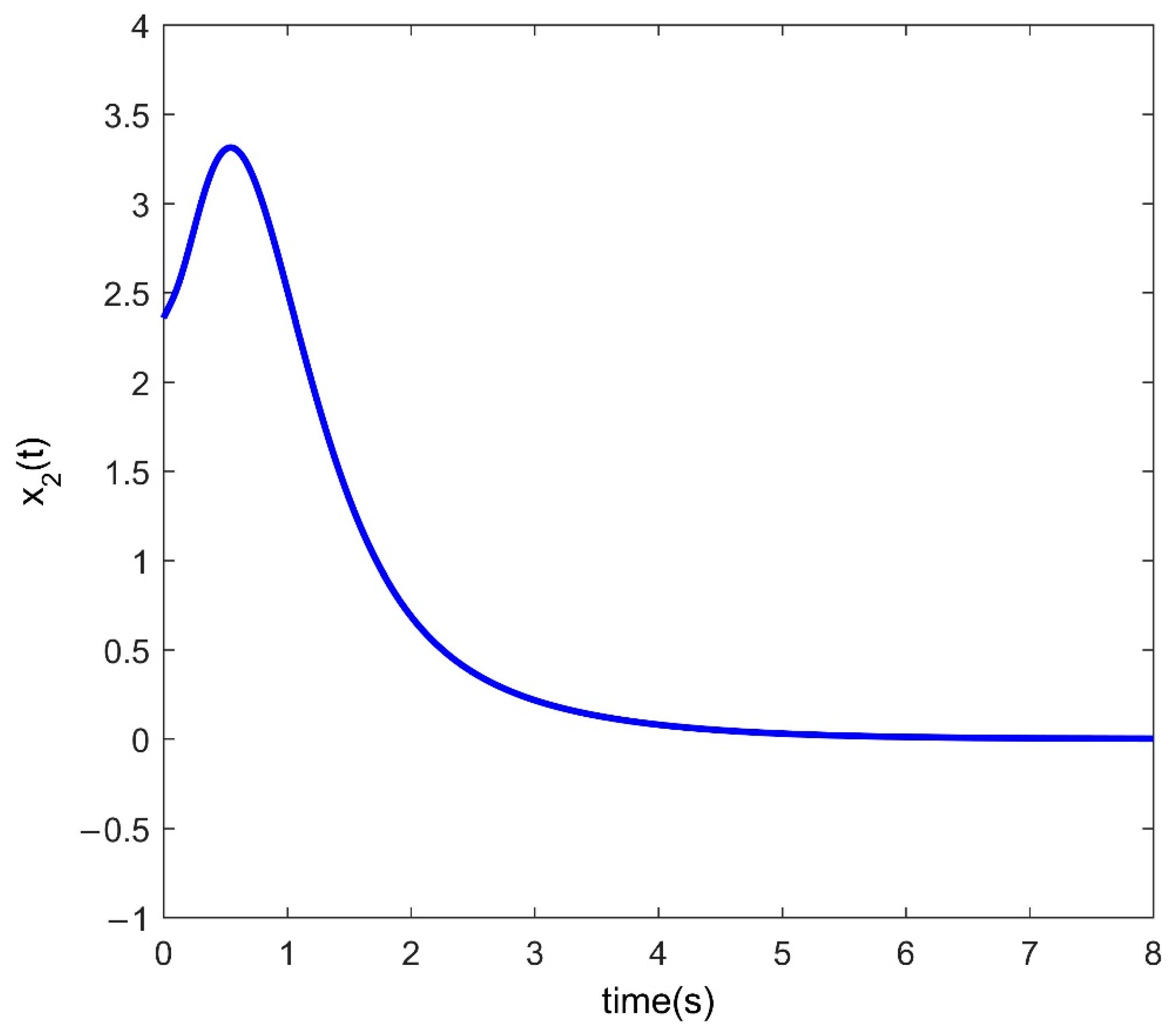
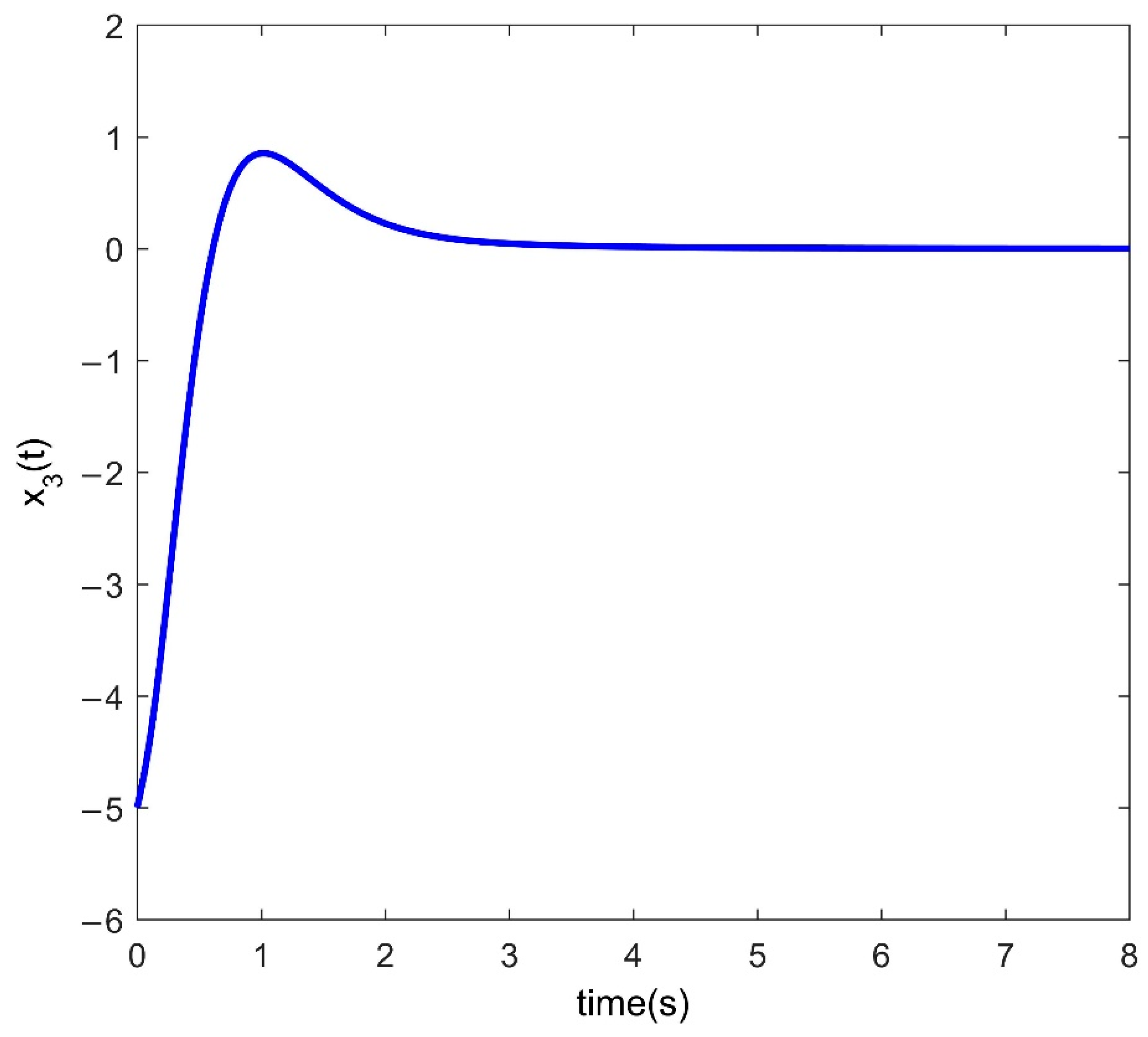
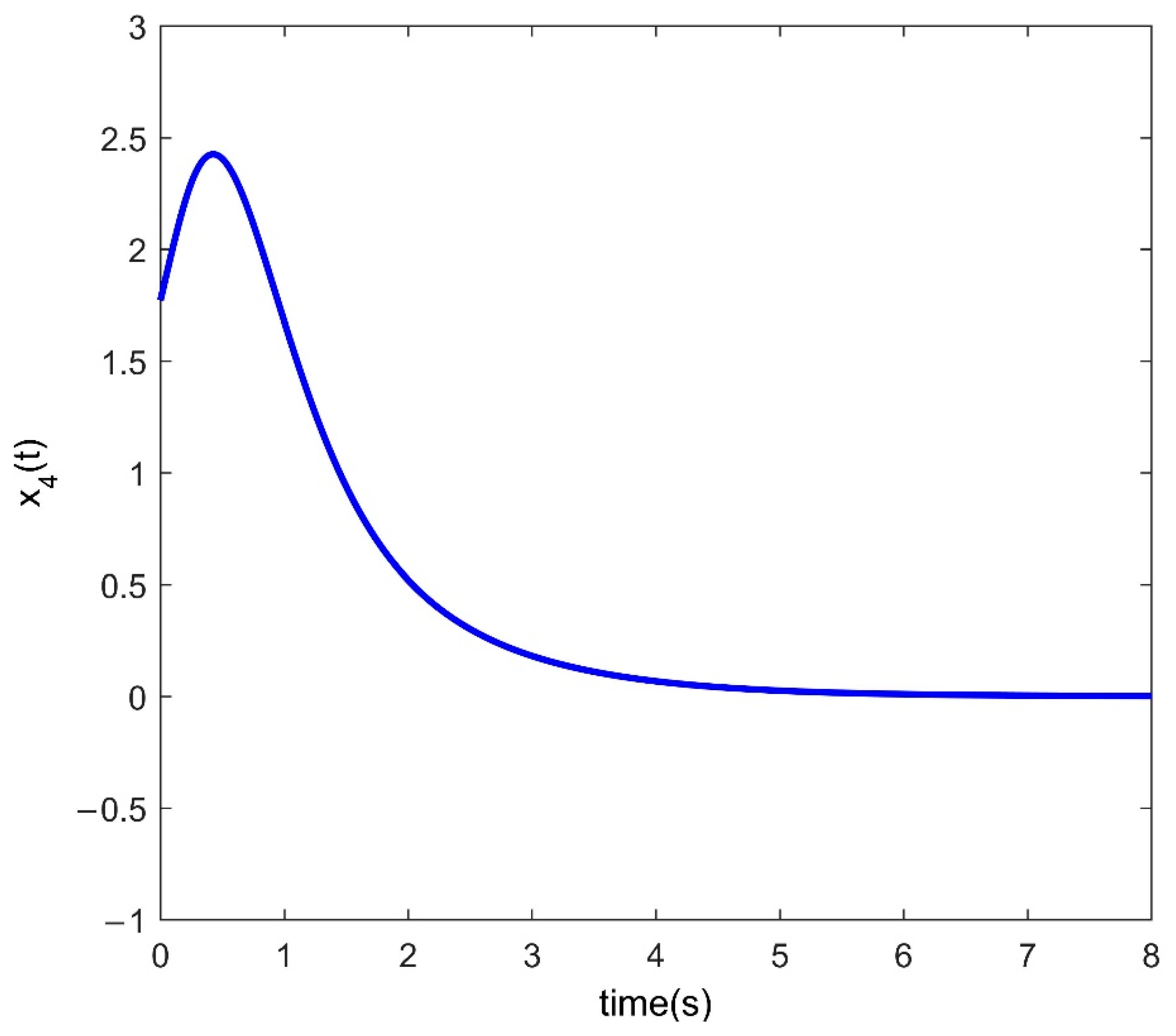
4. Numerical Examples

In this section, two numerical examples and a truck-trailer example are given to illustrate the advantages of the proposed method.

Example 1. Consider the following fuzzy singular system parameters which have two fuzzy rules.

$$\begin{array}{l}E=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right],A_1=\left[\begin{array}{cc}-2.8& 0\\ 0& -3.6\end{array}\right],A_2=\left[\begin{array}{cc}-1.8& 0\\ 0& -2.3\end{array}\right],\\ B_1=\left[\begin{array}{cc}-0.5& 0.1\\ 1.4& -0.1\end{array}\right],B_2=\left[\begin{array}{cc}-1.5& 0.5\\ 0.4& -0.3\end{array}\right],\\ B_{w1}=\left[\begin{array}{cc}0.3& 0.5\\ 1.5& 0.2\end{array}\right],B_{w2}=\left[\begin{array}{cc}0.2& 0\\ 1.5& 1.2\end{array}\right],\\ C_1=\left[\begin{array}{cc}-0.2& 1.4\\ 0.8& 1.2\end{array}\right],C_2=\left[\begin{array}{cc}-1.2& 0\\ 1.2& 1.5\end{array}\right].\end{array}$$

The purpose is to find the maximum delay $d_2$ to ensure that the system is admissible. The comparison results between the paper and the methods proposed in [50,51] ($d_1=0$) are shown in

Table 1. Maximum values for $d_2$.

Method	[50]	[51]	Theorem 1
$d_2$	3.25	3.3459	5.2381

. Obviously, Theorem 1 can obtain the maximum delay $d_2$ over those in references [50,51], which means that the algorithm proposed in this paper is less conservative.

Example 2.

Consider the fuzzy singular-system parameters as follows [41]:

$$\begin{array}{l}E=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right],A_1=\left[\begin{array}{cc}0& 1\\ -1& -2\end{array}\right],A_2=\left[\begin{array}{cc}0& a\\ -2& -2\end{array}\right],\\ B_1=\left[\begin{array}{cc}0.1& 0\\ 0.2& 0.1\end{array}\right],B_2=\left[\begin{array}{cc}0.1& 0\\ b& -0.5\end{array}\right],\\ B_{w1}=B_{w2}=\left[\begin{array}{c}1\\ 0\end{array}\right],C_1=C_2=\left[\begin{array}{cc}1& 1\end{array}\right].\end{array}$$

In order to explain how the proposed methods are less conservative, the $H_{\infty }$ performance index is used. We calculated the minimum attenuation levels for different values of a and b, with the comparisons listed in

Table 2. Minimum values of H_∞ performance γ.

a	2			5
b	0.3	0.7	0.95	0.8	0.83
Theorem 2 [52]	0.1908	0.4763	12.5166	2.8888	18.5937
Theorem 2 [53]	0.2913	0.6714	-	10.8072	-
Methods	0.2517	0.3568	0.8562	0.6524	0.7635

. It shows that the proposed method is more excellent than the methods in references [52,53].

Example 3. The truck-trailer models are expressed as follow [54].

$$\{\begin{array}{l}{\dot{x}}_1(t)=-\frac{v\overline{t}}{L{t}_0}{x}_1(t)+\frac{v\overline{t}}{l{t}_0}u(t)+\sigma w(t)\\ {\dot{x}}_2(t)=\frac{v\overline{t}}{L{t}_0}{x}_1(t)\\ {\dot{x}}_3(t)=\frac{v\overline{t}}{t_0}\left(x_2(t)+\frac{v\overline{t}}{2L}{x}_1(t)\right)\end{array}$$

(43)

where $x_1(t),x_2(t),x_3(t)$ represents the angular difference between the truck and trailer, the trailer’s angle, and the vertical position of trailer’s rear end. $w(t)$ is the disturbance. Consider the model parameters:

$$v=-1,\overline{t}=2,t_0=0.5,L=5.5,l=2.8,\sigma =1.$$

Similar to [54], a variable is introduced:

$$x_4(t)=x_2(t)-\frac{\overline{v}\overline{t}}{L{\overline{t}}_0}{x}_1(t)$$

(44)

Let $\theta (t)=x_2(t)+\frac{\overline{v}\overline{t}}{2L_0}{x}_1(t)$, then the following membership functions are obtained:

$$\begin{array}{l}{\mu }_1(\theta (t))=\{\begin{array}{ll}\frac{\sin \left(\theta (t)\right)-\delta \theta (t)}{\theta (t)\left(1-\delta \right)},& \hspace{1em}if\hspace{1em}\theta (t)\ne 0\hspace{1em}\hfill \\ 1,\hspace{1em}\hspace{1em}& \hspace{1em}if\hspace{1em}\theta (t)=0\hfill \end{array}\\ {\mu }_2(\theta (t))=1-{\mu }_1(\theta (t)),\hspace{1em}\delta =\frac{{10}^{-2}}{\pi }\end{array}$$

According to [50], system (41) can be described with TS fuzzy modeling, such that:

Mode Rule 1: IF $\theta (t)$ is about 0, THEN

$$E\dot{x}(t)=A_{1}x(t)+B_{1}u(t)+B_{w1}w(t)$$

(45)

Mode Rule 2: IF $\theta (t)$ is about $\pi$ or $-\pi$, THEN

$$E\dot{x}(t)=A_{2}x(t)+B_{2}u(t)+B_{w2}w(t)$$

(46)

where:

$$x(t)={\left[\begin{array}{cccc}{x}_1(t)& x_2(t)& x_3(t)& x_4(t)\end{array}\right]}^T$$

and:

$$E=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 0\end{array}\right],B_1=B_2=\left[\begin{array}{c}\frac{\overline{v}\overline{t}}{l{\overline{t}}_0}\\ 0\\ 0\\ 0\end{array}\right],B_{w1}=B_{w2}=\left[\begin{array}{c}\sigma \\ 0\\ 0\\ 0\end{array}\right],C_1=C_2={\left[\begin{array}{c}\sigma \\ 0\\ 0\\ 0\end{array}\right]}^T$$

$$A_1=\left[\begin{array}{cccc}-\frac{\overline{v}\overline{t}}{L{\overline{t}}_0}& 0& 0& 0\\ \frac{\overline{v}\overline{t}}{L{\overline{t}}_0}& 0& 0& 0\\ \frac{{\overline{v}}^2{\overline{t}}^2}{2L{\overline{t}}_0}& \frac{\overline{v}\overline{t}}{{\overline{t}}_0}& 0& 0\\ -\frac{\overline{v}\overline{t}}{L{\overline{t}}_0}& 1& 0& -1\end{array}\right],A_2=\left[\begin{array}{cccc}-\frac{\overline{v}\overline{t}}{L{\overline{t}}_0}& 0& 0& 0\\ \frac{\overline{v}\overline{t}}{L{\overline{t}}_0}& 0& 0& 0\\ \frac{\delta {\overline{v}}^2{\overline{t}}^2}{2L{\overline{t}}_0}& \frac{\delta \overline{v}\overline{t}}{{\overline{t}}_0}& 0& 0\\ -\frac{\overline{v}\overline{t}}{L{\overline{t}}_0}& 1& 0& -1\end{array}\right]$$

With the sampled-data controllers being described using TS fuzzy modeling, such that:

Controller Rule 1: IF $\theta (t)$ is about 0, THEN

$$u(t)=K_{1}x(t_k)$$

(47)

Controller Rule 2: IF $\theta (t)$ is about $\pi$ or $-\pi$, THEN

$$u(t)=K_{2}x(t_k)$$

(48)

Firstly, compared with [35,54,55], which use different methods for singular systems to obtain the maximum sampling period, our comparison results are listed in

Table 3. Maximum values of the upper bound $d_2$ ($d_1=0$).

Method	[35]	[54]	[55]	Theorem 1
$d_2$	0.25	0.264	0.453	0.628

. Choose the same sampling interval $d_1=0$, then, according to Theorem 2, the maximum sampling period can be obtained, such that $d_2=0.628$, which improves upon [35,54,55] by greater than 151.2%, 137.88%, and 38.63%, respectively. It is illustrated that the sampling period in the paper is longer than these references. Besides, the lower bound of the sampling interval is not considered in these references, which will lead to conservatism.

Assume that $d_1=1.0, d_2=1.7$ then, it can be obtained that ${\gamma }_{\min }=0.4925$. The fuzzy controller gains can be derived as:

$$\begin{array}{l}{K}_1=\left[\begin{array}{cccc}-1.5180& 0.5372& 0.7514& -0.3342\end{array}\right],\\ K_2=\left[\begin{array}{cccc}-1.5054& 0.5326& 0.7451& -0.3314\end{array}\right].\end{array}$$

The initial state is $x(0)=\left[\begin{array}{cccc}0.5\pi & 0.75\pi & -5& 1.77\end{array}\right]$, and the external disturbances are $w(t)=0.5\cos (t)$, the responses curve of the system’s state are shown in Figure 2, Figure 3, Figure 4 and Figure 5, respectively. Take Figure 3 as an example; Figure 3 is the responses curve of the trailer’s angle ($x_2\left(t\right)$). The initial state is $0.75\pi$, and the expected stable state is $0$. From Figure 3, this shows that after about 1 s of peak time and 4 s of stable time, the system state achieves the desired target, which shows that the system state is stable. Therefore, from Figure 2, Figure 3, Figure 4 and Figure 5, this illustrates that the state variables tend towards zero in a short time, which further illustrates that the proposed sampled-data controller makes the state variables stable and achieves good control performance under external disturbance.

5. Conclusions

The issue of sampled-data control for singular TS fuzzy systems is investigated in this paper. A proper LKF was established to alleviate the conservatism of the results. Then the conditions of asymptotical admissibility were presented by means of LMI. Finally, three examples were given to illustrate that the designed sampled-data controller is effective. The main achievements of this article are summarized as follows:

(1)

Through proper transformation, the research results in this paper can be extended to normal sampled-data systems. Hence, the proposed methods have universality;

(2)

The input delay approach is proposed to transform the system into a time-delay system so that many novel time-delay methods can be used;

(3)

Both the lower and upper bounds of the sampling period were considered, which has a wider application scope;

(4)

Reciprocally convex inequality is used to handle integral terms, such as LKF, meaning that the conservatism of the system has been greatly reduced.

However, the real sampling patterns are not fully captured, and the impulsive behavior of the system was not considered. In the future, the new control methods, such as reinforcement learning control, will be studied to improve the results of this paper.