Hot Primordial Regions with Anomalous Hydrogenless Chemical Composition
Abstract
:1. Introduction
2. Nucleosynthesis
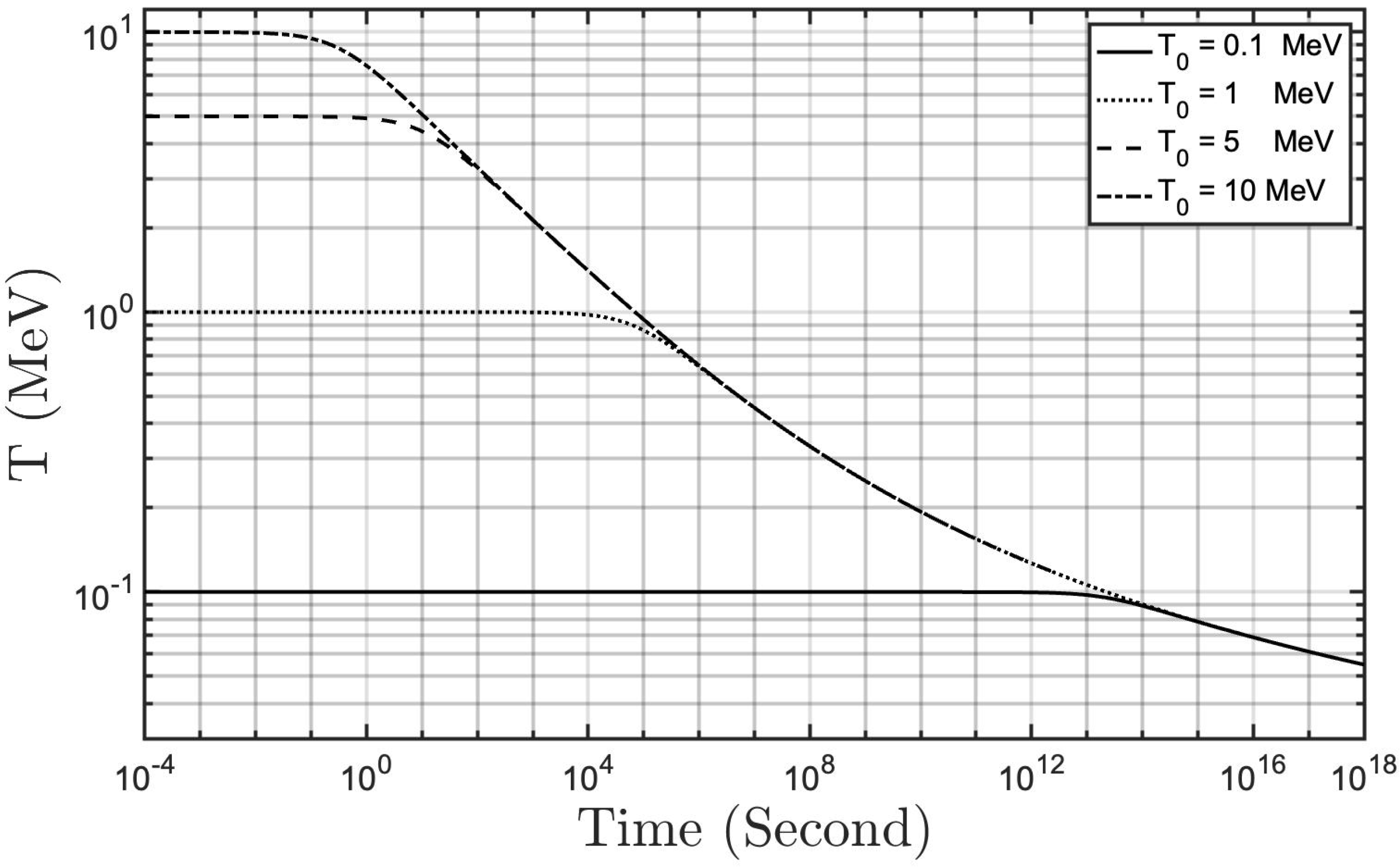
2.1. Temperature Evolution
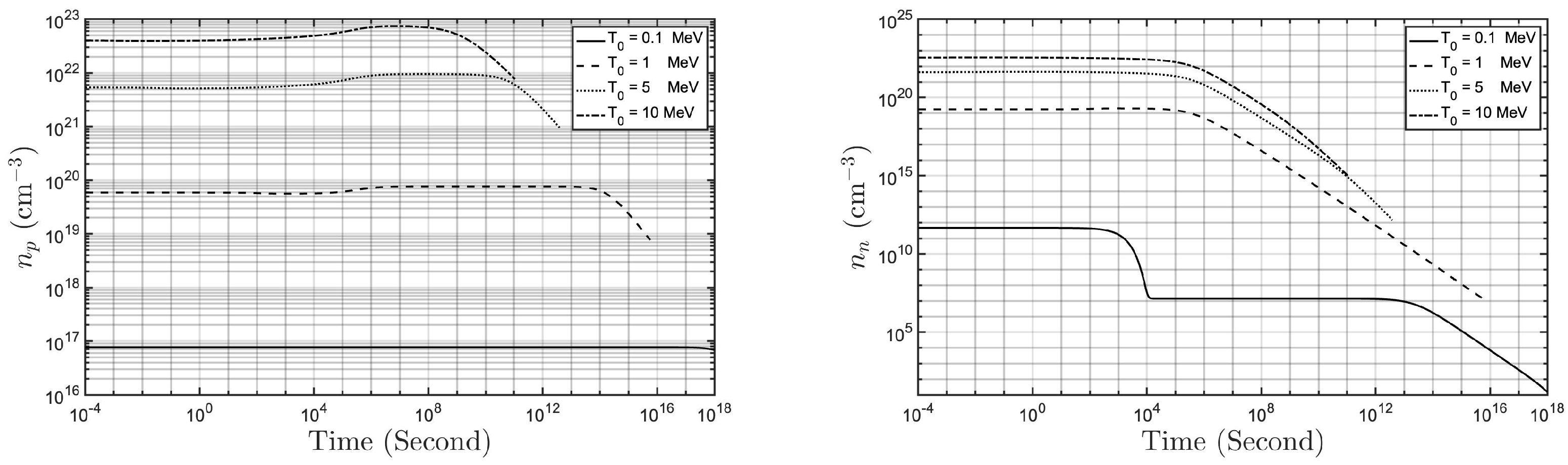
2.2. Abundances of Free Protons and Neutrons
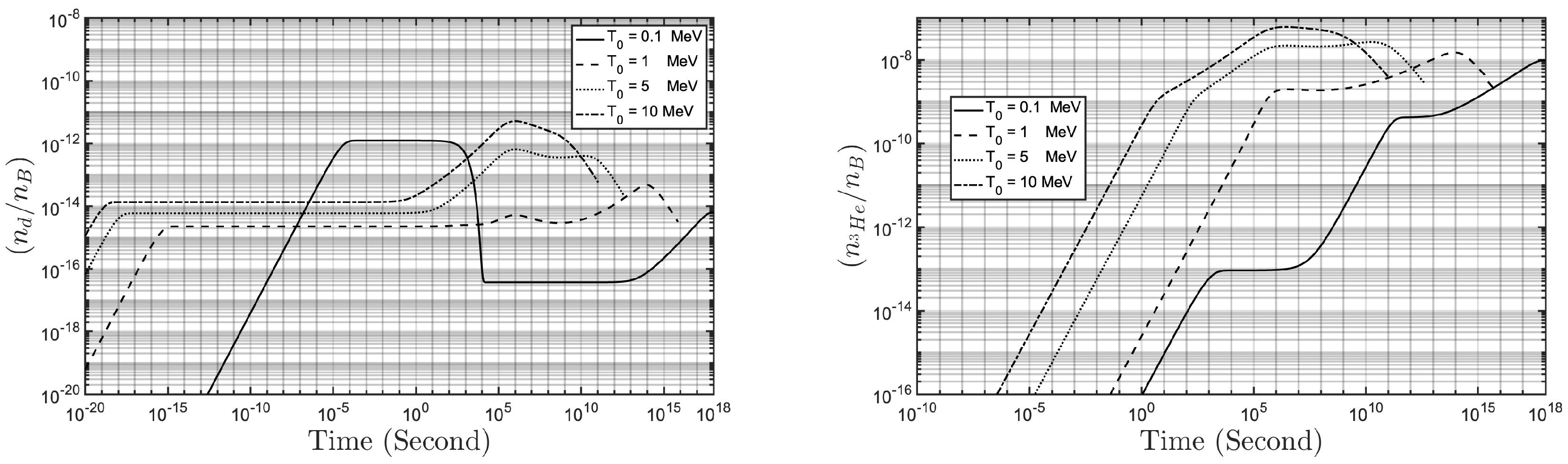
2.3. Abundances of Deuterium and Helium-3
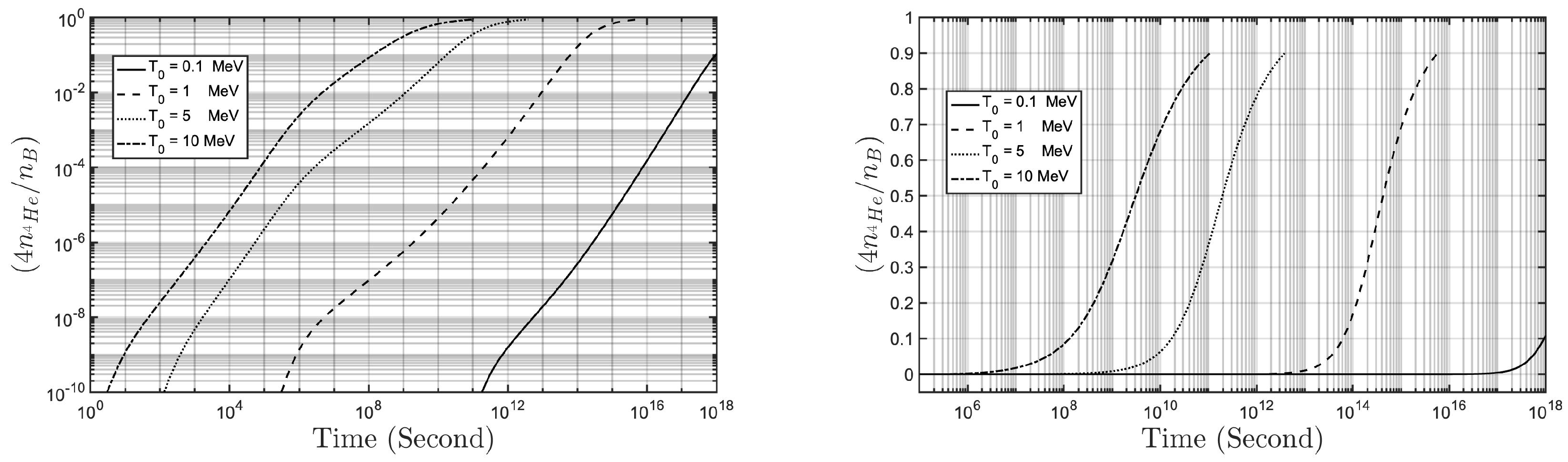
2.4. Abundance of Helium-4 with Heavier Elements
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
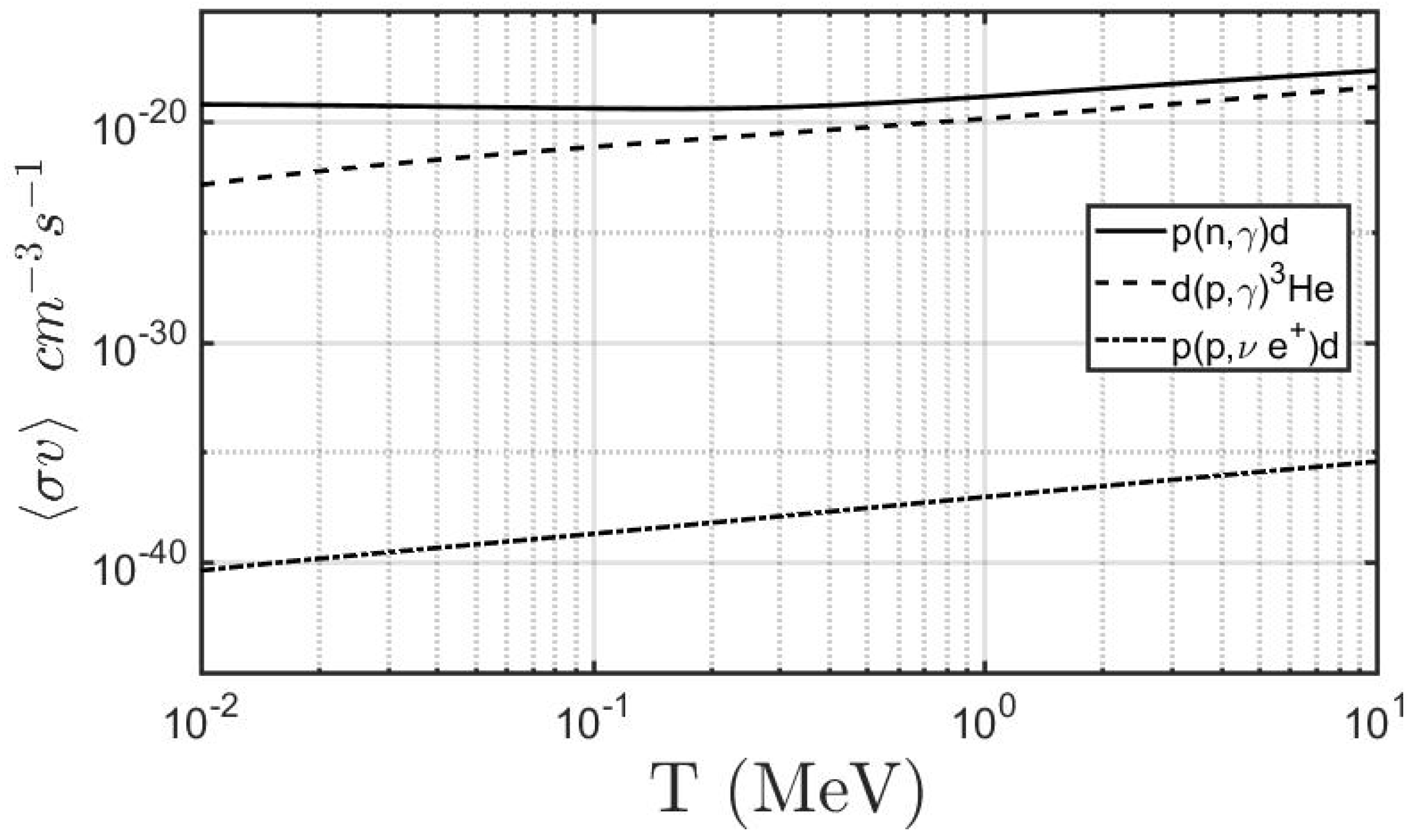
Appendix A. Reaction Rates and Cross-Sections
| Reaction | MeV b | b | MeV b |
|---|---|---|---|
| p(p,e)d | 3.94 × 10 | 4.61 × 10 | 2.96 × 10 |
| p(n,)d | 7.30 × 10 | −1.89 × 10 | 2.42 × 10 |
| d(p,)He | 0.20 × 10 | 5.60 × 10 | 3.10 × 10 |
| He(He,2p) | 5.18 | −2.22 | 0.80 |
References
- Kashlinsky, A.; Ali-Haïmoud, Y.; Clesse, S.; Garcia-Bellido, J.; Wyrzykowski, L.; Achucarro, A.; Amendola, L.; Annis, J.; Arbey, A.; Arendt, R.; et al. Electromagnetic probes of primordial black holes as dark matter. arXiv 2019, arXiv:1903.04424. [Google Scholar]
- Rubin, S.G.; Khlopov, M.Y.; Sakharov, A.S. Primordial black holes from nonequilibrium second order phase transition. Grav. Cosmol. 2000, 6, 51–58. [Google Scholar]
- Rubin, S.G.; Sakharov, A.S.; Khlopov, M.Y. The Formation of primary galactic nuclei during phase transitions in the early universe. J. Exp. Theor. Phys. 2001, 91, 921–929. [Google Scholar] [CrossRef] [Green Version]
- Khlopov, M.Y.; Rubin, S.G.; Sakharov, A.S. Primordial structure of massive black hole clusters. Astropart. Phys. 2005, 23, 265. [Google Scholar] [CrossRef] [Green Version]
- Ding, Q.; Nakama, T.; Silk, J.; Wang, Y. Detectability of Gravitational Waves from the Coalescence of Massive Primordial Black Holes with Initial Clustering. Phys. Rev. D 2019, 100, 103003. [Google Scholar] [CrossRef] [Green Version]
- Matsubara, T.; Terada, T.; Kohri, K.; Yokoyama, S. Clustering of primordial black holes formed in a matter-dominated epoch. Phys. Rev. D 2019, 100, 123544. [Google Scholar] [CrossRef] [Green Version]
- Young, S.; Byrnes, C.T. Initial clustering and the primordial black hole merger rate. JCAP 2020, 3, 004. [Google Scholar] [CrossRef]
- Kawasaki, M.; Murai, K.; Nakatsuka, H. Strong clustering of primordial black holes from Affleck-Dine mechanism. JCAP 2021, 10, 025. [Google Scholar] [CrossRef]
- Inman, D.; Ali-Haïmoud, Y. Early structure formation in primordial black hole cosmologies. Phys. Rev. D 2019, 100, 083528. [Google Scholar] [CrossRef] [Green Version]
- Afshordi, N.; McDonald, P.; Spergel, D.N. Primordial black holes as dark matter: The Power spectrum and evaporation of early structures. Astrophys. J. Lett. 2003, 594, L71–L74. [Google Scholar] [CrossRef] [Green Version]
- Jedamzik, K. Primordial Black Hole Dark Matter and the LIGO/Virgo observations. JCAP 2020, 09, 022. [Google Scholar] [CrossRef]
- De Luca, V.; Desjacques, V.; Franciolini, G.; Riotto, A. The clustering evolution of primordial black holes. JCAP 2020, 11, 028. [Google Scholar] [CrossRef]
- Pilipenko, S.; Tkachev, M.; Ivanov, P. Evolution of a primordial binary black hole due to interaction with cold dark matter and the formation rate of gravitational wave events. Phys. Rev. D 2022, 105, 123504. [Google Scholar] [CrossRef]
- Konoplich, R.; Rubin, S.; Sakharov, A.; Khlopov, M.Y. Formation of black holes in first-order phase transitions in the Universe. Astron. Lett. 1998, 24, 413–417. [Google Scholar]
- Deng, H.; Vilenkin, A.; Yamada, M. CMB spectral distortions from black holes formed by vacuum bubbles. J. Cosmol. Astropart. Phys. 2018, 2018, 59. [Google Scholar] [CrossRef] [Green Version]
- Dokuchaev, V.; Eroshenko, Y.; Rubin, S. Quasars formation around clusters of primordial black holes. Grav. Cosmol. 2005, 11, 99–104. [Google Scholar]
- Dokuchaev, V.I.; Eroshenko, Y.N.; Rubin, S.G. Early formation of galaxies initiated by clusters of primordial black holes. Astron. Rep. 2008, 52, 779–789. [Google Scholar] [CrossRef]
- Khromykh, L.A.; Kirillov, A.A. The gravitational dynamics of the primordial black holes cluster. J. Phys. Conf. Ser. 2019, 1390, 012090. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Konoplich, R.V.; Mignani, R.; Rubin, S.G.; Sakharov, A.S. Physical origin, evolution and observational signature of diffused antiworld. Astropart. Phys. 2000, 12, 367–372. [Google Scholar] [CrossRef] [Green Version]
- Khlopov, M.Y.; Rubin, S.G.; Sakharov, A.S. Possible origin of antimatter regions in the baryon dominated universe. Phys. Rev. D 2000, 62, 083505. [Google Scholar] [CrossRef] [Green Version]
- Belotsky, K.; El Kasmi, M.; Rubin, S. Neutrino Cooling of Primordial Hot Regions. Symmetry 2020, 12, 1442. [Google Scholar] [CrossRef]
- Belotsky, K.; El Kasmi, M.; Rubin, S. Neutrino cooling effect of primordial hot areas in dependence on its size. arXiv 2020, arXiv:2011.14221. [Google Scholar]
- Belotsky, K.; Golikova, Y.A.; Rubin, S. Local heating of matter in the early universe owing to the interaction of the Higgs field with a scalar field. Phys. At. Nucl. 2017, 80, 718–720. [Google Scholar] [CrossRef]
- Khlopov, M.; Paik, B.; Ray, S. Revisiting Primordial Black Hole Evolution. Axioms 2020, 9, 71. [Google Scholar] [CrossRef]
- Berezin, V.; Kuzmin, V.; Tkachev, I. Thin-wall vacuum domain evolution. Phys. Lett. B 1983, 120, 91–96. [Google Scholar] [CrossRef]
- Davoudiasl, H.; Denton, P.B.; Gehrlein, J. Supermassive Black Holes, Ultralight Dark Matter, and Gravitational Waves from a First Order Phase Transition. Phys. Rev. Lett. 2022, 128, 081101. [Google Scholar] [CrossRef]
- Dolgov, A.; Silk, J. Baryon isocurvature fluctuations at small scales and baryonic dark matter. Phys. Rev. D 1993, 47, 4244. [Google Scholar] [CrossRef]
- Dolgov, A.D. Massive and supermassive black holes in the contemporary and early Universe and problems in cosmology and astrophysics. Phys.-Uspekhi 2018, 61, 115. [Google Scholar] [CrossRef] [Green Version]
- Belotsky, K.M.; Dokuchaev, V.I.; Eroshenko, Y.N.; Esipova, E.A.; Khlopov, M.Y.; Khromykh, L.A.; Kirillov, A.A.; Nikulin, V.V.; Rubin, S.G.; Svadkovsky, I.V. Clusters of primordial black holes. Eur. Phys. J. C 2019, 79, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Carr, B.; Kuhnel, F. Primordial black holes as dark matter candidates. SciPost Phys. Lect. Notes 2022, 48, 1. [Google Scholar] [CrossRef]
- Bennett, D.P.; Udalski, A.; Bond, I.A.; Suzuki, D.; Ryu, Y.H.; Abe, F.; Barry, R.K.; Bhattacharya, A.; Donachie, M.; Fukui, A.; et al. A Planetary Microlensing Event with an Unusually Red Source Star: MOA-2011-BLG-291. AJ 2018, 156, 113. [Google Scholar] [CrossRef] [Green Version]
- Dolgov, A.D. Massive Primordial Black Holes. PoS 2020, MULTIF2019, 013. [Google Scholar] [CrossRef]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the elements in stars. Rev. Mod. Phys. 1957, 29, 547. [Google Scholar] [CrossRef] [Green Version]
- Clayton, D.D. Principles of Stellar Evolution and Nucleosynthesis; University of Chicago Press: Chicago, IL, USA, 1983. [Google Scholar]
- Iliadis, C. Nuclear Physics of Stars; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Angulo, C.; Arnould, M.; Rayet, M.; Descouvemont, P.; Baye, D.; Leclercq-Willain, C.; Coc, A.; Barhoumi, S.; Aguer, P.; Rolfs, C.; et al. A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 1999, 656, 3–183. [Google Scholar] [CrossRef]
- Fowler, W.A.; Caughlan, G.R.; Zimmerman, B.A. Thermonuclear reaction rates. Annu. Rev. Astron. Astrophys. 1967, 5, 525–570. [Google Scholar] [CrossRef]
- Lang, K.R. Astrophysical Formulae: Space, Time, Matter and Cosmology; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belotsky, K.M.; El Kasmi, M.M.; Rubin, S.G.; Solovyov, M.L. Hot Primordial Regions with Anomalous Hydrogenless Chemical Composition. Symmetry 2022, 14, 1452. https://doi.org/10.3390/sym14071452
Belotsky KM, El Kasmi MM, Rubin SG, Solovyov ML. Hot Primordial Regions with Anomalous Hydrogenless Chemical Composition. Symmetry. 2022; 14(7):1452. https://doi.org/10.3390/sym14071452
Chicago/Turabian StyleBelotsky, Konstantin M., Mohamed M. El Kasmi, Sergey G. Rubin, and Maxim L. Solovyov. 2022. "Hot Primordial Regions with Anomalous Hydrogenless Chemical Composition" Symmetry 14, no. 7: 1452. https://doi.org/10.3390/sym14071452
APA StyleBelotsky, K. M., El Kasmi, M. M., Rubin, S. G., & Solovyov, M. L. (2022). Hot Primordial Regions with Anomalous Hydrogenless Chemical Composition. Symmetry, 14(7), 1452. https://doi.org/10.3390/sym14071452







