Harmonic Balance Method to Analyze the Steady-State Response of a Controlled Mass-Damper-Spring Model
Abstract
1. Introduction
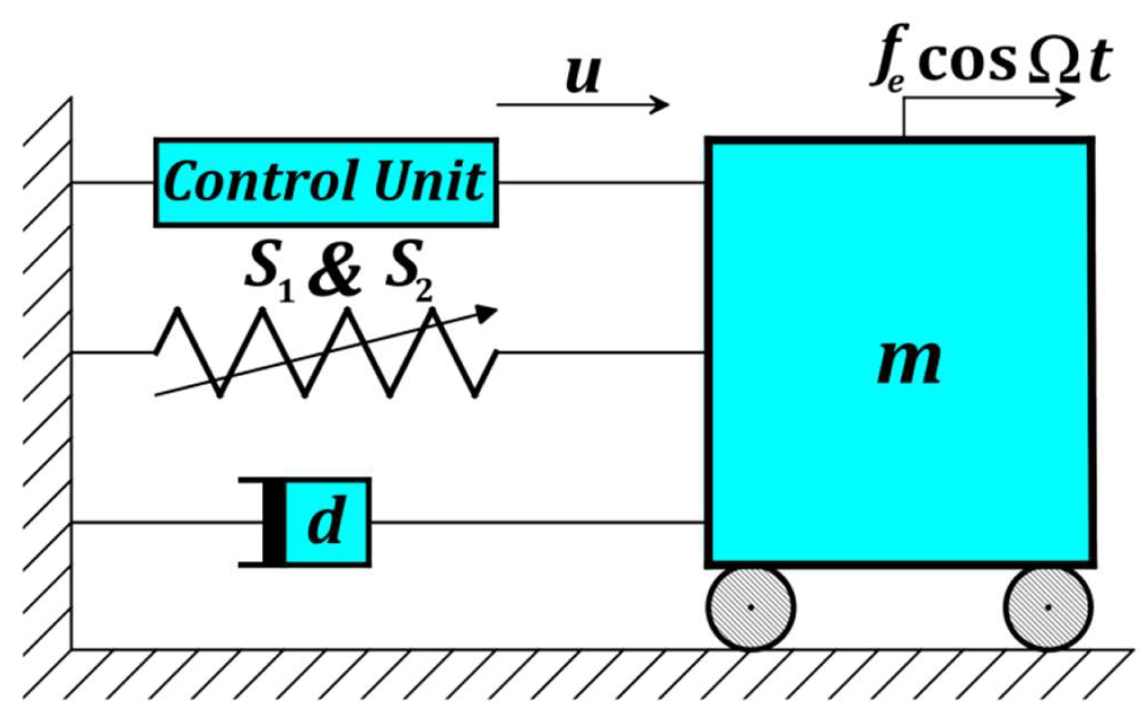
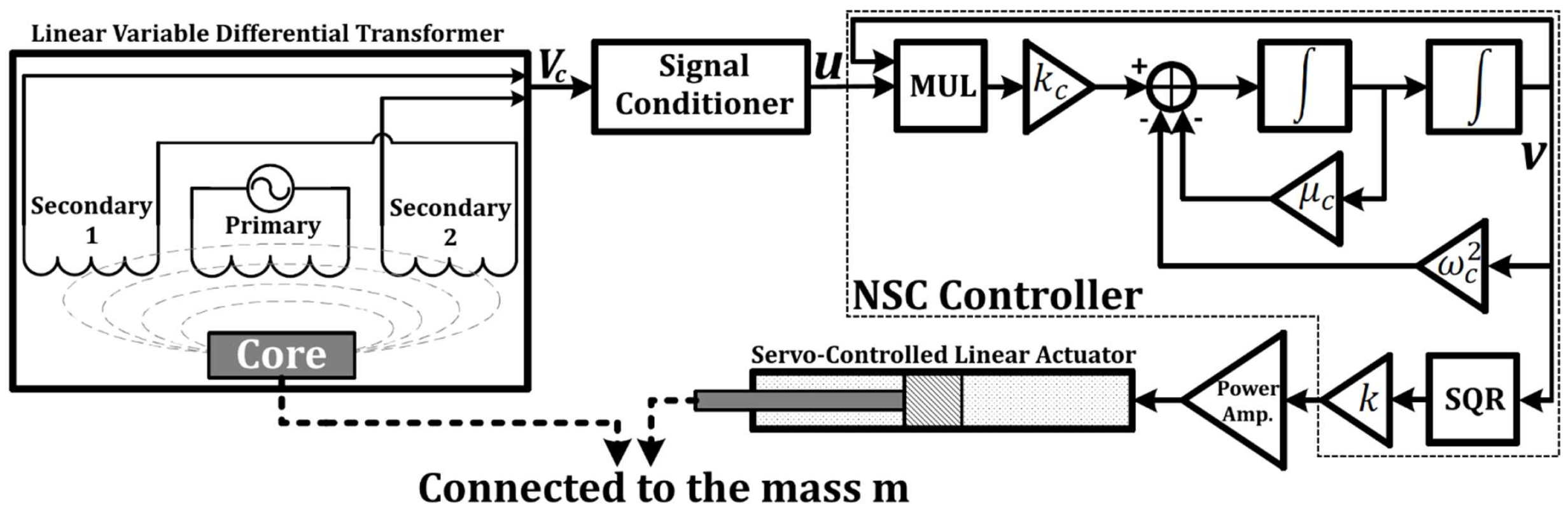
2. System Modelling and Harmonic Balance Method
3. Results and Discussion
4. Conclusions
- A.
- When the controller was OFF:
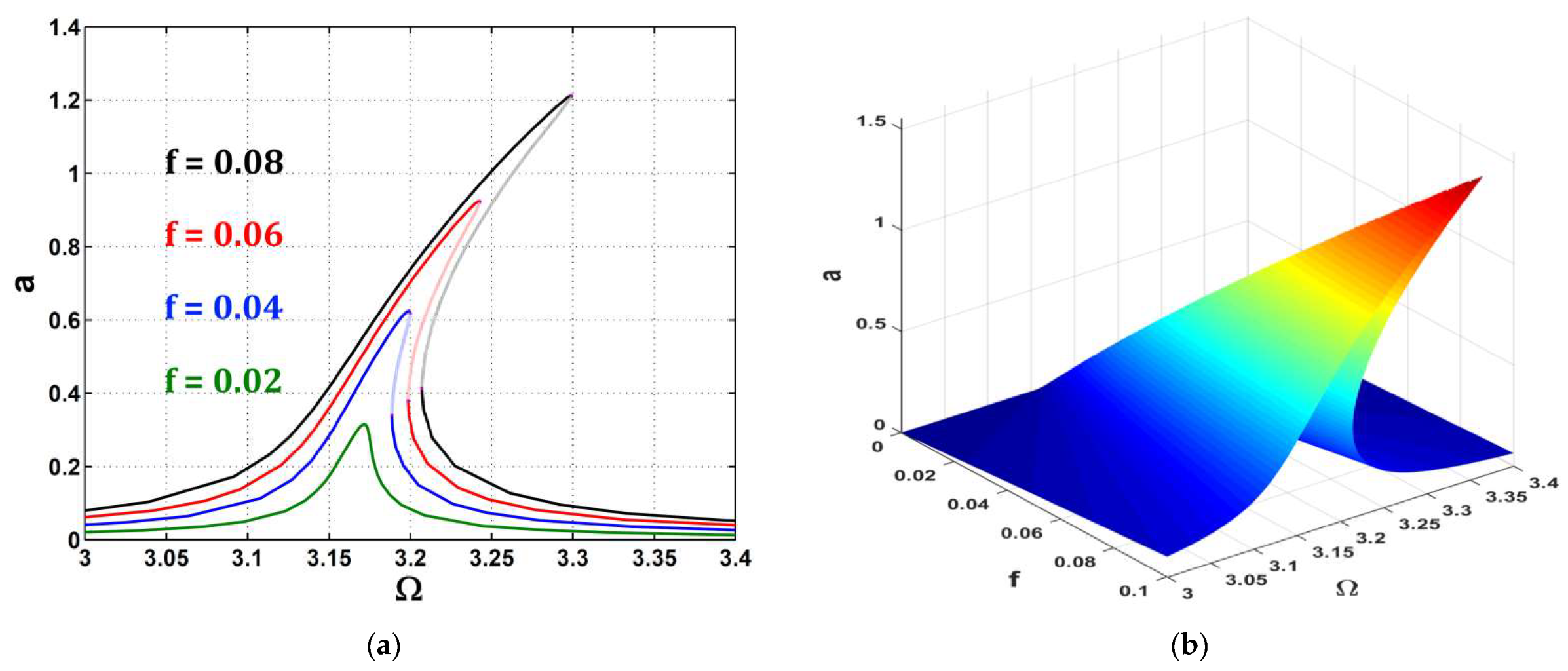
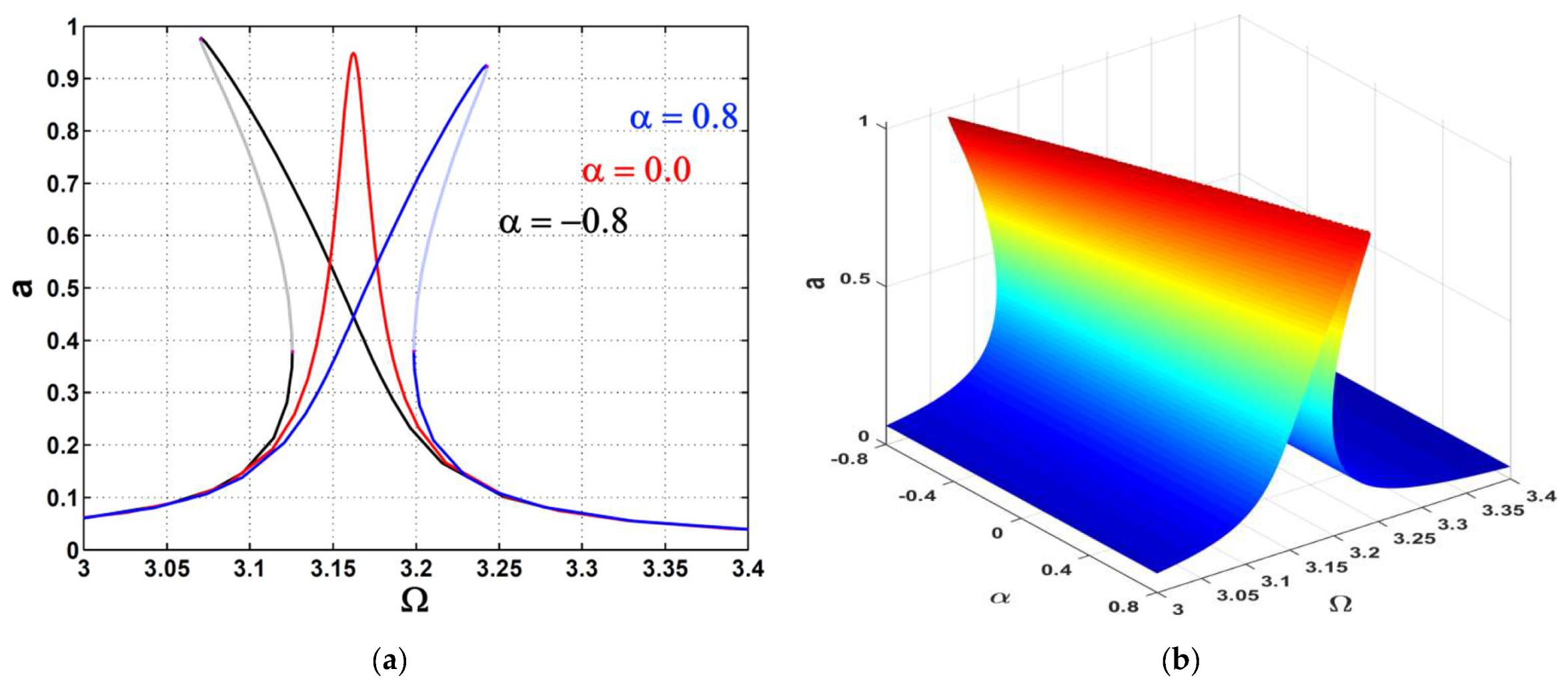
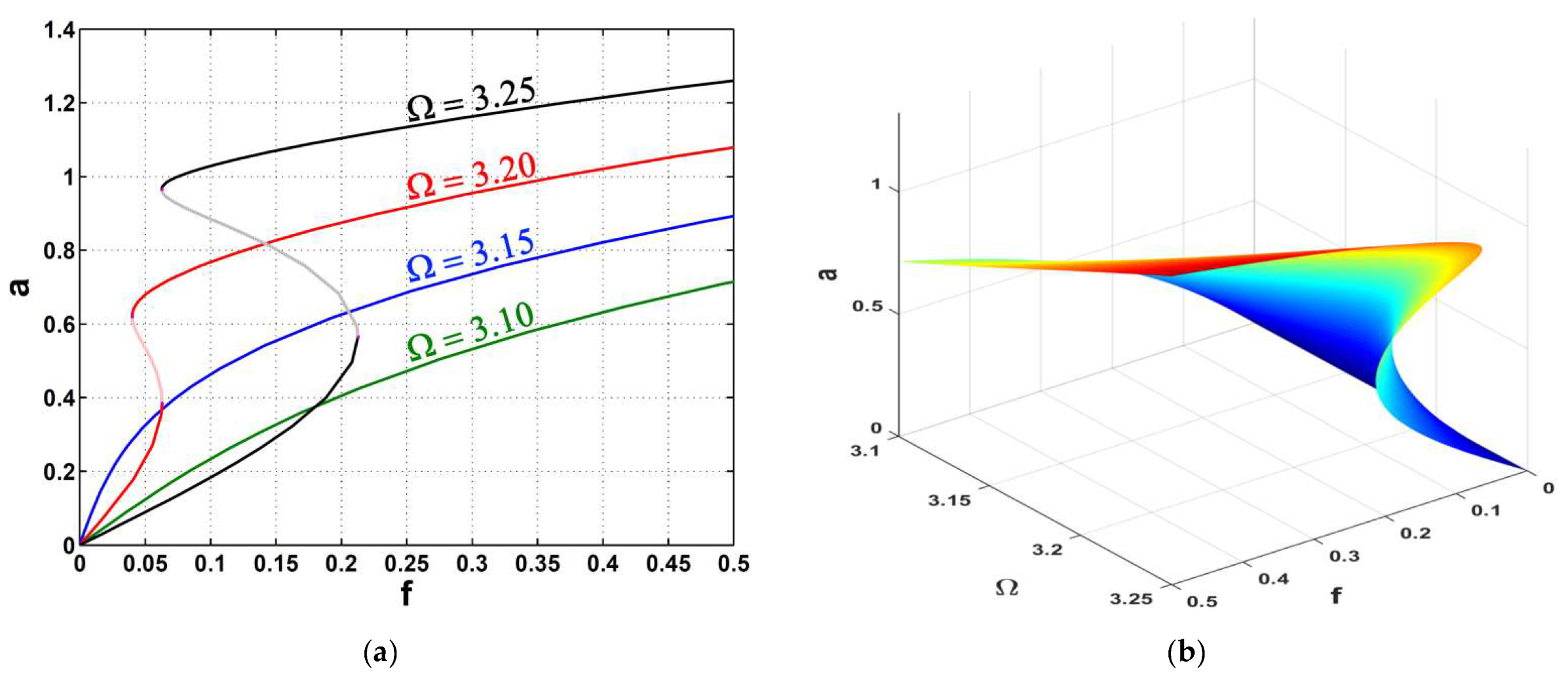
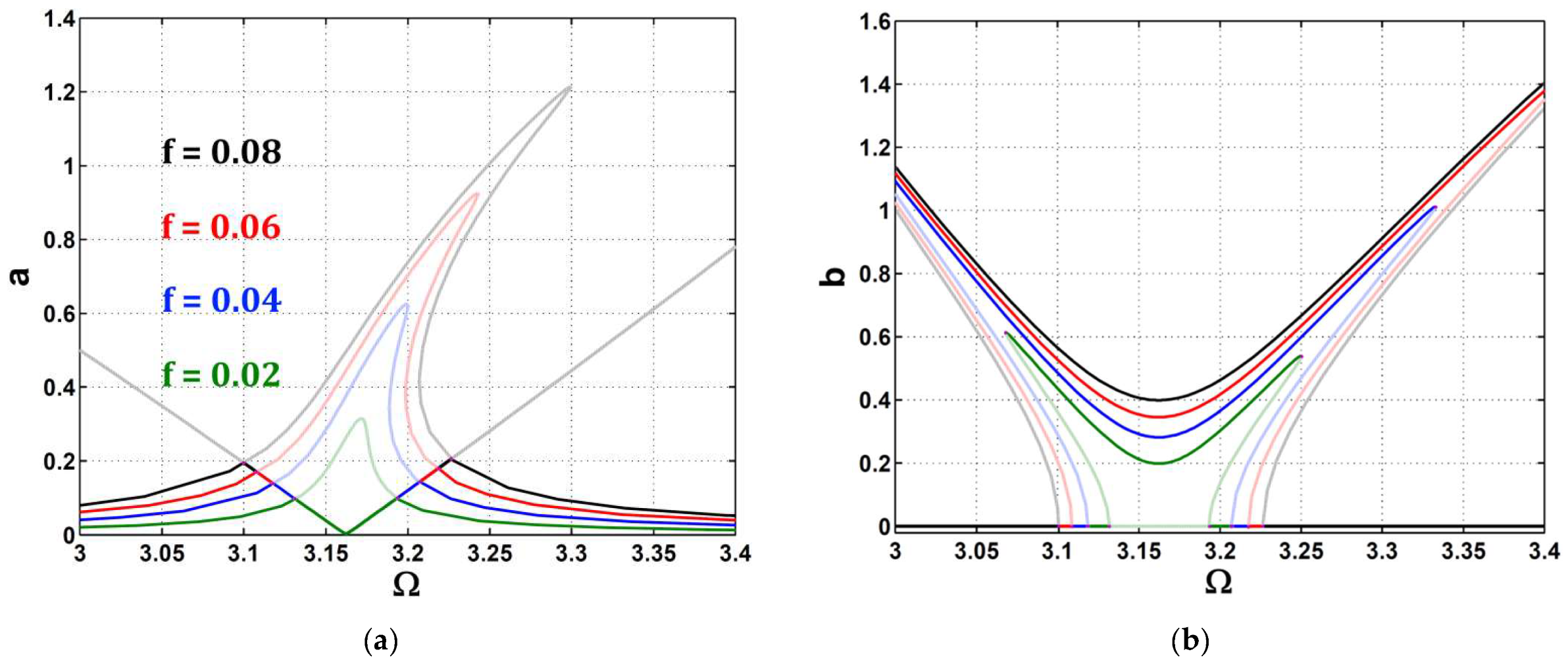
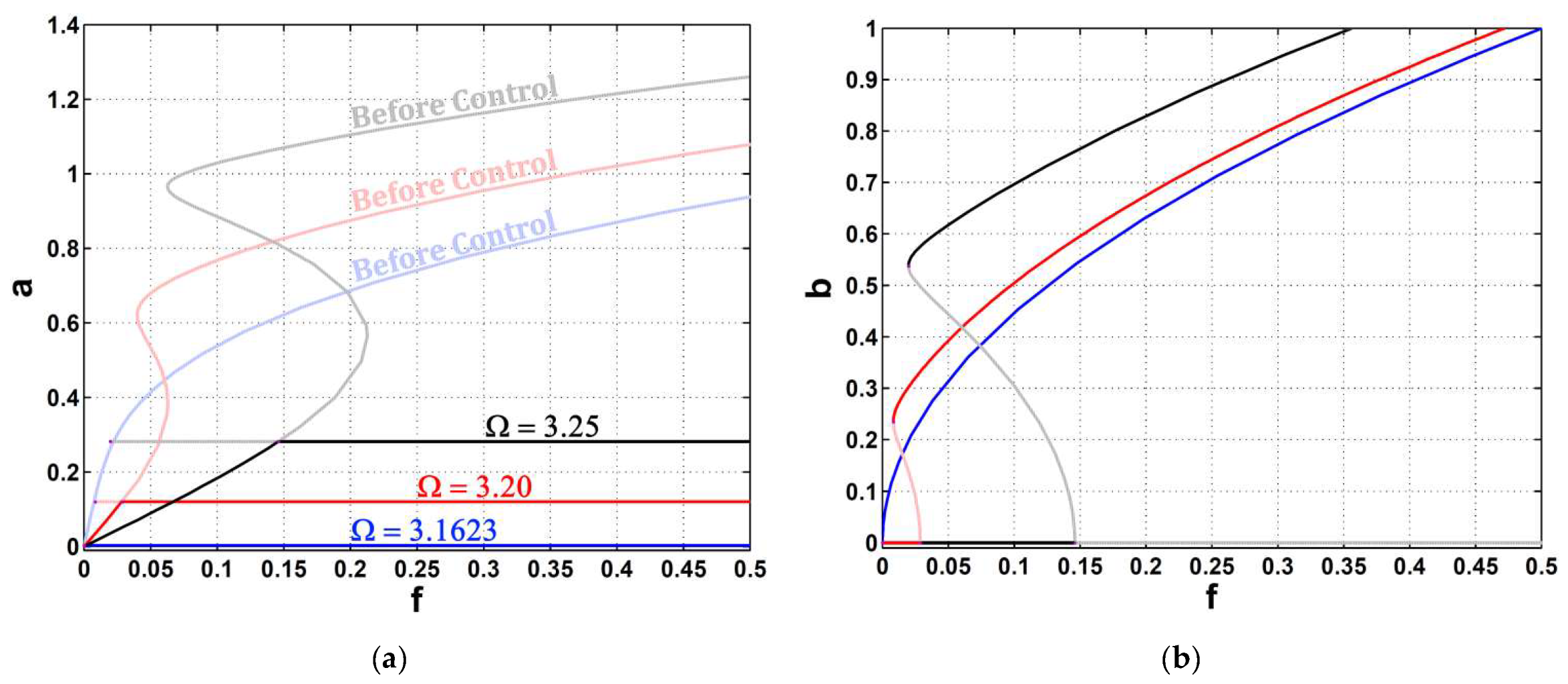
- The right-bending of the car’s vibration amplitude curve increased with the excitation force amplitude, which made the nonlinearity effect appear due to the spring’s hardening phenomenon.
- The jump phenomena displayed high to low states, and vice versa.
- The damping parameter could suppress the maximum amplitude, in addition to eliminating the existence of saddle-node points and therefore also the jump phenomena.
- The amplitude curve was exposed to a right-bending case (hardening phenomenon), a left-bending case (softening phenomenon), or a linear case depending on the sign of the cubic nonlinearity parameter.
- The excitation force amplitude and the damping factor could play an important role in tightening the range of the jump phenomena on the amplitude curve.
- B.
- When the controller was ON:
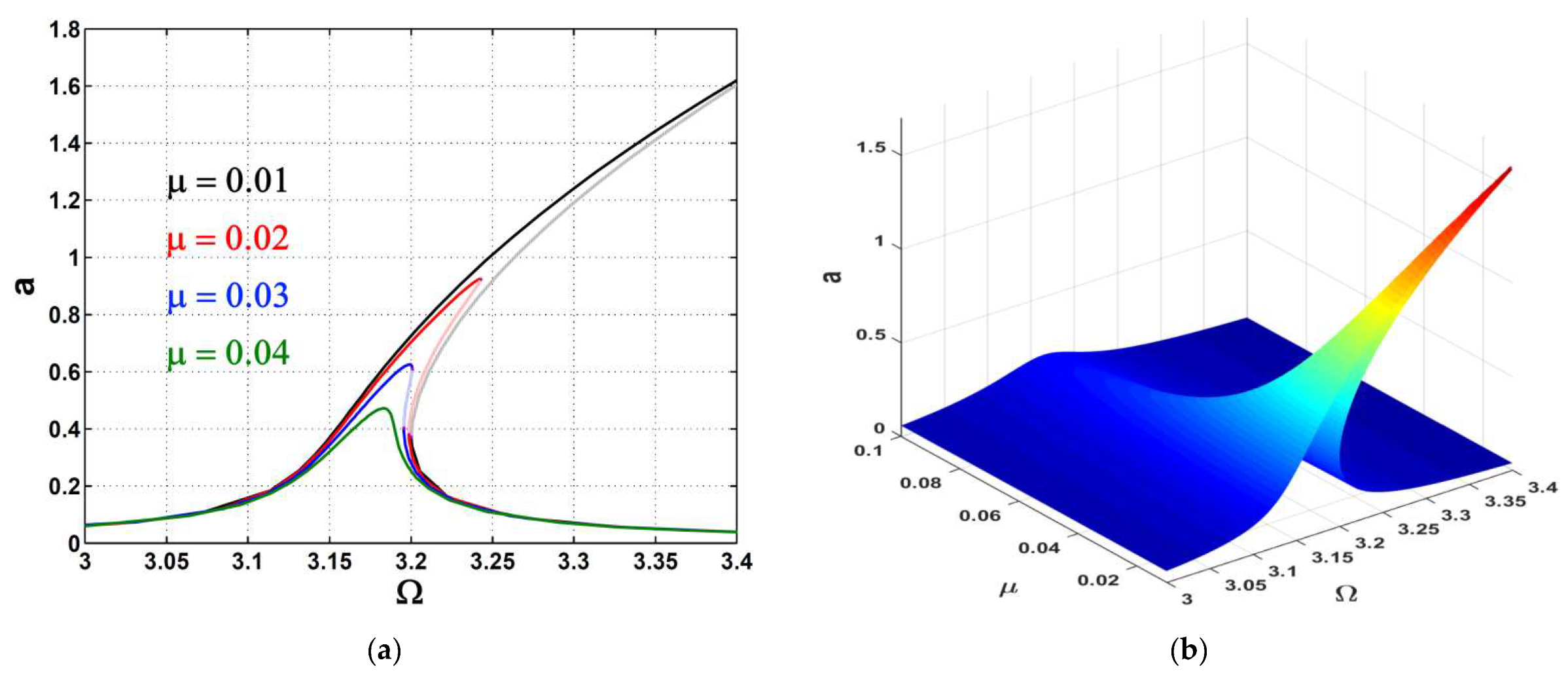
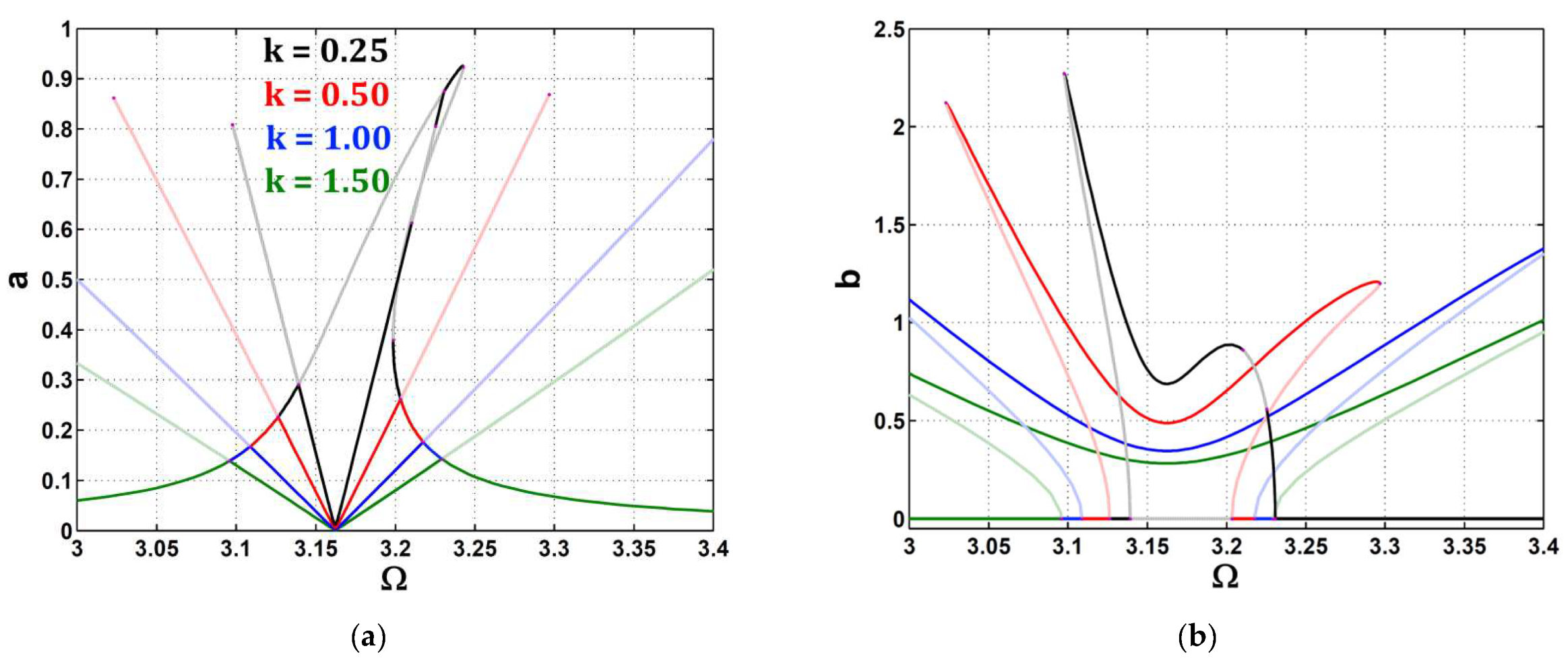
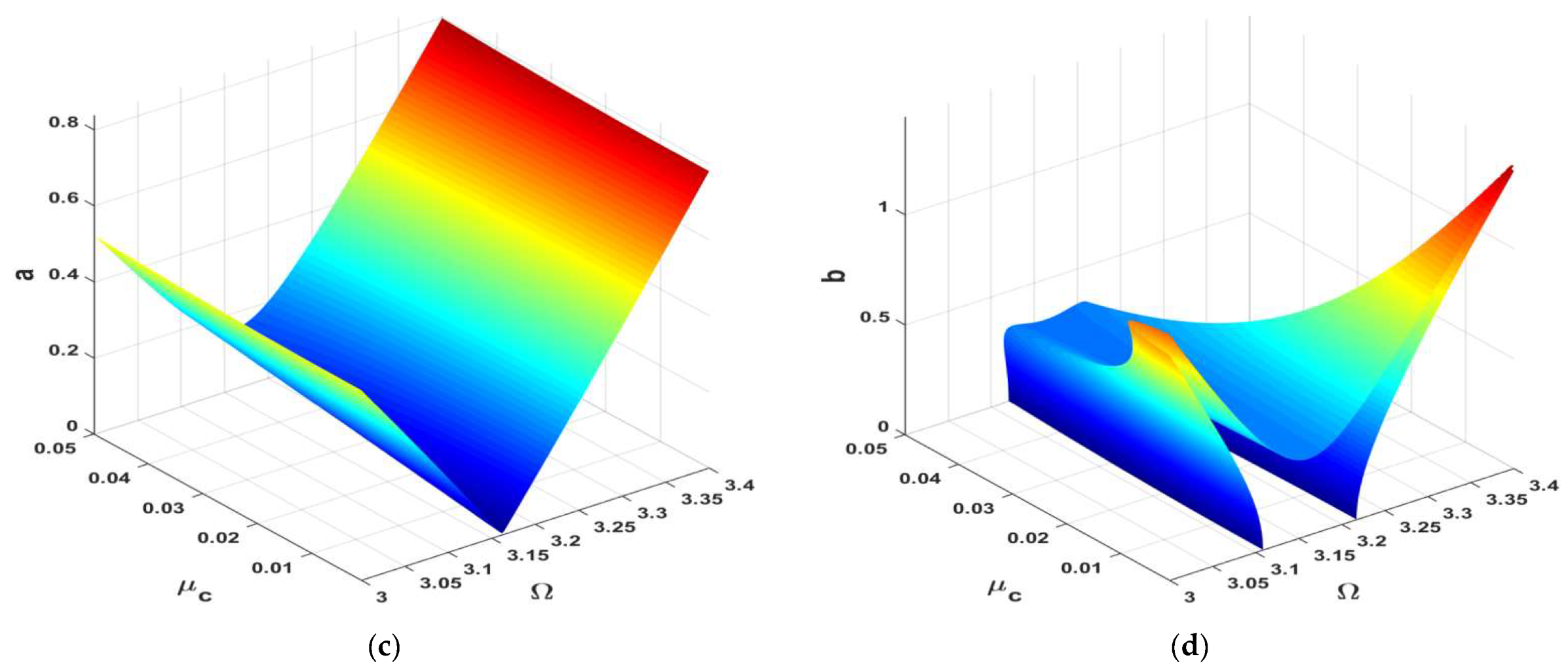
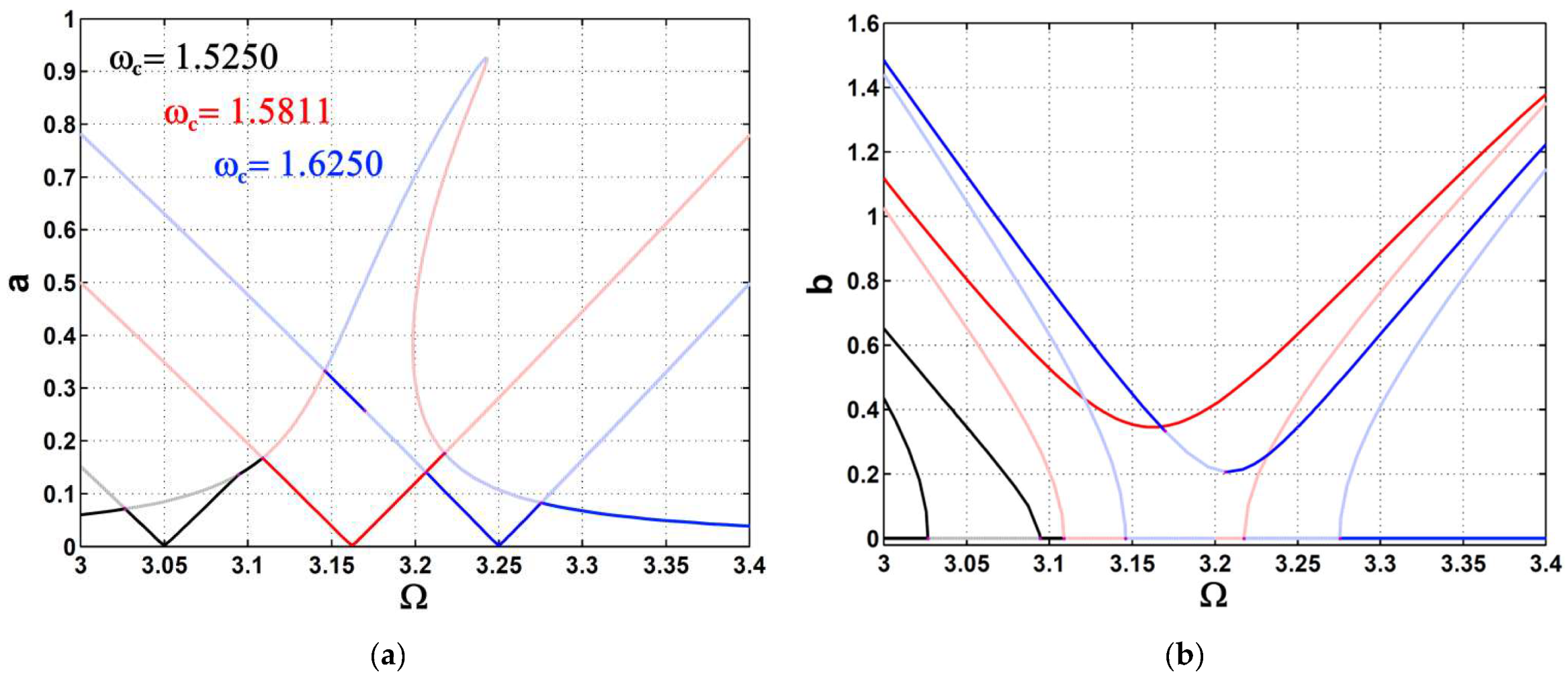
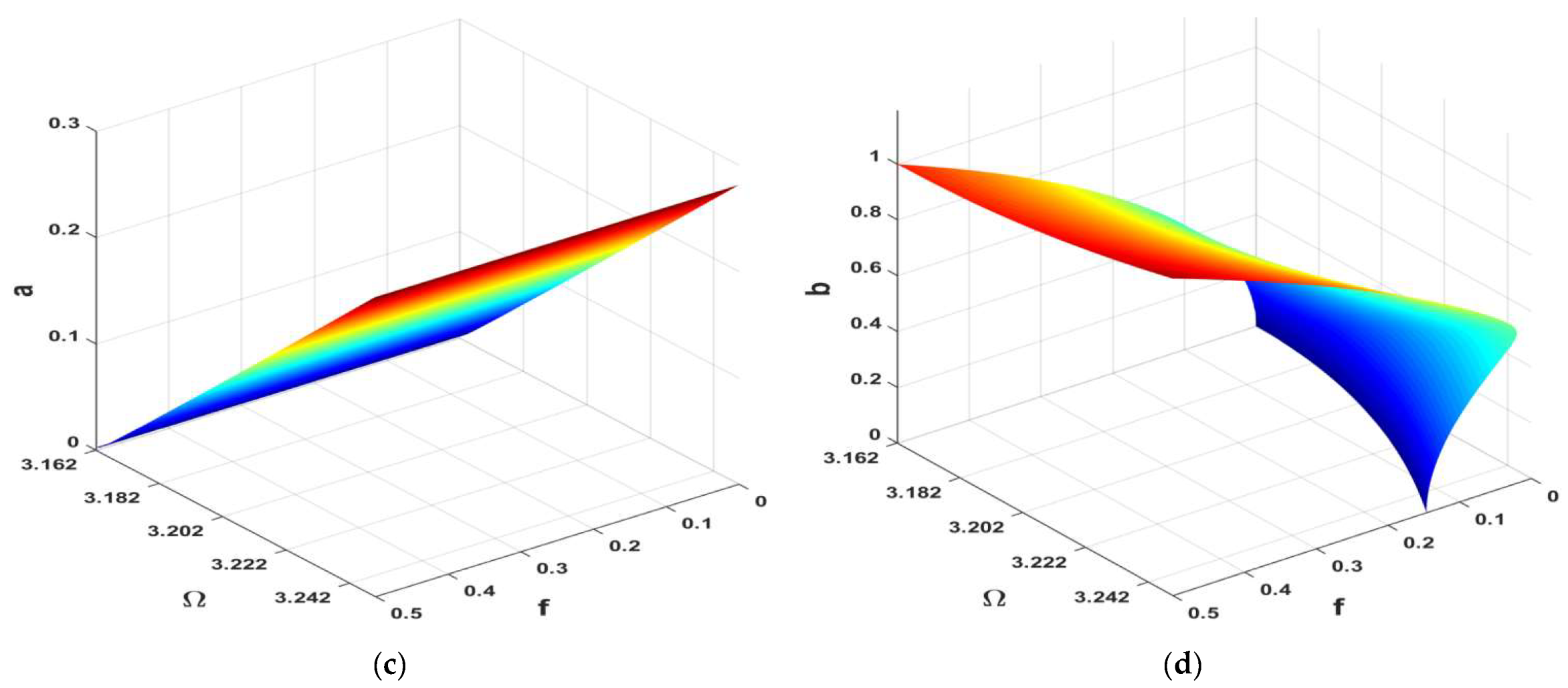
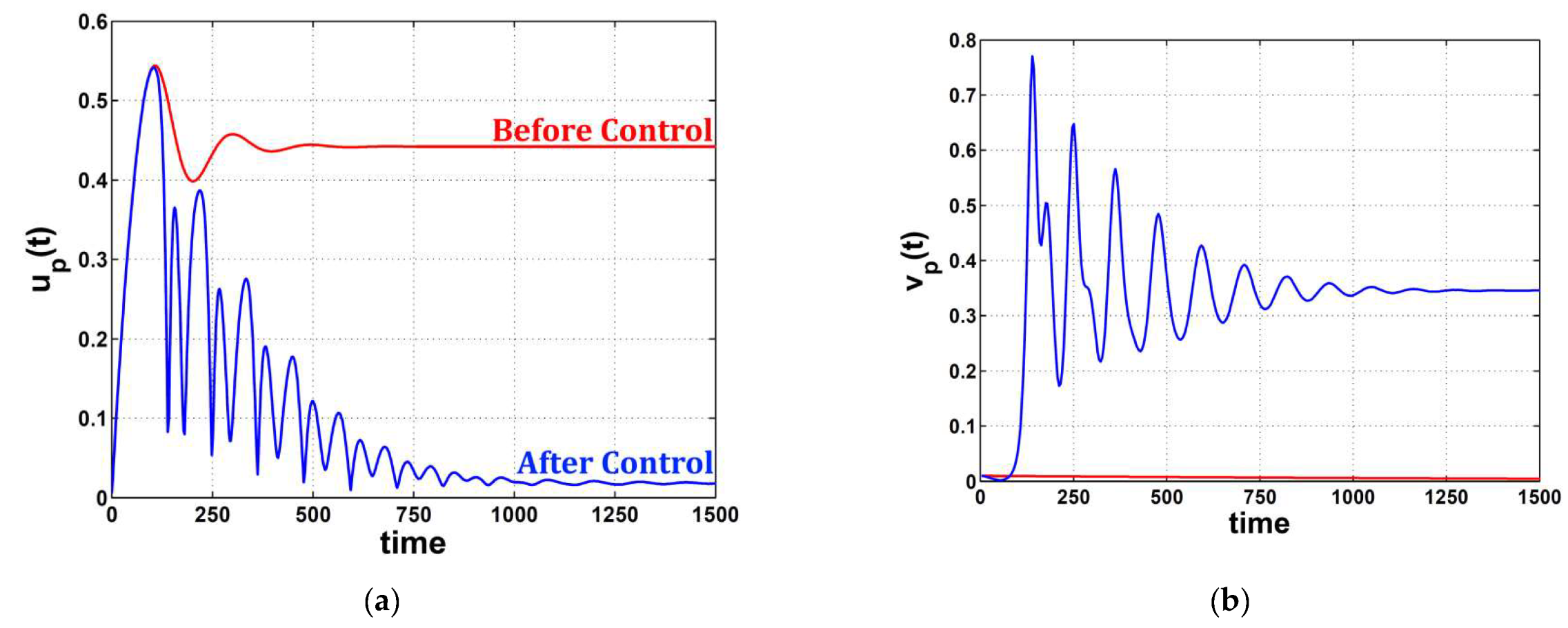
- The car’s amplitude took a new V-shaped path, departing from the previous path of higher values.
- The control and feedback gains could control the intersection band between the V-curve and the previous curve, where the bigger the gains were, the wider the V-curve became.
- The apex of the V-curve was at the point at which the system was designed to run.
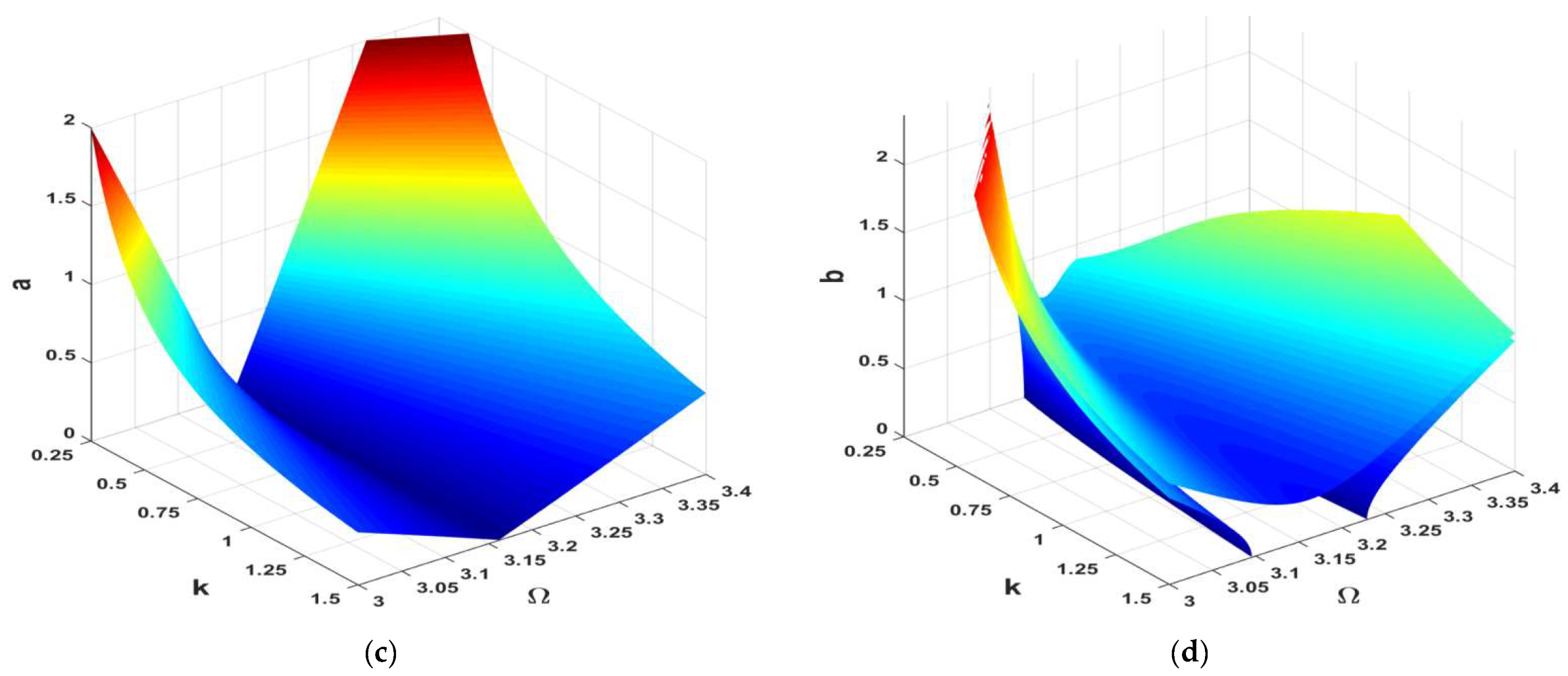
- Keeping the controller’s damping parameter at lower values took the car’s amplitude to its minimum level.
- The car’s amplitude was saturated at a specific level, keeping the V-curve unchanged even if the excitation force changed.
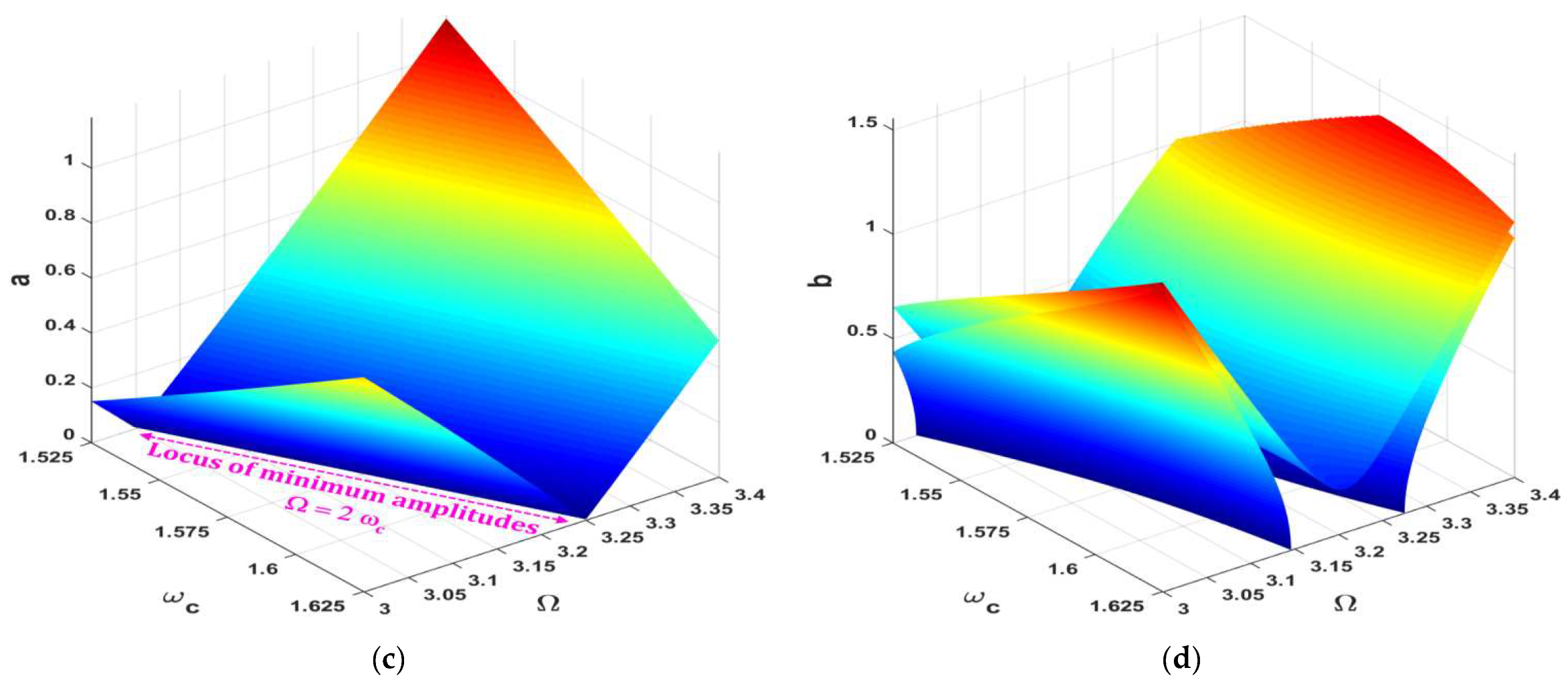
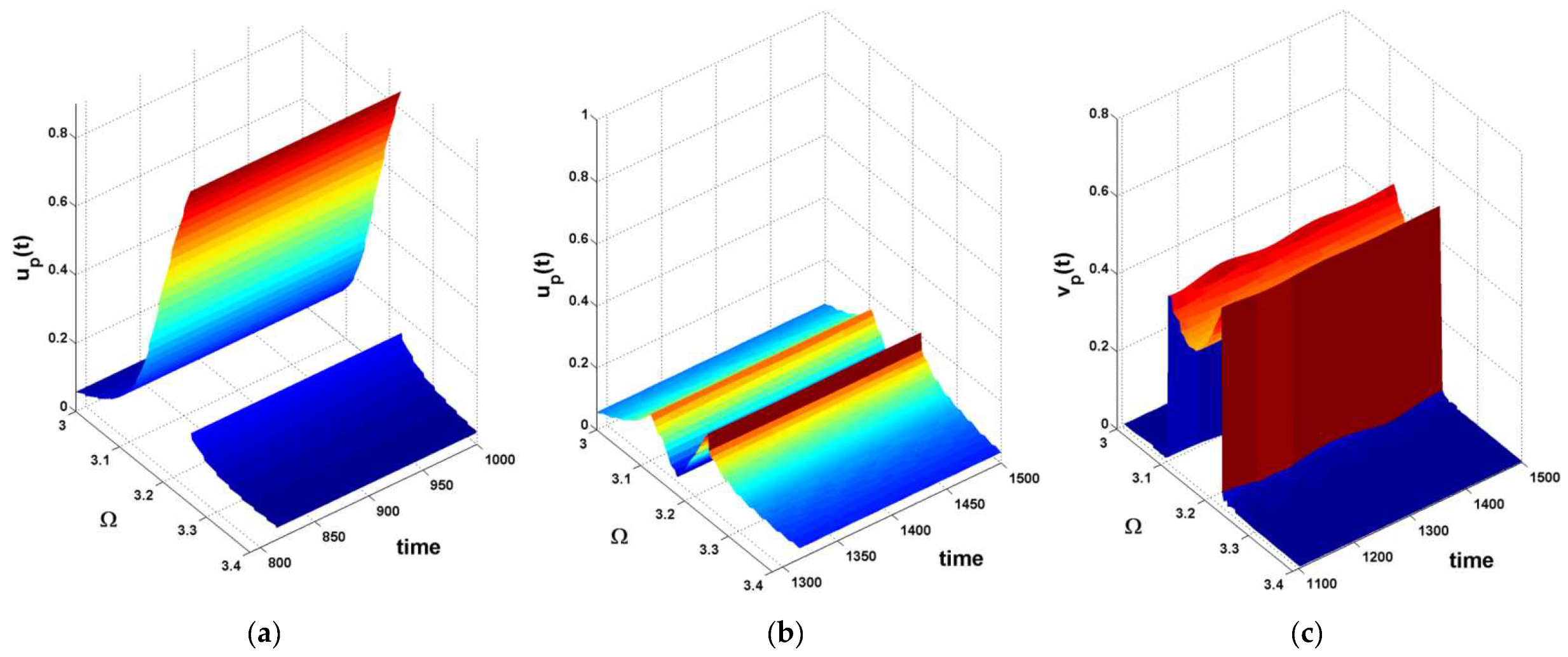
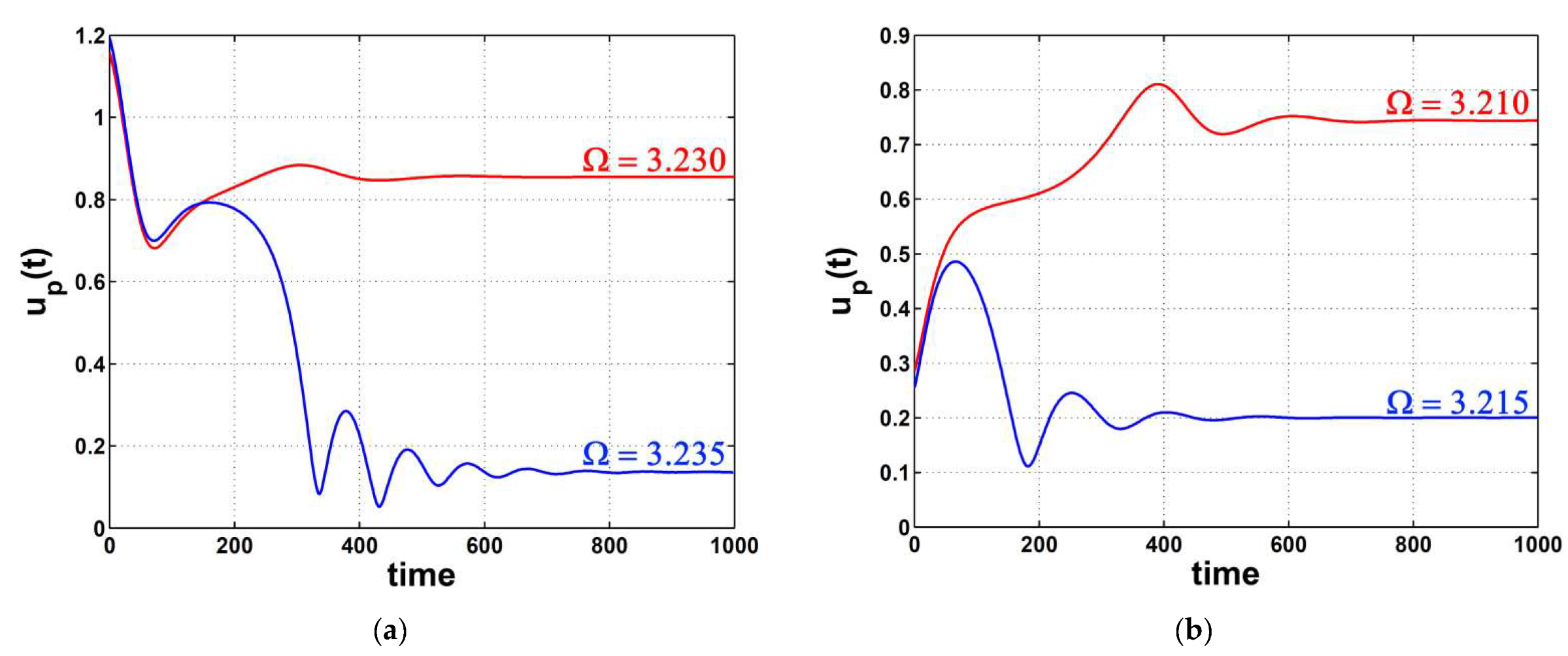
- The key to keeping the car’s amplitude at almost zero was to guarantee that even if the excitation frequency changed.
- In case of mistuning such that , the car’s amplitude could increase slightly with until a specific value of at which the amplitude could saturate independently of .
- The car’s vibrations were suppressed by about according to the numerical simulations of the studied model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Definition |
| Displacement of the car as a function of time | |
| Mass of the car | |
| Viscosity parameter of the dashpot | |
| Linear and cubic stiffness parameters of the spring | |
| Amplitude of the external excitation force | |
| Angular frequency of the external excitation | |
| The control signal as a function of time | |
| Damping parameter of the controller | |
| Angular natural frequency of the controller | |
| Gains of the control signal and the feedback signal | |
| Approximate amplitudes of and | |
| Approximate phases of and | |
| Floquet characteristic exponent |
References
- Hamdan, M.N.; Burton, T.D. On the steady state response and stability of non-linear oscillators using harmonic balance. J. Sound Vib. 1993, 166, 255–266. [Google Scholar] [CrossRef]
- Hassan, A. On the local stability analysis of the approximate harmonic balance solutions. Nonlinear Dyn. 1996, 10, 105–133. [Google Scholar] [CrossRef]
- Hamdan, M.N.; Shabaneh, N.H. On the period of large amplitude free vibration of conservative autonomous oscillators with static and inertia type cubic non-linearities. J. Sound Vib. 1997, 199, 737–750. [Google Scholar] [CrossRef]
- Maccari, A. Response of an oscillator moving along a parabola to an external excitation. Nonlinear Dyn. 2000, 23, 205–223. [Google Scholar] [CrossRef]
- Al-Qaisia, A.A.; Hamdan, M.N. Bifurcations and chaos of an immersed cantilever beam in a fluid and carrying an intermediate mass. J. Sound Vib. 2003, 253, 859–888. [Google Scholar] [CrossRef]
- Dunne, J.F. Subharmonic-response computation and stability analysis for a nonlinear oscillator using a split-frequency harmonic balance method. J. Comput. Nonlinear Dyn. 2006, 1, 221–229. [Google Scholar] [CrossRef]
- Malatkar, P.; Nayfeh, A.H. Steady-State dynamics of a linear structure weakly coupled to an essentially nonlinear oscillator. Nonlinear Dyn. 2007, 47, 167–179. [Google Scholar] [CrossRef]
- Zhang, B.; Billings, S.A.; Lang, Z.Q.; Tomlinson, G.R. A novel nonlinear approach to suppress resonant vibrations. J. Sound Vib. 2008, 317, 918–936. [Google Scholar] [CrossRef][Green Version]
- Carrella, A.; Brennan, M.J.; Kovacic, I.; Waters, T.P. On the force transmissibility of a vibration isolator with quasi-zero-stiffness. J. Sound Vib. 2009, 322, 707–717. [Google Scholar] [CrossRef]
- Gatti, G.; Brennan, M.J.; Kovacic, I. On the interaction of the responses at the resonance frequencies of a nonlinear two degrees-of-freedom system. Phys. D Nonlinear Phenom. 2010, 239, 591–599. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Nayfeh, N.A. Analysis of the cutting tool on a lathe. Nonlinear Dyn. 2011, 63, 395–416. [Google Scholar] [CrossRef]
- Luo, A.C.J.; O’Connor, D. Stable and unstable periodic solutions to the Mathieu-Duffing oscillator. In Proceedings of the IEEE 4th International Conference on Nonlinear Science and Complexity, NSC, Budapest, Hungary, 6–11 August 2012; pp. 201–204. [Google Scholar]
- Le, T.D.; Ahn, K.K. Experimental investigation of a vibration isolation system using negative stiffness structure. Int. J. Mech. Sci. 2013, 70, 99–112. [Google Scholar] [CrossRef]
- Ji, J.C.; Zhang, N. Suppression of the primary resonance vibrations of a forced nonlinear system using a dynamic vibration absorber. J. Sound Vib. 2010, 329, 2044–2056. [Google Scholar] [CrossRef]
- Ji, J.C.; Zhang, N. Suppression of super-harmonic resonance response using a linear vibration absorber. Mech. Res. Commun. 2011, 38, 411–416. [Google Scholar] [CrossRef]
- Ji, J.C. Secondary resonances of a quadratic nonlinear oscillator following two-to-one resonant Hopf bifurcations. Nonlinear Dyn. 2014, 78, 2161–2184. [Google Scholar] [CrossRef]
- Ji, J.C. Two families of super-harmonic resonances in a time-delayed nonlinear oscillator. J. Sound Vib. 2015, 349, 299–314. [Google Scholar] [CrossRef]
- Kamel, M.; Kandil, A.; El-Ganaini, W.A.; Eissa, M. Active vibration control of a nonlinear magnetic levitation system via Nonlinear Saturation Controller (NSC). Nonlinear Dyn. 2014, 77, 605–619. [Google Scholar] [CrossRef]
- Eissa, M.; Kandil, A.; El-Ganaini, W.A.; Kamel, M. Vibration suppression of a nonlinear magnetic levitation system via time delayed nonlinear saturation controller. Int. J. Non. Linear. Mech. 2015, 72, 23–41. [Google Scholar] [CrossRef]
- Hao, Z.; Cao, Q. The isolation characteristics of an archetypal dynamical model with stable-quasi-zero-stiffness. J. Sound Vib. 2015, 340, 61–79. [Google Scholar] [CrossRef]
- EL-Sayed, A.T.; Bauomy, H.S. Vibration suppression of subharmonic resonance response using a nonlinear vibration absorber. J. Vib. Acoust. Trans. ASME 2015, 137. [Google Scholar] [CrossRef]
- Motallebi, A.; Irani, S.; Sazesh, S. Analysis on jump and bifurcation phenomena in the forced vibration of nonlinear cantilever beam using HBM. J. Brazilian Soc. Mech. Sci. Eng. 2016, 38, 515–524. [Google Scholar] [CrossRef]
- Pérez-Molina, M.; Gil-Chica, J.; Fernández-Varó, E.; Pérez-Polo, M.F. Steady state, oscillations and chaotic behavior of a gas inside a cylinder with a mobile piston controlled by PI and nonlinear control. Commun. Nonlinear Sci. Numer. Simul. 2016, 36, 468–495. [Google Scholar] [CrossRef][Green Version]
- Zhou, S.; Song, G.; Sun, M.; Ren, Z. Nonlinear dynamic analysis of a quarter vehicle system with external periodic excitation. Int. J. Non. Linear. Mech. 2016, 84, 82–93. [Google Scholar] [CrossRef]
- Kandil, A.; Eissa, M. Improvement of positive position feedback controller for suppressing compressor blade oscillations. Nonlinear Dyn. 2017, 90, 1727–1753. [Google Scholar] [CrossRef]
- Kandil, A. Study of Hopf curves in the time delayed active control of a 2DOF nonlinear dynamical system. SN Appl. Sci. 2020, 2, 1924. [Google Scholar] [CrossRef]
- Silveira, M.; Wahi, P.; Fernandes, J.C.M. Effects of asymmetrical damping on a 2 DOF quarter-car model under harmonic excitation. Commun. Nonlinear Sci. Numer. Simul. 2017, 43, 14–24. [Google Scholar] [CrossRef]
- Kandil, A.; El-Gohary, H.A. Suppressing the nonlinear vibrations of a compressor blade via a nonlinear saturation controller. JVC/J. Vib. Control. 2018, 24, 1488–1504. [Google Scholar] [CrossRef]
- Hamed, Y.S.; Kandil, A. Influence of time delay on controlling the non-linear oscillations of a rotating blade. Symmetry 2021, 13, 85. [Google Scholar] [CrossRef]
- Zhou, S.; Song, G.; Li, Y.; Huang, Z.; Ren, Z. Dynamic and steady analysis of a 2-DOF vehicle system by modified incremental harmonic balance method. Nonlinear Dyn. 2019, 98, 75–94. [Google Scholar] [CrossRef]
- Kandil, A.; Hamed, Y.S. Tuned Positive Position Feedback Control of an Active Magnetic Bearings System with 16-Poles and Constant Stiffness. IEEE Access 2021, 9, 73857–73872. [Google Scholar] [CrossRef]
- Kandil, A.; Hamed, Y.S.; Alsharif, A.M. Rotor Active Magnetic Bearings System Control via a Tuned Nonlinear Saturation Oscillator. IEEE Access 2021, 9, 133694–133709. [Google Scholar] [CrossRef]
- Uemori, M.; Yabuno, H.; Ymamamoto, Y.; Matsumoto, S. Highly sensitive measurements of perturbations in stiffness of a resonator by virtual coupling with a virtual resonator. Nonlinear Dyn. 2021, 107, 1755–1764. [Google Scholar] [CrossRef]
- Kandil, A.; Hamed, Y.S.; Alsharif, A.M.; Awrejcewicz, J. 2D and 3D visualizations of the mass-damper-spring model dynamics controlled by a servo-controlled linear actuator. IEEE Access 2021, 9, 153012–153026. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Krack, M.; Gross, J. Harmonic Balance for Nonlinear Vibration Problems; Springer Nature: Cham, Switzerland, 2019. [Google Scholar]
- Nayfeh, A.H.; Balachandran, B. Applied Nonlinear Dynamics; Wiley: New York, NY, USA, 1995. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kandil, A.; Hamed, Y.S.; Awrejcewicz, J. Harmonic Balance Method to Analyze the Steady-State Response of a Controlled Mass-Damper-Spring Model. Symmetry 2022, 14, 1247. https://doi.org/10.3390/sym14061247
Kandil A, Hamed YS, Awrejcewicz J. Harmonic Balance Method to Analyze the Steady-State Response of a Controlled Mass-Damper-Spring Model. Symmetry. 2022; 14(6):1247. https://doi.org/10.3390/sym14061247
Chicago/Turabian StyleKandil, Ali, Y. S. Hamed, and Jan Awrejcewicz. 2022. "Harmonic Balance Method to Analyze the Steady-State Response of a Controlled Mass-Damper-Spring Model" Symmetry 14, no. 6: 1247. https://doi.org/10.3390/sym14061247
APA StyleKandil, A., Hamed, Y. S., & Awrejcewicz, J. (2022). Harmonic Balance Method to Analyze the Steady-State Response of a Controlled Mass-Damper-Spring Model. Symmetry, 14(6), 1247. https://doi.org/10.3390/sym14061247







