Conditioned Adaptive Control for an Uncertain Bioreactor with Input Saturation and Steep Settling Desired Output
Abstract
:1. Introduction
- −
- Contribution Ci. The effect of input constraint limits and desired output on the convergence of the tracking error during input saturation events is determined. In contrast, in current adaptive AES-based control (for instance [11,16,17,18]), the convergence of the tracking error is determined in terms of the controller parameters, not in terms of input constraint limits or desired out.
- −
- Contribution Cii. The upper limit of the input constraint guaranteeing output convergence during input saturation events is determined as a function of the model terms, but independent of the time derivative of the desired output and its limit. In contrast, this limit is not computed in common AES-based controllers (for instance [11,13,14,15,16,17,18,19]).
- −
- Contribution Ciii. Differently from [20], a new dead zone Lyapunov function is proposed which allows proving asymptotic convergence of the tracking error during input saturation events, considering desired output featuring settling behavior with a steep section.
2. Bioreactor Model, Reference Model, Control Goal, Materials and Methods
2.1. Bioreactor Model
2.2. Control Goal and Reference Model
2.3. Materials and Methods: Overview of the Method for Control Design and Stability Analysis
- −
- Definition of the input saturation conditions;
- −
- Definition of the tracking error dynamics, ;
- −
- Definition of the main features of the Lyapunov function for , , and of the gradient of , that is, ;
- −
- Determination of the expression;
- −
- Formulation of the control and update laws and determination of the expression for the case of no input saturation events, being the Lyapunov function;
- −
- Formulation of the control and update laws and the determination of the expression for the case of input saturation events;
- −
- Determination of the unified expression, combining saturation and no saturation events;
- −
- Determination of the convergence of the tracking error and boundedness of the updated parameter, for the whole closed-loop regime encompassing saturation and non-saturation events.
3. Control Algorithm, Controller Design, and Stability Analysis
- −
- The asymptotic convergence of the tracking error to the compact set is guaranteed, during the whole closed-loop regime in presence of input saturation events, and also it is guaranteed during input saturation events, considering high values occurring during some time lapses.
- −
- The condition for computing the limit for the input constraint is determined, which leads to asymptotic convergence of the tracking error in presence of input saturation events and is independent of .
- −
- A new dead zone Lyapunov function is proposed which allows proving the asymptotic convergence of the tracking error during input saturation events, considering desired output featuring settling behavior with a steep section.
3.1. Control Algorithm
3.2. Controller Design and Stability Analysis
3.3. Discussion of Results
- −
- The asymptotic convergence of the tracking error to the compact set is guaranteed, during the whole closed-loop regime in the presence of input saturation events, and also it is guaranteed during input saturation events, which is stated in Theorem 1, Tii.
- −
- The absence of an excessive increase in the updated parameter , is guaranteed, in the presence of input saturation events and high values occurring during some time lapses, which is stated in Theorem 1, Ti.
- −
- The condition (6) for computing is determined, which leads to an asymptotic convergence of the tracking error in the presence of input saturation events and is independent of . Condition (6) is included in Theorem 1.
- −
- The convergence rate of the tracking error during no saturation input events is achieved by properly setting the controller parameters;
- −
- The uncertainty on the substrate consumption rate is tackled by means of the updated parameter ;
- −
- The uncertainty on is tackled through the robustness strategy.
- −
- During input saturation events featuring , the first term of the expression is negative for zero ;
- −
- During input saturation events featuring , the first term depends on the upper saturation limit , the inflow concentration and the substrate consumption rate, and is rendered negative by using high enough values of . In the determination of , it is considered that the dilution rate must overcome the biological substrate consumption, to avoid substrate depletion, but the time varying nature of the feed substrate concentration is also taken into account. However, neither nor its bound are accounted in the value, because is vanishing;
- −
- The term of the expression may take on positive values, thus leading to positive . However, the tracking error convergence and parameter boundedness are yet to be obtained, due to the vanishing nature of . To prove these stability features, a new Lyapunov function of the tracking error is proposed, which is bounded for infinite values of the tracking error. The convergence of the tracking error is achieved even in the case of permanent input saturation.
4. Numerical Simulation
General Discussion on the Simulation Results
- −
- −
- Condition (6) for computing was adequate, as the asymptotic convergence of the tracking error was achieved.
- −
- There was no excessive increase in the updated parameter , which was also noticed during high values,
- −
- A fast convergence of the tracking error was achieved by properly setting the controller parameters,
- −
- The uncertainty on the substrate consumption rate was properly tackled by means of the updated parameter ;
- −
- The uncertainty on was properly tackled through the robustness strategy.
5. Conclusions
- −
- Contribution Ci. The effect of input constraint limits and desired output on the convergence of the tracking error during input saturation events was determined.
- −
- Contribution Cii. The upper limit of the input constraint guaranteeing output convergence during input saturation events was defined as a function of the model terms, but was independent of the time derivative of the desired output and its limit.
- −
- Contribution Ciii. A new dead zone Lyapunov function was proposed which allows proving the convergence of the tracking error during input saturation events, considering fast variation in the desired output.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Result (21)
References
- Alshammari, O.; Mahyuddin, M.N.; Jerbi, H. A Survey on Control Techniques of a Benchmarked Continuous Stirred Tank Reactor. J. Eng. Sci. Technol. 2018, 13, 3277–3296. [Google Scholar]
- Franco-de los Reyes, H.A.; Alvarez, J. Saturated Output-Feedback Control and State Estimation of a Class of Exothermic Tubular Reactors. J. Process Control 2022, 112, 78–95. [Google Scholar] [CrossRef]
- Bastin, G.; Dochain, D. On-Line Estimation and Adaptive Control of Bioreactors; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Méndez-Acosta, H.O.; Campos-Delgado, D.U.; Femat, R.; González-Alvarez, V. A Robust Feedforward/Feedback Control for an Anaerobic Digester. Comput. Chem. Eng. 2005, 29, 1613–1623. [Google Scholar] [CrossRef]
- Méndez-Acosta, H.O.; Palacios-Ruiz, B.; Alcaraz-González, V.; González-Álvarez, V.; García-Sandoval, J.P. A Robust Control Scheme to Improve the Stability of Anaerobic Digestion Processes. J. Process Control 2010, 20, 375–383. [Google Scholar] [CrossRef]
- Hägglund, T.; Shinde, S.; Theorin, A.; Thomsen, U. An Industrial Control Loop Decoupler for Process Control Applications. Control Eng. Pract. 2022, 123, 105138. [Google Scholar] [CrossRef]
- Zhou, Z.; Tang, G.; Huang, H.; Han, L.; Xu, R. Adaptive Nonsingular Fast Terminal Sliding Mode Control for Underwater Manipulator Robotics with Asymmetric Saturation Actuators. Control Theory Technol. 2020, 18, 81–91. [Google Scholar] [CrossRef]
- Shahriari-Kahkeshi, M. Dead-Zone Model-Based Adaptive Fuzzy Wavelet Control for Nonlinear Systems Including Input Saturation and Dynamic Uncertainties. Int. J. Fuzzy Syst. 2018, 20, 2577–2592. [Google Scholar] [CrossRef]
- Polycarpou, M.; Farrell, J.; Sharma, M. On-Line Approximation Control of Uncertain Nonlinear Systems: Issues with Control Input Saturation. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 543–548. [Google Scholar]
- Zhang, W.; Yi, W. Fuzzy Observer-Based Dynamic Surface Control for Input-Saturated Nonlinear Systems and Its Application to Missile Guidance. IEEE Access 2020, 8, 121285–121298. [Google Scholar] [CrossRef]
- Shao, K.; Tang, R.; Xu, F.; Wang, X.; Zheng, J. Adaptive Sliding Mode Control for Uncertain Euler–Lagrange Systems with Input Saturation. J. Frankl. Inst. 2021, 358, 8356–8376. [Google Scholar] [CrossRef]
- Gao, S.; Ning, B.; Dong, H. Fuzzy Dynamic Surface Control for Uncertain Nonlinear Systems under Input Saturation via Truncated Adaptation Approach. Fuzzy Sets Syst. 2016, 290, 100–117. [Google Scholar] [CrossRef]
- Min, H.; Xu, S.; Ma, Q.; Zhang, B.; Zhang, Z. Composite-Observer-Based Output-Feedback Control for Nonlinear Time-Delay Systems with Input Saturation and Its Application. IEEE Trans. Ind. Electron. 2018, 65, 5856–5863. [Google Scholar] [CrossRef]
- Zeinali, S.; Shahrokhi, M. Observer-Based Singularity Free Nonlinear Controller for Uncertain Systems Subject to Input Saturation. Eur. J. Control 2020, 52, 49–58. [Google Scholar] [CrossRef]
- Meng, R.; Chen, S.; Hua, C.; Qian, J.; Sun, J. Disturbance Observer-Based Output Feedback Control for Uncertain QUAVs with Input Saturation. Neurocomputing 2020, 413, 96–106. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, C.; Wang, J.; Hua, C. Adaptive Fuzzy Output Feedback Controller Design for a HAGC System with Input Saturation and Output Error Constraints. J. Frankl. Inst. 2022, 359, 2030–2057. [Google Scholar] [CrossRef]
- Li, H.; Liu, Q.; Kong, L.; Zhang, X. Design of Adaptive Tracking Controller Using Barrier Functions for Nonlinear Systems with Input Saturation. J. Frankl. Inst. 2020, 357, 12555–12570. [Google Scholar] [CrossRef]
- Sun, J.; Liu, C. Auxiliary-System-Based Composite Adaptive Optimal Backstepping Control for Uncertain Nonlinear Guidance Systems with Input Constraints. ISA Trans. 2020, 107, 294–306. [Google Scholar] [CrossRef]
- Askari, M.R.; Shahrokhi, M.; Khajeh Talkhoncheh, M. Observer-Based Adaptive Fuzzy Controller for Nonlinear Systems with Unknown Control Directions and Input Saturation. Fuzzy Sets Syst. 2017, 314, 24–45. [Google Scholar] [CrossRef]
- Golkani, M.A.; Seeber, R.; Reichhartinger, M.; Horn, M. Lyapunov-based Saturated Continuous Twisting Algorithm. Int. J. Robust Nonlinear Control 2021, 31, 3513–3527. [Google Scholar] [CrossRef]
- Dochain, D.; Perrier, M.; Guay, M. Extremum Seeking Control and Its Application to Process and Reaction Systems: A Survey. Math. Comput. Simul. 2011, 82, 369–380. [Google Scholar] [CrossRef]
- de Battista, H.; Jamilis, M.; Garelli, F.; Picó, J. Global Stabilisation of Continuous Bioreactors: Tools for Analysis and Design of Feeding Laws. Automatica 2018, 89, 340–348. [Google Scholar] [CrossRef]
- Picó, J.; de Battista, H.; Garelli, F. Smooth Sliding-Mode Observers for Specific Growth Rate and Substrate from Biomass Measurement. J. Process Control 2009, 19, 1314–1323. [Google Scholar] [CrossRef]
- Neria-González, M.I.; Domínguez-Bocanegra, A.R.; Torres, J.; Maya-Yescas, R.; Aguilar-López, R. Linearizing Control Based on Adaptive Observer for Anaerobic Sulphate Reducing Bioreactors with Unknown Kinetics. Chem. Biochem. Eng. Q. 2009, 23, 179–185. [Google Scholar]
- Slotine, J.-J.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Astrom, K.J.; Wittenmark, B. Adaptive Control; Addison-Wesley Publishing Company: Reading, MA, USA, 1995. [Google Scholar]
- Koo, K.-M. Stable Adaptive Fuzzy Controller with Time-Varying Dead-Zone. Fuzzy Sets Syst. 2001, 121, 161–168. [Google Scholar] [CrossRef]
- Wang, X.-S.; Su, C.-Y.; Hong, H. Robust Adaptive Control of a Class of Nonlinear Systems with Unknown Dead-Zone. Automatica 2004, 40, 407–413. [Google Scholar] [CrossRef]
- Ranjbar, E.; Yaghubi, M.; Abolfazl Suratgar, A. Robust Adaptive Sliding Mode Control of a MEMS Tunable Capacitor Based on Dead-Zone Method. Automatika 2020, 61, 587–601. [Google Scholar] [CrossRef]
- Hong, Q.; Shi, Y.; Chen, Z. Dynamics Modeling and Tension Control of Composites Winding System Based on ASMC. IEEE Access 2020, 8, 102795–102810. [Google Scholar] [CrossRef]
- Rincón, A.; Hoyos, F.E.; Candelo-Becerra, J.E. Adaptive Control for a Biological Process under Input Saturation and Unknown Control Gain via Dead Zone Lyapunov Functions. Appl. Sci. 2020, 11, 251. [Google Scholar] [CrossRef]
- Rincón, A.; Restrepo, G.M.; Hoyos, F.E. A Robust Observer—Based Adaptive Control of Second—Order Systems with Input Saturation via Dead-Zone Lyapunov Functions. Computation 2021, 9, 82. [Google Scholar] [CrossRef]
- Rincón, A.; Restrepo, G.M.; Sánchez, Ó.J. An Improved Robust Adaptive Controller for a Fed-Batch Bioreactor with Input Saturation and Unknown Varying Control Gain via Dead-Zone Quadratic Forms. Computation 2021, 9, 100. [Google Scholar] [CrossRef]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; Prentice-Hall PTR: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Liu, C.; Yue, X.; Zhang, J.; Shi, K. Active Disturbance Rejection Control for Delayed Electromagnetic Docking of Spacecraft in Elliptical Orbits. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2257–2268. [Google Scholar] [CrossRef]
- Shi, K.; Liu, C.; Sun, Z.; Yue, X. Coupled Orbit-Attitude Dynamics and Trajectory Tracking Control for Spacecraft Electromagnetic Docking. Appl. Math. Model. 2022, 101, 553–572. [Google Scholar] [CrossRef]
- Rincón, A.; Cuellar, J.A.; Valencia, L.F.; Sánchez, O.J. Cinética de Crecimiento de Gluconacetobacter Diazotrophicus Usando Melaza de Caña y Sacarosa: Evaluación de Modelos Cinéticos. Acta Biol. Colomb. 2019, 24, 38–57. [Google Scholar] [CrossRef]



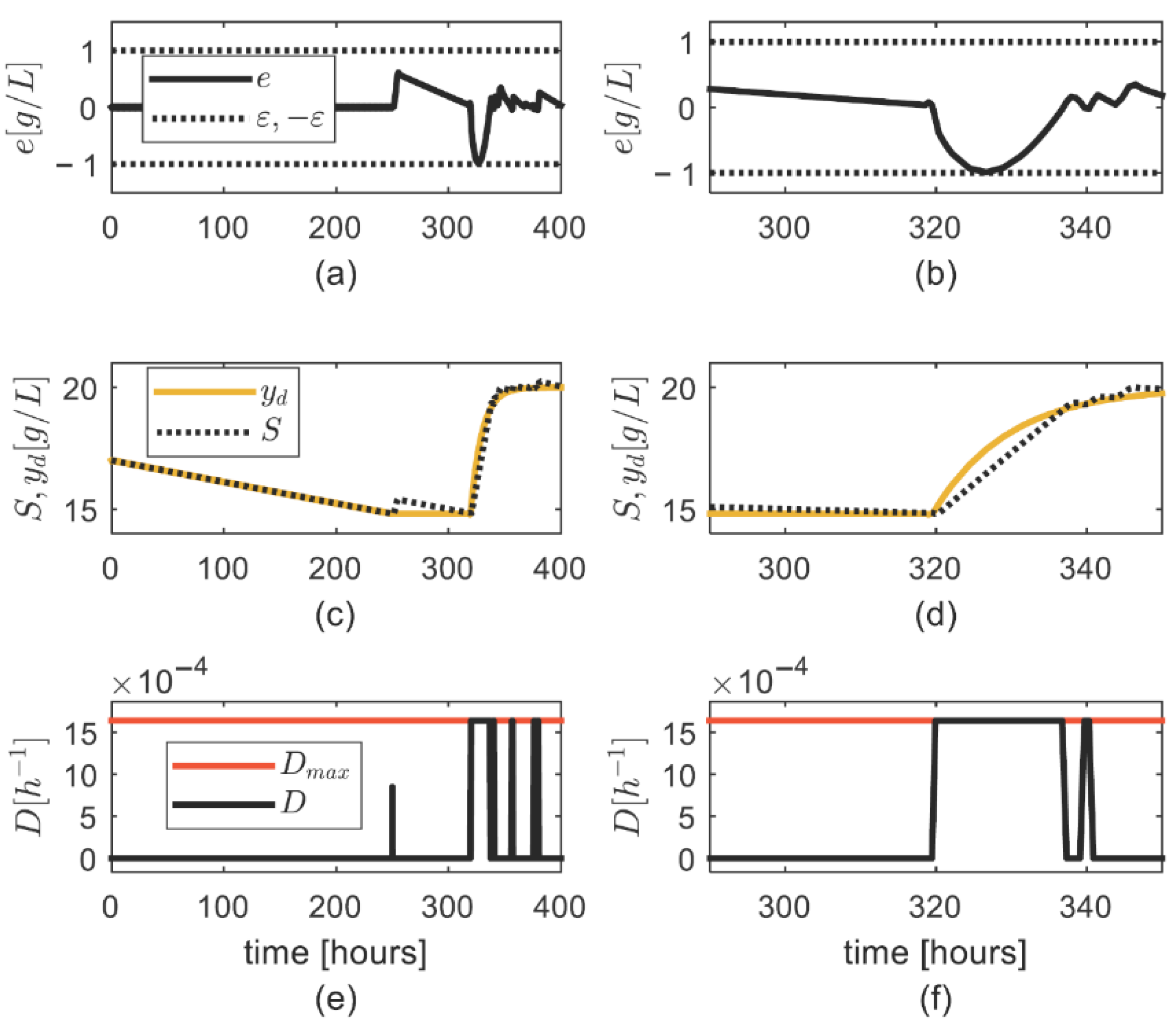
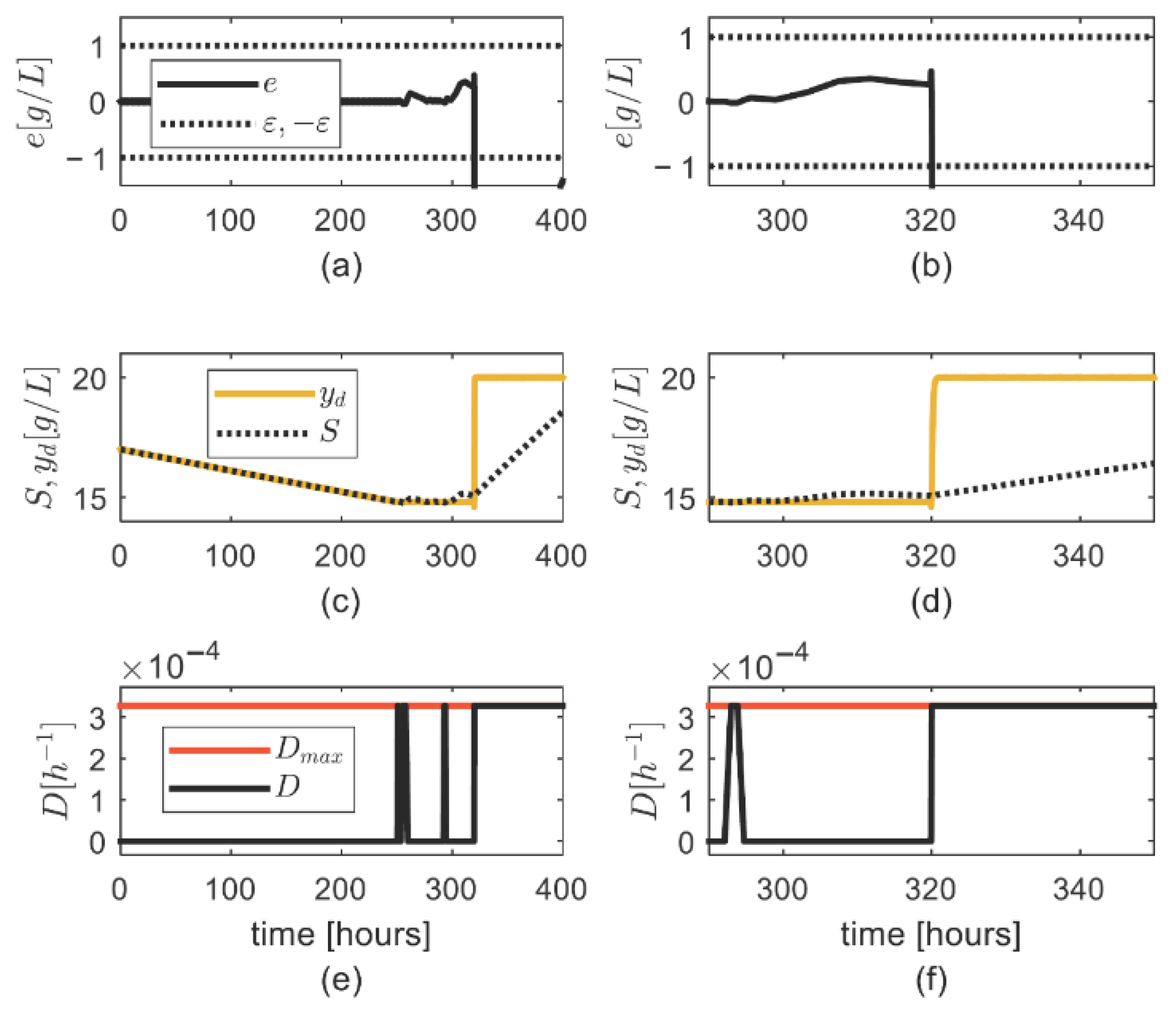
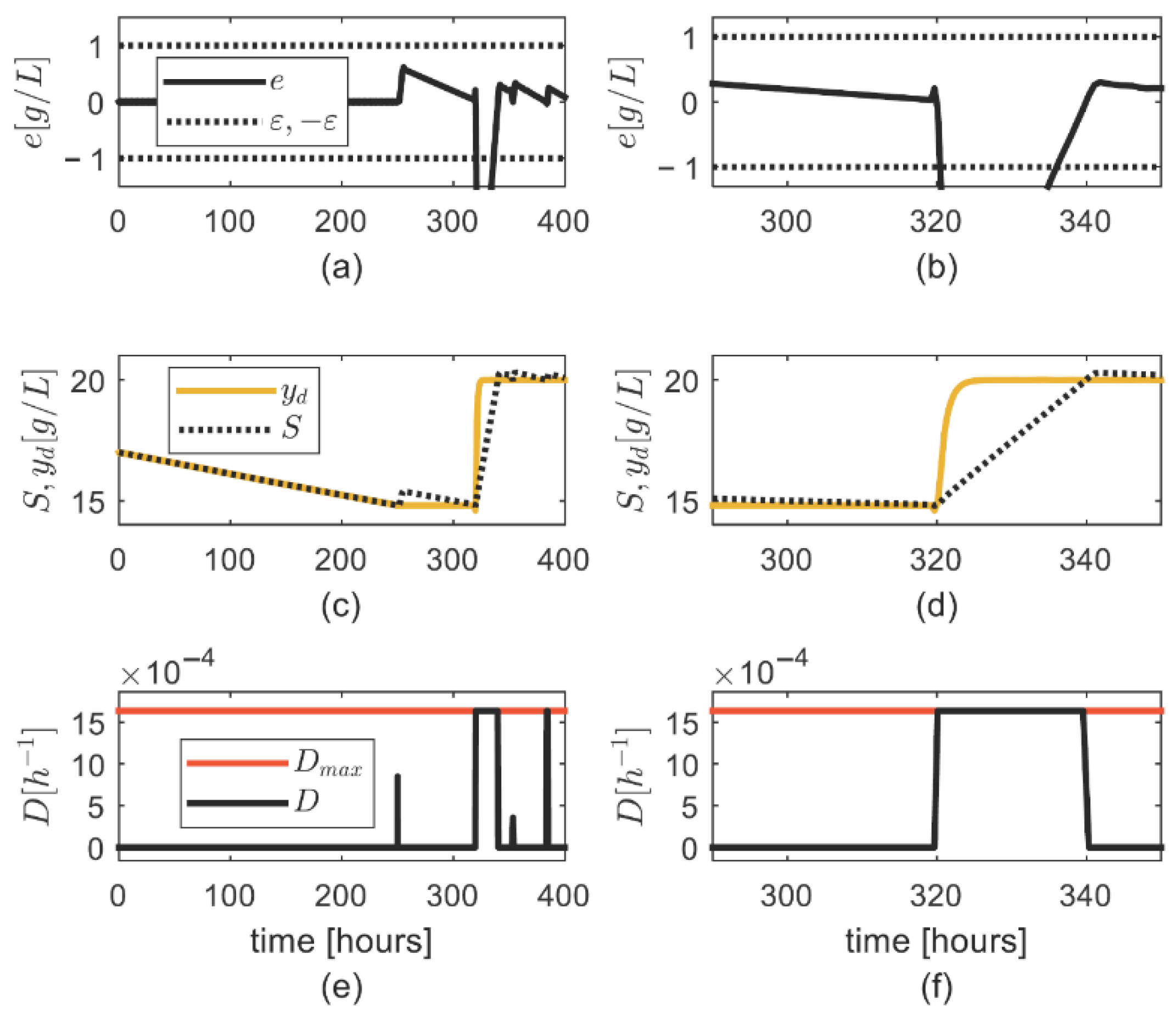
| Simulation Case | ||
|---|---|---|
| Case 1 | 0.0016 | 20 |
| Case 2 | 0.0016 | 0.1 |
| Case 3 | 0.000327 | 7 |
| Case 4 | 0.0016 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rincón, A.; Hoyos, F.E.; Candelo-Becerra, J.E. Conditioned Adaptive Control for an Uncertain Bioreactor with Input Saturation and Steep Settling Desired Output. Symmetry 2022, 14, 1232. https://doi.org/10.3390/sym14061232
Rincón A, Hoyos FE, Candelo-Becerra JE. Conditioned Adaptive Control for an Uncertain Bioreactor with Input Saturation and Steep Settling Desired Output. Symmetry. 2022; 14(6):1232. https://doi.org/10.3390/sym14061232
Chicago/Turabian StyleRincón, Alejandro, Fredy E. Hoyos, and John E. Candelo-Becerra. 2022. "Conditioned Adaptive Control for an Uncertain Bioreactor with Input Saturation and Steep Settling Desired Output" Symmetry 14, no. 6: 1232. https://doi.org/10.3390/sym14061232
APA StyleRincón, A., Hoyos, F. E., & Candelo-Becerra, J. E. (2022). Conditioned Adaptive Control for an Uncertain Bioreactor with Input Saturation and Steep Settling Desired Output. Symmetry, 14(6), 1232. https://doi.org/10.3390/sym14061232








