Two New Models for Dynamic Linear Elastic Beams and Simplifications for Double Symmetric Cross-Sections

Abstract

We present two new models for dynamic beams deduced from three dimensional theory of linear elasticity. The first model is deduced from virtual work considered for small beam sections. For the second model, we suppose a Taylor-Young expansion of the displacement field up to the fourth order in transverse dimensions of the beam. We consider the Fourier series expansion for considering Neumann lateral boundary conditions together with dynamical equations, we obtain a system of fifteen vector equations with the fifteen coefficients vector unknown of the displacement field. For beams with two fold symmetric cross sections commonly used (for example circular, square, rectangular, elliptical…), a unique decomposition of any three-dimensional loads is proposed and the symmetries of these loads is introduced. For these two theories, we show that the initial problem decouples into four subproblems. For an orthotropic material, these four subproblems are completely independent. For a monoclinic material, two subproblems are coupled and independent of the two other coupled subproblems. For the first model, we also give the detailed expression of these four subproblems when we consider the approximation of the displacement field used in the second model.

1. Introduction

Beams are very important engineering structures. Dimensions of the cross section of beams are much smaller than the third one, which is its length. To take advantage of this relative smallness, one may model the behavior of these structures by one-dimensional theory through certain dimensional reduction processes. The most popular approach relies on some kinematic assumptions which leads to classical beam theories, such as the Euler-Bernoulli theory, Timoshenko theory and the well-known Reddy’s third-order theory [1]. Various forms of this approach are used by Carrera and Giunta [2] and Carrera and Petrolo [3] to obtain results with a high degree of accuracy. Other authors consider first a rescaling of the initial physical problem and then apply the asymptotic analysis method (Trabucho and Viano [4], Zhao et al. [5]). Besides Trabucho and Viano [6] have proved rigourous convergence for their asymptotic model, they have to suppose an order of magnitude of both the imposed traction force and the body force. But what happens to other types of load scaling? This question is adressed in a systematic way in nonlinear setting by Meunier [7] and Marigo and Meunier [8]. They obtain a hierarchy of one dimensional beam models, each linked to specific load scaling. But in reality all effects predicted by this type of model are coupled and so it will be interesting to get a model independent of the order of the magnitude of the load.

However one dimensional beam theories deduced from the three dimensional theory of linear elasticity without any kinematic assumptions (except the necessary truncation of the Taylor-Young expansion of the displacement field at an optimal order) and any assumptions on the scaling of loads are scarce. The recent work of Schneider and Keinzler [9,10] is such as a theory presented in linear static elasticity. Their approach is based on a truncation of the potential energy at a given order and an estimation of the error made on the displacement field, it can be found in Schneider and Keinzler [10]. In the first part of this work, we extend the theory of Schneider and Keinzler [10] to dynamical problems. Indeed we obviously cannot consider Euler-Lagrange equations deduced from minimization of potential energy. So we obtain the dynamical problem by establishing virtual work of a small section of beam and then we generalize results of Schneider and Keinzler [9] to dynamical problems.

The most commonly used beam has a cross section with two symmetrical and perpendicular axes (circular, square, rectangular, elliptical…). For this type a cross sections, we will show that the initial problem can be decoupled into more simple four subproblems which can be independent in special cases. To this end, we begin by giving a unique decomposition of any three-dimensional loads and the symmetries of each introduced load is given.

For an orthotropic material, these four subproblems are completely independent. For a monoclinic material, two subproblems are coupled and independent of the two other coupled subproblems. For rectangular cross sections, Carrera and Petrolo [11] obtain very accurate numerical results by truncating the Taylor-young expansion of the displacement field at fifth order with respect to transverse dimensions of the cross section. Indeed we adopt this assumption and we give the explicit expression of the four subproblems when we consider this type of displacement fields.

In recent works [12,13,14,15,16,17,18,19] an another novel beam theory is deduced from the three-dimensional equilibrium equations and lateral boundary conditions (on the boundary of the cross section). The lateral boundary condition is expressed by considering the Fourier series expansion. Extension to dynamical problems is addressed in [18,19]. Thus in the second part of this work, we give this model and we state similar results as the ones obtained for the first beam model.

The main aim of this work is to give two new accurate theories for beams in linear elasticity deduced from three dimensional elasticity. The sole assumption is the series expansion of the displacement field which is assumed to be $C^{\infty }$ in transverse dimensions of the cross section (Section 4.1) or $C^5$ in transverse dimensions of the cross section (Section 4.4 and Section 5). The aim is not here to give more simplified versions of these models which require more assumptions [19,20]. For beams with double symmetric cross sections, we show that the initial problems decouples into four subproblems and we study the coupling between these subproblems.

2. Notation

Boldface letters represent vector-valued functions, tensors or spaces. Let (e₁, e₂, e₃) denote an orthonormal basis of the space ${ℝ}^3$. The colon: between two tensors means double contraction. For example, for two second-order tensors A and B: is used to denote the standard inner product of their associated matrices, i.e., A:B = A_ijB_ij We adopt the Einstein convention summation for repeated indices. The Euclidean scalar product (respectively vector product) of two vectors $\mathbf{a},\hspace{0.17em}\mathbf{b}$ is denoted by $\mathbf{a}\hspace{0.17em}\cdot \mathbf{b}$ (respectively $\mathbf{a}\hspace{0.17em}\wedge \mathbf{b}$). The tensorial product of two vectors $\mathbf{a},\hspace{0.17em}\mathbf{b}$ is the second order tensor $\mathbf{a}\hspace{0.17em}\otimes \mathbf{b}$ $\left({\left(\mathbf{a}\hspace{0.17em}\otimes \mathbf{b}\right)}_{ij}=a_i\hspace{0.17em}{b}_j\right).$ For a vector a, $\dot{\mathbf{a}}$ denotes the derivative of the vector a with respect to time t. For any tensors A depending on its position in the space $\mathbf{x}=x_1{\mathbf{e}}_1+x_2{\mathbf{e}}_2+x_3{\mathbf{e}}_3$, the derivative with respect to $x_i$ is denoted by ${\mathbf{A}}_{,\hspace{0.17em}i}$.

For a vectorial k-dimensional $2\mathbf{\pi }$ periodic $\left(\mathbf{F}\hspace{0.17em}\left(\mathsf{\theta }+2\mathbf{\pi }\right)=\mathbf{F}\hspace{0.17em}\left(\mathsf{\theta }\right)\right)$ function

$$\mathbf{F}:\mathsf{\theta }\in \left[-\mathbf{\pi },\hspace{0.17em}\mathbf{\pi }\right]\to \mathbf{F}\left(\mathsf{\theta }\right)\in {ℝ}^k$$

We assume that F is sufficiently regular to ensure that the Fourier series expansion of F is convergent

$$\mathbf{F}\left(\mathsf{\theta }\right)={\mathbf{F}}_0\hspace{0.17em}+{\displaystyle \sum _{n=1}^{\infty }{\mathbf{F}}_{c_n}}\cos n\mathsf{\theta }+{\mathbf{F}}_{s_n}\sin n\mathsf{\theta },$$

where ${\mathbf{F}}_0=\frac{1}{2\mathbf{\pi }}\hspace{0.17em}{\displaystyle {\int }_{-\mathbf{\pi }}^{\mathbf{\pi }}\mathbf{F}\left(\mathsf{\theta }\right)}\hspace{0.17em}d\mathsf{\theta }$, ${\mathbf{F}}_{c_n\hspace{0.17em}}\hspace{0.17em}=\frac{1}{\mathbf{\pi }}{\displaystyle {\int }_{-\mathbf{\pi }}^{\mathbf{\pi }}\mathbf{F}(\mathsf{\theta })\hspace{0.17em}\cos \left(n\mathsf{\theta }\right)\hspace{0.17em}d\mathsf{\theta }\hspace{0.17em}}$ and ${\mathbf{F}}_{s_n\hspace{0.17em}}\hspace{0.17em}=\frac{1}{\mathbf{\pi }}{\displaystyle {\int }_{-\mathbf{\pi }}^{\mathbf{\pi }}\mathbf{F}(\mathsf{\theta })\hspace{0.17em}\sin \left(n\mathsf{\theta }\right)\hspace{0.17em}d\mathsf{\theta }\hspace{0.17em}}$.

3. The Three-Dimensional Dynamical Problem

We consider a homogeneous straight beam with uniform cross section $\Sigma$ composed of a linear elastic material. The center of gravity of the cross section $\Sigma$ is G. A material point of the beam $\mathbf{B}=\Sigma \times \hspace{0.17em}\left[0,\hspace{0.17em}L\right]$ is $\mathbf{x}=x_i\hspace{0.17em}{\mathbf{e}}_i$. G$x_3$ is the direction of the mid-line of the beam and $\left(G,\hspace{0.17em}{x}_1,\hspace{0.17em}\hspace{0.17em}{x}_2\right)$ are principal directions of the uniform cross section $\Sigma$, then we have:

$${\displaystyle {\int }_{\Sigma }{x}_1}\hspace{0.17em}d\Sigma ={\displaystyle {\int }_{\Sigma }{x}_2}\hspace{0.17em}d\Sigma ={\displaystyle {\int }_{\Sigma }{x}_1}\hspace{0.17em}{x}_2\hspace{0.17em}d\Sigma =0.$$

(1)

We assume that axes G$x_1$ and G$x_2$ are axis of symmetry of this cross section.

Also we can observe that in this definition the boundary $\partial \mathbf{B}\hspace{0.17em}$ of the beam is composed of the cross sections at x₃ = 0 denoted by ${\Sigma }_0$ and $x_3=L$ denoted by ${\Sigma }_L$, and the remaining part, denoted by $\Gamma =\partial \Sigma \times \left[0,\hspace{0.17em}L\right]$, represents the lateral boundary of the beam.

The position vector of a point P in the cross-section $\Sigma$ is:

$$\mathbf{GP}=x_1\hspace{0.17em}{\mathbf{e}}_1+x_2\hspace{0.17em}{\mathbf{e}}_2.$$

(2)

To capture the small transverse dimension of the cross section we introduce a small parameter ρ₀ << L which characterizes the dimension of the cross section (transverse dimensions of the beam).

The elastic tensor E possesses the minor symmetries:

$$E_{ijkh}=E_{jikh}=E_{ijhk}$$

(3)

and the major symmetries

$$E_{ijkh}=E_{khij}$$

Moreover we assume that elastic energy is a positive-definite function of the symmetric second order strain tensor $\mathsf{\epsilon }$

$$\hspace{0.17em}\mathsf{\epsilon }:\mathbf{E}:\mathsf{\epsilon }>0 \mathrm{for} \mathrm{all} \hspace{0.17em}\mathsf{\epsilon }=\frac{1}{2}\left(\mathrm{Grad}\hspace{0.17em}\mathbf{u}\hspace{0.17em}+{\mathrm{Grad}}^T\mathbf{u}\right)\ne 0.$$

(4)

in which $\hspace{0.17em}{\left(\mathrm{Grad}\hspace{0.17em}\mathbf{u}\right)}_{ij}=u_{i,j}$$\hspace{0.17em}{\left({\mathrm{Grad}}^T\hspace{0.17em}\mathbf{u}\right)}_{ij}=u_{j,\hspace{0.17em}i}.$

The minor symmetries of the elastic tensor E implies that the elastic energy $\frac{1}{2}\hspace{0.17em}\mathsf{\epsilon }:\mathbf{E}:\mathsf{\epsilon }$ can be written in an another form $\hspace{0.17em}\frac{1}{2}\mathrm{Grad}\hspace{0.17em}\mathbf{u}:\hspace{0.17em}\mathbf{E}\hspace{0.17em}:\hspace{0.17em}\mathrm{Grad}\hspace{0.17em}\mathbf{u}$ since $\mathrm{Grad}\hspace{0.17em}\mathbf{u}\hspace{0.17em}=\hspace{0.17em}\mathsf{\epsilon }+\frac{1}{2}\left(\mathrm{Grad}\hspace{0.17em}\mathbf{u}\hspace{0.17em}-{\mathrm{Grad}}^T\mathbf{u}\right)$. Accordingly, $\mathsf{\epsilon }$ may be replaced by Grad u in the inequality expressing positive-definiteness of E. This in turn implies that the elastic moduli satisfy the strong-ellipticity condition

$$(\mathbf{v}\otimes \mathbf{w}):\mathbf{E}:(\mathbf{v}\otimes \mathbf{w})>0 \mathrm{for} \mathrm{all} \mathbf{v}\otimes \mathbf{w}\ne 0.$$

(5)

(reply 4) The space of symmetric second order tensors of the form $\frac{1}{2}\left(\mathbf{v}\otimes \mathbf{w}+\mathbf{w}\otimes \mathbf{v}\right)$ is strictly included in the space of all symmetric second order tensors then the strong ellipticity (5) does not imply the positive definite condition (4).

In this work we consider a general anisotropic elastic material which satisfies (4).

The beam is subjected to the body force f, the traction $\overline{\mathbf{T}}$ on the lateral surface $\Gamma ,$ the traction $\overline{\mathbf{t}}$ on the right edge ${\Sigma }_L\left(x_3=L\right)$. The displacement on the left edge ${\Sigma }_0\left(x_3=0\right),$ $\overline{\mathbf{u}}$ is prescribed. The initial conditions for the displacement field (respectively its time derivative) are denoted by ${\mathbf{u}}^0$ (respectively ${\dot{\mathbf{u}}}^0$). The dynamical problem is given by 3D equations of motion, boundary conditions and initial conditions

$$\mathrm{Div}\mathsf{\sigma }+ \mathbf{f} = \rho \hspace{0.17em}\ddot{\mathbf{u}} \mathrm{in} \mathbf{B},$$

(6)

$$\mathsf{\sigma }\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\mathbf{E}:\hspace{0.17em}\mathsf{\epsilon } \mathrm{in} \mathbf{B},$$

(7)

$$\mathsf{\sigma }\hspace{0.17em}.\hspace{0.17em}\mathbf{n}\hspace{0.17em}\hspace{0.17em}= \overline{\mathbf{T}} \mathrm{on} \Gamma ,$$

(8)

$$\mathsf{\sigma }.\hspace{0.17em}{\mathbf{e}}_3= \overline{\mathbf{t}} \mathrm{on} {\Sigma }_L,$$

(9)

$$\mathbf{u}=\overline{\mathbf{u}} \mathrm{on} {\Sigma }_0,$$

(10)

$$\mathbf{u}={\mathbf{u}}^0 \mathrm{in} \mathbf{B} \mathrm{and} \mathrm{at} t=0,$$

(11)

$$\stackrel{.}{\mathbf{u}}={\stackrel{.}{\mathbf{u}}}^0 \mathrm{in} \mathbf{B} \mathrm{and} \mathrm{at} t=0,$$

(12)

where Div is the three-dimensional divergence operator (Divσ = σ_ij,je_i ), n is the unit outward normal to the lateral boundary $\Gamma$ and $\rho$ is the density of the material.

For a consistent beam theory, one needs to make approximations to eliminate the cross section variable $\mathbf{x}\prime =(x_1,\hspace{0.17em}{x}_2)$. This approximation should be valid up to a certain order with respect to the order of magnitude ${\rho }_0$ which characterizes the transverse dimension of the cross section.

Thus, the consistency criterion is that for general smooth loadings ($\overline{\mathbf{T}}$,$\overline{\mathbf{t}}$ and $\overline{\mathbf{u}}$) each equation in the differential dynamical problem (6)–(10) should be satisfied. The main purpose of this work is to provide such a consistent beam theory and simplifications when the cross section is double symmetric.

In order to establish a beam theory in an asymptotically rigorous manner, we assume that applied data are sufficiently smooth.

4. Beam Theory Derived from Differential Dynamical Equations of a Small Piece of Sectional Beam

The starting point of our derivation is a consistent beam theory which results from equations of motion of an infinitesimal section of beam. For a beam with double symmetry cross section, we introduce a unique decomposition of loads. The problem can be decomposed into four subproblems decoupled in terms of stress resultant. After introducing series expansion of the displacement field, we study the link between the type of anisotropy and the coupling between the four subproblems. As truncation of the displacement field at fifth order in ${\rho }_0$, gives a sufficient accuracy for the approximation of the problem (see Carrera and Petrolo [11], Chen et al. [14,15]), we give for this approximation detailed expressions of the four subproblems which are decoupled for orthotropic materials.

4.1. Derivation of Vector Beam Dynamical Equations

Now we want to derive force dynamical equations and torque dynamical equations. In order to get this, we consider the following manipulation. Firstly we multiply an exact equilibrium Equation (6) by a virtual displacement field ${\mathbf{v}}^{*}$ which vanishes on Σ₀, and then we integrate by part in $\mathbf{V}=\Sigma \hspace{0.17em}\times \left[x_3,\hspace{0.17em}{x}_3+l\right]$. Secondly, we multiply the Neumann boundary condition (8) by ${\mathbf{v}}^{*}$ and then we integrate on $\tilde{\Gamma }=\partial \Sigma \hspace{0.17em}\times \left[x_3,\hspace{0.17em}{x}_3+l\right]$. Thirdly, we substract these relations and we obtain

$$\begin{array}{c}{\displaystyle {\int }_{\hspace{0.17em}\mathbf{V}}\left(\mathrm{Div}\hspace{0.17em}\mathsf{\sigma }+\mathbf{f}-\rho \hspace{0.17em} \ddot{\mathbf{u}}\right)\cdot \hspace{0.17em}}{\mathbf{v}}^{*}\hspace{0.17em}d\mathbf{V}-{\displaystyle {\int }_{\tilde{\Gamma }}\left(\mathsf{\sigma }\cdot \mathbf{n}- \overline{\mathbf{T}}\right)\hspace{0.17em}\cdot {\mathbf{v}}^{*}}d{x}_3\hspace{0.17em}ds=\\ {\displaystyle {\int }_{\Sigma }\left(\mathsf{\sigma }\left(x_3+l\right)\hspace{0.17em}\cdot {\mathbf{e}}_3\right)}\hspace{0.17em}\cdot {\mathbf{v}}^{*}\left(x_3+l\right)\hspace{0.17em}d\Sigma -{\displaystyle {\int }_{\Sigma }\left(\mathsf{\sigma }\left(x_3\right)\cdot \hspace{0.17em}{\mathbf{e}}_3\right)}\hspace{0.17em}\cdot {\mathbf{v}}^{*}\left(x_3\right)\hspace{0.17em}d\Sigma +\\ \hspace{0.17em}{\displaystyle {\int }_{x_3}^{x_3+l}\left({\displaystyle {\int }_{\hspace{0.17em}\Sigma \hspace{0.17em}}\mathbf{f}}\hspace{0.17em}\cdot {\mathbf{v}}^{*}d\hspace{0.17em}\Sigma \right)}\hspace{0.17em}d{x}_3+{\displaystyle {\int }_{x_3}^{x_3+l}\left({\displaystyle {\int }_{\hspace{0.17em}\partial \Sigma \hspace{0.17em}}\overline{\mathbf{T}}}\hspace{0.17em}\cdot {\mathbf{v}}^{*}\hspace{0.17em}d\hspace{0.17em}\Sigma \right)}\hspace{0.17em}d{x}_3-\\ {\displaystyle {\int }_{x_3}^{x_3+l}\left({\displaystyle {\int }_{\hspace{0.17em}\Sigma \hspace{0.17em}}\mathsf{\sigma }:\hspace{0.17em}\mathrm{grad}\hspace{0.17em}\left({\mathbf{v}}^{*}\right)}\hspace{0.17em}d\hspace{0.17em}\Sigma \right)}\hspace{0.17em}d{x}_3-{\displaystyle {\int }_{x_3}^{x_3+l}\left({\displaystyle {\int }_{\Sigma }\rho \hspace{0.17em}\ddot{\mathbf{u}}\hspace{0.17em}\cdot {\mathbf{v}}^{*}d\Sigma }\right)}\hspace{0.17em}d{x}_3\hspace{0.17em}=0.\end{array}$$

(13)

We divide the right hand side of (13) by l and when l goes to zero, we arrive at

$$\begin{array}{c}{\displaystyle {\int }_{\Sigma }\left(\left(\mathsf{\sigma }.\hspace{0.17em}{\mathbf{e}}_3\right)\cdot {\mathbf{v}}^{*}\right)}{\hspace{0.17em}}_{,\hspace{0.17em}3}\hspace{0.17em}d\Sigma \hspace{0.17em}+{\displaystyle {\int }_{\hspace{0.17em}\partial \Sigma \hspace{0.17em}}\overline{\mathbf{T}}}\hspace{0.17em}\cdot {\mathbf{v}}^{*}\hspace{0.17em}d\hspace{0.17em}\Sigma +{\displaystyle {\int }_{\hspace{0.17em}\Sigma }\mathbf{f}\hspace{0.17em}\cdot \hspace{0.17em}}{\mathbf{v}}^{*}\hspace{0.17em}d\hspace{0.17em}\Sigma -\\ {\displaystyle {\int }_{\hspace{0.17em}\Sigma }\rho \hspace{0.17em}\ddot{\mathbf{u}}\hspace{0.17em}\cdot {\mathbf{v}}^{*}}d\hspace{0.17em}\Sigma -{\displaystyle {\int }_{\hspace{0.17em}\Sigma \hspace{0.17em}}\mathsf{\sigma }:\hspace{0.17em}grad\hspace{0.17em}\left({\mathbf{v}}^{*}\right)}\hspace{0.17em}d\hspace{0.17em}\Sigma =0.\end{array}$$

(14)

In variational formulation (14), we consider test functions ${\mathbf{v}}^{*}\left(\mathbf{x}\right)=x_1^k\hspace{0.17em}{x}_2^{n-k}{\mathbf{v}}^{*}{}^{(k\hspace{0.17em},\hspace{0.17em}n-k)}\left(x_3\right)$ (for n$\in \hspace{0.17em}\mathbb{N}$ and k = 0, n)

$$\begin{array}{c}{m}_{i3,3}^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}\left(x_3\right)-k\hspace{0.17em}{m}_{i1}^{(k-1\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}n-k)}\left(x_3\right)-\left(n-k\right)\hspace{0.17em}{m}_{i2}^{(k,\hspace{0.17em}\hspace{0.17em}n-k-1)}\left(x_3\right)=\\ -p_i^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}\left(x_3\right)+q_i^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}\left(x_3\right),\end{array}$$

(15)

where

$$\begin{array}{c}{m}_{ij}^{(k,\hspace{0.17em}n-k)}\left(x_3\right)={\displaystyle {\int }_{\Sigma }{\mathsf{\sigma }}_{ij}}\hspace{0.17em}{x}_1^k\hspace{0.17em}{x}_2^{n-k}\hspace{0.17em}d\Sigma ,\\ p_i^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}\left(x_3\right)={\displaystyle {\int }_{\Sigma }\hspace{0.17em}{f}_i}\hspace{0.17em}{x}_1^k\hspace{0.17em}{x}_2^{n-k}\hspace{0.17em}d\Sigma +{\displaystyle {\int }_{\partial \hspace{0.17em}\Sigma }{\overline{T}}_i}\hspace{0.17em}{x}_1^k\hspace{0.17em}{x}_2^{n-k}\hspace{0.17em}d\left(\partial \Sigma \right) \mathrm{and}\\ q_i^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}\left(x_3\right)={\displaystyle {\int }_{\Sigma }\rho }\hspace{0.17em}{\ddot{u}}_i\hspace{0.17em}{x}_1^k\hspace{0.17em}{x}_2^{n-k}\hspace{0.17em}d\Sigma ,\end{array}$$

(16)

and by convention we set $m_{ij}^{(r,\hspace{0.17em}t)}\left(x_3\right)=0$ when r < 0 or $t<0$.

Now we have to introduce unidimensional boundary conditions involved by classical Neumann (respectively Dirichlet) boundary conditions (9) (respectively (10)). We obtain unidimensional Neumann boundary conditions by multiplying (9) by $x_1^k\hspace{0.17em}{x}_2^{n-k}$ and integrating over the cross section $\Sigma$

$$m_{i3}^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}={\overline{m}}_i^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}, \mathrm{at} x_3=L.$$

(17)

in which ${\overline{m}}_i^{(k,\hspace{0.17em}n-k)}={\displaystyle {\int }_{\Sigma }{\overline{t}}_i}\hspace{0.17em}{x}_1^k\hspace{0.17em}{x}_2^{n-k}\hspace{0.17em}d\Sigma .$

By assuming that $\mathbf{u}$ and $\overline{\mathbf{u}}$ can be expanded in series expansion in $\mathbf{x}\prime$ we assume that u and $\overline{\mathbf{u}}$ are $C^{\infty }$ in $\mathbf{x}\prime$), we can write the unidimensional Dirichlet boundary conditions

$$u_i^{(k,\hspace{0.17em}n-k)}={\overline{u}}_i^{(k,\hspace{0.17em}n-k)} \mathrm{at} x_3=0.$$

(18)

in which for n $\in \hspace{0.17em}\mathbb{N}$ and k = 0, n, z denotes a vector then we set ${\mathbf{z}}_{}^{(k,\hspace{0.17em}n-k)}\hspace{0.17em}\left(x_3\right)=\frac{{\partial }^n{\mathbf{z}}_{}}{\partial x_1^k\hspace{0.17em}\partial x_2^{n-k}}\left(\hspace{0.17em}0,\hspace{0.17em}0,x_3\right)$ with the convention ${\mathbf{z}}_{}^{(0,\hspace{0.17em}0)}\hspace{0.17em}\left(x_3\right)=\mathbf{z}\left(0,\hspace{0.17em}0,x_3\right).$

And finally, initial conditions are given by

$${\mathbf{u}}_{}^{\left(k,\hspace{0.17em}n-k\right)}={\mathbf{u}}_{}^{0\left(k,\hspace{0.17em}n-k\right)} \mathrm{for} x_3\in \left[0,L\right] \mathrm{and} t=0,$$

(19)

$${\dot{\mathbf{u}}}_{}^{\left(k,\hspace{0.17em}n-k\right)}={\dot{\mathbf{u}}}_{}^{0\left(k,\hspace{0.17em}n-k\right)} \mathrm{for} x_3\in \left[0,L\right] \mathrm{and} t=0.$$

(20)

Remark 1. 

If we insert the series expansion of the displacement fieldu(see expression (30) inSection 4.3) the expression ofq^{(k, n−k)}(16), we obtain

$${\mathbf{q}}_{}^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}=\rho {\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{l=0}^m\frac{{\ddot{\mathbf{u}}}^{(l\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}m-l)}}{l!\left(m-l\right)!}}\hspace{0.17em}}{I}^{\left(k+l,\hspace{0.17em}\hspace{0.17em}m+n-k-l\right)},$$

(21)

in which$I^{\left(p,\hspace{0.17em}\hspace{0.17em}q\right)}={\displaystyle {\int }_{\Sigma }{x}_1^p}{x}_2^q\hspace{0.17em}d\hspace{0.17em}\Sigma$is inertia.

For example, if we consider, the first three terms in (21) (m = 0,1,2, three terms vanish due to (1)) when k = n = 0, we see that

$${\mathbf{q}}_{}^{(0,\hspace{0.17em}\hspace{0.17em}0)}=\rho \left(\Sigma \hspace{0.17em}{\ddot{\mathbf{u}}}^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}+\frac{1}{2}\left(I^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\ddot{\mathbf{u}}}^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}2)}+I^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\ddot{\mathbf{u}}}^{(2\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}\right)\right)+.....,$$

(22)

In (22), the classical moment inertia, which appears in Euler-Bernoulli or Timoshenko beam theories, intervenes.

Remark 2. 

For practical applications on Neumann boundary${\Sigma }_L$, only the torsor of imposed vector traction (the resultant$\overline{\mathbf{R}}$and the moment of the torque$\overline{\mathbf{M}}$) is known. Nevertheless, the Neumann boundary condition (17) requires to know the prescribed stress vector$\overline{\mathbf{t}}$on${\Sigma }_L.$But next, we show that it can be determined if we assume that$\overline{\mathbf{t}}$is linear${\Sigma }_L$(but the choice is not unique)

$$\overline{\mathbf{t}}={\overline{\mathbf{t}}}_{}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\overline{\mathbf{t}}}_{}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{y}_1+{\overline{\mathbf{t}}}_{}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{y}_2.$$

Then we obviously have

$$\mathbf{R}\left( \overline{\mathbf{t}}\right)=\overline{\mathbf{R}},$$

(23)

$$\mathbf{M}\left( \overline{\mathbf{t}}\right)=\overline{\mathbf{M}},$$

(24)

in which$\mathbf{R}\left(\overline{\mathbf{t}}\right)={\displaystyle {\int }_{\Sigma } \overline{\mathbf{t}}\hspace{0.17em}}d\hspace{0.17em}\Sigma$and$\mathbf{M}\left(\overline{\mathbf{t}}\right)={\displaystyle {\int }_{\Sigma }\stackrel{\rightharpoonup }{\mathrm{GP}}\wedge \overline{\mathbf{t}}\hspace{0.17em}}d\hspace{0.17em}\Sigma .$

From (23), we obtain ${\overline{\mathbf{t}}}_{}^{\left(0,0\right)}=\overline{\mathbf{R}}$. But remains 3 scalar Equation (24) for six scalar unknowns ${\overline{\mathbf{t}}}_{}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}$ and ${\overline{\mathbf{t}}}_{}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}$. The two first equations give

$${\overline{t}}_3^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}=\frac{{\overline{M}}_1}{I^{\hspace{0.17em}\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}},$$

$${\overline{t}}_3^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}=-\frac{{\overline{M}}_2}{I^{\hspace{0.17em}\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}},$$

The last one gives

$${\overline{t}}_2^{\left(\hspace{0.17em}1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{I}^{\hspace{0.17em}\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}-{\overline{t}}_1^{\left(\hspace{0.17em}\hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{I}^{\hspace{0.17em}\left(\hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}2\right)}={\overline{M}}_3.$$

(25)

In view of the form of (25), let us assume that $I^{\hspace{0.17em}\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\overline{t}}_2^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}=-I^{\hspace{0.17em}\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\hspace{0.17em}{\overline{t}}_1^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}$, we obtain

$${\overline{t}}_2^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}=\frac{{\overline{M}}_3}{2\hspace{0.17em}{I}^{\hspace{0.17em}\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}},$$

$${\overline{t}}_1^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}=-\frac{{\overline{M}}_3}{2\hspace{0.17em}{I}^{\hspace{0.17em}\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}}.$$

Finally ${\overline{t}}_2^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}$ and ${\overline{t}}_1^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}$ remain indeterminate, we can assume that ${\overline{t}}_2^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}={\overline{t}}_1^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}=\frac{{\overline{t}}_2^{\left(\hspace{0.17em}\hspace{0.17em}1,\hspace{0.17em}0\right)}-{\overline{t}}_1^{\left(\hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}1\right)}}{2}=\frac{I^{\hspace{0.17em}\left(2,\hspace{0.17em}\hspace{0.17em}2\right)}}{4\hspace{0.17em}{I}^{\hspace{0.17em}\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{I}^{\hspace{0.17em}\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}}{\overline{M}}_3$.

So we can compute the higher order imposed vector term ${\overline{\mathbf{m}}}_{}^{(k,\hspace{0.17em}n-k)}$ as is required in boundary condition (17) in terms of $\overline{\mathbf{R}}$ and $\overline{\mathbf{M}}$.

For other classical type of boundary conditions, we have:

Clamped cross section: ${\mathbf{u}}_{}^{\left(k,\hspace{0.17em}\hspace{0.17em}l\right)}=0,$

Ball joint link: $\mathbf{u}=0$ for $\mathbf{x}\prime =0$$\left({\mathbf{u}}_{}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}=0\right)$ and σ (x).e₃ = 0 for $\mathbf{x}\prime \ne 0,$

Simply supported beam in direction $x_1$:$u_1=0$ at the points of $\partial \Sigma$ where the mechanical link acts and at the other points of the cross section, we have $\mathsf{\sigma }\left(\mathbf{x}\right).\hspace{0.17em}{\mathbf{e}}_3=0$ (free traction).

Now we show that with the unidimensional boundary conditions on the end cross sections of the beam (${\Sigma }_0$ and ${\Sigma }_L$), we can obtain variational formulation of the problem (15), (17)–(20). For example suppose that the cross section ${\Sigma }_0$ is clamped and the cross section ${\Sigma }_L$ is subjected to an imposed torsor ($\overline{\mathbf{R}}, \overline{\mathbf{M}}$). From the previous consideration ${\overline{\mathbf{m}}}^{(k,\hspace{0.17em}n-k)}$ is known. Firstly we multiply Equation (15) by a virtual displacement field ${\mathbf{u}}_{}^{\left(k,\hspace{0.17em}\hspace{0.17em}l\right)*}$. Secondly we integrate over the mid-line of the beam. Thirdly, we integrate by part the first term and we consider boundary condition (17) and the condition ${\mathbf{u}}_{}^{\left(k,\hspace{0.17em}\hspace{0.17em}l\right)*}\left(0\right).$ After truncation of the series expansion of the displacement field at a chosen order, this equation can be discretized by finite element.

Remark 3. 

We show that the classical force and moment equilibrium equations of a section of the beam are included in the system of differential Equation (15). Indeed, we choose a constant vector test function${\mathbf{v}}^{*}$in variational formulation (14) and we obtain the force dynamical equation of a cross section of the beam:

$$\mathbf{R}{\left(\mathbf{t}\right)}_{,\hspace{0.17em}3}+{\mathbf{p}}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}={\mathbf{q}}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)},$$

(26)

in which$\mathbf{R}\left(\mathbf{t}\right)={\displaystyle {\int }_{\Sigma }\mathbf{t}}\hspace{0.17em}d\Sigma$with$\mathbf{t}=\mathsf{\sigma }\hspace{0.17em}\cdot {\mathbf{e}}_3$(we see that$R_i\left(\mathbf{t}\right)=m_{i3}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}$).

We obtain the moment dynamical equation by successively choosing in (14) vectors test displacement field of the form ${\mathbf{v}}^{*}$ = $x_2\hspace{0.17em}{\mathbf{e}}_3,$ ${\mathbf{v}}^{*}$ = $-x_1\hspace{0.17em}{\mathbf{e}}_3,$ and ${\mathbf{v}}^{*}$ = $x_1\hspace{0.17em}{\mathbf{e}}_2-x_2\hspace{0.17em}{\mathbf{e}}_1$, we obtain the moment (or torque) dynamical equation for a section of the beam

$$\frac{d\hspace{0.17em}\mathbf{M}\left(\mathbf{t}\right)}{d\hspace{0.17em}{x}_3}+\tilde{\mathbf{M}}\left(\overline{\mathbf{T}}\right)+\mathbf{M}\left(\mathbf{f}\right)+\mathbf{T}=\mathbf{M}\left(\rho \hspace{0.17em}\ddot{\mathbf{u}}\right),$$

(27)

in which for any vectors v

$$\mathbf{M}\left(\mathbf{v}\right)={\displaystyle {\int }_{\Sigma }\stackrel{\rightharpoonup }{\mathrm{GP}}\wedge \mathbf{v}\hspace{0.17em}}d\hspace{0.17em}\Sigma =\hspace{0.17em}{\mathbf{e}}_1{\displaystyle {\int }_{\Sigma }{x}_2\hspace{0.17em}{v}_3}\hspace{0.17em}d\hspace{0.17em}\Sigma -{\mathbf{e}}_2{\displaystyle {\int }_{\Sigma }{x}_1\hspace{0.17em}{v}_3\hspace{0.17em}d\hspace{0.17em}\Sigma }\hspace{0.17em}+{\mathbf{e}}_3{\displaystyle {\int }_{\Sigma }(x_1\hspace{0.17em}{v}_2-x_2\hspace{0.17em}{v}_1)}\hspace{0.17em}d\hspace{0.17em}\Sigma ,$$

and for v = t, we have

$$\mathbf{M}\left(\mathbf{t}\right)=m_{33}^{(0,\hspace{0.17em}\hspace{0.17em}1)}\hspace{0.17em}{\mathbf{e}}_1-\hspace{0.17em}{m}_{33}^{(1\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}\hspace{0.17em}{\mathbf{e}}_2+\left(m_{23}^{(1,\hspace{0.17em}\hspace{0.17em}0)}-m_{13}^{(0,\hspace{0.17em}\hspace{0.17em}1)}\right){\mathbf{e}}_3,$$

$$\tilde{\mathbf{M}}\left(\overline{\mathbf{T}}\right)={\displaystyle {\int }_{\partial \hspace{0.17em}\Sigma }\stackrel{\rightharpoonup }{\mathrm{GP}}\wedge \overline{\mathbf{T}}\hspace{0.17em}}d\hspace{0.17em}\left(\partial \Sigma \right),$$

$$\mathbf{T}=-\hspace{0.17em}{\mathbf{e}}_1{\displaystyle {\int }_{\Sigma }{\mathsf{\sigma }}_{23}\hspace{0.17em}}d\hspace{0.17em}\Sigma +{\mathbf{e}}_2{\displaystyle {\int }_{\Sigma }{\mathsf{\sigma }}_{13}\hspace{0.17em}}d\hspace{0.17em}\Sigma =-\hspace{0.17em}{m}_{2\hspace{0.17em}3}^{(0,\hspace{0.17em}0)}\hspace{0.17em}{\mathbf{e}}_1\hspace{0.17em}+m_{1\hspace{0.17em}3}^{(0,\hspace{0.17em}0)}\hspace{0.17em}{\mathbf{e}}_2,$$

Then we see that

$$\tilde{\mathbf{M}}\left(\overline{\mathbf{T}}\right)+\mathbf{M}\left(\mathbf{f}\right)\hspace{0.17em}=\hspace{0.17em}{p}_3^{(0,\hspace{0.17em}\hspace{0.17em}1)}\hspace{0.17em}{\mathbf{e}}_1\hspace{0.17em}-\hspace{0.17em}\hspace{0.17em}{p}_3^{(1,\hspace{0.17em}\hspace{0.17em}0)}\hspace{0.17em}{\mathbf{e}}_2+\left(p_2^{(1,\hspace{0.17em}\hspace{0.17em}0)}-p_1^{(0,\hspace{0.17em}\hspace{0.17em}1)}\right){\mathbf{e}}_3.$$

As a consequence, we obviously see that we can find classical beam dynamical Equations (26) and (27) from (14). The unidimensional boundary problem (15), (17)–(20) is a well posed problem and is actually an exact representation of the three dimensional problem (6)–(12).

If we insert the linear part of the series expansion of the displacement field u (see expression (30) in Section 4.3), we obtain the expression for the torque dynamical terms of the right hand side of (27)

$$\mathbf{M}\left(\rho \ddot{u}\right)\hspace{0.17em}=\hspace{0.17em}{I}^{\left(0,\hspace{0.17em}2\right)}{\ddot{u}}_3^{\left(0,\hspace{0.17em}1\right)}{\mathbf{e}}_1-I^{\left(\hspace{0.17em}2,\hspace{0.17em}0\right)}{\ddot{u}}_3^{\left(1,\hspace{0.17em}0\right)}\hspace{0.17em}+\left(I^{\left(2,\hspace{0.17em}0\right)}{\ddot{u}}_2^{\left(\hspace{0.17em}1,0\right)}-I^{\left(0,\hspace{0.17em}2\right)}{\ddot{u}}_1^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\right){\mathbf{e}}_3.$$

(28)

In (28), the classical moment inertias appear.

4.2. The Decoupled Equations in Terms of Stress Resultants and Classification of Loads

4.2.1. Preliminary

The second order stress tensor resultant ${\mathbf{m}}_{}^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}$ are unknown in the exact one-dimensional Equation (15). If a specific stress resultant ${\mathbf{m}}_{}^{(k,\hspace{0.17em}\hspace{0.17em}n-k)}$ appears in two dynamical equations of type (15), by definition we say that these two equations are coupled. So two sets of equations of type (15) are independent if and only if the set of stress resultant appearing in two sets of equations is empty.

Let ${\mathbb{N}}_{q2}$ denote the quotient set of integers by 2, i.e., the set ${\mathbb{N}}_{q2}$ consists of precisely two elements: $e:\hspace{0.17em}=\{z\in \mathbb{N},\hspace{0.17em}\hspace{0.17em}z$ modulo 2 $=0\}$, the set of all even integers and $o:\hspace{0.17em}=\{z\in \mathbb{N},\hspace{0.17em}\hspace{0.17em}z$ modulo 2$=1\}$, the set of odd integers. If we use e and o as an upper index, the corresponding parity classes are meant, i.e.: $m_{ij}^{\left(o,\hspace{0.17em}e\right)}=\{m_{ij}^{\left(p,\hspace{0.17em}\hspace{0.17em}q\right)},\hspace{0.17em}\mathrm{with}\hspace{0.17em}p\hspace{0.17em}$ modulo 2 = 1 and q modulo $2=0\}.$ And then $m_{ij}^{\left(o,\hspace{0.17em}e\right)}\hspace{0.17em}$ represents a class of stress resultants $\left(\mathrm{for}\hspace{0.17em}\mathrm{example}\hspace{0.17em}{m}_{ij}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\in m_{ij}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}\right).$ We denote by $[.]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}},$ the mapping of integers to their parity class, i.e., $\left[9\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}}=\left[7\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}}=\left[1\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}}=o.$ Finally, we define the operator $K_i$

$$K_1\left(\left[i\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}},\hspace{0.17em}\left[j\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}}\right):\hspace{0.17em}=\left(\left[i+1\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}},\hspace{0.17em}\left[j\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}}\right),$$

$$K_2\left(\left[i\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}},\hspace{0.17em}\left[j\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}}\right):\hspace{0.17em}=\left(\left[i\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}},\hspace{0.17em}[j+1]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}}\right),$$

$$K_3\left(\left[i\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}},\hspace{0.17em}\left[j\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}}\right):\hspace{0.17em}=\left(\left[i\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}},\hspace{0.17em}\left[j\right]{\hspace{0.17em}}_{{\mathbb{N}}_{q2}}\right).$$

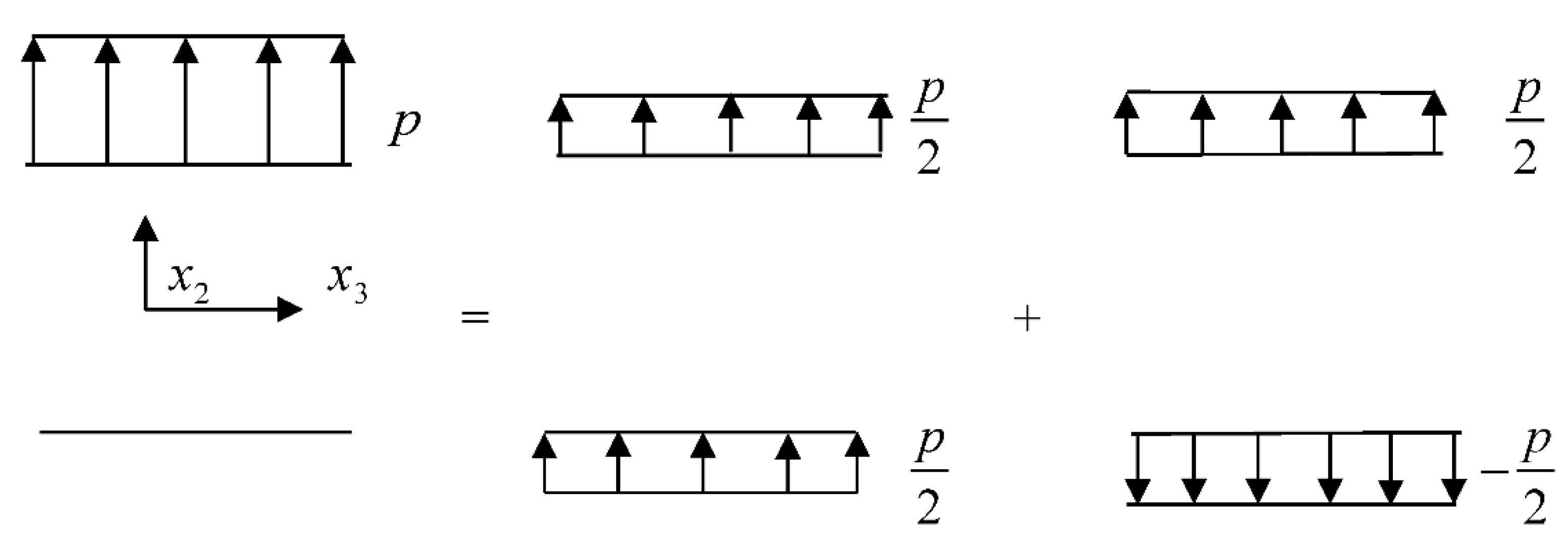
4.2.2. Classification of the Load Resultant

For beam with double symmetric cross section, any vectorial function G (which here represents $\overline{\mathbf{T}}$ and f) can be uniquely decomposed as follows

$$\mathbf{F}=\hspace{0.17em}\mathbf{F}{\hspace{0.17em}}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}+\mathbf{F}{\hspace{0.17em}}^{\left(e,\hspace{0.17em}\hspace{0.17em}o\right)}+\mathbf{F}{\hspace{0.17em}}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}+\mathbf{F}{\hspace{0.17em}}^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)},$$

(29)

in which

$$\hspace{0.17em}\mathbf{F}{\hspace{0.17em}}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}\left(\mathbf{x}\right)=\frac{1}{4}\left(\mathbf{F}\hspace{0.17em}\left(\mathbf{x}\right)+\mathbf{F}\hspace{0.17em}\left(x_1,\hspace{0.17em}-x_2,\hspace{0.17em}{x}_3\right)+\mathbf{F}\hspace{0.17em}\left(-x_1,\hspace{0.17em}{x}_2,\hspace{0.17em}{x}_3\right)+\mathbf{F}\hspace{0.17em}\left(-x_1,\hspace{0.17em}-x_2,\hspace{0.17em}{x}_3\right)\right),$$

$$\hspace{0.17em}\mathbf{F}{\hspace{0.17em}}^{\left(e,\hspace{0.17em}\hspace{0.17em}o\right)}\left(\mathbf{x}\right)=\frac{1}{4}\left(\mathbf{F}\hspace{0.17em}\left(\mathbf{x}\right)-\mathbf{F}\hspace{0.17em}\left(x_1,\hspace{0.17em}-x_2,\hspace{0.17em}{x}_3\right)+\mathbf{F}\hspace{0.17em}\left(-x_1,\hspace{0.17em}{x}_2,\hspace{0.17em}{x}_3\right)-\mathbf{F}\hspace{0.17em}\left(-x_1,\hspace{0.17em}-x_2,\hspace{0.17em}{x}_3\right)\right),$$

$$\hspace{0.17em}\mathbf{F}{\hspace{0.17em}}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}\left(\mathbf{x}\right)=\frac{1}{4}\left(\mathbf{F}\hspace{0.17em}\left(\mathbf{x}\right)+\mathbf{F}\hspace{0.17em}\left(x_1,\hspace{0.17em}-x_2,\hspace{0.17em}{x}_3\right)-\mathbf{F}\hspace{0.17em}\left(-x_1,\hspace{0.17em}{x}_2,\hspace{0.17em}{x}_3\right)-\mathbf{F}\hspace{0.17em}\left(-x_1,\hspace{0.17em}-x_2,\hspace{0.17em}{x}_3\right)\right),$$

$$\hspace{0.17em}\mathbf{F}{\hspace{0.17em}}^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}\left(\mathbf{x}\right)=\frac{1}{4}\left(\mathbf{F}\hspace{0.17em}\left(\mathbf{x}\right)-\mathbf{F}\hspace{0.17em}\left(x_1,\hspace{0.17em}-x_2,\hspace{0.17em}{x}_3\right)-\mathbf{F}\hspace{0.17em}\left(-x_1,\hspace{0.17em}{x}_2,\hspace{0.17em}{x}_3\right)+\mathbf{F}\hspace{0.17em}\left(-x_1,\hspace{0.17em}-x_2,\hspace{0.17em}{x}_3\right)\right).$$

We easily see that $\hspace{0.17em}\mathbf{F}{\hspace{0.17em}}^{\left(r,\hspace{0.17em}\hspace{0.17em}s\right)}$ has r-parity in $x_1$ and s-parity in $x_2$ ($\mathbf{F}\hspace{0.17em}$ has r-parity in $x_1$ i.e., $\hspace{0.17em}\mathbf{F}\hspace{0.17em}\left(\mathbf{x}\right)={\left(-1\right)}^r\mathbf{F}\hspace{0.17em}\left(-x_1,\hspace{0.17em}{x}_2,\hspace{0.17em}{x}_3\right)$ and $\hspace{0.17em}\mathbf{F}\hspace{0.17em}$ has s-parity in $x_2$ i.e.,$\hspace{0.17em}\mathbf{F}\hspace{0.17em}\left(\mathbf{x}\right)={\left(-1\right)}^s\mathbf{F}\hspace{0.17em}\left(x_1,\hspace{0.17em}-x_2,\hspace{0.17em}{x}_3\right)$).

From expression of type (29) for $\overline{\mathbf{T}}$ and f, we easily see that the sole non zero vector load ${\mathbf{p}}_{}^{(r,\hspace{0.17em}\hspace{0.17em}s)}$ is computed as follows

$${\mathbf{p}}_{}^{(r,\hspace{0.17em}\hspace{0.17em}s)}={\displaystyle {\int }_{\Sigma }\hspace{0.17em}{\mathbf{f}}^{\left({\left[r\right]}_{{\mathbb{N}}_{q2}},\hspace{0.17em}\hspace{0.17em}{\left[s\right]}_{{\mathbb{N}}_{q2}}\right)}}\hspace{0.17em}{x}_1^r\hspace{0.17em}{x}_2^s\hspace{0.17em}d\Sigma +{\displaystyle {\int }_{\partial \hspace{0.17em}\Sigma }{ \overline{\mathbf{T}}}^{\left({\left[r\right]}_{{\mathbb{N}}_{q2}},\hspace{0.17em}\hspace{0.17em}{\left[s\right]}_{{\mathbb{N}}_{q2}}\right)}}\hspace{0.17em}{x}_1^r\hspace{0.17em}{x}_2^s\hspace{0.17em}d\left(\partial \Sigma \right).$$

We can illustrate this decomposition by considering a beam with a rectangular cross-section, with the edge dimensions h in $x_2$-direction and b in $x_1$-direction. Let us consider a relevant load case for engineering practice defined by a constant positive load p on the top of the cross section ($x_2=\frac{h}{2}$)

$${\overline{T}}_1={\overline{T}}_3=0,{\overline{T}}_2=p,$$

$$\mathbf{f}=0.$$

Thus ${\overline{T}}_2$ is even in $x_1$ (${\overline{T}}_2$ is constant in $x_1$). This implies ${\overline{T}}_2^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}={\overline{T}}_2^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}=0.$

But in $x_2$-direction the load is neither even nor odd so the other two parts are given by (see Figure 1)

$${\overline{T}}_2^{\left(e,\hspace{0.17em}e\right)}\left(\frac{h}{2}\right)=\frac{p}{2},$$

$${\overline{T}}_2^{\left(e,\hspace{0.17em}e\right)}\left(-\frac{h}{2}\right)=\frac{p}{2},$$

$${\overline{T}}_2^{\left(e,\hspace{0.17em}o\right)}\left(\frac{h}{2}\right)=\frac{p}{2},$$

$${\overline{T}}_2^{\left(e,\hspace{0.17em}o\right)}\left(-\frac{h}{2}\right)=-\frac{p}{2}.$$

4.2.3. Decomposition of the Initial Problem into Four Subproblems

In this section, we generalize the results of Schneider and Kienzler [9]. The dynamical Equation (15) written in terms of stress resultants decouple in four subproblems. We identify each subproblem by a parity tuple $\left(r,\hspace{0.17em}t\right)\hspace{0.17em}{\mathbb{N}}_{q2}.$

These four independent subproblems are denoted by:

R (for this problem, the parity tuple is (e, e)),

B1 (for this problem, the parity tuple (o, e)),

B2 (for this problem, the parity tuple (e, o)),

S (for this problem, the parity tuple (o, o)).

For each of the subproblems, we give in

Table 1. Classification of components of the load resultants $p_i^{\left(r,\hspace{0.17em}\hspace{0.17em}t\right)}$ (also true for components of ${\mathbf{q}}_{}^{(r,\hspace{0.17em}\hspace{0.17em}t)}$ ) for the four subproblems R, B1, B2 and S (we define $K_i\left(p_j^{\left(r,\hspace{0.17em}\hspace{0.17em}t\right)}\right)=p_j^{\left(K_i\left(r,\hspace{0.17em}\hspace{0.17em}t\right)\right)}$ ).

Class	(r,t)	$K_1\left(p_1^{\left(r,\hspace{0.17em}\hspace{0.17em}t\right)}\right)$	$K_2\left(p_2^{\left(r,\hspace{0.17em}\hspace{0.17em}t\right)}\right)$	$K_3\left(p_3^{\left(r,\hspace{0.17em}t\right)}\right)$
R	(e,e)	$p_1^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}$	$p_2^{\left(e,\hspace{0.17em}o\right)}$	$p_3^{\left(e,\hspace{0.17em}e\right)}$
B1	(o,e)	$p_1^{\left(e,\hspace{0.17em}e\right)}$	$p_2^{\left(o,\hspace{0.17em}o\right)}$	$p_3^{\left(o,\hspace{0.17em}e\right)}$
B2	(e,o)	$p_1^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}$	$p_2^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}$	$p_3^{\left(e,\hspace{0.17em}\hspace{0.17em}o\right)}$
S	(o,o)	$p_1^{\left(e,\hspace{0.17em}\hspace{0.17em}o\right)}$	$p_2^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}$	$p_3^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}$

, the components of both load resultant ${\mathbf{p}}_{}^{(r,\hspace{0.17em}\hspace{0.17em}t)}$ and dynamical vector ${\mathbf{q}}_{}^{(r,\hspace{0.17em}\hspace{0.17em}t)}$ which intervene in each of this four subproblems.

In

Table 2. Classification of components of the stress resultants ${\mathbf{m}}_{}^{\left(r,\hspace{0.17em}\hspace{0.17em}t\right)}$ for the four subproblems R, B1, B2 and S (we define $K_i\left(m_{op}^{\left(r,\hspace{0.17em}\hspace{0.17em}t\right)}\right)=m_{op}^{\left(K_i\left(r,\hspace{0.17em}\hspace{0.17em}t\right)\right)}$).

Class	(r,t)	$K_1\hspace{0.17em}{K}_1$$\left(m_{11}^{\left(r,\hspace{0.17em}t\right)}\right)$	$K_1\hspace{0.17em}{K}_2$$\left(m_{12}^{\left(r,\hspace{0.17em}t\right)}\right)$	$K_1\hspace{0.17em}{K}_3$$\left(m_{13}^{\left(r,\hspace{0.17em}t\right)}\right)$	$K_2\hspace{0.17em}{K}_2$$\left(m_{22}^{\left(r,\hspace{0.17em}t\right)}\right)$	$K_2\hspace{0.17em}{K}_3$$\left(m_{23}^{\left(r,\hspace{0.17em}t\right)}\right)$	$K_3\hspace{0.17em}{K}_3$$\left(m_{33}^{\left(r,\hspace{0.17em}t\right)}\right)$
R	(e,e)	$m_{11}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{12}^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}$	$m_{13}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{22}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{23}^{\left(e,\hspace{0.17em}\hspace{0.17em}o\right)}$	$m_{33}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}$
B1	(o,e)	$m_{11}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{12}^{\left(e,\hspace{0.17em}\hspace{0.17em}o\right)}$	$m_{13}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{22}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{23}^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}$	$m_{33}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}$
B2	(e,o)	$m_{11}^{\left(e,\hspace{0.17em}\hspace{0.17em}o\right)}$	$m_{12}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{13}^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}$	$m_{13}^{\left(o,\hspace{0.17em}o\right)}$	$m_{23}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{33}^{\left(e,\hspace{0.17em}\hspace{0.17em}o\right)}$
S	(o,o)	$m_{11}^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}$	$m_{12}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{13}^{\left(e,\hspace{0.17em}\hspace{0.17em}o\right)}$	$m_{13}^{\left(e,\hspace{0.17em}o\right)}$	$m_{23}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}$	$m_{33}^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}$

, we give components of stress resultant $m_{ij}^{(q,\hspace{0.17em}\hspace{0.17em}r)}$ which intervene in each of these four subproblems.

4.3. The Anisotropic Coupling

For the determination of the anisotropic coupling it is necessary to express the unidimensional problem (15), (17)–(20) in terms of the displacement field. To this end, we take advantage of the smallness of the transverse dimension of the beam by taking complete series expansion in ${\mathbf{x}}^{\prime }$ (we assume that u is $C^{\infty }$ in $\mathbf{x}\prime$)

$$\mathbf{u}(\mathbf{x})={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{k=0}^n\frac{{\mathbf{u}}^{(k\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}n-k)}}{k!\left(n-k\right)!}}\left(x_3\right)\hspace{0.17em}{x}_1^k\hspace{0.17em}{x}_2^{n-k}},$$

(30)

The gradient of the displacement field (30) is for

$$\mathrm{Grad}\left(\mathbf{u}\left(x\right)\right)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{k=0}^n\frac{\mathrm{Grad}{\left(\mathbf{u}\right)}_{ij}^{(k\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}n-k)}\left(x_3\right)}{k!\left(n-k\right)!}}\hspace{0.17em}{\mathbf{e}}_i\otimes {\mathbf{e}}_j\hspace{0.17em}}{x}_1^k\hspace{0.17em}{x}_2^{n-k},$$

(31)

in which for $n\in \hspace{0.17em}\mathbb{N}\hspace{0.17em}and\hspace{0.17em}k=0,\hspace{0.17em}n$$\mathrm{Grad}{\left(\mathbf{u}\right)}_{ij}^{\left(k,\hspace{0.17em}\hspace{0.17em}n-k\right)}={\mathbf{u}}_i^{\left(k+1,\hspace{0.17em}\hspace{0.17em}n-k\right)}\hspace{0.17em}{\mathsf{\delta }}_{1j}+{\mathbf{u}}_i^{\left(k,\hspace{0.17em}\hspace{0.17em}n-k+1\right)}\hspace{0.17em}{\mathsf{\delta }}_{2j}+{\mathbf{u}}_{i,\hspace{0.17em}3}^{\left(k,\hspace{0.17em}\hspace{0.17em}n-k\right)}\hspace{0.17em}{\mathsf{\delta }}_{3j}.$

The series expansion of the components of the stress tensor is obtainable from the linear constitutive law (7) and the series expansion of the displacement gradient (31) (for n$\in \hspace{0.17em}\mathbb{N}$ and k = 0, n)

$$\mathsf{\sigma }\left(\mathbf{u}\hspace{0.17em}\left(\mathbf{x}\right)\right)={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{q=0}^n\frac{1}{q!(n-q)!}{\mathsf{\sigma }}_{}^{\left(q,\hspace{0.17em}n-q\right)}\left(\mathbf{u},\hspace{0.17em}{x}_3\right)x_1^q}{x}_2^{n-q}},$$

(32)

in which

$${\mathsf{\sigma }}_{ij}^{\left(q,\hspace{0.17em}p\right)}\left(\mathbf{u},\hspace{0.17em}{x}_3\right)=E_{ijk1}\hspace{0.17em}{u}_k^{(q+1\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right)+E_{ijk2}\hspace{0.17em}{u}_k^{(q\hspace{0.17em},\hspace{0.17em}p+1)}\left(x_3\right)+E_{ijk3}\hspace{0.17em}{u}_{k,3}^{(q\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right).$$

(33)

For studying the coupling of the one-dimensional subproblems, we define the effective shift $K_{eff}$ (that maps each index quadruple $\left(i,\hspace{0.17em}j,r,s\right)\hspace{0.17em}\in \hspace{0.17em}{\mathbb{N}}_{q2}^4$ to a mapping $\hspace{0.17em}{\mathbb{N}}_{q2}^2\hspace{0.17em}\to {\mathbb{N}}_{q2}^2$) defined by

$$K_{eff}:\left(i,j,r,s\right)\to K_i{K}_j{K}_r{K}_s.$$

Thus for dynamical problems, the main result of Schneider and Kienzler [9] remains true if we substitute ${\mathbf{p}}_{}^{(r,\hspace{0.17em}s)}$ by ${\mathbf{p}}_{}^{(r,\hspace{0.17em}s)}$ + ${\mathbf{q}}_{}^{(r,\hspace{0.17em}s)}$ in their argumentation and we can state that.

Theorem 1. 

For an anisotropic material, two subproblems $\left(t_1,\hspace{0.17em}{t}_2\right)\hspace{0.17em}\in \hspace{0.17em}{\mathbb{N}}_{q2}^2$ and$\left(t_3,\hspace{0.17em}{t}_4\right)\hspace{0.17em}\in \hspace{0.17em}{\mathbb{N}}_{q2}^2$are coupled if, and only if, there exists a nonzero component of the stiffness tensor$E_{ijrs}\ne 0$and$K_{eff}\left(i,j,r,s\right)$such that$K_{eff}\left(i,j,r,s\right)\left(t_1,t_2\right)=\left(t_3,t_4\right).$

This result implies the following two statements.

For an orthotropic material, where the planes of symmetry are given by the coordinate planes, the four subproblems are decoupled.

For a monoclinic material, where the plane of symmetry is given by two coordinate axes, we have coupled problems of pairwise two classical problems: If the symmetry plane is $x_1-x_3$, we have a coupled (R, B1) problem and a coupled (S, B2) problem. If the symmetry plane is $x_2-x_3$, we have a coupled (R, B2) problem and a coupled (S, B1) problem. If the symmetry plane is $x_1-x_2$, we have a coupled (R, S) problem and a coupled (B1, B2) problem.

4.4. Approximation of the Four Decoupled Subproblems for Orthotropic Anisotropy

In this subsection, we illustrate the first part of the Theorem 1 by giving expressions of the four independent subproblems for an orthotropic material. In practice it is not necessary to consider an infinite series expansion for the displacement field and the truncation of terms at least the order ${\rho }_0^5$ can be considered (Chen et al. [14,15], Pruchnicki et al. [16]). The total number of vector unknowns is fifteen (${\mathbf{u}}^{\left(p,\hspace{0.17em}n-p\right)}$ for n = 0 to 4 and p = 0, n). Thus exact expression of the displacement field (30) becomes (it is sufficient to assume that u is $C^5$ in $\mathbf{x}\prime$)

$$\mathbf{u}(\mathbf{x})={\displaystyle \sum _{n=0}^4{\displaystyle \sum _{k=0}^n\frac{{\mathbf{u}}^{(k\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}n-k)}}{k!\left(n-k\right)!}}\left(x_3\right)\hspace{0.17em}{x}_1^k\hspace{0.17em}{x}_2^{n-k}}+O\left({\rho }_0^5\right),$$

(34)

Now, we consider the complete expansion of the stress tensor involved by the approximation (34) of the displacement field

$$\mathsf{\sigma }\left(\mathbf{u}\left(\mathbf{x}\right)\right)={\displaystyle \sum _{n=0}^4{\displaystyle \sum _{q=0}^n\frac{1}{q!(n-q)!}{\mathsf{\sigma }}_{}^{\left(q,\hspace{0.17em}n-q\right)}\left(\mathbf{u},\hspace{0.17em}{x}_3\right)x_1^q}{x}_2^{n-q}},$$

(35)

For an orthotropic material, the stiffness tensor E is given by

$$\mathbf{E}=\left(\begin{array}{cccccc}{E}_{1111}& E_{1122}& E_{1133}& 0& 0& 0\\ & E_{2222}& E_{2233}& 0& 0& 0\\ & & E_{3333}& 0& 0& 0\\ \mathrm{S}& & & E_{1212}=G_{12}& 0& 0\\ & \mathrm{Y}& & & E_{1313}=G_{13}& 0\\ & & \mathrm{M}& & & E_{2323}=G_{23}\end{array}\right).$$

Thus for an orthotropic linear elastic material, the constitutive law (7) implies

$${\mathsf{\sigma }}_{11}^{\left(q,\hspace{0.17em}p\right)}\left(\mathbf{u},\hspace{0.17em}{x}_3\right)=E_{1111}\hspace{0.17em}{u}_1^{(q+1\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right)+E_{1122}\hspace{0.17em}{u}_2^{(q\hspace{0.17em},\hspace{0.17em}p+1)}\left(x_3\right)+E_{1133}\hspace{0.17em}{u}_{3,3}^{(q\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right),$$

(36)

$${\mathsf{\sigma }}_{22}^{\left(q,\hspace{0.17em}p\right)}\left(\mathbf{u},\hspace{0.17em}{x}_3\right)=E_{1122}\hspace{0.17em}{u}_1^{(q+1\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right)+E_{2222}\hspace{0.17em}{u}_2^{(q\hspace{0.17em},\hspace{0.17em}p+1)}\left(x_3\right)+E_{2233}\hspace{0.17em}{u}_{3,3}^{(q\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right),$$

(37)

$${\mathsf{\sigma }}_{33}^{\left(q,\hspace{0.17em}p\right)}\left(\mathbf{u},\hspace{0.17em}{x}_3\right)=E_{1133}\hspace{0.17em}{u}_1^{(q+1\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right)+E_{2233}\hspace{0.17em}{u}_2^{(q\hspace{0.17em},\hspace{0.17em}p+1)}\left(x_3\right)+E_{3333}\hspace{0.17em}{u}_{3,3}^{(q\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right),$$

(38)

$${\mathsf{\sigma }}_{12}^{\left(q,\hspace{0.17em}p\right)}\left(\mathbf{u},\hspace{0.17em}{x}_3\right)=G_{12}\hspace{0.17em}\left(u_2^{(q+1\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right)+u_1^{(q\hspace{0.17em},\hspace{0.17em}p+1)}\left(x_3\right)\right),$$

(39)

$${\mathsf{\sigma }}_{13}^{\left(q,\hspace{0.17em}p\right)}\left(\mathbf{u},\hspace{0.17em}{x}_3\right)=G_{13}\hspace{0.17em}\left(u_3^{(q+1\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right)+u_{1,3}^{(q\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right)\right),$$

(40)

$${\mathsf{\sigma }}_{23}^{\left(q,\hspace{0.17em}p\right)}\left(\mathbf{u},\hspace{0.17em}{x}_3\right)=G_{23}\left(u_3^{(q\hspace{0.17em},\hspace{0.17em}p+1)}\left(x_3\right)+u_{2,3}^{(q\hspace{0.17em},\hspace{0.17em}p)}\left(x_3\right)\right).$$

(41)

The displacement field u solution of unidimensional exact boundary problem (15), (17)–(20) can be uniquely decomposed as follows

$$\mathbf{u}={\mathbf{u}}_R+{\mathbf{u}}_{B1}+{\mathbf{u}}_{B2}+{\mathbf{u}}_S,$$

in which u_R solves the subproblem R, ${\mathbf{u}}_{B1}$ solves the subproblem B1, ${\mathbf{u}}_{B2}$ solves the subproblem B2, ${\mathbf{u}}_S$ solves the subproblem S.

Now we give expressions of successively subproblem R, subproblem B1, subproblem B2 and subproblem S. (for simplicity we denote by u the solution of each of these four subproblems). With the specific form of the displacement field given for each subproblem, we can get the components of stress tensor from formulae (36)–(41) and them we can compute the stress resultant $m_{i\hspace{0.17em}j}^{\left(r,\hspace{0.17em}t\right)}$ in terms of displacement field. For the sake of conciseness, we do not give these expressions. For boundary conditions, we apply Dirichlet type boundary conditions (18) for all coefficients of the expansion of the displacement field which intervenes in each subproblem. The same applies for initial conditions (11), (12). For Neumann boundary conditions, we consider boundary condition (17) for stress resultant $m_{i3}^{(p,\hspace{0.17em}q)}$ which intervenes in each subproblem (for example for subproblem R, we have to consider $m_{33}^{(0,\hspace{0.17em}0)},$ $m_{13}^{(1,\hspace{0.17em}0)},$ $m_{23}^{(0,\hspace{0.17em}1)}$, $m_{33}^{(0,\hspace{0.17em}2)}$, $m_{33}^{(2,\hspace{0.17em}0)}$, $m_{23}^{(0,\hspace{0.17em}3)}$, $m_{13}^{(1,\hspace{0.17em}2)}$, $m_{13}^{(3,\hspace{0.17em}0)}$, $m_{23}^{(2,\hspace{0.17em}1)},$ $m_{33}^{(2,\hspace{0.17em}2)},$ $m_{33}^{(0,\hspace{0.17em}4)},$ $m_{33}^{(4,\hspace{0.17em}0)})$. Thus for each subproblem, the total order of derivatives is equal to the total number of boundary conditions and these problems are well posed. The result of Table 1 can be applied for components of displacement ${\mathbf{u}}_{}^{\left(r,\hspace{0.17em}t\right)}$ which intervenes in each of the four subproblems.

(a) 

Subproblem R

Expansion of components of displacement (twelve displacement coefficients of type $u_i^{(r,\hspace{0.17em}s)}$)

$$u_1(\mathbf{x})=u_1^{\left(1,\hspace{0.17em}0\right)}\left(x_3\right)x_1+\frac{1}{2}{u}_1^{\left(1,\hspace{0.17em}2\right)}\left(x_3\right)x_1\hspace{0.17em}{x}_2^2\hspace{0.17em}+\frac{1}{6}{u}_1^{\left(3,\hspace{0.17em}0\right)}\left(x_3\right)x_1^3+O\left({\rho }_0^5\right),$$

(42)

$$u_2(\mathbf{x})=u_2^{(0\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_2^{}+\frac{1}{6}{u}_2^{(0\hspace{0.17em},\hspace{0.17em}3)}\left(x_3\right)x_2^3+\frac{1}{2}{u}_2^{(2\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_1^2{x}_2^{}++O\left({\rho }_0^5\right),$$

(43)

$$\begin{array}{c}{u}_3\left(\mathbf{x}\right)=u_3^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}\left(x_3\right)+\frac{1}{2}{u}_3^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}2)}\left(x_3\right)x_2^2+\frac{1}{2}{u}_3^{(2\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}\left(x_3\right)x_1^2+\frac{1}{4}{u}_3^{(2\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}2)}\left(x_3\right)x_1^2{x}_2^2+\\ \frac{1}{24}{u}_3^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}4)}\left(x_3\right)x_2^4+\frac{1}{24}{u}_3^{(4,\hspace{0.17em}\hspace{0.17em}0)}\left(x_3\right)x_1^4+O\left({\rho }_0^5\right),\end{array}$$

(44)

(a1) 

Twelve scalar dynamical equations

$$m_{33,3}^{(0,\hspace{0.17em}0)}\left(x_3\right)=-p_3^{(0,\hspace{0.17em}0)}\left(x_3\right)+q_3^{(0,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{13,3}^{(1,\hspace{0.17em}0)}\left(x_3\right)-\hspace{0.17em}{m}_{11}^{(0,\hspace{0.17em}0)}\left(x_3\right)=-p_1^{(1,\hspace{0.17em}0)}\left(x_3\right)+q_1^{(1,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{23,3}^{(0,\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{22}^{(0,\hspace{0.17em}0)}\left(x_3\right)=-p_2^{(0,\hspace{0.17em}1)}\left(x_3\right)+q_2^{(0,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{33,3}^{(0,\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{23}^{(0,\hspace{0.17em}1)}\left(x_3\right)=-p_3^{(0,\hspace{0.17em}2)}\left(x_3\right)+q_3^{(0,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{33,3}^{(2,\hspace{0.17em}0)}\left(x_3\right)-2\hspace{0.17em}{m}_{13}^{(1,\hspace{0.17em}0)}\left(x_3\right)=-p_3^{(2,\hspace{0.17em}0)}\left(x_3\right)+q_3^{(2,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{23,3}^{(0,\hspace{0.17em}3)}\left(x_3\right)-3\hspace{0.17em}{m}_{22}^{(0,\hspace{0.17em}2)}\left(x_3\right)=-p_2^{(0,\hspace{0.17em}3)}\left(x_3\right)+q_2^{(\hspace{0.17em}0,\hspace{0.17em}3)}\left(x_3\right),$$

$$m_{13,3}^{(1,\hspace{0.17em}2)}\left(x_3\right)-\hspace{0.17em}{m}_{11}^{(0,\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{12}^{(1,\hspace{0.17em}1)}\left(x_3\right)=-p_1^{(1,\hspace{0.17em}2)}\left(x_3\right)+q_1^{(1,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{13,3}^{(3,\hspace{0.17em}0)}\left(x_3\right)-3\hspace{0.17em}{m}_{11}^{(2\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)=-p_1^{(3,\hspace{0.17em}0)}\left(x_3\right)+q_1^{(3,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{23,3}^{(2,\hspace{0.17em}1)}\left(x_3\right)-2\hspace{0.17em}{m}_{12}^{(1\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{22}^{(2,\hspace{0.17em}0)}\left(x_3\right)=-p_2^{(2,\hspace{0.17em}1)}\left(x_3\right)+q_2^{(2,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{33,3}^{(2,\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{13}^{(1\hspace{0.17em},\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{23}^{(2,\hspace{0.17em}1)}\left(x_3\right)=-p_3^{(2,\hspace{0.17em}2)}\left(x_3\right)+q_3^{(2,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{33,3}^{(0,\hspace{0.17em}4)}\left(x_3\right)-4\hspace{0.17em}{m}_{23}^{(0,\hspace{0.17em}3)}\left(x_3\right)=-p_3^{(0,\hspace{0.17em}4)}\left(x_3\right)+q_3^{(0,\hspace{0.17em}4)}\left(x_3\right),$$

$$m_{33,3}^{(4,\hspace{0.17em}0)}\left(x_3\right)-4\hspace{0.17em}{m}_{13}^{(3\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)=-p_3^{(4,\hspace{0.17em}0)}\left(x_3\right)+q_3^{(4,\hspace{0.17em}0)}\left(x_3\right).$$

(b) 

Subproblem B1

Expansion of components of the displacement (twelve displacement coefficients of type $u_i^{(r,\hspace{0.17em}s)}$):

$$\begin{array}{c}{u}_1\left(\mathbf{x}\right)=u_1^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}\left(x_3\right)+\frac{1}{2}{u}_1^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}2)}\left(x_3\right)x_2^2+\frac{1}{2}{u}_1^{(2\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}\left(x_3\right)x_1^2+\frac{1}{4}{u}_1^{(2\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}2)}\left(x_3\right)x_1^2{x}_2^2+\\ \frac{1}{24}{u}_1^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}4)}\left(x_3\right)x_2^4+\frac{1}{24}{u}_1^{(4,\hspace{0.17em}\hspace{0.17em}0)}\left(x_3\right)x_1^4+O\left({\rho }_0^5\right),\end{array}$$

(45)

$$u_2(\mathbf{x})=u_2^{(1\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_1^{}{x}_2^{}+\frac{1}{6}{u}_2^{(1\hspace{0.17em},\hspace{0.17em}3)}\left(x_3\right)x_1^{}{x}_2^3+\frac{1}{6}{u}_2^{(3\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_1^3{x}_2^{}+O\left({\rho }_0^5\right),$$

(46)

$$u_3(\mathbf{x})=u_3^{(1\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)x_1^{}+\frac{1}{2}{u}_3^{(1\hspace{0.17em},\hspace{0.17em}2)}\left(x_3\right)x_1^{}{x}_2^2+\frac{1}{6}{u}_3^{(3\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)x_1^3+O\left({\rho }_0^5\right).$$

(47)

(b1) 

Twelve scalar dynamical equations

$$m_{13,3}^{(0,\hspace{0.17em}0)}\left(x_3\right)=-p_1^{(0,\hspace{0.17em}0)}\left(x_3\right)+q_1^{(0,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{33,\hspace{0.17em}3}^{(1,\hspace{0.17em}0)}\left(x_3\right)-\hspace{0.17em}{m}_{13}^{(0\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)=-p_3^{(1,\hspace{0.17em}0)}\left(x_3\right)+q_3^{(1,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{23,3}^{(1,\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{12}^{(0\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{22}^{(1,\hspace{0.17em}0)}\left(x_3\right)=-p_2^{(1,\hspace{0.17em}1)}\left(x_3\right)+q_2^{(1,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{13,3}^{(0,\hspace{0.17em}2)}\left(x_3\right)-\hspace{0.17em}2m_{12}^{(0,\hspace{0.17em}1)}\left(x_3\right)=-p_1^{(0,\hspace{0.17em}2)}\left(x_3\right)+q_1^{(0,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{13,3}^{(2,\hspace{0.17em}0)}\left(x_3\right)-\hspace{0.17em}2m_{11}^{(1,\hspace{0.17em}0)}\left(x_3\right)=-p_1^{(2,\hspace{0.17em}0)}\left(x_3\right)+q_1^{(2,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{33,3}^{(1,\hspace{0.17em}2)}\left(x_3\right)-\hspace{0.17em}{m}_{13}^{(0\hspace{0.17em},\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{23}^{(1,\hspace{0.17em}1)}\left(x_3\right)=-p_3^{(1,\hspace{0.17em}2)}\left(x_3\right)+q_3^{(1,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{33,3}^{(3,\hspace{0.17em}0)}\left(x_3\right)-3\hspace{0.17em}{m}_{13}^{(2\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)=-p_3^{(3,\hspace{0.17em}0)}\left(x_3\right)+q_3^{(3,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{23,3}^{(1,\hspace{0.17em}3)}\left(x_3\right)-\hspace{0.17em}{m}_{12}^{(0\hspace{0.17em},\hspace{0.17em}3)}\left(x_3\right)-3\hspace{0.17em}{m}_{22}^{(1,\hspace{0.17em}2)}\left(x_3\right)=-p_2^{(1,\hspace{0.17em}3)}\left(x_3\right)+q_2^{(1,\hspace{0.17em}3)}\left(x_3\right),$$

$$m_{23,3}^{(3,\hspace{0.17em}1)}\left(x_3\right)-3\hspace{0.17em}{m}_{12}^{(2\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{22}^{(3,\hspace{0.17em}0)}\left(x_3\right)=-p_2^{(3,\hspace{0.17em}1)}\left(x_3\right)+q_2^{(1,\hspace{0.17em}3)}\left(x_3\right),$$

$$m_{13,3}^{(2,\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{11}^{(1\hspace{0.17em},\hspace{0.17em}2)}\left(x_3\right)-\hspace{0.17em}2m_{12}^{(2,\hspace{0.17em}1)}\left(x_3\right)=-p_1^{(2,\hspace{0.17em}2)}\left(x_3\right)+q_1^{(2,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{13,3}^{(0,\hspace{0.17em}4)}\left(x_3\right)-4\hspace{0.17em}{m}_{12}^{(0,\hspace{0.17em}3)}\left(x_3\right)=-p_1^{(0,\hspace{0.17em}4)}\left(x_3\right)+q_1^{(0,\hspace{0.17em}4)}\left(x_3\right),$$

$$m_{13,3}^{(4,\hspace{0.17em}0)}\left(x_3\right)-4\hspace{0.17em}{m}_{11}^{(3\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)=-p_1^{(4,\hspace{0.17em}0)}\left(x_3\right)+q_1^{(4,\hspace{0.17em}0)}\left(x_3\right).$$

(c) 

Subproblem B2

Expression of components of the displacement (twelve displacement coefficients of type $u_i^{(r,\hspace{0.17em}s)}$):

$$u_1(\mathbf{x})=u_1^{(1\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_1\hspace{0.17em}{x}_2+\frac{1}{6}{u}_1^{(1\hspace{0.17em},\hspace{0.17em}3)}\left(x_3\right)x_1\hspace{0.17em}{x}_2^3+\frac{1}{6}{u}_1^{(3\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_1^3\hspace{0.17em}{x}_1^{}+O\left({\rho }_0^5\right),$$

(48)

$$\begin{array}{c}{u}_2\left(\mathbf{x}\right)=u_2^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}\left(x_3\right)+\frac{1}{2}{u}_2^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}2)}\left(x_3\right)x_2^2+\frac{1}{2}{u}_2^{(2\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}\left(x_3\right)x_1^2+\frac{1}{4}{u}_2^{(2\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}2)}\left(x_3\right)x_1^2{x}_2^2+\\ \frac{1}{24}{u}_2^{(0\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}4)}\left(x_3\right)x_2^4+\frac{1}{24}{u}_2^{(4\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}0)}\left(x_3\right)x_1^4+O\left({\rho }_0^5\right),\end{array}$$

(49)

$$u_3\left(\mathbf{x}\right)=u_3^{(0\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_2^{}+\frac{1}{6}{u}_3^{(0,\hspace{0.17em}3)}\left(x_3\right)x_2^3+\frac{1}{2}{u}_3^{(2\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_1^2{x}_2^{}+O\left({\rho }_0^5\right).$$

(50)

(c1) 

Twelve scalar dynamical equations

$$m_{23,3}^{(0,\hspace{0.17em}0)}\left(x_3\right)=-p_2^{(0,\hspace{0.17em}0)}\left(x_3\right)+q_2^{(0,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{33,3}^{(0,\hspace{0.17em}1)}\left(x_3\right)-m_{23}^{(0,\hspace{0.17em}0)}\left(x_3\right)=-p_3^{(0,\hspace{0.17em}1)}\left(x_3\right)+q_3^{(0,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{23,3}^{(0,\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{22}^{(0,\hspace{0.17em}1)}\left(x_3\right)=-p_2^{(0,\hspace{0.17em}2)}\left(x_3\right)+q_2^{(0,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{23,3}^{(2,\hspace{0.17em}0)}\left(x_3\right)-2\hspace{0.17em}{m}_{12}^{(1\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)=-p_2^{(2,\hspace{0.17em}0)}\left(x_3\right)+q_2^{(2,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{13,3}^{(1,\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{11}^{(0\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{12}^{(1,\hspace{0.17em}0)}\left(x_3\right)=-p_1^{(1,\hspace{0.17em}1)}\left(x_3\right)+q_1^{(1,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{33,3}^{(0,\hspace{0.17em}3)}\left(x_3\right)-3\hspace{0.17em}{m}_{23}^{(0,\hspace{0.17em}2)}\left(x_3\right)=-p_3^{(0,\hspace{0.17em}3)}\left(x_3\right)+q_3^{(0,\hspace{0.17em}3)}\left(x_3\right),$$

$$m_{33,3}^{(2,\hspace{0.17em}1)}\left(x_3\right)-2\hspace{0.17em}{m}_{13}^{(1\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{23}^{(2,\hspace{0.17em}0)}\left(x_3\right)=-p_3^{(2,\hspace{0.17em}1)}\left(x_3\right)+q_3^{(2,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{13,3}^{(1,\hspace{0.17em}3)}\left(x_3\right)-\hspace{0.17em}{m}_{11}^{(0,\hspace{0.17em}3)}\left(x_3\right)-3\hspace{0.17em}{m}_{12}^{(1,\hspace{0.17em}2)}\left(x_3\right)=-p_1^{(1,\hspace{0.17em}3)}\left(x_3\right)+q_1^{(1,\hspace{0.17em}3)}\left(x_3\right),$$

$$m_{13,3}^{(3,\hspace{0.17em}1)}\left(x_3\right)-3\hspace{0.17em}{m}_{11}^{(2,\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{12}^{(3,\hspace{0.17em}0)}\left(x_3\right)=-p_1^{(3,\hspace{0.17em}1)}\left(x_3\right)+q_1^{(3,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{23,3}^{(2,\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{12}^{(1\hspace{0.17em},\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{22}^{(2,\hspace{0.17em}1)}\left(x_3\right)=-p_2^{(2,\hspace{0.17em}2)}\left(x_3\right)+q_2^{(2,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{23,3}^{(0,\hspace{0.17em}4)}\left(x_3\right)-4\hspace{0.17em}{m}_{22}^{(0,\hspace{0.17em}3)}\left(x_3\right)=-p_2^{(0,\hspace{0.17em}4)}\left(x_3\right)+q_2^{(0,\hspace{0.17em}4)}\left(x_3\right),$$

$$m_{23,3}^{(4,\hspace{0.17em}0)}\left(x_3\right)-4\hspace{0.17em}{m}_{12}^{(3\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)=-p_2^{(4,\hspace{0.17em}0)}\left(x_3\right)+q_2^{(4,\hspace{0.17em}0)}\left(x_3\right).$$

(d) 

Subproblem S

Expession of components of the displacement (nine displacement coefficients of type $u_i^{(r,\hspace{0.17em}s)}$)

$$u_1\left(\mathbf{x}\right)=u_1^{(0\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)\hspace{0.17em}{x}_2+\frac{1}{6}{u}_1^{(0\hspace{0.17em},\hspace{0.17em}3)}\left(x_3\right)\hspace{0.17em}{x}_2^3+\frac{1}{2}{u}_1^{(2\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_1^2\hspace{0.17em}{x}_2^{}+O\left({\rho }_0^5\right),$$

(51)

$$u_2\left(\mathbf{x}\right)=u_2^{(1,\hspace{0.17em}0)}\left(x_3\right)x_1+\frac{1}{2}{u}_2^{(1\hspace{0.17em},\hspace{0.17em}2)}\left(x_3\right)x_1\hspace{0.17em}{x}_2^2+\frac{1}{6}{u}_2^{(3\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)x_1^3+O\left({\rho }_0^5\right),$$

(52)

$$u_3\left(\mathbf{x}\right)=u_3^{(1\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_1^{}{x}_2^{}+\frac{1}{6}{u}_3^{(1,\hspace{0.17em}3)}\left(x_3\right)x_1^{}{x}_2^3+\frac{1}{6}{u}_3^{(3\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)x_1^3{x}_2^{}+O\left({\rho }_0^5\right).$$

(53)

(d1) 

Nine scalar dynamical equations

$$m_{13,3}^{(0,\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{12}^{(0,\hspace{0.17em}0)}\left(x_3\right)=-p_1^{(0,\hspace{0.17em}1)}\left(x_3\right)+q_1^{(0,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{23,3}^{(1,\hspace{0.17em}0)}\left(x_3\right)-\hspace{0.17em}{m}_{12}^{(0\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)=-p_2^{(1,\hspace{0.17em}0)}\left(x_3\right)+q_2^{(1,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{33,3}^{(1,\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{13}^{(0\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{23}^{(1,\hspace{0.17em}0)}\left(x_3\right)=-p_3^{(1,\hspace{0.17em}1)}\left(x_3\right)+q_3^{(1,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{13,3}^{(0,\hspace{0.17em}3)}\left(x_3\right)-3\hspace{0.17em}{m}_{12}^{(0,\hspace{0.17em}2)}\left(x_3\right)=-p_1^{(0,\hspace{0.17em}3)}\left(x_3\right)+q_1^{(0,\hspace{0.17em}3)}\left(x_3\right),$$

$$m_{13,3}^{(2,\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{11}^{(1\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{12}^{(2,\hspace{0.17em}0)}\left(x_3\right)=-p_1^{(2,\hspace{0.17em}1)}\left(x_3\right)+q_1^{(2,\hspace{0.17em}1)}\left(x_3\right),$$

$$m_{23,3}^{(1,\hspace{0.17em}2)}\left(x_3\right)-\hspace{0.17em}{m}_{12}^{(0\hspace{0.17em},\hspace{0.17em}2)}\left(x_3\right)-2\hspace{0.17em}{m}_{22}^{(1,\hspace{0.17em}1)}\left(x_3\right)=-p_2^{(1,\hspace{0.17em}2)}\left(x_3\right)+q_2^{(1,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{23,3}^{(3,\hspace{0.17em}0)}\left(x_3\right)-3\hspace{0.17em}{m}_{12}^{(2\hspace{0.17em},\hspace{0.17em}0)}\left(x_3\right)=-p_2^{(3,\hspace{0.17em}0)}\left(x_3\right)+q_2^{(3,\hspace{0.17em}0)}\left(x_3\right),$$

$$m_{33,3}^{(1,\hspace{0.17em}3)}\left(x_3\right)-\hspace{0.17em}{m}_{13}^{(0\hspace{0.17em},\hspace{0.17em}3)}\left(x_3\right)-3\hspace{0.17em}{m}_{23}^{(1,\hspace{0.17em}2)}\left(x_3\right)=-p_3^{(1,\hspace{0.17em}2)}\left(x_3\right)+q_3^{(1,\hspace{0.17em}2)}\left(x_3\right),$$

$$m_{33,3}^{(3,\hspace{0.17em}1)}\left(x_3\right)-3\hspace{0.17em}{m}_{13}^{(2\hspace{0.17em},\hspace{0.17em}1)}\left(x_3\right)-\hspace{0.17em}{m}_{23}^{(3,\hspace{0.17em}0)}\left(x_3\right)=-p_3^{(3,\hspace{0.17em}1)}\left(x_3\right)+q_3^{(3,\hspace{0.17em}1)}\left(x_3\right).$$

In summary, we can observe that the initial problem is the union of subproblems R, B1, B2 and S (forty five dynamical equations with ninety boundary conditions). Obviously for general anisotropy only scalar dynamical equations are true.

5. Second Beam Theory Derived Directly from Both Dynamical Equations and Lateral Boundary Conditions

5.1. Derivation of the Theory

In this section, we present an another new model for beams which is linked to the idea presented in recent works ([12,14,15,16,17,18]). This modelization results from the approximation of the displacement field (34) given in Section 4.

Then the lateral boundary condition (8) will be considered by using the Fourier series expansion and the Taylor-Young expansion together with exact dynamical Equation (6). The aim will be to obtain a closed system of fifteen differential equations with fifteen unknowns displacement field u^(p,n−p) (for n = 0, 4 and p = 0, n). We will see that the advantage of this approach is that one knows the error made in every equation. We assume that the displacement field u is $C^5$ in $\mathbf{x}\prime$.

It is easy to see that both the gradient of the displacement field (34) and the stress tensor are accurate up to $O\left({\rho }_0^4\right)$

$$\mathrm{Grad}\hspace{0.17em}{\mathbf{u}}_{}={\displaystyle \sum _{n=0}^3{\displaystyle \sum _{k=0}^n\frac{1}{k!\left(n-k\right)!}\mathrm{Grad}{\hspace{0.17em}}^{(k\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}n-k)}\mathbf{u}}}+O\left({\rho }_0^4\right),$$

(54)

$$\mathsf{\sigma }\left(\mathbf{u}\hspace{0.17em}\left(\mathbf{x}\right)\right)={\displaystyle \sum _{n=0}^3{\displaystyle \sum _{q=0}^n\frac{1}{q!(n-q)!}{\mathsf{\sigma }}_{}^{\left(q,\hspace{0.17em}n-q\right)}{x}_1^q}{x}_2^{n-q}}+O\left({\rho }_0^4\right).$$

(55)

Now we consider the parametric equation of the lateral boundary (which is also the boundary $\partial \Sigma$ of the cross section $\Sigma$):

$$x_1\left(\theta \right)=r\left(\theta \right)\cos \left(\theta \right)$$

(56)

$$x_2\left(\theta \right)=r\left(\theta \right)\sin \left(\theta \right)$$

(57)

where r = $\Vert \mathbf{r}\Vert$ ($\mathbf{r}=\overrightarrow{GM}$, M belongs to the boundary $\partial \Sigma$ of the cross section $\Sigma$) is a given function of $\theta =\widehat{({\mathbf{e}}_1,\mathbf{r})}$ (the azimuthal angle on $x_1{x}_2$-plane), which describes the geometry of the lateral boundary. From parametric equations of the lateral boundary (56)–(57), we see that the components in $\left({\mathbf{e}}_1,\hspace{0.17em}{\mathbf{e}}_2\right)$ of the unit outward normal to $\partial \Sigma$ are

$$n_1\left(\theta \right)=v\left(\theta \right)\sin \theta +u\left(\theta \right)\cos \theta ,$$

$$n_2\left(\theta \right)=-v\left(\theta \right)\cos \theta +u\left(\theta \right)\sin \theta ,$$

in which $u\left(\theta \right)=\frac{r\hspace{0.17em}\left(\theta \right)\hspace{0.17em}}{\sqrt{r\prime \hspace{0.17em}{\left(\theta \right)}^2+r\hspace{0.17em}{\left(\theta \right)}^2}},$$v\left(\theta \right)=\frac{r\prime \left(\theta \right)\hspace{0.17em}}{\sqrt{r\prime \hspace{0.17em}{\left(\mathsf{\theta }\right)}^2+r\hspace{0.17em}{\left(\mathsf{\theta }\right)}^2}}$.

To satisfy the lateral traction condition (8) in a point-wise manner, we use the Fourier series expansion for the applied traction $\overline{\mathbf{T}}\left(\mathbf{x}\right)= \overline{\mathbf{T}}(r(\theta )\hspace{0.17em}\cos \theta ,\hspace{0.17em}\hspace{0.17em}r(\theta )\hspace{0.17em}\sin \theta ,\hspace{0.17em}{x}_3)=\widehat{\overline{\mathbf{T}}}\hspace{0.17em}(\theta ,\hspace{0.17em}{x}_3)$.

We assume that $\widehat{\overline{\mathbf{T}}}\hspace{0.17em}$ is a sufficiently regular function of $\theta$ to ensure that its Fourier series expansion is convergent:

$$\widehat{\overline{\mathbf{T}}}\hspace{0.17em}\left(\theta \right)=\widehat{\overline{\mathbf{T}}}{\hspace{0.17em}}_0\hspace{0.17em}+{\displaystyle \sum _{p=1}^{\infty }{\widehat{\overline{\mathbf{T}}}}_{c_p}}\cos p\hspace{0.17em}\theta +{\widehat{\overline{\mathbf{T}}}}_{s_p}\sin p\hspace{0.17em}\theta \hspace{0.17em}.$$

(58)

Thus the lateral boundary condition (8) gives

$$\begin{array}{c}{\displaystyle \sum _{n=0}^3}{\rho }_0^n{\displaystyle \sum _{q=0}^n}\frac{r_1^{\left(q,n-q\right)}\left(\theta \right)}{q!\left(n-q\right)!}{\mathsf{\sigma }}^{\left(q,n-q\right)}.e_1+{\displaystyle \sum _{n=0}^3}{\rho }_0^n{\displaystyle \sum _{q=0}^n}\frac{r_2^{\left(q,n-q\right)}\left(\theta \right)}{q!\left(n-q\right)!}{\mathsf{\sigma }}^{\left(q,n-q\right)}.e_2=\\ {\widehat{\overline{\mathbf{T}}}}_0\hspace{0.17em}+{\displaystyle \sum _{n=1}^4}{\widehat{\overline{\mathbf{T}}}}_{c_n\hspace{0.17em}}\cos n\theta +{\widehat{\overline{\mathbf{T}}}}_{s_n}\sin n\theta +O({\rho }_0^4),\end{array}$$

in which $r_1^{\left(q,\hspace{0.17em}n-q\right)}\left(\theta \right)={\left(\frac{r\left(\theta \right)}{{\rho }_0}\right)}^n{n}_1\left(\theta \right){\cos }^q\theta \hspace{0.17em}{\sin }^{n-q}\theta$, $r_2^{\left(q,\hspace{0.17em}n-q\right)}\left(\theta \right)={\left(\frac{r\left(\theta \right)}{{\rho }_0}\right)}^n{n}_2\left(\theta \right){\cos }^q\theta \hspace{0.17em}{\sin }^{n-q}\theta .$

The Fourier series expansions at the left hand side of (19) are computed. Then by equating the constant term and the coefficient of $\cos \hspace{0.17em}i\theta$ and $\sin \hspace{0.17em}i\theta$ (for i = 1, 2, 3, 4) on both sides of (19), nine vector equations, up to order $O({\rho }_0^4),$ are derived. For $i=0,$ we have

$${\displaystyle \sum _{n=0}^3{\rho }_0^n{\displaystyle \sum _{q=0}^n\frac{r_{1\hspace{0.17em}0}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}}{q!\left(n-q\right)!}{\mathsf{\sigma }}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}\cdot {\mathbf{e}}_1}}+{\displaystyle \sum _{n=0}^3{\rho }_0^n{\displaystyle \sum _{q=0}^n\frac{r_{2\hspace{0.17em}0}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}}{q!\left(n-q\right)!}}}\hspace{0.17em}{\mathsf{\sigma }}^{\left(q,\hspace{0.17em}n-q\right)}\cdot \hspace{0.17em}{\mathbf{e}}_2={\widehat{\overline{\mathbf{T}}}}_0\hspace{0.17em}+O({\rho }_0^4),$$

(59)

and for i = 1, 2, 3, 4, we obtain

$${\displaystyle \sum _{n=0}^3{\rho }_0^n{\displaystyle \sum _{q=0}^n\frac{r_{1\hspace{0.17em}\hspace{0.17em}{c}_i}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}}{q!\left(n-q\right)!}{\mathsf{\sigma }}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}\cdot {\mathbf{e}}_1}}+{\displaystyle \sum _{n=0}^3{\rho }_0^n{\displaystyle \sum _{q=0}^n\frac{r_{2\hspace{0.17em}{c}_i}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}}{q!\left(n-q\right)!}}}\hspace{0.17em}{\mathsf{\sigma }}^{\left(q,\hspace{0.17em}n-q\right)}\cdot {\mathbf{e}}_2={\widehat{\overline{\mathbf{T}}}}_{c_n\hspace{0.17em}}+O({\rho }_0^4)\hspace{0.17em},$$

(60)

$${\displaystyle \sum _{n=0}^3{\rho }_0^n{\displaystyle \sum _{q=0}^n\frac{r_{1\hspace{0.17em}\hspace{0.17em}{s}_i}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}}{q!\left(n-q\right)!}{\mathsf{\sigma }}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}\cdot \hspace{0.17em}{\mathbf{e}}_1}}+\hspace{0.17em}{\displaystyle \sum _{n=0}^3{\rho }_0^n{\displaystyle \sum _{q=0}^n\frac{r_{2\hspace{0.17em}\hspace{0.17em}{s}_i}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}}{q!\left(n-q\right)!}{\mathsf{\sigma }}^{\left(q,\hspace{0.17em}\hspace{0.17em}n-q\right)}\cdot {\mathbf{e}}_2}}={\widehat{\overline{\mathbf{T}}}}_{s_n}\hspace{0.17em}+O({\rho }_0^4),$$

(61)

where $r_{10}^{\left(q,\hspace{0.17em}n-q\right)},\hspace{0.17em}{r}_{1c_i}^{\left(q,\hspace{0.17em}n-q\right)},\hspace{0.17em}{r}_{1s_i}^{\left(q,\hspace{0.17em}n-q\right)}$ (respectively $r_{20}^{\left(q,\hspace{0.17em}n-q\right)},\hspace{0.17em}{r}_{2c_i}^{\left(q,\hspace{0.17em}n-q\right)},\hspace{0.17em}{r}_{2s_i}^{\left(q,\hspace{0.17em}n-q\right)}$) are the Fourier series expansion coefficients of $r_1^{\left(q,\hspace{0.17em}n-q\right)}$ (respectively $r_2^{\left(q,\hspace{0.17em}n-q\right)}$) (see Section 2 for analytical expressions).

For double symmetric cross sections, Equations (59)–(61) can be further simplified. We have the following results

Given $G{x}_1$ being the symmetrical axis of the cross section

if m is odd then

$$r_{1\hspace{0.17em}0}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,r_{1\hspace{0.17em}\hspace{0.17em}{c}_i}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,r_{2\hspace{0.17em}\hspace{0.17em}{s}_i}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,$$

(62)

if m is even then

$$r_{2\hspace{0.17em}0}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,r_{2\hspace{0.17em}\hspace{0.17em}{c}_i}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,r_{1\hspace{0.17em}\hspace{0.17em}{s}_i}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,$$

(63)

if l is odd then

$${\widehat{\overline{\mathbf{T}}}}_0^{(l,\hspace{0.17em}m)}={\widehat{\overline{\mathbf{T}}}}_{c_i}^{(l,\hspace{0.17em}m)}=0,$$

(64)

if l is even

$${\widehat{\overline{\mathbf{T}}}}_{s_i}^{(l,\hspace{0.17em}m)}{}_{\hspace{0.17em}}=0,$$

(65)

Given $G{x}_2$ being the symmetrical axis of the cross section

if l is even then $r_{1\hspace{0.17em}0}^{\left(l,\hspace{0.17em}m\right)}=0,$ if l is odd then

$$r_{2\hspace{0.17em}0}^{\left(l,\hspace{0.17em}m\right)}=0,$$

(66)

if i + l is even then

$$r_{1\hspace{0.17em}\hspace{0.17em}{c}_i}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,r_{2\hspace{0.17em}\hspace{0.17em}{s}_i}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,$$

(67)

if i + l is odd then

$$r_{1\hspace{0.17em}\hspace{0.17em}{s}_i}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,r_{2\hspace{0.17em}\hspace{0.17em}{c}_i}^{\left(l,\hspace{0.17em}\hspace{0.17em}m\right)}=0,$$

(68)

if m is odd then

$${\widehat{\overline{\mathbf{T}}}}_0^{(l,\hspace{0.17em}m)}=0,$$

(69)

if i + m is odd then

$${\widehat{\overline{\mathbf{T}}}}_{c_i}^{(l,\hspace{0.17em}m)}=0,$$

(70)

if i + m is even then

$${\widehat{\overline{\mathbf{T}}}}_{s_i}^{(l,\hspace{0.17em}m)}=0.$$

(71)

By taking into account of (62)–(71) for double symmetric cross sections, the nine Equations in (59)–(61) become

$$\begin{array}{c}{\rho }_0\left(r_{10}^{\left(1,\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+r_{20}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_2\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}0}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}\cdot {\mathbf{e}}_1+r_{2\hspace{0.17em}0}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_2+\frac{1}{3}{r}_{1\hspace{0.17em}0}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+\frac{1}{3}{r}_{2\hspace{0.17em}0}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\cdot {\mathbf{e}}_2\right)=\\ {\widehat{\overline{\mathbf{T}}}}_0^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}+O({\rho }_0^4),\end{array}$$

(72)

$$r_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+{\rho }_0^2\left(\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+r_{2\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_2+\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\cdot {\mathbf{e}}_1\right)={\widehat{\overline{\mathbf{T}}}}_{c_1}^{\left(e,\hspace{0.17em}o\right)}\hspace{0.17em}+O({\rho }_0^4),$$

(73)

$$r_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_2+{\rho }_0^2\left(\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_2+r_{1\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_1+\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\cdot {\mathbf{e}}_2\right)={\widehat{\overline{\mathbf{T}}}}_{s_1}^{\left(o,\hspace{0.17em}e\right)}\hspace{0.17em}+O({\rho }_0^4),$$

(74)

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{c}_2}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+r_{2\hspace{0.17em}{c}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_2\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}{c}_2\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}\cdot {\mathbf{e}}_1+r_{2\hspace{0.17em}{c}_2}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_2+\frac{1}{3}{r}_{1\hspace{0.17em}{c}_2}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+\frac{1}{3}{r}_{2\hspace{0.17em}{c}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\cdot {\mathbf{e}}_2\right)=\\ {\widehat{\overline{\mathbf{T}}}}_{c_2}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)}{}_{\hspace{0.17em}}\hspace{0.17em}+O({\rho }_0^4),\end{array}$$

(75)

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{s}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_1+r_{2\hspace{0.17em}{s}_2}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot \hspace{0.17em}{\mathbf{e}}_2\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{2\hspace{0.17em}\hspace{0.17em}{s}_2\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}\cdot \hspace{0.17em}{\mathbf{e}}_2+r_{1\hspace{0.17em}{s}_2}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot \hspace{0.17em}{\mathbf{e}}_1+\frac{1}{3}{r}_{2\hspace{0.17em}{s}_2}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_2+\frac{1}{3}{r}_{1\hspace{0.17em}{s}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\cdot {\mathbf{e}}_1\right)=\\ {\widehat{\overline{\mathbf{T}}}}_{s_2}^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}{}_{\hspace{0.17em}}+O({\rho }_0^4),\end{array}$$

(76)

$$r_{1\hspace{0.17em}{c}_1}^{\left(0,\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+{\rho }_0^2\left(\frac{1}{2}{r}_{1\hspace{0.17em}{c}_3}^{\left(2,\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(2,\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+r_{2\hspace{0.17em}{c}_3}^{\left(1,\hspace{0.17em}1\right)}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_2+\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\cdot {\mathbf{e}}_1\right)={\widehat{\overline{\mathbf{T}}}}_{c_3}^{\left(e,\hspace{0.17em}o\right)}+O({\rho }_0^4),$$

(77)

$$r_{2\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_2+{\rho }_0^2\left(\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_2+r_{1\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_1+\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\cdot {\mathbf{e}}_2\right)={\widehat{\overline{\mathbf{T}}}}_{s_3}^{\left(o,\hspace{0.17em}\hspace{0.17em}e\right)}\hspace{0.17em}+O({\rho }_0^4),$$

(78)

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{c}_4}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+r_{2\hspace{0.17em}{c}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_2\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{2\hspace{0.17em}{c}_4\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}\cdot {\mathbf{e}}_1+r_{2\hspace{0.17em}{c}_4}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_2+\frac{1}{3}{r}_{1\hspace{0.17em}{c}_4}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_1+\frac{1}{3}{r}_{2\hspace{0.17em}{c}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\cdot {\mathbf{e}}_2\right)=\\ {\widehat{\overline{\mathbf{T}}}}_{c_4}^{\left(e,\hspace{0.17em}e\right)}{}_{\hspace{0.17em}}+O({\rho }_0^4),\end{array}$$

(79)

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{s}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_1+r_{2\hspace{0.17em}{s}_4}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot \hspace{0.17em}{\mathbf{e}}_2\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{2\hspace{0.17em}\hspace{0.17em}{s}_4\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}\cdot {\mathbf{e}}_2+r_{1\hspace{0.17em}{s}_4}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}\cdot {\mathbf{e}}_1+\frac{1}{3}{r}_{2\hspace{0.17em}{s}_4}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}\cdot {\mathbf{e}}_2+\frac{1}{3}{r}_{1\hspace{0.17em}{s}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\cdot {\mathbf{e}}_1\right)=\\ {\widehat{\overline{\mathbf{T}}}}_{s_4}^{\left(o,\hspace{0.17em}o\right)}{}_{\hspace{0.17em}}+O({\rho }_0^4),\end{array}$$

(80)

The left hand side of Equations (72)–(80) represents the coefficients of the Fourier series expansion (58). We take into account the decomposition (29) and the results (64)–(65), (69)–(71) valid for double symmetric cross sections.

The nine Equations (72)–(80) contain fifteen vector unknowns ${\mathbf{u}}^{(k\hspace{0.17em},\hspace{0.17em}n-k)}$ $\left(0\le k\le n\le 4\right),$ and to have a closed system of differential equations, another six vector equations are needed which contain and only contain these fifteen unknowns.

For that purpose, we substitute (55) into the dynamical Equation (6), and we obtain

$${\displaystyle \sum _{n=0}^2{\displaystyle \sum _{q=0}^n\frac{1}{q!\left(n-q\right)!}\left({\mathrm{Div}}^{\left(q,\hspace{0.17em}n-q\right)}\mathsf{\sigma }+{\mathbf{f}}^{\left(q,\hspace{0.17em}n-q\right)}-\rho {\ddot{\mathbf{u}}}^{\left(q,\hspace{0.17em}n-q\right)}\right)+O\left({\rho }_0^3\right)}}=0,$$

(81)

in which ${\mathrm{Div}}^{\left(q,\hspace{0.17em}n-q\right)}\hspace{0.17em}\mathsf{\sigma }={\mathsf{\sigma }}_{}^{\left(q+1,\hspace{0.17em}n-q\right)}\cdot {\mathbf{e}}_1+{\mathsf{\sigma }}_{}^{\left(q,\hspace{0.17em}n-q+1\right)}\cdot {\mathbf{e}}_2+{\mathsf{\sigma }}_{,\hspace{0.17em}3}^{\left(q,\hspace{0.17em}n-q\right)}\cdot \hspace{0.17em}{\mathbf{e}}_3\hspace{0.17em}$ and ${\mathbf{f}}^{\left(q,\hspace{0.17em}n-q\right)}$ are the coefficients of the Taylor expansions of f.

Thus the six missing equations are given by

$${\mathrm{Div}}^{\left(q,\hspace{0.17em}n-q\right)}\mathsf{\sigma }+{\mathbf{f}}^{\left(q,\hspace{0.17em}n-q\right)}-\rho {\ddot{\mathbf{u}}}^{\left(q,\hspace{0.17em}n-q\right)}=\hspace{0.17em}0 \mathrm{for} n=0, 2 \mathrm{and} q=0, n$$

(82)

The linear dependence of ${\mathsf{\sigma }}^{(p,\hspace{0.17em}q)}$ in terms of higher-order displacement ${\mathbf{u}}_{}^{(q+1\hspace{0.17em},\hspace{0.17em}p)}$ and ${\mathbf{u}}_{}^{(q\hspace{0.17em},\hspace{0.17em}p+1)}$ (see constitutive law (33)) is a key feature of the dimension reduction procedure since this provides linear algebraic equations for the higher order coefficients which are readily to be eliminated to achieve a simple beam model. Thus Equations (72) and (75), (76), (79), (80) form a linear system for coefficients displacement ${\mathbf{u}}^{\left(4,0\right)},\hspace{0.17em}{\mathbf{u}}^{\left(3,1\right)},\hspace{0.17em}{\mathbf{u}}^{\left(2,2\right)},{\mathbf{u}}^{\left(1,3\right)}$ and ${\mathbf{u}}^{\left(0,\hspace{0.17em}4\right)}$ and then these coefficients displacement can be expressed in terms of lower order coefficients displacement. Also Equations (73) and (74), (77), (78) form a linear system for coefficients displacement ${\mathbf{u}}^{\left(3,0\right)},\hspace{0.17em}{\mathbf{u}}^{\left(2,1\right)},\hspace{0.17em}{\mathbf{u}}^{\left(1,2\right)}$ and ${\mathbf{u}}^{\left(0,3\right)}$ and thus these coefficients displacement can be expressed in terms of lower order coefficients displacement. We do not give these linear systems here since the aim of this work is not to give the complete development for solving this problem. Finally as explained in Section 4, it is easy to establish variational formulation of remaining dynamical Equation (82) which is necessary for finite element discretization.

As in Remark 2 of Section 4.1. we can show that with the unidimensional boundary conditions on the end cross sections of the beam (${\Sigma }_0$ and ${\Sigma }_L$), we can obtain variational formulation of Equation (82).

In the formulation of unidimensional problem (72)–(80) and (82), the moment inertia does not appear clearly but we can refer to Chen et al. [19]. Indeed, we neglect the body force (f = 0) and the lateral traction ($\overline{\mathbf{T}}=0$). For beam with circular cross section of radius $R_0$, for isotropic material and by considering more simplifying assumptions, it is shown in Chen et al. [19] that the unidimensional problem defined (72)–(80) and (82) can be reduced in four differential scalar equations for the leading displacement field ${\mathbf{u}}^{\left(0,0\right)}$ and the twist angle $\overline{\theta }=u_2^{\left(1,\hspace{0.17em}0\right)}-u_1^{\left(0,\hspace{0.17em}1\right)}$

$$E\hspace{0.17em}I\hspace{0.17em}{u}_{3,33}^{\left(0,\hspace{0.17em}0\right)}-\rho {\rm I}{\ddot{u}}_3^{\left(0,\hspace{0.17em}0\right)}=0,$$

$$E\hspace{0.17em}I\hspace{0.17em}{u}_{1,3333}^{\left(0,\hspace{0.17em}0\right)}-\rho {\rm I}{\ddot{u}}_{1,33}^{\left(0,\hspace{0.17em}0\right)}+\rho A\hspace{0.17em}{\ddot{u}}_1^{\left(0,\hspace{0.17em}0\right)}+\frac{{\left(\rho {\rm I}\right)}^2\hspace{0.17em}}{2GI}{\ddot{\ddot{u}}}_1^{\left(0,\hspace{0.17em}0\right)}=0,$$

$$E\hspace{0.17em}I\hspace{0.17em}{u}_{2,3333}^{\left(0,\hspace{0.17em}0\right)}-\rho {\rm I}{\ddot{u}}_{2,33}^{\left(0,\hspace{0.17em}0\right)}+\rho A\hspace{0.17em}{\ddot{u}}_2^{\left(0,\hspace{0.17em}0\right)}+\frac{{\left(\rho {\rm I}\right)}^2\hspace{0.17em}}{2GI}{\ddot{\ddot{u}}}_2^{\left(0,\hspace{0.17em}0\right)}=0,$$

$$G\hspace{0.17em}I\hspace{0.17em}{\overline{\theta }}_{,33}^{}-\rho {\rm I}\hspace{0.17em}\dot{\overline{\theta }}=0,$$

where E is the Young’s modulus, G is the shear modulus, $I=I^{\left(2,0\right)}=I^{\left(0,2\right)}=\frac{\mathbf{\pi }\hspace{0.17em}{R}_0^4}{4}$ is the moment inertia and $A=\mathbf{\pi }\hspace{0.17em}{R}_0^2$ is the area of the cross section.

We observe that the moment inertia comes from the Fourier series expansion coefficients of lateral boundary conditions in Equations (72)–(80).

5.2. Decomposition into Four Subproblems

As in Section 4, we can decompose the problem defined by Equations (72)–(80) and (82) into four subproblems defined as follows.

(a) 

Subproblem $\tilde{R}$

(for an orthotropic material the displacement field is given by Equations (42)–(44)).

This problem is defined by Equation (82) (for (n, q, i) = (0, 0, 3); (1, 0, 2); (2, 0, 3);

(1, 1, 1); (2, 2, 3)) and by the ${\mathbf{e}}_3$ component of (46), (75), (79), the ${\mathbf{e}}_1$ component of (73), (77), the ${\mathbf{e}}_2$ component of (74), (78)

(a1) 

Twelve scalar equations

$${\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}0\right)}+{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{33,\hspace{0.17em}3}^{\left(0,\hspace{0.17em}0\right)}+\hspace{0.17em}{f}_3^{\left(0,\hspace{0.17em}0\right)}-\rho \hspace{0.17em}{\ddot{u}}_3^{\left(0,\hspace{0.17em}0\right)}=0,$$

$${\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}2\right)}+{\mathsf{\sigma }}_{23,\hspace{0.17em}3}^{\left(0,\hspace{0.17em}1\right)}+\hspace{0.17em}{f}_2^{\left(0,\hspace{0.17em}1\right)}-\rho \hspace{0.17em}{\ddot{u}}_2^{\left(0,\hspace{0.17em}1\right)}=0,$$

$${\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}2\right)}+{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}3\right)}+{\mathsf{\sigma }}_{33,\hspace{0.17em}3}^{\left(0,\hspace{0.17em}2\right)}+\hspace{0.17em}{f}_3^{\left(0,\hspace{0.17em}2\right)}-\rho \hspace{0.17em}{\ddot{u}}_3^{\left(0,\hspace{0.17em}2\right)}=0,$$

$${\mathsf{\sigma }}_{11}^{\left(2,\hspace{0.17em}0\right)}+{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{13,\hspace{0.17em}3}^{\left(1,\hspace{0.17em}0\right)}+\hspace{0.17em}{f}_1^{\left(1,\hspace{0.17em}0\right)}-\rho \hspace{0.17em}{\ddot{u}}_1^{\left(1,\hspace{0.17em}0\right)}=0,$$

$${\mathsf{\sigma }}_{13}^{\left(3,\hspace{0.17em}0\right)}+{\mathsf{\sigma }}_{23}^{\left(2,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{33,\hspace{0.17em}3}^{\left(\hspace{0.17em}2,\hspace{0.17em}0\right)}+\hspace{0.17em}{f}_3^{\left(2,\hspace{0.17em}0\right)}-\rho \hspace{0.17em}{\ddot{u}}_3^{\left(2,\hspace{0.17em}0\right)}=0,$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}0}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}0}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{23}^{\left(\hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}1\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}0}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{2\hspace{0.17em}0}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{23}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}0}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{13}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}0}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{0\hspace{0.17em}3}^{\left(e,\hspace{0.17em}\hspace{0.17em}e\right)},\end{array}$$

$$r_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{11}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{11}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{11}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{c_1\hspace{0.17em}1}^{\left(e,\hspace{0.17em}o\right)}\hspace{0.17em},$$

$$r_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{22}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{1\hspace{0.17em}{s}_1}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{s_1\hspace{0.17em}2}^{\left(o,\hspace{0.17em}e\right)},$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{c}_2}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}{c}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}{c}_2\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{2\hspace{0.17em}{c}_2}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{23}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{c}_2}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{13}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{c}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{c_{2}3}^{\left(e,\hspace{0.17em}e\right)}\hspace{0.17em},\end{array}$$

$$r_{1\hspace{0.17em}\hspace{0.17em}{c}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{11}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_3}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{11}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}\hspace{0.17em}{c}_3}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{11}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{c_3\hspace{0.17em}1}^{\left(e,\hspace{0.17em}o\right)}\hspace{0.17em},$$

$$r_{2\hspace{0.17em}{s}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{2\hspace{0.17em}{s}_3}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{22}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{1\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{2\hspace{0.17em}{s}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{s_3\hspace{0.17em}2}^{\left(o,\hspace{0.17em}e\right)},$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{c}_4}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}{c}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}{c}_4\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{2\hspace{0.17em}{c}_4}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{23}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{c}_4}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{13}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{c}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{c_{4}3}^{\left(e,\hspace{0.17em}e\right)}.\end{array}$$

(b) 

Subproblem $\widetilde{\mathit{B}1}$

(for an orthotropic material the displacement field is given by formulas (45)–(47))

This problem is defined by Equation (82) (for (n, q, i) = (0, 0, 1); (2, 0, 1); (1, 1, 3);

(2, 1, 2)) (2, 2, 1); and by the ${\mathbf{e}}_1$ component of (46), (75), (79), the ${\mathbf{e}}_3$ component of (73), (79), the ${\mathbf{e}}_2$ component of (76), (80)

(b1) 

Twelve scalar equations

$${\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}0\right)}+{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{13,\hspace{0.17em}3}^{\left(0,\hspace{0.17em}0\right)}+\hspace{0.17em}{f}_3^{\left(0,\hspace{0.17em}0\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_1^{\left(0,\hspace{0.17em}0\right)}=0,$$

$${\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}2\right)}+{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}3\right)}+{\mathsf{\sigma }}_{13,\hspace{0.17em}3}^{\left(0,\hspace{0.17em}2\right)}+\hspace{0.17em}{f}_1^{\left(0,\hspace{0.17em}2\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_1^{\left(0,\hspace{0.17em}2\right)}=0,$$

$${\mathsf{\sigma }}_{13}^{\left(2,\hspace{0.17em}0\right)}+{\mathsf{\sigma }}_{23}^{\left(1,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{33,\hspace{0.17em}3}^{\left(1,\hspace{0.17em}0\right)}+\hspace{0.17em}{f}_3^{\left(1,\hspace{0.17em}0\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_3^{\left(1,\hspace{0.17em}0\right)}=0,$$

$${\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{22}^{\left(1,\hspace{0.17em}2\right)}+{\mathsf{\sigma }}_{23,\hspace{0.17em}3}^{\left(1,\hspace{0.17em}1\right)}+\hspace{0.17em}{f}_2^{\left(1,\hspace{0.17em}1\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_2^{\left(1,\hspace{0.17em}1\right)}=0,$$

$${\mathsf{\sigma }}_{11}^{\left(3,\hspace{0.17em}0\right)}+{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{13,\hspace{0.17em}3}^{\left(2,\hspace{0.17em}0\right)}+\hspace{0.17em}{f}_1^{\left(2,\hspace{0.17em}0\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_1^{\left(2,\hspace{0.17em}0\right)}=0,$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}0}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}0}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(\hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}1\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}0}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{2\hspace{0.17em}0}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}0}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{11}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}0}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{0\hspace{0.17em}1}^{(e,\hspace{0.17em}e)},\end{array}$$

$$r_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{13}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{13}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{23}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{13}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{c_{1}3}^{(e,\hspace{0.17em}\hspace{0.17em}o)}\hspace{0.17em},$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{c}_2}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}{c}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}{c}_2\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{2\hspace{0.17em}{c}_2}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{c}_2}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{11}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{c}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{c_{2\hspace{0.17em}}1}^{\left(e,\hspace{0.17em}e\right)}\hspace{0.17em},\end{array}$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{s}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}+r_{2\hspace{0.17em}{s}_2}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{22}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{2\hspace{0.17em}\hspace{0.17em}{s}_2\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{22}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{1\hspace{0.17em}{s}_2}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{s}_2}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{22}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{s}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{s_2\hspace{0.17em}2}^{\left(o,\hspace{0.17em}o\right)},\end{array}$$

$$r_{1\hspace{0.17em}{c}_3}^{\left(0,\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{13}^{\left(0,\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{1\hspace{0.17em}{c}_3}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{13}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}{c}_3}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{23}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{1\hspace{0.17em}{c}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{13}^{\left(0,\hspace{0.17em}2\right)}\right)=\hspace{0.17em}{\widehat{\overline{T}}}_{s_2\hspace{0.17em}2}^{\left(o,\hspace{0.17em}o\right)}$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{c}_4}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}{c}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}{c}_4\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{2\hspace{0.17em}{c}_4}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{c}_4}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{11}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{c}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{c_{4}1}^{\left(e,\hspace{0.17em}e\right)}\hspace{0.17em},\end{array}$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{s}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}+r_{2\hspace{0.17em}{s}_4}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{22}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{2\hspace{0.17em}\hspace{0.17em}{s}_4\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{22}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{1\hspace{0.17em}{s}_4}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{s}_4}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{22}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{s}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{s_4\hspace{0.17em}2}^{\left(o,\hspace{0.17em}\hspace{0.17em}o\right)}.\end{array}$$

(c) 

Subproblem$\widetilde{B2}$

(for an orthotropic material the displacement field is given by Equations (48)–(50))

The problem $\widetilde{B2}$ is obtained from Equation (82) (for (n, q, i) = (0, 0, 2); (1, 0, 3);

(2, 0, 2); m(2, 1, 1); (2, 2, 2); and by the ${\mathbf{e}}_2$ component of (46), (75), (79), the ${\mathbf{e}}_3$ component of (74), (78), the ${\mathbf{e}}_1$ component of (76), (80)

(c1) 

Twelve scalar equations

$${\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}2\right)}+{\mathsf{\sigma }}_{33,\hspace{0.17em}3}^{\left(0,\hspace{0.17em}1\right)}+\hspace{0.17em}{f}_3^{\left(0,\hspace{0.17em}1\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_3^{\left(0,\hspace{0.17em}1\right)}=0,$$

$${\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}2\right)}+{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}3\right)}+{\mathsf{\sigma }}_{23,\hspace{0.17em}3}^{\left(0,\hspace{0.17em}2\right)}+\hspace{0.17em}{f}_2^{\left(0,\hspace{0.17em}2\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_2^{\left(0,\hspace{0.17em}2\right)}=0,$$

$${\mathsf{\sigma }}_{11}^{\left(2,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}2\right)}+{\mathsf{\sigma }}_{13,\hspace{0.17em}3}^{\left(1,\hspace{0.17em}1\right)}+\hspace{0.17em}{f}_1^{\left(1,\hspace{0.17em}1\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_1^{\left(1,\hspace{0.17em}1\right)}=0,$$

$${\mathsf{\sigma }}_{12}^{\left(3,\hspace{0.17em}0\right)}+{\mathsf{\sigma }}_{22}^{\left(2,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{23,\hspace{0.17em}3}^{\left(2,\hspace{0.17em}0\right)}+\hspace{0.17em}{f}_2^{\left(2,\hspace{0.17em}0\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_2^{\left(2,\hspace{0.17em}0\right)}=0,$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}0}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}0}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{22}^{\left(\hspace{0.17em}0,\hspace{0.17em}\hspace{0.17em}1\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}0}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{2\hspace{0.17em}0}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{22}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}0}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}0}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{0\hspace{0.17em}2}^{(e,\hspace{0.17em}\hspace{0.17em}e)},\end{array}$$

$$r_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{23}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{1\hspace{0.17em}{s}_1}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{s_1\hspace{0.17em}3}^{(o,\hspace{0.17em}\hspace{0.17em}e)},$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{c}_2}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}{c}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}{c}_2\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{2\hspace{0.17em}{c}_2}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{22}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{c}_2}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{c}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{c_{2\hspace{0.17em}}2}^{(e,\hspace{0.17em}e)}\hspace{0.17em},\end{array}$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{s}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{11}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}+r_{2\hspace{0.17em}{s}_2}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{2\hspace{0.17em}\hspace{0.17em}{s}_2\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{1\hspace{0.17em}{s}_2}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{11}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{s}_2}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{s}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{11}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{s_2\hspace{0.17em}1}^{(o,\hspace{0.17em}\hspace{0.17em}o)},\end{array}$$

$$r_{2\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{23}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{1\hspace{0.17em}{s}_3}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{13}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{23}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{s_3\hspace{0.17em}3}^{(o,\hspace{0.17em}e)},$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{c}_4}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}{c}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{1\hspace{0.17em}{c}_4\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{2\hspace{0.17em}{c}_4}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{22}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{c}_4}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{c}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{22}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{c_{4\hspace{0.17em}}2}^{(e,\hspace{0.17em}e)}\hspace{0.17em},\end{array}$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{s}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{11}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}+r_{2\hspace{0.17em}{s}_4}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{2\hspace{0.17em}\hspace{0.17em}{s}_4\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{12}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{1\hspace{0.17em}{s}_4}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{11}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{s}_4}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{s}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{11}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{s_4\hspace{0.17em}1}^{(o,\hspace{0.17em}o)}.\end{array}$$

(d) 

Subproblem$\tilde{S}$

(for an orthotropic material the displacement field is given by Equations (51)–(53))

The subproblem $\tilde{S}$ is obtained from Equation (82) (for (n, q, i) = (1, 0, 1); (1, 1, 2); (2, 1, 3) and by the $e_2$ component of (73), (77), (79), the $e_1$ component of (74), (78), the $e_3$ component of (76), (80)

(d1) 

Nine scalar equations

$${\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}2\right)}+{\mathsf{\sigma }}_{13,\hspace{0.17em}3}^{\left(0,\hspace{0.17em}1\right)}+\hspace{0.17em}{f}_1^{\left(0,\hspace{0.17em}1\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_1^{\left(0,\hspace{0.17em}1\right)}=0,$$

$${\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}0\right)}+{\mathsf{\sigma }}_{22}^{\left(1,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{23,\hspace{0.17em}3}^{\left(1,\hspace{0.17em}0\right)}+\hspace{0.17em}{f}_2^{\left(1,\hspace{0.17em}0\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_2^{\left(1,\hspace{0.17em}0\right)}=0,$$

$${\mathsf{\sigma }}_{13}^{\left(2,\hspace{0.17em}1\right)}+{\mathsf{\sigma }}_{23}^{\left(1,\hspace{0.17em}2\right)}+{\mathsf{\sigma }}_{33,\hspace{0.17em}3}^{\left(1,\hspace{0.17em}1\right)}+\hspace{0.17em}{f}_3^{\left(1,\hspace{0.17em}1\right)}-\rho \hspace{0.17em}{\ddot{\mathbf{u}}}_3^{\left(1,\hspace{0.17em}1\right)}=0,$$

$$r_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{22}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{c_1\hspace{0.17em}2}^{(e,\hspace{0.17em}\hspace{0.17em}o)}\hspace{0.17em},$$

$$r_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{1\hspace{0.17em}{s}_1}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_1}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{s_1\hspace{0.17em}1}^{(o,\hspace{0.17em}\hspace{0.17em}e)},$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{s}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{13}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}+r_{2\hspace{0.17em}{s}_2}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{23}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{2\hspace{0.17em}\hspace{0.17em}{s}_2\hspace{0.17em}}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{23}^{\left(1,\hspace{0.17em}\hspace{0.17em}2\right)}+r_{1\hspace{0.17em}{s}_2}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{13}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{s}_2}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{23}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{s}_2}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{13}^{\left(0,\hspace{0.17em}\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{s_2\hspace{0.17em}3}^{(o,\hspace{0.17em}\hspace{0.17em}o)},\end{array}$$

$$r_{1\hspace{0.17em}\hspace{0.17em}{c}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_3}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{2\hspace{0.17em}\hspace{0.17em}{c}_3}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{22}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{1\hspace{0.17em}\hspace{0.17em}{c}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{c_3\hspace{0.17em}2}^{(e,\hspace{0.17em}\hspace{0.17em}o)}\hspace{0.17em},$$

$$r_{2\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}0\right)}+{\rho }_0^2\left(\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{12}^{\left(2,\hspace{0.17em}\hspace{0.17em}0\right)}+r_{1\hspace{0.17em}{s}_3}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{11}^{\left(1,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{2}{r}_{2\hspace{0.17em}\hspace{0.17em}{s}_3}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{12}^{\left(0,\hspace{0.17em}\hspace{0.17em}2\right)}\right)={\widehat{\overline{T}}}_{s_3\hspace{0.17em}1}^{(o,\hspace{0.17em}\hspace{0.17em}e)},$$

$$\begin{array}{c}{\rho }_0\left(r_{1\hspace{0.17em}{s}_4}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}\hspace{0.17em}{\mathsf{\sigma }}_{13}^{\left(0,\hspace{0.17em}\hspace{0.17em}1\right)}+r_{2\hspace{0.17em}{s}_4}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\hspace{0.17em}{\mathsf{\sigma }}_{23}^{\left(1,\hspace{0.17em}\hspace{0.17em}0\right)}\right)\\ +\frac{{\rho }_0^3}{2}\left(r_{2\hspace{0.17em}{s}_4\hspace{0.17em}}^{\left(1,\hspace{0.17em}2\right)}{\mathsf{\sigma }}_{23}^{\left(1,\hspace{0.17em}2\right)}+r_{1\hspace{0.17em}{s}_4}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}{\mathsf{\sigma }}_{13}^{\left(2,\hspace{0.17em}\hspace{0.17em}1\right)}+\frac{1}{3}{r}_{2\hspace{0.17em}{s}_4}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}{\mathsf{\sigma }}_{23}^{\left(3,\hspace{0.17em}\hspace{0.17em}0\right)}+\frac{1}{3}{r}_{1\hspace{0.17em}{s}_4}^{\left(0,\hspace{0.17em}3\right)}{\mathsf{\sigma }}_{13}^{\left(0,\hspace{0.17em}3\right)}\right)={\widehat{\overline{T}}}_{s_4\hspace{0.17em}3}^{(o,\hspace{0.17em}o)},\end{array}$$

For the four subproblems $\tilde{R},$ $\widetilde{B1},$ $\widetilde{B2}$ and $\tilde{S}$, the results of Theorem 1 remain true. Also we see that Table 1 remains true if we replace p by f. Table 2 is true if $m_{ij}^{\left(r,\hspace{0.17em}s\right)}$ is replaced by ${\mathsf{\sigma }}_{ij}^{\left(r,\hspace{0.17em}s\right)}.$

As we can see in the detailed formulation of the four subproblems $\tilde{R},$ $\widetilde{B1},$ $\widetilde{B2}$ and $\tilde{S}$, we give in

Table 3. Classification of components of the prescribed stress vector ${\overline{\mathbf{T}}}^{\left(r,\hspace{0.17em}\hspace{0.17em}t\right)}$ for the four subproblems $\tilde{R},$ $\widetilde{B1},$ $\widetilde{B2}$ and $\tilde{S}$.

$\tilde{R}$	${\overline{T}}_1^{(e,\hspace{0.17em}\hspace{0.17em}o)}$	${\overline{T}}_2^{(o,\hspace{0.17em}\hspace{0.17em}e)}$	${\overline{T}}_3^{(e,\hspace{0.17em}\hspace{0.17em}e)}$
$\widetilde{B1}$	${\overline{T}}_1^{(e,\hspace{0.17em}\hspace{0.17em}e)}$	${\overline{T}}_2^{(o,\hspace{0.17em}o)}$	${\overline{T}}_3^{(e,\hspace{0.17em}o)}$
$\widetilde{B2}$	${\overline{T}}_1^{(o,\hspace{0.17em}\hspace{0.17em}o)}$	${\overline{T}}_2^{(e,\hspace{0.17em}\hspace{0.17em}e)}$	${\overline{T}}_3^{(o,\hspace{0.17em}\hspace{0.17em}e)}$
$\tilde{S}$	${\overline{T}}_1^{(o,\hspace{0.17em}e)}$	${\overline{T}}_2^{(e,\hspace{0.17em}\hspace{0.17em}o)}$	${\overline{T}}_3^{(o,\hspace{0.17em}\hspace{0.17em}o)}$

, components of the prescribed stress vector ${\overline{\mathbf{T}}}^{\left(r,\hspace{0.17em}t\right)}$ which intervene in each of the four subproblems $\tilde{R},$ $\widetilde{B1},$$\widetilde{B2}$ and $\tilde{S}$.

6. Conclusions and Discussion

For linear elastic dynamical beams, we give two new unidimensional models rigorously deduced from a three dimensional elasticity. The first one is an extension to dynamical problems of the model previously justified for statical problems [10]. The second one is recently presented in [17,19]. In this model, the linearity of equations with respect to certain coefficients of the displacement field allows to eliminate nine coefficient vectors of the displacement field among fifteen unknowns vector coefficient of the displacement field. These two models can be easily extended to non linear hyperelastic beams but obviously, due to non linearity, results presented in this work cannot be applied.

For double symmetric cross sections and for orthotropic materials, we can show that the initial problem decouples in four independent subproblems. For a monoclinic material, two subproblems are coupled and independent of the two other coupled subproblems.

The decomposition of the initial problem into four more simple decoupled subproblems can be advantageously used for future numerical accurate works. To validate the second model [17,19], we intend to perform numerical tests by considering NURBS (non uniform rational B splines) discretization [21,22,23,24,25,26].