Abstract
Using the Lieb–Mattis ordering theorem of electronic energy levels, we identify the Hilbert space of the low energy sector of quantum Hall/Heisenberg ferromagnets at filling factor M for L Landau/lattice sites with the carrier space of irreducible representations of described by rectangular Young tableaux of M rows and L columns, and associated with Grassmannian phase spaces . We embed this N-component fermion mixture in Fock space through a Schwinger–Jordan (boson and fermion) representation of -spin operators. We provide different realizations of basis vectors using Young diagrams, Gelfand–Tsetlin patterns and Fock states (for an electron/flux occupation number in the fermionic/bosonic representation). -spin operator matrix elements in the Gelfand–Tsetlin basis are explicitly given. Coherent state excitations above the ground state are computed and labeled by complex matrix points Z on the Grassmannian phase space. They adopt the form of a displaced/rotated highest-weight vector, or a multinomial Bose–Einstein condensate in the flux occupation number representation. Replacing -spin operators by their expectation values in a Grassmannian coherent state allows for a semi-classical treatment of the low energy (long wavelength) -spin-wave coherent excitations (skyrmions) of quantum Hall ferromagnets in terms of Grasmannian nonlinear sigma models.
1. Introduction
The breakthrough in the development of new quantum technologies requires mathematical modeling and an adequate theoretical framework for the study of the underlying nuclear, atomic, molecular, optical and condensed matter systems. Algebraic, numerical, analytical and topological mathematical tools for dealing with complex many-body quantum systems are necessary to analyze their properties. In particular, for the understanding of new and exotic topological quantum phases of matter (characterized by topological numbers such as Chern, Pontryagin, Skyrmion (64), etc. and other winding numbers) and their exploitation for technological applications. Indeed, the discovery of new quantum phases of matter (mainly of a topological nature), their classification, analysis and understanding, is a very hot/topical subject. High-temperature superconductors and an emergent category two-dimensional materials provide new types of topological phases, sometimes characterized by exotic electronic (edge) states and currents remarkably robust to impurities and thermal fluctuations. Quantum Hall effect provides the paradigmatic example of a topological phase, but dispersion-less edge currents also appear in the absence of magnetic field, for example, in some graphene analogues (silicene, germanene, etc) with a strong spin–orbit coupling. Two-dimensional topological insulators (see [1] for a text book, [2,3] for reviews and [4] for progress and prospects) were predicted theoretically by Kane and Mele [5] using a two-dimensional graphene-like material model with spin–orbit interaction. They were first proposed [6] and observed experimentally [7] in mercury cadmium telluride (HgTe/CdTe) semiconductor quantum wells and later in other materials. Another rapidly developing field has to do with topological quantum computation; see [8] for Kitaev’s original proposal, [9] for a text book and [10] for a current perspective on Majorana zero modes. Topological quantum computation is an approach to fault-tolerant quantum computation in which the unitary quantum gates result from the braiding of certain topological quantum objects called “anyons”. Topological degrees of freedom promise to encode decoherence-resistant and scalable quantum information. For example, magnetic skyrmions are promising for technological applications, including spintronics and neuromorphic computing. They might be used as information carriers in future advanced memories, logic gates and computing devices (see [11,12,13] for bilayer systems). The creation and transmission of an isolated magnetic skyrmion in thin films is a key for future skyrmionics, which utilizes skyrmions as information carriers in advanced memories, logic gates and computing devices [11,12]. Therefore, a deeper fundamental/theoretical study of models related to this subject is justified by its future use in quantum technologies.
In this article we concentrate on the study of systems of interacting N-component fermions. Traditionally, the paradigmatic case for electrons is (spin 1/2), extensible to (flavor, color) components for leptons and quarks (see [14] for high energy consequences of topological quantum effects), (spin-isospin) components in nuclear physics, etc. The subject of fermions has been recently further fueled in condensed matter physics by the fact that symmetries can be extended to larger N in ultracold atomic gases (see, e.g., the text books [15,16,17] for a review). For example, fermionic alkaline-earth atomic gases trapped in optical lattices realize the generalization of the Hubbard model [18,19]. Exciting recent advances in cooling, trapping and manipulating more and more complex systems of this kind, make Feynman’s original ideas about the simulation of quantum systems and quantum information processing increasingly possible.
Here we want to revisit and deepen the particular subject of quantum Hall (Heisenberg-like) ferromagnets (QHF). As it is briefly reviewed in Appendix A, the exchange interaction for N-component planar electrons in a perpendicular magnetic field adopts the form of a QHF Hamiltonian
on a square lattice when written in terms of -spin operators realized in terms of creation and annihilation operators of an electron with component in a given Landau/lattice site of a given Landau level (namely, the lowest one). The sum over extends over all near-neighbor Landau/lattice sites, and is the exchange coupling constant (the spin stiffness for the XY model). Electrons become multicomponent when, for example, in addition to the usual spin components ↑ and ↓, they acquire extra “pseudospin” internal components associated: (a) with layer (for a multilayer arrangement), (b) with valley (such as in graphene and other 2D Dirac materials) and (c) with sub-lattice, etc. In addition, multilayer arrays introduce extra components (“flavors”) to the electron and much richness, so that the unitary group U also plays a fundamental role here. For example, twisted bilayer (and trilayer) graphene for “magic” angles exhibit interesting superconducting properties [20,21]. In the case of a bilayer quantum Hall system in the lowest Landau level, one Landau site can accommodate internal states (let us call them fermion “flavors/components”, in general); more schematically
where t and b make reference to the “top” and “bottom” layers, respectively. Since the electron field has degenerate components, the bilayer system possesses an underlying symmetry. Likewise, the ℓ-layer case carries a symmetry (see next Section 2 for more details).
For N-component electrons, the Pauli exclusion principle allows electrons per Landau/lattice site (the filling factor). Selecting a ground state ( denotes the Fock vacuum)
which fills all L Landau sites with the first M internal levels (i.e., for integer filling factor M), spontaneously breaks the symmetry since a general unitary transformation mixes the first M “spontaneously chosen” occupied internal levels with the unoccupied ones. The ground state is still invariant under the stability subgroup of transformations among the M occupied levels and the unoccupied levels, respectively. Therefore, the transformations that do not leave invariant are parametrized by the Grassmannian coset , which reduces to the well known sphere for spin components and electron per Landau site. The kind of irreducible representations (IRs) of related to Grassmann phase spaces are those described by rectangular Young tableaux of M rows and L columns, where L labels the corresponding IR, just as spin s does for .
The objective of this article is to describe the carrier Hilbert space associated with these representations, their coherent states (see, e.g., the standard text books [22,23]), and the classical limit. In the classical limit (large -spin representations), the collective operators become c-numbers (their coherent state expectation values, to be more precise), and the low energy (long wavelength) -spin-wave coherent excitations are named “skyrmions” (see, e.g., some recent books and thesis [24,25,26,27]). These coherent excitations turn out to be described by a ferromagnetic order parameter associated with this spontaneous symmetry breaking and labeled by complex matrices Z parametrizing the complex Grassmannian manifold (see later on Section 5 for more information about its structure). Actually, the classical dynamics associated with these quantum spin chains can be described by a Grassmannian nonlinear sigma model (NLM) [28,29,30,31,32,33], generalizing the NLM for the continuum dynamics of Heisenberg (anti)ferromagnets [34,35,36]. In references such as [30,31], N represents the number of fermion “flavors”, whereas L is referred to as the number of “colours” .
The organization of the paper is the following. In Section 2 we motivate the description of low energy sectors of QHF by representations linked rectangular Young tableaux, using the Lieb–Mattis ordering of electronic energy levels based on the pouring principle for Young tableaux. In Section 3, we develop this idea and construct the Hilbert space of N-component fermions occupying L Landau sites (integer filling factor M) making use of a bosonic realization of the -spin collective operators acting on Fock space states. The whole construction relies on the definition of a highest-weight (ground) state in Section 3.1, a “boson condensate” version of the ground state (3). We provide a representation of basis vectors in terms of Young tableaux, Gelfand–Tsetlin vectors and Fock (boson and fermion) states in Section 3.2. The monolayer case at filling factor , the bilayer case at filling factor and the trilayer case at are worked out as particular examples. General Hilbert-space dimension formulas are provided in Section 3.3. Matrix elements of the physical operators are provided in Section 4, together with the spectrum of Casimir operators, paying special attention to the quadratic Casimir operator since it is related with the exchange interaction Hamiltonian at low energies. Section 5 is devoted to the discussion of Grassmannian coherent states and the expectation values of -spin collective operators. coherent states can be seen as coherent excitations above the highest weight (ground) state in the form of Bose–Einstein condensates. Coherent states are essential to discuss the classical limit of large L representations of QHF in terms of NLMs on Grassmannian manifolds , of which we also comment in the second half of Section 5. The last Section 6 is devoted to conclusions and outlook. For completeness, and to be as self-contained as possible, we include in Appendix A a brief reminder on the derivation of QHF models from first principle (two-body exchange) interactions. The proof of propositions 1 and 2 is given in Appendix B and Appendix C, respectively. A more detailed relation between Gelfand–Tsetlin and Fock states is left for the Appendix D. The spin-pseudospin structure of basis states for bilayer QHF at filling factor is made explicit in the Appendix E. Explicit particular expressions of -spin matrices for and are given in Appendix F. Finally, general considerations about the highest weight state for Young tableaux of arbitrary shape are given in Appendix G.
2. U(N) Ferromagnetism and Lieb–Mattis Ordering of Electronic Energy Levels
Let us denote by the -dimensional carrier Hilbert space at site of the fully antisymmetric IR of described by the Young frames/diagrams of shape , that is, with M boxes on a single column. This is a convenient way of graphically representing (and symmetric group ) invariant subspaces, i.e., by Young diagrams of P boxes/particles
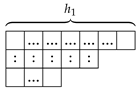 of shape , with , the number of boxes in row and the total number of particles. This is why h is also called a partition of P. We sometimes use the shorthand , obviating zero-box rows. Basis vectors of are the M-particle Slater determinants (in Fock and Young tableau notation)
of shape , with , the number of boxes in row and the total number of particles. This is why h is also called a partition of P. We sometimes use the shorthand , obviating zero-box rows. Basis vectors of are the M-particle Slater determinants (in Fock and Young tableau notation)
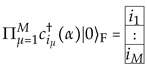 obtained by filling out columns of the corresponding Young diagram with components in strictly increasing order . The ground state (“highest weight”) vector (3) is just one example. One can see that there are exactly different arrangements of this kind (the dimension of ).
obtained by filling out columns of the corresponding Young diagram with components in strictly increasing order . The ground state (“highest weight”) vector (3) is just one example. One can see that there are exactly different arrangements of this kind (the dimension of ).

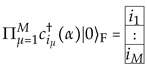
The Hilbert space of a QHF with L Landau/lattice sites at integer filling factor M is the -dimensional L-fold tensor product space . In Young tableau notation
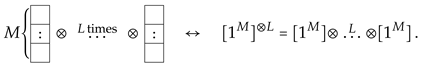
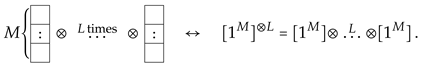
This tensor product representation of is reducible and it decomposes into a direct sum of irreducible representations of different shapes. For example, the Clebsch–Gordan decomposition of a tensor product of IRs of of shape , with filling factor , is represented by the following Young diagrams


The -particle ground state (3) is a vector of . In particular, for filling factor and lattice sites, is represented by the rectangular Young tableau
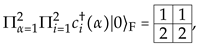 where rows are filled in a non-decreasing order. One can see that, for electron components, there are 20 different Young tableau arrangements of this kind, which is the dimension of the IR of given by the rectangular Young diagram of shape (see later on Section 3.3 for general dimension formulas). In fact, the corresponding dimensions for the tensor product decomposition (7) for is . Note that the ground state (3) is invariant under permutation of lattice sites (look at the Equations (A4) and (A5)); therefore, it will always belong to IRs of of rectangular shape
where rows are filled in a non-decreasing order. One can see that, for electron components, there are 20 different Young tableau arrangements of this kind, which is the dimension of the IR of given by the rectangular Young diagram of shape (see later on Section 3.3 for general dimension formulas). In fact, the corresponding dimensions for the tensor product decomposition (7) for is . Note that the ground state (3) is invariant under permutation of lattice sites (look at the Equations (A4) and (A5)); therefore, it will always belong to IRs of of rectangular shape
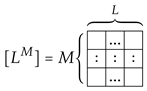 arising in the Clebsch–Gordan decomposition of the tensor product (6). The rectangular Young tableaux of shape are antisymmetric under the interchange of rows (electron components or “flavors”) and symmetric under the interchange of columns (lattice sites or “colors”).
arising in the Clebsch–Gordan decomposition of the tensor product (6). The rectangular Young tableaux of shape are antisymmetric under the interchange of rows (electron components or “flavors”) and symmetric under the interchange of columns (lattice sites or “colors”).

Let us show how Lieb–Mattis’ theorem [37], and some generalizations [38], also confer “dominance” to the rectangular Young diagrams ( such as in (7)) over the rest of diagrams arising in the Clebsch–Gordan decomposition of (6). The set of Young diagrams is partially ordered (not all P-particle diagrams can be compared for ) by the so called “dominance order” ⪰, such that
It is said that h dominates or that precedes h (). Intuitively, it means that one can go from h to by moving a certain number of boxes from upper rows to lower rows, so that h is “more symmetric”. Lieb–Mattis’ theorem [37] talks about the “pouring principle”, saying that can be “poured into” h. The theorem states that, under general conditions on the symmetric Hamiltonian of the system, if then [ for “pathologic” potentials], with the ground state energy inside each IR h of . From this, the following proposition can be demonstrated.
Proposition 1.
All Young diagrams arising in the Clebsch–Gordan direct sum decomposition of the L-fold tensor product (6) can be pored into the rectangular Young tableaux of shape . That is, the ground state for a QHF at filling factor M belongs to the carrier Hilbert space of the rectangular IR of inside the total Hilbert space .
The proof is made in the Appendix B. Note that states in are invariant under the permutation of lattice sites , thus becoming indistinguishable (“bosonized”). Another way of interpreting it is the following. Given the Fourier transform of -spin operators, the long-wavelength (low momentum/energy ) ground state excitations are described by the collective operators , which are invariant under site permutations . Moreover, the low-energy long-wavelength semi-classical () dynamics of QHF is described by a NLM which target space is the Grasmannian (the phase space associated with IRs with rectangular Young diagrams).
Once we have motivated/highlighted the dominant role of rectangular Young diagrams of shape at low energies, let us explicitly construct these representations in a boson realization of generators, together with their associated coherent states labeled by matrix points Z on the Grassmann phase space . These kind of representations have been studied in (mainly mathematically oriented) text books such as [39], but rarely associated with the low energy sector of spin systems such as the ones pursued in this article. This is why we think this discussion deserves attention.
3. Low Energy Sector of U(N) Quantum Hall Ferromagnets at Filling Factor M
3.1. Boson Realization of U(N)-Spin Operators, Fock Space, Highest-Weight State and Ladder Operators
In the quantum Hall approach, each electron occupies on average a surface area of (a Landau site, with the magnetic length) that is pierced by one magnetic flux quantum (see Appendix A for more information about this picture). This image allows a dual bosonic Schwinger realization of -spin operators
this time in terms of creation and annihilation boson operators of magnetic flux quanta attached to the electron with component (we use Greek indices for electron labels to avoid confusion). From the usual bosonic commutation relations we derive the -spin commutation relations
where is the usual Kronecker delta. This bosonic picture is quite common in algebraic approaches to nuclear and molecular structure [40,41,42], for example in the interacting boson model (IBM) [43]. Therefore, we have a representation of in Fock space made of Fock states
The exponent of indicates the number of Landau/lattice sites (flux quanta) available to the electron of flavor i (that is, the occupancy number ). We write and not because will later make reference to a row index of a Young diagram. Since IRs are finite-dimensional, we know that the representation of in Fock space must be reducible. In particular, -spin operators conserve the total number of particles [the linear Casimir operator of ]. According to Schur’s lemma, for a IR, every operator acting on the representation space and commuting with all must be trivial (a multiple of the identity). Note that the operators
close a Lie algebra, where we are writing the subscript to emphasize that this is different from all the other appearances of that are related to the “first” generators () of as a subgroup of . In fact, the operators are in general independent of , that is, can not be written in terms of (except for , when ) since they realize an independent Lie algebra. The operators preserve the IR space and they commute with all the -spin operators, i.e.,
Therefore, the operators can be consistently imposed as constraints on Fock state vectors to reduce the representation of in a consistent manner. Actually, since each electron has L Landau/lattice sites at its disposal (i.e., a total number of L flux quanta), then the constraint has to be imposed on physical states . This constraint is extended to for non-diagonal operators (see below in Equation (18) for the case of the highest weight vector). For the basis Fock states (13), the constraint in particular means that , the total number of Landau/lattice sites available to electron .
Our aim is to construct a state basis of the Hilbert space , carrying the IR of , given in terms of linear combinations of Fock states (13). The Hilbert space can be constructed from the so called “highest weight” HW (resp. lowest-weight) vector by applying lowering (resp. raising ) operators (see below for a more detailed explanation). This procedure reminds the standard construction of spin-j (Dicke) states from the highest (resp. lowest) weight state (resp. ) by applying ladder angular momentum operators (resp. ). Given a common eigenvector of , its weight is made of the corresponding eigenvalues , which count the number of electrons with flavor/component i; therefore, , the total number of particles, which is the value of the linear Casimir operator of . Any other state has lower weight than if the first non-vanishing coefficient of is positive. It is clear that the highest weight must be , which can also be read from the shape of the Young diagram (remember that we are discarding zeros). Let us state this in a more formal way. Before, for the sake of compact notation, we shall denote by
the and annihilation and creation operator matrices, respectively.
Proposition 2.
Let be the submatrix
of in (15), given by its first M columns (the leading principal submatrix of order M). Then the state
satisfies the highest weight (HW) conditions:
It is also normalized [ denotes the Pochhammer symbol] and invariant under transformations.
The proof is left for the Appendix C. The vector is the boson analogue of the fermion state in (3). The determinant structure of guarantees that this state is antisymmetric under electron exchange (i.e., under row exchange of ) as long as L is odd. Otherwise, a statistical transmutation occurs for the fermion mixture.
Let us identify the ladder operators. It can be seen that any other state is either zero or has lower weight than . Indeed, using the commutation relations (12),
Actually, from property (19), gives a non-zero vector of weight only when . The resulting vector has the same structure as but replacing column k, , of in by column j, of in (15). When , the weight component of is . When the weight component of is . Only the weight components and are shifted: increases by 1 and decreases by 1. Therefore, becomes of lower weight since the first non-vanishing coefficient of is . In this sense, , with acts as a lowering ladder operator. It transfers one electron from component k into component . Of special interest are the step 1 lowering operators , from which we can obtain the action of any other lowering operator making use of the recursion formulas
The same argument can be applied to raising ladder operators with . We shall provide an explicit expression for the matrix elements of step 1 lowering and raising operators for any IR of of a given HW in Section 4.
Let us see how to label and graphically represent basis states of any IR of shape h of in Young tableau and Gelfand notation. We shall pay special attention to the Hilbert space ,
3.2. Young Tableaux, Gelfand and Fock Basis States
Young tableaux are constructed by filling out rows (resp. columns) of the corresponding Young diagram with components in non-decreasing (resp. strictly increasing) order from left to right (resp. from top to bottom). For example, for filling factor , Landau sites and fermion components/flavors, the following Young tableau
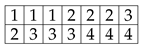 is in the standard form. The occupancy number described after (13) can be calculated as the number of times that the state i appears in the row (counting downwards) of the tableau. In the previous example we have
and zero the rest. It is clear that , that is, each electron has L Landau sites available (“it carries L flux quanta”). The highest weight vector in (17) is written in Young tableau notation as
is in the standard form. The occupancy number described after (13) can be calculated as the number of times that the state i appears in the row (counting downwards) of the tableau. In the previous example we have
and zero the rest. It is clear that , that is, each electron has L Landau sites available (“it carries L flux quanta”). The highest weight vector in (17) is written in Young tableau notation as
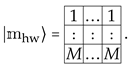
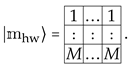
To subsequently write matrix elements of -spin operators in a compact form (see Section 4), it is convenient to introduce the Gelfand–Tsetlin notation for vectors as triangular patterns of non-negative integer numbers of the form
obeying the betweenness conditions
That is, each number in the pattern is constrained to vary between its two closest upper neighbors. Sometimes we shall denote a Gelfand pattern by its N rows . The relation between a Young tableau and the corresponding Gelfand pattern is built as follows (the prescription applies to a Young tableau of general shape, not only rectangular ):
- The top row is read off the shape of the tableau, and it coincides with the highest weight. In terms of the occupancy numbers , we have
- The second row is read off the shape of the tableau that remains after all boxes containing the component/flavor are removed, that is, .
- ⋯
- is read off the shape of the tableau that remains after all boxes containing the flavors are removed, that is, .
- ⋯
- is read off the shape of the tableau that remains after all remaining boxes containing are removed.
- Finally, is read off the shape of the tableau that remains after all remaining boxes containing are removed.
For example, for the Young tableau (22) we have
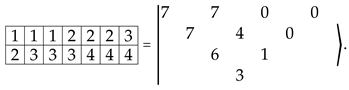
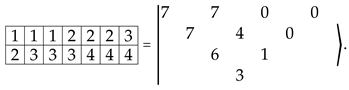
Let us work out some particular examples, for the sake of clarity, before stating more general formulas.
3.2.1. U(2) Quantum Hall Ferromagnet at Filling Factor
Let us describe the simplest example of a QHF where each Landau site accommodates electron with flavors, for example, a spin electron
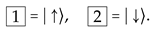
For L Landau sites, the Hilbert space basis vectors can be labeled by the number of spin-up (flavor ) electrons in Young tableau, Gelfand and Fock (boson and fermion) forms as
 where is the symmetric group of degree L and a permutation. Moreover, for this case, a Dicke state representation is also possible, with total angular momentum and spin third component . The highest () and lowest () weight states correspond to angular momentum third components and , respectively. The Hilbert space dimension is clearly . This is time for a clarification. Even though we are using the equality sign “=” in (29), to be precise, each of the vectors in those equalities belong to different vector spaces. That is, they are different mathematical ways of representing the same physical state. However, we will keep this little abuse of notation in the hope that no confusion arises.
where is the symmetric group of degree L and a permutation. Moreover, for this case, a Dicke state representation is also possible, with total angular momentum and spin third component . The highest () and lowest () weight states correspond to angular momentum third components and , respectively. The Hilbert space dimension is clearly . This is time for a clarification. Even though we are using the equality sign “=” in (29), to be precise, each of the vectors in those equalities belong to different vector spaces. That is, they are different mathematical ways of representing the same physical state. However, we will keep this little abuse of notation in the hope that no confusion arises.

3.2.2. U(4) Quantum Hall Ferromagnet at Filling Factor
Let us consider now a bilayer system (with top t and bottom b layers) where each Landau site accommodates electrons with flavors

The basis states of are given by the Gelfand vectors and their betweenness conditions
In this case, the basis vectors are indexed by four labels . Particular examples are the highest- and the lowest- weight states

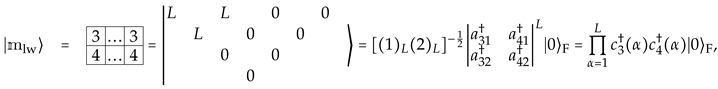 in Young tableau, Gelfand and Fock (boson and fermion) notation, respectively. The relation between Gelfand and Fock states for general L is a bit more involved for states other than the highest and lowest weight; therefore, we leave the general prescriptions for the Appendix D. An alternative basis for this case was, noted by
has been given in [44], where j (half-integer) represents an angular momentum and m (integer) is related to a population imbalance between layers t and b (both non-negative).
in Young tableau, Gelfand and Fock (boson and fermion) notation, respectively. The relation between Gelfand and Fock states for general L is a bit more involved for states other than the highest and lowest weight; therefore, we leave the general prescriptions for the Appendix D. An alternative basis for this case was, noted by
has been given in [44], where j (half-integer) represents an angular momentum and m (integer) is related to a population imbalance between layers t and b (both non-negative).

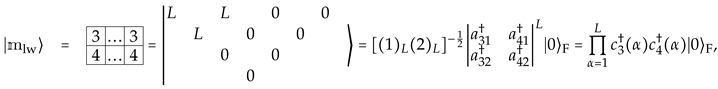
From the betweenness conditions (31), one can easily compute the dimension of the IR of as
Note that grows as for large L. We shall recover in Section 3.3 the expression (35) as a particular case of the so called “hook-length” general formula, which is a special case of the Weyl’s character formula (see, e.g., [39]).
In Appendix E we explicitly work out the case , for which , thus recovering the dimension of the totally antisymmetric IR of . The corresponding basis vectors for this case can be divided into two spin/pseudospin (layer) sectors, and we shall make use of them when writing Grassmannian coherent states later in Equation (60).
3.2.3. U(6) Quantum Hall Ferromagnet at Filling Factor
Let us consider now a trilayer system (with top t, central c, and bottom b layers) where each Landau site accommodates electrons with flavors
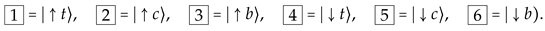
The basis states of are given by the Gelfand vectors indexed by 9 labels
In particular, the HW state
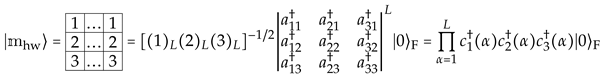 corresponds to the Gelfand vector with all 9 labels . As we did in (35), from the betweenness conditions (25) of these labels, one can compute the dimension
corresponds to the Gelfand vector with all 9 labels . As we did in (35), from the betweenness conditions (25) of these labels, one can compute the dimension
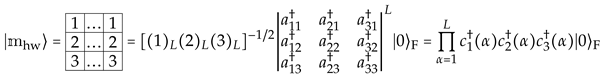
For we have , thus recovering the dimension of the totally antisymmetric IR of . Note that grows such as for large L.
3.3. General Dimension Formulas
The dimension of the carrier Hilbert space of a IR of with general HW (a partition of P) is given by the Weyl dimension formula (see, e.g., [39])
It can also be written with the so called “hook formula”
where is the length of the hook located at the box/cell position (row, column) of the corresponding Young diagram of shape . The hook is the set of cells/boxes such that and or and . The hook length is the number of cells/boxes in .
These formulas correspond to the number of independent Gelfand patterns fulfilling the betweenness conditions (25), and also to the number of different Young tableau arrangements.
For rectangular Yound diagrams the dimension formula (39) acquires the form
This formula reproduces the previous particular examples. Note that (conjugated representation).
4. Matrix Elements of U(N)-Spin Collective Operators
In this Section we shall provide explicit expressions for matrix elements of -spin operators (11) in the Gelfand–Tsetlin basis . We have already given some indications in Section 3.2. In fact, recursion formulas
allow us to obtain any non diagonal operator matrix element from the matrix elements of step 1 lowering and raising operators. Let us consider an arbitrary IR of of HW . Denoting by , the sum of k-th row of a pattern , and setting , the action of diagonal operators on an arbitrary Gelfand state is
which reproduces the expressions (19) for the highest-weight vector with rows for and for . The linear Casimir fulfills , the eigenvalue being the total number of particles.
Let us denote by the “auxiliary pattern” with 1 at place and zeros elsewhere [we call it “pattern” because it has the triangular shape, although it does not necessarily fulfill the betweenness conditions (25)]. The action of step 1 lowering and rising operators is given by [39]
with coefficients
where and whenever any indeterminacy arises. In fact, from the commutation relations (20), the weight of is given by
and therefore, becomes of lower weight than since the first non-vanishing coefficient of is . From the definition (45) one can prove that
which means that . Furthermore, applying induction and the recurrence formulas (42), we obtain . Therefore, we can construct proper hermitian -spin operators as: , and , , with the imaginary unit. In Appendix F we provide explicit expressions of these -spin matrix elements for particularly interesting cases.
For completeness, we shall provide the eigenvalues of the N invariant (Casimir) operators belonging to the enveloping algebra, whose expression is given by p powers of the operators as
where sum on repeated indices is understood. That is, is of degree p. We have already argued that with . For , the eigenvalue is the total number of particles. The eigenvalues of on the carrier Hilbert space of are given in [39] and they are constructed as follows. Let B a square matrix with entries
and let J be the all-ones matrix (that is, ). Then the spectrum of the Casimir operators is given by
where is the p-th power of B. The quadratic Casimir operator plays a fundamental role as the invariant part of the QHF Hamiltonian and we shall pay special attention to it. In particular, the eigenvalue of the quadratic Casimir operator is simply given in general by and, for the case of , the expression reduces to .
5. Grassmannian Coherent States and Nonlinear Sigma Models
5.1. Grassmannian Coherent States
We have seen in Proposition 2 that the HW (ground) state is invariant under the subgroup of . Therefore breaks the symmetry since a general rotation mixes the first M (“spontaneously chosen”) occupied internal orbitals with the remainder unoccupied ones. This structure is also very relevant for systems with particle-hole symmetry, such as in nuclear and molecular models [40,41,42,43]. -spin-wave excitations occur in QHF. These coherent excitations (named “skyrmions”) turn out to be described by a ferromagnetic order parameter associated with this spontaneous symmetry breaking and labeled by complex matrices Z parametrizing the complex Grassmannian coset . This parametrization is related to the Bruhat–Iwasawa block matrix decomposition (see, e.g., Chapter 3 of Ref. [39]) of the complexification of . For the fundamental N-dimensional representation, this block matrix decomposition reads
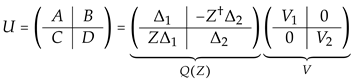 where A and D are invertible square complex matrices of orders M and , respectively, with
and are unitary matrices. The normalization matrix factors are related by the Woodbury matrix identity . Complex matrix points Z on the Grassmann manifold are associated with quotient representatives .
where A and D are invertible square complex matrices of orders M and , respectively, with
and are unitary matrices. The normalization matrix factors are related by the Woodbury matrix identity . Complex matrix points Z on the Grassmann manifold are associated with quotient representatives .
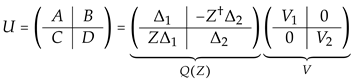
Let us firstly discuss the simplest case. The decomposition (50) for adopts the form
which is adapted to the quotient (the two-sphere), with the stereographic projection of a point (polar and azimuthal angles) of the sphere onto the complex plane . Let us consider filling factor . The creation operator matrix in (15) reduces to . Denote by the first column of in (52). Coherent excitations above the HW vector for filling factor can be written as a two-mode Bose–Einstein condensate of the form
where we are using the notation (28) for spin up and down states at a Landau site, respectively. That is, the spin coherent state adopts the form of a symmetric L-qubit state. The direct product structure (not entanglement between lattice sites) ensures the underlying translational invariance. For example, for the particular case of (spin ) we have
where we identify the spin triplet
basis written in terms of the usual Dicke (total angular momentum) states (with , the magnetic quantum number) already discussed after (29). In general, spin coherent states can be written in the Dicke basis as (see, e.g., [22,23] for standard references)
Even further, coherent states can also be created by applying a transformation/rotation on the HW vector
where is the spin lowering operator, and the relation between the complex coordinate y and the stereographic projection coordinate z arises from the application of the Baker–Campbell–Hausdorff–Zassenhaus factorization formula to the group [22,23]. Note that, in the tensor product representation of , all qubits/spins are rotated “in unison” to account for translation/permutation symmetry. Other non-symmetric definitions of spin coherent states are possible for the group product , in which every qubit/spin is rotated independently of each other (see, e.g., [45]). Here we restrict ourselves to spin (Bloch/atomic) symmetric coherent states introduced a long time ago by [46,47]. Haldane used them to study the semi-classical approximation of 1-D Heisenberg anti-ferromagnetic spin chains, whose continuum dynamics is described by NLMs [34,35,36].
All these construction can be extended to QHF at filling factor M as follows. Define as the first M columns of in (50) and split the creation operator matrix in (15) into a 2-block matrix , where makes reference to the first M columns (HW components) and to the last columns (LW components). Grassmannian coherent states (see [23] for related fermionic coherent states) are then labeled by the complex matrices Z and have the form of a Bose–Einstein condensate
Note that corresponds to the HW state (17). As for spin coherent states in (56), Grassmannian coherent states can also be written as a transformation/rotation of the HW vector as
where the relation between the complex matrices Y and Z [similar to the relation between y and z in (56)) now arises from the application of the Baker–Campbell–Hausdorff–Zassenhaus factorization formula to the group (see, e.g., [23] for related fermionic coherent states). Note that Grassmannian coherent states can be seen as a matrix version/extension of spin coherent states .
Let us explicitly work out a couple of examples related to the bilayer system () of Section 3.2.2. We shall denote the states such as in (30) and talk about spin and pseudo-spin or layer . For filling factor we have
where denotes a point on the complex projective space . For filling factor , the Hilbert space at each Landau/lattice site has dimension . In Appendix E we provide a basis (made of spin triplet and pseudo-spin triplet states) for adapted to the spin-layer intrinsic structure of this case. Coherent states here adopt the form
with a matrix point on the Grassmannian . can also be written in terms of Gelfand vectors as the rotation (58) with -spin operators given by their matrix elements (45) (see, e.g., Appendix F for some particular cases).
Coherent states are sometimes called “semi-classical” (they exhibit minimal uncertainty, etc.) and they are used as variational states to study the semiclassical and thermodynamic limit, specially in quantum phase transitions [48]. We have used coherent states, introduced by us in [44,49], to study their entanglement properties [50] and the phase diagram of bilayer quantum Hall systems at filling factor in [51,52], which turn out to reproduce previous results of Ezawa and collaborators [53,54]. Let us take a closer look to the role of Grasmannian coherent states to construct semi-classical models of QHF in terms of NLM.
5.2. Grassmannian Nonlinear Sigma Models
In order to study the semi-classical/thermodynamical limit of QHF, one has to replace -spin operators by their coherent state expectation values . Let us adopt a compact notation and denote by S the operator matrix with operator matrix entries . The corresponding coherent state expectation value matrix is
where is defined in (50). We have renormalized the matrix operator S by L to define the matrix expectation value as a density (intensive quantity), with a good thermodynamical limit . Moreover, we have shifted Cartan -spin operators by for convenience. The complex matrix plays the role of a ferromagnetic order parameter associated to the symmetry-breaking ground state. Let us take the continuum limit, that is, small lattice constant and large number of lattice sites , so that are coordinates on the plane and the finite difference becomes the derivative; that is, the order parameter becomes a matrix field at every point x of the plane. The low energy physics of the QH ferromagnet (when considering only nearest-neighbor interactions in the exchange energy (A9)) is then described by a NLM field theory with action
where means partial derivative with respect to time , is the gradient and is the scalar product. The first (kinetic) term of the action (62) is the Berry term (provided by the coherent state representation of the path integral quantization (see, e.g., [31,33] for more information about the origin of the Berry term, and [55] for the application of path-integral quantization to indistinguishable particle systems topologically confined by a magnetic field). The second term describes the energy cost when the order parameter is not uniform. The topological current
( is the Levi-Civita antisymmetric symbol in 1 + 2 dimensions) leads to the topological (Pontryagin) charge or Skyrmion number
See, e.g., Ref. [33] for more information.
Note that we do not have real field components for but only corresponding to the complex matrix Z. This is due to the constraints given by the N values (49) of the N Casimir operators (48). For example, the linear and quadratic Casimir values say that
For large L, the leading term for the expectation values of quadratic spin powers is (spin fluctuations are negligible in the classical limit). For , and , the linear and quadratic Casimir constraints reproduce the well known sphere equation for , and .
Since the kinetic (Berry) term involves a single time derivative, half of the Grassmannian fields Z are conjugate momenta of the other half (that is, The Grassmannian target space is a phase space), thus expecting independent spin-wave modes. Given the relation (61) between the order parameter and the Grassmann matrix Z, after a little bit of algebra, the spatial part (potential energy) of the Lagrangian (62) can be written in terms of minimal matrix fields Z as [56,57]
where we have used the expression (61) of in terms of in (50), together with the Woodbury matrix identity . It would be worth revising the classical limit of quantum Hall ferromagnets for large representations, considered long time ago by [28,29,30,31,32,33] for anti-ferromagnets, in boson/fermion mixture picture exposed in this article. This is work in progress.
6. Conclusions and Outlook
In this article we have presented several group-theoretical tools to study interacting N-component fermions on a lattice, such as quantum Hall ferromagnets arising from two-body exchange interactions. We have restricted ourselves to the lower energy permutation symmetry sector (according to the Lieb–Mattis theorem [37]) corresponding to fermion mixtures described by rectangular Young diagrams with M rows (the filling factor) and L columns (Landau/lattice sites). We have provided orthonormal basis vectors of the corresponding Hilbert space in terms of Youn tableaux, Gelfand–Tsetlin patterns and boson/fermion Fock states. We have written general matrix elements of -spin collective operators in the Gelfand–Tsetlin basis. Several particular examples have been explicitly worked out to better understand the general expressions, specially the case of bilayer quantum Hall systems at filling factor appearing in the literature [53,54,58,59,60,61,62,63,64,65] Dimension formulas for these irreducible representations of have also been provided. Special attention has been paid to the highest weight state, which can be associated with the ground state of the system. From this perspective, the “spontaneously chosen” ground state breaks the original symmetry and the associated ferromagnetic order parameter [the expectation value of collective -spin operators S in a Grassmannian coherent state ] describes coherent state excitations in the classical limit, whose dynamics is governed by a Grassmannian nonlinear sigma model.
Restricting to the dominant permutation symmetry sector is a common practice to reduce the computational complexity when dealing with quantum many-body systems. For example, critical and chaotic quantum systems of P, N-level/component, identical particles (“quNits”, a higher dimensional generalization of qubits for ) undergoing a quantum phase transition in the thermodynamic (classical) limit , are usually studied by restricting to the -dimensional (the number of ways of exciting P particles with N levels when order does not matter) totally symmetric sector in the -dimensional P-fold tensor product of N-dimensional (fundamental) irreducible representations of . Replacing by then reduces the size of the Hilbert space from to , which is a great simplification when and P is large. The justification of this restriction is that the ground state of the many-body system always belongs to totally symmetric representation, in accordance with the Lieb–Mattis ordering problem. In more physical terms, and for the particular example of the Dicke model of super-radiance [66], the assumption that the P atoms of -levels are indistinguishable (bosons) is admissible when the emitters are confined to a cavity volume much smaller than the scale of the wavelength ℓ of the optical transition. However, the role of mixed permutation symmetry sectors in many body quantum systems should not be disregarded at higher energies, and we have already made some steps in [67] for the case of critical N-level Lipkin–Meshkov–Glick atom models. Entanglement characterization of quantum phases in these systems have also been studied [68]. This is also our next step for quantum Hall ferromagnets.
Finally, concerning physical applications and quantum technological implementations, as we have already mentioned in the introduction, the subject of fermions and magnetism has been recently further fueled in condensed matter physics with exciting advances in cooling, trapping and manipulating fermionic alkaline-earth atoms trapped in optical lattices. Furthermore, magnetic Skyrmion materials display a robust topological magnetic structure, being a candidate for the next generation of spintronic memory devices. Multilayer quantum Hall arrangements, bearing larger symmetries, also display interesting new physics. Such is the case of superconducting properties of twisted bilayer (and trilayer) graphene predicted by [20] and observed by [21]. Therefore, this is a highly topical subject, in which we believe this article makes a novel (not standard) contribution of a fundamental nature. Further perspectives worth exploring have to do with the interplay between quantum information and quantum topological phases of matter. Namely, the identification of topological order by entanglement entropy (see, e.g., [69,70]). Indeed, quantum information concepts can be used to reformulate and characterize topological order. Some of us have already applied quantum information techniques to the characterization of topological insulator phases of graphene analogue [71,72,73,74,75] and fosforene [76,77]. Furthermore, Schur basis, such as the ones discussed here in terms of Young tableaux, have probed to be useful for efficient quNit circuits [78].
Author Contributions
Conceptualization, M.C.; methodology, M.C.; software, A.M.; validation, M.C., A.M. and J.G.; formal analysis, M.C.; investigation, M.C., A.M. and J.G.; resources, M.C.; data curation, M.C. and A.M.; writing—original draft preparation, M.C.; writing—review and editing, M.C., A.M. and J.G.; visualization, A.M.; supervision, M.C.; project administration, M.C.; funding acquisition, M.C. and J.G.. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish MICINN through the project PGC2018-097831-B-I00 and Junta de Andalucía through the projects SOMM17/6105/UGR, UHU-1262561, FQM-381 and FEDER/UJA-1381026. A.M. was funded by the Spanish MIU predoctoral fellowship FPU19/06376.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We all thank E. Pérez-Romero for his collaboration in the early stages of this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Quantum Hall Ferromagnets from Exchange Interactions
Let us briefly summarize how the Hamiltonian of a quantum Hall ferromagnet can be derived from fundamental microscopic two-body (let us say Coulomb) interactions between N-component electrons (see also [54]). The field theoretical expression of the Hamiltonian for two-body interactions between N-component electrons in 2-dimensional space is
where is the two-body potential and is the electron field, which can be expanded in terms of a set of one-body wave (Wannier) functions , localized around the lattice/Landau sites , with L the total number of lattice/landau sites as
In the case of quantum Hall systems in the Landau gauge (B is the constant perpendicular magnetic field and is the vector potential), the one-body functions are canonical (harmonic oscillator) coherent states
describing a plane wave propagating in the direction with momentum ( denotes the magnetic length). The probability of finding the electron at has a sharp peak at and a width , where (here denotes the -size of the system), because the wave number is quantized as , with n an integer. Thus, these states are represented by strips on a rectangular geometry occupying an area of and defining a von Neumann lattice (see, e.g., [54]). Therefore, the number of Landau/lattice sites enclosed by the system of area is , which coincides with the number of magnetic flux quanta penetrating the sample, that is, the ratio of the total magnetic flux to the magnetic flux quantum . In the symmetric gauge , the “strips in a rectangular geometry” image is replaced by “rings in a disk geometry”, where the linear momentum k is replaced by the angular momentum m (see [54] for more information).
The coefficients denote annihilation (creation) operators of electrons of component at site , fulfilling the usual anticommutation rules
It is also important to emphasize that these operators commute among different Landau/lattice sites, that is,
Let us denote by
The terms that effectively contribute to the energy are and , corresponding to the direct (D) and exchange (E) energies
where is the electron number operator at site . In the case of Coulomb interaction, the direct term represents the usual Coulomb energy between two charge distributions and localized around the Landau/lattice sites and , respectively. The exchange term has no classical counterpart and owes its origin to the Pauli exclusion principle. Note that vanishes when there is no overlap between the wave functions and at sites and (for example, for distant sites). One can define the -spin operators at site by
They allow one to write the exchange energy as a generalized Heisenberg spin–spin interaction
which depends on the relative -spin orientation at neighboring sites and . From here the name of “ quantum Hall ferromagnet”, where all -spins tend to be equally polarized (for ) to lower the exchange energy . This Hamiltonian is -invariant and therefore the -spin “direction” is spontaneously chosen. This invariance can be explicitly broken by adding Zeeman, pseudo-Zeeman, layer bias, etc., external couplings [54].
Appendix B. Proof of Proposition 1
We shall proceed by induction in L. The -fold tensor product representation of decomposes as
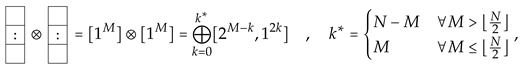 where we understand for all . It is clear that for all , in accordance with the dominance order definition (10). Now suppose that dominates over all Young diagrams arising in . Then, we have to prove by induction that dominates over all Young diagrams arising in .
where we understand for all . It is clear that for all , in accordance with the dominance order definition (10). Now suppose that dominates over all Young diagrams arising in . Then, we have to prove by induction that dominates over all Young diagrams arising in .
Firstly, we shall state an auxiliary lemma.
Lemma A1.
Let be any Young diagram of . The tensor product between and the totally antisymmetric IR leads to a decomposition into Young diagrams with shape
Proof.
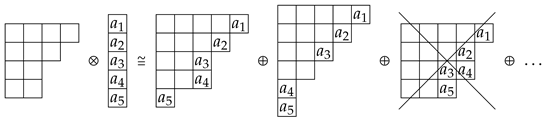
It is straightforward taking into consideration the multiplication rules of Young diagrams (Section 9.5.1 of [79]). Specially the one which states: Reading the resulting diagrams from right to left and starting with the top row, at any point must the number of ’s encountered exceed the number of previously encountered ’s. If we are multiplying any diagram with the totally antisymmetric (one column), every will appear only once in the new diagrams. Therefore, the aforementioned rule will limit by one the number of boxes per row that we can add to the original diagram to construct the new ones. For instance, using a diagram and the antisymmetric IR ,
 □
□

It is convenient to name the rectangular diagram as , and all Young diagrams arising from as , including the rectangular one (). Therefore, the dominance of is written as , or equivalently (10),
According to the Lemma A1, the tensor product generates the diagrams with and . Among them, there is a new rectangular diagram , with . The restriction implies , which leads to
and using Equation (A13),
Therefore, considering the dominance order definition, we arrive to , eventually proving that the rectangular Young diagram dominates the other diagrams arising from and concluding the proof by induction. ■
Appendix C. Proof of Proposition 2
Looking at the structure of
(where is the symmetric group of degree M and is the Levi-Civita symbol) it is clear that is made of particles, as desired. The basic boson commutation relations imply that or , where is a function and denotes the formal derivative with respect to the argument. Therefore, let us simply write . In order to prove (18), we have that
The last summation consists of replacing row by row inside the determinant , and therefore we have
which proves the constraint (18). To prove (19), we follow the same steps as for (18), that is
If , the last summation consists of replacing column j by column i inside the determinant , and therefore , which means that is invariant under the subgroup . If , then column j is absent from and , which means that is in fact invariant under the subgroup . Note the similarities with invariance properties of the ground state of Equation (3). This will be an important fact when discussing the Grassmannian structure associated with quantum Hall ferromagnets at filling factor M later in Section 5. The other possibilities for correspond to rising and lowering operators and will be discussed later.
It remains to prove that the squared norm of is given by in (17), where is the usual Pochhammer symbol. We proceed by mathematical induction. Firstly we prove that . Indeed,
Now we assume that and we shall prove that
Indeed, it can be shown that
The proof is cumbersome in general and we shall restrict ourselves to the more maneuverable case, which grasps the essence of the general case. In fact,
In general
To finish, we realize that , which concludes the proof by induction. ■
Appendix D. Relation between Gelfand–Tsetlin and Fock States
We already know the general expression of the HW state in Fock space, given by (17). In this expression, the leading principal minor of order M of plays a fundamental role. Remember that the square submatrix was obtained from in (15) by deleting the last columns. In the proof of Proposition 2, in the Appendix C, we argued that ladder operators replace column j by column i inside the minor . In general, we can obtain different minors of size , corresponding to the different ways one can choose M columns from the N columns of . Let , with (increasing order), denote one of these column choices and
the corresponding submatrix of . The cases (first M columns) and (last M columns) are special, since they are related to the highest- and lowest-weight states, respectively; actually, we are denoting simply by . There are several ways of attaching flux quanta to the electron with flavor .
For a given containing i, let us denote a composition (a partition where order matters) of in the sense that
[ means that we put i in the -th place]. Namely, for the example (22), we have () and we can arrange these compositions into planar tables, where sum on column i gives and sum on row i gives , as follows
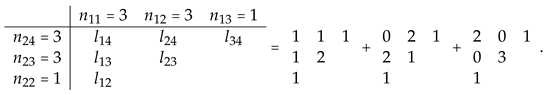
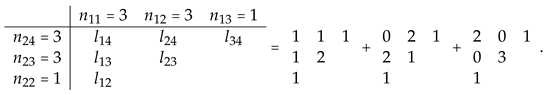
Denoting a minor of size of , a Gelfand state corresponds to the following (un-normalized) Fock state
where the sum is extended to all components associated with (or equivalently, to the occupancy numbers ). Note that is a homogeneous polynomial of degree in the creation operators . For example, taking into account the three components (A18) of the Gelfand state (27) for filling factor and flavors, the corresponding Fock state can be written as
This expression becomes simpler for highest and lowest weight states. For example, in (32) and (37) we have seen that the corresponding HW states for and are just given in terms of and (just one single component), respectively. In the same way, the lowest-weight state for and is given in terms of only in (33). The computation of compositions (A17) of the occupancy numbers for becomes more and more involved since the planar picture (A18) becomes a higher-dimensional arrangement.
Appendix E. Single Landau Site Hilbert Space Basis for a Bilayer U(4) QHF at M=2
Let us explicitly work out the case , and , for which the Hilbert space has dimension . The corresponding basis vectors for this case can be divided into two sectors: the spin-triplet pseudospin-singlet sector
 and the pseudospin-triplet spin-singlet sector
and the pseudospin-triplet spin-singlet sector



Appendix F. Explicit Particular Expressions of U(N)-Spin Matrix Elements
In Section 4, we have given general formulas (45) for the matrix coefficients of the -spin operators in the Gelfand basis for a given IR of characterized by the highest-weight (top row of the Gelfand vector in (24)). In this Appendix we provide particular examples to explain the underlying algorithm. Firstly, we need to order the Gelfand basis . For it, we choose an increasing order of the components of the Gelfand vector array (24) from top to bottom and from left to right, fulfilling the betweenness conditions (25). Schematically, the vectors of the basis are ordered within a list generated by nested indexes
For example, this ordering convention coincides with the order in which we add in Equation (35) the basis vectors of the representation of to compute its dimension. Note that the first basis vector is the lowest weight vector , whereas the last basis vector is the highest weight vector . Let us see some particular simple examples.
Appendix F.1. U(2)-Spin Matrices for M = 1 and L = 1
These matrices are in one-to-one correspondence to the SU(2) Pauli matrices (), , , plus identity.
Appendix F.2. U(2)-Spin Matrices for M = 1 and L = 2
These matrices are related to the SU(2) spin matrices, , , .
Appendix F.3. U(4)-Spin Matrices for M = 2 and L = 1
The rest of the matrices can be obtained using the commutation relations in Equation (42).
Appendix G. The Case of Non-Rectangular Young Tableaux
For a Young tableau of general shape , the HW state (17) is generalized to
where are leading (corner) principal minors of order n of (for , in general), such as in (A19); denotes a normalizing factor. This HW state satisfies the HW conditions:
If all components of are different, that is, , then all leading principal minors of are present in the product (A30) and the HW state is only invariant under (all internal/flavor states are occupied). In this case, the ferromagnetic order parameter associated with the symmetry breaking is labeled by complex parameters , parameterizing the coset (flag manifold) . See, e.g., [57] for the Bruhat–Iwasawa decomposition in this case.
References
- Bernevig, B.A. Topological Insulators and Topological Superconductors; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Kou, L.; Ma, Y.; Sun, Z.; Heine, T.; Chen, C. Two-Dimensional Topological Insulators: Progress and Prospects. J. Phys. Chem. Lett. 2017, 8, 1905–1919. [Google Scholar] [CrossRef] [PubMed]
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [PubMed]
- Konig, M.; Wiedmann, S.; Brune, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.L.; Zhang, S.C. Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef]
- Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef]
- Pachos, J.K. Introduction to Topological Quantum Computation; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Sarma, S.D.; Freedman, M.; Nayak, C. Majorana zero modes and topological quantum computation. NPJ Quantum Inf. 2015, 1, 15001. [Google Scholar] [CrossRef]
- Zhang, X.; Ezawa, M.; Zhou, Y. Magnetic skyrmion logic gates: Conversion, duplication and merging of skyrmions. Sci. Rep. 2015, 5, 9400. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, Y.; Ezawa, M.; Zhao, G.P.; Zhao, W. Magnetic skyrmion transistor: Skyrmion motion in a voltage-gated nanotrack. Sci. Rep. 2015, 5, 11369. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, Y.; Ezawa, M. Magnetic bilayer-skyrmions without skyrmion Hall effect. Nat. Commun. 2016, 7, 10293. [Google Scholar] [CrossRef]
- Jacak, J.E. Quantum mechanism of extremely high energy processes at neutron star collapse and of quasar luminosity. J. High Energy Phys. 2022, 2022, 2. [Google Scholar] [CrossRef]
- Pethick, C.J.; Smith, H. Bose-Einstein Condensation in Dilute Gases, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Lewenstein, M.; Sanpera, A.; Ahufinger, V. Ultracold Atoms in Optical Lattices: Simulating Quantum Many-Body Systems, 1st ed.; Oxford University Press: Oxford, UK, 2012. [Google Scholar] [CrossRef]
- Cazalilla, M.A.; Rey, A.M. Ultracold Fermi gases with emergent SU(N) symmetry. Rep. Prog. Phys. 2014, 77, 124401. [Google Scholar] [CrossRef] [PubMed]
- Honerkamp, C.; Hofstetter, W. Ultracold Fermions and the SU(N) Hubbard Model. Phys. Rev. Lett. 2004, 92, 170403. [Google Scholar] [CrossRef]
- Cazalilla, M.A.; Ho, A.F.; Ueda, M. Ultracold gases of ytterbium: Ferromagnetism and Mott states in an SU(6) Fermi system. New J. Phys. 2009, 11, 103033. [Google Scholar] [CrossRef]
- Bistritzer, R.; MacDonald, A.H. Moiré bands in twisted double-layer graphene. Proc. Natl. Acad. Sci. USA 2011, 108, 12233–12237. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Fatemi, V.; Demir, A.; Fang, S.; Tomarken, S.L.; Luo, J.Y.; Sanchez-Yamagishi, J.D.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018, 556, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Perelomov, A. Generalized Coherent States and Their Applications; Springer: Berlin/Heidelberg, Germeny, 1986. [Google Scholar] [CrossRef]
- Gazeau, J. Coherent States in Quantum Physics; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Seki, S.; Mochizuki, M. Skyrmions in Magnetic Materials; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Han, J.H. Skyrmions in Condensed Matter; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Finocchio, G.; Panagopoulos, C. (Eds.) Magnetic Skyrmions and Their Applications; Woodhead Publishing: Sawston, UK, 2021. [Google Scholar] [CrossRef]
- Zhang, S. Chiral and Topological Nature of Magnetic Skyrmions; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Affleck, I. The quantum Hall effects, σ-models at Θ = π and quantum spin chains. Nucl. Physics B 1985, 257, 397–406. [Google Scholar] [CrossRef]
- Affleck, I. Exact critical exponents for quantum spin chains, non-linear σ-models at Θ = π and the quantum hall effect. Nucl. Phys. B 1986, 265, 409–447. [Google Scholar] [CrossRef]
- Affleck, I. Critical behaviour of SU(N) quantum chains and topological non-linear σ-models. Nucl. Phys. B 1988, 305, 582–596. [Google Scholar] [CrossRef]
- Read, N.; Sachdev, S. Some features of the phase diagram of the square lattice SU(N) antiferromagnet. Nucl. Phys. B 1989, 316, 609–640. [Google Scholar] [CrossRef]
- Read, N.; Sachdev, S. Spin-Peierls, valence-bond solid, and Néel ground states of low-dimensional quantum antiferromagnets. Phys. Rev. B 1990, 42, 4568–4589. [Google Scholar] [CrossRef]
- Arovas, D.P.; Karlhede, A.; Lilliehöök, D. SU(N) quantum Hall skyrmions. Phys. Rev. B 1999, 59, 13147–13150. [Google Scholar] [CrossRef]
- Haldane, F. Continuum dynamics of the 1-D Heisenberg antiferromagnet: Identification with the O(3) nonlinear sigma model. Phys. Lett. A 1983, 93, 464–468. [Google Scholar] [CrossRef]
- Haldane, F.D.M. Nonlinear Field Theory of Large-Spin Heisenberg Antiferromagnets: Semiclassically Quantized Solitons of the One-Dimensional Easy-Axis Néel State. Phys. Rev. Lett. 1983, 50, 1153–1156. [Google Scholar] [CrossRef]
- Haldane, F.D.M. O(3) Nonlinear σ Model and the Topological Distinction between Integer- and Half-Integer-Spin Antiferromagnets in Two Dimensions. Phys. Rev. Lett. 1988, 61, 1029–1032. [Google Scholar] [CrossRef]
- Lieb, E.; Mattis, D. Theory of Ferromagnetism and the Ordering of Electronic Energy Levels. Phys. Rev. 1962, 125, 164–172. [Google Scholar] [CrossRef]
- Decamp, J.; Gong, J.; Loh, H.; Miniatura, C. Graph-theory treatment of one-dimensional strongly repulsive fermions. Phys. Rev. Res. 2020, 2, 023059. [Google Scholar] [CrossRef]
- Barut, A.; Raczka, R. Theory of Group Representations and Applications; Polish Scientific Publishers: Warszawa, Poland, 1980. [Google Scholar]
- Casten, R.; Lipas, P.; Warner, D.; Otsuka, T.; Heyde, K.; Draayer, J. Algebraic Approaches to Nuclear Structure: Interacting Boson and Fermion Models, 1st ed.; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar] [CrossRef]
- Frank, A.; Van Isacker, P. Algebraic Methods in Molecular and Nuclear Structure Physics; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Iachello, F.; Levine, R. Algebraic Theory of Molecules; Oxford University Press: Oxford, UK, 1995. [Google Scholar] [CrossRef]
- Iachello, F.; Arima, A. The Interacting Boson Model; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar] [CrossRef]
- Calixto, M.; Pérez-Romero, E. Coherent states on the GrassmannianU(4)/U(2)2: Oscillator realization and bilayer fractional quantum Hall systems. J. Phys. A Math. Theor. 2014, 47, 115302. [Google Scholar] [CrossRef]
- Sugita, A. Moments of generalized Husimi distributions and complexity of many-body quantum states. J. Phys. A Math. Gen. 2003, 36, 9081–9103. [Google Scholar] [CrossRef]
- Radcliffe, J.M. Some properties of coherent spin states. J. Phys. A Gen. Phys. 1971, 4, 313–323. [Google Scholar] [CrossRef]
- Arecchi, F.T.; Courtens, E.; Gilmore, R.; Thomas, H. Atomic Coherent States in Quantum Optics. Phys. Rev. A 1972, 6, 2211–2237. [Google Scholar] [CrossRef]
- Gilmore, R. Catastrophe Theory for Scientists and Engineers; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Calixto, M.; Pérez-Romero, E. Some properties of Grassmannian U(4)/U(2) x U(2) coherent states and an entropic conjecture. J. Phys. Math. Theor. 2015, 48, 495304. [Google Scholar] [CrossRef]
- Calixto, M.; Pérez-Romero, E. Interlayer coherence and entanglement in bilayer quantum Hall states at filling factorν = 2/λ. J. Physics Condens. Matter 2014, 26, 485005. [Google Scholar] [CrossRef] [PubMed]
- Calixto, M.; Peón-Nieto, C.; Pérez-Romero, E. Hilbert space and ground-state structure of bilayer quantum Hall systems at ν = 2/λ. Phys. Rev. B 2017, 95, 235302. [Google Scholar] [CrossRef]
- Calixto, M.; Peón-Nieto, C. Husimi function and phase-space analysis of bilayer quantum Hall systems at ν = λ. J. Stat. Mech. Theory Exp. 2018, 2018, 053112. [Google Scholar] [CrossRef]
- Hasebe, K.; Ezawa, Z.F. Grassmannian fields and doubly enhanced Skyrmions in the bilayer quantum Hall system at ν = 2. Phys. Rev. B 2002, 66, 155318. [Google Scholar] [CrossRef]
- Ezawa, Z. Quantum Hall Effects; World Scientific: Singapore, 2013. [Google Scholar] [CrossRef]
- Jacak, J.E. Application of path-integral quantization to indistinguishable particle systems topologically confined by a magnetic field. Phys. Rev. A 2018, 97, 012108. [Google Scholar] [CrossRef]
- MacFarlane, A. Generalizations of σ-models and CpN models, and instantons. Phys. Lett. B 1979, 82, 239–241. [Google Scholar] [CrossRef]
- Calixto, M.; Peón-Nieto, C.; Pérez-Romero, E. Coherent states for N-component fractional quantum Hall systems and their nonlinear sigma models. Ann. Phys. 2016, 373, 52–66. [Google Scholar] [CrossRef]
- Ezawa, Z.F.; Eliashvili, M.; Tsitsishvili, G. Ground-state structure in ν = 2 bilayer quantum Hall systems. Phys. Rev. B 2005, 71, 125318. [Google Scholar] [CrossRef]
- MacDonald, A.H.; Rajaraman, R.; Jungwirth, T. Broken-symmetry ground states in ν = 2 bilayer quantum Hall systems. Phys. Rev. B 1999, 60, 8817–8826. [Google Scholar] [CrossRef]
- Schliemann, J.; MacDonald, A.H. Bilayer Quantum Hall Systems at Filling Factor ν = 2: An Exact Diagonalization Study. Phys. Rev. Lett. 2000, 84, 4437–4440. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, A.; Sawada, A.; Kozumi, S.; Terasawa, D.; Shimoda, Y.; Ezawa, Z.F.; Kumada, N.; Hirayama, Y. Magnetotransport study of the canted antiferromagnetic phase in bilayer ν = 2 quantum Hall state. Phys. Rev. B 2006, 73, 165304. [Google Scholar] [CrossRef]
- Yang, K.; Das Sarma, S.; MacDonald, A.H. Collective modes and skyrmion excitations in graphene SU(4) quantum Hall ferromagnets. Phys. Rev. B 2006, 74, 075423. [Google Scholar] [CrossRef]
- Yang, K.; Moon, K.; Zheng, L.; MacDonald, A.H.; Girvin, S.M.; Yoshioka, D.; Zhang, S.C. Quantum ferromagnetism and phase transitions in double-layer quantum Hall systems. Phys. Rev. Lett. 1994, 72, 732–735. [Google Scholar] [CrossRef] [PubMed]
- Moon, K.; Mori, H.; Yang, K.; Girvin, S.M.; MacDonald, A.H.; Zheng, L.; Yoshioka, D.; Zhang, S.C. Spontaneous interlayer coherence in double-layer quantum Hall systems: Charged vortices and Kosterlitz-Thouless phase transitions. Phys. Rev. B 1995, 51, 5138–5170. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Moon, K.; Belkhir, L.; Mori, H.; Girvin, S.M.; MacDonald, A.H.; Zheng, L.; Yoshioka, D. Spontaneous interlayer coherence in double-layer quantum Hall systems: Symmetry-breaking interactions, in-plane fields, and phase solitons. Phys. Rev. B 1996, 54, 11644–11658. [Google Scholar] [CrossRef] [PubMed]
- Dicke, R.H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- Calixto, M.; Mayorgas, A.; Guerrero, J. Role of mixed permutation symmetry sectors in the thermodynamic limit of critical three-level Lipkin-Meshkov-Glick atom models. Phys. Rev. E 2021, 103, 012116. [Google Scholar] [CrossRef]
- Calixto, M.; Mayorgas, A.; Guerrero, J. Entanglement and U(D)-spin squeezing in symmetric multi-quDit systems and applications to quantum phase transitions in Lipkin–Meshkov–Glick D-level atom models. Quantum Inf. Process. 2021, 20, 304. [Google Scholar] [CrossRef]
- Jiang, H.C.; Wang, Z.; Balents, L. Identifying topological order by entanglement entropy. Nat. Phys. 2012, 8, 902–905. [Google Scholar] [CrossRef]
- Zeng, B.; Chen, X.; Zhou, D.L.; Wen, X.G. Quantum Information Meets Quantum Matter: From Quantum Entanglement to Topological Phases of Many-Body Systems; Springer Nature: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Calixto, M.; Romera, E. Identifying topological-band insulator transitions in silicene and other 2D gapped Dirac materials by means of Rényi-Wehrl entropy. EPL Europhys. Lett. 2015, 109, 40003. [Google Scholar] [CrossRef]
- Romera, E.; Calixto, M. Uncertainty relations and topological-band insulator transitions in 2D gapped Dirac materials. J. Phys. Condens. Matter 2015, 27, 175003. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Calixto, M.; Romera, E. Inverse participation ratio and localization in topological insulator phase transitions. J. Stat. Mech. Theory Exp. 2015, 2015, P06029. [Google Scholar] [CrossRef]
- Romera, E.; Calixto, M. Band inversion at critical magnetic fields in a silicene quantum dot. EPL Europhys. Lett. 2015, 111, 37006. [Google Scholar] [CrossRef][Green Version]
- Romera, E.; Calixto, M.; Bolivar, J. Information measures and topological-band insulator transitions in 2D-Dirac materials under external circularly polarized lasers, and static electric and magnetic fields. Phys. Stat. Mech. Appl. 2018, 511, 174–181. [Google Scholar] [CrossRef]
- Castaños, O.; Romera, E.; Calixto, M. Information theoretic analysis of Landau levels in monolayer phosphorene under magnetic and electric fields. Mater. Res. Express 2019, 6, 106316. [Google Scholar] [CrossRef]
- Calixto, M.; Romera, E.; Castaños, O. Analogies between the topological insulator phase of 2D Dirac materials and the superradiant phase of atom-field systems. Int. J. Quantum Chem. 2021, 121, e26464. [Google Scholar] [CrossRef]
- Bacon, D.; Chuang, I.L.; Harrow, A.W. Efficient Quantum Circuits for Schur and Clebsch-Gordan Transforms. Phys. Rev. Lett. 2006, 97, 170502. [Google Scholar] [CrossRef]
- Cvitanovic, P. Group Theory: Birdtracks, Lie’s and Exceptional Groups; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).