A New Flexible Univariate and Bivariate Family of Distributions for Unit Interval (0, 1)
Abstract
:1. Introduction
2. Brief Review and Methodology
- (i)
- ,
- (ii)
- is differentiable and monotonically non-decreasing, and
- (iii)
- and .
3. The NKw-G Family
4. Properties of the NKw-G Family
4.1. Quantile Function
4.2. Linear Representation for the NKw-G Density
4.3. Mathematical Properties
4.4. Estimation of Univariate G-Family Parameters
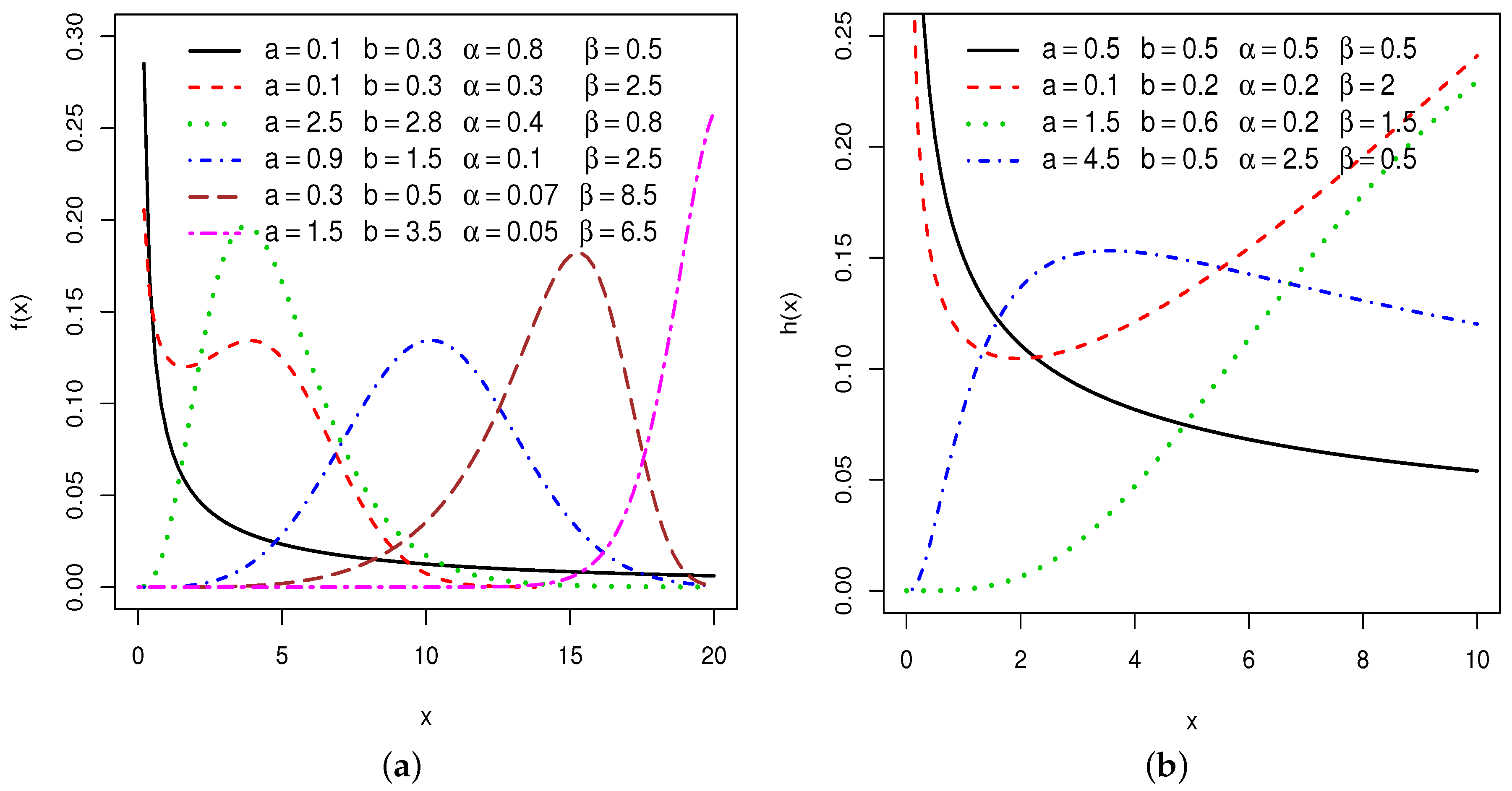
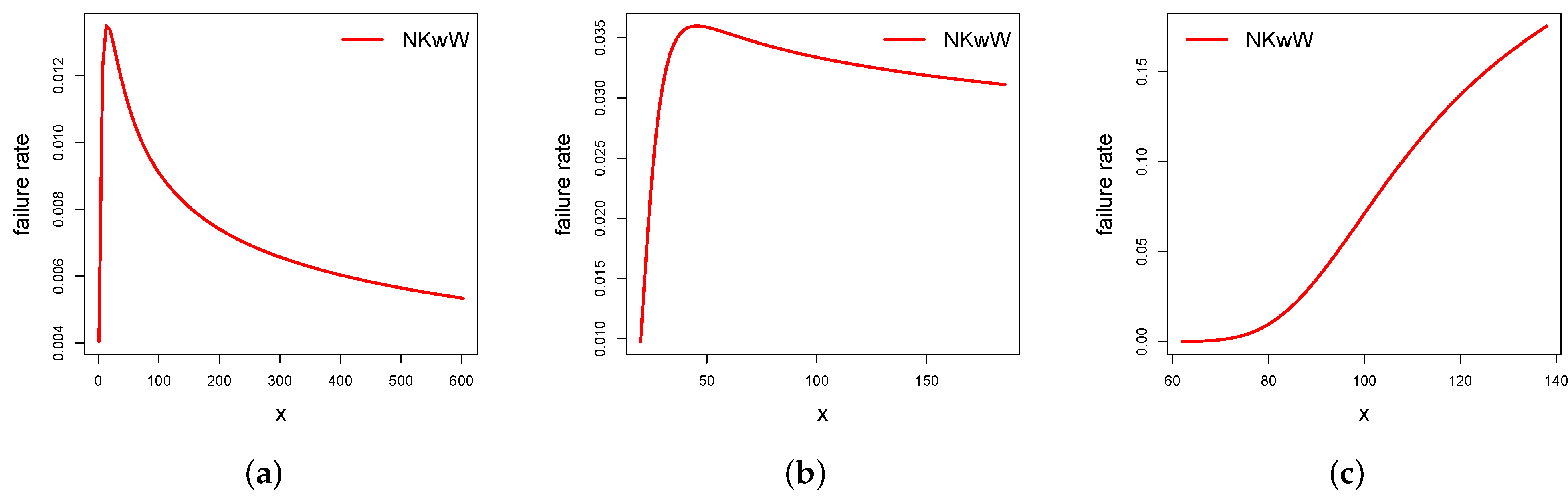
5. The Univariate NKwW Distribution
5.1. Properties of Univariate NKwW Model
5.2. Estimation of Univariate NKw Family Parameters
6. Simulation Study
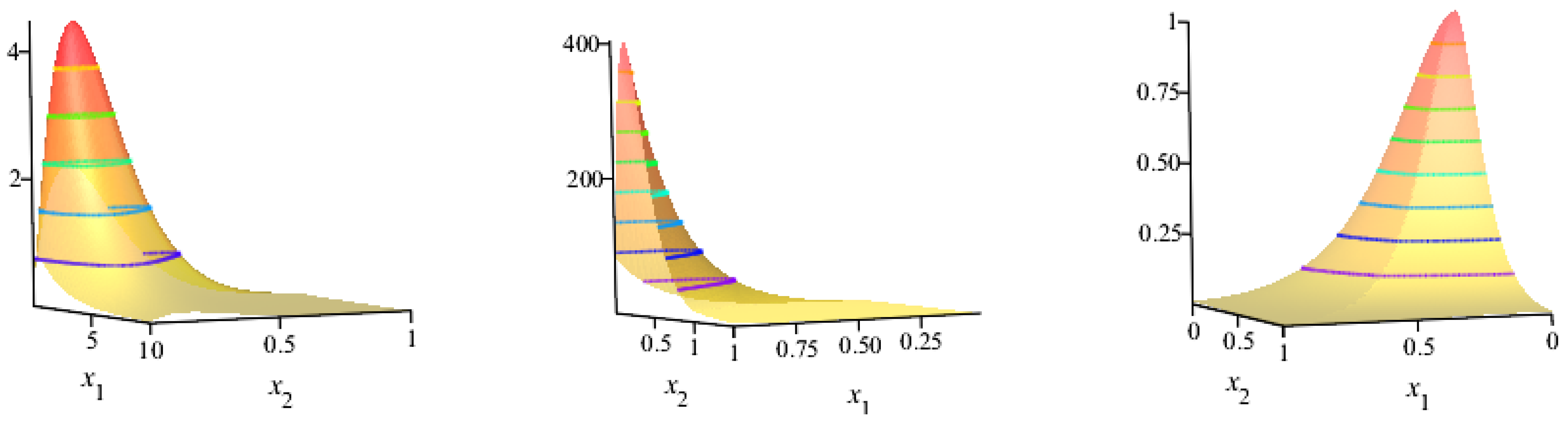
7. Bivariate New Kumaraswamy (BvNKw) G-Family
7.1. The MLE for the BvNKw-G Parameters
7.2. Kendall’s Rank Correlation ()
7.3. Simulation for the BvNKw-G Family
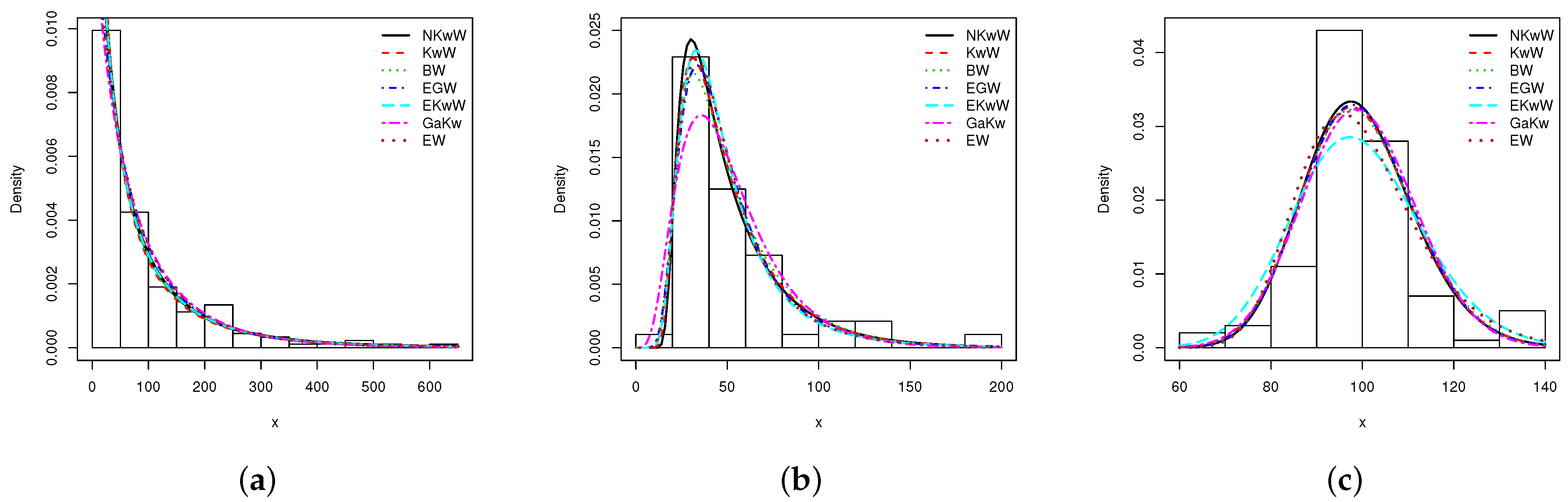
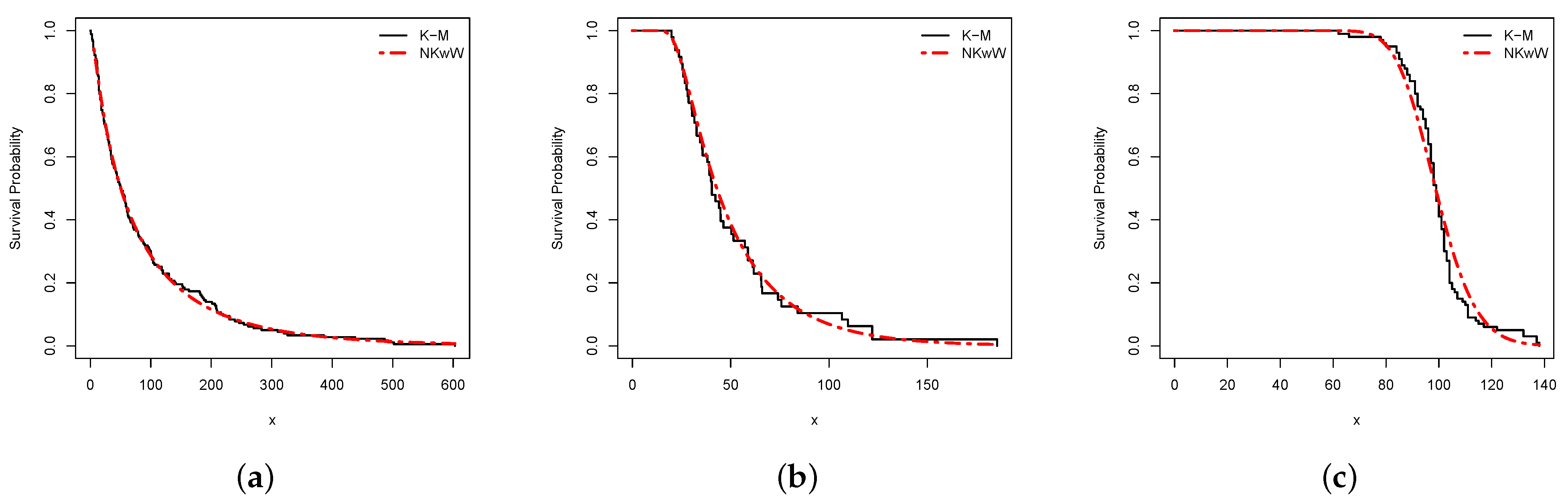
8. Empirical Illustrations of the Proposed Univariate Model
9. Empirical Illustration of the Proposed Bivariate Model
10. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat. Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; de-Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Zografos, K.; Balakrishnan, N. On families of beta- and generalized gamma generated distributions and associated inference. Stat. Methodol. 2009, 6, 344–362. [Google Scholar] [CrossRef]
- Shaw, W.T.; Buckley, I.R. The Alchemy of Probability Distributions: Beyond Gram-Charlier Expansions, and a Skew-Kurtotic-Normal Distribution from a Rank Transmutation Map. UCL Discovery Repository. 2009. Available online: http://discovery.ucl.ac.uk/id/eprint/643923 (accessed on 12 May 2022).
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef] [Green Version]
- Cordeiro, G.M.; Ortega, E.M.M.; Popović, B.V.; Pescim, R.R. The Lomax generator of distributions: Properties, minification process and regression model. Appl. Math. Comput. 2014, 247, 465–486. [Google Scholar] [CrossRef]
- Al-Aqtash, R.; Famoye, F.; Lee, C. On generating a new family of distributions using the logit function. J. Probab. Stat. Sci. 2015, 13, 135–152. [Google Scholar]
- Nasir, M.A.; Tahir, M.H.; Jamal, F.; Õzel, G. A new generalized Burr family of distributions for the lifetime data. J. Statist. Appl. Probab. 2017, 6, 401–417. [Google Scholar] [CrossRef]
- Lee, C.; Famoye, F.; Alzaatreh, A. Methods for generating families of univariate continuous distributions in the recent decades. WIREs Comput Stat. 2013, 5, 219–238. [Google Scholar] [CrossRef]
- Tahir, M.H.; Nadarajah, S. Parameter induction in continuous univariate distributions: Well-established G families. An. Acad. Bras. Ciênc. 2015, 87, 539–568. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M. Compounding of distributions: A survey and new generalized classes. J. Stat. Dist. Applic. 2016, 3, 35. [Google Scholar] [CrossRef] [Green Version]
- Alexander, C.; Cordeiro, G.M.; Ortega, E.M.M.; Sarabia, J.M. Generalized beta-generated distributions. Comput. Stat. Data Anal. 2012, 56, 1880–1897. [Google Scholar] [CrossRef]
- Rezaei, S.; Sadr, B.B.; Alizadeh, M.; Nadarajah, S. Topp-Leone generated family of distributions: Properties and applications. Commun. Stat. Theory Methods 2017, 46, 2893–2909. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Carrasco, J.M.F.; Ortega, E.M.M. A generalized modified Weibull distribution for lifetime modeling. Comput. Stat. Data Anal. 2008, 53, 450–462. [Google Scholar]
- Rocha, R.; Nadarajah, S.; Tomazella, V.; Louzada, F.; Eudes, A. New defective models based on the Kumaraswamy family of distributions with application to cancer data sets. Stat. Methods Med. Res. 2017, 26, 1737–1755. [Google Scholar] [CrossRef] [PubMed]
- Handique, L.; Chakraborty, S. A new four-parameter extension of Burr-XII distribution: Its properties and applications. Jpn. J. Stat. Data Sci. 2018, 1, 271–296. [Google Scholar] [CrossRef]
- Klakattawi, H.S. The Weibull-gamma distribution: Properties and applications. Entropy 2019, 21, 438. [Google Scholar] [CrossRef] [Green Version]
- Tahir, M.H.; Hussain, M.A.; Cordeiro, G.M.; El-Morshedy, M.; Eliwa, M.S. A new Kumaraswamy generalized family of distributions with properties, applications, and bivariate extension. Mathematics 2020, 8, 1989. [Google Scholar] [CrossRef]
- Kumaraswamy, P. Generalized probability density function for double bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Benkhelifa, L. The Marshall-Olkin extended generalized Lindley distribution: Properties and applications. Commun. Stat. Simul. Comput. 2017, 46, 8306–8330. [Google Scholar] [CrossRef]
- MacDonald, I.L. Does Newton-Raphson really fail? Stat. Methods Med. Res. 2014, 23, 308–311. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I. A multivariate exponential distribution. J. Am. Statist. Assoc. 1967, 62, 30–44. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, R.D. Bivariate generalized exponential distribution. J. Multivar. Anal. 2009, 100, 581–593. [Google Scholar] [CrossRef] [Green Version]
- Barreto-Souza, W.; Lemonte, A.J. Bivariate Kumaraswamy distribution: Properties and a new method to generate bivariate classes. Statistics 2013, 47, 1321–1342. [Google Scholar] [CrossRef]
- Ghosh, I.; Hamedani, G.G. On the Ristic-Balakrishnan distribution: Bivariate extension and characterizations. J. Statist. Theory Prac. 2018, 12, 436–449. [Google Scholar] [CrossRef] [Green Version]
- Eliwa, M.S.; El-Morshedy, M. Bivariate Gumbel-G family of distributions: Statistical properties, Bayesian and non-Bayesian estimation with application. Ann. Data Sci. 2019, 6, 39–60. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Alhussain, Z.A.; Atta, D.; Almetwally, E.M.; Eliwa, M.S. Bivariate Burr X generator of distributions: Properties and estimation methods with applications to complete and type-II censored samples. Mathematics 2020, 8, 264. [Google Scholar] [CrossRef] [Green Version]
- El-Morshedy, M.; Eliwa, M.S.; El-Gohary, A.; Khalil, A.A. Bivariate exponentiated discrete Weibull distribution: Statistical properties, estimation, simulation and applications. Math. Sci. 2020, 14, 29–42. [Google Scholar] [CrossRef] [Green Version]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Cordeiro, G.M.; Ortega, E.M.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Franklin Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]
- Lee, C.; Famoye, F.; Olumolade, O. Beta-Weibull distribution: Some properties and applications to censored data. J. Mod. Appl. Stat. Methods. 2007, 6, 173–186. [Google Scholar] [CrossRef]
- Oguntunde, P.E.; Odetunmibi, O.A.; Adejum, A.O. On the exponentiated generalized Weibull distribution: A generalization of the Weibull distribution. Indian J. Sci. Tech. 2015, 8. [Google Scholar] [CrossRef]
- Eissa, F.H. The exponentiated Kumaraswamy-Weibull distribution with application to real data. Int J. Stat. Prob. 2017, 6, 167–182. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Aristizábal, W.D.; Suárez, D.M.; Lozano, S. The gamma modified Weibull distribution. Chilean J. Statist. 2011, 6, 37–48. [Google Scholar]
- Pal, M.; Ali, M.M.; Woo, J. Exponentiated Weibull distribution. Statistica 2006, 2, 139–147. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Kus, C. A new lifetime distribution. Comput. Stat. Data Anal. 2007, 51, 4497–4509. [Google Scholar] [CrossRef]
- Asgharzadeh, A.; Bakouch, H.S.; Habibi, M. A generalized binomial exponential 2 distribution: Modeling and applications to hydrologic events. J. Appl. Statist. 2017, 44, 2368–2387. [Google Scholar] [CrossRef]
- Duncan, A.J. Quality Control and Industrial Statistics; Irwin: Homewood, IL, USA, 1974. [Google Scholar]
- Marinho, P.R.D.; Bourguignon, M.; Dias, C.R.B. Adequacy Model 1.0.8: Adequacy of Probabilistic Models and Generation of Pseudo-Random Numbers. 2013. Available online: http://cran.rproject.org/web/packages/AdequacyModel/AdequacyModel.pdf (accessed on 12 December 2013).
- Meintanis, S.G. Test of fit for Marshall-Olkin distributions with applications. J. Stat. Plann. Infer. 2007, 137, 3954–3963. [Google Scholar] [CrossRef]
- El-Gohary, A.; El-Bassiouny, A.H.; El-Morshedy, M. Bivariate exponentiated modified Weibull extension distribution. J. Stat. Appl. Probab. 2016, 5, 67–78. [Google Scholar] [CrossRef]
- El-Bassiouny, A.H.; EL-Damcese, M.; Abdelfattah, M.; Eliwa, M.S. Bivariate exponentaited generalized Weibull-Gompertz distribution. J. Appl. Probab. Stat. 2016, 11, 25–46. [Google Scholar]
- Eliwa, M.S.; El-Morshedy, M. Bivariate odd Weibull-G family of distributions: Properties, Bayesian and non-Bayesian estimation with bootstrap confidence intervals and application. J. Taibah Uni. Sci. 2020, 14, 331–345. [Google Scholar] [CrossRef] [Green Version]






| a | b | ||||||
|---|---|---|---|---|---|---|---|
| 0.5 | 2.5 | 0.5 | 0.5 | 0.9387 | 4.3451 | 45.8866 | 863.8300 |
| 2.5 | 2.5 | 0.5 | 1.5 | 2.8303 | 8.5624 | 27.5141 | 93.4544 |
| 0.9 | 1.2 | 0.5 | 1.8 | 2.3023 | 6.1339 | 18.3379 | 60.3563 |
| 5.0 | 3.0 | 1.0 | 3.0 | 1.2997 | 1.7046 | 2.2555 | 3.0102 |
| a | b | a | b | |||||
|---|---|---|---|---|---|---|---|---|
| Average | 0.914 | 1.501 | 0.1 | 2.515 | 0.913 | 1.501 | 0.1 | 2.509 |
| Bias | 0.014 | 0.001 | 0.0 | 0.011 | 0.013 | 0.001 | 0.0 | 0.009 |
| MSE | 0.005 | 0.000 | 0.0 | 0.004 | 0.005 | 0.000 | 0.0 | 0.003 |
| SD | 0.103 | 0.031 | 0.006 | 0.067 | 0.067 | 0.014 | 0.003 | 0.046 |
| Average SE | 0.013 | 0.004 | 0.001 | 0.009 | 0.006 | 0.001 | 0.001 | 0.004 |
| CP | 0.928 | 0.886 | 1.000 | 0.997 | 0.921 | 0.879 | 1.000 | 0.995 |
| LB | 0.345 | 13.020 | 0.245 | 0.913 | 1.016 | 10.341 | 0.395 | 0.982 |
| UB | 1.350 | 15.544 | 0.576 | 2.905 | 2.301 | 12.286 | 0.792 | 3.353 |
| a | b | a | b | |||||
| Average | 0.905 | 1.502 | 0.1 | 2.507 | 0.904 | 1.501 | 0.1 | 2.503 |
| Bias | 0.005 | 0.002 | 0.0 | 0.007 | 0.004 | 0.001 | 0.0 | 0.003 |
| MSE | 0.003 | 0.000 | 0.0 | 0.003 | 0.001 | 0.000 | 0.0 | 0.000 |
| SD | 0.062 | 0.023 | 0.003 | 0.061 | 0.028 | 0.008 | 0.002 | 0.024 |
| Average SE | 0.004 | 0.001 | 0.0001 | 0.004 | 0.001 | 0.0002 | 0.000 | 0.001 |
| CP | 0.93 | 0.910 | 1.000 | 0.99 | 0.947 | 0.988 | 1.000 | 0.982 |
| LB | 0.211 | 11.130 | 0.166 | 0.963 | 0.244 | 7.910 | 0.108 | 1.056 |
| UB | 0.983 | 14.164 | 0.452 | 2.585 | 0.795 | 11.150 | 0.366 | 2.205 |
| a | b | a | b | |||||
|---|---|---|---|---|---|---|---|---|
| Average | 2.519 | 2.775 | 0.405 | 0.831 | 2.520 | 2.775 | 0.404 | 0.821 |
| Bias | 0.019 | −0.025 | 0.005 | 0.031 | 0.020 | −0.025 | 0.004 | 0.021 |
| MSE | 0.168 | 0.054 | 0.007 | 0.012 | 0.148 | 0.051 | 0.006 | 0.007 |
| SD | 0.424 | 0.240 | 0.088 | 0.109 | 0.344 | 0.199 | 0.070 | 0.081 |
| Average SE | 0.058 | 0.033 | 0.012 | 0.015 | 0.039 | 0.022 | 0.007 | 0.008 |
| CP | 0.883 | 0.868 | 0.998 | 0.961 | 0.873 | 0.855 | 1.000 | 0.949 |
| LB | 13.682 | 15.354 | 3.052 | 1.379 | 6.780 | 12.997 | 1.213 | 1.269 |
| UB | 19.074 | 17.775 | 4.216 | 3.868 | 11.046 | 15.678 | 2.096 | 3.521 |
| a | b | a | b | |||||
| Average | 2.494 | 2.801 | 0.399 | 0.809 | 2.490 | 2.800 | 0.399 | 0.806 |
| Bias | −0.006 | 0.002 | −0.001 | 0.009 | −0.006 | 0.001 | −0.001 | 0.006 |
| MSE | 0.042 | 0.012 | 0.002 | 0.003 | 0.040 | 0.011 | 0.002 | 0.002 |
| SD | 0.218 | 0.117 | 0.044 | 0.053 | 0.217 | 0.112 | 0.042 | 0.041 |
| Average SE | 0.016 | 0.009 | 0.003 | 0.004 | 0.010 | 0.005 | 0.002 | 0.002 |
| CP | 0.866 | 0.870 | 0.988 | 0.940 | 0.848 | 0.899 | 0.998 | 0.879 |
| LB | 5.042 | 9.692 | 1.056 | 0.879 | 3.450 | 8.729 | 0.547 | 0.740 |
| UB | 9.145 | 12.739 | 1.839 | 2.921 | 7.240 | 12.422 | 1.122 | 2.520 |
| a | b | a | b | |||||
|---|---|---|---|---|---|---|---|---|
| Average | 0.590 | 5.525 | 1.740 | 1.566 | 0.539 | 5.512 | 1.609 | 1.550 |
| Bias | 0.090 | 0.025 | 0.240 | 0.066 | 0.039 | 0.012 | 0.109 | 0.050 |
| MSE | 0.102 | 0.017 | 0.446 | 0.260 | 0.041 | 0.007 | 0.157 | 0.143 |
| SD | 0.282 | 0.111 | 0.575 | 0.474 | 0.192 | 0.077 | 0.362 | 0.364 |
| Average SE | 0.039 | 0.016 | 0.077 | 0.070 | 0.021 | 0.008 | 0.039 | 0.038 |
| CP | 0.998 | 0.849 | 1.000 | 0.998 | 0.997 | 0.851 | 1.000 | 1.000 |
| LB | 3.631 | 56.393 | 58.803 | 1.329 | 1.044 | 42.404 | 11.521 | 1.173 |
| UB | 5.319 | 60.696 | 73.584 | 3.463 | 2.259 | 46.958 | 22.151 | 3.020 |
| a | b | a | b | |||||
| Average | 0.523 | 5.507 | 1.567 | 1.552 | 0.514 | 5.503 | 1.531 | 1.504 |
| Bias | 0.023 | 0.007 | 0.067 | 0.052 | 0.014 | 0.003 | 0.031 | 0.004 |
| MSE | 0.026 | 0.005 | 0.082 | 0.118 | 0.008 | 0.001 | 0.023 | 0.042 |
| SD | 0.148 | 0.071 | 0.256 | 0.337 | 0.086 | 0.032 | 0.142 | 0.199 |
| Average SE | 0.010 | 0.0043 | 0.017 | 0.023 | 0.004 | 0.001 | 0.006 | 0.009 |
| CP | 0.997 | 0.891 | 0.999 | 0.999 | 0.993 | 0.903 | 1.000 | 0.998 |
| LB | 0.556 | 35.430 | 7.104 | 1.033 | 0.340 | 25.285 | 4.695 | 1.009 |
| UB | 1.528 | 40.668 | 16.144 | 2.674 | 1.021 | 31.077 | 12.4051 | 2.271 |
| Average | 3.254 | 3.325 | 3.145 | 0.485 | 1.536 | 0.334 |
| Bias | 0.014 | 0.034 | 0.029 | −0.015 | 0.085 | 0.074 |
| MSE | 0.024 | 0.037 | 0.019 | 0.018 | 0.035 | 0.085 |
| SD | 0.021 | 0.031 | 0.014 | 0.012 | 0.027 | 0.079 |
| CP | 0.857 | 0.967 | 0.898 | 0.923 | 0.991 | 0.935 |
| LB | 2.987 | 2.854 | 2.334 | 0.259 | 1.183 | 0.227 |
| UP | 4.117 | 4.598 | 4.969 | 0.743 | 1.887 | 0.633 |
| Average | 3.165 | 3.214 | 3.098 | 0.489 | 1.523 | 0.321 |
| Bias | 0.008 | 0.023 | 0.015 | −0.011 | 0.049 | 0.036 |
| MSE | 0.008 | 0.017 | 0.012 | 0.012 | 0.024 | 0.056 |
| SD | 0.004 | 0.012 | 0.007 | 0.003 | 0.017 | 0.044 |
| CP | 0.998 | 0.876 | 0.964 | 0.876 | 0.910 | 0.962 |
| LB | 2.597 | 2.367 | 2.122 | 0.377 | 1.101 | 0.245 |
| UP | 3.911 | 3.637 | 3.876 | 0.864 | 2.018 | 0.886 |
| Average | 3.072 | 3.110 | 3.025 | 0.496 | 1.513 | 0.313 |
| Bias | 0.003 | 0.007 | 0.008 | −0.007 | 0.013 | 0.022 |
| MSE | 0.006 | 0.009 | 0.008 | 0.007 | 0.014 | 0.037 |
| SD | 0.001 | 0.004 | 0.002 | 0.001 | 0.007 | 0.024 |
| CP | 0.931 | 0.894 | 0.910 | 0.883 | 0.905 | 0.899 |
| LB | 2.157 | 2.367 | 2.110 | 0.159 | 1.017 | 0.119 |
| UP | 4.336 | 4.980 | 4.730 | 0.969 | 2.340 | 0.887 |
| Some Well—Established Models | Abbrivations |
|---|---|
| Kumaraswamy-Weibull | KwW |
| Beta-Weibull | BW |
| Exponentiated-generalized Weibull | EGW |
| Exponentiated Kumaraswamy-Weibull | EKwW |
| Gamma-Weibull | GaW |
| Exponentiated-Weibull | EW |
| Weibull | W |
| Model | a | b | |||
|---|---|---|---|---|---|
| NKwW | 1.4234 | 0.1476 | 0.1570 | 0.7035 | - |
| (0.3004) | (0.0123) | (0.0093) | (0.0059) | - | |
| KwW | 6.9878 | 0.1371 | 0.4437 | 0.6404 | |
| (0.0674) | (0.0104) | (0.0033) | (0.0026) | - | |
| BW | 3.8696 | 0.1436 | 0.3662 | 0.6566 | - |
| (0.7402) | (0.0124) | (0.0047) | (0.0063) | - | |
| EGW | 1.3659 | 1.6063 | 0.0128 | 0.7089 | - |
| (0.8344) | (0.4839) | (0.0103) | (0.1106) | - | |
| EKwW | 3.5743 | 0.1525 | 0.1756 | 0.7516 | 0.8511 |
| (0.1978) | (0.0192) | (0.0165) | (0.0110) | (0.0888) | |
| GaW | 1.2854 | - | 0.0174 | 0.7854 | - |
| (0.3523) | - | (0.0082) | (0.1273) | - | |
| EW | 1.5398 | - | 0.0188 | 0.7278 | - |
| (0.4638) | - | (0.0068) | (0.1143) | - | |
| W | - | - | 0.0118 | 0.9057 | - |
| - | - | (0.0010) | (0.0512) | - |
| Model | a | b | |||
|---|---|---|---|---|---|
| NKwW | 47.4853 | 0.2245 | 0.2413 | 0.8860 | - |
| (1.2203) | (0.0747) | (0.0365) | (0.0898) | - | |
| KwW | 54.7825 | 0.2041 | 0.1609 | 1.0252 | - |
| (0.1358) | (0.0382) | (0.0153) | (0.0276) | - | |
| BW | 23.0602 | 0.1940 | 0.1320 | 1.1080 | - |
| (8.7941) | (0.0324) | (0.0073) | (0.0068) | - | |
| EGW | 5.5966 | 10.5493 | 0.0090 | 0.7774 | - |
| (2.0458) | (5.6821) | (0.0041) | (0.1370) | - | |
| EKwW | 13.5103 | 0.2625 | 1.0662 | 0.6682 | 10.4554 |
| (1.4869) | (0.0374) | (0.0114) | (0.0093) | (3.4956) | |
| GaW | 14.7225 | - | 4.6144 | 0.4983 | - |
| (1.7239) | - | (0.1518) | (0.0217) | - | |
| EW | 113.6840 | - | 0.7698 | 0.4651 | - |
| (142.9147) | - | (1.0663) | (0.1165) | - | |
| W | - | - | 0.0171 | 1.7719 | - |
| - | - | (0.0015) | (0.1776) | - |
| Model | a | b | |||
|---|---|---|---|---|---|
| NKwW | 10.3003 | 1.9955 | 0.0179 | 2.0187 | - |
| (5.5072) | (0.9568) | (0.0029) | (0.3505) | - | |
| KwW | 12.3850 | 1.4312 | 0.0143 | 2.7814 | - |
| (6.5412) | (0.8195) | (0.0018) | (0.6625) | - | |
| BW | 6.8561 | 0.6098 | 0.0133 | 4.1015 | - |
| (4.8522) | (0.3226) | (0.0016) | (1.0461) | - | |
| EGW | 0.4074 | 8.6459 | 0.0171 | 3.5077 | - |
| (0.2631) | (5.8742) | (0.0037) | (0.7875) | - | |
| EKwW | 1.1559 | 3.1680 | 0.0096 | 3.0390 | 6.7019 |
| (0.2743) | (1.4522) | (0.0013) | (0.4169) | (2.1035) | |
| GaW | 14.4806 | - | 0.0353 | 2.1128 | - |
| (2.5218) | - | (0.0050) | (0.1240) | - | |
| EW | 42.8741 | - | 0.0199 | 2.1092 | - |
| (21.3162) | - | (0.0026) | (0.2529) | - | |
| W | - | - | 0.0095 | 7.5137 | - |
| - | - | (0.0001) | ( 0.5450) | - |
| KS | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | AIC | BIC | HQIC | AD | CvM | KS | p-Value | |
| NKwW | 976.7081 | 1961.4160 | 1974.1660 | 1966.5860 | 0.1954 | 0.0238 | 0.0377 | 0.9615 |
| KwW | 978.2675 | 1964.5350 | 1977.2850 | 1969.7050 | 0.2925 | 0.0313 | 0.0388 | 0.9501 |
| BW | 977.0803 | 1962.1610 | 1974.9100 | 1967.3300 | 0.2001 | 0.0219 | 0.0391 | 0.9470 |
| EGW | 978.7362 | 1965.4720 | 1978.2220 | 1970.6420 | 0.5620 | 0.0878 | 0.0420 | 0.9100 |
| EKwW | 977.6941 | 1963.3880 | 1979.3250 | 1969.8510 | 0.1918 | 0.0229 | 0.0388 | 0.9505 |
| GaW | 979.8445 | 1965.6890 | 1975.2510 | 1969.5660 | 0.7633 | 0.1219 | 0.0504 | 0.7530 |
| EW | 978.8859 | 1963.7720 | 1974.3340 | 1967.6490 | 0.5957 | 0.0935 | 0.0440 | 0.8797 |
| W | 981.1477 | 1966.2950 | 1975.6700 | 1968.8800 | 0.9755 | 0.1577 | 0.0567 | 0.6123 |
| KS | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | AIC | BIC | HQIC | AD | CvM | KS | p-Value | |
| NKwW | 215.0072 | 438.0144 | 445.4992 | 440.8429 | 0.1725 | 0.0235 | 0.0691 | 0.9761 |
| KwW | 215.5195 | 439.0389 | 446.5238 | 441.8675 | 0.2495 | 0.0347 | 0.0834 | 0.8924 |
| BW | 216.1573 | 440.3147 | 447.7995 | 443.1432 | 0.3387 | 0.0477 | 0.0973 | 0.7538 |
| EGW | 218.1801 | 444.3601 | 451.8449 | 447.1887 | 0.6147 | 0.0913 | 0.0973 | 0.7543 |
| EKwW | 216.8837 | 443.7674 | 453.1234 | 447.3031 | 0.4183 | 0.0609 | 0.0893 | 0.8387 |
| GaW | 219.4700 | 444.9401 | 450.5537 | 447.0615 | 0.8278 | 0.1250 | 0.1176 | 0.5203 |
| EW | 216.1707 | 438.7413 | 445.9549 | 440.4627 | 0.3006 | 0.0430 | 0.0763 | 0.9428 |
| W | 225.7065 | 455.4131 | 459.1555 | 456.8273 | 1.7286 | 0.2765 | 0.1399 | 0.3048 |
| KS | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | AIC | BIC | HQIC | AD | CvM | KS | p-Value | |
| NKwW | 391.4242 | 790.8485 | 801.2692 | 795.0659 | 2.1765 | 0.3684 | 0.1349 | 0.0525 |
| KwW | 391.6541 | 791.3081 | 801.7288 | 795.5256 | 2.2478 | 0.3781 | 0.1372 | 0.0463 |
| BW | 392.1492 | 792.2985 | 802.7192 | 796.5159 | 2.3690 | 0.3983 | 0.1446 | 0.0305 |
| EGW | 391.8419 | 791.6838 | 802.1045 | 795.9012 | 2.3105 | 0.3878 | 0.1417 | 0.0361 |
| EKwW | 393.8688 | 797.7376 | 810.7635 | 803.0094 | 2.3206 | 0.3892 | 0.1544 | 0.0170 |
| GaW | 393.0037 | 792.0073 | 799.8228 | 795.1704 | 2.5727 | 0.4276 | 0.1511 | 0.0208 |
| EW | 393.8216 | 793.6431 | 801.6586 | 796.8062 | 2.4039 | 0.4211 | 0.1363 | 0.0505 |
| W | 404.7118 | 813.4235 | 818.6339 | 815.5323 | 4.7488 | 0.7985 | 0.1978 | 0.0008 |
| Model | KS | KS p-Value | KS | KS p-Value | KS | KS p-Value | |||
| NKwW | 164.7087 | 0.1037 | 0.8212 | 163.6799 | 0.1165 | 0.6973 | 166.1881 | 0.1288 | 0.5716 |
| Model | |||||||
|---|---|---|---|---|---|---|---|
| Statistic | BvNKwW | BvW | BvExW | BvGPW | BvExMW | BvOWE | BvExWGz |
| 18.963 | 0.397 | 1.227 | 3.229 | 0.167 | 0.135 | 0.5474 | |
| SE | 0.025 | 0.063 | 0.772 | 4.252 | 0.281 | 0.9043 | |
| 17.646 | 0.274 | 0.382 | 1.983 | 0.061 | 0.302 | 0.1920 | |
| SE | 0.635 | 0.066 | 0.356 | 2.580 | 0.101 | 0.0001 | 0.3137 |
| 37.392 | 0.339 | 0.661 | 4.084 | 0.139 | 0.265 | 0.4437 | |
| SE | 0.985 | 0.067 | 0.454 | 5.340 | 0.227 | 0.7173 | |
| 4.689 | 0.083 | 0.012 | 0.037 | 85.918 | 0.025 | 0.4109 | |
| SE | 0.098 | 0.025 | 0.033 | 0.048 | 33.829 | 1.9960 | |
| 0.166 | – | 1.268 | – | 4.505 | – | 0.0797 | |
| SE | − | 0.609 | – | 6.924 | – | 1.2465 | |
| 14.473 | – | – | – | 0.025 | 1.094 | 0.0048 | |
| SE | 0.743 | – | – | – | 0.054 | 0.0325 | |
| – | – | – | – | – | – | 1.3582 | |
| SE | – | – | – | – | – | – | 1.3611 |
| 287.666 | 346.00 | 298.930 | 344.76 | 294.135 | 291.129 | 294.610 | |
| AIC | 587.332 | 700.00 | 607.860 | 697.53 | 600.280 | 592.259 | 603.220 |
| BIC | 596.997 | 706.44 | 615.914 | 703.97 | 609.945 | 600.313 | 07.082 |
| HQIC | 590.739 | 702.27 | 610.699 | 699.79 | 603.687 | 595.099 | 607.195 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Morshedy, M.; Tahir, M.H.; Hussain, M.A.; Al-Bossly, A.; Eliwa, M.S. A New Flexible Univariate and Bivariate Family of Distributions for Unit Interval (0, 1). Symmetry 2022, 14, 1040. https://doi.org/10.3390/sym14051040
El-Morshedy M, Tahir MH, Hussain MA, Al-Bossly A, Eliwa MS. A New Flexible Univariate and Bivariate Family of Distributions for Unit Interval (0, 1). Symmetry. 2022; 14(5):1040. https://doi.org/10.3390/sym14051040
Chicago/Turabian StyleEl-Morshedy, Mahmoud, Muhammad H. Tahir, Muhammad Adnan Hussain, Afrah Al-Bossly, and Mohamed S. Eliwa. 2022. "A New Flexible Univariate and Bivariate Family of Distributions for Unit Interval (0, 1)" Symmetry 14, no. 5: 1040. https://doi.org/10.3390/sym14051040
APA StyleEl-Morshedy, M., Tahir, M. H., Hussain, M. A., Al-Bossly, A., & Eliwa, M. S. (2022). A New Flexible Univariate and Bivariate Family of Distributions for Unit Interval (0, 1). Symmetry, 14(5), 1040. https://doi.org/10.3390/sym14051040









