The Application of the Modified Prim’s Algorithm to Restore the Power System Using Renewable Energy Sources

Abstract

The recent trends in the development of power systems are focused on the Self-Healing Grid technology fusing renewable energy sources. In the event of a failure of the power system, automated distribution grids should continue to supply energy to consumers. Unfortunately, there are currently a limited number of algorithms for rebuilding a power system with renewable energy sources. This problem is possible to solve by implementing restoration algorithms based on graph theory. This article presents the new modification of Prim’s algorithm, which has been adapted to operate on a power grid containing several power sources, including renewable energy sources. This solution is unique because Prim’s algorithm is ultimately dedicated to single-source graph topologies, while the proposed solution is adapted to multi-source topologies. In the algorithm, the power system is modeled by the adjacency matrices. The adjacency matrixes for the considered undirected graphs are symmetric. The novel logic is based on the original method of determining weights depending on active power, reactive power and active power losses. The developed solution was verified by performing a simulation on a test model of the distribution grid powered by a renewable energy source. The control logic concept was compared with the reference algorithms, which were chosen from the ideas representing available approaches based on graph theory present in the scientific publications. The conducted research confirmed the effectiveness and validity of the novel restoration strategy. The presented algorithm may be applied as a restoration logic dedicated to power distribution systems.

1. Introduction

The presence of renewable energy sources in the power system and the requirements of reliability in electrical energy supply imply the need for continuous development in the area of automation [1]. In addition to innovative solutions in the field of equipment and controllers, algorithms are extremely important, as they are responsible for the process of reconnecting consumers to the grid after a failure [2].

In electrical engineering, graph theory has a special place. This theory is applied not only in the field of electrical circuit analysis, but also in the power grid restoration algorithms [3]. Strategies based on graph theory can be divided into two types [4,5,6,7]. The first solution uses sectioning of grid topology into smaller fragments connected with power sources. In the second group of algorithms, there are logics using greedy algorithms, especially Prim’s algorithm [8].

As an example of the methods mentioned in the previous paragraph, the algorithm from [9] is used, which works in a hybrid way. This logic determines the skeleton of the network in the first stage through Prim’s algorithm, and in the second stage the power subsystems are determined. Prim’s algorithm is based on assigning weights to each power line, and the approach to this problem is contained in [10]. The application of the algorithm responsible for dividing the reconstructed network into feeder islands is possible by a logic based on a fuzzy neural network [11]. This method creates subnetworks characterized by stable operation. One of the less popular solutions is the logic using parallel systematic resampling [12]. This logic, resulting from graph theory based on graph convolutional network algorithms, can be applied to power system reconstruction [13]. The main disadvantage of this solution is its high complexity. There are also available solutions that have limited applications in the real world and this is, for example, the algorithm from [14], which is dedicated only to radial networks. The calculation efficiency is the only advantage of the logic. The main goal of the algorithms responsible for the restoration of power systems after a failure is to provide reliable access to the electricity.

The power system restoration methods developed so far [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] are dedicated to grids equipped with non-renewable energy sources. The presence of renewable energy sources in power systems requires the preparation of algorithms enabling network restoration that also take into account the kind of electricity generators [18]. Unfortunately, the number of publications dealing with the issue of logics dedicated to the restoration of a power grid supplied from renewable energy sources after a failure is limited. In [19], the algorithm designed to rebuild a power system after an islanding work, in which the loads receive electrical power also from renewable energy sources, is designed. A different approach to the problem is presented in [20], where a particle swarm optimalization algorithm is used to rebuild the grid. A similar solution is also presented in the article [21]. Furthermore, the use of energy storage systems in combination with PV power plants is studied [22]. Unfortunately, due to the significant cost of building this type of infrastructure, it is currently a theoretical issue with no prospects for application in the near future [23]. The limited number of publications in the field of restoration algorithms dedicated to cooperation with grids equipped with renewable energy sources is due to the lack of stable power supply by PV power stations or wind power plants [24].

The method of grid sectioning used for the restoration of power grids is characterized by high complexity as well as the use of additional algorithms supporting the decision-making process, including greedy algorithms [25]. In the first stage, the logic divides the existing topology into substructures related to the load, and then creates smaller power grids powered independently from separate energy sources. The resulting topologies are not interconnected. The logic based on Prim’s algorithm is characterized by a simpler methodology of operation than the method using sectioning; however, it requires appropriate adjustment to cooperate with power systems. This is due to the fact that in its original form, Prim’s algorithm is dedicated to single-source grids. As this algorithm is to be used in the power system topology supplied by more than one source, it is necessary to generalize this logic. Nevertheless, the speed of Prim’s algorithm is an extremely important advantage.

Another problem is the cooperation of the restoration algorithms with power grids powered by renewable energy sources [26]. These sources do not guarantee the access to constant power and their efficiency depends on the weather conditions [27]. This fact needs to be taken into consideration when using logics cooperating with such sources.

Technological development and the increasing presence of renewable energy sources in the power system demand the development of algorithms responsible for its restoration after emergencies. These algorithms should be characterized by reliability and short execution time. The performed operations through the control logic should guarantee the fastest possible delivery of electricity to consumers and should assure the stability of the restored power system.

The issues mentioned in the previous paragraphs imply the necessity to adapt the restoration algorithms to the cooperation with renewable energy sources through their appropriate modification. The proposal of logic applying a properly modified Prim’s algorithm is presented in the article. Additionally, the new method of calculating weights has been proposed. This method depends on the parameters characterizing power grids, i.e., active power, reactive power and active power losses. The prepared concept was verified during simulation studies. The proposed solution was compared with the reference logic, which was chosen on the basis of the analysis of the published algorithms in available scientific articles. The logic from [8] was considered the reference algorithm due to the fact that it is characterized by the advantages of solutions from [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].

2. The Presentation of the Problem

Prim’s algorithm is a logic using graph theory, which operates on the concepts of $E$ edges and $V$ vertices [34]. In mathematics, an undirected graph is defined as a pair: $G=\left(V,E\right)$. Mapping of the power system in the form of a graph can be realized in two ways. The first one consists of assigning the busbars to the vertices of the graph and the transmission lines to the edges. The second solution is adapted to the presence of switches in the power system, which are represented by the edges of the graph. In this case, the transmission lines are identical with vertices [35]. The presented methods of mapping the power supply grid as graphs are shown in Figure 1. In the paper, the scheme from Figure 1b is analyzed and developed.

The edges of $E$ of graph $G$ are assigned numerical values called weights w, which in science are related to the physical phenomenon under consideration. In the case of Prim’s algorithm used for the purposes of the power grid restoration strategy, these weights are the indicators depending on active power and reactive power. In [8], there are various mathematical dependencies that allow us to count the weights. One of the applied formulas is as follows [8]:

$$w_k=\frac{P_{PS0}+P_k+∆P_k}{P_s}$$

(1)

Equation (1) is related to the active power of the loads and losses of active power in the grid under the consideration. The advantage of using this equation in the modified Prim’s algorithm is its low mathematical complexity, which guarantees time-efficient calculations. The disadvantage of using this equation includes its low flexibility, which results from not taking into account the presence of reactive power in the power system. Thus, the grid topologies obtained by means of (1), are identical each time assuming that all power lines in the considered grid are technically efficient and there is no failure, e.g., short circuit.

Otherwise, the weights are expressed as the correlation between active and reactive power in the considered topology of the power system through [7]:

$$w_k=\frac{w_1^k}{b_1}·p+\frac{w_2^k}{b_2}·\left(1-p\right)$$

(2)

Parameters $w_1^k$ and $w_2^k$ are expressed in the following formulas [7]:

$$w_1^k=P_{PS0}+P_k$$

(3)

$$w_2^k=\left|Q_{PS0}+Q_k\right|$$

(4)

The values of $b_1$ and $b_2$ are calculated by [7]:

$$b_1=\min \left(P_{PS0}+P_k\right)$$

(5)

$$b_2=\min \left|Q_{PS0}+Q_k\right|$$

(6)

Using calculations (2) requires the specifying parameter $p$. For this purpose, a particle swarm optimalization (PSO) can be used, which operates according to the predefined indicators [36]. These indicators have to be adapted to the guidelines for the given restoration algorithm [37].

The disadvantages of the solution based on (2) are the lack of consideration of active power loss and high mathematical complexity compared to (1). The advantages include the relative influence of reactive power on the value of the weight representing the power line. Thanks to the presence of parameter $p$, it is possible to obtain different grid topologies, which indicate flexibility in applying Formula (2).

Prim’s algorithm used for the power system restoration is a modified logic in relation to its classical version [35]. The need to change this algorithm results from the fact that it has to be adapted to the topology of the power grid, which has more than one power source. Prim’s algorithm caters for a predefined set of edges with assigned weights and vertices; this generates the smallest possible sum of the edge weights with all vertices connected to each other. The resulting topology is called a minimal spanning tree. Prim’s algorithm starts with a vertex defined as a “root”. In each step, edges with the lowest possible weight are added to the structure starting from this point. An example of how Prim’s algorithm works is shown in Figure 2.

The minimum spanning tree can be determined using Kruskal’s algorithm. However, it is not applicable to power systems, because Kruskal’s algorithm starts from the node to which the line with the lowest weight is connected. As a result, Kruskal’s algorithm can connect transmission lines in such a way that they will not be energized (there will be islands of interconnected transmission lines not supplied by the power source). In the case of Prim’s algorithm, it is possible to define the node (root) from which the edges are connected, and each connected transmission line is always energized by the power source.

The other restoration algorithms based on graph theory use the method of sectioning grid topology into smaller sub-topologies that are related to energy sources. There are three phases of operation in these logics. In the first phase, called the coarsening phase, the $G_0$ graph is converted into smaller graphs $G_1$, $G_2$, $\dots$, $G_k$. The second stage, the partitioning phase, consists of assigning weights to the edges in the $G_k$ sub-graphs. In the uncoarsening and refinement phase, which is the last phase of the network topology partitioning method, the subnetwork system supplied from independent energy sources is rebuilt by merging the $G_{k-1}$, $G_{k-2}$, $\dots$, $G_1$, $G_0$ subgraphs [7]. The idea of the algorithm is presented in Figure 3.

Each of the logics described in the previous paragraphs has its advantages and disadvantages. The advantage of Prim’s algorithm over the method of grid sectioning into smaller topologies is a small complexity of logic and a fast calculation by digital systems. The complexity of the Prim’s algorithm is $O\left(V^2\right)$, where $V$ is the number of vertices in a graph. Prim’s algorithm complexity can be improved up to $O\left(E \log V\right)$using the Fibonacci heap, where $E$ is number of edges. The complexity of Prim’s algorithm using the Fibonacci heap is the same as in the case of Kruskal’s algorithm. The main advantage of the sectioning method is the possibility of creating subsystems which are powered from independent energy sources.

The development of a Smart Grid technology in connection with renewable energy sources implies the emergence of novel restoration algorithms creating micro-grids [38]. The most optimal solution is to combine the advantages of Prim’s algorithm and logic based on the power system sectioning. Implementation of this type of logic is possible by introducing the generalization of Prim’s algorithm, which is applicable to multi-source systems. These modifications require dealing with several problems.

First, it is necessary to develop a mathematical dependence expressing the weights which will reflect the operation of the power system and the presence of such parameters as active power, reactive power, and active power losses in it. The second problem is the preparation of logical conditions that will allow Prim’s algorithm to cooperate with the power grid supplied from several energy sources. The last issue that has to be taken into consideration in the algorithm is the specificity of the renewed energy sources, i.e., periodical generation of electric power by them, and thus the possibility of switching between the sources supplying the loads in the microgrids.

3. The Motivation and the Article’s Contribution

The previously described facts have motivated the authors of this paper to develop a new restoration algorithm that meets the previously mentioned conditions. This publication contains the following new contributions:

(1)

The new resuscitation algorithm for power systems based on a modification of Prim’s algorithm has been developed.

(2)

The prepared logic is adapted to work with a power system that has renewable energy sources in its topology.

(3)

For the developed algorithm, the authors have prepared a new method for determining the weights, which represent the power flows in the grid.

The proposed solutions were confirmed in simulation calculations. The simulations were performed on a modified model of the New England IEEE 39-bus system and power system model prepared by the authors.

4. The Restoration Algorithm—The Assumptions and the Control Logic

The algorithm must be adapted to the grid topology in which there are renewable energy sources and more than one electricity generator. The implementation of the control logic is based on the assumptions and conditions such as permissible voltage values on the busbars, permissible values of the current transmitted by power lines, etc.

4.1. Generation Capacity of Power Plants

For each of the electricity sources, there is a mathematical description that defines the limits of the generated power to the grid. Today in the existing topologies, nuclear power plants, coal power plants, wind farms and solar power plants are the most popular energy sources.

In the case of the power plants equipped with steam turbines, the power generated by them is limited by the rules of mechanics and thermodynamics. In the case of this type of energy source, the produced electric power is determined using the following formulas [39]:

$$P^2+Q^2=S^2\le {\left(V·I_{MAX}\right)}^2$$

(7)

$$P^2+{\left(Q+\frac{V^2}{x_d}\right)}^2\le {\left(\frac{E_q·V}{x_d}\right)}^2$$

(8)

$$P\ge \left(Q+\frac{V^2}{x_d}\right)·tan{\delta }_{MAX}$$

(9)

$$P_{Gmin}\le P\le P_{Gmax}$$

(10)

In the case of renewable energy sources, the power they generate depends on the weather conditions, e.g., the power produced by a solar power plant depends on the cloud cover and the power generated by a wind power plant depends on the wind speed. For a single wind turbine, the following equations and inequalities are relevant to determine the power it generates [40,41]:

$$P_{WT}=\{\begin{array}{c}0 if v\le v_{ci} \\ P_r·\frac{v-v_{ci}}{v_r-v_{ci}} if v_{ci}\le v\le v_r\\ \begin{array}{c}{P}_r if v_r\le v\le v_{co}\\ 0 if v\ge v_{co}\end{array}\end{array}$$

(11)

$$P_r=\frac{1}{2}·A_{WT}·c_p·{\rho }_a·{\eta }_r·{\eta }_{WT}·v_r^3$$

(12)

4.2. Power System Components’ Current and Voltage Limits

In the documentation, the operator of the power system defines the permissible voltage levels on the busbars, which result directly from the technological solutions used in the considered grid [42]. In the case of currents in transmission lines, the permissible values depend on the type of line [43].

For the analyses carried out in the article, it was assumed that the permissible voltage on the busbars ranged from 0.90 p.u. to 1.05 p.u. of the rated value for a given type of grid [7]. In the case of lines, the permissible current value cannot exceed their rated value [44].

4.3. A New Approach to Weights’ Calculations for Power System Representation as a Graph

In addition to the implementation of individual transmission lines and busbars in a matrix form, the use of graph algorithms requires the assignment of numerical values to the edges called weights. For the purposes of the implemented control logic, Formula (2) was modified, assuming that the weights are determined for the modified Prim’s algorithm, which connects the edges corresponding to the loads with the greatest demand for active power. The advantage of the presented formula in comparison to Equation (2) is considering the take-off of active power occurring in the power system. The formula used to calculate the weights is as follows:

$$w_k=\frac{w_1^{*k}}{c_1}·p_1+\frac{w_2^{*k}}{c_2}·p_2+\frac{w_3^{*k}}{c_3}·p_3$$

(13)

Parameters $w_1^{*k}$, $w_2^{*k}$, $w_3^{*k}$, $c_1$, $c_2$, and $c_3$ are determined from the following equations:

$$w_1^{*k}=P_{PS0}+P_k$$

(14)

$$w_2^{*k}=\frac{1 }{\left|Q_{PS0}+Q_k+∆Q_k\right| }$$

(15)

$$w_3^{*k}=\frac{1}{∆P_k}$$

(16)

$$c_1=\max \left(P_{PS0}+P_k\right)$$

(17)

$$c_2=\frac{1 }{\min \left|Q_{PS0}+Q_k+∆Q_k\right|}$$

(18)

$$c_3=\frac{1}{\min ∆P_k}$$

(19)

In the case of parameters $p_1$, $p_2$, and $p_3$, a simplifying equation can be used that links these quantities with each other:

$$p_1+p_2+p_3=1$$

(20)

Applying Equation (20) reduces the Formula (13) to the form:

$$w_k=\frac{w_1^{*k}}{c_1}·p_1+\frac{w_2^{*k}}{c_2}·p_2+\frac{w_3^{*k}}{c_3}·(1-p_1-p_2)$$

(21)

The following conditions must be met by $p_1$, $p_2$, and $p_3$:

$$p_1>0$$

(22)

$$p_2>0$$

(23)

$$p_2>0$$

(24)

The determination of the numerical value for the parameters $p_1$, $p_2$, and $p_3$ is possible using optimization algorithms. In this case, an effective approach is to use the PSO method with predefined conditions such as minimization of the time needed to connect all loads or connecting all loads while minimizing active power losses in the considered power system.

The method of calculating weights according to Equation (13) is applied to find the maximum spanning tree for the analyzed graph. The maximum spanning tree and the minimum spanning tree are the structures obtained by applying Prim’s algorithm. The relation (13) was adjusted in such a way that for the created maximum spanning tree, the active power losses were minimized, or the absolute value of the reactive power consumed by the grid created in this way was as close to zero as possible. The method for obtaining the maximum spanning tree consists of connecting the edges with the highest value of weights to the nodes (in the case of determining the minimum spanning tree Prim’s algorithm connects the edges with the highest value of weights to the nodes).

The rationale for using Prim’s algorithm for determining the maximum spanning tree and Formula (13) are discussed in the example used in Figure 4. In the considered topology, the following simplifying assumptions are made:

(1)

The DC grid is the considered topology, hence in Formula (13) $p_2=0$.

(2)

There are no active power losses in the considered grid, hence in Formula (13) p₃ = 0.

The application of Prim’s algorithm determining the minimum spanning tree and Equation (13) lead to the topology of Figure 4a, where loads with the total power of 0.8 p.u. are connected to the source with the power equal to 1.0 p.u. In the case of Figure 4b, the application of Prim’s algorithm for determining the maximum spanning tree allowed the connection of loads with the power of 1.0 p.u. From the economic point of view, the largest possible sale of electrical energy is the optimal solution. In the analyzed example, the effectiveness program applying Prim’s algorithm, which creates maximal spanning tree topology, and the use of the Formula (13) was shown.

4.4. Assumptions for the Logic of the Modified Prim’s Algorithm

Prim’s algorithm is dedicated to graph structures with a single power source. Its application in the logic responsible for the reconstruction of a power system requires appropriate modifications in the following aspects:

(1)

Adaptation of Prim’s algorithm to multi-source topologies.

(2)

Implementation of logical conditions responsible for the selection of the source for which a new supply line (edge) is to be connected at a given moment.

Obtaining the grid topology in which all the loads have been powered [29] is the reason to solve the previously mentioned dilemmas. This problem is discussed on the basis of Figure 5, where it is assumed that the transmission lines do not generate power losses. A DC grid is the considered grid, and the values of the weights are calculated using Formula (13). In case where there is no predefined logic responsible for the selection of the source to which the power line is to be connected and the sources are switched in the order of their numbering, as was realized in [8], the result is a tree topology where not all sources have been supplied. The example of such a topology obtained by Prim’s algorithm, responsible for the creation of maximum spanning tree, is shown in Figure 5a, where the applied Prim’s algorithm is not optimal (one source remains unpowered).

The elimination of the tree microgrids, where the loads remain unconnected to the energy source, is possible by using the following formulas described in [45]:

$$n^j=n_{all}^j-n_{cycle}^j$$

(25)

$${\alpha }^j=P_s^j-P_{PS0}^j$$

(26)

Formula (25) is used to select the power source to which the next power line is to be connected. The connection is made to the source for which the value of the $n^j$ coefficient is as small as possible. If two or more identical, and simultaneously smallest, values of $n^{\mathrm{j}}$ are obtained, then the source is selected on the basis of the $n^j$ coefficient. The power line is first connected to the source for which the largest possible value from Equation (26) was obtained. In the case where the same value has been obtained for several sources, which is at the same time the largest value of the ${\alpha }^j$, the source to which the power line should be connected is selected according to the assigned numbering, i.e., the first source in the order implemented in the program is selected. An example of the application of logic using Formulas (25) and (26) from [45] gained by the Prim’s algorithm responsible for the creation of the maximum spanning tree is presented in Figure 5b, where the obtained grid has all loads powered.

The assumptions presented in [45] are valid for the grids with non-renewable energy sources. In the case of renewable energy sources, the modified Prim’s algorithm from [45] does not allow for the proper connection of all loads to sources that do not depend on the weather conditions. The example of inappropriate and appropriate operations of the modified Prim’s algorithms is shown in Figure 6, where the considered grid is equipped with two energy sources (renewable source WT1 and non-renewable source G1). The analyses do not take into account the presence of reactive power and the power losses associated with the transmission lines. The modified Prim’s algorithm from [45] based on Equation (13) considered $p_1=1$ and $p_2=p_3=0$, which is used to obtain the topology of Figure 6a. The topology of Figure 6a guarantees reliable power delivery only to the loads connected to busbars BB2 and BB4. The loads from busbars BB3 and BB5 are supplied from a renewable source which depends on the weather conditions. The reduction in energy delivery at the output of the wind turbine may result in the disconnection of loads in order to ensure grid operation conditions in terms of frequency and power.

The right approach to solve this problem is to power the loads with non-renewable energy sources. This is possible because of the assumption that the renewable sources are considered by the logic in the same way as the loads nodes. This can be realized by using the numbers in the adjacency matrix. This matrix is a mathematical representation in the graphical form of a given topology that specifies what type of node the program is dealing with. Figure 6b shows the example of the obtained grid where each of the loads, as well as the renewable energy sources, are connected to each other.

The example of an adjacency matrix that is the representation of the case in Figure 6 is as follows:

$$\mathit{L}=\left[\begin{array}{cccccc}0& 2& 0& 2& 0& 0\\ 2& 0& 1& 0& 0& 0\\ 0& 1& 0& 0& 1& 1\\ 2& 0& 0& 0& 1& 0\\ 0& 0& 1& 1& 0& 1\\ 0& 0& 1& 0& 1& 0\end{array}\right]$$

(27)

In the matrix $\mathit{L}$, the number 0 indicates no transmission line between the pair of nodes; number 1 indicates the transmission line which may be connected to the nodes with loads and the transmission line which may be connected to the renewable source. The number 2 indicates the transmission line which may be connected directly to the non-renewable power sources and thus identifies the location of non-renewable power source nodes in the grid topology.

The last stage is the connection process between the microgrids obtained by using the modified Prim’s algorithm, and then connecting the other transmission lines. The order of connections is to be done according to the numbering of individual nodes. At the same time, it is necessary to check the power conditions for non-renewable power sources (it is not allowed to exceed the limits of operation power ranges for each power source).

It should be emphasized that the connections of the transmission lines occur in a predefined order that depends on the voltage level. The priority is always given to making connections for the highest voltage level and then it is done for structures with the lower voltage values.

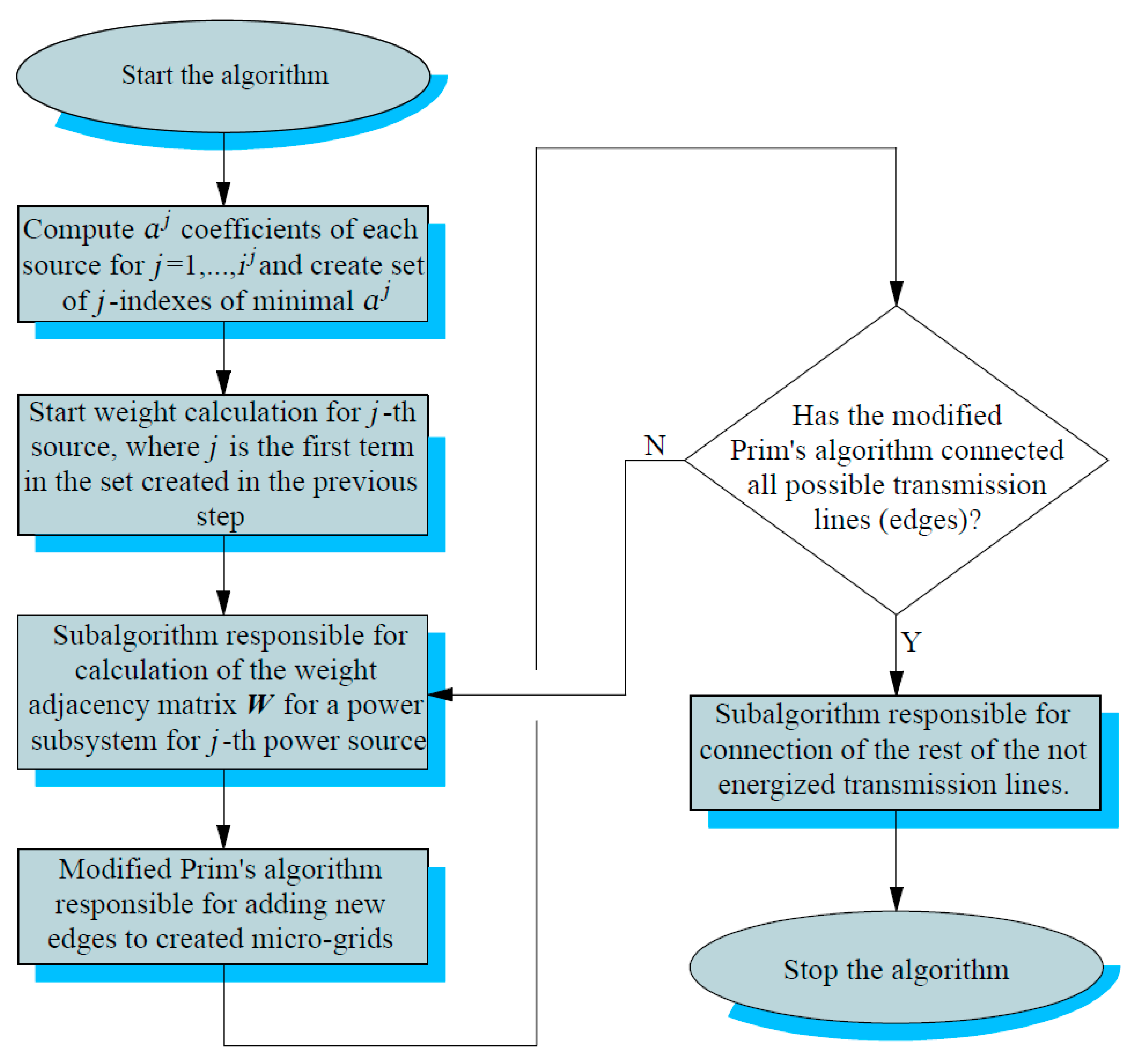
4.5. The New Power System Restoration Logic Applying the Modified Prim’s Algorithm

The logic using the modified Prim’s algorithm for the restoration of the power system is based on the assumptions presented in the previous part of the article and operates on the following matrices: $\mathit{\alpha }$, $\mathbf{∆}\mathit{P}$, $\mathbf{∆}\mathit{Q}$, ${\mathit{I}}_{PS}$, ${\mathit{I}}_r$, ${\mathit{I}}_W$, $\mathit{J}$, $\mathit{J}*$, $\mathit{J}**$, ${\mathit{J}}_{min}$, ${\mathit{k}}_{\mathit{w}}$, $\mathit{N}$, $\mathit{Q}$, ${\mathit{Q}}_{PS}$, $\mathit{P}$, ${\mathit{P}}_{PS}$, $\mathit{T}$, ${\mathit{V}}_{PS}$, ${\mathit{V}}_r$, ${\mathit{V}}_W$, $\mathit{W}$, ${\mathit{W}}_1$, ${\mathit{W}}_2$, ${\mathit{W}}_3$, and $\mathit{Z}$. The structure of the developed Algorithm 1 consists of Algorithms 2–5. At the start of the algorithm, the supply nodes are energized, i.e., the supply node is understood as the connection between the generator and the transformer. The logic in the graphical form is shown in Figure 7.

Algorithm 1.Algorithm dedicated to the restoration of the power system based on the modified Prim’s algorithm.

BEGIN $\hspace{1em}\mathbf{VARIABLES}: {\alpha }^j,{\alpha }^{j-1}, e, i^j,$ $j$$, j_c, n_{J*}$ $P_{PS0}^j, P_s^j, {\mathit{J}}^{*}$

$\hspace{1em}e:=0$ $\hspace{1em}j:=1$ $\hspace{1em}{n}_{J*}:=0$ $\hspace{1em}{\mathit{J}}^{*}:=[]$

$\hspace{1em}\mathbf{FOR} j=1$$\mathbf{TO} j=i^j$ DO $\hspace{1em}\hspace{1em} \mathrm{Calculate} P_s^j$$\mathrm{and} P_{PS0}^j$ $\hspace{1em}\hspace{1em} {\alpha }^j:=P_s^j-P_{PS0}^j$ $\hspace{1em}\hspace{1em} \mathbf{IF} j=1$$\mathbf{OR} \mathbf{(}j>1$$\mathbf{AND} {\alpha }^j<{\alpha }^{j-1}$) THEN $\hspace{1em}\hspace{1em}\hspace{1em} {\alpha }^{j-1}:={\alpha }^j$ $\hspace{1em}\hspace{1em}\hspace{1em} j_c:=j$     END IF $\hspace{1em}\hspace{1em} j:=j+1$    END FOR $\hspace{1em}\mathbf{WHILE} e=0$     Algorithm 1     Algorithm 2     Algorithm 3    END WHILE $\hspace{1em}\mathbf{WHILE} e=1$     Algorithm 4    END WHILE END

Algorithm 2.Algorithm responsible for weight’s calculations.

BEGIN   VARIABLES:$c_1, c_2, c_3, {∆P}_k, {∆Q}_k, k, i^j, i_c, i_n,i_s, p_1, p_2,p_3, P_s^j, P_{PSk}, Q_s^j, Q_{PSk}, v_n, v_c, v_s,$   $∆\mathit{P}$, $∆\mathit{Q}$, ${\mathit{I}}_W$, ${\mathit{k}}_W,$ ${\mathit{P}}_{PS}$, ${\mathit{Q}}_{PS}$, ${\mathit{V}}_W$, $\mathit{W}$, ${\mathit{W}}_1$, ${\mathit{W}}_2$, ${\mathit{W}}_3$,

$k:=1$   $c_1:=-1$   $c_2:=-1$   $c_3:=-1$   $∆\mathit{P}:=[]$   $∆\mathit{Q}:=[]$   ${\mathit{P}}_{PS}:=[]$   ${\mathit{Q}}_{PS}:=[]$   $\mathit{W}:=[]$   ${\mathit{W}}_{\mathbf{1}}:=[]$   ${\mathit{W}}_{\mathbf{2}}:=[]$   ${\mathit{W}}_{\mathbf{3}}:=[]$

FOR $k=1$ TO $k=i^j$ DO     ${\mathit{V}}_W:=[]$     ${\mathit{I}}_W:=[]$     $v_s:=0$     $v_c:=1$     $i_s:=0$     $i_c:=1$     Calculate $P_{PSk}, Q_{PSk}, ∆P_k, ∆Q_k, {\mathit{V}}_W$, ${\mathit{I}}_W$     IF $P_{PSk}^2+Q_{PSk}^2<\left(P_s^j\right)+\left(Q_s^j\right)$ THEN      $∆Q\left[k\right]:=∆Q_k$      $P_{PS}\left[k\right]:=P_{PSk}$      $Q_{PS}\left[k\right]:=Q_{PSk}$      FOR $v_c=1$ TO $v_n$ DO       IF $V_W\left[v_c\right]<0.9 p.u.$ OR $V\left[v_c\right]>1.05 p.u.$ THEN        $v_s:=1$        $v_c=v_n+1$       END IF      END FOR      IF $v_s=0$ THEN       FOR $i_c=1$ AND $i_s=0$ TO $i_n$ DO        IF $I_W\left[i_c\right]>1.0 p.u.$ THEN         $i_s:=1$         $i_c=i_n+1$        END IF       END FOR       IF $i_s=0$ THEN        $∆P\left[k\right]:=∆P_k$       ELSE        $∆P\left[k\right]:=-1$       END IF      ELSE        $∆P\left[k\right]:=-1$      END IF     ELSE      $∆P\left[k\right]:=-1$     END IF     IF $∆P_k=-1$ THEN      $W_1\left[k\right]:=-1$      $W_2\left[k\right]:=-1$      $W_3\left[k\right]:=-1$     ELSE      $W_1\left[k\right]:=P_{PSk}-∆P_k$      $W_2\left[k\right]:=\frac{1 }{\left|Q_{PSk}\right|}$      $W_3\left[k\right]:=\frac{1}{∆P_k}$     END IF     $k_W\left[k\right]:=k$     $k:=k+1$   END FOR   $k:=1$   FOR $k=1$ TO $i^j$ DO     IF $W_1\left[k\right]>c_1$THEN      $c_1:=W_1\left[k\right]$     END IF     IF $W_2\left[k\right]>c_1$THEN      $c_2:=W_2\left[k\right]$     END IF     IF $W_3\left[k\right]>c_1$THEN      $c_3:=W_3\left[k\right]$     END IF     $k:=k+1$   END FOR   $k:=1$   FOR $k=1$ TO $i^j$ DO     IF $c_1=-1$$\mathbf{OR} c_2=-1$$\mathbf{OR} c_3=-1$ THEN      $W\left[k\right]:=-1$     ELSE      $W\left[k\right]:=\frac{W_1\left[k\right]}{c_1}∆p_1+\frac{W_2\left[k\right]}{c_2}∆p_2+\frac{W_3\left[k\right]}{c_3}∆p_3$     END IF     $k:=k+1$   END FOR   $k:=1$ END

Algorithm 3.The modified Prim’s algorithm.

BEGIN   $\mathbf{VARIABLES}: i^j, j_c, k, k_{max}, n_{J*}, Q, u, v, w, w_{max}, w_s, {\mathit{J}}^{*}, \mathit{T}, \mathit{W}$

$w_s:=0$   $w_{max}:=0$   $k_{max}:=0$

FOR $k=1$ TO $i^j$ DO     IF $W\left[k\right]>w_{max}$ THEN      $w_{max}:=W\left[k\right]$      $k_{max}:=k$      $w_s:=1$    END IF   END FOR   IF $w_s=1$ THEN     $\mathrm{Connect} \mathrm{the} k_{max}$-th transmission line by updating T   ELSE     $n_{J*}:=n_{J*}+1$     $J^{*}\left[n_{J*}\right]=j_c$   END IF END

Algorithm 4.Algorithm responsible for the verification of a possible connection to Algorithm 2 already not energized by transmission lines.

BEGIN   $\mathbf{VARIABLES}: \mathit{\alpha }, \mathit{J}, {\mathit{J}}^{*}, {\mathit{J}}^{**}, {\mathit{J}}_{min}, \mathit{N}, e, l_1,l_2, l_3,l_4, l_5, l_6, l_7, {\alpha }_{max}, m$$, m_J$, $n$, $n_{J*}, n_{min},$   $P_{PS0}^j, P_s^j, z$

$\mathit{N}:=[]$   $\mathit{\alpha }:=[]$   $m:=1$   $n:=1$   $n_{min}:=-1$   ${\alpha }_{max}:=-1$   $l_1:=0$   $l_3:=0$   $l_4:=1$   $l_5:=0$   $l_6:=1$   $l_7:=1$

$\mathbf{FOR} m=1$$\mathbf{TO} m=m_J$ DO     $z:=0$     $\mathbf{FOR} n=1$$\mathbf{TO} n=n_{J*}$ DO       $\mathbf{IF} J\left[m\right]=J^{*}\left[n\right]$ THEN         $z:=1$       END IF       $n:=n+1$     END FOR      $m:=m+1$     $\mathbf{IF} z=0$ THEN       $l_1:=l_1+1$       $J^{**}\left[l_1\right]:=J\left[m\right]$     END IF   END FOR   $\mathbf{IF} l_1=0$ THEN     $e:=1$   ELSE     $\mathbf{FOR} l_2=1$ $\mathbf{TO} l_1$ DO       Calculate $n^j$ for $J^{**}\left[l_2\right]$       $l_3:=l_3+1$       $N\left[l_3\right]:=n^j$       $l_2:=l_2+1$     END FOR     $\mathbf{FOR} l_4=1$$\mathbf{TO} l_1$ DO       $\mathbf{IF} n_{min}=-1 AND N\left[l_4\right]>0$ THEN          $n_{min}:=N\left[l_4\right]$          $J_{min}\left[1\right]:=J^{**}\left[l_4\right]$       $\mathbf{ELSE} \mathbf{IF} N\left[l_4\right]\langle n_{min} AND n_{min}\rangle 0 AND N\left[l_4\right]>0$THEN          $n_{min}:=N\left[l_4\right]$          ${\mathit{J}}_{min}:=[]$          $J_{min}\left[1\right]:=J^{**}\left[l_4\right]$         $l_5:=1$       $\mathbf{ELSE} \mathbf{IF} N\left[l_4\right]=n_{min}$THEN          $l_5:=l_5+1$          $J_{min}\left[l_5\right]=J^{**}\left[l_4\right]$       END IF       $l_4:=l_4+1$      END FOR      $\mathbf{IF} {\mathit{J}}_{min}=[]$ THEN       $e:=1$      $\mathbf{ELSE} \mathbf{IF} l_5=1$THEN       $j_c=J_{min}\left[1\right]$      $\mathbf{ELSE} \mathbf{IF} l_5>1$ THEN       $\mathbf{FOR} l_6=1$$\mathbf{TO} l_5$ DO          Calculate ${\alpha }^j$ for $J_{min}\left[l_6\right]$          $\alpha \left[l_6\right]:$= ${\alpha }^j$          $l_6:=l_6+1$       END FOR       $\mathbf{FOR} l_7=1$$\mathbf{TO} l_5$ DO          IF $\alpha \left[l_7\right]>{\alpha }_{max}$ THEN            ${\alpha }_{max}:=\alpha \left[l_7\right]$            $j_c∆J_{min}\left[l_7\right]$            $l_7:=l_7+1$          END IF       END FOR     END IF   END IF END

Algorithm 5.Algorithm responsible for connection transmission lines not energized by Algorithm 4.

BEGIN   $\mathbf{VARIABLES}: b_{PQ}, i_c, i_n, i_s, j, j_{all},n_c, n_{all}, n_{ne}, v_c, v_n, v_s, P_s^j, P_{PS}^j, Q_s^j,Q_{PS}^j,{\mathit{I}}_{PS}, {\mathit{V}}_{PS}$

$n_{ne}:=1$   $n_c:=0$

Calculate $n_{all}$   $\mathbf{IF} n_{all}\ne 0$ THEN      FOR $n_{ne}=1$$\mathbf{TO} n_{ne}=n_{all}$ DO        $b_{PQ}:=0$        $v_s:=1$        $i_s:=1$        $j:=1$        FOR $j=1$ $AND b_{PQ}=0$TO $j=j_{all}$ DO          $\mathrm{Calculate} P_{PS}^j$and $Q_{PS}^j$          IF $\left(P_{PS}^j\right)+\left(Q_{PS}^j\right)<\left(P_s^j\right)+\left(Q_s^j\right)$ AND $b_{PQ}=0$ THEN            $b_{PQ}:=0$            $j:=j+1$          ELSE            $b_{PQ}:=1$          END IF        END FOR        IF $b_{PQ}=0$ THEN          Calculate ${\mathit{V}}_{PS}$          $v_s:=0$          $v_c:=1$          FOR $v_c=1 AND v_s=0 TO v_n DO$            IF $V_{PS}\left[v_c\right]<0.9 p.u.$ OR $V_{PS}\left[v_c\right]>1.05 p.u.$ THEN              $v_s:=1$              $v_c:=v_n+1$            END IF            $v_c:=v_c+1$          END FOR        END IF        IF $v_s=0$ THEN          Calculate ${\mathit{I}}_{PS}$          $i_s=0$          $i_c:=1$          FOR $i_c=1$ TO $i_n$ DO            IF $I_{PS}\left[i_c\right]>1.0 p.u.$ AND $i_s=0$ THEN              $i_s:=1$              $i_c:=i_n+1$            END IF            $i_c:=i_c+1$          END FOR        END IF        IF $i_s=0$ THEN          Connect the $n_{ne}$-th transmission line by updating T          $n_c:=n_c+1$        END IF        $n_{ne}:=n_{ne}+1$        IF $n_{all}=n_c$ OR $n_c=0$ THEN          $n_{ne}:=n_{all}+1$        ELSE IF $n_{ne}=n_{all}$ THEN          $n_{ne}:=1$          $n_c:=0$          Calculate $n_{all}$        END IF     END FOR   END IF END

5. The Test of the Logic Based on the Modified Prim’s Algorithm

The logic based on the modified Prim’s algorithm dedicated to the restoration of the power system after a malfunction was verified on test benchmarks. The solution described in [8] was used as the reference logic to compare with the presented control algorithm in the paper. The first reference logic was considered to be the study from [8] due to the significant recognition of this article through the citations currently amounting to over 90 cross-references in the various publications. The second reference logic is from the recent research article [45].

5.1. Power System Test Benchmarks

The tests of the designed restoration logic using the modified Prim’s algorithm were conducted on two test power system benchmarks. The first topology dedicated to computer simulations is a modified IEEE 39-bus system known as 10-machine New-England Power System, and the second case is a power system topology prepared by the authors of this article.

5.1.1. Modified IEEE 39-Bus System

The electrical power system used for simulation purposes has been modified to perform a simulation to verify the applicability of the prepared algorithm [46]. The scope of the changes to the IEEE 39-bus system is as follows [46]:

(1)

Transmission lines L06–07, L16–19, L16–24, L21–22, L22–23, L23–24 are redefined from single lines to two parallel lines with type and length according to the standard from [30]. The purpose of the change is to increase the transmission capacity of the mentioned lines in case of switching off, e.g., in line L21–22, a part of the energized lines (L16–24, L22–23, L23–24) is overloaded (transmitted current is higher than the rated value for a transmission line).

(2)

A renewable energy source in the form of wind power plants with the rated apparent power of 600 MVA, a power factor of 0.85 and a nominal voltage of 345 kVA are connected to the following busbars: BB14, BB17, and BB28.

The modified IEEE 39-bus system is shown in Figure 8.

5.1.2. Power System Test Topology Designed by the Authors

The power system used for the tests is shown in Figure 9. It consists of 27 transmission lines, 3 non-renewable energy sources, 3 renewable energy sources, 20 buses, and 17 loads. The benchmark is the topology operating at 20 kV. The data adopted for the transmission lines and loads are gathered in

Table 1. Line lengths of the power system model.

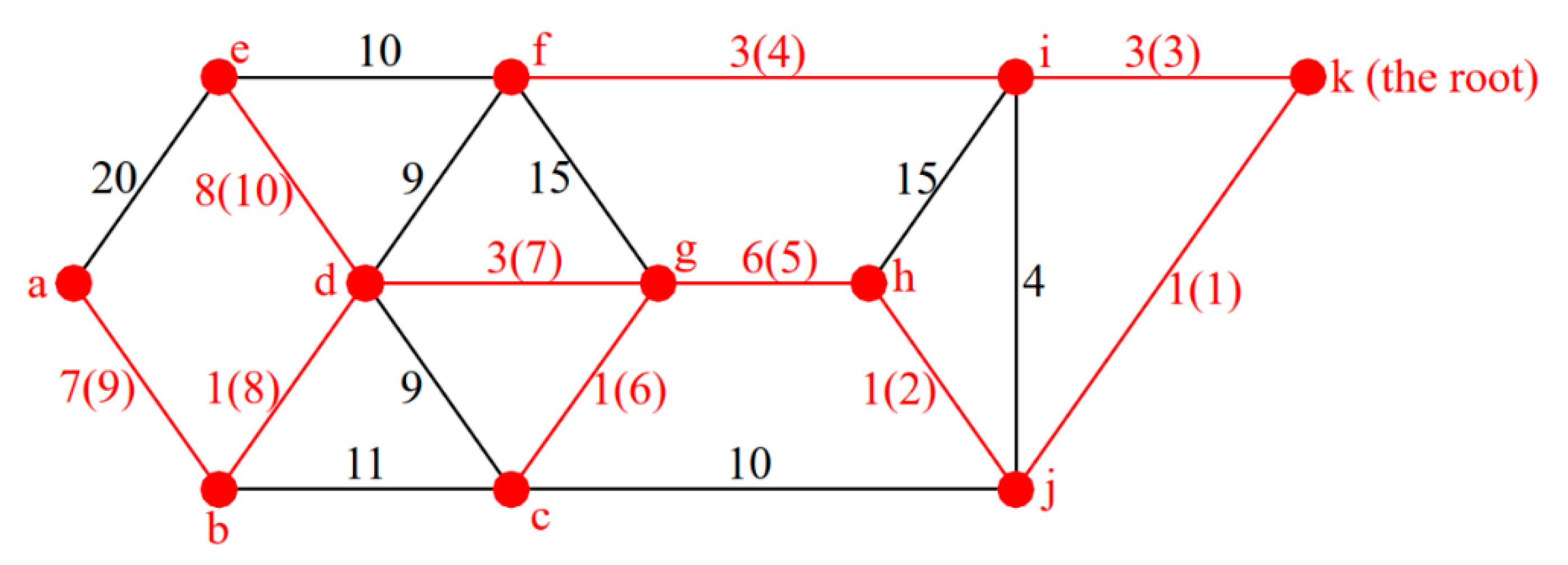
Tag of Line	Length of Line (km)	Tag of Line	Length of Line (km)	Tag of Line	Length of Line (km)
L1	9	L11	21	L21	7
L2	16	L12	14	L22	18
L3	13	L13	10	L23	8
L4	22	L14	18	L24	12
L5	19	L15	13	L25	15
L6	16	L16	8	L26	11
L7	11	L17	12	L27	12
L8	6	L18	7	L28	7
L9	17	L19	9	L29	18
L10	12	L20	15

and

Table 2. Loads of the power system model.

Tag of Load	Active Power of Load (MW)	Reactive Power of Load (MVar)	Tag of Load	Active Power of Load (MW)	Reactive Power of Load (MVar)
LB1	0.65	0.25	LB10	1.55	0.65
LB2	0.75	0.45	LB11	1.95	1.25
LB3	2.10	0.85	LB12	0.75	0.35
LB4	2.15	0.95	LB13	0.65	0.35
LB5	0.70	0.55	LB14	0.85	0.55
LB6	0.55	0.35	LB15	0.45	0.25
LB7	3.10	1.95	LB16	0.75	0.45
LB8	0.75	0.45	LB17	0.25	0.15
LB9	0.95	0.35	-	-	-

, respectively. The following assumptions were made for the test model:

(1)

All supply lines have the cross-section equal to 240 mm², their rated current is 425 A, resistance per unit $R_L^{\prime }=0.1292 \mathsf{\Omega }/\mathrm{km}$, reactance per unit $X_L^{\prime }=0.1099 \mathsf{\Omega }/\mathrm{km}$, and susceptance per unit $B_L^{\prime }=97.3894 \mathsf{\mu }\mathrm{S}/\mathrm{km}$.

(2)

Power losses in transformers are omitted and are thus not included in the grid topology.

(3)

The rated apparent power of each renewable source is 8 MVA.

(4)

The renewable energy sources in the test power system are wind turbines with the rated apparent power equal to 5 MVA each.

5.2. Results

The simulation calculations were performed for the two power grids, i.e., the grids in Figure 8 and Figure 9. The results of the tests were collected for different values of $p_1$, $p_2$, and $p_3$ in

Table 3. Simulation results for the modified IEEE 39-bus system.

The Algorithm Presented in the Paper			Sp (MVA)	Pp (MW)	Qp (MVar)	∆Pp (MW)	MLRPA (−)	MRPLPA (−)	tPA (ms)	MLRA (−)	tA (ms)
p1	p2	p3
0.333	0.333	0.333	4873.65	4212.86	767.38	18.76	0.688	27,.272	351	1.000	505
0.500	0.250	0.250	4873.65	4212.86	767.38	18.76	0.688	27.272	365	1.000	511
0.250	0.500	0.250	4873.65	4212.86	767.38	18.76	0.688	27.272	399	1.000	525
0.250	0.250	0.500	4873.65	4212.86	767.38	18.76	0.688	27.272	349	1.000	501
0.166	0.333	0.501	4873.65	4212.86	767.38	18.76	0.688	27.272	366	1.000	515
0.166	0.501	0.333	4873.65	4212.86	767.38	18.76	0.688	27.272	355	1.000	522
0.333	0.166	0.501	4873.65	4212.86	767.38	18.76	0.688	27.272	382	1.000	499
0.501	0.166	0.333	4873.65	4212.86	767.38	18.76	0.688	27.272	376	1.000	511
0.333	0.501	0.166	4873.65	4212.86	767.38	18.76	0.688	27.272	368	1.000	524
0.501	0.333	0.166	4873.65	4212.86	767.38	18.76	0.688	27.272	370	1.000	506
1.000	0.000	0.000	5179.64	5082.07	1000.59	21.77	0.830	26.230	377	1.000	513
0.000	1.000	0.000	4873.65	4212.86	767.38	18.76	0.688	27.272	352	1.000	507
0.000	0.000	1.000	4873.65	4212.86	767.38	18.76	0.688	27.272	378	1.000	512
The algorithm from the paper [8]			5179.64	5082.07	1000.59	21.77	0.830	26.230	380	-	-
The algorithm from the paper [45]			4158.29	4095.19	721.66	26.09	0.666	39.174	371	-	-

and

Table 4. Simulation results for the test system designed by the authors of the paper.

The Algorithm Presented in the Paper			Sp (MVA)	Pp (MW)	Qp (MVar)	∆Pp (MW)	MLRPA (−)	MRPLPA (−)	tPA (ms)	MLRA (−)	tA (ms)
p1	p2	p3
0.333	0.333	0.333	19.39	19.39	0.18	0.49	1.00	0.49	291	1.00	322
0.500	0.250	0.250	19.34	19.34	−0.33	0.44	1.00	0.44	288	1.00	319
0.250	0.500	0.250	19.34	19.34	−0.33	0.44	1.00	0.44	284	1.00	335
0.250	0.250	0.500	19.34	19.34	−0.33	0.44	1.00	0.44	292	1.00	333
0.166	0.333	0.501	19.34	19.34	−0.33	0.44	1.00	0.44	284	1.00	331
0.166	0.501	0.333	19.34	19.34	−0.33	0.44	1.00	0.44	290	1.00	325
0.333	0.166	0.501	19.34	19.34	−0.33	0.44	1.00	0.44	284	1.00	321
0.501	0.166	0.333	19.34	19.34	−0.33	0.44	1.00	0.44	283	1.00	330
0.333	0.501	0.166	19.34	19.34	−0.33	0.44	1.00	0.44	285	1.00	318
0.501	0.333	0.166	19.34	19.34	−0.33	0.44	1.00	0.44	292	1.00	325
1.000	0.000	0.000	19.34	19.34	−0.33	0.44	1.00	0.44	287	1.00	321
0.000	1.000	0.000	19.53	19.52	−0.48	0.62	1.00	0.62	293	1.00	326
0.000	0.000	1.000	19.35	19.35	0.23	0.45	1.00	0.45	288	1.00	317
The algorithm from the paper [8]			14.12	14.65	1.46	0.40	0.73	0.55	202	-	-
The algorithm from the paper [45]			12.48	12.34	1.86	0.19	0.65	0.29	210	-	-

, respectively. The algorithm from [45] was executed for $p_1=1$, $p_2=0$, and $p_3=0$.

In the case of the simulation studies for the modified IEEE 39-bus system model, they were carried out under the assumption that the BB19 bus is a single power node which consists of connected transformers T19–20, T19–33, T20–34, and generators PS04, PS05, and load LB20. The need for this assumption arises from the requirement specified in Algorithm 1, where power nodes that consist of connected energy sources and transformers must be defined at the start of the computational process.

The efficiency of the algorithm was verified by using quality factors defined as the following parameters:

○

the maximum load of the restored power system calculated by the modified Prim’s algorithm (before the start of the Algorithm 4):

$$MLRPA=\frac{P_p-∆P_p}{P_L}$$

(28)

○

the minimum real power loss of the restored power system calculated by the modified Prim’s algorithm (before the start of the Algorithm 4):

$$MLRPLPA=\frac{∆P_p}{MLRPA}$$

(29)

○

the maximum load of the restored power system by Algorithm 1:

$$MLRA=\frac{P_{pA}-∆P_{pA}}{P_L}$$

(30)

The $MLRPA$ parameter enables the verification of the number of loads connected to the power source through the modified Prim’s algorithm just before the start of Algorithm 4. The higher the value obtained from Formula (28), the more power is delivered to the customers. In casee where, for a larger number of computational variants depending on the $p$-parameters, an identical $MLRPA$ value is obtained, Formula (28) should be used as an additional indicator. This formula allows the identification of the case for which power losses in the topology created by the simulations are the lowest.

Based on the MLRPA and MRPLPA parameters, the optimal tree grid can be defined. This occurs for the case that is characterized by the largest possible value (maximum that can be equal to 1.00) for Equation (28) and the minimum value for Equation (29).

The effectiveness of Algorithm 1 is verified by checking whether all the loads that may not have been connected to the energy source through the operation of Algorithm 4 are powered. For this purpose, the $MLRA$ parameter is used, which is 1.00 in the case when electricity is supplied to each of the loads. For the analyzed topologies in Figure 8 and Figure 9, Algorithm 1 has connected all of the available lines.

In the case of a test model of the IEEE 39-bus system type, identical tree topologies were obtained both for the algorithm prepared by the authors of this paper with parameters $p_1=1$, $p_2=0$, $p_3=0$, and for the reference logic from [8]. This situation is due to the network topology for the IEEE 39-bus system benchmark, which consists predominantly of power sources, transformers, and constraints because of the physical values characterizing the transmission lines. For the other considered parameter settings $p_1$, $p_2$, and $p_3$ shown in Table 3, identical tree topologies were obtained, characterized by the same values of the determined $MLRPA$ and $MRPLPA$ coefficients. The algorithm in [8] and the algorithm in [45] do not have the implemented procedures that allow the rebuilding the power system in the case when the tree topologies obtained with the modified Prim’s algorithm did not supply all the loads. Thus, ultimately, the reference logics were not able to ensure a power supply to all of the customers. In the case of the solution proposed by the authors of this paper, eventually, Algorithm 4 made power to all the power lines present in the considered model, as evidenced by the $MLRA$ quality factor value of 1.00.

For the results obtained in Table 4 for the test model constituting the author’s study, it was found that in contrast to the new resuscitation logic, the reference algorithm from [8] did not make the power supply through the tree topology to all loads. This is due to the obtained $MLRPA$ values, which is 0.73 for the solution from [8], 0.65 for the algorithm from [45] and 1.00 for the other considered cases. In addition, the developed Algorithm 4 makes it possible to make the connection to the remaining transmission lines that are not energized by the modified Prim’s algorithm.

Formula (13) for the calculation of the weights is dedicated to the determination of the maximum spanning trees. The presence of the parameters $p_1$, $p_2$, and $p_3$ in this equation influences the obtained power topologies. According to [29], the obtained spanning tree networks for $p_1=0$, $p_2=0$, and $p_3=1$ will not necessarily be characterized by the minimum value of $∆P_p$. This is directly due to the influence of the order of the transmission lines attached by the greedy algorithm, which is Prim’s algorithm. This is confirmed by the results in Table 4, where the lowest value of $∆P_p$ was obtained for, e.g., $p_1=0.250$, $p_2=0.500$, and $p_3=0.250$.

Another indicator of the usability of the prepared algorithm is its execution time. Two times were distinguished in the analysis, i.e., the time to obtain the tree topology using Prim’s modified algorithm $t_{PA}$ and the time to energize all the transmission lines $t_A$. The obtained values of $t_{PA}$ and $t_A$ depend on the network topology with which they work. For the IEEE 39-bus system, the value of $t_{PA}$ did not exceed 400 ms, while did not exceed 525 ms. For the model used in Figure 9, $t_{PA}$ did not exceed 300 ms, while $t_A$ did not exceed 340 ms. The performance times of the algorithms from [8,45] are similar to those in Algorithm 1. The execution times of the simulation calculations prove the effectiveness of the proposed solution.

5.3. Dicussion

The problem of power supply reliability is an important subject of research in the field of electric power engineering [47], especially in the area of smart-grid technology [48]. The main objective of this paper was to prepare a control logic based on Prim’s algorithm that enables power system restoration after a fault. This goal is fulfilled.

The performed simulation studies showed that the prepared logic is adapted to work with the grids equipped with renewable energy sources. This is an advantage of the new solution in comparison to the algorithms of [8], as well as of [45], which are not dedicated to this kind of topology.

The research has shown that the algorithm allows the connection of all power lines present in the considered power grid. The reference solutions in [8,45] did not guarantee the delivery of electricity to all loads. Another advantage of the presented solution is the possibility to have an influence on the sequence of power line connections. This property results from the use of (13) to determine the weights and it is further discussed in [11].

The disadvantages of the presented algorithm include its high complexity compared to the solution in [8] or [45]. Nevertheless, this drawback is compensated by the previously mentioned advantages of the developed restoration logic.

6. Conclusions

This article presents a new control logic, which is a modification of Prim’s algorithm. The designed algorithm enables the effective reconstruction of the power system after the failure and disconnection of electricity receipts. The elaborated method has the following advantages:

(1)

The use of multi-parameter weights modeling power lines allows the loads to be powered in different orders of connection.

(2)

In comparison to the reference logic from [8,45], the algorithm provides the reconstruction of the power grid in which electrical energy is delivered to each of the loads.

(3)

The algorithm is fully adapted to the power grid, which has many sources that generate electricity, including topologies equipped with renewable energy sources.

The simulation tests have proven that the prepared algorithm is logically consistent and reliable. In the first phase of the operation of the designed Prim’s algorithm, islands powered solely by renewable energy sources were not formed. The advantage of this solution is that the priority is to ensure a s 23.2 supply of electricity to consumers. In addition, in contrast to the solution in [8], the developed control logic in an efficient way resulted in supplying the power to all loads in the considered test power systems. The justification of using Formula (13) for calculating the weights was also proved. Prim’s algorithm was adapted by this formula to generate grids based on the maximum spanning tree, while optimizing the start of active power. This feature also provides a significant advantage over the solution described in [8,45].