Extended Graph of Fuzzy Topographic Topological Mapping Model: ${\mathit{G}}_{\mathbf{0}}^{\mathbf{4}}\left({\mathit{F}\mathit{T}\mathit{T}\mathit{M}}_{\mathit{n}}^{\mathbf{4}}\right)$

Abstract

Fuzzy topological topographic mapping ($FTTM$) is a mathematical model that consists of a set of homeomorphic topological spaces designed to solve the neuro magnetic inverse problem. The key to the model is its topological structure that can accommodate electrical or magnetic recorded brain signal. A sequence of FTTM, $FTT{M}_n$, is an extension of FTTM whereby its form can be arranged in a symmetrical form, i.e., polygon. The special characteristic of $FTTM$, namely, the homeomorphisms between its components, allows the generation of new $FTTM$. The generated $FTTM$s can be represented as pseudo graphs. A pseudo-graph consists of vertices that signify the generated $FTTM$ and edges that connect their incidence components. A graph of pseudo degree zero, $G_0\left(FTT{M}_n^k\right),$ however, is a special type of graph where each of the $FTTM$ components differs from its adjacent. A researcher posted a conjecture on $G_0^3\left(FTT{M}_n^3\right)$ in 2014, and it was finally proven in 2021 by researchers who used their novel grid-based method. In this paper, the extended $G_0^3\left(FTT{M}_n^3\right)$, namely, the conjecture on $G_0^4\left(FTT{M}_n^4\right)$ that was posed in 2018, is narrated and proven using simple mathematical induction.

1. Introduction

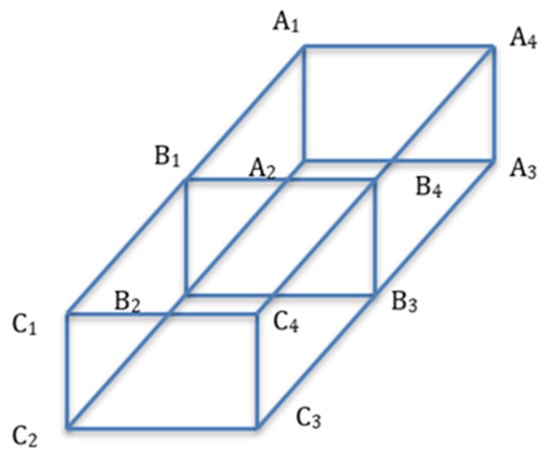
Fuzzy topographic topological mapping (FTTM) [1] was introduced to solve the neuro magnetic inverse problem, in particular, the sources of electroencephalography (EEG) signals recorded from an epileptic patient. Originally, the model is a 4-tuple of topological spaces and mappings of its respective homeomorphic mappings [2]. The topological spaces are magnetic plane (MC), base magnetic plane (BM), fuzzy magnetic field (FM) and topographic magnetic field (TM). The FTTM is defined formally as follows (see Figure 1).

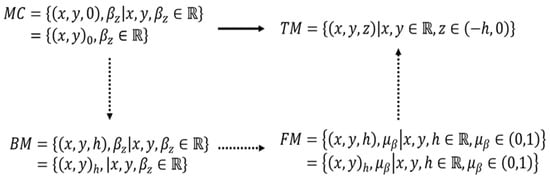
Figure 1. The FTTM.

Definition 1. 

([3]) Let $FTT{M}_i=\left(M{C}_i,B{M}_i,F{M}_i,T{M}_i\right)$ such that $M{C}_i,B{M}_i,F{M}_i,T{M}_i$ are topological spaces with $M{C}_i\cong B{M}_i\cong F{M}_i\cong T{M}_i$. Set of $FTT{M}_i$ is denoted by $FTTM=\left\{FTT{M}_i:i=1,2,3,\dots ,n\right\}$. Sequence of $nFTT{M}_i$ of FTTM is $FTT{M}_1,FTT{M}_2,FTT{M}_3,$ $FTT{M}_4,\dots ,FTT{M}_n$ such that $M{C}_i\cong M{C}_{i+1},B{M}_i\cong B{M}_{i+1},F{M}_i\cong F{M}_{i+1}$ and $T{M}_i\cong T{M}_{i+1}$.

There are many studies on ordinary and fuzzy hypergraphs available in the literature [4,5,6,7]. For example, O’Keeffe and Treacy [8] recently studied finite and periodic graphs and their embeddings in ordinary 3-D Euclidean space. Such isotopic and anisotropic graphs were discussed by the researchers. Poulik et al. [9] used a fuzzy graph to model wi-fi network system in a town, and Poulik and Ghoral [10] recently applied it for modeling of COVID-19 transmission. Similarly, Hassan et. al. [11] used a fuzzy graph to model COVID-19, and Hassan et al. [12] utilized a fuzzy graph for Malaysian banknote authentication purpose. However, the concept of FTTM as a graph was invented by Sayed and Ahmad [13]. Earlier, the sequence of FTTM was presented by Jamaian [14], whereby it is denoted as $FTT{M}_n.$ Basically, $FTT{M}_n$ is an extension of FTTM and is illustrated in the following Figure 2. It is arranged in a symmetrical form and can accommodate magnetoencephalography (MEG) [1] or electroencephalography (EEG) [15] signals, as well as grey scale image data [16]. This accommodative feature of FTTM is due to its homeomorphic structures.

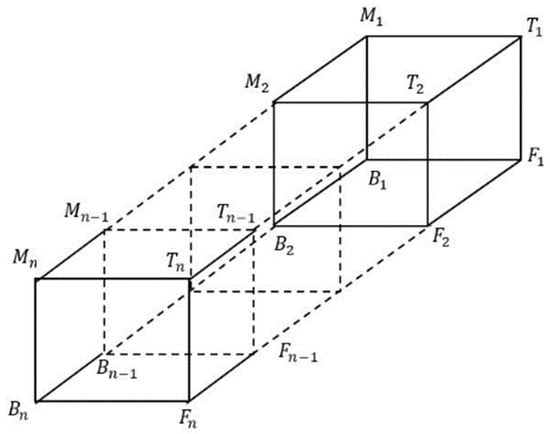
Figure 2. The sequence of $FTT{M}_n$.

2. Generalized FTTM

The FTTM structure can be generalized to any n number of components as well.

Definition 2. 

([17]) A $FTTM$ is defined as

$$FTT{M}_n=\left\{\left\{A_1,A_2,\mathrm{\dots },A_n\right\}:A_1\cong A_2\cong \mathrm{\dots }\cong A_n\right\}$$

(1)

such that $A_1, A_2, \mathrm{\dots }, A_n$ are the components of $FTT{M}_n$.

The model can be expanded to any k number of $FTTM$ versions, denoted as $FTT{M}_n^k$. The collection of $k$ version of $FTTM, \mathrm{in}\mathrm{short},FTT{M}_n^k$ is now simply called a sequence of $FTTM$.

Definition 3. 

([17]) A sequence of $k$ versions of $FTT{M}_n$ denoted by $\ast FTT{M}_n^k$ such that,

$$\ast FTT{M}_n^k=\{FTT{M}_n^1 ,FTT{M}_n^2, \mathrm{\dots }, FTT{M}_n^k$$

(2)

where $FTT{M}_n^1$ is the first version of $FTT{M}_n$ , the $FTT{M}_n^2$ is the second version of $FTT{M}_n$ and so forth.

Obviously, a new $FTTM$ can be generated from a combination of components from different versions of $FTTM$ due to their homeomorphisms.

Definition 4. 

([17]) A new $FTTM$ generated from $\ast FTT{M}_n^k$ is defined as

$$F=\left\{A_1^{m_1} ,A_2^{m_2} , . . . , A_n^{m_n}\right\}\in FTTM$$

(3)

where $0 \le m_1, m_2, . . . , m_n \le k$ and $m_i\ne m_j$ for at least one $i, j$.

A set of elements generated by $\ast FTT{M}_n^k$ is denoted by $G\left(\ast FTT{M}_n^k\right)$. Earlier researchers have shown that the number of $FTTM$ can be determined from $\ast FTT{M}_4^k$ using the geometrical features of its graph representation [1]. The amount of generated FTTM with four components is given by the following theorem.

Theorem 1. 

([1]) The number of generated $FTTM$ that can be created from $\ast FTT{M}_4^k$ is

$$\left|G\left(\ast FTT{M}_4^k\right)\right|=k^4-k$$

(4)

The extended version of Theorem 1 that includes n number of components of FTTM was posed by [1] earlier in 2014.

Theorem 2. 

([3]) The number of generated FTTM that can be created from $\ast FTT{M}_n^k$ is

$$\left|G\left(\ast FTT{M}_n^k\right)\right|=k^n-k$$

(5)

The following example is presented to illustrate Theorem 2.

Example 1. 

Consider $\ast FTT{M}_3^2$, with $FTT{M}_3^1=\left\{A_1^1,A_2^1, A_3^1\right\}$and $FTT{M}_3^2=\left\{A_1^2,A_2^2, A_3^2\right\}$, then $G\left(\ast FTT{M}_3^2\right)=\{\left\{A_1^1,A_2^2, A_3^1\right\}, \left\{A_1^1, A_2^1,A_3^2\right\},\left\{A_1^2,A_2^1,A_3^1\right\},\left\{A_1^2,A_2^2,A_3^1\right\}, \left\{A_1^2,A_2^1,A_3^2\right\},$$\left\{A_1^1,A_2^2,A_3^2\right\}$} that is $\left|G\left(\ast FTT{M}_3^2\right)\right|=2^3–2=6$as given by Theorem 2.

3. Extended Generalization of FTTM

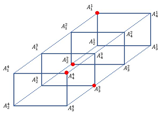
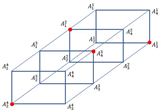
Furthermore, $\ast FTT{M}_n^k$ is an extended generalization of FTTM that can be represented by a graph of the sequence of $k$ number of polygons with $n$ sides or vertices. The polygon is arranged from back to front where the first polygon represents $FTT{M}_n^1$, the second polygon represents $FTT{M}_n^2$ and so forth. An edge is added to connect $FTT{M}_n^1$ to the $FTT{M}_n^2$ component wisely, similarly, for $FTT{M}_n^2$ and $FTT{M}_n^3$ and the rest (Figure 3).

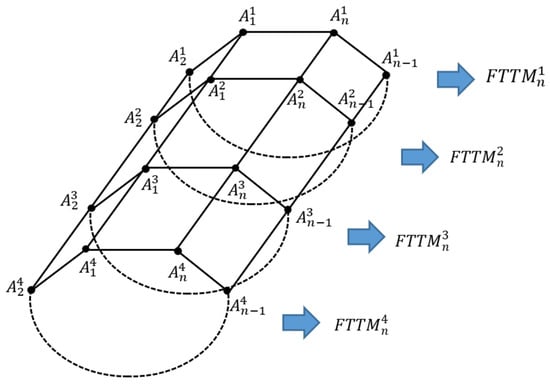
Figure 3. Graph of $\ast FTT{M}_n^k$ [18].

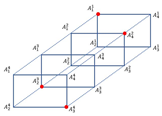
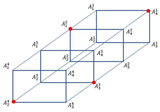
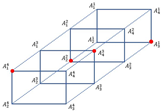
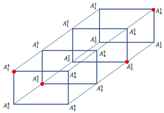
When a new $FTTM$ is obtained from $\ast FTT{M}_n^k$, then it is called a pseudo-graph of generated $FTTM$ and plotted on the skeleton of $\ast FTT{M}_n^k$. A generated element of a pseudo-graph consists of vertices that signify the generated $FTTM$ and edges that connect the incidence components. Two samples of pseudo-graphs are illustrated in Figure 4.

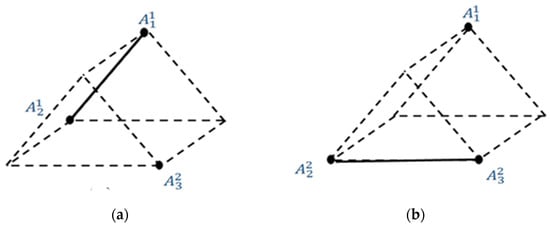
Figure 4. Pseudo graph: (a) $\left\{A_1^1,A_2^1,A_3^2\right\}$; (b) $\left\{A_1^1,A_2^2,A_3^2\right\}$ of $\ast FTT{M}_3^2$ [18].

Another concept related closely to the pseudo-graph is pseudo degree. It is defined as the sum of the pseudo degree from each component of the $FTTM$. The pseudo degree of a component is the number of other components that are adjacent to that particular component.

Definition 5. 

([17]) The $de{g}_p :FTTM\to Z$ defines the pseudo degree of $FTTM$ component. It maps a component of $F\in G\left(\ast FTT{M}_n^k\right)$ to an integer

$${\mathrm{deg}}_p\left(A_j^{m_j}\right)=\{\begin{array}{c}0; m_{j-1}\ne m_j\ne m_{j+1} \\ 1; m_{j-1}=m_j or m_j=m_{j+1}, \\ 2; m_{j-1}=m_j=m_{j+1}\end{array}$$

(6)

for $A_j^{m_j}\in FTTM$.

Definition 6. 

([17]) The $de{g}_{p}G :G\left(\ast FTT{M}_n^k\right)\to Z$ defines the pseudo degree of $FTTM$ graph. Let $F \in FTTM$

$$de{g}_{p}G\left(F\right)={\displaystyle \sum }_{i=1}^n{deg}_p{A}_i^{m_i}$$

(7)

where $F=\left\{A_1^{m_1} ,A_2^{m_2} , . . . , A_n^{m_n}\right\}\in G\left(\ast FTT{M}_n^k\right)$.

Definition 7. 

([17]) The set of elements generated by $\ast FTT{M}_n^k$ that have pseudo degree zero is

$$G_0\left(\ast FTT{M}_n^k \right)=\left\{F\in G\left(\ast FTT{M}_n^k\right)|de{g}_{p}G\left(F\right)=0 \right\}$$

(8)

In other words, vertices of $G_0\left(\ast FTT{M}_n^k\right)$ are all isolated.

From now on,

• $G_0\left(\ast FTT{M}_n^k\right)$ is simply denoted by $G_0\left(FTT{M}_n^k\right)$.
• $\left|G_0\left(FTT{M}_n^k\right)\right|$ denotes the cardinality of the set $G_0\left(FTT{M}_n^k\right)$.

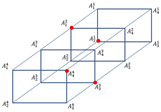
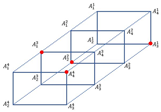
Example 2. 

(see Figure 5)

Figure 5. $FTT{M}_4^3$ [17].

$$\begin{array}{cc}FTTM{ }_4^3=\hfill & \left\{\left(A_1,A_2,A_3,A_4\right), \left(B_1,B_2,B_3,B_4\right), \left(C_1,C_2,C_3,C_4\right)\right\}\hfill \\ \hfill G_0\left(FTT{M}_4^3\right)& =\{\left(A_1,B_2,A_3,C_4\right), \left(A_1,B_2,C_3,B_4\right), \left(A_1,C_2,A_3,B_4\right), \left(A_1,C_2,B_3,C_4\right),\hfill \\ & \left(B_1,A_2,B_3,C_4\right),\left(B_1,A_2,C_3,A_4\right), \left(B_1,C_2,B_3,A_4\right), \left(B_1,C_2,A_3,C_4\right),\hfill \\ & \left(C_1,B_2,C_3,A_4\right), \left(C_1,B_2,A_3,B_4\right), \left(C_1,A_2,C_3,B_4\right), \left(C_1,A_2,B_3,A_4\right)\}\hfill \end{array}$$

(9)

$$Thus G_0\left(FTT{M}_4^3\right)=12.$$

Earlier, Elsafi proposed a conjecture in [3] related to the graph of pseudo degree, in particular, $G_0^3\left(FTT{M}_n^3\right)$.

Conjecture 1. 

([5])

$$\left|G_0^3\left(FTT{M}_n^3\right)\right|=\{\begin{array}{c}4\left|G_0^3\left(FTT{M}_{n-2}^3\right)\right|+12 , \mathrm{when}n\mathrm{is}\mathrm{even} \\ 4\left|G_0^3\left(FTT{M}_{n-2}^3\right)\right|+6, \mathrm{when}n\mathrm{is}\mathrm{odd}\end{array}$$

(10)

Conjecture 1 was finally proven successfully by Mukaram et al. [18] in 2021. In order to achieve it, the researchers developed an algorithm [15,17] to obtain some patterns of the conjecture (see Figure 6) for k = 3 and 4 before the analytical proof for $\left|G_0^3\left(FTT{M}_n^3\right)\right|$ was devised and presented in [18] using their novel grid-based method.

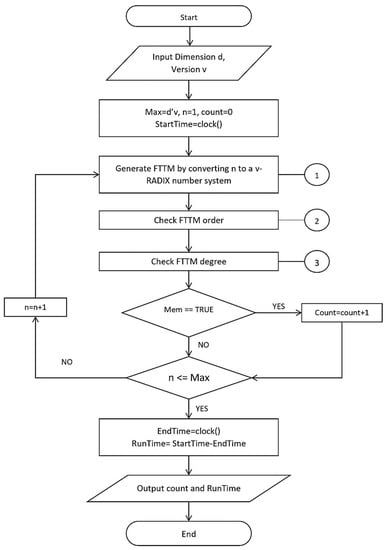
Figure 6. Flowchart for determining $\left|G_0\left(\ast FTT{M}_3^n\right)\right|$ [18].

Some interesting numerical results were obtained (see Table 1).

Table 1. $\left|G_0\left(FTT{M}_n^k\right)\right|$ for $4\le n\le 15$ and $k=3,4$ [18].

n	$\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}}^3\right)\right|$	$\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}}^4\right)\right|$
4	12	24
5	30	120
6	60	480
7	126	1680
8	252	5544
9	510	17,640
10	1020	54,960
11	2046	168,960
12	4092	515,064
13	8190	1,561,560
14	16,380	4,717,440
15	32,766	14,217,840

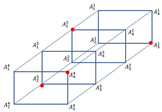
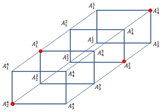
Example 3. 

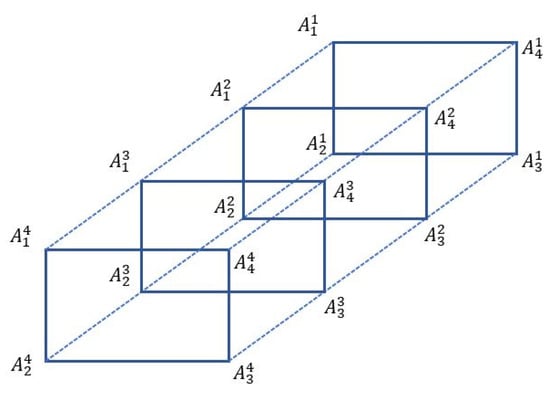
Consider $FTT{M}_4^4$ (see Figure 7) such that

$$FTT{M}_4^4=\left\{FTT{M}^1,FTT{M}^2,FTT{M}^3, FTT{M}^4\right\}$$

(11)

where $FTT{M}_4^1=\left\{A_1^1,A_2^1,A_3^1,A_4^1\right\},FTT{M}_4^2=\left\{A_1^2,A_2^2,A_3^2,A_4^2\right\},$ $FTT{M}_4^3=\left\{A_1^3,A_2^3,A_3^3,A_4^3\right\},$ $FTT{M}_4^4=\left\{A_1^4,A_2^4,A_3^4,A_4^4\right\}$.

Figure 7. $FTT{M}_4^4$.

Its pseudo degree zero elements are

$$\begin{array}{cc}\hfill \left| {\mathit{G}}_{\mathbf{0}}^{\mathbf{4}}\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathbf{4}}^{\mathbf{4}} \right)\right|=& \{\left\{A_1^1, A_2^2,A_3^3, A_4^4\right\}, \left\{A_1^1, A_2^2,A_3^4, A_4^3\right\}, \left\{A_1^1, A_2^3,A_3^2, A_4^4\right\}, \left\{A_1^1, A_2^3,A_3^4, A_4^2\right\},\hfill \\ & \left\{A_1^1, A_2^4,A_3^2, A_4^3\right\}, \left\{A_1^1, A_2^4,A_3^3, A_4^2\right\}, \left\{A_1^2, A_2^1,A_3^3, A_4^4\right\}, \left\{A_1^2, A_2^1,A_3^4, A_4^3\right\},\hfill \\ & \left\{A_1^2, A_2^3,A_3^1, A_4^4\right\}, \left\{A_1^2, A_2^3,A_3^4, A_4^1\right\}, \left\{A_1^2, A_2^4,A_3^1, A_4^3\right\}, \left\{A_1^2, A_2^4,A_3^3, A_4^1\right\},\hfill \\ & \left\{A_1^3, A_2^1,A_3^2, A_4^4\right\}, \left\{A_1^3, A_2^1,A_3^4, A_4^2\right\}, \left\{A_1^3, A_2^2,A_3^1, A_4^4\right\},\left\{A_1^3, A_2^2,A_3^4, A_4^1\right\},\hfill \\ & \left\{A_1^3, A_2^4,A_3^1, A_4^2\right\},\left\{A_1^3, A_2^4,A_3^2, A_4^1\right\},\left\{A_1^4, A_2^1,A_3^2, A_4^3\right\},\left\{A_1^4, A_2^1,A_3^3, A_4^2\right\},\hfill \\ & \left\{A_1^4, A_2^2,A_3^1, A_4^3\right\},\left\{A_1^4, A_2^2,A_3^3, A_4^1\right\},\left\{A_1^4, A_2^3,A_3^1, A_4^2\right\},\left\{A_1^4, A_2^3,A_3^2, A_4^1\right\}\}.\hfill \end{array}$$

(12)

and its geometrical representations are shown in Table 2.

Table 2. Geometrical features of Pseudo degree zero for $FTT{M}_4^4$ .

1.$FTT{M}_4^4=\left\{A_1^1, A_2^2,A_3^3, A_4^4\right\}$	2. $FTT{M}_4^4=\left\{A_1^1, A_2^2,A_3^4, A_4^3\right\}$
3. $FTT{M}_4^4=\left\{A_1^1, A_2^3,A_3^2, A_4^4\right\}$	4. $FTT{M}_4^4=\left\{A_1^1, A_2^3,A_3^4, A_4^2\right\}$
5. $FTT{M}_4^4=\left\{A_1^1, A_2^4,A_3^2, A_4^3\right\}$	6. $FTT{M}_4^4=\left\{A_1^1, A_2^4,A_3^3, A_4^2\right\}$
7. $FTT{M}_4^4=\left\{A_1^2, A_2^1,A_3^3, A_4^4\right\}$	8. $FTT{M}_4^4=\left\{A_1^2, A_2^1,A_3^4, A_4^3\right\}$
9. $FTT{M}_4^4=\left\{A_1^2, A_2^3,A_3^1, A_4^4\right\}$	10. $FTT{M}_4^4=\left\{A_1^2, A_2^3,A_3^4, A_4^1\right\}$
11. $FTT{M}_4^4=\left\{A_1^2, A_2^4,A_3^1, A_4^3\right\}$	12. $FTT{M}_4^4=\left\{A_1^2, A_2^4,A_3^3, A_4^1\right\}$
13. $FTT{M}_4^4=\left\{A_1^3, A_2^1,A_3^2, A_4^4\right\}$	14. $FTT{M}_4^4=\left\{A_1^3, A_2^1,A_3^4, A_4^2\right\}$
15. $FTT{M}_4^4=\left\{A_1^3, A_2^2,A_3^1, A_4^4\right\}$	16. $FTT{M}_4^4=\left\{A_1^3, A_2^2,A_3^4, A_4^1\right\}$
17. $FTT{M}_4^4=\left\{A_1^3, A_2^4,A_3^1, A_4^2\right\}$	18. $FTT{M}_4^4=\left\{A_1^3, A_2^4,A_3^2, A_4^1\right\}$
19. $FTT{M}_4^4=\left\{A_1^4, A_2^1,A_3^2, A_4^3\right\}$	20. $FTT{M}_4^4=\left\{A_1^4, A_2^1,A_3^3, A_4^2\right\}$
21. $FTT{M}_4^4=\left\{A_1^4, A_2^2,A_3^1, A_4^3\right\}$	22. $FTT{M}_4^4=\left\{A_1^4, A_2^2,A_3^3, A_4^1\right\}$
23. $FTT{M}_4^4=\left\{A_1^4, A_2^3,A_3^1, A_4^2\right\}$	24. $FTT{M}_4^4=\left\{A_1^4, A_2^3,A_3^2, A_4^1\right\}$

4. Conjecturing ${\mathit{G}}_{\mathbf{0}}^{\mathbf{4}}\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}}^{\mathbf{4}}\right)$

Mukaram et al. [17] conjectured $G_0^4\left(FTT{M}_n^4\right).$ Since Elsafi’s conjecture (see Conjecture 1) is presented in odd and even values of $n$, it was suspected that $G_0^4\left(FTT{M}_n^4\right)$ should exhibit a similar form as $\left|G_0\left(FTT{M}_n^3\right)\right|$. Table 3 and Table 4 list $G_0^4\left(FTT{M}_n^4\right)$ for odd and even $n$, respectively. The ratio of $\left|G_0\left(FTT{M}_n^4\right)\right| t\mathrm{o} \left|G_0\left(FTT{M}_{n-2}^4\right)\right|$ is then calculated.

Table 3. $G_0^4\left(FTT{M}_n^4\right)$ for odd $n\le 15$.

n	$\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}}^4\right)\right|$	$\frac{\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}}^4\right)\right|}{\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}-2}^4\right)\right|}$
5	120	-
7	1680	14
9	17,640	10.5
11	168,960	9.5782
13	1,561,560	9.24
15	14,217,840	9.104

Table 4. $G_0^4\left(FTT{M}_n^4\right)$ for even $n\le 14$.

n	$\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}}^4\right)\right|$	$\frac{\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}}^4\right)\right|}{\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}-2}^4\right)\right|}$
4	24	-
6	480	20
8	5544	11.55
10	54,960	9.9134
12	515,064	9.3
14	4,717,440	9.1589

From Table 3 and Table 4, the ratio seems to converge to 9. The equation is then conjectured to be as follows:

$$\left|G_0\left(FTT{M}_n^4\right)\right|=9\left|G_0\left(FTT{M}_{n-2}^4\right)\right|+I_n$$

(13)

such that $I_n$ is an unknown that needs to be determined.

In order to find $I_n$ the value of $\left|G_0\left(FTT{M}_n^4\right)\right|-9\left|G_0\left(FTT{M}_{n-2}^4\right)\right|$ for even (see Table 5) and odd (see Table 6) n must be determined.

Table 5. $I_n$ for even $n\le 14$.

$\mathit{n}$	${\mathit{I}}_{\mathit{n}}=\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}}^4\right)\right|-9\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}-2}^4\right)\right|$	$\frac{{\mathit{I}}_{\mathit{n}}}{{\mathit{I}}_{\mathit{n}-2}}$
6	264	-
8	1224	4.63
10	5064	4.13
12	20,424	4.03
14	81,864	4.00

Table 6. $I_n$ for odd $n\le 15$.

$\mathit{n}$	${\mathit{I}}_{\mathit{n}}=\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}}^4\right)\right|-9\left|{\mathit{G}}_0\left(\mathit{F}\mathit{T}\mathit{T}{\mathit{M}}_{\mathit{n}-2}^4\right)\right|$	$\frac{{\mathit{I}}_{\mathit{n}}}{{\mathit{I}}_{\mathit{n}-2}}$
7	600	-
9	2520	4.2
11	10,200	4.04
13	40,920	4.011
15	163,800	4.00

From Table 5 and Table 6, the ratio $\frac{I_n}{I_{n-2}}$ seems to converge to 4. The equation for $I_n$ is then conjectured to be as follows:

$$I_n=\{\begin{array}{c}4I_{n-2}+r_1 , \mathrm{when} n\mathrm{is} \mathrm{even} \\ 4I_{n-2}+r_2, \mathrm{when} n \mathrm{is} \mathrm{odd}\end{array}$$

(14)

Form Table 7, the following relation is then proposed

$$I_n=\{\begin{array}{c}4I_{n-2}+168 , \mathrm{when} n \mathrm{is} \mathrm{even} \\ 4I_{n-2}+120, \mathrm{when} n \mathrm{is} \mathrm{odd}\end{array}$$

(15)

Table 7. $r_1$ and $r_2$ for $n\le 15$.

n	${\mathit{I}}_{\mathit{n}}$	${\mathit{I}}_{\mathit{n}-2}$	${\mathit{r}}_1={\mathit{I}}_{\mathit{n}}-4{\mathit{I}}_{\mathit{n}-2}$	${\mathit{r}}_2={\mathit{I}}_{\mathit{n}}-4{\mathit{I}}_{\mathit{n}-2}$
6	264	-	-	-
7	600	-	-	-
8	1224	264	168	-
9	2520	600	-	120
10	5064	1224	168	-
11	10,200	2520	-	120
12	20,424	5064	168	-
13	40,920	10,200	-	120
14	81,864	20,424	168	-
15	163,800	40,920	-	120

Finally, a new conjecture, namely, $\left|G_0^4\left(\ast FTT{M}_n^4\right)\right|$ is stated formally.

Conjecture 2. 

$$\begin{gathered} \left|G_0^4\left(\ast FTT{M}_n^4\right)\right|=\{\begin{array}{c}9\left|G_0^4\left(\ast FTT{M}_{n-2}^4\right)\right|+I_n, n \mathrm{is} \mathrm{even},\\ 9\left|G_0^4\left(\ast FTT{M}_{n-2}^4\right)\right|+I_n, n \mathrm{is} \mathrm{odd}\end{array} \\ {I}_n=\{\begin{array}{c}4I_{n-2}+168, n \mathrm{is} \mathrm{even},\\ 4I_{n-2}+120, n \mathrm{is} \mathrm{odd}\end{array} \end{gathered}$$

(16)

for $n \ge 4$with $I_4=\left|G_0^4\left(\ast FTT{M}_4^4\right)\right|=24$and $I_5=\left|G_0^4\left(\ast FTT{M}_5^4\right)\right|=120$.

Example 4. 

When $n=6$,

$$\begin{array}{cc}\hfill \left|G_0^4\left(\ast FTT{M}_6^4\right)\right|& =9\left|G_0^4\left(\ast FTT{M}_4^4\right)\right|+I_6,\hfill \\ & =9\left|G_0^4\left(\ast FTT{M}_4^4\right)\right|+\left(4I_4+168\right)\hfill \\ & =9·24+\left(4I_4+168\right)\hfill \\ & =216+\left(4I_4+168\right)\hfill \\ & =384+4I_4 \hfill \\ & =384+4\left(24\right)\hfill \\ & =384+96 \hfill \\ & =480\hfill \end{array}$$

(17)

Example 5. 

When $n=9$,

$$\begin{array}{c}\left|G_0^4\left(\ast FTT{M}_9^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_7^4\right)\right|+I_9,\hfill \\ =9\left|G_0^4\left(\ast FTT{M}_7^4\right)\right|+\left[4I_7+120\right]\hfill \\ =9\left|G_0^4\left(\ast FTT{M}_7^4\right)\right|+\left[4\left(4I_5+120\right)+120\right]\hfill \\ =9\left|G_0^4\left(\ast FTT{M}_7^4\right)\right|+\left[4\left(4\left(120\right)+120\right)+120\right]\hfill \\ =9\left|G_0^4\left(\ast FTT{M}_7^4\right)\right|+\left[4\left(480+120\right)+120\right]\hfill \\ =9\left|G_0^4\left(\ast FTT{M}_7^4\right)\right|+\left[4\left(600\right)+120\right]\hfill \\ =9\left|G_0^4\left(\ast FTT{M}_7^4\right)\right|+\left[2400+120\right]\hfill \\ =9\left[9\left|G_0^4\left(\ast FTT{M}_5^4\right)\right|+I_7\right]+\left[2520\right]\hfill \\ =9\left[9\left(120\right)+I_7\right]+\left[2520\right]\hfill \\ =9\left[1080+\left(4I_5+120\right)\right]+\left[2520\right] \hfill \\ =9\left[1080+\left(4\left(120\right)+120\right)\right]+\left[2520\right]\hfill \\ =9\left[1080+\left(480+120\right)\right]+\left[2520\right]\hfill \\ =9\left[1080+600\right]+\left[2520\right]\hfill \\ =9\left[1680\right]+\left[2520\right]\hfill \\ =\left[15120\right]+\left[2520\right]\hfill \\ =17640\hfill \end{array}$$

(18)

The numerical patterns that can describe $\left|G_0\left(FTT{M}_n^4\right)\right|$ as in Table 3, Table 4, Table 5, Table 6 and Table 7 remain as open problems, hence, Conjecture 2 does as well, since the analytical proof of Conjecture 2 has not been provided.

5. The Theorem

In this section, we prove $\left|G_0\left(FTT{M}_n^4\right)\right|$, i.e., Conjecture 2, analytically using mathematical induction [19]. In doing so, a lemma and a couple of theorems are developed for the purpose.

Conjecture 2 can be divided into two parts, namely, the even and odd parts.

5.1. Even

First, the sub term of the even part, $I_n=4I_{n-2}+168$ for $n i\mathrm{s}\mathrm{even}$ and $n\ge 4$ with $I_4=24$ is considered. Here are some of its respective terms (see Table 8).

Table 8. I_n for n = 6, 8, 10, 12 and 14.

n	In
6	264
8	1224
10	5064
12	20,424
14	81,864

The expression can be deduced to a simpler form (see Table 9).

Table 9. I_n = 4I_n−2 + 168 for even number, n.

n	In = 4In−2 + 168
6	I6 = 4I4 + 168 = 4(24) + 168
8	I8 = 4I6 + 168 = 4(4(24) + 168) = 42(24) + (5)168
10	I10 = 4I8 + 168 = 4(42(24) + (5)168) + 168 = 43(24) + (21)168
12	I12 = 4I10 + 168 = 4(43(24) + (21)168 + 168 |= 44(24) + (85)168
⋮	⋮
4 + 2m	I4+2m = 4mI4 + (1 + 4m−1)168 = 4m(24) + (am)168 such that am = am−1 + 4m−1 with a0 = 0

As for the sequence $a_m=a_{m-1}+4^{m-1}$ with $a_0=0,$ it can be deduced further as follows.

Lemma 1. 

$a_m=a_{m-1}+4^{m-1}=1-\frac{4\left(1-4^{m-1}\right)}{3}$ with $a_0=0$ for $m\in \mathbb{N}$.

Proof. 

$$\begin{array}{c}{a}_1=a_0+4^0=0+1=1\hfill \\ a_2=a_1+4^1=1+4=5\hfill \\ a_3=a_2+4^2=5+16=21\hfill \\ a_4=a_3+4^3=21+64=85\hfill \\ ⋮⋮⋮⋮\\ a_m=a_{m-1}+4^{m-1}\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\displaystyle {\displaystyle \sum }_{i=1}^m}{a}_i& ={\displaystyle {\displaystyle \sum }_{i=0}^{m-1}}{a}_i+{\displaystyle {\displaystyle \sum }_{i=0}^{m-1}}{4}^i\hfill \\ & =a_0+{\displaystyle {\displaystyle \sum }_{i=1}^{m-1}}{a}_i+4^0+{\displaystyle {\displaystyle \sum }_{i=1}^{m-1}}{4}^i \hfill \\ & =0+{\displaystyle {\displaystyle \sum }_{i=1}^{m-1}}{a}_i+4^0+{\displaystyle {\displaystyle \sum }_{i=1}^{m-1}}{4}^i\hfill \\ & ={\displaystyle {\displaystyle \sum }_{i=1}^{m-1}}{a}_i+1+{\displaystyle {\displaystyle \sum }_{i=1}^{m-1}}{4}^i\hfill \end{array}$$

Therefore, ${\sum }_{i=1}^m{a}_i-{\sum }_{i=1}^{m-1}{a}_i=1+{\sum }_{i=1}^{m-1}{4}^i$which implies $a_m+{\sum }_{i=1}^{m-1}{a}_i-{\sum }_{i=1}^{m-1}{a}_i=1+{\sum }_{i=1}^{m-1}{4}^i$. Hence,$a_m=1+{\sum }_{i=1}^{m-1}{4}^i$, but then,${\sum }_{i=1}^{m-1}{4}^i$is a summation of a geometric series. If that is the case,

$$\begin{gathered} a_m=1+{\displaystyle {\displaystyle \sum }_{i=1}^{m-1}}{4}^i=1+\frac{4\left(1-4^{m-1}\right)}{1-4} \\ =1+\frac{4\left(1-4^{m-1}\right)}{-3} \\ =1-\frac{4\left(1-4^{m-1}\right)}{3} \end{gathered}$$

(20)

□

The deduction can be reinstated and proven as a theorem formally.

Theorem 3. 

$I_{4+2m}=4^m\left(24\right)+\left(a_m\right)168$such that$a_m=a_{m-1}+4^{m-1}$with$a_0=0$for$m\in \mathbb{N}$.

Proof. 

(by mathematical induction)

Now, by using Lemma 1.

$$\begin{array}{cc}\hfill I_{4+2m}& =4^m\left(24\right)+\left(a_m\right)168\hfill \\ & =4^m\left(24\right)+\left(1-\frac{4\left(1-4^{m-1}\right)}{3} \right)168\hfill \\ & =4^m\left(24\right)-\frac{4\left(1-4^{m-1}\right)}{3}168+168\hfill \\ & =4^m\left(24\right)-\left(1-4^{m-1}\right)224+168\hfill \\ & =4^m\left(24\right)+4^{m-1}\left(224\right)+168-224 \hfill \\ & =4^m\left(24\right)+4^{m-1}\left(224\right)-56\hfill \\ & =4\left(4^{m-1}\right)\left(24\right)+4^{m-1}\left(224\right)-56\hfill \\ & =\left(4^{m-1}\right)\left(96\right)+4^{m-1}\left(224\right)-56 \hfill \\ & =4^{m-1}\left(96+224\right)-56 \hfill \\ & =4^{m-1}\left(320\right)-56\hfill \end{array}$$

(21)

m = 1

$$I_{4+2\left(1\right)}=4^{1-1}\left(320\right)-56=4^0\left(320\right)-56=264=I_6$$

(22)

$m\Rightarrow m+1$

Assume $I_{4+2m}=4^{m-1}\left(320\right)-56$ is true. We need to show $I_{4+2\left(m+1\right)}=4^m\left(320\right)-56$.

Then, $I_{4+2\left(m+1\right)}=I_{4+2m+2}=4I_{4+2m+2-2}+168$.

Since

$$\begin{array}{cc}\hfill I_n& =4I_{n-2}+168\hfill \\ & =4I_{4+2m}+168\hfill \\ & =4\left(4^{m-1}\left(320\right)-56\right)+168 \sin \mathrm{ce}\mathrm{by}\mathrm{assumption}{I}_{4+2m}=4^{m-1}\left(320\right)-56\hfill \\ & =4^m\left(320\right)-224+168\hfill \\ & =4^m\left(320\right)-56\mathrm{as}\mathrm{required}.\hfill \end{array}$$

(23)

Thus,

$$I_{4+2m}=4^m\left(24\right)+\left(a_m\right)168\mathrm{such}\mathrm{that}{a}_m=a_{m-1}+4^{m-1} \mathrm{with}{a}_0=0\mathrm{for}m\in \mathbb{N}$$

(24)

□

The procedure to prove the even part has shown how we can deal with the odd part.

5.2. Odd

Second, the sub term of the odd part, namely, $I_n=4I_{n-2}+120$ for $n i\mathrm{s}\mathrm{odd}$ for $n>4$ with $I_5=120$. Here are some of its respective terms (see Table 10).

Table 10. $I_n$ for n = 7, 9, 11, 13 and 15.

$\mathit{n}$	${\mathit{I}}_{\mathit{n}}$
7	600
9	2520
11	10,200
13	40,920
15	163,800

The expression can be deduced to a simpler form (see Table 11).

Table 11. $I_n=4I_{n-2}+120$ for odd number, n.

n	${\mathit{I}}_{\mathit{n}}=4{\mathit{I}}_{\mathit{n}-2}+120$
7	$I_7=4I_5+120=4\left(120\right)+120$
9	$I_9=4I_7+120=4\left(4\left(120\right)+120\right)+120=4^2\left(120\right)+\left(5\right)120$
11	$I_{11}=4I_9+120=4\left(4^2\left(120\right)+\left(5\right)120\right)+120=4^3\left(120\right)+\left(21\right)120$
13	$I_{13}=4I_{11}+120=4\left(4^3\left(120\right)+\left(21\right)120\right)+120=4^4\left(120\right)+\left(85\right)120$
$⋮$	$⋮$
$5+2m$	$I_{5+2m}=4^m{I}_5+\left(1+4^{m-1}\right)120=4^m\left(120\right)+\left(a_m\right)120$ such that $a_m=a_{m-1}+4^{m-1}$ with $a_0=0$

The deduction on the odd part can be reinstated as a theorem formally.

Theorem 4. 

$$I_{5+2m}=4^m\left(120\right)+\left(a_m\right)120suchthat{a}_m=a_{m-1}+4^{m-1}with{a}_0=0form\in \mathbb{N}.$$

(25)

Proof. 

(by mathematical induction)

Now, using Lemma 1

$$\begin{array}{cc}\hfill I_{5+2m}& =4^m\left(120\right)+\left(a_m\right)120\hfill \\ & =4^m\left(120\right)+\left(1-\frac{4\left(1-4^{m-1}\right)}{3}\right)120\hfill \end{array}$$

(26)

$$\begin{array}{c}=4^m\left(120\right)-\frac{4\left(1-4^{m-1}\right)}{3}120+120\hfill \\ =4^m\left(120\right)-\left(1-4^{m-1}\right)160+120\hfill \\ =4^m\left(120\right)+4^{m-1}\left(160\right)+120-160 \hfill \\ =4^m\left(120\right)+4^{m-1}\left(160\right)-40\hfill \\ =4\left(4^{m-1}\right)\left(120\right)+4^{m-1}\left(160\right)-40\hfill \\ =4\left(4^{m-1}\right)\left(120\right)+4^{m-1}\left(160\right)-40\hfill \\ =\left(4^{m-1}\right)\left(480\right)+4^{m-1}\left(160\right)-40\hfill \\ =\left(4^{m-1}\right)\left(480\right)+4^{m-1}\left(160\right)-40\hfill \\ =4^{m-1}\left(640\right)-40\hfill \end{array}$$

m = 1

$$I_{5+2\left(1\right)}=4^{1-1}\left(640\right)-40=4^0\left(640\right)-40=600=I_7$$

(27)

$m\Rightarrow m+1$

Assume$I_{5+2m}=4^{m-1}\left(640\right)-40$is true. We need to show$I_{5+2\left(m+1\right)}=4^m\left(640\right)-40$.

Then,$I_{5+2\left(m+1\right)}=I_{5+2m+2}=4I_{5+2m+2-2}+120$since

$$\begin{array}{cc}\hfill I_n& =4I_{n-2}+120\hfill \\ & =4I_{5+2m}+12 \hfill \\ & =4\left(4^{m-1}\left(640\right)-40\right)+120 \sin \mathrm{ce}\mathrm{by}\mathrm{assumption}{I}_{5+2m}=4^{m-1}\left(640\right)-40\hfill \\ & =4^m\left(640\right)-160+12\hfill \\ & =4^m\left(640\right)-40\mathrm{as}\mathrm{required}.\hfill \end{array}$$

(28)

Thus,

$$I_{5+2m}=4^m\left(120\right)+\left(a_m\right)120\mathrm{such}\mathrm{that}{a}_m=a_{m-1}+4^{m-1}\mathrm{with}{a}_0=0\mathrm{for}m\in \mathbb{N}.$$

(29)

□.

Conjecture 2 is now simplified and composed to be a theorem as follows

Theorem 5. 

$$\begin{gathered} (i) \left|G_0^4\left(\ast FTT{M}_{4+2m}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{4+2m-2}^4\right)\right|+4^{m-1}\left(320\right)-56 \\ (ii) \left|G_0^4\left(\ast FTT{M}_{5+2m}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{5+2m-2}^4\right)\right|+4^{m-1}\left(640\right)-40 \end{gathered}$$

(30)

for$m\in \mathbb{N}$.

Proof. 

(by mathematical induction)

We are going to use the mathematical induction method to prove the conjecture (see Table 11).

m = 1

$$\begin{gathered} \left(\mathrm{i}\right)\left|G_0^4\left(\ast FTT{M}_6^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_4^4\right)\right|+4^0\left(320\right)-56 \\ =9\left(24\right)+320-56 \\ =480 \\ \left(\mathrm{ii}\right)\left|G_0^4\left(\ast FTT{M}_7^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_5^4\right)\right|+4^0\left(640\right)-40 \\ =9\left(120\right)+640-40 \\ =1680 \end{gathered}$$

(31)

$m\Rightarrow m+1$.

(i)

Assume$\left|G_0^4\left(\ast FTT{M}_{4+2m}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{4+2m-2}^4\right)\right|+4^{m-1}\left(320\right)-56$is true.

We need to show

$$\begin{array}{c}\left|G_0^4\left(\ast FTT{M}_{4+2\left(m+1\right)}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{4+2\left(m+1\right)-2}^4\right)\right|+4^m\left(320\right)-56\hfill \\ =9\left|G_0^4\left(\ast FTT{M}_{4+2m+2-2}^4\right)\right|+4^m\left(320\right)-56 \hfill \\ =9\left|G_0^4\left(\ast FTT{M}_{4+2m}^4\right)\right|+4^m\left(320\right)-56\hfill \end{array}$$

(32)

Look,

$$\left|G_0^4\left(\ast FTT{M}_{4+2\left(m+1\right)}^4\right)\right|=\left|G_0^4\left(\ast FTT{M}_{4+2m+2}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{4+2m+2-2}^4\right)\right|+I_n$$

(33)

Since

$$\begin{array}{c}\left|G_0^4\left(\ast FTT{M}_n^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{n-2}^4\right)\right|+I_n \hfill \\ =9\left|G_0^4\left(\ast FTT{M}_{4+2m}^4\right)\right|+I_n \hfill \\ =9\left|G_0^4\left(\ast FTT{M}_{4+2m}^4\right)\right|+4^m\left(320\right)-56 as required.\hfill \end{array}$$

(34)

since$I_n=I_{m+1}=4^{\left(m+1\right)-1}\left(320\right)-56$(Note: we start with$m=1,2\dots$).

(ii)

Assume$\left|G_0^4\left(\ast FTT{M}_{5+2m}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{5+2m-2}^4\right)\right|+4^{m-1}\left(640\right)-40$is true.

We need to show$\left|G_0^4\left(\ast FTT{M}_{5+2\left(m+1\right)}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{5+2\left(m+1\right)-2}^4\right)\right|+4^m\left(640\right)-40$. Look,

$$\left|G_0^4\left(\ast FTT{M}_{5+2\left(m+1\right)}^4\right)\right|=\left|G_0^4\left(\ast FTT{M}_{5+2m+2}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{5+2m+2-2}^4\right)\right|+I_n$$

(35)

since

$$\begin{array}{c}\left|G_0^4\left(\ast FTT{M}_n^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{n-2}^4\right)\right|+I_n \hfill \\ =9\left|G_0^4\left(\ast FTT{M}_{5+2m}^4\right)\right|+I_n \hfill \\ =9\left|G_0^4\left(\ast FTT{M}_{5+2m}^4\right)\right|+4^m\left(640\right)-40 as required.\hfill \end{array}$$

(36)

since$I_n=I_{m+1}=4^{\left(m+1\right)-1}\left(640\right)-40$(Note: we start with$m=1,2\dots$).

Therefore,

• $\left|G_0^4\left(\ast FTT{M}_{4+2m}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{4+2m-2}^4\right)\right|+4^{m-1}\left(320\right)-56$
• $\left|G_0^4\left(\ast FTT{M}_{5+2m}^4\right)\right|=9\left|G_0^4\left(\ast FTT{M}_{5+2m-2}^4\right)\right|+4^{m-1}\left(640\right)-40$

for$m\in \mathbb{N}$. □

6. Discussions

Fuzzy topological topographic mapping ($FTTM$) is a mathematical model that consists of a set of homeomorphic topological spaces designed originally to solve the neuro magnetic inverse problem. A sequence of FTTM denoted as $FTT{M}_n$ is an extension of FTTM that is arranged in a symmetrical form. It can be represented as a graph. The special characteristic of $FTTM$, namely, the homeomorphisms between its components, allows the generation of new $FTTMs$. Since 2019, $FTT{M}_n^3$ and $FTT{M}_n^4$ were generalized and introduced. The former means a sequence of three and the latter denotes a sequence of four FTTMs with n number of components, respectively. These arrangements can produce more $FTTM$s, i.e., generated FTTMs. Among the generated FTTMs are pseudo graphs. A graph of pseudo degree zero, $G_0\left(FTT{M}_n^k\right),$ is a special type of graph where each of the $FTTM$ components differs from its adjacent component, i.e., with isolated vertices. Initially, a researcher [3] posted a conjecture on $\left|G_0^3\left(FTT{M}_n^3\right)\right|$ in 2014, and it was finally proven in 2021 [18] using their novel grid-based method. Moreover, the latter researchers [17,18] also conjectured on $\left|G_0^4\left(FTT{M}_n^4\right)\right|$, which remains an open problem until today.

7. Conclusions

In this paper, the conjecture on $\left|G_0^4\left(FTT{M}_n^4\right)\right|$ is narrated, discussed and finally proven using mathematical induction. The methodology taken for proving $\left|G_0^4\left(FTT{M}_n^4\right)\right|$ is simpler and clearer than the grid-based method employed by [18]. Nevertheless, the methodology required to prove another pseudo degree zero, $G_0\left(FTT{M}_n^k\right)$ for $k=5, 6, 7, \dots .$ remains open. Certainly, it demands some related simulation works in order to identify and devise such methods of proving. Mathematical induction is a very common proving technique that involves integers. It can be considered whenever it is required. The technique can probably be adopted to prove other pseudo degree zero such as $G_0\left(FTT{M}_n^k\right)$ for $k=5, 6, 7, \dots$ or other similar complicated forms of sequences.