Quintessence Behavior of an Anisotropic Bulk Viscous Cosmological Model in Modified f(Q)-Gravity
Abstract
1. Introduction
2. Field Equations in -Gravity
3. Cosmological Solutions
4. Observational Constraints
Apparent Magnitude
5. Discussion of the Results
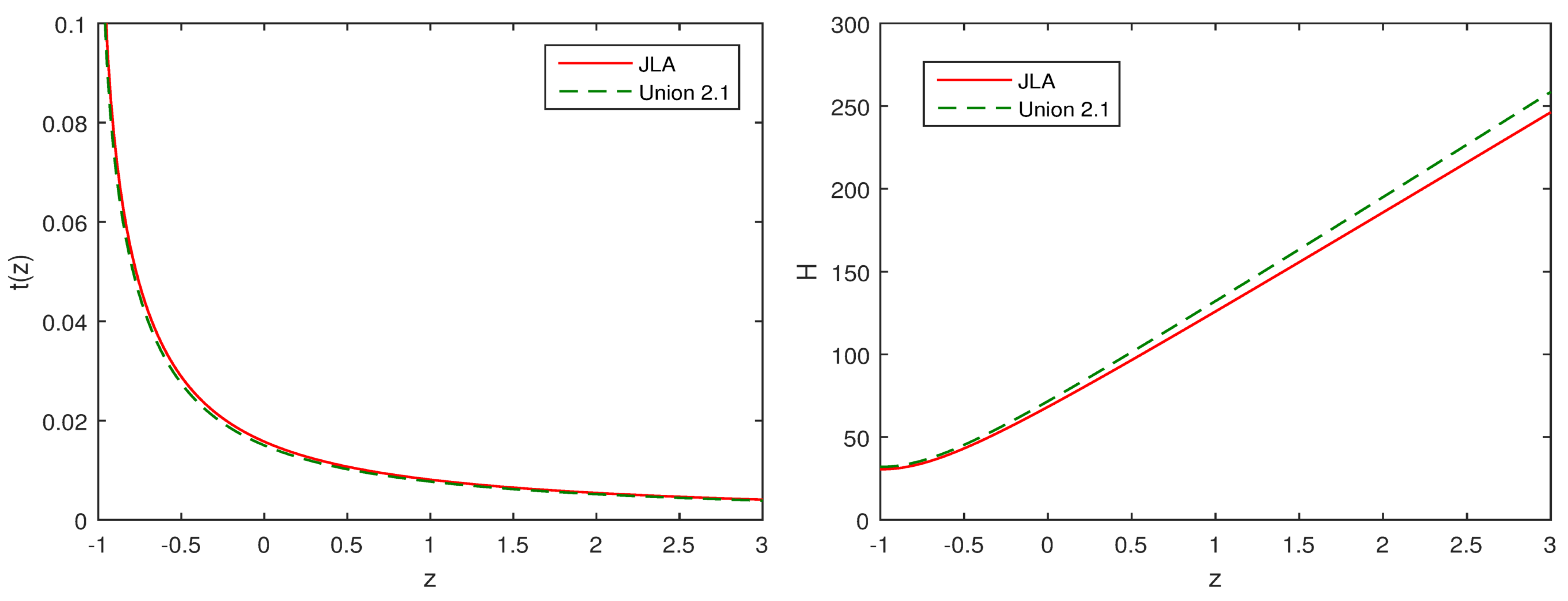
5.1. Age of the Present Universe
5.2. Statefinder Analysis
5.3. Om Diagnostics
6. Concluding Remarks
- In the model, the average scale factor is obtained by solving the field equations, and it depends on the values of model parameters .
- The derived model represents an accelerating universe evolution which has been transited from the decelerating phase.
- We have found the present value of EoS parameter for bulk-viscous fluid and it varies over positive to negative, which indicates the existence of dark energy in the late-time universe of the model.
- The skewness parameter for bulk-viscous fluid tends to zero, which is consistent with skewness property.
- We have found the bulk viscous coefficient as a decreasing function of cosmic time t, which may be a dark energy candidate.
- The model has a singularity at , since it is found that .
- The value of energy density as reveals the Big-Bang singularity in the model.
- The analysis of the statefinder parameters indicate that the derived model tends to the CDM model as .
- In the diagnostic analysis of our model, we have found that the universe in the derived model will have the quintessence-like dark energy at the late times.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Totani, T.; Yoshii, Y.; Sato, K. Evolution of the luminosity density in the universe: Implications for the nonzero cosmological constant. Astrophys. J. 1997, 483, L75. [Google Scholar] [CrossRef][Green Version]
- Meng, X.H.; Wang, P. Modified Friedmann equations in R-1-modified gravity. Class. Quant. Grav. 2003, 20, 4949. [Google Scholar] [CrossRef][Green Version]
- Wang, P.; Meng, X.H. Can vacuum decay in our universe? Class. Quant. Grav. 2005, 22, 283. [Google Scholar] [CrossRef]
- Perlmutter, S.; Gabi, S.; Goldhaber, G.; Goobar, A.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Pain, R.; et al. Measurements* of the Cosmological Parameters Ω and Λ from the First Seven Supernovae at z ≥ 0.35. Astrophys. J. 1997, 483, 565. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Valle, M.D.; Deustua, S.; Ellis, R.S.; Fabbro, S.; Fruchter, A.; Goldhaber, G.; Groom, D.E.; Hook, I.M.; et al. Discovery of a supernova explosion at half the age of the Universe. Nature 1998, 391, 51–54. [Google Scholar] [CrossRef]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Determination of cosmological parameters. Astrophys. J. Suppl. 2003, 148, 175–194. [Google Scholar] [CrossRef]
- Verde, L.; Heavens, A.F.; Percival, W.J.; Matarrese, S.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Cole, S.; Colless, M.; et al. The 2dF Galaxy Redshift Survey: The bias of galaxies and the density of the Universe. Mon. Not. R. Astron. Soc. 2002, 335, 432–440. [Google Scholar] [CrossRef]
- Hinshaw, G.; Weiland, J.L.; Hill, R.S.; Odegard, N.; Larson, D.; Bennett, C.L.; Dunkley, J.; Gold, B.; Greason, M.R.; Jarosik, N.; et al. Five-year wilkinson microwave anisotropy probe* observations: Data processing, sky maps, and basic results. Astrophys. J. Suppl. 2009, 180, 225–245. [Google Scholar] [CrossRef]
- Zlatev, I.; Wang, L.; Steinhardt, S. Quintessence, cosmic coincidence, and the cosmological constant. Phys. Rev. Lett. 1999, 82, 896–899. [Google Scholar] [CrossRef]
- Steinhardt, S.; Wang, L.; Zlatev, I. Cosmological tracking solutions. Phys. Rev. D 1999, 59, 123504. [Google Scholar] [CrossRef]
- Caldwell, R.; Kamionkowski, M.; Weinberg, N. Phantom energy: Dark energy with ω<-1 causes a cosmic doomsday. Phys. Rev. Lett. 2003, 91, 071301. [Google Scholar] [PubMed]
- Hassan, Z.; Mandal, S.; Sahoo, P.K. Traversable wormhole geometries in gravity. Fortschr. Phys. 2021, 69, 2100023. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Cosmological parameter results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Cao, W.; Liu, W.; Wu, X. Integrability of Kerr-Newman spacetime with cloud strings, quintessence and electromagnetic field. Phys. Rev. D 2022, 105, 124039. [Google Scholar] [CrossRef]
- Wu, X. A new interpretation of zero Lyapunov exponents in BKL time for Mixmaster cosmology. Res. Astron. Astrophys. 2010, 10, 211. [Google Scholar] [CrossRef]
- Ma, D.Z.; Wu, X.; Zhong, S.Y. Effects of the cosmological constant on chaos in an FRW scalar field universe. Res. Astron. Astrophys. 2009, 9, 1185. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Comm. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Hooft, G.T. Dimensional reduction in quantum gravity. arXiv 1993, arXiv:gr-qc/9310026. [Google Scholar]
- Li, M. A model of holographic dark energy. Phys. Lett. B 2004, 603, 1. [Google Scholar] [CrossRef]
- Eckart, C. The thermodynamics of irreversible processes. III. Relativistic theory of the simple fluid. Phys. Rev. 1940, 58, 919. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Butterworth Heinemann: New York, NY, USA, 1987. [Google Scholar]
- Israel, W. Nonstationary irreversible thermodynamics: A causal relativistic theory. Ann. Phys. 1976, 100, 310. [Google Scholar] [CrossRef]
- Israel, W.; Stewart, J.M. Thermodynamics of nonstationary and transient effects in a relativistic gas. Phys. Lett. 1976, 58, 213. [Google Scholar] [CrossRef]
- Murphy, G.L. Big-bang model without singularities. Phys. Rev. D 1973, 8, 4231. [Google Scholar] [CrossRef]
- Huang, W.H. Bianchi type I cosmological model with bulk viscosity. Phys. Lett. A 1998, 129, 429. [Google Scholar] [CrossRef]
- Jimenez, J.B.; Heisenberg, L.; Koivisto, T. Coincident general relativity. Phys. Rev. D 2018, 98, 044048. [Google Scholar] [CrossRef]
- Lazkoz, R.; Lobo, F.S.; Ortiz-Banos, M.; Salzano, V. Observational constraints of f(Q) gravity. Phys. Rev. D 2019, 100, 104027. [Google Scholar] [CrossRef]
- Mandal, S.; Sahoo, P.K.; Santos, J.R.L. Energy conditions in f(Q) gravity. Phys. Rev. D 2020, 102, 024057. [Google Scholar] [CrossRef]
- Koussour, M.; Shekh, S.H.; Bennai, M. Anisotropic nature of space-time in f(Q) gravity. Phys. Dark Univ. 2022, 36, 101051. [Google Scholar] [CrossRef]
- Mandal, S.; Wang, D.; Sahoo, P.K. Cosmography in f(Q) gravity. Phys. Rev. D 2020, 102, 124029. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.; Olmo, G.J.; Rubiera-Garcia, D. Coupling matter in modified Q gravity. Phys. Rev. D 2018, 98, 084043. [Google Scholar] [CrossRef]
- Dimakis, N.; Paliathanasis, A.; Christodoulakis, T. Quantum cosmology in f(Q) theory. Class. Quantum Grav. 2021, 38, 225003. [Google Scholar] [CrossRef]
- Koussour, M.; Pacif, S.K.J.; Bennai, M.; Sahoo, P.K. Dynamical dark energy models from a new Hubble parameter in f(Q) gravity. J. High Ener. Astrophys. 2022, 35, 43–51. [Google Scholar] [CrossRef]
- Jimenez, J.B.; Heisenberg, L.; Koivisto, T.; Pekar, S. Cosmology in f(Q) geometry. Phys. Rev. D 2020, 101, 103507. [Google Scholar] [CrossRef]
- Khyllep, W.; Paliathanasis, A.; Dutta, J. Cosmological solutions and growth index of matter perturbations in f(Q) gravity. Phys. Rev. D 2021, 103, 103521. [Google Scholar] [CrossRef]
- Barrow, J.D. The deflationary universe: An instability of the de Sitter universe. Phys. Lett. B 1987, 180, 335. [Google Scholar] [CrossRef]
- Brevik, I.; Odintsov, S.D. Cardy-Verlinde entropy formula in viscous cosmology. Phys. Rev. D 2002, 65, 067302. [Google Scholar] [CrossRef]
- Liu, D.J.; Li, X.Z. Dynamics of quintessence with thermal interactions. Phys. Lett. B 2005, 611, 8. [Google Scholar] [CrossRef]
- Fabris, J.C.; Goncalves, S.V.B.; de Sa Ribeiro, R. Bulk viscosity driving the acceleration of the universe. Gen. Relat. Gravit. 2006, 38, 495. [Google Scholar] [CrossRef]
- Li, B.; Barrow, J.D. Does bulk viscosity create a viable unified dark matter model? Phys. Rev. D 2009, 79, 103521. [Google Scholar] [CrossRef]
- Hipolito-Ricaldi, W.S.; Velten, H.E.S.; Zimdahl, W. Viscous dark fluid universe. Phys. Rev. D 2010, 82, 063507. [Google Scholar] [CrossRef]
- Avelino, A.; Nucamendi, U. Can a matter-dominated model with constant bulk viscosity drive the accelerated expansion of the universe? JCAP 2009, 2009, 006. [Google Scholar] [CrossRef]
- Avelino, A.; Nucamendi, U. Exploring a matter-dominated model with bulk viscosity to drive the accelerated expansion of the universe. JCAP 2010, 2010, 009. [Google Scholar] [CrossRef]
- Hassan, Z.; Mustafa, G.; Sahoo, P.K. Wormhole solutions in symmetric teleparallel gravity with noncommutative geometry. Symmetry 2021, 13, 1260. [Google Scholar] [CrossRef]
- Brevik, I.; Normann, B.D. Remarks on cosmological bulk viscosity in different epochs. Symmetry 2020, 12, 1085. [Google Scholar] [CrossRef]
- Cruz, N.; Gonzalez, E.; Jovel, J. Study of a viscous ΛWDM model: Non-equilibrium condition, entropy production, and cosmological constraints. Symmetry 2022, 14, 1866. [Google Scholar] [CrossRef]
- Singh, A.; Chaubey, R. Unified and bouncing cosmologies with inhomogeneous viscous fluid. Astrophys. Space Sci. 2021, 366, 15. [Google Scholar] [CrossRef]
- Raushan, R.; Singh, A.; Chaubey, R.; Singh, T. Universe with quadratic equation of state: A dynamical systems perspective. Int. J. Geom. Methods Mod. Phys. 2020, 17, 2050064. [Google Scholar] [CrossRef]
- Sharma, U.K.; Shweta; Mishra, A.K. Traversable wormhole solutions with non-exotic fluid in framework of f(Q) gravity. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250019. [Google Scholar] [CrossRef]
- Zimdahl, W.; Schwarz, D.J.; Balakin, A.B.; Pavon, D. Cosmic antifriction and accelerated expansion. Phys. Rev. D 2001, 64, 063501. [Google Scholar] [CrossRef]
- Zia, R.; Maurya, D.C.; Shukla, A.K. Transit cosmological models in modified f(Q,T) gravity. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150051. [Google Scholar] [CrossRef]
- Godani, N.; Samanta, G.C. FRW cosmology in f(Q,T) gravity. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150134. [Google Scholar] [CrossRef]
- Pradhan, A.; Maurya, D.C.; Dixit, A. Dark energy nature of viscus universe in f(R)-gravity with observational constraints. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150124. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R. Model-independent reconstruction of f(Q)non-metric gravity. Phys. Lett. B 2022, 832, 137229. [Google Scholar] [CrossRef]
- Koussour, M.; Shekh, S.H.; Bennai, M. Anisotropic f(Q) gravity model with bulk viscosity. arXiv 2022, arXiv:2203.10954. [Google Scholar]
- Maurya, D.C. Accelerating Scenarios of Viscus Fluid Universe in Modified f(T) Gravity. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250144. [Google Scholar] [CrossRef]
- Dixit, A.; Maurya, D.C.; Pradhan, A. Phantom dark energy nature of bulk-viscosity universe in modified f(Q)-gravity. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250198. [Google Scholar] [CrossRef]
- Xu, Y.; Li, G.; Harko, T.; Liang, S.D. f(Q,T) gravity. Eur. Phys. J. C 2019, 79, 1–19. [Google Scholar] [CrossRef]
- Thorne, K.S. Primordial element formation, primordial magnetic fields, and the isotropy of the universe. Astrophys. J. 1967, 148, 51. [Google Scholar] [CrossRef]
- Kantowski, R.; Sachs, R.K. Some spatially homogeneous anisotropic relativistic cosmological models. J. Math. Phys. 1966, 7, 433. [Google Scholar] [CrossRef]
- Kristian, J.; Sachs, R.K. Observations in cosmology. Astrophys. J. 1966, 143, 379. [Google Scholar] [CrossRef]
- Collins, C.B.; Glass, E.N.; Wilkinson, D.A. Exact spatially homogeneous cosmologies. Gen. Rel. Grav. 1980, 12, 805. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freemann and Company: San Francisco, CA, USA, 1973. [Google Scholar]
- Brevik, I.; Gron, O.; de Haro, J.; Odintsov, S.D.; Saridakis, E.N. Viscous cosmology for early-and late-time universe. Int. J. Mod. Phys. D 2017, 26, 1730024. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Elizalde, E.; Nojiri, S.I.; Odintsov, S.D. Observational constraints on dark energy with generalized equations of state. Phys. Rev. D 2006, 73, 043212. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Properties of singularities in the (phantom) dark energy universe. Phys. Rev. D 2005, 72, 023003. [Google Scholar] [CrossRef]
- Meng, X.H.; Dou, X. Singularities and entropy in bulk viscosity dark energy model. Commun. Theor. Phys. 2009, 52, 377. [Google Scholar] [CrossRef]
- Meng, X.H.; Ren, J.; Gaung, H.M. Friedmann cosmology with a generalized equation of state and bulk viscosity. Commun. Theor. Phys. 2007, 47, 379. [Google Scholar]
- Kumar, P.; Singh, C.P. New agegraphic dark energy model in Brans-Dicke theory with logarithmic form of scalar field. Astrophys. Space Sci. 2017, 362, 52. [Google Scholar] [CrossRef]
- Normann, B.D.; Brevik, I. Characteristic properties of two different viscous cosmology models for the future universe. Mod. Phys. Lett. A 2017, 32, 1750026. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended Gravity Cosmography. Int. J. Mod. Phys. D 2019, 28, 1930016. [Google Scholar] [CrossRef]
- Betoule, M.E.A.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble space telescope cluster supernova survey. V. Improving the dark-energy constraints above z > 1 and building an early-type-hosted supernova sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% determination of the local value of the Hubble constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder-new geometrical diagnostic of dark energy. JETP Lett. 2003, 77, 201. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Deep Saini, T.; Starobinsky, A.A. Exploring the expanding universe and dark energy using the Statefinder diagnostic. Mon. Not. R. Astron. Soc. 2003, 344, 1057–1074. [Google Scholar] [CrossRef]
- Sami, M.; Shahalam, M.; Skugoreva, M.; Toporensky, A. Cosmological dynamics of a nonminimally coupled scalar field system and its late time cosmic relevance. Phys. Rev. D 2012, 86, 103532. [Google Scholar] [CrossRef]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Two new diagnostics of dark energy. Phys. Rev. D 2008, 78, 103502. [Google Scholar] [CrossRef]
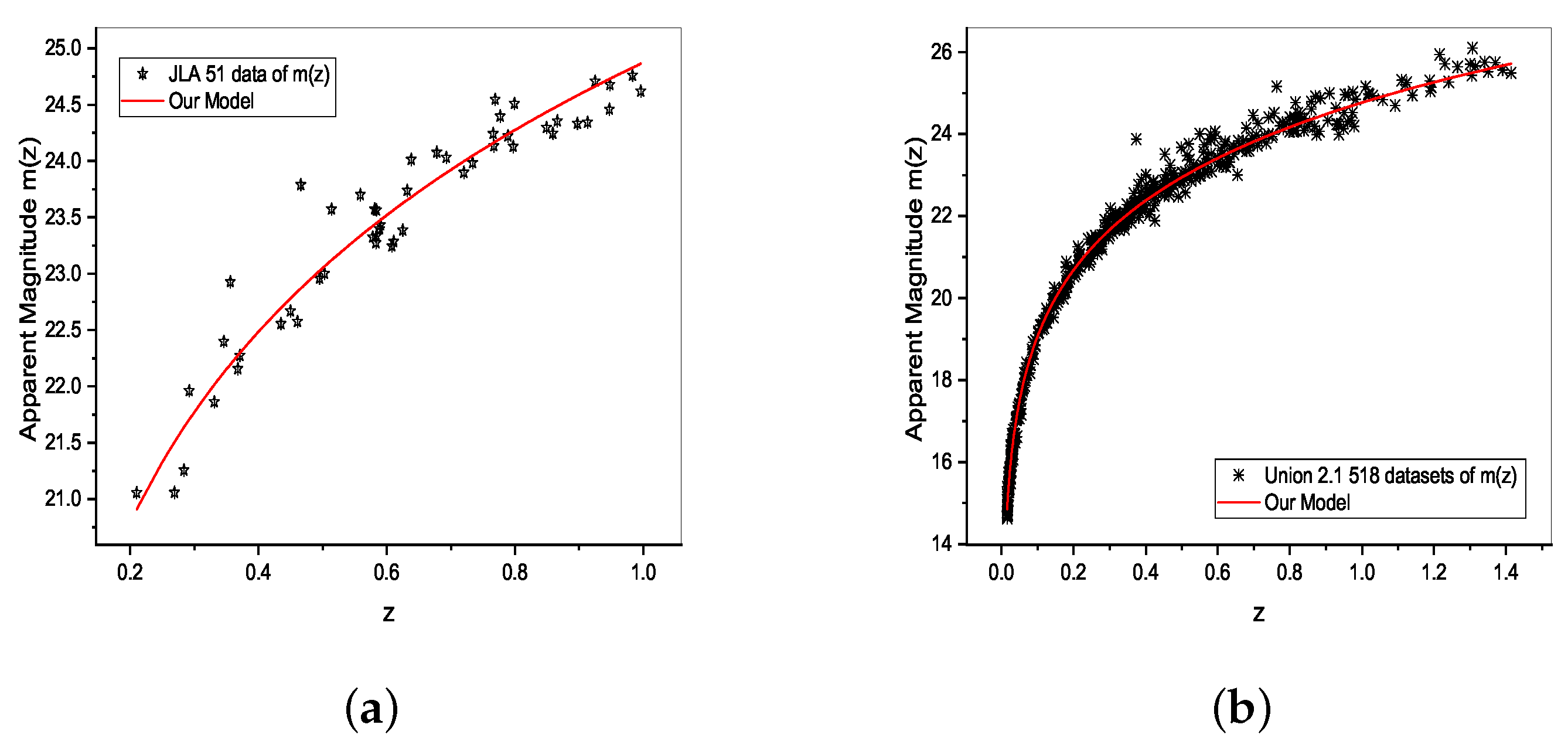
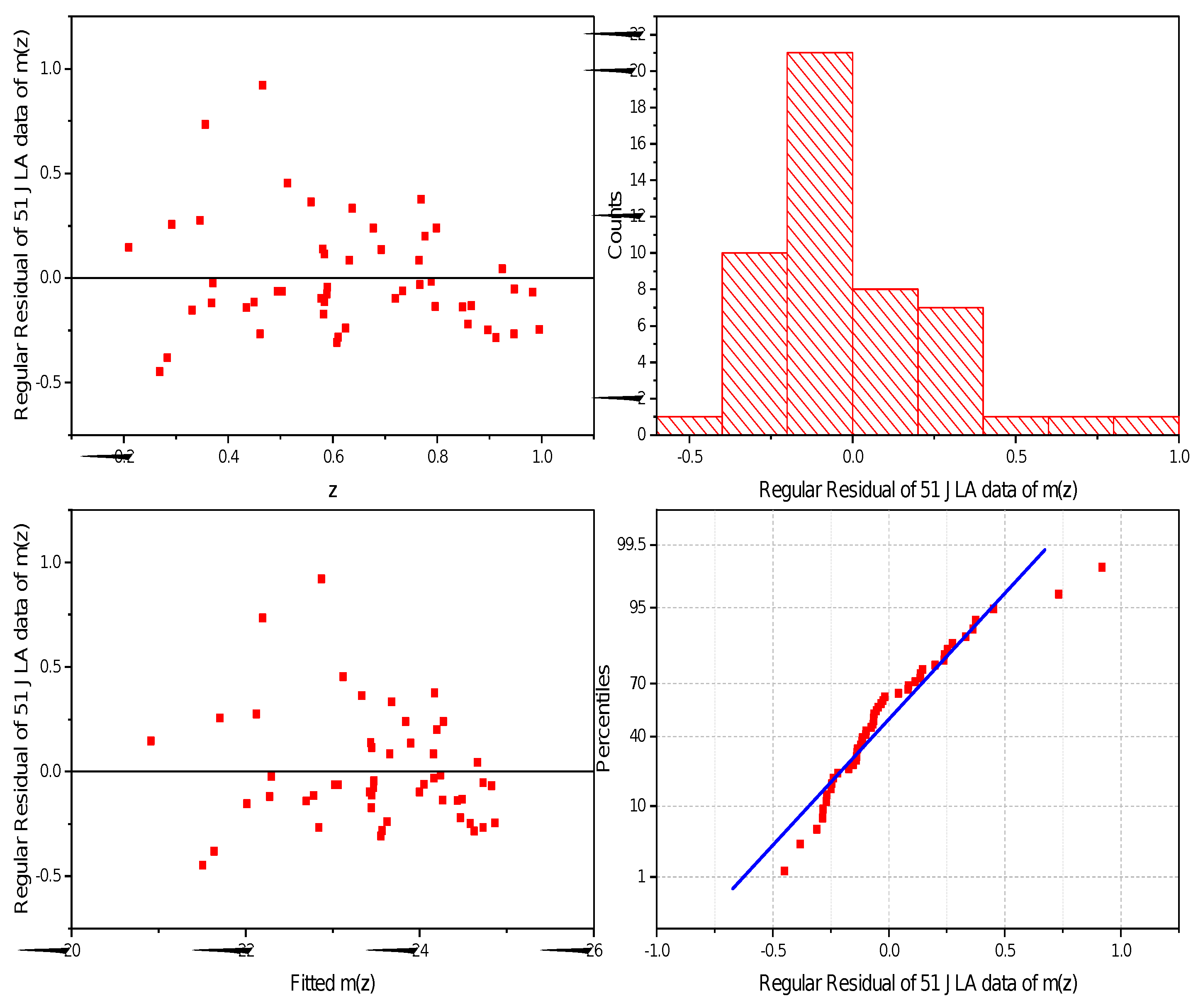
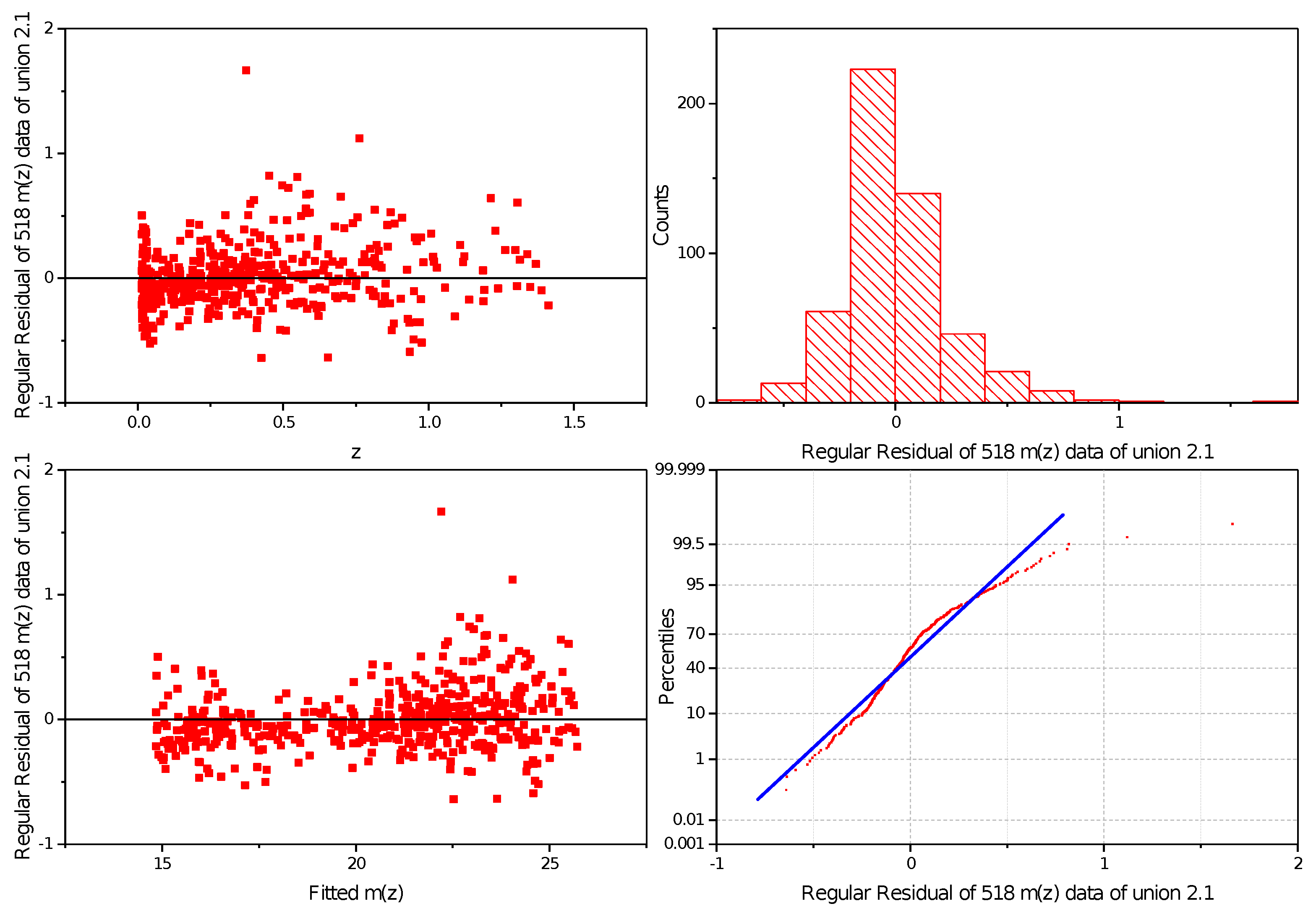

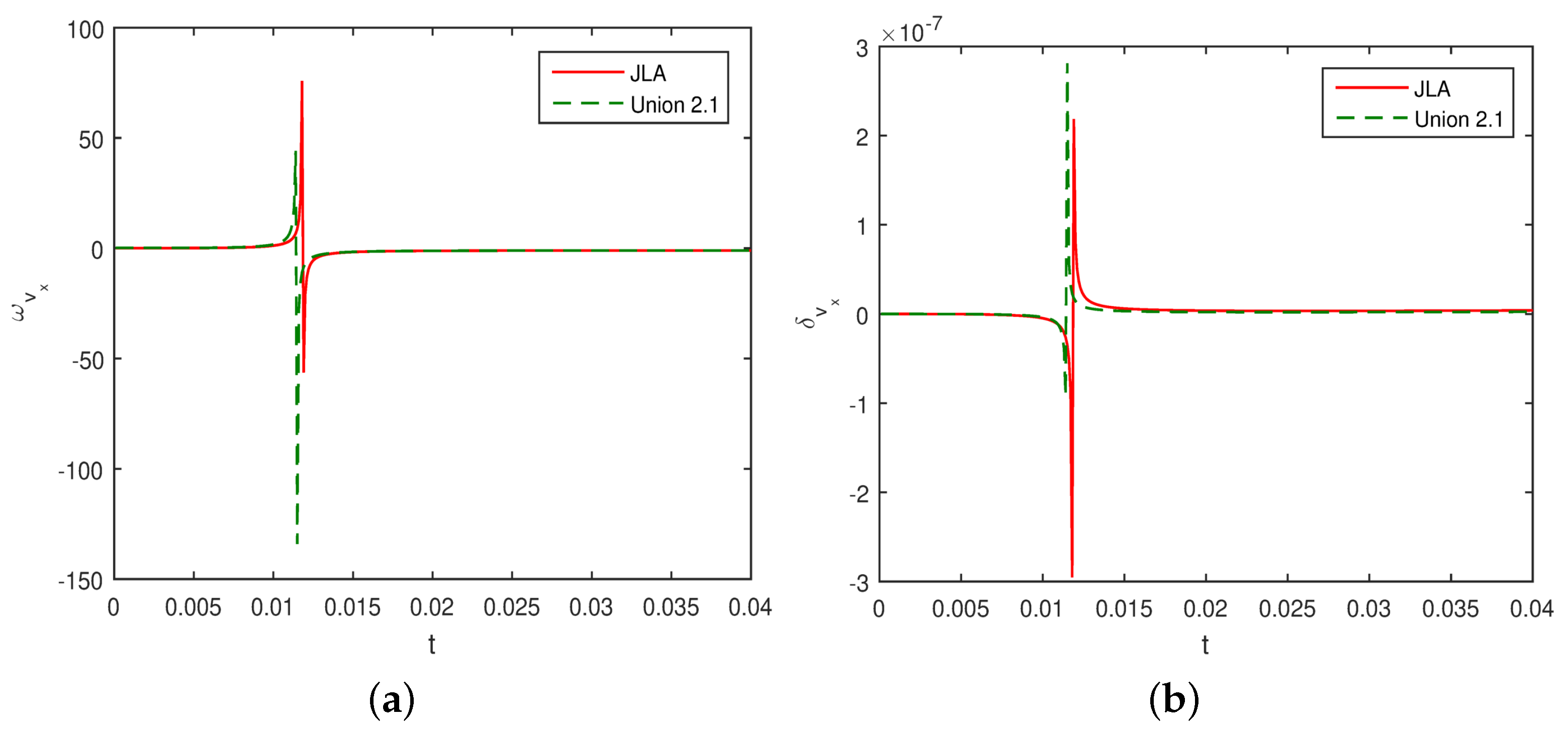
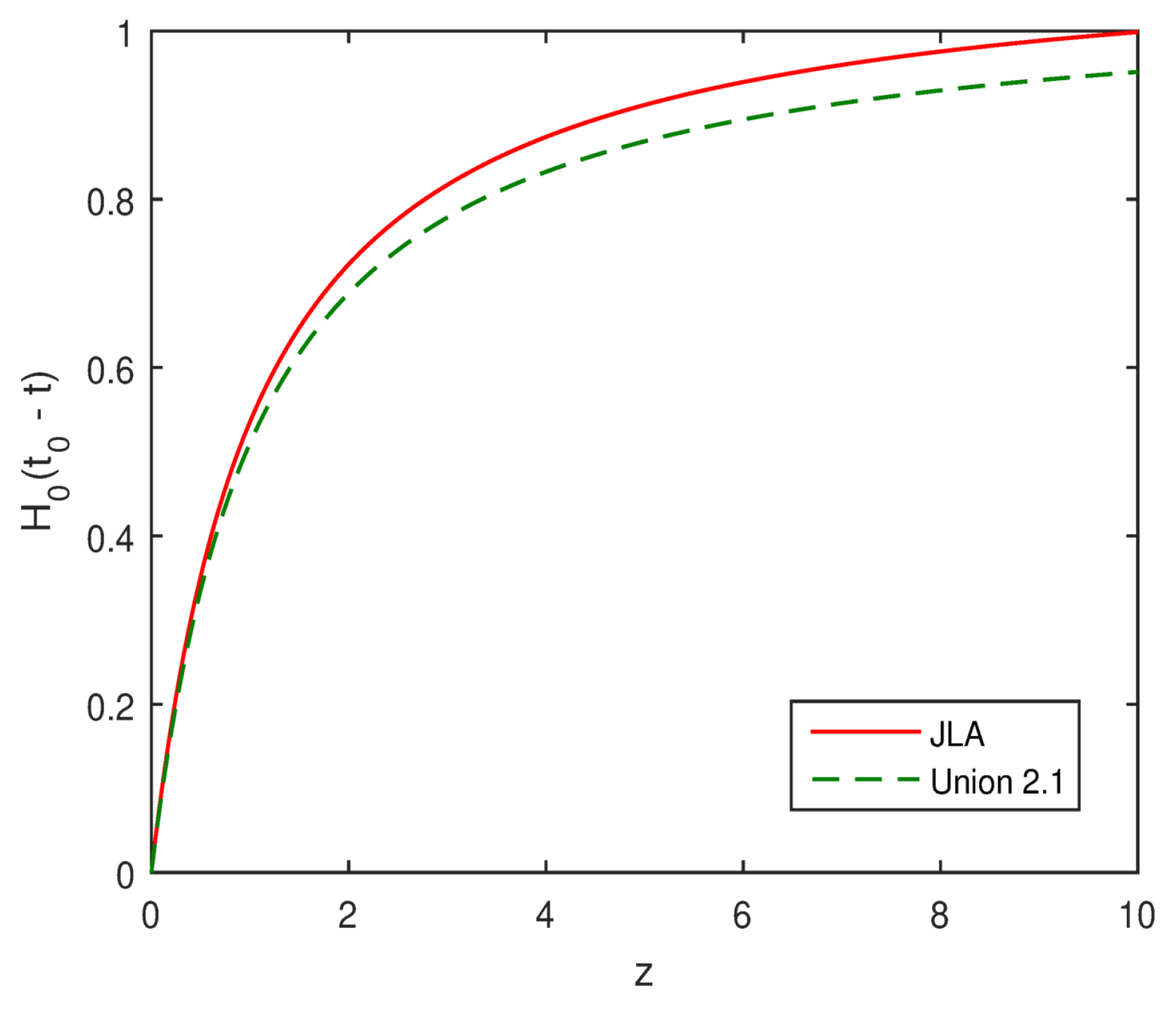
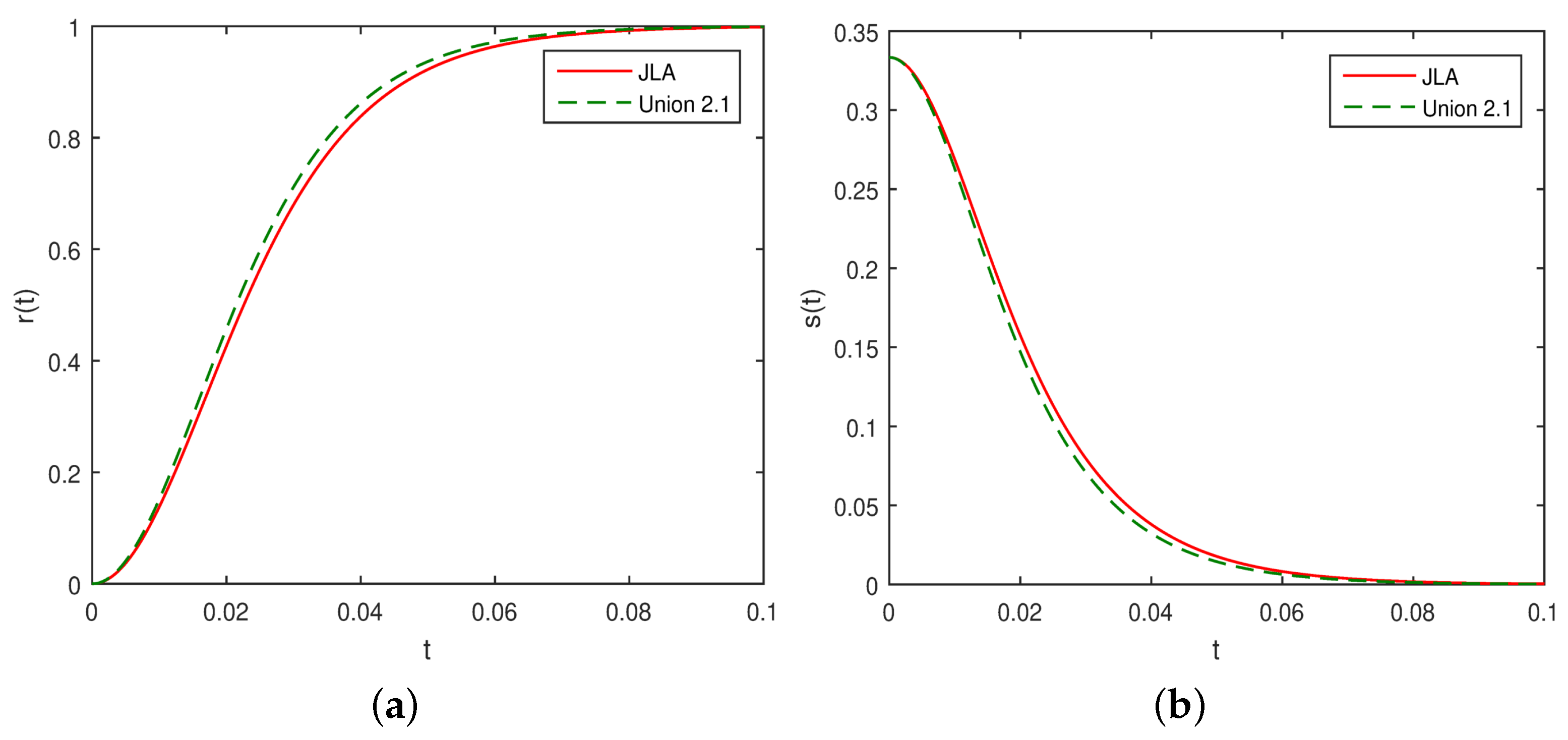
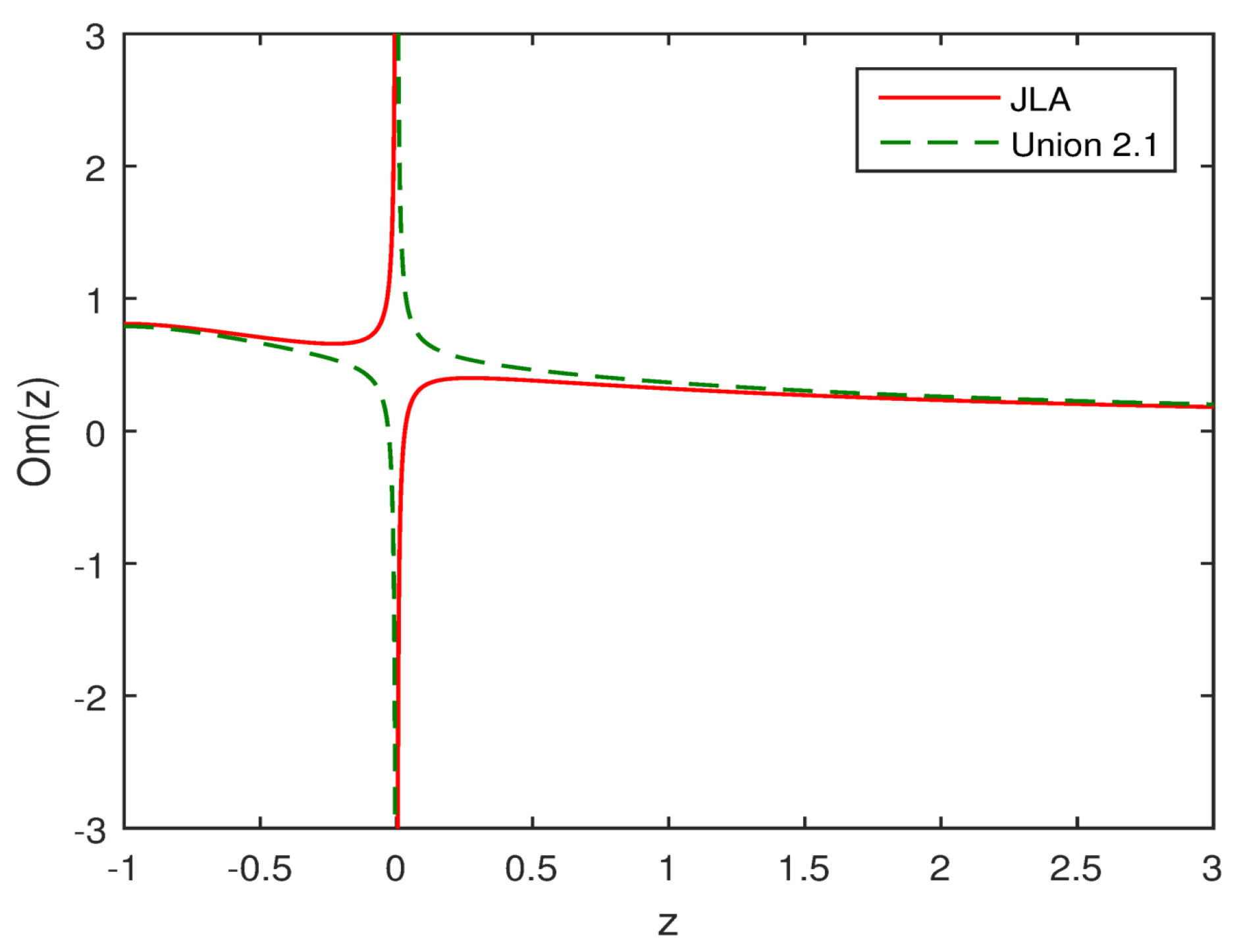
| Data | m | |||||
|---|---|---|---|---|---|---|
| JLA | 2 | 0.99998 | 70.00056 | 0.07228 | 0.92346 | |
| Union 2.1 | 2 | 0.97455 | 70.00000 | 0.05915 | 0.99404 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradhan, A.; Dixit, A.; Maurya, D.C. Quintessence Behavior of an Anisotropic Bulk Viscous Cosmological Model in Modified f(Q)-Gravity. Symmetry 2022, 14, 2630. https://doi.org/10.3390/sym14122630
Pradhan A, Dixit A, Maurya DC. Quintessence Behavior of an Anisotropic Bulk Viscous Cosmological Model in Modified f(Q)-Gravity. Symmetry. 2022; 14(12):2630. https://doi.org/10.3390/sym14122630
Chicago/Turabian StylePradhan, Anirudh, Archana Dixit, and Dinesh Chandra Maurya. 2022. "Quintessence Behavior of an Anisotropic Bulk Viscous Cosmological Model in Modified f(Q)-Gravity" Symmetry 14, no. 12: 2630. https://doi.org/10.3390/sym14122630
APA StylePradhan, A., Dixit, A., & Maurya, D. C. (2022). Quintessence Behavior of an Anisotropic Bulk Viscous Cosmological Model in Modified f(Q)-Gravity. Symmetry, 14(12), 2630. https://doi.org/10.3390/sym14122630








