Exploitation of Energy Optimal and Near-Optimal Control for Traction Drives with AC Motors

Abstract

The main contribution of this paper is the verification of a new train control system applied to the drive with a.c. motors that is energy near optimal with respect to electrical and mechanical energy minimization. All simulations are related to the one traction motor yielding its best exploitation. Load torque treated as a state variable consists of constant, linear, and quadratic components as a function of rotor speed. The required performance of the energy-saving control is rendered straightforward using precomputed energy optimal state variables or a prediction of losses for a symmetrical trapezoidal speed profile as the second alternative. An energy-saving reference position generator provides the state variables, which are faithfully followed by a feedback control based on field orientation, which is completed with a matched zero dynamic lag pre-compensator yielding prescribed closed-loop dynamics. Simulation results mutually compared confirm the capability of an overall drive control system to follow generated state variables for two different service conditions and the possibility of energy savings.

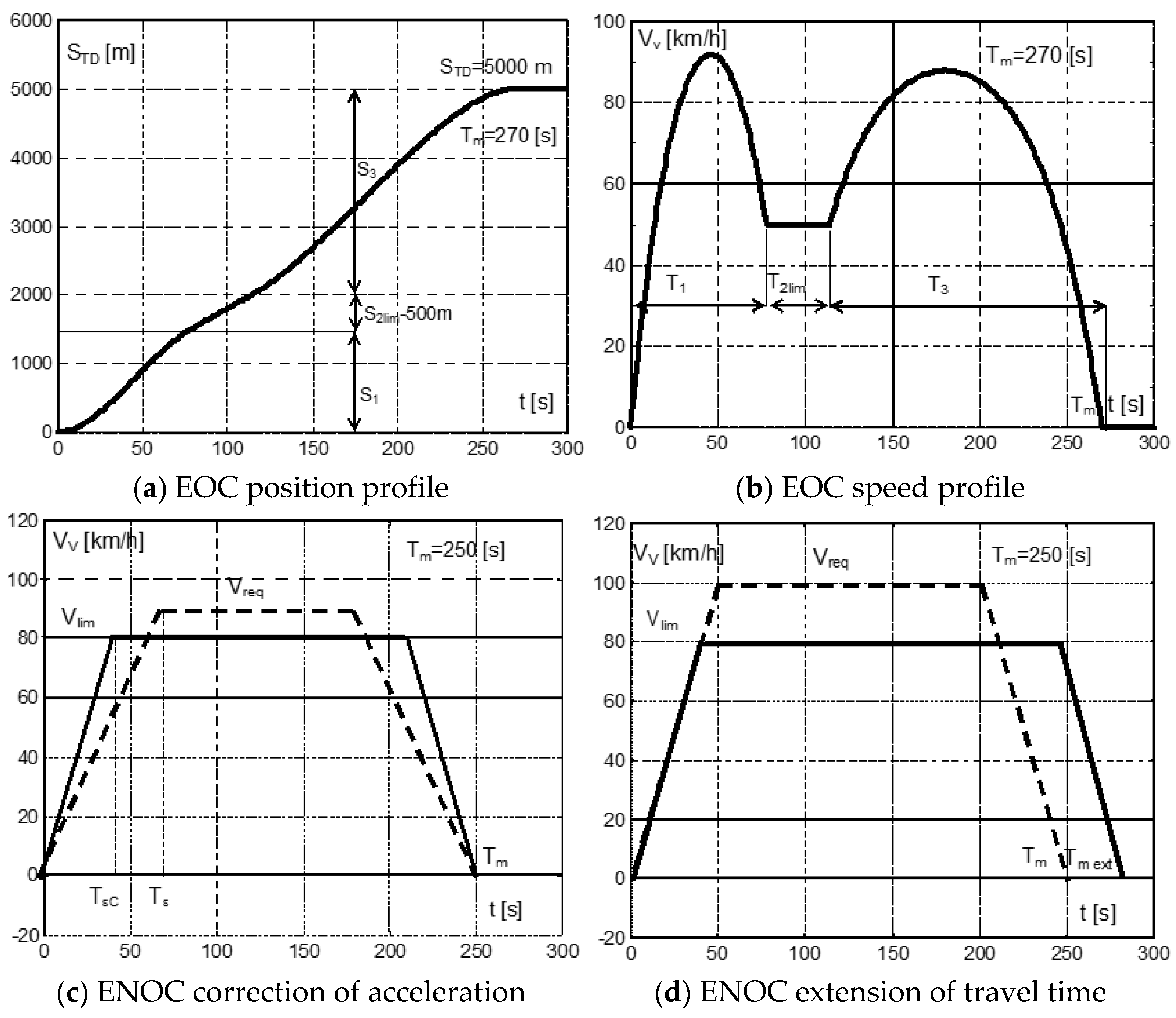
1. Introduction

The driving strategy of an electric traction vehicle has significant influence on energy consumption. In the era of vehicle control via varying resistances, the maximum acceleration and maximum track speed control strategies were widely used. This technique enabled reaching the track speed limit in the shortest amount of time and, at the same time, eliminating energy dissipation in resistors. The efficiency of such control was very low, and during the acceleration mode, nearly 50% of consumed energy was dissipated in resistors.

Substantial steps ahead brought the implementation of semiconductor converters and the construction of traction vehicles with a.c. motors (induction and synchronous). In this stage, the maximum acceleration and speed control strategies were implemented, and it was also the starting point of the development of energy-efficient train control (EETC), which can significantly reduce consumed energy and, in this way, contribute to the improvement of our environment and to the reduction of operating costs.

Nowadays, increased environmental concerns and rising energy prices require energy-efficient performance also in transportation systems with the improvement of railway [1] and road [2] vehicle control. This paper presents two different EETC strategies, which respect traction motor (TM) electrical and mechanical loss minimization for track without and with speed limit. The first strategy, “energy optimal control” (EOC), is based strictly on the mathematical Euler–Lagrange approach [3], while the second one, “energy near-optimal” (ENOC), is based on the precise prediction of TM losses and their minimization [4]. The ENOC approach is characterized by a symmetrical trapezoidal speed profile with a truly finite settling time. The total consumed energy of both strategies is evaluated twice via a sum of individual energy components and via the time integral of the input power and compared mutually to verify energy savings. For control of induction, TM principles of field-oriented control (FOC) are exploited due to a fast dynamical response and the possibility to control torque and field components of the stator current separately [5]. The FOC technique also has a large potential for reducing drive losses significantly.

The individual approaches to energy-efficient train movement differ significantly. Work [6] offers an extensive review (more than 90 references) on EETC and the related train timetabling from the first simple models to the advanced models and algorithms of the last decade, which take into account regenerative braking, track parameters, and speed limits. The optimal train control strategy is usually extended to the seven driving regimes: maximum acceleration, cruising, coasting, and maximum braking completed with (partial or full) regenerative braking during cruising or braking. Pontryagin’s maximum principle (PMP) is frequently used to determine optimal driving regimes, resulting in the optimal EETC under different conditions. The main problem here is to determine the optimal sequence of switching points between the driving regimes. Several models and numerical algorithms were developed to adjust these points for the design of the complete optimal train trajectories between two stops.

A multi-objective model for automatic train operation (ATO) of an urban railway is proposed in [7] by unifying dimensions of different objectives. The proposed model is built on multi-objective decisions with the penalty function based on the analysis of train performance and its operation environment. A genetic algorithm is then used to solve the model and to obtain the optimal speed profile corresponding to energy optimal control. A fuzzy logic controller is implemented to force the drive to follow recommended speed profiles. The proposed model was verified by simulations respecting train operation conditions and environments. Simulations confirmed 16% lower energy expenditures if compared with a real run and the robustness of the designed model against disturbances.

A new, more complex and robust model for finding the power and speed profiles that minimize the consumed energy of short railway journeys, which takes into account nonlinearity emerging in a real setting, is introduced in [8]. Discretization and reformulation of the designed model within the framework of dynamic programming allow for obtaining the optimal action for arbitrary initial points. In the end, the solution was implemented into a train simulator in order to estimate the energy reduction for several real examples of the metro trips. The presented study has shown that the proposed method could be implemented in a real system immediately, whereas more research is required in order to solve various real-life problems. The simulations confirm reduced energy consumption in the range of 8–25%.

The minimization of consumed traction energy based on PMP offers [9]. For a simplified train model, which has no speed limit, gradient, and regenerative braking, five subsequent control modes are supposed: maximum traction, partial traction, coasting, partial braking, and maximum braking. To form a complete speed trajectory the independent sections and costate variables are linked together using linking principles. As a next step, the development of a generally valid algorithm for solving differential equations of costate variables and complete speed trajectory is anticipated.

An online energy-saving driving strategy for a single metro train is proposed in [10]. For this purpose, a switched-mode dynamical model was developed with the capability of regenerative braking. The optimal train operation regime has fixed four operation modes: maximum traction, speed holding, coasting, and maximum braking. The determination of the optimal switching points is critical, as previously mentioned; therefore, a problem with switching points as the optimization variables has been formulated by exploiting the model predictive control (MPC) utilizing the exterior point penalty function. The proposed online algorithm with the switching times can respond to the disturbances during train operation, as well as to improve the computational efficiency. The feasibility and advantages of the proposed algorithm were verified in several case studies. The online multitrain energy-saving operation based on the switched-mode dynamical systems is considered as future work.

There are various approaches to energy-efficient train speed trajectories: the nonlinear continuous-time model and the continuous-space model of train operations are analyzed in [11], offering an integrated survey in this field (37 references). This work finds that analytical methods struggle to identify solutions under more realistic conditions, but numerical optimization methods do not always guarantee the optimal solution either. There are some available efficient optimal control software packages exploiting nonlinear programming to solve problems with optimal trajectory. Regardless of these solvers, some approximations are always required to formulate an efficient nonlinear train operation model. Therefore, any efficient approach has to compromise between computational accuracy and model efficiency.

The contribution of this paper is the direct application of EOC and ENOC strategies to the movement of a suburban train unit between two stops in a prescribed travel time and a comparison of their energy demands. The design of both control strategies requires knowledge of passive resistances to the train movement (constant, viscous, and quadratic drag component) as well as the average gradient of the route, which is added to the constant train resistance component to avoid necessary switching points. To ensure the same conditions for the comparison of the two control strategies, the regenerative braking is assumed.

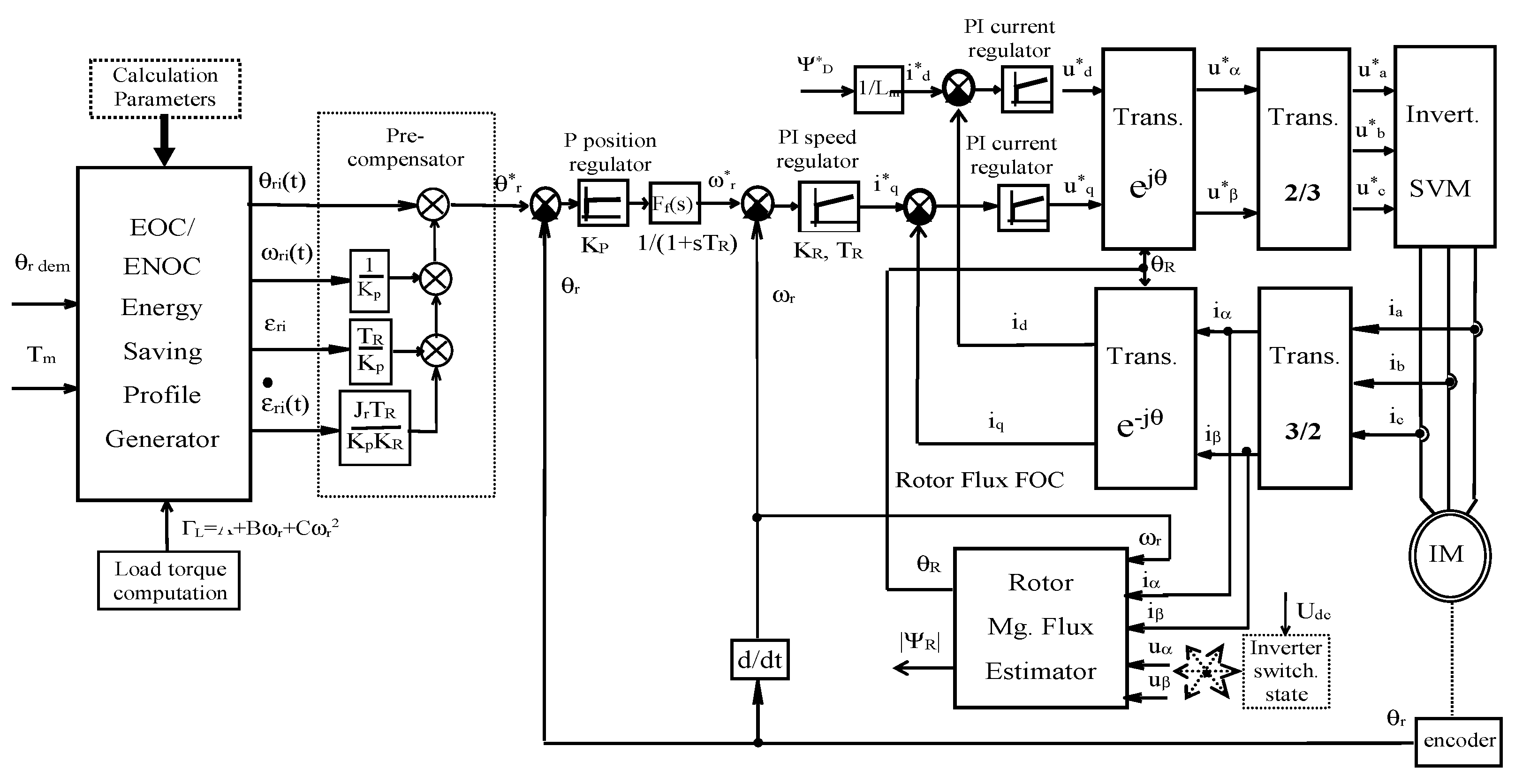
An overall math description of the control system for optimization then consists of four differential equations respecting vehicle dynamic, induction motor position, speed, and current dynamic [12]. Resulting speed profiles for routes without speed limits then consist of acceleration, cruising, and braking modes. The applications of the derived speed profiles to the routes with speed limits are also shown. The designed control structure for verification shown in Figure 1 consists of an EOC or ENOC energy-saving profile generator (position, speed, acceleration, and jerk) accomplished with pre-compensator and position controlled induction TM capable of precise tracking of generated state variables.

2. Theoretical Background

In previous work [13] (available as Open Access Journal) the background of EOC and ENOC of rotational drives was described in detail, therefore, the only parts necessary for implementation of these control strategies are listed further.

2.1. Energy Optimal Control

Energy optimal control is based on Euler–Lagrange optimization principles. The dynamical system for the optimization of a.c. drives consists of the differential equations for rotor position, θ_r; rotor speed, ω_r; and electric torque, γ_e containing a.c. TM current dynamic in which J_r is the moment of inertia on the shaft. Load torque, γ_L, is treated as a state variable. Therefore, the system is completed with its derivative, which is the function of the rotor speed having constant, A; linear, B; and quadratic, C, components, ${\mathsf{\gamma }}_{\mathrm{L}}=\hspace{0.17em}\mathrm{A}\hspace{0.17em}+\hspace{0.17em}\mathrm{B}{\mathsf{\omega }}_{\mathrm{r}}\hspace{0.17em}+\hspace{0.17em}\mathrm{C}{\mathsf{\omega }}_{\mathrm{r}}^2$. A derivative of load torque has the form: $\hspace{0.17em}\mathrm{d}{\mathsf{\gamma }}_{\mathrm{L}}/\mathrm{d}\mathrm{t}=\hspace{0.17em}\left(\mathrm{B}+\hspace{0.17em}2\mathrm{C}{\mathsf{\omega }}_{\mathrm{r}}\right)\hspace{0.17em}\mathrm{d}{\mathsf{\omega }}_{\mathrm{r}}/\mathrm{d}\mathrm{t}$ and

$$\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left[\begin{array}{c}{\mathsf{\theta }}_{\mathrm{r}}\\ {\mathsf{\omega }}_{\mathrm{r}}\\ {\mathsf{\gamma }}_{\mathrm{e}}\\ {\mathsf{\gamma }}_{\mathrm{L}}\end{array}\right]\hspace{0.17em}=\hspace{0.17em}\left[\begin{array}{cccc}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& 1& 0& 0\\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& 0& 1/{\mathrm{J}}_{\mathrm{r}}& -1/{\mathrm{J}}_{\mathrm{r}}\\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& -{\mathrm{k}}_{\mathsf{\omega }}& -{\mathrm{k}}_{\mathsf{\gamma }}& 0\\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& 0& \left(\mathrm{B}+2\mathrm{C}{\mathsf{\omega }}_{\mathrm{r}}\right)/{\mathrm{J}}_{\mathrm{r}}& \hspace{0.17em}\hspace{0.17em}-\hspace{0.17em}\left(\mathrm{B}+2\mathrm{C}{\mathsf{\omega }}_{\mathrm{r}}\right)/{\mathrm{J}}_{\mathrm{r}}\end{array}\right]\hspace{0.17em}\left[\begin{array}{c}{\mathsf{\theta }}_{\mathrm{r}}\\ {\mathsf{\omega }}_{\mathrm{r}}\\ {\mathsf{\gamma }}_{\mathrm{e}}\\ {\mathsf{\gamma }}_{\mathrm{L}}\end{array}\right]\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{c}0\\ 0\\ {\mathrm{k}}_{\mathrm{U}}\\ 0\end{array}\right]\hspace{0.17em}{\mathrm{u}}_{\mathrm{q}},$$

(1)

$$\hspace{0.17em}\hspace{0.17em}\mathrm{y}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{cccc}1& 0& 0& 0\end{array}\right]\hspace{0.17em}{\left[\begin{array}{cccc}{\mathsf{\theta }}_{\mathrm{r}}& {\mathsf{\omega }}_{\mathrm{r}}& {\mathsf{\gamma }}_{\mathrm{e}}& {\mathsf{\gamma }}_{\mathrm{L}}\end{array}\right]}^{\mathrm{T}}.$$

(2)

Constants of (1) for PMSM are defined as: ${\mathrm{k}}_{\mathsf{\gamma }}={\mathrm{R}}_{\mathrm{s}}/{\mathrm{L}}_{\mathrm{q}}$, ${\mathrm{k}}_{\mathsf{\omega }}=\mathrm{p}{\mathrm{k}}_{\mathrm{t}}{\mathsf{\Psi }}_{\mathrm{P}\mathrm{M}}/{\mathrm{L}}_{\mathrm{q}}$, and ${\mathrm{k}}_{\mathrm{U}}={\mathrm{k}}_{\mathrm{t}}/{\mathrm{L}}_{\mathrm{q}}$. The PMSM torque constant is ${\mathrm{k}}_{\mathrm{t}}=\mathrm{c}{\mathsf{\Psi }}_{\mathrm{P}\mathrm{M}}$, where $\mathrm{c}=3\mathrm{p}/2$ and ${\mathsf{\Psi }}_{\mathrm{PM}}$ are permanent magnet flux. For IM, the following constants are defined as: ${\mathrm{R}}_{\mathrm{c}}={\mathrm{R}}_{\mathrm{s}}+{\mathrm{R}}_{\mathrm{r}}{\left({\mathrm{L}}_{\mathrm{m}}/{\mathrm{L}}_{\mathrm{r}}\right)}^2$,${\mathrm{k}}_{\mathsf{\gamma }}={\mathrm{R}}_{\mathrm{c}}/\mathsf{\sigma }{\mathrm{L}}_{\mathrm{s}}$ ${\mathrm{k}}_{\mathsf{\omega }}=\mathrm{p}{\mathrm{k}}_{\mathrm{t}}{\mathsf{\Psi }}_{\mathrm{D}}\left({\mathrm{c}}_2/\mathsf{\sigma }{\mathrm{L}}_{\mathrm{s}}+1/{\mathrm{L}}_{\mathrm{m}}\right)$, and ${\mathrm{k}}_{\mathrm{U}}={\mathrm{k}}_{\mathrm{t}}/\mathsf{\sigma }{\mathrm{L}}_{\mathrm{s}}$. The IM torque constant, k_t = 3p${\mathsf{\Psi }}_{\mathrm{D}}$L_m/L_r, where for the vector control, ${\mathsf{\Psi }}_{\mathrm{D}}=\hspace{0.17em}{\mathrm{L}}_{\mathrm{m}}{\mathrm{i}}_{\mathrm{d}}$. The excitation voltage of both motors in the q axes is u_q. For the simplification of calculations further, a new constant, k_m, was defined as ${\mathrm{k}}_{\mathrm{m}}={\mathrm{k}}_{\mathrm{t}}^2/2{\mathrm{R}}_{\mathrm{c}}$. For details, see the Appendix A.

If Euler–Lagrange calculus is applied to the system, (1) then a highly nonlinear system (3) is obtained. This system consists of two derivatives of Lagrange coefficients, λ_1,2, and a derivative of rotor speed and rotor position can be solved only numerically:

$$\frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}\left[\begin{array}{c}{\mathsf{\lambda }}_1\\ {\mathsf{\lambda }}_2\\ {\mathsf{\omega }}_{\mathrm{r}}\\ {\mathsf{\theta }}_{\mathrm{r}}\end{array}\right]\hspace{0.17em}=\hspace{0.17em}\left[\begin{array}{cccc}\mathrm{B}/{\mathrm{J}}_{\mathrm{r}}& -1/{\mathrm{J}}_{\mathrm{r}}& 2\mathrm{B}/{\mathrm{J}}_{\mathrm{r}}& \hspace{0.17em}\hspace{0.17em}0\\ 0& 0& 0& \hspace{0.17em}\hspace{0.17em}0\\ {\mathrm{k}}_{\mathrm{m}}/{\mathrm{J}}_{\mathrm{r}}& 0& -\mathrm{B}/{\mathrm{J}}_{\mathrm{r}}& \hspace{0.17em}\hspace{0.17em}0\\ 0& 0& 1& \hspace{0.17em}\hspace{0.17em}0\end{array}\right]\hspace{0.17em}\left[\begin{array}{c}{\mathsf{\lambda }}_1\\ {\mathsf{\lambda }}_2\\ {\mathsf{\omega }}_{\mathrm{r}}\\ {\mathsf{\theta }}_{\mathrm{r}}\end{array}\right]\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{c}1/{\mathrm{J}}_{\mathrm{r}}\\ 0\\ -1/{\mathrm{J}}_{\mathrm{r}}\\ 0\end{array}\right]\mathrm{A}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}\left[\begin{array}{c}2\mathrm{C}{\mathsf{\lambda }}_1\\ 0\\ 0\\ 0\end{array}\right]{\mathsf{\omega }}_{\mathrm{r}}\hspace{0.17em}+\hspace{0.17em}\left[\begin{array}{c}3\mathrm{C}/{\mathrm{J}}_{\mathrm{r}}\\ 0\\ -\mathrm{C}/{\mathrm{J}}_{\mathrm{r}}\\ 0\end{array}\right]{\mathsf{\omega }}_{\mathrm{r}}^2.$$

(3)

A derived system (3) has to satisfy boundary conditions, which are as follows:

  for t = t₀         ω_r(t₀) = ω₀
                       θ_r(t₀) = θ_r0,
        for t = T_m         ω_r(T_m) = ω_m
                           ωθ_r(T_m) = θ_rd.

(4)

The solution of (3) for boundary conditions (4) offers a Matlab function, bvp4c.m (boundary value problem). Providing the points of approximation for an expected solution, this solver creates a mesh and determines a numerical solution by solving the differential equations resulting from the boundary conditions and the collocation conditions imposed on all subintervals. Subsequently, the solver estimates the error of the computed solution on each subinterval. If the solution does not satisfy the tolerance criteria, then the solver adapts the mesh and repeats the process. Resulting functions of acceleration, speed, and position then satisfy the minimum energy consumption.

2.2. Near-Optimal Control

The energy near-optimal approach described in [13] is based on the detailed prediction of copper and friction losses while exploiting the symmetrical trapezoidal profile of rotor speed. The total drive energy including predictable drive losses is then defined as:

$${\mathrm{W}}_{\mathrm{T}}\hspace{0.17em}=\hspace{0.17em}\frac{3}{2}{\displaystyle \underset{0}{\overset{{\mathrm{T}}_{\mathrm{m}}}{\int }}{\mathrm{R}}_{\mathrm{c}}{\mathrm{i}}_{\mathrm{q}}^2}\mathrm{d}\mathrm{t}\hspace{0.17em}+{\displaystyle \underset{0}{\overset{{\mathrm{T}}_{\mathrm{m}}}{\int }}\left(\mathrm{A}\hspace{0.17em}+\hspace{0.17em}\mathrm{B}\mathsf{\omega }\hspace{0.17em}+\hspace{0.17em}\mathrm{C}{\mathsf{\omega }}^2\right)}\hspace{0.17em}\mathsf{\omega }\mathrm{d}\mathrm{t}.$$

(5)

After integration over the maneuver time, T_m, as a function of the acceleration interval, T_ε, for a demanded position set point, θ_rd, total consumed energy, W_T results in:

$${\mathrm{W}}_{\mathrm{T}}=\hspace{0.17em}\frac{{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}^2}{{\left({\mathrm{T}}_{\mathrm{m}}-{\mathrm{T}}_{\mathsf{\epsilon }}\right)}^2}\hspace{0.17em}[\frac{{\mathrm{k}}_1}{{\mathrm{T}}_{\mathsf{\epsilon }}}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{\mathrm{k}}_{\mathrm{s}}\left({\mathrm{T}}_{\mathrm{m}}-\hspace{0.17em}\frac{4}{3}{\mathrm{T}}_{\mathsf{\epsilon }}\right)\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{\mathrm{k}}_3\frac{{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}^2}{{\left({\mathrm{T}}_{\mathrm{m}}-{\mathrm{T}}_{\mathsf{\epsilon }}\right)}^2}\left({\mathrm{T}}_{\mathrm{m}}-\hspace{0.17em}\frac{8}{5}{\mathrm{T}}_{\mathsf{\epsilon }}\right)\hspace{0.17em}\hspace{0.17em}+\hspace{0.17em}\hspace{0.17em}{\mathrm{k}}_5\frac{{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}^{}}{\left({\mathrm{T}}_{\mathrm{m}}-{\mathrm{T}}_{\mathsf{\epsilon }}\right)}\left({\mathrm{T}}_{\mathrm{m}}-\hspace{0.17em}\frac{3}{2}{\mathrm{T}}_{\mathsf{\epsilon }}\right)\hspace{0.17em}]\hspace{0.17em}\hspace{0.17em}+{\mathrm{k}}_{\mathrm{A}}{\mathrm{T}}_{\mathrm{m}}+\hspace{0.17em}{\mathrm{k}}_6{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}+\hspace{0.17em}\mathrm{A}{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}},$$

(6)

where ${\mathrm{k}}_1=\hspace{0.17em}3{\mathrm{R}}_{\mathrm{c}}\frac{{\mathrm{J}}_{\mathrm{r}}^2}{{\left(\mathrm{c}\mathsf{\Psi }\right)}^2}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}{\mathrm{k}}_2=\hspace{0.17em}\frac{3}{2}{\mathrm{R}}_{\mathrm{c}}\frac{{\mathrm{A}}^2}{{\left(\mathrm{c}\mathsf{\Psi }\right)}^2}+\mathrm{B},\hspace{0.17em}\hspace{0.17em}{\mathrm{k}}_3=\hspace{0.17em}\frac{3}{2}{\mathrm{R}}_{\mathrm{c}}\frac{{\mathrm{C}}^2}{{\left(\mathrm{c}\mathsf{\Psi }\right)}^2},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathrm{k}}_4=\hspace{0.17em}3{\mathrm{R}}_{\mathrm{c}}\frac{\mathrm{A}\mathrm{C}}{{\left(\mathrm{c}\mathsf{\Psi }\right)}^2},\hspace{0.17em}\hspace{0.17em}{\mathrm{k}}_5=\hspace{0.17em}3{\mathrm{R}}_{\mathrm{c}}\frac{\mathrm{B}\mathrm{C}}{{\left(\mathrm{c}\mathsf{\Psi }\right)}^2}\hspace{0.17em}+\hspace{0.17em}\mathrm{C}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mathrm{k}}_6=\hspace{0.17em}3{\mathrm{R}}_{\mathrm{c}}\frac{\mathrm{A}\mathrm{B}}{{\left(\mathrm{c}\mathsf{\Psi }\right)}^2},\hspace{0.17em}{\mathrm{k}}_{\mathrm{A}}=\hspace{0.17em}\frac{3}{2}{\mathrm{R}}_{\mathrm{c}}\frac{{\mathrm{A}}^2}{{\left(\mathrm{c}\mathsf{\Psi }\right)}^2}$ and ${\mathrm{k}}_{\mathrm{s}}=\hspace{0.17em}{\mathrm{k}}_2\hspace{0.17em}+\hspace{0.17em}{\mathrm{k}}_4$.

An optimized acceleration time, T_εopt, yielding energy demand minimization is determined via the derivative dW_T/dT_ε = 0 as:

$$\begin{array}{l}\frac{-4}{3}{\mathrm{k}}_{\mathrm{s}}{\mathrm{T}}_{\mathsf{\epsilon }}^5+\hspace{0.17em}\left[\frac{10}{3}{\mathrm{k}}_{\mathrm{s}}{\mathrm{T}}_{\mathrm{m}}+\hspace{0.17em}3{\mathrm{k}}_5{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}\right]{\mathrm{T}}_{\mathsf{\epsilon }}^4+\hspace{0.17em}\left[3{\mathrm{k}}_1-\hspace{0.17em}\frac{2}{3}{\mathrm{k}}_{\mathrm{s}}{\mathrm{T}}_{\mathrm{m}}^2-\hspace{0.17em}\frac{9}{2}{\mathrm{k}}_5{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}{\mathrm{T}}_{\mathrm{m}}-\hspace{0.17em}\frac{24}{5}{\mathrm{k}}_3{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}^2\right]{\mathrm{T}}_{\mathsf{\epsilon }}^3\hspace{0.17em}+\hspace{0.17em}\\ +\hspace{0.17em}\left[-7{\mathrm{k}}_1+\hspace{0.17em}\frac{2}{3}{\mathrm{k}}_{\mathrm{s}}{\mathrm{T}}_{\mathrm{m}}^3+\hspace{0.17em}\frac{3}{2}{\mathrm{k}}_5{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}{\mathrm{T}}_{\mathrm{m}}^2+\hspace{0.17em}\hspace{0.17em}\frac{12}{5}{\mathrm{k}}_3{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}^2{\mathrm{T}}_{\mathrm{m}}\right]{\mathrm{T}}_{\mathsf{\epsilon }}^2\hspace{0.17em}+\hspace{0.17em}5{\mathrm{k}}_1{\mathrm{T}}_{\mathrm{m}}^2{\mathrm{T}}_{\mathsf{\epsilon }}\hspace{0.17em}-\hspace{0.17em}\hspace{0.17em}{\mathrm{k}}_1{\mathrm{T}}_{\mathrm{m}}^3\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}0\hspace{0.17em}\end{array}$$

(7)

The Newton formula is used to solve this fifth-order algebraic equation and find the optimized acceleration time, T_εopt. The near-optimal acceleration time, T_εopt, determines also the optimal acceleration, ε_popt, as:

$${\mathsf{\epsilon }}_{\mathrm{p}\hspace{0.17em}\mathrm{o}\mathrm{p}\mathrm{t}}=\hspace{0.17em}\frac{{\mathsf{\theta }}_{\mathrm{r}\mathrm{d}}}{{\mathrm{T}}_{\mathsf{\epsilon }\hspace{0.17em}\mathrm{o}\mathrm{p}\mathrm{t}}\left({\mathrm{T}}_{\mathrm{m}}-{\mathrm{T}}_{\mathsf{\epsilon }\hspace{0.17em}\mathrm{o}\mathrm{p}\mathrm{t}}\right)}$$

(8)

During energy consumption analysis, it was found that the drive’s cruising speed can be kept to the minimum practicable values in the presence of any speed-dependent torque components (linear or quadratic) that decrease their energy expenditures. In contrast, any combination of these two components with constant friction brings the only one unique solution for maneuver time, T_m.

2.3. Energy Optimal and Near-Optimal Control with Speed Limits

The speed limits on the route require special attention. Different solutions are available, but the run of this section without speed limits can help to specify a suitable approach closer. Moreover, energy optimal and near-optimal control algorithms require treatment in different ways, as shown in Figure 2.

For EOC with a known position and length of slow motion, this task can be solved as three boundary conditions of three subsequent intervals. The first one with length, S_l, is from the starting point till the beginning of the interval with the limited speed, which is known. The second interval starts with the beginning of a limited speed motion, V_2lim, and the length of this section, S_2lim. The duration of this section is T_2lim = S_2lim/V_2lim. The third interval starts at the end of slow motion. Its length is S₃ and is known because the third interval finishes in the goal station. If, from the prescribed maneuver time, T_m is a subtracted duration of slow motion, T_2lim, then the sum of intervals T₁ and T₃ is obtained, T_m − T_2lim = (T₁ + T₃). The same is valid for distances, S_td − S_lim = S_l + S₃. Now the problem with proper switching times arises, as the first estimate of the first and third interval durations can be adjusted proportionally to their distances. From known distances, S_l and S₃, it is possible to adjust these intervals as T_l/T₃ = S_l/S₃.

For ENOC, there are also various possible solutions for speed limits on the route. Very small differences between required speed, V_req computed in ESPG, and speed limit V_lim for a given section can be solved by higher acceleration and deceleration with a necessary check of adhesion conditions. The corrected new value of acceleration and deceleration interval, T_εC, is:

$${\mathrm{T}}_{\mathsf{\epsilon }\hspace{0.17em}\hspace{0.17em}\mathrm{C}}=\hspace{0.17em}{\mathrm{T}}_{\mathrm{m}}\hspace{0.17em}-\mathsf{\kappa }\left({\mathrm{T}}_{\mathrm{m}}-\hspace{0.17em}{\mathrm{T}}_{\mathsf{\epsilon }}\right)\text{where}\hspace{0.17em}\mathsf{\kappa }\hspace{0.17em}=\hspace{0.17em}{\mathrm{V}}_{\mathrm{req}}/{\mathrm{V}}_{\lim }.$$

(9)

To keep the same acceleration and speed limit as computed for a run without restrictions, it is necessary to calculate the extension of the originally prescribed travel time, T_m, between two stops. The formula for travel time extension, T_mext, has the form:

$${\mathrm{T}}_{\mathrm{m}\hspace{0.17em}\hspace{0.17em}\mathrm{e}\mathrm{x}\mathrm{t}}=\hspace{0.17em}\hspace{0.17em}\mathsf{\kappa }{\mathrm{T}}_{\mathrm{m}}\hspace{0.17em}-{\mathrm{T}}_{\mathsf{\epsilon }}\left(\mathsf{\kappa }\hspace{0.17em}\hspace{0.17em}-\hspace{0.17em}\hspace{0.17em}\frac{1}{\mathsf{\kappa }}\right)$$

(10)

For a case study of energy-saving control strategies of traction drives, the example of a suburban train unit with parameters listed in Appendix A was chosen. All further computations are related to the one traction motor (TM). The relation between travel distance, S_TD, and TM rotor position, θ_r, is as:

$${\mathsf{\theta }}_{\mathrm{r}}=\hspace{0.17em}\hspace{0.17em}\frac{2\mathrm{u}}{{\mathrm{D}}_{\mathrm{w}\mathrm{a}}}\hspace{0.17em}{\mathrm{S}}_{\mathrm{T}\mathrm{D}}$$

(11)

where D_wa is the average diameter of the driving wheel, and u is the gear ratio between the rotor of TM and the driving wheel. The following relation determines the TM rotational speed, ω_r, as a function of vehicle velocity, V_V, as:

$${\mathsf{\omega }}_{\mathrm{r}}\hspace{0.17em}=\hspace{0.17em}\frac{\mathrm{u}}{1.8\hspace{0.17em}{\mathrm{D}}_{\mathrm{w}\mathrm{a}}}{\mathrm{V}}_{\mathrm{V}}$$

(12)

Constant, linear, and quadratic traction resistances to unit movement as a function of vehicle speed are defined as:

$${\mathrm{p}}_0\hspace{0.17em}=\hspace{0.17em}\mathrm{A}+\hspace{0.17em}\mathrm{B}{\mathrm{V}}_{\mathrm{V}}\hspace{0.17em}+\hspace{0.17em}\mathrm{C}{\mathrm{V}}_{\mathrm{V}}^2$$

(13)

and a suburban unit has the form: ${\mathrm{p}}_0\hspace{0.17em}=\hspace{0.17em}3.1+\hspace{0.17em}0.025{\mathrm{V}}_{\mathrm{V}}\hspace{0.17em}+0.00038{\mathrm{V}}_{\mathrm{V}}^2$. The relation between TM torque, Γ_TM, and unit traction force, F_t, is:

$${\mathsf{\Gamma }}_{\mathrm{T}\mathrm{M}}\hspace{0.17em}=\hspace{0.17em}\frac{{\mathrm{D}}_{\mathrm{w}\mathrm{a}}}{2\mathrm{m}\mathrm{u}}{\mathrm{F}}_{\mathrm{t}}$$

(14)

where m is the number of the train unit TMs. Train movement is described by differential equation:

$${\mathrm{m}}_{\mathrm{t}}\hspace{0.17em}\frac{{\mathrm{d}}^2{\mathrm{S}}_{\mathrm{T}\mathrm{D}}}{\mathrm{d}{\mathrm{t}}^2}\hspace{0.17em}=\hspace{0.17em}{\mathrm{F}}_{\mathrm{t}}\left(\mathrm{t},\mathrm{V}\right)\hspace{0.17em}-\hspace{0.17em}{\mathrm{F}}_{\mathrm{p}}\left(\mathrm{V}\right)\hspace{0.17em}-\hspace{0.17em}{\mathrm{F}}_{\mathrm{s}}\left({\mathrm{S}}_{\mathrm{T}\mathrm{D}}\right)-\hspace{0.17em}{\mathrm{F}}_{\mathrm{b}}\left(\mathrm{V}\right),$$

(15)

where m_t is the total mass of the train, S_TD is the travel distance between two stops, F_t is the traction force, F_p is the force covering vehicle resistance, F_s is the force covering slope resistance, and F_b is the braking force.

3. Verification of Energy Near-Optimal Control Strategies

The described train control strategies for the minimization of energy expenditures were verified by simulation for travel distance, S_TD = 5000 m, without and with speed limit when, for the route section between 1500 and 2000 m (S_lim = 500 m), the track speed was limited to 50 km/h. The strategies were implemented for a suburban traction unit with the maximum speed V_max = 100 km/h and two induction TMs with the total nominal power P_T = 1440 kW parameters, which are listed in Appendix A. The position control system shown in Figure 1 was used, including the FOC of TM.

The time functions of control variables (position, speed, current torque component, and energy consumption) during the run of a train unit without speed limit (in red) and with speed limit (in blue) for EOC and ENOC are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 for two various maneuver times, T_m. The profiles of the torque component and energy consumption are related to a single TM.

The train unit and TM control variables for an EOC run of a travel distance, S_TD = 5000 m, prescribed in a travel time, T_m = 270 s, are shown in Figure 3.

Figure 3a confirms that a required travel distance, S_TD, was reached by both EOC runs at a prescribed maneuver time, T_m = 270 s. The maximum speed for a journey without speed limit was V_max1 = 86.06 km/h, while a run with speed limit requires a higher maximum speed, V_max2 = 91.84 km/h, to keep the prescribed travel time.

Peaks of TM currents were I_q1 = 371.73 A and I_q2 = 648.64 A in motoring mode and I_q1 = 352.33 A and I_q2 = 403.09 A in braking mode. It means that the peak of a current for the run with speed limit was 1.74 higher in motoring mode and 1.14 higher in braking mode.

The measured energy consumptions of TM for an EOC run without speed limit were W_t1 = 2358.1 Wh and W_t2 = 2485.3 Wh for EOC with speed limit. It means that speed limit and the following acceleration to a new maximum speed, V_max2, is demanding 5.39% more energy (127.22 Wh).

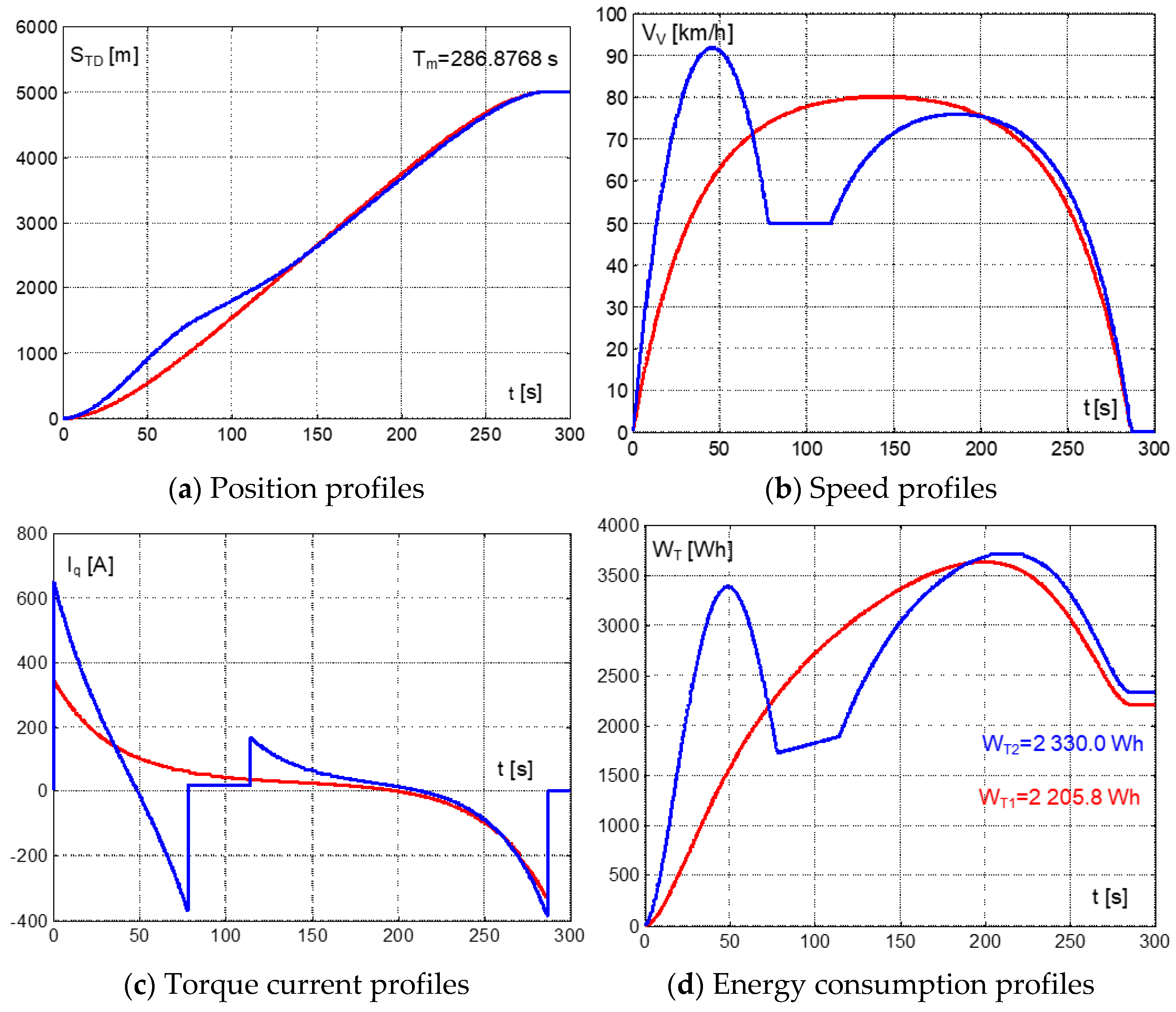
To compare results, the EOC and ENOC (related to Figure 7) travel time of EOC with speed limit was extended from the original T_m1 = 270 s to T_m2 = 286.876 s. Time profiles of this run are shown in Figure 4.

Figure 4a confirms that a required travel distance, S_TD = 5000 m, was reached at the prescribed maneuver times T_m1 and T_m2 by both runs. Without changes in boundary conditions, the maximums of speed for a journey without limit stood the same, V_max1 = 86.06 km/h and V_max2 = 91.84 km/h. There are no differences in motoring and braking currents for a run without speed limits (I_q1 = 371.73 A and I_q2 = 648.64 A), while for a run with speed limit, the peak of motoring current has the same value, I_q2 = 371.73 A, and braking current dropped to I_q2 = 386.85 A.

Interesting is energy consumption because there is no reason for its change during a run without speed limit (W_t1 = 2358.1 Wh), while the consumption of a run with speed limit dropped to W_t2 = 2330.0 Wh and is 1.19% lower (28.1 Wh) as compared with a run without speed limit. This difference in energy consumption can be explained with the lower average speed of the run with speed limit. To verify such influence of the prescribed travel time T_m, one more simulation for common travel time, T_m = 286.8768 s, was run and is shown in Figure 5.

As shown in Figure 5a, both position time profiles confirmed reaching the demanded travel distance 5000 m in the prescribed T_m. Figure 5b shows that there is a change in the time functions of speed, when the maximum speed without speed limit dropped now to V_max1 = 80.12 km/h, while there is no reason for a change of the maximum of speed with speed limit (V_max2 = 91.84 km/h) shown in Figure 4b.

The maximum of the torque current in motoring mode without speed limit dropped to I_q1 = 343.89 A (previously I_q1 = 371.73 A), and in a similar way, the braking torque current in this mode dropped to I_q1 = −334.21 A, while for the run with speed limit, the maximum speed stood the same.

These two runs confirmed that the consumed energy of TM with speed limit stood the same, W_t2 = 2330.0 Wh, while the consumption of a run without speed limit dropped to W_t1 = 2205.8 Wh, which is now 5.33% lower (124.2 Wh) if compared with a speed limit run. A comparison of energy consumptions in Figure 3 and Figure 5 reveals that the extension of travel time for 16.8768 s brought for a run without speed limit 6.46% energy savings (152.3 Wh), and the same is valid also for a run with speed limit with 6.25% energy savings (155.3 Wh).

In a similar way and under the same conditions (without and with speed limit), investigation of ENOC with symmetrical trapezoidal speed profile continued. Results of investigation are summarized in Figure 6, Figure 7 and Figure 8 for two prescribed maneuver times, T_m1 = 270 s and T_m2 = 286.8768 s.

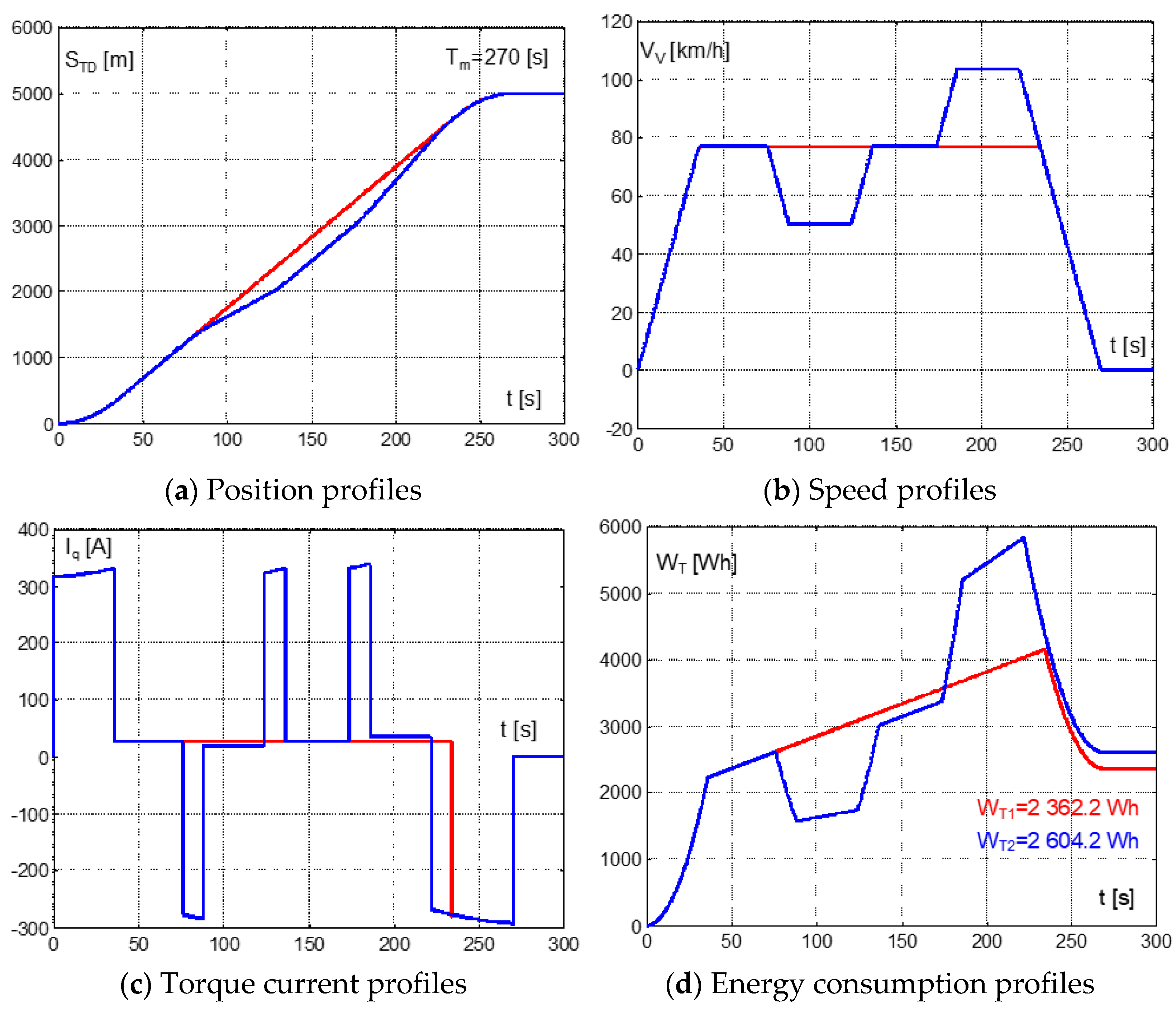
Figure 6a confirms that the required travel distance, S_TD, was reached at the prescribed maneuver time, T_m = 270 s, by both runs. The maximum speed for a journey without speed limit was V_max1 = 76.79 km/h, while the section S_lim = 500 m with the speed limit V_lim = 50 km/h requires a higher maximum speed, V_max2 = 103.55 km/h, to keep the prescribed travel time, T_m.

For motoring mode peaks of TM torque current, components were I_q1 = 330.39 A and I_q2 = 339.41 A, which is 2.75% higher for a run with speed limit. In braking mode, both currents’ minimums reached the same value. I_q1 = I_q2 = 292.9 A. The measured total energy consumptions of TM without speed limit were W_t1 = 2362.2 Wh and W_t2 = 2604.2 Wh with speed limit, which means that the speed limit, and following acceleration to a new speed maximum, V_max2, is 10.24% more energy demanding (242 Wh).

As it is derived in Section 2.3, there is a possibility for ENOC to keep the same acceleration together with the maximum of the cruising speed of both runs (without and with speed limit) under the assumption of travel time extension. Using (11), the required extension is T_ext = 16.8768 s, and a new prescribed travel time for a run with speed limit has the value T_mext = 286.8768 s. ENOC time profiles for an extended travel time of a run with speed limit are shown in Figure 7 for comparison together with results without speed limits of a previous run.

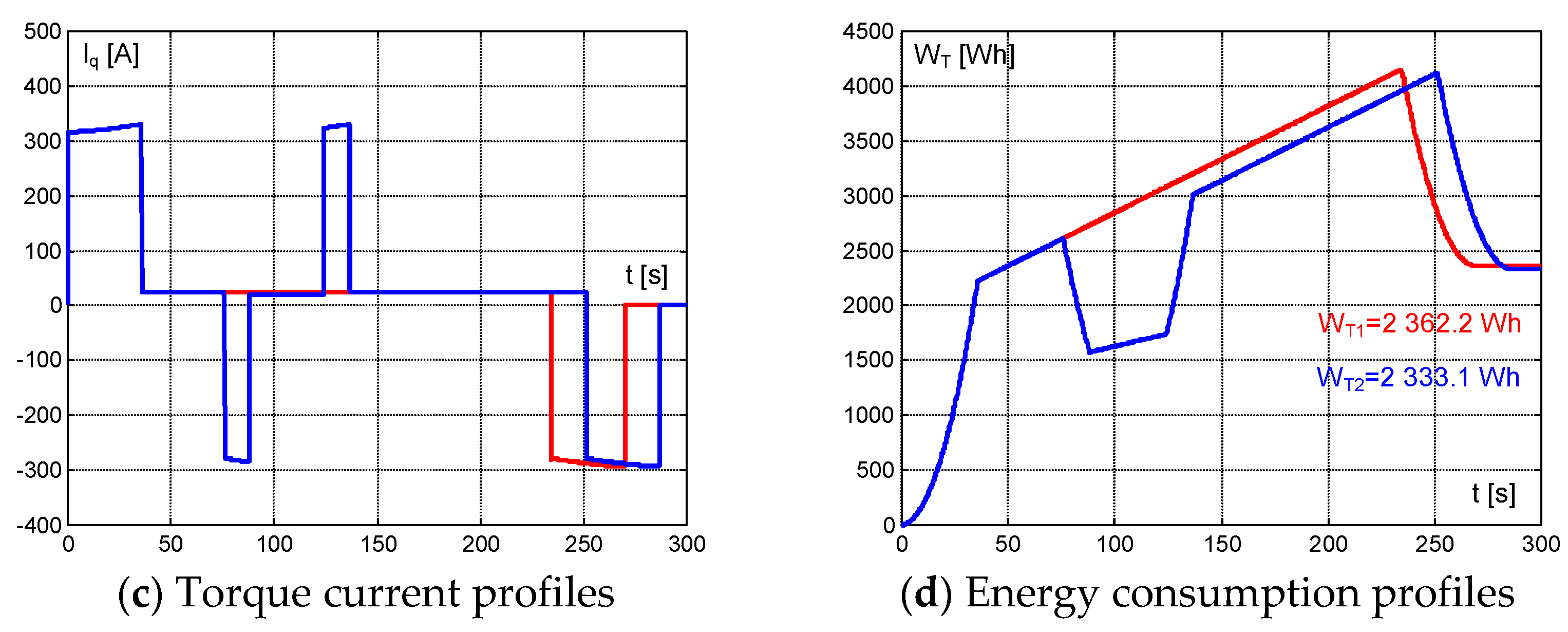
Figure 7a confirms that the required travel distance, S_TD, was reached at the prescribed maneuver times T_m1 = 270 s and T_m2 = 286.8768 s by both runs (without and with speed limit). The cruising speeds, V_max = 76.79 km/h, of both runs are now the same as well as the acceleration times, T_ε = 35.543 s.

The peaks of TM currents were I_q1 = I_q2 = 330.39 A in motoring mode and nearly the same at I_q1 = 293.05 A and I_q2 = 292.95 A in braking mode. The differences between motoring and braking currents are 37.49 and 37.44 A, respectively. There is no change in measured energy consumptions of the run without speed limit, W_t1 = 2362.2 Wh, and the consumption of the run with speed limit dropped to W_t2 = 2333.1 Wh, which is now 1.23% (29.1 Wh) lower than the run without speed limit with the travel time T_m = 270 s. This difference is explained again by the lower average speed of the run with speed limit.

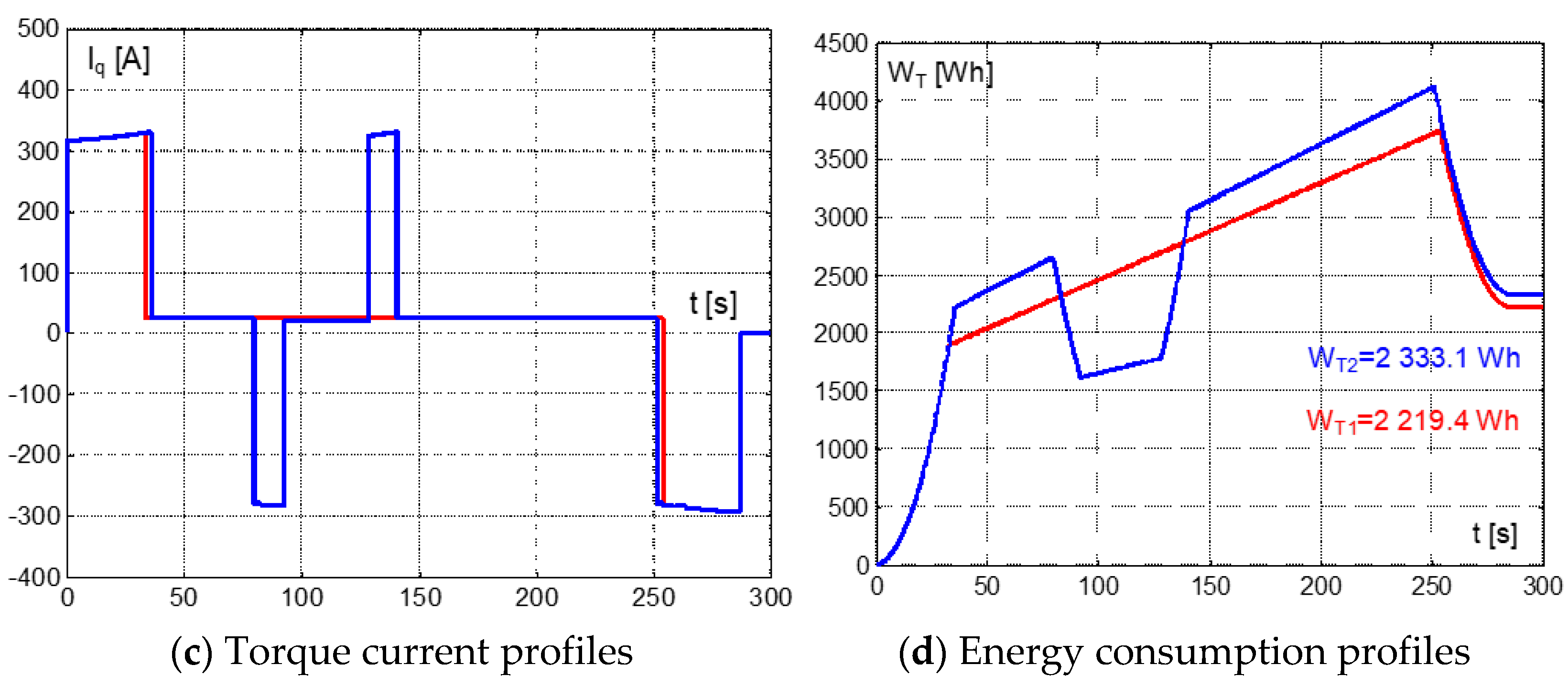
The influence of average speed was verified with a new run (with and without speed limit) for an extended maneuver time, T_m = 269.859 s, the results of which are shown in Figure 8. The simulations confirmed that TM energy consumptions of a run without speed limit dropped to the lowest value, W_t1 = 2219.4 Wh, while the consumption with speed limit stood the same at W_t2 = 2333.1 Wh. This consumption is now 1.31% (113.61 Wh) lower if compared with the speed limit run. Additionally, time functions of speed support the idea of a proportionality of energy consumption to average speed because the cruising speed for the run without speed limit dropped to V_max1 = 70.86 km/h, while the run with speed limit has the same value, V_max2 = 76.79 km/h.

The comparison of energy consumptions in Figure 6 and Figure 8 reveals that the extension of travel time for T_ext = 16.8768 s brought for a run without speed limit energy savings of 6.459% (152.3 Wh). The same is valid also for a run with speed limit when these energy savings are 6.056% (142.8 Wh), both related to the consumption for the travel time T_m = 270 s without speed limit.

From the results presented, it is evident that if EOC and ENOC strategies are compared mutually for an equal maneuver time, T_m, EOC is more efficient in all presented runs. For runs without speed limit and a travel time of T_m = 270 s, EOC brought energy savings of 0.17% (4.1 Wh), and for an extended travel time, T_m = 286.8768 s, due to speed limit, these savings are 0.13% (3.1 Wh). A comparison with a less suitable control strategy (triangular speed profile between two stops) was published in [13], where for a 3000 m run of the same unit, the differences in consumptions were higher (4.4% and 4.2% EOC and ENOC, respectively).

Possible energy savings by the extension of travel time were investigated in a previous work [14]. It is evident that halving a drive’s speed with a viscous torque component directly proportional to angular speed, ω_r, can bring 50% in energy savings due to power proportional to ${\mathsf{\omega }}_{\mathrm{r}}^2$. In a similar way, by halving a drive’s speed with a quadratic torque component directly proportional to the square of angular speed, ${\mathsf{\omega }}_{\mathrm{r}}^2$ can bring 75% of energy savings due to power proportional to ${\mathsf{\omega }}_{\mathrm{r}}^3$.

Mutual coupling between travel time, T_m; acceleration time, T_ε; and their influence on TM total energy consumption for ENOC is shown in Figure 9. As can be seen, the extension of travel time results in lower energy consumption. An example of travel time extension from T_m1 = 600 s to T_m2 = 900 s with T_ε1 = 66.46 s and T_ε = 75.56 s (green and yellow points, red point is valid for T_m = 270 s) can bring energy savings of 192.9 Wh (W_T1 = 1415.7 Wh, W_T2 = 1222.8 Wh). Real energy optimal consumption, W_Tmin = 1052.4 Wh, can be achieved for the travel time T_m = 4100.2 s, which is hardly acceptable for travelers on board as well as a timetable of railway service. Therefore, in general, the maximum speed of the unit should be kept to the minimum practicable values to satisfy passenger demands on the availability, precision, and density of railway service.

4. Conclusions

Two energy-saving control strategies based on Pontryagin’s maximum principle and a detailed prediction and minimization of TM’s losses were applied to a suburban train unit with a.c. induction TMs. The overall control system consists of an energy-saving profile generator, pre-compensator, and position-controlled induction TM respecting FOC principles. This structure eliminates a possible dynamic lag; therefore, precomputed energy optimal and near-optimal reference input functions are followed accurately, and a control system is forced to react as energy near optimal. A possible experimental implementation of proposed strategies in laboratory conditions was presented in [14]. The energy near-optimal control has the advantage of requiring less demanding computations and being easier to implement, resulting in constant acceleration and speed control.

To formulate a suitable model for a design of a train control system, some approximations are always required [6]. A proposed model for current torque component control exploits a constant moment of inertia in spite of its changes with the occupancy of the unit. Additionally, the average gradient of the track is supposed to be between two stops to avoid the computation of corresponding switching points. Similar simplifications of the proposed model are necessary also due to auxiliary drive operations, such as heating in the winter and air-conditioning through the summer. A further extension of this work should include optimization of an IM current magnetic flux component and inclusion of converter losses into a developed model. The results of this work can be applied to train units with automatic torque and speed control for a required travel time longer than the necessary time for time-optimal control.

The total energy expenditures of both control strategies were verified in two ways: the first as a time integral of motor input power, and then the second as the sum of individual energy components covering motor losses and energy delivered to the TM’s shaft. The lowest energy expenditures of an energy optimal control strategy were confirmed for all equivalent operational modes. The observed differences in energy expenditures are only small (0.17% and 0.13% without and with speed limit, respectively) due to the comparison of two energy-saving control strategies.