Stability and Existence of Solutions for a Tripled Problem of Fractional Hybrid Delay Differential Equations

Abstract

The purpose of this paper is to determine the existence of tripled fixed point results for the tripled symmetry system of fractional hybrid delay differential equations. We obtain results which support the existence of at least one solution to our system by applying hybrid fixed point theory. Similar types of stability analysis are presented, including Ulam–Hyers, generalized Ulam–Hyers, Ulam–Hyers–Rassias, and generalized Ulam–Hyers–Rassias. The necessary stipulations for obtaining the solution to our proposed problem are established. Finally, we provide a non-trivial illustrative example to support and enhance our analysis.

1. Introduction

The study of fractional derivatives is very important for many engineering applications as it utilizes differential equations which have a long history of application in many fields, including chemistry, physics and dynamical systems. The significance of fractional-order differential equations is that fractional-order types are more accurate than integer-order types because they have a greater degree of freedom [1,2,3]. Hybrid differential equations $(\mathbb{HDE}$s), which are one of the most common ways of representing perturbations in dynamical systems, have piqued the curiosity of many academics [4,5,6]. Many studies have involved the application of hybrid fixed point theory to $\mathbb{HDE}$s by incorporating various symmetry perturbations [7,8,9,10]. Before describing our investigation, we provide an overview of related studies addressing the identified problem. In 2013, Dhage established the existence and uniqueness of the following $\mathbb{HDE}$ solution:

$${\left[z\left(\varsigma \right)-\mathsf{\Lambda }\left(\varsigma ,z\left(\varsigma \right)\right)\right]}^{{}^{\prime }}=\mathsf{\Omega }\left(\varsigma ,z\left(\varsigma \right)\right),\varsigma \in \beth =\left[{\varsigma }_0,a+{\varsigma }_0\right],$$

(1)

and $z\left({\varsigma }_0\right)=z_0\in \mathbb{R},$ where $\mathsf{\Lambda },\mathsf{\Omega }\in C(\beth \times \mathbb{R},\mathbb{R})$ [8,11]. Subsequently, Lu et al. [5] generalized (1) by employing the Riemann–Liouville derivative to obtain a satisfactory relation between the analytical solution and the experimental results

$${\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-\mathsf{\Lambda }\left(\varsigma ,z\left(\varsigma \right)\right)\right)=\mathsf{\Omega }\left(\varsigma ,z\left(\varsigma \right)\right),\varsigma \in \beth ,$$

and $z\left({\varsigma }_0\right)=z_0\in \mathbb{R}$. In addition, Hilal et al. [6] proposed the $\mathbb{BVP}$ for fractional hybrid differential equations ($\mathbb{FHDE}$s), which included Caputo’s fractional-order derivative as follows:

$$\left\{\begin{array}{ll}{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(\frac{z\left(\varsigma \right)}{\mathsf{\Lambda }\left(\varsigma ,z\left(\varsigma \right)\right)}\right)=\mathsf{\Omega }\left(\varsigma ,z\left(\varsigma \right)\right),& \varsigma \in \beth ,\\ {\top }_1\left(\frac{z\left(0\right)}{\mathsf{\Lambda }\left(0,z\left(0\right)\right)}\right)+{\top }_2\left(\frac{z\left(\tau \right)}{\mathsf{\Lambda }\left(\tau ,z\left(\tau \right)\right)}\right)={\top }_3,\end{array}\right.$$

here $\mathsf{\Lambda }\in C\left(\beth \times \mathbb{R},\mathbb{R}-\left\{0\right\}\right),$$\mathsf{\Omega }\in C\left(\beth \times \mathbb{R},\mathbb{R}\right),{\top }_1,{\top }_2({\top }_1+{\top }_2\ne 0)$ and ${\top }_3$ are real values. Recently, Iqbal et al. [7] extended the work of [6] by adding a delay parameter to obtain the following $\mathbb{FHDDE}$

$$\left\{\begin{array}{ll}{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-\mathsf{\Lambda }\left(\varsigma ,z\left(\varsigma \right)\right)\right)=\mathsf{\Omega }\left(\varsigma ,c\left(\varsigma \right),c\left({\nu }_1\varsigma \right)\right),& \\ {}^C{\mathcal{D}}_{+0}^{\vartheta }\left(c\left(\varsigma \right)-\mathsf{\Lambda }\left(\varsigma ,c\left(\varsigma \right)\right)\right)=\mathsf{\Omega }\left(\varsigma ,z\left(\varsigma \right),z\left({\nu }_2\varsigma \right)\right),& \\ {}^C{\mathcal{D}}_{+0}^{\xi }z\left(0\right)={\mathsf{\Pi }}_{1}z({ð}_1),z^{\prime }\left(0\right)=0,\dots ,z^{\beta -2}\left(0\right)=0,& \widehat{C}{\mathcal{D}}_{+0}^{\xi }z\left(1\right)={\mathsf{\Pi }}_{2}z\left({ð}_2\right),\\ {}^C{\mathcal{D}}_{+0}^{\xi }c\left(0\right)={\mathsf{\Pi }}_{1}c\left({ð}_1\right),c^{\prime }\left(0\right)=0,\dots ,c^{{}^{\beta -2}}\left(0\right)=0,& \widehat{C}{\mathcal{D}}_{+0}^{\xi }c\left(1\right)={\mathsf{\Pi }}_{2}c\left({ð}_2\right),\end{array}\right.$$

where $\varsigma \in \left[0,1\right],v_1,v_2,\xi ,{ð}_1,{ð}_1\in (0,1),$${\mathsf{\Pi }}_1,$${\mathsf{\Pi }}_2$ are non-zero real values, ${}^C{\mathcal{D}}_{+0}^{\vartheta }$ is Caputo’s derivative, with $\vartheta \in (\beta -1,\beta );$ here $\beta \in \mathbb{N}$, $\beta \ge 3,$ $\mathsf{\Lambda }$ and $\mathsf{\Omega }$ are non-linear continuous functions. Samei et al. investigated the existence of solutions for the following hybrid Caputo–Hadamard fractional differential inclusion

$${}_H^C{\mathcal{D}}_{+0}^{\vartheta }\left(\frac{z\left(\varsigma \right)-\mathsf{\Theta }(\varsigma ,z\left(\varsigma \right),{\mathcal{I}}^{{\gamma }_1}{h}_1(\varsigma ,z\left(\varsigma \right)),\dots ,{\mathcal{I}}^{{\gamma }_n}{h}_n(\varsigma ,z\left(\varsigma \right)))}{\mathsf{\Lambda }(\varsigma ,z\left(\varsigma \right),{\mathcal{I}}^{{\eta }_1}z\left(\varsigma \right),\dots ,{\mathcal{I}}^{{\gamma }_m}z\left(\varsigma \right))}\right)\in \mathsf{\Omega }\left(\varsigma ,z\left(\varsigma \right)\right),$$

for $\varsigma \in [1,\tau ]$ and $z\left(1\right)={\mathsf{\mu }}_1\left(\varsigma \right)$, $z\left(\tau \right)={\mathsf{\mu }}_{\tau }\left(\varsigma \right)$, where ${}_H^C{\mathcal{D}}_{+0}^{\vartheta }$ and ${\mathcal{I}}^{\gamma }$ denote the Caputo–Hadamard fractional derivative and Hadamard integral of order $1<\vartheta \le 2$ and ${\gamma }_i>0$ for $i=1,2,\dots ,n$, respectively; functions $\mathsf{\Theta }:[1,\tau ]\times {\mathbb{R}}^{n+1}\to \mathbb{R}$, $\mathsf{\Lambda }:[1,\tau ]\times {\mathbb{R}}^{m+1}\to \mathbb{R}\backslash \left\{0\right\}$, $h_i:[1,\tau ]\times \mathbb{R}\to \mathbb{R}$, $i=1,2,\dots ,n$ are continuous, ${\mathsf{\mu }}_1,{\mathsf{\mu }}_{\tau }\in C([1,\tau ],\mathbb{R})$ and the multifunction $\mathsf{\Omega }:[1,\tau ]\times \mathbb{R}\to \mathcal{P}\left(\mathbb{R}\right)$ satisfies certain conditions [12]. Etemad et al. investigated the fractional hybrid multi-term Caputo integro-differential inclusion

$${}^C{\mathcal{D}}_{+0}^{\vartheta }\left(\frac{z\left(\varsigma \right)}{\mathsf{\Lambda }(\varsigma ,z\left(\varsigma \right),{\phi }_1\left(z\left(\varsigma \right)\right),\dots ,{\phi }_n\left(z\left(\varsigma \right)\right))}\right)\in \mathsf{\Omega }\left(\varsigma ,z\left(\varsigma \right),{\phi }_1\left(z\left(\varsigma \right)\right),\dots ,{\phi }_m\left(z\left(\varsigma \right)\right)\right),$$

with three-point integral hybrid boundary value conditions, where $\varsigma \in \beth =[0,1]$, ${}^C{\mathcal{D}}_{+0}^{\vartheta }$ denotes the fractional Caputo derivative of order $0<\vartheta \le 2$, $\mathsf{\Lambda }:[0,1]\times {\mathbb{R}}^{n+1}\to \mathbb{R}\backslash \left\{0\right\}$ is a continuous function and $\mathsf{\Omega }:[0,1]\times {\mathbb{R}}^{m+1}\to \mathcal{P}\left(\mathbb{R}\right)$ is a set-valued map via certain properties [13]. Ma in [14] considered three pairs of local and non-local group constraints for Ablowitz–Kaup–Newell–Segur matrix eigenvalue problems and generated three reduced non-local integrable non-linear Schrödinger hierarchies. They performed two group reductions of the Ablowitz–Kaup–Newell–Segur matrix spectral problems to derive a class of novel reduced non-local reverse-spacetime integrable modified Korteweg–de Vries equations [15].

A number of authors have sought innovative approaches to improve the various types of fractional-order differential equations. Stability analysis of fractional differential equation ($\mathbb{FDE}$) solutions was introduced to address this issue. In 1940, Ulam developed the novel concept of stability analysis to apply stability theory. In 1941, Hyers [16] then generalized the concept using a more advanced approach. Rassias [17,18] amplified the concept for the previously mentioned range to incorporate more types of stability, such as Ulam–Hyers–Rassias (UHR) and generalized Ulam–Hyers–Rassias ($\mathbb{G}$UHR). In bio-mathematics, applications of tripled systems of fractional-order epidemic models, such as susceptible-infected-susceptible and susceptible-infected-recovered models, with Caputo fractional-order derivative [19], have been developed. Papers [20,21,22,23,24,25] provide additional information on these stabilities and their applications.

In this paper, we demonstrate the requirements for at least one solution and analyze its stability for the following fractional hybrid delay differential equations ($\mathbb{FHDDE}$s) with non-homogeneous initial conditions and second-order quadratic perturbations

$$\left\{\begin{array}{l}{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right),\\ {}^C{\mathcal{D}}_{+0}^{\xi }\left(c\left(\varsigma \right)-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_2\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right),\\ {}^C{\mathcal{D}}_{+0}^{\delta }\left(s\left(\varsigma \right)-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_3\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right),\end{array}\right.$$

(2)

under conditions

$$z\left(\varsigma \right){|}_{\varsigma =0}=z_0,c\left(\varsigma \right){|}_{\varsigma =0}=c_0,s\left(\varsigma \right){|}_{\varsigma =0}=s_0,$$

(3)

where $\varsigma \in \gimel =\left[0,\tau \right],\tau >0,{}^C{\mathcal{D}}_{+0}$ is Caputo’s derivative, $\vartheta ,\xi ,\delta \in (0,1)$, $z_0,c_0,s_0$ are real numbers, $\nu =\left(0,1\right)$ is a delay parameter and ${\mathsf{\Lambda }}_i,$${\mathsf{\Omega }}_i:\gimel \times {\mathbb{R}}^3\to \mathbb{R}(i=1,2,3)$ are non-linear continuous functions. In addition, the hybrid fixed point theorem and other non-linear functional analysis outcomes are used to construct compatible criteria for the existence and uniqueness of the solution. The proposed system (2) is subjected to stability analysis in many directions. Finally, an example is presented to support our findings.

A brief outline of the paper is as follows: Section 2 provides the definitions and preliminary facts necessary for the analysis. We also review several definitions and properties of fractional-order integral and differential operators that will be utilized afterwards. In Section 3, we prove the existence of the problem (2). The existence, uniqueness and UH stability results for the problem (2) are also investigated. An example is given in Section 4. A concluding section completes the paper.

2. Preliminaries

In this section, we present notations and basic definitions which are useful for the derivation of our results. For supporting material to the current work, please see [3,11,26,27]. The Riemann–Liouville fractional integral of order $\vartheta \in {\mathbb{R}}^{+},$ for a function $z\left(\varsigma \right):\left[0,\tau \right]\to \mathbb{R}$ is given by

$${\mathcal{I}}^{\vartheta }z\left(\varsigma \right)=\frac{1}{\mathsf{\Gamma }\left(\vartheta \right)}{\int }_0^{\varsigma }{\left(\varsigma -u\right)}^{\vartheta -1}z\left(u\right)\mathrm{d}u,$$

provided that an integral exists. The Caputo derivative of order $\vartheta \in {\mathbb{R}}^{+}$ for $z\left(\varsigma \right)$ on $\left[0,\tau \right]$ is defined by

$${}^C{\mathcal{D}}_{+0}^{\vartheta }z\left(\varsigma \right)=\frac{1}{\mathsf{\Gamma }\left(\sigma -\vartheta \right)}{\int }_0^{\varsigma }{\left(\varsigma -u\right)}^{\sigma -\vartheta -1}{z}^{\left(\sigma \right)}\left(u\right)\mathrm{d}u,$$

where $\sigma =\left[\vartheta \right]+1$ and $\left[\vartheta \right]$ is the integer part of $\vartheta .$

Lemma 1

([1]). Differential operators and fractional-order integral are connected with the equation below

$${\mathcal{I}}^{\vartheta }\left[{}^C{\mathcal{D}}_{+0}^{\vartheta }z\left(\varsigma \right)\right]=z\left(\varsigma \right)+a_0+a_1\varsigma +a_2{\varsigma }^2+···+a_{\sigma -1}{\varsigma }^{\sigma -1},$$

for any $a_i\in \mathbb{R}(i=0,1,2,\dots ,\sigma -1)$, here $\sigma =\left[\vartheta \right]+1.$

Let $\mathbb{X},\mathbb{Y},\mathbb{Z}$ be Banach spaces having all continuous functions from $\gimel \to \mathbb{R}$ with a norm

$$∥z∥=max\left\{\left|z\left(\varsigma \right)\right|:\varsigma \in \gimel \right\},∥c∥=max\left\{\left|c\left(\varsigma \right)\right|:\varsigma \in \gimel \right\},∥s∥=max\left\{\left|s\left(\varsigma \right)\right|:\varsigma \in \gimel \right\}.$$

Then the product $\mathsf{\Xi }=\mathbb{X}\times \mathbb{Y}\times \mathbb{Z}$ is also a Banach space with the norm $∥\left(z,c,s\right)∥=∥z∥+∥c∥+∥s∥$, for each $(z,c,s)\in \Xi$.

As in Theorem 2.4 in [9], we can state the following Theorem.

Theorem 1.

Let O be a closed and bounded set so that $O\subset \Xi$ and the two operators $\Re :\Xi \to \Xi$, $\Im :O\to \Xi$ fulfil the following axioms

(1) 

ℜ is a contraction;

(2) 

ℑ is continuous and compact;

(3) 

$\left(z,c,s\right)=\Re \left(z,c,s\right)+\Im \left(z,c,s\right)$ for each $z,c,s\in \Xi$, implies $z,c,s\in O.$

Then the operator equations $\left(z,c,s\right)=\Re \left(z,c,s\right)+\Im \left(z,c,s\right)$ have a solution in $O.$

We now assume the following hypotheses in order to develop the results linked to the presence of the solution as well as to the study of functional stability:

(H${}_1$)

For positive real values $\omega ,\gamma$ and $\varkappa$, the functions ${\mathsf{\Lambda }}_1,{\mathsf{\Lambda }}_2$ and ${\mathsf{\Lambda }}_3$ satisfy the inequalities below: $\forall \varsigma \in \gimel$ and $z,\overline{z},c,\overline{c},s,\overline{s}\in \mathbb{R},$

$$\begin{array}{ll}\left|{\mathsf{\Lambda }}_1\left(\varsigma ,z,c,s\right)-{\mathsf{\Lambda }}_1\left(\varsigma ,\overline{z},\overline{c},\overline{s}\right)\right|& \le \omega \left(\left|z-\overline{z}\right|+\left|c-\overline{c}\right|+\left|s-\overline{s}\right|\right),\\ \left|{\mathsf{\Lambda }}_2\left(\varsigma ,z,c,s\right)-{\mathsf{\Lambda }}_2\left(\varsigma ,\overline{z},\overline{c},\overline{s}\right)\right|& \le \gamma \left(\left|z-\overline{z}\right|+\left|c-\overline{c}\right|+\left|s-\overline{s}\right|\right),\\ \left|{\mathsf{\Lambda }}_3\left(\varsigma ,z,c,s\right)-{\mathsf{\Lambda }}_3\left(\varsigma ,\overline{z},\overline{c},\overline{s}\right)\right|& \le \varkappa \left(\left|z-\overline{z}\right|+\left|c-\overline{c}\right|+\left|s-\overline{s}\right|\right);\end{array}$$

(H${}_2$)

For continuous functionals $p_i$, $b_i$, $d_i,e_i$$\left(i=1,2,3\right):\left[0,1\right]\to \mathbb{R},$ the functions ${\mathsf{\Omega }}_1,{\mathsf{\Omega }}_2$ and ${\mathsf{\Omega }}_3$ fulfil the following constraints

$$\begin{array}{ll}\left|{\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)\right|& \le p_1\left(\varsigma \right)+b_1\left(\varsigma \right)\left|z\left(\varsigma \right)\right|+d_1\left(\varsigma \right)\left|c\left(\varsigma \right)\right|+e_1\left(\varsigma \right)\left|s\left(\varsigma \right)\right|,\\ \left|{\mathsf{\Omega }}_2\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)\right|& \le p_2\left(\varsigma \right)+b_2\left(\varsigma \right)\left|z\left(\varsigma \right)\right|+d_2\left(\varsigma \right)\left|c\left(\varsigma \right)\right|+e_2\left(\varsigma \right)\left|s\left(\varsigma \right)\right|,\\ \left|{\mathsf{\Omega }}_3\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)\right|& \le p_3\left(\varsigma \right)+b_3\left(\varsigma \right)\left|z\left(\varsigma \right)\right|+d_3\left(\varsigma \right)\left|c\left(\varsigma \right)\right|+e_3\left(\varsigma \right)\left|s\left(\varsigma \right)\right|;\end{array}$$

(H${}_3$)

We present the notations below to prevent lengthy calculations and to help the reader comprehend the main results.

$${\ell }_i=\underset{\varsigma \in \left[0,1\right]}{\sup }\left|{\mathsf{\Lambda }}_i\left(\varsigma ,0,0,0\right)\right|,i=1,2,3,$$

(4)

and ${\eta }_i={\sup }_{\varsigma \in \gimel }\left|p_i\left(\varsigma \right)\right|,i=1,2,3,$

$$\begin{array}{ll}{J}_z& =\underset{\varsigma \in \gimel }{\sup }\left\{\left|b_i\left(\varsigma \right)\right|:i=1,2,3\right\},\\ J_c& =\underset{\varsigma \in \gimel }{\sup }\left\{\left|d_i\left(\varsigma \right)\right|:i=1,2,3\right\},\\ J_s& =\underset{\varsigma \in \gimel }{\sup }\left\{\left|e_i\left(\varsigma \right)\right|:i=1,2,3\right\},\end{array}$$

(5)

and $J=max\left\{J_z,J_c,J_s\right\}$.

Definition 1.

A function $\Re :\Xi \to \Xi$ is called $\rho -$Lipschitz for a positive real value ρ if the inequality below holds

$$\left|\Re \left(z,c,s\right)-\Re \left(\overline{z},\overline{c},\overline{s}\right)\right|\le \rho \left(\left|z-\overline{z}\right|+\left|c-\overline{c}\right|+\left|s-\overline{s}\right|\right),$$

$\forall \left(z,c,s\right),\left(\overline{z},\overline{c},\overline{s}\right)\in \Xi .$ Moreover, ℜ is said to be a strict contraction if $\rho <1.$

Definition 2.

A solution $z\left(\varsigma \right)\in C\left[0,\tau \right]$ of the $\mathbb{FDE}$ that is described as

$$\left\{\begin{array}{ll}{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)& \\ ={\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right),& \varsigma \in \gimel ,\\ z\left(\varsigma \right){|}_{\varsigma =0}=z_0,\end{array}\right.$$

(6)

• is UH stable if, for a constant ${\aleph }_{\vartheta ,\xi ,\delta ,D}>0$, so that, for each $\epsilon >0$, and for every solution $z\left(\varsigma \right)\in C\left[0,\tau \right]$, with the inequality below

  $$\left|{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)-{\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)\right|\le \epsilon ,$$

  (7)
  $\varsigma \in \gimel ,$ there is a unique solution $\mu \in C\left[0,\tau \right]$ of the $\mathbb{FDE}$ (6) with a constant ${\aleph }_{\vartheta ,\xi ,\delta ,D}>0$, so that $∥z-\mu ∥\le {\aleph }_{\vartheta ,\xi ,\delta ,D}$.
• is UHR stable, if we have $\hslash :\left(0,\infty \right)\to {\mathbb{R}}^{+}$, $(\hslash \left(0\right)=0)$, so that, for every solution $z\left(\varsigma \right)\in C\left[0,\tau \right]$ of (7), there is a unique solution $\mu \in C\left[0,\tau \right]$ of the $\mathbb{FDE}$ (6) with a constant ${\aleph }_{\vartheta ,\xi ,\delta ,D}>0$, so that $∥z-\mu ∥\le {\aleph }_{\vartheta ,\xi ,\delta ,D}\hslash \left(\epsilon \right)$.

We provide the following definitions of UHR and $\mathbb{G}$UHR stability for our considered system (6)

Definition 3.

$\mathbb{FDE}$ (6) is called

• UHR stable with respect to $w\in C\left(\left[0,\tau \right],\mathbb{R}\right)$ if there is a non-zero positive real value ${\aleph }_{w,D}$ and for every $\epsilon >0$, so that, for each solution $z\left(\varsigma \right)\in C\left[0,\tau \right]$ of the inequality

  $$\left|{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)-{\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)\right|\le \epsilon w\left(\varsigma \right),$$
  where $\varsigma \in \gimel ,$ there is a solution $\mu \in C\left[0,\tau \right]$ of the $\mathbb{FDE}$ (6) with a constant ${\aleph }_{w,D}>0$, so that $\left|z-\mu \right|\le {\aleph }_{w,D}w\left(\varsigma \right)$, for each $\varsigma \in \gimel$.
• $\mathbb{G}$UHR stable with respect to $w\in C\left(\left[0,\tau \right],\mathbb{R}\right)$ if there is a positive real number ${\aleph }_{w,D}$, so that, for each solution $z\left(\varsigma \right)\in C\left[0,\tau \right]$ of the inequality

  $$\left|{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)-{\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)\right|\le w\left(\varsigma \right),$$
  where $\varsigma \in \gimel ,$ there is a solution $\mu \in C\left[0,\tau \right]$ of the $\mathbb{FDE}$ (6) with a constant ${\aleph }_{w,D}>0$, so that $\left|z\left(\varsigma \right)-\mu \left(\varsigma \right)\right|\le {\aleph }_{w,D}w\left(\varsigma \right)$, for $\varsigma \in \gimel$.

3. Main Results

The following section considers the conditions in which the underlying $\mathbb{FHDDE}$s (2) can be solved. We begin by proving the following lemma.

Lemma 2.

Let $\mathsf{\Theta }:\gimel \to \mathbb{R},$ then the solution of the $\mathbb{FHDE}$

$$\left\{\begin{array}{ll}{}^C{\mathcal{D}}_{+0}^{\vartheta }\left[z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right]=\mathsf{\Theta }\left(\varsigma \right),& \vartheta \in (0,1],\varsigma \in \gimel ,\\ z\left(\varsigma \right){|}_{\varsigma =0}=z_0,\end{array}\right.$$

(8)

takes the form

$$z\left(\varsigma \right)=z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}+{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)+{\mathcal{I}}^{\vartheta }\left[\mathsf{\Theta }\left(\varsigma \right)\right].$$

(9)

Proof. 

Applying the integral ${\mathcal{I}}^{\vartheta }$ on ${}^C{\mathcal{D}}_{+0}^{\vartheta }z\left(\varsigma \right)$ and using Lemma 1, we have

$$z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)={\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\mathsf{\Theta }\left(u\right)\mathrm{d}u+b_0,b_0\in \mathbb{R}.$$

(10)

From the initial conditions ${\left.z\left(\varsigma \right)\right|}_{\varsigma =0}=z_0$, the Equation (10) transfers to (9) as

$$\begin{array}{ll}z\left(\varsigma \right)& =z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}+{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)+{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\mathsf{\Theta }\left(u\right)\mathrm{d}u.\end{array}$$

□

Theorem 2.

It should be noted that, according to Lemma 2, the proposed system $\mathbb{FHDDE}$s (2) is equivalent to the integral system below, $\varsigma \in \gimel ,$

$$\left\{\begin{array}{l}z\left(\varsigma \right)=z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ +{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u,}\\ \\ c\left(\varsigma \right)=c_0-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ +{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\xi -1}}{\mathsf{\Gamma }\left(\xi \right)}{\mathsf{\Omega }}_2\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u,}\\ \\ s\left(\varsigma \right)=s_0-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ +{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\delta -1}}{\mathsf{\Gamma }\left(\delta \right)}{\mathsf{\Omega }}_3\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u.}\end{array}\right.$$

(11)

Now, we have a theorem to produce the required result for at least one solution of the problem (2).

Theorem 3.

Problem (2) has at least one solution under assumptions (H${}_1$)–(H${}_3$) if the following condition is met

$${\rm Y}:=\left(\omega +\gamma +\varkappa +\frac{{\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{{\tau }^{\xi }}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{{\tau }^{\delta }}{\mathsf{\Gamma }\left(\delta +1\right)}\right)J<1.$$

(12)

Proof. 

Suppose a closed bounded set

$$O=\left\{\left(z,c,s\right)\in O:∥\left(z,c,s\right)∥\le \mathbb{R}\right\}\subset \Xi ,$$

where

$$\frac{\left[{\psi }_1+{\psi }_2+{\psi }_3+{\ell }_1+{\ell }_2+{\ell }_3+\frac{{\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{{\tau }^{\xi }}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{{\tau }^{\delta }}{\mathsf{\Gamma }\left(\delta +1\right)}\right]}{1-\left(\omega +\gamma +\varkappa +\frac{{\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{{\tau }^{\xi }}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{{\tau }^{\delta }}{\mathsf{\Gamma }\left(\delta +1\right)}\right)J}\le \mathbb{R},$$

and

$$\begin{array}{ll}{\psi }_1& ={\left|z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right|}_{\varsigma =0},\\ {\psi }_2& ={\left|c_0-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right|}_{\varsigma =0},\\ {\psi }_3& ={\left|s_0-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right|}_{\varsigma =0}.\end{array}$$

(13)

Let $\Re :\Xi \to \Xi$ and $\Im :O\to \Xi$ be operators defined by

$$\begin{array}{cc}\Re \left(z,c,s\right)& =\left({\Re }_1\left(z,c,s\right),{\Re }_2\left(z,c,s\right),{\Re }_3\left(z,c,s\right)\right),\\ \Im \left(z,c,s\right)& =\left({\Im }_1\left(z,c,s\right),{\Im }_2\left(z,c,s\right),{\Im }_3\left(z,c,s\right)\right).\end{array}$$

Then, we get, $\varsigma \in \gimel$,

$$\begin{array}{cc}{\Re }_1\left(z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)& ={\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right),\\ {\Re }_2\left(z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)& ={\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right),\\ {\Re }_3\left(z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)& ={\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right),\end{array}$$

(14)

and for $\varsigma \in \gimel ,$

$$\left\{\begin{array}{l}{\Im }_1\left(z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)=z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u,}\\ \\ {\Im }_2\left(z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)=c_0-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\xi -1}}{\mathsf{\Gamma }\left(\xi \right)}{\mathsf{\Omega }}_2\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u,}\\ \\ {\Im }_3\left(z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)=s_0-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\delta -1}}{\mathsf{\Gamma }\left(\delta \right)}{\mathsf{\Omega }}_3\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u.}\end{array}\right.$$

(15)

From (14) and (15), we obtain operator equations as

$$\Re \left(z,c,s\right)+\Im \left(z,c,s\right)=\left(z,c,s\right),\forall \varsigma \in \gimel ,$$

that is

$$\begin{array}{c}({\Re }_1\left(z,c,s\right),{\Re }_2\left(z,c,s\right),{\Re }_3\left(z,c,s\right))\\ +\left({\Im }_1\left(z,c,s\right),{\Im }_2\left(z,c,s\right),{\Im }_3\left(z,c,s\right)\right)=\left(z,c,s\right),\end{array}$$

this implies that

$${\Re }_1\left(z,c,s\right)+{\Im }_1\left(z,c,s\right)=z,{\Re }_2\left(z,c,s\right)+{\Im }_2\left(z,c,s\right)=c,{\Re }_3\left(z,c,s\right)+{\Im }_3\left(z,c,s\right)=s.$$

Now, we show that ℜ and ℑ fulfil the hypotheses of Theorem 1. For this, we prove that ℜ is Lipschitz on $\Xi$ with $\omega +\gamma +\varkappa >0$, and $\Im :O\to \Xi$ is completely continuous. Let $\left(z,c,s\right)\in \Xi ,$ then from (H${}_1$), we obtain that

$$\begin{array}{ll}\left|{\Re }_1\left(z,c,s\right)-{\Re }_1\left(\overline{z},\overline{c},\overline{s}\right)\right|& =\left|{\mathsf{\Lambda }}_1\left(\varsigma ,z,c,s\right)-{\mathsf{\Lambda }}_1\left(\varsigma ,\overline{z},\overline{c},\overline{s}\right)\right|\\ & \le \omega \left(\left|z-\overline{z}\right|+\left|c-\overline{c}\right|+\left|s-\overline{s}\right|\right)\\ & \le \omega \left(∥z-\overline{z}∥+∥c-\overline{c}∥+∥s-\overline{s}∥\right),\end{array}$$

$\forall \varsigma \in \gimel .$ Taking supremum over $\varsigma ,$ we have

$$\begin{array}{ll}∥{\Re }_1\left(z,c,s\right)& -{\Re }_1\left(\overline{z},\overline{c},\overline{s}\right)∥\le \omega \left(∥z-\overline{z}∥+∥c-\overline{c}∥+∥s-\overline{s}∥\right),\end{array}$$

(16)

$\forall \left(z,c,s\right),\left(\overline{z},\overline{c},\overline{s}\right)\in \Xi .$ Similarly, we can write

$$\begin{array}{ll}∥{\Re }_2\left(z,c,s\right)& -{\Re }_2\left(\overline{z},\overline{c},\overline{s}\right)∥\le \gamma \left(∥z-\overline{z}∥+∥c-\overline{c}∥+∥s-\overline{s}∥\right),\end{array}$$

(17)

and

$$\begin{array}{ll}∥{\Re }_3\left(z,c,s\right)& -{\Re }_3\left(\overline{z},\overline{c},\overline{s}\right)∥\le \varkappa \left(∥z-\overline{z}∥+∥c-\overline{c}∥+∥s-\overline{s}∥\right),\end{array}$$

(18)

$\forall \left(z,c,s\right),\left(\overline{z},\overline{c},\overline{s}\right)\in \Xi .$ Thus, ℜ is Lipschitz on $\Xi$ with a positive constant $\omega +\gamma +\varkappa ,$ from (16)–(18), one gets

$$\begin{array}{ll}∥\Re \left(z,c,s\right)& -\Re \left(\overline{z},\overline{c},\overline{s}\right)∥\le \left(\omega +\gamma +\varkappa \right)\left(∥z-\overline{z}∥+∥c-\overline{c}∥+∥s-\overline{s}∥\right).\end{array}$$

For continuity of $\Im ,$ suppose that $(z_{\beta },c_{\beta },s_{\beta })$ is a sequence in O converging to $\left(z,c,s\right)\in O,$ based on the Lebesgue dominated convergence theorem, we can write

$$\begin{array}{l}\underset{\beta \to \infty }{\lim }{\Im }_1\left(z_{\beta },c_{\beta },s_{\beta }\right)\left(\varsigma \right)=\underset{\beta \to \infty }{\lim }[z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z_{\beta }\left(\nu u\right),c_{\beta }\left(\nu u\right),s_{\beta }\left(\nu u\right)\right)\mathrm{d}u]\\ =z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\underset{\beta \to \infty }{lim}{\mathsf{\Omega }}_1\left(u,z_{\beta }\left(\nu u\right),c_{\beta }\left(\nu u\right),s_{\beta }\left(\nu u\right)\right)\mathrm{d}u\\ =z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u={\Im }_1\left(z,c,s\right)\left(\varsigma \right),\forall \varsigma \in \gimel .\end{array}$$

Analogously, we get, for each $\varsigma \in \gimel$,

$$\begin{gathered} \underset{\beta \to \infty }{\lim }{\Im }_2\left(z_{\beta },c_{\beta },s_{\beta }\right)\left(\varsigma \right)={\Im }_2\left(z,c,s\right)\left(\varsigma \right), \\ \underset{\beta \to \infty }{\lim }{\Im }_3\left(z_{\beta },c_{\beta },s_{\beta }\right)\left(\varsigma \right)={\Im }_3\left(z,c,s\right)\left(\varsigma \right). \end{gathered}$$

Now, we shall show $\Im (z_{\beta },c_{\beta },s_{\beta })$ is equicontinuous. So, we must conclude that ℑ is equicontinuous and uniformly bounded on $O.$ Assume $\left(z,c,s\right)\in O$ is any solution, then by (H${}_2$), we have

$$\begin{array}{ll}\left|{\Im }_1\left(z,c,s\right)\left(\varsigma \right)\right|& =|z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u|\\ & \le \left|z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\right|\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\left|{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\right|\mathrm{d}u\\ & \le {\psi }_1+\underset{\varsigma \in \gimel }{\sup }{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\left|p_1\left(u\right)\right|\mathrm{d}u+J\mathbb{R}\frac{{\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)},\end{array}$$

which leads to

$$∥{\Im }_1\left(z,c,s\right)∥\le {\psi }_1+\frac{\left({\eta }_1+J\mathbb{R}\right){\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}.$$

(19)

Follows the same scenario, we have

$$∥{\Im }_2\left(z,c,s\right)∥\le {\psi }_2+\frac{\left({\eta }_2+J\mathbb{R}\right){\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}$$

(20)

and

$$∥{\Im }_3\left(z,c,s\right)∥\le {\psi }_3+\frac{\left({\eta }_3+J\mathbb{R}\right){\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}.$$

(21)

Therefore, from (19)–(21), we obtain that

$$∥\Im \left(z,c,s\right)∥\le {\psi }_1+{\psi }_2+{\psi }_3+\frac{\left({\eta }_1+{\eta }_2+{\eta }_3+3J\mathbb{R}\right){\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}.$$

Thus, ℑ is a uniformly bounded operator on $O.$ Now, assume that $\varsigma ,\alpha \in \gimel$ with $\varsigma <\alpha ,$ then, for each $\left(z,c,s\right)\in O,$ we can write

$$\begin{array}{ll}|{\Im }_1\left(z,c,s\right)\left(\varsigma \right)& -{\Im }_1\left(z,c,s\right)\left(\alpha \right)|\\ & \le {\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}-{\left(\alpha -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\left|{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\right|\mathrm{d}u\\ & +{\int }_{\varsigma }^{\alpha }\frac{{\left(\alpha -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\left|{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\right|\mathrm{d}u\\ & \le \frac{2\left({\eta }_1+J\mathbb{R}\right)}{\mathsf{\Gamma }\left(\vartheta +1\right)}\left({\varsigma }^{\vartheta }-{\alpha }^{\vartheta }+2{\left(\alpha -\varsigma \right)}^{\vartheta }\right),\end{array}$$

which yields that

$$∥{\Im }_1\left(z,c,s\right)\left(\varsigma \right)-{\Im }_1\left(z,c,s\right)\left(\alpha \right)∥\le \frac{2\left({\eta }_1+J\mathbb{R}\right)}{\mathsf{\Gamma }\left(\vartheta +1\right)}\left[{\varsigma }^{\vartheta }-{\alpha }^{\vartheta }+2{\left(\alpha -\varsigma \right)}^{\vartheta }\right].$$

(22)

Similarly, we get

$$∥{\Im }_2\left(z,c,s\right)\left(\varsigma \right)-{\Im }_2\left(z,c,s\right)\left(\alpha \right)∥\le \frac{2\left({\eta }_2+J\mathbb{R}\right)}{\mathsf{\Gamma }\left(\vartheta +1\right)}\left[{\varsigma }^{\vartheta }-{\alpha }^{\vartheta }+2{\left(\alpha -\varsigma \right)}^{\vartheta }\right]$$

(23)

and

$$∥{\Im }_3\left(z,c,s\right)\left(\varsigma \right)-{\Im }_3\left(z,c,s\right)\left(\alpha \right)∥\le \frac{2\left({\eta }_3+J\mathbb{R}\right)}{\mathsf{\Gamma }\left(\vartheta +1\right)}\left[{\varsigma }^{\vartheta }-{\alpha }^{\vartheta }+2{\left(\alpha -\varsigma \right)}^{\vartheta }\right].$$

(24)

If $\varsigma \to \alpha ,$ then the right sides in (22)–(24) tend to zero. Furthermore, ${\Im }_1,{\Im }_2,{\Im }_3$ are bounded and continuous. Hence, from (22)–(24), we get

$$\begin{array}{ll}∥{\Im }_1\left(z,c,s\right)\left(\varsigma \right)& -{\Im }_1\left(z,c,s\right)\left(\alpha \right)∥\\ & +∥{\Im }_2\left(z,c,s\right)\left(\varsigma \right)-{\Im }_2\left(z,c,s\right)\left(\alpha \right)∥\\ & +∥{\Im }_3\left(z,c,s\right)\left(\varsigma \right)-{\Im }_3\left(z,c,s\right)\left(\alpha \right)∥\to 0,\mathrm{as}\varsigma \to \alpha ,\end{array}$$

that is, $\parallel \Im (z,c,s)\left(\varsigma \right)-\Im (z,c,s)\left(\alpha \right)\parallel \to 0$, as $\varsigma \to \alpha$. Hence, ℑ is uniformly continuous for each $\varsigma \in \gimel$ and $\left(z,c,s\right)\in O.$ So, ℑ is equicontinuous in $O.$ According to the Arzelá–Ascoli Theorem, ℑ is compact and, hence, completely continuous. Now, in order to show the postulate (H${}_3$) of Theorem 1, let $\left(z,c,s\right)\in O$ and, using the postulate (H${}_1$), we have

$$\begin{array}{ll}\left|\Re \left(z,c,s\right)\left(\varsigma \right)\right.& \left.+\Im \left(z,c,s\right)\left(\varsigma \right)\right|\\ & \le \left|\Re \left(z,c,s\right)\left(\varsigma \right)\right|+\left|\Im \left(z,c,s\right)\left(\varsigma \right)\right|\\ & \le \left|{\Re }_1\left(z,c,s\right)\left(\varsigma \right)\right|+\left|{\Re }_2\left(z,c,s\right)\left(\varsigma \right)\right|+\left|{\Re }_3\left(z,c,s\right)\left(\varsigma \right)\right|\\ & +\left|{\Im }_1\left(z,c,s\right)\left(\varsigma \right)\right|+\left|{\Im }_2\left(z,c,s\right)\left(\varsigma \right)\right|+\left|{\Im }_3\left(z,c,s\right)\left(\varsigma \right)\right|\\ & +{\psi }_1+{\psi }_2+{\psi }_3+\left|{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right|\\ & +\left|{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right|+\left|{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right|\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\left|{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\right|\mathrm{d}u\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\xi -1}}{\mathsf{\Gamma }\left(\xi \right)}\left|{\mathsf{\Omega }}_2\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\right|\mathrm{d}u\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\delta -1}}{\mathsf{\Gamma }\left(\delta \right)}\left|{\mathsf{\Omega }}_3\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\right|\mathrm{d}u,\end{array}$$

it follows that

$$\begin{array}{ll}\left|\Re \left(z,c,s\right)\left(\varsigma \right)\right.& \left.+\Im \left(z,c,s\right)\left(\varsigma \right)\right|\\ & \le {\psi }_1+{\psi }_2+{\psi }_3\\ & +\left|{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)-{\mathsf{\Lambda }}_1\left(\varsigma ,0,0,0\right)\right|\\ & +\left|{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)-{\mathsf{\Lambda }}_2\left(\varsigma ,0,0,0\right)\right|\\ & +\left|{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)-{\mathsf{\Lambda }}_3\left(\varsigma ,0,0,0\right)\right|\\ & +{\mathsf{\Lambda }}_1\left(\varsigma ,0,0,0\right)+{\mathsf{\Lambda }}_2\left(\varsigma ,0,0,0\right)+{\mathsf{\Lambda }}_3\left(\varsigma ,0,0,0\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}(\left|p_1\left(u\right)\right|+b\left(u\right)\left|z\left(u\right)\right|\\ & +d\left(u\right)\left|c\left(u\right)\right|+e\left(u\right)\left|s\left(u\right)\right|)\mathrm{d}u\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\xi -1}}{\mathsf{\Gamma }\left(\xi \right)}(\left|p_2\left(u\right)\right|+b\left(u\right)\left|z\left(u\right)\right|\\ & +d\left(u\right)\left|c\left(u\right)\right|+e\left(u\right)\left|s\left(u\right)\right|)\mathrm{d}u\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\delta -1}}{\mathsf{\Gamma }\left(\delta \right)}(\left|p_3\left(u\right)\right|+b\left(u\right)\left|z\left(u\right)\right|\\ & +d\left(u\right)\left|c\left(u\right)\right|+e\left(u\right)\left|s\left(u\right)\right|)\mathrm{d}u.\end{array}$$

(25)

Passing supremum over ℷ in (25), we have

$$\begin{array}{ll}∥\Re \left(z,c,s\right)& +\Im \left(z,c,s\right)∥\le {\psi }_1+{\psi }_2+{\psi }_3+\left(\omega +\gamma +\varkappa \right)J\mathbb{R}\\ & +{\ell }_1+{\ell }_2+{\ell }_3+\frac{\left({\eta }_1+J\mathbb{R}\right){\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{\left({\eta }_2+J\mathbb{R}\right){\tau }^{\xi }}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{\left({\eta }_3+J\mathbb{R}\right){\tau }^{\delta }}{\mathsf{\Gamma }\left(\delta +1\right)}\le \mathbb{R}.\end{array}$$

(26)

Hence, all the hypotheses of Theorem 1 are fulfilled. Then the system of $\mathbb{FHDDE}$s (2) has a solution in $O.$ □

4. Stability Results

This section focuses on demonstrating and analyzing the necessary and required criteria for UH, $\mathbb{G}$UH, UHR and $\mathbb{G}$UHR stability in the proposed three-fold problem solution (2).

Definition 4.

For $\epsilon =\left({\epsilon }_1,{\epsilon }_2,{\epsilon }_3\right)>0,$ a $\left(z,c,s\right)\in \Re$ is called a solution of

$$\left\{\begin{array}{l}|{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ -{\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)|<{\epsilon }_1,\\ |{}^C{\mathcal{D}}_{+0}^{\xi }\left(c\left(\varsigma \right)-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ -{\mathsf{\Omega }}_2\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)|<{\epsilon }_2,\\ |{}^C{\mathcal{D}}_{+0}^{\delta }\left(s\left(\varsigma \right)-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ -{\mathsf{\Omega }}_3\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)|<{\epsilon }_3,\end{array}\right.$$

for each $\varsigma \in \gimel$, if there are three functions ${⅁}_1,{⅁}_2,{⅁}_3\in C\left[0,\tau \right]$ which only depend on $z,c,s$, so that, $\forall \varsigma \in \gimel ,$

(i) 

$\left|{⅁}_1\left(\varsigma \right)\right|\le {\epsilon }_1,\left|{⅁}_2\left(\varsigma \right)\right|\le {\epsilon }_2,\left|{⅁}_3\left(\varsigma \right)\right|\le {\epsilon }_3$;

(ii) 

The perturbed system is defined by

$$\left\{\begin{array}{l}{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)+{⅁}_1\left(\varsigma \right),\\ {}^C{\mathcal{D}}_{+0}^{\xi }\left(c\left(\varsigma \right)-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_2\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)+{⅁}_2\left(\varsigma \right),\\ {}^C{\mathcal{D}}_{+0}^{\delta }\left(s\left(\varsigma \right)-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_3\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)+{⅁}_3\left(\varsigma \right).\end{array}\right.$$

(27)

In order to obtain the results for the underlying form, we make the following assumption:

(H${}_4$)

The three operators ${\mathsf{\Omega }}_1,{\mathsf{\Omega }}_2,{\mathsf{\Omega }}_3$ fulfil the more general Lipschitz type conditions below

$$\begin{array}{ll}\left|{\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)\right.& \left.-{\mathsf{\Omega }}_1\left(\varsigma ,\mu \left(\nu \varsigma \right),q\left(\nu \varsigma \right),\wp \left(\nu \varsigma \right)\right)\right|\\ & \le p_1\left(\varsigma \right)\left(\left|z-\mu \right|+\left|c-q\right|+\left|s-\wp \right|\right),\\ \left|{\mathsf{\Omega }}_2\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)\right.& \left.-{\mathsf{\Omega }}_2\left(\varsigma ,\mu \left(\nu \varsigma \right),q\left(\nu \varsigma \right),\wp \left(\nu \varsigma \right)\right)\right|\\ & \le p_2\left(\varsigma \right)\left(\left|z-\mu \right|+\left|c-q\right|+\left|s-\wp \right|\right),\\ \left|{\mathsf{\Omega }}_3\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)\right.& \left.-{\mathsf{\Omega }}_3\left(\varsigma ,\mu \left(\nu \varsigma \right),q\left(\nu \varsigma \right),\wp \left(\nu \varsigma \right)\right)\right|\\ & \le p_3\left(\varsigma \right)\left(\left|z-\mu \right|+\left|c-q\right|+\left|s-\wp \right|\right),\end{array}$$

$\forall p_1,p_2,p_3\in C\left[0,1\right].$

Lemma 3.

If the hypotheses $\left(i\right)$ and $\left(ii\right)$ are true, the solution $(z,c,s)\in \Xi$ of the following $\mathbb{FHDDE}$s

$$\left\{\begin{array}{l}{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)+{⅁}_1\left(\varsigma \right),\\ {}^C{\mathcal{D}}_{+0}^{\xi }\left(c\left(\varsigma \right)-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_2\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)+{⅁}_2\left(\varsigma \right),\\ {}^C{\mathcal{D}}_{+0}^{\delta }\left(s\left(\varsigma \right)-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_3\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)+{⅁}_3\left(\varsigma \right),\end{array}\right.$$

under conditions $z\left(\varsigma \right){|}_{\varsigma =0}=z_0$, $c\left(\varsigma \right){|}_{\varsigma =0}=c_0$, $s\left(\varsigma \right){|}_{\varsigma =0}=s_0$, which obeys the inequalities for $\varsigma \in \gimel$ as

$$\begin{array}{ll}\left|z\right(\varsigma )& -(-z_0+{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & -{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & -{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|\le \frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)},\\ \left|c\right(\varsigma )& -(-c_0+{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & -{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & -{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\xi -1}}{\mathsf{\Gamma }\left(\xi \right)}{\mathsf{\Omega }}_2\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|\le \frac{{\epsilon }_2}{\mathsf{\Gamma }\left(\xi +1\right)},\\ \left|s\right(\varsigma )& -(-s_0+{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & -{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & -{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\delta -1}}{\mathsf{\Gamma }\left(\delta \right)}{\mathsf{\Omega }}_3\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|\le \frac{{\epsilon }_3}{\mathsf{\Gamma }\left(\delta +1\right)}.\end{array}$$

(28)

Proof. 

Based on Theorem 2, we obtain a solution of the problem (27) for $\varsigma \in \gimel$ as

$$\left\{\begin{array}{l}z\left(\varsigma \right)=z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ +{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u}\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{⅁}_1\left(\varsigma \right)\mathrm{d}u,}\\ c\left(\varsigma \right)=c_0-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ +{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\xi -1}}{\mathsf{\Gamma }\left(\xi \right)}{\mathsf{\Omega }}_2\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u}\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\xi -1}}{\mathsf{\Gamma }\left(\xi \right)}{⅁}_2\left(\varsigma \right)\mathrm{d}u,}\\ s\left(\varsigma \right)=s_0-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ +{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\delta -1}}{\mathsf{\Gamma }\left(\delta \right)}{\mathsf{\Omega }}_3\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u}\\ {\displaystyle +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\delta -1}}{\mathsf{\Gamma }\left(\delta \right)}{⅁}_3\left(\varsigma \right)\mathrm{d}u.}\end{array}\right.$$

(29)

It is simple to obtain (28) using the solution provided by (29). □

Theorem 4.

Assume that (H${}_1$) and (H${}_4$) hold and consider Lemma 3 endowed with the condition ${\mho }_1+{\mho }_2+{\mho }_3\ne 1,$ where

$${\mho }_1=\omega +{\phi }_1,{\mho }_2=\gamma +{\phi }_2,{\mho }_3=\varkappa +{\phi }_3,$$

(30)

and

$$\begin{array}{ll}{\phi }_1& ={\int }_0^{\tau }\frac{{\left(\tau -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{p}_1\left(u\right)\mathrm{d}u,\\ {\phi }_2& ={\int }_0^{\tau }\frac{{\left(\tau -u\right)}^{\xi -1}}{\mathsf{\Gamma }\left(\xi \right)}{p}_2\left(u\right)\mathrm{d}u,\\ {\phi }_3& ={\int }_0^{\tau }\frac{{\left(\tau -u\right)}^{\delta -1}}{\mathsf{\Gamma }\left(\delta \right)}{p}_3\left(u\right)\mathrm{d}u.\end{array}$$

(31)

Then the solution of the problem (2) is UH and $\mathbb{G}$UH stable.

Proof. 

Let $\left(z,c,s\right)\in \Xi$ be an arbitrary solution of the problem (2) of $\mathbb{FHDDE}$s and $\left(\mu ,q,\wp \right)\in \Xi$ be the unique solution of the suggested problem (2). Consider

$$\begin{array}{ll}\left|\mu \left(\varsigma \right)-z\left(\varsigma \right)\right|& =|\mu \left(\varsigma \right)-(z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & +{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|\\ & \le |\mu \left(\varsigma \right)-({\mu }_0-{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right){|}_{\varsigma =0}\\ & +{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,\mu \left(\nu u\right),q\left(\nu u\right),\wp \left(\nu u\right)\right)\mathrm{d}u)|\\ & +\left|\right({\mu }_0-{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right){|}_{\varsigma =0}\\ & +{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)\\ & -(z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & +{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|,\end{array}$$

it follows that

$$\begin{array}{ll}\left|\mu \left(\varsigma \right)\right.& \left.-z\left(\varsigma \right)\right|\\ & \le \frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\left|{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)-{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right)\right|\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}|{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\\ & -{\mathsf{\Omega }}_1\left(u,\mu \left(\nu u\right),q\left(\nu u\right),\wp \left(\nu u\right)\right)|\mathrm{d}u\\ & \le \frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\omega \left(\left|\mu -z\right|+\left|q-c\right|+\left|\wp -s\right|\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\left|p_1\left(\varsigma \right)\right|\left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right)\mathrm{d}u.\end{array}$$

Hence,

$$\begin{array}{ll}∥\mu -z∥& \le \frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\omega \left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right)\\ & +\left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right){\phi }_1.\end{array}$$

(32)

Similarly, we have

$$\begin{array}{ll}∥q-c∥& \le \frac{{\epsilon }_2}{\mathsf{\Gamma }\left(\xi +1\right)}+\gamma \left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right)\\ & +\left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right){\phi }_2\end{array}$$

(33)

and

$$\begin{array}{ll}∥\wp -s∥& \le \frac{{\epsilon }_3}{\mathsf{\Gamma }\left(\delta +1\right)}+\varkappa \left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right)\\ & +\left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right){\phi }_3.\end{array}$$

(34)

From (32)–(34), we get

$$\begin{array}{ll}\left(1-\left(\omega +{\phi }_1\right)\right)∥\mu -z∥& -\left(\omega +{\phi }_1\right)∥q-c∥-\left(\omega +{\phi }_1\right)∥\wp -s∥\le \frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)},\end{array}$$

$$\begin{array}{ll}-\left(\gamma +{\phi }_2\right)∥\mu -z∥& +\left(1-\left(\gamma +{\phi }_2\right)\right)∥q-c∥-\left(\gamma +{\phi }_2\right)∥\wp -s∥\le \frac{{\epsilon }_2}{\mathsf{\Gamma }\left(\xi +1\right)},\end{array}$$

and

$$\begin{array}{ll}-\left(\varkappa +{\phi }_3\right)∥\mu -z∥& -\left(\varkappa +{\phi }_3\right)∥q-c∥+\left(1-\left(\varkappa +{\phi }_3\right)\right)∥\wp -s∥\le \frac{{\epsilon }_3}{\mathsf{\Gamma }\left(\delta +1\right)}.\end{array}$$

The inequalities above can be arranged as

$$\left[\begin{array}{lll}1-\left(\omega +{\phi }_1\right)& -\left(\omega +{\phi }_1\right)& -\left(\omega +{\phi }_1\right)\\ -\left(\gamma +{\phi }_2\right)& 1-\left(\gamma +{\phi }_2\right)& -\left(\gamma +{\phi }_2\right)\\ -\left(\varkappa +{\phi }_3\right)& -\left(\varkappa +{\phi }_3\right)& 1-\left(\varkappa +{\phi }_3\right)\end{array}\right]\left[\begin{array}{l}∥\mu -z∥\\ ∥q-c∥\\ ∥\wp -s∥\end{array}\right]\le \left[\begin{array}{l}\frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)}\\ \frac{{\epsilon }_2}{\mathsf{\Gamma }\left(\xi +1\right)}\\ \frac{{\epsilon }_3}{\mathsf{\Gamma }\left(\delta +1\right)}\end{array}\right].$$

Applying (30) in the above inequality, we have

$$\left[\begin{array}{l}∥\mu -z∥\\ ∥q-c∥\\ ∥\wp -s∥\end{array}\right]\le {\left[\begin{array}{lll}1-{\mho }_1& -{\mho }_1& -{\mho }_1\\ -{\mho }_2& 1-{\mho }_2& -{\mho }_2\\ -{\mho }_3& -{\mho }_3& 1-{\mho }_3\end{array}\right]}^{-1}\left[\begin{array}{l}\frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)}\\ \frac{{\epsilon }_2}{\mathsf{\Gamma }\left(\xi +1\right)}\\ \frac{{\epsilon }_3}{\mathsf{\Gamma }\left(\delta +1\right)}\end{array}\right].$$

(35)

By simplification and putting $D=1-\left({\mho }_1+{\mho }_2+{\mho }_3\right),$ (35) implies that

$$∥\mu -z∥\le \frac{1-\left({\mho }_2+{\mho }_3\right)}{D}\frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{{\mho }_1}{D}\frac{{\epsilon }_2}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{{\mho }_1}{D}\frac{{\epsilon }_3}{\mathsf{\Gamma }\left(\delta +1\right)},$$

(36)

$$∥q-c∥\le \frac{{\mho }_2}{D}\frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{1-\left({\mho }_1+{\mho }_3\right)}{D}\frac{{\epsilon }_2}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{{\mho }_2}{D}\frac{{\epsilon }_3}{\mathsf{\Gamma }\left(\delta +1\right)},$$

(37)

$$∥\wp -s∥\le \frac{{\mho }_3}{D}\frac{{\epsilon }_1}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{{\mho }_3}{D}\frac{{\epsilon }_2}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{1-\left({\mho }_1+{\mho }_2\right)}{D}\frac{{\epsilon }_3}{\mathsf{\Gamma }\left(\delta +1\right)}.$$

(38)

Hence, from (36)–(38) and taking $\epsilon =max\left\{{\epsilon }_1,{\epsilon }_2,{\epsilon }_3\right\},$ we have

$$∥\left(\mu ,q,\wp \right)-\left(z,c,s\right)∥\le {\aleph }_{\vartheta ,\xi ,\delta ,D},$$

where

$${\aleph }_{\vartheta ,\xi ,\delta ,D}=\frac{1}{D}\left[\frac{1}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{1}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{1}{\mathsf{\Gamma }\left(\delta +1\right)}\right].$$

Therefore, the solution of the suggested system (2) is UH stable. In addition, suppose that $\hslash \left(\epsilon \right)={\aleph }_{\vartheta ,\xi ,\delta ,D}$, which yields $\hslash \left(\epsilon \right)=0$. So the solution of the proposed problem (2) is $\mathbb{G}$UH stable. □

Now, the following hypothesis is assumed to be accurate in order to obtain the results below:

(H${}_5$)

For some given functions $w,$ r and $g,$ assume that the inequalities below are true

$$I^{\vartheta }w\left(\varsigma \right)\le {\daleth }_{w}w\left(\varsigma \right),I^{\xi }r\left(\varsigma \right)\le {\daleth }_{r}r\left(\varsigma \right),I^{\delta }g\left(\varsigma \right)\le {\daleth }_{g}g\left(\varsigma \right).$$

Lemma 4.

If the postulate $\left(H_5\right)$ holds, the solution $(z,c,s)\in \Xi$ of the following system

$$\left\{\begin{array}{l}{}^C{\mathcal{D}}_{+0}^{\vartheta }\left(z\left(\varsigma \right)-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)+w\left(\varsigma \right),\\ \\ {}^C{\mathcal{D}}_{+0}^{\xi }\left(c\left(\varsigma \right)-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_2\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)+r\left(\varsigma \right),\\ \\ {}^C{\mathcal{D}}_{+0}^{\delta }\left(s\left(\varsigma \right)-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\right)\\ ={\mathsf{\Omega }}_3\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)+g\left(\varsigma \right),\end{array}\right.$$

with conditions

$$z\left(\varsigma \right){|}_{\varsigma =0}=z_0,c\left(\varsigma \right){|}_{\varsigma =0}=c_0,s\left(\varsigma \right){|}_{\varsigma =0}=s_0,$$

(39)

obeys the relations given for each $\varsigma \in \gimel$

$$\begin{array}{ll}\left|z\right(\varsigma )& -(-z_0+{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & -{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & -{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|\\ & \le {\epsilon }_1{\daleth }_{w}w\left(\varsigma \right),\\ \\ \left|c\right(\varsigma )& -(-c_0+{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & -{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & -{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\xi -1}}{\mathsf{\Gamma }\left(\xi \right)}{\mathsf{\Omega }}_2\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|\\ & \le {\epsilon }_2{\daleth }_{r}r\left(\varsigma \right),\\ \\ \left|s\right(\varsigma )& -(-s_0+{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & -{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & -{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\delta -1}}{\mathsf{\Gamma }\left(\delta \right)}{\mathsf{\Omega }}_3\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|\\ & \le {\epsilon }_3{\daleth }_{g}g\left(\varsigma \right).\end{array}$$

(40)

Proof. 

As in Lemma (3), proof can be obtained. □

Theorem 5.

Under assumptions (H${}_1$), (H${}_4$), (H${}_5$) and Lemma 4 with

$${\mho }_1+{\mho }_2+{\mho }_3\ne 1,$$

the proposed system (2) is UHR and $\mathbb{G}$ UHR stable provided that (30) and (31) hold.

Proof. 

Let $\left(z,c,s\right)\in \Xi$ be a chosen point of the suggested system of $\mathbb{FHDDE}$s (2) and $\left(\mu ,q,\wp \right)\in \Xi$ be a unique solution of the considered problem (2); consider

$$\begin{array}{ll}\left|\mu \left(\varsigma \right)-z\left(\varsigma \right)\right|& =|\mu \left(\varsigma \right)-(z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & +{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|\\ & \le |\mu \left(\varsigma \right)-({\mu }_0-{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right){|}_{\varsigma =0}\\ & +{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,\mu \left(\nu u\right),q\left(\nu u\right),\wp \left(\nu u\right)\right)\mathrm{d}u)|\\ & +\left|\right({\mu }_0-{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right){|}_{\varsigma =0}\\ & +{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)\\ & -(z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\\ & +{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\mathrm{d}u)|,\end{array}$$

it follows that

$$\begin{array}{ll}\left|\mu \left(\varsigma \right)-z\left(\varsigma \right)\right|& \le {\epsilon }_1{\daleth }_{w}w\left(\varsigma \right)+|{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)\\ & -{\mathsf{\Lambda }}_1\left(\varsigma ,\mu \left(\varsigma \right),q\left(\varsigma \right),\wp \left(\varsigma \right)\right)|\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}|{\mathsf{\Omega }}_1\left(u,z\left(\nu u\right),c\left(\nu u\right),s\left(\nu u\right)\right)\\ & -{\mathsf{\Omega }}_1\left(u,\mu \left(\nu u\right),q\left(\nu u\right),\wp \left(\nu u\right)\right)|\mathrm{d}u\\ & \le {\epsilon }_1{\daleth }_{w}w\left(\varsigma \right)+\omega \left(\left|\mu -z\right|+\left|q-c\right|+\left|\wp -s\right|\right)\\ & +{\int }_0^{\varsigma }\frac{{\left(\varsigma -u\right)}^{\vartheta -1}}{\mathsf{\Gamma }\left(\vartheta \right)}\left|p_1\left(\varsigma \right)\right|\left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right)\mathrm{d}u.\end{array}$$

Therefore,

$$\begin{array}{ll}∥\mu -z∥& \le {\epsilon }_1{\daleth }_{w}w\left(\varsigma \right)+\omega \left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right)\\ & +{\phi }_1\left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right).\end{array}$$

(41)

Analogously

$$\begin{array}{ll}∥q-c∥& \le {\epsilon }_2{\daleth }_{r}r\left(\varsigma \right)+\gamma \left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right)\\ & +{\phi }_2\left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right)\end{array}$$

(42)

and

$$\begin{array}{ll}∥\wp -s∥& \le {\epsilon }_3{\daleth }_{g}g\left(\varsigma \right)+\varkappa \left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right)\\ & +{\phi }_3\left(∥\mu -z∥+∥q-c∥+∥\wp -s∥\right).\end{array}$$

(43)

Now, inequalities (41)–(43) can be written in matrix form as

$$\left[\begin{array}{l}∥\mu -z∥\\ ∥q-c∥\\ ∥\wp -s∥\end{array}\right]\le {\left[\begin{array}{lll}1-{\mho }_1& -{\mho }_1& -{\mho }_1\\ -{\mho }_2& 1-{\mho }_2& -{\mho }_2\\ -{\mho }_3& -{\mho }_3& 1-{\mho }_3\end{array}\right]}^{-1}\left[\begin{array}{l}{\epsilon }_1{\daleth }_{w}w\left(\varsigma \right)\\ {\epsilon }_2{\daleth }_{r}r\left(\varsigma \right)\\ {\epsilon }_3{\daleth }_{g}g\left(\varsigma \right)\end{array}\right].$$

(44)

Solving (44) and putting $D=1-\left({\mho }_1+{\mho }_2+{\mho }_3\right),$

$$max\left\{{\daleth }_{w}w\left(\varsigma \right),{\daleth }_{r}r\left(\varsigma \right),{\daleth }_{g}g\left(\varsigma \right)\right\}={\daleth }_{w}w\left(\varsigma \right)$$

and $\epsilon =max\left\{{\epsilon }_1,{\epsilon }_2,{\epsilon }_3\right\},$ we have

$$∥\mu -z∥+∥q-c∥+∥\wp -s∥\le {\aleph }_{w,D}w\left(\varsigma \right),$$

where ${\aleph }_{w,D}=\frac{3{\daleth }_w}{D}$. Therefore, the solution of the suggested system (2) is UHR stable with respect to w. Obviously, one can show that the considered Problem (2) is $\mathbb{G}$UHR stable with respect to w. □

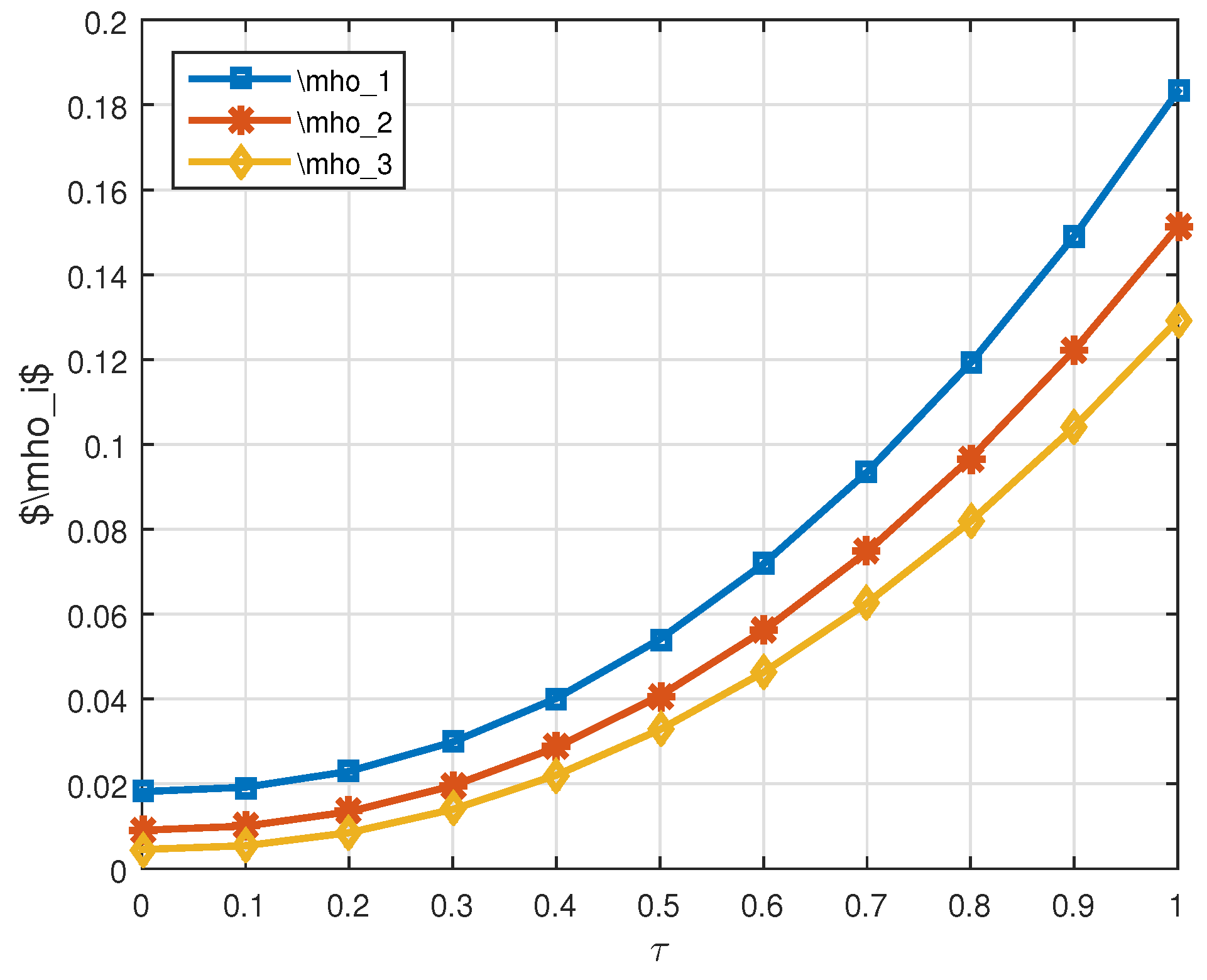
5. Supportive Example

To reinforce our study findings, we present the example below. All the experiments were carried out in MATLAB Ver. 8.5.0.197613 (R2015a) on a computer equipped with a CPU AMD Athlon(tm) II X2 245 at 2.90 GHz running under the operating system Windows 7.

Example 1.

Define the following system of $\mathbb{FHDDE}$s with $\tau =1$ so $\varsigma \in \gimel =\left[0,1\right]$ by

$$\left\{\begin{array}{l}{}^C{D}^{\frac{1}{5}}\left(z\left(\varsigma \right)-\frac{1}{55}\left(sin\varsigma +cos\left|z\left(\varsigma \right)\right|+c\left(\varsigma \right)+s\left(\varsigma \right)\right)\right)\\ =\frac{\varsigma }{5}\left(\varsigma +sin\left|z\left(\frac{\varsigma }{5}\right)\right|+c\left(\frac{\varsigma }{5}\right)+s\left(\frac{\varsigma }{5}\right)\right),\\ \\ {}^C{D}^{\frac{1}{6}}\left(c\left(\varsigma \right)-\frac{1}{110}\left(cos\varsigma +z\left(\varsigma \right)+cosc\left(\varsigma \right)+s\left(\varsigma \right)\right)\right)\\ =\frac{\varsigma }{6}\left(\varsigma +z\left(\frac{\varsigma }{5}\right)+sin\left|c\left(\frac{\varsigma }{5}\right)\right|+s\left(\frac{\varsigma }{5}\right)\right),\\ \\ {}^C{D}^{\frac{1}{7}}\left(s\left(\varsigma \right)-\frac{1}{220}\left(e^{\varsigma }+z\left(\varsigma \right)+c\left(\varsigma \right)+coss\left(\varsigma \right)\right)\right)\\ =\frac{\varsigma }{7}\left(\varsigma +z\left(\frac{\varsigma }{5}\right)+c\left(\frac{\varsigma }{5}\right)+sin\left|s\left(\frac{\varsigma }{5}\right)\right|\right),\end{array}\right.$$

(45)

under conditions

$$z\left(\varsigma \right){|}_{\varsigma =0}=1,c\left(\varsigma \right){|}_{\varsigma =0}=\frac{1}{2},s\left(\varsigma \right){|}_{\varsigma =0}=\frac{1}{4}.$$

(46)

Clearly, $\vartheta =\frac{1}{5}\in (0,1)$, $\xi =\frac{1}{6}\in (0,1)$, $\delta =\frac{1}{7}\in (0,1)$, $z_0=1\in \mathbb{R}$, $c_0=\frac{1}{2}\in \mathbb{R}$, $s_0=\frac{1}{4}\in \mathbb{R}$. From (45), we get

$$\begin{array}{ll}{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)& =\frac{1}{55}\left(sin\varsigma +cos\left|z\left(\varsigma \right)\right|+c\left(\varsigma \right)+s\left(\varsigma \right)\right),\\ {\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)& =\frac{1}{110}\left(cos\varsigma +z\left(\varsigma \right)+cos\left|c\left(\varsigma \right)\right|+s\left(\varsigma \right)\right),\\ {\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right)& =\frac{1}{220}\left(e^{\varsigma }+z\left(\varsigma \right)+c\left(\varsigma \right)+cos\left|s\left(\varsigma \right)\right|\right),\end{array}$$

and

$$\begin{array}{ll}{\mathsf{\Omega }}_1\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)& =\frac{\varsigma }{5}\left(\varsigma +sin\left|z\left(\frac{\varsigma }{5}\right)\right|+c\left(\frac{\varsigma }{5}\right)+s\left(\frac{\varsigma }{5}\right)\right),\\ {\mathsf{\Omega }}_2\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)& =\frac{\varsigma }{6}\left(\varsigma +z\left(\frac{\varsigma }{5}\right)+sin\left|c\left(\frac{\varsigma }{5}\right)\right|+s\left(\frac{\varsigma }{5}\right)\right),\\ {\mathsf{\Omega }}_3\left(\varsigma ,z\left(\nu \varsigma \right),c\left(\nu \varsigma \right),s\left(\nu \varsigma \right)\right)& =\frac{\varsigma }{7}\left(\varsigma +z\left(\frac{\varsigma }{5}\right)+c\left(\frac{\varsigma }{5}\right)+sin\left|s\left(\frac{\varsigma }{5}\right)\right|\right).\end{array}$$

Further, we can get $\omega =\frac{1}{55}$, $\gamma =\frac{1}{110}$, $\varkappa =\frac{1}{220}$, ${\eta }_1=\frac{1}{5}$, ${\eta }_2=\frac{1}{6}$, ${\eta }_3=\frac{1}{7}$, $p_1=p_2=p_3=\frac{{\varsigma }^2}{5}$, using (13) we have

$$\begin{array}{ll}{\psi }_1& =\left|z_0-{\mathsf{\Lambda }}_1\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\right|=|1-\frac{1}{55}\left(0+cos1+\frac{1}{2}+\frac{1}{4}\right)|\\ & =|1-\frac{1}{55}\times 1.2903|=0.9765,\\ {\psi }_2& =\left|c_0-{\mathsf{\Lambda }}_2\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\right|=|\frac{1}{2}-\frac{1}{110}\left(1+1+cos\frac{1}{2}+\frac{1}{4}\right)|\\ & =|\frac{1}{2}-\frac{1}{110}\times 3.1276|=0.4716,\\ {\psi }_3& =\left|s_0-{\mathsf{\Lambda }}_3\left(\varsigma ,z\left(\varsigma \right),c\left(\varsigma \right),s\left(\varsigma \right)\right){|}_{\varsigma =0}\right|=|\frac{1}{4}-\frac{1}{220}\left(1+1+\frac{1}{2}+cos\frac{1}{4}\right)|\\ & =|\frac{1}{4}-\frac{1}{220}\times 3.4689|=0.2342.\end{array}$$

using (4), we get

$$\begin{array}{ll}{\ell }_1& =\underset{\varsigma \in \left[0,1\right]}{\sup }\left|{\mathsf{\Lambda }}_1\left(\varsigma ,0,0,0\right)\right|\\ & =\underset{\varsigma \in \left[0,1\right]}{\sup }\left|\frac{1}{55}\left(sin\varsigma +cos\left|z\left(\varsigma \right)\right|+c\left(\varsigma \right)+s\left(\varsigma \right)\right)\right|=0.0153,\\ {\ell }_2& =\underset{\varsigma \in \left[0,1\right]}{\sup }\left|{\mathsf{\Lambda }}_2\left(\varsigma ,0,0,0\right)\right|\\ & =\underset{\varsigma \in \left[0,1\right]}{\sup }\left|\frac{1}{110}\left(cos\varsigma +z\left(\varsigma \right)+cos\left|c\left(\varsigma \right)\right|+s\left(\varsigma \right)\right)\right|=0.0091,\\ {\ell }_3& =\underset{\varsigma \in \left[0,1\right]}{\sup }\left|{\mathsf{\Lambda }}_3\left(\varsigma ,0,0,0\right)\right|\\ & =\underset{\varsigma \in \left[0,1\right]}{\sup }\left|\frac{1}{220}\left(e^{\varsigma }+z\left(\varsigma \right)+c\left(\varsigma \right)+cos\left|s\left(\varsigma \right)\right|\right)\right|=0.0124,\end{array}$$

and, by employing Equation (5), we obtain

$$\begin{array}{ll}{J}_z& =\underset{\varsigma \in \gimel }{\sup }\left\{\left|b_i\left(\varsigma \right)\right|:i=1,2,3\right\}=\underset{\varsigma \in \gimel }{\sup }\frac{\varsigma }{5}=\frac{1}{5},\\ J_c& =\underset{\varsigma \in \gimel }{\sup }\left\{\left|d_i\left(\varsigma \right)\right|:i=1,2,3\right\}=\underset{\varsigma \in \gimel }{\sup }\frac{\varsigma }{6}=\frac{1}{6},\\ J_s& =\underset{\varsigma \in \gimel }{\sup }\left\{\left|e_i\left(\varsigma \right)\right|:i=1,2,3\right\}=\underset{\varsigma \in \gimel }{\sup }\frac{\varsigma }{7}=\frac{1}{7},\end{array}$$

and so, $J=max\left\{\frac{1}{5},\frac{1}{6},\frac{1}{7}\right\}=\frac{1}{5}$. From (12), we deduce that

$$\begin{array}{ll}{\rm Y}& =\left(\omega +\gamma +\varkappa +\frac{{\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{{\tau }^{\xi }}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{{\tau }^{\delta }}{\mathsf{\Gamma }\left(\delta +1\right)}\right)J\\ & =\frac{1}{5}\left(0.0181+0.0090+0.0045+\frac{{\tau }^{\frac{1}{5}}}{\mathsf{\Gamma }\left(\frac{6}{5}\right)}+\frac{{\tau }^{\frac{1}{6}}}{\mathsf{\Gamma }\left(\frac{7}{6}\right)}+\frac{{\tau }^{\frac{1}{7}}}{\mathsf{\Gamma }\left(\frac{8}{7}\right)}\right)\simeq 0.6536<1.\end{array}$$

One can check these numerical results in Table 1 and can see a 2D plot of υ, $\mathbb{R}\ge$ and ${\phi }_i(i=1,2,3)$ in Figure 1a–c for $\tau \in [0,1]$.

Table 1. Numerical values of $\mathrm{Y}$ and ${\phi }_i(i=1,2,3)$ in Example 1.

			${\mathit{\phi }}_{\mathit{i}}\left(\mathit{\tau }\right)$
$\mathit{\tau }$	$\mathbf{Y}$	$\le \mathbb{R}$	${\mathbf{\phi }}_{\mathbf{1}}$	${\mathbf{\phi }}_{\mathbf{2}}$	${\mathbf{\phi }}_{\mathbf{3}}$
$0.00$	$0.0064$	$1.7301$	$0.0000$	$0.0000$	$0.0000$
$0.10$	$0.4445$	$7.0393$	$0.0010$	$0.0010$	$0.0009$
$0.20$	$0.4990$	$8.3475$	$0.0048$	$0.0043$	$0.0040$
$0.30$	$0.5340$	$9.3498$	$0.0117$	$0.0105$	$0.0095$
$0.40$	$0.5603$	$10.2100$	$0.0220$	$0.0195$	$0.0175$
$0.50$	$0.5817$	$10.9868$	$0.0359$	$0.0317$	$0.0282$
$0.60$	$0.5998$	$11.7089$	$0.0536$	$0.0470$	$0.0417$
$0.70$	$0.6155$	$12.3928$	$0.0753$	$0.0656$	$0.0581$
$0.80$	$0.6295$	$13.0488$	$0.1010$	$0.0877$	$0.0773$
$0.90$	$0.6421$	$13.6841$	$0.1309$	$0.1131$	$0.0995$
$1.00$	$0.6536$	$14.3037$	$0.1650$	$0.1421$	$0.1247$

Figure 1. Graphical representation of $\mathrm{Y}$$\le \mathbb{R}$ and ${\phi }_i(i=1,2,3)$ in Example 1 for $\tau \in [0,1]$.

Further,

$$\frac{\left[{\psi }_1+{\psi }_2+{\psi }_3+{\ell }_1+{\ell }_2+{\ell }_3+\frac{{\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{{\tau }^{\xi }}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{{\tau }^{\delta }}{\mathsf{\Gamma }\left(\delta +1\right)}\right]}{1-\left(\omega +\gamma +\varkappa +\frac{{\tau }^{\vartheta }}{\mathsf{\Gamma }\left(\vartheta +1\right)}+\frac{{\tau }^{\xi }}{\mathsf{\Gamma }\left(\xi +1\right)}+\frac{{\tau }^{\delta }}{\mathsf{\Gamma }\left(\delta +1\right)}\right)J}\simeq 14.3037\le \mathbb{R},$$

$${\phi }_1=0.1650,{\phi }_2=0.1421,{\phi }_3=0.1247,$$

Therefore, assumptions (H${}_1$), (H${}_2$), (H${}_3$) hold and so, by Theorem 3, the problem (45) has at least one solution. The red dotted lines in Figure 1b show that $\mathbb{R}$ must be more than $14.35$ for $\tau \in [0,1]$. So, applying Theorem 3, we conclude that the proposed Problem (45)

$$O=\left\{\left(z,c,s\right)\in \Xi :∥\left(z,c,s\right)∥\le \mathbb{R},\mathrm{s}.\mathrm{t}\mathbb{R}\ge 14.3037\right\}.$$

In addition to,

$${\mho }_1=\omega +{\phi }_1=0.1832,{\mho }_2=\gamma +{\phi }_2=0.1512,{\mho }_3=\varkappa +{\phi }_3=0.1292,$$

we obtain ${\mho }_1+{\mho }_2+{\mho }_3\simeq 0.4637\ne 1;$ this proves that the solution of (45) is UH stable, and the proposed solution is simply demonstrated to be $\mathbb{G}$UH stable.

One can check these numerical results in Table 2, which shows the numerical results of ${\mho }_i(i=1,2,3)$. A 2D plot of ${\mho }_i(i=1,2,3)$ is shown in Figure 2 for $\tau \in [0,1]$.

Table 2. Numerical values of ${\mho }_i(i=1,2,3)$ in Example 1.

	${\mho }_{\mathit{i}}\left(\mathit{\tau }\right)$
$\mathit{\tau }$	${\mho }_{\mathbf{1}}$	${\mho }_{\mathbf{2}}$	${\mho }_{\mathbf{3}}$	${\mho }_{\mathbf{1}}+{\mho }_{\mathbf{2}}+{\mho }_{\mathbf{3}}\ne \mathbf{1}$
$0.00$	$0.0182$	$0.0091$	$0.0045$	$0.0318$
$0.10$	$0.0192$	$0.0101$	$0.0054$	$0.0347$
$0.20$	$0.0230$	$0.0134$	$0.0085$	$0.0449$
$0.30$	$0.0299$	$0.0196$	$0.0140$	$0.0634$
$0.40$	$0.0402$	$0.0286$	$0.0221$	$0.0908$
$0.50$	$0.0541$	$0.0408$	$0.0328$	$0.1276$
$0.60$	$0.0718$	$0.0561$	$0.0463$	$0.1742$
$0.70$	$0.0935$	$0.0747$	$0.0626$	$0.2308$
$0.80$	$0.1192$	$0.0967$	$0.0819$	$0.2978$
$0.90$	$0.1491$	$0.1222$	$0.1041$	$0.3753$
$1.00$	$0.1832$	$0.1512$	$0.1293$	$0.4637$

Figure 2. Graphical representation of $\mho +i$ for $\tau \in [0,1]$ in Example 1.

Moreover, for $w\left(\varsigma \right)=r\left(\varsigma \right)=g\left(\varsigma \right)=\varsigma$; similarly, Theorem 5 states that the requirements of UHR and $\mathbb{G}$UHR stability can be easily satisfied.

6. Conclusions

In this paper, we defined a new fractional mathematical model of an $\mathbb{FHDDE}$ and investigated the qualitative behaviors of its solutions, including existence, uniqueness and stability. To confirm the existence criterion, we utilized the presumptions of the famous fixed point for the operator within the hybrid case. Modeling using systems of fractional differential equations is an important class of bio-mathematics, physics, applied chemistry and many other areas. The field has recently been extended to FDEs as well. BVPs have many applications in engineering and physical sciences. In addition, stability analysis in the Ulam–Hyers sense of a given system was considered. Finally, illustrations were provided to confirm the legitimacy of the results obtained.