From Five-Loop Scattering Amplitudes to Open Trees with the Loop-Tree Duality
Abstract
1. Introduction and Motivation
2. LTD Framework
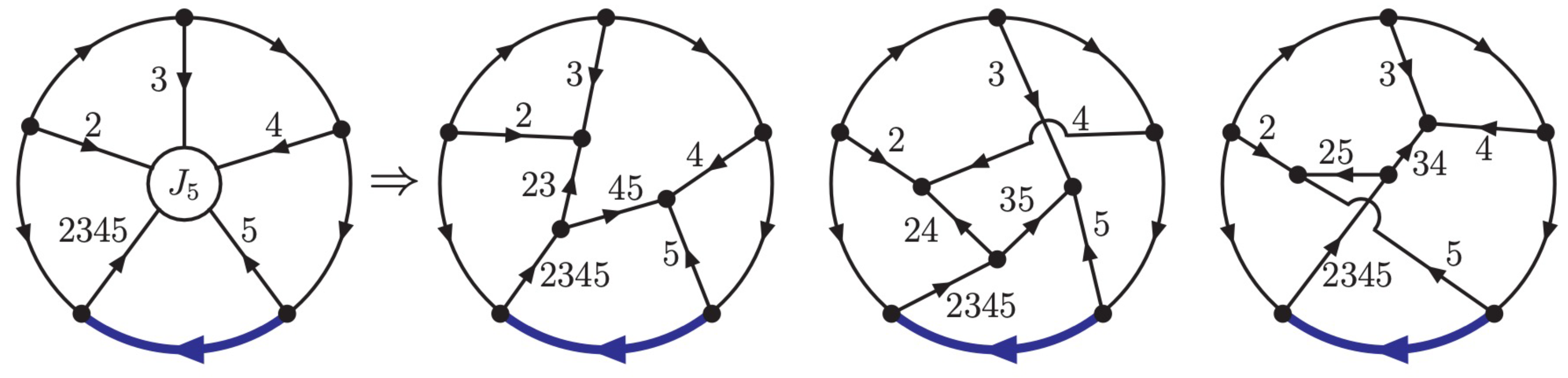
3. Universal Topology

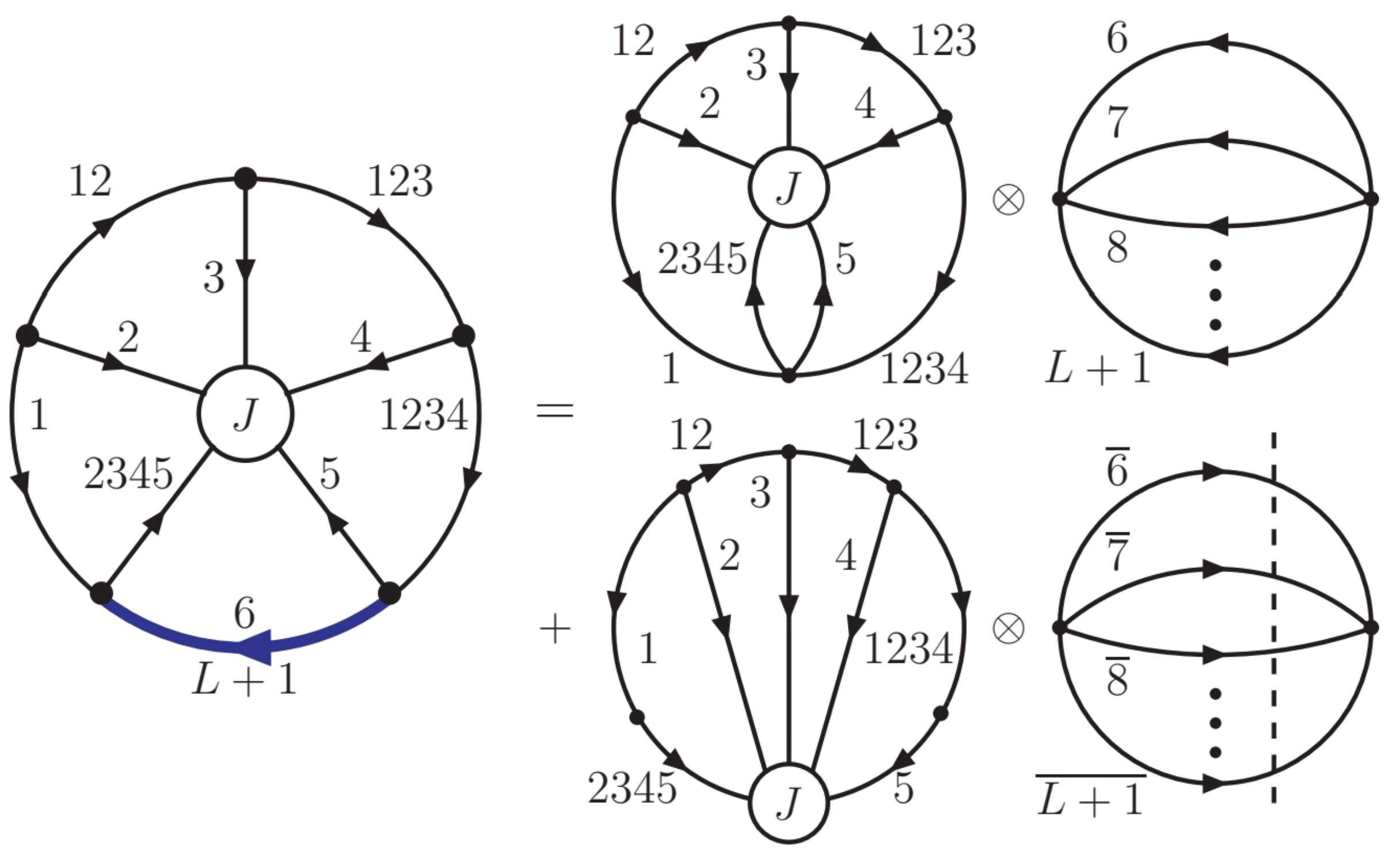
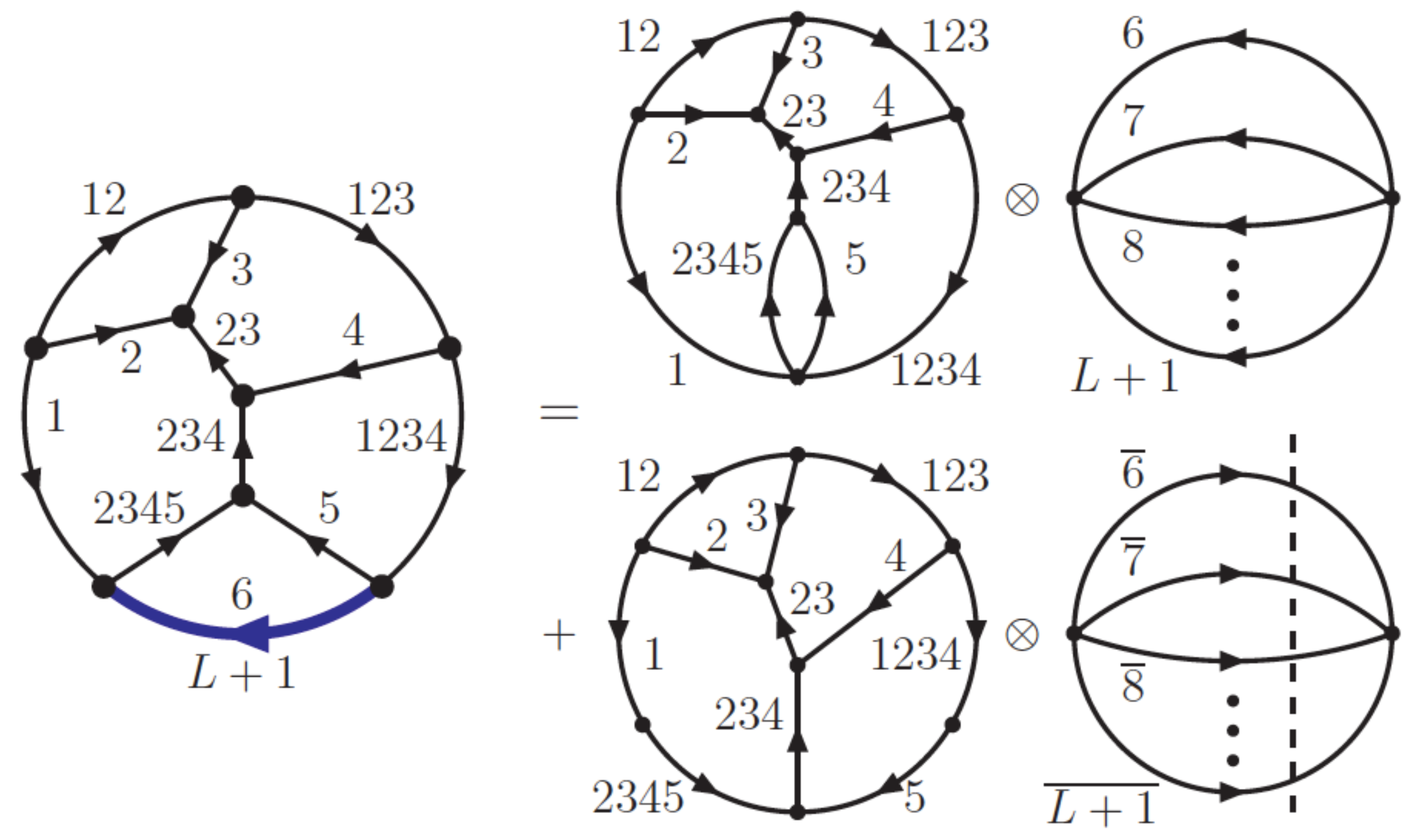
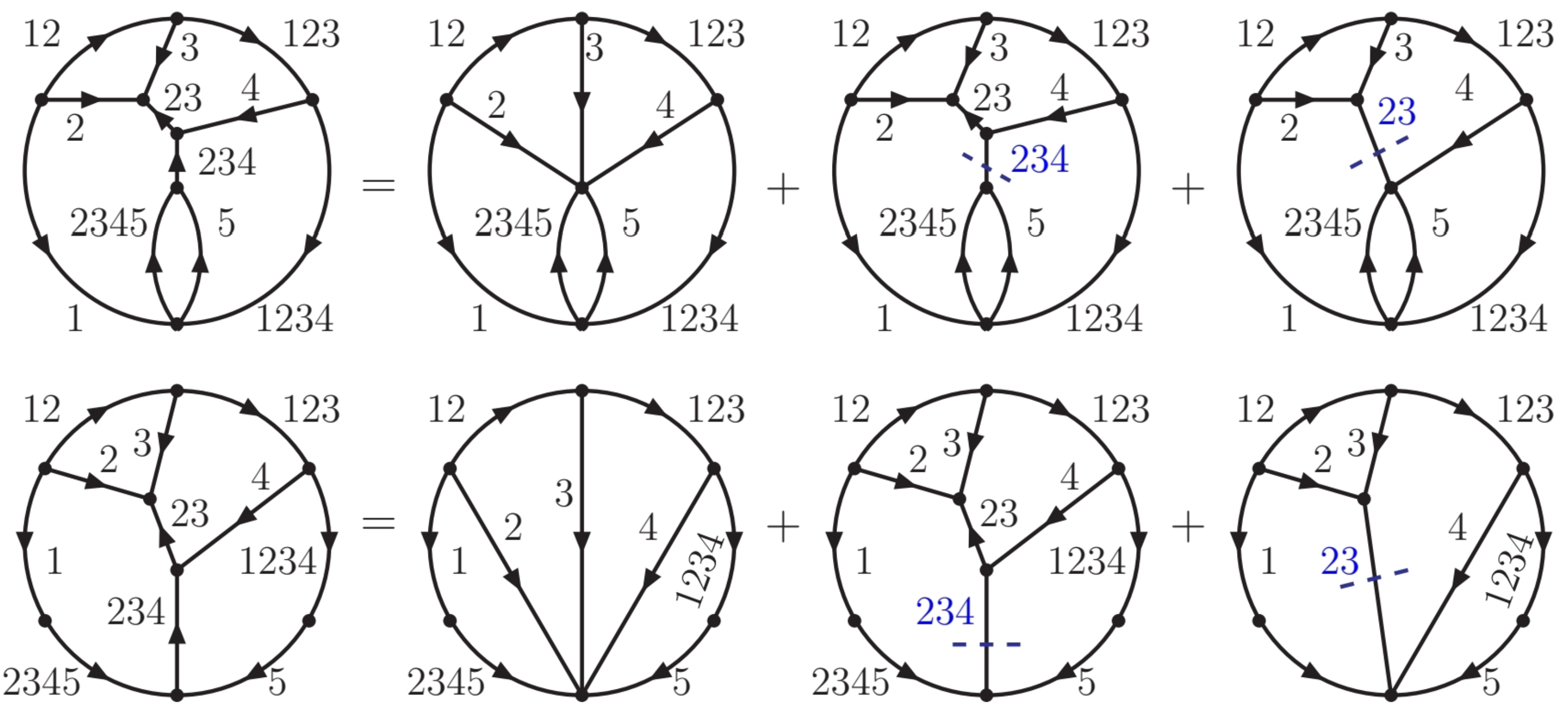
4. Specific Channels
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abada, A.; Abbrescia, M.; AbdusSalam, S.S.; Abdyukhanov, I.; Abelleira Fernandez, J.; Abramov, A.; Aburaia, M.; Acar, A.O.; Adzic, P.R.; Agrawal, P.; et al. FCC Physics Opportunities: Future Circular Collider Conceptual Design Report Volume 1. Eur. Phys. J. C 2019, 79, 474. [Google Scholar] [CrossRef]
- Bambade, P.; Barklow, T.; Behnke, T.; Berggren, M.; Brau, J.; Burrows, P.; Denisov, D.; Faus-Golfe, A.; Foster, B.; Fujii, K.; et al. The International Linear Collider: A Global Project. arXiv 2019, arXiv:1903.01629. [Google Scholar]
- Roloff, P.; de Blas, J.; Franceschini, R.; Riva, F.; Schnoor, U.; Spannoswsky, M.; Wells, J.D.; Wulzer, A.; Zupan, J.; Alipour-Fard, S.; et al. The Compact Linear e+e− Collider (CLIC): Physics Potential. arXiv 2018, arXiv:1812.07986. [Google Scholar]
- CEPC Study Group. CEPC Conceptual Design Report: Volume 2-Physics & Detector. arXiv 2018, arXiv:1811.10545. [Google Scholar]
- Gehrmann, T.; Kara, D. The Hb form factor to three loops in QCD. JHEP 2014, 9, 174. [Google Scholar] [CrossRef]
- Broggio, A.; Gnendiger, C.; Signer, A.; Stöckinger, D.; Visconti, A. Computation of H→gg in DRED and FDH: Renormalization, operator mixing, and explicit two-loop results. Eur. Phys. J. C 2015, 75, 418. [Google Scholar] [CrossRef]
- Page, B.; Pittau, R. Two-loop off-shell QCD amplitudes in FDR. JHEP 2015, 11, 183. [Google Scholar] [CrossRef]
- Cacciari, M.; Dreyer, F.A.; Karlberg, A.; Salam, G.P.; Zanderighi, G. Fully Differential Vector-Boson-Fusion Higgs Production at Next-to-Next-to-Leading Order. Phys. Rev. Lett. 2015, 115, 082002, Erratum in Phys. Rev. Lett. 2018, 120, 139901. [Google Scholar] [CrossRef]
- Aybat, S.M.; Dixon, L.J.; Sterman, G.F. The Two-loop anomalous dimension matrix for soft gluon exchange. Phys. Rev. Lett. 2006, 97, 072001. [Google Scholar] [CrossRef]
- Dreyer, F.A.; Karlberg, A. Vector-Boson Fusion Higgs Production at Three Loops in QCD. Phys. Rev. Lett. 2016, 117, 072001. [Google Scholar] [CrossRef]
- Catani, S. The Singular behavior of QCD amplitudes at two loop order. Phys. Lett. B 1998, 427, 161–171. [Google Scholar] [CrossRef]
- Bern, Z.; Del Duca, V.; Kilgore, W.B.; Schmidt, C.R. The infrared behavior of one loop QCD amplitudes at next-to-next-to leading order. Phys. Rev. D 1999, 60, 116001. [Google Scholar] [CrossRef]
- Becher, T.; Neubert, M. Infrared singularities of scattering amplitudes in perturbative QCD. Phys. Rev. Lett. 2009, 102, 162001, Erratum in Phys. Rev. Lett. 2013, 111, 199905. [Google Scholar] [CrossRef]
- Gehrmann-De Ridder, A.; Gehrmann, T.; Glover, E.W.N.; Heinrich, G. Infrared structure of e+ e- —> 3 jets at NNLO. JHEP 2007, 11, 58. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Moult, I.; Stewart, I.W.; Vita, G. Helicity Methods for High Multiplicity Subleading Soft and Collinear Limits. JHEP 2019, 5, 192. [Google Scholar] [CrossRef]
- Borinsky, M. Tropical Monte Carlo quadrature for Feynman integrals. arXiv 2020, arXiv:2008.12310. [Google Scholar]
- Chetyrkin, K.G.; Tkachov, F.V. Integration by Parts: The Algorithm to Calculate beta Functions in 4 Loops. Nucl. Phys. 1981, B192, 159–204. [Google Scholar] [CrossRef]
- Laporta, S. High precision calculation of multiloop Feynman integrals by difference equations. Int. J. Mod. Phys. A 2000, 15, 5087–5159. [Google Scholar] [CrossRef]
- Herzog, F. Geometric IR subtraction for final state real radiation. JHEP 2018, 8, 6. [Google Scholar] [CrossRef]
- Catani, S.; Seymour, M. The Dipole formalism for the calculation of QCD jet cross-sections at next-to-leading order. Phys.Lett. 1996, B378, 287–301. [Google Scholar] [CrossRef]
- Catani, S.; Seymour, M. A General algorithm for calculating jet cross-sections in NLO QCD. Nucl. Phys. 1997, B485, 291–419. [Google Scholar] [CrossRef]
- Catani, S.; Grazzini, M. Infrared factorization of tree level QCD amplitudes at the next-to-next-to-leading order and beyond. Nucl. Phys. B 2000, 570, 287–325. [Google Scholar] [CrossRef]
- de Florian, D.; Grazzini, M. Next-to-next-to-leading logarithmic corrections at small transverse momentum in hadronic collisions. Phys. Rev. Lett. 2000, 85, 4678–4681. [Google Scholar] [CrossRef]
- Catani, S.; Dittmaier, S.; Seymour, M.H.; Trocsanyi, Z. The Dipole formalism for next-to-leading order QCD calculations with massive partons. Nucl.Phys. 2002, B627, 189–265. [Google Scholar] [CrossRef]
- Frixione, S.; Kunszt, Z.; Signer, A. Three jet cross-sections to next-to-leading order. Nucl. Phys. 1996, B467, 399–442. [Google Scholar] [CrossRef]
- Frixione, S. A General approach to jet cross-sections in QCD. Nucl. Phys. B 1997, 507, 295–314. [Google Scholar] [CrossRef]
- Frixione, S.; Grazzini, M. Subtraction at NNLO. JHEP 2005, 6, 10. [Google Scholar] [CrossRef]
- Bozzi, G.; Catani, S.; de Florian, D.; Grazzini, M. The q(T) spectrum of the Higgs boson at the LHC in QCD perturbation theory. Phys. Lett. B 2003, 564, 65–72. [Google Scholar] [CrossRef][Green Version]
- Bozzi, G.; Catani, S.; de Florian, D.; Grazzini, M. Transverse-momentum resummation and the spectrum of the Higgs boson at the LHC. Nucl. Phys. B 2006, 737, 73–120. [Google Scholar] [CrossRef]
- Catani, S.; Grazzini, M. An NNLO subtraction formalism in hadron collisions and its application to Higgs boson production at the LHC. Phys. Rev. Lett. 2007, 98, 222002. [Google Scholar] [CrossRef]
- Catani, S.; Grazzini, M. QCD transverse-momentum resummation in gluon fusion processes. Nucl. Phys. B 2011, 845, 297–323. [Google Scholar] [CrossRef]
- Catani, S.; Cieri, L.; de Florian, D.; Ferrera, G.; Grazzini, M. Vector boson production at hadron colliders: Hard-collinear coefficients at the NNLO. Eur. Phys. J. C 2012, 72, 2195. [Google Scholar] [CrossRef]
- Catani, S.; Cieri, L.; de Florian, D.; Ferrera, G.; Grazzini, M. Universality of transverse-momentum resummation and hard factors at the NNLO. Nucl. Phys. B 2014, 881, 414–443. [Google Scholar] [CrossRef]
- Bonciani, R.; Catani, S.; Grazzini, M.; Sargsyan, H.; Torre, A. The qT subtraction method for top quark production at hadron colliders. Eur. Phys. J. C 2015, 75, 581. [Google Scholar] [CrossRef]
- Cieri, L.; Chen, X.; Gehrmann, T.; Glover, E.W.N.; Huss, A. Higgs boson production at the LHC using the qT subtraction formalism at N3LO QCD. JHEP 2019, 2, 96. [Google Scholar] [CrossRef]
- Catani, S.; Devoto, S.; Grazzini, M.; Kallweit, S.; Mazzitelli, J.; Sargsyan, H. Top-quark pair hadroproduction at next-to-next-to-leading order in QCD. Phys. Rev. D 2019, 99, 051501. [Google Scholar] [CrossRef]
- Buonocore, L.; Grazzini, M.; Tramontano, F. The qT subtraction method: Electroweak corrections and power suppressed contributions. Eur. Phys. J. C 2020, 80, 254. [Google Scholar] [CrossRef]
- Kosower, D.A. Antenna factorization of gauge theory amplitudes. Phys. Rev. D 1998, 57, 5410–5416. [Google Scholar] [CrossRef]
- Campbell, J.M.; Glover, E.W.N. Double unresolved approximations to multiparton scattering amplitudes. Nucl. Phys. B 1998, 527, 264–288. [Google Scholar] [CrossRef]
- Gehrmann-De Ridder, A.; Gehrmann, T.; Glover, E.W.N. Antenna subtraction at NNLO. JHEP 2005, 9, 56. [Google Scholar] [CrossRef]
- Daleo, A.; Gehrmann, T.; Maitre, D. Antenna subtraction with hadronic initial states. JHEP 2007, 4, 16. [Google Scholar] [CrossRef]
- Nigel Glover, E.W.; Pires, J. Antenna subtraction for gluon scattering at NNLO. JHEP 2010, 6, 96. [Google Scholar] [CrossRef]
- Currie, J.; Glover, E.W.N.; Wells, S. Infrared Structure at NNLO Using Antenna Subtraction. JHEP 2013, 4, 66. [Google Scholar] [CrossRef]
- Currie, J.; Gehrmann, T.; Glover, E.W.N.; Huss, A.; Niehues, J.; Vogt, A. N3LO corrections to jet production in deep inelastic scattering using the Projection-to-Born method. JHEP 2018, 5, 209. [Google Scholar] [CrossRef]
- Gehrmann, T.; Huss, A.; Niehues, J.; Vogt, A.; Walker, D.M. Jet production in charged-current deep-inelastic scattering to third order in QCD. Phys. Lett. B 2019, 792, 182–186. [Google Scholar] [CrossRef]
- Somogyi, G.; Trocsanyi, Z.; Del Duca, V. A Subtraction scheme for computing QCD jet cross sections at NNLO: Regularization of doubly-real emissions. JHEP 2007, 1, 70. [Google Scholar] [CrossRef]
- Somogyi, G.; Trocsanyi, Z. A Subtraction scheme for computing QCD jet cross sections at NNLO: Regularization of real-virtual emission. JHEP 2007, 1, 52. [Google Scholar] [CrossRef]
- Czakon, M. A novel subtraction scheme for double-real radiation at NNLO. Phys. Lett. 2010, B693, 259–268. [Google Scholar] [CrossRef]
- Czakon, M. Double-real radiation in hadronic top quark pair production as a proof of a certain concept. Nucl. Phys. B 2011, 849, 250–295. [Google Scholar] [CrossRef]
- Boughezal, R.; Melnikov, K.; Petriello, F. A subtraction scheme for NNLO computations. Phys. Rev. D 2012, 85, 034025. [Google Scholar] [CrossRef]
- Boughezal, R.; Liu, X.; Petriello, F. N-jettiness soft function at next-to-next-to-leading order. Phys. Rev. D 2015, 91, 094035. [Google Scholar] [CrossRef]
- Gaunt, J.; Stahlhofen, M.; Tackmann, F.J.; Walsh, J.R. N-jettiness Subtractions for NNLO QCD Calculations. JHEP 2015, 9, 58. [Google Scholar] [CrossRef]
- Magnea, L.; Maina, E.; Pelliccioli, G.; Signorile-Signorile, C.; Torrielli, P.; Uccirati, S. Local analytic sector subtraction at NNLO. JHEP 2018, 12, 107, Erratum in JHEP 2019, 6, 13. [Google Scholar] [CrossRef]
- Magnea, L.; Pelliccioli, G.; Signorile-Signorile, C.; Torrielli, P.; Uccirati, S. Analytic integration of soft and collinear radiation in factorised QCD cross sections at NNLO. JHEP 2021, 2, 37. [Google Scholar] [CrossRef]
- Heinrich, G. Collider Physics at the Precision Frontier. Phys. Rept. 2021, 922, 1–69. [Google Scholar] [CrossRef]
- Kreimer, D.; Yeats, K. Algebraic Interplay between Renormalization and Monodromy. arXiv 2021, arXiv:2105.05948. [Google Scholar]
- Borinsky, M.; Capatti, Z.; Laenen, E.; Salas-Bernárdez, A. Flow-oriented perturbation theory. arXiv 2022, arXiv:2210.05532. [Google Scholar]
- Catani, S.; Gleisberg, T.; Krauss, F.; Rodrigo, G.; Winter, J.C. From loops to trees by-passing Feynman’s theorem. JHEP 2008, 9, 65. [Google Scholar] [CrossRef]
- Buchta, S.; Chachamis, G.; Draggiotis, P.; Malamos, I.; Rodrigo, G. On the singular behaviour of scattering amplitudes in quantum field theory. JHEP 2014, 11, 14. [Google Scholar] [CrossRef]
- Tomboulis, E. Causality and Unitarity via the Tree-Loop Duality Relation. JHEP 2017, 5, 148. [Google Scholar] [CrossRef]
- Runkel, R.; Szőr, Z.; Vesga, J.P.; Weinzierl, S. Causality and loop-tree duality at higher loops. Phys. Rev. Lett. 2019, 122, 111603, Erratum in Phys. Rev. Lett. 2019, 123, 059902. [Google Scholar] [CrossRef] [PubMed]
- Capatti, Z.; Hirschi, V.; Kermanschah, D.; Ruijl, B. Loop-Tree Duality for Multiloop Numerical Integration. Phys. Rev. Lett. 2019, 123, 151602. [Google Scholar] [CrossRef] [PubMed]
- Aguilera-Verdugo, J.J.; Driencourt-Mangin, F.; Hernandez Pinto, R.J.; Plenter, J.; Ramirez-Uribe, S.; Renteria Olivo, A.E.; Rodrigo, G.; Sborlini, G.F.; Torres Bobadilla, W.J.; Tracz, S. Open loop amplitudes and causality to all orders and powers from the loop-tree duality. Phys. Rev. Lett. 2020, 124, 211602. [Google Scholar] [CrossRef]
- Aguilera-Verdugo, J.d.J.; Driencourt-Mangin, F.; Hernández-Pinto, R.J.; Plenter, J.; Prisco, R.M.; Ramírez-Uribe, N.S.; Rentería-Olivo, A.E.; Rodrigo, G.; Sborlini, G.; Torres Bobadilla, W.J.; et al. A Stroll through the Loop-Tree Duality. Symmetry 2021, 13, 1029. [Google Scholar] [CrossRef]
- Kromin, S.; Schwanemann, N.; Weinzierl, S. Amplitudes within causal loop-tree duality. Phys. Rev. D 2022, 106, 076006. [Google Scholar] [CrossRef]
- Capatti, Z.; Hirschi, V.; Pelloni, A.; Ruijl, B. Local Unitarity: A representation of differential cross-sections that is locally free of infrared singularities at any order. JHEP 2021, 4, 104. [Google Scholar] [CrossRef]
- Berghoff, M. Schwinger, ltd: Loop-tree duality in the parametric representation. JHEP 2022, 10, 178. [Google Scholar] [CrossRef]
- Runkel, R.; Szőr, Z.; Vesga, J.P.; Weinzierl, S. Integrands of loop amplitudes within loop-tree duality. Phys. Rev. D 2020, 101, 116014. [Google Scholar] [CrossRef]
- Buchta, S.; Chachamis, G.; Draggiotis, P.; Rodrigo, G. Numerical implementation of the loop–tree duality method. Eur. Phys. J. 2017, C77, 274. [Google Scholar] [CrossRef]
- Buchta, S. Theoretical foundations and applications of the Loop-Tree Duality in Quantum Field Theories. Ph.D Thesis, Universidad de Valencia, Valencia, Spain, 2015. arXiv:1509.07167. [Google Scholar]
- Driencourt-Mangin, F.; Rodrigo, G.; Sborlini, G.F.R.; Torres Bobadilla, W.J. Interplay between the loop-tree duality and helicity amplitudes. Phys. Rev. D 2022, 105, 016012. [Google Scholar] [CrossRef]
- Capatti, Z.; Hirschi, V.; Kermanschah, D.; Pelloni, A.; Ruijl, B. Numerical Loop-Tree Duality: Contour deformation and subtraction. JHEP 2020, 4, 96. [Google Scholar] [CrossRef]
- Kermanschah, D. Numerical integration of loop integrals through local cancellation of threshold singularities. JHEP 2022, 1, 151. [Google Scholar] [CrossRef]
- Driencourt-Mangin, F.; Rodrigo, G.; Sborlini, G.F. Universal dual amplitudes and asymptotic expansions for gg→H and H→γγ in four dimensions. Eur. Phys. J. C 2018, 78, 231. [Google Scholar] [CrossRef]
- Plenter, J. Asymptotic Expansions Through the Loop-Tree Duality. Acta Phys. Polon. B 2019, 50, 1983–1992. [Google Scholar] [CrossRef]
- Plenter, J.; Rodrigo, G. Asymptotic expansions through the loop-tree duality. Eur. Phys. J. C 2021, 81, 320. [Google Scholar] [CrossRef]
- Plenter, J. Asymptotic Expansions and Causal Representations through the Loop-Tree Duality. Ph.D Thesis, Universidad de Valencia, Valencia, Spain, 2022. [Google Scholar]
- Driencourt-Mangin, F.; Rodrigo, G.; Sborlini, G.F.R.; Torres Bobadilla, W.J. Universal four-dimensional representation of H→γγ at two loops through the Loop-Tree Duality. JHEP 2019, 2, 143. [Google Scholar] [CrossRef]
- Driencourt-Mangin, F. Four-dimensional representation of scattering amplitudes and physical observables through the application of the Loop-Tree Duality theorem. PhD Thesis, Universidad de Valencia, Valencia, Spain, 2019. arXiv:1907.12450. [Google Scholar]
- Aguilera-Verdugo, J.J.; Driencourt-Mangin, F.; Plenter, J.; Ramírez-Uribe, S.; Rodrigo, G.; Sborlini, G.F.; Torres Bobadilla, W.J.; Tracz, S. Causality, unitarity thresholds, anomalous thresholds and infrared singularities from the loop-tree duality at higher orders. JHEP 2019, 12, 163. [Google Scholar] [CrossRef]
- Hernandez-Pinto, R.J.; Sborlini, G.F.R.; Rodrigo, G. Towards gauge theories in four dimensions. JHEP 2016, 2, 44. [Google Scholar] [CrossRef]
- Sborlini, G.F.R.; Driencourt-Mangin, F.; Hernandez-Pinto, R.; Rodrigo, G. Four-dimensional unsubtraction from the loop-tree duality. JHEP 2016, 8, 160. [Google Scholar] [CrossRef]
- Sborlini, G.F.R.; Driencourt-Mangin, F.; Rodrigo, G. Four-dimensional unsubtraction with massive particles. JHEP 2016, 10, 162. [Google Scholar] [CrossRef]
- Ramírez-Uribe, S.; Hernández-Pinto, R.J.; Rodrigo, G.; Sborlini, G.F.R.; Torres Bobadilla, W.J. Universal opening of four-loop scattering amplitudes to trees. JHEP 2021, 4, 129. [Google Scholar] [CrossRef]
- Jesús Aguilera-Verdugo, J.; Hernández-Pinto, R.J.; Rodrigo, G.; Sborlini, G.F.R.; Torres Bobadilla, W.J. Mathematical properties of nested residues and their application to multi-loop scattering amplitudes. JHEP 2021, 2, 112. [Google Scholar] [CrossRef]
- Aguilera-Verdugo, J.J.; Hernandez-Pinto, R.J.; Rodrigo, G.; Sborlini, G.F.R.; Torres Bobadilla, W.J. Causal representation of multi-loop Feynman integrands within the loop-tree duality. JHEP 2021, 1, 69. [Google Scholar] [CrossRef]
- Bobadilla, W.J.T. Lotty – The loop-tree duality automation. Eur. Phys. J. C 2021, 81, 514. [Google Scholar] [CrossRef]
- Sborlini, G.F.R. Geometrical approach to causality in multiloop amplitudes. Phys. Rev. D 2021, 104, 036014. [Google Scholar] [CrossRef]
- Torres Bobadilla, W.J. Loop-tree duality from vertices and edges. JHEP 2021, 4, 183. [Google Scholar] [CrossRef]
- Capatti, Z.; Hirschi, V.; Kermanschah, D.; Pelloni, A.; Ruijl, B. Manifestly Causal Loop-Tree Duality. arXiv 2020, arXiv:2009.05509. [Google Scholar]
- Chetyrkin, K.G.; Misiak, M.; Munz, M. Beta functions and anomalous dimensions up to three loops. Nucl. Phys. B 1998, 518, 473–494. [Google Scholar] [CrossRef]
- Luthe, T.; Maier, A.; Marquard, P.; Schröder, Y. Towards the five-loop Beta function for a general gauge group. JHEP 2016, 7, 127. [Google Scholar] [CrossRef]
- Baikov, P.A.; Chetyrkin, K.G.; Kühn, J.H. Five-Loop Running of the QCD coupling constant. Phys. Rev. Lett. 2017, 118, 082002. [Google Scholar] [CrossRef]
- Herzog, F.; Ruijl, B.; Ueda, T.; Vermaseren, J.A.M.; Vogt, A. The five-loop beta function of Yang-Mills theory with fermions. JHEP 2017, 2, 90. [Google Scholar] [CrossRef]
- Herzog, F. Zimmermann’s forest formula, infrared divergences and the QCD beta function. Nucl. Phys. B 2018, 926, 370–380. [Google Scholar] [CrossRef]
- Bollini, C.G.; Giambiagi, J.J. Dimensional Renormalization: The Number of Dimensions as a Regularizing Parameter. Nuovo Cim. 1972, B12, 20–26. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Veltman, M.J.G. Regularization and Renormalization of Gauge Fields. Nucl. Phys. 1972, B44, 189–213. [Google Scholar] [CrossRef]
- Cicuta, G.M.; Montaldi, E. Analytic renormalization via continuous space dimension. Lett. Nuovo Cim. 1972, 4, 329–332. [Google Scholar] [CrossRef]
- Ashmore, J.F. A Method of Gauge Invariant Regularization. Lett. Nuovo Cim. 1972, 4, 289–290. [Google Scholar] [CrossRef]
- Capatti, Z.; Hirschi, V.; Ruijl, B. Local unitarity: Cutting raised propagators and localising renormalisation. JHEP 2022, 10, 120. [Google Scholar] [CrossRef]

| : | |||
| : | |||
| : | |||
| : | |||
| : |
| : | |||
| : | |||
| : | |||
| : | |||
| : |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Uribe, S.; Hernández-Pinto, R.J.; Rodrigo, G.; Sborlini, G.F.R. From Five-Loop Scattering Amplitudes to Open Trees with the Loop-Tree Duality. Symmetry 2022, 14, 2571. https://doi.org/10.3390/sym14122571
Ramírez-Uribe S, Hernández-Pinto RJ, Rodrigo G, Sborlini GFR. From Five-Loop Scattering Amplitudes to Open Trees with the Loop-Tree Duality. Symmetry. 2022; 14(12):2571. https://doi.org/10.3390/sym14122571
Chicago/Turabian StyleRamírez-Uribe, Selomit, Roger José Hernández-Pinto, Germán Rodrigo, and German F. R. Sborlini. 2022. "From Five-Loop Scattering Amplitudes to Open Trees with the Loop-Tree Duality" Symmetry 14, no. 12: 2571. https://doi.org/10.3390/sym14122571
APA StyleRamírez-Uribe, S., Hernández-Pinto, R. J., Rodrigo, G., & Sborlini, G. F. R. (2022). From Five-Loop Scattering Amplitudes to Open Trees with the Loop-Tree Duality. Symmetry, 14(12), 2571. https://doi.org/10.3390/sym14122571







