Abstract
In this study, an integer-order rabies model is converted into the fractional-order epidemic model. To this end, the Caputo fractional-order derivatives are plugged in place of the classical derivatives. The positivity and boundedness of the fractional-order mathematical model is investigated by applying Laplace transformation and its inversion. To study the qualitative behavior of the non-integer rabies model, two steady states and the basic reproductive number of the underlying model are worked out. The local and global stability is investigated at both the steady states of the fractional-order epidemic model. After analytic treatment, a structure-preserving numerical template is constructed to numerically solve the fractional-order epidemic model. Moreover, the positivity, boundedness and symmetry of the numerical scheme are examined. Lastly, numerical experiment and simulations are accomplished to substantiate the significant traits of the projected numerical design. Consequences of the study are highlighted in the closing section.
1. Introduction
Rabies is a deadly infectious disease caused by a virus, known as rabies. This virus belongs to the genus Lyssavirus, family Rhabdoviridae, and the order Mononegavirales. The rabies virus mainly affects the brains of the mammals [1,2]. The virus has become a serious risk for more than 150 countries of the globe. It is estimated that 55,000 casualties occur every year due to this deadly virus. The main cause of the rabies virus is the dogs’ bite [2,3]. An individual who becomes infected with the rabies virus and is left untreated dies in a short period of time after the appearance of symptoms [4]. The mathematical models for the rabies disease dynamics contain integer-order differential equations. Dogs, raccoons, bats and foxes are the animals that carry the rabies virus in their saliva and they transmit it to humans via bites [5]. The role of bites by wild animals and human causalities has been studied in various countries of the world [6,7]. Dogs, being the main source of the rabies virus in Africa and Asia, are responsible for its transmission around the globe.
The disease is transmitted to domestic animals and people through contact with tainted saliva. In previous years, bat rabies has arisen as a general medical issue in the United states and Europe [8]. In 2003, a large number individuals in South America passed away from rabies following the scratches of untamed animals, especially bats, then from dogs [9]. Rabies is a global issue, although numerous nations today are considered rabies-free (with no human cases) because of mass inoculation programs. Greece had been rabies from 1987 onward, until it reappeared in 2012 [10]. Rabies is a primary health problem in many populations dense with dogs, specifically in regions where fewer or no preventive measures are adopted (vaccination and remedy) for puppies and human beings. Remedy after exposure to the rabies virus is referred to as post-exposure prophylaxis (PEP), and vaccination earlier than exposure to the infection is known as pre-exposure prophylaxis. Many countries have developed the key concept of introducing the adjoint function to a differential equation by introducing an objective function [11].
The fractional-order derivatives have some important physical features, unlike the integer-order derivatives. One of the main features is the memory effect, which is an important part of biological models. This memory effect contains the history of the past that makes the immune system ready for invaders, such as bacteria, viruses, fungi and much more. Mathematically, a fractional-order derivative has the ability to capture a long range of dynamics of the physical phenomenon by adjusting a suitable value to the fractional-order parameter. The rate of disease dynamics is not same throughout the globe. These rates vary region-wise, depending upon the different conditions of environment, health, food, hygienic and so on. So, the use of fractional-order derivatives becomes inevitable to cover the infinitely many rates of infection according to the real situation. Further, these types of derivatives increase the stability of solutions [12,13]. Shi et al. (2022) studied a stochastic SEIRS rabies model with two patches of dog population. They investigated the existence and uniqueness of the global positive solutions. They also described the criteria for the ergodic stationary distribution [14]. Similarly, Ewald et al. (2020) reviewed various plans to alleviate the pathogens that will lead to the optimal control of the infection. They discussed the current trends in mathematical modeling and highlighted the possible features of the modeling for the human–pathogen interaction in the future [15].
It is not a simple and easy task to find the exact solutions of the nonlinear dynamical systems [16]. In some cases, it becomes more complex to find an exact solution due to the involvement of a number of parameters in the model. Additionally, in some models, the exact solution becomes almost impossible. So, the need for a numerical solution arises. In the literature, many numerical schemes exist for the classical or integer-order models [17,18,19,20,21,22]. On the other hand, a few schemes can be seen for fractional-order epidemic models. These schemes also have some flaws and deficiencies, such as divergence from the exact equilibrium points, negativity of the state variables and lack of stability. By considering these facts, an efficient numerical method is formulated to obtain the reliable numerical solutions. It is determined analytically and numerically that the new scheme converges toward the exact equilibrium state and provides positive solutions.
This paper is organized as follows: The model formulation, mathematical assumptions, mathematical flowchart and model equations are included in Section 2. The model analysis, basic reproduction number, and numerical simulations of the equilibria are mostly detailed in Section 3. We discuss the parameter values that lead to the numeric value of initial sequence ratio in Section 4. The outcomes and effectiveness of the study are discussed in Section 5.
2. Preliminaries
The purpose of the present section is to introduce crucial concepts and present the mathematical model under consideration in this work. To start with, we provide firstly the definition of Caputo fractional derivatives and their properties.
Definition 1
(Caputo [23]). Let m be a positive integer; suppose that and let . The Caputo fractional derivative of order λ of a function is defined as
Following the notation and conventions in the previous definition, it is well-known that the Laplace transform operator for the Caputo fractional derivative of the function f is given by the following expressions, for each as described in [24,25]
Definition 2.
The classical Mittag–Leffler function with a single parameter is the function given in closed form by
Meanwhile, the Mittag–Leffler function with two parameters and is provided by the formula (see Section 2 of [26])
Definition 3.
A value is a steady state of the system , if , for all (see [27,28]).
In our compartmental deterministic SIR model for rabies in human, the human population is divided into susceptible (S), infectious (I), and recovered (R) classes. These classes or compartments are functions that depend only on time. Moreover, this model may be represented as the system of ordinary differential equations [29]:
The parameters involved in systems (5)–(7) possess concrete physical connotations. For example, is the human recruitment rate, is the death due to rabies, is the constant rate, is the natural death rate, is the rate of rabies awareness, is the human vaccination rate, and is the rate of rabies treatment. Throughout, we will assume that all of them are positive constants.
For purposes of this work, the classic rabies model (5)–(7) is transformed in the scenario of fractional calculus as
and we will consider initial conditions of the form , and . We establish now some important properties on the solutions of this Caputo fractional model.
The proofs of Theorems 1 and 2 are given in Appendix A.
3. Analytical Results
The present section is devoted to establishing some properties on the solutions of epidemic model (8)–(10). To start with, it is important to notice that this epidemic model possesses two types of steady-state solutions, namely, a virus-free steady state (VFSS) and a virus-existing steady state (VESS).
To calculate the steady states of model (8)–(10), we assume that the solutions satisfy , for each . After some simplifications, it is possible to obtain the VFSS and the VESS. They are respectively represented by and , and they are provided by the following formulas:
Notice that when an infected individual appears among the individuals, then epidemics will exist in the population. Mathematically, this situation implies that the derivative of the infected population with respect to time is positive at the time that the infected individual is present. As a consequence, , which implies that in view that . Equivalently,
At the outset of epidemic, we have that S is approximately equal to . All this together yields that the basic reproductive number is given by
It is well-known that the basic reproductive number determines whether the disease will die out or persist in the population. Indeed, recall that when , then the disease will die out (no epidemic). Meanwhile, if , then the disease will become an epidemic. Moreover, the value of indicates that how contagious the disease is.
Next, we will investigate the stability of the steady states associated with the fractional model (8)–(10). To this end, two theorems are established.
Theorem 3.
The VFSS is locally asymptotically stable if .
The proof of Theorem 3 is given in Appendix A.
Theorem 4.
If , then the VESS is locally asymptotically stable.
Proof.
We proceed in the similar fashion as in the proof of the previous theorem. We calculate the matrix as in the previous result, and evaluate it now at the VESS. Then the eigenvalues of the matrix satisfy the quadratic equation
Under the hypothesis, notice that the independent coefficient as well as the coefficient of the linear term in this quadratic expression are positive. By the Routh–Hurwitz criterion, we conclude that the system is stable at the VESS. □
In order to prove the global stability of fractional system (8)–(10), we present an important lemma, which is as follows.
Lemma 1
([30]). Let be a continuous function. Then, for any time :
Theorem 5.
If , then the VFSS is globally asymptotically stable.
Proof.
Theorem 6.
If , then the VESS is globally asymptotically stable.
Proof.
In the same case as the disease-free equilibrium point, we assume to consider the Volterra-type Lyapunov function defined as
where, are all positive constants that can be chosen later. Then, by substituting Equation (17) into main model (8)–(10) and using Lemma 1, we reach the following:
After some computations, we obtain
Finally, by setting , we have
where for , and only if , . Therefore, it is concluded that system (8)–(10) is globally asymptotically stable. □
4. Numerical Results
This section is devoted to present a reliable structure-preserving numerical method for the solution of the continuous model (8)–(10). To that end, let and fix the time interval . Let us divide this temporal interval into identical sub-intervals with grid points given by
Here, , for each . For the sake of convenience, let us convey that , and , for each .
Definition 4.
Let Z be any of the functions S, I or R, and assume that . Then the nonstandard Grünwald–Letnikov approximation for the Caputo fractional derivative of Z of order λ at the time is given by
Here, is a suitable function, and
If , then it is easy to check that the coefficients and satisfy the following chains of inequalities for each :
- .
- .
Moreover, if , then and .
Using these conventions, the Grünwald–Letnikov nonstandard finite-difference (GL-NSFD) method employed to approximate the solutions of the epidemic model (8)–(10) is given by the system of discrete equations, for each :
By using Formula (21) in the system of Equations (22)–(24), we obtain
After some algebraic steps, it is possible to check that this system is equivalent to
The next results summarize the capability of the numerical method to preserve the positivity and the boundedness of approximations.
Theorem 7.
Suppose that ,, and . Then , and , for each
Proof.
The conclusion is true for by hypothesis. So, assume that the conclusion of this result is satisfied. Using Formulas (28)–(30), the induction hypothesis and the fact that all the coefficients are positive, it obviously follows that , and . The conclusion of this result follows now by mathematical induction. □
Theorem 8.
Suppose that , and are positive, and let . If or , then there are constants for each , such that
Proof.
For illustration purposes, we proceed recursively, though the proof could be carried out also using mathematical induction. Beforehand, add all three Equations (28)–(30) to obtain the following identity:
Notice that obviously satisfies the conclusion of the theorem. Letting now , it is easy to check that
where
It is obvious then that , and , where
The conclusion can be reached then recursively. □
The pseudocode of proposed numerical technique (28)–(30) is given in Algorithm 1.
| Algorithm 1: Pseudocode of proposed scheme (28)–(30). |
procedureFunction
|
Finally, we present some numerical simulations which assess the capability of the numerical scheme to preserve the positivity and the boundedness. To that end, we employ the parameters summarized in Table 1. Throughout, the initial conditions are given as , , . The results of our numerical simulations for both the VFSS and the VESS are provided in Figure 1 for various values of . The results show that the scheme is capable of preserving the positivity and the boundedness of the approximations. Moreover, they confirm the capability of the numerical model to preserve the stability of the steady-state solutions of the epidemiological system.
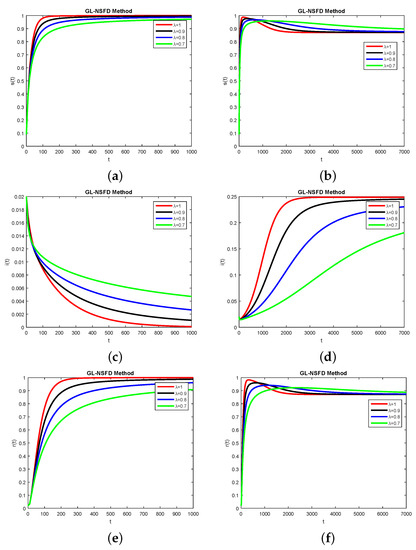
Figure 1.
Numerical simulations of the solutions for the continuous epidemic model investigated in this work, for the VFSS (left column) and the VESS (right column). The graphs present the dynamics for (top row), (middle row) and (bottom row). Various values of were employed in each case (see the legends). (a) for VFSS, (b) for VESS, (c) for VFSS, (d) for VESS, (e) for VFSS and (f) for VESS.
5. Conclusions
In this article, a classical rabies model is transformed into the fractional-order rabies model. As the fractional differential equation represents the class of differential equations by letting the different values of fractional-order parameter. So, the disease dynamics be understood deeply and concisely. The positivity and the boundedness properties of the fractional rabies model are explored with the help of the Laplace theory. Two steady states of the underlying model, i.e., the virus-free and virus-existing steady states, are worked out. The basic reproductive number of the fractional system is depicted. It is investigated that the non-integer order system is locally and globally stable at the virus-free steady state when , and for the system is locally and globally stable at the virus-existence steady state. For the numerical analysis, the robust numerical template is constructed. The significant features of this numerical design are the positivity, boundedness and convergence toward accurate steady states. These traits of the numerical design are identified by establishing some standard results. Moreover, simulations are presented to validate all of the key features of the novel numerical design.
Author Contributions
Conceptualization, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; methodology, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; software, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; validation, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; formal analysis, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; investigation, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; resources, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; data curation, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; writing—original draft preparation, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; writing—review and editing, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; visualization, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; supervision, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; project administration, Z.I., J.E.M.-D., N.A., A.J., M.R. and A.R.; funding acquisition, J.E.M.-D. All authors have read and agreed to the published version of the manuscript.
Funding
The corresponding author (J.E.M.-D.) acknowledges the financial support from the National Council for Science and Technology of Mexico (CONACYT) through grant A1-S-45928.
Data Availability Statement
Data will be available from the corresponding author (J.E.M.-D. upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Theorem A1.
Proof.
Let us define the norm function , and consider Equation (8). Bounding from below, it is easy to check that the following inequalities are satisfied:
Here, . As a consequence, , for each . Applying the Laplace operator on both sides of this inequality, using properties for this transform and rearranging terms to solve for , we readily obtain
After applying the inverse Laplace operator on (A2), we reach that . Similarly, it is possible to prove that and , for each . □
Proof.
Consider the system of equations for the fractional-order rabies model, and define , for each . Adding the three fractional differential equations of the mathematical model and rearranging terms, we obtain that
Applying Laplace transform on both sides of this equation, using the formula for the Laplace transform of Caputo derivatives and rearranging terms yields
Let . Applying now the inverse Laplace transform, we readily obtain
As a consequence, we obtain that . This implies that is bounded by M, which means that the solution is bounded in , for all . □
Theorem A3.
The VFSS is locally asymptotically stable if .
Proof.
Beforehand, observe that the function R does not appear in the expressions of the first two equations of system (8)–(10). So, for the analysis, we may consider only the first two equations of the epidemic model. Let us define then f and g as the following two functions of S and I:
Notice that the Jacobian matrix of this system of equations is given by
Evaluating now the Jacobian matrix on the VFSS, we readily obtain
After some algebraic calculations, we may readily check that the eigenvalues of the Jacobian matrix are the numbers
The number is obviously negative. Meanwhile, is likewise negative in view that . We conclude then that the VFSS is locally asymptotically stable, as desired. □
References
- Hayman, D.T.S.; Johnson, N.; Horton, D.L.; Hedge, J.; Wakeley, P.R.; Banyard, A.C.; Zhang, S.; Alhassan, A.; Fooks, A.R. Evolutionary history of rabies in Ghana. PLoS Neglected Trop. Dis. 2011, 5, e1001. [Google Scholar] [CrossRef] [PubMed]
- Kiddy, J.K.; Asamoah, K.; Oduro, F.T.; Bonyah, E.; Seidu, B. Modelling of Rabies Transmission Dynamics Using Optimal Control Analysis. J. Appl. Math. 2017, 2017, 2451237. [Google Scholar]
- Ega, T.T.; Luboobi, L.S.; Kuznetsov, D. Modeling the Dynamics of Rabies Transmission with Vaccination and Stability Analysis. Appl. Comput. Math. 2015, 4, 409–419. [Google Scholar]
- Demirci, E. A New Mathematical Approach for Rabies Endemy. Appl. Math. Sci. 2014, 8, 59–67. [Google Scholar] [CrossRef]
- Balcha, C.; Abdela, N. Review of Rabies Preventions and Control. Int. J. Public Health Sci. 2017, 6, 343–350. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Bartoszynki, R. On the Risk of Rabies; Mathematical Institute, Polish Academy of Sciences: Warsaw, Poland, 1975; pp. 355–377. [Google Scholar]
- Zarin, R.; Ahmed, I.; Kumam, P.; Zeb, A.; Din, A. Fractional modeling and optimal control analysis of rabies virus under the convex incidence rate. Results Phys. 2021, 28, 104665. [Google Scholar] [CrossRef]
- Wiraningsih, E.D.; Widodo; Aryati, L.; Toaha, S.; Lenhart, S. Optimal Control for SEIR Rabies Model between Dogs and Human with Vaccination Effect in dogs. In Proceedings of the 6th IMT-GT Conference on Mathematics, Statistics and Its Applications (ICMSA2010), Universiti Tunku Abdul Rahman, Kuala Lumpur, Malaysia, 3–4 November 2018. [Google Scholar]
- Tsiodras, S.; Dougas, G.; Baka, A.; Billinis, C.; Doudounakis, S.; Balaska, A.; Georgakopoulou, T.; Rigakos, G.; Kontos, V.; Tasioudi, K.E.; et al. Re-emergence of animal rabies in northern Greece and subsequent human exposure. Eurosurveillance 2013, 18, 20474. [Google Scholar]
- Warrel, M.J. Current rabies vaccines and prophylaxis schedules: Preventing rabies before and after exposure. Travel Med. Infect. Dis. 2012, 10, 1–15. [Google Scholar] [CrossRef]
- Arafa, A.A.M.; Rida, S.Z.; Khalil, M. A fractional-order model of HIV infection: Numerical solution and comparisons with data of patients. Int. J. Biomath. 2014, 7, 1450036. [Google Scholar] [CrossRef]
- Rihan, F.A.; Lakshmanan, S.; Hashish, A.H.; Rakkiyappan, R.; Ahmed, E. Fractional-order delayed predator–prey systems with Holling type-II functional response. Nonlinear Dyn. 2015, 80, 777–789. [Google Scholar] [CrossRef]
- Shi, Z.; Jiang, D.; Zhang, X.; Alsaedi, A. A stochastic SEIRS rabies model with population dispersal: Stationary distribution and probability density function. Appl. Math. Comput. 2022, 427, 127189. [Google Scholar] [CrossRef]
- Ewald, J.; Sieber, P.; Garde, R.; Lang, S.N.; Schuster, S.; Ibrahim, B. Trends in mathematical modeling of host–pathogen interactions. Cell. Mol. Life Sci. 2020, 77, 467–480. [Google Scholar] [CrossRef] [PubMed]
- Fernández, F.M. On some approximate methods for nonlinear models. Appl. Math. Comput. 2009, 215, 168–174. [Google Scholar] [CrossRef][Green Version]
- Dayan, F.; Rafiq, M.; Ahmed, N.; Raza, A.; Ahmad, M.O. A dynamical study of a fuzzy epidemic model of Mosquito-Borne Disease. Comput. Biol. Med. 2022, 148, 105673. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, N.; Macías-Díaz, J.E.; Raza, A.; Baleanu, D.; Rafiq, M.; Iqbal, Z.; Ahmad, M.O. Design, Analysis and Comparison of a Nonstandard Computational Method for the Solution of a General Stochastic Fractional Epidemic Model. Axioms 2022, 11, 10. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. An explicit dissipation-preserving method for Riesz space-fractional nonlinear wave equations in multiple dimensions. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 67–87. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. Numerical simulation of the nonlinear dynamics of harmonically driven Riesz-fractional extensions of the Fermi–Pasta–Ulam chains. Commun. Nonlinear Sci. Numer. Simul. 2018, 55, 248–264. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E. Numerical study of the transmission of energy in discrete arrays of sine-Gordon equations in two space dimensions. Phys. Rev. E 2008, 77, 016602. [Google Scholar] [CrossRef]
- Macías-Díaz, J.E.; Ahmed, N.; Rafiq, M. Analysis and Nonstandard Numerical Design of a Discrete Three-Dimensional Hepatitis B Epidemic Model. Mathematics 2019, 7, 1157. [Google Scholar] [CrossRef]
- Caputo, M. Linear model of dissipation whose q is almost frequency independent. II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Mittag-Leffler, M.G. Sur la nouvelle fonction Eα(x). Comptes Rendus Acad. Sci. Paris 1903, 137, 554–558. [Google Scholar]
- Mittag-Leffler, M.G. Sur la representation analytique d’une branche uniforme d’une fonction monogene. Acta Math. 1905, 29, 101–181. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. In Mathematics in Science and Engineering; Book Section 2; Elsevier: Amsterdam, The Netherlands, 1999; Volume 198, pp. 41–119. [Google Scholar]
- Li, Y.; Chen, Y.; Podlubny, I. Mittag–Leffler stability of fractional order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Biala, T.A.; Khaliq, A.Q.M. A fractional-order compartmental model for the spread of the COVID-19 pandemic. Commun. Nonlinear Sci. Numer. Simul. 2021, 98, 105764. [Google Scholar] [CrossRef] [PubMed]
- Jawaz, M.; Rehman, M.A.; Ahmed, N.; Baleanu, D.; Iqbal, M.S.; Rafiq, M.; Raza, A. Analysis and numerical effects of time-delayed rabies epidemic model with diffusion. Int. J. Nonlinear Sci. Numer. Simul. 2022. [Google Scholar] [CrossRef]
- Leon, C.V. Volterra Lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 75–85. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
