Mapping Properties of Associate Laguerre Polynomials in Leminiscate, Exponential and Nephroid Domain

Abstract

The function ${\mathcal{P}}_{\mathcal{L}}\left(z\right)=\sqrt{1+z}$ maps the unit disc $\mathbb{D}=\{z\in \mathbb{C}:|z|<1\}$ to a leminscate which is symmetric about the x-axis. The conditions on the parameters $\alpha$ and n, for which the associated Laguerre polynomial (ALP) ${\mathtt{L}}_n^{\alpha }$ maps unit disc into the leminscate domain, are deduced in this article. We also establish the condition under which a function involving ${\mathtt{L}}_n^{\alpha }$ maps $\mathbb{D}$ to a domain subordinated by ${\varphi }_{N_e}\left(z\right)=1-z+z^3/3$, ${\varphi }_e\left(z\right)=e^z$, and ${\varphi }_A\left(z\right)=1+Az$, $A\in (0,1]$. We provide several graphical presentations for a clear view of some of the obtained results. The possibilities for the improvements of the results are also highlighted.

1. Introduction

The generalized [1] or associated Laguerre polynomial (ALP) ${\mathtt{L}}_n^{\alpha }\left(z\right)$ is the solution of the differential equation

$$\begin{array}{c}\hfill z{y}^{″}\left(z\right)+(\alpha +1-z)y^{\prime }\left(z\right)+ny\left(z\right)=0,\alpha \in \mathbb{R},\end{array}$$

(1)

which is represented by the series

$$\begin{array}{c}\hfill {\mathtt{L}}_n^{\alpha }\left(z\right)=\sum _{i=0}^n{(-1)}^i\left(\begin{array}{c}n+\alpha \\ n-i\end{array}\right)\frac{z^i}{i!}=\frac{{(1+\alpha )}_n}{n!}{}_1{F}_1(-n;1+\alpha ;z),\end{array}$$

(2)

where ${}_1{F}_1$ is the confluent hypergeometric function, and ${\left(a\right)}_n$ is the well-known Pochhammer symbol defined as

$${\left(a\right)}_0=1,{\left(a\right)}_n=a(a+1)\dots (a+n-1),n\in \mathbb{N}.$$

The first few terms of the polynomial are given as

$$\begin{array}{cc}\hfill {\mathtt{L}}_0^{\alpha }\left(z\right)& =1,\hfill \\ \hfill {\mathtt{L}}_1^{\alpha }\left(z\right)& =-z+\alpha +1,\hfill \\ \hfill {\mathtt{L}}_2^{\alpha }\left(z\right)& =\frac{z^2}{2}-(\alpha +2)z+\frac{(\alpha +1)(\alpha +2)}{2},\hfill \\ \hfill {\mathtt{L}}_3^{\alpha }\left(z\right)& =-\frac{z^3}{6}+\frac{(\alpha +3)z^2}{2}-\frac{(\alpha +2)(\alpha +3)z}{2}+\frac{(\alpha +1)(\alpha +2)(\alpha +3)}{6}.\hfill \end{array}$$

ALP has its own significance in various branches of mathematics and physics and has a wide contribution in different aspects in mathematical research. The associated Laguerre polynomials are orthogonal with respect to the gamma distribution $e^{-z}{z}^{\alpha }dz$ on the interval $(0,\infty )$. The generalized Laguerre polynomials are widely used in many problems of quantum mechanics, mathematical physics and engineering. In quantum mechanics, the Schrödinger equation for the hydrogen-like atom is exactly solvable by separation of variables in spherical coordinates, and the radial part of the wave function is an ALP [2]. In mathematical physics, vibronic transitions in the Franck–Condon approximation can also be described by using Laguerre polynomials [3]. In engineering, the wave equation is solved for the time domain electric field integral equation for arbitrary shaped conducting structures by expressing the transient behaviors in terms of Laguerre polynomials [4]. The monographs by Szegó [5], and Andrews, Askey, and Roy [6] include a wealth of information about ALP and other orthogonal polynomial families.

In this study, we consider

$$\begin{array}{c}\hfill {\mathtt{F}}_{\alpha ,n}\left(z\right)=\frac{n!}{{(\alpha +1)}_n}{\mathtt{L}}_n^{\alpha }\left(z\right),z\in \mathbb{D}.\end{array}$$

(3)

The function ${\mathtt{F}}_{\alpha ,n}$ satisfies the normalization condition ${\mathtt{F}}_{\alpha ,n}\left(0\right)=1$ and is a solution of the differential equation

$$\begin{array}{c}\hfill z^2{y}^{″}\left(z\right)+(\alpha +1-z)z{y}^{\prime }\left(z\right)+nzy\left(z\right)=0.\end{array}$$

(4)

The following four functions are also important for this study.

$$\begin{array}{c}\hfill {\mathcal{P}}_{\mathcal{L}}\left(z\right)=\sqrt{1+z},{\varphi }_e\left(z\right)=e^z,{\varphi }_A\left(z\right)=1+Az\mathrm{and}{\varphi }_{N_e}\left(z\right)=1+z-\frac{z^3}{3}.\end{array}$$

The function ${\mathcal{P}}_{\mathcal{L}}$ maps $\mathbb{D}$ to a leminscate, ${\varphi }_A$ shifted $\mathbb{D}$ to a disc center at $(1,0)$ with radius $A\in [0,1)$, ${\varphi }_e$ maps $\mathbb{D}$ to the exponential domain, and ${\varphi }_{N_e}$ maps $\mathbb{D}$ to the neuphroid domain as shown in Figure 1.

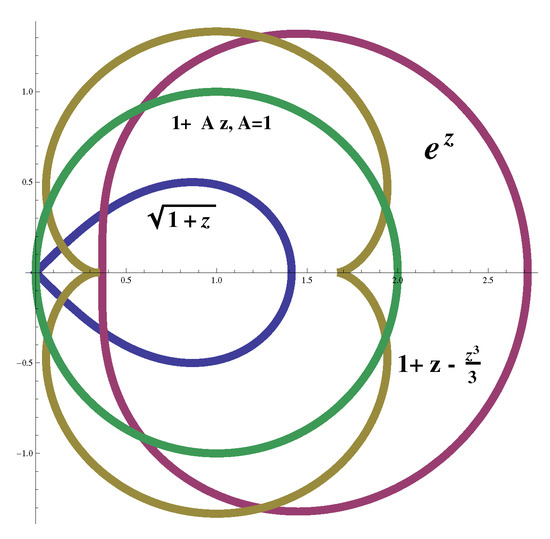
Figure 1. Boundary of ${\varphi }_{N_e}\left(\mathbb{D}\right)$, ${\mathcal{P}}_{\mathcal{L}}\left(\mathbb{D}\right)$, ${\varphi }_{A=1}\left(\mathbb{D}\right)$ and ${\varphi }_e\left(\mathbb{D}\right)$.

Let $\mathcal{A}$ denote the class of functions $\mathtt{f}$ in the open unit disk $\mathbb{D}=\{z:|z|<1\}$ and normalized by the conditions $f\left(0\right)=0=f^{\prime }\left(0\right)-1$. If f and g are analytic in $\mathbb{D}$, then f is subordinate to g, written $f\prec g,$ or $f\left(z\right)\prec g\left(z\right),$ $z\in \mathbb{D}$ if there is an analytic self-map $\omega$ of $\mathbb{D}$ satisfying $f\left(0\right)=g\left(0\right)$ and $f\left(z\right)=g\left(\omega \right(z\left)\right)$, $z\in \mathbb{D}$. Especially, if $g\left(z\right)$ is univalent in $\mathbb{D}$, then $f\left(z\right)\prec g\left(z\right)$ if and only if $f\left(0\right)=g\left(0\right)$ and $f\left(\mathbb{D}\right)\subset g\left(\mathbb{D}\right)$. It is worth noting here that ${\mathcal{P}}_{\mathcal{L}}$, ${\varphi }_{N_e}$, ${\varphi }_A$ and ${\varphi }_e$ are not subordinate to each other as it is clear from Figure 1 that the image of $\mathbb{D}$ by any one of these functions does not contain the image by others. Differential subordination is an important technique to study geometric functions theory. Details about this technique can be seen in [7,8].

Denote by ${\mathcal{S}}^{*}$ and $\mathcal{C}$, respectively the important subclasses of $\mathcal{A}$ consisting of univalent starlike and convex functions. Geometrically, $f\in {\mathcal{S}}^{*}$ if the linear segment $tw$, $0\le t\le 1,$ lies completely in $f\left(\mathbb{D}\right)$ whenever $w\in f\left(\mathbb{D}\right)$, while $f\in \mathcal{C}$ if $f\left(\mathbb{D}\right)$ is a convex domain. Related to these subclasses is the Cárathèodory class $\mathcal{P}$ consisting of analytic functions p satisfying $p\left(0\right)=1$ and $\mathrm{Re}p\left(z\right)>0$ in $\mathbb{D}$. Analytically, $f\in {\mathcal{S}}^{*}$ if $z{f}^{\prime }\left(z\right)/f\left(z\right)\in \mathcal{P}$, while $f\in \mathcal{C}$ if $1+z{f}^{″}\left(z\right)/f^{\prime }\left(z\right)\in \mathcal{P}$. It is well-known that the function $z{(1-z)}^{-2}$ is starlike and $z{(1-z)}^{-1}$ is convex in the unit disk $\mathbb{D}$.

A function $f\in \mathcal{A}$ is lemniscate convex if $1+z{f}^{″}\left(z\right)/f^{\prime }\left(z\right)$ lies in the region bounded by right half of lemniscate of Bernoulli given by $\{w:|w^2-1|=1\}$, which is equivalent to the subordination $1+z{f}^{″}\left(z\right)/f^{\prime }\left(z\right)\prec {\mathcal{P}}_{\mathcal{L}}\left(z\right)$. Similarly, the function f is lemniscate starlike if $z{f}^{\prime }\left(z\right)/f\left(z\right)\prec {\mathcal{P}}_{\mathcal{L}}\left(z\right)$. On the other hand, the function $f\in \mathcal{A}$ is lemniscate Carathéodory if $f^{\prime }\left(z\right))\prec {\mathcal{P}}_{\mathcal{L}}\left(z\right)$. Clearly, a lemniscate Carathéodory function is a Carathéodory function and hence is univalent.

The sufficient conditions of starlikeness associated with lemniscate of Bernoulli are obtained in [9]. A similar study associated with the exponential domain is conducted in [10]. One of the motivations of this work is the nephroid curve

$${\left({(u-1)}^2+v^2-\frac{4}{9}\right)}^3-\frac{4}{3}{v}^2=0.$$

Recently, the nephroid curve received attention of researchers in geometric functions theory thanks to the work by Wani and Swaminathan [11,12,13]. This two-cusped kidney-shaped curve was first studied by Huygens and Tschirnhausen in 1697. However, the word nephroid was first used by Richard A. Proctor in 1878 in his book The Geometry of Cycloids. For further details related to the nephroid curve, we refer to [11,14]. The radius of starlikeness and convexity for functions associated with the nephroid domain is discussed in [13]. In [12], the authors discuss the starlike and convex functions associated with the nephroid domain. The Fekete–Szegö kind of inequalities for certain subclasses of analytic functions in association with the nephroid domain is studied in [15].

Significant findings from the articles [9,10] are summarized, respectively, in Lemma 1 and Lemma 2, while Lemma 3 and Lemma 4 highlights the results from the reference [11]. The special functions, such as Bessel, Struve, Confluent hypergeometric and hypergeometric, are closely associated with the geometric functions theory. The geometric nature of these special functions associated with the leminisciate, the exponential and the nephroid domain are studied in [9,10,13]. The lemniscate convexity of generalized Bessel functions is studied in [9], while [10] deals with the exponential starlikeness and convexity of confluent hypergeometric, Lommel and Struve functions.

In this paper, motivated by the aforementioned works, we investigated the inclusion properties of the normalized function ${\mathtt{F}}_{\alpha ,n}$ involving ALP that maps the unit disc $\mathbb{D}$ into the lemniscate and the exponential domain, respectively, in Section 2 and Section 3. Section 4 deals with the results concerning the shifted disc $1+Az$, for $A\in [0,1]$. In Section 5, we derive the conditions under which integration associated with ${\mathtt{F}}_{\alpha ,n}$ maps $\mathbb{D}$ into the nephroid domain. All the results are interpreted graphically. Several options for the improvement are highlighted.

2. Mapping in the Lemniscate Domain

In this section, we derive the relation between $\alpha$ and n for which ${\mathtt{F}}_{\alpha ,n}$ maps $\mathbb{D}$ into ${\mathcal{P}}_{\mathcal{L}}\left(\mathbb{D}\right)$. To prove the main results related with the lemniscate, the following Lemma 1 is used.

Lemma 1 

([16]). Let $p\in \mathcal{H}[1,n]$ with $p\left(z\right)\not\equiv 1$ and $n\ge 1$. Let $\mathrm{\Omega }\subset \mathbb{C}$, and $\mathrm{\Psi }:{\mathbb{C}}^3\times \mathbb{D}\to \mathbb{C}$ satisfy

$$\begin{array}{c}\hfill \mathrm{\Psi }(r,s,t;z)\notin \mathrm{\Omega }\end{array}$$

whenever $z\in \mathbb{D},$ and for $m\ge n\ge 1$, $-\pi /4\le \theta \le \pi /4$,

$$\begin{array}{c}\hfill r=\sqrt{2cos\left(2\theta \right)}{e}^{i\theta },s=\frac{m{e}^{3i\theta }}{2\sqrt{2cos\left(2\theta \right)}}andRe\left((t+s)e^{-3i\theta }\right)\ge \frac{3m^2}{8\sqrt{2cos\left(2\theta \right)}}.\end{array}$$

(5)

If $\mathrm{\Psi }(p\left(z\right),z{p}^{\prime }\left(z\right),z^2{p}^{″}\left(z\right);z)\in \mathrm{\Omega }$ for $z\in \mathbb{D}$, then $p\left(z\right)\prec {\mathcal{P}}_{\mathcal{L}}\left(z\right)$ in $\mathbb{D}$.

In the case of two dimensions, if $\mathrm{\Psi }:{\mathbb{C}}^2\times \mathbb{D}\to \mathbb{C}$ satisfy $\mathrm{\Psi }(r,s;z)\notin \mathrm{\Omega }$ whenever $z\in \mathbb{D},$ and for $m\ge n\ge 1$, $-\pi /4\le \theta \le \pi /4$,

$$\begin{array}{c}\hfill r=\sqrt{2cos\left(2\theta \right)}{e}^{i\theta },s=\frac{m{e}^{3i\theta }}{2\sqrt{2cos\left(2\theta \right)}}.\end{array}$$

If $\mathrm{\Psi }(p\left(z\right),z{p}^{\prime }\left(z\right);z)\in \mathrm{\Omega }$ for $z\in \mathbb{D}$, then $p\left(z\right)\prec {\mathcal{P}}_{\mathcal{L}}\left(z\right)$ in $\mathbb{D}$.

Now we state and prove the main result for this section.

Theorem 1. 

For $4Re\left(\alpha \right)>16n+1$, ${\mathtt{F}}_{\alpha ,n}\left(z\right)\prec {\mathcal{P}}_{\mathcal{L}}\left(z\right)$.

Proof. 

Let $p\left(z\right)={\mathtt{F}}_{\alpha ,n}\left(z\right)$. Suppose that $\mathrm{\Omega }=\left\{0\right\}$. Define

$$\mathrm{\Psi }(p,z{p}^{\prime },z^2{p}^{″};z)=z^2{p}^{\prime \prime }\left(z\right)+(\alpha +1-z)z{p}^{\prime }\left(z\right)+nzp\left(z\right).$$

From (4), it follows $\mathrm{\Psi }(p,z{p}^{\prime },z^2{p}^{″};z)\in \mathrm{\Omega }$. To prove the result by using Lemma 1, it is enough to show $\mathrm{\Psi }(r,s,t;z)\notin \mathrm{\Omega }$ for r, s and t as stated in (5). Now

$$\begin{array}{cc}\hfill \left|\mathrm{\Psi }\right(r,s,t;z\left)\right|& =|t+(\alpha +1-z)s+nzr|\hfill \\ \hfill & >\left|\right(t+s)+(\alpha -z\left)s\right|-n\left|r\right|\hfill \\ \hfill & \ge \left|(t+s)e^{-3i\theta }+(\alpha -z)\frac{m}{2\sqrt{2cos\left(2\theta \right)}}\right|-n\sqrt{2cos\left(2\theta \right)}\hfill \\ \hfill & \ge \frac{3m^2}{8\sqrt{2cos\left(2\theta \right)}}+\frac{Re(\alpha -z)m}{2\sqrt{2cos\left(2\theta \right)}}-n\sqrt{2}\hfill \\ \hfill & \ge \frac{4Re\left(\alpha \right)-1}{8\sqrt{2}}-n\sqrt{2}>0,\hfill \end{array}$$

provided $4Re\left(\alpha \right)>16n+1$. □

A natural question arises for a fixed $n\in \mathbb{N}$: are the values ${\alpha }_0=(16n+1)/4$ the best possible in Theorem 1? To investigate it, we try to experiment through graphical representation of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$ and ${\mathcal{P}}_{\mathcal{L}}\left(\mathbb{D}\right)$. It is worth noting here that ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)\subset {\mathcal{P}}_{\mathcal{L}}\left(\mathbb{D}\right)$ when ${\mathtt{F}}_{\alpha ,n}\left(z\right)\prec {\mathcal{P}}_{\mathcal{L}}\left(z\right)$. We present our cases for $n=2,3,4$.

n = 2

By Theorem 1, ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)\subset {\mathcal{P}}_{\mathcal{L}}\left(\mathbb{D}\right)$ holds for $Re\left(\alpha \right)>8.25$. However, Figure 2 indicates that for real $\alpha$, the subordination property for which ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)\subset {\mathcal{P}}_{\mathcal{L}}\left(\mathbb{D}\right)$ follows for $\alpha >{\alpha }_0$ where the possible value ${\alpha }_0$ is any number in the interval $(4.1,4.3)$.

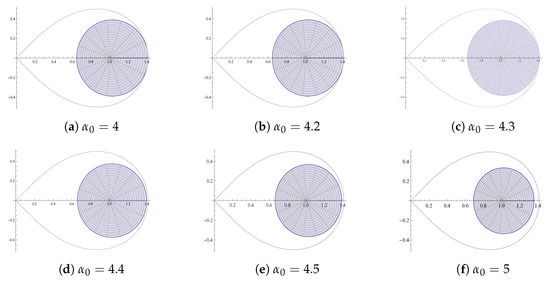Figure 2. Graph of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$ for fixed $n=2$.

n = 3

As per Theorem 1, in this case ${\alpha }_0$ is $12.25$. Figure 3 indicates that for real $\alpha$, the inclusion ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)\subset {\mathcal{P}}_{\mathcal{L}}\left(\mathbb{D}\right)$ holds for $\alpha >{\alpha }_0$ where the possible value of ${\alpha }_0$ is any number in the interval $(7.1,7.2)$.

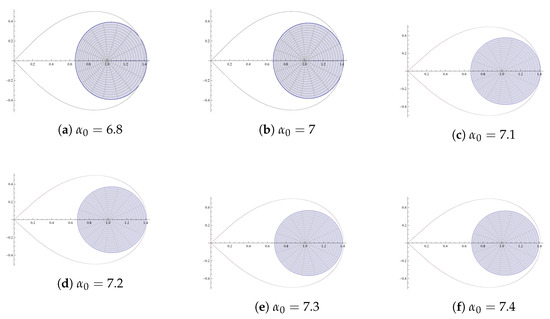Figure 3. Graph of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$ for fixed $n=3$.

n = 4

The expected value of ${\alpha }_0$ is $16.25$, but as per Figure 4, the value of ${\alpha }_0$ can be lower down to a number in $(10,10.2)$.

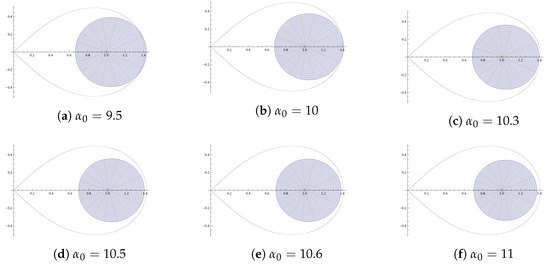Figure 4. Graph of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$ for fixed $n=4$.

3. Mapping in the Exponential Domain

Lemma 2 

([17]). Let $\mathrm{\Omega }\subset \mathbb{C}$, and $\mathrm{\Psi }:{\mathbb{C}}^3\times \mathbb{D}\to \mathbb{C}$ satisfy $\mathrm{\Psi }(r,s,t;z)\notin \mathrm{\Omega }$ whenever $z\in \mathbb{D},$ and for $m\ge 1$, $\theta \in (0,2\pi )$,

$$\begin{array}{c}\hfill r=e^{e^{i\theta }},s=m{e}^{i\theta }{e}^{e^{i\theta }}andRe\left(1+\frac{t}{s}\right)\ge m\left(1+cos\left(\theta \right)\right).\end{array}$$

(6)

If $\mathrm{\Psi }(p\left(z\right),z{p}^{\prime }\left(z\right),z^2{p}^{″}\left(z\right);z)\in \mathrm{\Omega }$ for $z\in \mathbb{D}$, then $p\left(z\right)\prec e^z$ in $\mathbb{D}$.

Now, we state and prove our main result to have the mapping properties in the exponential domain.

Theorem 2. 

For $Re\left(\alpha \right)>n+1$, ${\mathtt{F}}_{\alpha ,n}\left(z\right)\prec e^z$.

Proof. 

Let $p\left(z\right)={\mathtt{F}}_{\alpha ,n}\left(z\right)$. Suppose that $\mathrm{\Omega }=\left\{0\right\}$. Then,

$$\mathrm{\Psi }(p,z{p}^{\prime },z^2{p}^{″};z)=z^2{p}^{″}\left(z\right)+(\alpha +1-z)z{p}^{\prime }\left(z\right)+nzp\left(z\right)=0$$

Now

$$\begin{array}{cc}\hfill \left|\mathrm{\Psi }\right(r,s,t;z\left)\right|& =|t+(\alpha +1-z)s+nzr|\hfill \\ \hfill & >\left|\right(t+s)+(\alpha -z\left)s\right|-n\left|r\right|\hfill \\ \hfill & \ge \left|s\right|\left|\left(1+\frac{t}{s}\right)+(\alpha -z)\right|-n{e}^{cos\left(\theta \right)}\hfill \\ \hfill & =e^{cos\left(\theta \right)}\left(mRe\left(1+\frac{t}{s}\right)+mRe(\alpha -z)-n\right)\hfill \\ \hfill & \ge e^{-1}\left(m^2(1+cos\left(\theta \right))+m(Re\left(\alpha \right)-1)-n\right)\hfill \\ \hfill & \ge e^{-1}\left(Re\left(\alpha \right)-1-n\right)\ge 0\hfill \end{array}$$

provided $Re\left(\alpha \right)\ge n+1$. □

It is evident from Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$ and ${\varphi }_e\left(\mathbb{D}\right)$ that for real $\alpha$, the inclusion properties ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)\subset {\varphi }_e\left(\mathbb{D}\right)$ not only holds for $\alpha \ge n+1$ (as stated in the theorem), but also holds for $\alpha \ge n$. This indicates that there is a possibility for the improvement of Theorem 2.

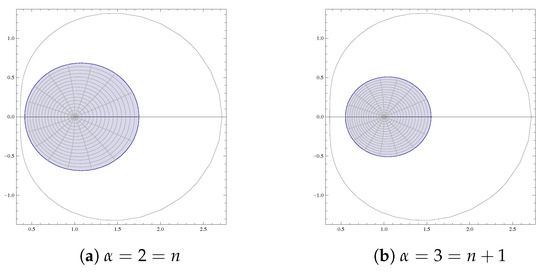
Figure 5. Graph of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$.

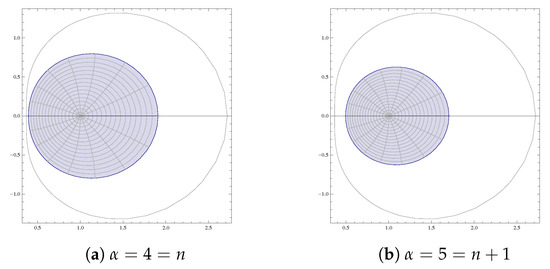
Figure 6. Graph of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$.

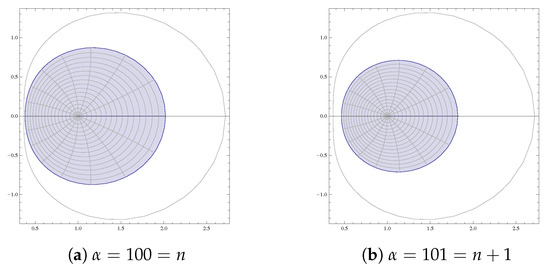
Figure 7. Graph of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$.

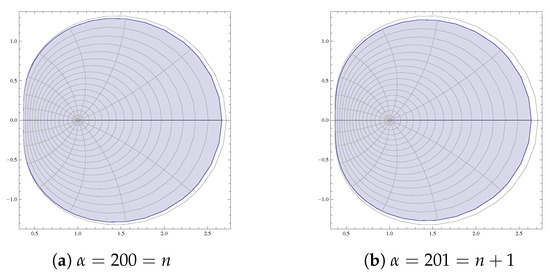
Figure 8. Graph of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$.

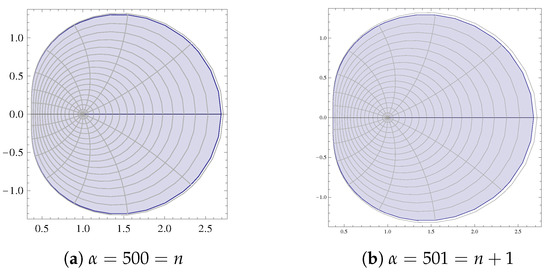
Figure 9. Graph of ${\mathtt{F}}_{\alpha ,n}\left(\mathbb{D}\right)$.

4. Mapping in Disc Center at $(\mathbf{0},\mathbf{1})$ and Radius $\mathit{A}\in (\mathbf{0},\mathbf{1}]$

The function ${\mathtt{f}}_{\mathtt{A}}\left(z\right)=1+Az$ for $A\in (0,1]$ maps the unit disc to a disc center at $(0,1)$ and radius A. In this section, we will derive conditions by which

Theorem 3. 

For $A\in \mathbb{C}$, $n\ge 1$ and $A\in (0,1]$, suppose that

$$\begin{array}{c}\hfill Re\left(\alpha \right)\ge \frac{n(A+1)}{A}.\end{array}$$

(7)

Then, ${\mathtt{f}}_{\alpha ,n}\left(z\right)\prec 1+Az$.

Proof. 

Consider

$$\begin{array}{c}\hfill q\left(z\right)=\sqrt{\frac{1}{A}\left({\mathtt{f}}_{\alpha ,n}\left(z\right)+A-1\right)}.\end{array}$$

(8)

A simplification gives

$$\begin{array}{cc}\hfill {\mathtt{f}}_{\alpha ,n}\left(z\right)& =A{q}^2\left(z\right)-A+1,{\mathtt{f}}_{\alpha ,n}^{\prime }\left(z\right)=2A{q}^{\prime }\left(z\right)q\left(z\right){\mathtt{f}}_{\alpha ,n}^{″}\left(z\right)=2A{q}^{″}\left(z\right)q\left(z\right)+2A{\left(q^{\prime }\left(z\right)\right)}^2.\hfill \end{array}$$

From (4) it follows that

$$\begin{array}{c}\hfill 2A{z}^2{q}^{″}\left(z\right)q\left(z\right)+2A{\left(z{q}^{\prime }\left(z\right)\right)}^2+2A(\alpha +1-z)z{q}^{\prime }\left(z\right)q\left(z\right)+nAz{q}^2\left(z\right)-nAz+nz=0.\end{array}$$

Let $\mathrm{\Omega }=\left\{0\right\}\subset \mathbb{C}$ and define $\psi {\mathbb{C}}^3\times \mathbb{D}\to \mathbb{C}$ as

$$\begin{array}{c}\hfill \psi (r,s,t;z)=2Atr+2A{s}^2+2A(\alpha +1-z)sr+nz(A{r}^2-A+1).\end{array}$$

(9)

It is clear from (9) that $\psi (q\left(z\right),z{q}^{\prime }\left(z\right),z{q}^{″}\left(z\right);z)\in \mathrm{\Omega }$. We shall apply Lemma 1 to show $\psi (r,s,t;z)\notin \mathrm{\Omega }$, which implies $q\left(z\right)\prec \sqrt{1+z}$.

Now, for $-\pi /4\le \theta \le \pi /4$, let

$$\begin{array}{c}\hfill r=\sqrt{2cos\left(2\theta \right)}{e}^{i\theta },s=\frac{m{e}^{3i\theta }}{2\sqrt{2cos\left(2\theta \right)}}.\end{array}$$

Applying elementary trigonometric identities, we have

$$r^2-1=2cos\left(2\theta \right)e^{2i\theta }-1=(2{cos}^2\left(2\theta \right)-1)+i2cos\left(2\theta \right)sin\left(2\theta \right)=e^{4i\theta }.$$

Substitute r, s and t in (5), and a simplification leads to

$$\begin{array}{cc}\hfill \left|\psi \right(r,s,t;z\left)\right|& =|2Atr+2A{s}^2+2A(\alpha +1-z)sr+nz(A{r}^2-A+1)|\hfill \\ \hfill & =|2Ar(t+s)+2A{s}^2+2A(\alpha -z)sr+Anz(r^2-1)+nz|\hfill \\ \hfill & >|e^{4i\theta }|\left(2A\sqrt{2cos\left(2\theta \right)}Re(t+s)e^{-3i\theta }+2A\frac{m^{2}Re\left(e^{2i\theta }\right)}{8cos\left(2\theta \right)}+ARe(\alpha -1)m\right)\hfill \\ \hfill & -nA|e^{4i\theta }|-n\hfill \\ \hfill & >2A\frac{3m^2}{8}+\frac{A{m}^2}{4}+ARe(\alpha -1)-n(A+1)\hfill \\ \hfill & >A+ARe\left(\alpha \right)-A-n(A+1)\ge 0\hfill \end{array}$$

when $Re\left(\alpha \right)\ge n(A+1)/A$. By Lemma 1, it is proved that $q\left(z\right)\prec \sqrt{1+z}$ which is equivalent to

$$\begin{array}{c}\hfill \sqrt{\frac{1}{A}\left({\mathtt{f}}_{\alpha ,n}\left(z\right)+A-1\right)}=\sqrt{1+w\left(z\right)},\end{array}$$

(10)

for some analytic function $w\left(z\right)$ such that $\left|w\right(z\left)\right|<1$. A simplification of (10) gives

$$\begin{array}{c}\hfill \frac{1}{A}\left({\mathtt{f}}_{\alpha ,n}\left(z\right)+A-1\right)=1+w\left(z\right)\Rightarrow {\mathtt{f}}_{\alpha ,n}\left(z\right)=1+Aw\left(z\right)\Rightarrow {\mathtt{f}}_{\alpha ,n}\left(z\right)\prec 1+Az.\end{array}$$

This completes the proof. □

Graphical representation indicates that there is a provision of improvement for a minimum value of $Re\left(\alpha \right)$ for fixed n and A. For example, set $n=1$ and $A=1/2$, and suppose that $\alpha$ is real. Then, by Theorem 3, ${\mathtt{f}}_{\alpha ,1}\left(z\right)\prec 1+z/2$ if $\alpha \ge 3$. However, Figure 10 clearly indicates that the result can hold for $\alpha \ge 1$. This claim can also be valid theoretically. The subordination ${\mathtt{f}}_{\alpha ,1}\left(z\right)\prec 1+Az$ is equivalent to

$$\begin{array}{c}\hfill |{\mathtt{f}}_{\alpha ,1}\left(z\right)-1|<A\Rightarrow \left|\frac{z}{\alpha +1}\right|<A\end{array}$$

which holds for $z\in \mathbb{D}$ if $A|\alpha +1|>1$. In particular, if $\alpha$ is a positive real number, and $A=1/2$, then ${\mathtt{f}}_{\alpha ,1}\left(z\right)\prec 1+(z/2)$ holds for $|\alpha +1|>2\Rightarrow \alpha >1.$

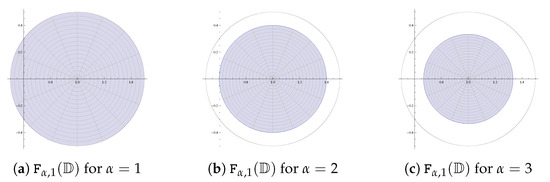
Figure 10. ${\mathtt{F}}_{\alpha ,1}\left(z\right)\prec 1+(z/2)$.

Similarly for $n=2$, as per Theorem 3, the subordination ${\mathtt{F}}_{\alpha ,2}\left(z\right)\prec 1+Az$ holds for $Re\left(\alpha \right)\ge 2(1+A)/A$. In particular, for real $\alpha$ and $A=1$, the subordination is true when $\alpha \ge 4$. However, a direct proof indicates that the subordination holds when

$$A|1+\alpha ||2+\alpha |>1+2|2+\alpha |.$$

Clearly, the second condition is better than the first condition (derived from Theorem 3). For example, if $\alpha$ is real and $A=1$, then ${\mathtt{F}}_{\alpha ,2}\left(z\right)\prec 1+z$ holds for $\alpha >1.3078$. The comparison can be seen in Figure 11.

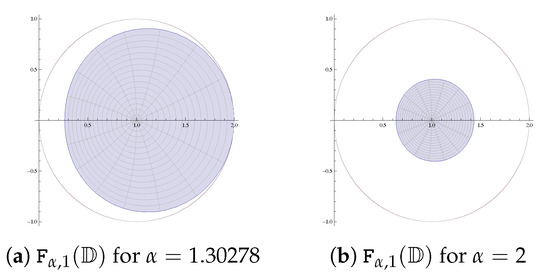
Figure 11. ${\mathtt{F}}_{\alpha ,2}\left(z\right)\prec 1+z$.

Based on the above facts, we can conclude that for certain special cases, Theorem 3 has a chance for improvement. Now, we state and prove an improved version of Theorem 3.

Theorem 4. 

For real $\alpha >-1$ and fixed $n\in \mathbb{N}$ and $A\in (0,1]$, suppose that ${\alpha }_0$ is the largest root of

$${}_1{F}_1(-n,1+\alpha ,-1)=1+A.$$

Then, the subordination ${\mathtt{F}}_{\alpha ,n}\left(z\right)\prec 1+Az$ holds for all $\alpha >{\alpha }_0$. The result is sharp as ${\alpha }_0$ is the best lowest value.

Proof. 

The subordination ${\mathtt{F}}_{\alpha ,n}\left(z\right)\prec 1+Az$ is equivalent to

$$\begin{array}{cc}\hfill \left|{\mathtt{F}}_{\alpha ,n}\left(z\right)-1\right|<A& =\left|\sum _{k=1}^n\frac{{(-n)}_k}{{(1+\alpha )}_{k}k!}{z}^k\right|<A.\hfill \end{array}$$

(11)

Now, for $\left|z\right|<1$, it follows

$$\begin{array}{c}\hfill \left|\sum _{k=1}^n\frac{{(-n)}_k}{{(1+\alpha )}_{k}k!}{z}^k\right|<\sum _{k=1}^n\frac{{|(-n)}_k|}{{(1+\alpha )}_{k}k!}={}_1{F}_1(-n,1+\alpha ,-1)-1.\end{array}$$

It can be easily verified that for a fixed n, the function $\alpha \to {}_1{F}_1(-n,1+\alpha ,-1)$ is decreasing; hence, the inequality (11) holds for $\alpha >{\alpha }_0$. Here, ${\alpha }_0>-1$ is the largest root of the equation

$${}_1{F}_1(-n,1+\alpha ,-1)=1+A.$$

This completes the proof. □

In the following Table 1 we have listed value of ${\alpha }_0$ for fixed n and A.

Table 1. The value of ${\alpha }_0$ for fixed A and n.

n/A	1	2	3	5	10	15
A = 1	0	1.30278	2.67882	5.49886	12.6531	19.8441
A = 1/2	1	3.37228	5.79852	10.6945	22.9951	35.3155
A = 1/3	2	5.40512	8.85262	15.7795	33.1391	50.5122
A = 1/4	3	7.42443	11.8837	20.8273	43.219	65.6208

5. Connection with the Nephroid Domain

In this section, we observe that $f\prec \sqrt{1+z}$ or $f\prec e^z$ do not always imply $f\nprec {\varphi }_{N_e}$. For example, consider the case when $n=100$ and $\alpha =101$, the polynomial

$$\frac{100!}{{\left(102\right)}_{100}}{L}_{100}^{101}\left(z\right)\prec \sqrt{1+z}\mathrm{but}\frac{100!}{{\left(102\right)}_{100}}{L}_{100}^{101}\left(z\right)\nprec {\varphi }_{N_e}$$

as shown in Figure 12a. Now define the function

$$\begin{array}{c}\hfill {\mathcal{X}}_{n,\alpha }\left(z\right)=1+\frac{1}{2}{\int }_0^z\frac{\frac{n!}{{(1+\alpha )}_n}{L}_n^{\alpha }\left(t\right)-1}{t}dt.\end{array}$$

(12)

In Figure 12b, we can see that

$${\mathcal{X}}_{100,101}\left(z\right)=1-\frac{50z}{101}{}_3{F}_3(1,1,-99;2,2,103,z)=1+\frac{1}{2}{\int }_0^z\frac{\frac{100!}{{\left(102\right)}_{100}}{L}_{100}^{101}\left(t\right)-1}{t}dt\prec {\varphi }_{N_e}.$$

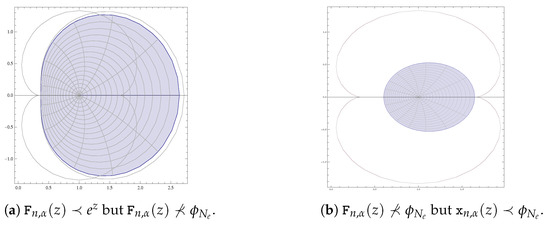
Figure 12. Comparison of ${\mathtt{F}}_{n,\alpha }$ and ${\mathcal{X}}_{n,\alpha }$.

To state the next result, let us generalize (12) as follows

$$\begin{array}{c}\hfill {\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)=1+\frac{1}{\beta }{\int }_0^z\frac{{\mathtt{F}}_{n,\alpha }\left(t\right)-1}{t}dt.\end{array}$$

(13)

We also consider the function

$$\begin{array}{c}\hfill {\mathcal{Y}}_{n,\alpha ,\beta }\left(z\right)=\frac{z^{-\frac{1}{\beta }}}{\beta }{\int }_0^z{\mathtt{F}}_{n,\alpha }\left(t\right)t^{\frac{1}{\beta }-1}dt.\end{array}$$

(14)

We need the following results in sequence.

Lemma 3 

([11]). Let $p:\mathbb{D}\to \mathbb{C}$ be analytic such that $p\left(0\right)=1$. Then, the following subordination implies $p\left(z\right)\prec {\varphi }_{N_{ϵ}}\left(z\right)$

(i) 

$p\left(z\right)+\beta z{p}^{\prime }\left(z\right)\prec \sqrt{1+z}$ for $\beta \ge 0.158379,$

(ii) 

$p\left(z\right)+\beta z{p}^{\prime }\left(z\right)\prec e^z$ for $\beta \ge 1.14016.$

Lemma 4 

([11]). Let $p:\mathbb{D}\to \mathbb{C}$ be analytic such that $p\left(0\right)=1$. Then the following subordination imply $p\left(z\right)\prec {\varphi }_{N_{ϵ}}\left(z\right)$

(i) 

$1+\beta z{p}^{\prime }\left(z\right)\prec \sqrt{1+z}$ for $\beta \ge 3(1-log(2)\approx 0.920558$,

(ii) 

$1+\beta \frac{z{p}^{\prime }\left(z\right)}{p\left(z\right)}\prec \sqrt{1+z}$ for $\beta \ge \frac{2\left(\sqrt{2}+log\left(2\right)-1-log(1+\sqrt{2}\right)}{log(5/3)}\approx 0.884792,$

(iii) 

$1+\beta \frac{z{p}^{\prime }\left(z\right)}{{\left(p\left(z\right)\right)}^2}\prec \sqrt{1+z}$ for $\beta \ge 5\left(\sqrt{2}+log\left(2\right)-1-log(1+\sqrt{2})\right)\approx 1.12994,$

(iv) 

$1+\beta z{p}^{\prime }\left(z\right)\prec e^z$ for $\beta \ge 1.97685$,

(v) 

$1+\beta \frac{z{p}^{\prime }\left(z\right)}{p\left(z\right)}\prec e^z$ for $\beta \ge 2.57995,$

(vi) 

$1+\beta \frac{z{p}^{\prime }\left(z\right)}{{\left(p\left(z\right)\right)}^2}\prec e^z$ for $\beta \ge 3.29476.$

The following subordination holds true.

Theorem 5. 

For $\beta >0$ and $Re\alpha >n+1$, the following subordination holds

(i) 

${\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)\prec {\varphi }_{N_e}$ for $\beta \ge 1.97685,$

(ii) 

$e^{{\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)-1}\prec {\varphi }_{N_e}$ for $\beta \ge 2.57995,$

(iii) 

${\mathcal{Y}}_{n,\alpha ,\beta }\left(z\right)\prec {\varphi }_{N_e}$ for $\beta \ge 1.14016.$

Proof. 

It is worth noting that for $Re\alpha >n+1$, Theorem 2 implies that

$${\mathtt{F}}_{n,\alpha }\left(z\right)\prec e^z.$$

Now, it follows from (13) that

$${\mathcal{X}}_{n,\alpha ,\beta }^{\prime }\left(z\right)=\frac{1}{\beta }\left(\frac{{\mathtt{F}}_{n,\alpha }\left(z\right)-1}{z}\right)\Rightarrow 1+\beta z{\mathcal{X}}_{n,\alpha ,\beta }^{\prime }\left(z\right)={\mathtt{F}}_{n,\alpha }\left(z\right).$$

Let us denote $p\left(z\right)=e^{{\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)-1}$; then, a logarithmic differentiation gives

$$\frac{p^{\prime }\left(z\right)}{p\left(z\right)}={\mathcal{X}}_{n,\alpha ,\beta }^{\prime }\left(z\right)\Rightarrow 1+\beta \frac{z{p}^{\prime }\left(z\right)}{p\left(z\right)}={\mathtt{F}}_{n,\alpha }\left(z\right).$$

Lastly, a derivative of ${\mathcal{Y}}_{n,\alpha ,\beta }\left(z\right)$ in (14) leads to

$${\mathcal{Y}}_{n,\alpha ,\beta }\left(z\right)+\beta z{\mathcal{Y}}_{n,\alpha ,\beta }^{\prime }\left(z\right)={\mathtt{F}}_{n,\alpha }\left(z\right).$$

The first three cases along with Lemma 4 (part (iv)–(vi)) helps to conclude the result, while the fourth case together with Lemma 3 (part (ii)) implies the result. □

As of a final result, we have the following that can be proved using Theorem 1 and Lemma 4 (part (i)–(iii)) and Lemma 3 (part (i)). We omit the details of the proof.

Theorem 6. 

For $\beta >0$ and $4Re\alpha >16n+1$, the following subordination holds

(i) 

${\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)\prec {\varphi }_{N_e}$ for $\beta \ge 0.920558,$

(ii) 

$e^{{\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)-1}\prec {\varphi }_{N_e}$ for $\beta \ge 0.884792,$

(iii) 

${\mathcal{Y}}_{n,\alpha ,\beta }\left(z\right)\prec {\varphi }_{N_e}$ for $\beta \ge 0.158379.$

Now, we are going to interpret the result obtained in Theorem 5 graphically. For this, we consider the special case where $\alpha =n+1$. In the case ${\mathcal{X}}_{n,n+1,\beta }\left(z\right)\subset {\varphi }_{N_e}\left(z\right)$, we set the smallest value of $\beta =1.97685$. Now, by judicious choice of n (we chose up to 5000), we can see through Figure 13 that ${\mathcal{X}}_{n,n+1,\beta }\left(\mathbb{D}\right)\subset {\varphi }_{N_e}\left(\mathbb{D}\right)$ holds. This indicates that in the case for all $n\ge 1$, the smallest value of $\beta =1.97685$ is sharp. However, in case of a fixed n, there is a possibility to lower the value of $\beta$ as presented in Table 2.

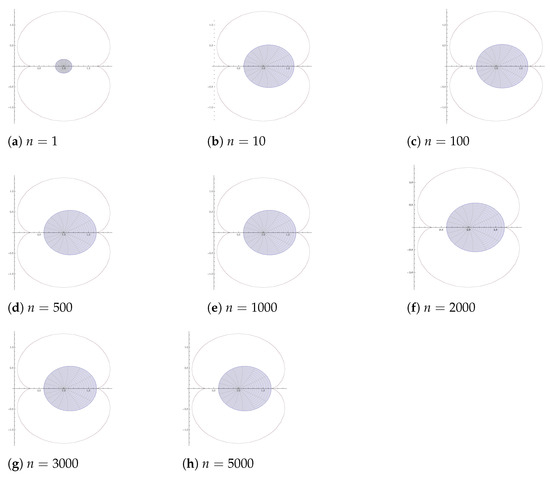
Figure 13. Graph of ${\mathcal{X}}_{n,n+1,\beta }\left(\mathbb{D}\right)$.

Table 2. ${\beta }_0$- possible lowest value of $\beta$ for a fixed n.

n	${\mathit{\beta }}_0$	n	${\mathit{\beta }}_0$
1	$0.5$	5	$1.26$
2	$0.79$	10	$1.47$
3	$0.98$	50	$1.8$
4	$1.2$	100	$1.89$

Clearly ${\beta }_0$ is approaching the value $1.97685$ for increasing n.

Similar analysis of results can also be computed for part of Theorem 5 ((ii) & (iii)) and Theorem 6. We avoid such details. However, this fact leads to an open problem as stated below

Problem 1 

(Open). Find the exact value of ${\beta }_0$ for all n, α such that ${\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)\prec {\varphi }_{N_e}\left(z\right)$; $e^{{\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)-1}\prec {\varphi }_{N_e}\left(z\right)$; and ${\mathcal{Y}}_{n,\alpha ,\beta }\left(z\right)\prec {\varphi }_{N_e}\left(z\right)$ holds for $\beta \ge {\beta }_0$.

6. Conclusions

By using results from the articles [9,10], we find the conditions on the parameter $\alpha$ and n such that

$$\begin{array}{c}\hfill {\mathtt{F}}_{\alpha ,n}\left(z\right)=\frac{n!}{{(\alpha +1)}_n}{\mathtt{L}}_n^{\alpha }\left(z\right),\end{array}$$

is starlike in the ${\mathcal{P}}_{\mathcal{L}}\left(\mathbb{D}\right)$, ${\varphi }_e\left(\mathbb{D}\right)$, ${\varphi }_A\left(\mathbb{D}\right)$. We also consider two integrals involving ${\mathtt{F}}_{n,\alpha }$, namely

$$\begin{array}{c}\hfill {\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)=1+\frac{1}{\beta }{\int }_0^z\frac{{\mathtt{F}}_{n,\alpha }\left(t\right)-1}{t}dt,\mathrm{and}{\mathcal{Y}}_{n,\alpha ,\beta }\left(z\right)=\frac{z^{-\frac{1}{\beta }}}{\beta }{\int }_0^z{\mathtt{F}}_{n,\alpha }\left(t\right)t^{\frac{1}{\beta }-1}dt.\end{array}$$

Then, using results from [11], we derive conditions on $\alpha ,\beta$ and n by which the functions ${\mathcal{X}}_{n,\alpha ,\beta }\left(z\right)$ and ${\mathcal{Y}}_{n,\alpha ,\beta }\left(z\right)$ are subordinated by ${\varphi }_{N_e}\left(z\right)$.

Different graphical presentations demonstrate that the findings in this study are valid. However, there is potential for improvement in a few instances. We conclude by emphasizing that the open cases regarding the function ${\mathtt{F}}_{n,\alpha }$ which are highlighted in this study are required for some alternative methods in contrast to those found in the references [9,10,11]. This could be an interesting topic for further study.