Mathematical Analysis of an SIVRWS Model for Pertussis with Waning and Naturally Boosted Immunity

Abstract

This work aims mainly to study the controllability of pertussis infection in the presence of waning and natural booster of pertussis immunity and to study their impact on the overall dynamics and disease outcomes. Therefore, an SIVRWS (Susceptible-Infected-Vaccinated-Recovered-Waned-Susceptible) model for pertussis infection spread in a demographically stationary, homogeneous, and fully symmetric mixing population is introduced. The model has been mathematically analyzed, where both equilibrium and stability analyses have been established, and uniform persistence of the model has been shown. The conditions on model parameters that ensure effective control of the infection have been derived. The effects of the interplay between waning and boosting pertussis immunity by re-exposure to Bordetella pertussis and vaccination on the dynamics have been investigated. The analytical results have been numerically confirmed and explained. The analysis reveals that ignoring the natural booster of immunity overestimates the endemic prevalence of the infection. Moreover, ignoring the differential susceptibility between secondary and primary susceptible individuals overestimates the critical vaccination coverage required to eliminate the infection. Moreover, the shorter the period of immunity acquired by either vaccination or experiencing natural infection, the higher the reproduction number and the endemic prevalence of infection, and therefore, the higher the effort needed to eliminate the infection.

1. Introduction

Mathematical modeling has gained much attention in the scientific community as it helps describe real problems and enables a better understanding of the system in consideration. It has been used to model problems in various fields including, but not limited to, physics, biology, chemistry, and economy [1,2,3]. More specifically, mathematical models have been used to model infectious diseases and help public health decision-makers obtain more insights into the dynamical spread and controllability of various infectious diseases [4,5,6,7,8,9,10,11]. Among these diseases is pertussis, which is highly contagious, fatal, re-emergent, and circulates worldwide. Its bacteria can easily spread directly from person to person through droplets produced during coughing, sneezing, or even talking. Generally, an infected individual can spread the disease when being in close contact with others within up to approximately one meter. Pertussis is highly incidental during winter and spring seasons among children below 5 years of age because children in this age group are not yet fully vaccinated.

Pertussis is endemic in the United States and most common among young children in developing countries, while it is highly incident among unvaccinated babies and increases again among teens in the developed world. Moreover, it is controllable with strategies based on vaccination [12]. However, it is evident that pertussis vaccines do not confer permanent immunity, yet the immunity acquired due to either vaccination or naturally experiencing pertussis infection declines/wanes with time [13,14,15].

The literature shows differences in the period of immunity acquired by vaccination and natural infection. More specifically, for a number of infectious diseases (e.g., measles, influenza A, COVID-19, and pertussis), the duration of immunity acquired by vaccination is shorter than that acquired by infection, as it is shown that naturally infected patients have higher antibody titer than vaccine recipients [16,17]. For the case of pertussis, definitely, these differences are evident, where in a study on the Senegal population for example, Broutin et al. [18] showed that the gap between two pertussis episodes is 7.1 years in unvaccinated children and 5.1 years in previously vaccinated children. However, Wendelboe et al. [15] showed that vaccine-acquired immunity lasts 4–12 years in children, while infection-acquired immunity wanes after 7–20 years.

The waned immunity is believed to be subsequently boosted by asymptomatic encounters with the infection [19,20]. The interplay between waning and boosting pertussis immunity by exposure to Bordetella pertussis and vaccination affects its transmission dynamics and needs a mathematical model for a true understanding. Various models that take these considerations into account have been developed and analyzed. For example, Carlsson et al. [21] introduced and studied a partial differential equation SIS model of waning and boosting (by repeated vaccination) with discrete immunity classes, but continuous age and time. However, Ehrhardt et al. [22] derived an SIR model to describe vaccination and the waning of immunity. The authors derived some qualitative results and introduced a finite difference scheme to solve the system. Moreover, Elbasha et al. [23] extended the basic SIRS model by including a compartment for imperfect vaccination to study the waning of immunity acquired either naturally or by immunization. In their model, the authors did not differentiate between primary susceptible, secondary susceptible, and waned-immunity individuals, but allowed for vaccinated individuals to either progress directly to the susceptible state or acquire the infection due to successful contact with infected ones. However, very recently, Opoku-Sarkodie et al. [24] extended the basic SIRS model to incorporate the waning and boosting of immunity due to repeated exposure to the infection in the absence of any vaccination scheme. The authors have mathematically analyzed how the different partitioning of the immune period into recovered and waned and varying boosting rates affect the dynamics of the model. In this paper, the last two-mentioned works have been extended by including routine vaccination (whose immunity wanes and has a shorter immunity period than that acquired by natural infection), including an independent compartment of waned individuals, and considering differences in susceptibility between primary and secondary susceptible individuals. Therefore, an SIVRWS (where W stands for waning) model is introduced and thoroughly analyzed. We are especially interested in investigating the effects of the interplay between waning and boosting immunity (by repeated exposure to the infection) on the overall dynamics. Other works include those by Barbarossa et al. [25] and Lavine et al. [20].

Our work is organized as follows. The model is formulated and proved to be well-posed in Section 2. Its equilibrium and stability analyses are shown in Section 3. Uniform persistence is shown in Section 4, while the controllability of pertussis infection is studied in Section 5. Section 6 shows the impact of waning and natural boosting of immunity on disease outcomes. Finally, the work is closed with a summary, conclusion, and future work in Section 7.

2. Model Formulation

The population of interest is assumed to be closed and demographically stationary. According to their epidemiological states, the individuals are categorized into six mutually independent groups. These are primary susceptible individuals (i.e., individuals who have never experienced the infection and whose proportion in the total population at time t is denoted by $S_1\left(t\right)$), vaccinated individuals (i.e., newborns who got vaccinated immediately after birth and whose proportion in the population at time t is denoted by $V\left(t\right)$), infected individuals (i.e., individuals who are infected and capable of transmitting the infection and whose proportion at time t is denoted by $I\left(t\right)$), recovered or boosted highly immune individuals (i.e., individuals who recently recovered from the infection or whose immunity have been naturally boosted due to re-exposure to the infection, and whose time-dependent proportion in the total population is denoted by $R\left(t\right)$), waned immunity individuals (i.e., individuals whose immunity acquired by vaccination or due to recovery after experiencing the infection, declined but are still protected from acquiring the infection and of proportion in the total population at time t is denoted by $W\left(t\right)$), and secondary susceptible individuals (i.e., individuals who partially lost their acquired immunity and whose proportion at time t is denoted by $S_2\left(t\right)$). The individuals in these compartments are asymmetric in their epidemiological status, but symmetric in their mixing behavior in the sense that they mix homogeneously. A brief description of the model variables is shown in Table 1.

Table 1. Physical meaning for model states.

Symbol	Description
$S_1\left(t\right)$	Time-dependent proportion of individuals who have never experienced the infection.
$V\left(t\right)$	Time-dependent proportion of individuals who got vaccinated immediately after birth.
$I\left(t\right)$	Time-dependent proportion of individuals who are infected and capable of transmitting the infection.
$R\left(t\right)$	Time-dependent proportion of individuals who recently recovered from the infection or whose immunity has been naturally boosted due to re-exposure to the infection.
$W\left(t\right)$	Time-dependent proportion of individuals, whose immunity acquired by vaccination or due to recovery after infection, declined but are still protected from acquiring the infection.
$S_2\left(t\right)$	Time-dependent proportion of individuals who partially lost their acquired immunity.

It is worth mentioning that the compartment of vaccinated individuals is recruited by newborns who got primarily immunized following the schedule of doses recommended by the World Health Organization (WHO) and the Center for Disease Control and Prevention (CDC). I.e., it is the routine pertussis vaccination recommended for infants. However, waned immunity individuals are those who lost some of their protective antibodies but still have at least a minimum level of antibodies that protects them against the causative antigen or the disease. The progressive loss of the protective antibodies moves an individual from the compartment of waned to that of secondary susceptible who are assumed to be partially protected against the disease.

It is assumed that individuals are born primarily susceptible and die naturally at the same rate $\mu$, where a proportion p of the newborns gets vaccinated at birth. Due to successful contacts with infected individuals, primary susceptible ones acquire the infection at an infection rate $\beta I$, where $\beta$ is the successful contact rate between $S_1$ and I individuals. Infected individuals recover from the infection at rate $\gamma$, but their naturally-acquired immunity declines, and they become waned at rate $\sigma$. The vaccine-acquired immunity for vaccinated individuals is assumed to decline at a rate $b\sigma$ and they become waned, where b is a rescaling parameter accounting for the relative loss in the vaccine-acquired with respect to the naturally-acquired immunity. The immunity of waned individuals either rises due to their contacts with infected individuals (at the rate $g\beta I$) or it continues to decline (at rate $\alpha$), where they become secondary susceptible, who may acquire the infection at a force of infection $r\beta I$, where $r\in [0,1]$ is the relative susceptibility of secondary susceptible with respect to primary susceptible individuals. A schematic diagram for the transition between the model states is shown in Figure 1 and a detailed description of the model parameters’ physical meaning is presented in Table 2. The parameter values have been chosen to represent (to a high extent) the case of pertussis, see Table 3. Therefore, the population dynamics is described by the following differential equation system

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{S}_1}{dt}}& =& (1-p)\mu -\beta S_{1}I-\mu S_1,\hfill \\ \hfill {\displaystyle \frac{dV}{dt}}& =& p\mu -(b\sigma +\mu )V,\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& =& \beta S_{1}I+r\beta S_{2}I-(\gamma +\mu )I,\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& =& \gamma I-(\sigma +\mu )R+g\beta IW,\hfill \\ \hfill {\displaystyle \frac{dW}{dt}}& =& b\sigma V+\sigma R-g\beta IW-(\mu +\alpha )W\hfill \\ \hfill {\displaystyle \frac{d{S}_2}{dt}}& =& \alpha W-r\beta S_{2}I-\mu S_2,\hfill \\ \hfill 1& =& S_1+V+I+R+W+S_2\hfill \end{array}$$

(1)

with initial conditions

$$S_1\left(0\right),V\left(0\right),I\left(0\right),W\left(0\right),R\left(0\right),S_2\left(0\right)⩾0$$

(2)

where all parameters are assumed to be positive, while the model states are defined on the set

$$\Omega =\{(S_1,V,I,R,W,S_2)\in {\mathbb{R}}_{+}^6:S_1+V+I+W+R+S_2=1\}.$$

The mathematical analysis of the basic properties of model (1) shows that $\Omega$ is positively invariant and model (1) has a unique time-dependent solution, see Appendix A for more details. This result is briefly stated in the following proposition.

Figure 1. Flowchart for the transition between model states.

Table 2. Model parameters’ description.

Parameter	Description	Dimension
$\mu$	Birth and natural death rate.	Time${}^{-1}$
$\beta$	Successful contact rate between primary susceptible and infected individuals.	Time${}^{-1}$
$\gamma$	Rate of recovery from the infection.	Time${}^{-1}$
$\sigma$	Recovered individuals’ rate of waning immunity	Time${}^{-1}$
$\alpha$	The progression rate of waned individuals to become secondary susceptible	Time${}^{-1}$
p	Proportion of newborns who get vaccinated immediately after birth.	Dimensionless
b	Relative loss in vaccine-acquired immunity with respect to naturally acquired immunity.	Dimensionless
r	Relative susceptibility of secondary susceptible with respect to primary susceptible individuals.	Dimensionless
g	A rescaling parameter that accounts for naturally boosting the immunity due to re-exposure to the infection.	Dimensionless

Table 3. Values of model parameters with references.

Parameter	Value	Range	Unit	Reference
$\mu$	$1/73$	-	per year	[26]
${\Re }_v$	13	[12–15]	Dimensionless	[27]
$\beta$	-	-	per year	Assumed
$\gamma$	25	[8.67–52]	per year	[12,28,29]
$\sigma$	0.05	[0.04–0.25]	per year	[12,15,28,29]
$\alpha$	0.16	-	per year	Assumed
p	0.83	[0.8–0.9]	Dimensionless	[30]
$b\sigma$	0.1	[0.083–0.25]	Dimensionless	[12,15,28,29]
b	2	-	Dimensionless	[12]
r	$0.8$	[0, 1]	Dimensionless	[12]
g	$0.3$	-	Dimensionless	Assumed

Proposition 1.

Model (1) has a unique time-dependent solution and any solution starting with non-negative initial conditions remains non-negative and ultimately bounded for all $t>0$. Moreover, the set Ω is positively invariant and attracts all solutions in ${\mathbb{R}}_{+}^6$.

3. Equilibrium and Stability Analyses

3.1. Infection-Free Equilibrium and the Control Reproduction Number

The equilibrium analysis of model (1) reveals that it has an infection-free equilibrium, given by $E_0={(S_{1_0},V_0,I_0,R_0,W_0,S_{2_0})}^{\prime }$ where

$$\begin{array}{ccc}\hfill S_{1_0}& =& 1-p,V_0=\frac{p\mu }{(b\sigma +\mu )},I_0=0,R_0=0,\hfill \\ \hfill W_0& =& \frac{p\mu b\sigma }{(b\sigma +\mu )(\mu +\alpha )},S_{2_0}=\frac{\alpha pb\sigma }{(b\sigma +\mu )(\mu +\alpha )}.\hfill \end{array}$$

(3)

Linearizing model (1) around the trivial equilibrium $E_0$ implies that the corresponding Jacobian matrix is

$$\left(\begin{array}{cccccc}-\mu & 0& -(1-p)\beta & 0& 0& 0\\ 0& -(b\sigma +\mu )& 0& 0& 0& 0\\ 0& 0& (1-p)\beta +r\beta S_{2_0}-(\gamma +\mu )& 0& 0& 0\\ 0& 0& \gamma +g\beta W_0& -(\sigma +\mu )& 0& 0\\ 0& b\sigma & -g\beta W_0& \sigma & -(\mu +\alpha )& 0\\ 0& 0& -r\beta S_{2_0}& 0& \alpha & -\mu \end{array}\right).$$

(4)

It is easy to check that this matrix has five negative eigenvalues given by $-\mu ,-\mu ,-(\alpha +\mu ),-(\sigma +\mu ),-(b\sigma +\mu )$, in addition to a sixth eigenvalue given by

$$\beta (1-p+r{S}_{2_0})-(\gamma +\mu )=\beta \left(1-p+\frac{\alpha rpb\sigma }{(b\sigma +\mu )(\mu +\alpha )}\right)-(\gamma +\mu ).$$

The last eigenvalue is negative if and only if

$$\frac{\beta }{(\gamma +\mu )}\left(1-p+\frac{\alpha rpb\sigma }{(b\sigma +\mu )(\mu +\alpha )}\right)<1.$$

(5)

Following the general approach shown by van den Driessche and Watmough [31], it is easy to check that the non-negative matrix F of the new infection terms, and the non-singular matrix V of the remaining transfer terms are given, respectively, by

$$F=(\beta S_{1_0}+r\beta S_{2_0}),V=(\gamma +\mu ).$$

Hence, the control reproduction number of model (1), denoted by ${\Re }_v$, is given by ${\Re }_v=\rho \left(F{V}^{-1}\right)$, where $\rho$ is the spectral radius (dominant eigenvalue) of the matrix $F{V}^{-1}$. Therefore,

$$\begin{array}{ccc}\hfill {\Re }_v& =& {\displaystyle \frac{\beta }{\gamma +\mu }}(S_{1_0}+r{S}_{2_0})\hfill \\ & =& \frac{\beta }{(\gamma +\mu )}\left(1-p+rp\times {\displaystyle \frac{\alpha }{\alpha +\mu }}\times {\displaystyle \frac{b\sigma }{b\sigma +\mu }}\right).\hfill \end{array}$$

(6)

Hence, the inequality (5) could be written as ${\Re }_v<1$. Therefore, all eigenvalues of the matrix in (4) are negative if and only if ${\Re }_v<1$, and we show the following proposition.

Proposition 2.

The infection-free equilibrium $E_0=(S_{1_0},V_0,I_0,R_0,W_0,S_{2_0})$ is locally asymptotically stable if and only if the control reproduction number ${\Re }_v<1$.

3.2. Endemic Equilibriums and the Bifurcation Direction

The equilibrium analysis shows further that model (1) has an endemic equilibrium, denoted by $E^{*}={(S_1^{*},V^{*},I^{*},R^{*},W^{*},S_2^{*})}^{\prime }$, where $I^{*}\ne 0$. This equilibrium is obtained by setting the derivatives in the left hand side of model (1) equal zero and solving the resulting algebraic equation system, for $I^{*}\ne 0$, to obtain the model state variables at equilibrium. Definitely, we have

$$\begin{array}{ccc}\hfill 0& =& (1-p)\mu -\beta S_1^{*}{I}^{*}-\mu S_1^{*},\hfill \\ \hfill 0& =& p\mu -(b\sigma +\mu )V^{*},\hfill \\ \hfill 0& =& \beta S_1^{*}{I}^{*}+r\beta S_2^{*}{I}^{*}-(\gamma +\mu )I^{*},\hfill \\ \hfill 0& =& \gamma I^{*}-(\sigma +\mu )R^{*}+g\beta I^{*}{W}^{*},\hfill \\ \hfill 0& =& b\sigma V^{*}+\sigma R^{*}-g\beta I^{*}{W}^{*}-(\mu +\alpha )W^{*},\hfill \\ \hfill 0& =& \alpha W^{*}-r\beta S_2^{*}{I}^{*}-\mu S_2^{*}.\hfill \end{array}$$

(7)

The first and second equations in (7) give

$$S_1^{*}=\frac{(1-p)\mu }{\mu +\beta I^{*}}\mathrm{and}{V}^{*}=\frac{p\mu }{(b\sigma +\mu )},$$

(8)

while the third equation in (7), for $I^{*}\ne 0$, leads to

$$S_1^{*}+r{S}_2^{*}=\frac{\gamma +\mu }{\beta }.$$

(9)

From the fourth and fifth equations in (7), we have

$$R^{*}=\frac{\gamma I^{*}+g\beta I^{*}{W}^{*}}{\sigma +\mu }and{W}^{*}=\frac{b\sigma V^{*}+\sigma R^{*}}{g\beta I^{*}+\mu +\alpha }.$$

(10)

From (10), we extract both $R^{*}$ and $W^{*}$ as

$$R^{*}=\frac{b\sigma p\mu g\beta I^{*}+\gamma I^{*}(b\sigma +\mu )(g\beta I^{*}+\mu +\alpha )}{(b\sigma +\mu )[\mu g\beta I^{*}+(\sigma +\mu )(\mu +\alpha )]},$$

(11)

$$W^{*}=\frac{b\sigma (\sigma +\mu )p\mu +\sigma (b\sigma +\mu )\gamma I^{*}}{(b\sigma +\mu )[\mu g\beta I^{*}+(\sigma +\mu )(\mu +\alpha )]}.$$

(12)

From the sixth equation in (7) and using (12), we obtain

$$S_2^{*}=\frac{\alpha (b\sigma (\sigma +\mu )p\mu +\sigma (b\sigma +\mu )\gamma I^{*})}{(\mu +r\beta I^{*})\left[(b\sigma +\mu )(\mu g\beta I^{*}+(\sigma +\mu )(\mu +\alpha ))\right]}.$$

(13)

Substituting from Equations (8) and (13) into Equation (9), we have

$$\frac{(1-p)\mu }{\mu +\beta I^{*}}+\frac{r\alpha (b\sigma (\sigma +\mu )p\mu +\sigma (b\sigma +\mu )\gamma I^{*})}{(\mu +r\beta I^{*})\left[(b\sigma +\mu )(\mu g\beta I^{*}+(\sigma +\mu )(\mu +\alpha ))\right]}=\frac{\gamma +\mu }{\beta }.$$

(14)

Now, we rewrite (14) in the form of a cubic polynomial equation of $\beta I^{*}$ as

$$F(\beta ,I^{*})=Q_1{\left(\beta I^{*}\right)}^3+Q_2{\left(\beta I^{*}\right)}^2+Q_3\left(\beta I^{*}\right)+Q_4=0$$

(15)

where

$$\begin{array}{ccc}\hfill Q_1& =& -rg\mu (\gamma +\mu ),\hfill \\ \hfill Q_2& =& rg{\mu }^2\beta (1-p)+r\alpha \gamma \sigma -r(\gamma +\mu )(\sigma +\mu )(\mu +\alpha )-rg{\mu }^2(\gamma +\mu )\hfill \\ & & -g{\mu }^2(\gamma +\mu ),\hfill \\ & =& rg{\mu }^2(\gamma +\mu )\left(\frac{\beta (1-p)}{\gamma +\mu }-1\right)-r\mu \left((\sigma +\mu )(\alpha +\mu )+\gamma (\alpha +\sigma +\mu )\right)\hfill \\ & & -g{\mu }^2(\gamma +\mu ),\hfill \\ \hfill Q_3& =& g{\mu }^3\beta (1-p)+r\mu \alpha \gamma \sigma +r\mu (\sigma +\mu )(\mu +\alpha )\beta (1-p)+\frac{\beta \alpha rp\mu b\sigma (\sigma +\mu )}{(b\sigma +\mu )}\hfill \\ & & -\mu (\sigma +\mu )(\mu +\alpha )(\gamma +\mu )-g{\mu }^3(\gamma +\mu )-r\mu (\sigma +\mu )(\mu +\alpha )(\gamma +\mu )\hfill \\ & =& g{\mu }^3(\gamma +\mu )\left(\frac{\beta (1-p)}{\gamma +\mu }-1\right)-r\mu [(\sigma +\mu )(\alpha +\mu )+\gamma (\alpha +\sigma +\mu )]\hfill \\ & & +\mu (\sigma +\mu )(\mu +\alpha )(\gamma +\mu )\left(\frac{\beta }{(\gamma +\mu )}\left(r(1-p)+\frac{\alpha rpb\sigma }{(b\sigma +\mu )(\mu +\alpha )}\right)-1\right),\hfill \\ \hfill Q_4& =& {\mu }^2(\sigma +\mu )(\mu +\alpha )\left(\beta (1-p)+\beta \frac{\alpha rpb\sigma }{(b\sigma +\mu )(\mu +\alpha )}-(\gamma +\mu )\right)\hfill \\ & =& {\mu }^2(\sigma +\mu )(\mu +\alpha )(\gamma +\mu )({\Re }_v-1).\hfill \end{array}$$

(16)

Equation (15) is a scalar equation in $I^{*}$. Each positive solution (i.e., $I^{*}>0$) gives rise to an endemic equilibrium. Once $I^{*}$ is known, we obtain the other components (namely, $S_1^{*}$, $R^{*}$, $W^{*}$ and $S_2^{*}$ ) of the endemic equilibrium $E^{*}$. The cubic Equation (15) could be seen as a bifurcation equation in the plane $(\beta ,I^{*})$, where $\beta$ is the bifurcation parameter. It has the bifurcation point $({\beta }_0,0)$, where

$${\beta }_0=\frac{(\gamma +\mu )(b\sigma +\mu )(\mu +\alpha )}{(1-p)(b\sigma +\mu )(\mu +\alpha )+\alpha rpb\sigma }.$$

(17)

In order to investigate the bifurcation direction at the point $({\beta }_0,0)$, we use the implicit function theorem [7]. Definitely, we have (for a complete derivation see Appendix B)

$$\frac{d{I}^{*}}{d\beta }{\mid }_{({\beta }_0,0)}=-\frac{F_{\beta }}{F_{I^{*}}}{\mid }_{({\beta }_0,0)},$$

where

$$F_{\beta }{\mid }_{({\beta }_0,0)}=\frac{\partial F}{\partial \beta }{\mid }_{({\beta }_0,0)}={\mu }^2(\sigma +\mu )(\mu +\alpha )[(1-p)+\frac{\alpha rpb\sigma }{(b\sigma +\mu )(\mu +\alpha )}]>0,$$

$$\begin{array}{ccc}\hfill F_{I^{*}}{\mid }_{({\beta }_0,0)}& =& \frac{\partial F}{\partial I^{*}}{\mid }_{({\beta }_0,0)}=\beta Q_3{\mid }_{\beta ={\beta }_0},\hfill \\ & =& g{\mu }^3(\gamma +\mu )(-\alpha rpb\sigma )-\Theta r\mu [(\sigma +\mu )(\alpha +\mu )+\gamma (\alpha +\sigma +\mu )]\hfill \\ & & +\mu (\sigma +\mu ){(\mu +\alpha )}^2(\gamma +\mu )(1-p)(b\sigma +\mu )(r-1)<0\hfill \end{array}$$

and $\Theta =(1-p)(b\sigma +\mu )(\mu +\alpha )+\alpha rpb\sigma .$ Hence,

$$\frac{d{I}^{*}}{d\beta }{\mid }_{({\beta }_0,0)}>0.$$

Therefore, the bifurcation direction at the point $({\beta }_0,0)$ is forward (i.e., supercritical). This result is briefly stated in the following proposition.

Proposition 3.

Model (1) shows forward (supercritical) bifurcation at the bifurcation point $({\beta }_0,0)$. The model does not exhibit backward bifurcation for ${\Re }_v<1$.

As equation (15) is cubic in $I^{*}$, it may have multiple supercritical endemic states (for ${\Re }_v>1$) and multiple subcritical endemic states (for ${\Re }_v<1$). To check the existence/non-existence of subcritical multiple equilibria, we apply Descartes’ rule of signs [32], on the polynomial in (15). Clearly, from (16), the coefficient $Q_1$, is always negative regardless of the values of the parameters. Moreover, if the control reproduction number ${\Re }_v<1$, then

$$\frac{\beta (1-p)}{\gamma +\mu }<1and\frac{\beta }{(\gamma +\mu )}\left(r(1-p)+\frac{\alpha rpb\sigma }{(b\sigma +\mu )(\mu +\alpha )}\right)<1.$$

Consequently, the coefficients $Q_2,Q_3$, and $Q_4$ are always negative, meaning that there are no sign changes. Hence, using the Descartes’ rule of signs, Equation (15) has no positive real root when ${\Re }_v<1$ and the endemic equilibrium exists only if ${\Re }_v>1$. The following proposition summarizes the above-obtained results.

Proposition 4.

Model (1) has no endemic equilibrium for ${\Re }_v<1$, and any endemic equilibrium does exist only if ${\Re }_v>1$.

It is worth mentioning that ${\Re }_v=1$ is equivalent to saying that $\beta ={\beta }_0$. Therefore, the bifurcation point (${\beta }_0,0$) in the plane $(\beta ,I^{*})$ is the same as the bifurcation point $(1,0)$ in the plane $({\Re }_v,I^{*})$. Figure 2 shows a bifurcation diagram for the endemic prevalence of the infection $I^{*}$ as a function of the reproduction number ${\Re }_v$, where all parameters (except $\beta$) have been kept fixed and with values as in Table 3. The figure shows further that $I^{*}$ increases initially with the increase in ${\Re }_v$ till reaching a peak and then decreases monotonically. In other words, higher values of the control reproduction number ${\Re }_v$ reduce the proportion of the infected population in the endemic situation.

Figure 2. A bifurcation diagram showing the endemic prevalence of infection as a function of the control reproduction number, with parameter values as shown in Table 3.

4. Uniform Persistence

Before going into detail on the persistence of the infection, we present a result on the global stability of the infection-free equilibrium. The global stability of the infection-free equilibrium $E_0$ is discussed by following the approach presented in Castillo-Chavez et al. [33]. Accordingly, model (1) could be rewritten as

$$\begin{array}{ccc}\hfill \frac{d{X}_1}{dt}& =& F(X_1,X_2),\hfill \\ \hfill \frac{d{X}_2}{dt}& =& G(X_1,X_2),G(X_1,0)=0,\hfill \end{array}$$

(18)

where $X_1=(S_1,V,R,W,S_2)\in {\mathbb{R}}^5$ denotes the components of uninfected individuals and $X_2=I\in \mathbb{R}$ denotes the components of infected individuals. Let $U_0=(X_1^0,0)$ denote the IFE of the model (18), which is equivalent to the IFE of model (1). Thus, the global stability of the infection-free equilibrium depends on the following two conditions.

$\left(C_1\right)$

For $\frac{d{X}_1}{dt}=F(X_1,0)$, $X_1^0$ is globally asymptotically stable.

$\left(C_2\right)$

$G(X_1,X_2)=A{X}_2-\widehat{G}(X_1,X_2)$, where $\widehat{G}(X_1,X_2)⩾0$ for $(X_1,X_2)\in \Omega$,

• where the Jacobian matrix $A=D_{X_2}G(X_1^0,0)$ has all non-negative off-diagonal elements, and $\Omega$ is the region where the model makes biological sense. Then, we present the following proposition, whose proof is deferred to Appendix C.

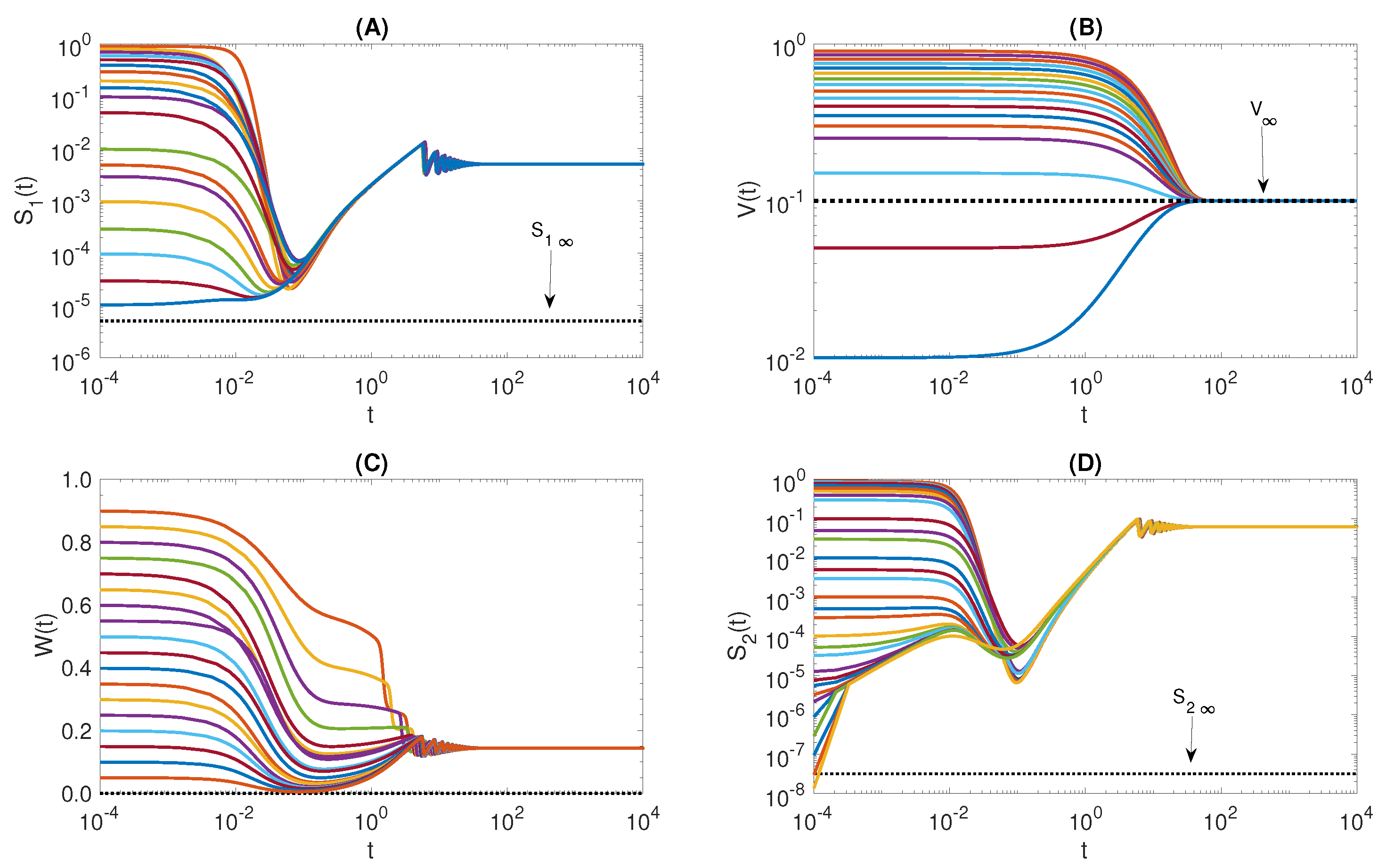
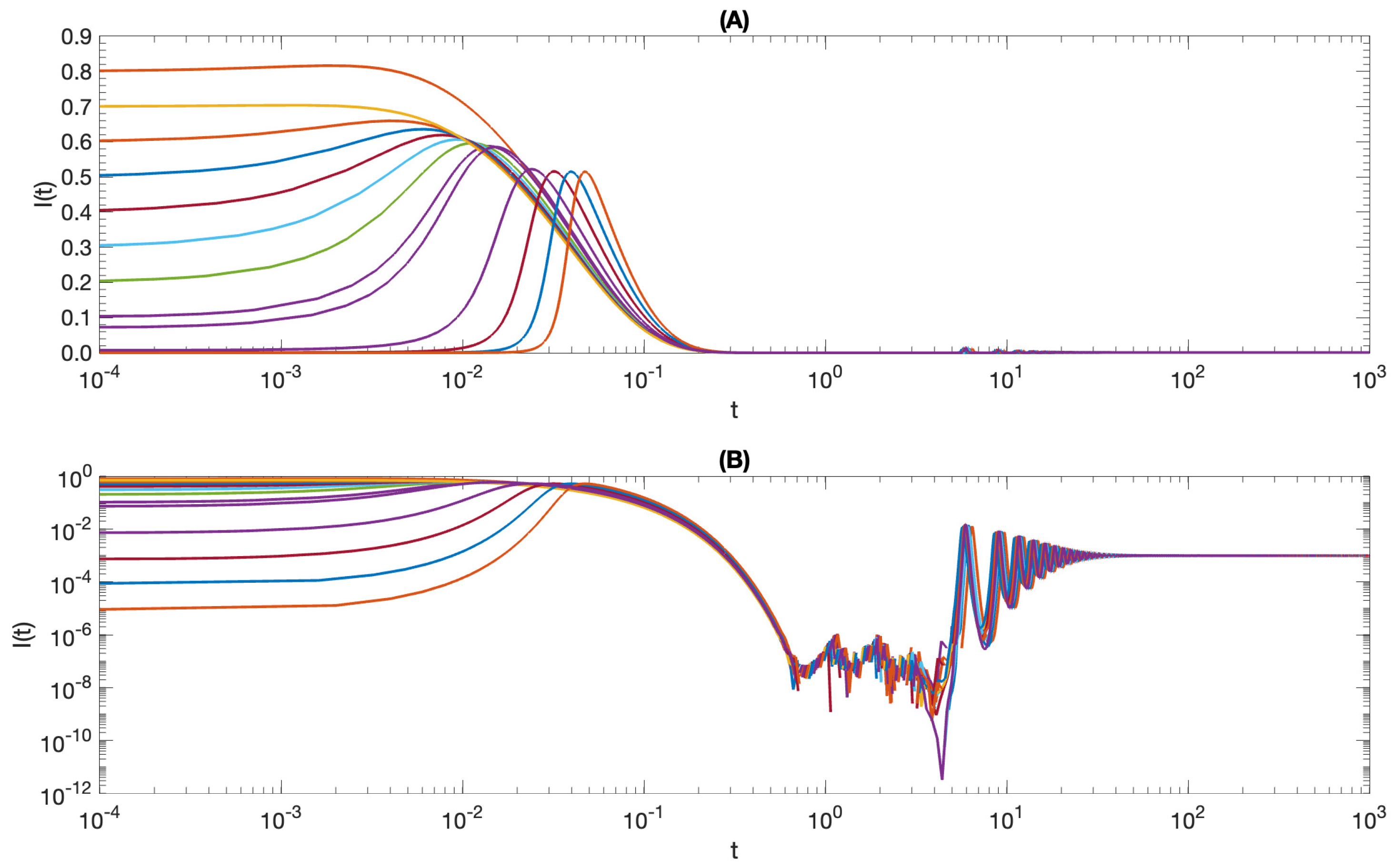
Proposition 5.

Infection-free equilibrium of model (1) is globally asymptotically stable in Ω if ${\Re }_v<1$ and above conditions are satisfied.

Based on the use of the Rung–Kutta method of order four, extensive simulations for model (1) have been performed and some of them are shown in Figure 3. The simulations show that all time-dependent solutions starting in the region $\Omega$ (with parameter values such that ${\Re }_v<1$, while keeping the other parameters as in Table 3) are attracted by the infection-free equilibrium $E_0$.

Figure 3. Time-dependent solutions, with various initial conditions, for the proportion of infected individuals $I\left(t\right)$. Each colored curve represents a solution. Simulations have been done with parameter values as shown in Table 3, except $\beta$ that has been chosen to keep the reproduction number ${\Re }_v=0.8<1$.

Now, we study the uniform persistence of the model (1). This model is said to be uniformly persistent [34,35] if there exists some $ϵ>0$ such that its time-dependent solution, with positive initial conditions, satisfies

$$\begin{array}{ccc}\hfill \underset{t\to \infty }{lim\; inf}{S}_1\left(t\right)& \ge & ϵ,\underset{t\to \infty }{lim\; inf}V\left(t\right)\ge ϵ,\underset{t\to \infty }{lim\; inf}I\left(t\right)\ge ϵ,\hfill \\ \hfill \underset{t\to \infty }{lim\; inf}R\left(t\right)& \ge & ϵ,\underset{t\to \infty }{lim\; inf}W\left(t\right)\ge ϵ,\underset{t\to \infty }{lim\; inf}{S}_2\left(t\right))\ge ϵ.\hfill \end{array}$$

(19)

We first show that the compartments of non-negative sub-populations $S_1\left(t\right),$$V\left(t\right)$, $W\left(t\right)$ and $S_2\left(t\right)$ are always uniformly persistent, regardless of the value of the control reproduction number ${\Re }_v$. Then, we prove the uniform persistence of the disease’s compartment $I\left(t\right)$ (when ${\Re }_v>1$), by using persistence results from Smith and Thieme [36].

Our proof is based on the use of the fluctuation lemma (see Appendix A of [36]). To this end, we let $f:[0,\infty )\to \mathbb{R}$ be a real-valued function, and the limit superior and the limit inferior of f as $t\to \infty$ be defined as

$$f_{\infty }=\underset{t\to \infty }{lim\; inf}f\left(t\right),f^{\infty }=\underset{t\to \infty }{lim\; sup}f\left(t\right).$$

To prove the persistence of the primary susceptible sub-population $S_1\left(t\right)$, we let $S_{1_{\infty }}=\underset{t\to \infty }{lim\; inf}{S}_1\left(t\right)$. On applying the fluctuation lemma, there exists a sequence $t_n\to \infty$ such that $S_1\left(t_n\right)\to S_{1_{\infty }}$ and ${\dot{S}}_1\left(t_n\right)\to 0$ as $n\to \infty$, where the over-dot indicates the derivative with respect to time t. If we apply this to the $S_1$-equation in model (1), we obtain

$${\dot{S}}_1\left(t_n\right)+\beta I\left(t_n\right)S_1\left(t_n\right)+\mu S_1\left(t_n\right)=(1-p)\mu .$$

From Proposition 1, we have ${lim}_{t\to \infty }(S_1\left(t\right)+V\left(t\right)+I\left(t\right)+R\left(t\right)+W\left(t\right)+S_2\left(t\right))=1$. Hence, $0\le I\left(t\right)\le 1$. Using this and letting $n\to \infty$, we obtain

$$S_{1_{\infty }}\ge {\displaystyle \frac{(1-p)\mu }{\beta +\mu }}>0.$$

Hence, $S_1\left(t\right)$ is always uniformly persistent.

Similarly, we apply the fluctuation lemma to the $V,W$ and $S_2$ equations in (1) and use the fact that $0\le I\left(t\right)\le 1$. There exists a sequence $t_n\to \infty$ such that $V\left(t_n\right)\to V_{\infty }$ and $\dot{V}\left(t_n\right)\to 0$ as $n\to \infty$. Hence,

$$V_{\infty }={\displaystyle \frac{p\mu }{b\sigma +\mu }}>0.$$

Moreover, there can exist a different sequence $t_n\to \infty$ such that $W\left(t_n\right)\to W_{\infty }$ and $\dot{W}\left(t_n\right)\to 0$ as $n\to \infty$. Hence,

$$W_{\infty }\ge {\displaystyle \frac{b\sigma V_{\infty }}{g\beta +\alpha +\mu }}\ge {\displaystyle \frac{pb\sigma \mu }{(g\beta +\alpha +\mu )(b\sigma +\mu )}}>0.$$

Finally, there can also exist another sequence $t_n\to \infty$ such that $S_2\left(t_n\right)\to S_{2_{\infty }}$ and ${\dot{S}}_2\left(t_n\right)\to 0$ as $n\to \infty$. Hence,

$$S_{2_{\infty }}\ge {\displaystyle \frac{\alpha W_{\infty }}{r\beta +\mu }}\ge {\displaystyle \frac{\alpha pb\sigma \mu }{(r\beta +\mu )(g\beta +\alpha +\mu )(b\sigma +\mu )}}>0.$$

Thus, the non-infected compartments $V\left(t\right),W\left(t\right)$ and $S_2\left(t\right)$ are also uniformly persistent. Therefore, we state the following proposition.

Proposition 6.

The time-dependent solutions of the non-infected sub-population compartments $S_1\left(t\right),V\left(t\right),W\left(t\right)$ and $S_2\left(t\right)$ are always uniformly persistent.

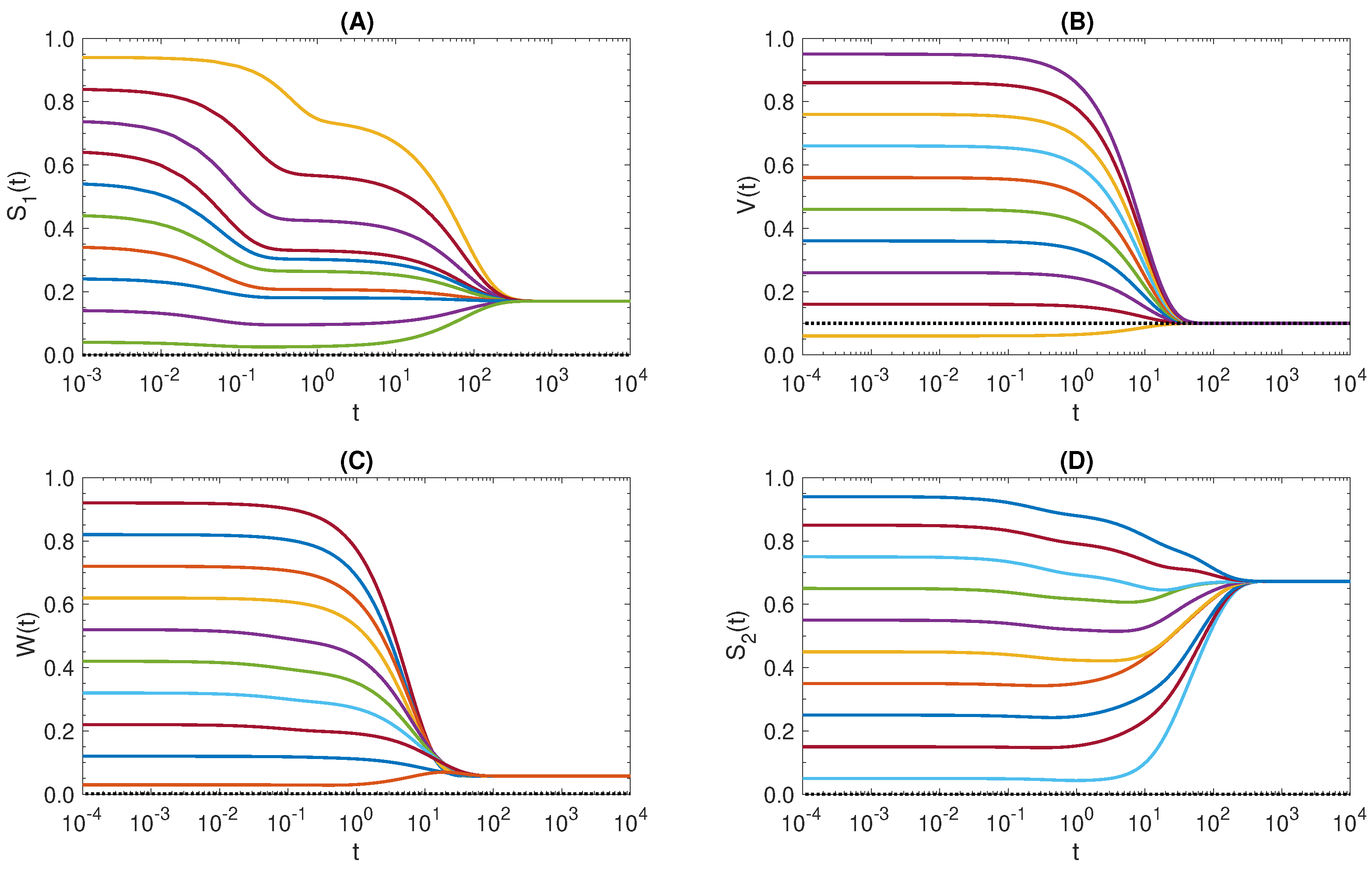
Figure 4 shows the time-dependent solution for the non-infected components $S_1\left(t\right),V\left(t\right),W\left(t\right)$ and $S_2\left(t\right)$ with various positive initial conditions and with values of parameters as in Table 3 except $\beta$ that has been chosen to restrict the reproduction number ${\Re }_v=0.8<1$. The simulations show that $S_{1\infty }=8.2347\times {10}^{-5},V_{\infty }=1.0\times {10}^{-1},W_{\infty }=1.2\times {10}^{-3}$ and $S_{2\infty }=8.1715\times {10}^{-6}>0$. Similar results have been obtained by solving with the same parameter values except for $\beta$ which is chosen such that ${\Re }_v=13>1$, see Figure 5.

Figure 4. Time-dependent solutions, with various initial conditions, for the proportion of non-infected sub-populations. Each colored curve represents a solution. The subfigures (A–D) show solutions of the proportion of primary susceptible $S_1\left(t\right)$, vaccinated $V\left(t\right)$, waned $W\left(t\right)$, and secondary susceptible $S_2\left(t\right)$ individuals, respectively. Simulations have been done with parameter values as shown in Table 3, except $\beta$ that has been chosen to keep the reproduction number ${\Re }_v=0.8<1$. The dotted horizontal line in each subfigure represents the infimum.

Figure 5. Time-dependent solutions, with various initial conditions, for the proportion of non-infected sub-populations. Each colored curve represents a solution. The subfigures (A–D) show solutions of the proportion of primary susceptible $S_1\left(t\right)$, vaccinated $V\left(t\right)$, waned $W\left(t\right)$, and secondary susceptible $S_2\left(t\right)$ individuals, respectively. Simulations have been done with parameter values as shown in Table 3, where the reproduction number ${\Re }_v=13>1$. The dotted horizontal line in each subfigure represents the infimum.

Now, we examine the uniform persistence of the disease when ${\Re }_v>1$ using the theory of uniform persistence [36]. To this end, we let $\Phi :{\mathbb{R}}_{+}\times \Omega ⟶\Omega$ be a continuous semiflow corresponding system (1) defined on the feasible state space $\Omega$. We define the persistence function

$$\rho :\Omega ⟶{\mathbb{R}}_{+}.$$

Now, we choose $\rho \left(x\right)=I\left(t\right)$ and define the sets

$$\begin{array}{ccc}\hfill {\Omega }_{+}& =& \{x\in \Omega :\rho (x)>0\},\hfill \\ \hfill {\Omega }_0& =& \Omega \setminus {\Omega }_{+}=\{x\in \Omega :\rho \left(x\right)=0\}\hfill \end{array}$$

where ${\Omega }_0$ is the invariant extinction space of $I\left(t\right)$ corresponding to $\rho$ (i.e., ${\Omega }_0$ is the collection of states in the absence of the disease). From proposition 1, the set $\Omega$ is positively invariant which implies that ${\Omega }_{+}$ and ${\Omega }_0$ are positively invariant and ${\Omega }_0$ is relatively closed under the semiflow $\Phi$. Now, we let $\omega \left(x\right)$ denote the $\omega$-limit set of a point in $\Omega$, where

$$\omega \left(x\right)=\{y\in \Omega :\exists t_{n}suchthat{t}_n\to \infty and\Phi (t_n,x)\to yasn\to \infty \},$$

and use the results shown in [36] (Chapter 8) to examine the set ${\cup }_{x\in {\Omega }_0}\omega \left(x\right)$. Clearly, all solutions starting in the extinction space ${\Omega }_0$ converge to the infection-free equilibrium. Therefore, ${\cup }_{x\in {\Omega }_0}\omega \left(x\right)=\left\{E_0\right\}$.

In the following, we prove the weak $\rho$-persistence using Theorem 8.17 in [36]. Using the terminology shown in [36], we let $M_1=\left\{E_0\right\}$. Therefore, ${\cup }_{x\in {\Omega }_0}\omega \left(x\right)\subset M_1$ where $M_1$ is isolated (due to unstability of $E_0$ when ${\Re }_v>1$, Proposition 2), compact, invariant and acyclic. We still have to prove that $M_1$ is weakly $\rho$-repelling. Then, by results from Chapter 8 of [36], we obtain the weak persistence.

Assume, by contradiction, that $M_1$ is not weakly $\rho$-repelling, i.e., there exists a solution of model (1) which converges to $E_0$ and $\rho \left(x\right)=I\left(t\right)>0$. Therefore, for any $ϵ>0$, and for sufficiently large t, we obtain

$$0<I\left(t\right)<ϵ,S_{1_0}-ϵ<S_1\left(t\right)<S_{1_0}+ϵ,S_{2_0}-ϵ<S_2\left(t\right)<S_{2_0}+ϵ.$$

Thus, for sufficiently large t, we can estimate ${\displaystyle \frac{dI}{dt}}$ as follows:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dI}{dt}}& =& \beta (S_1+r{S}_2)I\left(t\right)-(\gamma +\mu )I\left(t\right),\hfill \\ & >& \left(\beta (S_{1_0}+r{S}_{2_0})-(\gamma +\mu )-\beta (1+r)ϵ\right)I\left(t\right),\hfill \\ & =& \left({\Re }_v-1-{\displaystyle \frac{\beta }{\gamma +\mu }}(1+r)ϵ\right)(\gamma +\mu )I\left(t\right)>0\hfill \end{array}$$

which is positive if $ϵ$ is sufficiently small as follows from ${\Re }_v>1$. This contradicts $I\left(t\right)\to 0$. Hence, $M_1$ is weakly $\rho$-repelling and from Theorem 8.17 in [36], our flow $\Phi$ is uniformly weakly $\rho$-persistent.

Proposition 1 implies that the solutions of model (1) are ultimately bounded. Then, $\Phi :{\mathbb{R}}_{+}\times \Omega ⟶\Omega$ is point-dissipative and compact on $\Omega$ [37]. In view of Theorem 3.4.8 given by [38], $\Phi \left(t\right)$ has a compact global attractor in $\Omega$.

To prove the uniform (strong) persistence, we apply Theorem 4.5 shown in [36]. Clearly, model (1) generates a continuous flow on $\Omega$ and the subspaces $\Omega$, ${\Omega }_{+}$ and ${\Omega }_0$ are invariant. Moreover, the existence of a compact attractor in $\Omega$ is proved. Therefore, all conditions of Theorem 4.5 in [36] are satisfied from which we conclude that $\Phi$ is uniformly $\rho$-persistent (i.e., the disease $I\left(t\right)$ is uniformly persistent). Hence, we summarize the above results in the following proposition.

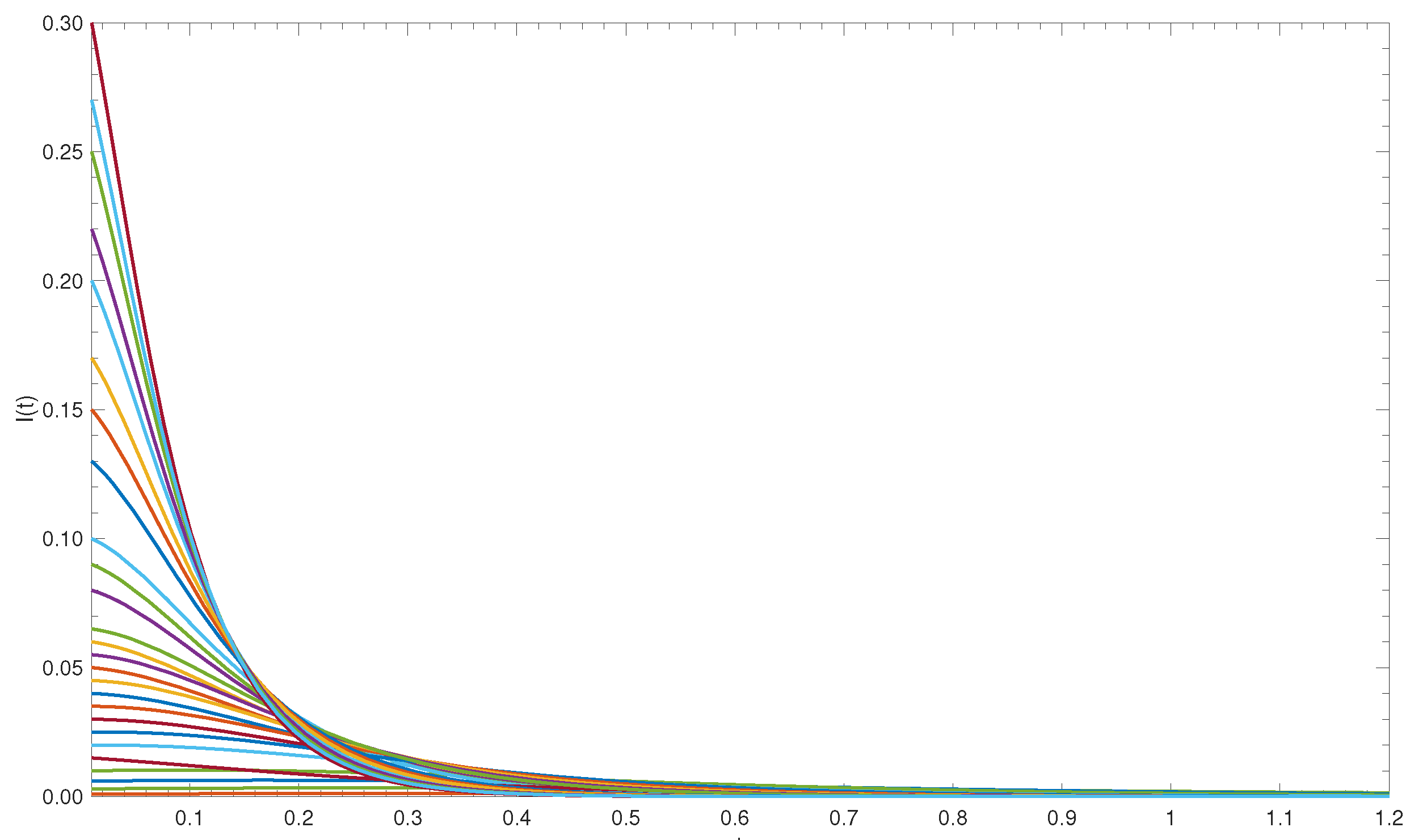
Proposition 7.

If ${\Re }_v>1$, then the semiflow Φ is uniformly ρ-persistent, i.e., the disease is uniformly persistent in the population. More precisely, there exists an $ϵ>0$ such that for any positive solution of model (1), $\underset{t\to \infty }{lim\; inf}I\left(t\right)\ge ϵ$.

Time-series analysis for the proportion of infected individuals, with parameter values as in Table 3, is shown in Figure 6. Figure 6A shows the solution with the Y-axis being in a linear scale, while Figure 6B shows the same trajectories in the logarithmic scale to better present the behavior of the solutions. It is clear that when $t\to \infty$, the value of $I\left(t\right)$ is bigger than some $ϵ>0$.

Figure 6. Time-dependent solutions, with various initial conditions, for the proportion of infected individuals $I\left(t\right)$, with parameter values as shown in Table 3, where the reproduction number ${\Re }_v=13>1$. Each colored curve represents a solution. Part (A) shows the results, with Y-axis being in a linear scale, while part (B) shows it in a logarithmic scale.

5. Controllability of the Infection

The above analysis showed that model (1) exhibits only forward bifurcation and that no endemic equilibrium exists for values of ${\Re }_v<1$. Therefore, the controllability of the infection is guaranteed by applying control measures aiming to reduce the value of ${\Re }_v$ to slightly below one. This is equivalent to having $\beta <{\beta }_v$, where

$$\begin{array}{ccc}\hfill {\beta }_v& =& \frac{(\gamma +\mu )(b\sigma +\mu )(\mu +\alpha )}{(1-p)(b\sigma +\mu )(\mu +\alpha )+\alpha rpb\sigma }\hfill \\ & =& (\gamma +\mu )/\left(1-p+r\times p\times {\displaystyle \frac{\alpha }{\alpha +\mu }}\times {\displaystyle \frac{b\sigma }{b\sigma +\mu }}\right)\hfill \\ & =& (\gamma +\mu )/\left(1-p+r\times p\times \left(1-{\displaystyle \frac{\mu }{\alpha +\mu }}\right)\times \left(1-{\displaystyle \frac{\mu }{b\sigma +\mu }}\right)\right)\hfill \\ & =& {\displaystyle \frac{\gamma +\mu }{1-p+r\times p\times \left(1-P_W\right)\times \left(1-P_V\right)}}\hfill \end{array}$$

(20)

is the critical contact rate separating the regions of disappearance and persistence of pertussis infection and the proportion

$$P_W={\displaystyle \frac{\mu }{\alpha +\mu }}={\displaystyle \frac{1}{\alpha +\mu }}/{\displaystyle \frac{1}{\mu }}$$

is the proportion of life spent in the waning immunity state, while the proportion

$$P_V={\displaystyle \frac{\mu }{b\sigma +\mu }}={\displaystyle \frac{1}{b\sigma +\mu }}/{\displaystyle \frac{1}{\mu }}$$

is the proportion of life spent in the vaccinated state.

Routine vaccination is considered one of the most important strategies applied to protect populations from the negative impact of infectious diseases and is represented here by the dimensionless parameter $p\in [0,1]$. A value of $p=0$ means that none of the new births receive the vaccine, while $p=1$ represents that all newborns get the shots. However, the ${\beta }_v$ represents here the critical contact rate (in the presence of vaccination) that separates between non-existence and existence of infection and is a function of p and some other model parameters. Of great interest is the dependence of ${\beta }_v$ on p. If ${\beta }_v\to \infty$ as $p\to 1$, then the infection is always controllable with strategies based on routine vaccination only [8,12]. However, if ${\beta }_v$ approaches a finite asymptote (say, ${\beta }^{\diamond }$) as $p\to 1$, then the infection is controllable only if control strategies (other than vaccination) are applied to reduce $\beta$ to slightly below ${\beta }^{\diamond }$, in addition to vaccinating a proportion $p>p^{\star }$, where

$$\begin{array}{ccc}\hfill p^{\star }& =& \left(1-\frac{\gamma +\mu }{\beta }\right)/\left(1-r\times {\displaystyle \frac{\alpha }{\alpha +\mu }}\times {\displaystyle \frac{b\sigma }{b\sigma +\mu }}\right)\hfill \end{array}$$

(21)

$$\begin{array}{ccc}& =& \left(1-\frac{\gamma +\mu }{\beta }\right)/\left(1-r\left(1-P_W\right)\left(1-P_V\right)\right)\hfill \end{array}$$

(22)

is the critical vaccination coverage required to eliminate pertussis infection. In fact, the value of ${\beta }^{\diamond }$ is

$${\beta }^{\diamond }={\displaystyle \frac{1}{r}}\times {\displaystyle \frac{\alpha +\mu }{\alpha }}\times {\displaystyle \frac{b\sigma +\mu }{b\sigma }}\times (\gamma +\mu )={\displaystyle \frac{1}{r}}\times {\displaystyle \frac{1}{1-P_W}}\times {\displaystyle \frac{1}{1-P_r}}\times (\gamma +\mu )$$

(23)

and represents the reinfection contact rate [8,12]. It is noteworthy that the critical vaccination coverage $p^{\star }$ decreases with the increase in either or both of $P_V$ and $P_W$ and increases with the increase in the rescaling parameter r. This means that ignoring the difference between susceptibilities of primary and secondary susceptible individuals overestimates the value of $p^{\star }$. However, the reinfection contact rate ${\beta }^{\diamond }$ increases with the increase in either of the proportions $P_W$ and $P_V$ and with the decline in r. The critical contact rate ${\beta }_v$ is depicted as a function of the vaccination coverage p for different values of the proportions $P_V,P_W$ and the scaling parameter r in Figure 7A–C, respectively. The figure shows that the region of infection’s controllability enlarges with the increase in the proportions $P_V$ and $P_W$ and the decrease in the relative susceptibility parameter r. In summary, we state the following proposition.

Figure 7. The critical contact rate ${\beta }_v$ as a function of the vaccination coverage level p for various values of $P_V,P_W$ and r, while keeping other model parameters’ value as shown in Table 3. The curve divides the ($p,\beta$) plane into the two regions of disappearance (below the curve) and persistence (above the curve) of infection. The subfigures (A,B) show that the disappearance region extends with the increase in the proportions $P_V$ and $P_W$, respectively, while the subfigure (C) shows that it increases with the decrease in the relative susceptibility r of secondary (with respect to primary) susceptible individuals.

Proposition 8.

If the successful contact rate β is less than the reinfection contact rate ${\beta }^{\diamond }$, then the infection is eliminated by vaccinating a proportion $p>p^{\star }$ of the newborns, while if $\beta >{\beta }^{\diamond }$, then the infection cannot be eliminated with a strategy based on vaccination solely, but other control strategies aiming at reducing β to slightly below ${\beta }^{\diamond }$ should be applied, in addition to vaccinating a proportion $p>p^{\star }$. Moreover, the possibility to control the infection enlarges with the increase in the proportion of life spent in the immunization and waning states and the decrease in the relative susceptibility of secondary (with respect to primary) susceptible individuals.

6. Impact of Waning and Natural Immune Boosting on Disease Outcomes

As explained in Section 2, the immunity acquired either due to vaccination or due to experiencing the infection declines and the individual’s status becomes waned. In model (1), the two parameters $\sigma$ and $\alpha$ determine the duration of acquired immunity and progression to become secondary susceptible, respectively. However, the natural immunity boosting is represented by the rescaling parameter $g\in [0,1]$ (times the force of infection $\lambda$), where a value of $g=0$ means that the natural boosting immunity is completely ignored. The parameter g does not appear explicitly in the formula of the reproduction number ${\Re }_v$. 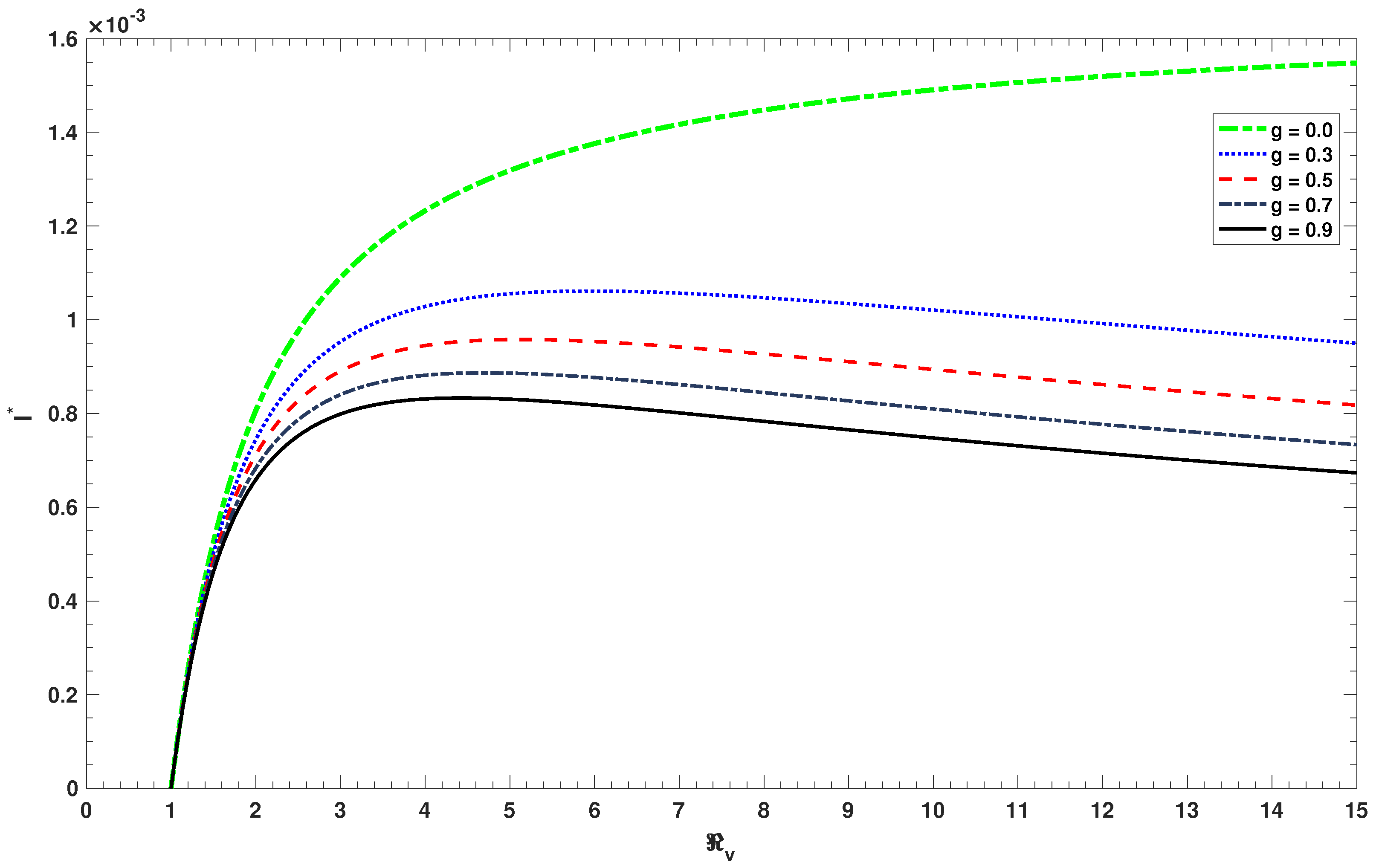However, it appears in the coefficients of the characteristic epidemiological Equation (15) and, therefore, affects the endemic prevalence of the infection.

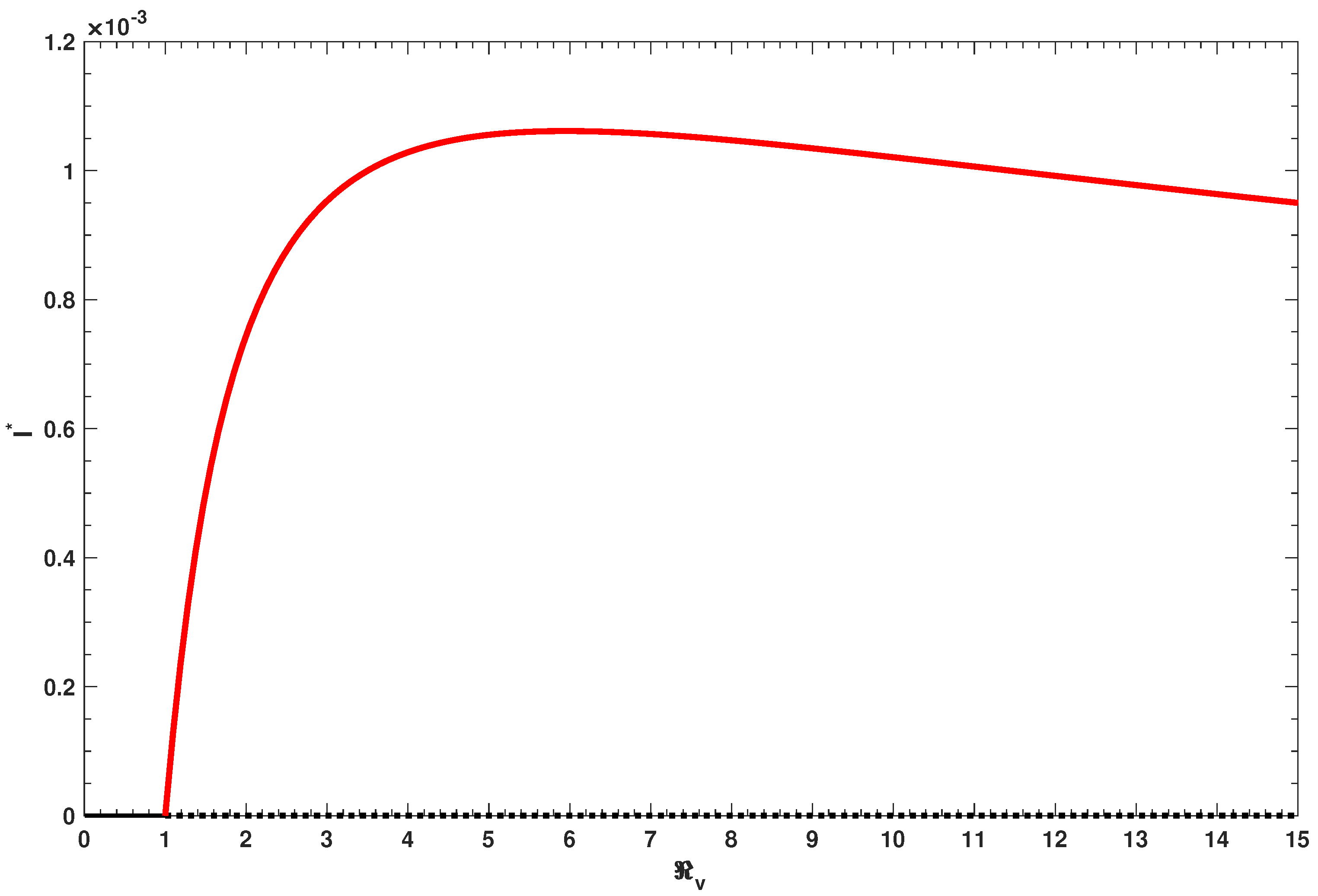
In the absence of natural booster immunity (i.e., $g=0$), the Equation (15) reduces from cubic to quadratic equation with simpler coefficients than in (16). In this case, the proportion of the infected population in the endemic situation reads

$$\overline{I}={\displaystyle \frac{B_1+\sqrt{B_1^2+4A_1{C}_1}}{2\beta A_1}}$$

(24)

where

$$\begin{array}{ccc}\hfill A_1& =& r\left((\sigma +\mu )(\alpha +\mu )+\gamma (\alpha +\sigma +\mu )\right),\hfill \\ \hfill B_1& =& r\alpha \gamma \sigma +(\sigma +\mu )(\mu +\alpha )\left(r\beta (1-p)-(1+r)(\gamma +\mu )\right)+\frac{rpb\sigma \alpha (\sigma +\mu )\beta }{(b\sigma +\mu )},\hfill \\ \hfill C_1& =& \mu (\sigma +\mu )(\mu +\alpha )(\gamma +\mu )({\Re }_v-1).\hfill \end{array}$$

The endemic prevalence of the infection $\overline{I}$ is depicted as a function of the control reproduction number ${\Re }_v$ for different values of the natural booster immunity parameter g and is presented in Figure 8. The figure shows that the proportion $\overline{I}$ increases monotonically with the increase in ${\Re }_v$, in the absence of natural booster immunity (i.e., if $g=0$). However, in the presence of natural booster immunity (i.e., if $g>0$), the endemic prevalence $\overline{I}$ increases monotonically in ${\Re }_v$ till reaching a maximum at some value of ${\Re }_v$ and then starts to decrease with the increase in ${\Re }_v$. This result could be read in a reverse way as follows. In the presence of natural booster immunity, reducing the control reproduction number ${\Re }_v$ increases the endemic prevalence of infection $\overline{I}$ till reaching a maximum level, and a further reduction in the value of ${\Re }_v$ to one (or slightly below one) forces a reduction in the endemic prevalence of infection $\overline{I}$ to zero. The figure also shows that the endemic prevalence of the infection $\overline{I}$ decreases with the increase in the natural booster immunity parameter g. Therefore, ignoring the natural booster immunity overestimates the endemic prevalence of infection and, in consequence, overestimates the effort needed to eliminate the infection.

Figure 8. The endemic prevalence of infection as a function of the control reproduction number with various values of the natural boosting immunity parameter g, where all other parameters have been kept fixed and with values as shown in Table 3.

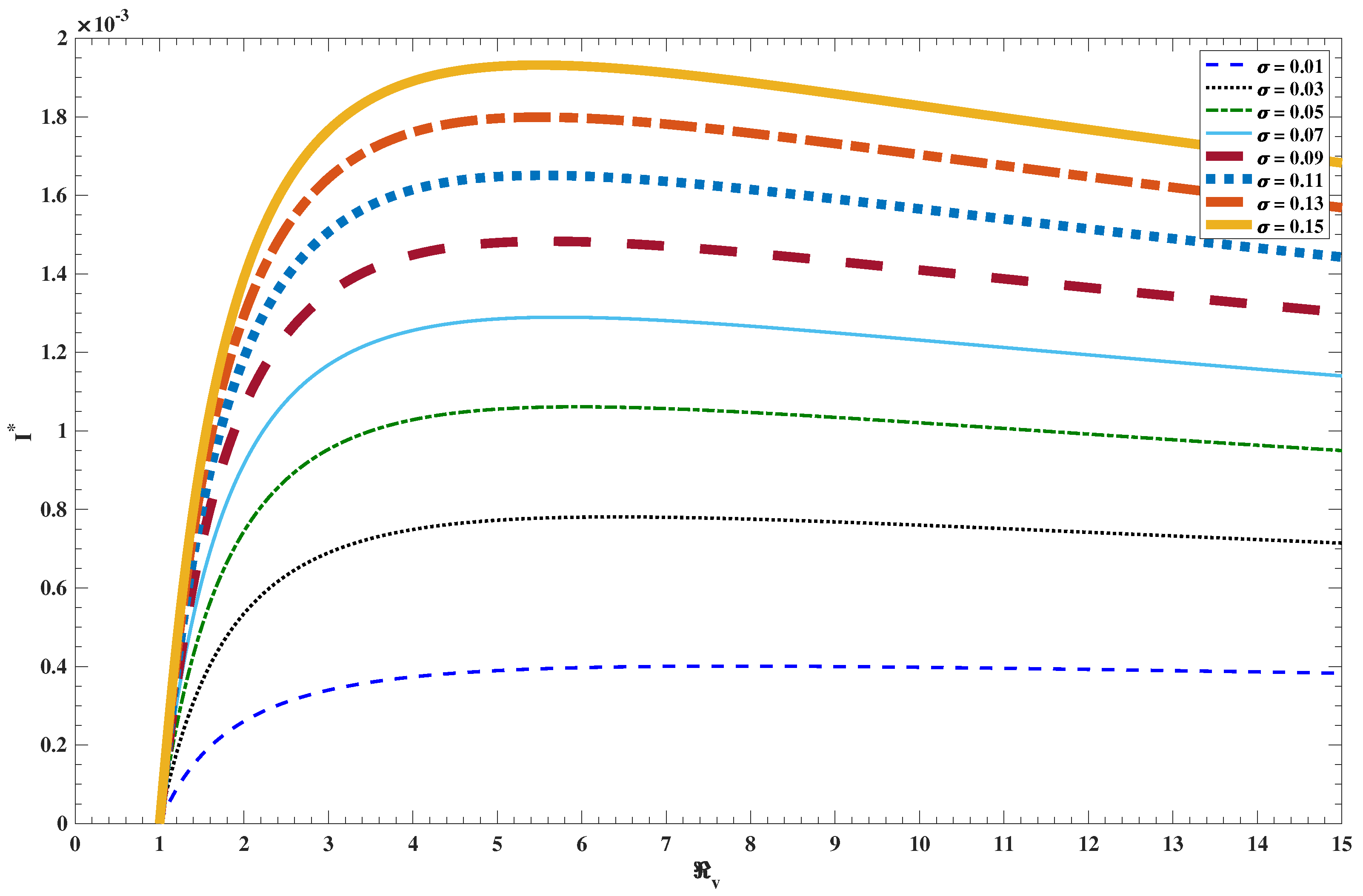
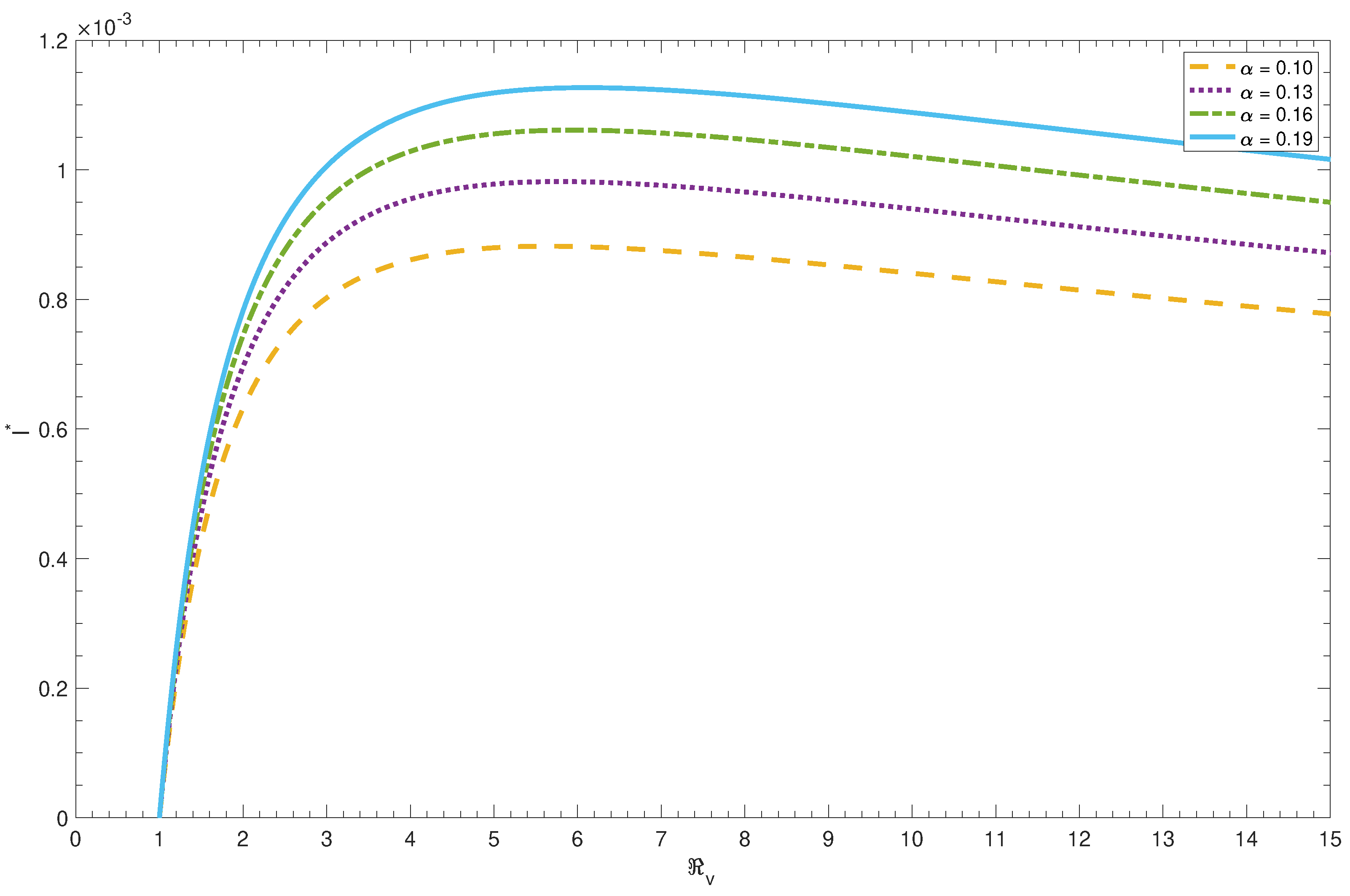
The waning of immunity and progression of secondary susceptible parameters $\sigma$ and $\alpha$ appear in both disease outcomes (i.e., ${\Re }_v$ and $I^{*}$). It is worth noting that ${\Re }_v$ increases with the increase in $\sigma$ and/or $\alpha$. Moreover, numerical simulations show that $\overline{I}$ increases with the increase in either $\sigma ,\alpha$ or both, see Figure 9 and Figure 10. In other words, any decline in the period of immunity acquired by either vaccination or naturally experiencing pertussis infection increases the reproduction number and the endemic prevalence of infection, and therefore, increases the effort needed to eliminate pertussis infection. Moreover, the endemic prevalence of pertussis infection rises with the increase in the progression rate of secondary susceptible individuals.

Figure 9. The endemic prevalence of infection $I^{*}$ as a function of the control reproduction number ${\Re }_v$ for several values of the rate $\sigma$ while the remaining parameters’ values have been kept as in Table 3.

Figure 10. The endemic prevalence of infection $I^{*}$ as a function of the control reproduction number ${\Re }_v$ for various values of the rate $\alpha$, while the other parameters’ value added are kept as shown in Table 3.

It is clear from (21) and (23) that increasing either or both of $\sigma$ and $\alpha$ decreases the reinfection contact rate ${\beta }^{\diamond }$ and increases the critical vaccination coverage required to eliminate the infection $p^{\star }$, which in turn increases the effort needed to eliminate the infection.

7. Summary, Conclusions and Future Work

Mathematical models have gained the attention of the scientific community as they help to understand the dynamic behavior of the phenomenon in concern [1,2]. The last few decades showed much interest in modeling infectious diseases and, in particular, the attempt to predict the most effective factors in containing an infectious disease [4,5,39]. Routine vaccination is one of the main strategies used to protect a population from infectious diseases. However, the immunity acquired either due to receiving the vaccine shots or due to naturally experiencing the infection wanes with time [14,15,40]. It is evident that re-exposure to Bordetella pertussis (after waning immunity) may trigger an immune response to protect against the infection while also boosting one’s immunity [20,41,42]. The effect of the interplay between waning and boosting of the infection on the overall dynamics is less understood. Therefore, a mathematical model of type SIRS (susceptible-infected-recovered-susceptible), with imperfect vaccination V and waning of immunity W, for pertussis infection that is spread in a homogeneously and symmetrically fully mixed population has been introduced and analyzed. The model differentiates between the susceptibility of individuals who acquire the infection for the first time and that of individuals who experienced it at least once before. Moreover, it considers the booster of immunity due to natural re-exposure to the infection after the waning of the acquired immunity.

The model has been mathematically analyzed, where the equilibrium and stability analyses have been studied. The model has a pertussis-free equilibrium $E_0$ that is shown to be locally and globally asymptotically stable if and only if the control reproduction number ${\Re }_v$ is less than one. Moreover, the model has an endemic equilibrium that is proved to be unique and to exist if and only if ${\Re }_v>1$. Moreover, the uniform persistence of all solutions has been proven.

The possibility to eliminate pertussis infection with a strategy based on vaccinating a proportion p of the newborns has been studied. The analysis shows that a reinfection contact rate level ${\beta }^{\diamond }$ (above which pertussis cannot be eliminated with active vaccination) does exist and control strategies other than vaccination should be applied to reduce the successful contact rate $\beta$ to slightly below ${\beta }^{\diamond }$ so that vaccinating a proportion $p>p^{*}$ of the newborns ensures effective control of pertussis infection. The analysis shows further that any decrease in the relative susceptibility r of secondary (with respect to primary) susceptible individuals and/or increase in either or both of the proportion of life spent in the vaccination state $P_V$ and in the waned-immunity state $P_W$ enlarges the region of infection’s controllability, which in turn increases the possibility to eliminate the infection and reduces the effort required to eliminate it (through reducing the critical vaccination coverage level $p^{\star }$). The results show that the reinfection contact rate ${\beta }^{\diamond }$ increases with the decrease in r. Thus, ignoring the differential susceptibility between primary and secondary susceptible individuals underestimates the reinfection contact rate threshold and overestimates the minimum vaccination coverage required to eliminate the infection.

The effect of waning immunity and natural immune boosting on disease outcomes has been studied. The analysis shows that:

• The higher the natural boosting immunity is, the lower the endemic prevalence of infection is. In other words, ignoring the natural boosting of immunity overestimates the endemic prevalence of infection;
• The faster the progression of secondary susceptible individuals is, the higher the endemic prevalence of infection is;
• The shorter the period of immunity acquired by either vaccination or experiencing natural infection, the higher the reproduction number and the endemic prevalence of infection, and therefore, the higher the effort needed to eliminate the infection is.

The dynamical behavior and the current results could be affected by taking further extensions, that are considered in forthcoming work, to include the differential infectivity and transmissibility of infected individuals who caught the infection for the first time and those who experienced it at least once before and are capable of transmitting it, taking into account real data.