Seismic Response Analysis of Uplift Terrain under Oblique Incidence of SV Waves
Abstract
1. Introduction
2. Methodology
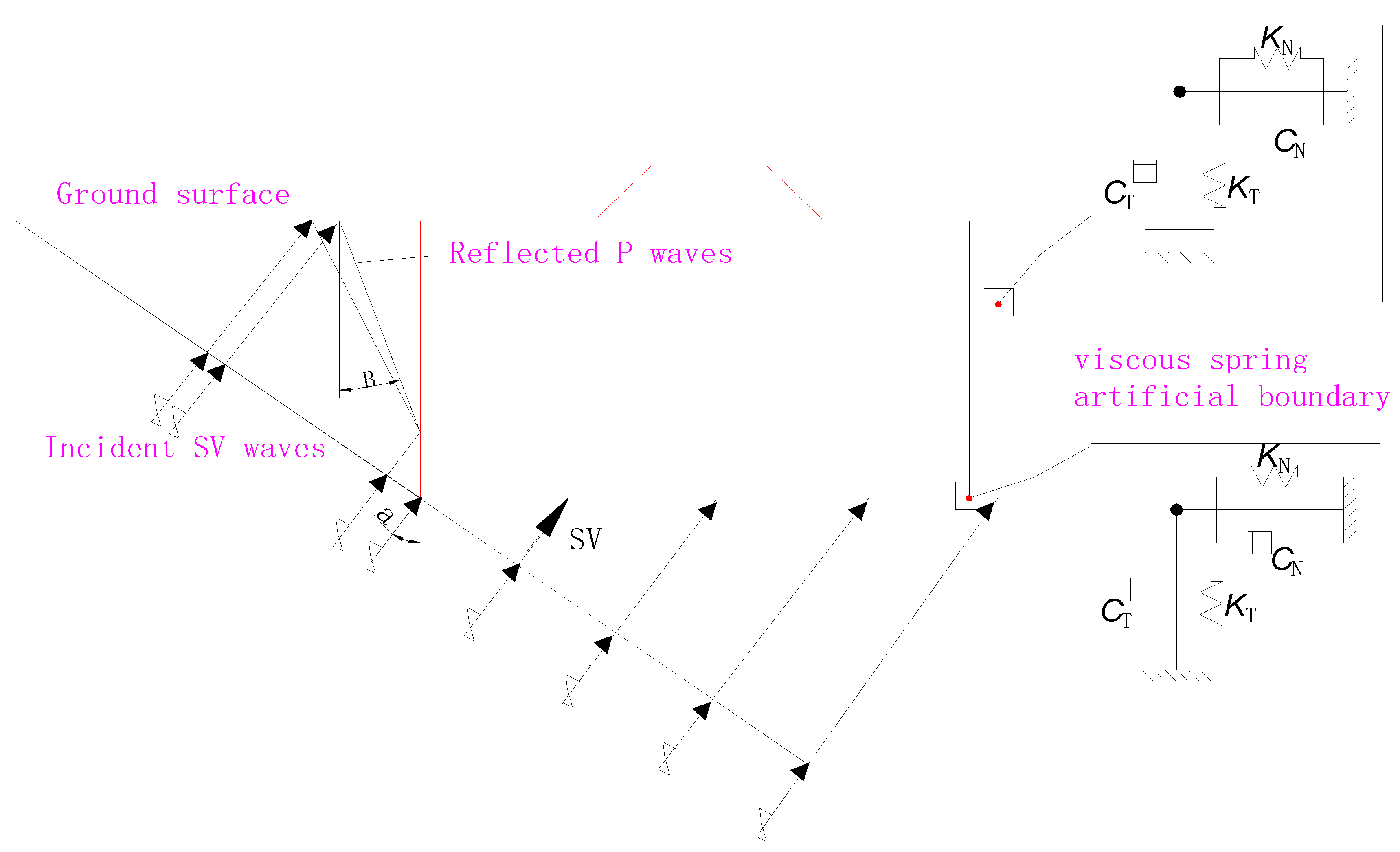
2.1. Establishment of Artificial Boundary
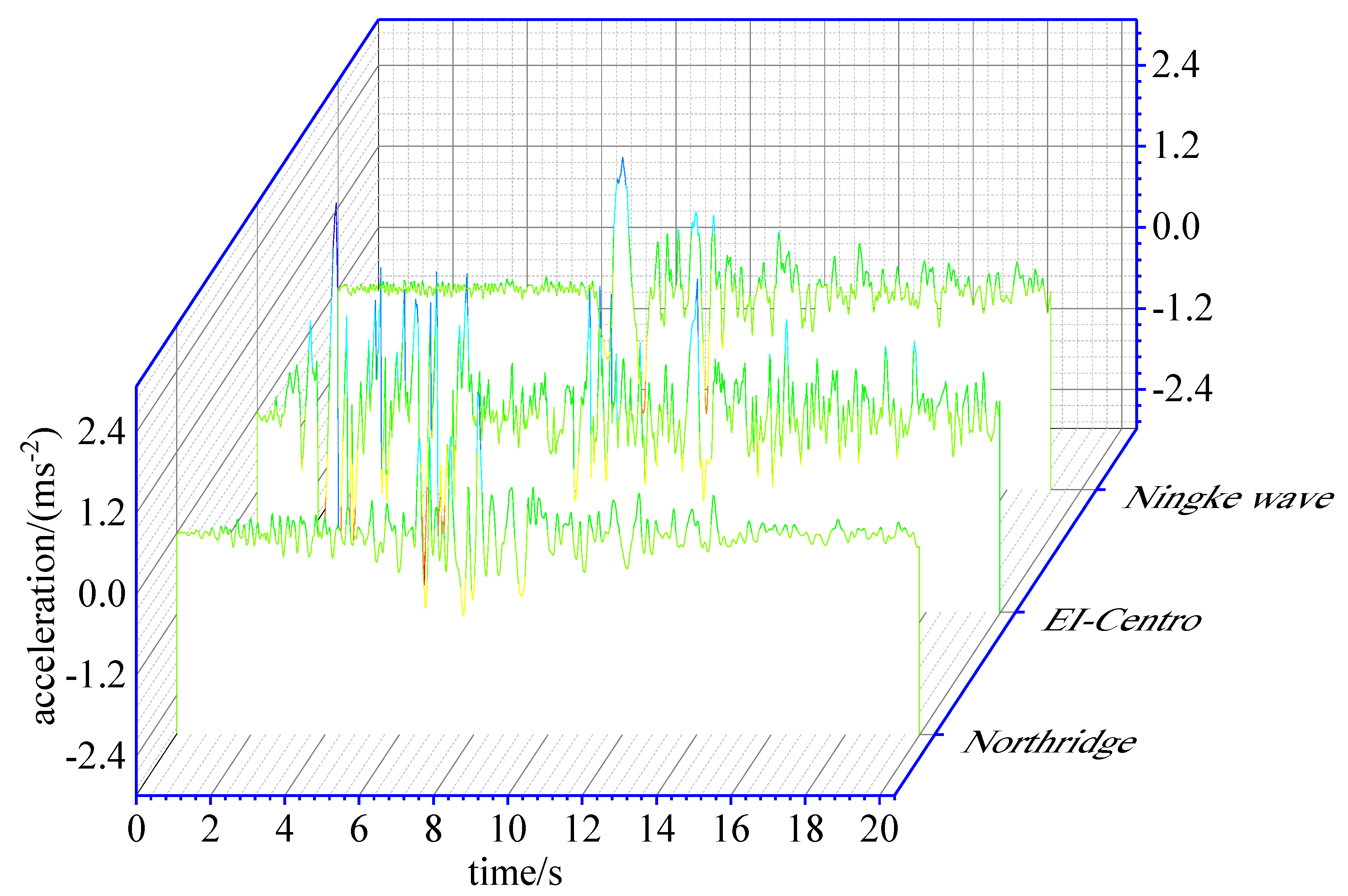
2.2. Input Method
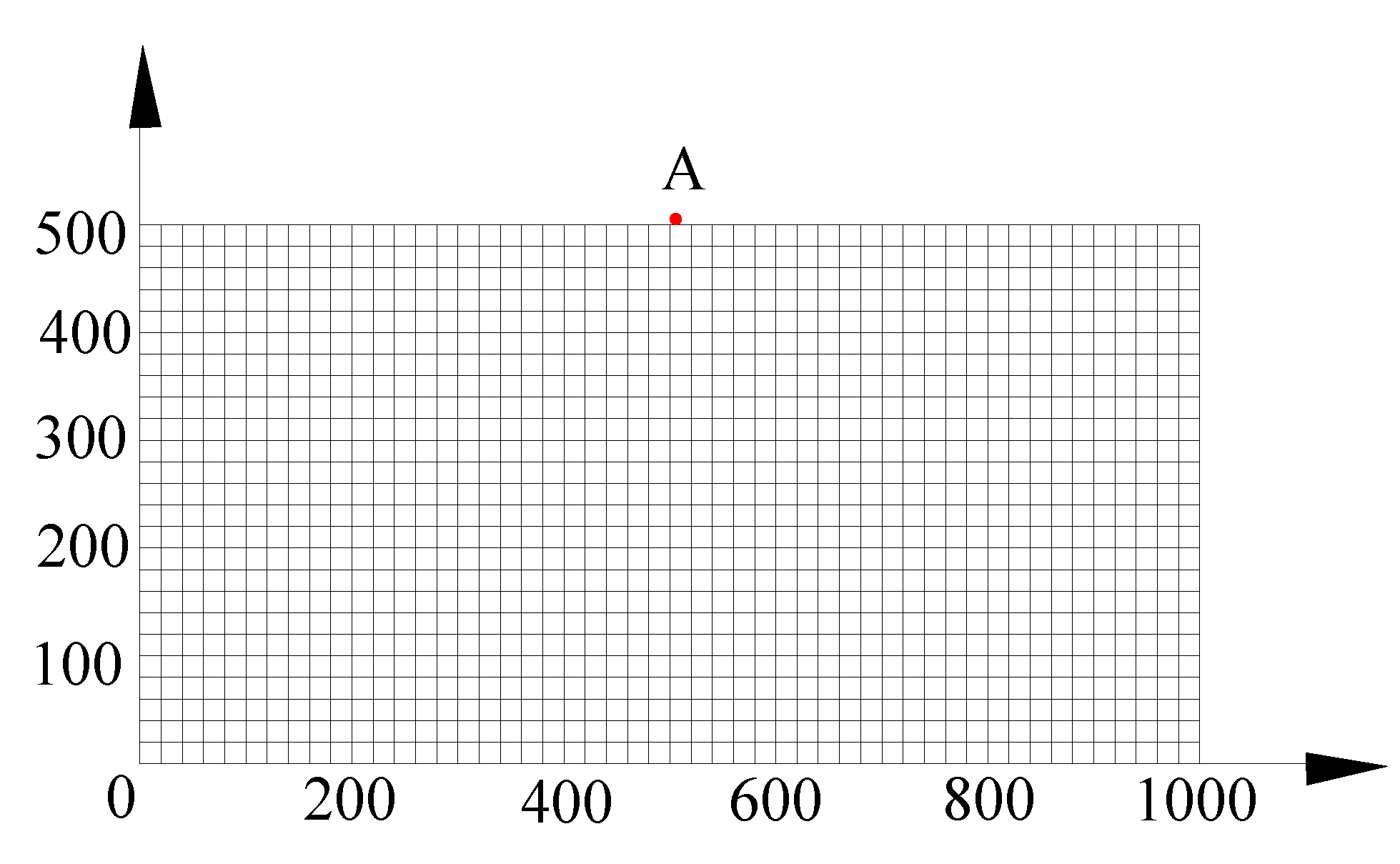
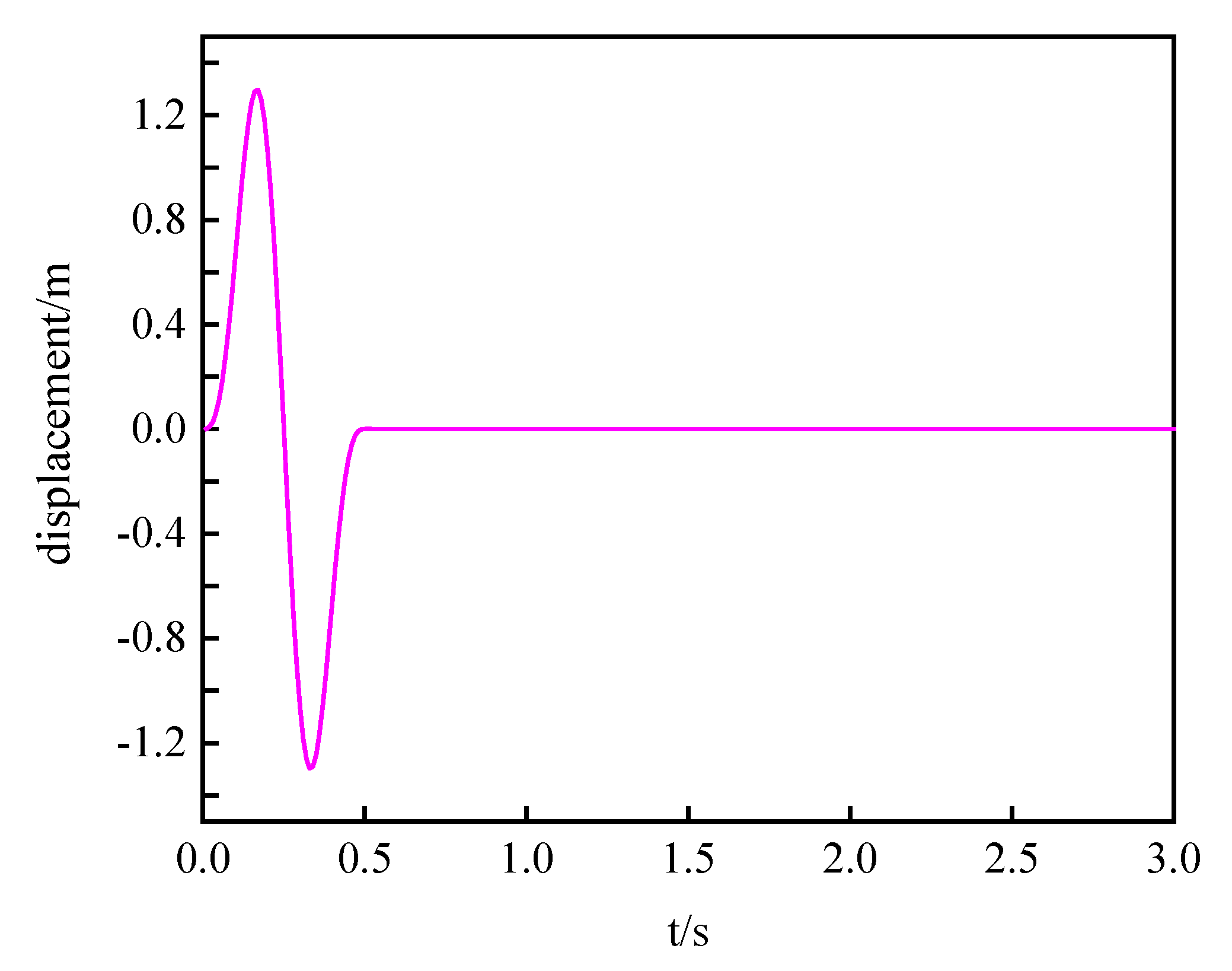
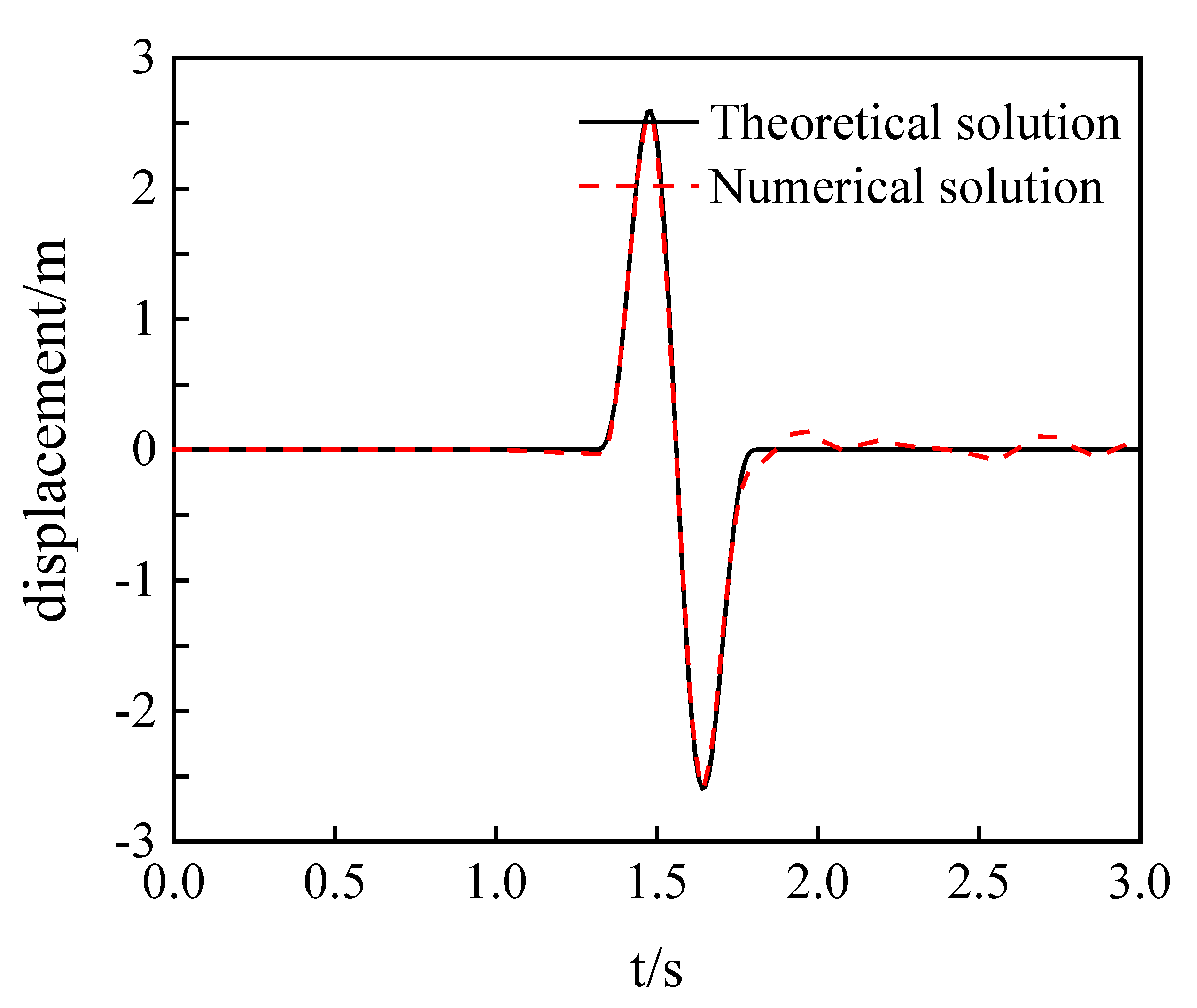
3. Seismic Input Verification
4. Seismic Response Analysis of Raised Terrain
4.1. Establishing Finite Element Model
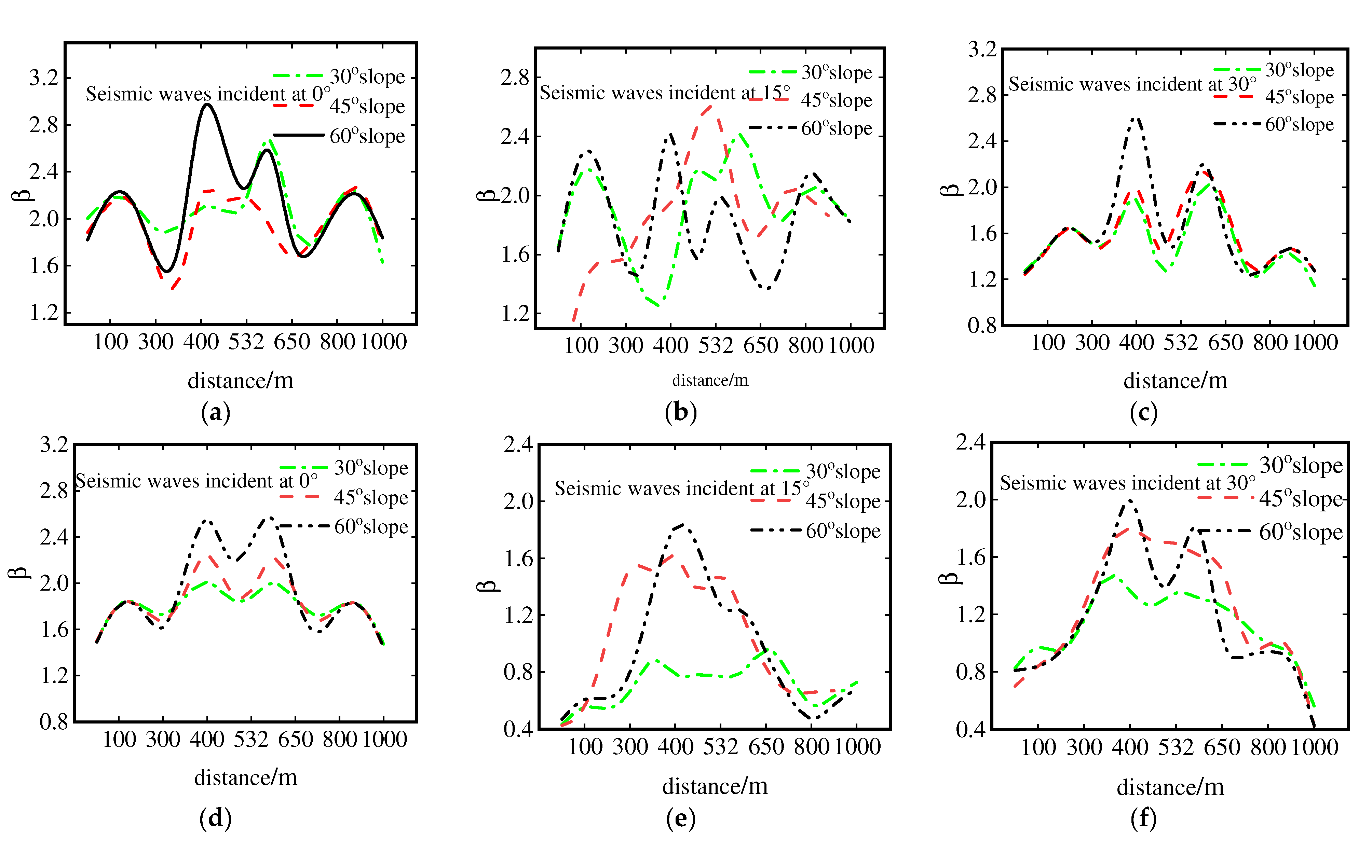
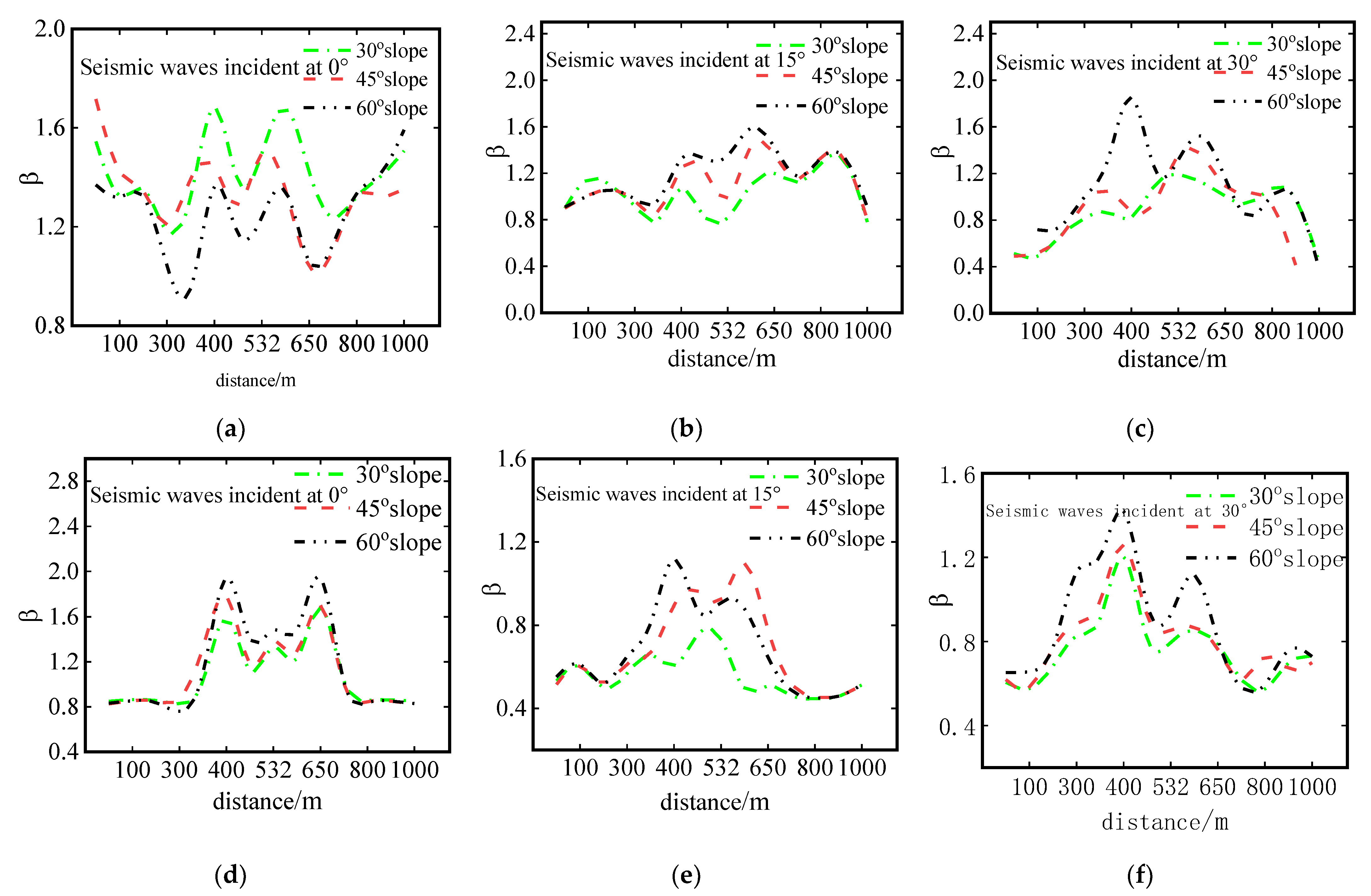
4.2. Response of Slope and Incident Angle to Ground Vibration of Raised Terrain
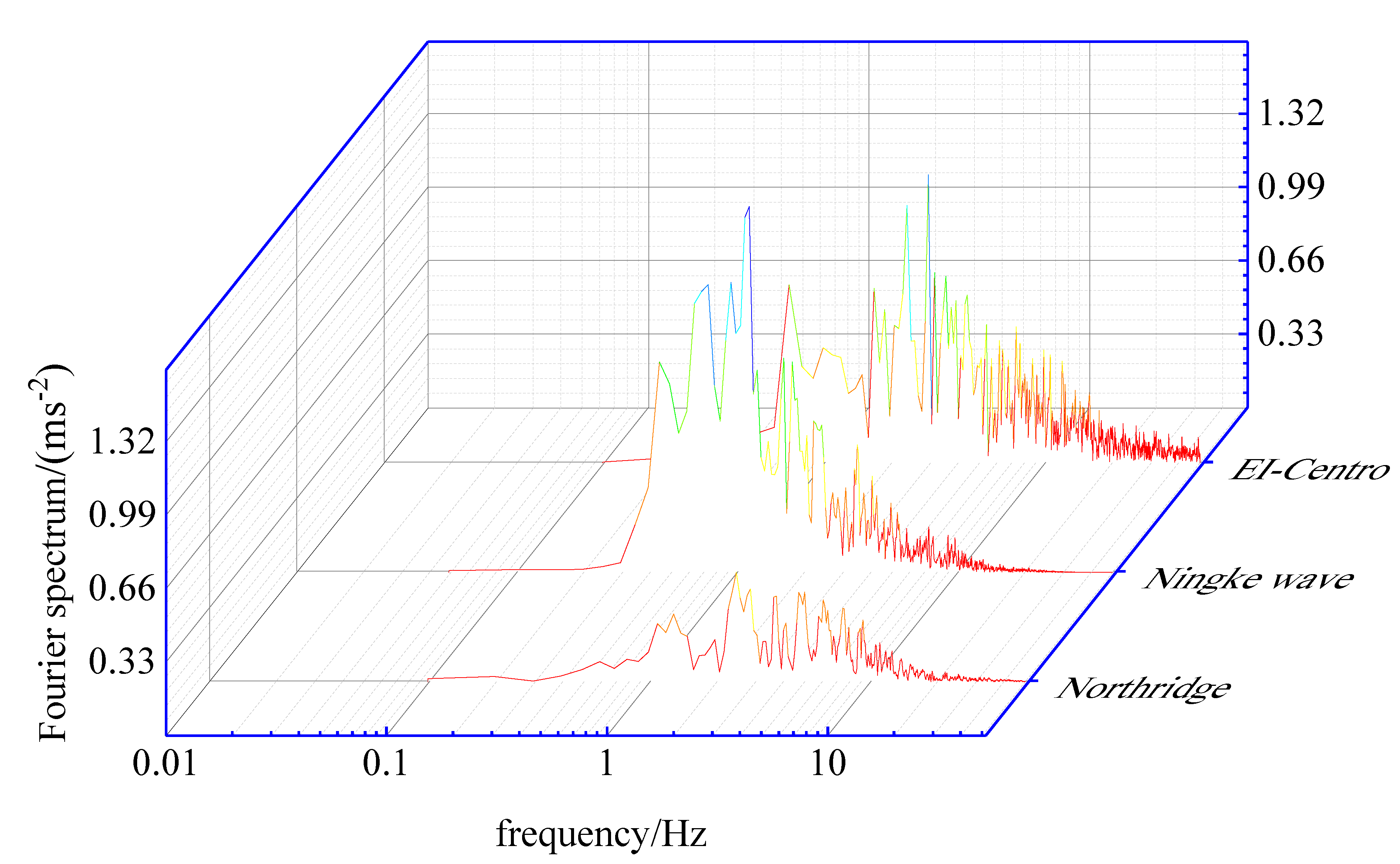
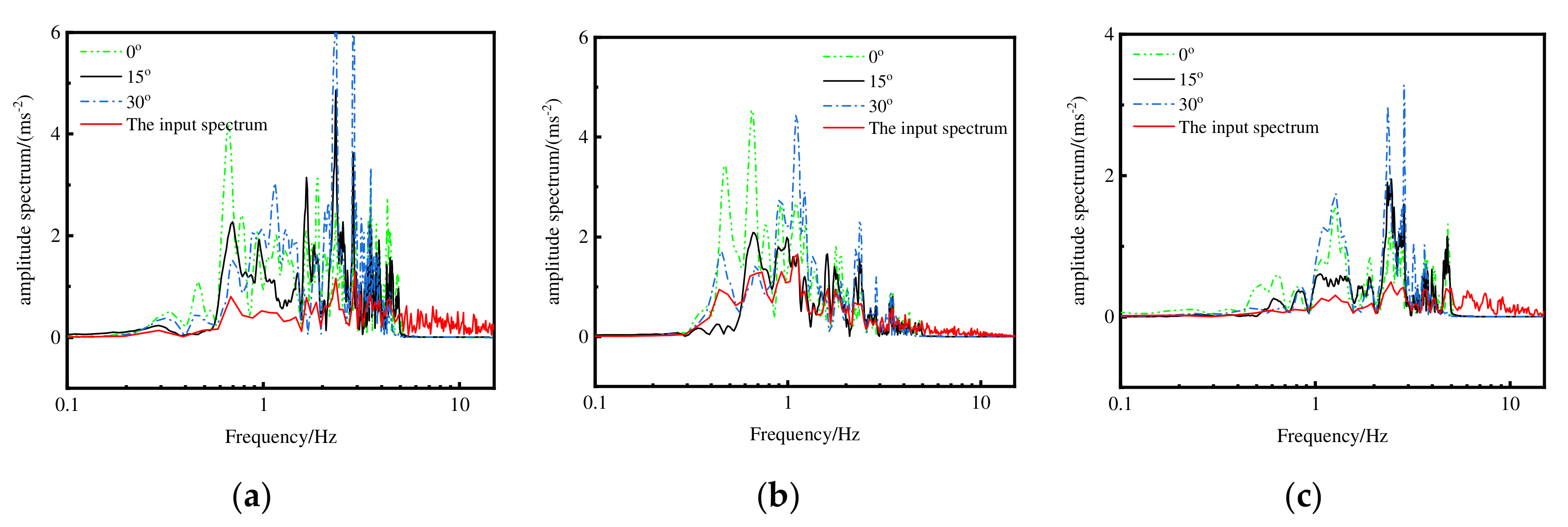
4.3. Effect of Topography on Fourier Spectrum of Ground Motion
5. Results
- (1)
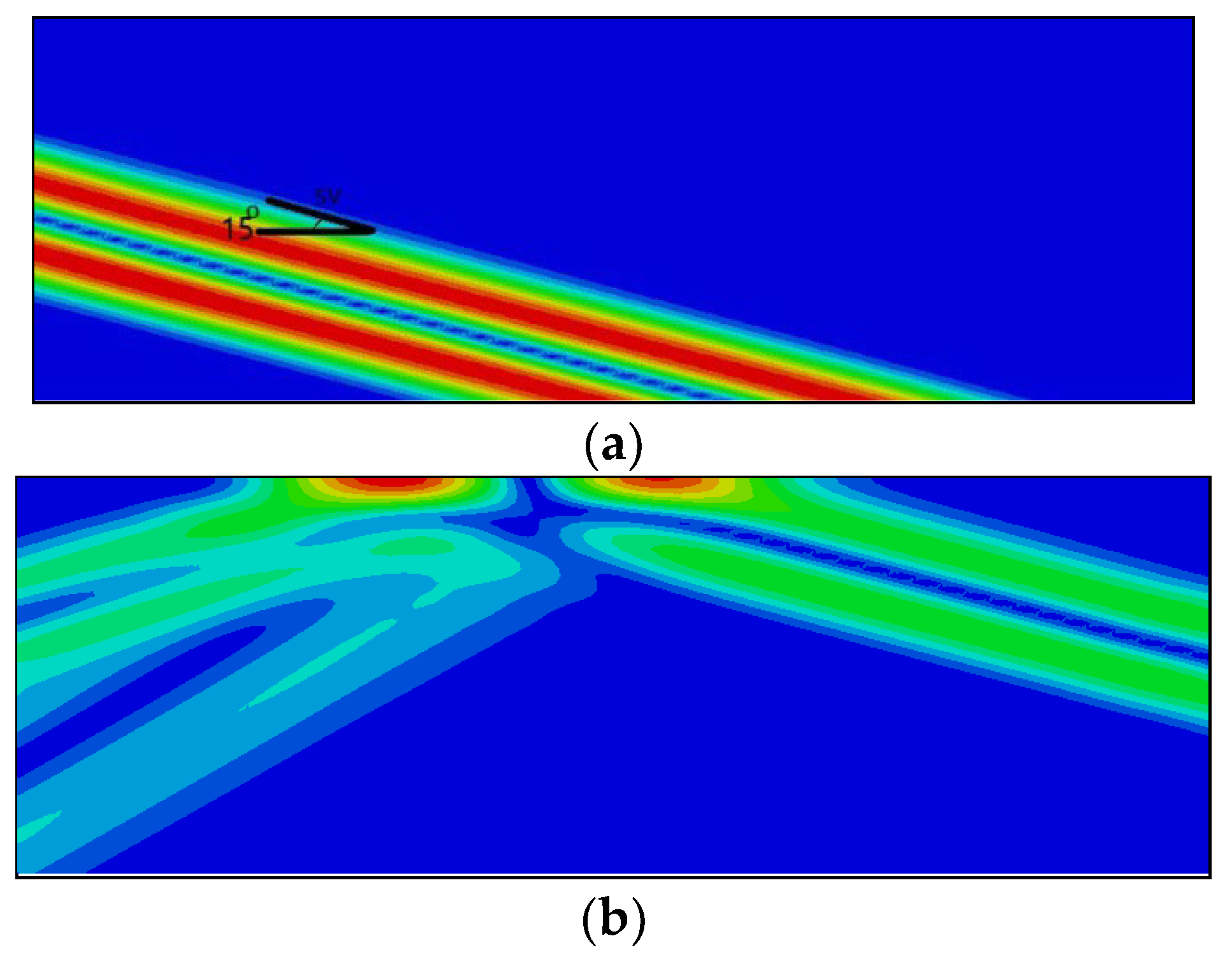
- When the slope is constant, the distribution of the oblique incident ground motion is much more complex than that of the vertical incident ground motion.
- (2)
- When the incident angle was constant, the amplification factor increased with the increase in the slope, and the left side of the site was larger than the right side. The amplification coefficients of the Y components were all less than two.
- (3)
- When the slope was fixed, with the increase of the incidence angle, the maximum value of the amplification coefficient shifted from the No. 7 monitoring point to the No. 5 monitoring point at the top of the slope, and the maximum value moved backward.
- (4)
- According to the Fourier spectrum curve diagram, the frequency was more obvious in the segment of 0.2~1 Hz, and the overall change was characterized by the larger Fourier spectrum value as the slope of the raised terrain increased.
- (5)
- When the El Centro wave was slanted into a 30° slope, the amplitude of the Fourier spectrum decreased with the increase of the incidence angle in the low-frequency band, and the amplitude of the Fourier spectrum increased with the increase of the incidence angle in the high-frequency band, and the change rate of the amplitude was the largest in the high-frequency band of 1–10 Hz.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sánchez-Sesma, F.J.; Campillo, M. Topographic effects for incident p, sv and rayleigh waves. Tectonophysics 1993, 218, 113–125. [Google Scholar] [CrossRef]
- Zhao, C.; Valliappan, S. Seismic wave scattering effects under different canyon topographic and geological conditions. Soil Dyn. Earthq. Eng. 1993, 12, 129–143. [Google Scholar] [CrossRef]
- Lee, S.J.; Komatitsch, D.; Huang, B.S.; Tromp, J. Effects of Topography on Seismic-Wave Propagation:An Example from Northern Taiwan. Bull. Seismol. Soc. Am. 2009, 99, 314–325. [Google Scholar] [CrossRef]
- Trifunac, M.D. Scattering of plane SH waves by a semi-cylindrical canyon. Earthq. Eng. Struct. Dyn. 1973, 1, 267–281. [Google Scholar] [CrossRef]
- Tsaur, D.H. Scattering and focusing of SH waves by a lower semielliptic convex topography. Bull. Seismol. Soc. Am. 2011, 101, 2212–2219. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Q.J.; Deng, P. Surface Motion of a Half-Space with a Semicylindrical Canyon under P, SV, and Rayleigh Waves. Bull. Seismol. Soc. Am. 2017, 107, 809–820. [Google Scholar] [CrossRef]
- Ba, Z.; Wang, Y.; Liang, J.; Lee, V.W. Wave scattering of plane p, sv, and sh waves by a 3d alluvial basin in a multilayered half-space. Bull. Seismol. Soc. Am. 2020, 110, 576–595. [Google Scholar] [CrossRef]
- Wong, H.L.; Trifunac, M.D. Scattering of plane SH waves by a semi-elliptical canyon. Earthq. Eng. Struct. Dyn. 1974, 3, 157–169. [Google Scholar] [CrossRef]
- Ohtsuki, A.; Harumi, K. Effect of topography and subsurface inhomogeneities on seismic SV waves. Earthq. Eng. Struct. Dyn. 1983, 11, 441–462. [Google Scholar] [CrossRef]
- Yuan, X.M.; Men, F.L. Scattering of plane SH waves by a semi-cylindrical hill. Earthq. Eng. Struct. Dyn. 1992, 21, 1091–1098. [Google Scholar] [CrossRef]
- Tsaur, D.H.; Chang, K.H. Scattering and focusing of SH waves by a convex circular-arctopography. Geophys. J. Int. 2009, 177, 222–234. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, L.M.; Li, X.Y.; Fan, R.L.; Zhang, J.J. Dynamic response of rock slopes to oblique incident SV waves. Eng. Geol. 2018, 247, 94–103. [Google Scholar] [CrossRef]
- Yin, C.; Li, W.H.; Zhao, C.G.; Kong, X.A. Impact of tensile strength and incident angles on a soil slope under earthquake SV-waves. Eng. Geol. 2019, 260, 105192. [Google Scholar] [CrossRef]
- Deeks, A.J.; Randolph, M.F. Axisymmetric time-domain transmitting boundaries. J. Eng. Mech. 1994, 120, 25–42. [Google Scholar] [CrossRef]
- Du, X.L.; Zhao, M.; Wang, J.T. A stress artificial boundary in FEA for near-field wave problem. Chin. J. Theor. Appl. Mech. 2006, 38, 49–56. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, M.; Ou, E.; Yan, S.; Du, J. Seismic Response Analysis of Uplift Terrain under Oblique Incidence of SV Waves. Symmetry 2022, 14, 2244. https://doi.org/10.3390/sym14112244
Cao M, Ou E, Yan S, Du J. Seismic Response Analysis of Uplift Terrain under Oblique Incidence of SV Waves. Symmetry. 2022; 14(11):2244. https://doi.org/10.3390/sym14112244
Chicago/Turabian StyleCao, Mingxing, Erfeng Ou, Songhong Yan, and Jiaxuan Du. 2022. "Seismic Response Analysis of Uplift Terrain under Oblique Incidence of SV Waves" Symmetry 14, no. 11: 2244. https://doi.org/10.3390/sym14112244
APA StyleCao, M., Ou, E., Yan, S., & Du, J. (2022). Seismic Response Analysis of Uplift Terrain under Oblique Incidence of SV Waves. Symmetry, 14(11), 2244. https://doi.org/10.3390/sym14112244




