Abstract
Understanding the evolutionary mechanisms of dynamic graphs is crucial since dynamic is a basic characteristic of real-world networks. The challenges of modeling dynamic graphs are as follows: (1) Real-world dynamics are frequently characterized by group effects, which essentially emerge from high-order interactions involving groups of entities. Therefore, the pairwise interactions revealed by the edges of graphs are insufficient to describe complex systems. (2) The graph data obtained from real systems are often noisy, and the spurious edges can interfere with the stability and efficiency of models. To address these issues, we propose a high-order topology-enhanced graph convolutional network for modeling dynamic graphs. The rationale behind it is that the symmetric substructure in a graph, called the maximal clique, can reflect group impacts from high-order interactions on the one hand, while not being readily disturbed by spurious links on the other hand. Then, we utilize two independent branches to model the distinct influence mechanisms of the two effects. Learnable parameters are used to tune the relative importance of the two effects during the process. We conduct link predictions on real-world datasets, including one social network and two citation networks. Results show that the average improvements of the high-order enhanced methods are 68%, 15%, and 280% over the corresponding backbones across datasets. The ablation study and perturbation analysis validate the effectiveness and robustness of the proposed method. Our research reveals that high-order structures provide new perspectives for studying the dynamics of graphs and highlight the necessity of employing higher-order topologies in the future.
1. Introduction
In the real world, there is a wealth of data that are frequently organized into non-Euclidean graph structures. For example, we may build a network to model social relationships, with nodes representing individuals and edges representing the existence of the friendship between individuals. Additionally, we can construct networks to model coauthor relationships, with nodes representing scholars and edges representing collaborative relationships between scholars.
A graph is more than just a form of data organization; it also provides a foundation upon which we can analyze, understand, and learn from complex systems in the real world. Graph representation learning is one of the research hotspots, with the goal of exploring and analyzing the connections between nodes in networks to help with tasks, such as node classification and link prediction [1,2]. Network embedding is the precursor to graph representation learning, which projects nodes into a low dimensional space while maintaining certain topological properties, such as locally linear embedding (LLE) [3], DeepWalk [4], Node2Vec [5], structural deep network embedding (SDNE) [6], etc. Inspired by the success of convolutional neural networks (CNNs), some researchers have redefined convolution for graph data. Bruna [7] transformed the graph signal from the spatial domain to the frequency domain through graph Fourier transformations and defined the graph convolution operation in the frequency domain. However, spectral methods have the disadvantage of high complexity, so Kipf [8] proposed graph convolutional networks (GCNs), which parameterize the convolution kernel in spectral methods to reduce complexity. GCN aggregates the information of each center node and its neighboring nodes to update the center node information. Inspired by this, some spatial methods have recently emerged to learn aggregation and update through attention mechanisms or recurrent neural networks (RNNs) [9,10].
The majority of graph neural networks (GNNs), like that mentioned above, focus on static graphs, while graphs in the real world evolve over time [11]. Dynamics in graphs should be captured to reflect reality better [12]. For example, individuals will develop new friendships, and scholars will form new co-authorships, all of which will generate new edges in relevant networks. Thus, the dynamic graph study has drawn attention from multiple fields [13]. Chen [14] found that studying protein complexes would benefit more from dynamic PPI networks than static ones. Berger [15] argued that studying the dynamic nature can help us to ask certain fundamental questions about the causes and consequences of social patterns. Holm [16] learned from the dynamic citation network and achieved a more accurate prediction of the trajectory of the number of citations. Dynamic graphs add a temporal dimension to network modeling and prediction, and this new dimension fundamentally affects the modeling of network properties [17]. Therefore, we need new models that take into account the time dimension to better capture the underlying mechanism and serve downstream tasks.
By introducing a temporal regularization term to static graph embedding methods, research has been conducted to extend static graphs to dynamic ones [18]. On the one hand, there are approaches to learning node embeddings by using the embedding vector of the previous time step as the initial value of the current time step [19]. On the other hand, dyngraph2vec [20] utilizes RNNs to learn the dynamic evolution of the graph after learning the structural properties of each time step with several nonlinear graph embedding layers. Likewise, graph convolutional neural network-based approaches mostly use GNNs to learn the node embeddings of each time step and then combine them with RNNs to learn the evolution mechanism of the node embeddings [21].
Regardless of the algorithms used, most methods learn node embeddings based on pairwise relationships. However, in some situations, they do not provide a satisfactory description, especially in those cases where more complex dynamics of group influence and reinforcement mechanisms exist [22]. Nodes within the same group may share attributes, exchange information frequently, or have similar functions. For example, in social networks, a group indicates common habits or social, cultural, and occupational backgrounds. Evidence has shown that groups can substantially affect the dynamics of systems [23]. Moreover, observations may bring noise and result in spurious links in graphs, which is even worse for modeling dynamic graphs when the noises accumulate over time [24].
Hence, we should value and explore the group influence and solve the problems brought by the spurious links to better model the dynamic graphs. Particularly, the high-order structures can reveal group affiliation in graphs, where the maximal clique is one well-known high-order structure on graphs [25]. It is a mesoscopic structure consisting of a group of densely interconnected nodes and, therefore, not easily affected by spurious links. Based on this, we propose a high-order topology-enhanced graph convolutional network for representing dynamic networks in the real world, namely social networks and co-authorship networks. Furthermore, since there are clear distinctions between the mechanisms of group influence and the mechanisms of pairwise effects on nodes in networks, we adopt a two-branch architecture to address this issue. The contribution of our work is threefold:
- We highlight the importance of group behaviors induced by high-order structures in graph dynamics. To model the different mechanisms of pairwise influence and group effects, we use a two-branch graph neural network, with one branch feeding the skeleton network and the other branch feeding the high-order structures.
- Our proposed method achieves optimal results on the link prediction task for three real-world network datasets, with a maximum improvement of 633%. The ablation study further verifies the effectiveness of introducing high-order information.
- We use learnable parameters to tune the relative importance of the strength of high-order and pairwise relationships, and further compare various schemes for combining high- and low-order information. We find that the simple linear combination of high- and low- order information can achieve satisfactory results.
2. Related Work
Graph representation learning has made considerable progress in the last few years. The related work can be divided into two categories: (1) static graph representation learning and (2) dynamic graph representation learning.
2.1. Static Graph Representation Learning
The spectral properties of graph matrices were used in early work on static graph representation learning, such as Laplacian Eigenmaps [26,27]. Laplacian Eigenmaps project the nodes onto a lower dimensional space, and the distance between point pairs is small when the corresponding edge weight is large, and vice versa. DeepWalk [4] is the forerunner that introduces neural network-based approaches to network embedding. It takes inspiration from a natural language processing (NLP) approach, interprets each node as a word, and generates a sentence from the node sequence collected from a random walk. Similar to DeepWalk, Node2vec [5] leverages the word2vec framework and uses random walks to build node sequences. Node2vec, on the other hand, can handle a weighted graph, and the magnitudes of the weights decide which neighbor node in a random walk is more likely to be sampled next. Moreover, it uses two parameters to alter the biased random walk process so that sampling is not done in an arbitrary depth-first or width-first manner. Large-scale information network embedding (LINE) [28] extends the proximity to the second order, where two nodes are alike if their neighbors overlap, and the degree of overlap indicates the similarity. Struc2vec [29] further explores the structural equivalence or identity of nodes. It assumes that node representations have no bearing on the properties of nodes or edges, and that the distance between node representations should be proportional to the structural similarity between them. Recently, researchers constructed graph neural networks (GNNs), which generalize convolutions on graphs to leverage the structure and attributes of graphs [8,9,30]. The capacity of GNNs to improve the representations of target nodes by aggregating the features of neighboring nodes in a supervised learning paradigm is largely responsible for their success [31]. However, they are designed for static graphs and are incapable of modeling evolutionary patterns in dynamic graphs.
2.2. Dynamic Graph Representation Learning
Some dynamic techniques extend static graph embedding techniques by adding regularization [18], with the goal of ensuring consistency over time steps. TIMERS [32] optimized the restart time of singular value decomposition (SVD) to process newly changed nodes and edges in dynamic networks in order to reduce error accumulation in time. DynGEM [33] employs a dynamically expanding deep autoencoder and incrementally initializes the current embedding from the previous time step to ensure stability and efficiency. DynamicTriad [34] relaxes the temporal smoothness assumption and models triadic closure processes to reflect the difference between characters of different vertices.
Combinations of GNNs and recurrent architectures are the most recent methodologies and are most pertinent to our work, with the former capturing graph information and the latter dealing with temporal dynamism. GCRN [35] proposes two architectures: Model 1 utilizes a stack of a graph-based CNN and RNN, and Model 2 uses convLSTM, which uses graph convolutions instead of the Euclidean 2D convolutions in the RNN definition. The key concept of GCRN is to merge graph convolution and recurrent architectures to model meaningful spatial structures and dynamic patterns simultaneously. The concept was also investigated by Manessia et al. [36]. They designed a waterfall dynamic-GC layer and a concatenated dynamic-GC layer [37]. The former is a copy of a regular graph convolutional layer, while the latter combines both graph convolutional features and plain vertex features. In addition to such combinations, EvolveGCN [21], which adapts the GCN model along the temporal dimension without resorting to node embeddings, can be used to further improve performance. The proposed approach captures the dynamism of the graph sequence by using an RNN to evolve the GCN parameters. For parameter evolution, two different architectures are being considered. While the H version includes node embedding in the recurrent network as an additional feature, the O version focuses solely on the changes in the network’s structure.
However, pairwise interactions are often not sufficient to characterize real-world network dynamics, where complex mechanisms of group influence and reinforcement exist. The aforementioned models learned directly from graphs are thus limited to modeling complex relationships between nodes, neglecting the importance of group effects.
3. Method
3.1. Definitions
A complex system that changes over time can be represented as a dynamic graph. Dynamic graphs are typically divided into two categories [38]:
Definition 1
(Continuous-time dynamic graph (CTDG)).CTDG starts from an initial static graph , and then a series of observations are conducted on over time. represents the observation of a set of events that occur at timestamp t, including node addition, node deletion, edge addition, edge deletion, etc. Each event can be represented by a tuple (event type; entity; timestamp). Snapshot , which is a static graph at time t, can be obtained by updating sequentially according to the observations .
Definition 2
(Discrete-time dynamic graph (DTDG)).DTDG is defined as a collection of static graphs observed at certain timestamps, , where is the snapshot at time t, and T is the number of the total observed time steps. Each snapshot is a graph with a node set , an edge set , and an adjacency matrix .
According to the definition, CTDG can be readily converted to DTDG, but DTDG cannot be converted back to CTDG due to the lack of detailed event information. Without loss of generality, in this paper, we focus on the discrete-time dynamic graph for ease of computation. Moreover, we use the union of node sets to replace the original node set for all time steps. By using this approach, the adjacency matrices are of the same size, and only the values of the entries are changing, making it easy to process using graph neural networks.
Definition 3
(k-Clique).A clique is a subset and , where any two vertices have an edge . In short, a clique is a complete graph composed of k vertices. Four vertices, for example, constitute a 4-clique if each of them is connected to the other three vertices. A clique implies a densely connected group of entities, whereas the maximal clique indicates the largest tightly-knit group to which an entity belongs.
3.2. High-Order Subgraph
Our objective is to enhance dynamic graph representation learning by considering group effects. To this end, we need to extract high-order subgraphs (as shown in Figure 1) from each graph snapshot since group affiliation can be revealed by the high-order structures in graphs. Here, the construction of the high-order subgraph involves allocating each node to the tightly grouped nodes defined by maximal cliques, which have long been recognized as an important component of real-world dynamic systems’ research, as evidenced by the work of Wasserman [39]. A maximal clique cannot be extended by adding another vertex to the set of maximal cliques because it is not a subset of a larger clique. The maximum clique in a graph is the maximal clique with the largest maximal clique.
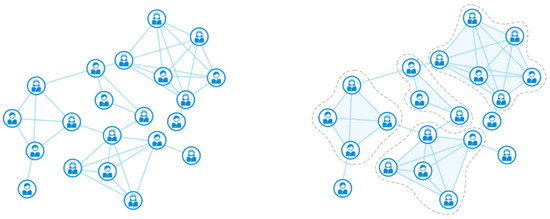
Figure 1.
Skeleton network and its high-order subgraphs.
3.3. Model
To extract the high-order subgraphs, we first list all the maximal cliques and rank them by size using the Bron–Kerbosch algorithm [40,41,42]. Then we start with the largest maximal clique, and assign related nodes to a group, as shown in Figure 2. We continuously partition the unassigned node into the largest group to which it belongs. Once a node has been assigned to a group, it is removed from the remaining smaller groups; nodes are only assigned to multiple groups in the case of equally sized maximal cliques. Ultimately, only nodes within the same group are connected by edges. While maximal clique refers to a group of nodes that are completely connected within a network, this definition is often overly restrictive. However, as networks are built from the observation of empirical data, spurious linkages may exist that muddle the pairwise relationships. The search for strictly clique-like groupings of nodes will not be easily confused by the spurious links (e.g., caused by data processing errors) in the dataset, as shown in Figure 3.
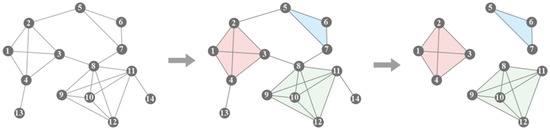
Figure 2.
Illustration of extracting high-order subgraphs.
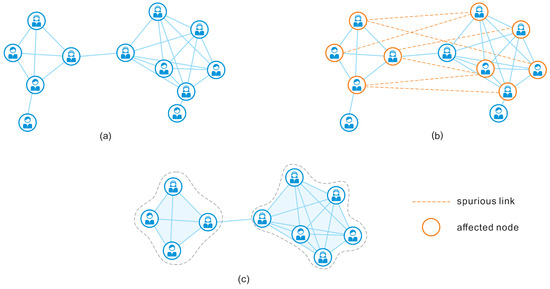
Figure 3.
Strictly clique-like groupings of nodes will not be easily confused by the spurious links in the dataset. (a) Original network; (b) Network with noise; (c) Strictly clique-like groupings for both (a,b).
To model the different mechanisms of pairwise influence and group effects, we use a two-branch graph neural network, as shown in Figure 4, with one branch feeding the 1-skeleton graph and another branch feeding the high-order structures. That is, two different graph convolutional networks are used to model the 1-skeleton network and the high-order subgraphs separately for each time step.
where is the activation function and and are trainable weight matrices. is the adjacency matrix of and is the adjacency matrix of the high-order subgraph induced from . denotes the node feature matrix, and represents the symmetric normalized Laplacian matrix. and are the representations obtained from the 1-skeleton branch and the high-order branch, carrying low- and high-order information, respectively. Note that we use a two-layer graph convolutional network to perceive a wider range of low-order information, while we use a single-layer graph convolutional network to ensure that nodes are only affected by their groups.
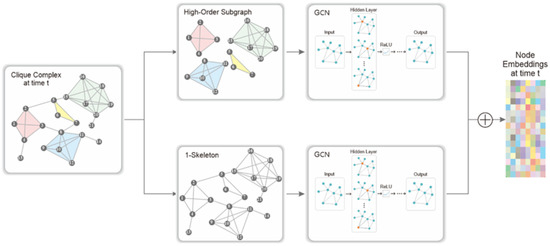
Figure 4.
Illustration of the two-branch module.
The representations obtained from the two branches are then combined to serve as the node representations at time t. Here, we use a linear combination to combine the two pieces of information as follows:
where the weights and are tuned by learning the relative importance of the strength of high-order and pairwise relationships.
Finally, deep learning techniques, such as RNNs, can be used to model the dynamic evolution of the learned graphs from historical graph snapshots. It is worth noting that our method works with any dynamic model that integrates GNN modules.
4. Experiments
4.1. Datasets
Social interaction processes are frequently driven by contagion and reinforcement, where group effects induced from high-order interactions are at work. Therefore, to verify the importance of considering high-order relationships in modeling the evolution of real-world networks, we choose one social network and two citation networks as the test datasets.
UCI (http://konect.cc/networks/opsahl-ucsocial, accessed on 20 March 2020): An online community of students from the University of California, Irvine. Each node represents a user, and each edge represents a message being received or sent between two users.
DBLP (http://konect.cc/networks/com-dblp/, accessed on 20 March 2020): A co-authorship network of the DBLP computer science bibliography, collected from 1995 to 2020. Each node represents an author, and the existence of edges indicates that the corresponding authors have co-published at least one paper.
HEP (http://konect.cc/networks/ca-cit-HepPh/, accessed on 20 March 2020): A co-authorship network of authors who submitted to the High Energy Physics - Phenomenology category in the e-print platform arxiv. The data are collected from January 1993 to April 2003.
Some details of these datasets are summarized as shown in Table 1. It is worth noting that the DBLP dataset is far sparser than the other two while having the highest number of nodes, making link prediction more challenging on DBLP than on the other two networks.

Table 1.
Details of datasets.
4.2. Baselines
We adopt different types of methodologies as baselines, which include unsupervised learning methods and supervised learning methods, to demonstrate the capabilities of our proposed method in the link prediction task. In particular, we choose the GCN-based models from baselines as the backbones of our two-branched model because they are easily adapted to our framework. The following is a basic overview of the baselines:
- GCN [8]. GCN is designed for static graph modeling. In the learning process, a single GCN is used for each graph snapshot, and the loss is accumulated over time. Only the information from the previous one time step is used to predict the subsequent one when this method is applied.
- GCN-GRU. A single GCN model is co-trained with a recurrent model using gated recurrent units (GRU), where one GCN models every time step and GRU learned from the sequential node embeddings.
- dyngraph2vec [20]. Three variations of the unsupervised graph representation model dyngraph2vec: (1) dyngraph2vecAE extends the autoencoders to the dynamic setting, (2) dyngraph2vecRNN utilizes sparsely connected long short-term memory (LSTM) networks, and (3) dyngraph2vecAERNN combines both autoencoders and LSTM networks.
- EvolveGCN [21]. It captures the mechanism of a dynamic graph by using an RNN to evolve the GCN parameters. Two different architectures, EvolveGCN-H and EvolveGCN-O, are designed to cope with different scenarios. The H version incorporates additional node embedding in the recurrent network, while the O version focuses on the structural change of the graph.
4.3. Tasks
The performance of the proposed methods is tested with the link prediction task in graphs, which has been widely studied in the literature [43]. The challenge entails forecasting new links that will form in a network in the future, given the existing state of the network. In this scenario, the task of link prediction is to leverage historical graph information up to time t and predict the existence of edges at time . For nodes i and j, we can concatenate their embeddings derived at time t and feed it into a multilayer perceptron (MLP) to obtain the probability of future linkage.
The performance is then assessed using the mean average precision (MAP), which is the mean of the average precision (AP) per edge. The weighted mean of precision achieved at each threshold is used to summarize a precision–recall curve, with the increase in recall from the previous threshold used as the weight:
where and are the recall and precision at the n-th threshold. The MAP value is robust and averages the predictions for all edges. High MAP values suggest that the model can make good predictions for most edges.
4.4. Experimental Results
For all three network datasets, we use the one-hot node-degree encoding as the input feature. Each dataset is split into training, validation, and test datasets following a 7:2:1 ratio. The number of epochs is set to 1000 with an early stop patience of 200. Other hyperparameters follow the default settings from original papers or released codes.
Table 2 and Figure 5 show the performance of all models for graph link prediction on the three datasets. Across each dataset, it is shown that the best results are all achieved by models enhanced with high-order information. When comparing the performance of the best models with the second best ones, the following can be found: on the UCI dataset, Egcn-O (Add) improves 53.33% over the original Egcn-O model; on the HEP dataset, GCN+GRU (Add) improves 9.63% over the original GCN+GRU model; and on the DBLP dataset, Egcn-H (Add) model improves 9.63% over dynARERNN by 235.93%. When comparing the high-order enhanced models with the backbones, we can see that 9 of the 12 high-order topology-enhanced models exceed the corresponding backbone models, with a maximum improvement of 633% for MAP and an average improvement of 173%. Among them, on the UCI dataset, the high-order enhanced models of GCN and GCN+GRU improve 115.79% and 20.00% over the original backbone models; on the HEP dataset, GCN+GRU (Add) improves 9.63% over the original GCN+GRU; and on the DBLP dataset, the high-order version of GCN improve 9.84%. In addition, since most of the best results are found in the augmented model with the Egcn model as the backbone, we specifically compare the original Egcn model with the augmented version, as shown in Figure 6.

Table 2.
The performance of link prediction.
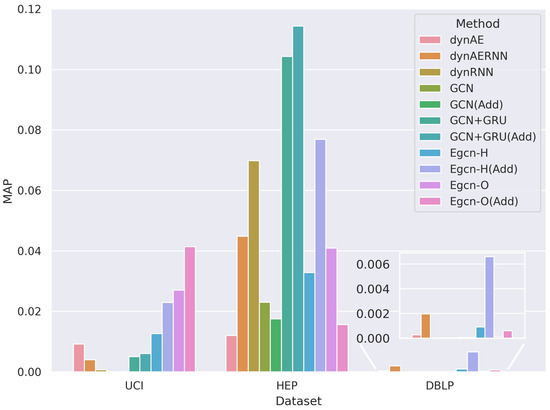
Figure 5.
Visualization of the performance of different methods on graph link prediction.
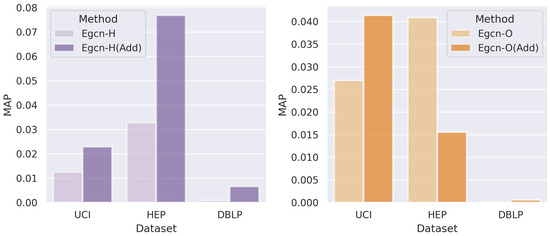
Figure 6.
Performance comparisons between the backbone methods and the enhanced versions.
Moreover, because the majority of the best results are found in the enhanced models with the Egcn models as the backbones, we compare the original Egcn models to the enhanced versions particularly, as illustrated in Figure 6.
On the UCI dataset, it is observed that adding the high-order branch to both versions of the Egcn-based model leads to a significant improvement. The Egcn-H (Add) improves MAP by 81.7% over the original Egcn-H model; Egcn-O performs the best among all baseline models, while the enhanced model further improves MAP by 53% over it. Although not all high-order topology-enhanced versions outperform the original model on the Hep-ph dataset, the enhanced version Egcn-H (Add) can increase the MAP by 134% over the original model (Egcn-H) and 88% over Egcn-O. As mentioned before, link prediction on the DBLP dataset is a rather difficult task. However, all of the enhanced versions outperform the backbones on the DBLP dataset, with the Egcn-H (Add) outperforming the Egcn-H by up to 633% and the Egcn-O (Add) outperforming the Egcn-O by 83%. Such a huge boost on DBLP may be due to the sparse nature of this dataset, resulting in many difficulties for other methods that only exploit the limited pairwise information in the graph skeleton.
It is worth noting that Egcn backbones perform worse on both the HEP and DBLP datasets than the unsupervised model dynAERNN. The same issue is raised in the Evolve-GCN work [21], where the authors explain that in this scenario, graph convolution does not appear to be powerful enough to capture the intrinsic similarity of the nodes, resulting in a considerably inferior starting place for dynamic models to catch up. However, by introducing higher-order graph branches, the enhanced Egcn models outperform the unsupervised models, which shows that the higher-order information can play a complementary role to node similarity learning.
5. Discussion
5.1. Enhanced Models with Different Schemes
We employ the weighted addition scheme (add) to combine the embeddings generated from the higher-order branch and the skeleton branch in previous experiments. To investigate the effect of different combination schemes on the model, we also compared the addition scheme to the following two approaches:
- ConcatThis scheme takes the form of the regularly used concatenation, and it is paired with one MLP to learn the final node representations.
- GatedThe gated scheme employs the reset gate to determine how to combine higher-order information with lower-order information, and the update gate defines the amount of lower-order information saved at the current time step.
Figure 7 shows the performance of the enhanced models with different schemes. It can be found that different combination schemes perform differently across datasets. On the UCI dataset and the DBLP dataset, the weighted addition schemes have the best performance. However, in the HEP dataset, the gated scheme paired with the Egcn-O backbone yields a considerable improvement (which the addition scheme is incapable of). Considering the fact that the gated update strategy requires more parameters and the weighted addition scheme can have a competitive performance in most circumstances, we recommend the addition scheme in practice.
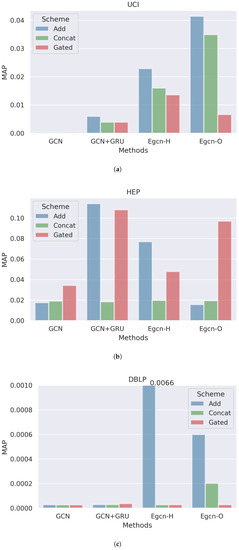
Figure 7.
The performance of enhanced models with different schemes on (a) UCI, (b) HEP, and (c) DBLP datasets.
5.2. The Effectiveness of Introducing High-Order Structures
To verify that the improvement is attributed to the introduction of high-order information and not just a result of an increase in the network capacity caused by the addition of a branch, we conducted 10 experiments using random subgraphs. Specifically, we randomly sampled subgraphs with nodes and node degrees consistent with the high-order subgraphs and also used a two-branch model to conduct link prediction; the results are shown in Figure 8. There are two lines on the box plot, with the top line representing the performance of the high-order topology-enhanced model, and the bottom one representing the result of the original model. It can be found that the random subgraphs also give a substantial boost to the model, indicating that increasing the network capacity does bring benefits. Meanwhile, the results based on the higher-order subgraphs are better than the mean and the median of the random subgraph-enhanced model, demonstrating that modeling high-order correlations can further improve performance. Although the performance of the high-order topology-enhanced model is slightly lower than the best performance of the random subgraph enhanced models, this suggests that there may be better structures in the network that can enhance the model. However, the mechanism for finding high-order subgraphs is certain, while the trial-and-error cost of finding the optimal structure using a random approach can be uncertain and challenging.
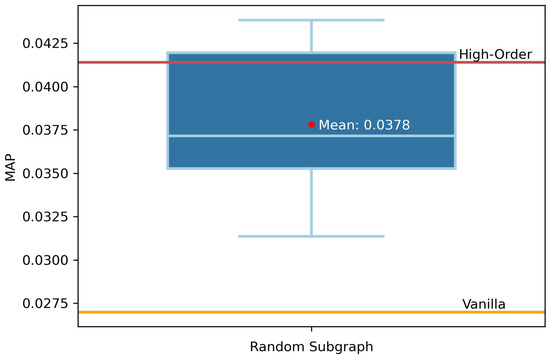
Figure 8.
Box plot of MAP in the random-enhanced model.
5.3. The Stability Brought by Introducing High-Order Structures
In order to demonstrate that introducing a stable structure, such as higher-order subgraphs, can make the model more robust, we test the baselines and the proposed methods with perturbed data by randomly adding edges. Specifically, we randomly generate 0.5–10% of fake edges in every time step, and the performance results of the backbones and their high-order versions are shown in Table 3.

Table 3.
Perturbation analysis.
It can be found that the performance of all models deteriorates as the perturbation increases, but regardless of the variation, the higher-order augmented models can perform better than the original model for different perturbations. When under 0.5%, 2%, 5%, and 10% perturbations, the higher-order augmented version of EGCN-H shows 52.19%, 3.46%, 83.06%, and 195.24% improvement compared to the original model, respectively, and the higher-order augmented version of EGCN-O shows 98.13%, 11.11%, 32.41%, and 100.00% improvement compared to the original model, respectively.
5.4. The Dataset
Since the improvement of the proposed method varies across datasets, we try to explain why the differences exist in terms of dataset characteristics. We evaluate the clustering coefficient in particular, which measures how close neighboring nodes are to being a clique in a graph. As shown in Figure 9, the clustering coefficient of the UCI dataset’s high-order subgraphs is less distinct from the original graph, and the clustering coefficient scores are generally low in both situations, while the clustering coefficient of the Hep-ph dataset’s high-order subgraphs is the greatest. In addition, we calculate the size of the maximum clique for each dataset. Table 4 shows that the UCI dataset has a maximum size of 5, HEP has 47, and 49% of UCI graph snapshots have no high-order cliques. These results indicate the importance of high-order information in dynamic graphs like UCI, since even a small amount of high-order information considerably improves performance on the UCI dataset. Additionally, because the size of the maximum clique is too large for a dataset like HEP, the high degree of node clustering in high-order subgraphs may lead to over-smoothing, resulting in less improvement of the model than on other datasets.
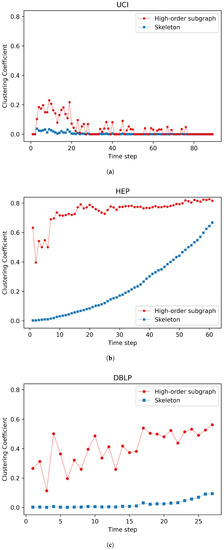
Figure 9.
Clustering coefficients of (a) UCI, (b) HEP, and (c) DBLP datasets.

Table 4.
The size of the maximum clique.
6. Conclusions
Graphs have been widely utilized to describe complex systems, resulting in many graph-based dynamic system modeling works. However, existing models typically learned directly from graphs are thus limited to modeling pairwise relationships between nodes and neglecting the importance of group effects. Therefore, we present a high-order improved graph convolutional network for modeling dynamic graphs, which uses a two-branch method to model high-order and pairwise relationships between nodes.
The results of link prediction experiments in three real-world networks show that the proposed method can considerably improve model performance. Moreover, when the original model fails in the task and falls short of the unsupervised method, it is found that adding high-order information can complement the gap and result in a substantial increase in model accuracy. The ablation study and perturbation analysis further verify the effectiveness and robustness of our model. Our findings reveal the limitations of using classical graph theory alone and highlight the significance of employing higher-order topologies in graphs in future works.
Author Contributions
Conceptualization, J.Z.; methodology, J.Z., L.Z. and H.L.; supervision, B.L. and H.L.; visualization, J.Z.; writing—original draft, J.Z.; writing—review and editing, J.Z. and Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China, Grant/Award Numbers 41871364 and 41871276, the High Performance Computing Platform of Central South University and HPC Central of Department of GIS, in providing HPC resources.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hamilton, W.L.; Ying, R.; Leskovec, J. Representation learning on graphs: Methods and applications. arXiv 2017, arXiv:1709.05584. [Google Scholar]
- Cai, H.; Zheng, V.W.; Chang, K.C.C. A Comprehensive Survey of Graph Embedding: Problems, Techniques, and Applications. IEEE Trans. Knowl. Data Eng. 2018, 30, 1616–1637. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Wang, D.; Cui, P.; Zhu, W. Structural deep network embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1225–1234. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. [Google Scholar]
- Aggarwal, C.; Subbian, K. Evolutionary network analysis: A survey. ACM Comput. Surv. (CSUR) 2014, 47, 1–36. [Google Scholar] [CrossRef]
- Šiljak, D. Dynamic graphs. Nonlinear Anal. Hybrid Syst. 2008, 2, 544–567. [Google Scholar] [CrossRef]
- Zaki, A.; Attia, M.; Hegazy, D.; Amin, S. Comprehensive survey on dynamic graph models. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 573–582. [Google Scholar] [CrossRef]
- Chen, B.; Fan, W.; Liu, J.; Wu, F.X. Identifying protein complexes and functional modules—From static PPI networks to dynamic PPI networks. Briefings Bioinform. 2014, 15, 177–194. [Google Scholar] [CrossRef]
- Berger-Wolf, T.Y.; Saia, J. A framework for analysis of dynamic social networks. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 523–528. [Google Scholar]
- Holm, A.N.; Plank, B.; Wright, D.; Augenstein, I. Longitudinal citation prediction using temporal graph neural networks. arXiv 2020, arXiv:2012.05742. [Google Scholar]
- Skarding, J.; Gabrys, B.; Musial, K. Foundations and modelling of dynamic networks using dynamic graph neural networks: A survey. arXiv 2020, arXiv:2005.07496. [Google Scholar]
- Zhu, L.; Guo, D.; Yin, J.; Ver Steeg, G.; Galstyan, A. Scalable temporal latent space inference for link prediction in dynamic social networks. IEEE Trans. Knowl. Data Eng. 2016, 28, 2765–2777. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Goyal, P.; Chhetri, S.R.; Canedo, A. dyngraph2vec: Capturing network dynamics using dynamic graph representation learning. Knowl.-Based Syst. 2020, 187, 104816. [Google Scholar] [CrossRef]
- Pareja, A.; Domeniconi, G.; Chen, J.; Ma, T.; Suzumura, T.; Kanezashi, H.; Kaler, T.; Schardl, T.B.; Leiserson, C.E. EvolveGCN: Evolving Graph Convolutional Networks for Dynamic Graphs. In Proceedings of the AAAI, New York, NY, USA, 7–12 February 2020; pp. 5363–5370. [Google Scholar]
- Lu, Z.; Wahlström, J.; Nehorai, A. Community detection in complex networks via clique conductance. Sci. Rep. 2018, 8, 5982. [Google Scholar] [CrossRef] [PubMed]
- Soundarajan, S.; Hopcroft, J. Using community information to improve the precision of link prediction methods. In Proceedings of the 21st International Conference on World Wide Web, Lyon, France, 16–20 April 2012; pp. 607–608. [Google Scholar]
- Cong, W.; Wu, Y.; Tian, Y.; Gu, M.; Xia, Y.; Mahdavi, M.; Chen, C.C.J. Dynamic Graph Representation Learning via Graph Transformer Networks. arXiv 2021, arXiv:2111.10447. [Google Scholar]
- Pardalos, P.M.; Xue, J. The maximum clique problem. J. Glob. Optim. 1994, 4, 301–328. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canda, 9–14 December 2002; pp. 585–591. [Google Scholar]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Ribeiro, L.F.; Saverese, P.H.; Figueiredo, D.R. struc2vec: Learning node representations from structural identity. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; pp. 385–394. [Google Scholar]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning convolutional neural networks for graphs. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 2014–2023. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, P.; Pei, J.; Wang, X.; Zhu, W. Timers: Error-bounded svd restart on dynamic networks. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Goyal, P.; Kamra, N.; He, X.; Liu, Y. Dyngem: Deep embedding method for dynamic graphs. arXiv 2018, arXiv:1805.11273. [Google Scholar]
- Zhou, L.; Yang, Y.; Ren, X.; Wu, F.; Zhuang, Y. Dynamic network embedding by modeling triadic closure process. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Seo, Y.; Defferrard, M.; Vandergheynst, P.; Bresson, X. Structured sequence modeling with graph convolutional recurrent networks. In Proceedings of the International Conference on Neural Information Processing, Siem Reap, Cambodia, 13–16 December 2018; Springer: Cham, Switzerland, 2018; pp. 362–373. [Google Scholar]
- Manessi, F.; Rozza, A.; Manzo, M. Dynamic graph convolutional networks. Pattern Recognit. 2020, 97, 107000. [Google Scholar] [CrossRef]
- Narayan, A.; Roe, P.H. Learning graph dynamics using deep neural networks. IFAC-PapersOnLine 2018, 51, 433–438. [Google Scholar] [CrossRef]
- Kazemi, S.M.; Goel, R.; Jain, K.; Kobyzev, I.; Sethi, A.; Forsyth, P.; Poupart, P. Representation Learning for Dynamic Graphs: A Survey. J. Mach. Learn. Res. 2020, 21, 1–73. [Google Scholar]
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994; p. 8. [Google Scholar]
- Bron, C.; Kerbosch, J. Algorithm 457: Finding all cliques of an undirected graph. Commun. ACM 1973, 16, 575–577. [Google Scholar] [CrossRef]
- Eppstein, D.; Löffler, M.; Strash, D. Listing all maximal cliques in sparse graphs in near-optimal time. In Proceedings of the International Symposium on Algorithms and Computation, Jeju Island, Korea, 15–17 December 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 403–414. [Google Scholar]
- Eppstein, D.; Löffler, M.; Strash, D. Listing all maximal cliques in large sparse real-world graphs. J. Exp. Algorithmics (JEA) 2013, 18, 3.1–3.21. [Google Scholar] [CrossRef]
- Srinivas, V.; Mitra, P. Link Prediction in Social Networks: Role of Power Law Distribution; Springer: New York, NY, USA, 2016. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).