On Fluxbrane Polynomials for Generalized Melvin-like Solutions Associated with Rank 5 Lie Algebras

Abstract

We consider generalized Melvin-like solutions corresponding to Lie algebras of rank 5 ($A_5$, $B_5$, $C_5$, $D_5$). The solutions take place in a D-dimensional gravitational model with five Abelian two-forms and five scalar fields. They are governed by five moduli functions $H_s\left(z\right)$ ($s=1,...,5$) of squared radial coordinates $z={\rho }^2$, which obey five differential master equations. The moduli functions are polynomials of powers $(n_1,n_2,n_3,n_4,n_5)=(5,8,9,8,5),(10,18,24,28,15),(9,16,21,24,25),(8,14,18,10,10)$ for Lie algebras $A_5$, $B_5$, $C_5$, $D_5$, respectively. The asymptotic behavior for the polynomials at large distances is governed by some integer-valued $5\times 5$ matrix $\nu$ connected in a certain way with the inverse Cartan matrix of the Lie algebra and (in $A_5$ and $D_5$ cases) with the matrix representing a generator of the ${\mathbb{Z}}_2$-group of symmetry of the Dynkin diagram. The symmetry and duality identities for polynomials are obtained, as well as asymptotic relations for solutions at large distances.

1. Introduction

In this article, we deal with a higher dimensional generalization of Melvin’s solution [1], which was studied earlier in reference [2].

The model from reference [2] is described by metric, n Abelian 2-forms, and $l\ge n$ scalar fields. Here, we study special solutions with $n=l=5$, which are governed by a $5\times 5$ Cartan matrices $\left(A_{ij}\right)$ corresponding to Lie algebras of rank 5: $A_5$, $B_5$, $C_5$, and $D_5$. We note that reference [2] contains a special subclass of fluxbrane solutions from reference [3].

We note that Melvin’s solution in the 4-dimensional space-time describes the gravitational field of a magnetic flux tube. The multidimensional analog of such a flux tube, supported by a certain configuration of the fields of forms, is referred to as a fluxbrane. The appearance of fluxbrane solutions was motivated in past decades by superstring/M-theory models. A physical relevance of such solutions is that they supply an appropriate background geometry for studying various processes, which involve branes, instantons, Kaluza–Klein monopoles, pair production of magnetically charged black holes, and other configurations that can be studied with a special kind of Kaluza–Klein reduction of a certain higher dimensional model in the presence of the $U\left(1\right)$ isometry subgroup. (The readers who are interested in generalizations of the Melvin solution and fluxbrane solutions may be addressed to references [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19], and references therein.)

The fluxbrane solutions from reference [3] were described by moduli functions $H_s\left(z\right)>0$ defined on $(0,+\infty )$, where $z={\rho }^2$ and $\rho$ is a proper radial coordinate. The moduli functions $H_s\left(z\right)$ were obeying n master equations (equivalent to Toda-like equations) governed by a matrix $\left(A_{s{s}^{\prime }}\right)$, and the following boundary conditions were imposed: $H_s(+0)=1$, $s=1,...,n$.

In reference [2] the matrix $\left(A_{s{s}^{\prime }}\right)$ was assumed to coincide with a Cartan matrix for some simple finite-dimensional Lie algebra $\mathcal{G}$ of rank n. In this case according to the conjecture from reference [3] the solutions to master equations with the boundary conditions $H_s(+0)=1$ imposed are polynomials

$$H_s\left(z\right)=1+\sum _{k=1}^{n_s}{P}_s^{\left(k\right)}{z}^k.$$

(1)

Here $P_s^{\left(k\right)}$ are constants, $P_s^{\left(n_s\right)}\ne 0$ and

$$n_s=2\sum _{s^{\prime }=1}^n{A}^{s{s}^{\prime }}.$$

(2)

with the notation assumed: $\left(A^{s{s}^{\prime }}\right)={\left(A_{s{s}^{\prime }}\right)}^{-1}$. Here, $n_s$ are integer numbers, which are components of the twice-dual Weyl vector on the basis of simple co-roots [20].

The functions $H_s$ (so-called “fluxbrane polynomials”) describe a special solution to open Toda chain equations [21,22], which correspond to simple finite-dimensional Lie algebra $\mathcal{G}$ [23].

Here we study the solutions corresponding to Lie algebras of rank 5. We prove some symmetry properties, as well as the so-called duality relations of fluxbrane polynomials. The duality relations describe the behavior of the solutions under the inversion $\rho \to 1/\rho$. They can be mathematically understood in terms of the groups of symmetry of Dynkin diagrams for the corresponding Lie algebras. For this work, these groups of symmetry are either identical (for Lie algebras $B_5$, $C_5$) or isomorphic to the group ${\mathbb{Z}}_2$ (for Lie algebras $A_5$, $D_5$). The duality identities may be used in deriving a $1/\rho$-expansion for solutions at large distances $\rho$. The corresponding asymptotic behaviors of the solutions are presented.

The analogous consideration was performed earlier for the case of Lie algebras of rank 2: $A_2$, $B_2=C_2$, $G_2$ in reference [24], and for Lie algebras of rank 3: $A_3$, $B_3$, $C_3$ in reference [25], for rank 4 non-exceptional Lie algebras $A_4$, $B_4$, $C_4$, $D_4$ in references [26,27] and for exceptional Lie algebra $F_4$ in [27]. Moreover, in reference [28], the conjecture from reference [3] was verified for the Lie algebra $E_6$ and certain duality relations for six $E_6$-polynomials were found.

2. The Setup and Generalized Melvin Solutions

We deal with the (smooth) manifold

$$M=(0,+\infty )\times M_1\times M_2,$$

(3)

where $M_1=S^1$ and $M_2$ is a $(D-2)$-dimensional manifold of signature $(-,+,...,+)$, which is supposed to be Ricci-flat.

The action of the model reads

$$S=\int d^{D}x\sqrt{\left|g\right|}\left\{R\left[g\right]-{\delta }_{ab}{g}^{MN}{\partial }_M{\phi }^a{\partial }_N{\phi }^b-\frac{1}{2}\sum _{s=1}^{5}exp\left[2{\overrightarrow{\lambda }}_s\overrightarrow{\phi }\right]{\left(F^s\right)}^2\right\}.$$

(4)

Here, $g=g_{MN}\left(x\right)d{x}^M\otimes d{x}^N$ is a (smooth) metric defined on M, $\overrightarrow{\phi }=\left({\phi }^a\right)\in {\mathbb{R}}^5$ is a vector that consists of scalar fields, $F^s=d{A}^s=\frac{1}{2}{F}_{MN}^{s}d{x}^M\wedge d{x}^N$ is a form of rank 2, ${\overrightarrow{\lambda }}_s=\left({\lambda }_s^a\right)\in {\mathbb{R}}^5$ is the vector of dilaton coupling constants, $s=1,...,5$; $a=1,...,5$. In (4) we denote $\left|g\right|\equiv |det(g_{MN}\left)\right|$, ${\left(F^s\right)}^2\equiv F_{M_1{M}_2}^s{F}_{N_1{N}_2}^s{g}^{M_1{N}_1}{g}^{M_2{N}_2}$.

We studied a family of exact solutions to the field equations, which correspond to the action (4) and depend on the radial coordinate $\rho$. These solutions read as follows [2] (for more general fluxbrane solutions, see [3])

$$\begin{array}{c}\hfill g=\left(\prod _{s=1}^5{H}_s^{2h_s/(D-2)}\right)\left\{d\rho \otimes d\rho +\left(\prod _{s=1}^5{H}_s^{-2h_s}\right){\rho }^{2}d\varphi \otimes d\varphi +g^2\right\},\end{array}$$

(5)

$$\begin{array}{c}\hfill exp\left({\phi }^a\right)=\prod _{s=1}^5{H}_s^{h_s{\lambda }_s^a},\end{array}$$

(6)

$$F^s=q_s\left(\prod _{l=1}^5{H}_l^{-A_{sl}}\right)\rho d\rho \wedge d\varphi ,$$

(7)

$s,a=1,...,5$, where $g^1=d\varphi \otimes d\varphi$ is a metric on a one-dimensional circle $M_1=S^1$ and $g^2$ is a metric of signature $(-,+,\cdots ,+)$ on the manifold $M_2$, which is supposed to be Ricci-flat. Here, $q_s\ne 0$ are constants.

In what follows, we denote $z={\rho }^2$. Here, the functions $H_s\left(z\right)>0$ obey the set of non-linear equations [2]

$$\frac{d}{dz}\left(\frac{z}{H_s}\frac{d}{dz}{H}_s\right)=P_s\prod _{l=1}^5{H}_l^{-A_{sl}},$$

(8)

with the boundary conditions imposed

$$H_s(+0)=1,$$

(9)

where

$$P_s=\frac{1}{4}{K}_s{q}_s^2,$$

(10)

$s=1,...,5$. Condition (9) prevents a possible appearance of the conic singularity for the metric at $\rho =+0$.

The parameters $h_s$ obey the following relations

$$h_s=K_s^{-1},K_s=B_{ss}>0,$$

(11)

where

$$B_{sl}\equiv 1+\frac{1}{2-D}+{\overrightarrow{\lambda }}_s{\overrightarrow{\lambda }}_l,$$

(12)

$s,l=1,...,5$. The formulae for the solutions contain the so-called “quasi-Cartan” matrix

$$\left(A_{sl}\right)=\left(2B_{sl}/B_{ll}\right).$$

(13)

Here, we study a multidimensional generalization of Melvin’s solution [1] for the case of five scalar fields and five 2-forms. In the case when scalar fields are absent, the original Melvin’s solution may be obtained here for $D=4$, one (electromagnetic) 2-form, $M_1=S^1$ ($0<\varphi <2\pi$), $M_2={\mathbb{R}}^2$, and $g^2=-dt\otimes dt+dx\otimes dx$.

3. Solutions Related to Simple Classical Rank 5 Lie Algebras

Here, we deal with solutions corresponding to Lie algebras $\mathcal{G}$ of rank 5. In this case, the matrix $A=\left(A_{sl}\right)$ should coincide with one of the Cartan matrices

$$\begin{array}{c}\left(A_{s{s}^{\prime }}\right)=\left(\begin{array}{ccccc}2& -1& 0& 0& 0\\ -1& 2& -1& 0& 0\\ 0& -1& 2& -1& 0\\ 0& 0& -1& 2& -1\\ 0& 0& 0& -1& 2\end{array}\right),\left(\begin{array}{ccccc}2& -1& 0& 0& 0\\ -1& 2& -1& 0& 0\\ 0& -1& 2& -1& 0\\ 0& 0& -1& 2& -2\\ 0& 0& 0& -1& 2\end{array}\right),\\ \left(\begin{array}{ccccc}2& -1& 0& 0& 0\\ -1& 2& -1& 0& 0\\ 0& -1& 2& -1& 0\\ 0& 0& -1& 2& -1\\ 0& 0& 0& -2& 2\end{array}\right),\left(\begin{array}{ccccc}2& -1& 0& 0& 0\\ -1& 2& -1& 0& 0\\ 0& -1& 2& -1& -1\\ 0& 0& -1& 2& 0\\ 0& 0& -1& 0& 2\end{array}\right).\end{array}$$

(14)

for $\mathcal{G}=A_5,B_5,C_5,D_5$, respectively.

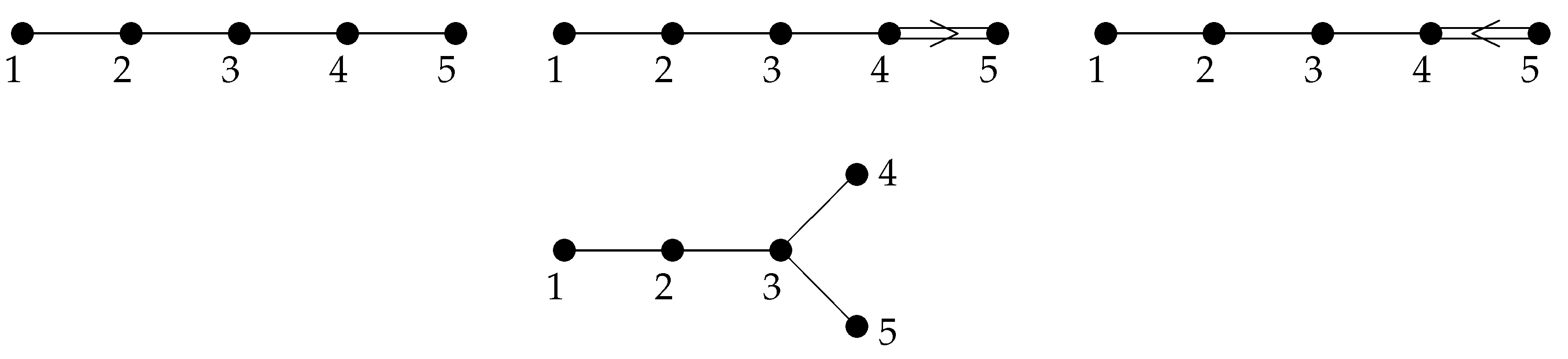
The graphical presentation of these matrices by Dynkin diagrams is given in Figure 1.

Figure 1. Dynkin diagrams for the Lie algebras $A_5,B_5,C_5,D_5$, respectively.

Due to (11)–(13), we obtain

$$K_s=\frac{D-3}{D-2}+{\overrightarrow{\lambda }}_s^2,$$

(15)

where $h_s=K_s^{-1}$, and

$${\overrightarrow{\lambda }}_s{\overrightarrow{\lambda }}_l=\frac{1}{2}{K}_l{A}_{sl}-\frac{D-3}{D-2}\equiv G_{sl},$$

(16)

$s,l=1,2,3,4$; (15) is a special case of (16).

Polynomials. Due to the conjecture from reference [3], the set of moduli functions $H_1\left(z\right),...,H_5\left(z\right)$, which obey Equations (8) and (9) with any matrix $A=\left(A_{sl}\right)$ from (14), are polynomials. Due to relation (2), the powers of these polynomials are the following ones: $(n_1,n_2,n_3,n_4,n_5)=(5,8,9,8,5),(10,18,24,28,15),(9,16,21,24,25),(8,14,18,10,10)$ for Lie algebras $A_5$, $B_5$, $C_5$, $D_5$, respectively.

Here, we verify (i.e., prove) the polynomial conjecture from reference [3] by solving the set of algebraic equations for the coefficients of the polynomials (1), which follow from master Equation (8).

In what follows (in this section), we present structures (or “truncated versions”) of these polynomials. In Appendix A, we present the total list of these polynomials, which were obtained by using a certain MATHEMATICA algorithm. Given Cartan matrix $A_{sl}$, this algorithm uses a polynomial ansatz (1) for $H_s\left(z\right)$ to write and solve Equation (8) as a system of non-linear algebraic equations on the corresponding polynomial coefficients $P_s^{\left(k\right)}$. The problem is that in the case of higher ranks, this system becomes quite complicated, so the direct use of built-in ‘solve’-like commands causes computational fails. To be more efficient, the algorithm uses the adapted computational procedure based on a certain recurrence property of the algebraic system under consideration. According to this property, among the full set of variables $P_s^{\left(k\right)}$ ($k=1,...,n_s$), one can single out a certain “starting” subset $P_s^{\left(k_0\right)}$, obeying the closed subsystem of equations, and resolving the remaining equations on each k-th step using the variables found in the previous step. As soon as all variables are found, the algorithm writes down the obtained fluxbrane polynomials and checks the correctness of the obtained solution by direct substitution into the original equations. After that, the algorithm directly verifies symmetry and duality properties for the obtained polynomials, which are discussed below.

Here, as in reference [23], we use the rescaled parameters

$$p_s=P_s/n_s.$$

(17)

$A_5$-case. For the Lie algebra $A_5$, the polynomials have the following structures

$H_1=$

$1+5p_{1}z+10p_1{p}_2{z}^2+10p_1{p}_2{p}_3{z}^3+5p_1{p}_2{p}_3{p}_4{z}^4+p_1{p}_2{p}_3{p}_4{p}_5{z}^5,$

$H_2=$

$1+8p_{2}z+(10p_1{p}_2+18p_2{p}_3)z^2+\cdots +(10p_1{p}_2^2{p}_3^2{p}_4+18p_1{p}_2^2{p}_3{p}_4{p}_5)z^6+8p_1{p}_2^2{p}_3^2{p}_4{p}_5{z}^7+p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8$,

$H_3=$

$1+9p_{3}z+(18p_2{p}_3+18p_3{p}_4)z^2+\cdots +(18p_1{p}_2^2{p}_3^2{p}_4{p}_5+18p_1{p}_2{p}_3^2{p}_4^2{p}_5)z^7+9p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8+p_1{p}_2^2{p}_3^3{p}_4^2{p}_5{z}^9$,

$H_4=$

$1+8p_{4}z+(18p_3{p}_4+10p_4{p}_5)z^2+\cdots +(18p_1{p}_2{p}_3{p}_4^2{p}_5+10p_2{p}_3^2{p}_4^2{p}_5)z^6+8p_1{p}_2{p}_3^2{p}_4^2{p}_5{z}^7+p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8$,

$H_5=$

$1+5p_{5}z+10p_4{p}_5{z}^2+10p_3{p}_4{p}_5{z}^3+5p_2{p}_3{p}_4{p}_5{z}^4+p_1{p}_2{p}_3{p}_4{p}_5{z}^5.$

$B_5$-case. For the Lie algebra $B_5$, we obtain the following structures of the polynomials

$H_1=$

$1+10p_{1}z+45p_1{p}_2{z}^2+\cdots +45p_1{p}_2{p}_3^2{p}_4^2{p}_5^2{z}^8+10p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^2{z}^9+p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5^2{z}^{10},$

$H_2=$

$$\begin{gathered} 1+18p_{2}z+(45p_1{p}_2+108p_2{p}_3)z^2+\cdots +(108p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^4+45p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^4)z^{16}+18p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^4{z}^{17}+ \\ {p}_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^4{z}^{18}, \end{gathered}$$

$H_3=$

$$\begin{gathered} 1+24p_{3}z+(108p_2{p}_3+168p_3{p}_4)z^2+\cdots +(168p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^6+108p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^6)z^{22}+24p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^6{z}^{23}+ \\ {p}_1^2{p}_2^4{p}_3^6{p}_4^6{p}_5^6{z}^{24}, \end{gathered}$$

$H_4=$

$$\begin{gathered} 1+28p_{4}z+(168p_3{p}_4+210p_4{p}_5)z^2+\cdots +(210p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^7+168p_1^2{p}_2^4{p}_3^5{p}_4^7{p}_5^8)z^{26}+28p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^8{z}^{27}+ \\ {p}_1^2{p}_2^4{p}_3^6{p}_4^8{p}_5^8{z}^{28}, \end{gathered}$$

$H_5=$

$1+15p_{5}z+105p_4{p}_5{z}^2+\cdots +105p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^4{z}^{13}+15p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^4{z}^{14}+p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^5{z}^{15}.$

$C_5$-case. For the Lie algebra $C_5$, the polynomials have the following structures

$H_1=$

$1+9p_{1}z+36p_1{p}_2{z}^2+\cdots +36p_1{p}_2{p}_3^2{p}_4^2{p}_5{z}^7+9p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8+p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^9,$

$H_2=$

$$\begin{gathered} 1+16p_{2}z+(36p_1{p}_2+84p_2{p}_3)z^2+\cdots +(84p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^2+36p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^2)z^{14}+16p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^2{z}^{15}+ \\ {p}_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^2{z}^{16}, \end{gathered}$$

$H_3=$

$$\begin{gathered} 1+21p_{3}z+(84p_2{p}_3+126p_3{p}_4)z^2+\cdots +(126p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^3+84p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^3)z^{19}+21p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^3{z}^{20}+ \\ {p}_1^2{p}_2^4{p}_3^6{p}_4^6{p}_5^3{z}^{21}, \end{gathered}$$

$H_4=$

$$\begin{gathered} 1+24p_{4}z+(126p_3{p}_4+150p_4{p}_5)z^2+\cdots +(150p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^3+126p_1^2{p}_2^4{p}_3^5{p}_4^7{p}_5^4)z^{22}+24p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^4{z}^{23}+ \\ {p}_1^2{p}_2^4{p}_3^6{p}_4^8{p}_5^4{z}^{24}, \end{gathered}$$

$H_5=$

$1+25p_{5}z+300p_4{p}_5{z}^2+\cdots +300p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^4{z}^{23}+25p_1^2{p}_2^4{p}_3^6{p}_4^8{p}_5^4{z}^{24}+p_1^2{p}_2^4{p}_3^6{p}_4^8{p}_5^5{z}^{25}.$

$D_5$-case. For the Lie algebra $D_5$, we obtain the following structures of the polynomials

$H_1=$

$1+8p_{1}z+28p_1{p}_2{z}^2+\cdots +28p_1{p}_2{p}_3^2{p}_4{p}_5{z}^6+8p_1{p}_2^2{p}_3^2{p}_4{p}_5{z}^7+p_1^2{p}_2^2{p}_3^2{p}_4{p}_5{z}^8,$

$H_2=$

$$\begin{gathered} 1+14p_{2}z+(28p_1{p}_2+63p_2{p}_3)z^2+\cdots +(63p_1^2{p}_2^3{p}_3^3{p}_4^2{p}_5^2+28p_1{p}_2^3{p}_3^4{p}_4^2{p}_5^2)z^{12}+14p_1^2{p}_2^3{p}_3^4{p}_4^2{p}_5^2{z}^{13}+ \\ {p}_1^2{p}_2^4{p}_3^4{p}_4^2{p}_5^2{z}^{14}, \end{gathered}$$

$H_3=$

$$\begin{gathered} 1+18p_{3}z+(63p_2{p}_3+45p_3{p}_4+45p_3{p}_5)z^2+\cdots +(45p_1^2{p}_2^4{p}_3^5{p}_4^3{p}_5^2+45p_1^2{p}_2^4{p}_3^5{p}_4^2{p}_5^3+63p_1^2{p}_2^3{p}_3^5{p}_4^3{p}_5^3)z^{16}+18p_1^2{p}_2^4{p}_3^5{p}_4^3{p}_5^3{z}^{17}+ \\ {p}_1^2{p}_2^4{p}_3^6{p}_4^3{p}_5^3{z}^{18}, \end{gathered}$$

$H_4=$

$1+10p_{4}z+45p_3{p}_4{z}^2+\cdots +45p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8+10p_1{p}_2^2{p}_3^3{p}_4^2{p}_5{z}^9+p_1{p}_2^2{p}_3^3{p}_4^2{p}_5^2{z}^{10},$

$H_5=$

$1+10p_{5}z+45p_3{p}_5{z}^2+\cdots +45p_1{p}_2^2{p}_3^2{p}_4{p}_5^2{z}^8+10p_1{p}_2^2{p}_3^3{p}_4{p}_5^2{z}^9+p_1{p}_2^2{p}_3^3{p}_4^2{p}_5^2{z}^{10}.$

Now we denote

$$H_s\equiv H_s\left(z\right)=H_s(z,\left(p_i\right)),\left(p_i\right)\equiv (p_1,p_2,p_3,p_4,p_5).$$

(18)

The polynomials have the following asymptotic behaviors

$$H_s=H_s(z,\left(p_i\right))\sim \left(\prod _{l=1}^5{\left(p_l\right)}^{{\nu }^{sl}}\right)z^{n_s}\equiv H_s^{as}(z,\left(p_i\right)),\mathrm{as}z\to \infty ,$$

(19)

where we denote by $\nu =\left({\nu }^{sl}\right)$ the integer-valued matrix, which has the form

$$\begin{array}{cc}\hfill \nu & =\left(\begin{array}{ccccc}1& 1& 1& 1& 1\\ 1& 2& 2& 2& 1\\ 1& 2& 3& 2& 1\\ 1& 2& 2& 2& 1\\ 1& 1& 1& 1& 1\end{array}\right),\left(\begin{array}{ccccc}2& 2& 2& 2& 2\\ 2& 4& 4& 4& 4\\ 2& 4& 6& 6& 6\\ 2& 4& 6& 8& 8\\ 1& 2& 3& 4& 5\end{array}\right),\left(\begin{array}{ccccc}2& 2& 2& 2& 1\\ 2& 4& 4& 4& 2\\ 2& 4& 6& 6& 3\\ 2& 4& 6& 8& 4\\ 2& 4& 6& 8& 5\end{array}\right),\hfill \\ \hfill & \left(\begin{array}{ccccc}2& 2& 2& 1& 1\\ 2& 4& 4& 2& 2\\ 2& 4& 6& 3& 3\\ 1& 2& 3& 2& 2\\ 1& 2& 3& 2& 2\end{array}\right)\hfill \end{array}$$

(20)

for Lie algebras $A_5,B_5,C_5,D_5$, respectively. It may be readily verified that the matrix $\nu =\left({\nu }^{sl}\right)$ obeys the following identity

$$\sum _{l=1}^5{\nu }^{sl}=n_s,s=1,2,3,4,5.$$

(21)

It should be noted that for Lie algebras $B_5$, $C_5$, the $\nu$-matrix coincides with the twice-inverse Cartan matrix $A^{-1}$, i.e.,

$$\nu \left(\mathcal{G}\right)=2A^{-1},\mathcal{G}=B_5,C_5,$$

(22)

while in the $A_5$ and $D_5$ cases, we have a more sophisticated relation

$$\nu \left(\mathcal{G}\right)=A^{-1}(I+P\left(\mathcal{G}\right)),\mathcal{G}=A_5,D_5.$$

(23)

Here, we denote by the I$5\times 5$ identity matrix and by $P\left(\mathcal{G}\right)$ - a matrix corresponding to a certain permutation $\sigma \in S_5$ ($S_5$ is the symmetric group) by the relation: $P=\left(P_j^i\right)=\left({\delta }_{\sigma \left(j\right)}^i\right)$, where $\sigma$ is the generator of the group $G=\{\sigma ,\mathrm{id}\}$. G is the group of symmetry of the Dynkin diagram for $A_5$ and $D_5$, which act on the set of the corresponding five vertices via their permutations. In fact, group G is isomorphic to the ${\mathbb{Z}}_2$ group. Here, we present the explicit forms for the permutation matrix P and the generator $\sigma$ for both Lie algebras $A_5,D_5$:

$$P\left(A_5\right)=\left(\begin{array}{ccccc}0& 0& 0& 0& 1\\ 0& 0& 0& 1& 0\\ 0& 0& 1& 0& 0\\ 0& 1& 0& 0& 0\\ 1& 0& 0& 0& 0\end{array}\right),\sigma :(1,2,3,4,5)\mapsto (5,4,3,2,1);$$

(24)

$$P\left(D_5\right)=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1\\ 0& 0& 0& 1& 0\end{array}\right),\sigma :(1,2,3,4,5)\mapsto (1,2,3,5,4).$$

(25)

We note that the above symmetry groups control certain identity properties for polynomials $H_s\left(z\right)$.

We denote ${\widehat{p}}_i=p_{\sigma \left(i\right)}$ for the $A_5$ and $D_5$ cases, and ${\widehat{p}}_i=p_i$ for $B_5$ and $C_5$ cases ($i=1,2,3,4,5$). The ordered set $\left({\widehat{p}}_i\right)$ is called a dual one to the ordered set $\left(p_i\right)$.

By using MATHEMATICA algorithms, we verified the validity of the following identities.

Symmetry relations.

Proposition 1. 

The fluxbrane polynomials, corresponding to Lie algebras for $A_5$ and $D_5$, obey for all $p_i$ and $z>0$ the following identities:

$$\begin{array}{ccc}& & H_{\sigma \left(s\right)}(z,\left(p_i\right))=H_s(z,\left({\widehat{p}}_i\right)),\hfill \end{array}$$

(26)

where $\sigma \in S_5$, $s=1,\cdots ,5$ is defined for each algebra by Equations (24), (25). Relations (26) may be called symmetry ones.

Duality relations.

Proposition 2. 

The fluxbrane polynomials, which correspond to Lie algebras $A_5$, $B_5$, $C_5$, $D_5$, satisfy for all $p_i>0$ and $z>0$ the following identities

$$H_s(z,\left(p_i\right))=H_s^{as}(z,\left(p_i\right))H_s(z^{-1},\left({\widehat{p}}_i^{-1}\right)),$$

(27)

$s=1,2,3,4,5$. Relations (27) may be called duality ones.

Fluxes. Now, we place our attention on the oriented 2-dimensional manifold $M_{*}=(0,+\infty )\times S^1$. We calculate the flux integrals over this manifold:

$${\mathsf{\Phi }}^s={\int }_{M_{*}}{F}^s=2\pi {\int }_0^{+\infty }d\rho \rho {\mathcal{B}}^s.$$

(28)

Here,

$${\mathcal{B}}^s=q_s\prod _{l=1}^5{H}_l^{-A_{sl}}.$$

(29)

Due to the results of reference [29], the flux integrals ${\mathsf{\Phi }}^s$ read

$${\mathsf{\Phi }}^s=4\pi n_s{q}_s^{-1}{h}_s,$$

(30)

$s=1,2,3,4,5$. Here, as in a general case [29], any flux ${\mathsf{\Phi }}^s$ depends upon one integration constant $q_s\ne 0$, while the integrand form $F^s$ depends upon all constants: $q_1,q_2,q_3,q_4,q_5$.

We also note that by placing $q_1=0$, we obtain the Melvin-type solutions corresponding to classical Lie algebras $A_4$, $B_4$, $C_4$, and $D_4$, respectively, which were analyzed in reference [26]. The case of rank 3 Lie algebras was considered in [25]. (For the case of the rank 2 Lie algebras, see reference [24].)

Special solutions. By putting $p_1=p_2=p_3=p_4=p_5=p>0$ we obtain binomial relations

$$H_s\left(z\right)=H_s(z;(p,p,p,p,p))={(1+pz)}^{n_s},$$

(31)

which obey the master Equations (8) with boundary conditions (9) imposed with parameters $q_s$, satisfying the following relations

$$\frac{1}{4}{K}_s{q}_s^2/n_s=p,$$

(32)

$s=1,2,3,4,5$.

Asymptotic relations.

Now we present the asymptotic relations as $\rho \to +\infty$ for the solution under consideration:

$$\begin{array}{c}\hfill g_{as}={\left(\prod _{l=1}^5{p}_l^{a_l}\right)}^{2/(D-2)}{\rho }^{2A}\{d\rho \otimes d\rho \\ \hfill +{\left(\prod _{l=1}^5{p}_l^{a_l}\right)}^{-2}{\rho }^{2-2A(D-2)}d\varphi \otimes d\varphi +g^2\},\end{array}$$

(33)

$$\begin{array}{c}\hfill {\phi }_{as}^a=\sum _{s=1}^5{h}_s{\lambda }_s^a(\sum _{l=1}^5{\nu }^{sl}ln{p}_l+2n_{s}ln\rho ),\end{array}$$

(34)

$$\begin{array}{c}\hfill F_{as}^s=q_s{p}_s^{-1}{p}_{\theta \left(s\right)}^{-1}{\rho }^{-3}d\rho \wedge d\varphi ,\end{array}$$

(35)

$a,s=1,2,3,4,5$, where

$$a_l=\sum _{s=1}^5{h}_s{\nu }^{sl},A=2{(D-2)}^{-1}\sum _{s=1}^5{n}_s{h}_s,$$

(36)

and in (35) we put $\theta =\sigma$ for $\mathcal{G}=A_5$, and $\theta =\mathrm{id}$ for $\mathcal{G}=B_5,C_5,D_5$.

Now, we explain the appearance of these asymptotical relations. Indeed, due to polynomial structures of moduli functions, we have

$$H_s\sim C_s{\rho }^{2n_s},C_s=\prod _{l=1}^5{\left(p_l\right)}^{{\nu }^{sl}},$$

(37)

as $\rho \to +\infty$. From (29), (37) and the equality ${\sum }_1^n{A}_{sl}{n}_l=2$, following from (2), we obtain

$${\mathcal{B}}^s\sim q_s{C}^s{\rho }^{-4},C^s=\prod _{l=1}^5{p}_l^{-{\left(A\nu \right)}_s^l}.$$

(38)

$s=1,2,3,4,5$.

Using (23) and (38) we have for the $A_5$-case

$$C^s=\prod _{l=1}^5{p}_l^{-{(I+P)}_s^l}=\prod _{l=1}^5{p}_l^{-{\delta }_s^l-{\delta }_{\sigma \left(s\right)}^l}=p_s^{-1}{p}_{\sigma \left(s\right)}^{-1}.$$

(39)

Similarly, due to (22) and (38), we obtain for Lie algebras $B_5$, $C_5$, $D_5$:

$$C^s=\prod _{l=1}^5{p}_l^{-2{\delta }_s^l}=p_s^{-2}.$$

(40)

We note that for $\mathcal{G}=B_5,C_5,D_5$ the asymptotic value of form $F_{as}^s$ depends on $q_s$, $s=1,2,3,4,5$. In the $A_5$-case, $F_{as}^s$ depends on $q_1$ and $q_5$ for $s=1,5$ and $q_2,q_4$ for $s=2,4$ and on $q_3$ for $s=3$.

4. Conclusions

In this paper, we studied a family of generalized multidimensional Melvin-type solutions which correspond to simple Lie algebras of rank 5: $\mathcal{G}=A_5,B_5,C_5,D_5$. Any solution of this family is ruled by a set of 5 polynomials $H_s\left(z\right)$ of powers $n_s$, $s=1,2,3,4,5$. The powers of these polynomials read: $(n_1,n_2,n_3,n_4,n_5)=(5,8,9,8,5),(10,18,24,28,15),(9,16,21,24,25),(8,14,18,10,10)$ for Lie algebras $A_5$, $B_5$, $C_5$, $D_5$, respectively. In Appendix A, we present all of these polynomials calculated by using a certain MATHEMATICA algorithm. In fact, these (so-called fluxbrane) polynomials determine special solutions to open Toda chain equations [23], which correspond to the Lie algebras under consideration and may be used in various areas of science.

The moduli parameters $p_s$ of polynomials $H_s\left(z\right)=H_s(z,\left(p_s\right))$ are related to parameters $q_s$ by the relation $p_s=K_s{q}_s^2/\left(4n_s\right)$, where $K_s$ depends upon the total dimension D and dilaton coupling vectors ${\overrightarrow{\lambda }}_s$ by the relation (15). For $D=4$, the parameters $q_s$ determine (up to a sign ±) the values of the colored magnetic fields on the axis of symmetry.

Here, we found the symmetry relations and the duality identities for our rank 5 fluxbrane polynomials. These identities may also be used in deriving $1/\rho$-expansion for solutions under consideration at large distances $\rho$, e.g. for asymptotic relations (as $\rho \to +\infty$), which were obtained in the paper.

By using the results of reference [23], one can construct black hole solutions corresponding to rank 5 Lie algebras for the model under consideration along the lines of how it was done in [26] for the rank 4 case. In the rank 5 case, one will need a thorough analysis of horizons in black hole metrics governed by fluxbrane polynomials extended to negative values of variable z. For the dyonic black hole solutions corresponding to rank 2 Lie algebras, such an analysis was started in references [30,31] (see also [32]). The proper analyses of black hole solutions corresponding to Lie algebras of ranks 3 and 4 are also desirable. This may be the subject of our future papers.

Appendix A.1. The List of Polynomials

$A_5$-case. For the Lie algebra $A_5\cong sl\left(6\right)$, the polynomials read

$H_1=$

$1+5p_{1}z+10p_1{p}_2{z}^2+10p_1{p}_2{p}_3{z}^3+5p_1{p}_2{p}_3{p}_4{z}^4+p_1{p}_2{p}_3{p}_4{p}_5{z}^5$

$H_2=$

$$\begin{gathered} 1+8p_{2}z+(10p_1{p}_2+18p_2{p}_3)z^2+(40p_1{p}_2{p}_3+16p_2{p}_3{p}_4)z^3+(20p_1{p}_2^2{p}_3+45p_1{p}_2{p}_3{p}_4+ \\ 5p_2{p}_3{p}_4{p}_5)z^4+(40p_1{p}_2^2{p}_3{p}_4+16p_1{p}_2{p}_3{p}_4{p}_5)z^5+(10p_1{p}_2^2{p}_3^2{p}_4+18p_1{p}_2^2{p}_3{p}_4{p}_5)z^6+ \\ 8p_1{p}_2^2{p}_3^2{p}_4{p}_5{z}^7+p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8 \end{gathered}$$

$H_3=$

$$\begin{gathered} 1+9p_{3}z+(18p_2{p}_3+18p_3{p}_4)z^2+(10p_1{p}_2{p}_3+64p_2{p}_3{p}_4+10p_3{p}_4{p}_5)z^3+(45p_1{p}_2{p}_3{p}_4+ \\ 36p_2{p}_3^2{p}_4+45p_2{p}_3{p}_4{p}_5)z^4+(45p_1{p}_2{p}_3^2{p}_4+36p_1{p}_2{p}_3{p}_4{p}_5+45p_2{p}_3^2{p}_4{p}_5)z^5+(10p_1{p}_2^2{p}_3^2{p}_4+ \\ 64p_1{p}_2{p}_3^2{p}_4{p}_5+10p_2{p}_3^2{p}_4^2{p}_5)z^6+(18p_1{p}_2^2{p}_3^2{p}_4{p}_5+18p_1{p}_2{p}_3^2{p}_4^2{p}_5)z^7+9p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8+ \\ {p}_1{p}_2^2{p}_3^3{p}_4^2{p}_5{z}^9 \end{gathered}$$

$H_4=$

$$\begin{gathered} 1+8p_{4}z+(18p_3{p}_4+10p_4{p}_5)z^2+(16p_2{p}_3{p}_4+40p_3{p}_4{p}_5)z^3+(5p_1{p}_2{p}_3{p}_4+45p_2{p}_3{p}_4{p}_5+ \\ 20p_3{p}_4^2{p}_5)z^4+(16p_1{p}_2{p}_3{p}_4{p}_5+40p_2{p}_3{p}_4^2{p}_5)z^5+(18p_1{p}_2{p}_3{p}_4^2{p}_5+10p_2{p}_3^2{p}_4^2{p}_5)z^6+ \\ 8p_1{p}_2{p}_3^2{p}_4^2{p}_5{z}^7+p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8 \end{gathered}$$

$H_5=$

$1+5p_{5}z+10p_4{p}_5{z}^2+10p_3{p}_4{p}_5{z}^3+5p_2{p}_3{p}_4{p}_5{z}^4+p_1{p}_2{p}_3{p}_4{p}_5{z}^5$

$B_5$-case. For the Lie algebra $B_5\cong so\left(11\right)$, we obtain

$H_1=$

$$\begin{gathered} 1+10p_{1}z+45p_1{p}_2{z}^2+120p_1{p}_2{p}_3{z}^3+210p_1{p}_2{p}_3{p}_4{z}^4+252p_1{p}_2{p}_3{p}_4{p}_5{z}^5+210p_1{p}_2{p}_3{p}_4{p}_5^2{z}^6+ \\ 120p_1{p}_2{p}_3{p}_4^2{p}_5^2{z}^7+45p_1{p}_2{p}_3^2{p}_4^2{p}_5^2{z}^8+10p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^2{z}^9+p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5^2{z}^{10} \end{gathered}$$

$H_2=$

$$\begin{gathered} 1+18p_{2}z+(45p_1{p}_2+108p_2{p}_3)z^2+(480p_1{p}_2{p}_3+336p_2{p}_3{p}_4)z^3+(540p_1{p}_2^2{p}_3+ \\ 1890p_1{p}_2{p}_3{p}_4+630p_2{p}_3{p}_4{p}_5)z^4+(3780p_1{p}_2^2{p}_3{p}_4+4032p_1{p}_2{p}_3{p}_4{p}_5+756p_2{p}_3{p}_4{p}_5^2)z^5+ \\ (2520p_1{p}_2^2{p}_3^2{p}_4+10206p_1{p}_2^2{p}_3{p}_4{p}_5+5250p_1{p}_2{p}_3{p}_4{p}_5^2+588p_2{p}_3{p}_4^2{p}_5^2)z^6+(12096p_1{p}_2^2{p}_3^2{p}_4{p}_5+ \\ 15120p_1{p}_2^2{p}_3{p}_4{p}_5^2+4320p_1{p}_2{p}_3{p}_4^2{p}_5^2+288p_2{p}_3^2{p}_4^2{p}_5^2)z^7+(5292p_1{p}_2^2{p}_3^2{p}_4^2{p}_5+22680p_1{p}_2^2{p}_3^2{p}_4{p}_5^2+ \\ 13500p_1{p}_2^2{p}_3{p}_4^2{p}_5^2+2205p_1{p}_2{p}_3^2{p}_4^2{p}_5^2+81p_2^2{p}_3^2{p}_4^2{p}_5^2)z^8+48620p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^2{z}^9+(81p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5^2+ \\ 2205p_1{p}_2^3{p}_3^2{p}_4^2{p}_5^2+13500p_1{p}_2^2{p}_3^3{p}_4^2{p}_5^2+22680p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^2+5292p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^3)z^{10}+(288p_1^2{p}_2^3{p}_3^2{p}_4^2{p}_5^2+ \\ 4320p_1{p}_2^3{p}_3^3{p}_4^2{p}_5^2+15120p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^2+12096p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^3)z^{11}+(588p_1^2{p}_2^3{p}_3^3{p}_4^2{p}_5^2+5250p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^2+ \\ 10206p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^3+2520p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^4)z^{12}+(756p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^2+4032p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^3+3780p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^4)z^{13}+ \\ (630p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^3+1890p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^4+540p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^4)z^{14}+(336p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^4+480p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^4)z^{15}+ \\ (108p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^4+45p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^4)z^{16}+18p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^4{z}^{17}+p_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^4{z}^{18} \end{gathered}$$

$H_3=$

$$\begin{gathered} 1+24p_{3}z+(108p_2{p}_3+168p_3{p}_4)z^2+(120p_1{p}_2{p}_3+1344p_2{p}_3{p}_4+560p_3{p}_4{p}_5)z^3+ \\ (1890p_1{p}_2{p}_3{p}_4+2016p_2{p}_3^2{p}_4+5670p_2{p}_3{p}_4{p}_5+1050p_3{p}_4{p}_5^2)z^4+(5040p_1{p}_2{p}_3^2{p}_4+ \\ 9072p_1{p}_2{p}_3{p}_4{p}_5+15120p_2{p}_3^2{p}_4{p}_5+12096p_2{p}_3{p}_4{p}_5^2+1176p_3{p}_4^2{p}_5^2)z^5+(2520p_1{p}_2^2{p}_3^2{p}_4+ \\ 43008p_1{p}_2{p}_3^2{p}_4{p}_5+11760p_2{p}_3^2{p}_4^2{p}_5+21000p_1{p}_2{p}_3{p}_4{p}_5^2+40824p_2{p}_3^2{p}_4{p}_5^2+14700p_2{p}_3{p}_4^2{p}_5^2+ \\ 784p_3^2{p}_4^2{p}_5^2)z^6+(27216p_1{p}_2^2{p}_3^2{p}_4{p}_5+42336p_1{p}_2{p}_3^2{p}_4^2{p}_5+126000p_1{p}_2{p}_3^2{p}_4{p}_5^2+27000p_1{p}_2{p}_3{p}_4^2{p}_5^2+ \\ 123552p_2{p}_3^2{p}_4^2{p}_5^2)z^7+(47628p_1{p}_2^2{p}_3^2{p}_4^2{p}_5+90720p_1{p}_2^2{p}_3^2{p}_4{p}_5^2+424710p_1{p}_2{p}_3^2{p}_4^2{p}_5^2+ \\ 3969p_2^2{p}_3^2{p}_4^2{p}_5^2+43200p_2{p}_3^3{p}_4^2{p}_5^2+98784p_2{p}_3^2{p}_4^3{p}_5^2+26460p_2{p}_3^2{p}_4^2{p}_5^3)z^8+(14112p_1{p}_2^2{p}_3^3{p}_4^2{p}_5+ \\ 434720p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^2+147000p_1{p}_2{p}_3^3{p}_4^2{p}_5^2+17496p_2^2{p}_3^3{p}_4^2{p}_5^2+408240p_1{p}_2{p}_3^2{p}_4^3{p}_5^2+86016p_2{p}_3^3{p}_4^3{p}_5^2+ \\ 117600p_1{p}_2{p}_3^2{p}_4^2{p}_5^3+82320p_2{p}_3^2{p}_4^3{p}_5^3)z^9+(1296p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5^2+291720p_1{p}_2^2{p}_3^3{p}_4^2{p}_5^2+567000p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^2+ \\ 370440p_1{p}_2{p}_3^3{p}_4^3{p}_5^2+37800p_2^2{p}_3^3{p}_4^3{p}_5^2+190512p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^3+387072p_1{p}_2{p}_3^2{p}_4^3{p}_5^3+90720p_2{p}_3^3{p}_4^3{p}_5^3+ \\ 24696p_2{p}_3^2{p}_4^3{p}_5^4)z^{10}+(10584p_1^2{p}_2^2{p}_3^3{p}_4^2{p}_5^2+52920p_1{p}_2^3{p}_3^3{p}_4^2{p}_5^2+960960p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^2+ \\ 127008p_1{p}_2^2{p}_3^3{p}_4^2{p}_5^3+680400p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^3+444528p_1{p}_2{p}_3^3{p}_4^3{p}_5^3+45360p_2^2{p}_3^3{p}_4^3{p}_5^3+126000p_1{p}_2{p}_3^2{p}_4^3{p}_5^4+ \\ 48384p_2{p}_3^3{p}_4^3{p}_5^4)z^{11}+(9408p_1^2{p}_2^3{p}_3^3{p}_4^2{p}_5^2+30618p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5^2+257250p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^2+252000p_1{p}_2^2{p}_3^4{p}_4^3{p}_5^2+ \\ 1605604p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^3+252000p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^4+257250p_1{p}_2{p}_3^3{p}_4^3{p}_5^4+30618p_2^2{p}_3^3{p}_4^3{p}_5^4+9408p_2{p}_3^3{p}_4^4{p}_5^4)z^{12}+ \\ (48384p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^2+126000p_1{p}_2^3{p}_3^4{p}_4^3{p}_5^2+45360p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5^3+444528p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^3+680400p_1{p}_2^2{p}_3^4{p}_4^3{p}_5^3+ \\ 127008p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^3+960960p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^4+52920p_1{p}_2{p}_3^3{p}_4^4{p}_5^4+10584p_2^2{p}_3^3{p}_4^4{p}_5^4)z^{13}+ \\ (24696p_1^2{p}_2^3{p}_3^4{p}_4^3{p}_5^2+90720p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^3+387072p_1{p}_2^3{p}_3^4{p}_4^3{p}_5^3+190512p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^3+37800p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5^4+ \\ 370440p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^4+567000p_1{p}_2^2{p}_3^4{p}_4^3{p}_5^4+291720p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^4+1296p_2^2{p}_3^4{p}_4^4{p}_5^4)z^{14}+ \\ (82320p_1^2{p}_2^3{p}_3^4{p}_4^3{p}_5^3+117600p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^3+86016p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^4+408240p_1{p}_2^3{p}_3^4{p}_4^3{p}_5^4+17496p_1^2{p}_2^2{p}_3^3{p}_4^4{p}_5^4+ \\ 147000p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^4+434720p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^4+14112p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^5)z^{15}+(26460p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^3+ \\ 98784p_1^2{p}_2^3{p}_3^4{p}_4^3{p}_5^4+43200p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^4+3969p_1^2{p}_2^2{p}_3^4{p}_4^4{p}_5^4+424710p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^4+90720p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^4+ \\ 47628p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^5)z^{16}+(123552p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^4+27000p_1{p}_2^3{p}_3^5{p}_4^4{p}_5^4+126000p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^4+ \\ 42336p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^5+27216p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^5)z^{17}+(784p_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^4+14700p_1^2{p}_2^3{p}_3^5{p}_4^4{p}_5^4+40824p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^4+ \\ 21000p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^4+11760p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^5+43008p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^5+2520p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^6)z^{18}+(1176p_1^2{p}_2^4{p}_3^5{p}_4^4{p}_5^4+ \\ 12096p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^4+15120p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^5+9072p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^5+5040p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^6)z^{19}+(1050p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^4+ \\ 5670p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^5+2016p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^6+1890p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^6)z^{20}+(560p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^5+1344p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^6+ \\ 120p_1{p}_2^3{p}_3^5{p}_4^6{p}_5^6)z^{21}+(168p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^6+108p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^6)z^{22}+24p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^6{z}^{23}+p_1^2{p}_2^4{p}_3^6{p}_4^6{p}_5^6{z}^{24} \end{gathered}$$

$H_4=$

$$\begin{gathered} 1+28p_{4}z+(168p_3{p}_4+210p_4{p}_5)z^2+(336p_2{p}_3{p}_4+2240p_3{p}_4{p}_5+700p_4{p}_5^2)z^3+(210p_1{p}_2{p}_3{p}_4+ \\ 5670p_2{p}_3{p}_4{p}_5+3920p_3{p}_4^2{p}_5+9450p_3{p}_4{p}_5^2+1225p_4^2{p}_5^2)z^4+(4032p_1{p}_2{p}_3{p}_4{p}_5+17640p_2{p}_3{p}_4^2{p}_5+ \\ 27216p_2{p}_3{p}_4{p}_5^2+49392p_3{p}_4^2{p}_5^2)z^5+(15876p_1{p}_2{p}_3{p}_4^2{p}_5+11760p_2{p}_3^2{p}_4^2{p}_5+21000p_1{p}_2{p}_3{p}_4{p}_5^2+ \\ 209916p_2{p}_3{p}_4^2{p}_5^2+19600p_3^2{p}_4^2{p}_5^2+74088p_3{p}_4^3{p}_5^2+24500p_3{p}_4^2{p}_5^3)z^6+(18816p_1{p}_2{p}_3^2{p}_4^2{p}_5+ \\ 195120p_1{p}_2{p}_3{p}_4^2{p}_5^2+202176p_2{p}_3^2{p}_4^2{p}_5^2+411600p_2{p}_3{p}_4^3{p}_5^2+87808p_3^2{p}_4^3{p}_5^2+158760p_2{p}_3{p}_4^2{p}_5^3+ \\ 109760p_3{p}_4^3{p}_5^3)z^7+(5292p_1{p}_2^2{p}_3^2{p}_4^2{p}_5+277830p_1{p}_2{p}_3^2{p}_4^2{p}_5^2+35721p_2^2{p}_3^2{p}_4^2{p}_5^2+425250p_1{p}_2{p}_3{p}_4^3{p}_5^2+ \\ 961632p_2{p}_3^2{p}_4^3{p}_5^2+176400p_1{p}_2{p}_3{p}_4^2{p}_5^3+238140p_2{p}_3^2{p}_4^2{p}_5^3+771750p_2{p}_3{p}_4^3{p}_5^3+164640p_3^2{p}_4^3{p}_5^3+ \\ 51450p_3{p}_4^3{p}_5^4)z^8+(109760p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^2+1292760p_1{p}_2{p}_3^2{p}_4^3{p}_5^2+308700p_2^2{p}_3^2{p}_4^3{p}_5^2+537600p_2{p}_3^3{p}_4^3{p}_5^2+ \\ 470400p_1{p}_2{p}_3^2{p}_4^2{p}_5^3+907200p_1{p}_2{p}_3{p}_4^3{p}_5^3+2731680p_2{p}_3^2{p}_4^3{p}_5^3+411600p_2{p}_3{p}_4^3{p}_5^4+137200p_3^2{p}_4^3{p}_5^4)z^9+ \\ (7056p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5^2+666680p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^2+1029000p_1{p}_2{p}_3^3{p}_4^3{p}_5^2+340200p_2^2{p}_3^3{p}_4^3{p}_5^2+190512p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^3+ \\ 4484844p_1{p}_2{p}_3^2{p}_4^3{p}_5^3+833490p_2^2{p}_3^2{p}_4^3{p}_5^3+2268000p_2{p}_3^3{p}_4^3{p}_5^3+576240p_2{p}_3^2{p}_4^4{p}_5^3+525000p_1{p}_2{p}_3{p}_4^3{p}_5^4+ \\ 2163672p_2{p}_3^2{p}_4^3{p}_5^4+38416p_3^2{p}_4^4{p}_5^4)z^{10}+(81648p_1^2{p}_2^2{p}_3^2{p}_4^3{p}_5^2+1132320p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^2+2621472p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^3+ \\ 4939200p_1{p}_2{p}_3^3{p}_4^3{p}_5^3+1632960p_2^2{p}_3^3{p}_4^3{p}_5^3+1524096p_1{p}_2{p}_3^2{p}_4^4{p}_5^3+1128960p_2{p}_3^3{p}_4^4{p}_5^3+ \\ 3591000p_1{p}_2{p}_3^2{p}_4^3{p}_5^4+1000188p_2^2{p}_3^2{p}_4^3{p}_5^4+2721600p_2{p}_3^3{p}_4^3{p}_5^4+1100736p_2{p}_3^2{p}_4^4{p}_5^4)z^{11}+ \\ (166698p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5^2+257250p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^2+272160p_1^2{p}_2^2{p}_3^2{p}_4^3{p}_5^3+6419812p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^3+ \\ 1190700p_1{p}_2^2{p}_3^2{p}_4^4{p}_5^3+3111696p_1{p}_2{p}_3^3{p}_4^4{p}_5^3+882000p_2^2{p}_3^3{p}_4^4{p}_5^3+2666720p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^4+ \\ 6431250p_1{p}_2{p}_3^3{p}_4^3{p}_5^4+2480058p_2^2{p}_3^3{p}_4^3{p}_5^4+2500470p_1{p}_2{p}_3^2{p}_4^4{p}_5^4+540225p_2^2{p}_3^2{p}_4^4{p}_5^4+ \\ 3358656p_2{p}_3^3{p}_4^4{p}_5^4+144060p_2{p}_3^2{p}_4^4{p}_5^5)z^{12}+(65856p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^2+987840p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5^3+ \\ 1778112p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^3+5551504p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^3+403200p_1^2{p}_2^2{p}_3^2{p}_4^3{p}_5^4+10190880p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^4+ \\ 2744000p_1{p}_2^2{p}_3^2{p}_4^4{p}_5^4+9560880p_1{p}_2{p}_3^3{p}_4^4{p}_5^4+4000752p_2^2{p}_3^3{p}_4^4{p}_5^4+1053696p_2{p}_3^3{p}_4^5{p}_5^4+ \\ 470400p_1{p}_2{p}_3^2{p}_4^4{p}_5^5+635040p_2{p}_3^3{p}_4^4{p}_5^5)z^{13}+(493920p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^3+714420p_1^2{p}_2^2{p}_3^3{p}_4^4{p}_5^3+ \\ 2160900p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^3+529200p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^3+1852200p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5^4+3333960p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^4+ \\ 291600p_1^2{p}_2^2{p}_3^2{p}_4^4{p}_5^4+21364200p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^4+291600p_2^2{p}_3^4{p}_4^4{p}_5^4+3333960p_1{p}_2{p}_3^3{p}_4^5{p}_5^4+ \\ 1852200p_2^2{p}_3^3{p}_4^5{p}_5^4+529200p_1{p}_2^2{p}_3^2{p}_4^4{p}_5^5+2160900p_1{p}_2{p}_3^3{p}_4^4{p}_5^5+714420p_2^2{p}_3^3{p}_4^4{p}_5^5+493920p_2{p}_3^3{p}_4^5{p}_5^5)z^{14}+ \\ (635040p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^3+470400p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^3+1053696p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^4+4000752p_1^2{p}_2^2{p}_3^3{p}_4^4{p}_5^4+ \\ 9560880p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^4+2744000p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^4+10190880p_1{p}_2^2{p}_3^3{p}_4^5{p}_5^4+403200p_2^2{p}_3^4{p}_4^5{p}_5^4+ \\ 5551504p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^5+1778112p_1{p}_2{p}_3^3{p}_4^5{p}_5^5+987840p_2^2{p}_3^3{p}_4^5{p}_5^5+65856p_2{p}_3^3{p}_4^5{p}_5^6)z^{15}+ \\ (144060p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^3+3358656p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^4+540225p_1^2{p}_2^2{p}_3^4{p}_4^4{p}_5^4+2500470p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^4+ \\ 2480058p_1^2{p}_2^2{p}_3^3{p}_4^5{p}_5^4+6431250p_1{p}_2^3{p}_3^3{p}_4^5{p}_5^4+2666720p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^4+882000p_1^2{p}_2^2{p}_3^3{p}_4^4{p}_5^5+ \\ 3111696p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^5+1190700p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^5+6419812p_1{p}_2^2{p}_3^3{p}_4^5{p}_5^5+272160p_2^2{p}_3^4{p}_4^5{p}_5^5+ \\ 257250p_1{p}_2{p}_3^3{p}_4^5{p}_5^6+166698p_2^2{p}_3^3{p}_4^5{p}_5^6)z^{16}+(1100736p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^4+2721600p_1^2{p}_2^3{p}_3^3{p}_4^5{p}_5^4+ \\ 1000188p_1^2{p}_2^2{p}_3^4{p}_4^5{p}_5^4+3591000p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^4+1128960p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^5+1524096p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^5+ \\ 1632960p_1^2{p}_2^2{p}_3^3{p}_4^5{p}_5^5+4939200p_1{p}_2^3{p}_3^3{p}_4^5{p}_5^5+2621472p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^5+1132320p_1{p}_2^2{p}_3^3{p}_4^5{p}_5^6+ \\ 81648p_2^2{p}_3^4{p}_4^5{p}_5^6)z^{17}+(38416p_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^4+2163672p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^4+525000p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^4+ \\ 576240p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^5+2268000p_1^2{p}_2^3{p}_3^3{p}_4^5{p}_5^5+833490p_1^2{p}_2^2{p}_3^4{p}_4^5{p}_5^5+4484844p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^5+ \\ 190512p_1{p}_2^2{p}_3^4{p}_4^6{p}_5^5+340200p_1^2{p}_2^2{p}_3^3{p}_4^5{p}_5^6+1029000p_1{p}_2^3{p}_3^3{p}_4^5{p}_5^6+666680p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^6+ \\ 7056p_2^2{p}_3^4{p}_4^6{p}_5^6)z^{18}+(137200p_1^2{p}_2^4{p}_3^4{p}_4^5{p}_5^4+411600p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^4+2731680p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^5+ \\ 907200p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^5+470400p_1{p}_2^3{p}_3^4{p}_4^6{p}_5^5+537600p_1^2{p}_2^3{p}_3^3{p}_4^5{p}_5^6+308700p_1^2{p}_2^2{p}_3^4{p}_4^5{p}_5^6+ \\ 1292760p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^6+109760p_1{p}_2^2{p}_3^4{p}_4^6{p}_5^6)z^{19}+(51450p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^4+164640p_1^2{p}_2^4{p}_3^4{p}_4^5{p}_5^5+ \\ 771750p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^5+238140p_1^2{p}_2^3{p}_3^4{p}_4^6{p}_5^5+176400p_1{p}_2^3{p}_3^5{p}_4^6{p}_5^5+961632p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^6+ \\ 425250p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^6+35721p_1^2{p}_2^2{p}_3^4{p}_4^6{p}_5^6+277830p_1{p}_2^3{p}_3^4{p}_4^6{p}_5^6+5292p_1{p}_2^2{p}_3^4{p}_4^6{p}_5^7)z^{20}+ \\ (109760p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^5+158760p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^5+87808p_1^2{p}_2^4{p}_3^4{p}_4^5{p}_5^6+411600p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^6+ \\ 202176p_1^2{p}_2^3{p}_3^4{p}_4^6{p}_5^6+195120p_1{p}_2^3{p}_3^5{p}_4^6{p}_5^6+18816p_1{p}_2^3{p}_3^4{p}_4^6{p}_5^7)z^{21}+(24500p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^5+ \\ 74088p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^6+19600p_1^2{p}_2^4{p}_3^4{p}_4^6{p}_5^6+209916p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^6+21000p_1{p}_2^3{p}_3^5{p}_4^7{p}_5^6+11760p_1^2{p}_2^3{p}_3^4{p}_4^6{p}_5^7+ \\ 15876p_1{p}_2^3{p}_3^5{p}_4^6{p}_5^7)z^{22}+(49392p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^6+27216p_1^2{p}_2^3{p}_3^5{p}_4^7{p}_5^6+17640p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^7+ \\ 4032p_1{p}_2^3{p}_3^5{p}_4^7{p}_5^7)z^{23}+(1225p_1^2{p}_2^4{p}_3^6{p}_4^6{p}_5^6+9450p_1^2{p}_2^4{p}_3^5{p}_4^7{p}_5^6+3920p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^7+5670p_1^2{p}_2^3{p}_3^5{p}_4^7{p}_5^7+ \\ 210p_1{p}_2^3{p}_3^5{p}_4^7{p}_5^8)z^{24}+(700p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^6+2240p_1^2{p}_2^4{p}_3^5{p}_4^7{p}_5^7+336p_1^2{p}_2^3{p}_3^5{p}_4^7{p}_5^8)z^{25}+(210p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^7+ \\ 168p_1^2{p}_2^4{p}_3^5{p}_4^7{p}_5^8)z^{26}+28p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^8{z}^{27}+p_1^2{p}_2^4{p}_3^6{p}_4^8{p}_5^8{z}^{28} \end{gathered}$$

$H_5=$

$$\begin{gathered} 1+15p_{5}z+105p_4{p}_5{z}^2+(280p_3{p}_4{p}_5+175p_4{p}_5^2)z^3+(315p_2{p}_3{p}_4{p}_5+1050p_3{p}_4{p}_5^2)z^4+ \\ (126p_1{p}_2{p}_3{p}_4{p}_5+1701p_2{p}_3{p}_4{p}_5^2+1176p_3{p}_4^2{p}_5^2)z^5+(840p_1{p}_2{p}_3{p}_4{p}_5^2+3675p_2{p}_3{p}_4^2{p}_5^2+ \\ 490p_3{p}_4^2{p}_5^3)z^6+(2430p_1{p}_2{p}_3{p}_4^2{p}_5^2+1800p_2{p}_3^2{p}_4^2{p}_5^2+2205p_2{p}_3{p}_4^2{p}_5^3)z^7+(2205p_1{p}_2{p}_3^2{p}_4^2{p}_5^2+ \\ 1800p_1{p}_2{p}_3{p}_4^2{p}_5^3+2430p_2{p}_3^2{p}_4^2{p}_5^3)z^8+(490p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^2+3675p_1{p}_2{p}_3^2{p}_4^2{p}_5^3+840p_2{p}_3^2{p}_4^3{p}_5^3)z^9+ \\ (1176p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^3+1701p_1{p}_2{p}_3^2{p}_4^3{p}_5^3+126p_2{p}_3^2{p}_4^3{p}_5^4)z^{10}+(1050p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^3+315p_1{p}_2{p}_3^2{p}_4^3{p}_5^4)z^{11}+ \\ (175p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^3+280p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^4)z^{12}+105p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^4{z}^{13}+15p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^4{z}^{14}+p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^5{z}^{15} \end{gathered}$$

$C_5$-case. For the Lie algebra $C_5\cong sp\left(5\right)$, we find

$$\begin{array}{cc}{H}_1=\hfill & 1+9p_{1}z+36p_1{p}_2{z}^2+84p_1{p}_2{p}_3{z}^3+126p_1{p}_2{p}_3{p}_4{z}^4+126p_1{p}_2{p}_3{p}_4{p}_5{z}^5+84p_1{p}_2{p}_3{p}_4^2{p}_5{z}^6+\hfill \\ & 36p_1{p}_2{p}_3^2{p}_4^2{p}_5{z}^7+9p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8+p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^9\hfill \\ H_2=\hfill & 1+16p_{2}z+(36p_1{p}_2+84p_2{p}_3)z^2+(336p_1{p}_2{p}_3+224p_2{p}_3{p}_4)z^3+(336p_1{p}_2^2{p}_3+1134p_1{p}_2{p}_3{p}_4+\hfill \\ & 350p_2{p}_3{p}_4{p}_5)z^4+(2016p_1{p}_2^2{p}_3{p}_4+2016p_1{p}_2{p}_3{p}_4{p}_5+336p_2{p}_3{p}_4^2{p}_5)z^5+(1176p_1{p}_2^2{p}_3^2{p}_4+\hfill \\ & 4536p_1{p}_2^2{p}_3{p}_4{p}_5+2100p_1{p}_2{p}_3{p}_4^2{p}_5+196p_2{p}_3^2{p}_4^2{p}_5)z^6+(4704p_1{p}_2^2{p}_3^2{p}_4{p}_5+5376p_1{p}_2^2{p}_3{p}_4^2{p}_5+\hfill \\ & 1296p_1{p}_2{p}_3^2{p}_4^2{p}_5+64p_2^2{p}_3^2{p}_4^2{p}_5)z^7+12870p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8+(64p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5+1296p_1{p}_2^3{p}_3^2{p}_4^2{p}_5+\hfill \\ & 5376p_1{p}_2^2{p}_3^3{p}_4^2{p}_5+4704p_1{p}_2^2{p}_3^2{p}_4^3{p}_5)z^9+(196p_1^2{p}_2^3{p}_3^2{p}_4^2{p}_5+2100p_1{p}_2^3{p}_3^3{p}_4^2{p}_5+4536p_1{p}_2^2{p}_3^3{p}_4^3{p}_5+\hfill \\ & 1176p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^2)z^{10}+(336p_1^2{p}_2^3{p}_3^3{p}_4^2{p}_5+2016p_1{p}_2^3{p}_3^3{p}_4^3{p}_5+2016p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^2)z^{11}+(350p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5+\hfill \\ & 1134p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^2+336p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^2)z^{12}+(224p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^2+336p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^2)z^{13}+(84p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^2+\hfill \\ & 36p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^2)z^{14}+16p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^2{z}^{15}+p_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^2{z}^{16}\hfill \\ H_3=\hfill & 1+21p_{3}z+(84p_2{p}_3+126p_3{p}_4)z^2+(84p_1{p}_2{p}_3+896p_2{p}_3{p}_4+350p_3{p}_4{p}_5)z^3+(1134p_1{p}_2{p}_3{p}_4+\hfill \\ & 1176p_2{p}_3^2{p}_4+3150p_2{p}_3{p}_4{p}_5+525p_3{p}_4^2{p}_5)z^4+(2646p_1{p}_2{p}_3^2{p}_4+4536p_1{p}_2{p}_3{p}_4{p}_5+\hfill \\ & 7350p_2{p}_3^2{p}_4{p}_5+5376p_2{p}_3{p}_4^2{p}_5+441p_3^2{p}_4^2{p}_5)z^5+(1176p_1{p}_2^2{p}_3^2{p}_4+18816p_1{p}_2{p}_3^2{p}_4{p}_5+\hfill \\ & 8400p_1{p}_2{p}_3{p}_4^2{p}_5+25872p_2{p}_3^2{p}_4^2{p}_5)z^6+(10584p_1{p}_2^2{p}_3^2{p}_4{p}_5+68112p_1{p}_2{p}_3^2{p}_4^2{p}_5+2304p_2^2{p}_3^2{p}_4^2{p}_5+\hfill \\ & 16464p_2{p}_3^3{p}_4^2{p}_5+18816p_2{p}_3^2{p}_4^3{p}_5)z^7+(48510p_1{p}_2^2{p}_3^2{p}_4^2{p}_5+48384p_1{p}_2{p}_3^3{p}_4^2{p}_5+8400p_2^2{p}_3^3{p}_4^2{p}_5+\hfill \\ & 66150p_1{p}_2{p}_3^2{p}_4^3{p}_5+24696p_2{p}_3^3{p}_4^3{p}_5+7350p_2{p}_3^2{p}_4^3{p}_5^2)z^8+(784p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5+65142p_1{p}_2^2{p}_3^3{p}_4^2{p}_5+\hfill \\ & 75264p_1{p}_2^2{p}_3^2{p}_4^3{p}_5+91854p_1{p}_2{p}_3^3{p}_4^3{p}_5+14336p_2^2{p}_3^3{p}_4^3{p}_5+29400p_1{p}_2{p}_3^2{p}_4^3{p}_5^2+17150p_2{p}_3^3{p}_4^3{p}_5^2)z^9+\hfill \\ & (5376p_1^2{p}_2^2{p}_3^3{p}_4^2{p}_5+18900p_1{p}_2^3{p}_3^3{p}_4^2{p}_5+196812p_1{p}_2^2{p}_3^3{p}_4^3{p}_5+42336p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^2+72576p_1{p}_2{p}_3^3{p}_4^3{p}_5^2+\hfill \\ & 12600p_2^2{p}_3^3{p}_4^3{p}_5^2+4116p_2{p}_3^3{p}_4^4{p}_5^2)z^{10}+(4116p_1^2{p}_2^3{p}_3^3{p}_4^2{p}_5+12600p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5+72576p_1{p}_2^3{p}_3^3{p}_4^3{p}_5+\hfill \\ & 42336p_1{p}_2^2{p}_3^4{p}_4^3{p}_5+196812p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^2+18900p_1{p}_2{p}_3^3{p}_4^4{p}_5^2+5376p_2^2{p}_3^3{p}_4^4{p}_5^2)z^{11}+(17150p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5+\hfill \\ & 29400p_1{p}_2^3{p}_3^4{p}_4^3{p}_5+14336p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5^2+91854p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^2+75264p_1{p}_2^2{p}_3^4{p}_4^3{p}_5^2+65142p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^2+\hfill \\ & 784p_2^2{p}_3^4{p}_4^4{p}_5^2)z^{12}+(7350p_1^2{p}_2^3{p}_3^4{p}_4^3{p}_5+24696p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^2+66150p_1{p}_2^3{p}_3^4{p}_4^3{p}_5^2+8400p_1^2{p}_2^2{p}_3^3{p}_4^4{p}_5^2+\hfill \\ & 48384p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^2+48510p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^2)z^{13}+(18816p_1^2{p}_2^3{p}_3^4{p}_4^3{p}_5^2+16464p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^2+\hfill \\ & 2304p_1^2{p}_2^2{p}_3^4{p}_4^4{p}_5^2+68112p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^2+10584p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^2)z^{14}+(25872p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^2+\hfill \\ & 8400p_1{p}_2^3{p}_3^5{p}_4^4{p}_5^2+18816p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^2+1176p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^3)z^{15}+(441p_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^2+5376p_1^2{p}_2^3{p}_3^5{p}_4^4{p}_5^2+\hfill \\ & 7350p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^2+4536p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^2+2646p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^3)z^{16}+(525p_1^2{p}_2^4{p}_3^5{p}_4^4{p}_5^2+3150p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^2+\hfill \\ & 1176p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^3+1134p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^3)z^{17}+(350p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^2+896p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^3+84p_1{p}_2^3{p}_3^5{p}_4^6{p}_5^3)z^{18}+\hfill \\ & (126p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^3+84p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^3)z^{19}+21p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^3{z}^{20}+p_1^2{p}_2^4{p}_3^6{p}_4^6{p}_5^3{z}^{21}\hfill \\ H_4=\hfill & 1+24p_{4}z+(126p_3{p}_4+150p_4{p}_5)z^2+(224p_2{p}_3{p}_4+1400p_3{p}_4{p}_5+400p_4^2{p}_5)z^3+(126p_1{p}_2{p}_3{p}_4+\hfill \\ & 3150p_2{p}_3{p}_4{p}_5+7350p_3{p}_4^2{p}_5)z^4+(2016p_1{p}_2{p}_3{p}_4{p}_5+20832p_2{p}_3{p}_4^2{p}_5+7056p_3^2{p}_4^2{p}_5+\hfill \\ & 12600p_3{p}_4^3{p}_5)z^5+(15288p_1{p}_2{p}_3{p}_4^2{p}_5+29400p_2{p}_3^2{p}_4^2{p}_5+57344p_2{p}_3{p}_4^3{p}_5+23814p_3^2{p}_4^3{p}_5+\hfill \\ & 8750p_3{p}_4^3{p}_5^2)z^6+(22752p_1{p}_2{p}_3^2{p}_4^2{p}_5+14400p_2^2{p}_3^2{p}_4^2{p}_5+50400p_1{p}_2{p}_3{p}_4^3{p}_5+178752p_2{p}_3^2{p}_4^3{p}_5+\hfill \\ & 50400p_2{p}_3{p}_4^3{p}_5^2+29400p_3^2{p}_4^3{p}_5^2)z^7+(16758p_1{p}_2^2{p}_3^2{p}_4^2{p}_5+180900p_1{p}_2{p}_3^2{p}_4^3{p}_5+98304p_2^2{p}_3^2{p}_4^3{p}_5+\hfill \\ & 98784p_2{p}_3^3{p}_4^3{p}_5+50400p_1{p}_2{p}_3{p}_4^3{p}_5^2+279300p_2{p}_3^2{p}_4^3{p}_5^2+11025p_3^2{p}_4^4{p}_5^2)z^8+(3136p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5+\hfill \\ & 143472p_1{p}_2^2{p}_3^2{p}_4^3{p}_5+163296p_1{p}_2{p}_3^3{p}_4^3{p}_5+89600p_2^2{p}_3^3{p}_4^3{p}_5+321600p_1{p}_2{p}_3^2{p}_4^3{p}_5^2+194400p_2^2{p}_3^2{p}_4^3{p}_5^2+\hfill \\ & 274400p_2{p}_3^3{p}_4^3{p}_5^2+117600p_2{p}_3^2{p}_4^4{p}_5^2)z^9+(29400p_1^2{p}_2^2{p}_3^2{p}_4^3{p}_5+233100p_1{p}_2^2{p}_3^3{p}_4^3{p}_5+322812p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^2+\hfill \\ & 516096p_1{p}_2{p}_3^3{p}_4^3{p}_5^2+315000p_2^2{p}_3^3{p}_4^3{p}_5^2+142200p_1{p}_2{p}_3^2{p}_4^4{p}_5^2+147456p_2^2{p}_3^2{p}_4^4{p}_5^2+255192p_2{p}_3^3{p}_4^4{p}_5^2)z^{10}+\hfill \\ & (50400p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5+50400p_1{p}_2^3{p}_3^3{p}_4^3{p}_5+75264p_1^2{p}_2^2{p}_3^2{p}_4^3{p}_5^2+932400p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^2+268128p_1{p}_2^2{p}_3^2{p}_4^4{p}_5^2+\hfill \\ & 550368p_1{p}_2{p}_3^3{p}_4^4{p}_5^2+470400p_2^2{p}_3^3{p}_4^4{p}_5^2+98784p_2{p}_3^3{p}_4^5{p}_5^2)z^{11}+(17150p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5+229376p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5^2+\hfill \\ & 255150p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^2+78400p_1^2{p}_2^2{p}_3^2{p}_4^4{p}_5^2+1544004p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^2+78400p_2^2{p}_3^4{p}_4^4{p}_5^2+255150p_1{p}_2{p}_3^3{p}_4^5{p}_5^2+\hfill \\ & 229376p_2^2{p}_3^3{p}_4^5{p}_5^2+17150p_2{p}_3^3{p}_4^5{p}_5^3)z^{12}+(98784p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^2+470400p_1^2{p}_2^2{p}_3^3{p}_4^4{p}_5^2+550368p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^2+\hfill \\ & 268128p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^2+932400p_1{p}_2^2{p}_3^3{p}_4^5{p}_5^2+75264p_2^2{p}_3^4{p}_4^5{p}_5^2+50400p_1{p}_2{p}_3^3{p}_4^5{p}_5^3+50400p_2^2{p}_3^3{p}_4^5{p}_5^3)z^{13}+\hfill \\ & (255192p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^2+147456p_1^2{p}_2^2{p}_3^4{p}_4^4{p}_5^2+142200p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^2+315000p_1^2{p}_2^2{p}_3^3{p}_4^5{p}_5^2+\hfill \\ & 516096p_1{p}_2^3{p}_3^3{p}_4^5{p}_5^2+322812p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^2+233100p_1{p}_2^2{p}_3^3{p}_4^5{p}_5^3+29400p_2^2{p}_3^4{p}_4^5{p}_5^3)z^{14}+\hfill \\ & (117600p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^2+274400p_1^2{p}_2^3{p}_3^3{p}_4^5{p}_5^2+194400p_1^2{p}_2^2{p}_3^4{p}_4^5{p}_5^2+321600p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^2+\hfill \\ & 89600p_1^2{p}_2^2{p}_3^3{p}_4^5{p}_5^3+163296p_1{p}_2^3{p}_3^3{p}_4^5{p}_5^3+143472p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^3+3136p_2^2{p}_3^4{p}_4^6{p}_5^3)z^{15}+(11025p_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^2+\hfill \\ & 279300p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^2+50400p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^2+98784p_1^2{p}_2^3{p}_3^3{p}_4^5{p}_5^3+98304p_1^2{p}_2^2{p}_3^4{p}_4^5{p}_5^3+180900p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^3+\hfill \\ & 16758p_1{p}_2^2{p}_3^4{p}_4^6{p}_5^3)z^{16}+(29400p_1^2{p}_2^4{p}_3^4{p}_4^5{p}_5^2+50400p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^2+178752p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^3+\hfill \\ & 50400p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^3+14400p_1^2{p}_2^2{p}_3^4{p}_4^6{p}_5^3+22752p_1{p}_2^3{p}_3^4{p}_4^6{p}_5^3)z^{17}+(8750p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^2+\hfill \\ & 23814p_1^2{p}_2^4{p}_3^4{p}_4^5{p}_5^3+57344p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^3+29400p_1^2{p}_2^3{p}_3^4{p}_4^6{p}_5^3+15288p_1{p}_2^3{p}_3^5{p}_4^6{p}_5^3)z^{18}+\hfill \\ & (12600p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^3+7056p_1^2{p}_2^4{p}_3^4{p}_4^6{p}_5^3+20832p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^3+2016p_1{p}_2^3{p}_3^5{p}_4^7{p}_5^3)z^{19}+(7350p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^3+\hfill \\ & 3150p_1^2{p}_2^3{p}_3^5{p}_4^7{p}_5^3+126p_1{p}_2^3{p}_3^5{p}_4^7{p}_5^4)z^{20}+(400p_1^2{p}_2^4{p}_3^6{p}_4^6{p}_5^3+1400p_1^2{p}_2^4{p}_3^5{p}_4^7{p}_5^3+224p_1^2{p}_2^3{p}_3^5{p}_4^7{p}_5^4)z^{21}+\hfill \\ & (150p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^3+126p_1^2{p}_2^4{p}_3^5{p}_4^7{p}_5^4)z^{22}+24p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^4{z}^{23}+p_1^2{p}_2^4{p}_3^6{p}_4^8{p}_5^4{z}^{24}\hfill \\ H_5=\hfill & 1+25p_{5}z+300p_4{p}_5{z}^2+(700p_3{p}_4{p}_5+1600p_4^2{p}_5)z^3+(700p_2{p}_3{p}_4{p}_5+9450p_3{p}_4^2{p}_5+\hfill \\ & 2500p_4^2{p}_5^2)z^4+(252p_1{p}_2{p}_3{p}_4{p}_5+10752p_2{p}_3{p}_4^2{p}_5+15876p_3^2{p}_4^2{p}_5+26250p_3{p}_4^2{p}_5^2)z^5+\hfill \\ & (4200p_1{p}_2{p}_3{p}_4^2{p}_5+39200p_2{p}_3^2{p}_4^2{p}_5+37800p_2{p}_3{p}_4^2{p}_5^2+78400p_3^2{p}_4^2{p}_5^2+17500p_3{p}_4^3{p}_5^2)z^6+\hfill \\ & (16200p_1{p}_2{p}_3^2{p}_4^2{p}_5+25600p_2^2{p}_3^2{p}_4^2{p}_5+16800p_1{p}_2{p}_3{p}_4^2{p}_5^2+245000p_2{p}_3^2{p}_4^2{p}_5^2+44800p_2{p}_3{p}_4^3{p}_5^2+\hfill \\ & 132300p_3^2{p}_4^3{p}_5^2)z^7+(22050p_1{p}_2^2{p}_3^2{p}_4^2{p}_5+115200p_1{p}_2{p}_3^2{p}_4^2{p}_5^2+202500p_2^2{p}_3^2{p}_4^2{p}_5^2+25200p_1{p}_2{p}_3{p}_4^3{p}_5^2+\hfill \\ & 617400p_2{p}_3^2{p}_4^3{p}_5^2+99225p_3^2{p}_4^4{p}_5^2)z^8+(4900p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5+198450p_1{p}_2^2{p}_3^2{p}_4^2{p}_5^2+353400p_1{p}_2{p}_3^2{p}_4^3{p}_5^2+\hfill \\ & 691200p_2^2{p}_3^2{p}_4^3{p}_5^2+137200p_2{p}_3^3{p}_4^3{p}_5^2+627200p_2{p}_3^2{p}_4^4{p}_5^2+30625p_3^2{p}_4^4{p}_5^3)z^9+(50176p_1^2{p}_2^2{p}_3^2{p}_4^2{p}_5^2+\hfill \\ & 798504p_1{p}_2^2{p}_3^2{p}_4^3{p}_5^2+145152p_1{p}_2{p}_3^3{p}_4^3{p}_5^2+280000p_2^2{p}_3^3{p}_4^3{p}_5^2+405000p_1{p}_2{p}_3^2{p}_4^4{p}_5^2+1048576p_2^2{p}_3^2{p}_4^4{p}_5^2+\hfill \\ & 296352p_2{p}_3^3{p}_4^4{p}_5^2+245000p_2{p}_3^2{p}_4^4{p}_5^3)z^{10}+(235200p_1^2{p}_2^2{p}_3^2{p}_4^3{p}_5^2+491400p_1{p}_2^2{p}_3^3{p}_4^3{p}_5^2+\hfill \\ & 1411200p_1{p}_2^2{p}_3^2{p}_4^4{p}_5^2+340200p_1{p}_2{p}_3^3{p}_4^4{p}_5^2+1075200p_2^2{p}_3^3{p}_4^4{p}_5^2+180000p_1{p}_2{p}_3^2{p}_4^4{p}_5^3+\hfill \\ & 518400p_2^2{p}_3^2{p}_4^4{p}_5^3+205800p_2{p}_3^3{p}_4^4{p}_5^3)z^{11}+(179200p_1^2{p}_2^2{p}_3^3{p}_4^3{p}_5^2+56700p_1{p}_2^3{p}_3^3{p}_4^3{p}_5^2+\hfill \\ & 490000p_1^2{p}_2^2{p}_3^2{p}_4^4{p}_5^2+2118900p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^2+313600p_2^2{p}_3^4{p}_4^4{p}_5^2+793800p_1{p}_2^2{p}_3^2{p}_4^4{p}_5^3+\hfill \\ & 268800p_1{p}_2{p}_3^3{p}_4^4{p}_5^3+945000p_2^2{p}_3^3{p}_4^4{p}_5^3+34300p_2{p}_3^3{p}_4^5{p}_5^3)z^{12}+(34300p_1^2{p}_2^3{p}_3^3{p}_4^3{p}_5^2+945000p_1^2{p}_2^2{p}_3^3{p}_4^4{p}_5^2+\hfill \\ & 268800p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^2+793800p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^2+313600p_1^2{p}_2^2{p}_3^2{p}_4^4{p}_5^3+2118900p_1{p}_2^2{p}_3^3{p}_4^4{p}_5^3+\hfill \\ & 490000p_2^2{p}_3^4{p}_4^4{p}_5^3+56700p_1{p}_2{p}_3^3{p}_4^5{p}_5^3+179200p_2^2{p}_3^3{p}_4^5{p}_5^3)z^{13}+(205800p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^2+\hfill \\ & 518400p_1^2{p}_2^2{p}_3^4{p}_4^4{p}_5^2+180000p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^2+1075200p_1^2{p}_2^2{p}_3^3{p}_4^4{p}_5^3+340200p_1{p}_2^3{p}_3^3{p}_4^4{p}_5^3+\hfill \\ & 1411200p_1{p}_2^2{p}_3^4{p}_4^4{p}_5^3+491400p_1{p}_2^2{p}_3^3{p}_4^5{p}_5^3+235200p_2^2{p}_3^4{p}_4^5{p}_5^3)z^{14}+(245000p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^2+\hfill \\ & 296352p_1^2{p}_2^3{p}_3^3{p}_4^4{p}_5^3+1048576p_1^2{p}_2^2{p}_3^4{p}_4^4{p}_5^3+405000p_1{p}_2^3{p}_3^4{p}_4^4{p}_5^3+280000p_1^2{p}_2^2{p}_3^3{p}_4^5{p}_5^3+\hfill \\ & 145152p_1{p}_2^3{p}_3^3{p}_4^5{p}_5^3+798504p_1{p}_2^2{p}_3^4{p}_4^5{p}_5^3+50176p_2^2{p}_3^4{p}_4^6{p}_5^3)z^{15}+(30625p_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^2+\hfill \\ & 627200p_1^2{p}_2^3{p}_3^4{p}_4^4{p}_5^3+137200p_1^2{p}_2^3{p}_3^3{p}_4^5{p}_5^3+691200p_1^2{p}_2^2{p}_3^4{p}_4^5{p}_5^3+353400p_1{p}_2^3{p}_3^4{p}_4^5{p}_5^3+\hfill \\ & 198450p_1{p}_2^2{p}_3^4{p}_4^6{p}_5^3+4900p_2^2{p}_3^4{p}_4^6{p}_5^4)z^{16}+(99225p_1^2{p}_2^4{p}_3^4{p}_4^4{p}_5^3+617400p_1^2{p}_2^3{p}_3^4{p}_4^5{p}_5^3+\hfill \\ & 25200p_1{p}_2^3{p}_3^5{p}_4^5{p}_5^3+202500p_1^2{p}_2^2{p}_3^4{p}_4^6{p}_5^3+115200p_1{p}_2^3{p}_3^4{p}_4^6{p}_5^3+22050p_1{p}_2^2{p}_3^4{p}_4^6{p}_5^4)z^{17}+\hfill \\ & (132300p_1^2{p}_2^4{p}_3^4{p}_4^5{p}_5^3+44800p_1^2{p}_2^3{p}_3^5{p}_4^5{p}_5^3+245000p_1^2{p}_2^3{p}_3^4{p}_4^6{p}_5^3+16800p_1{p}_2^3{p}_3^5{p}_4^6{p}_5^3+25600p_1^2{p}_2^2{p}_3^4{p}_4^6{p}_5^4+\hfill \\ & 16200p_1{p}_2^3{p}_3^4{p}_4^6{p}_5^4)z^{18}+(17500p_1^2{p}_2^4{p}_3^5{p}_4^5{p}_5^3+78400p_1^2{p}_2^4{p}_3^4{p}_4^6{p}_5^3+37800p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^3+\hfill \\ & 39200p_1^2{p}_2^3{p}_3^4{p}_4^6{p}_5^4+4200p_1{p}_2^3{p}_3^5{p}_4^6{p}_5^4)z^{19}+(26250p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^3+15876p_1^2{p}_2^4{p}_3^4{p}_4^6{p}_5^4+\hfill \\ & 10752p_1^2{p}_2^3{p}_3^5{p}_4^6{p}_5^4+252p_1{p}_2^3{p}_3^5{p}_4^7{p}_5^4)z^{20}+(2500p_1^2{p}_2^4{p}_3^6{p}_4^6{p}_5^3+9450p_1^2{p}_2^4{p}_3^5{p}_4^6{p}_5^4+700p_1^2{p}_2^3{p}_3^5{p}_4^7{p}_5^4)z^{21}+\hfill \\ & (1600p_1^2{p}_2^4{p}_3^6{p}_4^6{p}_5^4+700p_1^2{p}_2^4{p}_3^5{p}_4^7{p}_5^4)z^{22}+300p_1^2{p}_2^4{p}_3^6{p}_4^7{p}_5^4{z}^{23}+25p_1^2{p}_2^4{p}_3^6{p}_4^8{p}_5^4{z}^{24}+p_1^2{p}_2^4{p}_3^6{p}_4^8{p}_5^5{z}^{25}\hfill \end{array}$$

$D_5$-case. For the Lie algebra $D_5\cong so\left(10\right)$, we find the following polynomials

$$\begin{array}{cc}{H}_1=\hfill & 1+8p_{1}z+28p_1{p}_2{z}^2+56p_1{p}_2{p}_3{z}^3+(35p_1{p}_2{p}_3{p}_4+35p_1{p}_2{p}_3{p}_5)z^4+56p_1{p}_2{p}_3{p}_4{p}_5{z}^5+\hfill \\ & 28p_1{p}_2{p}_3^2{p}_4{p}_5{z}^6+8p_1{p}_2^2{p}_3^2{p}_4{p}_5{z}^7+p_1^2{p}_2^2{p}_3^2{p}_4{p}_5{z}^8\hfill \\ H_2=\hfill & 1+14p_{2}z+(28p_1{p}_2+63p_2{p}_3)z^2+(224p_1{p}_2{p}_3+70p_2{p}_3{p}_4+70p_2{p}_3{p}_5)z^3+(196p_1{p}_2^2{p}_3+\hfill \\ & 315p_1{p}_2{p}_3{p}_4+315p_1{p}_2{p}_3{p}_5+175p_2{p}_3{p}_4{p}_5)z^4+(490p_1{p}_2^2{p}_3{p}_4+490p_1{p}_2^2{p}_3{p}_5+896p_1{p}_2{p}_3{p}_4{p}_5+\hfill \\ & 126p_2{p}_3^2{p}_4{p}_5)z^5+(245p_1{p}_2^2{p}_3^2{p}_4+245p_1{p}_2^2{p}_3^2{p}_5+1764p_1{p}_2^2{p}_3{p}_4{p}_5+700p_1{p}_2{p}_3^2{p}_4{p}_5+\hfill \\ & 49p_2^2{p}_3^2{p}_4{p}_5)z^6+3432p_1{p}_2^2{p}_3^2{p}_4{p}_5{z}^7+(49p_1^2{p}_2^2{p}_3^2{p}_4{p}_5+700p_1{p}_2^3{p}_3^2{p}_4{p}_5+1764p_1{p}_2^2{p}_3^3{p}_4{p}_5+\hfill \\ & 245p_1{p}_2^2{p}_3^2{p}_4^2{p}_5+245p_1{p}_2^2{p}_3^2{p}_4{p}_5^2)z^8+(126p_1^2{p}_2^3{p}_3^2{p}_4{p}_5+896p_1{p}_2^3{p}_3^3{p}_4{p}_5+490p_1{p}_2^2{p}_3^3{p}_4^2{p}_5+\hfill \\ & 490p_1{p}_2^2{p}_3^3{p}_4{p}_5^2)z^9+(175p_1^2{p}_2^3{p}_3^3{p}_4{p}_5+315p_1{p}_2^3{p}_3^3{p}_4^2{p}_5+315p_1{p}_2^3{p}_3^3{p}_4{p}_5^2+196p_1{p}_2^2{p}_3^3{p}_4^2{p}_5^2)z^{10}+\hfill \\ & (70p_1^2{p}_2^3{p}_3^3{p}_4^2{p}_5+70p_1^2{p}_2^3{p}_3^3{p}_4{p}_5^2+224p_1{p}_2^3{p}_3^3{p}_4^2{p}_5^2)z^{11}+(63p_1^2{p}_2^3{p}_3^3{p}_4^2{p}_5^2+28p_1{p}_2^3{p}_3^4{p}_4^2{p}_5^2)z^{12}+\hfill \\ & 14p_1^2{p}_2^3{p}_3^4{p}_4^2{p}_5^2{z}^{13}+p_1^2{p}_2^4{p}_3^4{p}_4^2{p}_5^2{z}^{14}\hfill \\ H_3=\hfill & 1+18p_{3}z+(63p_2{p}_3+45p_3{p}_4+45p_3{p}_5)z^2+(56p_1{p}_2{p}_3+280p_2{p}_3{p}_4+280p_2{p}_3{p}_5+\hfill \\ & 200p_3{p}_4{p}_5)z^3+(315p_1{p}_2{p}_3{p}_4+315p_2{p}_3^2{p}_4+315p_1{p}_2{p}_3{p}_5+315p_2{p}_3^2{p}_5+1575p_2{p}_3{p}_4{p}_5+\hfill \\ & 225p_3^2{p}_4{p}_5)z^4+(630p_1{p}_2{p}_3^2{p}_4+630p_1{p}_2{p}_3^2{p}_5+2016p_1{p}_2{p}_3{p}_4{p}_5+5292p_2{p}_3^2{p}_4{p}_5)z^5+\hfill \\ & (245p_1{p}_2^2{p}_3^2{p}_4+245p_1{p}_2^2{p}_3^2{p}_5+9996p_1{p}_2{p}_3^2{p}_4{p}_5+1225p_2^2{p}_3^2{p}_4{p}_5+5103p_2{p}_3^3{p}_4{p}_5+\hfill \\ & 875p_2{p}_3^2{p}_4^2{p}_5+875p_2{p}_3^2{p}_4{p}_5^2)z^6+(5616p_1{p}_2^2{p}_3^2{p}_4{p}_5+12600p_1{p}_2{p}_3^3{p}_4{p}_5+3528p_2^2{p}_3^3{p}_4{p}_5+\hfill \\ & 2520p_1{p}_2{p}_3^2{p}_4^2{p}_5+2520p_2{p}_3^3{p}_4^2{p}_5+2520p_1{p}_2{p}_3^2{p}_4{p}_5^2+2520p_2{p}_3^3{p}_4{p}_5^2)z^7+(441p_1^2{p}_2^2{p}_3^2{p}_4{p}_5+\hfill \\ & 17172p_1{p}_2^2{p}_3^3{p}_4{p}_5+2205p_1{p}_2^2{p}_3^2{p}_4^2{p}_5+7875p_1{p}_2{p}_3^3{p}_4^2{p}_5+2205p_2^2{p}_3^3{p}_4^2{p}_5+2205p_1{p}_2^2{p}_3^2{p}_4{p}_5^2+\hfill \\ & 7875p_1{p}_2{p}_3^3{p}_4{p}_5^2+2205p_2^2{p}_3^3{p}_4{p}_5^2+1575p_2{p}_3^3{p}_4^2{p}_5^2)z^8+(2450p_1^2{p}_2^2{p}_3^3{p}_4{p}_5+5600p_1{p}_2^3{p}_3^3{p}_4{p}_5+\hfill \\ & 16260p_1{p}_2^2{p}_3^3{p}_4^2{p}_5+16260p_1{p}_2^2{p}_3^3{p}_4{p}_5^2+5600p_1{p}_2{p}_3^3{p}_4^2{p}_5^2+2450p_2^2{p}_3^3{p}_4^2{p}_5^2)z^9+(1575p_1^2{p}_2^3{p}_3^3{p}_4{p}_5+\hfill \\ & 2205p_1^2{p}_2^2{p}_3^3{p}_4^2{p}_5+7875p_1{p}_2^3{p}_3^3{p}_4^2{p}_5+2205p_1{p}_2^2{p}_3^4{p}_4^2{p}_5+2205p_1^2{p}_2^2{p}_3^3{p}_4{p}_5^2+7875p_1{p}_2^3{p}_3^3{p}_4{p}_5^2+\hfill \\ & 2205p_1{p}_2^2{p}_3^4{p}_4{p}_5^2+17172p_1{p}_2^2{p}_3^3{p}_4^2{p}_5^2+441p_2^2{p}_3^4{p}_4^2{p}_5^2)z^{10}+(2520p_1^2{p}_2^3{p}_3^3{p}_4^2{p}_5+2520p_1{p}_2^3{p}_3^4{p}_4^2{p}_5+\hfill \\ & 2520p_1^2{p}_2^3{p}_3^3{p}_4{p}_5^2+2520p_1{p}_2^3{p}_3^4{p}_4{p}_5^2+3528p_1^2{p}_2^2{p}_3^3{p}_4^2{p}_5^2+12600p_1{p}_2^3{p}_3^3{p}_4^2{p}_5^2+5616p_1{p}_2^2{p}_3^4{p}_4^2{p}_5^2)z^{11}+\hfill \\ & (875p_1^2{p}_2^3{p}_3^4{p}_4^2{p}_5+875p_1^2{p}_2^3{p}_3^4{p}_4{p}_5^2+5103p_1^2{p}_2^3{p}_3^3{p}_4^2{p}_5^2+1225p_1^2{p}_2^2{p}_3^4{p}_4^2{p}_5^2+9996p_1{p}_2^3{p}_3^4{p}_4^2{p}_5^2+\hfill \\ & 245p_1{p}_2^2{p}_3^4{p}_4^3{p}_5^2+245p_1{p}_2^2{p}_3^4{p}_4^2{p}_5^3)z^{12}+(5292p_1^2{p}_2^3{p}_3^4{p}_4^2{p}_5^2+2016p_1{p}_2^3{p}_3^5{p}_4^2{p}_5^2+630p_1{p}_2^3{p}_3^4{p}_4^3{p}_5^2+\hfill \\ & 630p_1{p}_2^3{p}_3^4{p}_4^2{p}_5^3)z^{13}+(225p_1^2{p}_2^4{p}_3^4{p}_4^2{p}_5^2+1575p_1^2{p}_2^3{p}_3^5{p}_4^2{p}_5^2+315p_1^2{p}_2^3{p}_3^4{p}_4^3{p}_5^2+315p_1{p}_2^3{p}_3^5{p}_4^3{p}_5^2+\hfill \\ & 315p_1^2{p}_2^3{p}_3^4{p}_4^2{p}_5^3+315p_1{p}_2^3{p}_3^5{p}_4^2{p}_5^3)z^{14}+(200p_1^2{p}_2^4{p}_3^5{p}_4^2{p}_5^2+280p_1^2{p}_2^3{p}_3^5{p}_4^3{p}_5^2+280p_1^2{p}_2^3{p}_3^5{p}_4^2{p}_5^3+\hfill \\ & 56p_1{p}_2^3{p}_3^5{p}_4^3{p}_5^3)z^{15}+(45p_1^2{p}_2^4{p}_3^5{p}_4^3{p}_5^2+45p_1^2{p}_2^4{p}_3^5{p}_4^2{p}_5^3+63p_1^2{p}_2^3{p}_3^5{p}_4^3{p}_5^3)z^{16}+18p_1^2{p}_2^4{p}_3^5{p}_4^3{p}_5^3{z}^{17}+\hfill \\ & p_1^2{p}_2^4{p}_3^6{p}_4^3{p}_5^3{z}^{18}\hfill \\ H_4=\hfill & 1+10p_{4}z+45p_3{p}_4{z}^2+(70p_2{p}_3{p}_4+50p_3{p}_4{p}_5)z^3+(35p_1{p}_2{p}_3{p}_4+175p_2{p}_3{p}_4{p}_5)z^4+\hfill \\ & (126p_1{p}_2{p}_3{p}_4{p}_5+126p_2{p}_3^2{p}_4{p}_5)z^5+(175p_1{p}_2{p}_3^2{p}_4{p}_5+35p_2{p}_3^2{p}_4^2{p}_5)z^6+(50p_1{p}_2^2{p}_3^2{p}_4{p}_5+\hfill \\ & 70p_1{p}_2{p}_3^2{p}_4^2{p}_5)z^7+45p_1{p}_2^2{p}_3^2{p}_4^2{p}_5{z}^8+10p_1{p}_2^2{p}_3^3{p}_4^2{p}_5{z}^9+p_1{p}_2^2{p}_3^3{p}_4^2{p}_5^2{z}^{10}\hfill \\ H_5=\hfill & 1+10p_{5}z+45p_3{p}_5{z}^2+(70p_2{p}_3{p}_5+50p_3{p}_4{p}_5)z^3+(35p_1{p}_2{p}_3{p}_5+175p_2{p}_3{p}_4{p}_5)z^4+\hfill \\ & (126p_1{p}_2{p}_3{p}_4{p}_5+126p_2{p}_3^2{p}_4{p}_5)z^5+(175p_1{p}_2{p}_3^2{p}_4{p}_5+35p_2{p}_3^2{p}_4{p}_5^2)z^6+(50p_1{p}_2^2{p}_3^2{p}_4{p}_5+\hfill \\ & 70p_1{p}_2{p}_3^2{p}_4{p}_5^2)z^7+45p_1{p}_2^2{p}_3^2{p}_4{p}_5^2{z}^8+10p_1{p}_2^2{p}_3^3{p}_4{p}_5^2{z}^9+p_1{p}_2^2{p}_3^3{p}_4^2{p}_5^2{z}^{10}\hfill \end{array}$$