A Novel Discrete-Time Chaos-Function-Based Random-Number Generator: Design and Variability Analysis

Abstract

This paper presents a novel discrete-time (DT) chaotic map-based random-number generator (RNG), namely the Siponi map, which is a modification of the Logistic map. The Logistic map is usually applied to cryptosystems, mainly for the purposes of generating random numbers. In addition to being easy to implement, it has a better security level than other nonlinear functions. However, it can only process positive real-number inputs. Our proposed map is a deterministic function that can process positive and negative real values. We explored the map comprehensively and investigated its characteristics and parameters. We calculated the optimum parameter values using empirical and theoretical mathematical models to yield the maximum randomness of a sequence of bits. The limit variation of the maximum parameter value was determined based on a practical information measure. Empirical verification was performed for the Siponi map to generate bit sequences unrelated to the previous bit with high entropy values, and we found the extractor function threshold value to be 0.5, while the parameter control was −2 or 2. Using our proposed map, a simple RNG without post-processing passed DieHard statistical tests and all the tests on the NIST SP 800-22. Finally, we have implemented a Siponi map-based RNG on the FPGA board and demonstrated that the sources used are LUT = 4086, DSP = 62, and register = 2206.

1. Introduction

Random number sequences are utilized as keys for the encryption/decryption process, including in symmetric cryptographic system applications, as a salt to the hash function, and as a nonce function applied to cryptographic protocols [1]. The need for random number sequences is greater in many cryptographic applications, and these sequences play a crucial role in various security services. Therefore, processes that generate precise random sequence numbers are essential for cryptographic applications.

A unique key for encryption/decryption processes is achieved by employing a random-number generator (RNG) implemented through automatic methods [2]. The process of obtaining randomness plays a significant role in generating key sequences that can be utilized on cryptosystems, sequences which are difficult for unauthorized parties to solve [1].

The RNG encompasses a series of processes that generate a bitstream that have unpredictable or random values but also have specific distribution patterns. Pseudo-random-number generators (PRNGs) and true random-number generators (TRNGs) are the two main classes of RNG. PRNGs, also called deterministic RNGs, use the specific amount of the seed as the input, and its output is derived from the deterministic function of the seed. Therefore, the randomness of the resulting output depends on the seed. Pseudo-random numbers appear random if no identical values occur in the seed [3]. TRNGs use a non-deterministic source as an entropy source and a processing function as an entropy-distillation process. Physical quantities that can serve as an entropy source are noise in electronic circuits and other random-seeming waveforms/phenomena. A distillation process must be performed to overcome the weakness of the entropy source that generates nonrandom numbers. The harvesting method and post-processing are two entropy distillation processes. For cryptosystems, the output of TRNGs must be unpredictable [2]. In reality, however, several physical sources can be predicted. Therefore, combining various sources as TRNGs inputs is recommended, although this does not guarantee the generation of statistically random numbers series [3].

Chaos is a dynamic system that exhibits non-periodic behavior. A discrete-time chaotic (DTC) system can be utilized in RNG applications as the entropy source for the TRNG design. DTC systems are nonlinear dynamic systems that are very sensitive to changes in initial conditions [4,5,6,7]. Due to high sensitivity, chaos could be utilized as a deterministic function for generating random bits. Furthermore, the advantages of implementing DTCs are of use when there are fewer resources and are convenient when applied to cryptography. In a chaos system, the entropy source used is the inherent noise of the system, which is amplified by the positive feedback loop through the output signal for each iteration [8]. Other advantages are the integrity and quality of the bits produced. Therefore, this system is acceptable for random number generation processes [6,9,10,11]. The logistic map [10,11,12,13], tent map [6], and Bernoulli map [8] represent one-dimensional (1D) chaos systems that are commonly used to generate these numbers.

The Logistic map is a simple 1D chaos system widely applied to cryptosystems, especially for random-number generation processes [11,14,15,16,17]. In addition to being easy to implement on hardware, this chaos system has a better level of security than the linear function chaos system. The Logistics map is only able to process input in the form of positive real numbers $x_0\in (0,1)$ and produce positive real-number outputs, $x_{n+1}\in (0,1)$. However, in the random-number generation process, without using post-processing, this chaotic system can generate a series of random bits with entropy values close to 1 and no correlation between bits.

Several researchers [9,16,18,19] have modified a 1D chaos system that can process positive and negative real input numbers, $x_0\in (-1,1)$, alternately. The map’s input value represents a non-ideal condition often encountered when the map is applied to a complex circuit. This condition will produce a biased and correlated binary circuit [9]. Map functions obtained from the modifications made can generate a series of random bits with very high entropy values (close to 1). However, these functions are not able to generate a statistically random number series. Therefore, the post-processing of the output data is required to minimize this condition. The most widely used post-processing steps for RNG applications include Von-Neumann [20], bit skipping, XOR, LFSR shuffler, and hash functions [12,21].

Based on some of the arguments above, in this study, we propose a new chaos function named the Siponi map, a modification of the Logistic map. This new chaos function is a dual-side-deterministic function, which is capable of processing positive and negative real values, $x_0\in (-1,1)$. It has a more comprehensive range of parameters, $x_{n+1}\in (-1,1)$, where $n\ge$ 0. The Siponi map could be applied to the RNG to generate a series of bits with random entropies close to 1. Furthermore, we have carried out an analysis using an empirical approach and a mathematical model to obtain a threshold value for generating independent and identically distributed binary sequences. We have performed several randomness performance tests on the generated bit sets using several statistical tests, including NIST SP 800-22 and the DieHard statistical test. In addition, the Siponi map implementation has been compared with another RNG-based 1D chaos system capable of processing real input values, $x_0\in (-1,1)$.

The paper includes five sections. Section 1 describes the research background. Section 2 reviews the DTC system and logistic map as a modified chaotic function. Section 3 explains the Siponi map as a proposed map function and the method of determining threshold values for acquiring an identically distributed bit sequence. Section 4 describes the proposed map application for the random-number generator, results, and analysis. Section 5 presents the conclusions of our experiment. This study used Matlab R2021 in the Siponi map design and simulation process. Furthermore, the function was implemented on the ZedBoard Zynq 7000 to generate a series of random numbers.

2. Preliminaries

2.1. Discrete-Time Chaotic Map

The chaotic map represents a dynamic system that exhibits non-periodic behavior, and it is a nonlinear dynamic system that is very sensitive to changes in the initial conditions [4,5,7]. Due to this sensitivity, chaos can be utilized as a deterministic function for generating random bits [7,9,10,22,23,24]. The dynamic system is a deterministic function whose output is entirely determined by the initial parameter values and initial conditions [4]. RNG-based chaotic systems can be classified as discrete-time (DT) or continuous-time (CT) systems, depending on the fundamental dynamics. In a CT chaotic system, the differential equations define the future state in relation to the current state variables; however, in a DTC system, the future state described by the function equation depends on the current state value. In other words, a DTC map exhibits the chaotic system behavior that is formed by the iteration of the system outputs into the system at each run time.

The operation of DTC RNGs requires an external clock signal to drive the chaotic dynamics. Therefore, the generation and evolution speed of the time series forming the chaotic trajectories depend on the clock frequency. The main components of a DTC RNG system are a nonlinear transfer function circuit, a sample-hold circuit, and a clock source. These components are shown in Figure 1.

A 1D chaos system is a simple dynamic system that is widely used to generate random numbers. The Logistic map, tent map, and Bernoulli map represent 1D chaos systems that are commonly used in this process. The Logistic map is a nonlinear chaos system, and, in addition to being easy to implement, the Logistic map also provides an appropriate level of security [4,11,19].

2.2. Logistic Map

The Logistic map is a 1D chaos system that is very popular in cryptography and other fields. The Logistic map is a recursive function with a particular parameter value and requires low computation to generate good chaotic conditions. It is described by:

$$x_{n+1}=r{x}_n(1-x_n),n=0,1,...,$$

(1)

where r is a parameter that lies in the interval $(0,4]$, and $x_n\in (0,1)$. Hence, the definition of the Logistic map indicates that $x_n:(0,1)$→$(0,1)$. The Lyapunov exponents and bifurcation diagram represent the chaotic properties of the Logistic map that are obtained from calculations and plots. The Logistic map is very sensitive to changes in the initial conditions, especially when the parameter value (r) is 4. This property can be plotted in the Lyapunov exponent. As presented in Figure 2, the plot will be positive when r = 4.

The bifurcation diagram presents values close to the system’s asymptotic (fixed points, periodic orbits, or chaotic attractors) as a system parameters function. It can be used to determine the sensitivity level of a chaotic system. The plot of the bifurcation diagram depends on the parameter values. Figure 3 indicates a Logistic map bifurcation diagram and presents the highest sensitivity level as $r=4$.

The Logistic map has been applied as a dynamic system for generating random numbers that pass statistical tests; thus, a logistic map-based RNG algorithm is feasible for application in cryptography [25]. Although some researchers have modified the Logistic map to apply the Logistic map to cryptosystems, changes in the parameter values and generated data distribution must be considered [26,27].

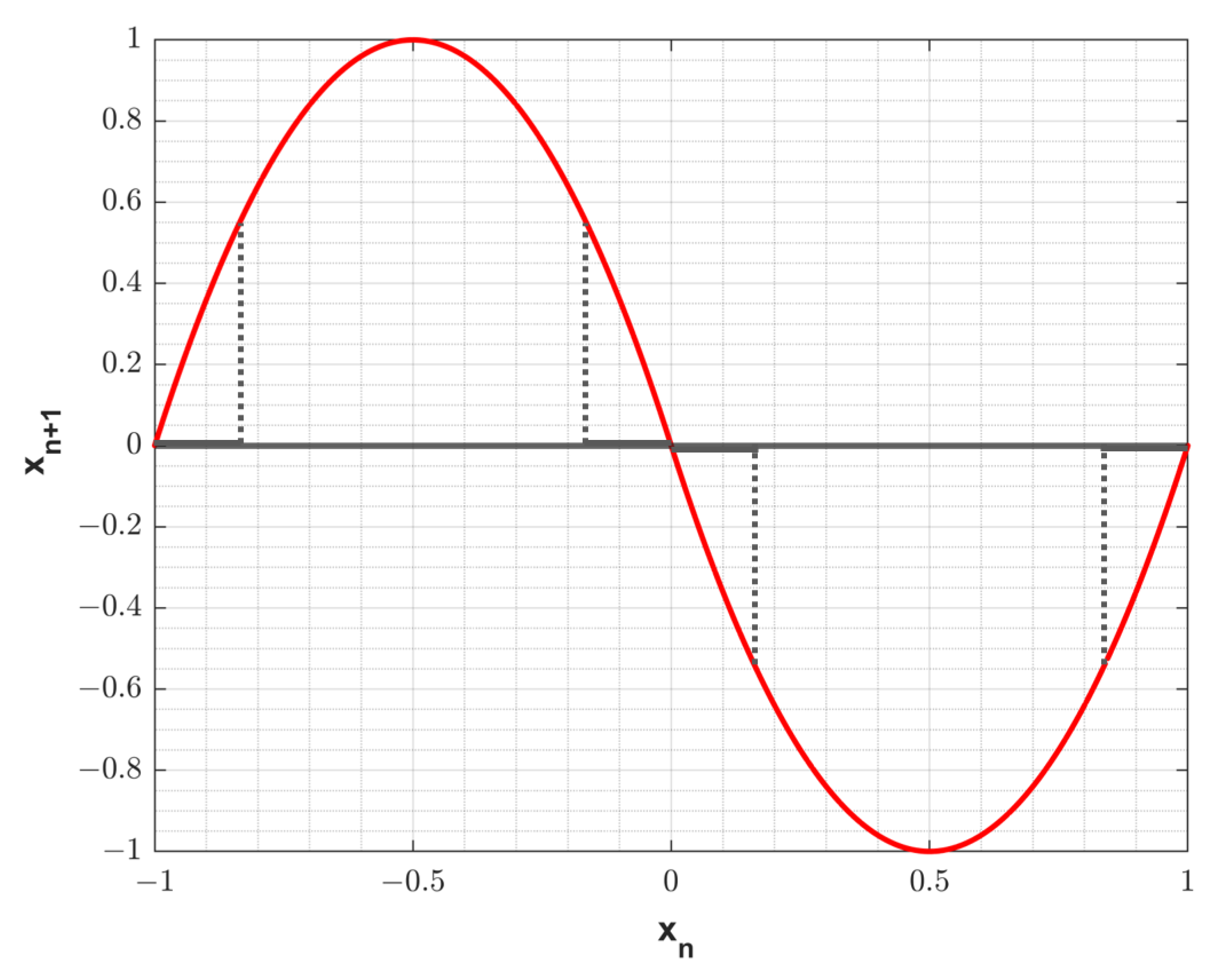
3. Proposed Map

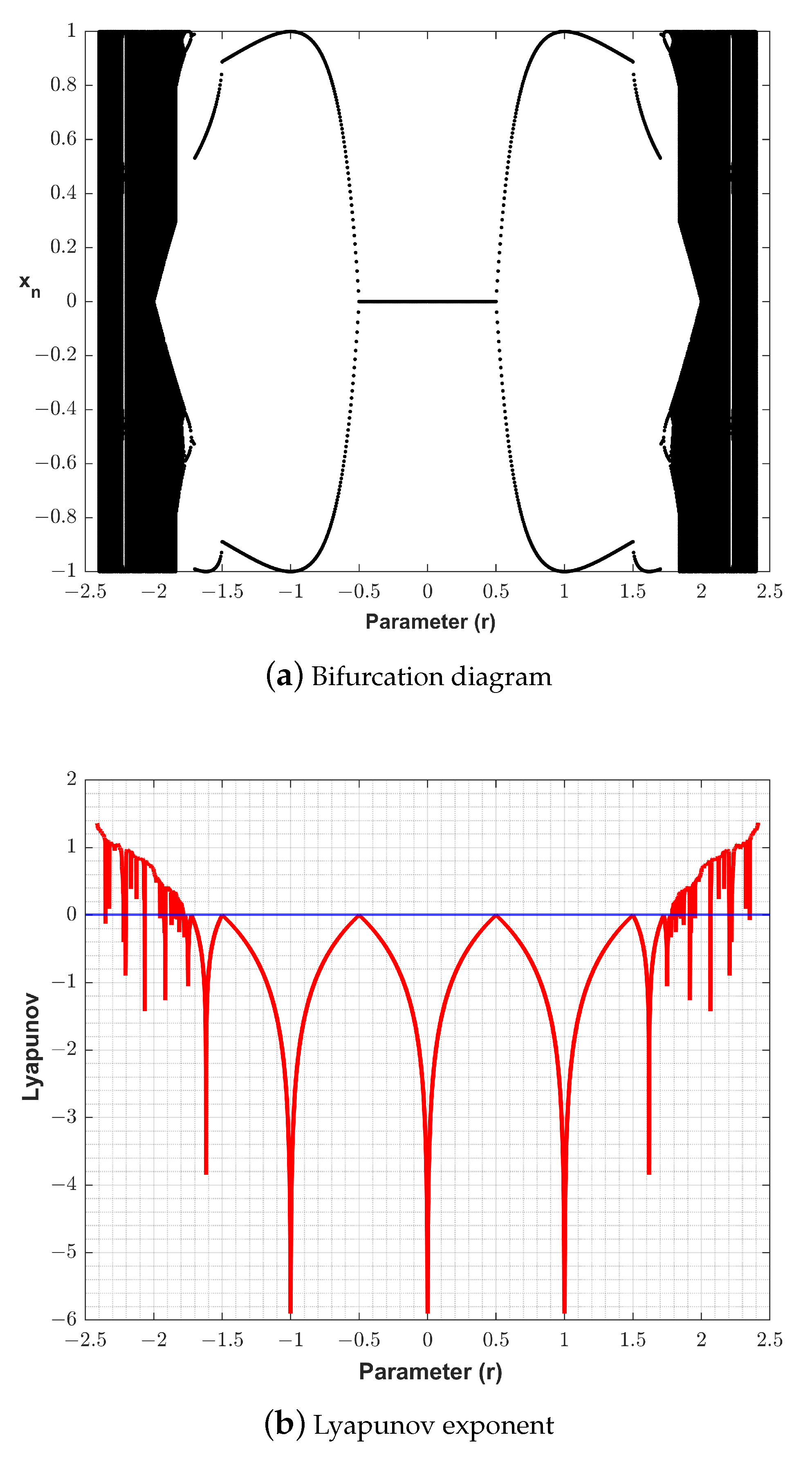
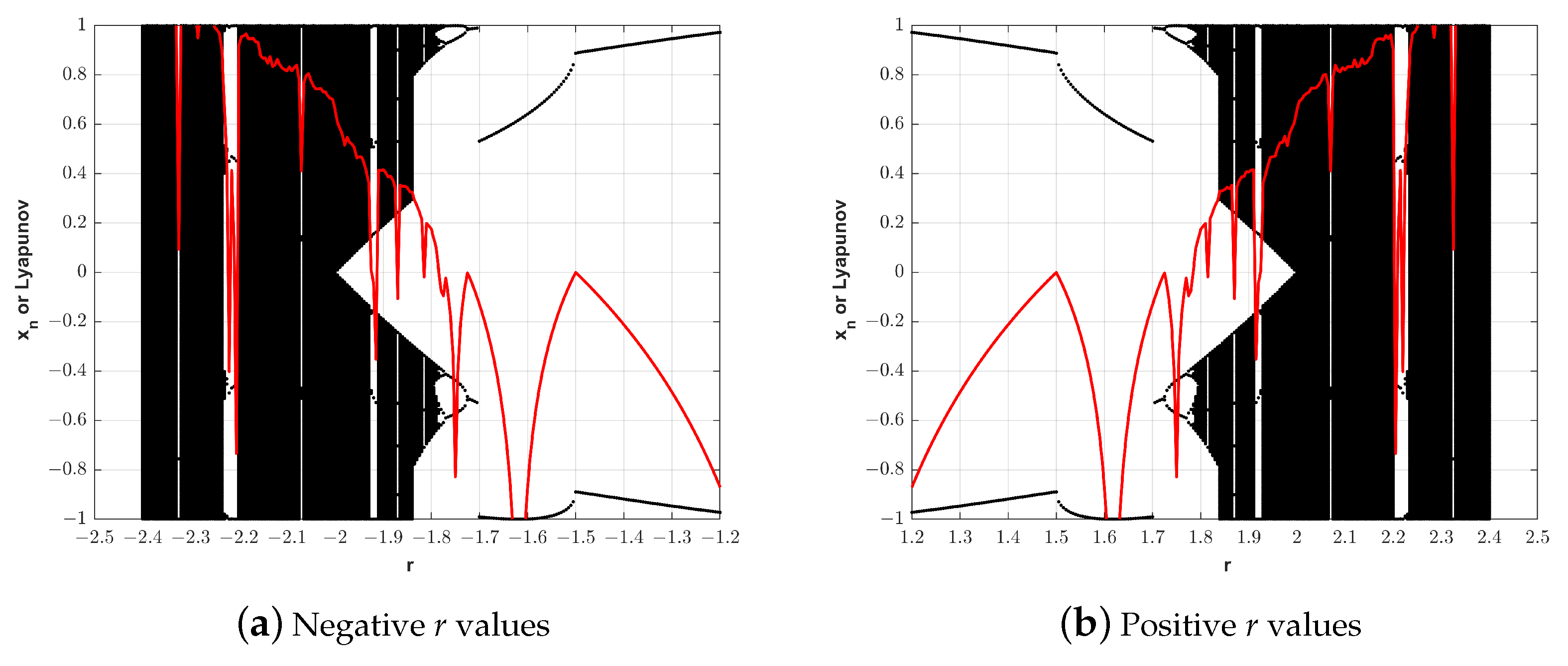
3.1. Siponi Map

We propose a novel DTC system named the Siponi map, which modifies the logistic map. This system generates output values that alternate between positive and negative values, which facilitates the implementation of modifications under non-ideal conditions [28]. Furthermore, the Siponi map will produce the same output in absolute values, because the resulting values are symmetric, despite alternating between positive and negative.

The map modification is defined as X over the interval $I=(-1,1)$ and $I\ne 0$. A partition point divides I into two segments, as shown in (2). Different functions define it for each segment; these are well known as $X_1$ and $X_2$ [26,27].

$$X=x_{n+1}=\left\{\begin{array}{cc}{X}_1,\hfill & \hfill -1<x_n<0\\ X_2,\hfill & \hfill 0<x_n<1,\end{array}\right.$$

(2)

where $x_n\in (-1,1)$. In a Siponi map, positive input value generates negative output value, an vice versa. Therefore, the recursive equation of the Siponi map is as follows:

$$X=x_{n+1}=\left\{\begin{array}{cc}-r^2{x}_n\left(\frac{2}{\left|r\right|}+x_n\right),\hfill & -1<x_n<0\hfill \\ -r^2{x}_n\left(\frac{2}{\left|r\right|}-x_n\right),\hfill & 0<x_n<1,\hfill \end{array}\right.$$

(3)

where r is a real number, $r\in [-2.4,0)$, and $r\in (0,2.4]$. Figure 4 presents the output of (3) for input values $x_n\in (-1,1)$ and $x_n\ne 0$. Different r values will provide different curves.

Equation (3) could be applied to define bifurcation diagrams from chaotic maps according to alterations of r. The bifurcation diagram serves to identify the chaotic behavior of a system. Employing (3), we obtain the plot of the bifurcation diagram as in Figure 5a. The diagram shows values ranging from $r=2$ to $r=2.41$ and $r=-2.41$ to $r=-2$, generating a real-number output with the maximum range of $[-1,1]$. As demonstrated in Figure 5b, those parameters generate positive Lyapunov exponential values, indicating high sensitivity.

The cobweb plot or Verhulst diagram of the Siponi map function with an initial value, $x_0$, is represented in Figure 6. Therefore, the plot could define a point on the map curve as the endpoint in a particular iteration of the Siponi map function. The cobweb plot assists in visualizing successive iterations of the deterministic function and investigating the qualitative behavior of the 1D-iterated function.

The proposed map is very sensitive to alterations in the initial conditions. Two different initial values will produce different outputs. Furthermore, it is highlighted in Figure 7 how if a slight change occurs in the initial value, a different trajectory will be delivered.

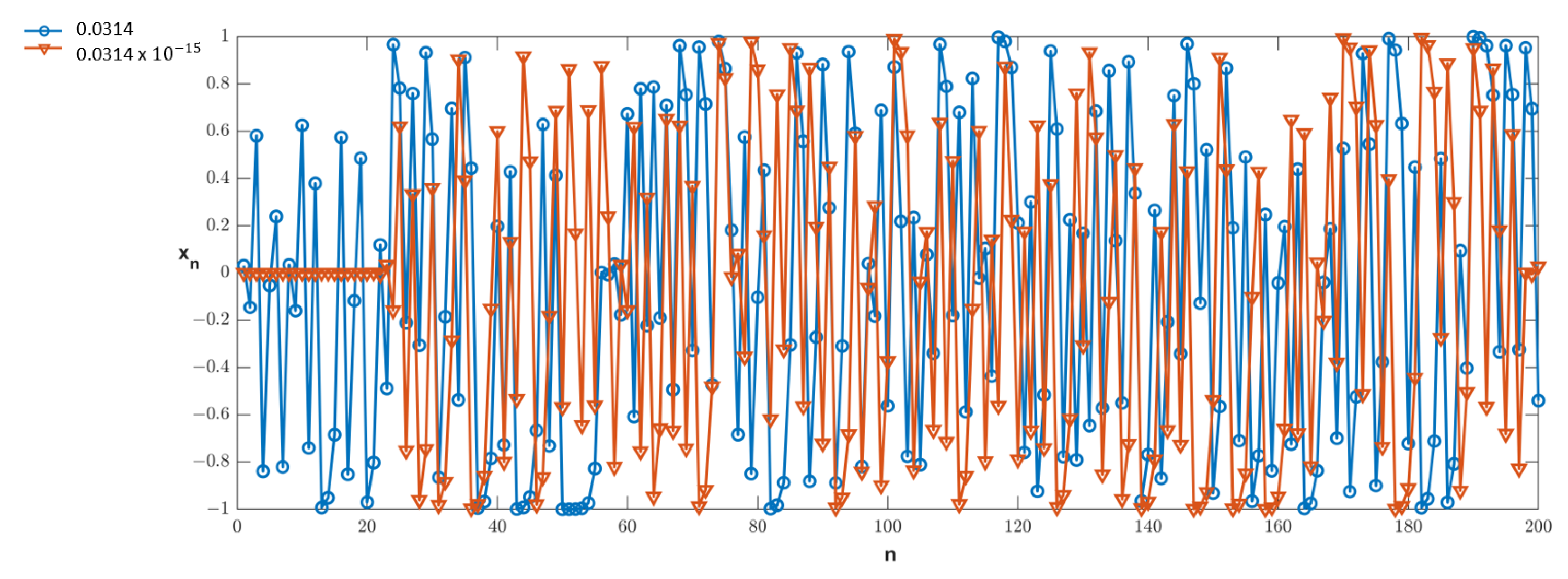
3.2. Keyspace Analysis of the Proposed Map

Cryptographic applications can be used for various kinds of attacks, including brute-force attacks. In order to prevent an attack, it is possible to increase the keyspace of the secret keys or seed values, which are greater than $2^{100}$ [29].

The Siponi map resulted in several parameters: the initial conditions $x_n\in (-1,1)$, where $x_n\ne 0$, and several control parameters $\left(r\right)$. Figure 8 indicates that several control parameters have positive Lyapunov exponential values that provide real output numbers with a maximum range $[-1,1]$ when $r=[2,2.41]$. This condition is also similar for $r=[-2,41,-2]$. Furthermore, as shown in Figure 9a,b, the values of the control parameters are $r\in [-2.41,-2.33]$, $[-2.32,-2.235]$, $[-2.2,-2.075]$, $[-2.065,-2]$, $[2,2.065]$, $[2.075,2.2]$, $[2.235,2.32]$, $[2.33,2.41]$.

The IEEE floating-point standard indicates the double floating-point precision as ${10}^{-16}$ [30]. It allows the value of x to be one of ${10}^{16}$ values and could be any value in the range $\left(\right(-2.41-(-2.33))+(-2.32-(-2.235))+(-2.2-(-2.075))+(-2.065-(-2))+(2-2.065)+(2.075-2.2)+(2.235-2.32)+(2.33-2.41\left)\right)$×${10}^{16}=0.71$ × ${10}^{16}$. The Siponi map is a chaotic system that could generate an output value of $x_{n+1}\in [-1,1]$. In order to generate this value, the keyspace that could be produced is $0.71$ × $2$ × ${10}^{16}$ × ${10}^{16}$ = $1.42$ × ${10}^{32}$ ≈ $2^{107}$.

Table 1. Keyspace comparison.

Study	Control Parameter	Initial Value	Keyspace
Proposed work	$r\in [-2.41,-2.33]$, $[-2.32,-2.235]$, $[-2.2,-2.075]$, $[-2.065,-2]$, $[2,2.065]$, $[2.075,2.2]$, $[2.235,2.32]$, $[2.33,2.41]$	$x_n\in (-1,1)$,$x_n\ne 0$	$1.42$ × ${10}^{32}\approx 2^{107}$
[31]	$r\in [4,31]$	$x_n\in (0,1)$	27 × ${10}^{32}\approx 2^{111}$
[33]	$r\in [3.5699,4]$	$x_n\in (0,1)$	0.4301 × ${10}^{32}\approx 2^{104}$
[32]	$r\in (0,4]$	$x_n\in (0,1)$	4 × ${10}^{32}\approx 2^{108}$
[34]	$r\in [3.999,4]$	$x_n\in (0,1)$	0.001 × ${10}^{32}\approx 2^{99}$
[35]	$r\in [0,1]$	$x_n\in (0,1)$	1 × ${10}^{32}\approx 2^{106}$

compares the keyspace range of the proposed method with other research methods. Other research methods have the initial ($x_n$), and the final ($x_{n+1}$) values are (0, 1], whereas the output of the Siponi map is at $[-1,1]$. Based on the comparison results, several methods [31,32] could produce larger keyspaces than the Siponi map. However, the proposed method satisfies the keyspace requirement and is capable of resisting brute-force attacks.

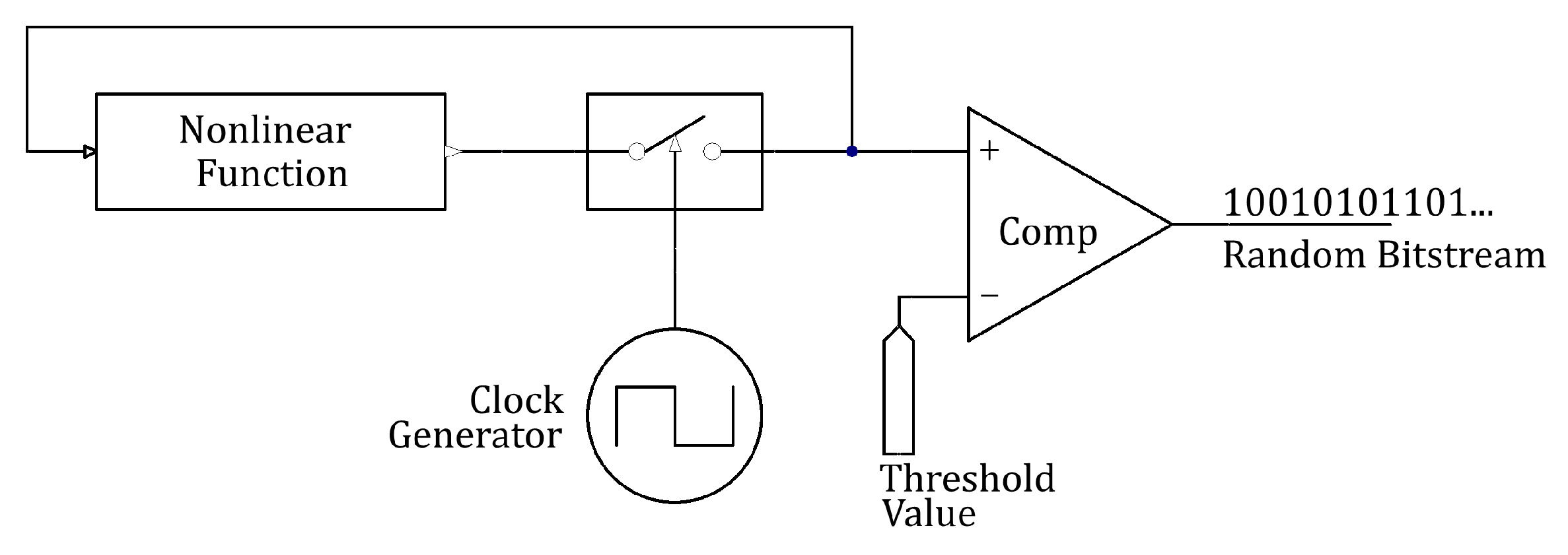
4. Application to Random-Bit Generator

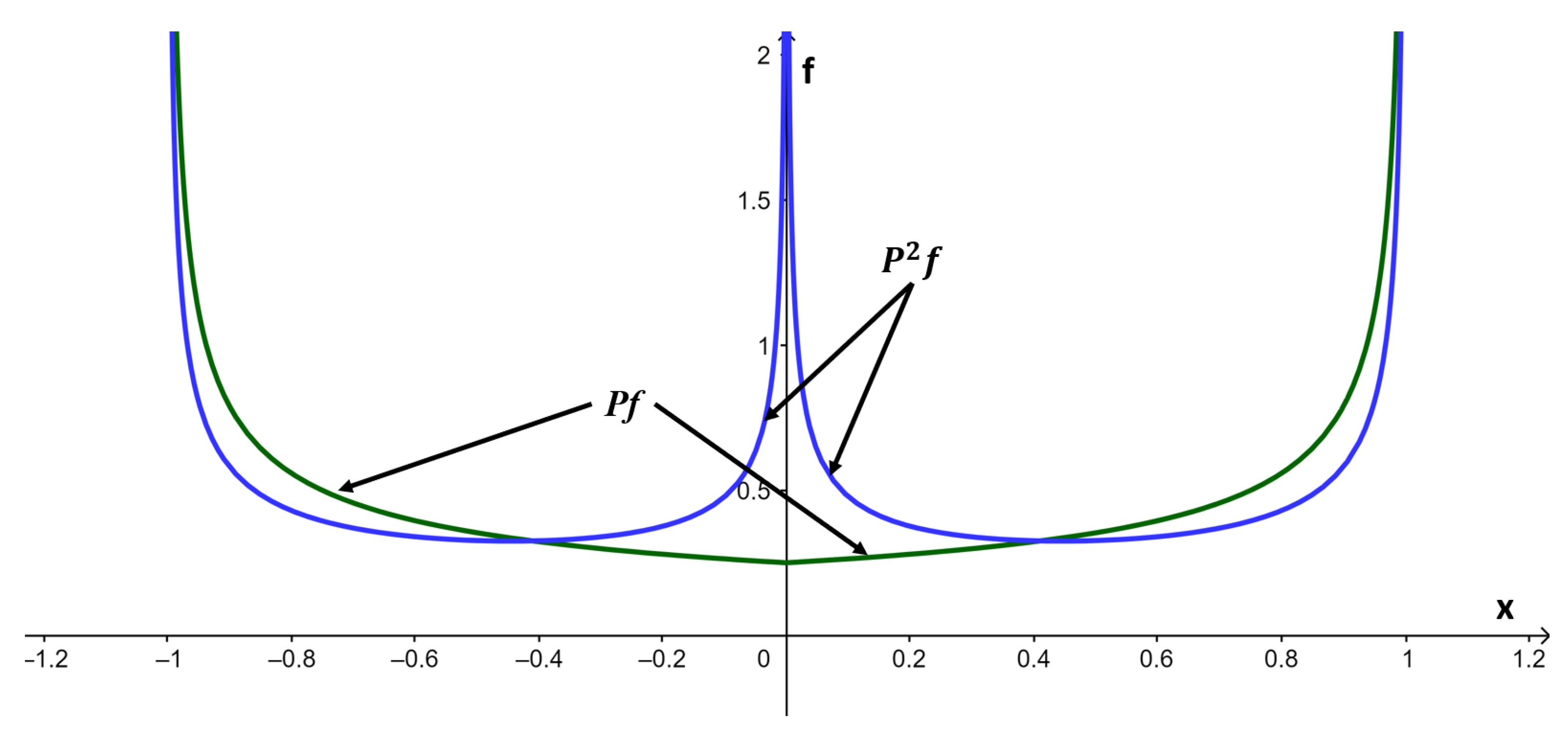
4.1. Entropy Source

This research is divided into several stages. In the initial stage, the RNG entropy source is selected. A clock system with a frequency of 10 MHz is used as the entropy source. Furthermore, the sampling and hold (S/H) process is performed for the clock to produce the real value that becomes the initial value of the deterministic function. Chaos is the deterministic function, and so the input values must not be repeated.

The S/H process produces different values. To ensure a variety of different values, we examine the real numbers that are acquired from the S/H process. The results show that as many as $3\times {10}^5$ of the outputs of the S/H process do not include identical numbers.

4.2. Determine the Threshold Value

The output of the Siponi chaotic system is a real positive or negative number, $x_{n+1}\in \mathbb{R}$. The resulting output values are converted to their absolute values. RNG imperfections or non-ideal conditions will produce biases in the resulting binary sequence. To avoid this, the entropy value of the output binary sequence must be close or equal to 1. Therefore, comparing the chaos outputs with a threshold value $\left(T_h\right)$ is a method for acquiring a bit sequence with the expected entropy value. There are two ways to determine the Siponi map threshold value; these methods are discussed below.

4.2.1. Empirical Probability Density Function (Empirical PDF)

The empirical PDF [36] is used to statistically analyze the distribution of map function outputs to determine the threshold value. This can be achieved by utilizing the time sequences of the RNGs model generated. The empirical PDF comprises the following steps.

• Creating a histogram of the frequency distribution of the map function output values $|x_{n+1}|,|x_{n+1}|\in [0,1]$.
• Dividing $|x_{n+1}|$ by n non-intersecting discrete intervals, the jth interval is:

  $$\left[\right(\mathrm{j}-1)/\mathrm{n},\mathrm{j}/\mathrm{n})\mathrm{j}=1,\dots \mathrm{n}$$

  (4)
• Selecting the initial value $x_0$ and calculating the resulting value for each iteration based on the equation:

  $$x_0,x_1=X\left(x_0\right),x_2=X\left(x_1\right)=X\left(X\left(x_0\right)\right),\dots ,x_N,$$

  where N is the number of iterations, and $N>>n$.
• Determining the fraction, $f_j$, of a j th interval:

  $${\mathrm{f}}_{\mathrm{j}}=\frac{\mathrm{n}}{\mathrm{N}}\left\{\mathrm{number}\mathrm{of}{\mathrm{x}}_{\mathrm{k}}\in \left(\frac{\mathrm{j}-1}{\mathrm{n}},\frac{\mathrm{j}}{\mathrm{n}}\right),\mathrm{k}=1,\dots ,\mathrm{N}\right\}$$

  (5)

In this process, the histogram is generated using iterations $N={10}^6$ and $n={10}^2$. The resulting histogram plot is symmetrical, with the distribution of values concentrated between 0 and 1 with a minimum at 1/2. We have conducted experiments using different control parameter values, resulting in different histograms. As described in Section 3.2, the Siponi map has several control parameters that produce the maximum range [−1, 1]. However, not all parameter values could produce a symmetric histogram plot. Figure 10 indicates the results of histogram generation for several values of r. Based on the experiments, the values of $r=-2$ and $r=2$ produce a concentrated symmetric histogram plot between 0 and 1, as represented in Figure 10g,h. Therefore, the Siponi map control parameters utilized to generate random bit sequences are $r=-2$ and 2.

The threshold value $\left(T_h\right)$ is determined by summing up the frequencies of the first histogram until a certain histogram yields $N/2$. The interval value for the $N/2$ frequencies shows the desired $T_h$ value. If the number of histograms $\left(n\right)$ being processed increases, then the value of $T_h$ obtained is more accurate. Using this empirical method, for $N={10}^6$ and $n=3000$, we obtain $T_h=0.5$.

4.2.2. Optimal Theoretical Threshold Determination for Identical Bit Generation

The output of the Siponi map is converted to an absolute value, and we assume that the final transformations are $X_1\left(x\right):(0,1)\to [-1,0)$ and $X_2\left(x\right):(-1,0)\to (0,1]$ with a large number of initial values, N. To analyze the PDF of the resulting output, the counter-image of a map function should be used [36]. As illustrated in Figure 11, the counter-image consists of the union areas of two sets denoted by the heavy lines on the x-axis. The domain area $X_1\left(x\right):(0,1)\to [-1,0)$ is equal to $X_2\left(x\right):(-1,0)\to (0,1]$.

The Frobenius–Perron operator $\left(P\right)$ is utilized to analyze the PDF transformation $X.$ For the first transformation, define the operator $\left(Pf\right)$ for the map functions $X_1\left(x\right)$ as $:[-1,0]\to [0,1]$, and $X_2\left(x\right):[0,1]\to [-1,0]$.

$$Pf\left(x\right)=\left\{\begin{array}{c}\frac{d}{dx}{\int }_{X_1^{-1}\left((-x,0)\right)}f\left(u\right)du\hfill \\ \frac{d}{dx}{\int }_{X_2^{-1}\left((0,x)\right)}f\left(u\right)du,\hfill \end{array}\right.$$

(6)

where $X_1^{-1}$ is the counter-image over the interval $\left(\right[-x,0\left]\right)$, and $X_2^{-1}$ is the counter-image $\left(\right[0,x\left]\right)$. Before applying Equation (6), it is necessary to determine several points on the map function, as shown in Figure 11, using the inverse function of the simple equation for $X_1^{-1}$ and $X_2^{-1}$, as follows:

$$X^{-1}\left([-x,x]\right)=\left[-1,-\frac{1}{r}-\frac{1}{r}\sqrt{1-x}\right]\cup \left[-\frac{1}{r}+\frac{1}{r}\sqrt{1-x},0\right]\cup \left[0,\frac{1}{r}-\frac{1}{r}\sqrt{1+x}\right]\cup \left[\frac{1}{r}+\frac{1}{r}\sqrt{1+x},1\right].$$

Applying the Frobenius–Perron concept, Equation (6) changes as follows:

$$Pf\left(x\right)=\left\{\begin{array}{cc}\frac{d}{dx}{\int }_{-1}^{-1/r-1/r\sqrt{1-x}}f\left(u\right)du+{\int }_{-1/r+1/r\sqrt{1-x}}^{0}f\left(u\right)du,\hfill & x\in [0,1]\hfill \\ \frac{d}{dx}{\int }_0^{1/r-1/r\sqrt{1+x}}f\left(u\right)du+{\int }_{1/r+1/r\sqrt{1+x}}^{1}f\left(u\right)du,\hfill & x\in [-1,0]\hfill \end{array}\right..$$

The results of the differentiation process are as follows:

$$Pf\left(x\right)=\left\{\begin{array}{cc}\frac{1}{2r\sqrt{1-x}}\left\{f\left(-\frac{1}{r}-\frac{1}{r}\sqrt{1-x}\right)+f\left(-\frac{1}{r}+\frac{1}{r}\sqrt{1-x}\right)\right\},\hfill & x\in [0,1]\hfill \\ \frac{1}{2r\sqrt{1+x}}\left\{f\left(\frac{1}{r}-\frac{1}{r}\sqrt{1+x}\right)+f\left(\frac{1}{r}+\frac{1}{r}\sqrt{1+x}\right)\right\},\hfill & x\in [-1,0]\hfill \end{array}\right..$$

(7)

For this case, we utilized the initial density $f\left(x\right)\equiv 0.5$; furthermore, we substituted all instances of $f\left(x\right)$ inside brackets in (7) with the constant 0.5.

All the resulting output values are converted to absolute values in the second transformation. With the result that the output is on the positive y-axis, Equation (7) turns into the following equation:

$$\begin{array}{cc}& P\left(Pf\left(x\right)\right)=P^{2}f\left(x\right)\hfill \\ & P^{2}f\left(x\right)=\left\{\begin{array}{c}\frac{\sqrt{r}}{4r^2\sqrt{1-x}}\left(\frac{1}{\sqrt{1-\sqrt{1-x}}}+\frac{1}{\sqrt{1+\sqrt{1-x}}}\right),\mathrm{for}x\in [0,1]\hfill \\ \frac{\sqrt{r}}{4r^2\sqrt{1+x}}\left(\frac{1}{\sqrt{1-\sqrt{1+x}}}+\frac{1}{\sqrt{1+\sqrt{1+x}}}\right),\mathrm{for}x\in [-1,0]\hfill \end{array}\right..\hfill \end{array}$$

The plots of $Pf$ and $P^{2}f$ for the first and the second transformation are shown in Figure 12. Furthermore, the asymptotic evolution of the parallel density to the time iteration is:

$$f_{\infty }\left(x\right)=\underset{n\to \infty }{lim}{P}^{n}f\left(x\right)=1.$$

Applying the cumulative distribution function:

$$F\left(x\right)={\int }_{-\infty }^{T_h}{f}_{\infty }\left(x\right)dx=T_h.$$

(8)

Entropy is a mathematical measure that indicates the amount of information provided by an observation [37]. In the RNG, the entropy value must be maximal to generate a sequence number with a high level of randomness. The maximum value of entropy for a sequence bit is 1. Therefore, the optimum threshold ($T_h$) for the output of the proposed chaotic function allows the generation of bits with high entropy. The probability determination of bit 0 and bit 1 from an entropy source allows for the use of the PDF, as below:

$$p=P_0={\int }_0^{T_h}{f}_x\left(x\right)dx=T_h$$

(9)

$$q=P_1={\int }_{T_h}^1{f}_x\left(x\right)dx=1-T_h=1-P_0.$$

(10)

Using Shannon’s entropy:

$$H=-\sum _{\mathrm{i}=0}^1{P}_i{log}_2{P}_i=-\left(p{log}_{2}p+q{log}_{2}q\right),$$

(11)

for sequences with high randomness, substitute 1 for H as a maximum value of entropy:

$$\begin{array}{c}1=-\left(T_h{log}_2{T}_h+\left(1-T_h\right){log}_2\left(1-T_h\right)\right)\\ 1/2=T_h^{T_h}{\left(1-T_h\right)}^{\left(1-T_h\right)}.\end{array}$$

$T_h=p=0.5$ is obtained by using $dH\left(T_h\right)/\left(d{T}_h\right)=0$, as shown in Figure 13.

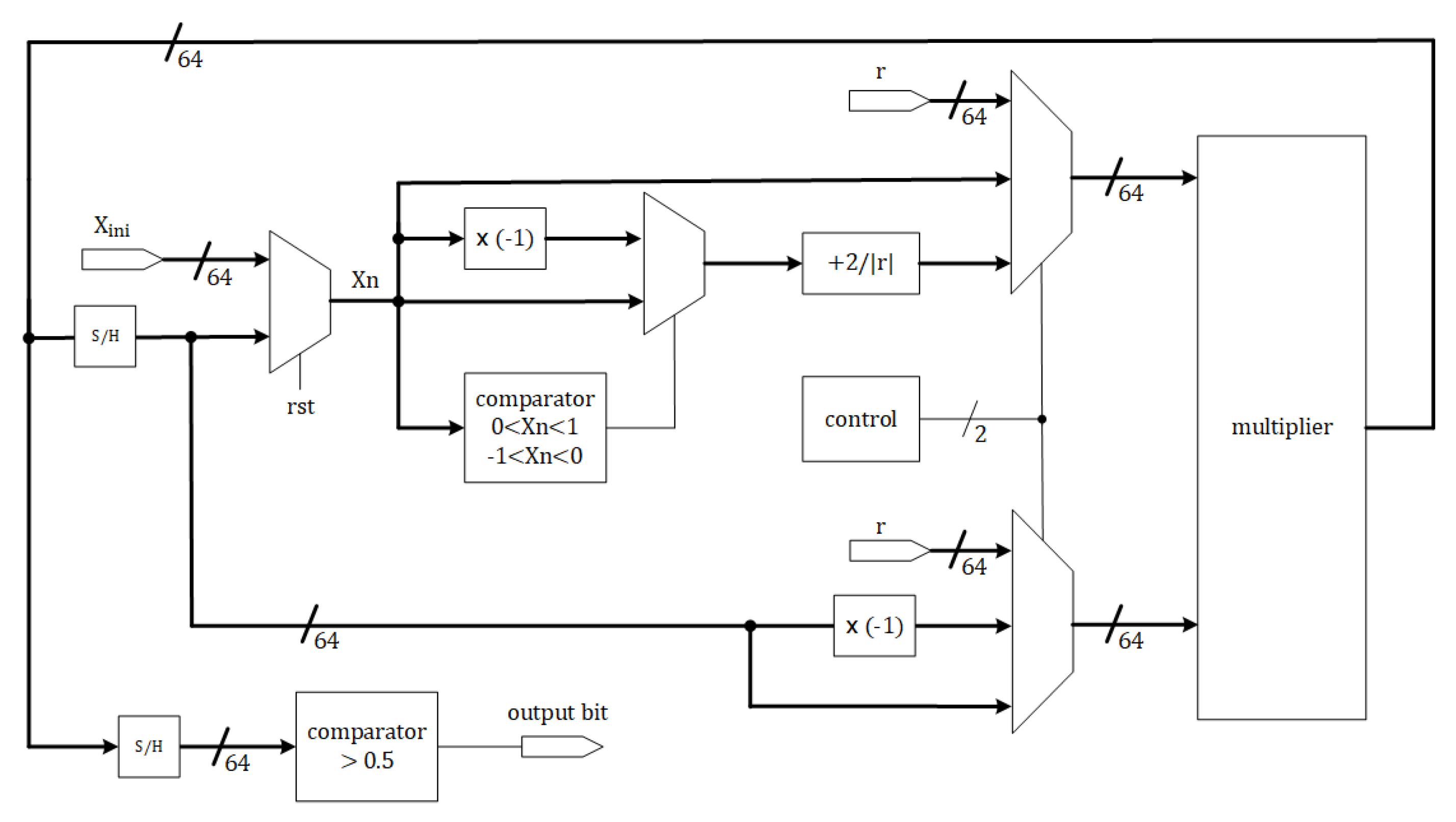
4.3. The Proposed Random-Bit Generator

To verify that the proposed map function could generate a sequence of random bits, we implemented the function as shown in Figure 1. The values generated by each iteration of the map function were then compared with the resulting $T_h$ values. The result of the comparison is a sequence bits of 0 and 1 acquired based on the following equation:

$$y_{n+1}=\left\{\begin{array}{cc}0,\hfill & \hfill |x_{n+1}|\le T_h\\ 1,\hfill & \hfill |x_{n+1}|>T_h,\end{array}\right.$$

(12)

where $T_h$ = 0.5. Furthermore, the randomness level of the resulting bits sequence is proven by statistical tests.

4.4. Analysis of Autocorrelation and Entropy

Some of the analyses we performed on the outputs generated by the proposed map based on the random-bit generator are listed below.

4.4.1. Autocorrelation Analysis

Autocorrelation, commonly referred to as serial correlation, is the correlation of a bit with the previous bit in the same sequence. An autocorrelation test on a bit sequence determines the distribution of the bits 0 and 1. In addition, this test is an alternative test for checking the randomness of a sequence of bits [38], which is calculated using the following equation:

$$r_k=\frac{{\sum }_{t=1}^{N-k}\left(z_t-\overline{z}\right)\left(z_{t+k}-\overline{z}\right)}{{\sum }_{t=1}^N{\left(z_t-\overline{z}\right)}^2},$$

(13)

where,

• k, number of lags
• N, number of observations
• $r_k$, autocorrelation value with lag k
• $z_t$, observation value of data variable to - t
• $z_{(t+k)}$, the value of the following variable observation
• $\overline{z}$, the average value of the observation data.

Table 2. Autocorrelation of random bit sequences.

Sequences	Minimum Value	Maximum Value
First sequence	$-0.0595$	$0.05615$
Second sequence	$-0.07279$	$0.08154$
Third sequence	$-0.0752$	$0.07026$
Fourth sequence	$-0.06821$	$0.07333$

presents the maximum and minimum values of the autocorrelation test (except the first lag). The test results indicate no correlation between one bit and the previous bit in a series of bits. The minimum and maximum autocorrelation values for each sequence are in the range’s confidence limits, that is, $-0.0949$ and $0.0949$. Therefore, the resulting sequences are random.

4.4.2. Entropy Analysis

Theoretically, implementing the proposed map on the RNG could generate a bit sequence that is distributed independently and unpredictably. We calculated the entropy value of each resulting bit sequence to prove this. This value represents the distribution of bits 0 and 1 in a sequence. The uncertainty of the next generated bit value could be found by Shannon’s theory. Furthermore, the entropy value of a binary sequence is obtained using (11).

The entropy value generated by the Siponi map can be compared with another map, that is, the zigzag map [9]. Its value measures the bit quality resulting from both chaotic map functions, which can process negative and positive inputs. These two deterministic functions produce 300 entropy values for 300 sequences, each containing ${10}^6$ bits.

The parameter value used is 2, which is an ideal parameter value for Siponi and zigzag maps. The comparison of the resulting entropy values is shown in Figure 14, which indicates that the Siponi map generates bit sequences that have higher entropy values than those of the zigzag map. An entropy value close to 1 indicates that the probability of bit 0 and bit 1 is almost certainly $P\left(0\right)=$$P\left(1\right)=0.5$. Therefore, bit 0 and bit 1 in the binary sequence generated by the Siponi map are distributed more independently and unexpectedly than in the sequence generated by the zigzag map.

4.5. Statistical Analysis

In order to prove that our proposed chaos method could generate a sequence of random numbers, we evaluated the resulting binary output using the NIST 800-22 and DieHard statistical tests. These tests can detect statistical weaknesses in a design. The sample size and delivery requirements for a sequence of random numbers follow each test suite’s documentation provisions.

4.5.1. NIST SP 800-22

We performed a statistical performance analysis of our proposed method using the NIST 800-22 statistical test suite. We evaluated 1 Gbit of data, which was divided into 1000 sequences. NIST 800-22 consists of 15 empirical tests, each of which will produce a p-value that indicates the probability of an ideal RNG. The p-values are compared at the significance level $\left(\alpha \right)=0.01$, with p-values greater than $\alpha$ indicating that the sequences are random and accepted. The value $\alpha =0.01$ indicates that, in 100 binary sequences, one sequence is rejected. A p-value $\ge 0.01$ shows that the confidence level of an apparently random sequence is $99\%$. Therefore, the sequence of bits generated by the proposed method is random and presents p-values greater than $\alpha$, as shown in

Table 3. NIST 800-22 test result on RNG based on Siponi map with $\alpha =0.01$, parameter $r=2$.

Statistical Test	Our Proposed Method without Post-Processing		[9] with Post-Processing	[9] without Post-Processing
	Proportion	p-Value	p-Value	p-Value
Frequency	$0.984$	$0.328297$	$0.575479$	$0.047704$
Block Frequency	$0.986$	$0.154629$	$0.410214$	$0.94278$
Cumulative Sums	$0.984$	$0.422638$	$0.975089$	$0.03606$
Runs	$0.987$	$0.173770$	$0.044596$	$0.689421$
Longest Run	$0.986$	$0.439122$	$0.024845$	$0.553323$
Rank	$0.991$	$0.091487$	$0.98771$	$0.445713$
FFT	$0.991$	$0.176657$	$0.871131$	$0.721176$
Non-Overlapping Template	$0.996$	$99.32\%$	$100\%$	$99.32\%$
Overlapping Template	$0.986$	$0.197981$	$0.736301$	$0.510453$
Universal	$0.986$	$0.358641$	NA	NA
Approximate Entropy	$0.992$	$0.257004$	$0.513673$	$0.431503$
Random Excursions	$0.992138$	$0.374107$	NA	NA
Random Excursions Variant	$0.998428$	$0.714256$	NA	NA
Serial	$0.992$	$0.585209$	$0.548205$	Failed
Linear Complexity	$0.986$	$0.639202$	$0.082259$	$0.017841$

.

In addition to p-values, NIST 800-22 also produces a proportion value that represents the proportion of sequences that passed the given test. The proportion of a sequence should be within a particular interval, which is calculated using the following formula:

$$(1-\alpha )\pm 3\sqrt{\frac{(1-\alpha )\alpha }{m}},$$

(14)

where m is the number of sequences. Using (14), we should generate sequences with proportions in the interval of 0.9804–0.9994, with $m=1000$. Based on the NIST 800-22 test, Table 3 shows that the output of our method has proportion values that lie within the interval of the proportion.

We compared the results of our proposed method with those of other studies. In Table 3, columns 4 and 5 show the results of the NIST tests produced by the DTC using zigzag maps as proposed by [9], with and without the use of post-processing. Table 3 shows that the proposed method (without post-processing) passed the NIST 800-22 test, and the successful Non-Overlapping Template test passing rate was $99.32\%$. In contrast, the passing rate for the Non-Overlapping Template test using the method in [9] was also equal to $99.32\%$, and, although it failed the Serial test, it passed all tests when using post-processing.

4.5.2. DieHard

DieHard is a statistical test that can be utilized to determine whether a sequence of numbers is random. George Marsagli developed DieHard in 1995 [39]. It consists of 16 tests, and each test generates a p-value = [0, 1). A sequence of numbers fails the test when it obtains a p-value = 1 or 0 on six or more suite tests.

Table 4. DieHard test results.

Statistical Test	Our Proposed Map	[22]
	p-Value	p-Value Avr
Birthday spacing	0.991533	0.02393
Overlapping permutation	0.875032 ≤ p ≤ 0.946973	Failed
Binary rank 31 × 31	0.979577	0.78890
Binary rank 32 × 32	0.997424	0.43108
Binary rank 6 × 8	0.629602	0.39575
Bitstream	0.84723 ≤ p ≤ 0.96382	Failed
OPSO, OQSO, DNA	0.1869 ≤ p ≤ 0.9714	Failed
Count the ones 01	0.6663	0.08874
Count the ones 02	0.393787 ≤ p ≤ 0.924297	0.07288
Parking Lot	0.312673	0.32397
Minimum distance	0.297187	Failed
3DS spheres	0.41720	0.01264
Squeeze	0.947457	Failed
Overlapping sum	0.772100	0.40466
Runs	0.122128 ≤ p ≤ 0.559110	0.85040
Craps	0.12659	F ailed

presents the results of the randomness test using the DieHard test suites. Implementing the proposed map on the RNG generates a bit sequence; every 32 ASCII bits are written in 8 hexadecimal digits. DieHard could test the data with a minimum amount of 80 Mbit. The total data tested in this study is 100 Mbit. Moreover, the test results of these data indicate that the p-values for all types of tests are in the interval range [0, 1), and, based on Ref. [39], the number sequence passed the DieHard test.

Table 4 also shows the results of number sequence testing generated by modifying the PRNG-based logistic map proposed by [22], which fails six DieHard suit tests. Based on these results, the Siponi map is proven to generate a series of random numbers.

4.6. Analysis of Speed

We analyzed the speed of the RNG process with the proposed chaos function. The mean speed required for the nonlinear function block to process the initial value and produce a chaotic output of the floating point is approximately $3987.5$ Mbit/s. The average speed required to process an initial value and generate a sequence of bits, which are the outputs of the comparator as in Figure 1, is $124.61$ Mbit/s. These results indicate that the chaotic function proposed is fast enough to produce a sequence of bits using the IEEE 754-2008 standard for floating-point numbers or a random bit sequence using a comparator block with a threshold value.

4.7. Implementation on FPGA Board

The RNG-based Siponi map architecture on hardware is presented in Figure 15. Although there are three multiplication operations in the Siponi map equation, we designed the system using only one multiplier. In addition, to match our tests on Matlab, we used double-precision floating points for processing floating-point numbers.

There are four steps in this architecture, and they are as follows:

• Controlling parameter multiplication $\left(r^2\right)$.
• Multiplying the outcome of the preceding step by $x_n$.
• Multiplying the second step’s outcome with $(+2/|r\left|\right)$.
• Sampling the data output and holding it for comparison with the threshold value of $0.5$.

A Siponi map-based RNG is implemented on the Altera Cyclone 3 EP3C16F484 board to generate bit sequences. The map equation’s mathematical operations impact how many resources are used by FPGA. In this regard, a summary of RNG’s resource consumption based on the proposed map is given in

Table 5. Chaos-based RNG map resource consumption on the Altera Cyclone 3 EP3C16F484.

Function	DSP	LUT	Register
altfp_mult0	18	554	533
lpm_mux0	0	128	0
lpm_mux1	0	64	0
altfp_compare0	0	169	3
altfp_div0	44	1522	1028
altfp_add_sub0	0	1649	642
Total	62	4086	2206

.

The Siponi map implementation on the FPGA consumes more resources than the implementation of several chaotic functions (which was performed by [40]). The proposed map allows for division and multiple multiplication operations, which increase the usage of FPGA resources.

We utilize the clock unit, because it allows us to implement FPGAs of different types and brands without restriction. With a clock frequency of 40 MHz, the Altera Cyclone 3 EP3C16F484 generates 1.428 Mbit/s of random data. Running one loop of the Siponi map takes 28 clocks in total.

Table 6. The amount of time needed for each mathematical operation.

Operation	Clock Cycle
Multiplication $r.r$	8 clocks
Multiplication $\left(r^2{x}_n\right)$	8 clocks
Multiplication $\left(r^2{x}_n\right)(+2/|r\left|\right)$	8 clocks
Sample and hold data output to compare with $T_h=0.5$	4 clocks

presents the time each mathematical operation on the Siponi map takes.

5. Conclusions

The Siponi map, a novel discrete-time chaotic system based on a Logistic map, was proposed. According to the results of Lyapunov’s exponential and bifurcation analysis, the proposed map has high sensitivity when $r=2$ to $r=2.41$ and $r=-2.41$ to $r=-2$. Furthermore, the keyspace analysis results show that the proposed map generates a keyspace of $2^{107}$, which makes the map’s implementation in the cryptographic system resistant to brute-force attacks.

We created a random-bit generator using the Siponi map. Utilizing an empirical and theoretical PDF analysis of the Siponi map equation with control parameters $r=-2$ and $r=2$, we explored whether the threshold value $T_h=0.5$ could generate a sequence of bits with an average entropy close to 1 and no correlation between the bits in the sequence. According to NIST SP 800-22 and the DieHard statistical suites tests, the bit sequences are also random. A Siponi-map-based RNG requires 4086 LUT, 2206 registers, and 62 DSP to be implemented on an Altera Cyclone 3 EP3C16F484 FPGA. In addition, the total number of clocks required to complete one loop of the Siponi map is 28.