A Novel Discrete-Time Chaos-Function-Based Random-Number Generator: Design and Variability Analysis
Abstract
1. Introduction
2. Preliminaries
2.1. Discrete-Time Chaotic Map
2.2. Logistic Map
3. Proposed Map
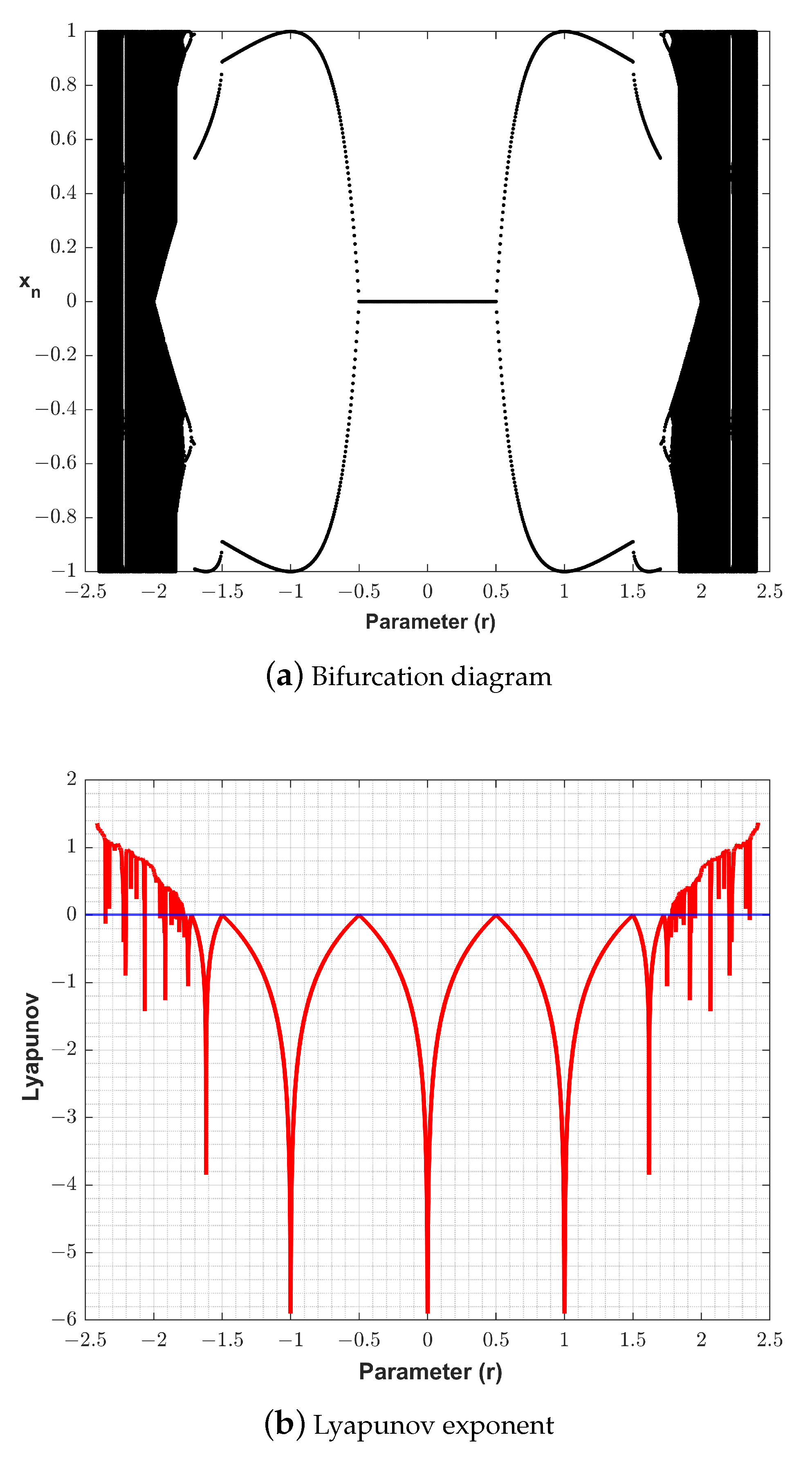
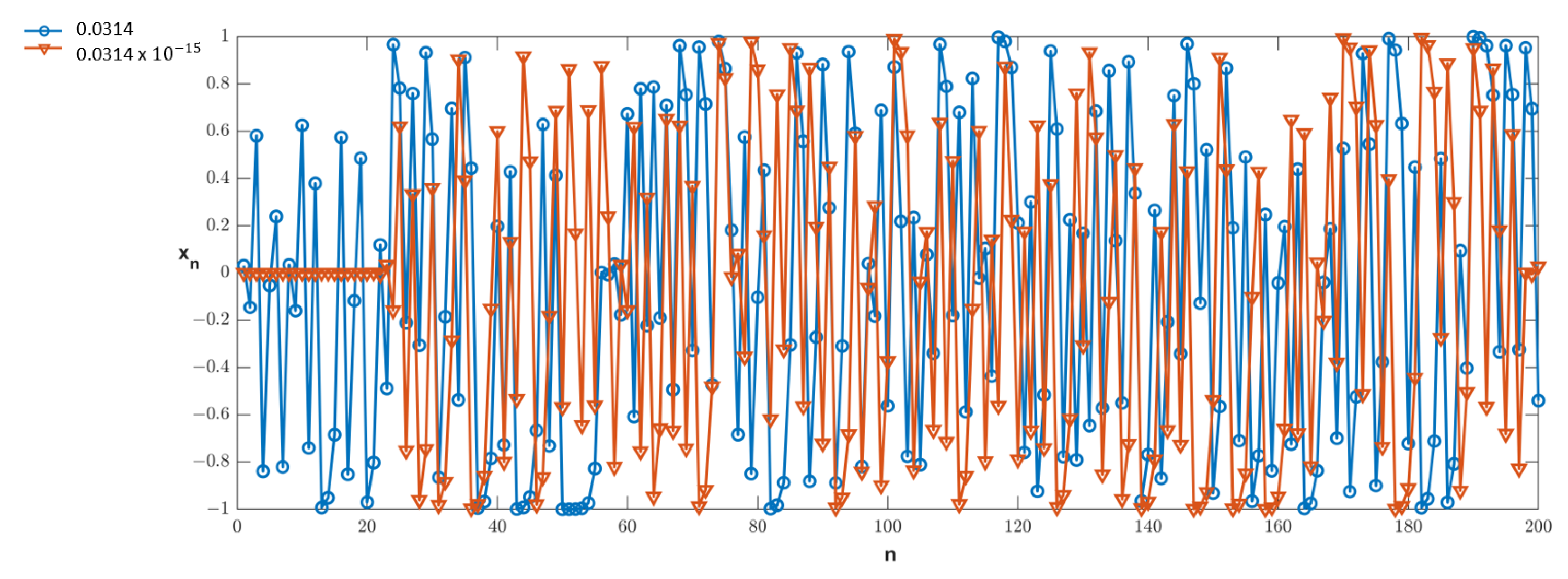
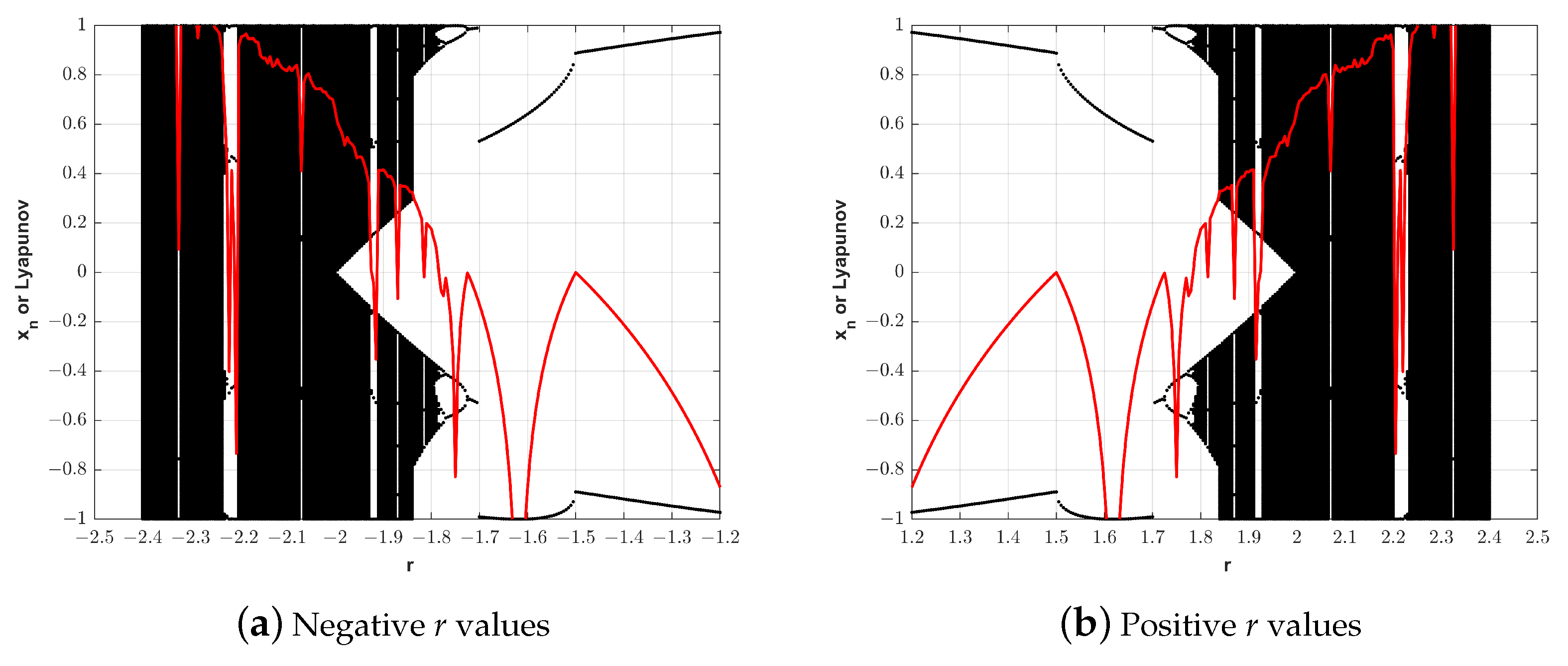
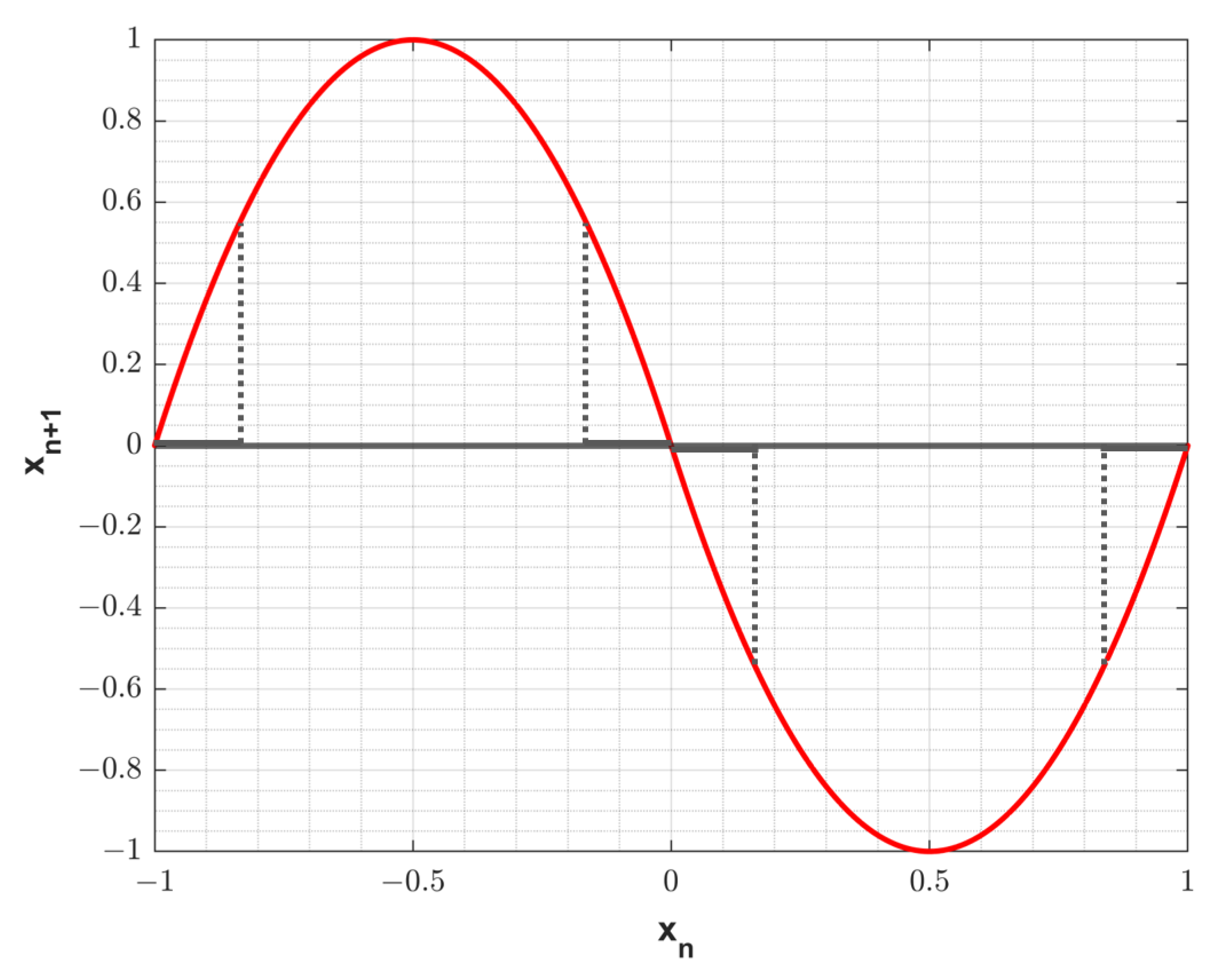
3.1. Siponi Map
3.2. Keyspace Analysis of the Proposed Map
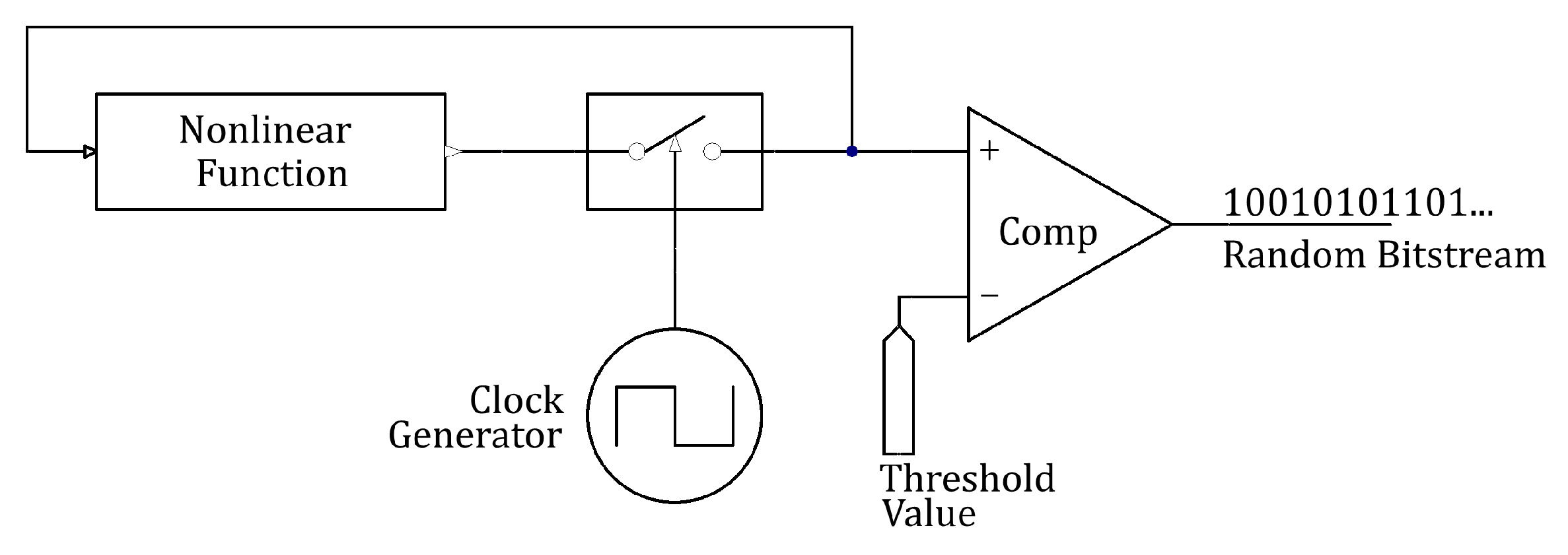
4. Application to Random-Bit Generator
4.1. Entropy Source
4.2. Determine the Threshold Value
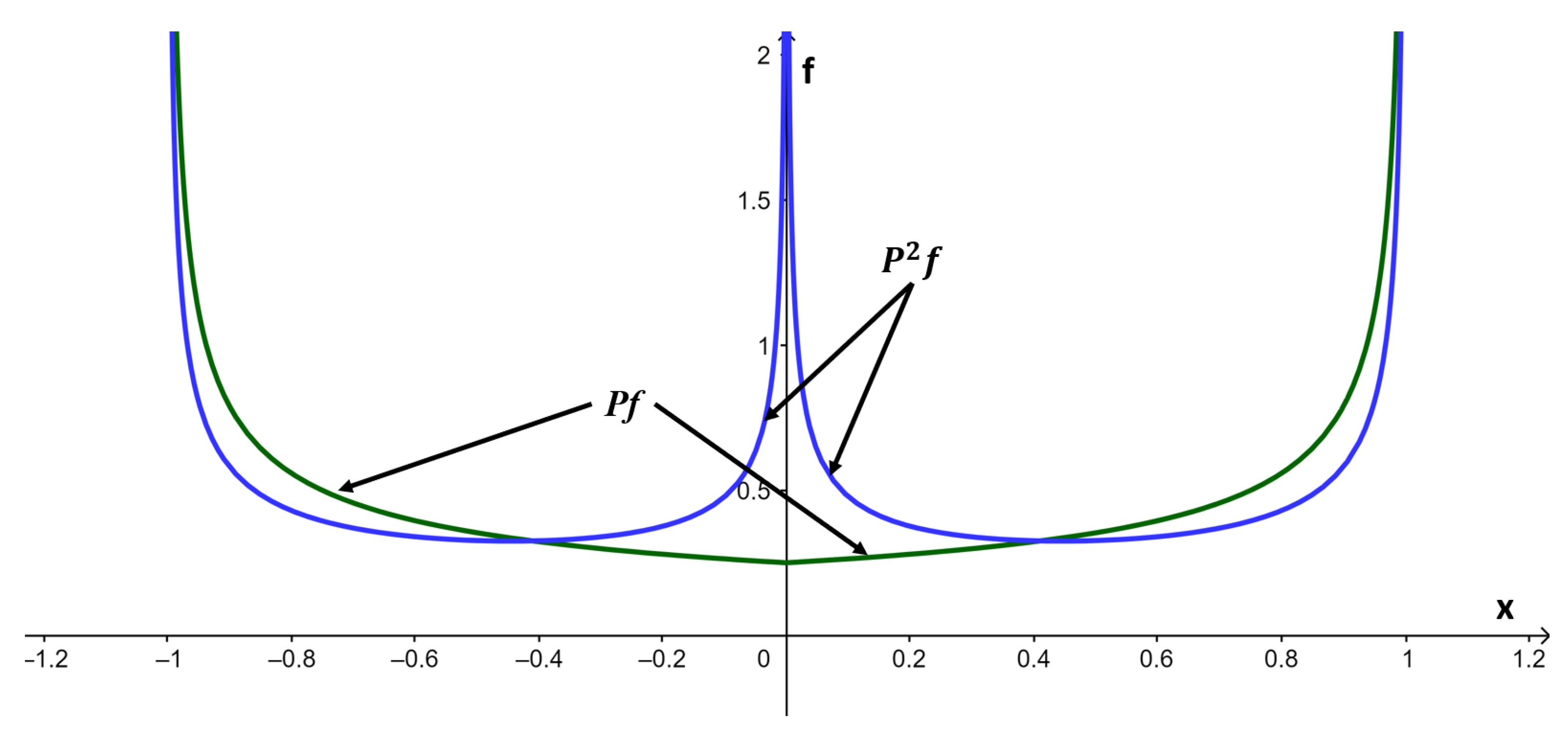
4.2.1. Empirical Probability Density Function (Empirical PDF)
- Creating a histogram of the frequency distribution of the map function output values .
- Dividing by n non-intersecting discrete intervals, the jth interval is:
- Selecting the initial value and calculating the resulting value for each iteration based on the equation:where N is the number of iterations, and .
- Determining the fraction, , of a j th interval:
4.2.2. Optimal Theoretical Threshold Determination for Identical Bit Generation
4.3. The Proposed Random-Bit Generator
4.4. Analysis of Autocorrelation and Entropy
4.4.1. Autocorrelation Analysis
- k, number of lags
- N, number of observations
- , autocorrelation value with lag k
- , observation value of data variable to - t
- , the value of the following variable observation
- , the average value of the observation data.
4.4.2. Entropy Analysis
4.5. Statistical Analysis
4.5.1. NIST SP 800-22
4.5.2. DieHard
4.6. Analysis of Speed
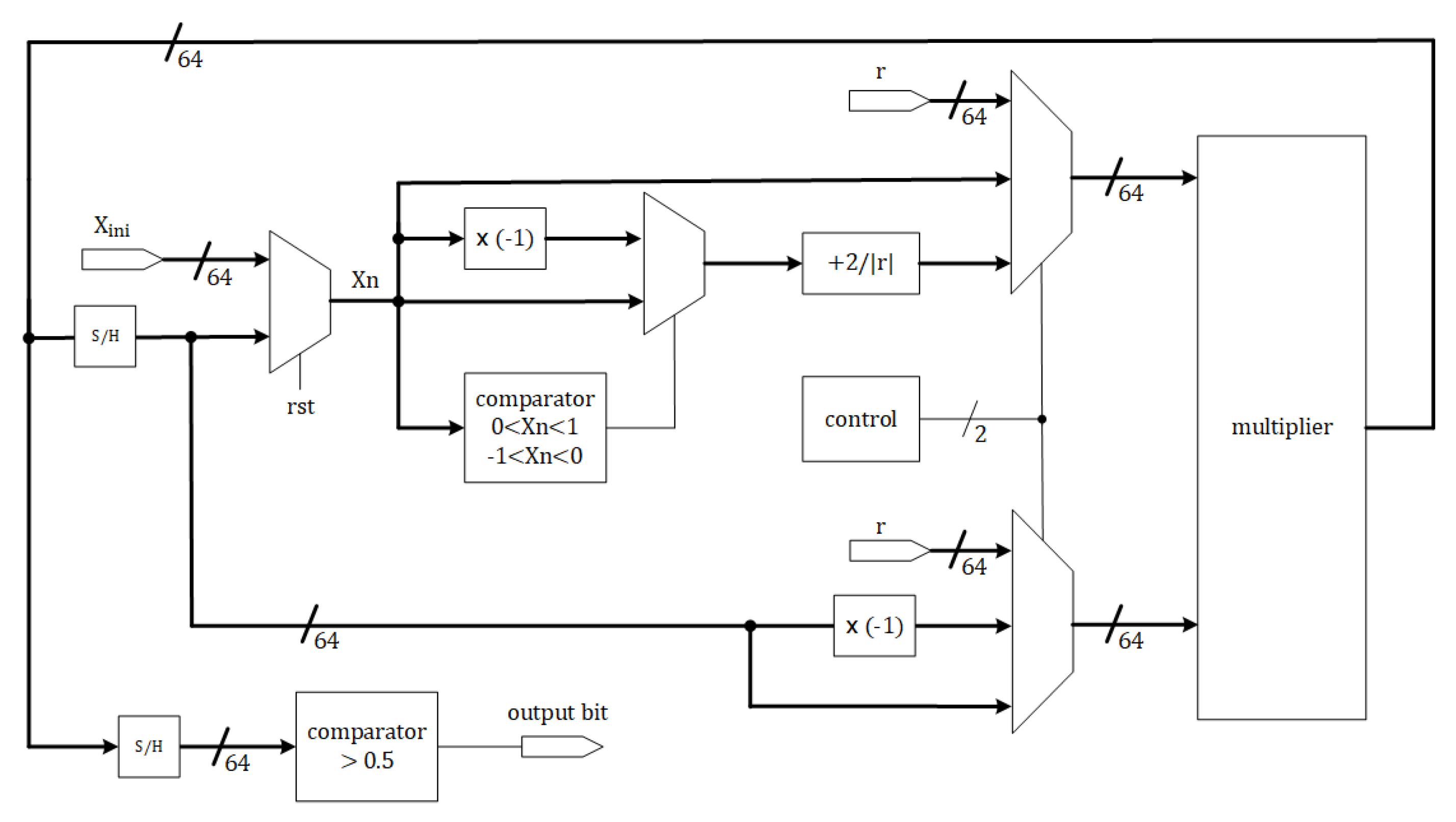
4.7. Implementation on FPGA Board
- Controlling parameter multiplication .
- Multiplying the outcome of the preceding step by .
- Multiplying the second step’s outcome with .
- Sampling the data output and holding it for comparison with the threshold value of .
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Menezes, A.J.; Van Oorschot, P.C.; Vanstone, S.A. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Bruce, S. Applied Cryptography: Protocols, Algorithms, and Source Code in C; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Technical Report; Booz-Allen and Hamilton Inc Mclean va: Fairfax, VA, USA, 2001. [Google Scholar]
- Kocarev, L.; Lian, S. Chaos-Based Cryptography: Theory, Algorithms and Applications; Springer Science & Business Media: Berlin, Heidelberg, Germany, 2011; Volume 354. [Google Scholar]
- Ciçek, I.; Pusane, A.E.; Dündar, G. A novel dual entropy core true random number generator. In Proceedings of the 2013 8th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2013; pp. 332–335. [Google Scholar]
- Cicek, I.; Pusane, A.E.; Dundar, G. A novel design method for discrete time chaos based true random number generators. Integration 2014, 47, 38–47. [Google Scholar] [CrossRef]
- Pareschi, F.; Setti, G.; Rovatti, R. A fast chaos-based true random number generator for cryptographic applications. In Proceedings of the 2006 32nd European Solid-State Circuits Conference, Montreaux, Switzerland, 19–21 September 2006; pp. 130–133. [Google Scholar]
- Callegari, S.; Rovatti, R.; Setti, G. Embeddable ADC-based true random number generator for cryptographic applications exploiting nonlinear signal processing and chaos. IEEE Trans. Signal Process. 2005, 53, 793–805. [Google Scholar] [CrossRef]
- Nejati, H.; Beirami, A.; Ali, W.H. Discrete-time chaotic-map truly random number generators: Design, implementation, and variability analysis of the zigzag map. Analog Integr. Circuits Signal Process. 2012, 73, 363–374. [Google Scholar] [CrossRef]
- Moysis, L.; Volos, C.; Jafari, S.; Munoz-Pacheco, J.M.; Kengne, J.; Rajagopal, K.; Stouboulos, I. Modification of the logistic map using fuzzy numbers with application to pseudorandom number generation and image encryption. Entropy 2020, 22, 474. [Google Scholar] [CrossRef] [PubMed]
- Moysis, L.; Tutueva, A.; Volos, C.; Butusov, D.; Munoz-Pacheco, J.M.; Nistazakis, H. A two-parameter modified logistic map and its application to random bit generation. Symmetry 2020, 12, 829. [Google Scholar] [CrossRef]
- Magfirawaty; Suryadi, M.T.; Ramli, K. Performance analysis of zigzag map and hash function to generate random number. In Proceedings of the 2017 International Conference on Electrical Engineering and Informatics (ICELTICs), Banda Aceh, Indonesia, 18–20 October 2017; pp. 297–301. [Google Scholar]
- Han, C. An image encryption algorithm based on modified logistic chaotic map. Optik 2019, 181, 779–785. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Z.; Li, L.; Zou, X. A low-cost low-power ring oscillator-based truly random number generator for encryption on smart cards. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 608–612. [Google Scholar] [CrossRef]
- Cao, J.; Chugh, R. Chaotic behavior of logistic map in superior orbit and an improved chaos-based traffic control model. Nonlinear Dyn. 2018, 94, 959–975. [Google Scholar]
- Alawida, M.; Samsudin, A.; Teh, J.S.; Alshoura, W.H. Digital cosine chaotic map for cryptographic applications. IEEE Access 2019, 7, 150609–150622. [Google Scholar] [CrossRef]
- Dhall, S.; Pal, S.K.; Sharma, K. A chaos-based probabilistic block cipher for image encryption. J. King Saud Univ. Comput. Inf. Sci. 2018, 34, 1533–1543. [Google Scholar] [CrossRef]
- Kodỳtek, F.; Lórencz, R. A design of ring oscillator based PUF on FPGA. In Proceedings of the 2015 IEEE 18th International Symposium on Design and Diagnostics of Electronic Circuits & Systems, Belgrade, Serbia, 22–24 April 2015; pp. 37–42. [Google Scholar]
- Magfirawaty; Lestari, A.A.; Suryadi, M.; Ramli, K. Modified logistic maps for discrete time chaos based random number generator. In Proceedings of the 2018 International Conference on Electrical Engineering and Computer Science (ICECOS), Pangkal Pinang, Indonesia, 2–4 October 2018; pp. 391–396. [Google Scholar]
- Von Neumann, J. 13. various techniques used in connection with random digits. Appl. Math. Ser. 1951, 12, 3. [Google Scholar]
- Dang, Q. Recommendation for Applications Using Approved Hash Algorithms; Special Publication (NIST SP); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2012. Available online: https://tsapps.nist.gov/publication/getpdf.cfm?pubid=911479 (accessed on 16 September 2022).
- Merah, L.; Lorenz, P.; Adda, A.P. A New and Efficient Scheme for Improving the Digitized Chaotic Systems from Dynamical Degradation. IEEE Access 2021, 9, 88997–89008. [Google Scholar] [CrossRef]
- Cicek, I.; Pusane, A.E.; Dundar, G. An integrated dual entropy core true random number generator. IEEE Trans. Circuits Syst. II Express Briefs 2016, 64, 329–333. [Google Scholar] [CrossRef]
- Jessa, M.; Jaworski, M. Randomness of a combined TRNG based on the ring oscillator sampling method. In Proceedings of the ICSES 2010 International Conference on Signals and Electronic Circuits, Gliwice, Poland, 7–10 September 2010; pp. 323–326. [Google Scholar]
- Patidar, V.; Sud, K.K.; Pareek, N.K. A pseudo random bit generator based on chaotic logistic map and its statistical testing. Informatica 2009, 33, 441–452. [Google Scholar]
- Borujeni, S.E.; Ehsani, M.S. Modified logistic maps for cryptographic application. Appl. Math. 2015, 6, 773. [Google Scholar] [CrossRef]
- Huang, W. Constructing an opposite map to a specified chaotic map. Nonlinearity 2005, 18, 1375. [Google Scholar] [CrossRef]
- Beirami, A.; Nejati, H.; Massoud, Y. A performance metric for discrete-time chaos-based truly random number generators. In Proceedings of the 2008 51st Midwest Symposium on Circuits and Systems, Knoxville, TN, USA, 10–13 August 2008; pp. 133–136. [Google Scholar]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Kahan, W. IEEE standard 754 for binary floating-point arithmetic. Lect. Notes Status IEEE 1996, 754, 11. [Google Scholar]
- Irfan, M.; Ali, A.; Khan, M.A.; Ehatisham-ul Haq, M.; Mehmood Shah, S.N.; Saboor, A.; Ahmad, W. Pseudorandom number generator (PRNG) design using hyper-chaotic modified robust logistic map (HC-MRLM). Electronics 2020, 9, 104. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Ma, J.; He, H. A pseudorandom number generator based on piecewise logistic map. Nonlinear Dyn. 2016, 83, 2373–2391. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, H. Pseudo-random number generator based on logistic chaotic system. Entropy 2019, 21, 960. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.; Cruz-Hernández, C.; Cardoza-Avendaño, L.; Méndez-Ramírez, R. A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dyn. 2017, 87, 407–425. [Google Scholar] [CrossRef]
- Behnia, S.; Akhavan, A.; Akhshani, A.; Samsudin, A. A novel dynamic model of pseudo random number generator. J. Comput. Appl. Math. 2011, 235, 3455–3463. [Google Scholar] [CrossRef][Green Version]
- Lasota, A.; Mackey, M.C. Chaos, Fractals, and Noise: Stochastic Aspects of Dynamics; Springer Science & Business Media: Berlin, Heidelberg, Germany, 1998; Volume 97. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Ma, X.; Xu, F.; Xu, H.; Tan, X.; Qi, B.; Lo, H.K. Postprocessing for quantum random-number generators: Entropy evaluation and randomness extraction. Phys. Rev. A 2013, 87, 062327. [Google Scholar] [CrossRef]
- Marsaglia, G. The Marsaglia Random Number CDROM Including the Diehard Battery of Tests of Randomness. 2008. Available online: https://web.archive.org/web/20160125103112/http:/stat.fsu.edu/pub/diehard/ (accessed on 16 September 2022).
- De la Fraga, L.G.; Torres-Pérez, E.; Tlelo-Cuautle, E.; Mancillas-López, C. Hardware implementation of pseudo-random number generators based on chaotic maps. Nonlinear Dyn. 2017, 90, 1661–1670. [Google Scholar] [CrossRef]








| Study | Control Parameter | Initial Value | Keyspace |
|---|---|---|---|
| Proposed work | , , , , , , , | , | × |
| [31] | 27 × | ||
| [33] | 0.4301 × | ||
| [32] | 4 × | ||
| [34] | 0.001 × | ||
| [35] | 1 × |
| Sequences | Minimum Value | Maximum Value |
|---|---|---|
| First sequence | ||
| Second sequence | ||
| Third sequence | ||
| Fourth sequence |
| Statistical Test | Our Proposed Method without Post-Processing | [9] with Post-Processing | [9] without Post-Processing | |
|---|---|---|---|---|
| Proportion | p-Value | p-Value | p-Value | |
| Frequency | ||||
| Block Frequency | ||||
| Cumulative Sums | ||||
| Runs | ||||
| Longest Run | ||||
| Rank | ||||
| FFT | ||||
| Non-Overlapping Template | ||||
| Overlapping Template | ||||
| Universal | NA | NA | ||
| Approximate Entropy | ||||
| Random Excursions | NA | NA | ||
| Random Excursions Variant | NA | NA | ||
| Serial | Failed | |||
| Linear Complexity | ||||
| Statistical Test | Our Proposed Map | [22] |
|---|---|---|
| p-Value | p-Value Avr | |
| Birthday spacing | 0.991533 | 0.02393 |
| Overlapping permutation | 0.875032 ≤ p ≤ 0.946973 | Failed |
| Binary rank 31 × 31 | 0.979577 | 0.78890 |
| Binary rank 32 × 32 | 0.997424 | 0.43108 |
| Binary rank 6 × 8 | 0.629602 | 0.39575 |
| Bitstream | 0.84723 ≤ p ≤ 0.96382 | Failed |
| OPSO, OQSO, DNA | 0.1869 ≤ p ≤ 0.9714 | Failed |
| Count the ones 01 | 0.6663 | 0.08874 |
| Count the ones 02 | 0.393787 ≤ p ≤ 0.924297 | 0.07288 |
| Parking Lot | 0.312673 | 0.32397 |
| Minimum distance | 0.297187 | Failed |
| 3DS spheres | 0.41720 | 0.01264 |
| Squeeze | 0.947457 | Failed |
| Overlapping sum | 0.772100 | 0.40466 |
| Runs | 0.122128 ≤ p ≤ 0.559110 | 0.85040 |
| Craps | 0.12659 | F ailed |
| Function | DSP | LUT | Register |
|---|---|---|---|
| altfp_mult0 | 18 | 554 | 533 |
| lpm_mux0 | 0 | 128 | 0 |
| lpm_mux1 | 0 | 64 | 0 |
| altfp_compare0 | 0 | 169 | 3 |
| altfp_div0 | 44 | 1522 | 1028 |
| altfp_add_sub0 | 0 | 1649 | 642 |
| Total | 62 | 4086 | 2206 |
| Operation | Clock Cycle |
|---|---|
| Multiplication | 8 clocks |
| Multiplication | 8 clocks |
| Multiplication | 8 clocks |
| Sample and hold data output to compare with | 4 clocks |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magfirawaty, M.; Lestari, A.A.; Nurwa, A.R.A.; MT, S.; Ramli, K. A Novel Discrete-Time Chaos-Function-Based Random-Number Generator: Design and Variability Analysis. Symmetry 2022, 14, 2122. https://doi.org/10.3390/sym14102122
Magfirawaty M, Lestari AA, Nurwa ARA, MT S, Ramli K. A Novel Discrete-Time Chaos-Function-Based Random-Number Generator: Design and Variability Analysis. Symmetry. 2022; 14(10):2122. https://doi.org/10.3390/sym14102122
Chicago/Turabian StyleMagfirawaty, Magfirawaty, Andriani Adi Lestari, Agus Reza Aristiadi Nurwa, Suryadi MT, and Kalamullah Ramli. 2022. "A Novel Discrete-Time Chaos-Function-Based Random-Number Generator: Design and Variability Analysis" Symmetry 14, no. 10: 2122. https://doi.org/10.3390/sym14102122
APA StyleMagfirawaty, M., Lestari, A. A., Nurwa, A. R. A., MT, S., & Ramli, K. (2022). A Novel Discrete-Time Chaos-Function-Based Random-Number Generator: Design and Variability Analysis. Symmetry, 14(10), 2122. https://doi.org/10.3390/sym14102122









