The Analytical Solutions of Stochastic-Fractional Drinfel’d-Sokolov-Wilson Equations via (G′/G)-Expansion Method

Abstract

Fractional–stochastic Drinfel’d–Sokolov–Wilson equations (FSDSWEs) forced by multiplicative Brownian motion are assumed. This equation is employed in mathematical physics, plasma physics, surface physics, applied sciences, and population dynamics. The $(G^{\prime }/G)$-expansion method is utilized to find rational, hyperbolic, and trigonometric stochastic solutions for FSDSWEs. Because of the priority of FSDSWEs, the derived solutions are more useful and effective in understanding various important physical phenomena. Furthermore, we used the MATLAB package to create 3D graphs for specific solutions in order to investigate the effect of fractional-order and Brownian motions on the solutions of FSDSWEs.

1. Introduction

Nonlinear evolution equation (NLEE) research has focused on many areas of nonlinear science, including geochemistry, plasma physics, solid-state physics, fluid mechanics, optical fibers, nuclear physics, and chemical physics. Many authors planned to create traveling wave solutions for NLEEs by using a variety of analytical and numerical approaches. To achieve exact solutions to these equations, a various of methods were used, such as Darboux transformation [1], sine–cosine [2,3], Hirota’s function [4], $(G^{\prime }/G)$-expansion [5,6,7], the robust method [8], the Lyapunov functional [9], gamma transform correction methods [10], state damping control [11], perturbation [12,13], Riccati–Bernoulli sub-ODE [14], $exp(-\varphi (\varsigma \left)\right)$-expansion [15], tanh-sech [16,17], and the Jacobi elliptic function [18,19].

Recently, random perturbations in practically physical systems have arisen from a wide range of external inputs. They cannot be ignored, since noise can create statistical characteristics and important phenomena. Therefore, stochastic differential equations (SDEs) appeared and became important in modeling phenomena in atmosphere, fluid mechanics, oceanography, chemistry, physics, biology, and other sciences [20,21,22,23]. On the other hand, fractional derivatives are used to represent several important phenomena, including anomalous diffusion, electrochemistry, acoustics, image processing, and electromagnetism. One of the advantages of fractional models is that they can be described more accurately than integer models can, which pushed us to define several major and useful fractional models. In general, finding exact solutions to SDEs with fractional derivatives is more difficult than finding exact solutions to classical ones.

As a result, the following stochastic-fractional Drinfel’d–Sokolov–Wilson equations (SFDSWEs) are considered:

$$d\psi +\left[{\gamma }_1\phi {\mathbb{T}}_x^{\delta }\phi \right]dt=\rho \psi d\beta ,$$

(1)

$$d\phi +[{\gamma }_2{\mathbb{T}}_{xxx}^{\delta }\phi +{\gamma }_3\psi {\mathbb{T}}_x^{\delta }\phi +{\gamma }_4\phi {\mathbb{T}}_x^{\delta }\psi ]dt=\rho \phi d\beta ,$$

(2)

where $\psi =\psi (x,t)$, $\phi =\phi (x,t)$ and ${\gamma }_i$ for $i=1,2,3,4$ are nonzero constants. $T^{\delta },$ for $0<\delta \le 1$, is the conformable derivative (CD) [24]. $\beta =\beta \left(t\right)$ is a standard Brownian motion (SBM), and $\rho$ is the noise strength.

Drinfel’d–Sokolov–Wilson equations (DSWEs) (1) and (2) with $\delta =1$ and $\rho =0$ develop from shallow-water wave models that Drinfel’d and Sokolov [25,26] first provided, and Wilson later refined [27]. Additionally, this model is employed in surface physics, plasma physics, applied sciences, population dynamics, and mathematical physics. Because of the significance of DSWEs, a number of researchers proposed the exact solutions for this system via different approaches, including tanh and extended tanh methods [28], the homotopy analysis method [29], the $F-$ expansion method [30], the truncated Painlevè method [31], and the exp-function method [32]. A few authors also used various approaches, such as the discrimination system for polynomial [33] and Jacobi elliptical function method [34], to find accurate solutions for fractional DSW.

The originality of this work is to obtain a wide range of stochastic–fractional solutions for SFDSWEs (1) and (2), including hyperbolic, rational, and trigonometric functions, by utilizing the $(G^{\prime }/G)$-expansion method. This study is the first to acquire stochastic–fractional solutions of SFDSWEs by using the $(G^{\prime }/G)$-expansion method in the presence of noise and fractional derivatives. In addition, we used MATLAB tools to build 3D plots for some of the solutions of SFDSWEs (1) and (2), created in this work to highlight how the SBM influences these solutions. Lastly, we deduce that the noise term and fractional-order impact the stability and symmetry of the obtained solutions.

The rest of this paper is organized as follows: In Section 2, we introduce the definitions and properties of CD and SBM. In Section 3, we explain the $(G^{\prime }/G)$-expansion method. In Section 4, to derive the wave equation for SFDSWEs (1) and (2), we employ a suitable wave transformation. In Section 5, we obtain the analytic solutions of SFDSWEs (1) and (2). In Section 6, we address the impact of the SBM and fractional order on the solutions. Section 7 presents the paper’s conclusion.

2. Preliminaries

We now introduce the definitions and properties of CD and SBM. We define CD as follows:

Definition 1

([24]). The CD of $P:R^{+}\to R$ of order δ is defined as follows:

$${\mathbb{T}}_x^{\delta }P\left(z\right)=\underset{\kappa \to 0}{lim}\frac{P(z+\kappa z^{1-\delta })-P\left(z\right)}{\kappa }.$$

Theorem 1

([24]). Assume that $P_1,P_2:R^{+}\to R$ are δ differentiable functions, then

$${\mathbb{T}}_x^{\delta }(P_1\circ P_2)\left(z\right)=z^{1-\delta }{P}_2^{\prime }\left(x\right)P_1\left(P_2\left(x\right)\right).$$

The CD had the following properties:

• $T_z^{\delta }[c_1{P}_1\left(z\right)+c_2{P}_2\left(z\right)]=c_1{T}_x^{\delta }{P}_1\left(z\right)+c_2{T}_x^{\delta }{P}_2\left(z\right),c_1,c_2\in R,$
• $T_z^{\delta }\left[C\right]=0,C$ is a constant,
• $T_z^{\delta }\left[z^k\right]=k{z}^{k-\delta },k\in \mathbb{R},$
• $T_z^{\delta }P\left(x\right)=z^{1-\delta }\frac{dP}{dx}.$

Definition 2

([35]). Stochastic process ${\left\{\beta \left(t\right)\right\}}_{t\ge 0}$ is an SBM if

• $\beta \left(0\right)=0,$
• For $t_1<t_2,$$\beta \left(t_1\right)-\beta \left(t_2\right)$ is independent,
• $\beta \left(t\right),$$t\ge 0$ is a continuous function of t,
• $\beta \left(t_2\right)-\beta \left(t_1\right)$ has normal distribution with variance $t_2-t_1$ and mean 0.

Lemma 1

([35]). $E\left(e^{\alpha \beta \left(t\right)}\right)=e^{\frac{1}{2}{\alpha }^{2}t}$ for $\alpha \ge 0$.

3. The $({\mathit{G}}^{\prime }/\mathit{G})$-Expansion Method Description

It is helpful to outline the main steps presented in [5]:

1.

First, a general form of the nonlinear equation in the fractional space of stochastic processes is considered:

$$P(u{\beta }_t,u,u_t,{\mathbb{T}}_x^{\delta }\psi ,{\mathbb{T}}_{xx}^{\delta }\psi ,\dots )=0.$$

(3)

2.

To obtain the traveling wave equation of Equation (3), we introduce

$$\psi (t,x)=u\left(\xi \right)e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\xi =\frac{1}{\delta }{x}^{\delta }+\theta t,$$

(4)

where the localized wave solution $u\left(\xi \right)$ is a deterministic function, and $\theta$ is a constant. As a result, we perform the following changes:

$$\begin{array}{ccc}\hfill \frac{\partial \psi }{\partial t}& =& (-\theta u^{\prime }+\rho u\frac{d\beta }{dt}+\frac{1}{2}{\rho }^{2}u-\frac{1}{2}{\rho }^{2}u)e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\hfill \\ \hfill {\mathbb{T}}_x^{\delta }\psi & =& u^{\prime }{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\hfill \\ & & ⋮⋮⋮⋮⋮\hfill \\ \hfill {\mathbb{T}}_{x^n}^{\delta }\psi & =& u^{\left(n\right)}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\hfill \end{array}$$

(5)

where $+\frac{1}{2}{\rho }^{2}u$ is the itô correction term. Using (5) changes the PDE (3) to a stochastic ordinary differential equation (SODE):

$$P(u{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},u^{‵}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},u^{‵‵}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\dots )=0.$$

3.

To remove the stochastic term from Equation (6), we took an expectation on both sides to obtain a deterministic ODE in the following form:

$$P(u,u^{‵},u^{‵‵},\dots )=0.$$

(6)

4.

The ansatz is introduced:

$$u=\sum _{k=0}^N{\hslash }_k{\left[\frac{G^{\prime }}{G}\right]}^k,\mathrm{such}\mathrm{that}{\hslash }_N\ne 0,$$

(7)

where G solves the second ODE:

$$G^{″}+\lambda G^{\prime }+\nu G=0,$$

(8)

where $\lambda ,\nu$ are undefined constants. In most situations, N is a positive integer that is calculated. Putting (7) into ODE (6) yields an equation in powers of $G^{\prime }/G$.

5.

To calculate parameter N, we follow these steps: First, we define the degree of u as $D\left[u\right]=N.$ Second, we determine the highest order nonlinear and highest-order derivatives in Equation (6) as follows:

$$D\left[\frac{d^{n}u}{d{\xi }^n}\right]=N+n,$$

and

$$D\left[u^p{\left(\frac{d^{n}u}{d{\xi }^n}\right)}^s\right]=pN+s(N+n).$$

With the N calculated, the coefficients of $G^{\prime }/G$ are equated in the obtained equation. As a result, a set of algebraic equations containing ${\hslash }_k$ ($k=0,1,\dots ,N$), $\nu$, and $\lambda$ are produced. We then solve the system to find these constants. Next, relying on the sign of $\Delta ={\lambda }^2-4\nu ,$ we have the solutions of Equation (6).

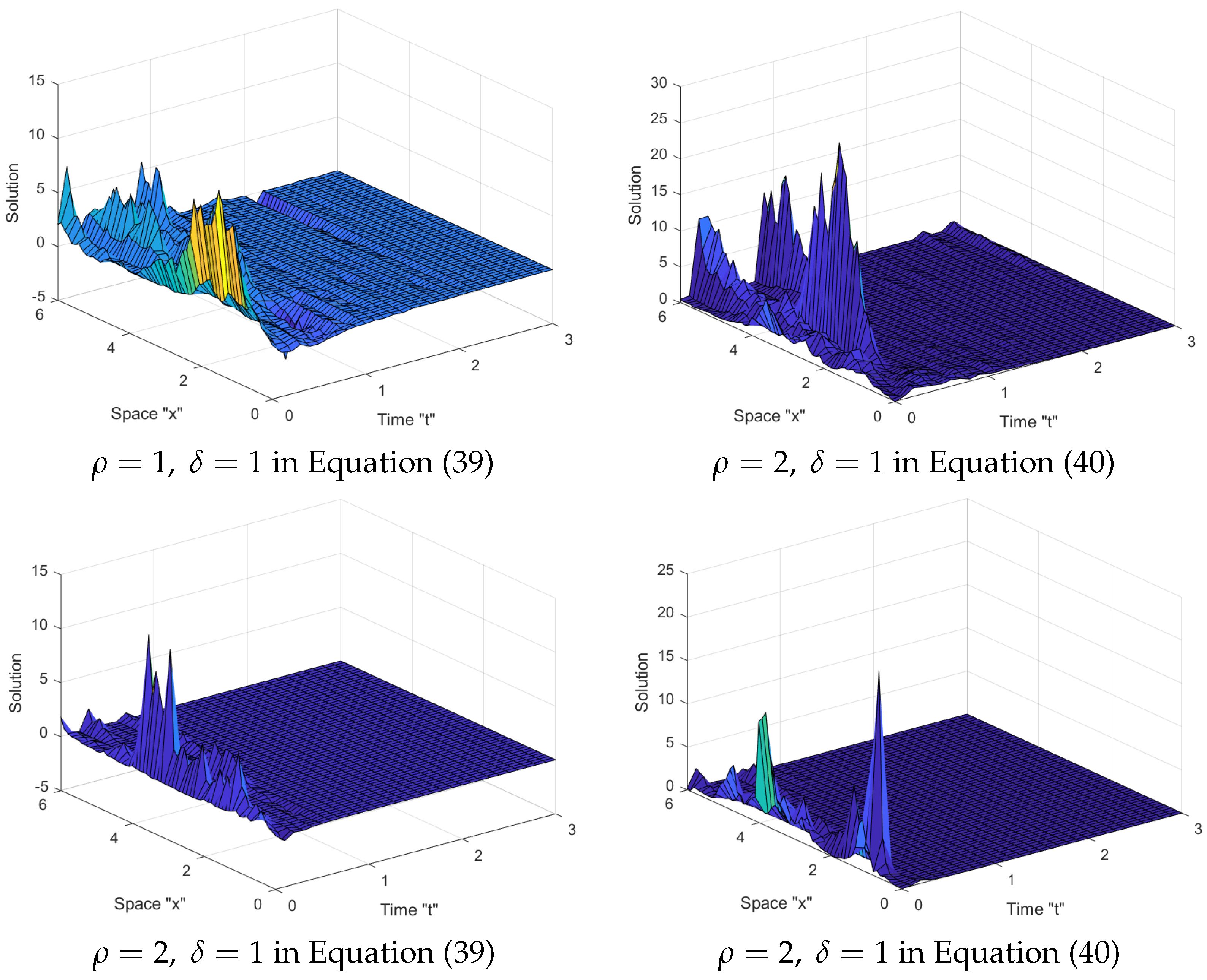
4. Wave Equation for SFDSWEs

To construct the wave equation for SFDSWEs (1) and 2), we apply the following wave transformation:

$$\psi (x,t)=v\left(\xi \right)e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\phi (x,t)=u\left(\xi \right)e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\xi =\frac{1}{\delta }{x}^{\delta }+\theta t,$$

(9)

where v and u are real deterministic functions. Substituting Equation (9) into Equations (1) and (2), and utilizing

$$\begin{array}{ccc}\hfill d\psi & =& [\theta v^{\prime }dt+\rho vd\beta ]e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\hfill \\ \hfill d\phi & =& [\theta u^{\prime }dt+\rho ud\beta ]e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\hfill \\ \hfill {\mathbb{T}}_x^{\delta }\phi & =& u^{\prime }{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},{\mathbb{T}}_x^{\delta }\psi =v^{\prime }{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\hfill \\ \hfill {\mathbb{T}}_{xxx}^{\delta }\phi & =& u^{‴}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},\hfill \end{array}$$

(10)

we obtain

$$\begin{array}{ccc}\hfill \theta v^{\prime }+{\gamma }_{1}u{u}^{\prime }{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)}& =& 0,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill \theta u^{\prime }+{\gamma }_2{u}^{‴}+{\gamma }_{3}v{u}^{\prime }{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)}+{\gamma }_{4}u{v}^{\prime }{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)}& =& 0.\hfill \end{array}$$

(12)

By taking expectation $\mathbb{E}(·)$ for Equations (11) and (12), we have

$$\begin{array}{ccc}\hfill \theta v^{\prime }+{\gamma }_{1}u{u}^{\prime }{e}^{-\frac{1}{2}{\rho }^{2}t}\mathbb{E}\left(e^{\rho \beta \left(t\right)}\right)& =& 0,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill \theta u^{\prime }+{\gamma }_2{u}^{‴}+[{\gamma }_{3}v{u}^{\prime }+{\gamma }_{4}u{v}^{\prime }]e^{-\frac{1}{2}{\rho }^{2}t}\mathbb{E}\left(e^{\rho \beta \left(t\right)}\right)& =& 0.\hfill \end{array}$$

(14)

Using Lemma 4, we obtain

$$\begin{array}{ccc}\hfill \theta v^{\prime }+{\gamma }_{1}u{u}^{\prime }& =& 0,\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill \theta u^{\prime }+{\gamma }_2{u}^{‴}+{\gamma }_{3}v{u}^{\prime }+{\gamma }_{4}u{v}^{\prime }& =& 0.\hfill \end{array}$$

(16)

Integrating Equation (15), we have

$$v=-\frac{{\gamma }_1}{\theta }{u}^2+C,$$

(17)

where C is the constant of the integral. Putting Equation (17) into (16) and utilizing Equation (15), we have

$${\gamma }_2{u}^{‴}-[\frac{{\gamma }_1{\gamma }_3}{2\theta }+\frac{{\gamma }_1{\gamma }_4}{\theta }]u^2{u}^{\prime }+[\theta +C{\gamma }_3]u^{\prime }=0.$$

(18)

Integrating Equation (18), we obtain the following wave equation:

$$u^{″}-{\ell }_1{u}^3+{\ell }_{2}u=0,$$

(19)

where

$${\ell }_1=\frac{{\gamma }_1{\gamma }_3}{6{\gamma }_2\theta }+\frac{{\gamma }_1{\gamma }_4}{3{\gamma }_2\theta }\mathrm{and}{\ell }_2=\frac{\theta }{{\gamma }_2}+\frac{C{\gamma }_3}{{\gamma }_2}.$$

5. Analytical Solutions of SFDSWEs

Assuming that the solution of (19) has the form (7), by equating the order of $u^3$ and $u^{″}$ in (7), we have $N=1$. Now, rewriting Equation (7) with $N=1,$ we attain

$$u\left(\xi \right)={\hslash }_0+{\hslash }_1\left[\frac{G^{\prime }}{G}\right].$$

(20)

Putting Equation (20) into Equation (19) and utilizing Equation (8), we obtain:

$$\begin{array}{ccc}& & (2{\hslash }_1-{\ell }_1{\hslash }_1^3){\left[\frac{G^{\prime }}{G}\right]}^3+(3\lambda {\hslash }_1-3{\ell }_1{\hslash }_0{\hslash }_1^2){\left[\frac{G^{\prime }}{G}\right]}^2\hfill \\ & & +({\lambda }^2{\hslash }_1+2{\hslash }_1\nu -3{\ell }_1{\hslash }_1{\hslash }_0^2+{\ell }_2{\hslash }_1)\left[\frac{G^{\prime }}{G}\right]\hfill \end{array}$$

$$+(\nu \lambda {\hslash }_1-{\ell }_1{\hslash }_0^2{\hslash }_1+{\ell }_2{\hslash }_0)=0.$$

Setting each coefficient of ${\left[\frac{G^{\prime }}{G}\right]}^j$ for $j=3,2,1,0$ equal zero:

$$2{\hslash }_1-{\ell }_1{\hslash }_1^3=0,$$

$$3\lambda {\hslash }_1-3{\ell }_1{\hslash }_0{\hslash }_1^2=0,$$

$${\lambda }^2{\hslash }_1+2{\hslash }_1\nu -3{\ell }_1{\hslash }_1{\hslash }_0^2+{\ell }_2{\hslash }_1=0,$$

and

$$\nu \lambda {\hslash }_1-{\ell }_1{\hslash }_0^3+{\ell }_2{\hslash }_0=0.$$

Solving this system, we have for ${\ell }_1>0$:

$${\hslash }_1=\pm \sqrt{\frac{2}{{\ell }_1}},\lambda =\mathrm{any}\mathrm{real}\mathrm{number},{\hslash }_0=\pm \frac{\lambda }{\sqrt{2{\ell }_1}},\nu =\frac{{\lambda }^2}{4}-\frac{{\ell }_2}{2}.$$

(21)

The roots of auxiliary Equation (8) are:

$$\frac{-\lambda }{2}\pm \sqrt{\frac{{\ell }_2}{2}}.$$

(22)

There are three sets for the solutions of Equation (8) relying on the value of ${\ell }_2.$

Set I: If ${\ell }_2=0$, then Roots (22) are equal, and the solution of Equation (8) is:

$$G\left(\xi \right)=c_{1}exp\left(\frac{-\lambda }{2}\xi \right)+c_2\xi exp\left(\frac{-\lambda }{2}\xi \right),$$

where $c_1,c_2$ are constants. Hence, the solution of Equation (19) by using Equation (20) is:

$$u\left(\xi \right)=\pm \sqrt{\frac{2}{{\ell }_1}}\left[\frac{c_2}{c_1+c_2\xi }\right].$$

(23)

Consequently, the exact solutions of SFDSWEs (1-2) in this status are rational as follows:

$$\phi (x,t)=\pm \sqrt{\frac{2}{{\ell }_1}}\left[\frac{c_2}{c_1+c_2\xi }\right]e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(24)

$$\psi (x,t)=\left\{-\frac{2{\gamma }_1}{\theta {\ell }_1}{\left[\frac{c_2}{c_1+c_2\xi }\right]}^2+C\right\}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

where $\xi =\frac{1}{\delta }{x}^{\delta }+\theta t.$

Set II: If ${\ell }_2<0$, then Roots (22) are complex, and the solution of Equation (8) is:

$$G\left(\xi \right)=exp\left(\frac{-\lambda }{2}\xi \right)\left[c_{1}cos\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)+c_{2}sin\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)\right].$$

Hence, the solution of Equation (19) is:

$$u\left(\xi \right)=\pm \frac{-c_1\sqrt{\frac{-{\ell }_2}{{\ell }_1}}sin\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)+c_2\sqrt{\frac{-{\ell }_2}{{\ell }_1}}cos\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)}{c_{1}cos\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)+c_{2}sin\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)}.$$

(25)

Therefore, the solutions of SFDSWEs (1) and (2) in this status are trigonometric, as follows:

$$\phi (x,t)=\pm \left[\frac{-c_1\sqrt{\frac{-{\ell }_2}{{\ell }_1}}sin\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)+c_2\sqrt{\frac{-{\ell }_2}{{\ell }_1}}cos\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)}{c_{1}cos\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)+c_{2}sin\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)}\right]e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(26)

$$\psi (x,t)=\left\{C-{\displaystyle \frac{{\gamma }_1}{\theta }}{\left[\frac{-c_1\sqrt{\frac{-{\ell }_2}{{\ell }_1}}sin\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)+c_2\sqrt{\frac{-{\ell }_2}{{\ell }_1}}cos\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)}{c_{1}cos\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)+c_{2}sin\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)}\right]}^2\right\}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(27)

where $\xi =\frac{1}{\delta }{x}^{\delta }+\theta t.$

Set III: If ${\ell }_2>0$, then Roots (22) are real and distinct, and the solution of Equation (8) is:

$$G\left(\xi \right)=c_{1}exp\left[(\frac{-\lambda }{2}+\sqrt{\frac{{\ell }_2}{2}})\xi \right]+c_{2}exp\left[(\frac{-\lambda }{2}-\sqrt{\frac{{\ell }_2}{2}})\xi \right].$$

Therefore, the solution of Equation (19) is:

$$u\left(\xi \right)=\pm \sqrt{\frac{{\ell }_2}{{\ell }_1}}\frac{c_{1}exp\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)+c_{2}exp\left(-\sqrt{\frac{{\ell }_2}{2}}\xi \right)}{c_{1}exp\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)+c_{2}exp\left(-\sqrt{\frac{{\ell }_2}{2}}\xi \right)}.$$

(28)

Consequently, the solutions of SFDSWEs (1) and (2) in this status are hyperbolic as follows:

$$\phi (x,t)=\pm \sqrt{\frac{{\ell }_2}{{\ell }_1}}\frac{c_{1}exp\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)+c_{2}exp(-\sqrt{\frac{{\ell }_2}{2}}\xi )}{c_{1}exp\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)+c_{2}exp(-\sqrt{\frac{{\ell }_2}{2}}\xi )}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(29)

$$\psi (x,t)=\left\{C-\frac{{\ell }_2{\gamma }_1}{{\ell }_1\theta }{\left[\frac{c_{1}exp\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)+c_{2}exp\left(-\sqrt{\frac{{\ell }_2}{2}}\xi \right)}{c_{1}exp\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)+c_{2}exp\left(-\sqrt{\frac{{\ell }_2}{2}}\xi \right)}\right]}^2\right\}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(30)

where $\xi =\frac{1}{\delta }{x}^{\delta }+\theta t.$

Special Cases:

Case 1: setting $c_2=0$ in Equations (26) and (27), we obtain for ${\ell }_2<0$:

$$\phi (x,t)=\pm \sqrt{\frac{-{\ell }_2}{{\ell }_1}}tan\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(31)

$$\psi (x,t)=\left\{C+\frac{{\ell }_2{\gamma }_1}{{\ell }_1\theta }{tan}^2\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)\right\}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)}.$$

(32)

Case 2: setting $c_1=0$ in Equations (26) and (27), we obtain for ${\ell }_2<0$:

$$\phi (x,t)=\pm \sqrt{\frac{-{\ell }_2}{{\ell }_1}}cot\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(33)

$$\psi (x,t)=\left\{C+\frac{{\ell }_2{\gamma }_1}{{\ell }_1\theta }{cot}^2\left(\sqrt{\frac{-{\ell }_2}{2}}\xi \right)\right\}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)}.$$

(34)

Case 3: setting $c_1=c_2=1$ in Equations (26) and (27), we obtain for ${\ell }_2<0$:

$$\phi (x,t)=\pm \sqrt{\frac{-{\ell }_2}{{\ell }_1}}\left[sec\left(\sqrt{-2{\ell }_2}\xi \right)-tan\left(\sqrt{-2{\ell }_2}\xi \right)\right]e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)}.$$

(35)

$$\psi (x,t)=\left\{C+\frac{{\ell }_2{\gamma }_1}{{\ell }_1\theta }{\left[sec\left(\sqrt{-2{\ell }_2}\xi \right)-tan\left(\sqrt{-2{\ell }_2}\xi \right)\right]}^2\right\}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(36)

or

$$\phi (x,t)=\pm \sqrt{\frac{-{\ell }_2}{{\ell }_1}}\left[\frac{1}{sec\left(\sqrt{-2{\ell }_2}(\xi \right)+tan\left(\sqrt{-2{\ell }_2}\xi \right)}\right]e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)}.$$

(37)

$$\psi (x,t)=\left\{C+\frac{{\ell }_2{\gamma }_1}{{\ell }_1\theta }{\left[\frac{1}{sec\left(\sqrt{-2{\ell }_2}\xi \right)+tan\left(\sqrt{-2{\ell }_2}\xi \right)}\right]}^2\right\}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)}.$$

(38)

Case 4: setting $c_1=c_2=1$ in Equations (29) and (30), we obtain for ${\ell }_2>0$:

$$\phi (x,t)=\pm \sqrt{\frac{{\ell }_2}{{\ell }_1}}tanh\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(39)

$$\psi (x,t)=\left\{C-\frac{{\ell }_2{\gamma }_1}{{\ell }_1\theta }{tanh}^2\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)\right\}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)}.$$

(40)

Case 5: setting $c_1=1,c_2=-1$ in Equations (29) and (30), we obtain for ${\ell }_2>0$:

$$\phi (x,t)=\pm \sqrt{\frac{{\ell }_2}{{\ell }_1}}coth\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)e^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(41)

$$\psi (x,t)=\left\{C-\frac{{\ell }_2{\gamma }_1}{{\ell }_1\theta }{coth}^2\left(\sqrt{\frac{{\ell }_2}{2}}\xi \right)\right\}{e}^{(\rho \beta \left(t\right)-\frac{1}{2}{\rho }^{2}t)},$$

(42)

where $\xi =\frac{1}{\delta }{x}^{\delta }+\theta t.$

Remark 1.

If we set $\rho =0$, $\delta =1$ in Equations (39)–(42), we have the same results as those reported in [28].

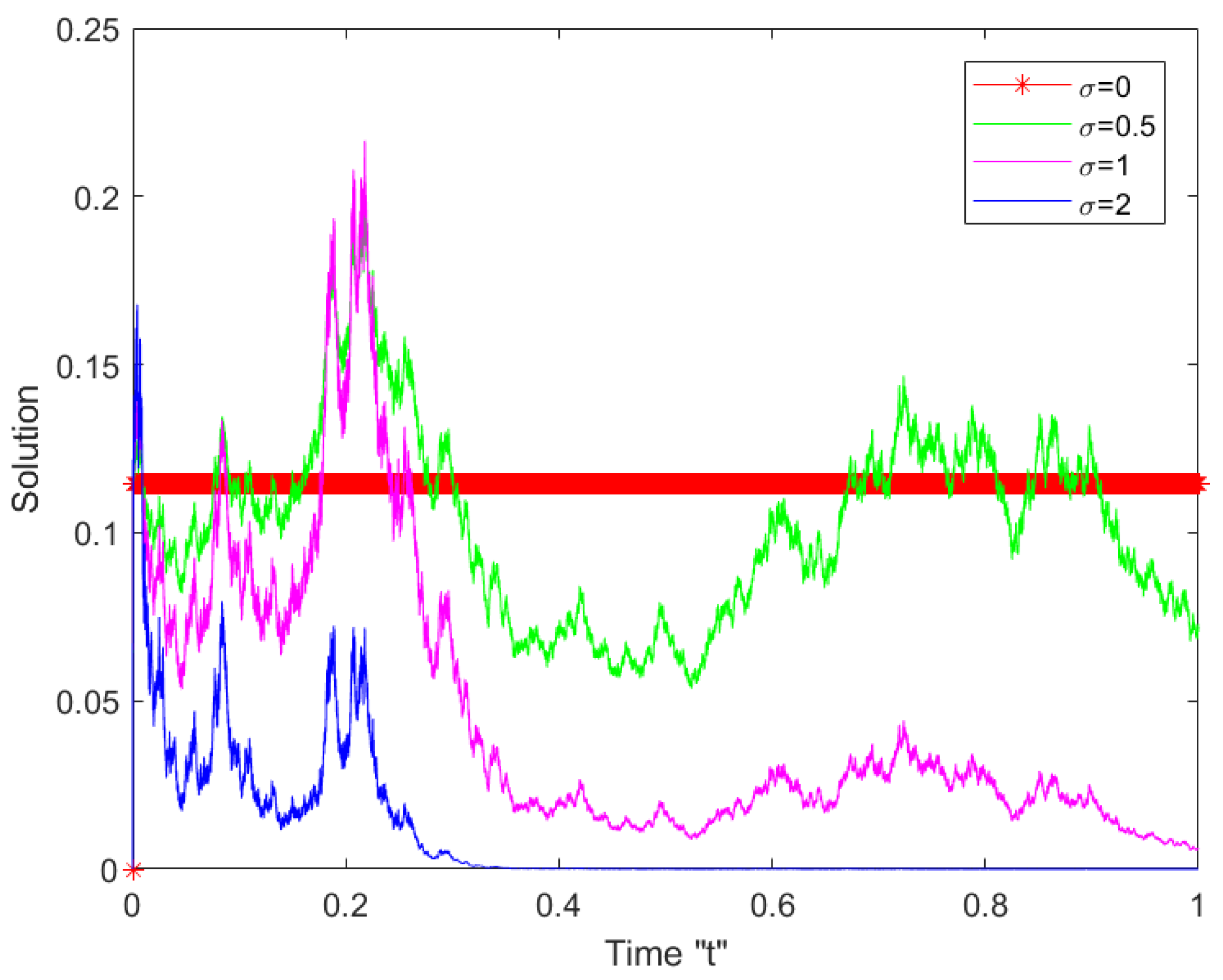
6. Effect of Noise and Fractional Order on the Solutions

The impact of the fractional order and noise on the achieved solutions of FSDSWEs (1) and (2) is examined. The destabilizing and stabilizing effects induced by noisy terms in deterministic systems are now well-understood according to the literature on the subject [36,37] and the references therein. The significance of these effects in interpreting the long-term behavior of actual systems is beyond dispute. Now, to show the impact of noise on the obtained solutions of FSDSWEs (1) and (2), let us plot the graphs for some solutions, such as (39) and (40), by utilizing MATLAB tools with $C=0,{\gamma }_1=1$, ${\gamma }_2=-1$, ${\gamma }_3={\gamma }_4=3$ and $\theta =-3$. Then ${\ell }_1=0.5$ and ${\ell }_2=3.$

First, the impact of noise: In Figure 1, when $\rho =0,$ there was some irregularity in the surface and it was not flat.

In Figure 2, if the noise strength appeared and increased, the surface became significantly flatter.

In Figure 3, we drew a two-dimensional graph representing the solution $\phi (x,t)$ in Equation (39) to illustrate our previous results as follows:

Second, the impact of fractional derivatives: Figure 4 and Figure 5 if $\rho =0$ show that, as $\delta$ increased, the surface was extended:

7. Conclusions

In this work, we studied the stochastic–fractional Drinfel’d–Sokolov–Wilson equations. These equations are used in plasma physics, surface physics, applied sciences, population dynamics, and mathematical physics. The exact stochastic–fractional solutions to SFDSWEs (1) and (2) were successfully attained by utilizing the $(G^{\prime }/G)$-expansion method. We acquired different types of solutions, including hyperbolic, rational, and trigonometric functions. Due to the significance of SFDSWEs, the obtained solutions are more important for and beneficial in comprehending a variety of crucial physical phenomena that have appeared in applied sciences, population dynamics, plasma physics, and surface physics. Moreover, we applied MATLAB software to discuss how the fractional order and multiplicative noise affected the solutions of SFDSWEs. From our results, we concluded that the solutions were stabilized around zero by multiplicative Brownian motion. Additionally, when the fractional derivative increased, the surface expanded. In future studies, SFDSWEs (1) and (2) may be taken into account with either additive noise or infinite dimension multiplicative noise.