Deflection Angle and Shadow of the Reissner–Nordström Black Hole with Higher-Order Magnetic Correction in Einstein-Nonlinear-Maxwell Fields
Abstract
1. Introduction
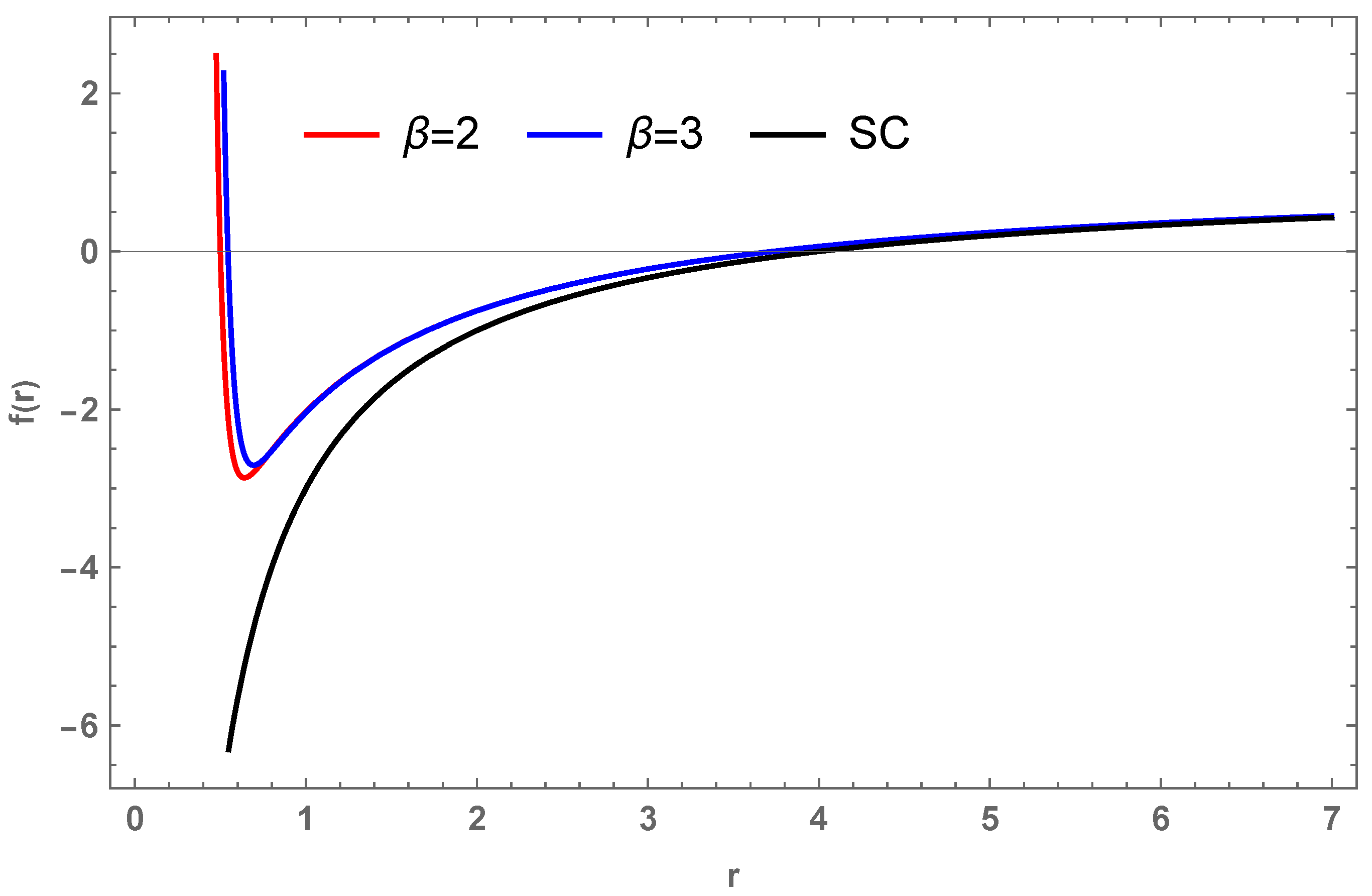
2. Brief Review of Reissner–Nordström Black Hole with Higher-Order Magnetic Correction in Einstein-Nonlinear-Maxwell Fields
3. Weak Deflection Angle Using Gauss–Bonnet Theorem
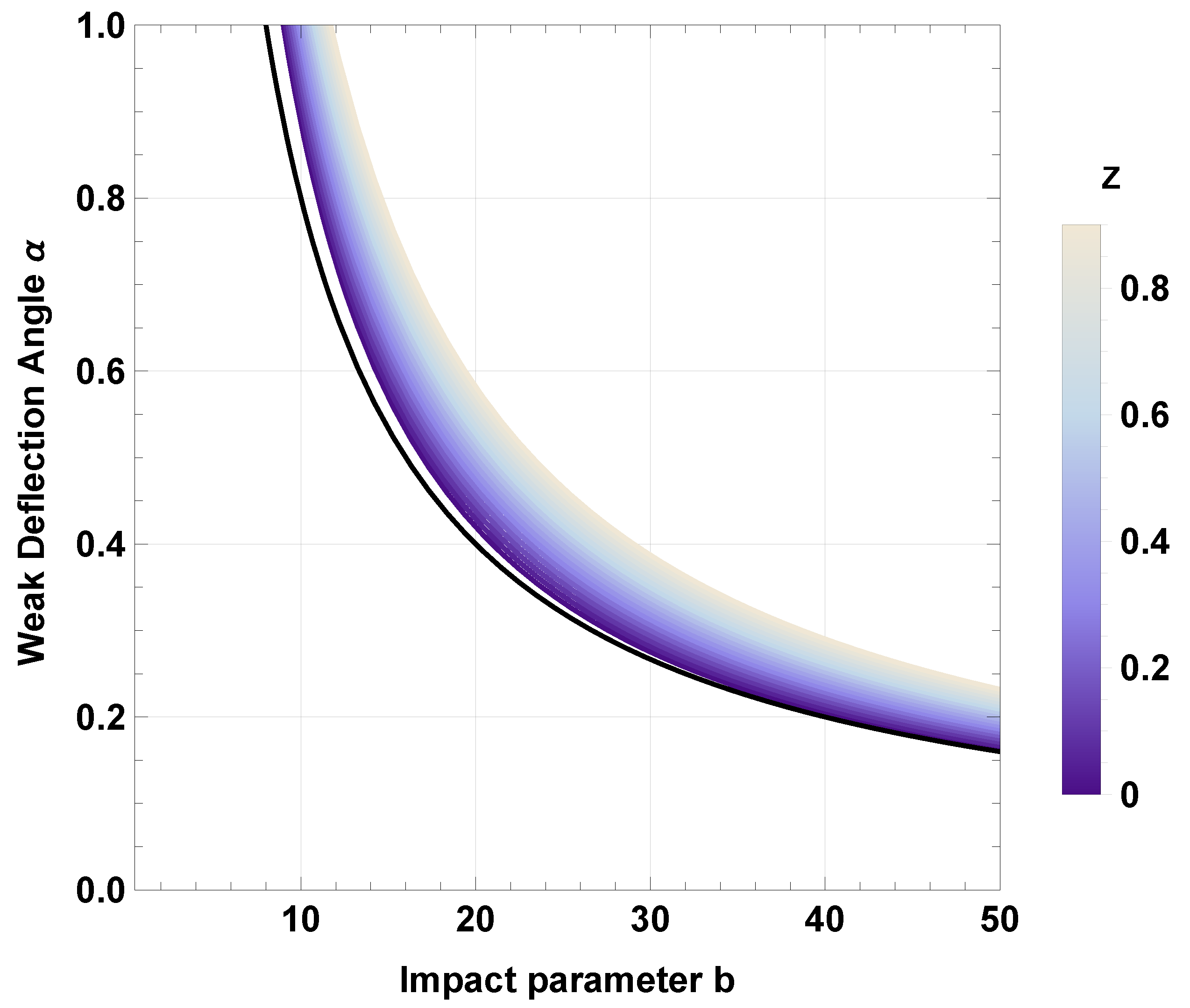
Calculation of Weak Deflection Angle Using Keeton–Petters Formalism
4. Weak Deflection Angle of Massive Particles
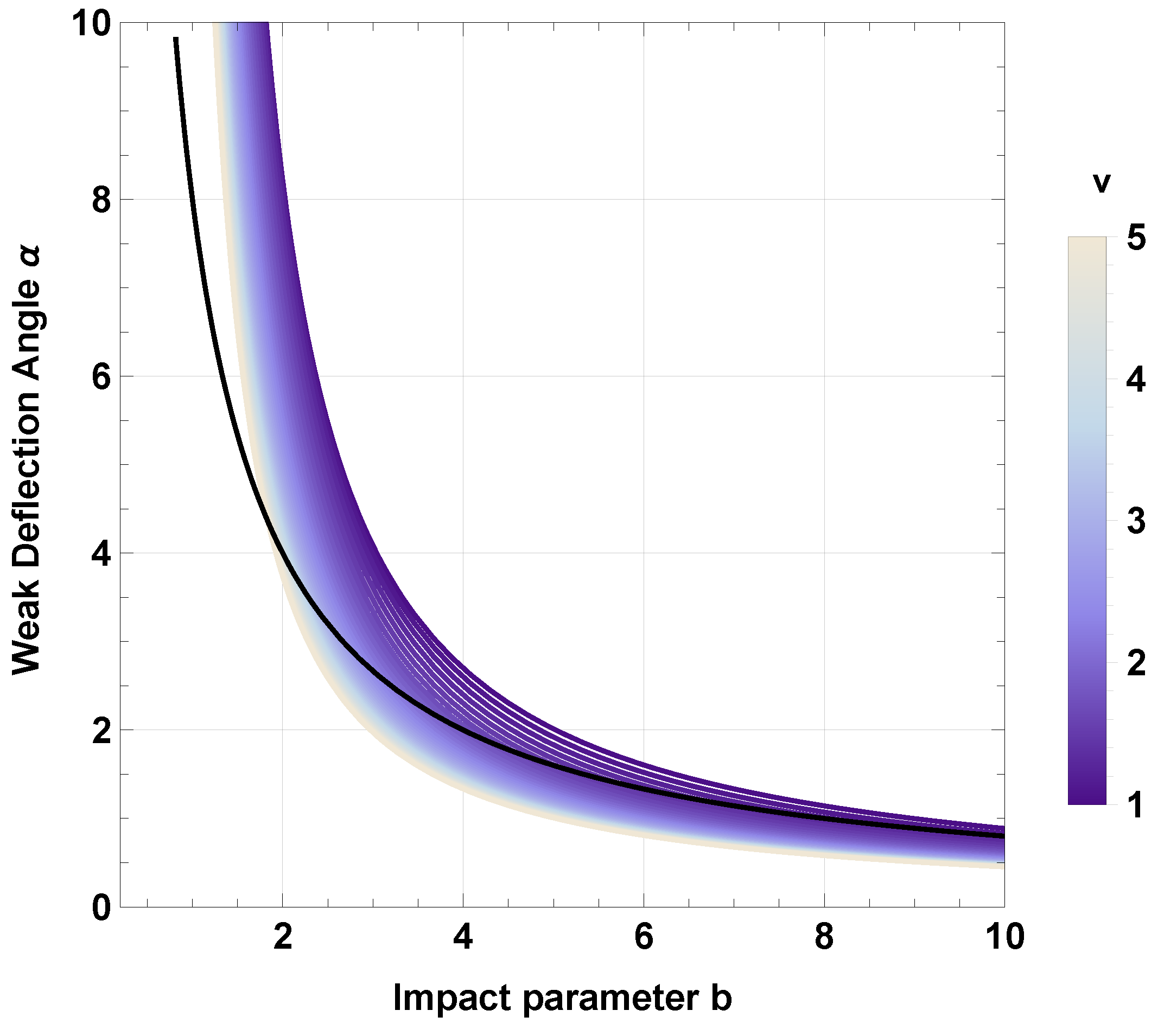
5. Weak Deflection Angle in Plasma Medium and Dark Matter
5.1. Weak Deflection Angle in Plasma Medium
5.2. Weak Deflection Angle in Dark Matter Medium
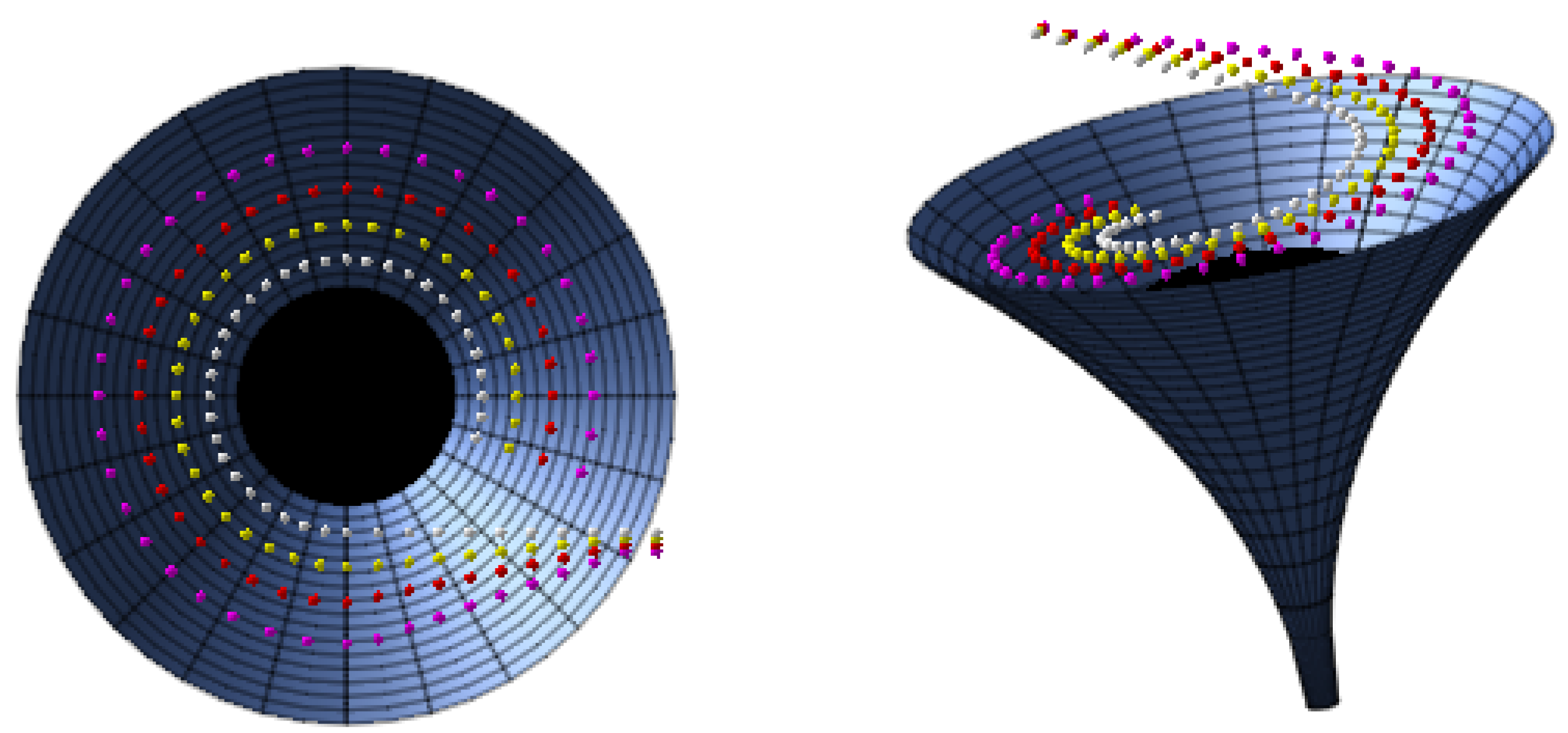
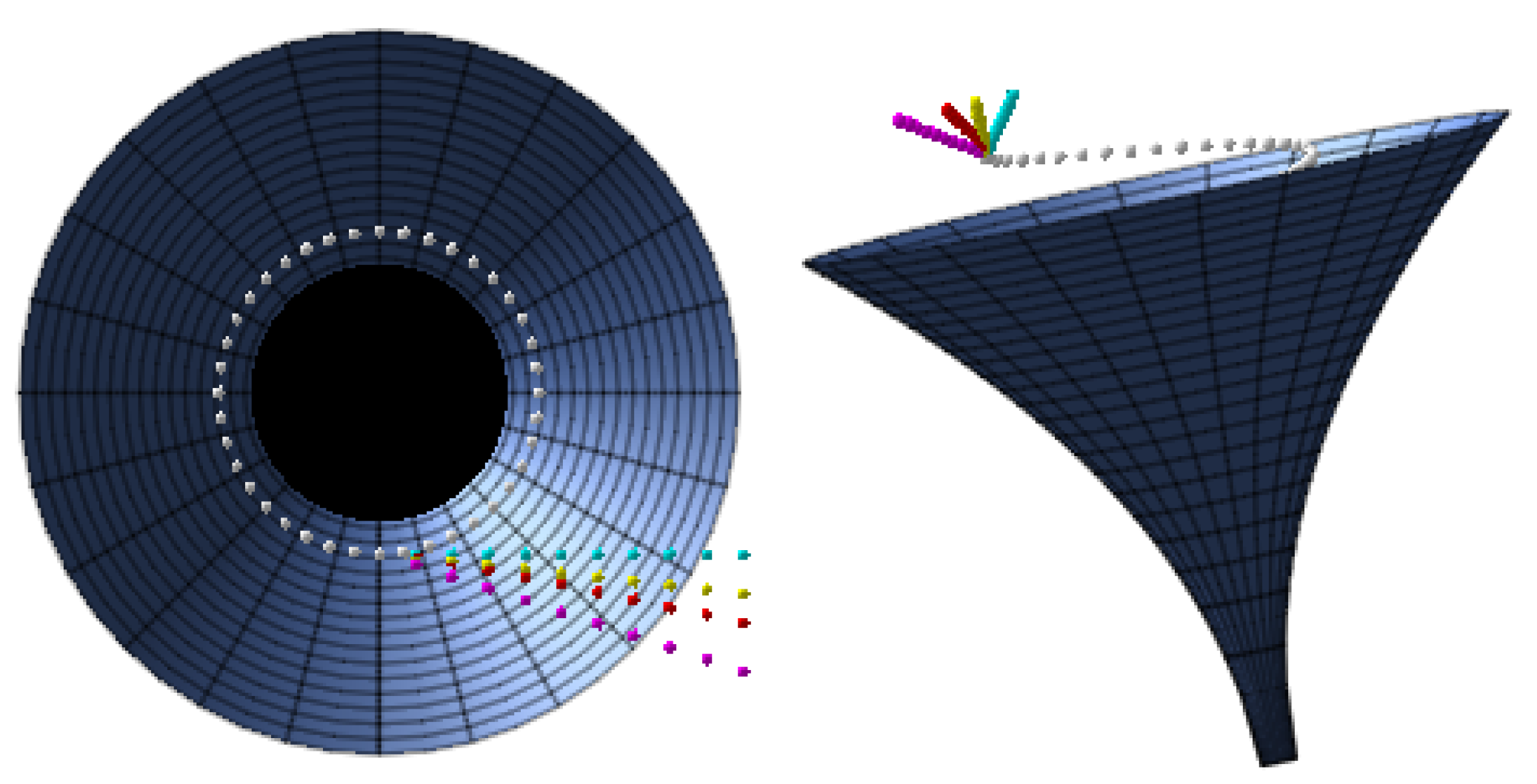
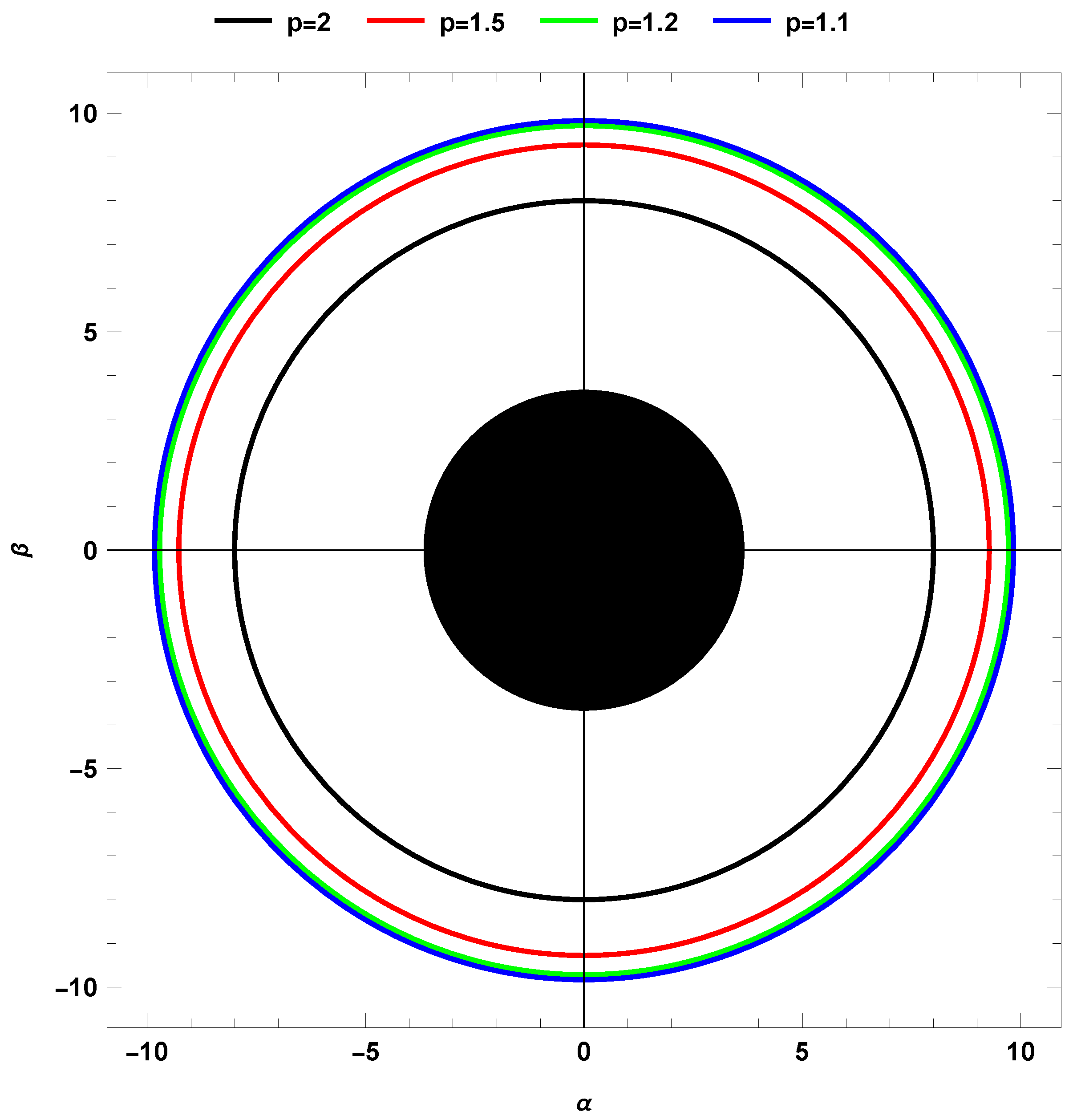
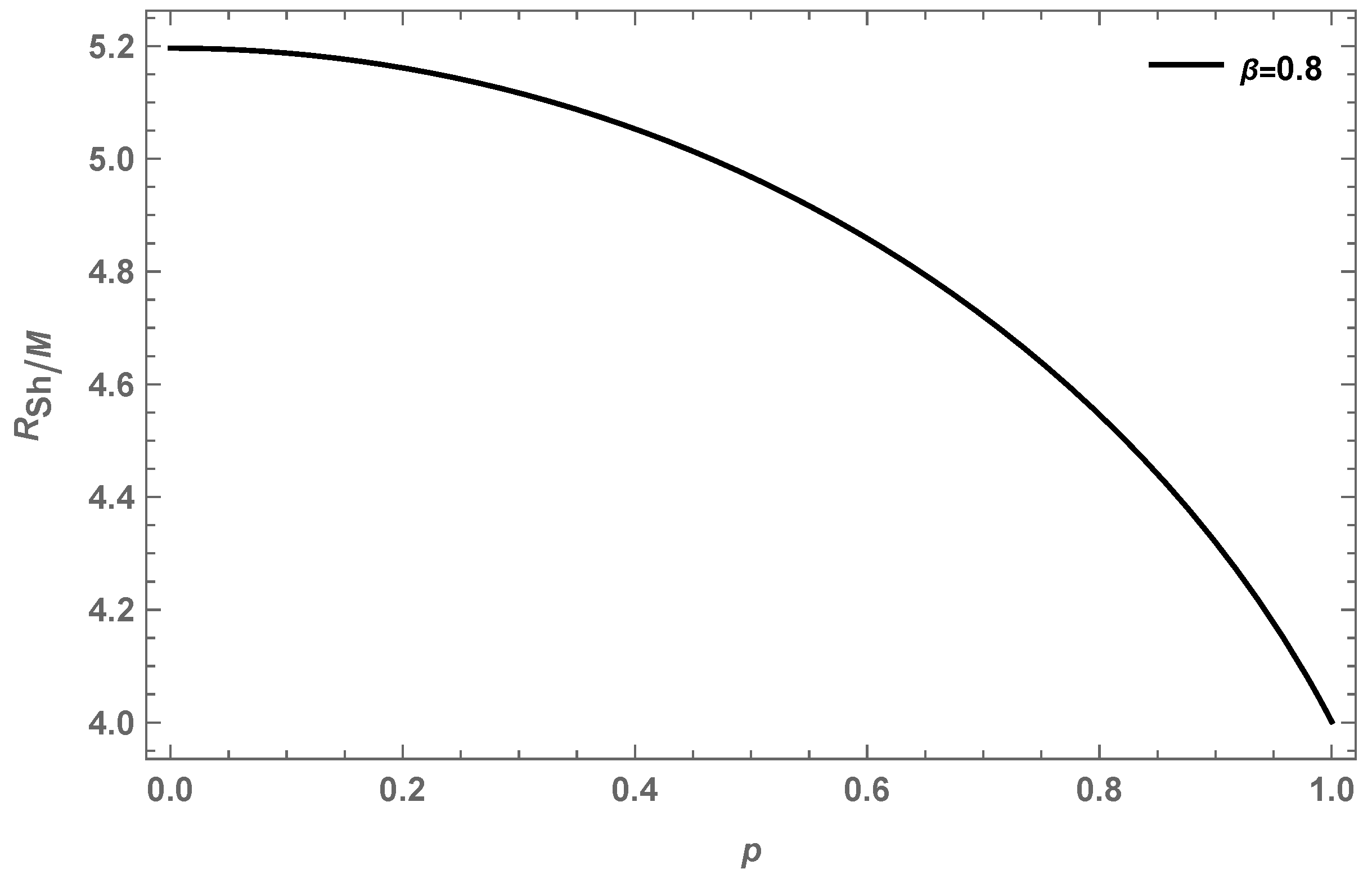
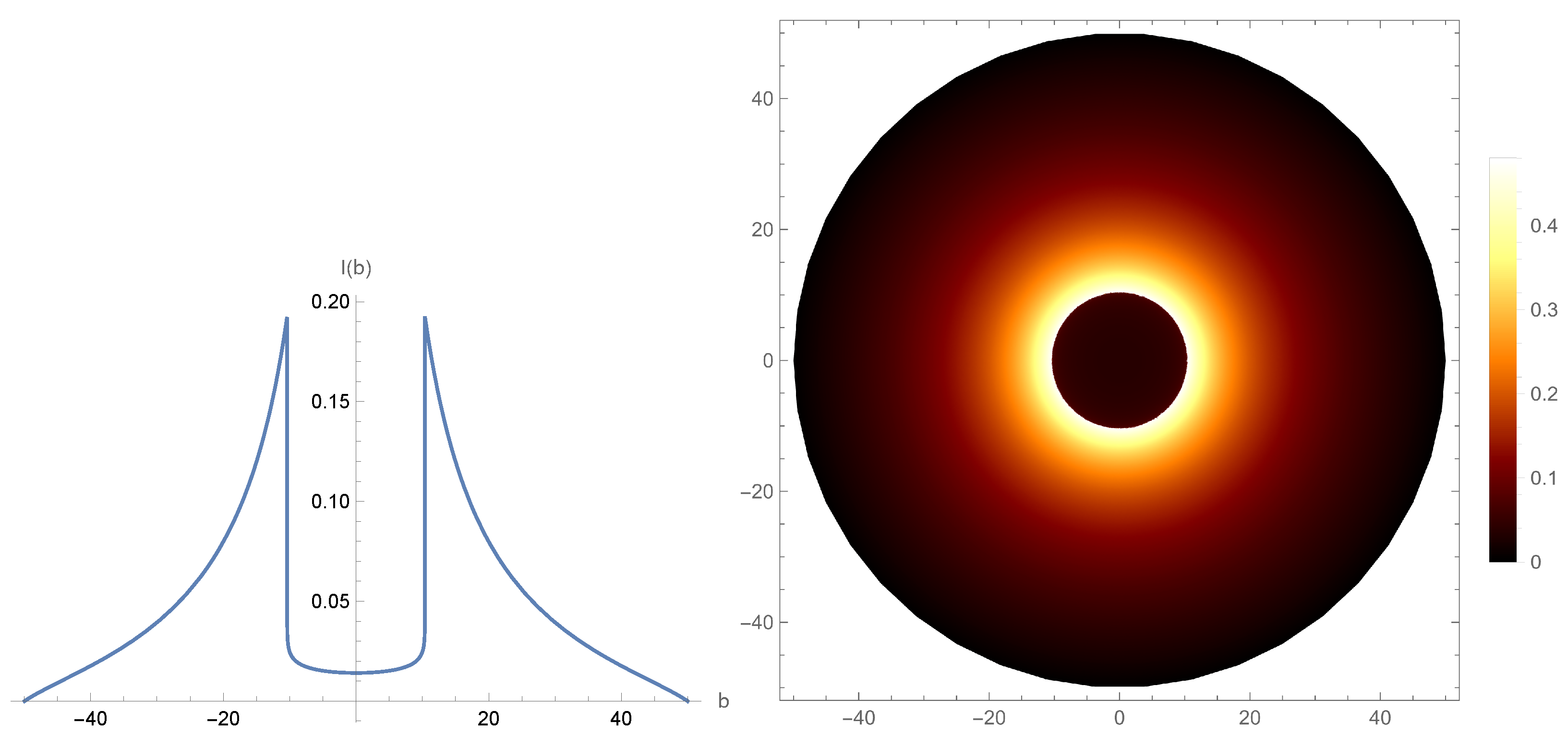
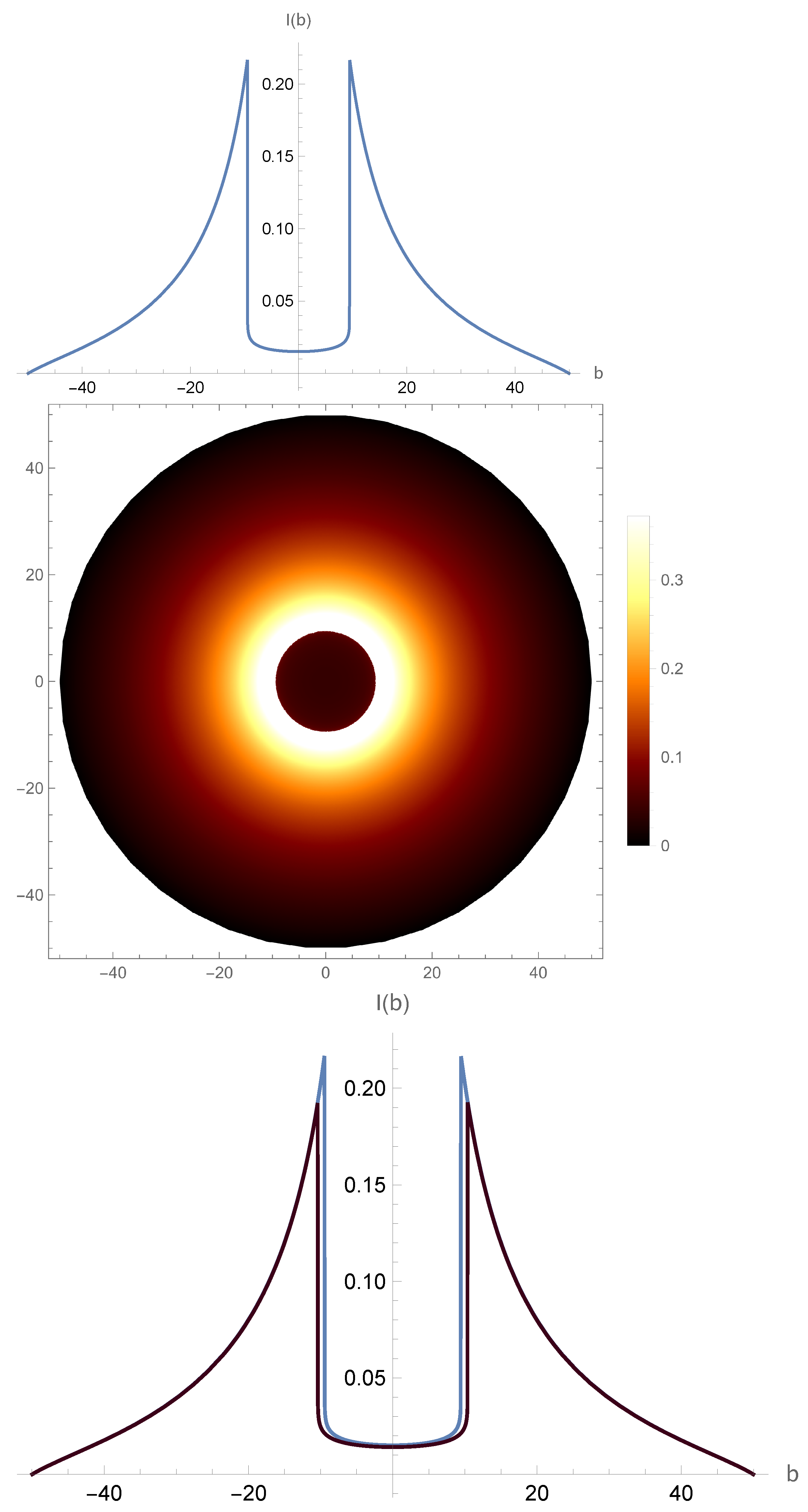
6. Shadow of the Black Hole
Spherically in-Falling Accretion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Einstein, A. The Foundation of the General Theory of Relativity. Ann. Phys. 1916, 49, 769–822. [Google Scholar] [CrossRef]
- Akiyama, K. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Martí-Vidal, I. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Synge, J.L. The Escape of Photons from Gravitationally Intense Stars. Mon. Not. R. Astron. Soc. 1966, 131, 463–466. [Google Scholar] [CrossRef]
- Luminet, J.P. Image of a spherical black hole with thin accretion disk. Astron. Astrophys. 1979, 75, 228–235. [Google Scholar]
- Bozza, V. Gravitational lensing in the strong field limit. Phys. Rev. D 2002, 66, 103001. [Google Scholar] [CrossRef]
- NASA_ESA_CSA; STScI. First Images from the James Webb Space Telescope. 2022. Available online: https://doi.org/nasa.gov/webbfirstimages#tab1-5 (accessed on 1 July 2021).
- Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Gravitational lensing by naked singularities. Phys. Rev. D 2002, 65, 103004. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Narasimha, D.; Chitre, S.M. Role of the scalar field in gravitational lensing. Astron. Astrophys. 1998, 337, 1–8. [Google Scholar]
- Virbhadra, K.S.; Keeton, C.R. Time delay and magnification centroid due to gravitational lensing by black holes and naked singularities. Phys. Rev. D 2008, 77, 124014. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Relativistic images of Schwarzschild black hole lensing. Phys. Rev. D 2009, 79, 083004. [Google Scholar] [CrossRef]
- Adler, S.L.; Virbhadra, K.S. Cosmological constant corrections to the photon sphere and black hole shadow radii. arXiv 2022, arXiv:2205.04628. [Google Scholar] [CrossRef]
- Hasse, W.; Perlick, V. Gravitational lensing in spherically symmetric static space-times with centrifugal force reversal. Gen. Rel. Grav. 2002, 34, 415–433. [Google Scholar] [CrossRef]
- Perlick, V. On the Exact gravitational lens equation in spherically symmetric and static space-times. Phys. Rev. D 2004, 69, 064017. [Google Scholar] [CrossRef]
- Perlick, V.; Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Black hole shadow in an expanding universe with a cosmological constant. Phys. Rev. D 2018, 97, 104062. [Google Scholar] [CrossRef]
- He, G.; Zhou, X.; Feng, Z.; Mu, X.; Wang, H.; Li, W.; Pan, C.; Lin, W. Gravitational deflection of massive particles in Schwarzschild-de Sitter spacetime. Eur. Phys. J. C 2020, 80, 835. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Compactness of supermassive dark objects at galactic centers. arXiv 2022, arXiv:2204.01792. [Google Scholar]
- Virbhadra, K.S. Distortions of images of Schwarzschild lensing. arXiv 2022, arXiv:2204.01879. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Werner, M.C. Applications of the Gauss–Bonnet theorem to gravitational lensing. Class. Quant. Grav. 2008, 25, 235009. [Google Scholar] [CrossRef]
- Werner, M.C. Gravitational lensing in the Kerr-Randers optical geometry. Gen. Rel. Grav. 2012, 44, 3047–3057. [Google Scholar] [CrossRef]
- Övgün, A. Light deflection by Damour-Solodukhin wormholes and Gauss–Bonnet theorem. Phys. Rev. D 2018, 98, 044033. [Google Scholar] [CrossRef]
- Övgün, A. Weak field deflection angle by regular black holes with cosmic strings using the Gauss–Bonnet theorem. Phys. Rev. D 2019, 99, 104075. [Google Scholar] [CrossRef]
- Övgün, A. Deflection Angle of Photons through Dark Matter by Black Holes and Wormholes Using Gauss–Bonnet Theorem. Universe 2019, 5, 115. [Google Scholar] [CrossRef]
- Li, Z.; Övgün, A. Finite-distance gravitational deflection of massive particles by a Kerr-like black hole in the bumblebee gravity model. Phys. Rev. D 2020, 101, 024040. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, G.; Övgün, A. Circular Orbit of a Particle and Weak Gravitational Lensing. Phys. Rev. D 2020, 101, 124058. [Google Scholar] [CrossRef]
- Kumaran, Y.; Övgün, A. Weak Deflection Angle of Extended Uncertainty Principle Black Holes. Chin. Phys. C 2020, 44, 025101. [Google Scholar] [CrossRef]
- Kumaran, Y.; Övgün, A. Deriving weak deflection angle by black holes or wormholes using Gauss–Bonnet theorem. Turk. J. Phys. 2021, 45, 247–267. [Google Scholar] [CrossRef]
- Övgün, A.; Kumaran, Y.; Javed, W.; Abbas, J. Effect of Horndeski theory on weak deflection angle using the Gauss–Bonnet theorem. Int. J. Geom. Meth. Mod. Phys. 2022, 2250192. [Google Scholar] [CrossRef]
- Övgün, A.; Sakallı, I.; Saavedra, J. Shadow cast and Deflection angle of Kerr-Newman-Kasuya spacetime. JCAP 2018, 10, 41. [Google Scholar] [CrossRef]
- Okyay, M.; Övgün, A. Nonlinear electrodynamics effects on the black hole shadow, deflection angle, quasinormal modes and greybody factors. JCAP 2022, 1, 9. [Google Scholar] [CrossRef]
- Javed, W.; Abbas, J.; Övgün, A. Deflection angle of photon from magnetized black hole and effect of nonlinear electrodynamics. Eur. Phys. J. C 2019, 79, 694. [Google Scholar] [CrossRef]
- Javed, W.; Abbas, J.; Övgün, A. Effect of the Hair on Deflection Angle by Asymptotically Flat Black Holes in Einstein-Maxwell-Dilaton Theory. Phys. Rev. D 2019, 100, 044052. [Google Scholar] [CrossRef]
- Javed, W.; Babar, R.; Övgün, A. Effect of the dilaton field and plasma medium on deflection angle by black holes in Einstein-Maxwell-dilaton-axion theory. Phys. Rev. D 2019, 100, 104032. [Google Scholar] [CrossRef]
- Javed, W.; Hamza, A.; Övgün, A. Effect of nonlinear electrodynamics on the weak field deflection angle by a black hole. Phys. Rev. D 2020, 101, 103521. [Google Scholar] [CrossRef]
- Javed, W.; Babar, R.; Övgün, A. The effect of the Brane-Dicke coupling parameter on weak gravitational lensing by wormholes and naked singularities. Phys. Rev. D 2019, 99, 084012. [Google Scholar] [CrossRef]
- Javed, W.; Abbas, J.; Övgün, A. Effect of the Quintessential Dark Energy on Weak Deflection Angle by Kerr-Newmann Black Hole. Ann. Phys. 2020, 418, 168183. [Google Scholar] [CrossRef]
- Ishihara, A.; Suzuki, Y.; Ono, T.; Kitamura, T.; Asada, H. Gravitational bending angle of light for finite distance and the Gauss–Bonnet theorem. Phys. Rev. D 2016, 94, 084015. [Google Scholar] [CrossRef]
- Takizawa, K.; Ono, T.; Asada, H. Gravitational deflection angle of light: Definition by an observer and its application to an asymptotically nonflat spacetime. Phys. Rev. D 2020, 101, 104032. [Google Scholar] [CrossRef]
- Ono, T.; Asada, H. The effects of finite distance on the gravitational deflection angle of light. Universe 2019, 5, 218. [Google Scholar] [CrossRef]
- Ishihara, A.; Suzuki, Y.; Ono, T.; Asada, H. Finite-distance corrections to the gravitational bending angle of light in the strong deflection limit. Phys. Rev. D 2017, 95, 044017. [Google Scholar] [CrossRef]
- Ono, T.; Ishihara, A.; Asada, H. Gravitomagnetic bending angle of light with finite-distance corrections in stationary axisymmetric spacetimes. Phys. Rev. D 2017, 96, 104037. [Google Scholar] [CrossRef]
- Pantig, R.C.; Rodulfo, E.T. Weak deflection angle of a dirty black hole. Chin. J. Phys. 2020, 66, 691–702. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Pantig, R.C.; Övgün, A.; Abdujabbarov, A.; Demir, D. Quasiperiodic oscillations, weak field lensing and shadow cast around black holes in Symmergent gravity. arXiv 2022, arXiv:2206.06599. [Google Scholar]
- Pantig, R.C.; Övgün, A. Dark matter effect on the weak deflection angle by black holes at the center of Milky Way and M87 galaxies. Eur. Phys. J. C 2022, 82, 391. [Google Scholar] [CrossRef]
- Pantig, R.C.; Övgün, A. Testing dynamical torsion effects on the charged black hole’s shadow, deflection angle and greybody with M87* and Sgr A* from EHT. arXiv 2022, arXiv:2206.02161. [Google Scholar]
- Pantig, R.C.; Övgün, A. Dehnen halo effect on a black hole in an ultra-faint dwarf galaxy. arXiv 2022, arXiv:2202.07404. [Google Scholar] [CrossRef]
- Uniyal, A.; Pantig, R.C.; Övgün, A. Probing a nonlinear electrodynamics black hole with thin accretion disk, shadow and deflection angle with M87* and Sgr A* from EHT. arXiv 2022, arXiv:2205.11072. [Google Scholar]
- Javed, W.; Aqib, M.; Övgün, A. Effect of the magnetic charge on weak deflection angle and greybody bound of the black hole in Einstein-Gauss–Bonnet gravity. Phys. Lett. B 2022, 829, 137114. [Google Scholar] [CrossRef]
- Jusufi, K.; Werner, M.C.; Banerjee, A.; Övgün, A. Light Deflection by a Rotating Global Monopole Spacetime. Phys. Rev. D 2017, 95, 104012. [Google Scholar] [CrossRef]
- Javed, W.; Hussain, I.; Övgün, A. Weak deflection angle of Kazakov–Solodukhin black hole in plasma medium using Gauss–Bonnet theorem and its greybody bonding. Eur. Phys. J. Plus 2022, 137, 148. [Google Scholar] [CrossRef]
- Javed, W.; Abbas, J.; Kumaran, Y.; Övgün, A. Weak deflection angle by asymptotically flat black holes in Horndeski theory using Gauss–Bonnet theorem. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150003. [Google Scholar] [CrossRef]
- Övgün, A. Weak Deflection Angle of Black-bounce Traversable Wormholes Using Gauss–Bonnet Theorem in the Dark Matter Medium. Turk. J. Phys. 2020, 44, 465–471. [Google Scholar] [CrossRef]
- El Moumni, H.; Masmar, K.; Övgün, A. Weak deflection angle of light in two classes of black holes in nonlinear electrodynamics via Gauss–Bonnet theorem. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250094. [Google Scholar] [CrossRef]
- Javed, W.; Khadim, M.B.; Övgün, A.; Abbas, J. Weak gravitational lensing by stringy black holes. Eur. Phys. J. Plus 2020, 135, 314. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgün, A. Gravitational Lensing by Rotating Wormholes. Phys. Rev. D 2018, 97, 024042. [Google Scholar] [CrossRef]
- Fu, Q.M.; Zhao, L.; Liu, Y.X. Weak deflection angle by electrically and magnetically charged black holes from nonlinear electrodynamics. Phys. Rev. D 2021, 104, 024033. [Google Scholar] [CrossRef]
- Crisnejo, G.; Gallo, E. Weak lensing in a plasma medium and gravitational deflection of massive particles using the Gauss–Bonnet theorem. A unified treatment. Phys. Rev. D 2018, 97, 124016. [Google Scholar] [CrossRef]
- Keeton, C.R.; Petters, A.O. Formalism for testing theories of gravity using lensing by compact objects. I. Static, spherically symmetric case. Phys. Rev. D 2005, 72, 104006. [Google Scholar] [CrossRef]
- Jaroszynski, M.; Kurpiewski, A. Optics near kerr black holes: Spectra of advection dominated accretion flows. Astron. Astrophys. 1997, 326, 419. [Google Scholar]
- Bambi, C. A code to compute the emission of thin accretion disks in non-Kerr space-times and test the nature of black hole candidates. Astrophys. J. 2012, 761, 174. [Google Scholar] [CrossRef]
- Kruglov, S.I. The shadow of M87* black hole within rational nonlinear electrodynamics. Mod. Phys. Lett. A 2020, 35, 2050291. [Google Scholar] [CrossRef]
- Allahyari, A.; Khodadi, M.; Vagnozzi, S.; Mota, D.F. Magnetically charged black holes from non-linear electrodynamics and the Event Horizon Telescope. JCAP 2020, 2, 3. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Roy, R.; Tsai, Y.D.; Visinelli, L. Horizon-scale tests of gravity theories and fundamental physics from the Event Horizon Telescope image of Sagittarius A*. arXiv 2022, arXiv:2205.07787. [Google Scholar]
- Roy, R.; Vagnozzi, S.; Visinelli, L. Superradiance evolution of black hole shadows revisited. Phys. Rev. D 2022, 105, 083002. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Visinelli, L. Hunting for extra dimensions in the shadow of M87*. Phys. Rev. D 2019, 100, 024020. [Google Scholar] [CrossRef]
- Khodadi, M.; Lambiase, G.; Mota, D.F. No-hair theorem in the wake of Event Horizon Telescope. JCAP 2021, 09, 028. [Google Scholar] [CrossRef]
- Khodadi, M.; Allahyari, A.; Vagnozzi, S.; Mota, D.F. Black holes with scalar hair in light of the Event Horizon Telescope. JCAP 2020, 09, 026. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G. Black Hole Parameter Estimation from Its Shadow. Astrophys. J. 2020, 892, 78. [Google Scholar] [CrossRef]
- Khodadi, M.; Lambiase, G. Probing the Lorentz Symmetry Violation Using the First Image of Sagittarius A*: Constraints on Standard-Model Extension Coefficients. arXiv 2022, arXiv:2206.08601. [Google Scholar]
- Lambiase, G.; Mastrototaro, L. Neutrino pair annihilation above black-hole accretion disks in modified gravity. arXiv 2022, arXiv:2205.09785. [Google Scholar] [CrossRef]
- Kumar, R.; Ghosh, S.G. Rotating black holes in 4D Einstein-Gauss–Bonnet gravity and its shadow. JCAP 2020, 7, 053. [Google Scholar] [CrossRef]
- Rahaman, F.; Singh, K.N.; Shaikh, R.; Manna, T.; Aktar, S. Shadows of Lorentzian traversable wormholes. Class. Quant. Grav. 2021, 38, 215007. [Google Scholar] [CrossRef]
- Belhaj, A.; Benali, M.; El Balali, A.; El Moumni, H.; Ennadifi, S.E. Deflection angle and shadow behaviors of quintessential black holes in arbitrary dimensions. Class. Quant. Grav. 2020, 37, 215004. [Google Scholar] [CrossRef]
- Belhaj, A.; Belmahi, H.; Benali, M.; El Hadri, W.; El Moumni, H.; Torrente-Lujan, E. Shadows of 5D black holes from string theory. Phys. Lett. B 2021, 812, 136025. [Google Scholar] [CrossRef]
- Belhaj, A.; Belmahi, H.; Benali, M. Superentropic AdS black hole shadows. Phys. Lett. B 2021, 821, 136619. [Google Scholar] [CrossRef]
- Guo, S.; Li, G.R.; Liang, E.W. Influence of accretion flow and magnetic charge on the observed shadows and rings of the Hayward black hole. Phys. Rev. D 2022, 105, 023024. [Google Scholar] [CrossRef]
- Sun, C.; Liu, Y.; Qian, W.L.; Yue, R. Shadows of magnetically charged rotating black holes surrounded by quintessence *. Chin. Phys. C 2022, 46, 065103. [Google Scholar] [CrossRef]
- Gralla, S.E.; Holz, D.E.; Wald, R.M. Black Hole Shadows, Photon Rings, and Lensing Rings. Phys. Rev. D 2019, 100, 024018. [Google Scholar] [CrossRef]
- Ma, T.C.; Zhang, H.X.; He, P.Z.; Zhang, H.R.; Chen, Y.; Deng, J.B. Shadow cast by a rotating and nonlinear magnetic-charged black hole in perfect fluid dark matter. Mod. Phys. Lett. A 2021, 36, 2150112. [Google Scholar] [CrossRef]
- Övgün, A.; Sakallı, I. Testing generalized Einstein–Cartan–Kibble–Sciama gravity using weak deflection angle and shadow cast. Class. Quant. Grav. 2020, 37, 225003. [Google Scholar] [CrossRef]
- Pantig, R.C.; Rodulfo, E.T. Rotating dirty black hole and its shadow. Chin. J. Phys. 2020, 68, 236. [Google Scholar] [CrossRef]
- Reggie, P.C.; Paul, K.Y.; Rodulfo, E.T.; Ali, O. Shadow and weak deflection angle of extended uncertainty principle black hole surrounded with dark matter. Ann. Phys. 2022, 436, 168722. [Google Scholar] [CrossRef]
- Övgün, A. Black hole with confining electric potential in scalar-tensor description of regularized 4-dimensional Einstein-Gauss–Bonnet gravity. Phys. Lett. B 2021, 820, 136517. [Google Scholar] [CrossRef]
- Çimdiker, I.; Demir, D.; Övgün, A. Black hole shadow in symmergent gravity. Phys. Dark Univ. 2021, 34, 100900. [Google Scholar] [CrossRef]
- Kuang, X.M.; Övgün, A. Strong gravitational lensing and shadow constraint from M87* of slowly rotating Kerr-like black hole. arXiv 2022, arXiv:2205.11003. [Google Scholar]
- Herdeiro, C.A.R.; Pombo, A.M.; Radu, E.; Cunha, P.V.P.; Sanchis-Gual, N. The imitation game: Proca stars that can mimic the Schwarzschild shadow. JCAP 2021, 4, 51. [Google Scholar] [CrossRef]
- Shaikh, R.; Kocherlakota, P.; Narayan, R.; Joshi, P.S. Shadows of spherically symmetric black holes and naked singularities. Mon. Not. Roy. Astron. Soc. 2019, 482, 52–64. [Google Scholar] [CrossRef]
- Shaikh, R. Black hole shadow in a general rotating spacetime obtained through Newman-Janis algorithm. Phys. Rev. D 2019, 100, 024028. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Eiró, N.A.; Herdeiro, C.A.R.; Lemos, J.P.S. Lensing and shadow of a black hole surrounded by a heavy accretion disk. JCAP 2020, 3, 35. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E. EHT constraint on the ultralight scalar hair of the M87 supermassive black hole. Universe 2019, 5, 220. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Herdeiro, C.A.R. Shadows and strong gravitational lensing: A brief review. Gen. Rel. Grav. 2018, 50, 42. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Kleihaus, B.; Kunz, J.; Radu, E. Shadows of Einstein–dilaton–Gauss–Bonnet black holes. Phys. Lett. B 2017, 768, 373–379. [Google Scholar] [CrossRef]
- Vincent, F.H.; Gourgoulhon, E.; Herdeiro, C.; Radu, E. Astrophysical imaging of Kerr black holes with scalar hair. Phys. Rev. D 2016, 94, 084045. [Google Scholar] [CrossRef]
- Afrin, M.; Kumar, R.; Ghosh, S.G. Parameter estimation of hairy Kerr black holes from its shadow and constraints from M87*. Mon. Not. Roy. Astron. Soc. 2021, 504, 5927–5940. [Google Scholar] [CrossRef]
- Jha, S.K.; Rahaman, A. Lorentz violation and noncommutative effect on superradiance scattering off Kerr-like black hole and on the shadow of it. arXiv 2021, arXiv:2111.02817. [Google Scholar]
- Zeng, X.X.; Zhang, H.Q.; Zhang, H. Shadows and photon spheres with spherical accretions in the four-dimensional Gauss–Bonnet black hole. Eur. Phys. J. C 2020, 80, 872. [Google Scholar] [CrossRef]
- He, K.J.; Tan, S.C.; Li, G.P. Influence of torsion charge on shadow and observation signature of black hole surrounded by various profiles of accretions. Eur. Phys. J. C 2022, 82, 81. [Google Scholar] [CrossRef]
- Dokuchaev, V.I.; Nazarova, N.O. Visible shapes of black holes M87* and SgrA*. Universe 2020, 6, 154. [Google Scholar] [CrossRef]
- Bambi, C.; Freese, K.; Vagnozzi, S.; Visinelli, L. Testing the rotational nature of the supermassive object M87* from the circularity and size of its first image. Phys. Rev. D 2019, 100, 044057. [Google Scholar] [CrossRef]
- Meng, Y.; Kuang, X.M.; Tang, Z.Y. Photon regions, shadow observables and constraints from M87* of a charged rotating black hole. arXiv 2022, arXiv:2204.00897. [Google Scholar] [CrossRef]
- Chen, C.Y. Testing black hole equatorial reflection symmetry using Sgr A* shadow images. arXiv 2022, arXiv:2205.06962. [Google Scholar] [CrossRef]
- Chen, Y.; Roy, R.; Vagnozzi, S.; Visinelli, L. Superradiant evolution of the shadow and photon ring of Sgr A*. arXiv 2022, arXiv:2205.06238. [Google Scholar] [CrossRef]
- Wang, M.; Chen, S.; Jing, J. Chaotic Shadows of Black Holes: A Short Review. arXiv 2022, arXiv:2205.05855. [Google Scholar] [CrossRef]
- Bronzwaer, T.; Falcke, H. The Nature of Black Hole Shadows. Astrophys. J. 2021, 920, 155. [Google Scholar] [CrossRef]
- Falcke, H.; Melia, F.; Agol, E. Viewing the shadow of the black hole at the galactic center. Astrophys. J. Lett. 2000, 528, L13. [Google Scholar] [CrossRef]
- Wei, S.W.; Zou, Y.C.; Liu, Y.X.; Mann, R.B. Curvature radius and Kerr black hole shadow. JCAP 2019, 8, 30. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X.; Mann, R.B. Intrinsic curvature and topology of shadows in Kerr spacetime. Phys. Rev. D 2019, 99, 041303. [Google Scholar] [CrossRef]
- Abdolrahimi, S.; Mann, R.B.; Tzounis, C. Distorted Local Shadows. Phys. Rev. D 2015, 91, 084052. [Google Scholar] [CrossRef]
- Adair, C.; Bueno, P.; Cano, P.A.; Hennigar, R.A.; Mann, R.B. Slowly rotating black holes in Einsteinian cubic gravity. Phys. Rev. D 2020, 102, 084001. [Google Scholar] [CrossRef]
- Abdolrahimi, S.; Mann, R.B.; Tzounis, C. Double Images from a Single Black Hole. Phys. Rev. D 2015, 92, 124011. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zinhailo, A.F. Quasinormal modes, stability and shadows of a black hole in the 4D Einstein–Gauss–Bonnet gravity. Eur. Phys. J. C 2020, 80, 1049. [Google Scholar] [CrossRef]
- Konoplya, R.A. Shadow of a black hole surrounded by dark matter. Phys. Lett. B 2019, 795, 1–6. [Google Scholar] [CrossRef]
- Konoplya, R.A. Quantum corrected black holes: Quasinormal modes, scattering, shadows. Phys. Lett. B 2020, 804, 135363. [Google Scholar] [CrossRef]
- Chakhchi, L.; El Moumni, H.; Masmar, K. Shadows and optical appearance of a power-Yang-Mills black hole surrounded by different accretion disk profiles. Phys. Rev. D 2022, 105, 064031. [Google Scholar] [CrossRef]
- Perlick, V.; Tsupko, O.Y. Calculating black hole shadows: Review of analytical studies. Phys. Rept. 2022, 947, 1–39. [Google Scholar] [CrossRef]
- Clifton, T.; Carrilho, P.; Fernandes, P.G.S.; Mulryne, D.J. Observational Constraints on the Regularized 4D Einstein-Gauss–Bonnet Theory of Gravity. Phys. Rev. D 2020, 102, 084005. [Google Scholar] [CrossRef]
- Maldacena, J. Comments on magnetic black holes. JHEP 2021, 4, 79. [Google Scholar] [CrossRef]
- Zhang, S.J.; Zhang, H.X.; Shao, L.; Deng, J.B.; Hu, X.R. Bardeen black hole in magnetically charged four-dimensional Einstein-Gauss–Bonnet gravity. arXiv 2021, arXiv:2112.11869. [Google Scholar]
- Mazharimousavi, S.H.; Halilsoy, M. Electric and magnetic black holes in a new nonlinear electrodynamics model. Ann. Phys. 2021, 433, 168579. [Google Scholar] [CrossRef]
- Bardeen, J. Non-singular general-relativistic gravitational collapse. In Proceedings of the International Conference GR5, Tbilisi, USSR, 1968; p. 174. [Google Scholar]
- Frolov, V.P. Remarks on non-singular black holes. EPJ Web Conf. 2018, 168, 01001. [Google Scholar] [CrossRef]
- Falciano, F.T.; Peñafiel, M.L.; Perez Bergliaffa, S.E. Entropy bounds and nonlinear electrodynamics. Phys. Rev. D 2019, 100, 125008. [Google Scholar] [CrossRef]
- Obukhov, V.V. Algebra of symmetry operators for Klein-Gordon-Fock equation. Symmetry 2021, 13, 727. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; Chicago University Press: Chicago, IL, USA, 1984. [Google Scholar] [CrossRef]
- Ruggiero, M.L. Light bending in f(T) gravity. Int. J. Mod. Phys. D 2016, 25, 1650073. [Google Scholar] [CrossRef]
- Li, Z.; He, G.; Zhou, T. Gravitational deflection of relativistic massive particles by wormholes. Phys. Rev. D 2020, 101, 044001. [Google Scholar] [CrossRef]
- Latimer, D.C. Dispersive Light Propagation at Cosmological Distances: Matter Effects. Phys. Rev. D 2013, 88, 063517. [Google Scholar] [CrossRef]
- Psaltis, D. Gravitational Test Beyond the First Post-Newtonian Order with the Shadow of the M87 Black Hole. Phys. Rev. Lett. 2020, 125, 141104. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Martí-Vidal, I. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar]
- Bambi, C. Can the supermassive objects at the centers of galaxies be traversable wormholes? The first test of strong gravity for mm/sub-mm very long baseline interferometry facilities. Phys. Rev. D 2013, 87, 107501. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumaran, Y.; Övgün, A. Deflection Angle and Shadow of the Reissner–Nordström Black Hole with Higher-Order Magnetic Correction in Einstein-Nonlinear-Maxwell Fields. Symmetry 2022, 14, 2054. https://doi.org/10.3390/sym14102054
Kumaran Y, Övgün A. Deflection Angle and Shadow of the Reissner–Nordström Black Hole with Higher-Order Magnetic Correction in Einstein-Nonlinear-Maxwell Fields. Symmetry. 2022; 14(10):2054. https://doi.org/10.3390/sym14102054
Chicago/Turabian StyleKumaran, Yashmitha, and Ali Övgün. 2022. "Deflection Angle and Shadow of the Reissner–Nordström Black Hole with Higher-Order Magnetic Correction in Einstein-Nonlinear-Maxwell Fields" Symmetry 14, no. 10: 2054. https://doi.org/10.3390/sym14102054
APA StyleKumaran, Y., & Övgün, A. (2022). Deflection Angle and Shadow of the Reissner–Nordström Black Hole with Higher-Order Magnetic Correction in Einstein-Nonlinear-Maxwell Fields. Symmetry, 14(10), 2054. https://doi.org/10.3390/sym14102054






