An Improved Equilibrium Optimizer Algorithm and Its Application in LSTM Neural Network
Abstract
:1. Introduction
2. Equilibrium Optimizer Algorithm and Its Improvement
2.1. Description of Equilibrium Optimizer Algorithm
- (1)
- Initialization: In the initial state of the optimization process, the equilibrium concentration is unknown. Therefore, the algorithm performs random initialization within the upper and lower limits of each optimization variable.where and represent the lower limit and upper limit vector of the optimized variable, respectively; denotes the random number vector of individual i, the dimension of which is consistent with that of the optimized space. The value of each element is a random number ranging from 0 to 1.
- (2)
- Update of the balance pool: The equilibrium state in Equation (2) is selected from the five current optimal candidate solutions to improve the global search capability of the algorithm and avoid the prospect of falling into low-quality local optimal solutions. The equilibrium state pool formed by these candidate solutions is expressed as follows:where represent the best solution found through the iteration so far; refers to the average of these four solutions. The probability is identical for these five candidate solutions selected, that is, 0.2.
- (3)
- Index term F: To better balance the local search and global search of the algorithm, Equation (3) is improved as follows:where, represents the weight constant coefficient of the global search; indicates the symbolic function; both represent a random number vector, the dimension of which is consistent with the optimized space dimension. The value of each element is a random number ranging from 0 to 1.
- (4)
- Generation rate G: To enhance the local optimization capability of the algorithm, the generation rate is designed as follows:where:when , the algorithm achieves balance between global optimization and local optimization.
- (5)
- Solution update: To address the update optimization problem, the solution of the algorithm is updated as follows according to Equation (2):is obtained using Equation (9), and represents the unit. The right side of Equation (10) is comprised of three terms. The first one is an equilibrium concentration, while the second and third ones represent the changes in concentration.
2.2. Improved Equilibrium Optimizer (IEO)
2.2.1. Improved Strategies for EO
- (1)
- Population initialization based on chaos theory
- (2)
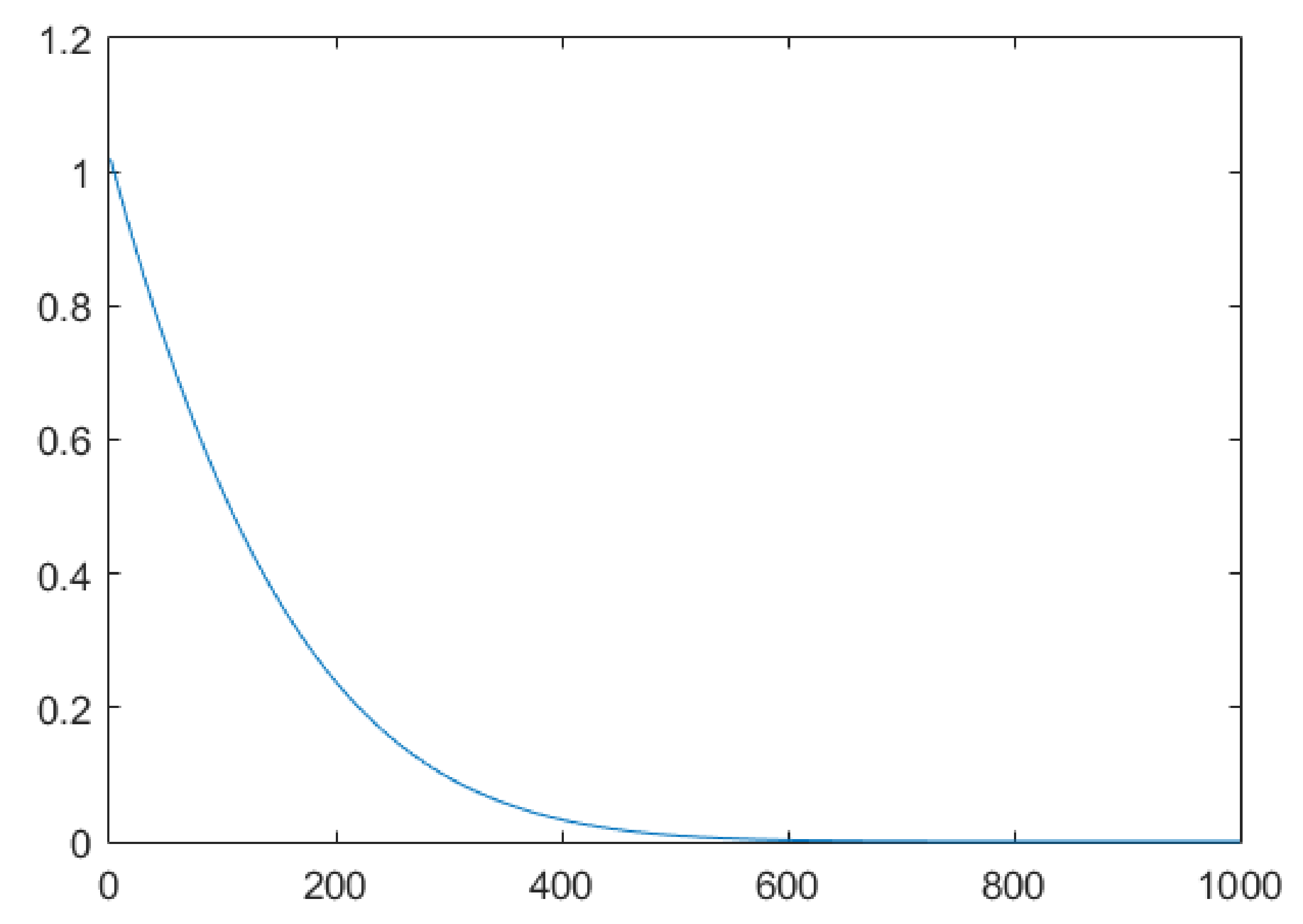
- Adaptive inertia weights Based on the nonlinear decreasing strategy
2.2.2. IEO Algorithm Process
- (1)
- The parameters are initialized, including , , and , Then the maximum number of iterations and the fitness function of the candidate concentration are set;
- (2)
- The fitness value of each object is calculated according to Equation (5), including: , , , , and ;
- (3)
- Calculation is performed for according to Equation (6), and the concentration of each search object is updated using Equation (15);
- (4)
- The output result is saved when the maximum number of iterations is reached.
| Algorithm 1 Pseudo-code of the IEO algorithm. |
| Initialisation: particle populations i = 1, …., n; |
| free parameters a1;a2; GP: a1 = 2; a2 = 1; GP = 0.5; |
| While (Iter < Max_iter) do |
| for (i = 1:number of particles(n)) do |
| Calculate fitness of i-th particle |
| if (fit() < fit()) then |
| Replace with and fit() with () |
| Else if (fit() > fit() & fit() < fit()) then |
| Replace with and fit() with (); |
| Else if (fit() > fit() & fit() > fit() & fit() < fit()) then |
| Replace with and fit() with () |
| else fit() > fit() & fit() > fit() & fit() > fit() & fit() < fit() |
| Replace with and fit() with (); |
| end if |
| end for |
| Construct the equilibrium pool |
| Accomplish memory saving (if Iter > 1) |
| Assign |
| For I = 1:number of particles(n) |
| Randomly choose one candidate from the equilibrium pool(vector) |
| Generate random vectors of λ, r |
| Construct |
| Construct |
| Construct |
| Construct |
| Update concentrations |
| end for |
| Iter = Iter+1 |
| End while |
2.3. Numerical Optimization Experiments
2.3.1. Experimental Settings and Algorithm Parameters
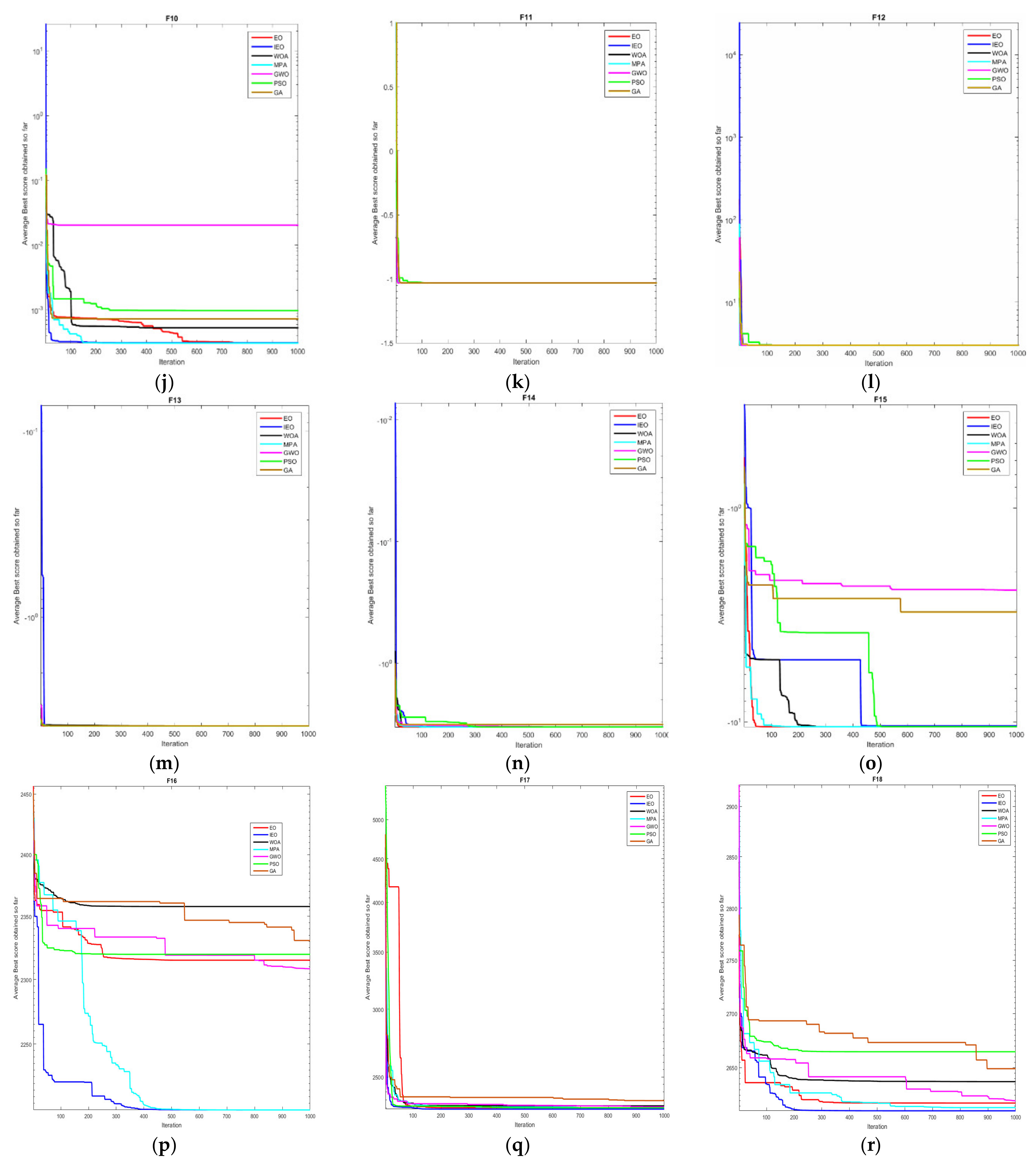
2.3.2. Benchmark Test Functions
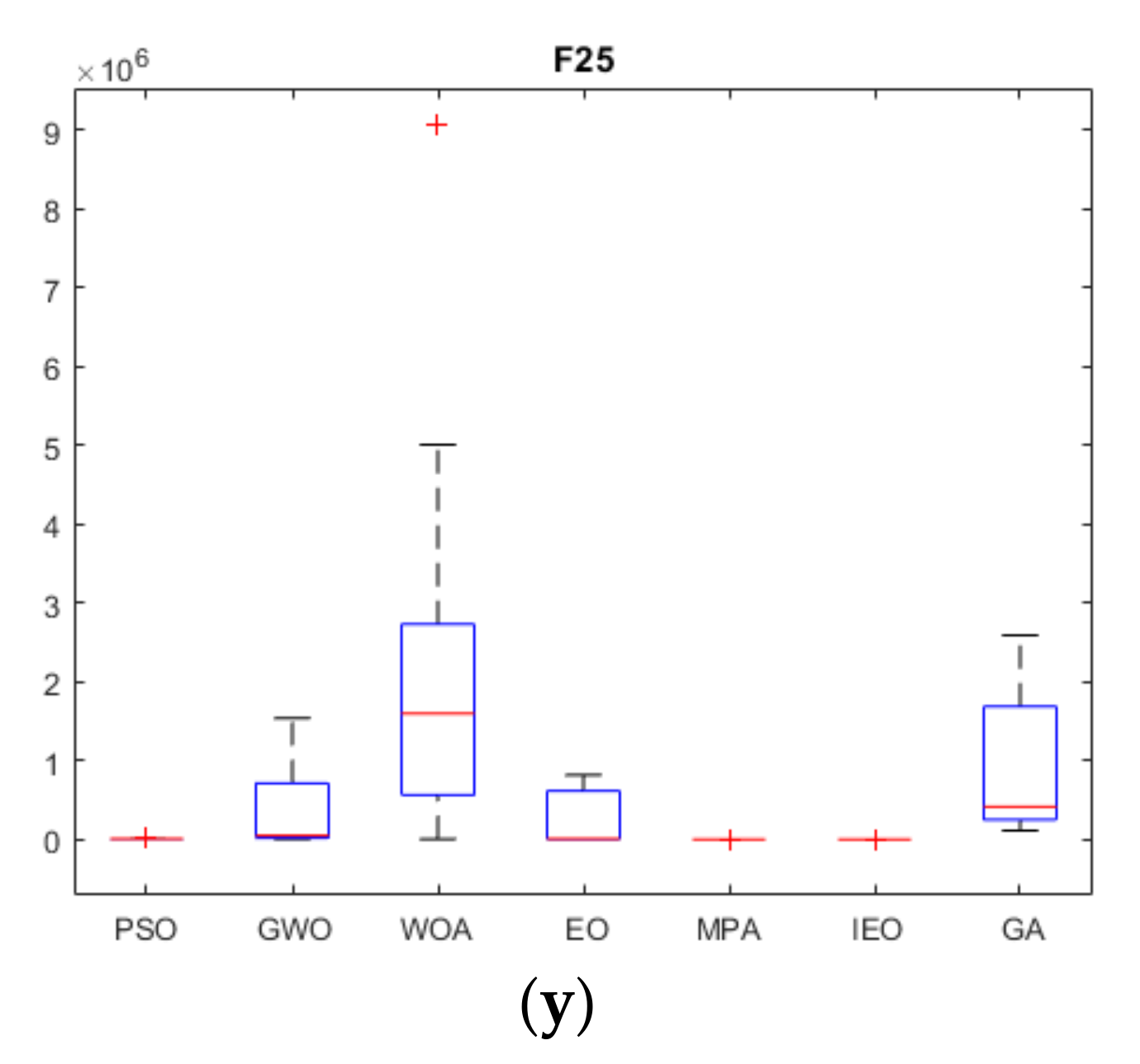
2.3.3. Experimental Results and Analysis
3. LSTM Model Optimization by Improved IEO Algorithm
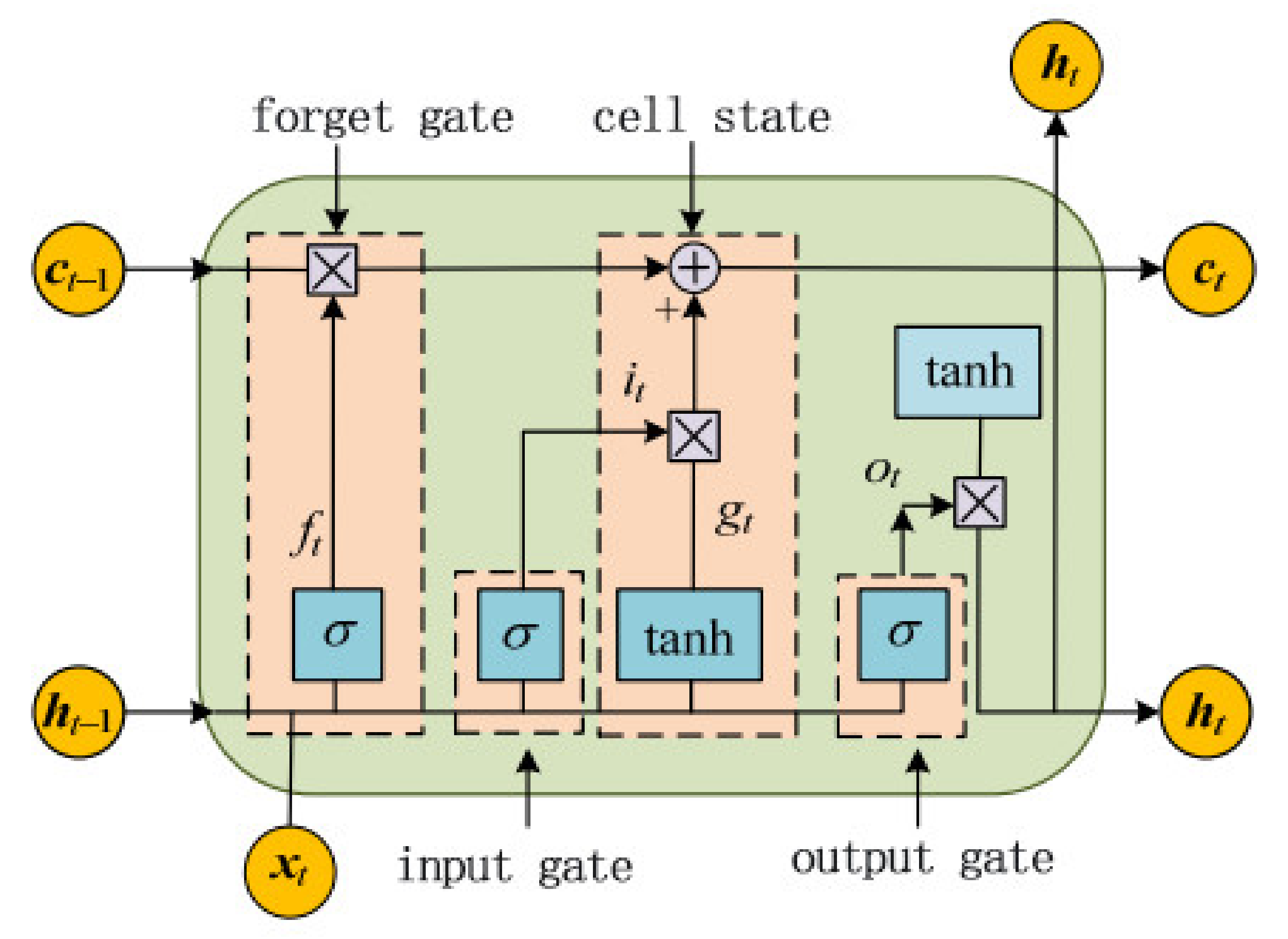
3.1. Basic Model of LSTM
3.2. LSTM Based on Improved EO
- (1)
- The relevant parameters are initialized. The parameters of the IEO algorithm are initialized, including: population size, fitness function, are free parameter assignment. The parameters of the LSTM algorithm are initialized by setting the time window, the initial learning rate, the number of initial iterations, and the size of the packet. In this paper, the error is treated as a fitness function, which is expressed as follows:where D represents the training set, m denotes the number of samples in the training set, indicates the predicted sample label, means the original sample label, and is a function. If , = 1; otherwise, = 0.
- (2)
- The LSTM parameters are set as required to form the corresponding particles. The particle structure is (, , ). Among them, represents the LSTM learning rate, indicates the number of iterations, suggests the size of the bag. The particles mentioned above are the objects of IEO optimization.
- (3)
- The concentration is updated according to Equation (15). According to the newly-obtained concentration, calculate the fitness value and then update the individual optimal concentration and the global optimal concentration of the particles.
- (4)
- If the number of iterations reaches the maximum number of times of iteration, that is, 30, the LSTM model trained on the optimal particles will output the prediction value; otherwise, return to step (3) for continued iteration.
- (5)
- The optimal parameters are substituted into the LSTM model, for constructing obtaining the IEO-LSTM model.
| Algorithm 2 Pseudo-code of the IEO-LSTM on oil prediction. |
| Input: |
| Training samples set: trainset_input, trainset_output |
| LSTM initialization parameters |
| Output: IEO-LSTM model |
| 1. Initialize the LSTM model: |
| assign parameters para = [lr,epoch,batch_size] = [0.01,100,256]; |
| loss = categorical_crossentropy, optimizer = adam |
| 2. Set IEO equalization parameters and Import trainset to Optimization: Parameters:para = [lr,epoch,batch_size] Ll para = [0.001,1, 1, 1, 1, 1]; % Set lower limit for merit search Ul para = [0.01, 100,256, 100, 100,100]; % Set the upper limit of merit seeking IEO_para = [ll,ul,trainset_input, trainset_output, num_epoch = 30]; Get_fitness_position ((IEO)) = length(find((trainset_output - LSTM(trainset- input)~ = 0))/length(trainset_output); % Find the best Concentration to minimize the LSTM error rate return para_best to LSTM model; save (‘IEO-LSTM.mat’,’LSTM’) |
3.3. Actual Application in Oil Layer Prediction
3.3.1. Design of Oil Layer Prediction System
- (1)
- Data acquisition and preprocessing
- (2)
- Selection of sample set and attribute reduction
- (3)
- IEO-LSTM modeling
- (4)
- Prediction
| Algorithm 3 Pseudo-code of the oil prediction system based on IEO-LSTM. |
| Input: |
| Training samples set: trainset_input, trainset_output, testset |
| Test samples set: testset |
| Output: Parameter optimization value Prediction results of the test samples set |
| 1. Original data initialization, Divide the trainset and testset |
| 2. Initialize the LSTM model: |
| assign parameters para = [lr,epoch,batch_size] = [0.01,100,256]; |
| loss = categorical_crossentropy, optimizer = adama; |
| 3. Set IEO equalization parameters and Import trainset to Optimization: 4. Set IEO equalization parameters and Import trainset to Optimization: Parameters:para = [lr,epoch,batch_size] ll =[0.001,1, 1]; % Set lower limit for merit search ul = [0.01, 100, 256]; % Set the upper limit of merit seeking para = IEO[ll,ul,trainset_input, trainset_output, num_epoch = 30]; Get_fitness_position () = length(find((trainset_output—LSTM(trainset- input)~ = 0))/length(trainset_output); % Find the best Concentration to minimize the LSTM error rate return para_best to LSTM model; save (‘IEO-LSTM.mat’,’LSTM’); 5. Import test samples set to IEO-LSTM load(‘IEO-LSTM.mat’) predictset = IEO-LSTM(testset) return predictset |
3.3.2. Practical Application
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A




| Function | IEO | EO | WOA | MPA | GWO | PSO | GA | ||
|---|---|---|---|---|---|---|---|---|---|
| Unimodal Benchmark Functions | F1 | Ave | 0.00 × 10+00 | 2.45 × 10−85 | 1.41 × 10−30 | 3.27 × 10−21 | 1.07 × 10−58 | 0.32 × 10+00 | 0.55 × 10+00 |
| Std | 0.00 × 10+00 | 9.08 × 10−85 | 4.91 × 10−30 | 4.61 × 10−21 | 2.77 × 10−58 | 0.21 × 10+00 | 1.23 × 10+00 | ||
| F2 | Ave | 0.00 × 10+00 | 2.91 × 10−48 | 1.06 × 10−21 | 0.07 × 10+00 | 1.36 × 10−34 | 1.04 × 10+00 | 0.01 × 10+00 | |
| Std | 0.00 × 10+00 | 2.92 × 10−48 | 2.39 × 10−21 | 0.11 × 10+00 | 1.40 × 10−34 | 0.46 × 10+00 | 0.01 × 10+00 | ||
| F3 | Ave | 0.00 × 10+00 | 1.77 × 10−21 | 5.39 × 10−07 | 2.78 × 10+02 | 9.25 × 10−16 | 8.14 × 10+01 | 8.46 × 10+02 | |
| Std | 0.00 × 10+00 | 8.45 × 10−21 | 2.93 × 10−06 | 4.00 × 10+02 | 2.44 × 10−15 | 2.13 × 10+01 | 1.62 × 10+02 | ||
| F4 | Ave | 0.00 × 10+00 | 2.84 × 10−21 | 0.73 × 10−01 | 6.78 × 10+00 | 1.84 × 10−14 | 1.51 × 10+00 | 4.56 × 10+00 | |
| Std | 0.00 × 10+00 | 9.26 × 10−21 | 0.40 × 10+00 | 2.94 × 10+00 | 3.40 × 10−14 | 0.22 × 10+00 | 0.59 × 10+00 | ||
| F5 | Ave | 6.70 × 10−05 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.09 × 10+00 | 0.07 × 10+00 | 0.11 × 10+00 | |
| Std | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.03 × 10+00 | 0.01 × 10+00 | 0.04 × 10+00 | ||
| Multimodal Benchmark Functions | F6 | Ave | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 4.84 × 10+01 | 0.00 × 10+00 |
| Std | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 3.44 × 10+00 | 3.97 × 10+00 | ||
| F7 | Ave | 8.84 × 10−16 | 5.15 × 10−15 | 7.40 × 10+00 | 9.69 × 10−12 | 0.00 × 10+00 | 1.20 × 10+00 | 0.18 × 10+00 | |
| Std | 0.00 × 10+00 | 1.45 × 10−15 | 9.90 × 10+00 | 6.13 × 10−12 | 0.00 × 10+00 | 0.73 × 10+00 | 0.15 × 10+00 | ||
| F8 | Ave | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.60 × 10+00 | 0.01 × 10+00 | 0.66 × 10+00 | |
| Std | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.00 × 10+00 | 0.09 × 10+00 | 0.01 × 10+00 | 0.19 × 10+00 | ||
| Fifixed-Dimenstion Multimodal Benchmark Functions | F9 | Ave | 1.00 × 10+00 | 1.00 × 10+00 | 2.11 × 10+00 | 1.00 × 10+00 | 0.16 × 10+00 | 2.18 × 10+00 | 1.00 × 10+00 |
| Std | 2.12 × 10−17 | 1.11 × 10−16 | 2.50 × 10+00 | 2.47 × 10−16 | 0.84 × 10+00 | 2.01 × 10+00 | 8.84 × 10−12 | ||
| F10 | Ave | 3.58 × 10−04 | 3.69 × 10−49 | 0.00 × 10+00 | 3.07 × 10−04 | 1.62 × 10−04 | 5.61 × 10−04 | 2.69 × 10−03 | |
| Std | 1.54 × 10−04 | 2.36 × 10−04 | 0.00 × 10+00 | 4.09 × 10−15 | 3.33 × 10−04 | 4.38 × 10−04 | 4.84 × 10−03 | ||
| F11 | Ave | −1.03 × 10+00 | −1.03 × 10+00 | −1.03 × 10+00 | −1.03 × 10+00 | −1.03 × 10+00 | −1.03 × 10+00 | −1.03 × 10+00 | |
| Std | 5.63 × 10−06 | 2.04 × 10+16 | 4.2 × 10−07 | 4.46 × 10−01 | 5.46 × 10−09 | 6.64 × 10−16 | 2.39 × 10−08 | ||
| F12 | Ave | 3.00 × 10+00 | 3.00 × 10+00 | 3.00 × 10+00 | 3.00 × 10+00 | 3.00 × 10+00 | 3.00 × 10+00 | 3.00 × 10+00 | |
| Std | 5.95 × 10−17 | 4.96 × 10−16 | 4.22 × 10−15 | 1.95 × 10−15 | 2.29 × 10−02 | 1.38 × 10−15 | 2.45 × 10−07 | ||
| F13 | Ave | −3.86 × 10+00 | −3.86 × 10+00 | −3.85 × 10+00 | −3.86 × 10+00 | 0.51 × 10+00 | −3.86 × 10+00 | −3.86 × 10+00 | |
| Std | 3.17 × 10−16 | 2.15 × 10−15 | 0.00 × 10+00 | 2.42 × 10−15 | 2.73 × 10−15 | 2.68 × 10−15 | 2.85 × 10−8 | ||
| F14 | Ave | −3.32 × 10+00 | -−3.28 × 10+00 | −2.98 × 10+00 | −3.32 × 10+00 | −2.84×10+00 | −3.26 × 10+00 | −3.27 × 10+00 | |
| Std | 1.59 × 10−15 | 0.06 × 10+00 | 0.38 × 10+00 | 1.14 × 10−11 | 4.68 × 10−2 | 6.05 × 10−2 | 5.99 × 10−2 | ||
| F15 | Ave | −1.05 × 10+1 | −10.27 × 10+00 | −9.34 × 10+00 | −1.05 × 10+1 | −7.11 × 10+00 | −7.25 × 10+00 | −7.77 × 10+00 | |
| Std | 1.92 × 10−07 | 1.48 × 10+00 | 2.41 × 10+00 | 3.89 × 10−11 | 3.11 × 10+00 | 3.66 × 10+00 | 3.73 × 10+00 | ||
| Composition Functions | F16 | Ave | 2.20 × 10+03 | 2.30 × 10+03 | 2.33 × 10+03 | 2.20 × 10+03 | 2.31 × 10+03 | 2.32 × 10+03 | 2.28 × 10+03 |
| Std | 6.54 × 10−07 | 4.13 × 10+01 | 4.34 × 10+01 | 8.66 × 10−06 | 2.28 × 10+01 | 6.34 × 10+01 | 5.84 × 10+01 | ||
| F17 | Ave | 2.28 × 10+3 | 2.30 × 10+03 | 2.36 × 10+03 | 2.28 × 10−06 | 2.31 × 10+03 | 2.37 × 10+03 | 2.41 × 10+03 | |
| Std | 0.54 × 10+00 | 0.35 × 10+00 | 1.43 × 10+02 | 3.38 × 10+01 | 8.52 × 10+00 | 3.20 × 10+02 | 1.00 × 10+02 | ||
| F18 | Ave | 2.61 × 10+03 | 2.62 × 10+03 | 2.65 × 10+03 | 2.61 × 10+03 | 2.62 × 10+03 | 2.71 × 10+03 | 2.65 × 10+03 | |
| Std | 3.55 × 10+00 | 8.76 × 10+00 | 2.88 × 10+01 | 5.06 × 10+00 | 1.04 × 10+01 | 4.18 × 10+01 | 1.28 × 10+01 | ||
| F19 | Ave | 2.63 × 10+02 | 2.74 × 10+03 | 2.76 × 10+03 | 2.51 × 10+03 | 2.75 × 10+03 | 2.77 × 10+02 | 2.79 × 10+03 | |
| Std | 5.13 × 10+00 | 4.30 × 10+00 | 6.11 × 10+01 | 3.58 × 10+01 | 1.40 × 10+01 | 1.16 × 10+02 | 2.31 × 10+01 | ||
| F20 | Ave | 2.91 × 10+03 | 2.92 × 10+03 | 2.95 × 10+03 | 2.88 × 10+03 | 2.94 × 10+03 | 2.90 × 10+03 | 2.99 × 10+02 | |
| Std | 2.29 × 10+01 | 2.39 × 10+02 | 2.36 × 10+01 | 2.09 × 10+01 | 2.68 × 10+01 | 8.60 × 10+01 | 8.07 × 10+01 | ||
| F21 | Ave | 2.78 × 10+03 | 3.03 × 10+03 | 3.60 × 10+03 | 2.79 × 10+03 | 3.23 × 10+03 | 3.08 × 10+03 | 3.20 × 10+03 | |
| Std | 5.11 × 10+01 | 3.07 × 10+02 | 6.33 × 10+02 | 1.10 × 10+02 | 4.32 × 10+02 | 3.57 × 10+02 | 2.17 × 10+02 | ||
| F22 | Ave | 3.08 × 10+03 | 3.09 × 10+03 | 3.13 × 10+03 | 3.09 × 10+03 | 3.10 × 10+03 | 3.16 × 10+03 | 3.14 × 10+03 | |
| Std | 0.33 × 10+00 | 6.52 × 10+00 | 4.27 × 10+01 | 0.22 × 10+00 | 2.11 × 10+01 | 7.44 × 10+01 | 3.53 × 10+01 | ||
| F23 | Ave | 3.11 × 10+03 | 3.32 × 10+03 | 3.41 × 10+03 | 3.12 × 10+03 | 3.34 × 10+03 | 3.19 × 10+03 | 3.62 × 10+03 | |
| Std | 5.57 × 10−05 | 1.41 × 10+02 | 1.77 × 10+02 | 5.00 × 10−05 | 9.99 × 10+01 | 6.07 × 10+01 | 2.02 × 10+02 | ||
| F24 | Ave | 3.15 × 10+03 | 3.18 × 10+03 | 3.36 × 10+03 | 3.14 × 10+03 | 3.22 × 10+03 | 3.26 × 10+03 | 3.30 × 10+03 | |
| Std | 3.14 × 10+00 | 3.47 × 10+01 | 1.12 × 10+02 | 8.63 × 10+00 | 5.49 × 10+01 | 8.77 × 10+01 | 8.67 × 10+01 | ||
| F25 | Ave | 4.73 × 10+03 | 3.35 × 10+05 | 9.75 × 10+05 | 3.40 × 10+03 | 1.03 × 10+06 | 1.08 × 10+04 | 1.39 × 10+06 | |
| Std | 3.51 × 10+01 | 4.11 × 10+05 | 8.97 × 10+05 | 3.51 × 10+01 | 1.09 × 10+06 | 4.96 × 10+03 | 1.10 × 10+06 |
References
- Ma, X.S.; Li, Y.L.; Yan, L. A comparative review of traditional multi-objective optimization methods and multi-objective genetic algorithms. Electr. Drive Autom. 2010, 32, 48–53. [Google Scholar]
- Koziel, S.; Michalewicz, Z. Evolutionary Algorithms, homomorphous mappings, and constrained parameter optimization. Evol. Comput. 1999, 7, 19–44. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Fister, I.; Yang, X.S.; Brest, J.; Fister, D. A Brief Review of Nature-Inspired Algorithms for Optimization. Elektrotehniski Vestn. Electrotech. Rev. 2013, 80, 116–122. [Google Scholar]
- Brezočnik, L.; Fister, I.; Podgorelec, V. Swarm Intelligence Algorithms for Feature Selection: A Review. Appl. Sci. 2018, 8, 9. [Google Scholar] [CrossRef] [Green Version]
- Omran, M.; Engelbrecht, A.; Salman, A. Particle Swarm Optimization Methods for Pattern Recognition and Image Processing. Ph.D. Thesis, University of Pretoria, Pretoria, South Africa, 2004. [Google Scholar]
- Martens, D.; Baesens, B.; Fawcett, T. Editorial survey: Swarm intelligence for data mining. Mach. Learn. 2010, 82, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Zhang, J.; Xia, K.; He, Z.; Fan, S. Dynamic Multi-Swarm Differential Learning Quantum Bird Swarm Algorithm and Its Application in Random Forest Classification Model. Comput. Intell. Neurosci. 2020, 2020, 6858541. [Google Scholar] [CrossRef] [PubMed]
- Alejo-Reyes, A.; Cuevas, E.; Rodríguez, A.; Mendoza, A.; Olivares-Benitez, E. An Improved Grey Wolf Optimizer for a Supplier Selection and Order Quantity Allocation Problem. Mathematics 2020, 8, 1457. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2018, 165, 169–196. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Pan, Y.-K.; Xia, K.-W.; Niu, W.-J.; He, Z.-P. Semisupervised SVM by Hybrid Whale Optimization Algorithm and Its Application in Oil Layer Recognition. Math. Probl. Eng. 2021, 2021, 5289038. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Engineering Optimisation by Cuckoo Search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- He, Z.; Xia, K.; Niu, W.; Aslam, N.; Hou, J. Semisupervised SVM Based on Cuckoo Search Algorithm and Its Application. Math. Probl. Eng. 2018, 2018, 8243764. [Google Scholar] [CrossRef] [Green Version]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Yang, W.B.; Xia, K.W.; Li, T.J.; Xie, M.; Song, F. A Multi-Strategy Marine Predator Algorithm and Its Application in Joint Regularization Semi-Supervised ELM. Mathematics 2021, 9, 291. [Google Scholar] [CrossRef]
- Pierezan, J.; Coelho, L. Coyote Optimization Algorithm: A New Metaheuristic for Global Optimization Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Kiong, S.C.; Ong, P.; Sia, C.K. A carnivorous plant algorithm for solving global optimization problems. Appl. Soft Comput. 2020, 98, 106833. [Google Scholar]
- Yang, W.B.; Xia, K.W.; Li, T.J.; Xie, M.; Song, F.; Zhao, Y.L. An Improved Transient Search Optimization with Neighborhood Dimensional Learning for Global Optimization Problems. Symmetry 2021, 13, 244. [Google Scholar] [CrossRef]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Transient search optimization: A new meta-heuristic optimization algorithm. Appl. Intell. 2020, 50, 3926–3941. [Google Scholar] [CrossRef]
- Afshin, F.; Mohammad, H.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2019, 191, 105190. [Google Scholar]
- Yang, L.Q. A novel improved equilibrium global optimization algorithm based on Lévy flight. Astronaut. Meas. Technol. 2020, 40, 66–73. [Google Scholar]
- Feng, Y.H.; Liu, J.Q.; He, Y.C. Dynamic population firefly algorithm based on chaos theory. J. Comput. Appl. 2013, 54, 796–799. [Google Scholar]
- Wu, G.; Mallipeddi, R.; Ponnuthurai, N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real Parameter Optimization; Nanyang Technological University: Singapore, 2010. [Google Scholar]
- Gooijer, J.; Hyndman, R.J. 25 years of time series forecasting. In Monash Econometrics & Business Statistics Working Papers; Monash University: Clayton, Australia, 2005; Volume 22, pp. 443–473. [Google Scholar]
- Caraka, R.E.; Chen, R.C.; Yasin, H.; Suhartono, S.; Lee, Y.; Pardamean, B. Hybrid Vector Autoregression Feedforward Neural Network with Genetic Algorithm Model for Forecasting Space-Time Pollution Data. Indones. J. Sci. Technol. 2021, 6, 243–268. [Google Scholar] [CrossRef]
- Caraka, R.E.; Chen, R.C.; Toharudin, T.; Pardamean, B.; Yasin, H.; Wu, S.H. Prediction of Status Particulate Matter 2.5 using State Markov Chain Stochastic Process and Hybrid VAR-NN-PSO. IEEE Access 2019, 7, 161654–161665. [Google Scholar] [CrossRef]
- Suhartono, S.; Prastyo, D.D.; Kuswanto, H.; Lee, M.H. Comparison between VAR, GSTAR, FFNN-VAR and FFNN-GSTAR Models for Forecasting Oil Production. Mat. Malays. J. Ind. Appl. Math. 2018, 34, 103–111. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2017, 270, 654–669. [Google Scholar] [CrossRef] [Green Version]
- Toharudin, T.; Pontoh, R.S.; Caraka, R.E.; Zahroh, S.; Lee, Y.; Chen, R.C. Employing Long Short-Term Memory and Facebook Prophet Model in Air Temperature Forecasting. Commun. Stat. Simul. Comput. 2021. (Early Access). [Google Scholar] [CrossRef]
- Wu, C.H.; Lu, C.C.; Ma, Y.-F.; Lu, R.-S. A new forecasting framework for bitcoin price with LSTM. In Proceedings of the IEEE International Conference on Data Mining Workshops, Singapore, 17–20 November 2018; pp. 168–175. [Google Scholar]
- Helmini, S.; Jihan, N.; Jayasinghe, M.; Perera, S. Sales Forecasting Using Multivariate Long Short Term Memory Networks. PeerJ 2019, 7, e27712v1. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2017, 6, 1662–1669. [Google Scholar] [CrossRef]
- Saeed, A.; Li, C.; Danish, M.; Rubaiee, S.; Tang, G.; Gan, Z.; Ahmed, A. Hybrid Bidirectional LSTM Model for Short-Term Wind Speed Interval Prediction. IEEE Access 2020, 8, 182283–182294. [Google Scholar] [CrossRef]
- Venskus, J.; Treigys, P.; Markevičiūtė, J. Unsupervised marine vessel trajectory prediction using LSTM network and wild bootstrapping techniques. Nonlinear Anal. Model. Control. 2021, 26, 718–737. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, Z.; Hu, F.; Zhu, J.; Tang, Q.; Liang, Y. An automatic diagnosis of arrhythmias using a combination of CNN and LSTM technology. Electronics 2020, 9, 121. [Google Scholar] [CrossRef] [Green Version]
- Bai, J.; Xia, K.; Lin, Y.; Wu, P. Attribute Reduction Based on Consistent Covering Rough Set and Its Application. Complexity 2017, 2017, 8986917. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Zhao, J.; Gao, Y.; Sotelo, M.A.; Li, Z. Lane Work-schedule of Toll Station Based on Queuing Theory and PSO-LSTM Model. IEEE Access 2020, 8, 84434–84443. [Google Scholar] [CrossRef]
- Wen, H.; Zhang, D.; Lu, S.Y. Application of GA-LSTM model in highway traffic flow prediction. J. Harbin Inst. Technol. 2019, 51, 81–95. [Google Scholar]


| Function | Dim | Range | |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| 30 | [−10, 10] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−100, 100] | 0 | |
| 30 | [−1.28, 1.28] | 0 | |
| 30 | [−5.12, 5.12] | 0 | |
| 30 | [−32, 32] | 0 | |
| 30 | [−600, 600] | −418.9829 × 5 | |
| 2 | [−65, 65] | 1 | |
| 4 | [−5, 5] | 0.00030 | |
| 2 | [−5, 5] | −1.0316 | |
| 2 | [−2, 2] | 3 | |
| 3 | [1, 3] | −3.86 | |
| 6 | [0, 1] | −3.32 | |
| 4 | [0, 10] | −10.5363 | |
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 | ||
| 30 | 0 |
| Well | Attributes |
|---|---|
| Original results () | GR,DT,SP,WQ,LLD,LLS,DEN,NPHI,PE,U,TH,K,CALI |
| Reduction results () | GR, DT,SP,LLD,LLS, DEN, K |
| Original results () | AC,CNL,DEN,GR,RT,RI,RXO,SP,R2M,R025,BZSP,RA2,C1,C2,CALI,RINC,PORT,VCL,VMA1,VMA6,RHOG,SW,VO,WO,PORE,VXO,VW,so,rnsy,rsly,rny,AC1 |
| Reduction results () | AC,GR,RT,RXO,SP |
| Original results () | AC,CALI,GR,NG,RA2,RA4,RI,RM,RT,RXO,SP |
| Reduction results () | AC,NG,RI,SP |
| Decision attribute | where–1, 1 represents the dry layer and oil layer respectively. |
| Well | Depth (m) | Training Set | Depth (m) | Test Set | ||
|---|---|---|---|---|---|---|
| Oil Layer | Dry Layer | Oil Layer | Dry Layer | |||
| 3150~3330 | 122 | 1319 | 3330~3460 | 115 | 925 | |
| 1180~1255 | 65 | 496 | 1230~1300 | 40 | 360 | |
| 1150~1250 | 65 | 736 | 1233~1260 | 104 | 112 | |
| Attributes | GR | DT | SP | LLD | LLS | DEN | K |
|---|---|---|---|---|---|---|---|
| Boundary | [6, 200] | [152, 462] | [−167, −68] | [0, 25000] | [0, 3307] | [1, 4] | [0, 5] |
| Attributes | AC | GR | RT | RXO | SP |
|---|---|---|---|---|---|
| Boundary | [54, 140] | [27, 100] | [2, 90] | [1, 328] | [−32, −6] |
| Attributes | AC | NG | RI | SP |
|---|---|---|---|---|
| Boundary | [0, 571] | [0, 42] | [−1, 81] | [−50, 28] |
| Optimization Algorithm | Oil | Learning Rate | Epochs | Batch Size | ACC | MSE | RMSE | MAE |
|---|---|---|---|---|---|---|---|---|
| LSTM | o1 | 0.01 | 100 | 256 | 0.8837 | 0.2049 | 0.4887 | 0.2341 |
| o2 | 0.01 | 100 | 256 | 0.8937 | 0.1765 | 0.0519 | 0.0826 | |
| o3 | 0.01 | 100 | 256 | 0.9095 | 0.1561 | 0.4896 | 0.1971 | |
| PSO_LSTM | o1 | 0.0098 | 86 | 103 | 0.9025 | 0.1697 | 0.3925 | 0.1137 |
| o2 | 0.0011 | 42 | 154 | 0.9154 | 0.0937 | 0. 035 | 0.0985 | |
| o3 | 0.003 | 52 | 75 | 0.8859 | 0.0952 | 0.3131 | 0.0933 | |
| GA_LSTM | o1 | 0.0082 | 20 | 200 | 0.9084 | 0.6732 | 0.8587 | 0.7368 |
| o2 | 0.0082 | 54 | 167 | 0.8979 | 0.0753 | 0.2853 | 0.0877 | |
| o3 | 0.0038 | 29 | 176 | 0.9132 | 0.1368 | 0.3368 | 0.1404 | |
| EO_LSTM | o1 | 0.0089 | 28 | 163 | 0.9231 | 0.1481 | 0.2347 | 0.5442 |
| o2 | 0.0081 | 45 | 127 | 0.9183 | 0.0605 | 0.0375 | 0.0116 | |
| o3 | 0.0049 | 56 | 155 | 0.9203 | 0.0795 | 0.2353 | 0.0793 | |
| IEO_LSTM | o1 | 0.0030 | 29 | 137 | 0.9433 | 0.1023 | 0.3781 | 0.4544 |
| o2 | 0.0082 | 43 | 109 | 0.9371 | 0.041 | 0.0212 | 0.0107 | |
| o3 | 0.0027 | 53 | 128 | 0.9661 | 0.0323 | 0.2016 | 0.0571 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, P.; Xia, K.; Pan, Y.; Fan, S. An Improved Equilibrium Optimizer Algorithm and Its Application in LSTM Neural Network. Symmetry 2021, 13, 1706. https://doi.org/10.3390/sym13091706
Lan P, Xia K, Pan Y, Fan S. An Improved Equilibrium Optimizer Algorithm and Its Application in LSTM Neural Network. Symmetry. 2021; 13(9):1706. https://doi.org/10.3390/sym13091706
Chicago/Turabian StyleLan, Pu, Kewen Xia, Yongke Pan, and Shurui Fan. 2021. "An Improved Equilibrium Optimizer Algorithm and Its Application in LSTM Neural Network" Symmetry 13, no. 9: 1706. https://doi.org/10.3390/sym13091706
APA StyleLan, P., Xia, K., Pan, Y., & Fan, S. (2021). An Improved Equilibrium Optimizer Algorithm and Its Application in LSTM Neural Network. Symmetry, 13(9), 1706. https://doi.org/10.3390/sym13091706







