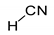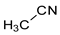Next Article in Journal
Estimating the Reattachment Length by Realizing a Comparison between URANS k-Omega SST and LES WALE Models on a Symmetric Geometry
Next Article in Special Issue
Symmetry in Acid-Base Chemistry
Previous Article in Journal
On Special Differential Subordinations Using Fractional Integral of Sălăgean and Ruscheweyh Operators
Previous Article in Special Issue
Quantum-Chemical Search for Keto Tautomers of Azulenols in Vacuo and Aqueous Solution
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Symmetry
Volume 13
Issue 9
10.3390/sym13091554
symmetry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Push–Pull Effect on the Gas-Phase Basicity of Nitriles: Transmission of the Resonance Effects by Methylenecyclopropene and Cyclopropenimine π-Systems Substituted by Two Identical Strong Electron Donors

by
Ewa D. Raczyńska
1,*,
Jean-François Gal
2,*,
Pierre-Charles Maria
2 and
Hamid Saeidian
3,*
1
Department of Chemistry, Warsaw University of Life Sciences (SGGW), ul. Nowoursynowska 159c, 02-776 Warszawa, Poland
2
Institut de Chimie de Nice, UMR 7272, Université Côte d’Azur, Parc Valrose, 06108 Nice, France
3
Department of Science, Payame Noor University (PNU), Teheran P.O. Box 19395-4697, Iran
*
Authors to whom correspondence should be addressed.
Symmetry 2021, 13(9), 1554; https://doi.org/10.3390/sym13091554
Submission received: 28 June 2021 / Revised: 10 August 2021 / Accepted: 18 August 2021 / Published: 24 August 2021
(This article belongs to the Special Issue Symmetry in Acid-Base Chemistry)
Browse Figures
Versions Notes

Abstract

:
The gas-phase basicity of nitriles can be enhanced by a push–pull effect. The role of the intercalated scaffold between the pushing group (electron-donor) and the pulling (electron-acceptor) nitrile group is crucial in the basicity enhancement, simultaneously having a transmission function and an intrinsic contribution to the basicity. In this study, we examine the methylenecyclopropene and the N-analog, cyclopropenimine, as the smallest cyclic π systems that can be considered for resonance propagation in a push–pull system, as well as their derivatives possessing two strong pushing groups (X) attached symmetrically to the cyclopropene scaffold. For basicity and push–pull effect investigations, we apply theoretical methods (DFT and G2). The effects of geometrical and rotational isomerism on the basicity are explored. We establish that the protonation of the cyano group is always favored. The push–pull effect of strong electron donor X substituents is very similar and the two π-systems appear to be good relays for this effect. The effects of groups in the two cyclopropene series are found to be proportional to the effects in the directly substituted nitrile series X–C≡N. In parallel to the basicity, changes in electron delocalization caused by protonation are also assessed on the basis of aromaticity indices. The calculated proton affinities of the nitrile series reported in this study enrich the gas-phase basicity scale of nitriles to around 1000 kJ mol−1.

1. Introduction

Nitriles are usually considered weak bases because of the unfavorable sp hybridization of the nitrogen atom and the high s character, being adverse to electron pair sharing with acids. Nevertheless, their gas-phase basicity, as experimentally measured or calculated, may be increased by the push–pull effect. This effect occurs when a strong electron-donating group pushes its electron density toward the electron-accepting cyano group through a conjugated system [1]. Several examples can be found in a review reporting on the gas-phase basicity values of nitriles [2]. For example, 3-(dimethylamino)acrylonitrile (CH3)2N−CH=CH−C≡N, which is protonated preferentially on the cyano group, displays a proton affinity (897 kJ mol−1) close to that of methylamine (899 kJ mol−1) [3,4]. The calculated proton affinities of nitriles bearing strong electron-donating groups, such as phosphazeno and diphosphazeno substituents, can exceed 1000 kJ mol−1 [2,5,6]. Inserting a group with at least one double bond (e.g., vinyl group) in the dimethyl cyanamide skeleton (CH3)2N−C≡N, leading to (CH3)2N−CH=CH−C≡N, significantly enhances the push–pull effect, increasing the proton affinity from 852 to 897 kJ mol−1 [3,4]. For this reason, the search for even more efficient resonance-transmitting systems of the push–pull effect seems to be a promising strategy for increasing the C≡N basicity.
In this study, we extended earlier quantum chemical investigations of strong basic nitriles in the gas phase [5,6] to two series of nitriles (I and II) possessing interesting π-π- and n-π-conjugated systems or groups (Figure 1). First, we included in our study, for comparison with previous reports and for investigation of the substituent effects, nitriles containing simple acyclic π-systems such as H2C=Z (1) and H2C=CH−CH=Z (2) [2], as well as nitriles with different cyclic scaffolds displaying strong electron delocalization (aromaticity), such as cyclopropene (3) [7], 1,3,5-cycloheptatriene (5) [8,9], and “quinoid” fragments (6 and 7) [10]. Additionally, the methylenecyclopropene (3)-conjugated system (with Z: CH) and its heteroatomic analog (with Z: N) was hypothesized to be an efficient resonance-transmitting unit between various pushing substituents and the site of protonation [7,10,11,12,13,14,15,16,17]; therefore, we also decided to study the gas-phase protonation of the nitrile series shown in Figure 2, for which the two X substituents are electron-donating or pushing groups of medium or strong power, such as Me, NR2, N=C(NR2)2, and N=P(NR2)3 (R: H and Me) attached to the cyclopropenylidene ring.
The cyclopropenimine (or cyclopropeneimine, less common name) skeleton (Z: N) has a special status among the heteroatomic analogs of methylenecyclopropene. It is present in many systems, which have been largely studied experimentally and theoretically, in particular in the last ten years, as platforms for developing superbases and organocatalysts [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. The imino bond carrying a nitrile group on the nitrogen, >C=N−CN, is present in molecules of biological interest, in particular the neonicotinoids [35,36,37], and in materials developed for their electronic applications [38,39,40]. These articles, as well as others dealing with similar functionalities, refer to the corresponding families as N-cyano-imines or cyano-imines. On the other hand, the IUPAC nomenclature describes these compounds (Z: N) as cyanamide (H2N−CN) derivatives, with the series Z: CH being defined as acetonitrile derivatives (see Table S1 in the Supplementary Materials (SM) for IUPAC names for series 1–6). To avoid confusion, and to focus on our objective of comparing nitrile basicity values, we adopted names indicating a priority for the nitrile group. This choice does not imply a priori that the favored gas-phase protonation site is the nitrile group, although previous studies have shown that this site is often the most basic group preferred in push–pull nitriles.
In the study presented here, we aimed to compare the methylenecyclopropene (CPC) and the cyclopropeneimine (CPN) systems as push–pull relays (or resonance transmission units) using the basicity of the cyano group as the probe. In the CPN series, the imino-nitrogen is also a concurrent basic site due to the intrinsically higher basicity of the imino N atom in comparison with the cyano nitrogen, while the most favored protonation site is yet to be determined. The electronic structure of CPC and CPN confers to these systems specific aromaticity properties [13]. The analogous phenomena are related to the relationships of the nitriles series (Figure 1) with the other groups (4–6). Consequently, we considered possible structural variations for neutral and protonated forms, as well as all reasonable potential protonation sites. About 200 isomeric structures were analyzed at various quantum chemical levels. We used the Gaussian series of software programs and employed DFT methods for all derivatives, as well as the G2 approach for selected simple nitriles. For more computational details, see the next section and SM. For selected isomers, bond length alternations, including the aromaticity of the cycles, were discussed. Gas-phase basicity parameters (proton affinity, PA; gas-phase basicity, GB) for N sites in each isomer were calculated and conformational and substituent effects were investigated. For compounds presenting isomers with close energies, we estimated the macroscopic PA and GB values corresponding to the isomeric mixtures.
Monosubstituted CPC and CPN, with only one substituent on the cyclopropene cycle and with unsymmetrically disubstituted structures bearing two different substituents on the cycle, pose specific problems because of their Z/E isomerism. These compounds are also particularly interesting as models for the additivity (or non-additivity) of strong electron donation in push–pull systems. For these reasons, the basicity of these unsymmetrical molecules will be described in a separate forthcoming publication.

2. Conceptual Approaches and Computational Methods

DFT calculations at the B3LYP/6-311++G(d,p) level [41,42,43] were performed for geometry optimization without symmetry constraints, as well as for gas-phase basicity estimations of an extended series of nitriles, given in Figure 1 and Figure 2, including those based on methylenecyclopropene and cyclopropenimine scaffolds. For the selected structures, the B3LYP/311+G(d,p) level [41,42,43] was also employed to reach our previous DFT-PA scale for push–pull nitriles [5,6]. This level of theory was chosen for nitrogen bases by Koppel and co-workers [44] and is used for PA prediction of guanidines, phosphazenes, biguanides, and other imines [7,45]. For small molecules (I.1–I.3, and II.1–II.3), the G2 theory [46,47] was additionally applied. Some computational details are included in SM.
We performed quantum chemical calculations for a series of nitriles (I with Z: CH) and for a series of α-imino nitriles (II with Z: N) containing simple π-π-conjugated systems (1–6 in Figure 1), as well as for those possessing two electron-donating substituents attached to the cyclopropene ring, in order to explore the transmission of their cross-pushing effects to the pulling cyano group through the π-π-conjugated CPC and CPN scaffold (7–12 in Figure 2). Calculations were performed for neutral derivatives and for their monoprotonated forms. When more than one nitrogen atom (N-cyano) was present in the molecule (N-imino or N-amino), potential protonated forms were considered to indicate the favored site of protonation for investigated nitriles in the gas phase. The most significant structural phenomena that may dictate basicity of the investigated derivatives were taken into account for the neutral and monoprotonated forms. Selected thermochemical data for all considered species of simple nitriles (Table S2) and CPC and CPN derivatives containing large substituents (Table S3) are included in SM.
Gas-phase basicity parameters, namely the PA (proton affinity) and GB (gas-phase basicity), for the potential sites of monoprotonation in each isomer of CH and N derivatives were determined according to Equations (1) and (2), respectively [3]. In these equations, B and BH+ correspond to the neutral and monoprotonated forms, while their H and G correspond to the enthalpy and Gibbs energy, respectively, calculated at 298 K. For the proton, the following values were used: H298(H+) = 6.2 kJ mol−1 and G298(H+) = −26.3 kJ mol−1 [48,49].
PA = H298(B) + H298(H+) − H298(BH+)
GB = G298(B) + G298(H+) − G298(BH+)
The geometry-based HOMA (harmonic oscillator model of aromaticity) [50] and HOMED (harmonic oscillator model of electron delocalization) indices [51], both originating from the HOMA idea proposed by Kruszewski and Krygowski [52,53], were estimated for fragments of selected neutral and monoprotonated forms of nitriles and imino nitriles according to Equation (3). In this equation, n, α, Ro, and Rx are the number of bonds in a considered fragment, the normalization constant (different for different bonds of CC and CN), the optimum bond length for the reference molecule (also different for different CC and CN bonds), and the calculated bond lengths for the studied fragment, respectively:
HOMA or HOMED = 1 − (ΣαΣ[Ro − Rx]2)/n
The HOMA and HOMED procedures are analogous, although their parametrizations (α and Ro) are different. For example, the HOMA and HOMED descriptors are equal to unity for aromatic benzene and s-triazine; however, zero is not the same in the HOMA and HOMED scales—HOMED = 0 for the Kekulé structure of benzene with non-delocalized C–C and C=C bonds [54], similar to the original HOMA, whereas HOMA = 0 for the hypothetical structure of benzene with moderately delocalized C–C and C=C bonds [50]. In HOMED(0), the bond lengths of ethane and ethene were taken for the C–C and C=C bonds in the Kekulé structure of benzene, whereas those of 1,3-butadiene were used for the hypothetical structure of benzene in HOMA(0). These differences in the reference bond lengths lead to the negative HOMA values for hydrocarbons being less delocalized than the structure taken for HOMA(0) [55,56]. On the other hand, both HOMED and HOMA are equal to zero for the Kekulé structure of s-triazine with non-delocalized C–N and C=N bonds. In both cases, C–N in methylamine and C=N in methylimine were employed for the reference single and double bond lengths, respectively. The differences in zero on the two HOMA and HOMED scales lead to some discrepancies between the HOMA and HOMED values for heterocompounds [54]; hence, it is recommended that the HOMA index be used for the delocalized systems containing the same types of bonds, e.g., hydrocarbons, while the HOMED index should be used for any π-π, n-π, or σ-π delocalized heterocompounds [51,54,57,58]. In this study, the HOMA index (α = 257.7 and Ro = 1.388) [50] was applied for cyclic fragments containing only CC bonds, while the HOMED index was applied for selected fragments with CC and CN bonds. The HOMED parameters used for the CC and CN bonds are given in Table S4 (SM).
Electron delocalization in a π-electron-conjugated cycle (aromaticity) can also be related to the induced ring currents. The magnetic susceptibility of the ring indicates its aromatic character, which can be measured using the nucleus-independent chemical shift (NICS) descriptor [59,60]. According to the computational NICS procedure proposed by Schleyer and co-workers, the absolute magnetic shielding can be calculated at the ring center using the Gaussian ghost atom Bq as the probe [59,60,61]. In this study, the NICS index at a distance of 1 Å above the ring plane was used as the trustable criterion for aromaticity determination. The negative and positive values of NICS indicate the aromaticity and antiaromaticity of the ring, respectively.

3. Results and Discussion

3.1. Gas-Phase Basicity of Simple Nitriles

The two DFT levels of theory for B3LYP/311+G(d,p) and B3LYP/6-311++G(d,p), referred to as DFT1 and DFT2, respectively, applied for selected derivatives lead to very similar basicity parameters (PA and GB) for the cyano and imino N sites, and consequently to analogous DFT gas-phase basicity scales. For simple molecules optimized at the two DFT levels, the geometry parameters are identical. Only their energy parameters slightly differ. Note that the geometry and energy (including basicity) parameters for compounds I.9 and II.9 depend not much on Me conformation. In our case, the differences in gas-phase basicity data predictions were not larger than 0.5 kJ mol−1.
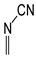
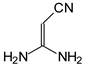
For simple nitriles, the PAs calculated here for the cyano and imino N (Z) atoms, together with data for DFT, G2, and G4 from the literature, are summarized in Table 1. Generally, applications of the DFT methods lead to considerably higher PAs (and GBs) for the N-cyano site than those of the Gn theories (differences 10–20 kJ mol−1), with the exception of HCN. On the other hand, the DFT and G2 methods predict similar PAs for the N-imino site in series II (differences lower than 10 kJ mol−1). Consequently, the differences between the PA(N-cyano) and PA(N-imino) dramatically change when going from DFT to G2 levels. This means that the favored site of monoprotonation can be predicted without any doubt when the DFT-calculated ΔPA for the cyano and imino N atoms is higher than 20 kJ mol−1. In other cases, a conclusion on favored monoprotonation sites should be carefully derived on the basis of DFT calculations.

3.2. Isomeric Phenomena in Neutral Forms

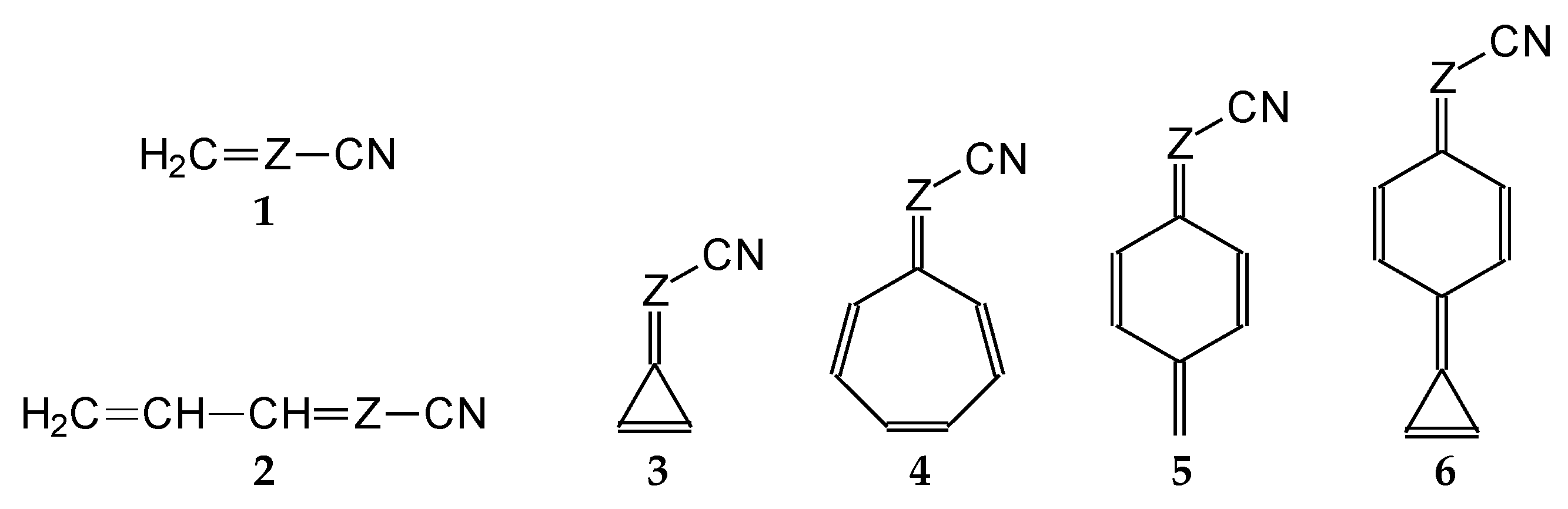
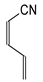
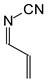
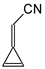
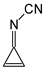
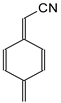
Among derivatives of simple π-π-conjugated series I and II (Figure 1), two geometrical isomers about the C=C and C=N double bonds (a and b) and their two rotational isomers about the C–C bond (c and d) can be distinguished for compounds I.2 and II.2 (Chart S1 in SM). Four isomeric structures with different stability levels are, thus, possible for the neutral forms of I.2 and II.2. We found that at the DFT level of theory, the Gibbs energy of structure I.2a is lower than that of I.2b (by only 1 kJ mol−1) and is significantly lower than those of the less favorable structures c and d. On the other hand, the G2 level of theory predicted the reverse. In the case of neutral α-imino nitriles II.2, the stability order of structures a–d at the DFT levels is analogous to that for I.2. The presence of the imino N atom only affects the relative Gibbs energies (ΔGs), although by no more than 4 kJ mol−1. Slight differences occur at the G2 level. The isomer a has the lowest G similarly, as found at the DFT levels. The isomer b has higher G by 2 kJ mol−1. For both derivatives (I.2 and II.2), the isomers c and d may be neglected in the isomeric mixtures owing to their high ΔGs (≥10 kJ mol−1); hence, their basicity data calculated at different levels of theory are not compared in Table 1.
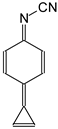
The structural investigations for simple π-π-conjugated nitriles encouraged us to perform an extended analysis of isomeric phenomena for the series, in which the push–pull effect is transmitted by the CPC or by the CPN scaffolds (Figure 2). When large donor substituents (guanidino N=C(NR2)2 and phosphazeno N=P(NR2)3 groups) are introduced at the cyclopropene ring, rotational isomerism about the single C–X bonds can affect geometric and energetic parameters and cannot be neglected for these derivatives. Note that rotation of the Me groups was not studied here in detail for I.11, I.12, II.11, and II.12, because for compounds I.9 and II.9, we observed only slight structural and energetic effects.
Although prototropic tautomerism (amino–imino conversions) may additionally occur for guanidino derivatives with two N=C(NH2)2 groups, this phenomenon can be neglected owing to the very strong electron-accepting effect of the C2C=Z–C≡N fragment, as well as the commonly known rule based on the Brønsted theory and substituent effects that pulling groups strongly stabilize the imino tautomer of weaker basicity [64,65]. According to this rule, the labile protons are preferentially bonded to the amino N atoms in guanidine and the imino N atoms of the two guanidine groups are linked to the C2C=Z–C≡N fragment, leading to the following favored tautomeric form, [(H2N)2C=N]2C2C=Z–C≡N, for I.10 (Z: CH) and II.10 (Z: N). Replacement of H by Me at the amino N atoms in I.11 and II.11 eliminates amino-imino tautomerism in the guanidine group. The same is true for the diphosphazeno derivatives I.12 and II.12.
In order to reduce the number of drawings for the representation of the possible isomers of I.10–I.12 and II.10–II.12, the guanidino and phosphazeno groups are abbreviated here as N=Y(NR2)n, where R is H or Me, Y is C or P, and n is 2 or 3, respectively. If we look at the single-bonds of Cring–N=Y(NR2)n, about which rotations are possible, four major isomers are possible (not including methyl group rotations), which we examined separately for each derivative regarding the C=Z moiety; therefore, we decided to analyze these four particular isomers (a, b, c, and d in Chart S2 in SM) for derivatives I.10–I.12 and II.10–II.12. In our analyses, we neglected other intermediate positions as well as the minor conformational changes induced by the methyl group rotations. The relative Gibbs energies calculated at the DFT1 or DFT2 level for a–d of the neutral CH and N derivatives are summarized in Chart S2 (SM). They indicate some differences in stability of a–d in I and II. Generally, the isomer a is favored (except I.10), and in some cases c is also favored (I.10, I.11, and I.12). Possible intramolecular interactions in selected nitriles that can influence their stability are shown in Figures S1 and S2 (SM).

3.3. Possible and Favored Sites of Monoprotonation

For compounds containing different functional groups, such as cyano, imino, and amino groups, the N atom(s) are potential sites of protonation. Quantum chemical methods have an advantage in that they allow the possibility of investigating all potential sites of protonation, then indicating the atom(s) that can preferentially bind one proton. On the basis of our calculations performed for series I and II of simple π-π-conjugated nitriles and imino nitriles given in Figure 1, we can conclude that the cyano N atom is the favored site of protonation. Generally, imines are much stronger bases than nitriles [1,2,3,4,32]; however, the combination of the strong electron-accepting effect of the cyano group, considerably decreasing the basicity of the imino N atom, and the push–pull effect on the nitrile, increasing its basicity, reverse the usual order. Consequently, the difference in Gibbs energies between the imino-protonated cation (C=NH+) and the cyano-protonated cation (C≡NH+) is not lower than 20 kJ mol−1; therefore, the imino-protonated isomers can be neglected (<0.1%) for monoprotonated forms, at least for the simple systems considered in Chart S3 (SM).
We paid particular attention to the two derivatives, I.2 and II.2, which display isomeric phenomena about the double C=C and C=N bonds and about the single C–C bond, not only for the neutral molecules (Chart S1 in SM), but also for their monoprotonated forms (Chart S3 in SM). We found that for the cyano-protonated forms of I.2 and II.2, the structure a is favored at each level of theory applied here for basicity prediction (DFT and Gn). Its Gibbs energy is lower than that of structure b by more than 5 kJ mol−1. The other cyano-protonated isomers (c and d) have higher Gibbs energies than a and can be considered as minor (c) or even as rare (d) forms in the isomeric mixture of monoprotonated I.2 and II.2. The imino-protonated isomers a–d of II.2 can be neglected, as their ΔGs are exceptionally high (≥50 kJ mol−1).
The cyano N atom also appears to be the preferred site of protonation for the derivatives given in Figure 2, containing additional N atoms in the substituents, for which Z is CH or N. For example, protonation of the amino N atoms at the syn- (a) and anti-position (b) regarding C≡N for the diamino derivatives I.8 and II.8 leads to monocations (Chart S4 in SM), for which the DFT1-calculated Gs are dramatically higher than those of the cyano-protonated forms (by ca. 180 and 210 kJ mol−1, respectively). For II.8 (Z: N), this effect seems to be stronger due to an additional pull effect of the imino group. Since it is commonly recognized that amines are stronger bases than nitriles, the reverse orders of Gs for the cyano- and amino-protonated forms of I.8 and II.8 confirm very strong push–pull effects in these molecules between the amino and cyano groups through the CPC or CPN scaffolds. The protonation at the imino nitrogen in II.8 is unfavored by the strong electron-accepting effect of the cyano group combined with the push–pull effect on the nitrile, as already mentioned. The Gibbs energy of the imino-protonated form is higher than that of the cyano monocation by more than 40 kJ mol−1. An analogous difference (37 kJ mol−1 at the DFT2 level) is found for the cyclopropenimine derivative II.9 containing two NMe2 groups, indicating also that the cyano N atom is preferentially protonated.
Taking into account the negligible probability of amino protonation in I.8 and II.8, as well as in the investigated earlier series of amino, amidino, guanidino, and phosphazeno nitriles possessing the substituent directly linked with the cyano group, X–C≡N [5,6], the amino-protonated forms for other CPC (I.10–I.12) and CPN derivatives (II.10–II.12) were not considered in this study; however, two extreme conformations (syn and anti regarding C=Z) for the guanidino and phosphazeno groups, which are possible for the cyano and imino-protonated forms and analogously as neutral forms (Chart S2 in SM), have to be considered. As such, DFT calculations were performed for four isomers (a–d) of each monoprotonated form (cyano and imino). Their relative Gibbs energies are summarized in Chart S5 (SM).
The DFT results indicate Ncyano as the favored site of protonation in the gas phase for all disubstituted derivatives. Generally, the isomer b has the lowest Gibbs energy for the cyano monocation, probably owing to possible favorable intramolecular interactions (see Figure S3 and discussion in SM for diguanidino derivatives). For the diphosphazeno CH derivative I.12, isomer d is favored in the monoprotonation reaction leading to the cyano monocation of the lowest Gibbs energy. For other derivatives with large substituents, this isomer belongs to the minor form. The probability of protonation of the imino N (Z) seems to be very low (ΔG > 15 kJ mol−1). The same is true for the imino N (X), particularly for N derivatives, where the electron-accepting effect of the imino C=N(Z) group increases ΔGs between the cyano and imino (X) protonated forms. An exception is the diguanidino CH derivative I.11, for which some isomers of the Nimino (guanidino) protonated forms (ΔG < 20 kJ mol−1) cannot be neglected in the isomeric mixture. A tentative explanation for this phenomenon is the polarizability effect of Me-groups in I.11 that increases the PA of imino N(X) to a higher degree than that of cyano N (Table S5 in SM). When compared to I.10, the ΔGs decrease for isomers a–c of I.11.

3.4. Gas-Phase Basicity of N Atoms in Isomers

For compounds I.2 and II.2, for which two types of isomerism (geometrical about a double C=C or C=N bond and rotational about a single C–C bond) can be considered for neutral (Chart S1 in SM) and monoprotonated forms (Chart S3 in SM), we calculated the basicity parameters, namely the PAs and GBs (Table S5 in SM), for each potential site of protonation (cyano and imino N atoms) in four isomers (a–d). Comparing the DFT-calculated PAs for two pairs of isomers, a and b and separately c and d (Figure 3), the effects of E/Z isomerism on basicity of the cyano N atom are slightly stronger for the second pair of these isomers (ca. 10 kJ mol−1) than for the first one (3–6 kJ mol−1). On the other hand, comparing the PAs of the two other pairs of isomers, a and c and separately b and d, the effects of rotational isomerism seem to be slightly weaker (1–2 and 6–7 kJ mol−1, respectively) than those of E/Z isomerism. Generally, the structural (isomeric) effects on PA(Ncyano) are not very strong for I.2 and II.2 (ΔPA ≤ 10 kJ mol−1). For II.2, the analogous effects on PA(Nimino) are only slightly stronger; ΔPAs do not exceed 13 kJ mol−1.
For I.8 and II.8 containing the CPC or CPN scaffold with two NH2 groups, gas-phase basicity values were estimated for the cyano, imino, and amino N atoms. Figure 4 presents the PAs calculated for these sites. When we compare the PAs estimated for N atoms in I.8 and II.8 to those estimated at the same level of theory (DFT1) for cross-n-π-conjugated derivatives without the CPC or CPN fragment, (H2N)2C=CH–C≡N and (H2N)2C=N–C≡N [6], we can see that the CPC or CPN part increases the PA of the cyano N atom in I.8 and II.8 by ca. 60 kJ mol−1. To a higher degree (by ca. 70 kJ mol−1), this part also increases the PA of the imino N atom in II.8, but it does not change the general order of basicity parameters: PA(Ncyano) > PA(Nimino) > PA(Namino). All of these increases of gas-phase basicity for the imino and cyano N atoms give information about the particular transmission of the electron-donating (push) effects of two NH2 groups through the CPC or CPN transmitter to C=N and next to C≡N, and also about particular electron delocalization effects in the system. Note that the CPC or CPN part only slightly changes the PAs of the amino N atoms (by 0–15 kJ mol−1). The PAs estimated for the amino groups in I.8 and II.8 are considerably lower (by 50–100 kJ mol−1) than the experimental PA of ammonia at 853.6 kJ mol−1 [3]. This observation, together with earlier reports on strong PA decreases for amino groups in push–pull nitriles [5,6], allows us to omit PA estimations for all NH2 and for all NMe2 groups in other derivatives.
Taking into account the rotational isomerism of substituent X about the single C–X bond for neutral (Chart S2 in SM) and monoprotonated forms (Chart S5 in SM) of disubstituted CPC or CPN derivatives bearing large groups (I.10–I.12 and II.10–II.12), we calculated the PAs and GBs for the potential sites of protonation (Ncyano and Nimino) in possible individual isomers, where substituent X adopts a syn or anti conformation regarding Z=N. The basicity data (PA and GB) estimated by the DFT1 or DFT2 methods are included in Table S5 (SM). Since the neutral isomer d of I.10–I.12 and II.10–II.12 is not stable and during optimization goes to another more stable isomer (b or c) or to another molecule, PAs and GBs are given in Table S5 (SM) only for three rotamers (a–c). Some exceptions were also found for cyano-N-protonated II.12c, which is not stable at the DFT2 level and after optimization transforms into II.12b. This observation shed some light on the energy barrier of the CNH+ group rotation about the C=Z bond. This barrier seems to be negligible in the protonated form.
The differences in PAs for extreme rotamers a–c of I.10–I.12 and II.10–II.12 are considerably larger than those for conformational isomers of compounds I.2 and II.2 (Table S5 in SM). For the favored site of protonation (Ncyano) in CH derivatives, the strongest effect (ΔPA 34 kJ mol−1) is observed for isomers of I.10 possessing two N=C(NH2)2 groups, for which PA varies from 985 (isomer a) to 1019 kJ mol−1 (isomer b), and the weakest effect (ΔPA 22 kJ mol−1) for isomers of I.12 containing two N=P(NMe2)3 groups, for which PA varies from 1066 (isomer a) to 1088 kJ mol−1 (isomer b). For isomers of I.11 with two N=C(NMe2)2 groups, the difference in PAs (27 kJ mol−1) is lower than that for isomers of I.10, although larger than that for isomers of I.12. Analogous PA variations are found for isomers of N derivatives (37, 28, and 22 kJ mol−1 for II.10, II.11, and II.12, respectively). For the N-imino sites, changes in the conformation of X substituents lead to ΔPAs higher than 20 kJ mol−1 and lower than 40 kJ mol−1 for the CH derivative.
The differences in PAs for individual isomers quantitatively inform us about the strong sensitivity of N-sites in terms of structural changes in compounds with large flexible substituents. They also provide information how significant errors can be made in PA prediction when conformational analysis is not considered and when PA is calculated only for rotamers of neutral and protonated forms that do not correspond to true energy minima. For example, on the basis of DFT calculations performed only for conformation a of I.11a (Figure 5), one could conclude that the CH derivative does not belong to the family of nitriles, because PA(Ncyano) is lower (by ca. 11 kJ mol−1) than the PA of the imino N atom in the guanidino group at the syn-position regarding C≡N.

3.5. Substituent Effects in the Simple Nitrile Series

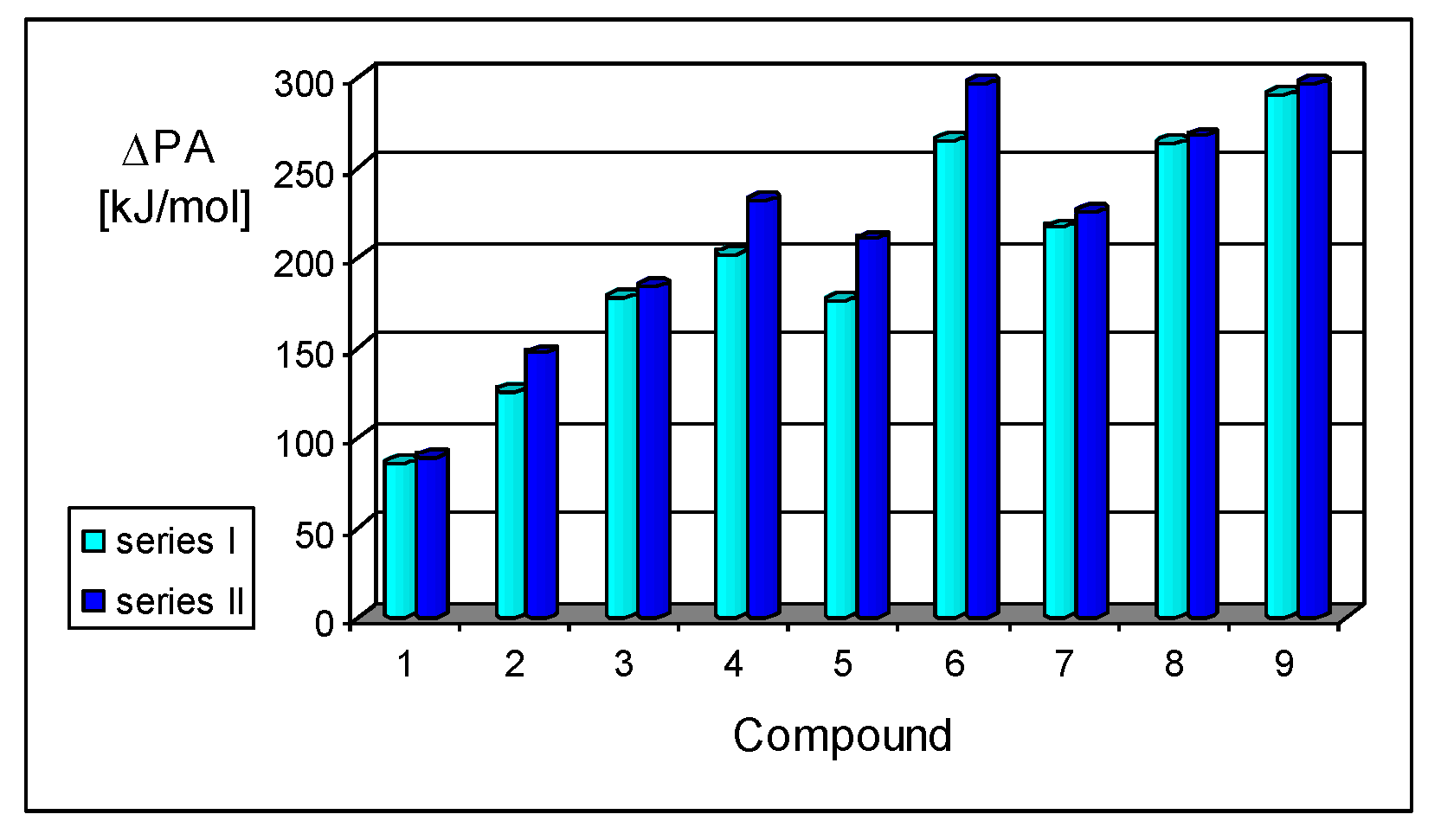
On the basis of our DFT calculations, we considered all compounds studied as functional nitriles in the gas phase, because protonation occurs on the nitrile group. Consequently, we investigated the substituent effects in the two series of nitriles (I and II). First, we compared the PAs of acyclic and cyclic nitriles containing H2C=CH–CH=Z (2) and (HC)2C=Z (3) with those possessing the simplest π-electron group, H2C=Z (1). Compounds 2 and 3 are the π-π-conjugated systems and have the same numbers of heavy atoms and π-electrons, although they exhibit completely different PAs. When proceeding from I.1 to I.2 and I.3, and also from II.1 to II.2 and II.3, the total electronic effects for the cyclic part (HC=CH closed in the ring) in I.3 and II.3 (ca. 90 kJ mol−1) are about twice those for the acyclic part (H2C=CH in acyclic group) in I.2 and II.2 (ca. 40 kJ mol−1). The analogous effects of the HC=CH part in the ring increase the PAs of I.6 and II.6 (by ca. 90 kJ mol−1) when going from I.5 and II.5, respectively. Interestingly, the π-π-conjugated compounds I.4 and II.4 possess higher PAs (by 20–30 kJ mol−1) than their constitutional isomers I.5 and II.5. This analysis of substituent effects on the PAs of simple nitriles evidently showed an exceptionally large increase in basicity for derivatives containing CPC, methylene-1,3,5-cycloheptatriene, methylenequinoid, methylenequinoidcyclopropene, and their heteroanalog-transmitting systems. The basicity orders of the investigated nitriles are a consequence of their exceptional internal electronic effects, which are discussed in detail below.
Assessment of the gas-phase basicity data for all simple derivatives of series I and II summarized in Table S5a (SM) led to additional observations concerning gas-phase internal effects. The total electronic substituent effects, measured as differences between the PAs of simple nitriles of series I and II (compounds 1–9, including only 2a) and that of HCN calculated at the same level of theory, vary from ca. 90 kJ mol−1 for 1 to ca. 300 kJ mol−1 for 9 (Figure 6). The greater size of the π-π-conjugated group and stronger electronic pushing effects of n-π-conjugated X substituents are related to the higher PA values. Moreover, replacement of the CH group in series I by the imino N (Z) atom in series II does not always affect the basicity of nitriles in the same way. For example, differences between PAs of the CPC derivatives I.3 and I.7–I.9 and of the CPN derivatives II.3 and II.7–II.9 are close to those between PAs of I.1 and II.1 (<10 kJ mol−1), whereas those between the other π-π-conjugated derivatives are considerable higher, being close to 20 and 30 kJ mol−1 for acyclic (I.2 and II.2) and cyclic (I.4–I.6 and II.4–II.6) molecules, respectively.
This variations of the relative PAs indicate that the electron-donating effects of π-π-conjugated groups in series I of simple nitriles 1–9 containing different transmitter parts are not identical but somewhat parallel to those in series II; however, we can distinguish some subfamilies for the investigation of substituent effects, with one subfamily containing compounds 4, 5, and 6 (1,3,5-cycloheptatriene, quinoid, and quinoid cyclopropene derivatives, respectively), for which the electron-donating effect is considerably stronger in series II than in series I; and the other subfamily with compounds 3, 7, 8, and 9, for which the differences in electron-donating effects in series I and II are smaller than those for the first family but analogous to those in CH and N derivatives of 1 (see Figure S4 in SM). Interestingly, all simple nitriles 3, 7, 8, and 9 in the second subfamily possess a cyclopropene part with two X (X: H, Me, NH2, and NMe2). Taking this simple observation into account, we included derivatives (10–12) containing larger X substituents (X: N=C(NH2)2, N=C(NMe2)2, and N=P(Nme2)3), for which the effects of isomerism on PAs were investigated. In this way, we could directly compare the total electronic effects of all X substituents in series I of CPC derivatives with those in the CPN series II.

3.6. Substituent Effects in the Methylenecyclopropene and Cyclopropeneimine Series

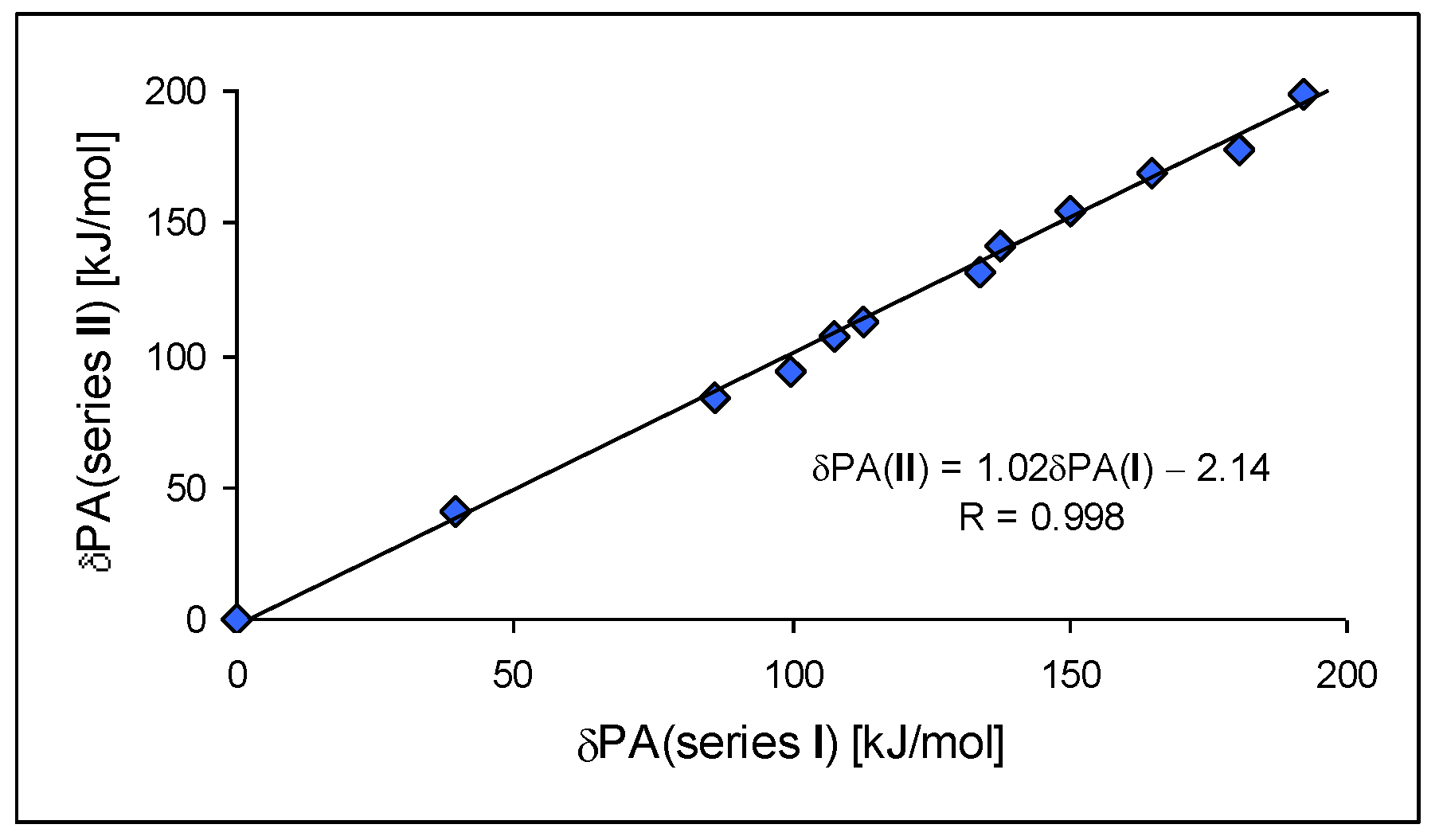
For investigation of the substituent effects in the CPC (I.7–I.12) and CPN series (II.7–II.12), we used the unsubstituted CH (I.3) and N (II.3) compounds as reference (parent) molecules. We calculated the differences between the PA of substituted derivatives (or its isomers) and the PA of the parent molecules. These differences, abbreviated as δPA, correspond to the total substituent effects of two X groups in CPC and CPN derivatives. They vary from 0 (for H) to ca. 200 kJ mol−1 (for two phosphazeno groups in b conformation). Since the basicity data found at the DFT1 and DFT2 levels for simple derivatives did not differ significantly (differences in PAs lower than 0.5 kJ mol−1), we compared the estimated δPAs of CH derivatives with those of N derivatives, without indication of the DFT method used for calculation, as shown in Figure 7. We found an interesting linear relationship between δPAs determined for series I and II. The slope of the regression line close to unity (correlation coefficient R = 0.998) indicates that introduction of the N imino atom in series II does not significantly perturb π-π conjugation or transmission of substituent (pushing) effects through the π-π-conjugated systems to the cyano N site.
The strong electron-donating effects of the two X substituents (push–pull cross-effects) can additionally explain the higher PA/GB values of disubstituted versus unsubstituted series I and II. As expected, the orders of basicity increase for series I and II are analogous to that for nitriles X–C≡N, substituted directly by the X group, containing H, Me, NH2, NMe2, N=C(NH2)2, N=C(NMe2)2, and N=P(NMe2)3 [6]. Conformation of the large substituents, and consequently favorable and unfavorable intramolecular interactions of functional groups, are additional significant (but not main) factors that affect basicity parameters for investigated disubstituted CPC and CPN derivatives. 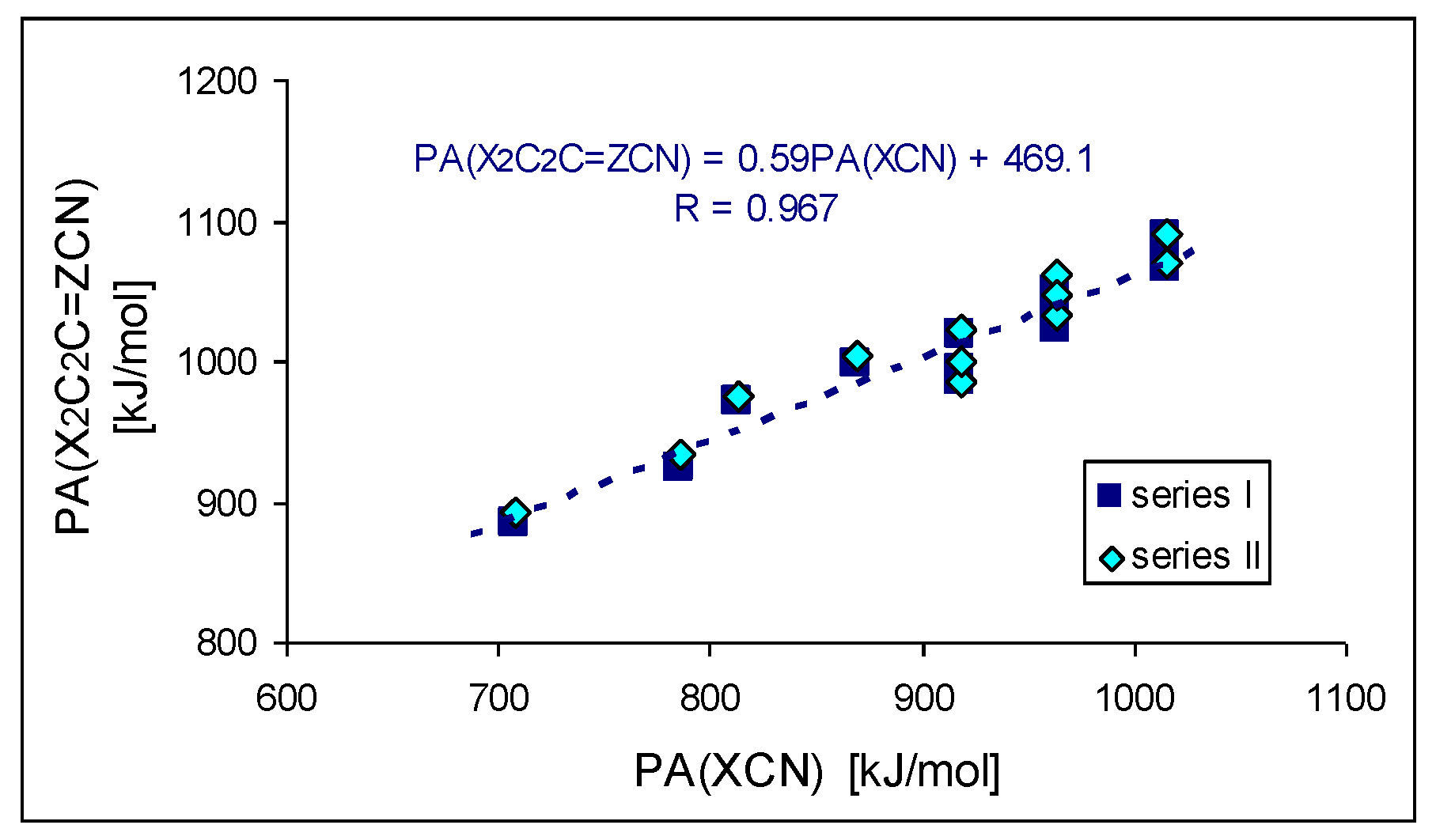Figure 8 shows the linear trend (R > 0.95) between the DFT-estimated PAs of series I and II and X–C≡N studied previously [6]. The cross-push–pull effects of the two X substituents in series I and II (CPC and CPN derivatives, respectively) seem to be attenuated by the cyclo-C2C=Z scaffold (slope ca. 0.6). For a more limited series of substituents (X: H, NH2, NMe2, data from Table 1 and ref. [6]), the comparison of calculated PAs for the two disubstituted cyclopropene systems cyclo-X2C2C=Z–C≡N and X2C=Z–C≡N (substituted by 3 and 1, respectively) give a slope (Figure 8) of 0.7, which can be viewed as a transmission factor of substituent effects (see Figure S5 in SM). The cyclopropene scaffolds somewhat reduce the electron donor effect as compared to direct substitution in X–C≡N or to transmission by intercalating the C=Z double bond. Nevertheless, the substituted CPC and CPN molecules still present PAs larger than X–C≡N and X2C=Z–C≡N analogs. This is due to the basicity enhancement of the nitrile functional group by the intrinsic effects (polarizability and resonance) of the scaffold cyclo-X2C2C=Z.

3.7. Changes in Electron Delocalization Caused by Protonation

Electron delocalization in organic conjugated systems can be related to their bond lengths. For delocalized systems, single and double bond lengths are usually different from those for the corresponding non-conjugated molecules. Depending on the conjugation strength, they are more or less close to those of aromatic systems (e.g., CC 1.394 and CN 1.334 Å for benzene and s-triazine, respectively, calculated at the DFT1 level) [51]. Observations of DFT-calculated geometric parameters for simple π-π-conjugated nitriles and imino nitriles, as well as for more complex disubstituted CPC and CPN derivatives, show significant variations of single and double bond lengths when proceeding from neutral to protonated forms; for example, the Z=C double bond lengthens and the Z–Ccyano single bond shortens (see Table S6 in SM for selected nitriles). Analogous changes also take place for other single and double bonds in investigated systems. Generally, single bonds shorten and double bonds lengthen. This alternation is a consequence of differences in resonance hybrids for the neutral and protonated forms (Scheme S1 in SM), but does not lead to full equalization of bond lengths—even for cyclic fragments—as it does benzene and s-triazine.
To quantitatively describe changes in electron delocalization for simple neutral and cyano N protonated derivatives, the geometry-based HOMED index [51,54] has been applied. Based on the geometries, optimized at the DFT1 level, HOMEDs have been calculated for selected fragments using equation (3) and parameters from Table S4 (SM). Generally, the estimated HOMEDs increase when the number of heavy atoms and π bonds increase, and also when proceeding from the neutral to cyano N protonated forms (Figure 9). Moreover, they are higher for the cyclic derivatives I.3 and II.3 than for the acyclic ones I.2 and II.2 containing the same number of heavy atoms and π bonds. They are also higher for cyclic I.4 and II.4 than for cyclic I.5 and II.5, both being isomeric forms, and additionally for bicyclic I.6 and II.6 than for monocyclic I.5 and II.5. The highest HOMEDs (>0.9), close to those for aromatic compounds (HOMED ≈ 1), are found for the entire group R in R–C≡NH+ of I.3, II.3, I.4, II.4, I.6, and II.6 as well as for their cyclic fragment(s). For these monocations, we can distinguish the resonance structures with well delocalized 3-membered (cyclopropenyl) and 7-membered cyclic (cycloheptatrienyl) cations as well as of the neutral benzene ring (Scheme S1 in SM). This tendency confirms strong electron delocalization in the cyclic fragments that become aromatic for unsubstituted systems.
In the case of CPC and CPN derivatives substituted by two X groups (I.7–I.12 and II.7–II.12): Me, NH2, NMe2, N=C(NH2)2, N=C(NMe2)2, and N=P(NMe2)3, substituents X additionally participate in electron and charge delocalization (Scheme S2 in SM). The Me groups are σ-π hyperconjugated and the other groups are n-π conjugated with the ring, and next with the cyano group. Hence, larger number of resonance structures can be written and stronger electron delocalization can be expected than for I.3 and II.3 (Scheme S1 in SM), although differences between the resonance hybrids of the neutral and cyano protonated forms have analogous origin as those for simple π-π conjugated systems (Scheme S1 in SM). Consequently, the HOMED indices increase for disubstituted derivatives when compared to unsubstituted ones (I.3 and II.3).
For example, the DFT1-estimated HOMEDs change for the cyclopropenylidene scaffold (C2C=) when going from the neutral to protonated form of I.7, I.8, I.9, I.10a, I.10b, and I.10c (Table 2). Analogous changes are found for the C2C=CH fragment with slightly lower HOMEDs. The corresponding imino derivatives of series II display similar HOMED trends for the cyclopropene ring and cyclopropenimine part (C2C=N) when going from the neutral to protonated form. The introduction of N atom in series II increases HOMEDs already for neutral molecules. This is a consequence of possible intramolecular interactions between functional groups that increase electron delocalization. Hence, smaller HOMED changes take place in protonation reaction for derivatives of series II.
Note that for n-π-conjugated pushing substituents (X: NH2, NMe2, N=C(NH2)2), saturation of electron delocalization can be observed for neutral disubstituted 3-membered cycles (HOMEDs between 0.9 and 1.0). The effect of the strong pushing groups causes a step toward electron delocalization in the high PA/GB range for these derivatives (Figure 10). Their exceptionally strong gas-phase basicity is rather a consequence of push–pull effects—analogous to those for series X–C≡N (Figure 8)—which occur between the substituent X and site of protonation (cyano N) through the C2C=Z fragment. Electron delocalization appears be the second factor that enhances the PA/GB range for push–pull nitriles.
The additional estimations of the HOMA and NICS indices for cyclic parts in selected simple nitriles shown in Table 3 confirm increases of the electron delocalization and the magnetic susceptibility of the ring when proceeding from the neutral molecule to its cyano N-protonated form (C≡NH+) in both series of nitriles I and II, and also in series II when going from the neutral form to its imino monocation (ZH+ for Z = N). Generally, negative NICS values are found for the neutral and monoprotonated structures. An exception is the neutral nitrile I.4, for which a positive NICS value (close to zero) is found.

3.8. Macroscopic Basicity Values

For polyfunctional compounds displaying isomerism, gas-phase basicity parameters (PAs and GBs) can be estimated using quantum chemical methods for separate isomers, as well as for their isomeric mixtures. A distinction between the two approaches can be made using different terminology and different microscopic basicity levels for individual isomers and for their mixtures. The microscopic basicity parameters discussed in the previous subchapter refer to partial equilibria for individual isomers, BiH+ → Bi + H+, whereas the macroscopic basicity parameters correspond to the global equilibrium for the isomeric mixture, y1B1H+ + y2B2H+ + y3B3H+ +… → x1B1 + x2B2 + x3B3 +…+ H+. Each isomer mole fraction xi in the neutral isomeric mixture can be found on the basis of the relative Gibbs energies calculated for neutral individual isomers: xi ≈ (exp(–ΔG(Bi)/RT))/(Σ1n[exp(–ΔG(Bi)/RT)]). In a similar way, the isomer mole fractions yi in the isomeric mixture of monocations can be estimated on the basis of the relative Gibbs energies calculated for the corresponding protonated isomers: yi ≈ (exp(–ΔG(BiH+)/RT))/(Σ1n[exp(–ΔG(BiH+)/RT)]). As discussed above, the microscopic PAs and GBs indicate the basicity of selected sites of protonation for separate isomers, which can be distinguished as major, minor, and rare, as appropriate. They can be applied for analysis of the pure internal effects in individual isomers. The macroscopic PA or GB values give general information on the basicity of the isomeric mixture in the monoprotonation reaction, and can be compared with basicity data for other molecules already placed in the PA or GB scales in order to characterize its strength. For newly synthesized compounds, the predicted PA or GB can also be useful when selecting reference bases for experimental PA or GB determination.
To our knowledge, the gas-phase basicity values of the simple derivatives I.2 and II.2, which exhibit various types of isomerism (E/Z and rotational) and can exist in mixtures of the four isomers, have not yet been experimentally determined. There is only a theoretical report on the microscopic basicity values of the two isomers I.2a and I.2b [2]. Considering the four isomers (a–d), we found that microscopic PAs and GBs do not differ very much (Figure 3), while the favored neutral and protonated forms correspond to the same isomer. In such cases, the macroscopic PAs and GBs are not very different from the microscopic ones for the favored isomer. Using the relative Gibbs energies for the rotamers a and c of the E form and separately for the rotamers b and d of the Z form, we obtained the following PAs and GBs at the DFT1 level: 834.0 and 805.6 for E-I.2, 828.3 and 799.5 for Z-I.2, 854.7 and 826.7 for E-II.2, 851.8 and 824.3 kJ mol−1 for Z-II.2.
If we assume that protonation of the cyano N atom reduces the energy barrier for E/Z isomerization, we can estimate the macroscopic basicity for the mixture of the four isomers a–d (Scheme S3 in SM). For this consideration, we take the following observation into account. First, the DFT-calculated double C=Z bonds significantly lengthen (e.g., from 1.348 to 1.369 Å for I.2a and from 1.289 to 1.312 Å for II.2a) and the single Z–CN bonds shorten (e.g., from 1.421 to 1.384 Å for I.2a and from 1.332 to 1.269 Å for II.2a) when going from the neutral to cyano-protonated forms. For estimation of the isomer mole fractions xi and yi, in the neutral and protonated isomeric mixtures of the four isomers a–d, we used the corresponding relative Gibbs energies between b–d and a found at the DFT1 level (Chart S1 and S3 in SM). The percentage contents calculated for individual isomers in the isomeric mixtures of the neutral and protonated forms and the macroscopic PAs and GBs estimated for the monoprotonation equilibria are included in Scheme S3 (SM). Indeed, the macroscopic PAs and GBs shown in Table 4 are not very different from the microscopic PAs and GBs of the favored isomer a given in Table S5 (SM).
The macroscopic PAs and GBs were estimated for all derivatives (Z: CH and N) with two large substituents. For the estimations, we considered only major and minor isomers with ΔG < 25 kJ mol−1 that contribute significantly in the PAs and GBs of the isomeric mixtures. As shown below, the macroscopic PAs and GBs estimated for I.10–I.12 and II.10–II.12 differ from the microscopic ones found for individual isomers. The reasons are as follows. First, the microscopic basicity data strongly depend on the syn and anti conformation of X groups. Second, the favored conformation for the neutral form (Chart S2 in SM) is not the same as that for the monocation (Chart S5 in SM). Next, intramolecular interactions in I.10–I.12 and II.10–II.12 that influence their relative Gibbs energies seem to not always be analogous when proceeding from guanidino to phosphazeno groups and from CH (series I) to N (series II) derivatives (vide infra). Consequently, the estimated macroscopic PAs and GBs may be placed between the lowest and highest PAs and GBs for individual isomers or close to one of them.
For the CH and N derivatives containing two N=C(NH2)2 groups (I.10 and II.10, Scheme S4 in SM), in the isomeric mixture three isomers are important for the neutral form (Chart S2 in SM) and four isomers for the monoprotonated form (Chart S5 in SM). The imino-protonated forms are not significant and they can be neglected in the isomeric mixture of monocation. For estimation of the isomer mole fractions xi and yi in the isomeric mixtures, we used the corresponding relative Gibbs energies found for neutral and protonated isomers. The macroscopic PAs and GBs estimated at the DFT1 level (Table 4) are between the lowest (for isomers a) and the highest (for isomer b) microscopic PAs and GBs (Table S5 in SM).
Some imino-N-protonated forms, particularly guanidino protonated isomers (Chart S5 in SM), have to be considered for the CH and N derivatives containing two N=C(NMe2)2 groups (I.11 and II.11). Methylation of amino groups seems to increase the basicity of the guanidino N imino atom in comparison to the cyano N atom. For estimation of the macroscopic PAs and GBs, we used the isomers mole fractions calculated from the ΔGs of three neutral isomers (Chart S2 in SM), four isomers of cyano monocations, and the isomers of imino-N-protonated forms, for which ΔG < 25 kJ mol−1 (Chart S5 in SM). The DFT2-estimated macroscopic PAs and GBs (Table 4) are also between the lowest and highest microscopic PAs and GBs calculated for the isomers a and b (Table S5 in SM).
Particular cases are diphosphazeno CH and N derivatives (I.12 and II.12), for which isomeric preferences are different for both the neutral (isomer c for I.12 and isomer a for II.12, see in Chart S2 in SM) and monoprotonated forms (isomer d for I.12 and isomer b for II.12, see in Chart S5 in SM); hence, these differences strongly affect the macroscopic PAs and GBs estimated at the DFT2 level (Scheme S6 in SM). For the N derivative, they are between the lowest and highest microscopic PA and GB calculated for the isomers a and b of II.12, although for the CH derivative they are close to the highest microscopic PA and GB values found for I.12b (Table S5 in SM). Consequently, II.12 seems to be a weaker base than I.12 at the DFT2 level (Table 4). This order of basicity data is reversed in comparison to other derivatives of series I and II. For simple nitriles investigated here that do not exhibit rotational isomerism, N derivatives are stronger bases than CH derivatives (Figure 6). The analogous trend is found for individual isomers of I.10–I.12 and II.10–II.12. They obey linear relationship given in Figure 7. The exceptionally high macroscopic PA and GB values for the diphosphazeno CH derivative I.12 result from the strong stability of the cyano-protonated isomer d. For the N derivative II.12, this isomer belongs to the rare form, similar to the diguanidino N derivative II.10d.

3.9. New π-π- and n-π-Conjugated Nitriles on the DFT-PA Scale

In our previous studies on the gas-phase basicity of push–pull nitriles [5,6], we investigated series of compounds with strong pushing groups, such as R2N, R2N–CH=CH, R2N–CH=N, (R2N)2C=N, (R2N)3P=N, and (R2N)3P=N(R2N)2P=N, directly linked to the pulling C≡N group. In this way, we extended the DFT basicity scale for nitriles up to superbasic 1,8-bis(dimethylamino)naphthalene (DMAN, experimental PA 1028.2 kJ mol−1 [3]). The most basic nitrile in this series with the biphosphazene group (Me2N)3P=N(Me2N)2P=N has a DFT-calculated PA value even higher than that of DMAN by ca. 30 kJ mol−1 [6].
The new simple π-π-conjugated nitriles investigated here containing methylenecyclopropene, methylene-1,3,5-cycloheptatriene, methylenequinoid, and methylenequinoidcyclopropene, as well as their heteroanalog transmitter systems, seem to be very promising for the future extension of the PA scale for nitriles. Their unsubstituted derivatives (I.3–I.6 and II.3–II.6) already display higher PAs (Table 1) than the push–pull dimethylcyanamide Me2N–C≡N (DFT-calculated PA 868.7 kJ mol−1 [6]). Substitution of CPC and CPN parts by two NMe2 groups in I.9 and II.9 leads to derivatives with PAs (Table 1) higher than those of phosphazenenitrile (H2N)3P=N–C≡N (DFT calculated PA 978.8 kJ mol−1 [6]). The positions of all these simple new π-π-conjugated nitrile bases (I.1–I.9 and II.1–II.9) on the DFT-calculated PA scale are given in Figure 11.
Although the simple nitriles with unsubstituted transmitter parts (I.3–I.6 and II.3–II.6) investigated here are weaker bases than the strongest base studied previously [6], namely biphosphazenenitrile (Me2N)3P=N(Me2N)2P=N–C≡N (DFT-calculated PA 1055.5 kJ mol−1), we show here that substitution of the cyclopropene ring in I.3 and II.3 by two pushing groups increases the PAs by ca. 200 kJ mol−1 (Figure 7). Diphosphazene derivatives (I.12 and II.12, macroscopic PA 1088 and 1079 kJ mol−1, respectively; Table 4) are the strongest bases in the current DFT-calculated PA scale for nitriles. This observation suggests that analogous substitution of the methylenequinoid, methylene-1,3,5-cycloheptatriene, and methylenequinoidcyclopropene transmitters and their N analogs by two strong pushing groups in I.4–I.6 and II.4–II.6 may lead to derivatives for which the DFT-calculated PAs will be close to the limit of the experimental PA scale for push–pull N imino bases (PA < 1200 kJ mol−1) [1]. Transmission of the strong pushing effects in such π-π-conjugated systems has already been proved in the literature for imines by quantum-chemical methods [7,8,10].

4. Conclusions

On the basis of our quantum chemical estimations of proton affinities (mainly DFT and also Gn for some parent systems), we proposed new π-π- and n-π-conjugated nitrogen bases reaching PA values above 1000 kJ mol−1. Using the electron acceptor (pulling) nitrile functional group as a probe, we explored the efficiency of the methylenecyclopropene (CPC) and cyclopropenimine (CPN) π-systems (3 with Z: CH and N, respectively, in Figure 1) as resonance transmission scaffolds for strong electron donor (pushing) substituents. By applying robust DFT methods, we analyzed the effects of pushing groups X (NH2, NMe2, (H2N)2C=N, (M2N)2C=N, and (Me2N)3P=N) linked to 2- and 3-positions of the cyclopropene ring on the gas-phase basicity of the cyano N site in compounds I.8–I.12 and II.8–II.12 (Figure 2).
As the CPN and pushing X groups contain N atoms (imino and amino) that are potential sites of protonation, we carefully examined various neutrals and monocations in possible conformations to determine the structures of their most favored forms. In all cases for the favored isomers, the nitrile N atom emerges as the strongest basic site. The cyano group in the two CPC and CPN series have similar calculated proton affinities, with a small advantage for the later.
The CPC and CPN scaffolds efficiently transmit the push–pull effect from the X to CN group with very similar transmission power (Figure 7). Although the transmission of the X donor effect is ca. 60% of that found for X–C≡N (Figure 8), the calculated PAs of the two series of nitriles containing the cyclopropene ring and bearing two electron donor X substituents are larger than their X–C≡N and X2C=Z–C≡N analogs (Figure 11). The enhanced PAs for investigated nitriles can be attributed to the extended electron delocalization and polarizability resulting from the intercalation of the CPC and CPN π-systems.
The gas-phase basicity values calculated for the cyano N atom in nitriles containing the methylene-1,3,5-cycloheptatriene, methylenequinoid, and methylenequinoidcyclopropene and their heteroanalog transmitter π-systems (derivatives I.4–I.6 and II.4–II.6, respectively) also reveal some similarities; however, the imino N (Z) effect seems to be stronger for these larger scaffolds than that for the CPN derivatives (Figure 6). Nitriles I.6 and II.6 (Table 1) exhibit the highest PAs in series of simple parent compounds (without pushing X groups). Their exceptionally high PAs (973 and 1004 kJ mol−1, respectively) and the strong pushing effects of the two phosphazene groups in II.12 containing the CPN system when compared to the parent system II.3 (ca. 200 kJ mol−1) lead us to believe that the basicity values of derivatives containing two pushing groups at the cyclopropene ring in II.6 can reach PA values of 1200 kJ mol−1. Note that in solution, simple nitriles are exceptionally weak N bases (pKas of monofunctional RCN in water ca. –10) [66,67]. Nitriles have only been protonated in sulfuric acid and oleum systems [66]. It will be interesting to study in the future the theoretical pKas of push–pull nitriles to indicate first the favored site of protonation (particularly in nitriles containing the guanidine and phosphazene pushing groups), and next to estimate solvent effects. For Me2N–CH=N–C≡N, the imino N atom has been found to be the favored site of protonation at the PCM (water)//HF/6-31G* level for both geometrical isomers (E and Z) [68].
The degrees of electron delocalization in the π-π-conjugated transmitter systems were described by applying two aromaticity descriptors, namely structural (HOMA) and magnetic (NICS) indices. The cyclopropene π-systems exhibit a significant π-electron delocalization in neutral nitriles (stronger than that in π-π-conjugated butadiene—the reference molecule for the C–C and C=C bonds in the HOMA procedure—and weaker than that in aromatic benzene). The cyano protonation amplifies electron and charge delocalization and these scaffolds display stronger aromatic characters, as indicated by more negative NISC indices (Table 3). The same is true for larger π-electron cycles (Figure 9), which display analogous variations of aromaticity indices; however, the aromatic character of the transmitter π-systems seems to be less dependent on the electron donor effect of the X groups (NH2, NMe2, (H2N)2C=N, (M2N)2C=N, and (Me2N)3P=N) than the basicity of the electron acceptor cyano group (Figure 10). We found that the push–pull effect between X and C≡N is the main factor that enhances the PAs of nitriles (Figure 8). Despite slight attenuation of the substituent effect by the cyclic π-systems, as compared to shorter conjugated systems, the intrinsic basicity enhancement of the nitrile functional group by the CPC and CPN scaffolds leads to highly basic nitriles.

Supplementary Materials

The following is available online at https://www.mdpi.com/article/10.3390/sym13091554/s1: docx file Nitriles_SM_Symmetry.

Author Contributions

E.D.R., supervision, methodology, computational, writing, editing. J.-F.G., project administration, supervision, writing. P.-C.M., supervision, writing. H.S., methodology, computation, writing. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available as supplementary material.

Acknowledgments

J.F.G. and P.C.M. thank the Université Côte d’Azur and the Institut de Chimie de Nice (CNRS UMR 7272) for their continuous support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C. Enhanced Basicity of Push-Pull Nitrogen Bases in the Gas Phase. Chem. Rev. 2016, 116, 13454–13511. [Google Scholar] [CrossRef] [PubMed]
  2. Bouchoux, G. Gas phase basicities of polyfunctional molecules. Part 6: Cyanides and isocyanides. Mass Spectrom. Rev. 2018, 37, 533–564. [Google Scholar] [CrossRef] [PubMed]
  3. Hunter, E.P.; Lias, S.G. Evaluated Gas Phase Basicities and Proton Affinities of Molecules: An Update. J. Phys. Chem. Ref. Data 1998, 27, 413–656. [Google Scholar] [CrossRef]
  4. NIST Chemistry WebBook, NIST Standard Reference Database, No. 69; Linstrom, P.J.; Mallard, W.G. (Eds.) National Institute of Standards and Technology: Gaithersburg, MD, USA, 2014. Available online: http://webbook.nist.gov/chemistry (accessed on 7 May 2021).
  5. Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C. Exceptional proton affinities of push–pull nitriles substituted by the guanidino and phosphazeno groups. RSC Adv. 2015, 5, 25513–25517. [Google Scholar] [CrossRef]
  6. Raczyńska, E.D.; Makowski, M.; Maria, P.-C.; Gal, J.-F. Can Nitriles Be Stronger Bases than Proton Sponge in the Gas Phase? A Computational Analysis. J. Phys. Chem. A 2015, 119, 8225–8236. [Google Scholar] [CrossRef] [PubMed]
  7. Maksić, Z.B.; Kovačević, B.; Vianello, R. Advances in Determining the Absolute Proton Affinities of Neutral Organic Molecules in the Gas Phase and Their Interpretation: A Theoretical Account. Chem. Rev. 2012, 112, 5240–5270. [Google Scholar] [CrossRef] [PubMed]
  8. Valadbeigi, Y. Superbasicity of 1,3,5-cycloheptatriene derivatives and their proton sponges in gas phase. Chem. Phys. Let. 2017, 689, 1–7. [Google Scholar] [CrossRef]
  9. Gilani, M.; Saeidian, H.; Mirjafary, Z. Harnessing aromaticity and intramolecular hydrogen bondingto tailor organosuperbases by using 2,4,6-cycloheptatriene-1-imine scaffold. Struct. Chem. 2020, 31, 1545–1551. [Google Scholar] [CrossRef]
  10. Despotović, I.; Maksić, Z.B.; Vianello, R. Computational design of Brønsted neutral organic superbases-[3]iminoradialenes and quinonimines are important synthetic targets. New J. Chem. 2007, 31, 52–62. [Google Scholar] [CrossRef]
  11. Höltzl, T.; Nguyen, M.T.; Veszprémi, T. Mono-, di-, tri- and tetraphosphatriafulvenes: Electronic structure and aromaticity. J. Mol. Struct. (THEOCHEM) 2007, 811, 27–35. [Google Scholar] [CrossRef]
  12. Saeidian, H.; Mirjafary, Z. Engineering non-ionic carbon super- and hyperbases by a computational DFT approach: Substituted allenes have unprecedented cation affinities. New J. Chem. 2020, 44, 12967–12977. [Google Scholar] [CrossRef]
  13. Wang, Y.; Fernández, I.; Duvall, M.; Wu, J.I.-C.; Li, Q.; Frenking, G.; Schleyer, P.v.R. Consistent Aromaticity Evaluations of Methylenecyclopropene Analogues. J. Org. Chem. 2010, 75, 8252–8257. [Google Scholar] [CrossRef]
  14. Burk, P.; Abboud, J.-L.M.; Koppel, I.A. Aromaticity of substituted cyclopropenes: A theoretical study. J. Phys. Chem. A 1996, 100, 6992–6997. [Google Scholar] [CrossRef]
  15. Merchant, M.; González-Luque, R.; Roos, B.O. A theoretical determination of the electronic spectrum of Methylenecyclopropene. Theor. Chim. Acta 1996, 94, 143–154. [Google Scholar] [CrossRef]
  16. Bachrach, S.M.; Liu, M. Structure, topological electron density analysis and aromaticity of 4-heterosubstituted methylenecyclopropenes: X=CCH=CH, X = CH2, NH, O, SiH2, PH and S. J. Phys. Org. Chem. 1991, 4, 242–250. [Google Scholar] [CrossRef]
  17. Norden, T.D.; Staley, S.W.; Taylor, W.H.; Harmony, M.D. Electronic character of methylenecyclopropene: Microwave spectrum, structure, and dipole moment. J. Am. Chem. Soc. 1986, 108, 7912–7918. [Google Scholar] [CrossRef]
  18. Bandar, J.S.; Lambert, T.H. Enantioselective Brønsted base catalysis with chiral cyclopropenimines. J. Am. Chem. Soc. 2012, 134, 5552–5555. [Google Scholar] [CrossRef]
  19. Bandar, J.S.; Lambert, T.H. Cyclopropenimine-Catalyzed Enantioselective Mannich Reactions of tert-Butyl Glycinates with N-Boc-Imines. J. Am. Chem. Soc. 2013, 135, 11799–11802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  20. Bandar, J.S.; Sauer, G.S.; Wulff, W.D.; Lampert, T.H.; Vetticatt, M.J. Transition State Analysis of Enantioselective Brønsted Base Catalysis by Chiral Cyclopropenimines. J. Am. Chem. Soc. 2014, 136, 10700–10707. [Google Scholar] [CrossRef] [Green Version]
  21. Bandar, J.S.; Barthelme, A.; Mazori, A.Y.; Lambert, T.H. Structure–activity relationship studies of cyclopropenimines as enantioselective Brønsted base catalysts. Chem. Sci. 2015, 6, 1537–1547. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Nacsa, E.D.; Lambert, T.H. Higher-order cyclopropenimine superbases: Direct neutral Brønsted base catalyzed Michael reactions with α-aryl esters. J. Am. Chem. Soc. 2015, 137, 10246–10253. [Google Scholar] [CrossRef] [Green Version]
  23. Belding, L.; Dudding, T. Synthesis and Theoretical Investigation of a 1,8-Bis (bis (diisopropylamino) cyclopropeniminyl) naphthalene Proton Sponge Derivative. Chem. Eur. J. 2014, 20, 1032–1037. [Google Scholar] [CrossRef] [PubMed]
  24. Belding, L.; Stoyanov, P.; Dudding, T. Synthesis, Theoretical Analysis, and Experimental pKa Determination of a Fluorescent, Nonsymmetric, In–Out Proton Sponge. J. Org. Chem. 2016, 81, 6–13. [Google Scholar] [CrossRef] [PubMed]
  25. Belding, L.; Stoyanov, P.; Dudding, T. Phase-transfer catalysis via a proton sponge: A bifunctional role for biscyclopropenimine. J. Org. Chem. 2016, 81, 553–558. [Google Scholar] [CrossRef]
  26. Guest, M.; Le Sueur, R.; Pilkington, M.; Dudding, T. Development of an Unsymmetrical Cyclopropenimine-Guanidine Platform for Accessing Strongly Basic Proton Sponges and Boron-Difluoride Diaminonaphthalene Fluorophores. Chem. Eur. J. 2020, 26, 8608–8620. [Google Scholar] [CrossRef] [PubMed]
  27. Çiftcioğlu, G.A.; Trindle, C. Computational estimates of thermochemistry and pKa values of cyclopropenyl imine superbases. Int. J. Quantum Chem. 2014, 114, 392–399. [Google Scholar] [CrossRef]
  28. Krawczyk, H.; Dzięgielewski, M.; Deredas, D.; Albrecht, A.; Albrecht, Ł. Chiral Iminophosphoranes-An Emerging Class of Superbase Organocatalysts. Chem. Eur. J. 2015, 21, 10268–10277. [Google Scholar] [CrossRef]
  29. Barić, D.; Dragičevič, I.; Kovačević, B. Cyclopropenimine as a hydrogen bond acceptor-towards the strongest non-phosphorus superbases. Tetrahedron 2014, 70, 8571–8576. [Google Scholar] [CrossRef]
  30. Barić, D.; Kovačević, B. Cyclopropenimine as pincer ligand and strong electron donor in proton sponges. J. Phys. Org. Chem. 2016, 29, 750–758. [Google Scholar] [CrossRef]
  31. Saadat, K.; Shiri, A.; Kovačević, B. Substituted troponimines: When aromatization of the conjugate acid leads to very strong neutral organic superbases. New J. Chem. 2018, 42, 14568–14575. [Google Scholar] [CrossRef]
  32. Bouchoux, G. Gas phase basicities of polyfunctional molecules. Part 5: Non-aromatic sp2 nitrogen containing compounds. Mass Spectrom. Rev. 2018, 37, 139–170. [Google Scholar] [CrossRef]
  33. Cao, W.; Liu, X.; Feng, X. Chiral organobases: Properties and applications in asymmetric catalysis. Chin. Chem. Lett. 2018, 29, 1201–1208. [Google Scholar] [CrossRef]
  34. Wang, Y.-H.; Cao, Z.-Y.; Li, Q.-H.; Lin, G.-Q.; Zhou, J.; Tian, P. Activating Pronucleophiles with High pKa Values: Chiral Organo-Superbases. Angew. Chem. Int. Ed. 2020, 59, 8080–8090. [Google Scholar] [CrossRef]
  35. Casida, J.E. Neonicotinoid metabolism: Compounds, substituents, pathways, enzymes, organisms, and relevance. J. Agric. Food Chem. 2011, 59, 2923–2931. [Google Scholar] [CrossRef] [PubMed]
  36. Zhou, L.-Y.; Zhang, L.-J.; Sun, S.-L.; Ge, F.; Mao, S.-Y.; Ma, Y.; Liu, Z.-H.; Dai, Y.-J.; Yuan, S. Degradation of the Neonicotinoid Insecticide Acetamiprid via the N-Carbamoylimine Derivate (IM-1-2) Mediated by the Nitrile Hydratase of the Nitrogen-Fixing Bacterium Ensifer meliloti CGMCC 7333. J. Agric. Food Chem. 2014, 62, 9957–9964. [Google Scholar] [CrossRef]
  37. Zhang, H.; Wei, Z.; Zhang, A.H.; Yu, S. Access to Cyanoimines Enabled by Dual Photoredox/Copper-Catalyzed Cyanation of O-Acyl Oximes. Org. Lett. 2020, 22, 7315–7320. [Google Scholar] [CrossRef]
  38. Peltier, J.-D.; Heinrich, B.; Donnio, B.; Jeannin, O.; Rault-Berthelot, J.; Jacques, E.; Poriel, C. N-Cyanoimine as an electron-withdrawing functional group for organic semiconductors: Example of dihydroindacenodithiophene positional isomers. J. Mater. Chem. C 2018, 6, 13197–13210. [Google Scholar] [CrossRef]
  39. Zarren, G.; Nisar, B.; Sher, F. Synthesis of anthraquinone-based electroactive polymers: A critical review. Mater. Today Sustain. 2019, 5, 100019. [Google Scholar] [CrossRef]
  40. Hodsden, T.; Thorley, K.J.; Basu, A.; White, A.J.P.; Wang, C.; Mitchell, W.; Glöcklhofer, F.; Anthopoulos, T.D.; Heeney, M. The influence of alkyl group regiochemistry and backbone fluorination on the packing and transistor performance of N-cyanoimine functionalised indacenodithiophenes. Mater. Adv. 2021, 2, 1706–1714. [Google Scholar] [CrossRef]
  41. Becke, A.D. Density Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  42. Lee, C.; Yang, W.; Parr, R.G. Density-functional exchange-energy approximation with correct asymptotic behaviour. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Hehre, W.J.; Radom, L.; Schleyer, P.v.R.; Pople, J.A. Ab initio Molecular Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
  44. Kaljurand, I.; Koppel, I.A.; Kütt, A.; Rõõm, E.-I.; Rodima, T.; Koppel, I.; Mishima, M.; Leito, I. Experimental gas-phase basicity scale of superbasic phosphazenes. J. Phys. Chem. A 2007, 111, 1245–1250. [Google Scholar] [CrossRef] [PubMed]
  45. Leito, I.; Koppel, I.A.; Koppel, I.; Kaupmees, K.; Tshepelevitsh, S.; Saame, J. Basicity limits of neutral organic superbases. Angew. Chem. Int. Ed. 2015, 54, 9262–9265. [Google Scholar] [CrossRef] [PubMed]
  46. Curtiss, L.A.; Raghavachari, K.; Trucks, G.W.; Pople, J.A. Gaussian-2 theory for molecular energies of first-and second-row compounds. J. Chem. Phys. 1991, 94, 7221–7230. [Google Scholar] [CrossRef]
  47. Curtiss, L.A.; Raghavachari, K.; Pople, J.A. Gaussian-2 theory using reduced Møller–Plesset orders. J. Chem. Phys. 1993, 98, 1293–1298. [Google Scholar] [CrossRef]
  48. Bartmess, J.E. Thermodynamics of the electron and the proton. J. Phys. Chem. 1994, 98, 6420–6424. [Google Scholar] [CrossRef]
  49. Fifen, J.J.; Dhaouadi, Z.; Nsangou, M. Revision of the Thermodynamics of the Proton in Gas Phase. J. Phys. Chem. A 2014, 118, 11090–11097. [Google Scholar] [CrossRef]
  50. Krygowski, T.M. Crystallographic studies of inter-and intramolecular interactions reflected in aromatic character of π-electron systems. J. Chem. Inform. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
  51. Raczyńska, E.D.; Hallmann, M.; Kolczyńska, K.; Stępniewski, T.M. On the harmonic oscillator model of electron delocalization (HOMED) index and its application to heteroatomic π-electron systems. Symmetry 2010, 2, 1485–1509. [Google Scholar] [CrossRef] [Green Version]
  52. Kruszewski, J.T.; Krygowski, M. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [Google Scholar] [CrossRef]
  53. Kruszewski, J.T.; Krygowski, M. Aromaticity of thiophene, pyrrole and furan in terms of aromaticity indices and Hammett ρ constants. Bull. Acad. Pol. Sci. Sér. Sci. Chim. 1974, 22, 871–876. [Google Scholar]
  54. Raczyńska, E.D. Application of the Extended HOMED (Harmonic Oscillator Model of Aromaticity) Index to Simple and Tautomeric Five-Membered Heteroaromatic Cycles with C, N, O, P, and S Atoms. Symmetry 2019, 11, 146. [Google Scholar] [CrossRef] [Green Version]
  55. Ostrowski, S.; Dobrowolski, J.C. What does the HOMA index really measure? RSC Adv. 2014, 4, 44158–44161. [Google Scholar] [CrossRef]
  56. Dobrowolski, J.C.; Ostrowski, S. On the HOMA index of some acyclic and conducting systems. RSC Adv. 2015, 5, 9467–9471. [Google Scholar] [CrossRef]
  57. Krygowski, T.M.; Szatyłowicz, H.; Stasiuk, O.A.; Dominikowska, J.; Palusiak, M. Aromaticity from the viewpoint of molecular geometry: Application to planar systems. Chem. Rev. 2014, 114, 6383–6422. [Google Scholar] [CrossRef] [PubMed]
  58. Raczyńska, E.D. Quantum-chemical studies on the favored and rare isomers of isocytosine. Comput. Theor. Chem. 2017, 1121, 58–67. [Google Scholar] [CrossRef]
  59. Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef] [PubMed]
  60. Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-independent chemical shifts (NICS) as an aromaticity criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
  61. Gershoni-Poranne, R.; Stanger, A. Magnetic criteria of aromaticity. Chem. Soc. Rev. 2015, 44, 6597–6615. [Google Scholar] [CrossRef] [PubMed]
  62. Smith, B.J.; Radom, L. Assigning absolute values to proton affinities: A differentiation between competing scales. J. Am. Chem. Soc. 1993, 115, 4885–4888. [Google Scholar] [CrossRef]
  63. Smith, B.J.; Radom, L. Calculation of proton affinities using the G2 (MP2, SVP) procedure. J. Phys. Chem. 1995, 99, 6468–6471. [Google Scholar] [CrossRef]
  64. Elguero, J.; Marzin, C.; Katritzky, A.R.; Linda, P. The Tautomerism of Heterocycles; Academic Press: New York, NY, USA, 1976. [Google Scholar]
  65. Raczyńska, E.D.; Kosińska, W.; Ośmiałowski, B.; Gawinecki, R. Tautomeric equilibria in relation to pi-electron delocalization. Chem. Rev. 2005, 105, 3561–3612. [Google Scholar] [CrossRef] [PubMed]
  66. Deno, N.C.; Gaugler, R.W.; Wisotsky, M.J. The base strengths and chemical behavior of nitriles in sulfuric acid and oleum systems. J. Org. Chem. 1966, 31, 1967–1968. [Google Scholar] [CrossRef]
  67. Perrin, D.D. Dissociation Constants of Organic Bases in Aqueous Solution; Butterworth: London, UK, 1965. [Google Scholar]
  68. Makowski, M.; Raczyńska, E.D.; Chmurzyński, L. Ab initio study of possible and preferred basic site(s) in polyfunctional N1,N1-dimethyl-N2-cyanoformamidine. J. Phys. Chem. A 2001, 105, 869–874. [Google Scholar] [CrossRef]
Symmetry 13 01554 g001 550
Figure 1. Simple π-π-conjugated nitriles: series I (Z: CH) and series II (Z: N).
Figure 1. Simple π-π-conjugated nitriles: series I (Z: CH) and series II (Z: N).
Symmetry 13 01554 g001
Symmetry 13 01554 g002 550
Figure 2. Series of nitriles derived from methylenecyclopropene and cyclopropenimine (series I with Z: CH and series II with Z: N, respectively) containing electron-donating substituents.
Figure 2. Series of nitriles derived from methylenecyclopropene and cyclopropenimine (series I with Z: CH and series II with Z: N, respectively) containing electron-donating substituents.
Symmetry 13 01554 g002
Symmetry 13 01554 g003 550
Figure 3. Variations of PAs estimated at the DFT1 level (in kJ mol−1 at 298 K) for N atoms in four isomers (2a–2d) of I.2 (Z: CH, in normal style) and II.2 (Z: N, shown in italics).
Figure 3. Variations of PAs estimated at the DFT1 level (in kJ mol−1 at 298 K) for N atoms in four isomers (2a–2d) of I.2 (Z: CH, in normal style) and II.2 (Z: N, shown in italics).
Symmetry 13 01554 g003
Symmetry 13 01554 g004 550
Figure 4. Comparison of PAs estimated at the DFT1 level (in kJ mol−1 at 298 K) for N atoms in I.8 (Z: CH) and II.8 (Z: N, values in italics) with those found previously at the same level of theory for analogous cross-n-π-conjugated derivatives without CPC or CPN fragments.
Figure 4. Comparison of PAs estimated at the DFT1 level (in kJ mol−1 at 298 K) for N atoms in I.8 (Z: CH) and II.8 (Z: N, values in italics) with those found previously at the same level of theory for analogous cross-n-π-conjugated derivatives without CPC or CPN fragments.
Symmetry 13 01554 g004
Symmetry 13 01554 g005 550
Figure 5. Variations of PAs estimated at the DFT2 level (in kJ mol−1 at 298 K) for N atoms in three rotamers (11a–11c) of diguanidino derivatives (I.11 (Z: CH) and II.8 (Z = N, values in italics)).
Figure 5. Variations of PAs estimated at the DFT2 level (in kJ mol−1 at 298 K) for N atoms in three rotamers (11a–11c) of diguanidino derivatives (I.11 (Z: CH) and II.8 (Z = N, values in italics)).
Symmetry 13 01554 g005
Symmetry 13 01554 g006 550
Figure 6. Variations of PAs relative to HCN estimated at the DFT1 level for Z: CH (I.1–I.9) and Z: N (II.1–II.9) derivatives (ΔPA in kJ mol−1 at 298 K).
Figure 6. Variations of PAs relative to HCN estimated at the DFT1 level for Z: CH (I.1–I.9) and Z: N (II.1–II.9) derivatives (ΔPA in kJ mol−1 at 298 K).
Symmetry 13 01554 g006
Symmetry 13 01554 g007 550
Figure 7. Linear relationship between the total substituent effects (δPA in kJ mol−1 at 298 K) in the methylenecyclopropene series (I) and in the cyclopropenimine series (II) estimated at the DFT1 or DFT2 level.
Figure 7. Linear relationship between the total substituent effects (δPA in kJ mol−1 at 298 K) in the methylenecyclopropene series (I) and in the cyclopropenimine series (II) estimated at the DFT1 or DFT2 level.
Symmetry 13 01554 g007
Symmetry 13 01554 g008 550
Figure 8. Linear trend between DFT-estimated PAs of disubstituted cyclopropene derivatives X2C2C=Z–CN and X–CN (X: H, Me, NH2, NMe2, N=C(NH2)2, N=C(NMe2)2, and N=P(NMe2)3).
Figure 8. Linear trend between DFT-estimated PAs of disubstituted cyclopropene derivatives X2C2C=Z–CN and X–CN (X: H, Me, NH2, NMe2, N=C(NH2)2, N=C(NMe2)2, and N=P(NMe2)3).
Symmetry 13 01554 g008
Symmetry 13 01554 g009 550
Figure 9. Change of HOMEDs for selected structures when going from the neutral to protonated forms (italicized values for series II) estimated at the DFT1 level.
Figure 9. Change of HOMEDs for selected structures when going from the neutral to protonated forms (italicized values for series II) estimated at the DFT1 level.
Symmetry 13 01554 g009
Symmetry 13 01554 g010 550
Figure 10. Plots between HOMEDs for C2C=Z fragments and PAs estimated at the DFT1 level for selected derivatives of series I (Z: CH) and II (Z: N) with X: H, Me, NH2, NMe2, and N=C(NH2)2.
Figure 10. Plots between HOMEDs for C2C=Z fragments and PAs estimated at the DFT1 level for selected derivatives of series I (Z: CH) and II (Z: N) with X: H, Me, NH2, NMe2, and N=C(NH2)2.
Symmetry 13 01554 g010
Symmetry 13 01554 g011 550
Figure 11. Simple π-π- and n-π-conjugated nitriles I.1–I.9 and II.1–II.9 on the DFT-calculated PA scale of push–pull nitriles.
Figure 11. Simple π-π- and n-π-conjugated nitriles I.1–I.9 and II.1–II.9 on the DFT-calculated PA scale of push–pull nitriles.
Symmetry 13 01554 g011
Table
Table 1. Comparison of PAs (in kJ mol−1 at 298 K) for selected nitriles and imino nitriles calculated with different levels of theory, together with experimental values when available.
Table 1. Comparison of PAs (in kJ mol−1 at 298 K) for selected nitriles and imino nitriles calculated with different levels of theory, together with experimental values when available.
LevelBasePA(Ncyano)BasePA(Ncyano)PA(Nimino)
B3LYP/6-311++G(d,p) Symmetry 13 01554 i001707.9 a Symmetry 13 01554 i002785.8 a
B3LYP/6-311+G(d,p)708.0 b785.5 a
G2712.0 c780.1 c
G2MP2713.8 d781.7 c
G4MP2 781.2 e
Exp.712.9 f779.2 f
B3LYP/6-311++G(d,p) Symmetry 13 01554 i003
I.1		793.4 a Symmetry 13 01554 i004
II.1		797.5 a738.3 a
B3LYP/6-311+G(d,p)793.3 a797.4 a738.3 a
G2784.7 a785.3 a743.0 a
G2MP2785.4 a786.2 a743.7 a
G4MP2783.8 e
Exp.784.7 f
B3LYP/6-311++G(d,p) Symmetry 13 01554 i005 Symmetry 13 01554 i006
B3LYP/6-311+G(d,p)913.6 b917.8 b864.9 b
G2895.4 g900.8 g867.9 g
G2MP2896.0 g901.9 g867.4 g
B3LYP/6-311++G(d,p) Symmetry 13 01554 i007
I.2a		834.1 a Symmetry 13 01554 i008
II.2a		854.7 a807.6 a
B3LYP/6-311+G(d,p)834.0 a854.7 a807.6 a
G2814.3 a831.0 a802.1 a
G2MP2814.5 a831.3 a802.3 a
G4MP2812.2 e
B3LYP/6-311++G(d,p) Symmetry 13 01554 i009
I.2b		828.4 a Symmetry 13 01554 i010
II.2b		851.8 a815.1 a
B3LYP/6-311+G(d,p)828.3 a851.7 a815.1 a
G2809.0 a827.6 a809.0 a
G2MP2809.2 a828.0 a809.1 a
G4MP2806.8 e
B3LYP/6-311++G(d,p) Symmetry 13 01554 i011
I.3		885.5 a Symmetry 13 01554 i012
II.3		892.1 a841.7 a
B3LYP/6-311+G(d,p)885.4 a892.1 a841.6 a
G2867.6 a875.1 a845.0 a
G2MP2867.9 a875.8 a845.5 a
B3LYP/6-311++G(d,p) Symmetry 13 01554 i013
I.4		910.0 a Symmetry 13 01554 i014
II.4		939.3 a909.0 a
B3LYP/6-311+G(d,p)910.1 a939.3 a909.3 a
B3LYP/6-311++G(d,p) Symmetry 13 01554 i015
I.5		884.1 a Symmetry 13 01554 i016
II.5		918.5 a892.6 a
B3LYP/6-311+G(d,p)884.1 a918.4 a892.7 a
B3LYP/6-311++G(d,p) Symmetry 13 01554 i017
I.6		972.9 a Symmetry 13 01554 i018
II.6		1004.4 a987.1 a
B3LYP/6-311+G(d,p)972.9 a1004.3 a987.0 a
B3LYP/6-311++G(d,p)
B3LYP/6-311+G(d,p)		 Symmetry 13 01554 i019
I.7		924.7 a
924.6 a		 Symmetry 13 01554 i020
II.7		933.2 a
933.1 a		897.3 a
897.3 a
B3LYP/6-311++G(d,p)
B3LYP/6-311+G(d,p)		 Symmetry 13 01554 i021
I.8		971.6 a
971.5 a		 Symmetry 13 01554 i022
II.8		975.6 a
975.6 a		935.4 a
935.3 a
B3LYP/6-311++G(d,p) Symmetry 13 01554 i023
I.9		998.1 a Symmetry 13 01554 i024
II.9		1004.6 a967.6 a
B3LYP/6-311+G(d,p)998.5 a1004.5 b967.4 a
a Data taken from this study. b Taken from ref. [6]. c Taken from ref. [62]. d Taken from ref. [63]. e Taken from ref. [2]. f Taken from ref. [3]. g Taken from ref. [5].
Table
Table 2. HOMED indices estimated at the DFT1 level for the rings in selected neutral and monoprotonated cyano (C≡NH+) nitriles.
Table 2. HOMED indices estimated at the DFT1 level for the rings in selected neutral and monoprotonated cyano (C≡NH+) nitriles.
HOMED(C2C=)HOMED(C2C=Z)
SeriesXIsomerNeutralC≡NH+NeutralC≡NH+
Z: CHMeI.70.8600.9620.8280.965
NH2I.80.9270.9880.9110.980
NMe2I.90.9540.9940.9420.976
N=C(NH2)2I.10a0.9090.9990.9070.976
I.10b0.9170.99980.9010.987
I.10c0.9290.9990.9190.981
Z: NMeII.70.9310.9810.8910.978
NH2II.80.9730.9860.9500.987
NMe2II.90.9910.9740.9760.972
N=C(NH2)2II.10a0.9800.9890.9790.973
II.10b0.9820.9810.9660.972
II.10c0.9760.9840.9680.980
Table
Table 3. HOMA and NICS indices estimated at the DFT2 level for the rings in selected neutral and monoprotonated cyano (C≡NH+) and imino (ZH+) nitriles. See Table 1 for structures.
Table 3. HOMA and NICS indices estimated at the DFT2 level for the rings in selected neutral and monoprotonated cyano (C≡NH+) and imino (ZH+) nitriles. See Table 1 for structures.
Number of AtomsNeutralC≡NH+ZH+ (Z: N)
CompoundIn the RingHOMANICSHOMANICSHOMANICS
I.330.17−9.080.69−11.79--
I.470.452.700.88−5.65--
I.63
6		0.20
0.43		−8.10
−2.53		0.73
0.79		−10.51
−6.65		--
I.930.62−9.340.82−9.76--
II.330.48−9.940.87−12.400.91−12.25
II.470.57−1.480.92−7.260.92−7.23
II.63
6		0.33
0.47		−8.48
−3.71		0.75
0.81		−10.99
−7.10		0.79
0.85		−10.36
−7.53
II.930.75−8.540.71−8.860.85−8.92
Table
Table 4. Macroscopic PAs and GBs (in kJ mol−1 at 298 K) estimated at the DFT1 or DFT2 level for nitriles displaying isomerism. See Table 1 for structures.
Table 4. Macroscopic PAs and GBs (in kJ mol−1 at 298 K) estimated at the DFT1 or DFT2 level for nitriles displaying isomerism. See Table 1 for structures.
CompoundPAGBCompoundPAGB
I.2834.0 a805.6 aII.2854.9 a826.9 a
I.10995.5 a971.0 aII.101011.8 a987.1 a
I.111035.1 b1004.7 bII.111043.2 b1015.2 b
I.121087.5 b1059.3 bII.121079.2 b1052.4 b
a DFT1. b DFT2.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C.; Saeidian, H. Push–Pull Effect on the Gas-Phase Basicity of Nitriles: Transmission of the Resonance Effects by Methylenecyclopropene and Cyclopropenimine π-Systems Substituted by Two Identical Strong Electron Donors. Symmetry 2021, 13, 1554. https://doi.org/10.3390/sym13091554

AMA Style

Raczyńska ED, Gal J-F, Maria P-C, Saeidian H. Push–Pull Effect on the Gas-Phase Basicity of Nitriles: Transmission of the Resonance Effects by Methylenecyclopropene and Cyclopropenimine π-Systems Substituted by Two Identical Strong Electron Donors. Symmetry. 2021; 13(9):1554. https://doi.org/10.3390/sym13091554

Chicago/Turabian Style

Raczyńska, Ewa D., Jean-François Gal, Pierre-Charles Maria, and Hamid Saeidian. 2021. "Push–Pull Effect on the Gas-Phase Basicity of Nitriles: Transmission of the Resonance Effects by Methylenecyclopropene and Cyclopropenimine π-Systems Substituted by Two Identical Strong Electron Donors" Symmetry 13, no. 9: 1554. https://doi.org/10.3390/sym13091554

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop