Centralising Monoids with Low-Arity Witnesses on a Four-Element Set

Abstract

As part of a project to identify all maximal centralising monoids on a four-element set, we determine all centralising monoids witnessed by unary or by idempotent binary operations on a four-element set. Moreover, we show that every centralising monoid on a set with at least four elements witnessed by the Mal’cev operation of a Boolean group operation is always a maximal centralising monoid, i.e., a co-atom below the full transformation monoid. On the other hand, we also prove that centralising monoids witnessed by certain types of permutations or retractive operations can never be maximal.

1. Introduction

There are various notions of symmetry in the sciences and in mathematics. Algebraic structures are usually considered symmetric if they have a lot of automorphisms or, more generally, endomorphisms. For a universal algebra (a structure without relations) the automorphism group/endomorphism monoid consists of all those permutations/self-maps of the carrier set that commute with all fundamental operations of the algebra. Studying commuting operations in more generality leads to the notion of the centraliser clone of an algebra, or simply of a set of operations if the carrier set is understood from the context. The unary part of the centraliser (clone) is then exactly the endomorphism monoid of the algebra, and the fundamental operations of the algebra are said to witness this monoid.

This article is concerned with algebras on a specific carrier set A that are ‘maximally symmetric’ in the sense that their endomorphism monoid is a co-atom in the lattice of all possible endomorphism monoids of algebras on A. As the monoids in this lattice are the unary parts of (all) centraliser clones on A, they are called centralising monoids, and the co-atoms of this lattice are also referred to as maximal centralising monoids.

The study of centralisers in algebra goes back to Cohn [1] (Chapter III.3), and notably to Kuznecov [2] who first established logical methods for their investigation, exploiting closure under operations whose graphs are primitive positively definable from given operations. Kuznecov allegedly also discovered all 25 centraliser clones among Post’s lattice, a fact later re-proved by Hermann [3]. Danil’čenko [4,5,6,7] continued the work of Kuznecov by determining all 2986 centraliser clones on sets of three elements [8,9]. On carrier sets of size four and beyond, currently no good overview of the lattice of centralisers exists. Between 1974 and 1976 Harnau [10,11,12,13,14,15] worked on centralisers of unary operations, which are dual to centralising monoids in terms of the Galois connection induced by commutation of finitary operations (see Section 2). Centralising monoids of single unary operations, i.e., monounary algebras, were investigated in [16,17,18], showing, for example, which centralising monoids of this type are equal to the centralising monoid they describe as a witness [16] (Theorem 4.1, p. 8, Theorem 5.1, p. 10), and which of them have a unique unary operation as their witness [18] (Theorems 3.1 and 3.3, p. 4659 et seq.). Research on centralising monoids was further pushed forward in a series of papers [19,20,21,22,23,24,25] by Machida and Rosenberg, linking in particular maximal centralising monoids to the five types of functions appearing in Rosenberg’s Classification Theorem [26] for minimal clones. As a consequence, all 192 centralising monoids on three-element sets were determined in [21,23], and all 10 maximal centralising monoids among them were identified.

This research is part of the project, begun in [27], to take the results of [23] to the next level, that is, to determine all maximal centralising monoids on four-element carrier sets. According to Proposition 3 it is necessary for this to find all centralising monoids on $\left\{0,1,2,3\right\}$ induced by single functions of each of the five types of Rosenberg’s Theorem and to determine the ones among them which are maximal proper transformation monoids under set inclusion. As an initial step centralising groups of majority operations and semiprojections were studied in [28]. Extending the methods of [23], the case of majority operations on $\left\{0,1,2,3\right\}$ was already completed in [27], and further investigated under a different aspect in [29]. In this article we tackle the cases of unary operations (permutations of prime order and non-identical retractive operations), binary idempotent operations and ternary minority operations arising as Mal’cev operations corresponding to Boolean groups.

We determine all centralising monoids on $4=\left\{0,1,2,3\right\}$ witnessed by binary idempotent operations, and we classify both the witnessing operations and the monoids up to conjugacy by inner automorphisms from $Sym4$. We also exhibit the maximal monoids among them, in general, and again, up to conjugacy. With respect to unary operations, we establish that on every carrier set of size at least four, every single transposition or every product of disjoint transpositions without fixed points and every non-identical retraction witnesses a centralising monoid which is a co-atom in the lattice of those centralising monoids witnessed by sets of unary operations, that is, in the lattice of endomorphism monoids of unary algebras. However, we also show that, given at least four elements, no transposition and no permutation with a single fixed point, as well as no retraction fixing all but one element can ever witness a maximal centralising monoid. For $\left\{0,1,2,3\right\}$ we improve this by showing that no permutation at all will witness a maximal centralising monoid. Finally, based on results of Länger and Pöschel [30] about strongly constantively rigid relational systems, we give a new proof of the known fact [21] (Theorem 5.1) that the centralising monoid of a constant on an at least three-element set is indeed maximal. We use the same technique to prove that—with the exception of the two-element set—the centralising monoid of a Mal’cev operation of a Boolean group is always maximal.

2. Preliminaries

We start by introducing basic notation with respect to sets, functions and relations, followed by fundamental facts regarding their Galois theory based on preservation and commutation. We also give a brief overview of formal concept analysis in order to be able to switch between different Galois connections. In the second part of this section we present background theory on clones, in particular centraliser clones, and centralising monoids that we shall use extensively to derive our main results.

2.1. Notation and Basic Concepts

We write $\mathbb{N}=\left\{0,1,2\dots \right\}$ for the set of all natural numbers (finite ordinals) and ${\mathbb{N}}_{+}$ for the positive ones. It will be convenient for us to understand every $n\in \mathbb{N}$ as the set of its ordinal predecessors $n=\left\{0,\dots ,n-1\right\}$ as in the von Neumann model of natural numbers. The cardinality (size) of a set A is denoted by $\left|A\right|$; if $\left|A\right|<{\aleph }_0$, then we often pick a canonical representative for it, e.g., $n=\left\{0,\dots ,n-1\right\}$ where $n=\left|A\right|$.

Given sets $A,B,C$ and functions $f:A⟶B$ and $g:B⟶C$, we denote their composition by $g\circ f:A⟶C$ and mean the function mapping each element $a\in A$ to $(g\circ f)\left(a\right):=g\left(f\right(a\left)\right)\in C$. The set of all functions from A to B is symbolised as $B^A$. If $f\in B^A$ and $U\subseteq A$, $V\subseteq B$, we write $f\left[U\right]$ for the image $\left\{\left.f\left(u\right)\phantom{u\in U}\right|u\in U\right\}$ and $f^{-1}\left[V\right]$ for the preimage $\left\{\left.x\in A\phantom{f\left(x\right)\in V}\right|f\left(x\right)\in V\right\}$. The full image of f is also denoted as $im\left(f\right):=f\left[A\right]$. The restriction of f to an arbitrary subset $U\subseteq A$ is the function ${f|}_U:U⟶B$ mapping $x\in U$ to ${f|}_U\left(x\right):=f\left(x\right)$.

For $n\in \mathbb{N}$ we understand tuples $\mathit{x}\in A^n$ as maps from $n=\left\{0,\dots ,n-1\right\}$ to A that are simply written as $\mathit{x}=(x_0,\dots ,x_{n-1})$. Sometimes we allow ourselves to deviate from this standard notation if some other indexing like $\mathit{x}=(a,b,c)$ or $\mathit{x}=(x_1,\dots ,x_n)$ seems more convenient. As tuples $\mathit{x}\in A^n$ are maps, we have in particular $im\left(\mathit{x}\right)=\left\{x_0,\dots ,x_{n-1}\right\}$ and we can compose with $f\in B^A$ or $\alpha \in n^I$, giving $f\circ \mathit{x}=(f\left(x_0\right),\dots ,f\left(x_{n-1}\right))\in B^n$ and re-indexed tuples $\mathit{x}\circ \alpha ={\left(x_{\alpha \left(i\right)}\right)}_{i\in I}\in A^I$.

For a set A and $n\in \mathbb{N}$, every $f\in {\mathcal{O}}_A^{\left(n\right)}:=A^{A^n}$ is said to be an n-ary operation on A. We collect all finitary (non-nullary) operations on A in the set ${\mathcal{O}}_A={\bigcup }_{n\in {\mathbb{N}}_{+}}{\mathcal{O}}_A^{\left(n\right)}$. For $F\subseteq {\mathcal{O}}_A$ and $n\in \mathbb{N}$ we write $F^{\left(n\right)}$ for $F\cap {\mathcal{O}}_A^{\left(n\right)}$; in particular ${\mathcal{O}}_A^{\left(n\right)}={\left({\mathcal{O}}_A\right)}^{\left(n\right)}$ for $n>0$. For $i\in n\in \mathbb{N}$ the n-ary projection onto the coordinate i is the operation $e_i^{\left(n\right)}\in {\mathcal{O}}_A^{\left(n\right)}$ given by $e_i^{\left(n\right)}\left(\mathit{x}\right):=x_i$ for $\mathit{x}\in A^n$. We write shortly ${id}_A:=e_0^{\left(1\right)}$ for the identity operation on A, and we use ${\mathcal{J}}_A=\left\{\left.e_i^{\left(n\right)}\phantom{i\in n\in \mathbb{N}}\right|i\in n\in \mathbb{N}\right\}$ for the set of all projections. For $a\in A$ the n-ary constant with value a is the map $c_a^{\left(n\right)}\in {\mathcal{O}}_A^{\left(n\right)}$ satisfying $c_a^{\left(n\right)}\left(\mathit{x}\right)=a$ for all $\mathit{x}\in A^n$. We collect all constant operations on A in the set $C_A=\left\{\left.c_a^{\left(n\right)}\phantom{a\in A\wedge n\in {\mathbb{N}}_{+}}\right|a\in A\wedge n\in {\mathbb{N}}_{+}\right\}$. We also need some more specific operations given by identities. An operation $f\in {\mathcal{O}}_A$ is idempotent, if it satisfies $f(x,\dots ,x)=x$ for all $x\in A$. A ternary operation $f\in {\mathcal{O}}_A^{\left(3\right)}$ is called a majority operation, if $f(x,x,y)=f(x,y,x)=f(y,x,x)=x$ for all $x,y\in A$; it is called a minority operation if $f(x,x,y)=f(x,y,x)=f(y,x,x)=y$ for all $x,y\in A$; finally, it is a Mal’cev operation if $f(x,x,y)=f(y,x,x)=y$ for all $x,y\in A$. Among unary operations we need permutations $f\in SymA$, i.e., bijective self-maps $f\in {\mathcal{O}}_A^{\left(1\right)}$, and retractive operations $f\in {\mathcal{O}}_A^{\left(1\right)}$ satisfying $f\circ f=f$ (sometimes also called idempotent since they are idempotent elements in the semigroup $⟨{\mathcal{O}}_A^{\left(1\right)};\circ ⟩$).

For all $m,n\in \mathbb{N}$ and $g_1,\dots ,g_n\in {\mathcal{O}}_A^{\left(m\right)}$, we can form $(g_1,\dots ,g_n):A^m⟶A^n$, called the tupling of $g_1,\dots ,g_n$, sending $\mathit{x}\in A^m$ to $(g_1\left(\mathit{x}\right),\dots ,g_n\left(\mathit{x}\right))\in A^n$. In this way, we can compose finitary operations $g_1,\dots ,g_n\in {\mathcal{O}}_A^{\left(m\right)}$ with $f\in {\mathcal{O}}_A^{\left(n\right)}$ as $f\circ (g_1,\dots ,g_n)$. A (concrete) clone of non-nullary operations on A is any set $F\subseteq {\mathcal{O}}_A$ that is closed under this form of composition and satisfies ${\mathcal{J}}_A\subseteq F$.

For $m\in \mathbb{N}$ an m-ary relation on a set A is any subset $\varrho \subseteq A^m$ of m-tuples. Any m-ary operation $f\in {\mathcal{O}}_A^{\left(m\right)}$ can be understood as an $(m+1)$-ary relation via its graph $f^{•}:=\left\{\left.(x_1,\dots ,x_m,g(x_1,\dots ,x_m))\phantom{x_1,\dots ,x_m\in A}\right|x_1,\dots ,x_m\in A\right\}$. We extend this notation element-wise to sets of operations by putting $F^{•}:=\left\{\left.f^{•}\phantom{f\in F}\right|f\in F\right\}$ for $F\subseteq {\mathcal{O}}_A$. A binary relation $\varrho \subseteq A^2$ is just a set of pairs; we define its inverse (sometimes also called dual) to be ${\varrho }^{-1}:=\left\{\left.(y,x)\phantom{(x,y)\in \varrho }\right|(x,y)\in \varrho \right\}$. A binary $\varrho \subseteq A^2$ is symmetric if ${\varrho }^{-1}\subseteq \varrho$, and reflexive if $(x,x)\in \varrho$ for all $x\in A$. If $\varrho$ is reflexive, symmetric and transitive, that is $(x,y),(y,z)\in \varrho$ implies $(x,z)\in \varrho$ for all $x,y,z\in A$, then $\varrho$ belongs to $Eq\left(A\right)$, the set of all equivalence relations on A. By ${\mathcal{R}}_A=\left\{\left.\varrho \subseteq A^m\phantom{m\in {\mathbb{N}}_{+}}\right|m\in {\mathbb{N}}_{+}\right\}$ we denote the set of all finitary relations on A.

While functions can be composed, new relations can be constructed from given ones using logical expressions. A primitive positive formula $\phi$ (in prenex normal form) over a given relational signature consists of a prefix of finitely many existentially quantified variables (possibly none) followed by a finite non-empty conjunction of atomic predicates that correspond to the given signature (relations) and have been substituted by some tuple of variables. If the relation symbols are associated with concrete relations, the set of all satisfying value assignments to (a superset of) the free variables of $\phi$ determines a finitary relation on A, which is called primitive positively definable from the given relations. For a finite carrier set A, a set $Q\subseteq {\mathcal{R}}_A$ is said to be a relational clone on A if it contains the diagonal ${\Delta }_A:=\left\{\left.(x,x)\phantom{x\in A}\right|x\in A\right\}$ and is closed under all relations that are primitive positively definable from members of Q (for infinite carrier sets stronger closure properties are required). As this is an implicational definition, all relational clones on A form a closure system. The least relational clone on A containing a particular set $R\subseteq {\mathcal{R}}_A$ will be denoted by ${\left[R\right]}_{{\mathcal{R}}_A}$ and is computed by adding to R all relations that are primitive positively definable from $R\cup \left\{{\Delta }_A\right\}$.

Clones of operations and relational clones are connected in the following way: for $m,n\in \mathbb{N}$ and $f:A^n⟶A$, $\varrho \subseteq A^m$ we say that f preserves $\varrho$ if and only if $\varrho$ is a subuniverse of the algebra ${⟨A;f⟩}^m$. This means that for every $(r_0,\dots ,r_{n-1})\in {\varrho }^n$ the m-tuple obtained by the composition $f\circ (r_0,\dots ,r_{n-1})$ of f with the tupling of $r_0,\dots ,r_{n-1}$ stays inside $\varrho$, that is, for every $(m\times n)$-matrix $R\in A^{m\times n}$ the columns of which all belong to $\varrho$, the m-tuple obtained by applying f row-wise to R remains in $\varrho$. We then call $\varrho$ an invariant of f or f a polymorphism of $\varrho$. The preservation relation induces a Galois connection between ${\mathcal{O}}_A$ and ${\mathcal{R}}_A$, giving rise to the derivation operators $Q\mapsto {Pol}_{A}Q$ and $F\mapsto {Inv}_{A}F$, collecting all polymorphisms in ${\mathcal{O}}_A$ of every relation $\varrho \in Q\subseteq {\mathcal{R}}_A$ and all invariant relations $\varrho \in {\mathcal{R}}_A$ for all given operations $f\in F\subseteq {\mathcal{O}}_A$, respectively. Moreover, we declare for $n\in \mathbb{N}$ and $F\subseteq {\mathcal{O}}_A$, $Q\subseteq {\mathcal{R}}_A$ that ${Pol}_A^{\left(n\right)}F:={\left({Pol}_{A}F\right)}^{\left(n\right)}$ and ${Inv}_A^{\left(n\right)}Q:={\left({Inv}_{A}Q\right)}^{\left(n\right)}$. Now for every $Q\subseteq {\mathcal{R}}_A$ the set ${Pol}_{A}Q$ forms a clone on A, and for every $F\subseteq {\mathcal{O}}_A$ the invariants ${Inv}_{A}F$ are a relational clone containing ∅ (since we omit nullary operations in our clones). Therefore, ${Inv}_A{Pol}_{A}Q\supseteq {\left[Q\cup \left\{\varnothing \right\}\right]}_{{\mathcal{R}}_A}$ and ${Pol}_A{Inv}_{A}F$ contains the clone generated by F. On finite carrier sets A, these inclusions are equalities [31,32]; for infinite A local interpolation operators (and a strengthened definition of relational clone) need to be added to close the gap [33,34].

Besides the Galois connection induced by preservation, we shall encounter several other Galois connections that differ by the inducing relation or by restrictions of the domains they link. Switching between them and the associated closure systems can be expressed well in the framework of formal concept analysis [35,36], providing terminology, notation and theory for the manipulation of Galois connections on a general level. The basic object of formal concept analysis is that of a formal context $\mathbb{K}=(G,M,I)$ where $I\subseteq G\times M$ is any binary relation between sets G (commonly called objects) and M (usually called attributes). A context $\mathbb{K}$ induces two derivation operators of a Galois connection between G and M in the natural way, and specifies exactly between which sets this Galois connection is to be understood. The Galois closed sets on the side of objects are called extents and the ones on the side of attributes are referred to as intents. When we keep the relation I, but pass on to a subset $H\subseteq G$ of the objects or $N\subseteq M$ of the attributes (or both), we form a subcontext ${\mathbb{K}}^{\prime }=(H,N,I\cap (H\times N))$. Though technically incorrect, it is customary to omit the intersection $\cap (H\times N)$ when specifying a subcontext, as the restriction becomes clear from stating the sets of objects and attributes. How the lattices of Galois closed sets (extents and intents) of $\mathbb{K}$ and ${\mathbb{K}}^{\prime }$ are related is discussed in Chapter 3 of [35] (p. 97 et seqq.). We will mostly aim for context manipulations where the closure system of intents (and thus the lattice structure) does not change, such as object clarification and object reduction. We shall explain more details at the appropriate place in the text and give pointers to the literature there.

Centrally for this paper will be the Galois connection of commutation given by the context ${\mathbb{K}}_{\mathrm{c}}=\left({\mathcal{O}}_A,{\mathcal{O}}_A,\perp \right)$. In this respect we say that an n-ary operation $f\in {\mathcal{O}}_A^{\left(n\right)}$ commutes with an m-ary operation $g\in {\mathcal{O}}_A^{\left(m\right)}$, if $g\left(f\left(X\right)\right)=f\left(g\left(X^T\right)\right)$ holds for any matrix $X\in A^{m\times n}$, where $f\left(X\right):={\left(f\left(X\right(i,·\left)\right)\right)}_{i\in m}$ denotes the tuple obtained by applying f row-wise to the matrix X, and similarly for g and the transposed matrix $X^T$. This commutation condition will be denoted by $f\perp g$; it is easy to see that it is a symmetric property, i.e., we have $f\perp g$ if and only if $g\perp f$. Therefore, the two Galois derivatives induced by ${\mathbb{K}}_{\mathrm{c}}$ coincide: they map $F\subseteq {\mathcal{O}}_A$ to its centraliser $F^{*}=\left\{\left.g\in {\mathcal{O}}_A\phantom{\forall f\in F:g\perp f}\right|\forall f\in F:g\perp f\right\}$, and the associated closure operator sends F to $F^{**}$, the bicentraliser of F. A routine verification shows that $g\in F^{*}\iff g\in {Pol}_A{F}^{•}\iff g^{•}\in {Inv}_{A}F$ holds for $F\cup \left\{g\right\}\subseteq {\mathcal{O}}_A$, so $F^{*}={Pol}_A{F}^{•}$, i.e., commutation can be rephrased in terms of preservation of graphs of operations. Hence, up to isomorphism, ${\mathbb{K}}_{\mathrm{c}}$ is the subcontext of finitary operations and relations with preservation, where ${\mathcal{R}}_A$ is restricted to ${\left[{\mathcal{O}}_A\right]}^{•}$.

As mentioned in the introduction, when studying centralising monoids we only look at the unary parts $F^{*\left(1\right)}$ of centraliser clones, that is to say, we are dealing with the subcontext $\mathbb{K}:=\left({\mathcal{O}}_A,{\mathcal{O}}_A^{\left(1\right)},\perp \cap \left({\mathcal{O}}_A\times {\mathcal{O}}_A^{\left(1\right)}\right)\right)$, briefly $\left({\mathcal{O}}_A,{\mathcal{O}}_A^{\left(1\right)},\perp \right)$, of ${\mathbb{K}}_{\mathrm{c}}$. The intents of $\mathbb{K}$, i.e., Galois closed sets $M=F^{*\left(1\right)}$ for some $F\subseteq {\mathcal{O}}_A$, are exactly all centralising monoids on A. Moreover, every set $F\subseteq {\mathcal{O}}_A$ describing M in this way, is a witness of M, and we can equivalently express that M is witnessed by F via saying that $M=End⟨A;F⟩$. A centralising monoid $M\subseteq {\mathcal{O}}_A^{\left(1\right)}$ is maximal if it is a co-atom in the intent lattice of $\mathbb{K}$, i.e., a proper centralising monoid which is maximal under set inclusion.

2.2. Fundamental Results on Clones, Centralisers and Centralising Monoids

The following simple observation exhibits necessary conditions that can be used to describe functions in a particular centraliser clone (or its unary part). The utility of said conditions was already observed by Harnau, cf. Lemma 2.6 and Satz 2.15 of [10], in the context of centralisers of single unary operations $f\in {\mathcal{O}}_A^{\left(1\right)}$.

Lemma 1.

For every set $F\subseteq {\mathcal{O}}_A$ we have $F^{*}={Pol}_A{\left[F^{•}\right]}_{{\mathcal{R}}_A}$. In particular, we have

$$\begin{array}{cc}\hfill F^{*}& \subseteq {Pol}_A\left\{\left.ker\left(f\right)\phantom{f\in F}\right|f\in F\right\},\hfill \\ \hfill F^{*}& \subseteq {Pol}_A\left\{\left.im\left(f\right)\phantom{f\in F}\right|f\in F\right\},\hfill \\ \hfill F^{*}& \subseteq {Pol}_A\left\{\left.fix\left(f\right)\phantom{f\in F}\right|f\in F\right\},\hfill \end{array}$$

where for $n\in \mathbb{N}$ and $f\in {\mathcal{O}}_A^{\left(n\right)}$

$$\begin{array}{cc}\hfill ker\left(f\right)& :=\left\{\left.(x_1,\dots ,x_n,y_1,\dots ,y_n)\in A^{2n}\phantom{f(x_1,\dots ,x_n)=f(y_1,\dots ,y_n)}\right|f(x_1,\dots ,x_n)=f(y_1,\dots ,y_n)\right\},\hfill \\ \hfill im\left(f\right)& :=f\left[A^n\right],\hfill \\ \hfill fix\left(f\right)& :=\left\{\left.x\in A\phantom{f(x,\dots ,x)=x}\right|f(x,\dots ,x)=x\right\}.\hfill \end{array}$$

Proof. 

We have $F^{*}={Pol}_A{F}^{•}\supseteq {Pol}_A{\left[F^{•}\right]}_{{\mathcal{R}}_A}\supseteq {Pol}_A{Inv}_A{Pol}_A{F}^{•}={Pol}_A{F}^{•}$, following directly from the definition of commutation. Clearly, $fix\left(f\right)$ is primitive positively definable from the graph of f, $im\left(f\right)=\left\{\left.y\in A\phantom{\exists x_1,\dots ,x_n\in A:f(x_1,\dots ,x_n)=y}\right|\exists x_1,\dots ,x_n\in A:f(x_1,\dots ,x_n)=y\right\}$ is too, and $ker\left(f\right)=\left\{\left.(\mathit{x},\mathit{y})\in A^{2n}\phantom{\exists z\in A:f\left(\mathit{x}\right)=z\wedge f\left(\mathit{y}\right)=z}\right|\exists z\in A:f\left(\mathit{x}\right)=z\wedge f\left(\mathit{y}\right)=z\right\}$ as well.    □

Second, we recollect the following helpful characterisation of centralising monoids.

Lemma 2

(cf. [21] (Lemma 2.2)). For a set $M\subseteq {\mathcal{O}}_A^{\left(1\right)}$ the following facts are equivalent:

(a)

M is a centralising monoid, i.e., there is $F\subseteq {\mathcal{O}}_A$ such that $M=F^{*\left(1\right)}$.

(b)

$M=M^{**\left(1\right)}$, i.e., M is witnessed by $M^{*}$.

Proof. 

If $M=F^{*\left(1\right)}$ for some $F\subseteq {\mathcal{O}}_A$, then $M^{**\left(1\right)}={\left({\left(F^{*\left(1\right)}\right)}^{*}\right)}^{*\left(1\right)}=F^{*\left(1\right)}=M$ by virtue of the Galois derivatives ${}^{*}$ and ${}^{*\left(1\right)}$. Conversely, if $M=M^{**\left(1\right)}$, then M is a centralising monoid witnessed by $F=M^{*}$.    □

Lemma 2 shows that every centralising monoid $M=F^{*\left(1\right)}$ has a largest possible witness, as generally $M\subseteq F^{*}$, so $F\subseteq M^{*}$. We now turn to maximal centralising monoids. Being co-atoms in the lattice of intents of $\mathbb{K}=\left({\mathcal{O}}_A,{\mathcal{O}}_A^{\left(1\right)},\perp \right)$, they correspond via that Galois connection of commutation to an atom F in the lattice of extents of $\mathbb{K}$. Such an atom must be generated (as an extent) by a single non-trivial object $f\in {\mathcal{O}}_A\setminus {\mathcal{O}}_A^{\left(1\right)*}$, i.e., $F={\left\{f\right\}}^{*\left(1\right)*}$. For the co-atom $M=F^{*\left(1\right)}$ this means $M=F^{*\left(1\right)}={\left\{f\right\}}^{*\left(1\right)**\left(1\right)}={\left\{f\right\}}^{*\left(1\right)}$ by virtue of the Galois connection given by $\mathbb{K}$. So M is singly witnessed by a non-trivial operation f; however, even more is known about these witnesses: they can always be chosen as a generator of a minimal clone of minimum arity, a so-called minimal function.

Proposition 3

(Theorem 3.2 in [21], Proposition 2.2 in [27]). For any maximal centralising monoid $M\subseteq {\mathcal{O}}_A^{\left(1\right)}$ on a finite set A there is a minimal function $f\in M^{*}\setminus {\mathcal{O}}_A^{\left(1\right)*}$ (generating a minimal clone) such that $M={\left\{f\right\}}^{*\left(1\right)}$.

Minimal functions are separated by Rosenberg’s Classification Theorem [26] for minimal clones into five distinct categories ((II) is a special case of (V), but is often listed on its own).

Theorem 4

(See [26]). On a finite set A every minimal function f is of one of the following types:

(I)

$f\in {\mathcal{O}}_A^{\left(1\right)}$ and $f\in SymA$ is a permutation of prime order or a retractive operation $f\circ f=f\ne {id}_A$;

(II)

$f\in {\mathcal{O}}_A^{\left(2\right)}$ is idempotent, i.e., $f\circ ({id}_A,{id}_A)={id}_A$;

(III)

$f\in {\mathcal{O}}_A^{\left(3\right)}$ is a ternary (minority) Mal’cev operation arising as $f(x,y,z):=x+y+z$ for $x,y,z\in A$ from a Boolean group $⟨A;+⟩$;

(IV)

$f\in {\mathcal{O}}_A^{\left(3\right)}$ is a ternary majority operation;

(V)

$f\in {\mathcal{O}}_A^{\left(n\right)}$ is a proper semiprojection of arity n where $3\le n\le \left|A\right|$.

In this paper, we address centralising monoids witnessed by a minimal function of types (I)–(III) with a special focus on the set $\left\{0,1,2,3\right\}$; those relating to type (IV) have already been considered in [27], the ones of type (V) are part of ongoing research.

Before we can tend to this problem in more detail, we need further background information on clones, such as the centraliser of a constant operation.

Lemma 5

(Lemma 1.9 in [10], Lemma 5.2 in [21]). For any $n\in \mathbb{N}$ and $a\in A$ we have ${\left\{c_a^{\left(n\right)}\right\}}^{*}={Pol}_A\left\{\left\{a\right\}\right\}=\left\{\left.f\in {\mathcal{O}}_A\phantom{a\in fix\left(f\right)}\right|a\in fix\left(f\right)\right\}$.

Proof. 

Let $m\in \mathbb{N}$ and $f\in {\mathcal{O}}_A^{\left(m\right)}$. We have $f\perp c_a^{\left(n\right)}$ if and only if for all $x_{11},\dots ,x_{mn}\in A$ the condition

$$\begin{array}{cc}\hfill f(a,\dots ,a)& =f(c_a^{\left(n\right)}(x_{11},\dots ,x_{1n}),\dots ,c_a^{\left(n\right)}(x_{m1},\dots ,x_{mn}))\hfill \\ \hfill & =c_a^{\left(n\right)}(f(x_{11},\dots ,x_{m1}),\dots ,f(x_{1n},\dots ,x_{mn}))=a\hfill \end{array}$$

holds, that is, exactly if $f(a,\dots ,a)=a$, i.e., precisely if $a\in fix\left(f\right)$, or $f\in {Pol}_A\left\{\left\{a\right\}\right\}$.    □

Corollary 6

(Lemma 5.3 in [21]). The centraliser $C_A^{\left(1\right)*}=C_A^{*}$ is the clone of all idempotent operations.

Proof. 

We have $C_A^{\left(1\right)*}={\bigcap }_{a\in A}{\left\{c_a^{\left(1\right)}\right\}}^{*}={\bigcap }_{a\in A}{Pol}_A\left\{\left\{a\right\}\right\}={Pol}_A\left\{\left.\left\{a\right\}\phantom{a\in A}\right|a\in A\right\}$ due to Lemma 5.    □

The following characterisation is also very well known.

Lemma 7.

For a clone F on any set A the following statements are equivalent:

(a)

F is a clone of idempotent operations, i.e., $F\subseteq {Pol}_A\left\{\left.\left\{a\right\}\phantom{a\in A}\right|a\in A\right\}$.

(b)

For every $f\in F$ and all $a\in A$ we have $f(a,\dots ,a)=a$.

(c)

$F^{\left(1\right)}=\left\{{id}_A\right\}$.

Proof. 

Condition (b) simply spells out the preservation of every singleton set $\left\{a\right\}$ in (a). From this it follows that every $f\in F^{\left(1\right)}$ satisfies $f\left(a\right)=a$ for every $a\in A$, i.e., $f={id}_A$. For F contains all projections, (b) implies (c). Now since F is a clone, with every $f\in F$ also $f\circ ({id}_A,\dots ,{id}_A)\in F^{\left(1\right)}$. If (c) holds, then $f\circ ({id}_A,\dots ,{id}_A)\in \left\{{id}_A\right\}$, and this shows statement (b).    □

Lemma 8.

For any set A we have $({\mathcal{J}}_A\cup C_A)\cap C_A^{\left(1\right)*}={\mathcal{J}}_A$.

Proof. 

For $\left|A\right|<2$ this is trivially true. For $\left|A\right|\ge 2$, no constant map is idempotent, so, by Corollary 6, $({\mathcal{J}}_A\cup C_A)\cap C_A^{\left(1\right)*}$ can only consist of projections. The converse inclusion is trivial.    □

When proving that a certain centralising monoid is maximal, it will be necessary to compute the centralising monoid $M^{**\left(1\right)}$ generated by some set $M\subseteq {\mathcal{O}}_A^{\left(1\right)}$ and to show that it is the full transformation monoid on A. To do this we shall always demonstrate the seemingly stronger condition that the centraliser of M is trivial. The following lemma shows that this is in fact a necessary step to take whenever $\left|A\right|\ge 3$.

Lemma 9.

For any set A with $\left|A\right|\ge 3$ and any subset $M\subseteq {\mathcal{O}}_A$ the following statements are equivalent:

(a)

$M^{**\left(1\right)}={\mathcal{O}}_A^{\left(1\right)}$.

(b)

$M^{**}={\mathcal{O}}_A$.

(c)

$M^{*}={\mathcal{J}}_A$.

Proof. 

The implications (c)$\Rightarrow \left(\mathsf{b}\right)\Rightarrow$(a) are obvious as every function commutes with projections. Now, if (a) holds, then ${\mathcal{O}}_A^{\left(1\right)}\subseteq M^{**}$, which is equivalent to $F:=M^{*}\subseteq {\mathcal{O}}_A^{\left(1\right)*}$. By Lemma 1, this means the functions in F preserve the kernel of any unary operation, so they preserve every equivalence relation on A. Therefore, $F\subseteq {Pol}_{A}Eq\left(A\right)$, and for $\left|A\right|\ge 3$ the latter clone equals ${\mathcal{J}}_A\cup C_A$ as is shown in Example 3.3 of [30] (p. 136). Now $F\subseteq {\mathcal{O}}_A^{\left(1\right)*}\subseteq C_A^{\left(1\right)*}$ implies that $F\subseteq ({\mathcal{J}}_A\cup C_A)\cap C_A^{\left(1\right)*}$, so Lemma 8 shows that (c) must be satisfied.    □

Note that for $\left|A\right|=2$, Lemma 9 fails as, e.g., the clone L of all affine linear functions, which is the centraliser of the (ternary minority) Mal’cev function on the two-element set, contains all unary operations. So $L^{**}=L⊊{\mathcal{O}}_A$, but $L^{**\left(1\right)}=L^{\left(1\right)}={\mathcal{O}}_A^{\left(1\right)}$.

To establish for a subset $M\subseteq {\mathcal{O}}_A$ condition (c) of Lemma 9 or to prove at least $M^{*\left(1\right)}=\left\{{id}_A\right\}$, we shall exploit a theorem of Länger and Pöschel [30] on (strongly) constantively rigid systems of (binary) relations.

Proposition 10

(cf. [30] (Theorem 2.13, p. 136, Theorem 2.3, p. 133)). Let A be any (finite or infinite) set with $\left|A\right|\ge 4$, $F\subseteq {\mathcal{O}}_A$ and let $Q\subseteq {Inv}_A^{\left(2\right)}F$ satisfy the following two separation conditions (see Definition 2.7, p. 134 et seq. in [30])

(B)

for all pairwise distinct $x,y,z\in A$ there is $\varrho \in Q$ such that $(x,y)\in \varrho \not\ni (x,z)$;

(D)

for all pairwise distinct $x,y,z,u\in A$ there is $\varrho \in Q$ such that $(x,y)\in \varrho \not\ni (z,u)$.

Then $F^{\left(1\right)}\subseteq \left\{{id}_A\right\}\cup C_A^{\left(1\right)}$; moreover, if all relations in Q are reflexive, then $F\subseteq {\mathcal{J}}_A\cup C_A$.

Proof. 

By our assumption we have $F\subseteq {Pol}_{A}Q$ and, in particular, $F^{\left(1\right)}\subseteq {Pol}_A^{\left(1\right)}Q$. We use Theorem 2.13 of [30] to infer that Q is constantively rigid, i.e., ${Pol}_A^{\left(1\right)}Q\subseteq {\mathcal{J}}_A\cup C_A$, wherefore $F^{\left(1\right)}\subseteq \left\{{id}_A\right\}\cup C_A^{\left(1\right)}$. If, additionally, Q only contains reflexive relations, then Theorem 2.3 of [30] states that constantive rigidity of Q is equivalent to strong constantive rigidity, that is, $F\subseteq {Pol}_{A}Q\subseteq {\mathcal{J}}_A\cup C_A$.    □

Remark 11.

There are two more conditions, (A) and (C), in [30], which can also be employed to ensure (strong) constantive rigidity of systems Q of (binary reflexive) relations, see, e.g., Theorems 2.11 and 2.12 of [30]. In particular, via Theorem 2.12, (B) and (C) together may be used to obtain (strong) constantive rigidity also when $\left|A\right|=3$, and (C) automatically follows from (B) if all the relations in Q are symmetric (see Lemma 2.8 in [30]), for example, equivalence relations. More concrete constantively rigid systems of relations are provided in Section 3 of [30], some of them also being strongly constantively rigid.

Corollary 12.

Let A be any set with $\left|A\right|\ge 4$ and $M\subseteq {\mathcal{O}}_A$ be such that for each $a\in A$ there is $s\in M$ satisfying $a\notin fix\left(s\right)$. Moreover assume that $Q\subseteq {\left[M^{•}\right]}_{{\mathcal{R}}_A}^{\left(2\right)}$ satisfies conditions (B) and (D), then $M^{*\left(1\right)}=\left\{{id}_A\right\}$; if all the relations in Q are reflexive, then $M^{*}={\mathcal{J}}_A$; if, moreover, the relations used to satisfy (B) are reflexive and symmetric, then the result also follows for $\left|A\right|=3$.

Proof. 

Let $F:=M^{*}$ in Proposition 10 and note that ${\left[M^{•}\right]}_{{\mathcal{R}}_A}\subseteq {Inv}_A{Pol}_A{M}^{•}={Inv}_A{M}^{*}$. So Proposition 10 entails that $M^{*\left(1\right)}=F^{\left(1\right)}\subseteq {\mathcal{J}}_A\cup C_A$ and $M^{*}=F\subseteq {\mathcal{J}}_A\cup C_A$ under the reflexive assumption. If the relations used in (b) are reflexive and symmetric, we combine the reasoning of Proposition 10 with Remark 11 to get $F\subseteq {\mathcal{J}}_A\cup C_A$ also for $\left|A\right|=3$. Finally, $F\cap C_A=\varnothing$, for the supposition of $c_a^{\left(n\right)}\in F=M^{*}$ for some $a\in A$ and $n\in \mathbb{N}$ would imply $M\subseteq {\left\{c_a^{\left(n\right)}\right\}}^{*}=\left\{\left.f\in {\mathcal{O}}_A\phantom{a\in fix\left(f\right)}\right|a\in fix\left(f\right)\right\}$, see Lemma 5, which contradicts the assumption on M.    □

Corollary 13.

Let A be any set with $\left|A\right|\ge 3$ and $M\subseteq {\mathcal{O}}_A$ be such that for each $a\in A$ there is $s\in M$ satisfying $a\notin fix\left(s\right)$. Moreover assume that

(B’)

for all pairwise distinct $x,y,z\in A$ there is $s\in M^{\left(1\right)}$ such that $s\left(y\right)=s\left(x\right)\ne s\left(z\right)$,

(D’)

for all pairwise distinct $x,y,z,u\in A$ there is $s\in M^{\left(1\right)}$ such that $s\left(x\right)=s\left(y\right)$ and $s\left(z\right)\ne s\left(u\right)$,

then $M^{*}={\mathcal{J}}_A$.

Proof. 

Use Corollary 12 on the equivalence relations $\left\{\left.ker\left(s\right)\phantom{s\in M^{\left(1\right)}}\right|s\in M^{\left(1\right)}\right\}\subseteq {Inv}_A^{\left(2\right)}{M}^{*}$.    □

Corollary 14.

Let A be any set with $\left|A\right|\ge 4$ and $M\subseteq {\mathcal{O}}_A$ be such that for each $a\in A$ there is $s\in M$ satisfying $a\notin fix\left(s\right)$. Moreover assume that

(B”)

for all pairwise distinct $x,y,z\in A$ there is $s\in M^{\left(1\right)}$ such that $s\left(y\right)=s\left(x\right)\ne s\left(z\right)$ or $s\left(x\right)=y$ or $s\left(y\right)=x\ne s\left(z\right)$,

(D”)

for all pairwise distinct $x,y,z,u\in A$ there is $s\in M^{\left(1\right)}$ satisfying one of the conditions $s\left(x\right)=s\left(y\right)\wedge s\left(z\right)\ne s\left(u\right)$ or $s\left(x\right)=y\wedge s\left(z\right)\ne u$ or $s\left(y\right)=x\wedge s\left(u\right)\ne z$,

then $M^{*\left(1\right)}=\left\{{id}_A\right\}$.

Proof. 

Use the set $Q:=\left\{\left.ker\left(s\right)\phantom{s\in M^{\left(1\right)}}\right|s\in M^{\left(1\right)}\right\}\cup M^{\left(1\right)}{}^{•}\cup \left\{\left.{s^{•}}^{-1}\phantom{s\in M^{\left(1\right)}}\right|s\in M^{\left(1\right)}\right\}\subseteq {Inv}_A^{\left(2\right)}{M}^{*}$ in Corollary 12.    □

3. Monoids Witnessed by Unary Operations

There are two types of unary minimal functions in Rosenberg’s Theorem 4. The first are permutations of prime order, that is, their cycle structure consists only of fixed points and cycles of length p for some prime p. The second are idempotent or retractive operations $f\in {\mathcal{O}}_A^{\left(1\right)}$, which satisfy $f\circ f=f\ne {id}_A$. These are exactly those non-identical unary operations which fix every point of their image.

3.1. Computational Results for $\{0,1,2,3\}$

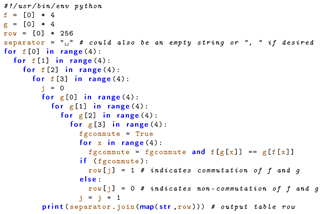
We started by computing a commutation table of all 256 unary operations on the set $A=\left\{0,1,2,3\right\}$, i.e., the formal context ${\mathbb{K}}_1=\left({\mathcal{O}}_A^{\left(1\right)},{\mathcal{O}}_A^{\left(1\right)},\perp \right)$ in the language of [35,36]. Being a $256\times 256$ Boolean matrix this table is already confusingly big and we therefore do not present it here. For purposes of verification, in Listing 1 we have instead added simple Python code that allows anybody to reproduce such a table if desired. Using standard algorithms presented in Section 2.1 of [35] or Chapter 2 of [36], one may compute from ${\mathbb{K}}_1$ that there are exactly 1485 centralising monoids on $\left\{0,1,2,3\right\}$ that can be witnessed by sets of unary operations. However, we are only interested in the co-atoms of this large lattice. By virtue of the Galois connection represented by ${\mathbb{K}}_1$, every co-atom M is the Galois derivative $N^{*\left(1\right)}$ of an atom N on the dual side of the Galois connection. Since in the lattice of closed sets of any closure operator the atoms must be singly generated, it follows that $N={\left\{f\right\}}^{*\left(1\right)*\left(1\right)}$ for a single unary function $f\in {\mathcal{O}}_A^{\left(1\right)}$ and so $M=N^{*\left(1\right)}={\left\{f\right\}}^{*\left(1\right)*\left(1\right)*\left(1\right)}={\left\{f\right\}}^{*\left(1\right)}$. Hence, to obtain the co-atoms, we only need to iterate over the 255 rows of ${\mathbb{K}}_1$ belonging to each $f\in {\mathcal{O}}_A^{\left(1\right)}\setminus \left\{{id}_A\right\}$ (or just the unary f from Rosenberg’s Theorem) and check, which ${\left\{f\right\}}^{*\left(1\right)}$ are maximal under set inclusion.

The result is that there are 49 co-atoms in the lattice of closed sets of ${\mathbb{K}}_1$, and subsequently we shall explain our computational findings in terms of the types of unary operations from Rosenberg’s Theorem, i.e., permutations of prime order and non-identical retractions. In the following two subsections we shall then give theoretical evidence why the 49 co-atoms arise on $\left\{0,1,2,3\right\}$. It is worth noting that these 49 co-atoms in the lattice belonging to ${\mathbb{K}}_1$ are merely candidates for maximal centralising monoids, and we shall indeed demonstrate that some co-atoms of ${\mathbb{K}}_1$ fail to be maximal among all centralising monoids, that is, are no co-atoms with respect to $\left({\mathcal{O}}_A,{\mathcal{O}}_A^{\left(1\right)},\perp \right)$.

Listing 1.

Python code to print a commutation table (0-1-matrix) for all 256 unary operations f on $\left\{0,1,2,3\right\}$, where rows and columns are enumerated in lectic order of the value tables $f\circ (0,1,2,3)$ from $(0,0,0,0),(0,0,0,1),(0,0,0,2),\dots ,(3,3,3,3)$.

On a four-element set there are three types of permutations of prime order: three-cycles, transpositions or products of two disjoint transpositions. Up to conjugacy these can be represented by the following three functions on $\left\{0,1,2,3\right\}$: $(0,1,2)$, $(0,1)$, $(0,1)(2,3)$. There are $2·\left(\genfrac{}{}{0pt}{}{4}{1}\right)=8$ three-cycles (4 choices of the unique fixed point and 2 for the image of the first cycle element), but it will turn out that centralising monoids witnessed by these operations are not maximal (Lemma 16), not even with respect to ${\mathbb{K}}_1$. However, the monoids described by the other prime permutations are maximal when considered among the monoids witnessed by only unary operations (i.e., the closure system of ${\mathbb{K}}_1$). Yet again, they will not be maximal in the lattice of all centralising monoids on $\left\{0,1,2,3\right\}$, see Corollary 22. We have $\left(\genfrac{}{}{0pt}{}{4}{2}\right)=6$ transpositions (choosing the two transposed elements) and $\frac{1}{2}·\left(\genfrac{}{}{0pt}{}{4}{2}\right)=3$ products of disjoint transpositions since such a function can be obtained by choosing the first transposed pair or the second one. Altogether there are 9 prime permutations (of order 2) that describe maximal monoids of ${\mathbb{K}}_1$.

The non-trivial retractive functions on a four-element set can be separated into the following types: being constant (one-element image, there are 4 such functions), having a two-element image, or having a three-element image (there are $\left(\genfrac{}{}{0pt}{}{4}{3}\right)·\left(\genfrac{}{}{0pt}{}{3}{1}\right)=12$ such functions, first choosing the image and then the value of the element outside the image within it). The retractions with a two-element image can moreover be split up into those mapping the two elements outside the image to the same value and those mapping them to both distinct values of the image. In both subcases we have $\left(\genfrac{}{}{0pt}{}{4}{2}\right)·2=12$ functions as we need to choose the two-element image and then one of two ways how the elements outside the image can be mapped into it. Retractions of all four types witness centralising monoids that are maximal among those centralising monoids witnessed by unary functions, see Corollary 27, and there are $3·12+4=40$ non-trivial retractions on $\left\{0,1,2,3\right\}$. Moreover, it is known from Theorem 5.1 of [21] that ${\left\{c_a^{\left(1\right)}\right\}}^{*\left(1\right)}$ with $a\in A$ is a maximal centralising monoid in general (that is on any finite set A with $\left|A\right|\ge 3$ in the lattice of all centralising monoids), so the 4 centralising monoids of constants are co-atoms with respect to $\left({\mathcal{O}}_A,{\mathcal{O}}_A^{\left(1\right)},\perp \right)$, not just ${\mathbb{K}}_1$. In total, we have $40+9=49$ centralising monoids on $\left\{0,1,2,3\right\}$ that are maximal in the 1485-element lattice of those monoids that can be witnessed by sets of unary operations. These can be grouped together into 6 conjugacy types that can be represented as ${\left\{(0,1)\right\}}^{*\left(1\right)}$, ${\left\{(0,1)(2,3)\right\}}^{*\left(1\right)}$, ${\left\{c_0^{\left(1\right)}\right\}}^{*\left(1\right)}$, ${\left\{f_{24}\right\}}^{*\left(1\right)}$, ${\left\{f_{16}\right\}}^{*\left(1\right)}$ and ${\left\{f_{17}\right\}}^{*\left(1\right)}$ where the retractions $f_{24}$, $f_{16}$ and $f_{17}$ are given as $f_{24}\circ (0,1,2,3)=(0,1,2,0)$, $f_{16}\circ (0,1,2,3)=(0,1,0,0)$ and $f_{17}\circ (0,1,2,3)=(0,1,0,1)$. From the explicit calculations (and the characterisations in the following subsections) it follows that

$$\begin{array}{cccc}\hfill \left|{\left\{(0,1)\right\}}^{*\left(1\right)}\right|& =16\hfill & \hfill \left|{\left\{(0,1)(2,3)\right\}}^{*\left(1\right)}\right|& =16\hfill \\ \hfill \left|{\left\{c_0^{\left(1\right)}\right\}}^{*\left(1\right)}\right|& =64\hfill & \hfill \left|{\left\{f_{24}\right\}}^{*\left(1\right)}\right|& =36\hfill \\ \hfill \left|{\left\{f_{16}\right\}}^{*\left(1\right)}\right|& =20\hfill & \hfill \left|{\left\{f_{17}\right\}}^{*\left(1\right)}\right|& =16.\hfill \end{array}$$

As $(0,1)(2,3)$ has no fixed points but $(0,1)$ and $f_{17}$ have, the monoid ${\left\{(0,1)(2,3)\right\}}^{*\left(1\right)}$ does not contain constant operations (cf. Lemma 5) but ${\left\{(0,1)\right\}}^{*\left(1\right)}$ and ${\left\{f_{17}\right\}}^{*\left(1\right)}$ do. Therefore, $⟨{\left\{(0,1)\right\}}^{*\left(1\right)};\circ ⟩\ncong ⟨{\left\{(0,1)(2,3)\right\}}^{*\left(1\right)};\circ ⟩\ncong ⟨{\left\{f_{17}\right\}}^{*\left(1\right)};\circ ⟩$. Furthermore, computations show that $⟨{\left\{(0,1)\right\}}^{*\left(1\right)};\circ ⟩$ has 96 binary term functions, but $⟨{\left\{f_{17}\right\}}^{*\left(1\right)};\circ ⟩$ has 262 of them, so $⟨{\left\{(0,1)\right\}}^{*\left(1\right)};\circ ⟩\ncong ⟨{\left\{f_{17}\right\}}^{*\left(1\right)};\circ ⟩$. Therefore, the co-atoms of the lattice of intents of ${\mathbb{K}}_1$ fall into exactly 6 distinct isomorphism classes of monoids. Moreover, we computed that all 1485 monoids in the lattice of intents of ${\mathbb{K}}_1$ can be separated into 106 classes up to element-wise conjugacy (cf. Section 4 for more explanation).

3.2. Monoids Witnessed by Permutations

In Lemma 4.11 of [27] (see also Lemma 4.10 of [37]) we provided a characterisation of when a finitary operation $f\in {\mathcal{O}}_A$ on a finite set A commutes with a permutation $s\in SymA$, based on examining orbits of the permutation group generated by s. Under the assumption that f is a function the given condition was sufficient to ensure that $f\perp s$, but blindly fulfilling the orbit condition could also lead to some value assignments for f that would contradict the assumption of f being a function. Thus, some care had to be taken when working with Lemma 4.11 from [27], but this was never much of an issue when studying majority operations f on small sets as in [27]. Here we improve the mentioned characterisation by placing an additional necessary condition on the choice of the function values such that no contradictions can occur.

Lemma 15.

For a finite set A, $n\in {\mathbb{N}}_{+}$ and $s\in SymA$ let $S:={⟨\left\{s\right\}⟩}_{SymA}$ be the permutation group generated by s and $T\subseteq A^n$ be a transversal of the orbits of the action of S on $A^n$ via $(\tilde{s},\mathit{x})\mapsto \tilde{s}\circ \mathit{x}$. For $f\in {\mathcal{O}}_A^{\left(n\right)}$ we have $f\perp s$ if and only if for every $\mathit{x}\in T$ the length of the orbit of $f\left(\mathit{x}\right)$ under S divides the length ℓ of the orbit of $\mathit{x}$ under S and $f(s^j\circ \mathit{x})=s^j\left(f\left(\mathit{x}\right)\right)$ for all exponents j satisfying $1\le j<\ell$.

In particular if for all $\mathit{x}\in T$ a value $f\left(\mathit{x}\right)$ is chosen such that the size of the orbit of $f\left(\mathit{x}\right)$ is a divisor of the size ℓ of the orbit of $\mathit{x}$, then there is a unique extension of this partial definition to an n-ary function $f\in {\left\{s\right\}}^{*}$ by defining $f(s^j\circ \mathit{x}):=s^j\left(f\left(\mathit{x}\right)\right)$ for all $1\le j<\ell$ and $\mathit{x}\in T$.

Proof. 

Let $m:=\left|S\right|$ be the order of s. Lemma 4.11 of [27] shows that $f\perp s$ if and only if for all $\mathit{x}\in T$ the condition $f(s^j\circ \mathit{x})=s^j\left(f\left(\mathit{x}\right)\right)$ holds for all $0\le j<m$. The length ℓ of the orbit of $\mathit{x}$ is the least common multiple of the lengths of the orbits of the entries of $\mathit{x}$ and each of these lengths divides m, so ℓ divides m. So $f(s^j\circ \mathit{x})=s^j\left(f\left(\mathit{x}\right)\right)$ for all $1\le j<\ell$ follows from $f\perp s$. If t is the size of the orbit of $f\left(\mathit{x}\right)$, then this orbit is $\left\{\left.s^j\left(f\left(\mathit{x}\right)\right)\phantom{0\le j<t}\right|0\le j<t\right\}$ and $s^t\left(f\left(\mathit{x}\right)\right)=f\left(\mathit{x}\right)$. Writing $\ell =q·t+r$ with $0\le r<t$, it follows from the definition of ℓ and the commutation condition that

$$f\left(\mathit{x}\right)=f(s^{\ell }\circ \mathit{x})=f(s\circ s^{\ell -1}\circ \mathit{x})=s\left(f(s^{\ell -1}\circ \mathit{x})\right)=s\left(s^{\ell -1}\left(f\left(\mathit{x}\right)\right)\right)=s^{\ell }\left(f\left(\mathit{x}\right)\right)=s^r\left(f\left(\mathit{x}\right)\right),$$

so $r=0$ as the elements ${\left(s^j\left(f\left(\mathit{x}\right)\right)\right)}_{0\le j<t}$ are pairwise distinct. Therefore, $f\perp s$ implies that t divides ℓ.

Conversely, if for fixed $\mathit{x}\in T$ we have $f(s^j\circ \mathit{x})=s^j\left(f\left(\mathit{x}\right)\right)$ for all $1\le j<\ell$ and t divides ℓ, where t is the size of the orbit of $f\left(\mathit{x}\right)$, then $s^t\left(f\left(\mathit{x}\right)\right)=f\left(\mathit{x}\right)$ and we can show by induction on $i\in \mathbb{N}$ that $s^{i\ell }\left(f\left(\mathit{x}\right)\right)=f\left(\mathit{x}\right)$. The case $i=0$ is trivial and the step from i to $i+1$ simplifies to $s^{\ell }\left(s^{i\ell }\left(f\left(\mathit{x}\right)\right)\right)=s^{\ell }\left(f\left(\mathit{x}\right)\right)=s^{qt}\left(f\left(\mathit{x}\right)\right)=s^t(\cdots s^t\left(f\left(\mathit{x}\right)\right))=f\left(\mathit{x}\right)$ by repeated application of $s^t\left(f\left(\mathit{x}\right)\right)=f\left(\mathit{x}\right)$. Therefore, for every $0\le j<\ell$ and $i\in \mathbb{N}$ we obtain $s^{i\ell +j}\left(f\left(\mathit{x}\right)\right)=s^j\left(s^{i\ell }\left(f\left(\mathit{x}\right)\right)\right)=s^j\left(f\left(\mathit{x}\right)\right)=f(s^j\circ \mathit{x})$ by our assumption. By the definition of ℓ we have $s^{\ell }\circ \mathit{x}=\mathit{x}$ and thus get $s^{i\ell +j}\circ \mathit{x}=s^j\circ s^{\ell }\circ \cdots \circ s^{\ell }\circ \mathit{x}=s^j\circ \mathit{x}$; therefore, $s^{i\ell +j}\left(f\left(\mathit{x}\right)\right)=f(s^j\circ \mathit{x})=f(s^{i\ell +j}\circ \mathit{x})$. This means $s^m\left(f\left(\mathit{x}\right)\right)=f(s^m\circ \mathit{x})$ for all $m\in \mathbb{N}$, which implies commutation, see, e.g., Lemma 4.11 in [27].

If the divisor condition on $f\left(\mathit{x}\right)$ is satisfied for $\mathit{x}\in T$ with orbit of size ℓ, then certainly $f(s^j\circ \mathit{x}):=s^j\left(f\left(\mathit{x}\right)\right)$ can (and must to ensure $f\in {\left\{s\right\}}^{*}$) be defined for $1\le j<\ell$ as the tuples ${\left(s^j\circ \mathit{x}\right)}_{0\le j<\ell }$ are pairwise distinct by the choice of ℓ as the size of the orbit of $\mathit{x}$. For T is a transversal of the orbits on $A^n$, this completely defines a function $f\in {\mathcal{O}}_A^{\left(n\right)}$; the second part of the proof above shows that such f actually commutes with s due to the divisor condition. □

From Lemma 15 it follows again for every n-ary $f\in {\left\{s\right\}}^{*}$ that if $s\circ \mathit{x}=\mathit{x}$, that is, $\mathit{x}\in {(fix\left(s\right))}^n$, then $f\left(\mathit{x}\right)$ must belong to an orbit of size 1. Hence, $f\left(\mathit{x}\right)\in fix\left(s\right)$ and $f\in {Pol}_A\left\{fix\left(s\right)\right\}$. So we obtain once more one of the necessary conditions for functions in the centraliser that were given in Lemma 1.

We can easily adapt an argument of Harnau’s [10] (Lemma 2.9, p. 345), given for centraliser clones of unary operations, to centralising monoids. This shows that on a four-element set no three-cycle can witness a maximal centralising monoid (nor a maximal centraliser clone, by Harnau’s result).

Lemma 16.

Let A be a set with $2\le \left|A\right|<{\aleph }_0$, and $s\in SymA$ be a permutation such that ${\left\{s\right\}}^{*\left(1\right)}$ is a maximal centralising monoid, then the number of fixed points of s is not 1.

Proof. 

Assume for a contradiction that $s\in SymA$ witnesses a maximal centralising monoid and has $a\in A$ as its unique fixed point. Since ${\left\{s\right\}}^{*\left(1\right)}$ is maximal, we have $s^p={id}_A\ne s$ for some prime p. Applying the above Lemmas 1 and 5 we then conclude that ${\left\{s\right\}}^{*}\subseteq {Pol}_A\left\{\left\{a\right\}\right\}={\left\{c_a^{\left(1\right)}\right\}}^{*}$, so ${\left\{s\right\}}^{*\left(1\right)}\subseteq {\left\{c_a^{\left(1\right)}\right\}}^{*\left(1\right)}⊊{\mathcal{O}}_A^{\left(1\right)}$ due to $\left|A\right|\ge 2$. As $s\ne {id}_A$, its cycle representation has at least one p-cycle $(a_1,\dots ,a_p)$, and $a\notin \left\{a_1,\dots ,a_p\right\}$ because it is fixed by s. We define $f\in {Pol}_A^{\left(1\right)}\left\{\left\{a\right\}\right\}={\left\{c_a^{\left(1\right)}\right\}}^{*\left(1\right)}$ by $f\left(a_1\right):=a_1$ and $f\left(x\right):=a$ for all $x\in A\setminus \left\{a_1\right\}$. If f were to commute with s, then Lemma 15 (or the definition) would imply that $a=f\left(a_2\right)=f\left(s\left(a_1\right)\right)=s\left(f\left(a_1\right)\right)=s\left(a_1\right)=a_2$ contradicting $a\notin \left\{a_1,\dots ,a_p\right\}$. Hence, $f\in {\left\{c_a^{\left(1\right)}\right\}}^{*\left(1\right)}\setminus {\left\{s\right\}}^{*}$, so ${\left\{s\right\}}^{*\left(1\right)}⊊{\left\{c_a^{\left(1\right)}\right\}}^{*\left(1\right)}⊊{\mathcal{O}}_A^{\left(1\right)}$ and ${\left\{s\right\}}^{*\left(1\right)}$ cannot be a maximal centralising monoid (not even maximal among just those witnessed by unary operations). □

The following lemma describes (for the case when ℓ is a prime) the centralising monoids witnessed by permutations of prime order.

Lemma 17.

Let $s\in SymA$ be a permutation on a finite set A that is a product of $t\ge 0$ disjoint cycles of length $\ell \ge 2$ and has $\left|A\right|-t·\ell$ fixed points. That is, s is of the form $s={\prod }_{0\le i<t}(a_0^i,\dots ,a_{\ell -1}^i)$ where $a_j^i\ne a_{j^{\prime }}^{i^{\prime }}$ for distinct $(i,j)\ne (i^{\prime },j^{\prime })$, $0\le i,i^{\prime }<t$, $0\le j,j^{\prime }<\ell$, and $fix\left(s\right)=A\setminus \left\{\left.a_j^i\phantom{0\le i<t\wedge 0\le j<\ell }\right|0\le i<t\wedge 0\le j<\ell \right\}$. Then $f\in {\left\{s\right\}}^{*\left(1\right)}$ holds if and only if both of the following conditions are satisfied:

(a)

$f\in {Pol}_A^{\left(1\right)}\left\{fix\left(s\right)\right\}$, and

(b)

for all $0\le i<t$ the value $f\left(a_0^i\right)\in A$ is arbitrary, but $f\left(a_j^i\right)=s^j\left(f\left(a_0^i\right)\right)$ for all $1\le j<\ell$.

Proof. 

We simplify the condition given in Lemma 15. A transversal of the orbits of the cyclic permutation group generated by s is given by $T=\left\{\left.a_0^i\phantom{0\le i<t}\right|0\le i<t\right\}\cup fix\left(s\right)$. The condition in Lemma 15 expressed for those $x\in T$ that are fixed by s is exactly equivalent to $f\in {Pol}_A\left\{fix\left(s\right)\right\}$ since the only positive divisor of 1 is 1. For all $x\in T\setminus fix\left(s\right)$, i.e., $x=a_0^i$ for some $0\le i<t$, the length of the orbit generated by x is ℓ, so the divisibility condition in Lemma 15 is fulfilled for any choice of the value $f\left(x\right)=f\left(a_0^i\right)\in A$ as the only orbit sizes are 1 or ℓ. The remaining part of the condition translates to the equality of $f\left(a_j^i\right)=f\left(s^j\left(a_0^i\right)\right)=f\left(s^j\left(x\right)\right)$ and $s^j\left(f\left(x\right)\right)=s^j\left(f\left(a_0^i\right)\right)$ for all $1\le j<\ell$. □

When $\left|A\right|\ge 2$ and $t\ge 1$, that is, $s\ne {id}_A$, it is easy to see that ${\left\{s\right\}}^{*\left(1\right)}⊊{\mathcal{O}}_A^{\left(1\right)}$, because we can define $f\in {\mathcal{O}}_A^{\left(1\right)}\setminus {\left\{s\right\}}^{*\left(1\right)}$ with $f\left(a_1^0\right)\ne s\left(f\left(a_0^0\right)\right)$, thereby violating condition (b) of Lemma 17. The following corollary is also evident.

Corollary 18.

Let $A\supseteq \left\{0,1\right\}$ be a finite set and $s:=(0,1)$ be a transposition. Then ${\left\{s\right\}}^{*\left(1\right)}$ equals

$$\left\{\left.f\in {Pol}_A^{\left(1\right)}\left\{A\setminus \left\{0,1\right\}\right\}\phantom{f\circ (0,1)\in \left\{(0,1),(1,0)\right\}\cup \left\{\left.(a,a)\phantom{a\in A\setminus \left\{0,1\right\}}\right|a\in A\setminus \left\{0,1\right\}\right\}}\right|f\circ (0,1)\in \left\{(0,1),(1,0)\right\}\cup \left\{\left.(a,a)\phantom{a\in A\setminus \left\{0,1\right\}}\right|a\in A\setminus \left\{0,1\right\}\right\}\right\};$$

moreover, for $A=\left\{0,1,2,3\right\}$ we have

$${\left\{(0,1)\right\}}^{*\left(1\right)}=\left\{\left.f\in {Pol}_A^{\left(1\right)}\left\{\left\{2,3\right\}\right\}\phantom{f\circ (0,1)\in \left\{(0,1),(1,0)\right\}\cup \left\{\left.(a,a)\phantom{a\in \left\{2,3\right\}}\right|a\in \left\{2,3\right\}\right\}}\right|f\circ (0,1)\in \left\{(0,1),(1,0)\right\}\cup \left\{\left.(a,a)\phantom{a\in \left\{2,3\right\}}\right|a\in \left\{2,3\right\}\right\}\right\}.$$

Next we prove that the centraliser of any proper supermonoid of a centralising monoid witnessed by a fixed-point free product of disjoint transpositions or a single transposition with at least two fixed points is idempotent. Hence, by Lemma 7, the centralising monoid of such a transposition is maximal in the lattice of all centralising monoids witnessed by unary operations (the intent lattice of ${\mathbb{K}}_1$).

Lemma 19.

For a permutation $s\in SymA$ on A with $4\le \left|A\right|<{\aleph }_0$ of order two that can be written as a fixed-point free product $s=(a_1,a_2)(a_3,a_4)\cdots (a_{k-1},a_k)$ of disjoint transpositions where $A=\left\{a_1,\dots ,a_k\right\}$ and any transformation monoid $M⊋{\left\{s\right\}}^{*\left(1\right)}$, the centraliser clone $M^{*}$ contains only idempotent operations, i.e., $M^{*\left(1\right)}=\left\{{id}_A\right\}$. Hence, if $M=M^{*\left(1\right)*\left(1\right)}$, then $M={\mathcal{O}}_A^{\left(1\right)}$.

Proof. 

We use Corollary 14 to show that $M^{*\left(1\right)}=\left\{{id}_A\right\}$ for every monoid $M⊋{\left\{s\right\}}^{*\left(1\right)}$. Note that s has only two-cycles, so $fix\left(s\right)=\varnothing$ and ${\left\{s\right\}}^{*\left(1\right)}$ is fully described by condition (b) of Lemma 17. Transversals of the orbits are given by picking exactly one element from each cycle, and any assignment of values to (some of) the elements of the transversal can be completed to a function $g\in {\left\{s\right\}}^{*\left(1\right)}\subseteq M$, cf. Lemmas 17 and 15.

In particular, for every $a\in A$ we can pick $b\in A\setminus \left\{a\right\}$ and the partial definition $g\left(a\right):=b\ne a$ can be extended to some $g\in {\left\{s\right\}}^{*\left(1\right)}\subseteq M$ with $a\notin fix\left(g\right)$. Hence, the initial assumption of Corollary 14 is satisfied. To show condition (B”), take distinct $x,y,z\in A$ and extend the partial definition $g\left(x\right):=y\ne z$ to some $g\in {\left\{s\right\}}^{*\left(1\right)}\subseteq M$. For condition (D”) consider distinct $x,y,z,u\in A$ and some $h\in M\setminus {\left\{s\right\}}^{*}$. Since h does not commute with s there is $a\in A$ such that for $b:=s\left(a\right)$, $p:=h\left(a\right)$ and $q:=h\left(b\right)$ the inequality $q=h\left(b\right)=h\left(s\right(a\left)\right)\ne s\left(h\right(a\left)\right)=s\left(p\right)$ holds. We can define some $g\in {\left\{s\right\}}^{*\left(1\right)}$ with $g\left(p\right)=g\left(q\right)=y$. Namely, if $p=q$, this is clear, and if $q\ne p$, then $q\notin \left\{p,s\left(p\right)\right\}$ and thus belongs to a different orbit than p, wherefore the assignment of y on a transversal containing $\left\{p,q\right\}$ can be extended to some $g\in {\left\{s\right\}}^{*\left(1\right)}$. Moreover, we define $\tilde{g}\left(x\right):=a$ and $\tilde{g}\left(z\right):=b$. If $z=s\left(x\right)$, then this assignment is compatible with condition (b) of Lemma 17 because $\tilde{g}\left(s\left(x\right)\right)=\tilde{g}\left(z\right)=b=s\left(a\right)=s\left(\tilde{g}\left(x\right)\right)$, so it can be extended to some $\tilde{g}\in {\left\{s\right\}}^{*\left(1\right)}$. If $z\ne s\left(x\right)$, then $z\notin \left\{x,s\left(x\right)\right\}$ and thus belongs to a distinct orbit than x, wherefore the given assignment on a transversal including $\left\{x,z\right\}$ can be extended to some $\tilde{g}\in {\left\{s\right\}}^{*\left(1\right)}$. As a consequence, we have $g\circ h\circ \tilde{g}\in M$, and it satisfies $g\left(h\left(\tilde{g}\left(x\right)\right)\right)=g\left(h\left(a\right)\right)=g\left(p\right)=y$ and $g\left(h\left(\tilde{g}\left(z\right)\right)\right)=g\left(h\left(b\right)\right)=g\left(q\right)=y\ne u$. Invoking Corollary 14, $M^{*\left(1\right)}=\left\{{id}_A\right\}$, and by Lemma 7, $M^{*}$ has only idempotent operations. □

Lemma 20.

For any finite set $A\supseteq \left\{0,1,2,3\right\}$, a transposition $f=(0,1)$ and a transformation monoid $M⊋{\left\{f\right\}}^{*\left(1\right)}$, the centraliser clone $M^{*}$ consists only of idempotent operations, i.e., $M^{*}\subseteq {Pol}_A\left\{\left.\left\{a\right\}\phantom{a\in A}\right|a\in A\right\}$. Hence, $M^{*\left(1\right)}=\left\{{id}_A\right\}$, and if $M=M^{*\left(1\right)*\left(1\right)}$, then $M={\mathcal{O}}_A^{\left(1\right)}$.

Proof. 

We have to show that all functions in $M^{*}$ preserve all singletons of A. For every $a\in fix\left(f\right)$ we have $c_a^{\left(1\right)}\in {\left\{f\right\}}^{*\left(1\right)}\subseteq M$ by Lemma 5, so $M^{*}\subseteq {\left\{\left.c_a^{\left(1\right)}\phantom{a\in fix\left(f\right)}\right|a\in fix\left(f\right)\right\}}^{*}$. Thus, again by Lemma 5, we get $M\subseteq {Pol}_A\left\{\left.\left\{a\right\}\phantom{a\in fix\left(f\right)}\right|a\in fix\left(f\right)\right\}$. It only remains to show that $M^{*}\subseteq {Pol}_A\left\{\left\{0\right\},\left\{1\right\}\right\}$, and for this task we shall exploit that there is some $h\in M\setminus {\left\{f\right\}}^{*\left(1\right)}$.

Subsequently we distinguish cases how h might look like according to Corollary 18. The first case is that $h\notin {Pol}_A\left\{fix\left(f\right)\right\}$, i.e., there is some $t\notin \left\{0,1\right\}$ such that $h\left(t\right)\in \left\{0,1\right\}$. By the above, $\left\{f,c_t^{\left(1\right)}\right\}\subseteq {\left\{f\right\}}^{*\left(1\right)}\subseteq M$, and then $\left\{h\circ c_t^{\left(1\right)},f\circ h\circ c_t^{\left(1\right)}\right\}=\left\{c_0^{\left(1\right)},c_1^{\left(1\right)}\right\}\subseteq M$. Again by Lemma 5 we infer $M^{*}\subseteq {\left\{c_0^{\left(1\right)},c_1^{\left(1\right)}\right\}}^{*}={Pol}_A\left\{\left\{0\right\},\left\{1\right\}\right\}$. From now on assume that $h\in {Pol}_A\left\{A\setminus \left\{0,1\right\}\right\}$. The second case is that one of $h\left(0\right),h\left(1\right)$ belongs to $fix\left(f\right)$, but $h\left(0\right)\ne h\left(1\right)$. If $h\left(1\right)\in fix\left(f\right)$, then we can use $h\circ f\in M$ instead, where $h\left(f\right(0\left)\right)=h\left(1\right)$ is in $fix\left(f\right)$ and still $h\left(f\right(0\left)\right)=h\left(1\right)\ne h\left(0\right)=h\left(f\right(1\left)\right)$. Therefore, no generality is lost in assuming that $h\left(1\right)\ne h\left(0\right)=:a\in fix\left(f\right)$.

As a subcase we assume that $h\left(b\right)=h\left(0\right)=a$ for all $b\in fix\left(f\right)$. By Lemma 17 there is $g\in {\left\{f\right\}}^{*\left(1\right)}$ with $g\left(h\right(0\left)\right)=g\left(a\right)=a$ and $g\left(x\right)=t$ for all $x\in A\setminus \left\{a\right\}$ where $t\in fix\left(f\right)\setminus \left\{a\right\}$. Such a t exists as $\left|A\right|\ge 4$; in particular $g\left(h\right(1\left)\right)=t$. Since $c_t^{\left(1\right)}\in M$, the singleton $\left\{t\right\}=im\left(c_t^{\left(1\right)}\right)$ is primitive positively definable from $M^{•}$ (see Lemma 1), therefore so is

$$\begin{array}{cc}\hfill {(g\circ h)}^{-1}\left[\left\{t\right\}\right]& =\left\{\left.x\in A\phantom{\exists y\in A:g\circ h\left(x\right)=y\wedge y\in \left\{t\right\}}\right|\exists y\in A:g\circ h\left(x\right)=y\wedge y\in \left\{t\right\}\right\}\hfill \\ \hfill & =\left\{\left.x\in A\phantom{\exists y,z\in A:g\circ h\left(x\right)=y\wedge c_t^{\left(1\right)}\left(z\right)=y}\right|\exists y,z\in A:g\circ h\left(x\right)=y\wedge c_t^{\left(1\right)}\left(z\right)=y\right\}=\left\{1\right\}.\hfill \end{array}$$

Likewise, we can define ${(g\circ h\circ f)}^{-1}\left[\left\{t\right\}\right]=\left\{0\right\}$ from $M^{•}$ due to $\left\{c_t^{\left(1\right)},f,g,h\right\}\subseteq M$. Consequently, every function in $M^{*}$ preserves $\left\{0\right\}$ and $\left\{1\right\}$.

The opposite subcase is that there is $b\in fix\left(f\right)$ with $h\left(b\right)\ne h\left(0\right)=a\in fix\left(f\right)$. The function $g_1\in {\mathcal{O}}_A^{\left(1\right)}$ defined via $g_1\left(x\right)=x$ for $x\in \left\{0,1\right\}$ and $g_1\left(x\right)=b$ for $x\in fix\left(f\right)$ belongs to ${\left\{f\right\}}^{*\left(1\right)}$ by Corollary 18. Take again $t\in fix\left(f\right)\setminus \left\{a\right\}$ and define $g_2\in {\mathcal{O}}_A^{\left(1\right)}$ by $g_2\left(a\right)=a$ and $g_2\left(x\right)=t$ for all $x\in A\setminus \left\{a\right\}$; by Lemma 17, $g_2\in {\left\{f\right\}}^{*\left(1\right)}$. As $h\left(1\right)$ and $h\left(b\right)$ are distinct from a, it follows that $g_2\circ h\circ g_1\left(0\right)=a$ and $g_2\circ h\circ g_1\left(x\right)=t$ for all $x\in A\setminus \left\{0\right\}$. Likewise $g_2\circ h\circ g_1\circ f\left(1\right)=a$ and $g_2\circ h\circ g_1\circ f\left(x\right)=t$ for all $x\in A\setminus \left\{1\right\}$. Therefore, ${(g_2\circ h\circ g_1)}^{-1}\left[\left\{a\right\}\right]=\left\{0\right\}$ and ${(g_2\circ h\circ g_1\circ f)}^{-1}\left[\left\{a\right\}\right]=\left\{1\right\}$, and as above these preimages are primitive positively definable from $M^{•}$ as $\left\{g_1,g_2,h,f,c_a^{\left(1\right)}\right\}\subseteq M$. Hence, $M^{*}\subseteq {Pol}_A\left\{\left\{0\right\},\left\{1\right\}\right\}$. This finishes the second case where $h\left(0\right)\ne h\left(1\right)$ and one of them is fixed by f.

The remaining case is when $h\in {Pol}_A\left\{fix\left(f\right)\right\}\setminus {\left\{f\right\}}^{*}$, but the second case does not take place, i.e., none of $h\left(0\right),h\left(1\right)$ is fixed by f. This implies $\left\{h\left(0\right),h\left(1\right)\right\}\subseteq \left\{0,1\right\}$ and, moreover $h\left(0\right)=h\left(1\right)$, because $h\notin {\left\{f\right\}}^{*}$, see Corollary 18. Let us assume that $h\left(0\right)=h\left(1\right)=0$, for otherwise, we might consider $f\circ h\in M$, which operates identically to h on $fix\left(f\right)$ and has swapped values compared to h on $\left\{0,1\right\}$. Certainly, $0\in fix\left(h\right)$. If it is the only fixed point, then $fix\left(h\right)=\left\{0\right\}$ and $fix(f\circ h)=\left\{1\right\}$. By Lemma 1 both of these sets are primitive positively definable from $M^{•}$ since $f,h\in M$. Therefore, $M^{*}\subseteq {Pol}_A\left\{\left\{0\right\},\left\{1\right\}\right\}$.

Now let us assume that there is $a\in A\setminus \left\{0,1\right\}=fix\left(f\right)$ such that $\left\{0,a\right\}\subseteq fix\left(h\right)$ and let $b\in fix\left(f\right)\setminus \left\{a\right\}$. By Lemma 17, the functions $g_a,g_b\in {\mathcal{O}}_A^{\left(1\right)}$, defined by $g_z\left(x\right)=x$ for $x\in \left\{0,1\right\}$ and $g_z\left(x\right)=z$ for $x\in fix\left(f\right)$ and both $z\in \left\{a,b\right\}$, belong to ${\left\{f\right\}}^{*\left(1\right)}\subseteq M$. We have $h\circ g_a\left(x\right)=0$ for $x\in \left\{0,1\right\}$ and $h\circ g_a\left(x\right)=h\left(a\right)=a$ for $x\in fix\left(f\right)$ since $a\in fix\left(h\right)$. Therefore $fix(h\circ g_a)=\left\{0,a\right\}$. Likewise, $g_b\circ h\circ g_a\left(x\right)=0$ for $x\in \left\{0,1\right\}$ and $g_b\circ h\circ g_a\left(x\right)=g_b\left(a\right)=b$ for $x\in fix\left(f\right)$ since $a\in fix\left(f\right)$. Thus, $fix(g_b\circ h\circ g_a)=\left\{0,b\right\}$. As $h\circ g_a,g_b\circ h\circ g_a\in M$, these sets of fixed points are primitive positively definable from $M^{•}$ (Lemma 1), and so is their intersection $\left\{0\right\}=\left\{0,b\right\}\cap \left\{0,a\right\}$, where we use that $b\ne a$ by the choice of b. Similarly, $fix(f\circ h\circ g_a)=\left\{1,a\right\}$ and $fix(f\circ g_b\circ h\circ g_a)=\left\{1,b\right\}$, and hence $\left\{1\right\}=\left\{1,a\right\}\cap \left\{1,b\right\}$ is primitive positively definable from $M^{•}$, as well. We conclude that $M^{*}\subseteq {Pol}_A\left\{\left\{0\right\},\left\{1\right\}\right\}$. □

Lemma 21.

For any finite set $A\supseteq \left\{0,1,2\right\}$ and the transposition $s=(0,1)$, let a binary operation $b\in {\mathcal{O}}_A^{\left(2\right)}$ be defined by $b(x,y):=s\left(y\right)$ if $x\in A\setminus \left\{0,1\right\}$, $b(x,y):=y$ if $y\in A\setminus \left\{0,1\right\}$ and $b(x,y):=x$ if $x,y\in \left\{0,1\right\}$. Then b is idempotent and ${\left\{b\right\}}^{*\left(1\right)}={\left\{s\right\}}^{*\left(1\right)}\dot{\cup }\left\{c_0^{\left(1\right)},c_1^{\left(1\right)}\right\}$.

Proof. 

We first note that b is well defined since $A\setminus \left\{0,1\right\}=fix\left(s\right)$ and thus for any $x,y\in fix\left(s\right)$ we have $s\left(y\right)=y=b(x,y)$. In particular, $b(y,y)=y$ for $y\in fix\left(s\right)$, and $b(y,y)=y$ for $y\in \left\{0,1\right\}$, too. Hence, $b(y,y)=y$ for all $y\in A$, so b is idempotent.

As b is idempotent, Corollary 6 yields that $b\in C_A^{\left(1\right)*}$, i.e., $C_A^{\left(1\right)}\subseteq {\left\{b\right\}}^{*\left(1\right)}$. So, first, we take any $f\in {\left\{s\right\}}^{*\left(1\right)}$ and prove that it commutes with b. For this we consider any $x,y\in A$ and want to show that $b\left(f\right(x),f(y\left)\right)=f\left(b\right(x,y\left)\right)$. This is clear from idempotence of b if $x=y$; thus, we distinguish three more cases re $x\ne y$. Assume first that $f\left(x\right)\in fix\left(s\right)$; hence $b\left(f\right(x),f(y\left)\right)=s\left(f\right(y\left)\right)=f\left(s\right(y\left)\right)$. Now if also $x\in fix\left(s\right)$, then $b(x,y)=s\left(y\right)$ and so $f\left(b\right(x,y\left)\right)=f\left(s\right(y\left)\right)=b\left(f\right(x),f(y\left)\right)$. Otherwise, $x\in \left\{0,1\right\}$ and we distinguish two subcases. If $y\in fix\left(s\right)$, then $b(x,y)=y$, wherefore we get $b\left(f\right(x),f(y\left)\right)=f\left(s\right(y\left)\right)=f\left(y\right)=f\left(b\right(x,y\left)\right)$. Alternatively, $x,y\in \left\{0,1\right\}$ and $b(x,y)=x$. Since $x\ne y$, we have $s\left(y\right)=x$, and so $b\left(f\right(x),f(y\left)\right)=f\left(s\right(y\left)\right)=f\left(x\right)=f\left(b\right(x,y\left)\right)$.

Our second case is that $f\left(y\right)\in fix\left(s\right)$, whence $b\left(f\right(x),f(y\left)\right)=f\left(y\right)$. Clearly, if also $y\in fix\left(s\right)$, then $f\left(b\right(x,y\left)\right)=f\left(y\right)=b\left(f\right(x),f(y\left)\right)$. Hence, suppose that $y\in \left\{0,1\right\}$. We get now that $b\left(f\right(x),f(y\left)\right)=f\left(y\right)=s\left(f\right(y\left)\right)=f\left(s\right(y\left)\right)$, using that $f\left(y\right)\in fix\left(s\right)$ and $f\in {\left\{s\right\}}^{*\left(1\right)}$. If $x\in fix\left(s\right)$, then $b(x,y)=s\left(y\right)$ and $b\left(f\right(x),f(y\left)\right)=f\left(s\right(y\left)\right)=f\left(b\right(x,y\left)\right)$. Finally, the subcase $x,y\in \left\{0,1\right\}$ with $x\ne y$ remains, which is treated as shown at the end of the previous paragraph.

The third and last case is that $f\left(x\right),f\left(y\right)\in A\setminus fix\left(s\right)=\left\{0,1\right\}$. Then $x,y$ must belong to $\left\{0,1\right\}$ as $f\in {\left\{s\right\}}^{*\left(1\right)}\subseteq {Pol}_A\left\{fix\left(s\right)\right\}$ by Lemma 17. From the definition of b we now infer $b(x,y)=x$ and also $b\left(f\right(x),f(y\left)\right)=f\left(x\right)=f\left(b\right(x,y\left)\right)$.

For the opposite inclusion we consider any $f\in {\left\{b\right\}}^{*\left(1\right)}$ that is not constant and have to show $f\in {\left\{s\right\}}^{*\left(1\right)}$. First we demonstrate that $f\in {Pol}_A^{\left(1\right)}\left\{fix\left(s\right)\right\}$. Taking any $y\in fix\left(s\right)$, we have $b(x,y)=y$. Since $f\notin C_A$, there is $x\in A$ such that $f\left(x\right)\ne f\left(y\right)$. Now the commutation condition with respect to b gives $b\left(f\right(x),f(y\left)\right)=f\left(b\right(x,y\left)\right)=f\left(y\right)$. Because $f\left(x\right)\ne f\left(y\right)$, this is not possible if $f\left(y\right)\in \left\{0,1\right\}$, i.e., we obtain $f\left(y\right)\in fix\left(s\right)$.

Knowing now that $f\in {Pol}_A\left\{fix\left(s\right)\right\}$ we consider any $y\in A$ and with it $2\in fix\left(s\right)$, whence also $f\left(2\right)\in fix\left(s\right)$. The definition of b implies $s\left(f\right(y\left)\right)=b\left(f\right(2),f(y\left)\right)$ and $b(2,y)=s\left(y\right)$, wherefore $s\left(f\right(y\left)\right)=b\left(f\right(2),f(y\left)\right)=f\left(b\right(2,y\left)\right)=f\left(s\right(y\left)\right)$ because we have $f\in {\left\{b\right\}}^{*}$. This shows that $f\in {\left\{s\right\}}^{*}$ as desired. Finally, if $f=c_a^{\left(1\right)}\in {\left\{b\right\}}^{*\left(1\right)}$ and $a\notin \left\{0,1\right\}$, then $a\in fix\left(s\right)$ and so Lemma 5 shows $s\in {\left\{c_a^{\left(1\right)}\right\}}^{*\left(1\right)}$, i.e., $c_a^{\left(1\right)}\perp s$. □

Corollary 22.

Assume $4\le \left|A\right|<{\aleph }_0$ and let $s\in SymA$ be a transposition or a product of disjoint transpositions without fixed points. Then ${\left\{s\right\}}^{*\left(1\right)}$ is a co-atom in the lattice of all centralising monoids on A witnessed by unary operations. However, the centralising monoid of a transposition is never a maximal centralising monoid, and the centralising monoid of a product of two disjoint transpositions fails to be maximal in the case where $\left|A\right|=4$.

Proof. 

Maximality in the lattice of centralising monoids witnessed by unary operations (that is with respect to the closure operator $X\mapsto X^{*\left(1\right)*\left(1\right)}$) follows from Lemmas 19 and 20. That transpositions do not yield co-atoms in the lattice of all centralising monoids is a consequence of Lemma 21. Finally, we consider a product s of two disjoint transpositions on $A=\left\{0,1,2,3\right\}$, which we can represent up to conjugacy as $s=\left(03\right)\left(12\right)$. If we represent unary operations u on $\left\{0,1,2,3\right\}$ as integer numbers ${\sum }_{j=0}^{3}u\left(j\right)4^{3-j}$, then we have ${\left\{s\right\}}^{*\left(1\right)}=\left\{15,27,39,51,78,90,102,114,141,153,165,177,204,216,228,240\right\}$. It can be seen from Table 4 in [27] that the centralising monoid witnessed by the majority operation $f_{20}$ (see Table 1 in [27]) contains all these unary operations and, for example, all unary constants. Therefore, we have ${\left\{s\right\}}^{*\left(1\right)}\cup C_{\left\{0,1,2,3\right\}}^{\left(1\right)}⊊{\left\{f_{20}\right\}}^{*\left(1\right)}⊊{\mathcal{O}}_A^{\left(1\right)}$, whence $s=\left(03\right)\left(12\right)$ does not witness a maximal centralising monoid on $\left\{0,1,2,3\right\}$. □

3.3. Monoids Witnessed by Retractive Operations

We now turn our attention from permutations of prime order to unary retractive operations $f\in {\mathcal{O}}_A^{\left(1\right)}$ (also called idempotent unary operations), that is, such $f:A⟶A$ where $f\circ f=f$. This property for $f\in {\mathcal{O}}_A^{\left(1\right)}$ is equivalent to ${f|}_{im\left(f\right)}={id}_A{|}_{im\left(f\right)}$, wherefore $fix\left(f\right)=im\left(f\right)$ for any retraction $f\in {\mathcal{O}}_A^{\left(1\right)}$. It follows that the only surjective retraction $f\in {\mathcal{O}}_A^{\left(1\right)}$ is the one fixing every point of A, so $f={id}_A$. In other words, if $f\in {\mathcal{O}}_A^{\left(1\right)}\setminus \left\{{id}_A\right\}$ is a non-identical retraction, then the set of fixed points (image) $fix\left(f\right)$ is a proper subset of A.

Lemma 23.

Let A be any set, $n\in {\mathbb{N}}_{+}$ and $f\in {\mathcal{O}}_A^{\left(1\right)}$ with $f\circ f=f$. For $h\in {\mathcal{O}}_A^{\left(n\right)}$ we have $h\perp f$ if and only if $h\in {Pol}_A\left\{fix\left(f\right)\right\}$ and for all $\mathit{x}\in A^n\setminus {(fix\left(f\right))}^n$ the condition $h\left(\mathit{x}\right)\in f^{-1}\left[\left\{h(f\circ \mathit{x})\right\}\right]$ is satisfied.

In particular, since for every $\mathit{x}\in A^n$ the tuple $f\circ \mathit{x}\in {(im\left(f\right))}^n={(fix\left(f\right))}^n$, for any choice of values $h\left(\mathit{x}\right)\in fix\left(f\right)$ for $\mathit{x}\in {(fix\left(f\right))}^n$ there are (generally not unique) extensions $h\in {\left\{f\right\}}^{*\left(n\right)}$.

Proof. 

For every individual $\mathit{x}\in A^n$ the commutation condition $f\left(h\right(\mathit{x}\left)\right)=h(f\circ \mathit{x})$ can equivalently be restated as $h\left(\mathit{x}\right)\in f^{-1}\left[\left\{h(f\circ \mathit{x})\right\}\right]$. For all $\mathit{x}\in A^n\setminus {(fix\left(f\right))}^n$ we use the reformulation, while for all $\mathit{x}\in {(fix\left(f\right))}^n$ we keep the original condition, which simplifies to $f\left(h\right(\mathit{x}\left)\right)=h\left(\mathit{x}\right)$ as $f\circ \mathit{x}=\mathit{x}$. However, this is just expressing that $h\left(\mathit{x}\right)\in fix\left(f\right)$ for every $\mathit{x}\in {(fix\left(f\right))}^n$, i.e., that $h\in {Pol}_A\left\{fix\left(f\right)\right\}$.

For the second part of the lemma, we observe that once values $h\left(\mathit{x}\right)\in fix\left(f\right)$ are selected for each tuple $\mathit{x}\in {(fix\left(f\right))}^n$, the condition $h\left(\mathit{x}\right)\in f^{-1}\left[\left\{h(f\circ \mathit{x})\right\}\right]$ determines the values on all remaining tuples since $f\circ \mathit{x}\in {(fix\left(f\right))}^n$. The choices of values of h in the preimages can be made independently of each other without leading to contradictions, i.e., all possible choices for h described above indeed produce a function $h\in {\left\{f\right\}}^{*}$. □

For any retraction $f\in {\mathcal{O}}_A^{\left(1\right)}$ and any element $x\in fix\left(f\right)=im\left(f\right)$, we can write $f^{-1}\left[\left\{x\right\}\right]=\left\{x\right\}\cup A_x$ where $A_x\subseteq A\setminus fix\left(f\right)$ is possibly empty. Every $A_x\ne \varnothing$ adds a requirement to the commutation condition, and (for unary operations) it is useful to rephrase Lemma 23 in terms of these sets.

Corollary 24.

For a retraction $f\in {\mathcal{O}}_A^{\left(1\right)}$ let $I:=\left\{\left.x\in fix\left(f\right)\phantom{A_x:=f^{-1}\left[\left\{x\right\}\right]\setminus \left\{x\right\}\ne \varnothing }\right|A_x:=f^{-1}\left[\left\{x\right\}\right]\setminus \left\{x\right\}\ne \varnothing \right\}$. Then

$${\left\{f\right\}}^{*\left(1\right)}=\left\{\left.h\in {Pol}_A^{\left(1\right)}\left\{fix\left(f\right)\right\}\phantom{\forall j\in I\forall a\in A_j:\begin{array}{cc}\hfill \left(h\right(j)=:i\in I& \wedge h\left(a\right)\in \left\{i\right\}\cup A_i)\vee \hfill \\ \hfill \left(h\right(j)\notin I& \wedge h\left(a\right)=h\left(j\right))\hfill \end{array}}\right|\forall j\in I\forall a\in A_j:\begin{array}{cc}\hfill \left(h\right(j)=:i\in I& \wedge h\left(a\right)\in \left\{i\right\}\cup A_i)\vee \hfill \\ \hfill \left(h\right(j)\notin I& \wedge h\left(a\right)=h\left(j\right))\hfill \end{array}\right\}.$$

Proof. 

We use Lemma 23 for $n=1$ and note that for $j\in I$ and $a\in A_j$ we have $f\left(a\right)=j$ and $h\left(f\right(a\left)\right)=h\left(j\right)=:i\in fix\left(f\right)$. So $f^{-1}\left[\left\{h\left(f\right(a\left)\right)\right\}\right]=f^{-1}\left[\left\{i\right\}\right]=\left\{i\right\}\cup A_i$, which equals just $\left\{i\right\}=\left\{h\left(j\right)\right\}$ whenever $i\in fix\left(f\right)\setminus I$. □

It is evident that we have ${\left\{f\right\}}^{*\left(1\right)}⊊{\mathcal{O}}_A^{\left(1\right)}$ for any retraction $f\in {\mathcal{O}}_A^{\left(1\right)}\setminus \left\{{id}_A\right\}$. Namely, since $f\ne {id}_A$, we have $fix\left(f\right)=im\left(f\right)⊊A$, and picking some $a\in A\setminus fix\left(f\right)$, we have $c_a^{\left(1\right)}\notin {Pol}_A^{\left(1\right)}\left\{fix\left(f\right)\right\}$, so $c_a^{\left(1\right)}\in {\mathcal{O}}_A^{\left(1\right)}\setminus {\left\{f\right\}}^{*\left(1\right)}$ by Corollary 24.

Lemma 25.

Let $f\in {\mathcal{O}}_A^{\left(1\right)}$ be a retraction, $I:=\left\{\left.x\in fix\left(f\right)\phantom{A_x:=f^{-1}\left[\left\{x\right\}\right]\setminus \left\{x\right\}\ne \varnothing }\right|A_x:=f^{-1}\left[\left\{x\right\}\right]\setminus \left\{x\right\}\ne \varnothing \right\}$. Assume that $M\subseteq {\mathcal{O}}_A^{\left(1\right)}$ is a transformation monoid with ${\left\{f\right\}}^{*\left(1\right)}⊊M$, then the centraliser $M^{*}$ is a clone of idempotent operations, i.e., $M^{*\left(1\right)}=\left\{{id}_A\right\}$. So, if $M=M^{*\left(1\right)*\left(1\right)}$, then $M={\mathcal{O}}_A^{\left(1\right)}$.

Proof. 

According to Lemma 7, we have to show that the functions in $M^{*}$ preserve all singletons of A. Thus, the goal is to show $\left\{t\right\}\in {\left[M^{•}\right]}_{{\mathcal{R}}_A}\subseteq {Inv}_A{Pol}_A{M}^{•}={Inv}_A{M}^{*}$ for all $t\in A$, that is, to primitive positively define the singletons $\left\{t\right\}$ from the graphs of the functions in M. If $t\in fix\left(f\right)$, then $c_t^{\left(1\right)}\in {\left\{f\right\}}^{*\left(1\right)}\subseteq M$ by Lemma 5, and therefore $M^{*}\subseteq {Pol}_A\left\{\left.\left\{t\right\}\phantom{t\in fix\left(f\right)}\right|t\in fix\left(f\right)\right\}$ by Lemma 1 as $im\left(c_t^{\left(1\right)}\right)=\left\{t\right\}$. Hence, it only remains to primitive positively define $\left\{t\right\}\in {\left[M^{•}\right]}_{{\mathcal{R}}_A}$ for all $t\in A\setminus fix\left(f\right)$, and, in fact, it is sufficient for this to define $\left\{a\right\}\in {\left[M^{•}\right]}_{{\mathcal{R}}_A}$ for some specific $a\in A\setminus fix\left(f\right)$. Namely, if $\left\{a\right\}\in {\left[M^{•}\right]}_{{\mathcal{R}}_A}$ and we have any other $t\in A\setminus (fix\left(f\right)\cup \left\{a\right\})$, then there is $h_{a,t}\in {\left\{f\right\}}^{*\left(1\right)}\subseteq M$ with $h_{a,t}\left(a\right)=t$, so $\left\{t\right\}=h_{a,t}\left[\left\{a\right\}\right]\in {\left[M^{•}\right]}_{{\mathcal{R}}_A}$. Let $j:=f\left(a\right)$ so $a\in A_j$. If $t\in A_j$, too, then we define $h_{a,t}\in {Pol}_A\left\{fix\left(f\right)\right\}$ by $h_{a,t}\left(a\right):=t$ and $h_{a,t}\left(x\right):=x$ for $x\in A\setminus \left\{a\right\}$. Then for all $i\in I$ and $x\in A_i$ we have $h_{a,t}\left(i\right)=i$ and the condition in Corollary 24 turns into $h_{a,t}\left(x\right)\in \left\{i\right\}\cup A_i$, which is satisfied for a as $a,t\in A_j$ and clearly holds for all other x. So $h_{a,t}\in {\left\{f\right\}}^{*\left(1\right)}$. If $t\in A_{\ell }$ with $\ell \in I\setminus \left\{j\right\}$, we put $h_{a,t}\left(j\right):=\ell$, $h_{a,t}\left(x\right):=t$ for $x\in A_j$ and $h_{a,t}\left(x\right):=x$ else. Clearly, $h_{a,t}\in {Pol}_A\left\{fix\left(f\right)\right\}$ as $h_{a,t}\left(j\right)=\ell \in fix\left(f\right)$ and $h_{a,t}\left(i\right)=i$ for all $i\in I\setminus \left\{j\right\}$. For such i and $x\in A_i$ we have $h_{a,t}\left(x\right)=x\in \left\{i\right\}\cup A_i$, and for j and $x\in A_j$ we have $h_{a,t}\left(x\right)=t\in \left\{\ell \right\}\cup A_{\ell }$, so Corollary 24 yields that $h_{a,t}\in {\left\{f\right\}}^{*\left(1\right)}$.

Now, to establish $\left\{a\right\}\in {\left[M^{•}\right]}_{{\mathcal{R}}_A}$ for at least one $a\in A\setminus fix\left(f\right)$, we shall exploit the existence of $h\in M\setminus {\left\{f\right\}}^{*\left(1\right)}$. According to Corollary 24 there may be two reasons why $h\notin {\left\{f\right\}}^{*\left(1\right)}$. The first case is that $h\notin {Pol}_A\left\{fix\left(f\right)\right\}$. This means there is $t\in fix\left(f\right)$ such that $a:=h\left(t\right)\in A\setminus fix\left(f\right)$. Then $h\circ c_t^{\left(1\right)}=c_a^{\left(1\right)}\in M$, and Lemma 1 shows $M^{*}\subseteq {Pol}_A\left\{a\right\}$, so $\left\{a\right\}=im\left(c_a^{\left(1\right)}\right)$ is primitive positively definable from $M^{•}$.

The second case why $h\notin {\left\{f\right\}}^{*\left(1\right)}$ is that $h\in {Pol}_A\left\{fix\left(f\right)\right\}$ but there is $j\in I$ and $a\in A_j$ with $h\left(a\right)\notin f^{-1}\left[\left\{h\left(j\right)\right\}\right]$. Referring to Corollary 24, we distinguish as subcases whether $\ell :=h\left(j\right)\in I$ or not. First suppose that $\ell \in I$, then $h\left(a\right)\notin f^{-1}\left[\left\{\ell \right\}\right]=\left\{\ell \right\}\cup A_{\ell }$, that is, $a\in h^{-1}\left[B\right]\not\ni j$ where $B:=A\setminus (A_{\ell }\cup \left\{\ell \right\})$. Hence, $a\in h^{-1}\left[B\right]\cap \left\{a,j\right\}$ being a subset of $A\setminus \left\{j\right\}\cap \left\{a,j\right\}=\left\{a\right\}$, i.e., $\left\{a\right\}=h^{-1}\left[B\right]\cap \left\{a,j\right\}$. We define $g\in {Pol}_A^{\left(1\right)}\left\{fix\left(f\right)\right\}$ by $g\left(a\right):=a$ and $g\left(x\right):=j$ for $x\in A\setminus \left\{a\right\}$. For all $i\in I$ and $x\in A_i$ we have $g\left(x\right)\in \left\{a,j\right\}\subseteq \left\{j\right\}\cup A_j$, which is in accordance with Corollary 24 since $g\left(i\right)=j$. Thus, $g\in {\left\{f\right\}}^{*\left(1\right)}\subseteq M$ and $im\left(g\right)=\left\{a,j\right\}$. To define a function $\tilde{g}\in {\left\{f\right\}}^{*\left(1\right)}$ with $im\left(\tilde{g}\right)=B$, we observe that there is $t\in fix\left(f\right)\setminus \left\{\ell \right\}$, for otherwise $f=c_{\ell }^{\left(1\right)}$, contradicting $h\left(a\right)\notin f^{-1}\left[\left\{h\left(j\right)\right\}\right]$. We let $\tilde{g}\left(x\right):=x$ for $x\in fix\left(f\right)\setminus \left\{\ell \right\}$ and $\tilde{g}(\ell ):=t\in fix\left(f\right)\setminus \left\{\ell \right\}$, then $\tilde{g}\in {Pol}_A^{\left(1\right)}\left\{fix\left(f\right)\right\}$. For $x\in A_{\ell }$ we define $\tilde{g}\left(x\right):=t\in \left\{t\right\}\cup A_t$, which agrees with Corollary 24 as $\tilde{g}(\ell )=t$. Finally, for $x\in A_i$ where $i\in I\setminus \left\{\ell \right\}$, we put $\tilde{g}\left(x\right):=x$, which also complies with Corollary 24. Hence, $\tilde{g}\in {\left\{f\right\}}^{*\left(1\right)}\subseteq M$ and $im\left(\tilde{g}\right)=B$. Therefore, we get $\left\{a\right\}=h^{-1}[im\left(\tilde{g}\right)]\cap im\left(g\right)\in {\left[M^{•}\right]}_{{\mathcal{R}}_A}$.

The remaining subcase of the second case is that $h\in {Pol}_A\left\{fix\left(f\right)\right\}$ and $\ell \in fix\left(f\right)\setminus I$. By the condition in Corollary 24, we have $h\left(a\right)\in A\setminus \left\{h\left(j\right)\right\}=A\setminus \left\{\ell \right\}$ for the violating element $a\in A_j$ with $j\in I$. Thus, we get $a\in h^{-1}[A\setminus \left\{\ell \right\}]\cap \left\{a,j\right\}\subseteq A\setminus \left\{j\right\}\cap \left\{a,j\right\}=\left\{a\right\}$, that is, $\left\{a\right\}=h^{-1}[A\setminus \left\{\ell \right\}]\cap \left\{a,j\right\}$. To define a unary operation $\widehat{g}\in {\left\{f\right\}}^{*\left(1\right)}$ having $im\left(\widehat{g}\right)=A\setminus \left\{\ell \right\}$, we note that $I\ne \varnothing$, as otherwise $fix\left(f\right)=A$, i.e., $f={id}_A$ and then ${\mathcal{O}}_A^{\left(1\right)}\supseteq M⊋{\left\{f\right\}}^{*\left(1\right)}$ would be violated. We pick some $i\in I$ and define $\widehat{g}(\ell ):=i$ and $\widehat{g}\left(x\right):=x$ for $x\in A\setminus \left\{\ell \right\}$. By Corollary 24 we have $\widehat{g}\in {\left\{f\right\}}^{*\left(1\right)}\subseteq M$ because $\ell \notin I$. Clearly, $im\left(\widehat{g}\right)=A\setminus \left\{\ell \right\}$, and so $\left\{a\right\}=h^{-1}[im\left(\widehat{g}\right)]\cap im\left(g\right)\in {\left[M^{•}\right]}_{{\mathcal{R}}_A}$ where we are re-using $g\in {\left\{f\right\}}^{*\left(1\right)}\subseteq M$ with $im\left(g\right)=\left\{a,j\right\}$ from above. □

Lemma 25 covers in particular such retractions for which the image contains all elements except for one. For these we can show that they never witness maximal centralising monoids.

Lemma 26.

Let $a\in A$ and $f\in {\mathcal{O}}_A^{\left(1\right)}$ be a retraction with $fix\left(f\right)=A\setminus \left\{a\right\}$. Moreover, let $g\in {\mathcal{O}}_A^{\left(2\right)}$ be given by $g(x,y):=f\left(x\right)$ if $(x,y)\ne (a,a)$ and $g(a,a):=a$. Then g is a binary idempotent operation and ${\left\{g\right\}}^{*\left(1\right)}={\left\{f\right\}}^{*\left(1\right)}\dot{\cup }\left\{c_a^{\left(1\right)}\right\}$.

Proof. 

Clearly, for every $x\in A\setminus \left\{a\right\}$ we have $g(x,x)=f\left(x\right)=x$; moreover, $g(a,a)=a$, so $g\in C_A^{\left(1\right)*}$ is idempotent (Corollary 7) and so $C_A^{\left(1\right)}\subseteq {\left\{g\right\}}^{*\left(1\right)}$. Consider now any $h\in {\left\{f\right\}}^{*\left(1\right)}$; we have to show that $h\in {\left\{g\right\}}^{*}$. For this take $(x,y)\in A^2$. First we assume that $(x,y)\ne (a,a)$. There is $t\in \left\{x,y\right\}$ with $t\in A\setminus \left\{a\right\}=fix\left(f\right)$. Since by Corollary 24 $h\in {\left\{f\right\}}^{*\left(1\right)}\subseteq {Pol}_A\left\{fix\left(f\right)\right\}$, we have $h\left(t\right)\in fix\left(f\right)$, i.e., $h\left(t\right)\ne a$, so $\left(h\right(x),h(y\left)\right)\ne (a,a)$. Now the definition of g implies $g\left(h\right(x),h(y\left)\right)=f\left(h\right(x\left)\right)=h\left(f\right(x\left)\right)=h\left(g\right(x,y\left)\right)$. The remaining possibility is that $(x,y)=(a,a)$, and here $h\left(g\right(a,a\left)\right)=h\left(a\right)=g\left(h\right(a),h(a\left)\right)$, for g is idempotent. Therefore, $h\in {\left\{g\right\}}^{*}$.

Conversely, let $h\in {\left\{g\right\}}^{*\left(1\right)}$. If $h=c_t^{\left(1\right)}$ for some $t\ne a$, then $h\in {\left\{f\right\}}^{*}$ because t belongs to $A\setminus \left\{a\right\}=fix\left(f\right)$, cf. Lemma 5. Now consider $h\in {\left\{g\right\}}^{*\left(1\right)}\setminus C_A$ and any $x\in A$. As h is not constant, there is $y\in A$ such that $h\left(y\right)\ne h\left(x\right)$. It certainly follows that $\{(x,y),(h\left(x\right),h\left(y\right))\}\subseteq A^2\setminus \left\{(a,a)\right\}$, so $h\left(f\right(x\left)\right)=h\left(g\right(x,y\left)\right)=g\left(h\right(x),h(y\left)\right)=f\left(h\right(x\left)\right)$. We conclude that $h\in {\left\{f\right\}}^{*\left(1\right)}$. □

Corollary 27.

Let $f\in {\mathcal{O}}_A^{\left(1\right)}\setminus \left\{{id}_A\right\}$ be any non-identical retraction, then ${\left\{f\right\}}^{*\left(1\right)}$ is maximal in the lattice of all centralising monoids on A witnessed by unary operations. In particular this holds for retractions $f\in {\mathcal{O}}_A^{\left(1\right)}$ with $fix\left(f\right)=A\setminus \left\{a\right\}$ for some $a\in A$; however, these do not witness a maximal centralising monoid.

Proof. 

Maximality with respect to the closure system of the operator $X\mapsto X^{*\left(1\right)*\left(1\right)}$ follows from Lemma 25; for functions with a single non-fixed point non-maximality in general is evident from Lemma 26. □

Lemma 25 and Corollary 27 deal with all non-identical retractions on any set and successfully explain our computational results regarding those centralising monoids on $A=\left\{0,1,2,3\right\}$ that can be witnessed by just unary operations. For retractions fixing all but one element, we have that the centralising monoid is never maximal; for constant retractions it is known that the centralising monoid is always maximal, see Corollary 29 below. For the other types of centralising monoids witnessed by non-constant retractions, we currently do not know more than what is stated in Corollary 27. On a four-element set there are two types of such retractions, both having a two-element image. Our computations from [27] and Section 4 show that the corresponding monoids are not contained in any proper centralising monoid witnessed by a unary or (idempotent) binary or majority operation on $A=\left\{0,1,2,3\right\}$, but at the moment we cannot exclude that there might be a monoid witnessed by a semiprojection, which is properly larger.

We conclude the discussion of monoids witnessed by retractions by giving a short and new proof of the fact that on sets with at least three elements every centralising monoid witnessed by a constant is actually maximal. This has been shown before in [21] (Theorem 5.1, p. 157).

Lemma 28.

Let A be a set with $\left\{0,1,2\right\}\subseteq A$ and $M\subseteq {\mathcal{O}}_A$ be a set of operations satisfying $M⊋{\left\{c_0^{\left(1\right)}\right\}}^{*\left(1\right)}=T_0^{\left(1\right)}={Pol}_A^{\left(1\right)}\left\{\left\{0\right\}\right\}$, then $M^{*}={\mathcal{J}}_A$.

Proof. 

By Lemma 5, ${\left\{c_0^{\left(1\right)}\right\}}^{*\left(1\right)}={Pol}_A^{\left(1\right)}\left\{\left\{0\right\}\right\}=T_0^{\left(1\right)}=\left\{\left.f\in {\mathcal{O}}_A^{\left(1\right)}\phantom{0\in fix\left(f\right)}\right|0\in fix\left(f\right)\right\}$, and since there is $s\in M\setminus T_0^{\left(1\right)}$, there is $s\in M$ with $0\notin fix\left(s\right)$. Moreover, $c_0^{\left(1\right)}\in T_0^{\left(1\right)}\subseteq M$, and $a\notin fix\left(c_0^{\left(1\right)}\right)$ for any $a\in A\setminus \left\{0\right\}$. Hence, the initial precondition of Corollary 13 has been established. We shall use the operations from $T_0^{\left(1\right)}\subseteq M$ to obtain conditions (B’) and (D’). For this let $x,y,z,u\in A$ be pairwise distinct. If $z=0$, then $s_0\in T_0^{\left(1\right)}$ defined by $s_0\left(0\right):=0$ and $s_0\left(a\right):=1$ for $a\in A\setminus \left\{0\right\}$ shows (B’); if $z\ne 0$, then $s_1\in T_0^{\left(1\right)}$ defined by $s_1\left(x\right)=s_1\left(y\right)=s_1\left(0\right):=0$ and $s_1\left(a\right):=1$ for $a\in A\setminus \left\{0,x,y\right\}$ shows (B’). Similarly, if $u=0$, then $s_0\in T_0^{\left(1\right)}$ establishes (D’), and if $u\ne 0$, then $s_3\in T_0^{\left(1\right)}$ given as $s_3\left(u\right):=1$ and $s_3\left(a\right):=0$ for $a\in A\setminus \left\{u\right\}$ shows (D’). Now Corollary 13 entails $M^{*}={\mathcal{J}}_A$. □

Corollary 29

([21] (Theorem 5.1, p. 157)). For any set A with $\left|A\right|\ge 3$ and $a\in A$, the monoid $T_a^{\left(1\right)}={\left\{c_a^{\left(1\right)}\right\}}^{*\left(1\right)}$ is a maximal centralising monoid.

Proof. 

If $M\subseteq {\mathcal{O}}_A^{\left(1\right)}$ is a centralising monoid with $M⊋T_a^{\left(1\right)}$, then we have $M^{*}={\mathcal{J}}_A$ from Lemma 28, and so $M=M^{**\left(1\right)}={\mathcal{O}}_A^{\left(1\right)}$ by a combination of Lemmas 2 and 9. □

3.4. Results

We summarise the results of the current section in the following theorem.

Theorem 30.

Let A be a finite set and $f\in {\mathcal{O}}_A^{\left(1\right)}\setminus \left\{{id}_A\right\}$ be a unary minimal function from Theorem 4. If

• $\left|A\right|\ge 4$ and $f\in SymA$ is a transposition of just two elements,
• $\left|A\right|\ge 4$ is even and $f\in SymA$ is a product of disjoint transpositions without fixed points,
• $f=f\circ f$ is any (non-identical) retraction,

then ${\left\{f\right\}}^{*\left(1\right)}⊊{\mathcal{O}}_A^{\left(1\right)}$ is a centralising monoid that is maximal among those monoids on A witnessed by unary operations. If $\left|A\right|\ge 3$ and f is constant, then ${\left\{f\right\}}^{*\left(1\right)}$ is always a maximal centralising monoid. Moreover, if

• $\left|A\right|\ge 4$ and $f\in SymA$ is a transposition of just two elements,
• $\left|A\right|\ge 2$ and $f\in SymA$ has a single fixed point,
• $\left|A\right|=4$ and $f\in SymA$ is a product of two disjoint transpositions (without fixed points),
• f is a retraction with $im\left(f\right)=A\setminus \left\{a\right\}$ for some $a\in A$,

then ${\left\{f\right\}}^{*\left(1\right)}$ is not a co-atom (maximal) in the lattice of all centralising monoids on A.

Proof. 

The positive statements follow from Corollaries 22, 27 and 29; the negative statements from Lemma 16 and again Corollaries 22 and 27. □

Corollary 31.

On a four-element set no maximal centralising monoid is witnessed by a permutation nor a retraction with a three-element image; however all constants witness maximal centralising monoids. Moreover, every permutation of order 2 and every non-identical retraction witnesses a centralising monoid forming a co-atom in the lattice of all centralising monoids witnessed by unary operations.

4. Monoids Witnessed by Binary Idempotent Operations

Each binary idempotent operation $g\in C_A^{*\left(2\right)}$ satisfies $g(x,x)=x$ for all $x\in A$. Therefore, on $A=\left\{0,1,2,3\right\}$ there are $4^{4^2-4}=4^{12}=16,777,216$ binary idempotent operations, which are candidates for binary minimal functions. In a very similar way as shown in Listing 1 we used a (slightly more complicated) c++ implementation to brute force enumerate all these binary operations g, and for each of them produced a characteristic vector in ${\left\{0,1\right\}}^{256}$ of ${\left\{g\right\}}^{*\left(1\right)}$. Whenever we found some $\tilde{g}\in C_A^{*\left(2\right)}$ with ${\left\{\tilde{g}\right\}}^{*\left(1\right)}={\left\{g\right\}}^{*\left(1\right)}$ for a previously enumerated g, we did not store ${\left\{\tilde{g}\right\}}^{*\left(1\right)}$, that is, we dropped duplicate rows from the context ${\mathbb{K}}_2:=\left(C_A^{*\left(2\right)},{\mathcal{O}}_A^{\left(1\right)},\perp \right)$. We also removed the binary projections that describe the full transformation monoid ${\mathcal{O}}_A^{\left(1\right)}$. The result is a subcontext ${\mathbb{K}}_2^{\prime }=\left(G,{\mathcal{O}}_A^{\left(1\right)},\perp \right)$ with a $10,263$-element subset $G\subseteq C_A^{*\left(2\right)}$ of binary idempotent non-projections that has the same closure system of monoids (intents) as ${\mathbb{K}}_2$.

Using again algorithms from [35,36], we calculated that there are $17,013$ centralising monoids on a four-element set that can be witnessed by some set of binary idempotent operations (and clearly $10,263$ of them can be witnessed by just a single such operation). These numbers are of interest as they give the highest currently available lower bounds for the cardinality of the lattice ${\mathcal{C}}_A$ of centraliser clones on $A=\left\{0,1,2,3\right\}$, which is totally unexplored at the moment. We see a steep increase of these cardinalities as the size of A grows:

$$\begin{array}{cccc}\left|A\right|:\hfill & 2& 3& 4\\ \left|{\mathcal{C}}_A\right|:\hfill & {25}^{\left[8\right] (\mathrm{p.} 155), \left[3\right] (\mathrm{Figures} 5 \mathrm{and} 6, \mathrm{pp.} 3158, 3162)}& {2986}^{\left[8\right] (\mathrm{p.} 155), \left[9\right] (\mathrm{p.} 125 \mathrm{et} \mathrm{seqq.})}& \ge 17,013\end{array}$$

Removing duplicate rows from ${\mathbb{K}}_2$ is just one way of simplifying a formal context, known as object clarification in the terminology of [35]. Another idea is to omit a row described by $g\in C_A^{*\left(2\right)}$ if there is $H\subseteq G\setminus \left\{g\right\}$ such that ${\left\{g\right\}}^{*\left(1\right)}={\bigcap }_{h\in H}{\left\{h\right\}}^{*\left(1\right)}=H^{*\left(1\right)}$, i.e., if the row can be obtained as an intersection of other rows. This operation is known as object or row reduction, see [35] (p. 24), and leaves only functions $g\in G$ where the monoid ${\left\{g\right\}}^{*\left(1\right)}$ is ⋂-irreducible in the lattice of centralising monoids belonging to ${\mathbb{K}}_2$. One can object reduce ${\mathbb{K}}_2^{\prime }$ to a context ${\mathbb{K}}_2^{†}=\left(\tilde{G},{\mathcal{O}}_A^{\left(1\right)},\perp \right)$ where $\left|\tilde{G}\right|=1236$ and ${\mathbb{K}}_2^{†}$ has the same closure system of monoids as ${\mathbb{K}}_2^{\prime }$ and ${\mathbb{K}}_2$. That is, only 1236 out of all $4^{12}$ binary idempotent operations, those in $\tilde{G}$, suffice to witness all $17,013$ centralising monoids that can be witnessed by any selection of binary idempotent operations on $\left\{0,1,2,3\right\}$. We have listed these in the Appendix B; it is a simple task to reproduce ${\mathbb{K}}_2^{†}$ from them.

In the same way as explained in Section 3.1 one can iterate over the rows of ${\mathbb{K}}_2^{\prime }$ (or ${\mathbb{K}}_2^{†}$) to find the proper centralising monoids in the closure system that are maximal under set inclusion. We found that there are 612 centralising monoids that are inclusion maximal among those witnessed by binary idempotent operations, and their single witnesses are those operations in Appendix B that are marked by ↑. Again, these 612 monoids are not necessarily maximal centralising monoids, just candidates, they still need to be compared to the candidates witnessed by other types of minimal functions (unary, Mal’cev, majority—see Tables 4 and 5 in [27], and semiprojections). As the case of semiprojections has not been computed yet, we defer any comparisons of the different candidates for maximal centralising monoids to a point when all the data will be available. Let us summarise the main results of this section:

Theorem 32.

On $A=\left\{0,1,2,3\right\}$ there are exactly $17,013$ centralising monoids that can be witnessed by sets of binary idempotent operations; 612 of these are co-atoms under inclusion. All these monoids are witnessed by subsets of the 1236-element subset $\tilde{G}\subseteq C_A^{*\left(2\right)}$ (see Appendix B, the 612 co-atoms are marked there by ↑ and correspond to the functions with indices 1, 4, 6, 10, 12, 19, 20, 21, 31, 33, 35, 36, 39, 44, 49, 50, 68, 69, 70, 71, 97, 135, 151, 153, 156, 159, 166, 168, 169, 347, 348, 351, 372, 377, 396, 412, 442, 454, 563, 618, 627, 657, 658, 659, 697, 762, 771, 774, 779, 780, 933, 934, 979, 981, 982, 983, 984, 986, 997, 1002, 1003, 1011, 1013, 1018, 1020, 1022, 1026, 1028, 1029, 1033, 1038, 1042, 1049, 1137, 1180, 1181, 1187 and their conjugates (cf. below and Appendix C) 11, 15, 16, 17, 22, 25, 26, 30, 42, 43, 48, 51, 53, 55, 56, 58, 61, 63, 65, 67, 75, 78, 81, 86, 87, 88, 92, 96, 98, 105, 107, 108, 110, 111, 113, 114, 118, 123, 124, 125, 126, 127, 128, 129, 130, 133, 136, 139, 143, 146, 148, 149, 150, 154, 157, 164, 165, 172, 173, 174, 177, 178, 180, 182, 183, 184, 186, 187, 188, 190, 191, 192, 196, 197, 198, 199, 200, 202, 203, 204, 208, 211, 214, 216, 217, 219, 222, 229, 230, 236, 237, 238, 240, 241, 242, 244, 245, 246, 249, 250, 251, 252, 253, 255, 256, 259, 260, 263, 264, 269, 270, 272, 276, 277, 279, 280, 281, 283, 284, 287, 288, 294, 297, 298, 299, 301, 303, 304, 306, 307, 308, 309, 313, 314, 320, 321, 322, 325, 326, 330, 333, 334, 335, 336, 337, 338, 339, 342, 343, 344, 345, 353, 354, 361, 362, 365, 366, 368, 369, 373, 376, 378, 382, 384, 385, 387, 389, 393, 395, 397, 399, 400, 401, 404, 405, 408, 410, 411, 413, 415, 416, 420, 421, 423, 426, 429, 439, 443, 446, 448, 449, 451, 452, 456, 459, 461, 462, 463, 466, 470, 471, 472, 475, 476, 477, 479, 480, 481, 483, 484, 485, 487, 502, 506, 510, 511, 512, 519, 520, 523, 527, 528, 529, 535, 536, 537, 539, 543, 544, 545, 546, 549, 550, 551, 554, 555, 557, 560, 561, 562, 569, 571, 572, 575, 577, 579, 580, 581, 582, 586, 595, 600, 601, 602, 604, 607, 608, 612, 613, 614, 615, 619, 620, 623, 625, 626, 629, 634, 635, 636, 639, 640, 642, 645, 646, 647, 648, 650, 655, 656, 660, 662, 669, 670, 671, 672, 673, 676, 678, 679, 682, 683, 684, 685, 686, 691, 696, 699, 700, 702, 703, 704, 707, 708, 709, 712, 714, 715, 716, 718, 722, 723, 724, 727, 728, 730, 731, 732, 733, 734, 735, 738, 739, 740, 741, 742, 744, 745, 748, 751, 752, 753, 754, 757, 759, 761, 764, 765, 766, 768, 775, 776, 777, 778, 782, 785, 786, 790, 791, 793, 794, 796, 800, 803, 804, 811, 812, 813, 815, 818, 819, 820, 822, 824, 825, 826, 827, 828, 829, 830, 831, 832, 833, 834, 835, 836, 837, 838, 846, 847, 848, 849, 851, 852, 854, 855, 858, 861, 865, 867, 868, 872, 873, 874, 875, 876, 879, 881, 882, 886, 887, 888, 889, 890, 891, 893, 894, 895, 896, 901, 913, 914, 915, 916, 917, 918, 922, 923, 925, 927, 939, 941, 943, 945, 946, 948, 949, 951, 952, 954, 955, 956, 962, 964, 967, 968, 969, 970, 971, 972, 973, 974, 975, 976, 990, 991, 992, 993, 994, 995, 998, 999, 1000, 1006, 1007, 1015, 1021, 1023, 1030, 1034, 1037, 1043, 1044, 1045, 1046, 1056, 1059, 1060, 1062, 1067, 1069, 1070, 1071, 1072, 1078, 1080, 1081, 1082, 1084, 1087, 1088, 1089, 1095, 1097, 1099, 1100, 1106, 1107, 1108, 1109, 1110, 1111, 1118, 1119, 1121, 1122, 1123, 1126, 1127, 1130, 1131, 1141, 1143, 1145, 1146, 1147, 1156, 1158, 1159, 1160, 1161, 1162, 1168, 1170, 1171, 1172, 1173, 1174, 1185, 1186, 1202, 1204, 1205, 1206, 1219, 1220, 1221, 1222, 1223, 1224, 1225, 1226, 1233, 1235, 1236).

Proof. 

Straightforward (time consuming) computation from the given data. □

As in [27], we also use conjugation by inner automorphisms to simplify the situation. We define the conjugate $f^s\in {\mathcal{O}}_A^{\left(n\right)}$ of an n-ary operation $f\in {\mathcal{O}}_A^{\left(n\right)}$ by a permutation $s\in SymA$ via $f^s\left(\mathit{x}\right):=s(f(s^{-1}\circ \mathit{x})$ for all $\mathit{x}\in A^n$. We say that operations $f,g\in {\mathcal{O}}_A^{\left(n\right)}$ are conjugate if there is $s\in SymA$ such that $g=f^s$, and we can hence form conjugacy classes of functions from this equivalence relation. It is helpful to extend the conjugation notation to sets $F\subseteq {\mathcal{O}}_A$ by an element-wise definition: for $s\in SymA$ we stipulate $F^s:=\left\{\left.f^s\phantom{f\in F}\right|f\in F\right\}$. Clearly, this conjugation notion respects any composition structure that F may have. The following observation is an immediate consequence from the fact that $s:⟨A;{\left(f\right)}_{f\in {\mathcal{O}}_A}⟩⟶⟨A;{\left(f^s\right)}_{f\in {\mathcal{O}}_A}⟩$ is an isomorphism and $f\mapsto f^s$ is injective.

Lemma 33

(cf. Observation 5.4 in [27]). For all $n\in \mathbb{N}$, $F\subseteq {\mathcal{O}}_A$ and permutations $s\in SymA$ we have $F^{s*\left(n\right)}={F^{*\left(n\right)}}^s$.

Proof. 

We have $F^{s*\left(n\right)}={\left\{\left.f^s\phantom{f\in F}\right|f\in F\right\}}^{*\left(n\right)}={\bigcap }_{f\in F}{\left\{f\right\}}^{s*\left(n\right)}={\bigcap }_{f\in F}{{\left\{f\right\}}^{*\left(n\right)}}^s$ from [27]. By the injectivity of $f\mapsto f^s$ the latter equals ${\left[{\bigcap }_{f\in F}{\left\{f\right\}}^{*\left(n\right)}\right]}^s={\left[F^{*\left(n\right)}\right]}^s$. □

Mainly relevant in the context of centralising monoids is the case $n=1$ of Lemma 33, where it states that the conjugate by s of a centralising monoids witnessed by F is the centralising monoid witnessed by the conjugate $F^s$ of F. As the centralising monoid $F^{*\left(1\right)}$ is isomorphic to its conjugate via $f\mapsto f^s$, it is a useful initial step to simplify a large list of monoids given by witnesses via separating conjugacy classes of the witnesses. In a second turn one can then classify the remaining monoids according to element-wise conjugacy.

In this respect we obtained the following results: the $10,263$ idempotent binary non-projections constituting the objects G of ${\mathbb{K}}_2^{\prime }$ can be classified into 2274 conjugacy types by inner automorphisms. Similarly, the 1236 binary operations in $\tilde{G}\subseteq G$ can be grouped together into 142 conjugacy classes (their representatives are marked in Appendix B by over- or underlining), and the 612 idempotent binary operations describing maximal elements with respect to ${\mathbb{K}}_2$ fall into 77 conjugacy types (representatives are marked in Appendix B by ↑ and over- or underlining, the monoids are listed in Appendix A, the classification of witnesses into conjugacy classes is given in Appendix C). The respective numbers of monoids up to element-wise conjugacy are therefore at most as big as these values, but generally reduce further. For example, the 1236 monoids ${\left\{g\right\}}^{*\left(1\right)}$ for $g\in \tilde{G}$ can be separated into 83 classes up to element-wise conjugacy. They correspond to those operations in Appendix B that are overlined. The other numbers are contained in the following theorem.

Theorem 34.

Let $A=\left\{0,1,2,3\right\}$. Up to element-wise conjugacy there are exactly 923 centralising monoids that can be witnessed by subsets of $C_A^{*\left(2\right)}$, 563 proper ones that can be witnessed by singletons, and 42 that are inclusion maximal proper monoids (among monoids witnessed by binary idempotent non-projections). These 42 monoids are shown in Appendix A.1 and correspond to those operations in Appendix B that are overlined and marked with ↑.

5. Monoids Witnessed by Mal’cev Operations of Boolean Groups

In this section, we are going to consider a set A carrying a Boolean group $⟨A;+,-,0⟩$, i.e., fulfilling the law $x+x\approx 0$. Such a group is necessarily Abelian, and since every non-unit element has order two, there is a natural ${\mathbb{Z}}_2$-vector space structure on A by defining $1·a:=a$ and $0·a:=0$ for all $a\in A$. It follows from this that if A is finite, then $\left|A\right|=2^d$ for some $d\in \mathbb{N}$. As the group is Boolean, it satisfies $-x\approx x$ and any linear combinations simply reduce to sums. All identities holding in A clearly also transfer to its powers, and notationally we shall not distinguish between the (infix) addition on A or on a power, as it is common in linear algebra.

Following case (III) of Rosenberg’s Theorem 4, we consider the Mal’cev (minority) operation $f\in {\mathcal{O}}_A^{\left(3\right)}$ given as $f(x,y,z):=x-y+z=x+y+z$ for $x,y,z\in A$. Our goal is to prove via Corollary 12 that ${\left\{f\right\}}^{*\left(1\right)}$ always is a maximal centralising monoid on A, given $\left|A\right|\ge 4$.

From the theory of maximal clones on finite sets, the centraliser of the Mal’cev operation of any Abelian p-group for prime p is very well known, see, e.g., [38] (4.3.13 Lemma, p. 107) and note that the quaternary relation ${\varrho }_{\mathbf{G}}$ given in [38] (4.3.12 Definition, p. 106) is a variable permutation of the graph $f^{•}$ of the Mal’cev operation f of $\mathbf{G}$. We here state the characterisation only for $p=2$, where we can replace ‘−’ by ‘+’.

Lemma 35.

Let $⟨A;+,-,0⟩$ be a Boolean group and $f\in {\mathcal{O}}_A^{\left(3\right)}$ be its Mal’cev operation and $g\in {\mathcal{O}}_A^{\left(n\right)}$ with $n\in \mathbb{N}$. For $L:={\left\{f\right\}}^{*}$ we have

$$\begin{array}{cc}\hfill g\in L& \iff \forall \mathit{x},\mathit{y},\mathit{z}\in A^n:\begin{array}{cc}\hfill g(\mathit{x}+\mathit{y}+\mathit{z})& =g(f\circ (\mathit{x},\mathit{y},\mathit{z}\left)\right)\hfill \\ \hfill & =f\left(g\right(\mathit{x}),g(\mathit{y}),g(\mathit{z}\left)\right)=g\left(\mathit{x}\right)+g\left(\mathit{y}\right)+g\left(\mathit{z}\right)\hfill \end{array}\hfill \\ \hfill & \iff \forall \mathit{x},\mathit{y},\mathit{z},\mathit{u}\in A^n:\mathit{u}=\mathit{x}+\mathit{y}+\mathit{z}\Rightarrow g\left(\mathit{u}\right)=g\left(\mathit{x}\right)+g\left(\mathit{y}\right)+g\left(\mathit{z}\right)\hfill \\ \hfill & \iff \forall \mathit{x},\mathit{y},\mathit{z},\mathit{u}\in A^n:\mathit{x}+\mathit{y}+\mathit{z}+\mathit{u}=\mathbf{0}\Rightarrow g\left(\mathit{x}\right)+g\left(\mathit{y}\right)+g\left(\mathit{z}\right)+g\left(\mathit{u}\right)=0\hfill \\ \hfill & \iff g:{⟨A;+,-,0⟩}^n⟶⟨A;+,-,0⟩\mathrm{is}{\mathbb{Z}}_2-\mathrm{affine}\mathrm{linear}.\hfill \end{array}$$

Since the centraliser $L={\left\{f\right\}}^{*}$ of the Mal’cev operation of a p-group is the clone of affine (linear) functions, it will be necessary to review a few basic facts regarding affine functions and affine (in)dependence.

Elements $a_1,\dots ,a_n$ in an affine space A are affinely independent if and only if for every linear combination $0={\lambda }_1{a}_1+\cdots +{\lambda }_n{a}_n$ with ${\lambda }_1+\cdots +{\lambda }_n=0$ necessarily all coefficients vanish: ${\lambda }_1=\cdots ={\lambda }_n=0$. Rephrasing this, they are affinely dependent precisely if there is a linear combination $0={\lambda }_1{a}_1+\cdots +{\lambda }_n{a}_n$ with ${\lambda }_1+\cdots +{\lambda }_n=0$ with some non-zero coefficients in it. Of course, we can remove all the coefficients which are zero from the sum without changing this condition. Thus, $\left\{a_1,\dots ,a_n\right\}$ are affinely dependent if and only if there is a subset $\varnothing \ne S\subseteq \left\{a_1,\dots ,a_n\right\}$ and non-zero coefficients ${\lambda }_s$ for $s\in S$ such that $0={\sum }_{s\in S}{\lambda }_{s}s$ and ${\sum }_{s\in S}{\lambda }_s=0$. In the context of an affine space over ${\mathbb{Z}}_2$, all ${\lambda }_s\in {\mathbb{Z}}_2\setminus \left\{0\right\}=\left\{1\right\}$ are equal to 1. Hence, over ${\mathbb{Z}}_2$ a set $\left\{a_1,\dots ,a_n\right\}$ is affinely dependent if there is a non-empty subset $S\subseteq \left\{a_1,\dots ,a_n\right\}$ with ${\sum }_{s\in S}s=0$ and $0={\sum }_{s\in S}1=\left|S\right|mod2$. Thus, $a_1,\dots ,a_n$ are affinely independent over ${\mathbb{Z}}_2$ if every non-empty sum of evenly many of these elements is distinct from the zero-vector 0.

The following special cases of affine independence over ${\mathbb{Z}}_2$ will be relevant for our proof: $a_1,a_2\in A$ are affinely independent if and only if $a_1\ne a_2$ since $a_1+a_2=0$ is equivalent to $a_1=a_2$; three general elements $a_1,a_2,a_3\in A$ are affinely independent if and only if $\left|\left\{a_1,a_2,a_3\right\}\right|=3$, i.e., they are pairwise distinct. Moreover, $a_1,a_2,a_3,a_4\in A$ are affinely independent exactly if $\left|\left\{a_1,a_2,a_3,a_4\right\}\right|=4$ and $a_1+a_2+a_3+a_4\ne 0$. Therefore, four pairwise distinct elements $a_1,a_2,a_3,a_4$ of A are affinely independent precisely if $a_1+a_2+a_3+a_4\ne 0$.

The importance of affine independence in our situation comes from the following extendability property, which is part of a typical introductory course to linear algebra (see, e.g., Satz 6.3.6 in [39] (p. 156)).

Proposition 36.

Let A and $A^{\prime }$ be affine spaces over the same field and $B\subseteq A$ be an affine basis of A. Then for every partial assignment ${\left(g\left(b\right)\right)}_{b\in B}\in {A^{\prime }}^B$ there is a unique extension to an affine linear map $g:A⟶A^{\prime }$.

Since every affinely independent set $I\subseteq A$ can be extended to an affine basis $B\subseteq A$, every partial assignment ${\left(g\left(x\right)\right)}_{x\in I}\in {A^{\prime }}^I$ is extendable to an affine map $g:A⟶A^{\prime }$.

Lemma 37.

For a Boolean group $⟨A;+,-,0⟩$ with $\left|A\right|\ge 4$ and its associated Mal’cev operation $f\in {\mathcal{O}}_A^{\left(3\right)}$, let $M\subseteq {\mathcal{O}}_A^{\left(1\right)}$ be a monoid satisfying $M⊋{\left\{f\right\}}^{*\left(1\right)}=L^{\left(1\right)}$; then $M^{*}={\mathcal{J}}_A$.

Proof. 

By the assumption there is some unary $h\in M\subseteq {\mathcal{O}}_A^{\left(1\right)}$ with $h\notin {\left\{f\right\}}^{*}$, i.e., the condition given in Lemma 35 is falsified by h. We proceed through a series of claims.

Claim 1.

There are pairwise distinct affinely dependent $x,y,z,u\in A$ for which there is a function $g\in M$ with $(x,y)\in ker\left(g\right)$ and $(z,u)\notin ker\left(g\right)$.

Proof. 

To prove this claim we use the operation $h\notin {\left\{f\right\}}^{*\left(1\right)}$. This means there are (affinely dependent) $x+y+z+u=0$ in A for which $h\left(x\right)+h\left(y\right)+h\left(z\right)+h\left(u\right)\ne 0$. If any two elements from $(x,y,z,u)$ were equal, then because of $x+y+z+u=0$ also the other two would have to be equal. It would follow that $h\left(x\right)+h\left(y\right)+h\left(z\right)+h\left(u\right)=0$ for it would be a sum of two pairs of equal summands. This contradicts the assumption on $x,y,z,u$. Therefore, we know that $x+y+z+u=0$ and $h\left(x\right)+h\left(y\right)+h\left(z\right)+h\left(u\right)\ne 0$ and $x,y,z,u$ are pairwise distinct. These conditions are completely symmetric under permutation of the four values. If there are any two that are sent by h to the same value, then because of $0\ne h\left(x\right)+h\left(y\right)+h\left(z\right)+h\left(u\right)$ the other two are not in the kernel of h, and h and some permutation of $(x,y,z,u)$ will show Claim 1. Now let us assume that all four h-values are pairwise distinct. Then $h\left(x\right),h\left(y\right),h\left(z\right),h\left(u\right)$ are affinely independent, and by Proposition 36 we choose some affine linear map $g\in L^{\left(1\right)}\subseteq M$ satisfying $g\left(h\right(y\left)\right):=h\left(x\right)$ and $g\left(h\right(w\left)\right):=h\left(w\right)$ for $w\in \left\{x,z,u\right\}$. Then $g\circ h\in M$ and $g\circ h\left(x\right)=h\left(x\right)=g\circ h\left(y\right)$, $g\circ h\left(z\right)=h\left(z\right)\ne h\left(u\right)=g\circ h\left(u\right)$, i.e., $(x,y)\in ker(g\circ h)$ and $(z,u)\notin ker(g\circ h)$. So $g\circ h$ will show Claim 1. □

Claim 2.

For all pairwise distinct affinely dependent $x,y,z,u\in A$ there is a function $g\in M$ with $(x,y)\in ker\left(g\right)$ and $(z,u)\notin ker\left(g\right)$.

Proof. 

By Claim 1 there are affinely dependent pairwise distinct elements $x,y,z,u\in A$ and $g\in M$ with $g\left(x\right)=g\left(y\right)$ and $g\left(z\right)\ne g\left(u\right)$. Now consider any other affinely dependent quadruple $(a,b,c,d)$ with pairwise distinct entries. Dependency means precisely that $x+y+z+u=0$ and $a+b+c+d=0$, or equivalently, $u=x+y+z$ and $d=a+b+c$. However, as $a,b,c$ are pairwise distinct, these points are affinely independent. Via Proposition 36 we choose an affine linear map $g^{\prime }\in L^{\left(1\right)}\subseteq M$ such that $g^{\prime }\left(a\right)=x$, $g^{\prime }\left(b\right)=y$ and $g^{\prime }\left(c\right)=z$. Since $g^{\prime }\in L^{\left(1\right)}={\left\{f\right\}}^{*}$, it follows (see Lemma 35) that $g^{\prime }\left(d\right)=g^{\prime }\left(a\right)+g^{\prime }\left(b\right)+g^{\prime }\left(c\right)=x+y+z=u$. Thus, $g\circ g^{\prime }\left(a\right)=g\left(x\right)=g\left(y\right)=g\circ g^{\prime }\left(b\right)$ and $g\circ g^{\prime }\left(c\right)=g\left(z\right)\ne g\left(u\right)=g\circ g^{\prime }\left(d\right)$, wherefore we obtain $(a,b)\in ker(g\circ g^{\prime })$ but $(c,d)\notin ker(g\circ g^{\prime })$. Hence, $g\circ g^{\prime }\in M$ shows Claim 2. □

Claim 3.

For all pairwise distinct elements $x,y,z,u\in A$ there exists a function $g\in M$ such that $(x,y)\in ker\left(g\right)$ and $(z,u)\notin ker\left(g\right)$; i.e., $g\left(x\right)=g\left(y\right)$ but $g\left(z\right)\ne g\left(u\right)$.

Proof. 

Let $x,y,z,u\in A$ be pairwise distinct. If they are affinely dependent, the result follows from Claim 2; hence suppose that $x,y,z,u$ are affinely independent. In this case we use Proposition 36 to construct $g\in L^{\left(1\right)}\subseteq M$ with $g\left(x\right)=g\left(y\right)=g\left(z\right)=0\ne g\left(u\right)$, so that $(x,y)\in ker\left(g\right)$ and $(z,u)\notin ker\left(g\right)$. □

We now take advantage of Corollary 12 to complete the proof of Lemma 37. Condition (D’) is provided by Claim 3; condition (B’) holds as any pairwise distinct $x,y,z\in A$ are affinely independent, and so we may again rely on Proposition 36 to pick some $g\in L^{\left(1\right)}\subseteq M$ with $g\left(y\right)=g\left(x\right)\ne g\left(z\right)$. Similarly, for each $a\in A$ this single point is affinely independent, and so Proposition 36 can be invoked to define some $g\in L^{\left(1\right)}\subseteq M$ with $g\left(a\right)\ne a$, i.e., $a\notin fix\left(g\right)$. Consequently, Corollary 12 implies $M^{*}={\mathcal{J}}_A$.

Theorem 38.

Let $⟨A;+,-,0⟩$ be a Boolean group with $\left|A\right|\ge 4$ and $f\in {\mathcal{O}}_A^{\left(3\right)}$ be the associated Mal’cev operation. Then $L^{\left(1\right)}={\left\{f\right\}}^{*\left(1\right)}$ is a maximal centralising monoid on A.

Proof. 

If $M\subseteq {\mathcal{O}}_A^{\left(1\right)}$ is a centralising monoid satisfying $L^{\left(1\right)}⊊M$, then $M^{*}={\mathcal{J}}_A$ by Lemma 37. We now use Lemmas 2 and 9 to infer $M={\mathcal{O}}_A^{\left(1\right)}$. Moreover, $\left|A\right|\ge 4>2$ ensures that $L^{\left(1\right)}⊊{\mathcal{O}}_A^{\left(1\right)}$. Namely, take pairwise distinct $x,y,z\in A$ and let $u:=x+y+z$. Since $\left|\left\{x,y,z\right\}\right|=3$, $u\notin \left\{x,y,z\right\}$. We define $h\left(u\right)\ne 0$ and $h\left(a\right):=0$ for $a\in A\setminus \left\{u\right\}$, in particular $h\left(x\right)=h\left(y\right)=h\left(z\right)=0$. If h were affine linear, then, by Lemma 35, we would have $h\left(u\right)=h\left(x\right)+h\left(y\right)+h\left(z\right)=0+0+0=0$, contradicting the definition of h. Hence, $h\in {\mathcal{O}}_A^{\left(1\right)}\setminus L^{\left(1\right)}$. □

Remark 39.

Four-element sets are the smallest ones where Theorem 38 (non-vacuously) holds. Three-element sets do not support Boolean groups—for this reason monoids witnessed by Mal’cev operations did not appear in the analyses given in [21,23]; and for $\left|A\right|\le 2$ we have $L^{\left(1\right)}={\mathcal{O}}_A^{\left(1\right)}$, the full transformation monoid. Hence, in these cases ${\left\{f\right\}}^{*\left(1\right)}=L^{\left(1\right)}$ fails to be a maximal centralising monoid.

Appendix A.1

Centralising monoids being maximal w.r.t. ${\mathbb{K}}_2$, witnessed by 77 conjugacy types of binary idempotent functions $g_i$ (part 1: monoids representing one of 42 conjugacy classes). The indices $i\in \left\{1,\dots ,1236\right\}$ of the witnesses refer to the overlined operations listed in Appendix B; the unary operations u in the monoids are coded via their base-4-representation ${\sum }_{j=0}^{3}u\left(j\right)4^{3-j}$.

$$\begin{array}{cc}\hfill {\left\{g_1\right\}}^{*\left(1\right)}=\{& 0,1,2,3,4,6,7,8,9,11,12,13,14,16,18,19,24,27,28,30,32,33,35,36,39,\hfill \\ & 44,45,48,49,50,52,54,56,57,85,170,255\}\hfill \\ \hfill {\left\{g_4\right\}}^{*\left(1\right)}=\{& 0,3,4,7,8,11,16,19,24,27,32,35,36,39,85,170,252,255\}\hfill \\ \hfill {\left\{g_6\right\}}^{*\left(1\right)}=\{& 0,1,2,3,5,10,11,15,16,18,19,26,27,31,32,33,37,48,49,53,85,170,171,\hfill \\ & 175,186,255\}\hfill \\ \hfill {\left\{g_{10}\right\}}^{*\left(1\right)}=\{& 0,3,11,16,19,27,32,85,170,171,252,254,255\}\hfill \\ \hfill {\left\{g_{12}\right\}}^{*\left(1\right)}=\{& 0,4,8,11,16,24,27,32,36,85,170,239,248,251,255\}\hfill \\ \hfill {\left\{g_{19}\right\}}^{*\left(1\right)}=\{& 0,1,10,11,16,26,27,85,160,161,170,171,176,177,186,255\}\hfill \\ \hfill {\left\{g_{20}\right\}}^{*\left(1\right)}=\{& 0,10,11,15,16,26,27,31,85,160,170,186,240,255\}\hfill \\ \hfill {\left\{g_{21}\right\}}^{*\left(1\right)}=\{& 0,2,3,8,10,11,12,14,15,16,18,19,24,26,27,28,30,31,85,160,162,163,\hfill \\ & 168,170,171,172,174,175,240,242,243,248,250,251,252,254,255\}\hfill \\ \hfill {\left\{g_{31}\right\}}^{*\left(1\right)}=\{& 0,1,2,3,5,7,10,11,15,17,19,27,34,35,39,51,85,87,95,119,170,171,\hfill \\ & 175,187,255\}\hfill \\ \hfill {\left\{g_{33}\right\}}^{*\left(1\right)}=\{& 0,1,3,8,9,11,17,19,25,27,51,59,85,87,119,162,170,255\}\hfill \\ \hfill {\left\{g_{35}\right\}}^{*\left(1\right)}=\{& 0,1,3,11,17,19,27,51,85,87,119,163,170,171,187,255\}\hfill \\ \hfill {\left\{g_{36}\right\}}^{*\left(1\right)}=\{& 0,8,17,19,25,27,49,51,57,59,85,93,162,170,247,255\}\hfill \\ \hfill {\left\{g_{39}\right\}}^{*\left(1\right)}=\{& 0,2,3,8,10,11,12,14,15,19,27,85,87,93,95,160,162,163,168,170,171,\hfill \\ & 172,174,175,240,242,243,245,247,248,250,251,252,253,254,255\}\hfill \\ \hfill {\left\{g_{44}\right\}}^{*\left(1\right)}=\{& 0,4,8,12,16,24,27,32,36,39,48,85,170,223,239,247,251,255\}\hfill \\ \hfill {\left\{g_{49}\right\}}^{*\left(1\right)}=\{& 0,8,16,24,27,48,85,162,170,174,223,251,255\}\hfill \\ \hfill {\left\{g_{50}\right\}}^{*\left(1\right)}=\{& 0,8,12,16,19,24,27,85,162,170,174,220,223,243,251,255\}\hfill \\ \hfill {\left\{g_{68}\right\}}^{*\left(1\right)}=\{& 0,1,2,3,4,8,12,21,22,23,25,27,29,30,42,63,85,86,87,89,91,93,94,\hfill \\ & 106,127,170,255\}\hfill \\ \hfill {\left\{g_{69}\right\}}^{*\left(1\right)}=\{& 0,4,8,12,21,23,25,27,42,61,63,85,89,106,170,255\}\hfill \\ \hfill {\left\{g_{70}\right\}}^{*\left(1\right)}=\{& 0,3,4,8,23,27,85,87,89,91,170,252,253,255\}\hfill \\ \hfill {\left\{g_{71}\right\}}^{*\left(1\right)}=\{& 0,1,2,3,5,6,7,10,11,15,21,22,23,26,27,31,42,43,47,63,85,86,87,90,\hfill \\ & 91,95,106,107,111,127,170,171,175,191,255\}\hfill \\ \hfill {\left\{g_{97}\right\}}^{*\left(1\right)}=\{& 0,21,27,42,45,54,63,85,106,170,191,213,255\}\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\left\{g_{151}\right\}}^{*\left(1\right)}=\{& 0,1,2,3,6,7,11,27,84,85,168,170,252,255\}\hfill \\ \hfill {\left\{g_{153}\right\}}^{*\left(1\right)}=\{& 0,5,10,11,26,27,80,85,160,161,170,175,176,177,250,255\}\hfill \\ \hfill {\left\{g_{156}\right\}}^{*\left(1\right)}=\{& 0,1,2,3,4,5,8,10,11,12,14,15,26,27,30,31,80,81,84,85,160,162,163,\hfill \\ & 168,170,171,172,174,175,240,242,243,248,250,251,252,254,255\}\hfill \\ \hfill {\left\{g_{159}\right\}}^{*\left(1\right)}=\{& 0,1,2,3,6,11,27,84,85,87,168,170,252,253,255\}\hfill \\ \hfill {\left\{g_{166}\right\}}^{*\left(1\right)}=\{& 0,4,8,9,11,12,24,25,27,56,57,59,81,85,93,162,170,243,247,255\}\hfill \\ \hfill {\left\{g_{168}\right\}}^{*\left(1\right)}=\{& 0,1,2,3,4,5,7,8,10,11,12,13,14,15,24,27,80,81,83,84,85,87,92,93,\hfill \\ & 95,160,162,163,168,170,171,172,174,175,240,241,242,243,244,245,\hfill \\ & 247,248,250,251,252,253,254,255\}\hfill \\ \hfill {\left\{g_{169}\right\}}^{*\left(1\right)}=\{& 0,5,10,15,27,80,85,95,160,170,175,228,240,245,250,255\}\hfill \\ \hfill {\left\{g_{347}\right\}}^{*\left(1\right)}=\{& 0,5,10,11,14,15,16,21,26,27,30,31,32,37,42,48,53,63,64,69,74,75,\hfill \\ & 78,79,80,85,90,91,94,95,96,101,106,112,117,127,128,133,138,144,\hfill \\ & 149,154,160,165,170,192,197,207,208,213,223,240,245,255\}\hfill \\ \hfill {\left\{g_{348}\right\}}^{*\left(1\right)}=\{& 0,5,10,16,21,27,32,42,64,69,78,80,85,95,117,127,128,138,160,170,\hfill \\ & 175,186,191,213,223,234,239,245,250,255\}\hfill \\ \hfill {\left\{g_{351}\right\}}^{*\left(1\right)}=\{& 0,5,10,15,16,21,27,30,32,42,47,48,58,63,64,69,80,85,128,138,143,\hfill \\ & 160,170,175,176,186,191,192,202,207,224,234,239,240,250,255\}\hfill \\ \hfill {\left\{g_{372}\right\}}^{*\left(1\right)}=\{& 0,5,11,14,16,21,27,30,64,69,75,78,80,85,91,94,170,175,186,191,234,\hfill \\ & 239,250,255\}\hfill \\ \hfill {\left\{g_{377}\right\}}^{*\left(1\right)}=\{& 0,21,22,27,64,85,106,149,170,191,233,234,255\}\hfill \\ \hfill {\left\{g_{396}\right\}}^{*\left(1\right)}=\{& 0,21,23,27,39,42,43,61,62,63,64,85,106,128,149,170,192,255\}\hfill \\ \hfill {\left\{g_{412}\right\}}^{*\left(1\right)}=\{& 0,21,22,23,25,26,27,29,30,31,37,38,39,41,42,43,45,46,47,53,54,55,\hfill \\ & 57,58,59,61,62,63,64,85,128,170,192,255\}\hfill \\ \hfill {\left\{g_{454}\right\}}^{*\left(1\right)}=\{& 0,27,45,54,85,106,127,149,170,191,213,234,255\}\hfill \\ \hfill {\left\{g_{563}\right\}}^{*\left(1\right)}=\{& 0,5,10,27,78,80,85,95,160,170,175,177,228,245,250,255\}\hfill \\ \hfill {\left\{g_{618}\right\}}^{*\left(1\right)}=\{& 0,4,8,19,27,85,93,116,170,205,243,251,255\}\hfill \\ \hfill {\left\{g_{658}\right\}}^{*\left(1\right)}=\{& 0,20,23,24,27,36,39,40,43,65,66,77,78,85,113,114,125,126,129,130,\hfill \\ & 141,142,170,177,178,189,190,212,215,216,219,228,231,232,235,255\}\hfill \\ \hfill {\left\{g_{697}\right\}}^{*\left(1\right)}=\{& 0,5,27,30,75,78,80,85,170,175,177,180,225,228,250,255\}\hfill \\ \hfill {\left\{g_{762}\right\}}^{*\left(1\right)}=\{& 0,10,17,27,68,78,85,95,160,170,177,187,228,238,245,255\}\hfill \\ \hfill {\left\{g_{1187}\right\}}^{*\left(1\right)}=\{& 0,27,45,54,78,85,99,120,135,156,170,177,201,210,228,255\}\hfill \end{array}$$

Appendix A.2

Centralising monoids $M_i:={\left\{g_i\right\}}^{*\left(1\right)}$ being maximal w.r.t. ${\mathbb{K}}_2$, witnessed by 77 conjugacy types of binary idempotent functions $g_i$ (part 2: monoids conjugate to the 42 ones shown in Appendix A.1). The indices $i\in \left\{1,\dots ,1236\right\}$ of the witnesses refer to the (over- or underlined) operations listed in Appendix B; the unary operations u in the monoids are coded via their base-4-representation ${\sum }_{j=0}^{3}u\left(j\right)4^{3-j}$.

$$\begin{array}{cc}\hfill M_{135}=\{& 0,16,21,27,31,32,42,46,48,59,63,85,170,213,223,255\}=M_{69}^{\left(321\right)}\hfill \\ \hfill M_{442}=\{& 0,27,41,42,85,106,127,128,149,170,213,214,255\}=M_{377}^{\left(12\right)}\hfill \\ \hfill M_{627}=\{& 0,4,8,27,85,89,93,120,170,201,243,251,255\}=M_{97}^{\left(0231\right)}\hfill \\ \hfill M_{657}=\{& 0,3,7,11,19,23,27,35,39,43,67,71,75,83,85,87,91,99,103,107,131,\hfill \\ & 135,139,147,151,155,163,167,170,171,252,253,254,255\}=M_{412}^{\left(0321\right)}\hfill \\ \hfill M_{659}=\{& 0,3,23,27,39,43,67,85,86,87,131,169,170,171,252,253,254,255\}=M_{396}^{\left(03\right)}\hfill \\ \hfill M_{771}=\{& 0,15,16,27,31,80,85,90,95,154,158,170,207,219,223,255\}=M_{35}^{\left(310\right)}\hfill \\ \hfill M_{774}=\{& 0,11,15,16,27,31,80,85,91,95,170,174,203,207,219,223,251,255\}=M_{33}^{\left(310\right)}\hfill \\ \hfill M_{779}=\{& 0,10,11,14,15,26,27,30,31,74,75,78,79,85,90,91,94,95,160,161,164,\hfill \\ & 165,170,176,177,180,181,224,225,228,229,240,241,244,245,255\}=M_{658}^{\left(123\right)}\hfill \\ \hfill M_{780}=\{& 0,2,3,8,10,11,12,14,15,26,27,30,31,74,75,78,79,85,86,87,89,90,91,\hfill \\ & 93,94,95,160,162,163,165,166,167,168,169,170,171,172,173,174,175,240,\hfill \\ & 242,243,245,246,247,248,249,250,251,252,253,254,255\}=M_{347}^{\left(02\right)\left(13\right)}\hfill \\ \hfill M_{933}=\{& 0,23,27,63,85,89,113,125,149,170,177,189,215,219,243,255\}=M_{19}^{\left(0123\right)}\hfill \\ \hfill M_{934}=\{& 0,23,27,60,85,105,113,125,150,170,177,189,195,215,219,255\}=M_{153}^{\left(0123\right)}\hfill \\ \hfill M_{979}=\{& 0,27,42,43,85,87,103,155,168,170,171,213,232,234,255\}=M_{12}^{\left(0231\right)}\hfill \\ \hfill M_{981}=\{& 0,26,27,32,85,101,138,154,170,186,202,218,239,255\}=M_{151}^{\left(02\right)\left(13\right)}\hfill \\ \hfill M_{982}=\{& 0,26,27,42,43,85,101,152,154,155,168,170,171,216,\hfill \\ & 218,232,234,255\}=M_4^{\left(0231\right)}\hfill \\ \hfill M_{983}=\{& 0,26,27,32,85,101,117,138,154,170,186,202,223,239,255\}=M_{159}^{\left(02\right)\left(13\right)}\hfill \\ \hfill M_{984}=\{& 0,26,27,42,85,101,117,154,155,170,223,234,255\}=M_{10}^{\left(0231\right)}\hfill \\ \hfill M_{986}=\{& 0,27,32,85,117,138,159,170,186,202,223,239,255\}=M_{377}^{\left(013\right)}\hfill \end{array}$$

$$\begin{array}{cc}\hfill M_{997}=\{& 0,21,27,59,63,85,89,166,170,174,213,219,251,255\}=M_{70}^{\left(0132\right)}\hfill \\ \hfill M_{1002}=\{& 0,21,27,31,53,59,63,85,89,93,166,170,174,247,251,255\}=M_{50}^{\left(310\right)}\hfill \\ \hfill M_{1003}=\{& 0,21,27,59,63,85,89,127,166,170,174,251,255\}=M_{49}^{\left(310\right)}\hfill \\ \hfill M_{1011}=\{& 0,2,3,27,32,34,35,48,50,51,85,87,117,119,136,138,139,147,168,170,171,\hfill \\ & 184,186,187,204,206,207,221,223,236,238,239,252,253,254,255\}=M_{351}^{\left(320\right)}\hfill \\ \hfill M_{1013}=\{& 0,2,25,27,32,34,57,59,85,87,117,119,136,138,145,147,168,170,177,\hfill \\ & 179,221,223,253,255\}=M_{372}^{\left(0132\right)}\hfill \\ \hfill M_{1018}=\{& 0,25,27,42,59,85,102,153,155,170,187,213,238,255\}=M_{20}^{\left(210\right)}\hfill \\ \hfill M_{1020}=\{& 0,24,26,27,32,48,85,101,138,152,154,155,170,186,207,216,218,219,\hfill \\ & 239,255\}=M_{166}^{\left(210\right)}\hfill \\ \hfill M_{1022}=\{& 0,24,27,40,43,48,85,101,154,170,207,216,219,232,235,255\}=M_{36}^{\left(210\right)}\hfill \\ \hfill M_{1026}=\{& 0,2,3,27,35,85,86,137,168,169,170,252,255\}=M_{377}^{\left(310\right)}\hfill \\ \hfill M_{1028}=\{& 0,2,3,27,32,34,48,51,85,86,87,101,102,117,119,136,138,153,154,168,\hfill \\ & 169,170,177,204,207,221,223,252,253,255\}=M_{348}^{\left(013\right)}\hfill \\ \hfill M_{1029}=\{& 0,2,3,26,27,32,34,35,48,50,51,85,86,87,101,102,103,117,118,119,\hfill \\ & 136,138,139,153,154,155,168,169,170,171,184,185,186,187,204,206,\hfill \\ & 207,221,222,223,236,237,238,239,252,253,254,255\}=M_{168}^{\left(210\right)}\hfill \\ \hfill M_{1033}=\{& 0,2,25,27,32,34,57,59,85,86,87,101,102,103,117,118,119,136,138,\hfill \\ & 153,154,155,168,169,170,171,185,186,187,221,222,223,237,238,239,\hfill \\ & 253,254,255\}=M_{156}^{\left(210\right)}\hfill \\ \hfill M_{1038}=\{& 0,3,27,43,48,51,85,86,87,101,102,103,117,118,119,153,154,155,\hfill \\ & 169,170,171,185,186,187,204,207,221,222,223,237,238,239,\hfill \\ & 252,253,254,255\}=M_{39}^{\left(210\right)}\hfill \\ \hfill M_{1042}=\{& 0,25,26,27,41,42,43,57,58,59,85,86,87,101,102,103,117,118,119,\hfill \\ & 153,154,155,169,170,171,185,186,187,221,222,223,237,238,239,\hfill \\ & 253,254,255\}=M_{21}^{\left(210\right)}\hfill \\ \hfill M_{1049}=\{& 0,27,32,48,85,138,156,170,186,207,210,239,255\}=M_{454}^{\left(01\right)}\hfill \\ \hfill M_{1137}=\{& 0,27,39,60,78,85,105,114,141,150,170,177,195,216,228,255\}=M_{697}^{\left(321\right)}\hfill \\ \hfill M_{1180}=\{& 0,27,40,60,78,85,105,125,130,150,170,177,195,215,228,255\}=M_{563}^{\left(13\right)}\hfill \\ \hfill M_{1181}=\{& 0,27,40,60,78,85,105,125,130,150,170,190,195,215,235,255\}=M_{169}^{\left(02\right)}\hfill \end{array}$$