New Conservation Laws and Exact Cosmological Solutions in Brans–Dicke Cosmology with an Extra Scalar Field
Abstract
1. Introduction
2. Cosmological Model
3. Quadratic First Integrals for a Class of Second-Order ODEs with Linear Damping
3.1. Case
3.2. Case
3.3. Case
3.4. Case
4. Cosmological Exact Solutions
4.1. Case
4.2. Case
4.3. Case
4.4. Case
4.4.1. Subcase
4.4.2. Subcase
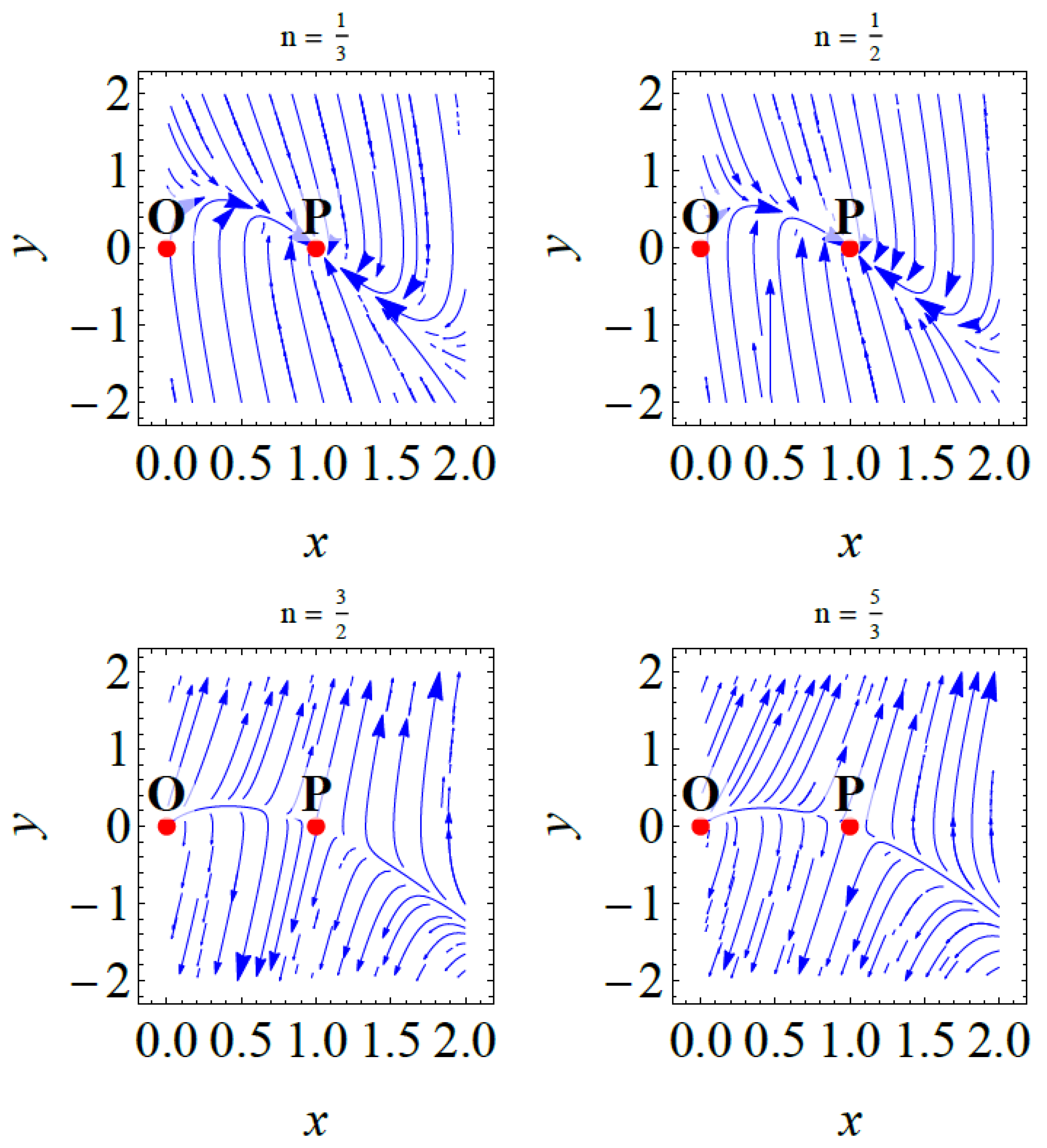
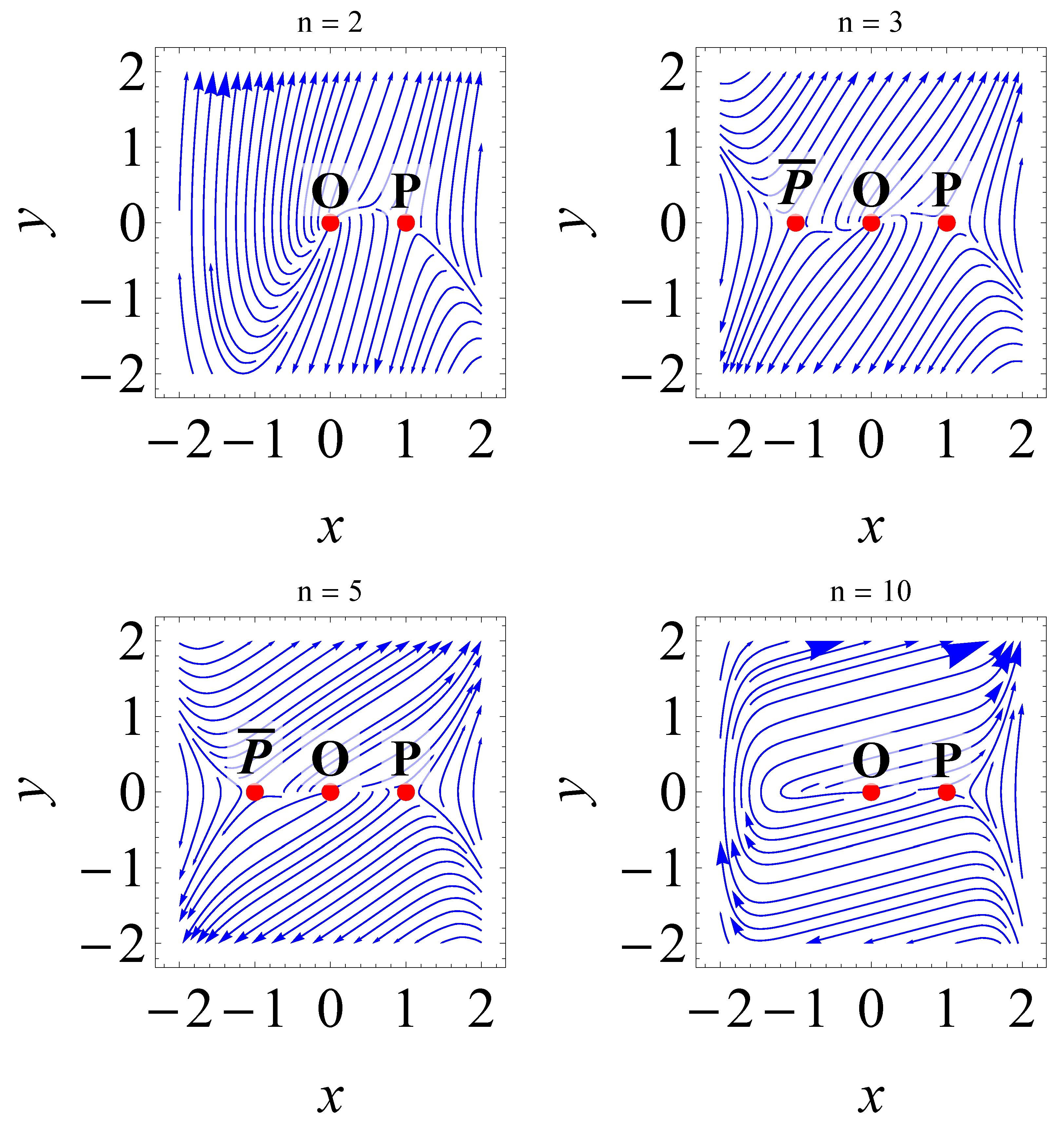
5. Stability of Scaling Solutions
Case
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Deustua, S.; Fabbro, S.; Goldhaber, G.; Groom, D.E.; Kim, A.G.; Kim, M.Y.; Knop, R.A.; Nugent, P.; et al. Cosmology from Type Ia supernovae. Bull. Am. Astron. Soc. 1997, 29, 1351. [Google Scholar]
- Riess, A.G.; Strolger, L.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Gold, B.; Challis, P.J.; Filippenko, A.V.; Jha, S.; Li, W.; et al. NewHubble Space TelescopeDiscoveries of Type Ia Supernovae at z>=1: Narrowing Constraints on the Early Behavior of Dark Energy. Astrophys. J. 2007, 659, 98–121. [Google Scholar] [CrossRef]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.S.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. Thehubble space telescopecluster supernova survey. v. improving the dark-energy constraints abovez> 1 and building an early-type-hosted supernova sample. Astrophys. J. 2012, 746, 85. [Google Scholar] [CrossRef]
- di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quantum Gravity 2021, 2103. [Google Scholar] [CrossRef]
- Starobinsky, A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Müller, V.; Schmidt, H.-J.; Starobinsky, A. The stability of the de Sitter space-time in fourth order gravity. Phys. Lett. B 1988, 202, 198–200. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.; Starobinsky, A. Inflationary universe generated by the combined action of a scalar field and gravitational vacuum polarization. Phys. Lett. B 1985, 157, 361–367. [Google Scholar] [CrossRef]
- Wald, R.M. Asymptotic behavior of homogeneous cosmological models in the presence of a positive cosmological constant. Phys. Rev. D 1983, 28, 2118–2120. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. Phys. Rev. D 1977, 15, 2738–2751. [Google Scholar] [CrossRef]
- Hawking, S.; Moss, I. Supercooled phase transitions in the very early universe. Phys. Lett. B 1982, 110, 35–38. [Google Scholar] [CrossRef]
- Sato, K. First-order phase transition of a vacuum and the expansion of the Universe. Mon. Not. R. Astron. Soc. 1981, 195, 467–479. [Google Scholar] [CrossRef]
- Barrow, J.D.; Ottewill, A. The stability of general relativistic cosmological theory. J. Phys. A Math. Gen. 1983, 16, 2757–2776. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J.E. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406–3427. [Google Scholar] [CrossRef]
- Barrow, J.D.; Saich, P. Scalar-field cosmologies. Class. Quantum Gravity 1993, 10, 279–283. [Google Scholar] [CrossRef]
- Brans, C.H.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Faraoni, V. Cosmology in Scalar-Tensor Gravity, Fundamental Theories of Physics; Kluwer Academic Press: Dordrecht, The Netherlands, 2004; Volume 139. [Google Scholar]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- O’Hanlon, J. Intermediate-Range Gravity: A Generally Covariant Model. Phys. Rev. Lett. 1972, 29, 137–138. [Google Scholar] [CrossRef]
- Nicolis, A.; Rattazzi, R.; Trincherini, E. Galileon as a local modification of gravity. Phys. Rev. D 2009, 79, 064036. [Google Scholar] [CrossRef]
- Deffayet, C.; Esposito-Farese, G.; Vikman, A. Covariant Galileon. Phys. Rev. D 2009, 79. [Google Scholar] [CrossRef]
- Belinchón, J.A.; Harko, T.; Mak, M.K. Exact scalar–tensor cosmological models. Int. J. Mod. Phys. D 2017, 26, 1750073. [Google Scholar] [CrossRef]
- Fomin, I.V.; Chervon, S.V. Exact and slow-roll solutions for exponential power-law inflation connected with f(R) gravity and observational constraints. arXiv 2006, arXiv:2006.16074. [Google Scholar]
- Fomin, I.V.; Chervon, S.; Maharaj, S.D. A new look at the Schrödinger equation in exact scalar field cosmology. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950022. [Google Scholar] [CrossRef]
- Saridakis, E.; Tsamparlis, M. Symmetry inheritance of conformal Killing vectors. J. Math. Phys. 1991, 32, 1541–1551. [Google Scholar] [CrossRef]
- Shapovalov, V.N. Stäckel spaces. Sib. Math. J. 1979, 20, 790. [Google Scholar] [CrossRef]
- Obukhov, V. Separation of variables in Hamilton-Jacobi and Klein-Gordon-Fock equations for a charged test particle in the Stäckel spaces of type. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150033. [Google Scholar] [CrossRef]
- Osetrin, E.; Osetrin, K. Pure radiation in space-time models that admit integration of the eikonal equation by the separation of variables method. J. Math. Phys. 2017, 58, 112504. [Google Scholar] [CrossRef]
- Tsamparlis, M.; Paliathanasis, A. The generic model of general relativity. Arab. J. Math. 2019, 8, 201–254. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Dark Energy: Theory and Observations; Cambrdige University Press: Cambridge, UK, 2010. [Google Scholar]
- Demiański, M.; De Ritis, R.; Marmo, G.; Platania, G.; Rubano, C.; Scudellaro, P.; Stornaiolo, C. Scalar field, nonminimal coupling, and cosmology. Phys. Rev. D 1991, 44, 3136–3146. [Google Scholar] [CrossRef] [PubMed]
- Dimakis, N.; Giacomini, A.; Paliathanasis, A. Integrability from point symmetries in a family of cosmological Horndeski Lagrangians. Eur. Phys. J. C 2017, 77, 458. [Google Scholar] [CrossRef]
- Dimakis, N.; Terzis, P.A.; Christodoulakis, T. Integrability of the mixmaster model. Phys. Rev. D 2019, 99, 023536. [Google Scholar] [CrossRef]
- Papagiannopoulos, G.; Barrow, J.D.; Basilakos, S.; Giacomini, A.; Paliathanasis, A. Dynamical symmetries in Brans-Dicke cosmology. Phys. Rev. D 2017, 95, 024021. [Google Scholar] [CrossRef]
- Tsamparlis, M.; Paliathanasis, A. Symmetries of Differential Equations in Cosmology. Symmetry 2018, 10, 233. [Google Scholar] [CrossRef]
- Katzin, G.H. Related integral theorem. II. A method for obtaining quadratic constants of the motion for conservative dynamical systems admitting symmetries. J. Math. Phys. 1973, 14, 1213–1217. [Google Scholar] [CrossRef]
- Katzin, G.H.; Levine, J. Geodesic first integrals with explicit path-parameter dependence in Riemannian space–times. J. Math. Phys. 1981, 22, 1878–1891. [Google Scholar] [CrossRef]
- Katzin, G.H.; Levine, J. Time-dependent quadratic constants of motion, symmetries, and orbit equations for classical particle dynamical systems with time-dependent Kepler potentials. J. Math. Phys. 1982, 23, 552–563. [Google Scholar] [CrossRef]
- Horwood, J.T. Higher order first integrals in classical mechanics. J. Math. Phys. 2007, 48, 102902. [Google Scholar] [CrossRef]
- Tsamparlis, M.; Mitsopoulos, A. Quadratic first integrals of autonomous conservative dynamical systems. J. Math. Phys. 2020, 61, 072703. [Google Scholar] [CrossRef]
- Tsamparlis, M.; Mitsopoulos, A. First integrals of holonomic systems without Noether symmetries. J. Math. Phys. 2020, 61, 122701. [Google Scholar] [CrossRef]
- Mukherjee, P.; Chakrabarti, S. Exact solutions and accelerating universe in modified Brans–Dicke theories. Eur. Phys. J. C 2019, 79, 681. [Google Scholar] [CrossRef]
- Giacomini, A.; Leon, G.; Paliathanasis, A.; Pan, S. Cosmological evolution of two-scalar fields cosmology in the Jordan frame. Eur. Phys. J. C 2020, 80, 1–31. [Google Scholar] [CrossRef]
- Cid, A.; Leon, G.; Leyva, Y. Intermediate accelerated solutions as generic late-time attractors in a modified Jordan-Brans-Dicke theory. J. Cosmol. Astropart. Phys. 2016, 2016, 27. [Google Scholar] [CrossRef][Green Version]
- Jamil, M.; Momeni, D.; Myrzakulov, R. Noether symmetry of F(T) cosmology with quintessence and phantom scalar fields. Eur. Phys. J. C 2012, 72, 2137. [Google Scholar] [CrossRef]
- Paliathanasis, A. Dynamics of chiral cosmology. Class. Quantum Gravity 2020, 37, 195014. [Google Scholar] [CrossRef]
- Dimakis, N.; Paliathanasis, A. Crossing the phantom divide line as an effect of quantum transitions. Class. Quantum Gravity 2021, 38, 075016. [Google Scholar] [CrossRef]
- Brown, A.R. Hyperbolic Inflation. Phys. Rev. Lett. 2018, 121, 251601. [Google Scholar] [CrossRef] [PubMed]
- Coley, A.A.; Hoogen, R.V.D. Dynamics of multi-scalar-field cosmological models and assisted inflation. Phys. Rev. D 2000, 62, 023517. [Google Scholar] [CrossRef]
- Cai, Y.-F.; Saridakis, E.; Setare, M.R.; Xia, J.-Q. Quintom cosmology: Theoretical implications and observations. Phys. Rep. 2010, 493, 1–60. [Google Scholar] [CrossRef]
- Choi, K.-Y.; Kim, S.A.; Kyae, B. Primordial curvature perturbation during and at the end of multi-field inflation. Nucl. Phys. B 2012, 861, 271–289. [Google Scholar] [CrossRef]
- Lyth, D.H. Generating the curvature perturbation at the end of inflation. JCAP 2005, 11, 6. [Google Scholar] [CrossRef][Green Version]
- Langlois, D.; Renaux-Peterl, S. Perturbations in generalized multi-field inflation. JCAP 2008, 804, 17. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.; Oikonomou, V. Ghost-free F (R) gravity with Lagrange multiplier constraint. Phys. Lett. B 2017, 775, 44–49. [Google Scholar] [CrossRef]
- Capozziello, S.; Matsumoto, J.; Nojiri, S.; Odintsov, S.D. Dark energy from modified gravity with Lagrange multipliers. Phys. Lett. B 2010, 693, 198–208. [Google Scholar] [CrossRef]
- Chervon, S.V.; Fomin, I.V.; Pozdeeva, E.O.; Sami, M.; Vernov, S.Y. Superpotential method for chiral cosmological models connected with modified gravity. Phys. Rev. D 2019, 100, 063522. [Google Scholar] [CrossRef]
- da Silva, M.R.M.C. A transformation approach for finding first integrals of motion of dynamical systems. Int. J. Non Linear Mech. 1974, 9, 241. [Google Scholar] [CrossRef]
- Sarlet, W.; Bahar, L. A direct construction of first integrals for certain non-linear dynamical systems. Int. J. Non-Linear Mech. 1980, 15, 133–146. [Google Scholar] [CrossRef]
- Mitsopoulos, A.; Tsamparlis, M. Quadratic first integrals of time-dependent dynamical systems of the form . Mathematics 2021, 9, 1503. [Google Scholar] [CrossRef]
- Karpathopoulos, L.; Paliathanasis, A.; Tsamparlis, M. Lie and Noether point symmetries for a class of nonautonomous dynamical systems. J. Math. Phys. 2017, 58, 082901. [Google Scholar] [CrossRef]
- Katzin, G.H.; Levine, J. Dynamical symmetries and constants of the motion for classical particle systems. J. Math. Phys. 1974, 15, 1460–1470. [Google Scholar] [CrossRef]
- Prince, G.E.; Eliezer, C.J. Symmetries of the time-dependent N-dimensional oscillator. J. Phys. A Math. Gen. 1980, 13, 815–823. [Google Scholar] [CrossRef]
- Stephani, H.; Kramer, D.; Maccallum, M.; Hoenselaers, C.; Herlt, E. Exact Solutions to Einstein’s Field Equations, 2nd ed.; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Stephani, H. A new interior solution of Einstein’s field equations for a spherically symmetric perfect fluid in shear-free motion. J. Phys. A Math. Gen. 1983, 16, 3529–3532. [Google Scholar] [CrossRef]
- Srivastana, D.C. Exact solutions for shear-free motion of spherically symmetric perfect fluid distributions in general relativity. Class. Quant. Grav. 1987, 4, 1093. [Google Scholar] [CrossRef]
- Leach, P.G.L.; Maharaj, S.D. A first integral for a class of time-dependent anharmonic oscillators with multiple anharmonicities. J. Math. Phys. 1992, 33, 2023–2030. [Google Scholar] [CrossRef]
- Leach, P.G.L.; Maartens, R.; Maharaj, S.D. Self-similar solutions of the generalized Emden-Fowler equation. Int. J. Non-Linear Mech. 1992, 27, 575. [Google Scholar] [CrossRef]
- Maharaj, S.D.; Leach, P.G.L.; Maartens, R. Expanding spherically symmetric models without shear. Gen. Relativ. Gravit. 1996, 28, 35–50. [Google Scholar] [CrossRef]
- Duarte, L.G.S.; Moreira, I.C.; Euler, N.; Steeb, W.-H. Invertible point transformations, Lie symmetries and the Painlevé test for the equation d2x/dt2 + f1(t)dx/dt + f2(t)x + f3(t)xn = 0. Phys. Scr. 1991, 43, 449–451. [Google Scholar] [CrossRef]
- Liddle, A.; Scherrer, R.J. Classification of scalar field potentials with cosmological scaling solutions. Phys. Rev. D 1998, 59, 023509. [Google Scholar] [CrossRef]
- Uzan, J.P. Effects of a scalar fifth force on the dynamics of a charged particle as a new experimental design to test chameleon theories. Phys. Rev. D 1999, 59, 123510. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mitsopoulos, A.; Tsamparlis, M.; Leon, G.; Paliathanasis, A. New Conservation Laws and Exact Cosmological Solutions in Brans–Dicke Cosmology with an Extra Scalar Field. Symmetry 2021, 13, 1364. https://doi.org/10.3390/sym13081364
Mitsopoulos A, Tsamparlis M, Leon G, Paliathanasis A. New Conservation Laws and Exact Cosmological Solutions in Brans–Dicke Cosmology with an Extra Scalar Field. Symmetry. 2021; 13(8):1364. https://doi.org/10.3390/sym13081364
Chicago/Turabian StyleMitsopoulos, Antonios, Michael Tsamparlis, Genly Leon, and Andronikos Paliathanasis. 2021. "New Conservation Laws and Exact Cosmological Solutions in Brans–Dicke Cosmology with an Extra Scalar Field" Symmetry 13, no. 8: 1364. https://doi.org/10.3390/sym13081364
APA StyleMitsopoulos, A., Tsamparlis, M., Leon, G., & Paliathanasis, A. (2021). New Conservation Laws and Exact Cosmological Solutions in Brans–Dicke Cosmology with an Extra Scalar Field. Symmetry, 13(8), 1364. https://doi.org/10.3390/sym13081364