Sensitivity of KM3NeT to Violation of Equivalence Principle
Abstract
1. Introduction
2. Neutrino Oscillations in the Presence Of VEP
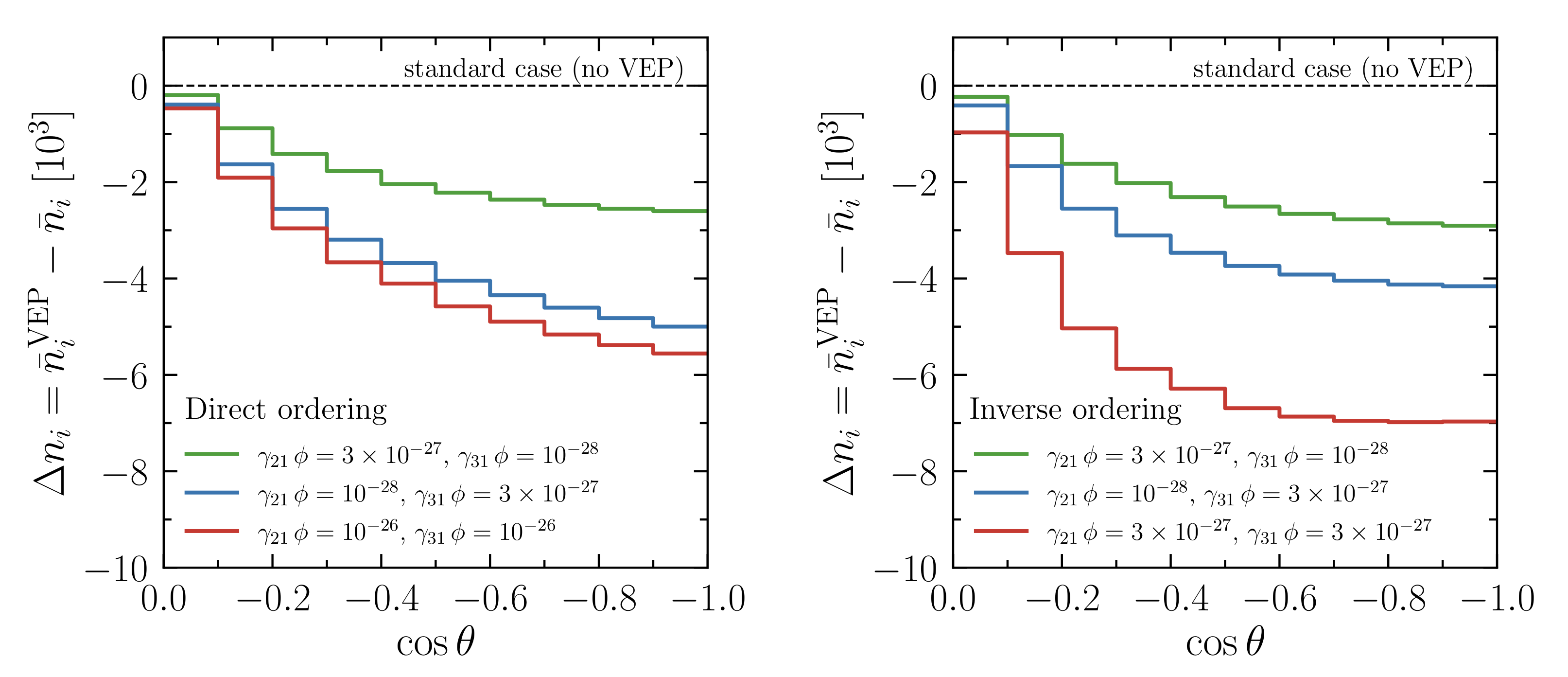
3. Forecast Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wagner, T.A.; Schlamminger, S.; Gundlach, J.H.; Adelberger, E.G. Torsion-balance tests of the weak equivalence principle. Class. Quant. Grav. 2012, 29, 184002. [Google Scholar] [CrossRef]
- Overduin, J.; Mitcham, J.; Warecki, Z. Expanded solar-system limits on violations of the equivalence principle. Class. Quant. Grav. 2014, 31, 015001. [Google Scholar] [CrossRef][Green Version]
- Hohensee, M.A.; Leefer, N.; Budker, D.; Harabati, C.; Dzuba, V.A.; Flambaum, V.V. Limits on Violations of Lorentz Symmetry and the Einstein Equivalence Principle using Radio-Frequency Spectroscopy of Atomic Dysprosium. Phys. Rev. Lett. 2013, 111, 050401. [Google Scholar] [CrossRef]
- Damour, T.; Schaefer, G. New tests of the strong equivalence principle using binary pulsar data. Phys. Rev. Lett. 1991, 66, 2549–2552. [Google Scholar] [CrossRef] [PubMed]
- Horvat, R. Pulsar velocities due to a violation of the equivalence principle by neutrinos. Mod. Phys. Lett. A 1998, 13, 2379–2384. [Google Scholar] [CrossRef]
- Barkovich, M.; Casini, H.; D’Olivo, J.C.; Montemayor, R. Pulsar motions from neutrino oscillations induced by a violation of the equivalence principle. Phys. Lett. B 2001, 506, 20–26. [Google Scholar] [CrossRef]
- Pantaleone, J.T.; Halprin, A.; Leung, C.N. Neutrino mixing due to a violation of the equivalence principle. Phys. Rev. D 1993, 47, R4199–R4202. [Google Scholar] [CrossRef] [PubMed]
- Butler, M.N.; Nozawa, S.; Malaney, R.A.; Boothroyd, A.I. Gravitationally induced neutrino oscillations. Phys. Rev. D 1993, 47, 2615–2618. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Krastev, P.I.; Leung, C.N. Solar neutrinos and the principle of equivalence. Phys. Rev. D 1995, 52, 1770–1779. [Google Scholar] [CrossRef]
- Halprin, A.; Leung, C.N.; Pantaleone, J.T. A Possible violation of the equivalence principle by neutrinos. Phys. Rev. D 1996, 53, 5365–5376. [Google Scholar] [CrossRef] [PubMed]
- Mureika, J.R.; Mann, R.B. Mass or gravitationally induced neutrino oscillations? A Comparison of B-8 neutrino flux spectra in a three generation framework. Phys. Lett. B 1996, 368, 112–118. [Google Scholar] [CrossRef]
- Mureika, J.R.; Mann, R.B. Three flavor gravitationally induced neutrino oscillations and the solar neutrino problem. Phys. Rev. D 1996, 54, 2761–2778. [Google Scholar] [CrossRef] [PubMed]
- Mureika, J.R. An Investigation of equivalence principle violations using solar neutrino oscillations in a constant gravitational potential. Phys. Rev. D 1997, 56, 2408–2418. [Google Scholar] [CrossRef]
- Mansour, S.W.; Kuo, T.K. Solar neutrinos and the violation of equivalence principle. Phys. Rev. D 1999, 60, 097301. [Google Scholar] [CrossRef]
- Gago, A.M.; Nunokawa, H.; Zukanovich Funchal, R. The Solar neutrino problem and gravitationally induced long wavelength neutrino oscillation. Phys. Rev. Lett. 2000, 84, 4035–4038. [Google Scholar] [CrossRef] [PubMed]
- Casini, H.; D’Olivo, J.C.; Montemayor, R. VEP oscillation solutions to the solar neutrino problem. Phys. Rev. D 2000, 61, 105004. [Google Scholar] [CrossRef]
- Majumdar, D.; Raychaudhuri, A.; Sil, A. Solar neutrino results and violation of the equivalence principle: An Analysis of the existing data and predictions for SNO. Phys. Rev. D 2001, 63, 073014. [Google Scholar] [CrossRef]
- Gasperini, M. Testing the Principle of Equivalence with Neutrino Oscillations. Phys. Rev. D 1988, 38, 2635–2637. [Google Scholar] [CrossRef] [PubMed]
- Gasperini, M. Experimental Constraints on a Minimal and Nonminimal Violation of the Equivalence Principle in the Oscillations of Massive Neutrinos. Phys. Rev. D 1989, 39, 3606–3611. [Google Scholar] [CrossRef]
- Minakata, H.; Nunokawa, H. Testing the principle of equivalence by solar neutrinos. Phys. Rev. D 1995, 51, 6625–6634. [Google Scholar] [CrossRef]
- Valdiviesso, G.A.; Guzzo, M.M.; de Holanda, P.C. Probing new limits for the Violation of the Equivalence Principle in the solar–reactor neutrino sector as a next to leading order effect. Phys. Lett. B 2011, 701, 240–247. [Google Scholar] [CrossRef]
- Foot, R.; Volkas, R.R.; Yasuda, O. Up-down atmospheric neutrino flux asymmetry predictions for various neutrino oscillation scenarios. Phys. Lett. B 1998, 421, 245–249. [Google Scholar] [CrossRef]
- Foot, R.; Volkas, R.R.; Yasuda, O. Confronting solutions to the atmospheric neutrino anomaly involving large angle neutron(mu) —> neutron(e) oscillations with Super-Kamiokande and CHOOZ. Phys. Lett. B 1998, 433, 82–87. [Google Scholar] [CrossRef]
- Fogli, G.L.; Lisi, E.; Marrone, A.; Scioscia, G. Testing violations of special and general relativity through the energy dependence of muon-neutrino <—> tau-neutrino oscillations in the Super-Kamiokande atmospheric neutrino experiment. Phys. Rev. D 1999, 60, 053006. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, M.C.; Maltoni, M. Status of global analysis of neutrino oscillation data. In Proceedings of the 5th Workshop on Neutrino Oscillations and their Origin (NOON2004), Tokyo, Japan, 11–15 February 2004. [Google Scholar] [CrossRef]
- Gonzalez-Garcia, M.C.; Halzen, F.; Maltoni, M. Physics reach of high-energy and high-statistics icecube atmospheric neutrino data. Phys. Rev. D 2005, 71, 093010. [Google Scholar] [CrossRef]
- Battistoni, G.; Becherini, Y.; Cecchinib, S.; Cozzi, M.; Dekhissi, H.; Esposito, L.S.; Giacomelli, G.; Giorgini, M.; Mandrioli, G.; Manzoor, S.; et al. Search for a Lorentz invariance violation contribution in atmospheric neutrino oscillations using MACRO data. Phys. Lett. B 2005, 615, 14–18. [Google Scholar] [CrossRef]
- Morgan, D.; Winstanley, E.; Thompson, L.F.; Brunner, J.; Thompson, L.F. Neutrino telescope modelling of Lorentz invariance violation in oscillations of atmospheric neutrinos. Astropart. Phys. 2008, 29, 345–354. [Google Scholar] [CrossRef][Green Version]
- Abbasi, R.; Abdou, Y.; Ackermann, M.; Adams, J.; Ahlers, M.; Andeen, K.; Auffenberg, J.; Bai, X.; Baker, M.; Barwick, S.W.; et al. Determination of the Atmospheric Neutrino Flux and Searches for New Physics with AMANDA-II. Phys. Rev. D 2009, 79, 102005. [Google Scholar] [CrossRef]
- Pakvasa, S.; Simmons, W.A.; Weiler, T.J. Test of Equivalence Principle for Neutrinos and Anti-neutrinos. Phys. Rev. D 1989, 39, 1761. [Google Scholar] [CrossRef]
- Guzzo, M.M.; Nunokawa, H.; Tomas, R. Testing the principle of equivalence by supernova neutrinos. Astropart. Phys. 2002, 18, 277–286. [Google Scholar] [CrossRef]
- Minakata, H.; Smirnov, A.Y. High-energy cosmic neutrinos and the equivalence principle. Phys. Rev. D 1996, 54, 3698–3705. [Google Scholar] [CrossRef]
- Iida, K.; Minakata, H.; Yasuda, O. A Test of the equivalence principle by long baseline neutrino oscillation experiments. Mod. Phys. Lett. A 1993, 8, 1037–1046. [Google Scholar] [CrossRef]
- Mann, R.B.; Sarkar, U. Test of the equivalence principle from neutrino oscillation experiments. Phys. Rev. Lett. 1996, 76, 865–868. [Google Scholar] [CrossRef]
- Esmaili, A.; Gratieri, D.R.; Guzzo, M.M.; de Holanda, P.C.; Peres, O.L.G.; Valdiviesso, G.A. Constraining the violation of the equivalence principle with IceCube atmospheric neutrino data. Phys. Rev. D 2014, 89, 113003. [Google Scholar] [CrossRef]
- Díaz, F.N.; Hoefken, J.; Gago, A.M. Effects of the Violation of the Equivalence Principle at DUNE. Phys. Rev. D 2020, 102, 055020. [Google Scholar] [CrossRef]
- Tino, G.M.; Cacciapuoti, L.; Capozziello, S.; Lambiase, G.; Sorrentino, F. Precision Gravity Tests and the Einstein Equivalence Principle. Prog. Part. Nucl. Phys. 2020, 112, 103772. [Google Scholar] [CrossRef]
- Aslanides, E.; Aubert, J.J.; Basa, S. A Deep Sea Telescope for High-Energy Neutrinos. Available online: https://antares.in2p3.fr/Publications/proposal/proposal99/proposal.pdf (accessed on 1 April 2021).
- Soldner-Rembold, S.; Aartsen, M.G. Letter of Intent: The Precision IceCube Next Generation Upgrade (PINGU). arXiv 2014, arXiv:1401.2046. [Google Scholar]
- Barwick, S.W. ARIANNA: A New Concept for UHE Neutrino Detection. In Proceedings of the 30th International Cosmic Ray Conference, Merida, Yucatan, Mexico, 3–11 July 2007. [Google Scholar]
- Meures, T. The Askar’yan Radio Array, an UHE-neutrino detector at South Pole. Proc. Int. Sch. Phys. Fermi 2012, 182, 321–325. [Google Scholar] [CrossRef]
- Martineau-Huynh, O.; Bustamante, M.; Carvalho, W.; Charrier, D.; Jon5, S.D.; de Vries, K.D.; Fang, K.; Feng, Z.; Finley, C.; Gou, Q.; et al. The Giant Radio Array for Neutrino Detection. EPJ Web Conf. 2016, 116, 03005. [Google Scholar] [CrossRef]
- Schulz, O. The IceCube DeepCore. AIP Conf. Proc. 2009, 1085, 783–786. [Google Scholar] [CrossRef]
- Blaufuss, E.; Kopper, C.; Haack, C. The IceCube-Gen2 High Energy Array. PoS 2016, ICRC2015, 1146. [Google Scholar] [CrossRef]
- Ageron, M.; Sánchez, J.A.A.; Samara, I.A.; Albert, A.; Ameli, F.; André, M.; Anghinolfi, M.; Anton, G.; Anvar, S.; Ardid, M.; et al. ANTARES: The first undersea neutrino telescope. Nucl. Instrum. Meth. A 2011, 656, 11–38. [Google Scholar] [CrossRef]
- Belolaptikov, I.A.; Bezrukov, L.B.; Borisovets, B.A.; Budnev, N.M.; Bugaev, E.V.; Chensky, A.G.; Danilchenko, I.A.; Djilkibaev, J.-A.M.; Dobrynin, V.I.; Domogatsky, G.V.; et al. The Baikal underwater neutrino telescope: Design, performance and first results. Astropart. Phys. 1997, 7, 263–282. [Google Scholar] [CrossRef]
- Riccobene, G. Status and development of KM3NeT/ARCA. PoS 2017, NOW2016, 54. [Google Scholar] [CrossRef]
- Kappes, A. KM3NeT: A Next Generation Neutrino Telescope in the Mediterranean Sea. arXiv 2007, arXiv:0711.0563. [Google Scholar]
- Goldschmidt, A. The IceCube detector. In Proceedings of the 27th International Cosmic Ray Conference, Hamburg, Germany, 7–15 August 2001. [Google Scholar]
- Karle, A.; Ahrens, J.; Bahcall, J.N.; Bai, X.; Becka, T.; Becker, K.-H.; Besson, D.Z.; Berley, D.; Bernardini, E.; Bertrand, D.; et al. Icecube—The next generation neutrino telescope at the south pole. Nucl. Phys. B Proc. Suppl. 2003, 118, 388–395. [Google Scholar] [CrossRef]
- Fiorillo, D.F.G.; Mangano, G.; Morisi, S.; Pisanti, O. IceCube constraints on Violation of Equivalence Principle. JCAP 2021, 4, 079. [Google Scholar] [CrossRef]
- Adrián-Martínez, S.; Ageron, M.; Aharonian, F.; Aiello, S.; Albert, A.; Ameli, F.; Anassontzis, E.; Andre, M.; Androulakis, G.; Anghinolfi, M.; et al. Letter of intent for KM3NeT 2.0. J. Phys. G 2016, 43, 084001. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alispach, C.; Allison, P.; Amin, N.M.; et al. IceCube-Gen2: The Window to the Extreme Universe. J. Phys. G 2021, 48, 060501. [Google Scholar] [CrossRef]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Particle Physics. PTEP 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Samarai, I.A.; Altmann, D.; Andeen, K.; Anderson, T.; et al. Neutrino Interferometry for High-Precision Tests of Lorentz Symmetry with IceCube. Nat. Phys. 2018, 14, 961–966. [Google Scholar] [CrossRef]
- Kenyon, I.R. A Recalculation of the Gravitational Mass Difference Between the K0 and K¯0 Mesons. Phys. Lett. B 1990, 237, 274–277. [Google Scholar] [CrossRef]
- Honda, M.; Kajita, T.; Kasahara, K.; Midorikawa, S.; Sanuki, T. Calculation of atmospheric neutrino flux using the interaction model calibrated with atmospheric muon data. Phys. Rev. D 2007, 75, 043006. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chianese, M.; Fiorillo, D.F.G.; Mangano, G.; Miele, G.; Morisi, S.; Pisanti, O. Sensitivity of KM3NeT to Violation of Equivalence Principle. Symmetry 2021, 13, 1353. https://doi.org/10.3390/sym13081353
Chianese M, Fiorillo DFG, Mangano G, Miele G, Morisi S, Pisanti O. Sensitivity of KM3NeT to Violation of Equivalence Principle. Symmetry. 2021; 13(8):1353. https://doi.org/10.3390/sym13081353
Chicago/Turabian StyleChianese, Marco, Damiano F. G. Fiorillo, Gianpiero Mangano, Gennaro Miele, Stefano Morisi, and Ofelia Pisanti. 2021. "Sensitivity of KM3NeT to Violation of Equivalence Principle" Symmetry 13, no. 8: 1353. https://doi.org/10.3390/sym13081353
APA StyleChianese, M., Fiorillo, D. F. G., Mangano, G., Miele, G., Morisi, S., & Pisanti, O. (2021). Sensitivity of KM3NeT to Violation of Equivalence Principle. Symmetry, 13(8), 1353. https://doi.org/10.3390/sym13081353





