The Improvement of Elliptic Curve Factorization Method to Recover RSA’s Prime Factors
Abstract
:1. Introduction
2. Overviews of RSA and ECC
2.1. RSA
2.2. Elliptic Curve Cryptography
3. Overviews of Integer Factorization Algorithms
3.1. Special-Purpose Factoring
3.2. General-Purpose Factoring
| Algorithm 1 ECM |
| Input:n, P = (x1, y1) |
Output:p, q
|
4. Overviews of Quantum Computer and Shor’s Factoring
5. The Proposed Method
| Algorithm 2 Generating the ECC over Finite Field |
| Input:n |
Output: P = (x1, y1), 2P = (x2, y2), a, b, x3 (3P = (x3, y3)), x4 (4P = (x4, y4)), m3, m4
|
| Algorithm 3 F-ECM |
| Input:n, P = (x1, y1), 2P = (x2, y2), a, b, x3, x4, m3, m4 |
Output:p, q
|
6. Loop Analysis
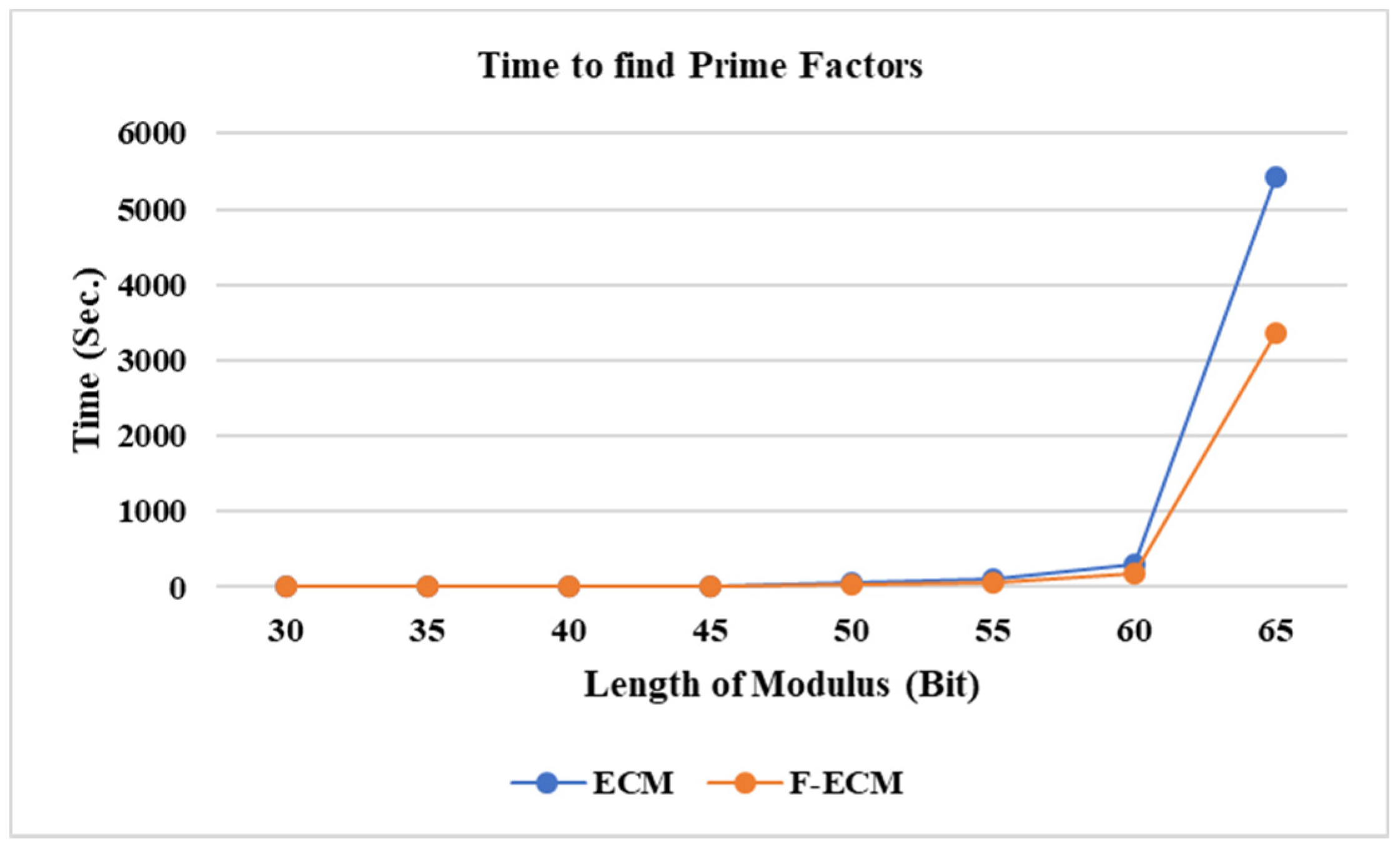
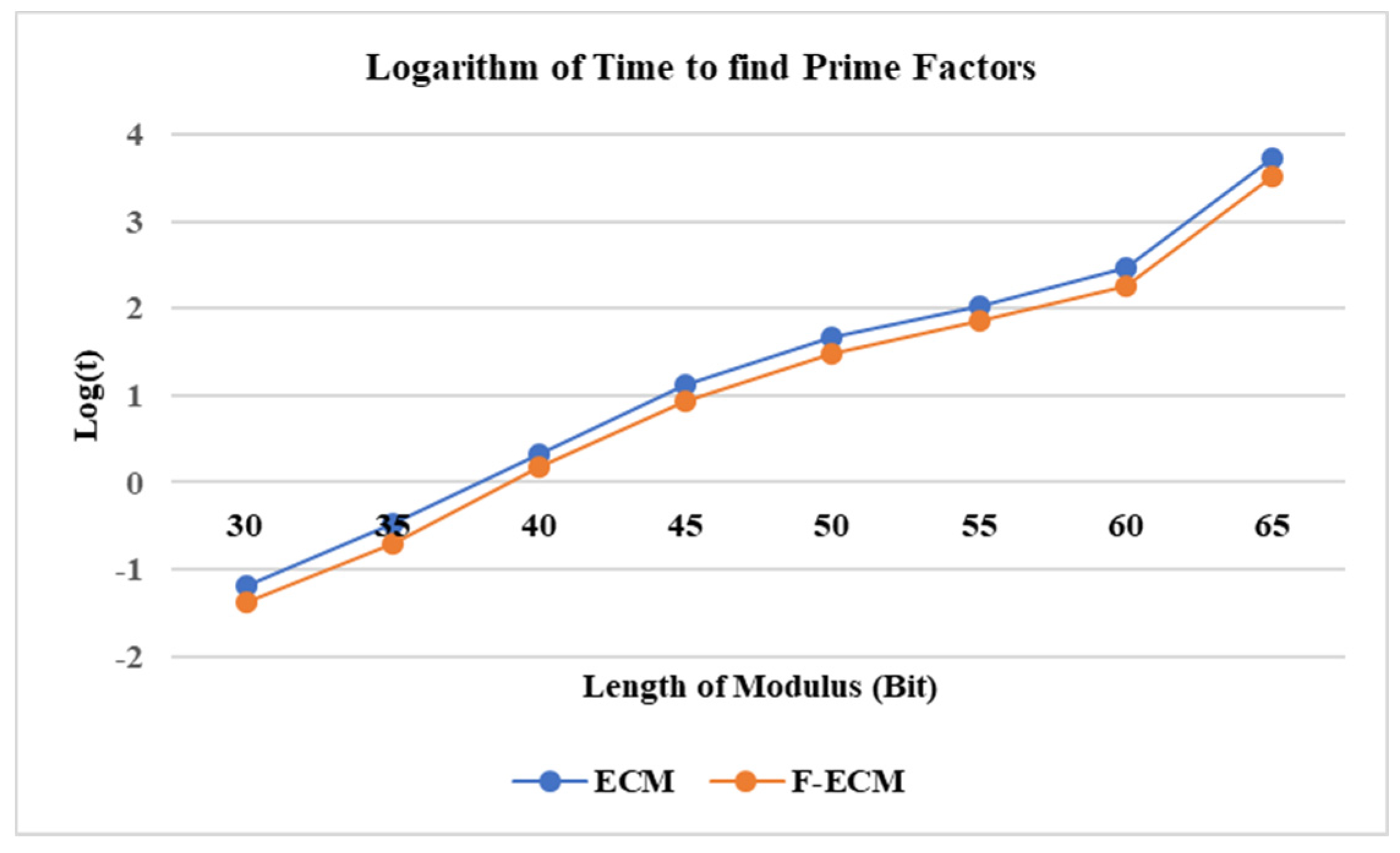
7. Experimental Results
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Diffie, W.; Hellman, M.E. New directions in cryptography. IEEE Trans. Inf. Theory 1976, 22, 644–654. [Google Scholar] [CrossRef] [Green Version]
- Sitalakshmi, V.; Anthony, O. New Method of Prime Factorisation-Based Attacks on RSA Authentication in IoT. Cryptography 2019, 3, 20. [Google Scholar]
- Ruzai, W.N.A.; Ariffin, M.R.K.; Asbullah, M.A.; Mahad, Z.; Nawawi, A. On the Improvement Attack upon Some Variants of RSA Cryptosystem via the Continued Fractions Method. IEEE Access 2020, 8, 80997–81006. [Google Scholar] [CrossRef]
- Sharma, P.; Gupta, A.K.; Vijay, A. Modified Integer Factorization Algorithm using V-Factor Method. In Proceedings of the International Conference on Advanced Computing & Communication Technologies, Rohtak, India, 7–8 January 2012; pp. 423–425. [Google Scholar]
- Koblitz, N. Elliptic Curve Cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Miller, V.S. Uses of elliptic curves in cryptography. Lect. Notes Comput. Sci. 1986, 218, 417–428. [Google Scholar]
- Amadori, A.; Pintore, F.; Sala, M. On the discrete logarithm problem for prime-field elliptic curves. Finite Fields Appl. 2018, 51, 168–182. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.C.; Chang, T.Y.; Hwang, M.S. A new anonymous conference key distribution system based on the elliptic curve discrete logarithm problem. Comput. Stand. Interfaces 2003, 25, 141–145. [Google Scholar] [CrossRef]
- Su, P.C.; Change, H.K.C.; Lu, L.H. ID-based threshold digital signature schemes on the elliptic curve discrete logarithm problem. Appl. Math. Comput. 2005, 164, 757–772. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Zhou, Q.; Tian, C.; Zhang, H.; Yu, J.; Li, F. How to securely outsource the extended Euclidean algorithm for large-scale polynomials over finite fields. Inf. Sci. 2020, 512, 641–660. [Google Scholar] [CrossRef]
- Hazmi, I.; Gebali, F.; Ibrahim, A. High Speed and Low Area Complexity Extended Euclidean Inversion Over Binary Fields. IEEE Trans. Consum. Electron. 2019, 65, 408–417. [Google Scholar] [CrossRef]
- Horng, S.J.; Tzeng, S.F.; Fan, P.; Wang, X.; Li, T.; Khan, M.K. Secure Convertible Undeniable Signature Scheme Using Extended Euclidean Algorithm without Random Oracles. KSII Trans. Internet Inf. Syst. 2013, 7, 1512–1532. [Google Scholar]
- Eisentrager, K.; Lauter, K.; Montgomery, P.L. Fast Elliptic curve arithmetic and improved Weil pairing evaluation. Lect. Notes Comput. Sci. 2003, 2612, 343–354. [Google Scholar]
- Obaidat, M.; Brown, J.; Obeidat, S.; Rawashdeh, M. A Hybrid Dynamic Encryption Scheme for Multi-Factor Verification: A Novel Paradigm for Remote Authentication. Sensors 2020, 20, 4212. [Google Scholar] [CrossRef]
- Singh, L.D.; Debbrama, T. A new approach to Elliptic curve cryptography. In Proceedings of the International Conference on Advanced Communication Control and Computing Technologies, Ramanathapuram, India, 8–10 May 2014; pp. 78–82. [Google Scholar]
- Tange, H.; Anderson, B. Attacks and Countermeasures on AES and ECC. In Proceedings of the International Symposium on Wireless Personal Multimedia Communications, Atlantic City, NJ, USA, 24–27 June 2013; pp. 1–5. [Google Scholar]
- Somsuk, K.; Sanemueang, C. The New Modified Methodology to Solve ECDLP Based on Brute Force Attack. Adv. Intell. Syst. Comput. 2019, 769, 255–264. [Google Scholar]
- Nidhi, L.; Anurag, P.; Shishupal, K. Modified Trial Division Algorithm Using KNJ-Factorization Method to Factorize RSA Public Key Encryption. In Proceedings of the International Conference on Contemporary Computing and Informatics, Mysore, India, 27–29 November 2014; pp. 992–995. [Google Scholar]
- Raghunandan, K.R.; Aithal, G.; Shetty, S. Comparative Analysis of Encryption and Decryption Techniques Using Mersenne Prime Numbers and Phony Modulus to Avoid Factorization Attack of RSA. In Proceedings of the International Conference on Advanced Mechatronic Systems, Kusatsu, Japan, 26–28 August 2019; pp. 152–157. [Google Scholar]
- Somsuk, S.; Chiawchanwattana, T.; Sanemueang, C. Estimating the new Initial Value of Trial Division Algorithm for Balanced Modulus to Decrease Computation Loops. In Proceedings of the International Joint Conference on Computer Science and Software Engineering, Chonburi, Thailand, 10–12 July 2019; pp. 137–141. [Google Scholar]
- Ambedkar, B.R.; Gupta, A.; Gautam, P.; Bedi, S.S. An Efficient Method to Factorize the RSA Public Key Encryption. In Proceedings of the International Conference on Communication Systems and Network Technologies, Katra, India, 3–5 June 2011; pp. 108–111. [Google Scholar]
- Wu, M.E.; Tso, R.; Sun, H.M. On the improvement of Fermat factorization using a continued fraction technique. Future Gener. Comput. Syst. 2014, 30, 162–168. [Google Scholar] [CrossRef]
- Somsuk, K. The improvement of initial value closer to the target for Fermat’s factorization algorithm. J. Discret. Math. Sci. Cryptogr. 2018, 21, 1573–1580. [Google Scholar] [CrossRef]
- Tahir, R.R.M.; Asbullah, M.A.; Ariffin, M.R.K.; Mahad, Z. Determination of a Good Indicator for Estimated Prime Factor and Its Modification in Fermat’s Factoring Algorithm. Symmetry 2021, 13, 735. [Google Scholar] [CrossRef]
- Somsuk, K.; Tientanopajai, K. An Improvement of Fermat’s Factorization by Considering the Last m Digits of Modulus to Decrease Computation Time. Int. J. Netw. Secur. 2017, 19, 99–111. [Google Scholar]
- Omar, K.; Szalay, L. Sufficient conditions for factoring a class of large integers. J. Discret. Math. Sci. Cryptogr. 2010, 13, 95–103. [Google Scholar]
- Pollard, J.M. Theorems of factorization and primality testing. Math. Proc. Camb. Philos. Soc. 1974, 76, 521–528. [Google Scholar] [CrossRef]
- Murat, S. Generalized Trial Division. Int. J. Contemp. Math. Sci. 2011, 6, 59–64. [Google Scholar]
- Lenstra, H.W., Jr. Factoring integers with elliptic curves. Ann. Math. 1987, 126, 649–673. [Google Scholar] [CrossRef] [Green Version]
- Macariu, G.; Petcu, D. Parallel Multiple Polynomial Quadratic Sieve on Multi-Core Architectures. In Proceedings of the International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Timisoara, Romania, 26–29 September 2017; pp. 59–65. [Google Scholar]
- Gaj, K.; Kwon, S.; Baier, P.; Kohlbrenner, P.; Le, H.; Khaleeluddin, M.; Bachimanchi, R.; Rogawski, M. Area-Time Efficient Implementation of the Elliptic Curve Method of Factoring in Reconfigurable Hardware for Application in the Number Field Sieve. IEEE Trans. Comput. 2010, 59, 1264–1280. [Google Scholar] [CrossRef]
| Algorithm | Computation Costs | |||
|---|---|---|---|---|
| I | M | S | G | |
| F-ECM | 2 | 15 | 4 | 3 |
| ECM | 5 | 10 | 5 | 6 |
| Algorithm | Computation Costs | |||
|---|---|---|---|---|
| I | M | S | G | |
| F-ECM | 8 | 57 | 16 | 9 |
| ECM | 16 | 32 | 16 | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somsuk, K. The Improvement of Elliptic Curve Factorization Method to Recover RSA’s Prime Factors. Symmetry 2021, 13, 1314. https://doi.org/10.3390/sym13081314
Somsuk K. The Improvement of Elliptic Curve Factorization Method to Recover RSA’s Prime Factors. Symmetry. 2021; 13(8):1314. https://doi.org/10.3390/sym13081314
Chicago/Turabian StyleSomsuk, Kritsanapong. 2021. "The Improvement of Elliptic Curve Factorization Method to Recover RSA’s Prime Factors" Symmetry 13, no. 8: 1314. https://doi.org/10.3390/sym13081314
APA StyleSomsuk, K. (2021). The Improvement of Elliptic Curve Factorization Method to Recover RSA’s Prime Factors. Symmetry, 13(8), 1314. https://doi.org/10.3390/sym13081314





