Abstract
This study investigated the stability of structural motifs via molecular dynamics, using α-α-corners as an example. A molecular dynamics experiment was performed on a sample of α-α-corners selected by the authors from the PDB database. For the first time during a molecular dynamics experiment, we investigated the characteristics of structural motifs by describing their geometry, including the interplanar distance, area of polygon of the helices projections intersection, and torsion angles between axes of helices in helical pairs. The torsion angles for the constriction amino acids in the equilibrium portion of the molecular dynamics trajectory were analyzed. Using the molecular dynamics method, α-α-corners were found to be autonomous structures that are stable in aquatic environments.
1. Introduction
Simple structural motifs are a current focus of researchers. These consist of two elements of the secondary structure, which are characterized by unique folding of the polypeptide chain in space. This interest in structural motifs is due to the uniqueness of the structures and their ability to act as focuses in the process of protein folding [1]. Structural motifs can be used as starting structures to identify possible folds in a polypeptide chain when modeling protein structures. They can also be used as stable structures in studies to predict the tertiary structure of a protein.
Previously, Efimov [1] presented a classification of structural motifs, including two α-helices, with unique folds of the polypeptide chain in space (α-α-corners, α-α-hairpins, and L-shaped and V-shaped structures). Types of helical pairs are presented in the Figure 1.
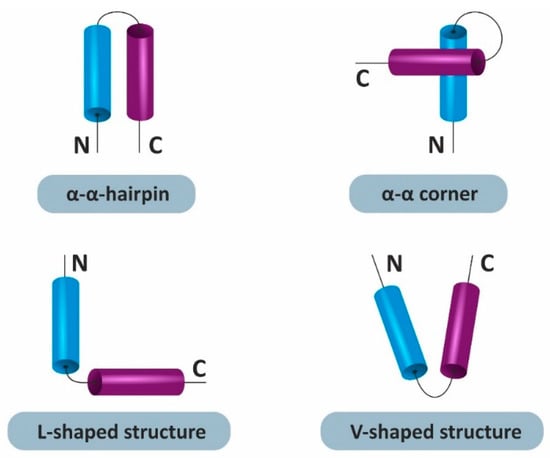
Figure 1.
Types of the helical pairs, including two α-helices, with unique folds of the polypeptide chain in space.
The α-α-hairpin motif is a supersecondary structure comprising two adjacent α-helices in the chain, which are constricted and packed antiparallel. The hairpin can be left or right, depending on how the second α-helix is located relative to the first. The length of the constrictions between the helices can also differ, and each standard α-α-hairpin contains hydrophobic, hydrophilic, and glycine residues at strictly defined locations [2].
Supersecondary L- and V-shaped structures are formed by two helices. Proline plays a special role in the formation of L-shaped structures and promotes a link between two α-helices. Similar to studs, L-shaped structures can be right-handed or left-handed [3]. V-shaped structures are also very similar to α-α-hairpins, in which the unconnected ends of α-helices are very far from each other; they also appear as L-shaped structures. In V-shaped structures, α-helices have a length that does not exceed three to four turns.
One of the most common structural motifs in homologous and non-homologous proteins is the α-α-corner [4]. This supersecondary structure is formed by two adjacent α-helices along the polypeptide chain, connected by a constriction and packed orthogonally in space. In proteins, α-α-corners occur in the form of a left supercoil. Their sequences have a definite arrangement in chains of hydrophobic, hydrophilic, and glycine residues. The side chains of residues buried in the hydrophobic core are hydrophobic. Hydrophilic side chains or other polar groups can be recessed into a hydrophobic core (or other hydrophobic environment) if they participate in the formation of hydrogen or ionic bonds [1]. Thus, each α-helix must have at least one hydrophobic residue per turn; in this case, hydrophobic residues should be located on one side of the α-helix and form a continuous hydrophobic cluster [4].
Previously [5,6,7,8], we investigated the geometric characteristics of double-helical structures. Important characteristics of helical pairs include inter-helical distances, the torsion angles between helical axes in helical pairs, the number of amino acids between helixes, the length of the helixes, and the area and perimeter of the intersection of helical projections. In a previous study [9], we formulated rules for the classification of double-helical motifs based on the geometric and spatial characteristics of their packing.
In proteins, α-helices are tightly packed. Two α-helices are packed most densely when there is an antiparallel, perpendicular, and canted orientation between the helices; examples of such packing include the supersecondary structures α-α-corners, α-α-hairpins, and L-shaped and V-shaped structures (Figure 1). The most studied α-α-corners are those with short constrictions. The constriction represents the disordered part of the molecule, and each amino acid residue within the constriction has a certain conformation from the allowed regions on the Ramachandran map. Since the conformational change in the molecule chain is significant (close to rotation), the conformations of residues in the short constriction are clamped within a narrower range. These patterns were noted in [4] and require a comprehensive study and statistical analysis.
Many small proteins exist that comprise only one or two known structural motifs, indicating that such structural motifs are stable [4]. The stability of α-α-corners was demonstrated indirectly in 1993 by Canadian researchers F. Tsai and J. Sherman (University of British Columbia, Canada) in an experimental study using the circular dichroism method [10]. In that study, using a synthetic horse methemoglobin peptide (residues 80–108) with α-α-corner folding as an example, the conformation was found to be autonomously stable outside the protein structure. Thus, in water, the peptide forms a moderately helical shape and acquires a form close to that of the peptide in the solvent trifluoroethanol, which mimics the hydrophobic environment of the peptide in the intact protein molecule [10].
In addition, we independently proposed and tested a hypothesis on the autonomous stability of structural motifs in computational experiments of molecular dynamics (MD) [11,12]. In this work, the trajectories obtained using MD were studied in detail, considering stability. For the first time, using supersecondary structures of the α-α-corner type, α-α-corners with a short constriction as autonomous structures were found to be stable in a water environment.
This work is a continuation of our earlier studies on the stability of these structural motives. It is focused on a visual analysis of molecular dynamics trajectories and on a numerical analysis of geometric characteristics of the structures. For the first time, the characteristics of structural motifs describing their geometry were obtained and investigated during a molecular dynamics experiment, as follows: the interplanar distance, the intersection area of helical projections, the angle φ between the helical axes, and the torsion angle θ between the helical axes of a pair, the sign of which is the chirality of the structure. We analyzed the φ and ψ angles for the constriction amino acids in the equilibrium section of the MD trajectory.
2. Materials and Methods
The study was performed using 50 structural motifs of the α-α-corner type, which were obtained from the PDB database [12,13]. The secondary structures of proteins were determined using the DSSP method, as described by Kabsch and Sander [14]. Secondary structures are designated as follows: H, α-helix; B, residue in isolated β-bridge; E, extended strand, participates in the β-ladder; G, helix 310; I, π-helix; T, hydrogen-bonded turn; S, bend; and C, coil.
MD modeling of the molecular fragment of the α-α-corner and subsequent analyses were performed using the AMBER 11 software package [15]. Dynamic simulations were performed with consideration of the water environment. During preparation of the initial data, a complex surrounded by water molecules was placed in the cell under periodic boundary conditions (PBCs). The number of water molecules for each molecular fragment differed; however, the thickness of the water layer from the edge of the molecular fragment to the cell boundary of the periodic boundary conditions was 9 Å. The force parameters of the water molecules were selected according to the TIP3P model [16]. The simulation was performed in a force field ff03 [17,18] at 300 K. Initially, the energy of the system was minimized at a fixed position of the coordinates of Cα atoms of protein. This aimed to streamline the atomic interactions and distribute water molecules evenly in the PBC cell. Then, the system was heated slightly at a constant volume, and the position of the Cα atoms was fixed. This is necessary to correctly align the water molecules surrounding the model α-α-corner relative to the boundaries of the PBC cell. This warm-up lasted for 10 ps. Furthermore, the energy of the model was minimized in two successive stages, with a partial weakening of the forces fixing the positions of the atoms of the α-α-corner molecule in space. In the next stage, the entire system was heated without restrictions to 300 K at a constant volume. After heating for 10 ps, the simulation was performed at a constant pressure for 15 ps. In this case, the cell with periodic boundary conditions was adjusted in order to obtain a given density of the medium in the system. Consequently, the system reached a state with the desired parameters, from which the MD trajectory with a duration of 11 ns was further calculated at a constant pressure of 1 atm.
3. Results
This study investigated the hypothesis that structural motifs, such as α-α-corners, possess autonomous stability. In this case, autonomous stability is understood as the stability of the spatial structure of the studied structural motif separately from the protein molecule containing the structure. To conduct an MD experiment on the stability of structural motifs, a sample of α-α-corners was obtained from globular proteins with resolved 3D structures by X-ray structural analysis and nuclear magnetic resonance, registered in the PDB database. The sample consisted of 50 α-α-corners and included proteins with the coordinates of the atoms forming these structures and the serial number of the helical pair in the protein globule (Table 1).

Table 1.
List of selected globular proteins indicating the coordinates of the atoms of structural motifs of the α-α-corner type and the serial number of the helical pair in the protein.
As shown in Table 1, the selected helical pairs belong to proteins of predominantly bacterial origin. All proteins were globular, with a rich content of α-helices. The molecular weights of the selected proteins ranged from 7 to 82 kDa. High values were observed for the aliphatic index of the studied proteins, most of which exceeded 70. The aliphatic index reflects the relative content of hydrophobic amino acid residues and the volume occupied by amino acid side groups. Values above 70 are believed to correspond to proteins with a high content of hydrophobic amino acids; therefore, such proteins are stable and thermostable. The selected proteins were found to exert similar functional activity; all possess natural molecular partners, since they are enzymes or DNA-binding proteins.
To confirm the stability of the corners under study, we performed a computational experiment in which the following were investigated: change in the conformation of the corner constriction in each of the 5000 frames of the MD experiment by recording the values of the torsion angles of each amino acid residue of the irregular region; change in the values of the geometric characteristics of the studied motifs during the experiment; and the intersection area of the helical projections, the interplanar distance, and the angles between helical axes of the pair.
All structural motifs possess their own conformational patterns, based on the distribution of the values of the φ and ψ angles on the Ramachandran map. To describe the conformation of the polypeptide chain, the following nomenclature is used [4]: α, αL, and β regions on the Ramachandran map correspond to the right α-helix, left helix, and β-structure, respectively.
Thus, the conformation of each residue of the polypeptide chain is indicated by one of the nomenclature symbols. The conformation of a supersecondary structure of the α-α-corner type with a short constriction can be represented as a template:
where n and m are the number of α-helix residues and αLββ is a connection pattern. According to the distribution of the limiting values of the φ and ψ angles on the Ramachandran map for all possible regions, a conformational description of the residues of irregular regions for the studied structures was determined as follows:
αmαLββαn
The entire sample of structural motifs was subdivided into subsets, depending on the constriction pattern: αLββ, ααLββ, αLββα, αLβαLαL, and εαLαLαLββ. Distributions of the φ and ψ angle values on the Ramachandran map and histograms of the distributions of the geometric characteristics of the α-α-corners of each subset are presented in the Supplementary Material. Most of the structures comprised the first subset, with the constricted structures satisfying the αLββ pattern (38 α-α-corners). As an example, Figure 2 shows the results of the conformational analysis along the MD trajectory for the α-α-corner found in PDB ID 1P48 (coordinates of its entry into this protein: 106–137; serial number of the helical pair in the protein molecule: 2).
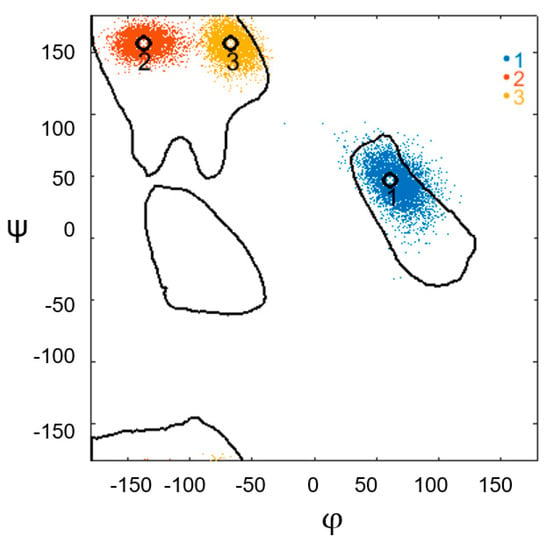
Figure 2.
Change in the conformation of the constriction of the α-α-corner found in PDBID 1P48 (Cα: 106–137) during the MD experiment, based on the values of the torsion angles φ and ψ of each amino acid residue of the irregular region. The colored dots represent the torsion angles of the amino acid constriction for each point of the trajectory. The legend on the right indicates the sequence of amino acids in the constriction: blue denotes the first amino acid, red denotes the second amino acid, and orange denotes the third amino acid of the constriction. Black circles represent the values of the φ and ψ angles of the experimental structure before the start of the MD experiment. Each point is denoted by a serial number, which represents the constriction amino acids of the experimental structure.
Figure 2 demonstrates the stability of the structure by preserving the φ and ψ angles; that is, preserving the conformation of the corner constriction in each of 5000 frames of the MD experiment. The calculated values of the torsion angles of each amino acid residue of the constriction during the experiment lie within the region recorded before the experiment.
The histograms in Figure 3 show the changes in the quantities that describe the geometry of the α-α-corner PDB ID 1P48 (Cα: 106–137) during the MD experiment. The upper-left histogram reflects the change in the interplanar distance between the helixes; the upper-right histogram reflects the change in the intersection area of the helical projections; the lower-left histogram shows the change in the φ angle value between the helical axes of the structural motif; and the lower-right histogram shows the change in the θ angle value between the helical axes of the studied motif PDB ID 1P48 (Cα: 106–137). In each histogram, the triangles mark the values of the studied quantities before the start of the MD experiment. For a given corner, the triangles mark the center of each histogram, which indicates that the structure has high geometric stability. According to the results of the experiment, most corners with a short constriction (three amino acids) satisfying the αLββ pattern are stable structures.
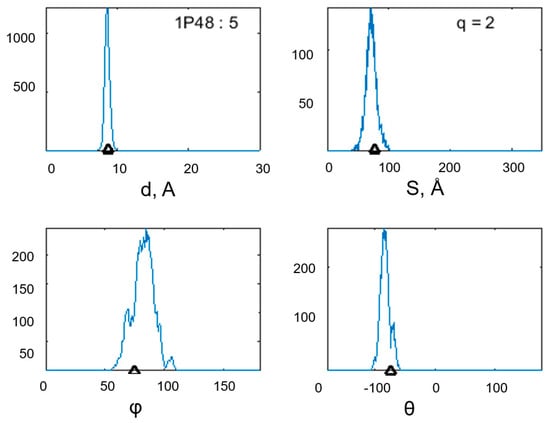
Figure 3.
Changes in the geometric characteristics of the α-α-corner PDB ID 1P48 (Cα: 106–137) during the MD experiment: the interplanar distance between the helixes, the intersection area of the helical projections, and the φ and θ angles between the helical axes of the structural motif. In the captions for each histogram, the mean value and standard deviation are given. In the figure with the histogram of the interplanar distance, the structure identifier is duplicated; in the figure with the histogram, the total charge of the structure is shown. Black triangles mark the values of the studied quantities before the start of the MD experiment.
However, this is not always the case. The results of the MD experiment show that the geometric stability of the structure could be observed, despite the disturbed angular stability of the amino acids in the irregular region. An example of such a structural motif is the α-α-corner of PDB ID 1B9M (Cα: 34–59) (Figure 4 and Figure 5). As shown in Figure 4, this corner initially has a short constriction, consisting of three amino acids, and satisfies the αLββ template. However, during the MD experiment, the constriction conformation changes as follows: the torsion angles of the first amino acid of the constriction from the αL region pass into the β region; the angles of the second amino acid change and are localized at the initial values of the third amino acid but still remain in the β; torsion angles of the third amino acid from the β region during the experiment pass into the α region. The stability of the irregular region of this supersecondary structure was disturbed. However, its geometric characteristics provide information on the autonomous stability of this structure in an aquatic environment (see Figure 5). Figure 5 illustrates the distribution of the geometric characteristics of the structure during the MD experiment. The figure shows that the geometry of this motive is not violated. The interplanar spacing, d, between the helices before the start of the experiment was approximately 10 Å, and during the experiment, the distribution of d values was single-mode and around the initial value. Histograms showing the distribution of values for the φ and θ angles between the helical axes and the area of intersection of the helical projections of the structural motif also support the stability of the α-α-corner PDB ID 1B9M (Cα: 34–59). Notably, during the experiment, the intersection area of the helixes had a slightly smaller value than before the experiment; that is, the initial value was not in the center of the histogram. This may indicate that the instability of the constriction conformation influenced the stability of this characteristic. However, overall, all characteristics support the stability of this structure.
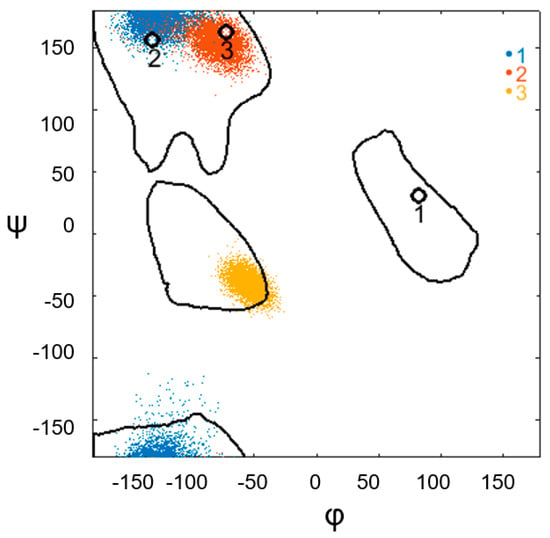
Figure 4.
Change in the conformation of the α-α-corner PDB ID 1B9M (Cα: 34–59) during the MD experiment, obtained by recording the values of the torsion angles φ and ψ of each amino acid residue in the irregular region. The colored dots indicate the φ and ψ angles of the constriction amino acids for each point of the trajectory. The legend on the right indicates the sequence of amino acids in the constriction: blue denotes the first amino acid, red denotes the second amino acid, and orange denotes the third amino acid of the constriction. Black circles represent the values of the φ and ψ angles of the experimental structure before the start of the MD experiment. Each point is denoted with a serial number, which represents the constriction amino acids of the experimental structure.
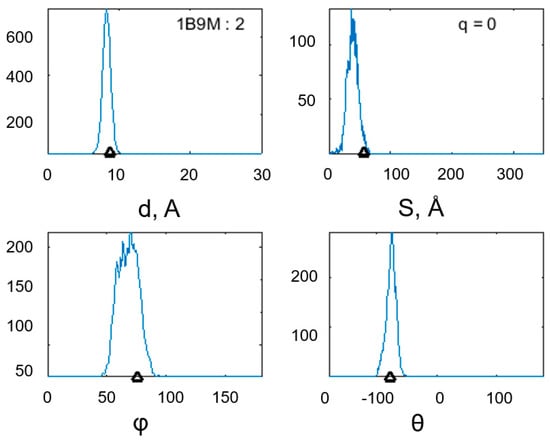
Figure 5.
Distribution of the geometric characteristics of the α-α-corner PDB ID 1B9M (Cα: 34–59) during the MD experiment: the interplanar distance between the helixes, the intersection area of the helical projections, and the φ and θ angles between the helical axes of the structural motif. In the figure with the histogram of the interplanar distance, the structure identifier is duplicated, and in the figure with the histogram of the, the total charge of the structure is shown. Black triangles mark the values of the studied quantities before the start of the MD experiment.
Next, we investigated the structures for which the first or last amino acid of the constriction falls into region α on the Ramachandran map. These are structures with constrictions that match the ααLββ and αLββα patterns. Generally, these amino acids should be referred to as α-helices and not as constrictions. Their appearance in the connection is a consequence of using the DSSP program, which identifies the secondary structure by angles as well as hydrogen bonds. For structures with a connection of this type, there is no fundamental difference in the behavior of the MD experiment from structures with an αLββL type waist between the helices. The experimental results indicate that these corners are stable structures. In addition, in some cases, the angular stability of the amino acids of the irregular region is violated, but the results of the MD experiment confirm the geometric stability of the structure.
Among the structures selected for the experiment were the two α-α-corners PDB ID 2NX4 (Cα: 8–40) and PDB ID 2OEM (Cα:360–385), with the constriction patterns αLβαLαL and εαLαLαLββ, respectively. The length of the constriction of the α-α-corner of PDB ID 2OEM (Cα: 360–385) is four, and the irregular region between the helices of the PDB ID 2NX4 structure (Cα: 8–40) consists of six amino acids. Figure 6 and Figure 7 illustrate the conformational changes in the constriction of the α-α-corner of PDB ID 2NX4 (Cα: 8–40) by recording the values of the torsion angles φ and ψ of each amino acid residue of the irregular region during the MD experiment on the Ramachandran map. During the experiment, the region of the torsion angles φ and ψ for the first, second, third, and fourth amino acids of the constriction did not change region: the values of the torsion angles φ and ψ of the first amino acid were recorded in the region ε; the second, third, and fourth were localized in the region α. Values for the torsion angles φ and ψ of the fifth and sixth amino acids of the irregular region before the beginning of the experiment were in the β region. During the MD experiment, the angles of the fifth amino acid presented a strong scatter, with scatter in the α region and scatter in the lower region of the β region. The angles of the sixth amino acid were localized around the initial value of the torsion angles of the fifth amino acid but remained in the β region.
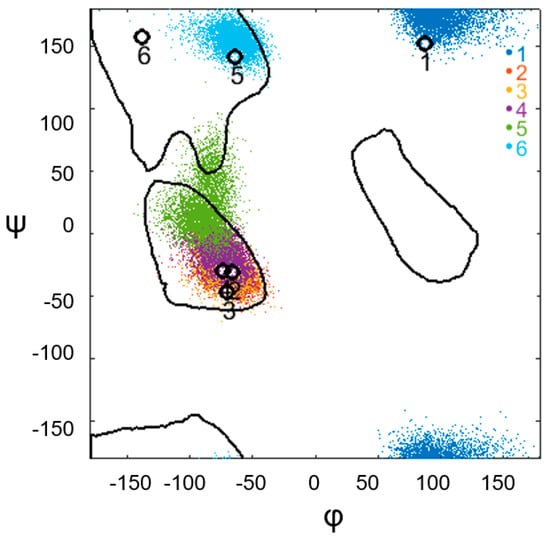
Figure 6.
Conformational changes in the constriction of the α-α-corner of PDB ID 2NX4 (Cα: 8–40) during the MD experiment, obtained by recording the values of the torsion angles φ and ψ for each amino acid residue of the irregular region. The colored dots indicate the φ and ψangles of the constriction amino acids for each point of the trajectory. The legend on the right indicates the sequence of amino acids in the constriction: blue denotes the first amino acid, red denotes the second amino acid, orange denotes the third amino acid, purple denotes the fourth amino acid, light green denotes the fifth amino acid, and blue denotes the sixth amino acid of the constriction. Black circles representthe values of the φ and ψ angles of the experimental structure before the start of the MD experiment. Each point is denoted by a serial number, which represents the constriction amino acids of the experimental structure.
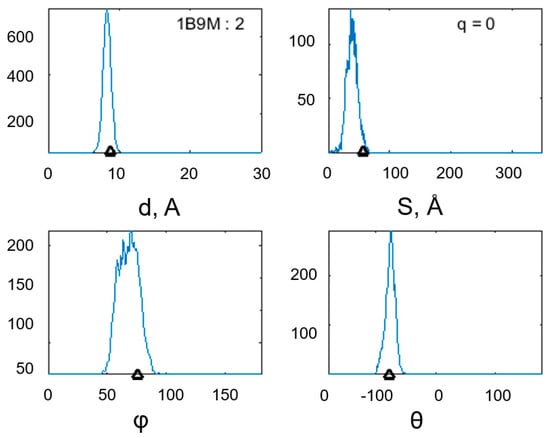
Figure 7.
Distribution of the values for the geometric characteristics of the α-α-corner PDB ID 2NX4 (Cα: 8–40) during the MD experiment: the interplanar distance between the helixes, the intersection area of the helical projections, and the φ and θ angles between the helical axes of the structural motif. In the histogram showing the interplanar distance, the structure identifier is duplicated, and in the histogram, the total charge of the structure is shown. Black triangles mark the values of the studied quantities before the start of the MD experiment.
The geometric characteristics of the α-α-corner of PDB ID 2NX4 (Cα: 8–40) during the MD experiment confirmed the stability of the structure (see Figure 7). The two-mode distribution of values for the interplanar distance between the helixes and the intersection area of the helical projections should be noted; however, the initial values of the studied quantities are within the histograms, which indicates stability.
Generally, the conformation of the α-α-corner constriction was less stable. Residue conformations of the short constriction are clamped within a narrower range and fit well within the angle constraints; therefore, α-α-corners with a short constriction are more stable structures. Conformational analysis made it possible to separate the class of structures with a short waist from the others. This revealed the appearance of some residues in the ε-conformation for structures with a longer constriction. Thus, it can be assumed that the conformation and waist length of such structures contribute to the stability of the structure. However, it should be noted that long-drawn α-α-corners possess structural motives that are less studied.
The distribution of values for the geometric characteristics of the structures under study during the MD experiment are described in Table S1 and Figure S1 (Supplementary Materials), which summarizes the data obtained during the MD experiment for all participating structures. The Supplementary Material provides visual illustrations of the distributions of values for all of the investigated geometric characteristics during the MD experiment for each structure.
4. Conclusions
In this study, we tested the autonomous stability of structural motifs in computational experiments using MD. For the first time on a sample of supersecondary structures of the α-α-corner type, we used MD to perform a conformational analysis of the irregular region between the helices and investigated the geometric characteristics of these structures. The stability of the spatial structure of the structural motif was tested separately for protein molecules containing this structure. We found that almost all motifs presented autonomous stability in an aqueous medium, and the conformation of the structures was maintained during molecular dynamics, with some features as described above.
The main observation from this study was that compact α-α-corners are stable outside the protein molecule and can be studied as independent motifs. Dense packing in the space of α-α-corners and, consequently, high stability are provided by multiple hydrogen bonds, which help to stabilize α-helices, and van der Waals interactions of side polar and charged radicals of amino acids with each other and with solvent molecules.
The characterization of geometric parameters and MD studies of α-α-corners outside the protein structure will benefit a wide range of biomedical challenges. MD study of the α-α-corner motif, which is small in terms of the number of atoms compared with the whole protein molecule, is characterized by its high performance, lower requirements for computing resources, and low costs.
Isolated helical pairs (including α-α-corners) are of interest for the study of structural changes caused by amino acid substitutions in the protein, or post-translational modifications. Important research in medical proteomics includes studies on the molecular basis of diseases associated with modified, aberrant forms of proteins that are not present in healthy people: so-called proteoinopathies. Proteinopathies are often caused by genetic polymorphisms, alternative splicing, and post-translational protein modifications [19]. Examples of diagnostically significant aberrant protein forms include amyloid beta isomers in Alzheimer’s disease [20], osteopontin b and c splice isoforms in prostate cancer [21], an amino acid substitution in protein C7 in type II diabetes [22], and an amino acid substitution in the Ras protein in pancreatic and colorectal cancers [23].
Post-translational modifications, specific to serological proteins of patients with colorectal cancer, are localized in helical pairs, including the α-α-corners. It is likely that the identified post-translational modifications modulate the biological function of a protein, while the protein is associated with oncogenesis [9].
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/sym13071193/s1. Table S1: The results of calculating the geometric characteristics of the structural blocks of protein molecules using the molecular dynamics experiment.
Author Contributions
Conceptualization, D.A.T. and A.L.K.; methodology V.R.R. and L.I.K.; software, formal analysis, A.V.E., D.A.T. and L.I.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work was done in the framework of the Russian Federation fundamental research program for the long-term period for 2021–2030.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Archive-information about the 3D shapes of proteins (PDB IDs) of proteins is presented in the database PDB (https://www.rcsb.org/ (accessed on 1 June 2021)).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Efimov, A.V. Standard structures in proteins. Prog. Biophys. Mol. Biol. 1993, 60, 201–239. [Google Scholar] [CrossRef]
- Brazhnikov, E.V.; Efimov, A.V. Structure of α-α-hairpins with short connections in globular proteins. Mol. Biol. 2001, 35, 89–97. [Google Scholar] [CrossRef]
- Efimov, A.V. L-shaped structure of two α-helices with a proline residue between them. Mol. Biol. 1992, 26, 1370–1376. (In Russian) [Google Scholar]
- Efimov, A.V. New supersecondary structure of proteins: α-α-corner. Mol. Biol. 1984, 18, 1524–1537. (In Russian) [Google Scholar]
- Tikhonov, D.A.; Kulikova, L.I.; Efimov, A.V. Statistical analysis of the internal distances of helical pairs in protein molecules. Math. Biol. Bioinf. 2016, 11, 170–190. (In Russian) [Google Scholar] [CrossRef]
- Tikhonov, D.A.; Kulikova, L.I.; Efimov, A.V. The Study of interhelical angles in the structural motifs formed by two helices. Math. Biol. Bioinf. 2017, 12, 83–101. (In Russian) [Google Scholar] [CrossRef] [Green Version]
- Tikhonov, D.A.; Kulikova, L.I.; Efimov, A.V. Analysis of the Torsion Angles between Helical Axes inPairs of 745 Helices in Protein Molecules. Math. Biol. Bioinf. 2018, 13, t17–t28. [Google Scholar] [CrossRef]
- Tikhonov, D.A.; Kulikova, L.I.; Efimov, A.V. Relationship between the interhelical packing angles and the length of α-helices in proteins. Mol. Biol. 2020, 54, 292–298. [Google Scholar] [CrossRef]
- Tikhonov, D.; Kulikova, L.; Kopylov, A.; Malsagova, K.; Stepanov, A.; Rudnev, V.; Kaysheva, A. super secondary structures of proteins with post-translational modifications in colon cancer. Molecules 2020, 25, 3144. [Google Scholar] [CrossRef] [PubMed]
- Tsai, F.C.; Sherman, J.C. Circular dichroism analysis of a synthetic peptide corresponding to the α-α-corner motif of hemoglobin. Biochem. Biophys. Res. Commun. 1993, 196, 435–439. [Google Scholar] [CrossRef]
- Rudnev, V.R.; Pankratov, A.N.; Kulikova, L.I.; Dedus, F.F.; Tikhonov, D.A.; Efimov, A.V. Recognition and stability analysis of structural motifs of α-α-corner type in globular proteins. Math. Biol. Bioinf. 2013, 8, 398–406. [Google Scholar] [CrossRef]
- Rudnev, V.R.; Pankratov, A.N.; Kulikova, L.I.; Dedus, F.F.; Tikhonov, D.A.; Efimov, A.V. Conformational analysis of structural motifs of α-α-corner in the computational experiment of molecular dynamics. Math. Biol. Bioinf. 2014, 9, 575–584. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein databank. Nucleic Acids Res. 2020, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Cheatham, T.E.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M.C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003, 24, 1999–2012. [Google Scholar] [CrossRef]
- Lee, M.C.; Duan, Y. Distinguish protein decoys by using a scoring function based on a new Amber force field, short molecular dynamics simulations, and the generalized Born solvent model. Proteins 2004, 55, 620–634. [Google Scholar] [CrossRef] [PubMed]
- Kelleher, N.L. A cell-based approach to the human proteome project. J. Am. Soc. Mass Spectrom 2012, 23, 1617–1624. [Google Scholar] [CrossRef] [Green Version]
- Indeykina, M.I.; Popov, I.A.; Kozin, S.A.; Kononikhin, A.S.; Kharybin, O.N.; Tsvetkov, P.O.; Makarov, A.A.; Nikolaev, E.N. Capabilities of MS for analytical quantitative determination of the ratio of α- and βAsp7 isoforms of the amyloid-β peptide in binary mixtures. Anal. Chem. 2011, 8, 3205–3210. [Google Scholar] [CrossRef]
- Tilli, T.M.; Mello, K.D.; Ferreira, L.B.; Matos, A.R.; Accioly, M.T.S.; Faria, P.A.; Bellahcène, A.; Castronovo, V.; Gimba, E.R. Both osteopontin-c and osteopontin-b splicing isoforms exert pro-tumorigenic roles in prostate cancer cells. Prostate 2012, 72, 1688–1699. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.D.; Sun, L.; Yu, D.X.; Li, R.X.; Li, H.X.; Yu, Z.J.; Sheng, Q.H.; Lin, X.; Zeng, R.; Wu, J.R. Quantitative detection of single amino acid polymorphisms by targeted proteomics. Mol. Cell. Biol. 2011, 3, 309–315. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Chaerkady, R.; Wu, J.; Hwang, H.J.; Papadopoulos, N.; Kopelovich, L.; Maitra, A.; Matthaei, H.; Eshleman, J.R.; Hruban, R.H.; et al. Mutant proteins as cancer-specific biomarkers. Proc. Natl. Acad. Sci. USA 2011, 108, 2444–2449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).