Quantum Information in the Protein Codes, 3-Manifolds and the Kummer Surface
Abstract
:1. Introduction
2. Algebraic Geometrical Models of Secondary Structures
2.1. The Gieseking Manifold
2.2. The Hypercartographic Group
2.3. Fundamental Groups of 3-Manifolds
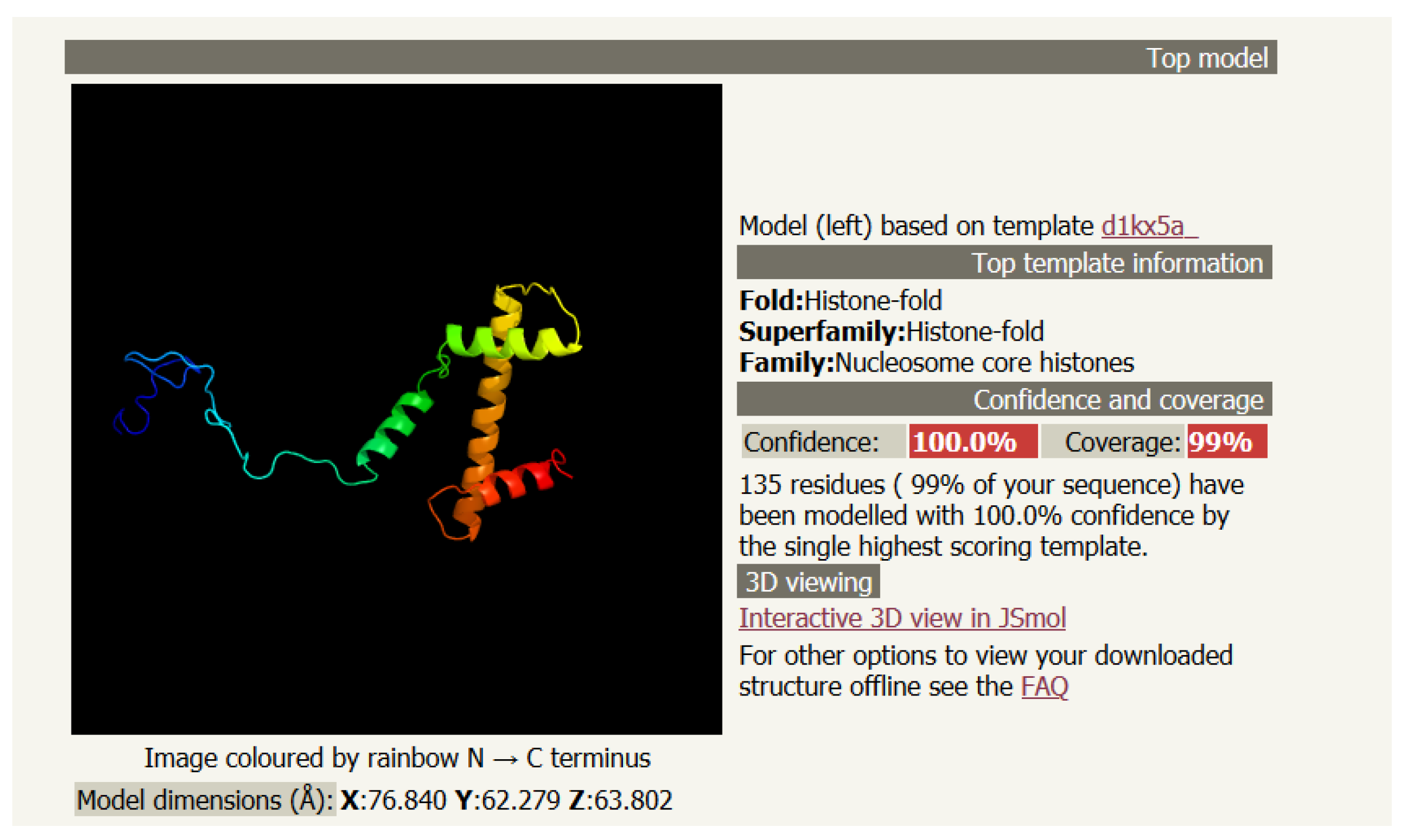
3. Secondary Structure with Helices: Drosophila Melanogaster Histone H3 (PDB 6PWE_1)
3.1. The Primary (Linear) Structure
- IVFSNVK–T-TLVKPKSEMARTKQTARKSTGGKAPRKQLATKAARKSAPATGGVKKPHRYRPGTVALREIRRYQKSTELLIRKLPFQRLVREIAQDFKTDLRFQSSAVMALQEASEAYLVGLFEDTNLCAIHAKRVTIMPKDIQLARRIRGERA-ADTALTCR-SASVLYNRSFS
3.2. The Secondary Structure
- CCCCCCCCCCCCCCCCCHHHHCHHHHCCCCCCCCCCCCCCCCCCCCHHHHHHHCCCCC
- CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCHHHHHHHHHHHHCC
- CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCHHHHHHHHHHHHCCC
- CCCCCCCCCCCCCCCCCCCCHHHHHCCCCCCCCCCCCCCCCCCHHHHHHHHHHHHHCC
- HHHHHCCCCHHHHHHHHHHHCCCCCCCCHHHHHHHHHHHHHHHHHHHHHHHHCHHHH
- CCHHHCCCHHHHHHHHHHHHCCCCCCCCHHHHHHHHHHHHHHHHHHHHHHHHHHHHC
- HHHHHHHHHHHHHHHHHHHHHCCCCCCCHHHHHHHHHHHHHHHHHHHHHHHHHHHHC
- HHHHHHHHHHHHHHHHHHCCCCCCCCCCHHHHHHHHHHHHHHHHHHHHHHHHHHHHC
- CCCCCCHHHHHHHHHHCCCCC
- CCCCCCHHHHHHHHHHCCCCC
- CCCCCCHHHHHHHHHHCCCCC
- CCCCCCHHHHHHHHHHHCCCC
4. Secondary Structures with Helices and Sheets: Myelin P2, Carbonic Anhydrase and the Lsm 1-7 Complex
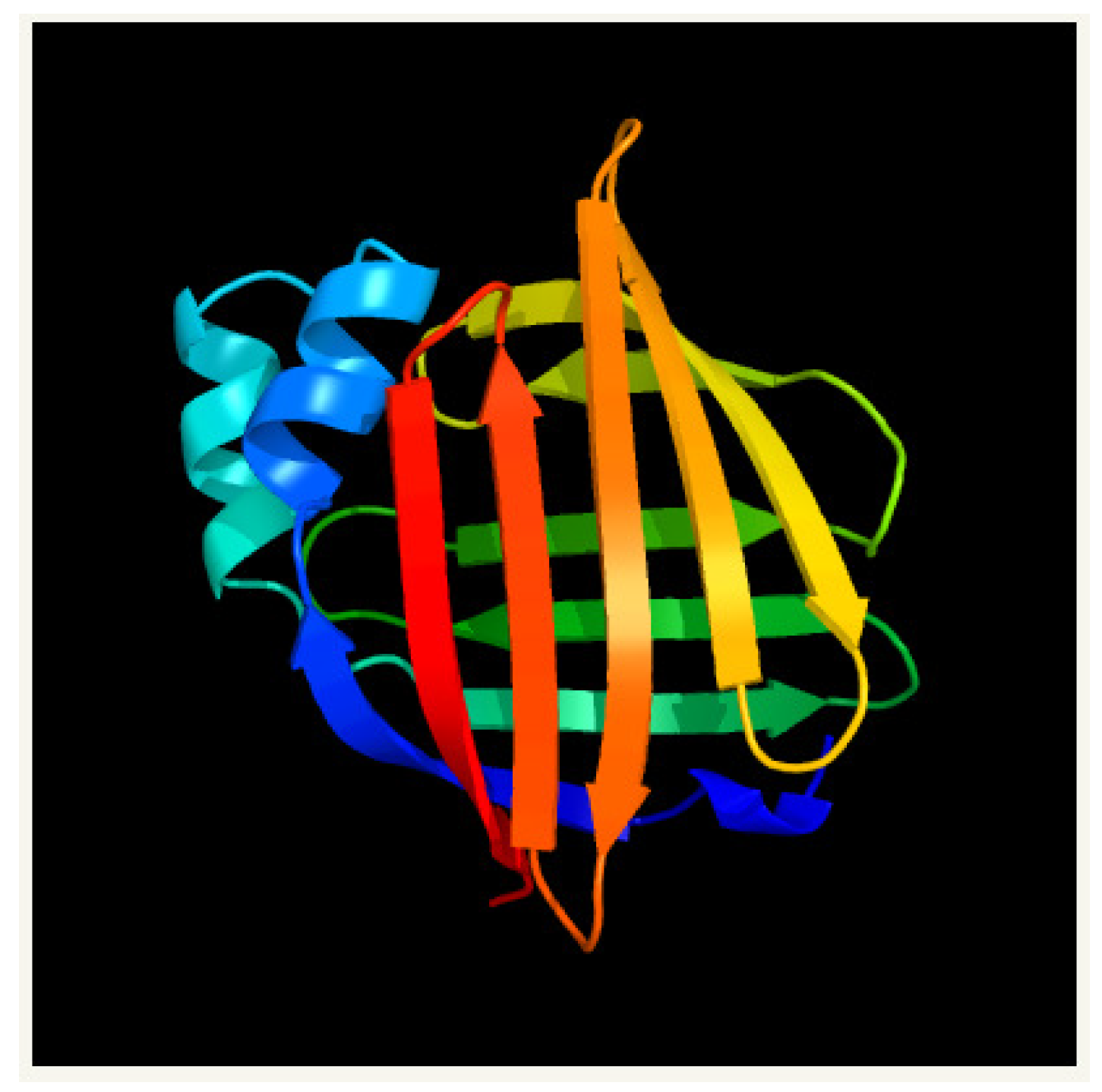
4.1. Myelin P2 for Homo Sapiens (PDB 2WUT)
- GMSNKFLGTWKLVSSENFDDYMKALGVGLATRKLGNLAKPTVIISKKGDIITIRTESTFKN
- CCCHHCCEEEEEEEECCHHHHHHHCCCCHHHHHHHHHCCCEEEEEEECCEEEEEEECCCC
- CCCHHCCEEEEEECCCCHHHHHHHCCCCHHHHHHHHHCCCEEEEEEECCEEEEEEECCCC
- CCCCCCEEEEEEEEECCHHHHHHHHCCCHHHHHHHHCCCCEEEEEEECCEEEEEEECCCC
- CCCCCCEEEEEEEEECCHHHHHHHCCCCHHHHHHHHCCCCEEEEEEECCEEEEEEECCCC
- TEISFKLGQEFEETTADNRKTKSIVTLQRGSLNQVQRWDGKETTIKRKLVNGKMVAECKM
- CCCHHCCEEEEEEEECCHHHHHHHCCCCHHHHHHHHHCCCEEEEEEECCEEEEEEECCCC
- EEEEEEEECCEEEEECCCCCEEEEEEEEECCEEEEEEECCCCEEEEEEEEECCEEEEEEEE
- EEEEEEECCCEEEEECCCCCEEEEEEEEECCEEEEEEECCCCCEEEEEEEECCEEEEEEEE
- EEEEEEECCCEEEEECCCCCEEEEEEEEECCEEEEEEECCCCCEEEEEEEECCEEEEEEEE
- KGVVCTRIYEKV
- CCEEEEEEEEEC
- CCEEEEEEEEEC
- CCEEEEEEEEEC
- CCEEEEEEEEEC
4.2. The 3-Fold Symmetric Complex for Gamma-Carbonic Anhydrase (PDB 1QRE)
4.3. The Hfq Protein Complex of Escherichia coli (PDB 1HK9)
- GAMAKGQSLQDPFLNALRRERVPVSIYLVNGIKLQGQIESFDQFVILLKNTVSQMVYKHAISTVVPSRPVSHHSCCCCCCCCCHHHHHHHHHHCCCCEEEEEECCCEEEEEEEECCCEEEEEECCCEEEEEEEEEEEEEECCCCCCCCCCCCCCCCHHHHHHHHHHHCCCCEEEEEECCEEEEEEEEEECEEEEEEECCCEEEEEEEEEEEEECCCCCCCCCCCCCCCCCCHHHHHHHHHHCCCEEEEEEECCEEEEEEEEEECCEEEEEECCCCEEEEEEEEEEEEECCEEEECCCCCCCCCCCCHHHHHHHHHCCCCEEEEECCCCEEEEEEEEECCCEEEEEECCCEEEEEEEEEEEEECCCCCCCC
4.4. Other n-Fold Symmetric Complexes
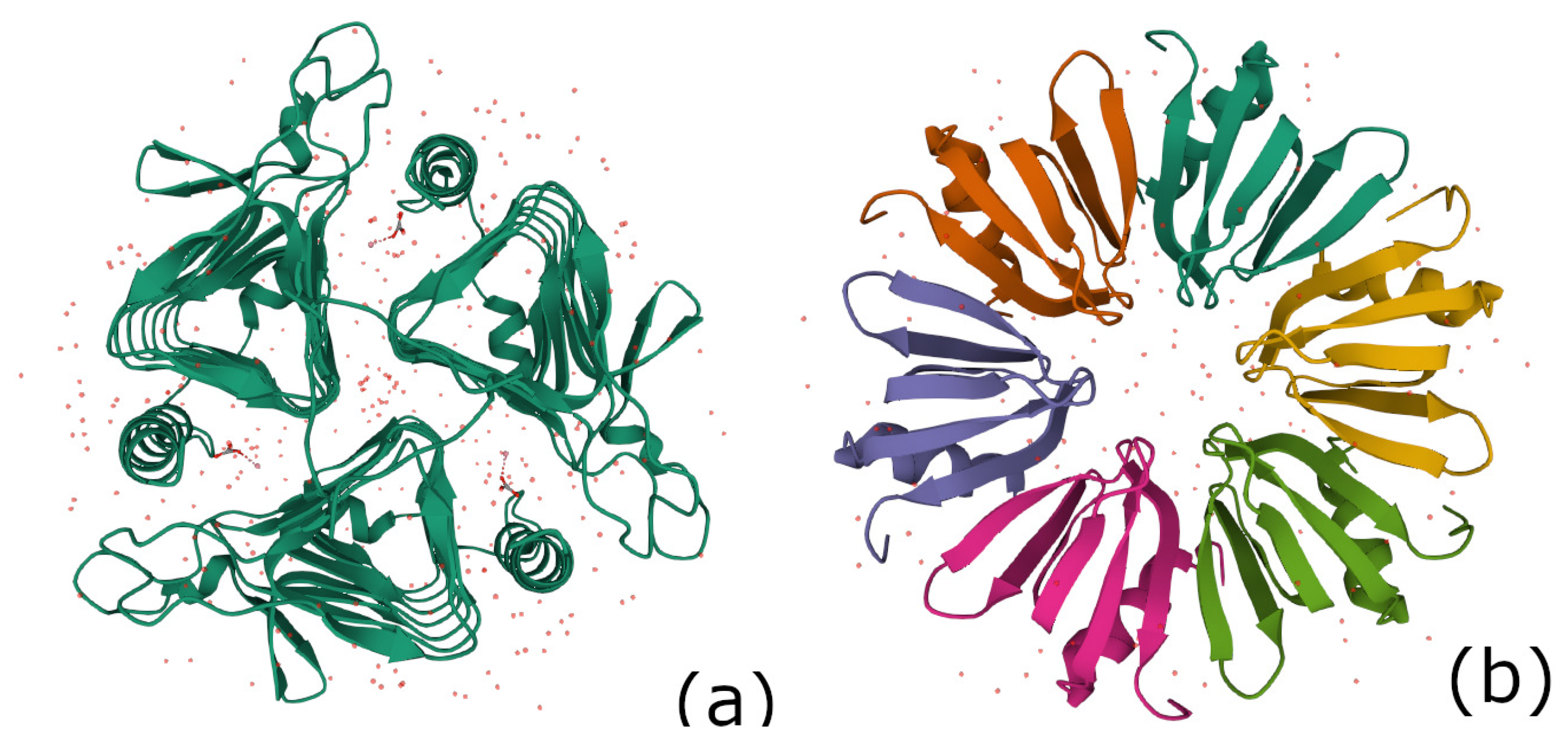
4.4.1. The 5-Fold Symmetric H2A-H2B Complex in Nucleoplasmin (PDB 2XQL)
4.4.2. The 5-Fold Symmetric Acetylcholine Receptor (PDB 2BG9)
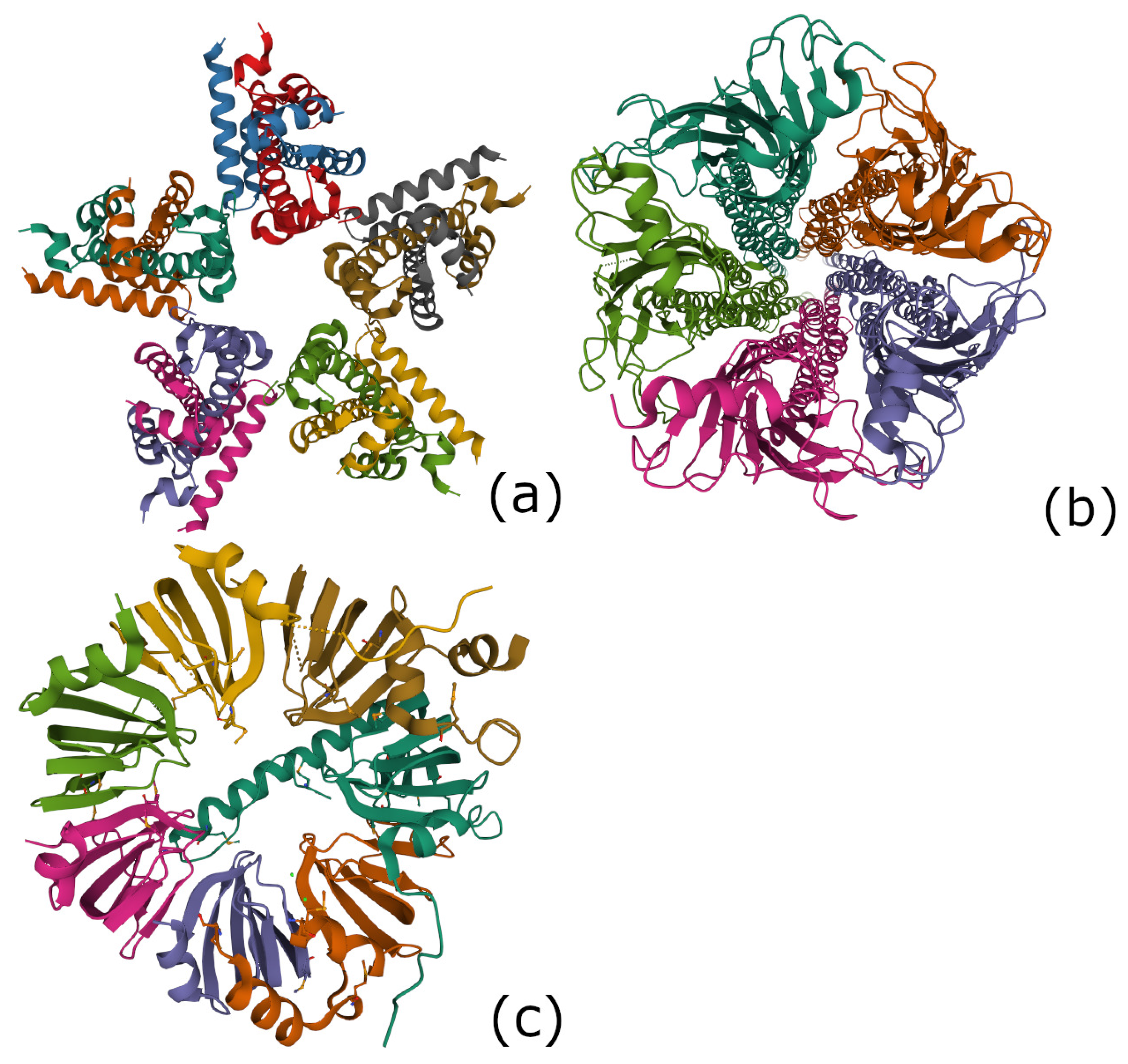
4.4.3. The 7-Fold Symmetric Lsm 1-7 Complex in the Spliceosome (PDB 4M75)
4.4.4. Encoding a Protein with the Characters of the Finite Group
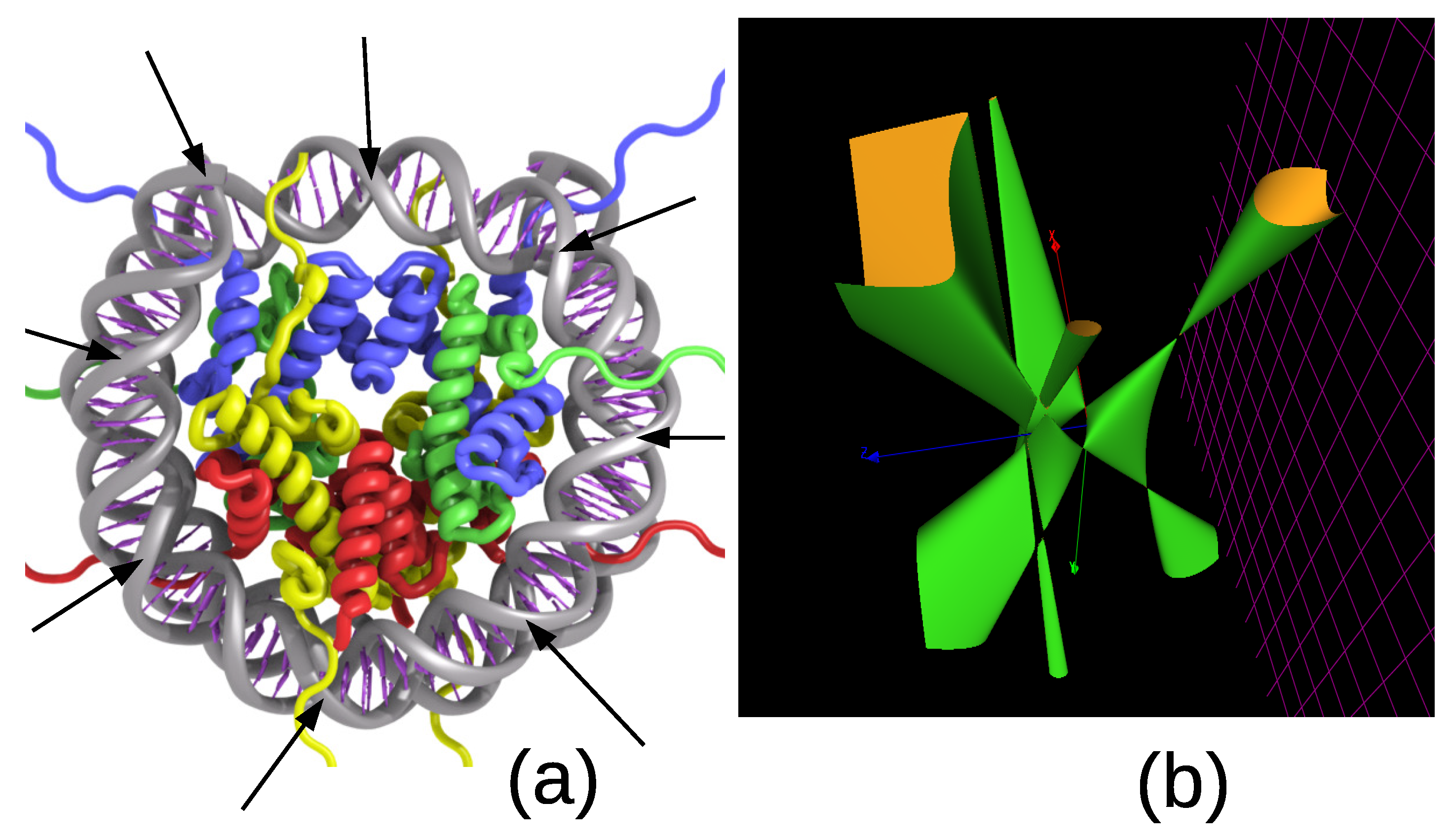
5. The 8-Fold Symmetric Histone Complex of the Nucleosome: 3WKJ in the Protein Data Bank
6. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Bartlett, S.D. Powered by magic. Nature 2014, 510, 345–347. [Google Scholar] [CrossRef] [PubMed]
- Planat, M.; Gedik, Z. Magic informationally complete POVMs with permutations. R. Soc. Open Sci. 2017, 4, 170387. [Google Scholar] [CrossRef] [Green Version]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Group geometrical axioms for magic states of quantum computing. Mathematics 2019, 7, 948. [Google Scholar] [CrossRef] [Green Version]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Fang, F.; Irwin, K. Complete quantum information in the DNA genetic code. Symmetry 2020, 12, 1993. [Google Scholar] [CrossRef]
- Planat, M.; Chester, D.; Aschheim, R.; Amaral, M.M.; Fang, F.; Irwin, K. Finite groups for the Kummer surface: The genetic code and quantum gravity. Quantum Rep. 2021, 3, 68–79. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Informationally complete characters for quark and lepton mixings. Symmetry 2020, 12, 1000. [Google Scholar] [CrossRef]
- The Protein Data Bank. Available online: https://pdb101.rcsb.org/ (accessed on 1 January 2021).
- Dang, Y.; Gao, J.; Wang, J.; Heffernan, R.; Hanson, J.; Paliwal, K.; Zhou, Y. Sixty-five years of the long march in protein secondary structure prediction: The final strech? Brief. Bioinform. 2018, 19, 482–494. [Google Scholar]
- Pauling, L.; Corey, R.B.; Branson, H.R. The structure of proteins: Two hydrogen-bonded helical configurations of the polypeptide chain. Proc. Natl. Acad. Sci. USA 1951, 37, 205–211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pauling, L.; Corey, R.B. Configurations of polypeptide chains with favored orientations around single bonds: Two new pleated sheets. Proc. Natl. Acad. Sci. USA 1951, 37, 729–740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adams, C.C. The noncompact hyperbolic 3-manifold of minimal volume. Proc. Am. Math. Soc. 1987, 4, 100. [Google Scholar]
- Grothendieck, A. Sketch of a Programme, Written in 1984 and Reprinted with Translation in L. Schneps ans P. Lochak eds, Geometric Galois Actions 1. Around Grothendieck’s Esquisse d’un Programme, 2. The Inverse Galois Problem, Moduli Spaces and Mapping Class Groups (Cambridge University Press, 1997); (b) The Grothendieck Theory of Dessins d’Enfants, Schneps, L., Lochak, P., Eds. (Cambridge Univ. Press, 1994). Available online: https://webusers.imj-prg.fr/~leila.schneps/grothendieckcircle/EsquisseEng.pdf (accessed on 1 January 2021).
- Lando, S.K.; Zvonkin, A.K. Graphs on Surfaces and Their Applications; Springer: Berlin, Germany, 2004. [Google Scholar]
- Jones, G.; Singerman, D. Maps, hypermaps and triangle groups. In Geometric Galois Actions 1. Around Grothendieck’s Esquisse d’un Programme; Schneps, L., Lochak, P., Eds.; Cambridge University Press: Cambridge, UK, 1994; pp. 115–145. [Google Scholar]
- Planat, M.; Giorgetti, A.; Holweck, F.; Saniga, M. Quantum contextual finite geometries from dessins d’enfants. Int. J. Geom. Mod. Phys. 2015, 12, 1550067. [Google Scholar] [CrossRef] [Green Version]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Universal quantum computing and three-manifolds, Universal quantum computing and three-manifolds. Symmetry 2018, 10, 773. [Google Scholar] [CrossRef] [Green Version]
- Thurston, W.P. Three-Dimensional Geometry and Topology; Princeton University Press: Princeton, NJ, USA, 1997; Volume 1. [Google Scholar]
- Adams, C.C. The newest inductee in the number hall of fame. Math. Mag. 1998, 71, 341–349. [Google Scholar] [CrossRef]
- Milnor, J. Hyperbolic geometry: The first 150 years. Bull. Am. Math. Soc. 1982, 6, 9–24. [Google Scholar] [CrossRef] [Green Version]
- Culler, M.; Dunfield, N.M.; Goerner, M.; Weeks, J.R. SnapPy, a Computer Program for Studying the Geometry and Topology of 3-Manifolds. Available online: http://snappy.math.uic.edu/ (accessed on 1 January 2021).
- Fominikh, E.; Garoufalidis, S.; Goerner, M.; Tarkaev, V.; Vesnin, A. A census of tetrahedral hyperbolic manifolds. Exp. Math. 2016, 25, 466–481. [Google Scholar] [CrossRef] [Green Version]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum computing, Seifert surfaces and singular fibers. Quantum Rep. 2019, 1, 12–22. [Google Scholar] [CrossRef] [Green Version]
- Jones, D.T. Protein secondary structure prediction based on position-specific scoring matrices. J. Mol. Biol. 1999, 292, 195–202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mirabello, C.; Pollastri, G. Porter, PaleAle 4.0: High-accuracy prediction of protein secondary structure and relative solvent accessibility. Bioinformatics 2013, 29, 2056–2058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kelley, L.A.; Mezulis, S.; Yates, C.M.; Wass, M.N.; Sternberg, M.J.E. The Phyre2 web portal for protein modeling, prediction and analysis. Nat. Protoc. 2015, 10, 845–858. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Sun, S.; Li, Z.; Zhang, R.; Xu, J. Accurate de novo prediction of protein contact map by ultra-deep learning model. PLoS Comput. Biol. 2017, 13, e1005324. [Google Scholar] [CrossRef] [Green Version]
- Genbank. Available online: https://www.ncbi.nlm.nih.gov/genbank/ (accessed on 1 January 2021).
- Nucleic Acid Sequence “Massager”. Available online: http://biomodel.uah.es/en/lab/cybertory/analysis/massager.htm (accessed on 1 January 2021).
- Translate. Available online: https://web.expasy.org/translate/ (accessed on 1 January 2021).
- Dutta, S.; Akey, I.V.; Dingwall, C.; Hartman, K.H.; Laue, T.; Nolte, R.T.; Head, J.F.; Akey, C.W. The crystal structure of nucleoplasmin-core: Implications for histone binding and nucleosome assembly. Mol. Cell 2001, 8, 841–853. [Google Scholar] [CrossRef]
- Sauter, C.; Basquin, J.; Suck, D. Sm-Like proteins in eubacteria: The crystal structure of the Hfq protein from Escherichia coli. Nucleic Acids Res. 2003, 31, 4091. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lührmann, W.C.L. Spliceosome, structure and function. Cold Spring Harb. Perspect. Biol. 2011, 3, a003707. [Google Scholar]
- Bosma, W.; Cannon, J.J.; Fieker, C.; Steel, A. (Eds.) Handbook of Magma Functions, 2.23th ed.; 2017; p. 5914. Available online: http://magma.maths.usyd.edu.au/magma/ (accessed on 10 April 2021).
- Tozzi, A.; Peters, J.F.; Fingelkurts, A.A.; Marijuàn, P.C. Brain Projective Reality: Novel Clothes for the Emperor. Reply to comments on “Topodynamics of metastable brains” by Tozzi et al. Phys. Life Rev. 2017, 21, 46–55. [Google Scholar] [CrossRef]
- Irwin, K.; Amaral, M.; Chester, D. The Self-Simulation hypothesis interpretation of quantum mechanics. Entropy 2020, 22, 247. [Google Scholar] [CrossRef] [Green Version]
- Jones, G.A. Maps on surfaces and Galois groups. Math. Slovaca 1997, 47, 1–33. [Google Scholar]
- Planat, M. Geometry of contextuality from Grothendieck’s coset space. Quantum Inf. Process. 2015, 14, 2563–2575. [Google Scholar] [CrossRef]
- Koch, R.M.; Ramgoolam, S. From matrix models and quantum fields to Hurwitz space and the absolute Galois group. arXiv 2010, arXiv:1002.1634. [Google Scholar]
- Aspinwall, P.S. K3 surfaces and string duality. In Fields, Strings and Duality, TASI 1996; Efthimiou, C., Greene, B., Eds.; World Scientific: Singapore, 1997; pp. 421–540. [Google Scholar]
| Index | 1 | 2 | 3 | 4 | 5 |
| 3-man | m000 | K4a1, ooct02_00001 | ntet03_00000 | m206, otet04_00002 | m407, ntet05_00007 |
| m204, ntet04_00000 | m405, ncube01_00001 | ||||
| P | (1,1) | (2,1) | (3,1) | (4,1) | (5,1) |
| (12,3) | (20,3) | ||||
| Index | 6 | 7 | 8 | 9 | 10 |
| 3-man | s961, otet06_00003 | y886, ntet07_00000 | t12839, otet06_00007 | ||
| x252, ntet06_00004 | t12840, otet08_00002 | ||||
| ntet06_00005 | ntet08_00002 | ||||
| P | (6,2) | (7,1) | (8,1) | (9,1) | (10,2) |
| (12,3) | (24,3) | ||||
| (24,13) | (24,13) | ||||
| (96,70), (192,201) | (9,1), (648,705) | (10,2), (20,3), | |||
| lacking P | (72,39) | (320,1635) | |||
| extra P | , | (216,53), , | , |
| Protein | Model | |
|---|---|---|
| H3 (6PWE_1) | PSIPRED | [1,1,1,1,2, 2,1,3,5,5 .,.,.,.,.] |
| H3 | PHYRE2 | [1,1,1,1,3, 4,1,5,10,10 .,.,.,.,.] |
| H3 | PORTER | [1,1,1,2,2, 3,1,12,6,5 .,.,.,.,.] |
| H3 | RAPTORX | [1,1,1,1,2, 1,1,2,3,3 .,.,.,.,.] |
| m000 | Gieseking | [1,1,1,2,2, 3,1,4,3,5, 4,14,1,5,10] |
| trefoil | [1,1,2,3,2, 8,7,10,18,28, 27,88,134,171,354] | |
| figure-of-eight | [1,1,1,2,4, 11,9,10,11,38, 26,62,39,89,228] | |
| (0,1) | [1,1,1,2,2, 5,1,2,2,4, 3,17,1,1,2] | |
| singular fiber II* | [1,1,2,2,1, 5,3,2,4,1, 1,12,3,3,4] |
| Protein | aa | Model | |
|---|---|---|---|
| myelin P2 (2WUT) | 133 | PSIPRED | [1, 3, 13, 84, 336, 4216] |
| 2WUT | PHYRE2 | [1, 3, 7, 26, 164, 10,669] | |
| 2WUT | PORTER | [1, 3, 7, 26, 135, 871] | |
| 2WUT | RAPTORX | [1, 3, 10, 59, 348, 2899] | |
| . | (336,118) | [1, 3, 7, 30, 122, 991] | |
| . | (384,5589) | [1, 3, 7, 34, 130, 999] | |
| carbonic anhydrase (1QRE_1) | 247 | PSIPRED | [1, 3, 10, 43, 135, 1071] |
| 1QRE_1 | PHYRE2 | [1, 3, 7, 26, 149, 1085] | |
| 1QRE_1 | PORTER | [1, 3, 7, 26, 415, 4382] | |
| 1QRE_1 | RAPTORX | [1, 3, 10, 35, 106, 804] | |
| . | (336,118) | [1, 3, 7, 30, 150, 883] | |
| . | (384,5589) | [1, 3, 10, 47, 148, 1015] | |
| protein Hfq (1HK9_1) | 74 | PSIPRED | [1, 7, 17, 114, 1145, 14,275] |
| 1HK9_1 | PHYRE2 | [1, 7, 14, 149, 1458, 21,756] | |
| 1HK9_1 | PORTER | [1, 3, 7, 26, 97, 624, 4163, 34,470] | |
| 1HK9_1 | RAPTORX | [1, 3, 10, 51, 162, 1434] | |
| . | (336,118) | [1, 3, 7, 26, 134, 912] | |
| . | (384,5589) | [1, 3, 7, 34, 146, 894] | |
| H2A-H2B (2XQL_1) | 91 | PHYRE2 | [1, 3, 7, 26, 103, 688] |
| 2XQL_1 | RAPTORX | [1, 3, 7, 26, 165, 2272] | |
| . | (336,118) | [1, 3, 7, 26, 130, 943] | |
| . | (384,5589) | [1, 3, 7, 26, 136, 967] | |
| acetylcholin receptor (2BG9_1) | 370 | PSIPRED | [1, 3, 10, 35, 151, 1023] |
| 2BG9_1 | PHYRE2 | [1, 7, 11, 92,288, 2087] | |
| 2BG9_1 | PORTER | [1, 7, 11, 92, 239, 2058] | |
| 2BG9_1 | RAPTORX | [1, 3, 7, 34, 169, 1432] | |
| . | [1, 3, 10, 47, 124, 1026] | ||
| . | [1, 3, 7, 30, 140, 931] | ||
| Lsm 1-7 complex (4M75_1) | 144 | PSIPRED | [1, 3, 16, 81, 184, 1800] |
| 4M75_1 | PHYRE2 | [1, 7, 14, 201, 705, 8850] | |
| 4M75_1 | PORTER | [1, 3, 7, 26, 139, 1118] | |
| 4M75_1 | RAPTORX | [1, 3, 7, 26, 125, 747] | |
| . | [1, 3, 7, 34, 145, 948] | ||
| . | [1, 3, 10, 35, 135, 975] | ||
| na | oriented hypermaps | [1, 3, 7, 26, 97, 624, 4163, 34,470] | |
| ooct02_00017 | 3-manifold | [1, 3, 7, 26, 40, 231] | |
| ooct02_00006 | 3-manifold | [1, 3, 10, 43, 112, 802] | |
| noct02_00024 | 3-manifold | [1, 3, 10, 43, 117, 804] | |
| ooct02_00009 | 3-manifold | [1,3,7,30,105, 649] | |
| ooct04_00001 | 3-manifold | [1, 3, 7, 34, 43, 240, 254] | |
| L7a1 | 3-manifold link | [1, 3, 7, 34, 75, 377, 807] | |
| ooct03_00019 | 3-manifold | [1, 7, 11, 85, 95, 240, 492] |
| (336,118) | dimension | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| d-dit, d = 29 | 29 | 785 | |||||||||
| amino acid | . | M | W | C | F | Y | . | . | H | Q | |
| order | 1 | 2 | 3 | 4 | 4 | 6 | 7 | 7 | 7 | 8 | |
| char | Cte | Cte | Cte | ||||||||
| polar req. | . | 5.3 | 5.2 | 4.8 | 5.0 | 5.4 | . | . | 8.4 | 8.6 | |
| (336,118) | dimension | 2 | 2 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 4 |
| d-dit, d = 29 | |||||||||||
| amino acid | N | K | E | D | I | Stop | . | . | . | . | |
| order | 14 | 14 | 14 | 21 | 21 | 21 | 21 | 21 | 21 | 21 | |
| char | Cte | Cte | Cte | ||||||||
| polar req. | 10.0 | 10.1 | 12.5 | 13.0 | 10 | 15 | . | . | . | . | |
| (336,118) | dimension | 4 | 4 | 4 | f 4 | 4 | 4 | 6 | 6 | 6 | |
| d-dit, d = 29 | |||||||||||
| amino acid | V | P | T | A | G | . | L | S | R | ||
| order | 28 | 28 | 28 | 42 | 42 | 42 | 42 | 42 | 42 | ||
| char | |||||||||||
| polar req. | 5.6 | 6.6 | 6.6 | 7.0 | 7.9 | . | 4.9 | 7.5 | 9.1 |
| (384,5589) | dimension | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 |
| d-dit, d = 37 | 37 | 1333 | 1333 | 1333 | 1361 | 1367 | . | ||||
| amino acid | . | . | M | W | . | . | . | . | . | . | |
| char | Cte | Cte | Cte | Cte | Cte | Cte | Cte | ||||
| (384,5589) | dimension | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 |
| d-dit, d = 37 | 1367 | ||||||||||
| amino acid | C | F | Y | H | Q | N | K | E | D | . | |
| char | Cte | ||||||||||
| (384,5589) | dimension | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| d-dit, d = 37 | 1367 | 1367 | 1367 | 1367 | |||||||
| amino acid I | Stop | . | . | . | . | . | . | . | V | ||
| char | Cte | Cte | Cte | Cte | Cte | Cte | |||||
| (384,5589) | dimension | 4 | 4 | 4 | 4 | 6 | 6 | 6 | |||
| d-dit, d = 37 | 701 | 1365 | 1365 | ||||||||
| amino acid | P | T | A | G | L | S | R | ||||
| char | Cte |
| A | B | C | D |
| B | A | D | C |
| C | D | A | B |
| D | C | B | A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Planat, M.; Aschheim, R.; Amaral, M.M.; Fang, F.; Irwin, K. Quantum Information in the Protein Codes, 3-Manifolds and the Kummer Surface. Symmetry 2021, 13, 1146. https://doi.org/10.3390/sym13071146
Planat M, Aschheim R, Amaral MM, Fang F, Irwin K. Quantum Information in the Protein Codes, 3-Manifolds and the Kummer Surface. Symmetry. 2021; 13(7):1146. https://doi.org/10.3390/sym13071146
Chicago/Turabian StylePlanat, Michel, Raymond Aschheim, Marcelo M. Amaral, Fang Fang, and Klee Irwin. 2021. "Quantum Information in the Protein Codes, 3-Manifolds and the Kummer Surface" Symmetry 13, no. 7: 1146. https://doi.org/10.3390/sym13071146
APA StylePlanat, M., Aschheim, R., Amaral, M. M., Fang, F., & Irwin, K. (2021). Quantum Information in the Protein Codes, 3-Manifolds and the Kummer Surface. Symmetry, 13(7), 1146. https://doi.org/10.3390/sym13071146







