Abstract
Neuroevolutionary models are used to predict magnetic hysteresis for barium hexaferrites (to predict magnetic hysteresis for barium hexaferrites). Magnetic hysteresis for a specific set of samples of barium hexaferrite doped with titanium were measured experimentally at room temperature and reported before. Neural networks are trained using these experimental data in order to generate magnetization and predict magnetic hysteresis for various concentrations of titanum. We present the prediction for various methods of neural calculations and the deviations from actual data results were negligible. Finally, the predictions of magnetic hysteresis are summerized for the titanume concentration between 0.0 and 1.0.
1. Introduction
The advancement in technology is due to advancement in science and material science. Magnetic materials have been extensively used and investigated over the years. The hexaferrite, first discovered in the 1950s, has been developed and used as significant electronic materials in the previous decades. They played a vital role in the advancement of technology and industry [1]. These ferrites are magnetic ceramics formed from iron oxides combined chemically with one or more other metals and have a cubic or hexagonal crystal structure [2,3]. The hexaferrite forms a group of complex oxides and can be categorized based on chemical composition and crystal structure [4]. The ferromagnetic and ferrimagnetic materials show a nonlinear relation between the magnetization M of the sample and the applied H. The hysteresis loop displays the magnetization M of the sample with the variation of the applied field H. From the hysteresis loop, important characteristic parameters of the material can be derived. These parameters include the saturation magnetization Ms, the remnant magnetization or the remanence Mr, and the coercive field Hc, which defines the magnetic hardness of the material [5]. Many research works were carried out to investigate the influence of the dopants on the magnetic properties of M-type hexaferrite [6,7,8,9,10,11,12]. Magnetic hysteresis of magnetic materials has a major effect on devices that contain these magnetic materials. These devices include power systems since it is related closely to residual flux in transformer cores. In addition to other devices that contain a magnetic core, such as recording equipment and actuators. Therefore it is very important to develop a method for predicting the hysteresis of the magnetic material. There are two methods to simulate hysteresis loops: Physical method and phenomenological method. In either method the results should reflect properly the magnetic properties of the material. There are several reported works that have simulated hysteresis loops. More generally, the complication of the preparation method for some hexagonal ferrites could lead to less information about magnetic properties. A computer model for hysteresis can be of great help in this case. Artificial Neural Networks have been used for many years to compute the magnetic properties of nonlinear materials [13,14,15,16]. Xu et al. used feed forward NN that were trained to generate symmetrical magnetic hysteresis loops with accuracy [17]. Madayam et al. studied hysteresis for the ferromagnetic materials with modeling that included the radial function approach by breaking the B-H loop into three regions: The initial magnetization, the falling, and the rising branches [18]. Saliah and Lowther reported principles of radial basis functions (RBF) and cerebpllum manipulator control (CMAC) neural networks and demonstrated their capabilities with magnetic hysteresis behavior identification, verifying their work by numerical examples [19]. I. Kucuk measured dynamics hysteresis for soft magnetic toroids wound cores made from SiFe thin strips over a wide frequency range [20]. A dynamical hysteresis loop prediction model developed using a neural network genetic algorithm from measurements with an acceptable prediction capability for hysteresis loops of toroidal cores was also reported [20]. Kuezmann and coworkers introduced a neural network model for magnetic hysteresis based on the function approximation capability of NN. Their work described the behavior of ferromagnetic materials in the rolling and transverse direction of an isotropic material [21]. Akharzadeh et al. showed that NNs can be used to predict the satisfactory features of some observed hysteric behavior and therefore NNs can be used for many interesting applications [22].
However there should be an agreement between calculated and measured hysteresis and consequently magnetic properties. The effects of titanium substitution on the magnetic and structural properties of the barium hexaferrites prepared according to the formula BaFeTiO with x = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0 were reported previously [23]. The main aim of the present work is to use artificial neural networks to generate the hysteresis and magnetic properties of these as prepared compounds and predict hysteresis and magnetic properties even for different compositions.
The rest of this paper is organized as follows. Section 2 presents the problem formulation. The proposed neuroevolutionary Model is discussed in Section 3. Section 4 discusses the evaluation measures. Results and discussions are presented in Section 5. Finally, the findings of this research are concluded in Section 6.
2. Problem Formulation
Many research works were executed to investigate the influence of dopants on the magnetic properties of hexaferrite [6,7,8,9,10,11,12]. Magnetic hysteresis of the magnetic materials has a significant effect on devices that contain these magnetic materials. These devices include power systems since it is related closely to the residual flux in transformer cores. In addition to other devices that contain a magnetic core, such as recording equipment and actuators. Therefore it is essential to develop a method for predicting the hysteresis of magnetic material. The hexaferrite materials show a nonlinear relation between the applied magnetic field and the magnetization of the sample. They form a group of complex oxides and can be classified based on the chemical composition and crystal structure [4]. The hysteresis loop displays the behavior of the magnetization of the sample with the variation of the applied magnetic field. From the hysteresis loop, many characteristic parameters of the material can be derived. These parameters include the saturation magnetization Ms, the remnant magnetization or the remanence Mr, and the coercive field, Hc, which defines the magnetic hardness of the material [5]. The effects of titanium substitution on the magnetic and structural properties of the barium hexaferrite prepared according to the formula BaFeTiO with x = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0 were reported previously [23]. The main aim of the present work is to use Artificial Neural Networks (ANN) and experimental data to generate the hysteresis and the magnetic properties of these as prepared compounds, and then predict hysteresis and magnetic properties for different concentrations and even different compositions. However, there should be an agreement between the calculated and measured hysteresis and consequently, between measured and calculated magnetic properties. In this work, a proposed neuroevolutionary model will be described by a three-component model: The neural network topology, the optimizer, and the fitness function.
3. Neuroevolutionary Model
The proposed neuroevolutionary model can be described as three main components: The neural network topology, the optimizer, and the fitness function [24,25,26,27,28]. Thus we describe each of these components.
- Neural network topology: Artificial Neural Networks (ANNs) are intelligent learning algorithms inspired by biological neural networks. The objective of an ANN is to perform information analysis and knowledge extraction in a way that is analogous to the biological neurons process. The topology of the ANN can be represented as a connected directed graph in which the artificial neurons are the nodes, and the weighted connections are the links between the nodes. ANNs models have a layered structure. Where it includes the input and output layers, and in between is the hidden layer(s). Each layer consists a set of neurons, while each neuron has an activation unit. Different activation functions could be used. Equation (1) shows the Sigmoid activation function which is selected for the proposed model:Mainly, ANNs learn the relationships between inputs and outputs by repeatedly learning and adjusting the weights of the connections and modifying the network structure. Training ANNs requires finding the weights by determining a loss (objective) function. A typical multilayer perceptron neural network has an input layer I of N number of nodes. A set of hidden layer(s) H where each hidden layer h has m number of nodes. And an output layer O with k number of nodes. Each connection between any two neurons i and j is associated with a weight . Furthermore, each neuron has a bias value b for adjusting the output and better converge toward optimality. For prediction, the input is fed into the hidden layer, where the output of the input layer is represented by . At the hidden layer, the output from the previous layer (input) is multiplied by the weights and summed out, as given in Equation (2). Where is the associated bias of hidden layer:The value of inside the neuron is transformed using an activation function. Thus, the output of the last hidden layer will go through the output layer.
- The optimizer: This component is responsible for finding the best possible parameters of the neural network that minimize a predefined error criterion. Two optimizers are used for this task: Genetic Algorithm (GA) and Particle Swarm Optimization (PSO). Both optimizers are selected due to their popularity in the literature and their consideration as ones of the most well-regarded metaheuristic algorithms.
- -
- PSO is a population-based optimization algorithm by Russell Eberhard and James Kennedy in 1995 [29]. It represents the social behavior of the movement of a bird flock or school of fish [30]. Like other population-based algorithms, PSO initializes a preliminary population for the first generation representing the initial set of potential solutions which are called particles [31]. It then tries to search for the optimal solution by updating the speed and position of the set of particles through the course of generations [32]. The algorithm keeps track of two best fitness values: The pbest and gbest. At a specific generation, pbest is the best fitness value corresponding to the best particle for the generation whereas gbest is the best global fitness value obtained across all the generations reached so far [30].
- -
- GA is a population-based optimization algorithm by John Holland in the early 1970s [33]. It uses a population of individuals at each generation which represent the potential solutions for the generation. It is based on evolutionary operators which are: Selection, crossover, mutation, and elitism. The evolutionary operators are used to find other possible solutions at the next generation in the aim of finding the optimal solution [34]. At each generation, the fitness values of the individuals are evaluated and are used by the evolutionary operators at the next generation. Finally, the best individual with the best fitness value at the last generation is selected and is considered as the solution obtained from running the algorithm [33].
In both optimizers, the solution is represented as a vector of the parameters of the network that will be optimized. In this case each solution is formed as a set of weights between the input layer and the hidden layer, the weights between the hidden layer and the output layer, and the biases of all neurons. Figure 1 illustrates the structure of the solution in the neuroevolutionary algorithm and how it maps to the structure of the network.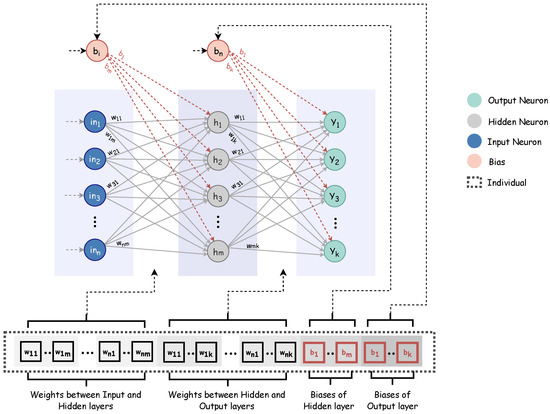 Figure 1. Solution representation in the neuroevolutionary model.
Figure 1. Solution representation in the neuroevolutionary model. - The fitness function: This component is used to evaluate and determine the quality of the candidate solutions which were generated by the optimizer. This value used to by the optimizer, which in this case is either GA or PSO, to guide the search process toward more quality solutions. In this work, MSE is used, which is widely adopted in the literature as a cost function for different machine learning models. Therefore the fitness function is to minimize the MSE value.
Overall, the flowchart of the neuroevolutionary algorithm can be described as shown in Figure 2.
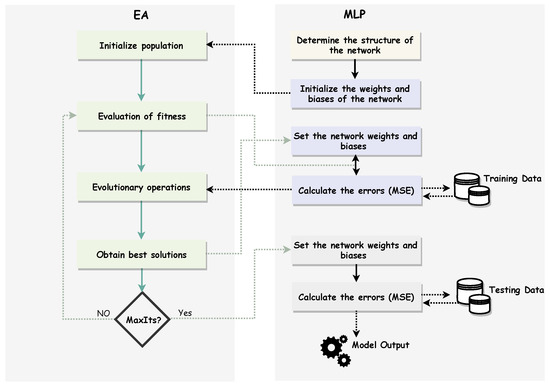
Figure 2.
Flow of the main processes of the neuroevolutionary model.
4. Evaluation Measures
In order to evaluate the best generated neuroevolutionary models, the following five evaluation measures are used:
5. Results and Discussion
The magnetic properties are experimentally generated from hysteresis loops. We reported the magnetic properties generated from the hysteresis loops of BaFeTiO with different titanium concentration (x = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0) and these hysteresis loops are shown in Figure 3 [23]. The main objective of this work is to generate these hysteresis loops of these as prepared compounds utilizing ANN for the same samples and predict from the hysteresis loops the magnetic properties for different compositions. We used the last 34 experimental data points to predict the corresponding values by using trained NNs.
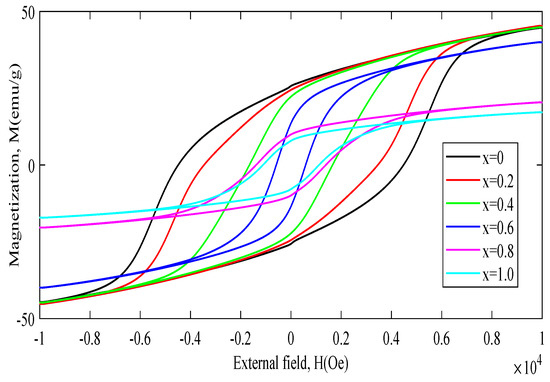
Figure 3.
Hysteresis loops for the samples BaFeTiO (x = 0.0 to 1.0) sintered at 1000 C.
The neuroevolutionary model proposed in this work is implemented using Python 3.7 and EvoloPy [35]. EvoloPy is an open source library that includes nature-inspired optimization algorithms for global optimization written in Python. Two well-regarded algorithms are selected from EvoloPy to optimize NN, namely; GA and PSO. The number of hidden neurons in GA and PSO is set to , which is equal 3. In addition, the number of hidden layers is one. Both models are compared to the classical back propagation (BP) algorithm and Linear Regression (LR). Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 show the evaluation measures for GA, PSO, BP, and LR based on the set of data points for the system under study for each value of x starting from 0.0, to 1.0 with a step of 0.2. That is, a table of results is shown for each value of x.

Table 1.
Performance results for the last 34 data points for the BaFeTiO (x = 0.0) at 1000 C. (The best result is marked in bold font).

Table 2.
Performance results for the last 34 data points for the BaFeTiO (x = 0.2) at 1000 C.

Table 3.
Performance results for the last 34 data points for the BaFeTiO (x = 0.4) at 1000 C.

Table 4.
Performance results for the last 34 data points for the BaFeTiO (x = 0.6) at 1000 C.

Table 5.
Performance results for the last 34 data points for the BaFeTiO (x = 0.8) at 1000 C.

Table 6.
Performance results for the last 34 data points for the BaFeTiO (x = 1.0) at 1000 C.
Examining the listed results in the tables, it can be clearly noticed that the error in terms of all measures decreases for all models when the value of x increases. Therefore, the lowest error values are shown in Table 6. It can be noted that with the exception of the first two cases when the value of x = 0 and x = 0.2, the GA and PSO show superior results to BP and LR, with a slight advantage for GA. In addition, the GA model shows more stable results compared to PSO in terms of lower stdv values.
Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 show the actual and predicted values for the last 34 data points for the BaFeTiO (x = 0.8) at 1000 C. using GA, PSO, BP, and LR. The approximation curves verify that the ability of proposed algorithms to represent the behavior of the process.
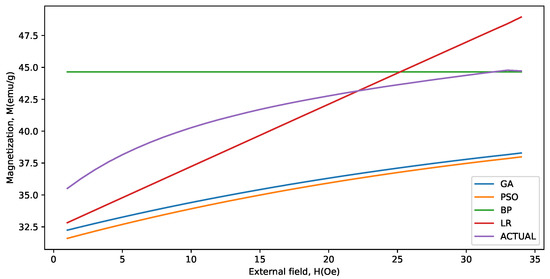
Figure 4.
Actual and predicted values for the last 34 data points for the BaFeTiO (x = 0.0) at 1000 C.
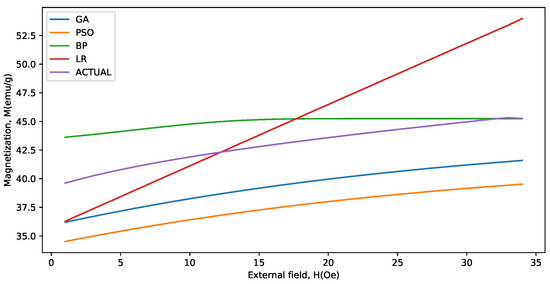
Figure 5.
Actual and predicted values for the last 34 data points for the BaFeTiO (x = 0.2) at 1000 C.
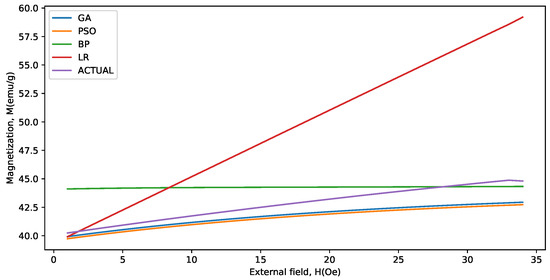
Figure 6.
Actual and predicted values for the last 34 data points for the BaFeTiO (x = 0.4) at 1000 C.
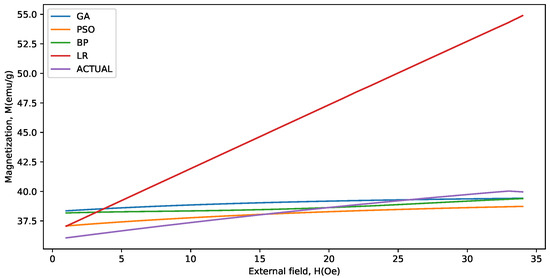
Figure 7.
Actual and predicted values for the last 34 data points for the BaFeTiO (x = 0.6) at 1000 C.
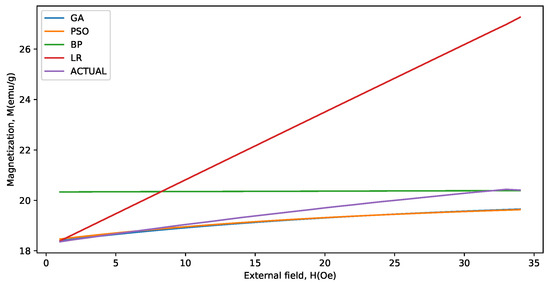
Figure 8.
Actual and predicted values for the last 34 data points for the BaFeTiO (x = 0.8) at 1000 C.
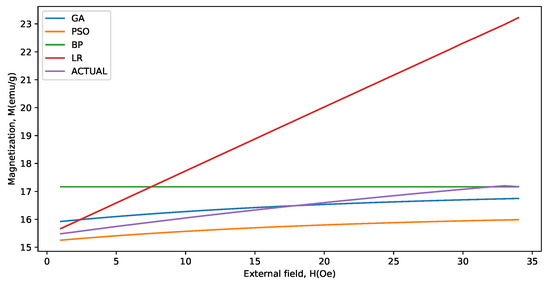
Figure 9.
Actual and predicted values for the last 34 data points for the BaFeTiO (x = 1.0) at 1000 C.
6. Conclusions
Neuroevolutionary models were used to predict magnetic hysteresis for barium hexaferrites. Magnetic hysteresis for a specific set of samples of barium hexaferrite doped with titanium were measured experimentally at room temperature and reported. Neural networks were trained using 34 data experimental data points. Using the various model, the magnetization of barium hexaferrites for various concentrations of titanium were then calculated. The predictions for various methods of neural calculations and the deviations from actual data results were summarized. The deviations between actual experimental data results and the predicted ones were negligible for all models. However, the GA method was arguably the best technique with low deviations. Finally, we conclude that the magnetic hysteresis could be predicted for the whole set of experimental data for samples with various titanum concentration between 0.0 and 1.0.
Author Contributions
Conceptualization, L.A. and A.R.A.D.; Methodology, L.A. and I.A.; Software, L.A., I.A. and H.F.; Writing—original draft, L.A.; Writing—review & editing, A.R.A.D., I.A. and H.F.; Formal Analysis, L.A. and A.R.A.D.; Visualization, I.A. and H.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sugimoto, M. The past, present, and future of ferrites. J. Am. Ceram. Soc. 1999, 82, 269–280. [Google Scholar] [CrossRef]
- Cochardt, A. Recent ferrite magnet developments. J. Appl. Phys. 1966, 37, 1112–1115. [Google Scholar] [CrossRef]
- Pullar, R.C. Hexagonal ferrites: A review of the synthesis, properties and applications of hexaferrite ceramics. Prog. Mater. Sci. 2012, 57, 1191–1334. [Google Scholar] [CrossRef]
- Koutzarova, T.; Kolev, S.; Ghelev, C.; Grigorov, K.; Nedkov, I. Structural and magnetic properties and preparation techniques of nanosized M-type hexaferrite powders. In Advances in Nanoscale Magnetism; Springer: Berlin, Germany, 2009; pp. 183–203. [Google Scholar]
- Awadallah, A.M.; Sami, M. Effects of Preparation Conditions and Metal ion Substitutions for Barium and Iron on the Properties of M-Type Barium Hexaferrites. Ph.D. Thesis, The University of Jordan, Amman, Jordan, 2012. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Q.; Yang, H. Synthesis, characterization, and magnetic properties of nanocrystalline BaFe12O19 Ferrite. Curr. Appl. Phys. 2009, 9, 1375–1380. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Kostishyn, V.G.; Panina, L.V.; Trukhanov, A.V.; Turchenko, V.A.; Tishkevich, D.I.; Trukhanova, E.L.; Yakovenko, O.S.; Matzui, L.Y.; et al. Effect of gallium doping on electromagnetic properties of barium hexaferrite. J. Phys. Chem. Solid. 2017, 111, 142–152. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Kostishyn, V.G.; Panina, L.V.; Trukhanov, A.V.; Turchenko, V.A.; Tishkevich, D.I.; Trukhanova, E.L.; Yakovenko, O.S.; Matzui, L.Y. Investigation into the structural features and microwave absorption of doped barium hexaferrites. Dalton Trans. 2017, 46, 9010–9021. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Salem, M.M.; Trukhanova, E.L.; Panina, L.V.; Kostishyn, V.G.; Darwish, M.A.; Trukhanov, A.V.; Zubar, T.I.; Tishkevich, D.I.; et al. Preparation and investigation of structure, magnetic and dielectric properties of (BaFe11.9Al0.1O19)1-x-(BaTiO3)x bicomponent ceramics. Ceram. Int. 2018, 44, 21295–21302. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Turchenko, V.A.; Trukhanov, A.V.; Tishkevich, D.I.; Trukhanova, E.L.; Zubar, T.I.; Karpinsky, D.V.; Kostishyn, V.G.; Panina, L.V.; et al. Magnetic and dipole moments in indium doped barium hexaferrites. J. Magn. Magn. Mater. 2018, 457, 83–96. [Google Scholar] [CrossRef]
- Trukhanov, S.V.; Trukhanov, A.V.; Turchenko, V.A.; Kostishyn, V.G.; Panina, L.V.; Kazakevich, I.S.; Balagurov, A.M. Structure and magnetic properties of BaFe11.9In0.1O19 hexaferrite in a wide temperature range. J. Alloys Compd. 2016, 689, 383–393. [Google Scholar] [CrossRef]
- Turchenko, V.A.; Trukhanov, S.V.; Balagurov, A.M.; Kostishyn, V.G.; Trukhanov, A.V.; Panina, L.V.; Trukhanova, E.L. Features of crystal structure and dual ferroic properties of BaFe12-xMexO19 (Me = In3+ and Ga3+; x = 0.1–1.2). J. Magn. Magn. Mater. 2018, 464, 139–147. [Google Scholar] [CrossRef]
- Kuczmann, M.; Iványi, A. A new neural-network-based scalar hysteresis model. IEEE Trans. Magn. 2002, 38, 857–860. [Google Scholar] [CrossRef]
- Nussbaum, C.; Pfutzner, H.; Booth, T.; Baumgartinger, N.; Ilo, A.; Clabian, M. Neural networks for the prediction of magnetic transformer core characteristics. IEEE Trans. Magn. 2000, 36, 313–329. [Google Scholar] [CrossRef]
- Mohammed, O.A.; Uler, F.G. A state space approach and formulation for the solution of nonlinear 3-D transient eddy current problems. IEEE Trans. Magn. 1992, 28, 1111–1114. [Google Scholar] [CrossRef]
- Nussbaum, C.; Booth, T.; Ilo, A.; Pfützner, H. A neural network for the prediction of performance parameters of transformer cores. J. Magn. Magn. Mater. 1996, 160, 81–83. [Google Scholar] [CrossRef]
- Xu, Q.F.; Refsum, A. Analysis of some numerical models of hysteresis loops. In Proceedings of the 1993 2nd International Conference on Advances in Power System Control, Operation and Management, APSCOM-93, Hong Kong, China, 7–10 December 1993; IET: Stevenage, UK, 1993; pp. 734–737. [Google Scholar]
- Eval, N.T. INTERNATI9NAL SEMINAR’DAY OF’DIFFRACTION’94 SAINT PETERSBURG, MAY 30-JUNE 3, 1994. Nondestr. Test. Eval. 1994, 11, 369–376. [Google Scholar]
- Saliah, H.H.; Lowther, D.A. The use of neural networks in magnetic hysteresis identification. Phys. B Condens. Matter 1997, 233, 318–323. [Google Scholar] [CrossRef]
- Kucuk, I. Prediction of hysteresis loop in magnetic cores using neural network and genetic algorithm. J. Magn. Magn. Mater. 2006, 305, 423–427. [Google Scholar] [CrossRef]
- Kuczmann, M.; Iványi, A. Neural network model of magnetic hysteresis. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2002, 21, 364–376. [Google Scholar] [CrossRef]
- Akbarzadeh, V.; Davoudpour, M.; Sadeghian, A. Neural network modeling of magnetic hysteresis. In Proceedings of the 2008 IEEE International Conference on Emerging Technologies and Factory Automation, Hamburg, Germany, 15–18 December 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1267–1270. [Google Scholar]
- Dairy, A.R.A.; Al-Hmoud, L.A.; Khatatbeh, H.A. Magnetic and structural properties of barium hexaferrite nanoparticles doped with titanium. Symmetry 2019, 11, 732. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Alqatawna, J.F. Optimizing feedforward neural networks using krill herd algorithm for e-mail spam detection. In Proceedings of the 2015 IEEE Jordan Conference on Applied Electrical Engineering and Computing Technologies (AEECT), Amman, Jordan, 3–5 November 2015; pp. 1–5. [Google Scholar]
- Faris, H.; Aljarah, I.; Al-Madi, N.; Mirjalili, S. Optimizing the learning process of feedforward neural networks using lightning search algorithm. Int. J. Artif. Intell. Tools 2016, 25, 1650033. [Google Scholar] [CrossRef]
- Faris, H.; Mirjalili, S.; Aljarah, I. Automatic selection of hidden neurons and weights in neural networks using grey wolf optimizer based on a hybrid encoding scheme. Int. J. Mach. Learn. Cybern. 2019, 10, 2901–2920. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S.; Al-Madi, N.; Sheta, A.; Mafarja, M. Evolving neural networks using bird swarm algorithm for data classification and regression applications. Clust. Comput. 2019, 22, 1317–1345. [Google Scholar] [CrossRef]
- Al-Badarneh, I.; Habib, M.; Aljarah, I.; Faris, H. Neuro-evolutionary models for imbalanced classification problems. J. King Saud Univ. Comput. Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Dong, P.T. A review of convergence analysis of particle swarm optimization. Int. J. Grid Distrib. Comput. 2013, 6, 117–128. [Google Scholar]
- Esperanza, G.-G.; Fernández-Martínez, J.L. A brief historical review of particle swarm optimization (PSO). J. Bioinform. Intell. Control 2012, 1, 3–16. [Google Scholar]
- Qinghai, B. Analysis of particle swarm optimization algorithm. Comput. Inf. Sci. 2010, 3, 180. [Google Scholar]
- Kumar, M.; Husain, M.; Upreti, N.; Gupta, D. Genetic algorithm: Review and application. Int. J. Inf. Technol. Knowl. Manag. 2010, 2, 451–454. [Google Scholar] [CrossRef]
- Srinivas, M.; Patnaik, L.M. Genetic algorithms: A survey. Computer 1994, 27, 17–26. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Mirjalili, S.; Castillo, P.A.; Guervós, J.J.M. EvoloPy: An Open-source Nature-inspired Optimization Framework in Python. In Proceedings of the IJCCI (ECTA), Porto, Portugal, 9–11 November 2016; pp. 171–177. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).