An Auxetic System Based on Interconnected Y-Elements Inspired by Islamic Geometric Patterns

Abstract

A 2D mechanical metamaterial exhibiting perfectly auxetic behavior, i.e., Poisson’s ratio of $-1$, is proposed in this paper drawing upon inspiration from an Islamic star formed by circumferential arrangement of eight squares, such as the one found at the exterior of the Ghiyathiyya Madrasa in Khargird, Iran (built 1438–1444 AD). Each unit of the metamaterial consists of eight pairs of pin-jointed Y-shaped rigid elements, whereby every pair of Y-elements is elastically restrained by a spiral spring. Upon intermediate stretching, each metamaterial unit resembles the north dome of Jameh Mosque, Iran (built 1087–1088 AD), until the attainment of the fully opened configuration, which resembles a structure in Agra, India, near the Taj Mahal. Both infinitesimal and finite deformation models of the effective Young’s modulus for the metamaterial structure were established using strain energy approach in terms of the spiral spring stiffness and geometrical parameters, with assumptions to preserve the eight-fold symmetricity of every metamaterial unit. Results indicate that the prescription of strain raises the effective Young’s modulus in an exponential manner until full extension is attained. This metamaterial is useful for applications where the overall shape of the structure must be conserved in spite of uniaxial application of load, and where deformation is permitted under limited range, which is quickly arrested as the deformation progresses.

1. Introduction

By nature, a material contracts laterally when stretched longitudinally and expands laterally when compressed longitudinally, as illustrated in Figure 1 (left). For this reason, an elastic property known as Poisson’s ratio has been defined as

$$v_{12}=-\frac{{\epsilon }_{22}}{{\epsilon }_{11}}$$

(1)

where ${\epsilon }_{11}$ is the applied strain in the direction parallel to the $O{x}_1$ axis, while ${\epsilon }_{22}$ is the resulting strain in the direction parallel to the $O{x}_2$ axis. Since these orthogonal strains possess opposite signs, a negative sign has been historically incorporated so as to give a positive Poisson’s ratio. However, there exists a class of material which behave in the opposite manner, i.e., they expand laterally when stretched longitudinally and contract laterally when compressed longitudinally, as depicted in Figure 1 (right). Since the orthogonal strains possess equal signs, the definition of Poisson’s ratio, as described in Equation (1), would therefore give negative values. Negative Poisson’s ratio materials occur naturally in certain zeolites, such as alpha-cristobalites [1,2], and can be developed by compression of foams [3,4] as well as in some composite designs [5,6]. With the advent of 3D printing and other precision materials processing techniques, auxetic metamaterials have been developed [7,8]; these materials derive their properties from the designed microarchitectures rather than from properties of the base materials. The literature on auxetic systems is too voluminous to be fairly cited, and so the reader is referred only to the lists of exhaustive references collated in generic review papers on auxetic materials and structures [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] and review papers on specific areas, such as auxetic textiles or fabrics [26,27,28,29], auxetic nanomaterials [30,31], chiral-based auxetics [32], applications of auxetic materials [33,34], and metamaterials with auxetic and negative stiffness inclusions [35], as well as monographs [36,37,38], across the field of auxetics. It suffices to mention that while the Poisson’s ratio of anisotropic materials has no bounds, i.e., $-\infty <v<\infty$ [39,40], in the case of isotropic materials the bounds of Poisson’s ratio are $-1\le v\le 1$ for two-dimensional systems and $-1\le v\le 1/2$ for three-dimensional systems, i.e.,

$$-1\le v\le \frac{1}{D-1}$$

(2)

where $D=2$ and $D=3$ indicate two- and three-dimensional systems, respectively [41]. Regardless of two-dimensional or three-dimensional systems, the lower bounds of Poisson’s ratio for both isotropic systems are common, i.e., $v=-1$, which is known as perfect auxetics. This means that upon application of uniaxial tension or uniaxial compression a two-dimensional system undergoes equi-biaxial strain while a three-dimensional system undergoes equi-triaxial strain, so that the overall shape is conserved.

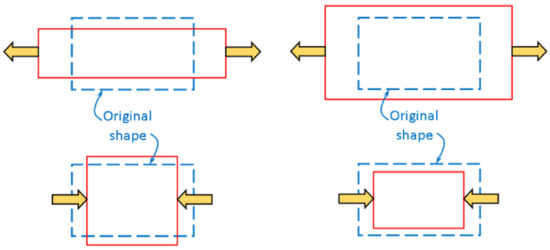
Figure 1. Deformation of conventional materials (left column) and auxetic materials (right column) in response to uniaxial tension (top row) and uniaxial compression (bottom row).

Of late, the fields of auxetic and other metamaterials have been enriched by inspiration from Islamic motifs [42,43,44,45,46]. In addition, there have been recent works that appraise the various symmetry aspects of auxetic systems [47,48,49,50,51,52]. In this paper, consideration is given to a perfectly auxetic 2D metamaterial system that is inspired by an eight-pointed Islamic star pattern that is formed from a circumference of eight squares. A historically famous example of this eight-pointed star is found at the exterior of the Ghiyathiyya madrasa, which was built in 1438–1444 at Khargird, Iran, as shown in Figure 2a, with its idealized version depicted in Figure 2b. In order to enhance structural stability in producing a repetitive pattern in square array, each eight-pointed star is connected to its four nearest neighbors via overlapping of the on-axes squares. An example of overlapping corners in Islamic geometric pattern is found in the Nasrid carved stucco ornament of the Alhambra palace. For visual aid, four red, tilted, dashed squares are superposed onto the carved stucco ornament as shown in Figure 2c. In the context of the currently considered metamaterial, a group of two-by-two-unit cells are interconnected to each other via overlapping of the on-axes squares as illustrated in Figure 2d. It will later be shown that upon stretching the metamaterial, it deforms into the pattern that resembles the north dome of Jameh Mosque, Isfahan, shown in Figure 2e, that was constructed by Taj al-Mulk in year 1087–1088. It will further be shown that at maximum stretching, each metamaterial unit transforms into a regular octagon that is connected with four other octagons. This pattern can be found worldwide due to its simplicity but, for consistency within the context of Islamic motifs, Figure 2f shows an example of this geometrical pattern in a structure at Agra, India, near the Taj Mahal.

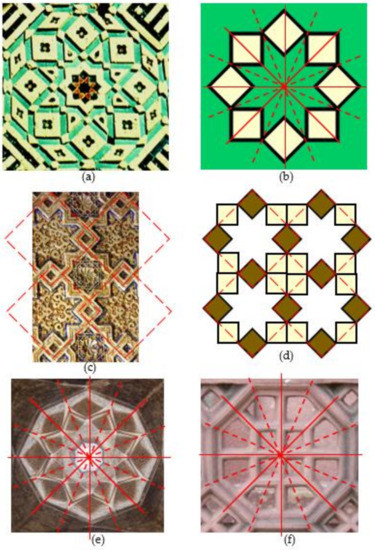
Figure 2. (a) An example of eight-pointed star constructed from eight squares found at the exterior of the Ghiyathiyya madrasa in Khargird, Iran (1438–1444), and (b) its idealized form. (c) Four units of squares interlaced at their corners from the Nasrid carved stucco ornament of the Alhambra and (d) a schematic of four metamaterial units interlaced at the on-axes squares. (e) The north dome of Jameh Mosque, Isfahan, that was constructed by Taj al-Mulk in 1087–1088, and (f) a structure near the Taj Mahal in Agra features an alternative combination of octagons and tilted squares resembling the partially and fully stretched metamaterial displayed in Figure 4c,h, respectively.

Although each unit of the metamaterial possesses eight-fold symmetry, as indicated by the continuous and dashed red lines in Figure 2b,e,f, the interconnection in square array reduces the entire metamaterial structure into four-fold symmetry, as denoted by the continuous red lines. The main novelty is the use of rigid Y-elements that are assembled in such a manner so as to exhibit perfect auxeticity that additionally manifests a range of exquisite Islamic geometrical designs throughout the entire deformation process. In other words, while the microstructure encounters changes to its geometry during the deformation process, the changed geometry at every stage conforms to the various Islamic geometrical patterns.

2. Analysis

The basic unit for the construction of the metamaterial is the Y-shaped element shown in Figure 3a. Each Y-element consists of three arms of equal length $l$ but of unequal angular spacing. Specifically, two of the arms are at $90°$ angle, while the third arm is at $135°$ from the other two arms. As such, the first two arms are termed “near arms” and the third arm is called the “far arm”. Two Y-elements are connected to one another at their junctions by pin-joints to form a pair of Y-elements, as shown in Figure 3b. Some molecular examples for this pair of Y-elements can be approximated by metallocene, which is a compound comprising two cyclopentadienyl anions $\left({\mathrm{C}}_5{\mathrm{H}}_5^{-}\right)$ bound to a metal M in the oxidation state II, thereby resulting in the general chemical formula $\mathrm{M}{\left({\mathrm{C}}_5{\mathrm{H}}_5\right)}_2$, such as ferrocene where M = Fe or cobaltocene where M = Co. To attain the Y-shaped structure, three of the H atoms are replaced with long rigid groups.

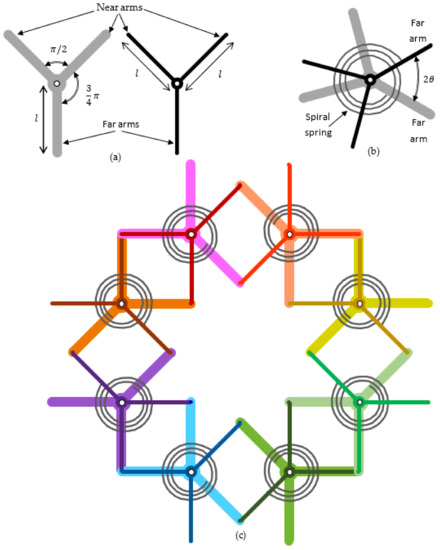
Figure 3. (a) Definitions of the near and far arms for a pair of Y-elements and (b) the angular offset $2\theta$ for a pair of hinged Y-elements based on the angle formed between two far arms, with a spiral spring to produce angular elastic resistance. (c) A unit of the presently considered metamaterial formed by eight pairs of Y-elements.

Elastic resistance to relative rotational motion between the paired Y-elements in the metamaterial is implemented by incorporating a spiral spring between them, with each end of the spiral spring connected to the far arm for each Y-element. The angle formed between the two far arms is defined as $2\theta$ such that if the two far arms are symmetrically positioned with reference to an axis, the half-angle $\theta$ defines the subtending angle of each far arm with reference to the corresponding axis. Each pair of Y-elements is interconnected to its neighboring pair of Y-elements via pin-joints at the ends of their arms, as shown in Figure 3c, such that the eight-pointed star indicated in Figure 2b is manifested. In the molecular version, the tip of the rigid long group is attached to the end of a rigid long group from a neighboring metallocene to permit bond bending as an analogy of the pin-joints, so that the elastic resistance is supplied by the bond bending energy.

For visual clarity, each Y-element in Figure 3c is allocated a different color with the upper Y-element represented as thinner and darker lines so as not to obscure the lower Y-elements. It can be seen that the four sides in each square is formed by two pairs of Y-elements. Specifically, the on-axes squares are formed by far arms while the off-axes squares are formed by near arms. If a unit of the metamaterial is considered in isolation, it possesses eight springs, each of spring constant $k$. If a metamaterial unit is fully surrounded by neighboring units, each spring is shared with the adjacent neighbor, therefore halving this number to an equivalence of four springs per metamaterial unit. For a very large number of $m\times n$ metamaterial units, the number of springs can therefore be approximated as $4mn$.

A gradual biaxial opening up of each metamaterial unit from its original or reference state, similar to Figure 2b or Figure 3c, through its intermediate deformation akin to Figure 2e, and finally to its fully opened configuration resembling Figure 2f is illustrated in Figure 4. From the original state in its closed configuration shown in Figure 4a, the equi-biaxial enlargement of each metamaterial unit is made possible by a counter-rotating action in each pair of Y-elements such that the squares deform into rhombi. The combination of rhombi shown in Figure 4c resembles the north dome of Jameh Mosque, Isfahan, depicted in Figure 2e. Additional counter-rotation of the pairs of Y-elements further elongates and narrows the rhombi until each rhombus collapses into a line, such that the metamaterial unit eventually transforms into a regular octagon, as indicated in Figure 4h. Throughout the entire deformation process, the area of every rhombus decreases while the effective area of each metamaterial increases. In addition, the eight-fold symmetry of each metamaterial unit is conserved throughout the entire deformation mechanism. There exists, therefore, a mathematical relationship between the rotation of the Y-elements and the equi-biaxial strain, as well as a limit to the extent of the rotation and the corresponding strain. Having demonstrated the manner in which a single isolated metamaterial unit deforms under the action of applied uniaxial strain, a visual representation on how each metamaterial unit is interlaced with its neighbors from its originally closed configuration to its fully-opened configuration will be displayed next.

Figure 4. (a–h) Gradual change of one unit of the considered metamaterial from the closed configuration to the fully opened configuration. Spiral springs and pin-joints are not shown for clarity. Figure 4c,h comparable to Figure 2e,f.

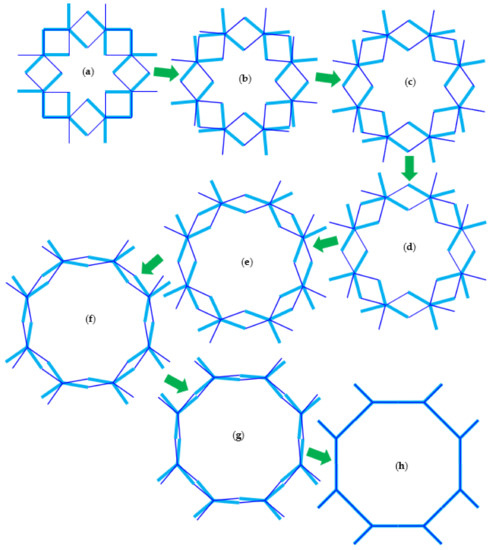
Figure 5 shows four metamaterial units, arranged in a two-by-two array of metamaterials, interlaced at their on-axes squares. These four interconnected metamaterial units are at various stages of deformation. For ease of tracking, a pair of Y-elements is colored in red and pink, such that the angular offset between their far arms is identified as $2\theta$. Starting from $2\theta =90°$ in its original reference state indicated in Figure 5a, an initial deformation at which $2\theta =60°$ reveals another type of star being formed. Specifically, this is a four-pointed star that is located diagonally from each metamaterial unit. With reference to Figure 5b, the four-pointed star is manifested in between the four adjacent metamaterial units. Upon further deformation to $2\theta =30°$ as shown in Figure 5c each metamaterial unit closely resembles a circle, during which the four-pointed star becomes blunter. In addition, a loop encircling the four-pointed star resembles a smaller circle, such that at this stage of deformation the metamaterial resembles overlapping larger circles in square array as well as intermittent smaller circles also in square array, as illustrated in Figure 5d. Finally, at the fully opened configuration whereby $2\theta =0°$ in Figure 5e, the metamaterial units transform into regular octagons while the blunt four-pointed stars and their encircling loops collapse into tilted squares that are arranged in rectangular array. The general framework involves searching for geometrical designs that consist of repetitive patterns that can be modified to exhibit the desired overall material properties and the use of physical principles to derive a suite of effective material behavior. In the current investigation, the metamaterial structure is inspired by a star pattern found in a class of Islamic geometrical design, which can be modified to manifest perfect auxeticity $\left(v=-1\right)$ while the effective Young’s modulus is formulated, as will be shown later, by means of energy method. This metamaterial structure can be formed using precision additive manufacturing, wherein the stresses are transferred parallel to the axis for each arm of a Y-element, and stress transfers from one pair of Y-elements to its neighboring pair through the pin-joints. Specifically, such a metamaterial structure can be processed by 3D printing using two types of materials, namely materials that are comparatively rigid to form the Y-elements, while the more elastic materials are used to form the spiral springs. In the subsequent analysis, the following assumptions are made in order for each metamaterial unit to retain its eight-fold symmetry and for the metamaterial’s square array to retain its four-fold symmetry consistently throughout the entire deformation process:

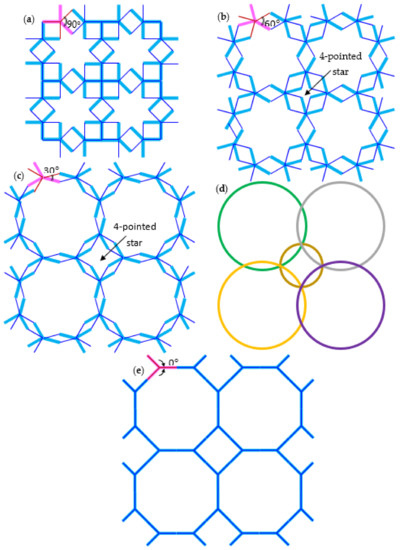
Figure 5. A two-by-two unit of the currently considered metamaterial at (a) the closed configuration where $2\theta =90°$ and (b) with a slightly opened configuration where $2\theta =60°$ upon prescription of uniaxial strain. Further equi-biaxial opening of the metamaterial micro-lattice at (c) $2\theta =30°$ leads to (d) a tiled pattern formed from overlapping circles, until (e) the fully opened configuration is attained where $2\theta =0°$. Note that the closed configuration corresponds to Figure 2b with the connections based on overlapping, or sharing, of the on-axes squares akin to Figure 2d. The configuration for each unit of Figure 5b commensurates with Figure 2e while that of Figure 5e resembles the structure furnished in Figure 2f. Spiral springs and pin-joints are not shown for clarity.

(a)

All Y-elements rotate by the same magnitude;

(b)

All springs, including those at the edges, encounter the same amount of twisting;

(c)

The preservation of overall shape is not only due to perfect auxeticity, whereby $v=-1$, but also due to the preservation of the edges, e.g., straight edges remain straight upon uniaxial stretching.

Typically, springs located on the edge would have to be allowed to rotate by a different amount than interior springs but this is not implemented to preserve symmetry.

A quadrant of a metamaterial unit, with the unnecessary lines removed, is furnished in Figure 6 for analysis, in which $l$ is the arm length for the Y-element and $\theta$ is half of the angular offset for each pair of Y-elements. With reference to Figure 6, the half-dimensions of the metamaterial unit $X_1$ and $X_2$ as measured along the $O{x}_1$ and $O{x}_2$ axes are equal by virtue of symmetry, and can be generally written as

$$X_1=X_2=\left(1+\sqrt{2}\right)l\cos \theta$$

(3)

for $0<\theta <\pi /4$, from which substitution of $\theta =\pi /4$ gives the original half-dimensions

$$X_1^0=X_2^0=\left(1+\frac{1}{\sqrt{2}}\right)l$$

(4)

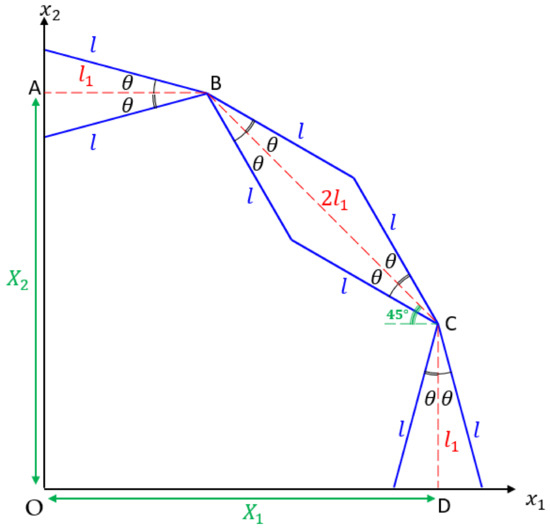
Figure 6. A quadrant of a metamaterial unit for analysis. Spiral springs, pin-joints, and unnecessary lines have been removed for clarity.

For reasons of geometrical symmetry as well as kinematical symmetry, the subsequent analysis considers only the dimension along the $O{x}_1$ axis and its changes thereof. Upon application of load, we have an incremental change to the dimension as

$$d{X}_1=-\left(1+\sqrt{2}\right)l\sin \theta d\theta$$

(5)

that gives the incremental effective strain

$$d{\epsilon }_{eff}=\frac{d{X}_1}{X_1}=-\tan \theta d\theta$$

(6)

Substituting $\theta =\pi /4$ for the reference state, we have the infinitesimal strain

$$d{\epsilon }_{eff}^0=-d\theta$$

(7)

Due to the large deformation involved, we adopt the true strain definition ${\epsilon }_{eff}=\int d{\epsilon }_{eff}$ to give

$${\epsilon }_{eff}=\ln \frac{X_1}{X_1^0}=\ln \left(\sqrt{2}\cos \theta \right)$$

(8)

The effective Young’s modulus, $E_{eff}$, can be established by energy approach, whereby the local mechanism, in the form of potential energy stored within the spiral springs during counter rotation of the Y-element pairs, is matched against the global deformation, in the form of overall strain energy for the entire metamaterial structure. Suppose each Y-element rotates by a magnitude of $d\theta$, the counter-rotating mechanism for each pair of Y-elements means that the spring encounters an angular change of $2d\theta$. The torsional load of $T=-k\left(2d\theta \right)$ for each spring would therefore give the potential energy stored per spring as

$$U=\frac{1}{2}k{\left(2d\theta \right)}^2$$

(9)

For $m\times n$ number of metamaterial units, there are $4mn+2\left(m+n\right)$ number of springs. Therefore, the total energy stored for an $m\times n$ unit array of this metamaterial is

$$U_{Tot}=8\left(mn+\frac{m}{2}+\frac{n}{2}\right)k{\left(d\theta \right)}^2$$

(10)

if every Y-element rotates by $d\theta$. The strain energy stored in each unit of the metamaterial is $U=0.5V{E}_{eff}{\epsilon }_{eff}^2$ in which the volume of each metamaterial unit is $V=\left(2X_1\right)\left(2X_2\right)\left(2h_Y+h_S\right)$, where $2X_1=2X_2$ are the side dimensions of each metamaterial unit while $h_Y$ and $h_S$ are the thicknesses of each Y-element and the spring, respectively. Writing $h=2h_Y+h_S$ for the entire metamaterial thickness and substituting $X_1$ and $X_2$ from Equation (3), we have the strain energy for each metamaterial unit

$$U=2h{\left(1+\sqrt{2}\right)}^2{l}^2{\cos }^2\theta E_{eff}{\epsilon }_{eff}^2$$

(11)

Hence, for an $m\times n$ array of metamaterial units we have the total strain energy

$$U_{Tot}=2mnh\left(3+2\sqrt{2}\right)l^2{\cos }^2\theta E_{eff}{\epsilon }_{eff}^2$$

(12)

Note that the factor $mn+m/2+n/2$ in Equation (10) is related to the metamaterial units’ borders, where the spiral springs are located, while the factor $mn$ in Equation (12) is due to the number of metamaterial units. Equating both expressions of the total energy and imposing $m,n\to \infty$, one obtains the effective Young’s modulus

$$E_{eff}=\frac{4k}{\left(3+2\sqrt{2}\right)h{l}^2{\cos }^2\theta } \frac{{\left(d\theta \right)}^2}{{\epsilon }_{eff}^2}$$

(13)

With reference to Equation (7) and $\theta =\pi /4$ for infinitesimal deformation, we have the infinitesimal effective Young’s modulus

$$E_{eff}=\frac{8k}{\left(3+2\sqrt{2}\right)h{l}^2}$$

(14)

For large deformation, there is a need to express the Y-element rotation $d\theta$ in terms of the strain. Perusal of Equation (8) gives

$$\cos \theta =\frac{e^{{\epsilon }_{eff}}}{\sqrt{2}}$$

(15)

Since $\theta ={\theta }_0+d\theta$ where ${\theta }_0=\pi /4$, one obtains

$$d\theta =-\frac{\pi }{4}+{\cos }^{-1}\left(\frac{e^{{\epsilon }_{eff}}}{\sqrt{2}}\right)$$

(16)

for which the strain changes from ${\epsilon }_{eff}=0$ to ${\epsilon }_{eff}=\ln 2$ as the half-angle of the Y-element pairs changes from $\theta =\pi /4$ in its original state to $\theta =0$ in its fully opened configuration. Therefore, substituting Equations (15) and (16) into Equation (13) yields

$$E_{eff}=\frac{8k}{\left(3+2\sqrt{2}\right)h{l}^2}\frac{{\epsilon }_{eff}^{-2}}{e^{2{\epsilon }_{eff}}} {\left[-\frac{\pi }{4}+{\cos }^{-1}\left(\frac{e^{{\epsilon }_{eff}}}{\sqrt{2}}\right)\right]}^2$$

(17)

It can be easily seen that the effective Young’s modulus is undefined at ${\epsilon }_{eff}=0$. As such, Equation (14) is used for obtaining the effective Young’s modulus at ${\epsilon }_{eff}=0$ while Equation (17) is to be adopted for ${\epsilon }_{eff}>0$. Under the effect of changed environmental temperature, the resulting change in the arc length and curvature of the spiral spring cause a change to the angle $\theta$, which induces counter-rotating action for each pair of the Y-elements, thereby leading to an overall change in size for each metamaterial unit. As such, a change in temperature alters the size of the entire metamaterial structure at constant shape, thereby retaining its symmetry. At high energy levels, the Y-elements can no longer be assumed rigid, such that application of uniaxial load would reduce the metamaterial to two-fold symmetry.

3. Results and Discussion

The first discussion entails the relationship between the prescribed uniaxial strain and the amount of rotation in each Y-element. This relationship is described by Equation (16), for which a visual representation is furnished in Figure 7 (top). The more simplified linear relationship, as described by Equation (7), is valid only for very small strain. For this reason, the global strain to local rotation relationship described by Equation (7) can be discarded in favor of Equation (16).

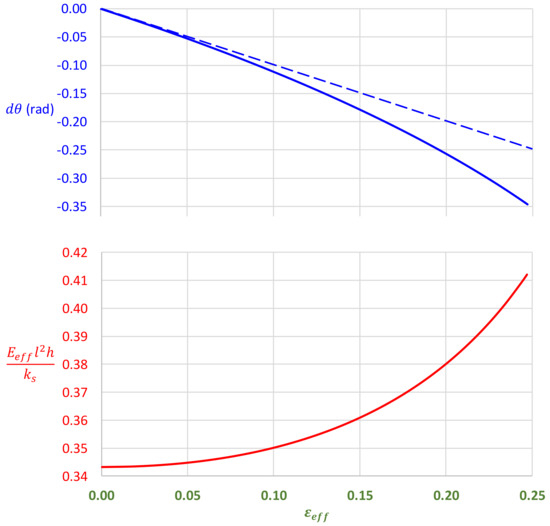
Figure 7. Effect of prescribed strain on the angular change of the Y-element, with the straight dashed line denoting infinitesimal model (top) and the dimensionless effective Young’s modulus for $m,n\to \infty$ (bottom).

Notwithstanding the above suggestion, Equation (7) is nevertheless useful for enabling the effective Young’s modulus to be calculated for infinitesimal deformation because this modulus is undefined at zero strain based on the finite deformation model, and independent from the strain based on the infinitesimal deformation model. As such, Figure 7 (bottom) shows a plot of dimensionless Young’s modulus based on Equation (17) for ${\epsilon }_{eff}>0$ and Equation (14) at ${\epsilon }_{eff}=0$. The plot graphically shows that the effective Young’s modulus can be enhanced by in-plane stretching.

4. Conclusions and Recommendations

A 2D metamaterial that exhibits perfect auxeticity, i.e., a Poisson’s ratio of $-1$ and hence achieving shape conservation during in-plane uniaxial loading, has been introduced herein by inspiration from an Islamic geometric pattern in the form of an eight-pointed star for each unit consisting of eight squares arranged in a circumference. Constructed via an intricate connection of rigid Y-elements, elastic restraint is implemented by incorporation of spiral springs between each pair of Y-elements. During application of uniaxial stretching, the metamaterial deforms in such a manner that each unit resembles the north dome of Jameh Mosque, Isfahan, and similar-looking Islamic architectures and designs. Results indicate that the effective Young’s modulus increases exponentially with the prescribed strain. Arising from the adopted assumptions and modeling approach, the following aspects of symmetry are attained for the currently investigated metamaterial:

(a)

The resulting in-plane strain is equi-biaxial $\left({\epsilon }_{11}={\epsilon }_{22}\right)$ under uniaxial loading;

(b)

Every unit of the metamaterial preserves its eight-fold symmetry throughout the entire stretching process;

(c)

The metamaterial array preserves its four-fold symmetry throughout the entire stretching process;

(d)

The effective Young’s modulus, $E_{eff}$, along either axis is the same.

In view of the high level of symmetry and asymmetry in Islamic geometrical patterns that have been developed for many centuries, it is herein recommended that further survey be made on other Islamic art and architectural designs in order to conceptualize other metamaterials with novel, especially negative, properties.