Machine Learning-Based Pulse Wave Analysis for Early Detection of Abdominal Aortic Aneurysms Using In Silico Pulse Waves
Abstract
1. Introduction
2. Materials and Methods
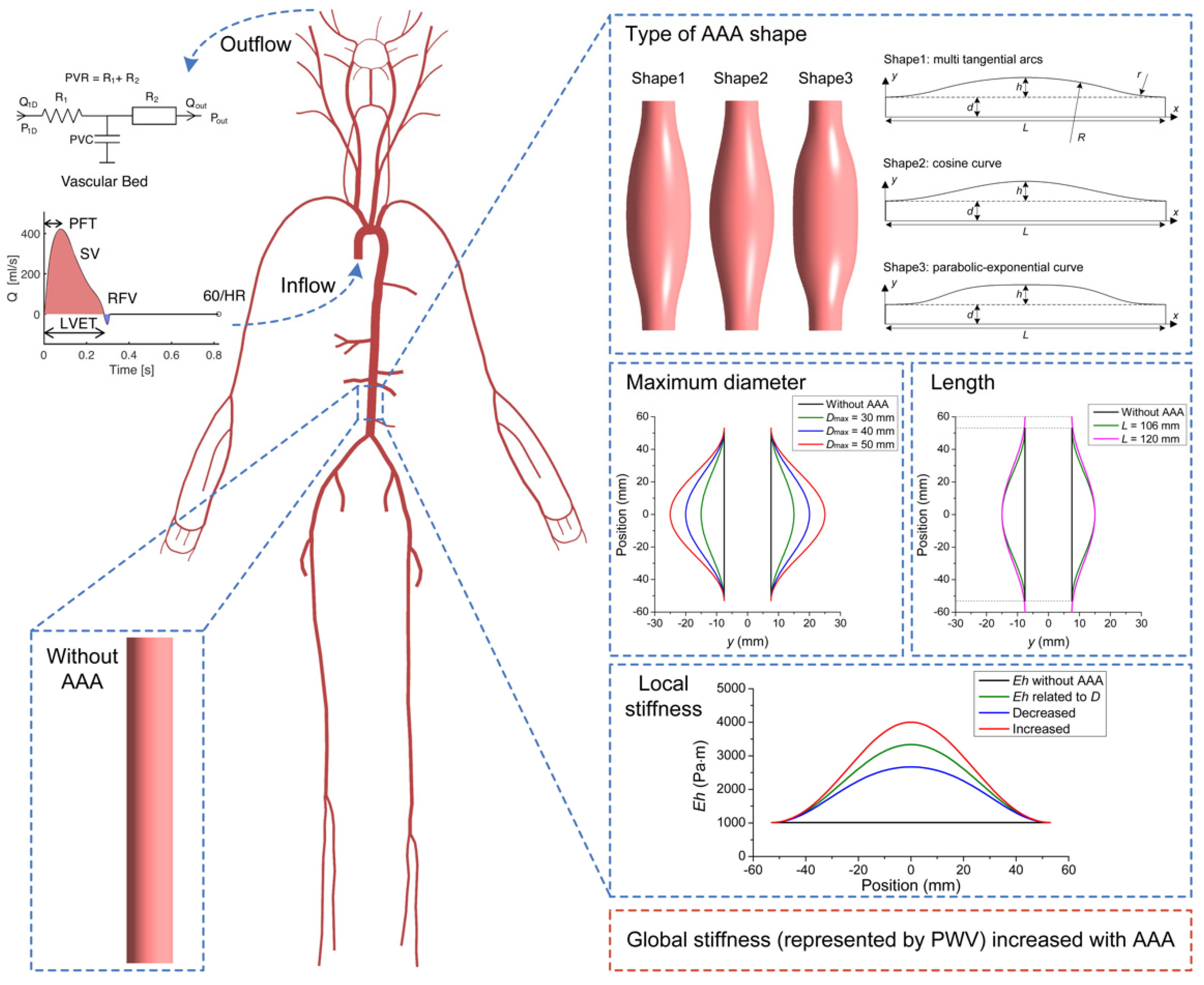
2.1. Modelling Pulse Waves in Baseline Subjects with and without AAAs
2.2. Parameter Sensitivity Analysis
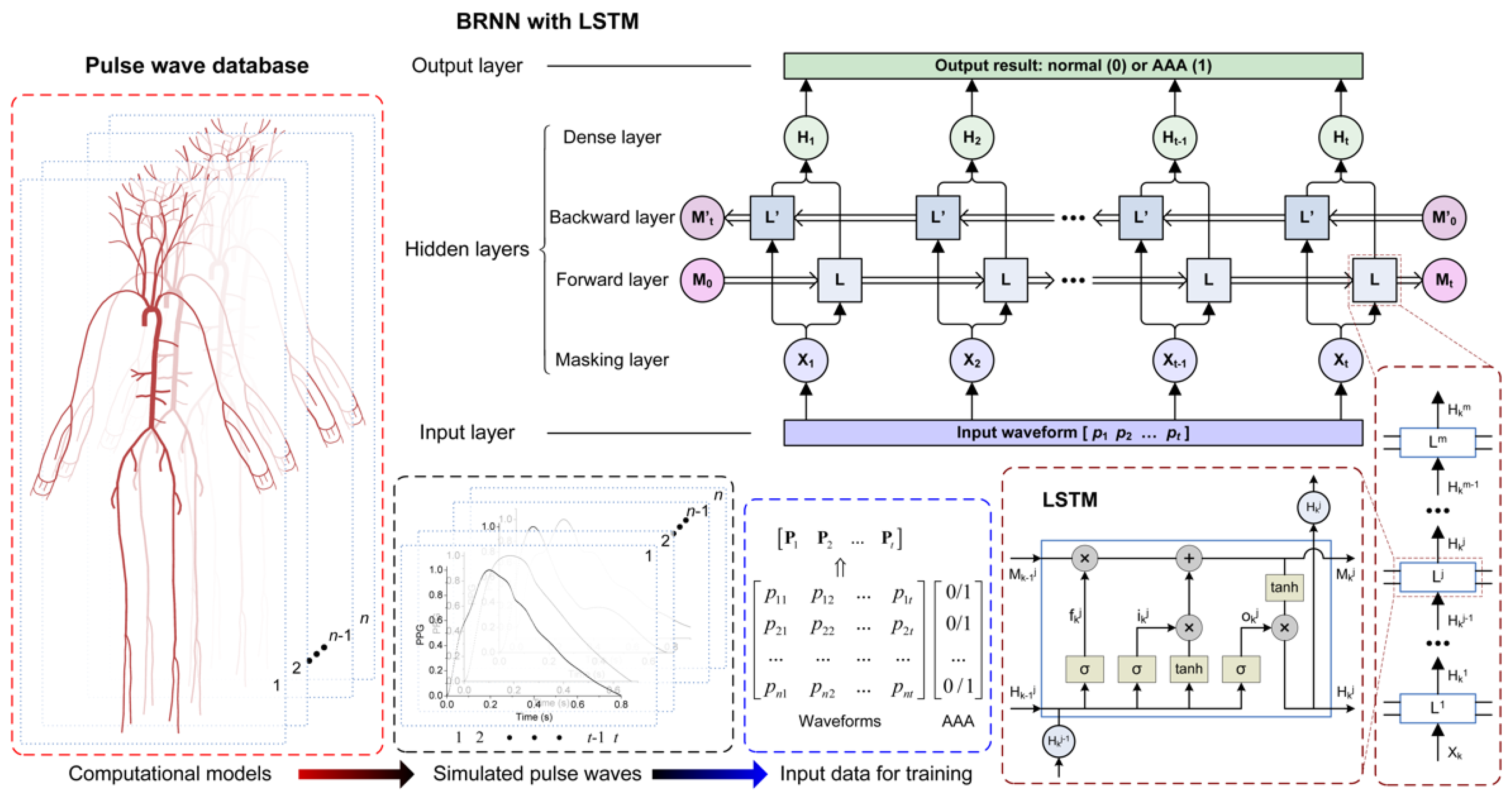
2.3. Database of In Silico Pulse Waves
2.3.1. Modelling a Database of Pulse Waves in Subjects with and without an AAA
2.3.2. Extracting Pulse Wave Indexes
2.4. Machine Learning-Based Pulse Wave Analysis
2.4.1. Recurrent Neural Network
2.4.2. Training and Testing
3. Results
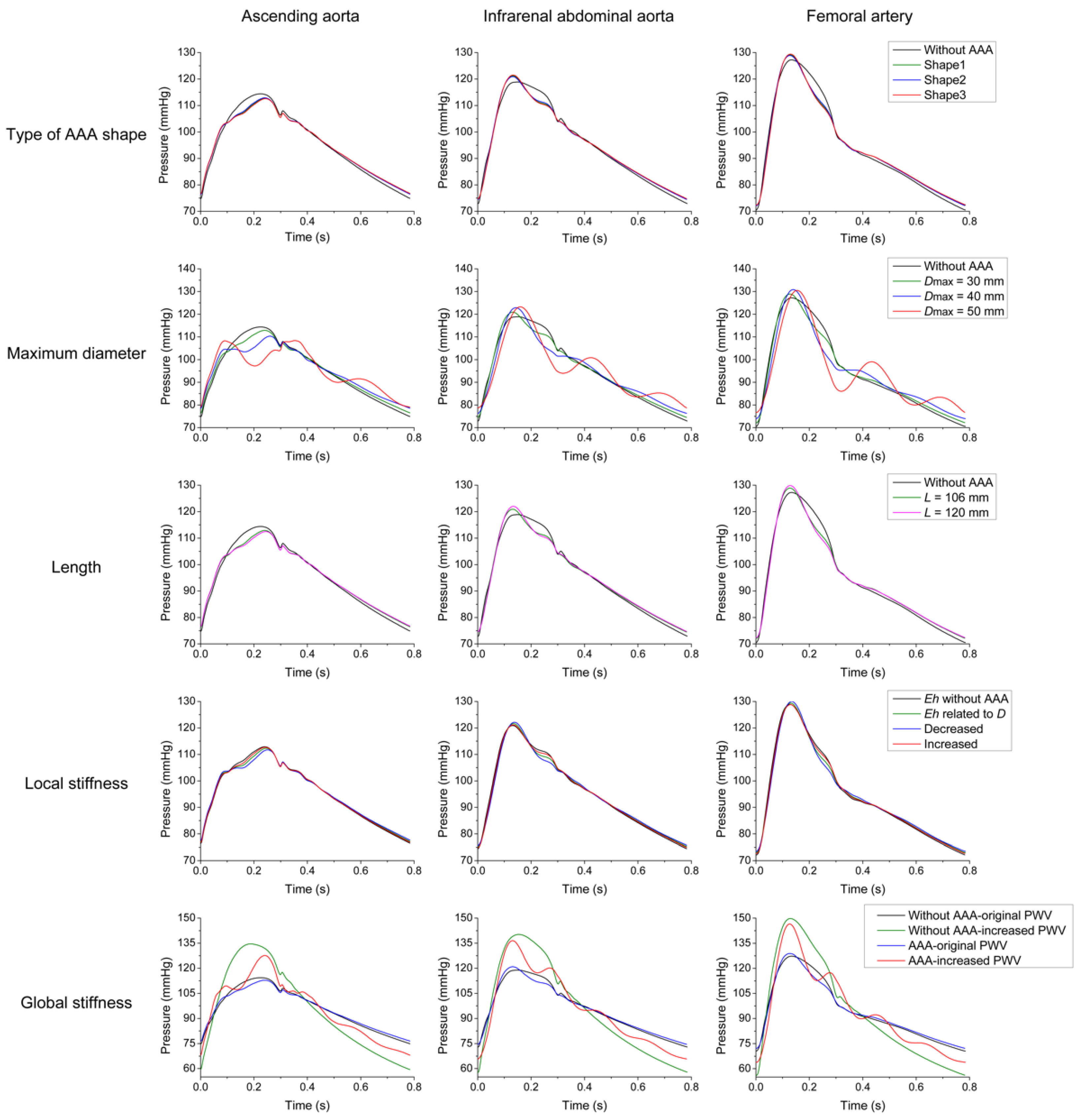
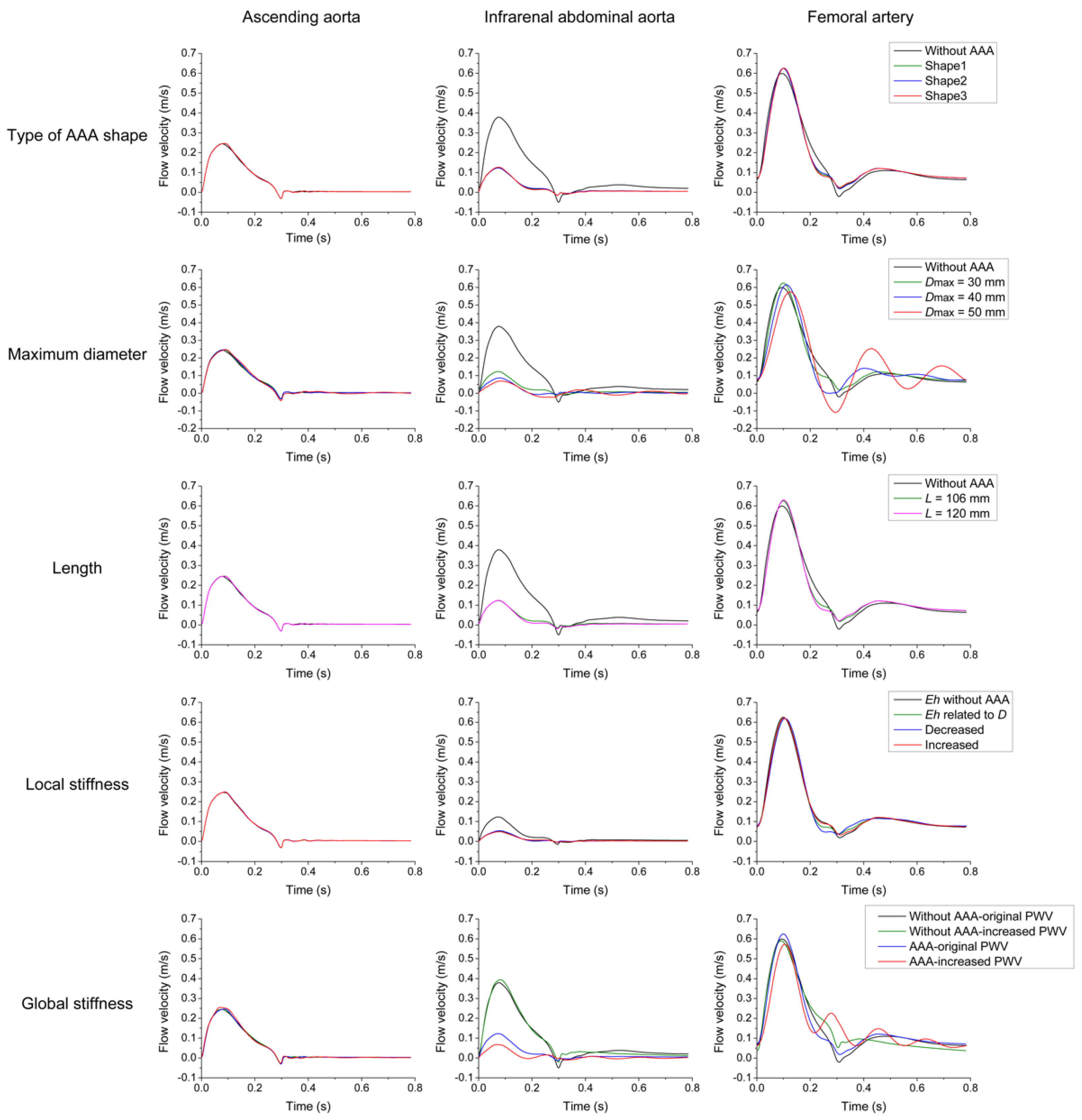
3.1. Parameter Sensitivity Analysis
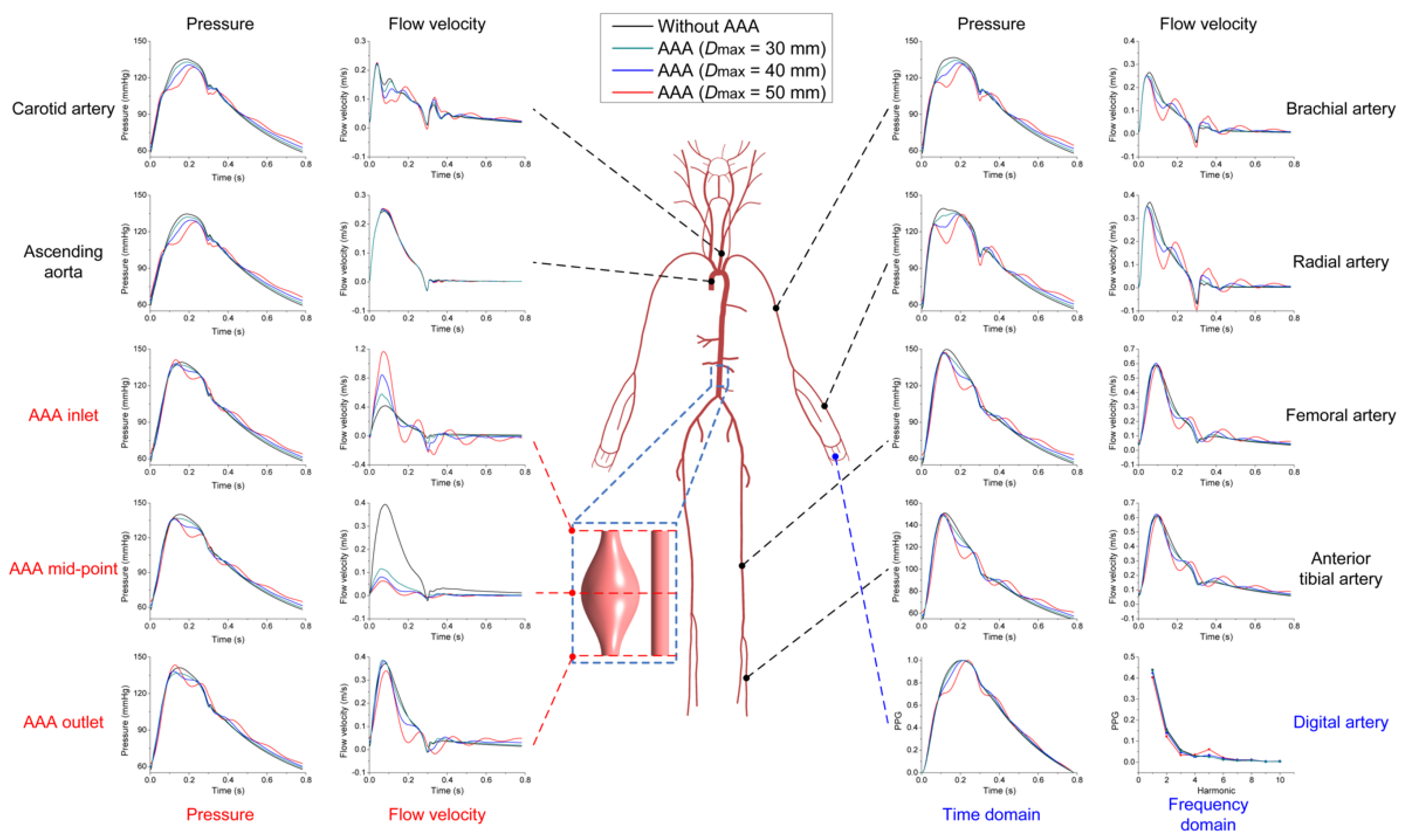
3.2. Effects of AAA on Pulse Waveforms and Comparison with the Literature
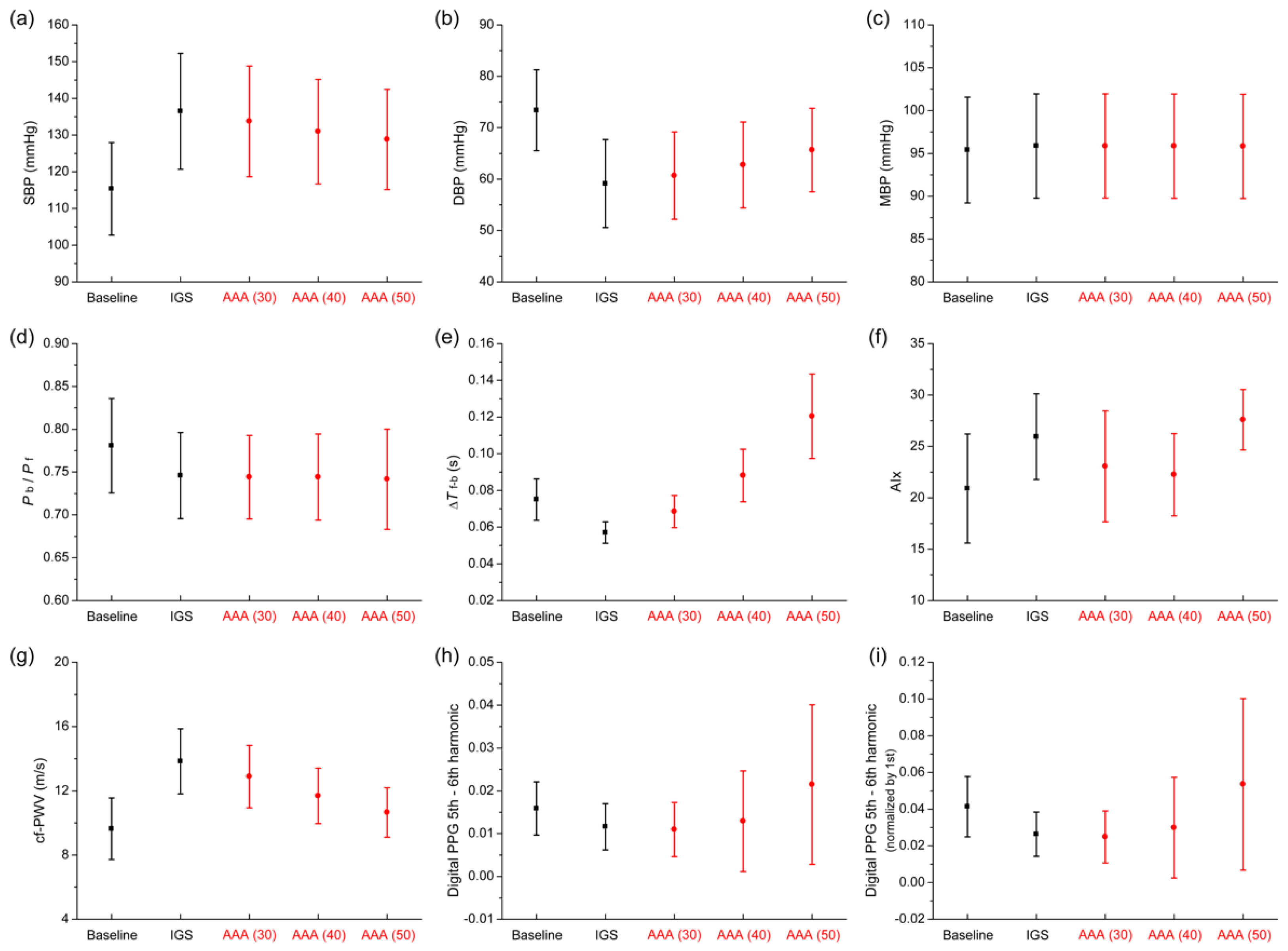
3.3. Comparison of Pulse Wave Indexes Extracted from the Pulse Wave Database
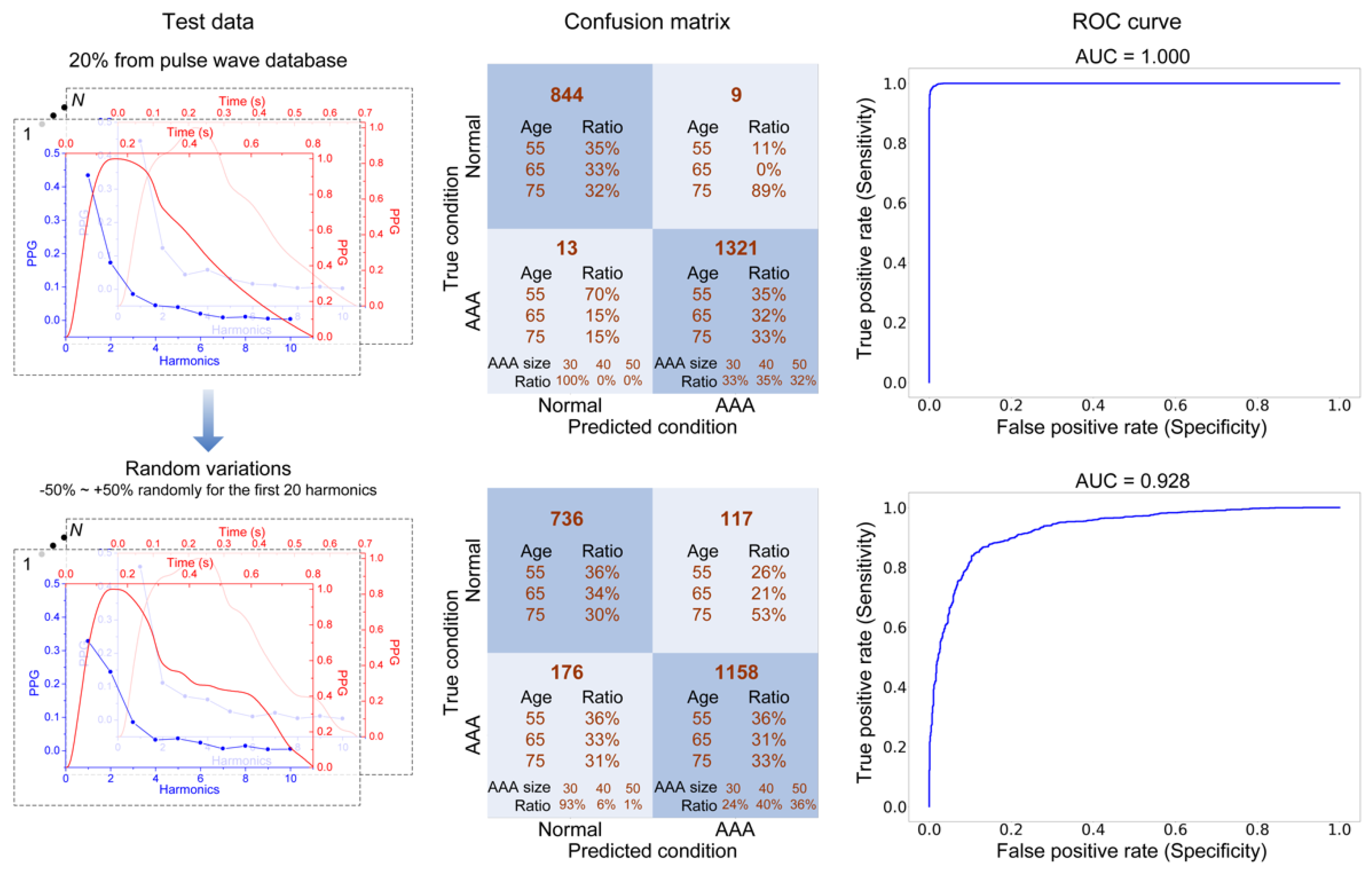
3.4. AAA Early Detection Using Machine Learning
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sakalihasan, N.; Limet, R.; Defawe, O.D. Abdominal aortic aneurysm. Lancet 2005, 365, 1577–1589. [Google Scholar] [CrossRef]
- Golledge, J.; Muller, J.; Daugherty, A.; Norman, P. Abdominal aortic aneurysm: Pathogenesis and implications for management. Arterioscler. Thromb. Vasc. Biol. 2006, 26, 2605–2613. [Google Scholar] [CrossRef]
- Scott, R.A.P.; Ashton, H.A.; Kay, D.N. Abdominal aortic aneurysm in 4237 screened patients: Prevalence, development and management over 6 years. Br. J. Surg. 1991, 78, 1122–1125. [Google Scholar] [CrossRef]
- Kent, K.C. Abdominal aortic aneurysms. N. Engl. J. Med. 2014, 371, 2101–2108. [Google Scholar] [CrossRef] [PubMed]
- Upchurch, G.R.; Schaub, T.A. Abdominal aortic aneurysm. Am. Family Physician 2006, 73, 1198–1204. [Google Scholar]
- Aggarwal, S.; Qamar, A.; Sharma, V.; Sharma, A. Abdominal aortic aneurysm: A comprehensive review. Exp. Clin. Cardiol. 2011, 16, 11–15. [Google Scholar]
- Wells, C.E.; Pugh, N.D.; Woodcock, J.P. Abdominal aortic aneurysm detection by common femoral artery Doppler ultrasound waveform analysis. J. Med. Eng. Technol. 2011, 35, 34–39. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wood, M.M.; Romine, L.E.; Lee, Y.K.; Richman, K.M.; O’Boyle, M.K.; Paz, D.A.; Chu, P.K.; Pretorius, D.H. Spectral doppler signature waveforms in ultrasonography: A review of normal and abnormal waveforms. Ultrasound Q. 2010, 26, 83–99. [Google Scholar] [CrossRef]
- Elgendi, M. PPG Signal Analysis: An Introduction Using MATLAB®; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Chakshu, N.K.; Sazonov, I.; Nithiarasu, P. Towards Enabling a Cardiovascular Digital Twin for Human Systemic Circulation Using Inverse Analysis. Biomech. Model. Mechanobiol. 2020. [Google Scholar] [CrossRef] [PubMed]
- Tavallali, P.; Razavi, M.; Pahlevan, N.M. Artifcial intelligence estimation of carotid-femoral pulse wave velocity using carotid waveform. Sci. Rep. 2018, 8, 1014. [Google Scholar] [CrossRef] [PubMed]
- Biswas, D.; Everson, L.; Liu, M.; Panwar, M.; Verhoef, B.-E.; Patki, S.; Kim, C.H.; Acharyya, A.; Van Hoof, C.; Konijnenburg, M.; et al. CorNET: Deep learning framework for PPG-based heart rate estimation and biometric identification in ambulant environment. IEEE Trans. Biomed. Eng. 2019, 13, 282–291. [Google Scholar] [CrossRef] [PubMed]
- Jones, G.; Parr, J.; Nithiarasu, P.; Pant, S. Machine learning for detection of stenoses and aneurysms: Application in a physiologically realistic virtual patient database. arXiv 2021, arXiv:2103.00599. [Google Scholar]
- Charlton, P.H.; Harana, J.M.; Vennin, S.; Li, Y.; Chowienczyk, P.; Alastruey, J. Modelling arterial pulse waves in healthy ageing: A database for in silico evaluation of haemodynamics and pulse wave indexes. Am. J. Physiol. Heart Circulatory Physiol. 2019, 317, H1062–H1085. [Google Scholar] [CrossRef] [PubMed]
- Jones, G.; Parr, J.; Nithiarasu, P.; Pant, S. A physiologically realistic virtual patient database for the study of arterial haemodynamics. arXiv 2021, arXiv:2102.10655. [Google Scholar]
- Wang, T.; Liang, F.; Li, L.; Zhang, W.; Wang, G.; Wang, J.; Zhang, C.; Qi, X. A computational model-based study on the exchangeability of hepatic venous pressure gradients measured in multiple hepatic vein. Med. Eng. Phys. 2020, 84, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Liang, F.; Zhou, Z.; Qi, X. Global sensitivity analysis of hepatic venous pressure gradient (HVPG) measurement with a stochastic computational model of the hepatic circulation. Comput. Biol. Med. 2018, 97, 124–136. [Google Scholar] [CrossRef] [PubMed]
- Vilalta, G.; Nieto, F.; Vaquero, C.; Vilalta, J.A. Quantitative indicator of abdominal aortic aneurysm rupture risk based on its geometric parameters. World Acad. Sci. Eng. Technol. 2010, 70, 181–185. [Google Scholar]
- Giannoglou, G.; Giannakoulas, G.; Soulis, J.; Chatzizisis, Y.; Perdikides, T.; Melas, N.; Parcharidis, G.; Louridas, G. Predicting the risk of rupture of abdominal aortic aneurysms by utilizing various geometrical parameters revisiting the diameter criterion. Angiology 2006, 57, 487–494. [Google Scholar] [CrossRef]
- Li, Z.; Kleinstreuer, C. A new wall stress equation for aneurysm-rupture prediction. Ann. Biomed. Eng. 2005, 33, 209–213. [Google Scholar] [CrossRef]
- Venkatasubramaniam, A.K.; Fagan, M.J.; Mehta, T.; Mylankal, K.J.; Ray, B.; Kuhan, G.; Chetter, I.C.; McCollum, P.T. A comparative study of aortic wall stress using finite element analysis for ruptured and non-ruptured abdominal aortic aneurysms. Eur. J. Vasc. Endovasc. Surg. 2004, 28, 168–176. [Google Scholar]
- Lindquist Liljeqvist, M.; Hultgren, R.; Siika, A.; Gasser, T.C.; Roy, J. Gender, smoking, body size, and aneurysm geometry influence the biomechanical rupture risk of abdominal aortic aneurysms as estimated by finite element analysis. J. Vasc. Surg. 2017, 65, 1014–1022. [Google Scholar] [CrossRef] [PubMed]
- Volokh, K.Y.; Vorp, D.A. A model of growth and rupture of abdominal aortic aneurysm. J. Biomech. 2008, 41, 1015–1021. [Google Scholar] [CrossRef] [PubMed]
- Grytsan, A.; Watton, P.N.; Holzapfel, G.A. A thick-walled fluid–solid-growth model of abdominal aortic aneurysm evolution: Application to a patient-specific geometry. J. Biomech. Eng. 2015, 137, 031008. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, J.D.; Holzapfel, G.A. Mechanics, mechanobiology, and modeling of human abdominal aorta and aneurysms. J. Biomech. 2012, 45, 805–814. [Google Scholar] [CrossRef]
- Figueroa, C.A.; Taylor, C.A.; Yeh, V.; Chiou, A.J.; Zarins, C.K. Effect of curvature on displacement forces acting on aortic endografts: A 3-dimensional computational analysis. J. Endovasc. Ther. 2009, 16, 284–294. [Google Scholar] [CrossRef]
- Gindre, J.; Bel-Brunon, A.; Kaladji, A.; Duménil, A.; Rochette, M.; Lucas, A.; Haigron, P.; Combescure, A. Finite element simulation of the insertion of guidewires during an EVAR procedure: Example of a complex patient case, a first steptoward patient-specific parameterized models. Int. J. Numer. Method Biomed. Eng. 2015, 31, e02716. [Google Scholar] [CrossRef]
- Casciaro, M.E.; Alfonso, M.A.; Craiem, D.; Alsac, J.M.; El-Batti, S.; Armentano, R.L. Predicting the effect on pulse wave reflection of different endovascular repair techniques in abdominal aortic aneurysm using 1D patient-specific models. Health Technol. 2016, 6, 173–179. [Google Scholar] [CrossRef]
- Fraser, K.H.; Meagher, S.; Blake, J.R.; Easson, W.J.; Hoskins, P.R. Characterization of an abdominal aortic velocity waveform in patients with abdominal aortic aneurysm. Ultrasound Med. Biol. 2008, 34, 73–80. [Google Scholar] [CrossRef]
- Taylor, C.A.; Cheng, C.P.; Espinosa, L.A.; Tang, B.T.; Parker, D.; Herfkens, R.J. In vivo quantification of blood flow and wall shear stress in the human abdominal aorta during lower limb exercise. Ann. Biomed. Eng. 2002, 30, 402–408. [Google Scholar] [CrossRef]
- Les, A.S.; Yeung, J.J.; Schultz, G.M.; Herfkens, R.J.; Dalman, R.L.; Taylor, C.A. Supraceliac and infrarenal aortic flow in patients with abdominal aortic aneurysms: Mean flows, waveforms, and allometric scaling relationships. Cardiovasc. Eng. Technol. 2010, 1, 39–51. [Google Scholar] [CrossRef]
- Wang, T.; Alastruey, J.; Liang, F. A computational model-based study on the effect of abdominal aortic aneurysm on pulse wave morphology. Artery Res. 2020, 26, S10–S11. [Google Scholar] [CrossRef]
- Sazonov, I.; Khir, A.W.; Hacham, W.S.; Boileau, E.; Carson, J.M.; van Loon, R.; Ferguson, C.; Nithiarasu, P. A novel method for non-invasively detecting the severity and location of aortic aneurysms. Biomech. Model. Mechanobiol. 2017, 16, 1225–1242. [Google Scholar] [CrossRef]
- Safaei, S. Simulating Blood Flow in an Anatomical Arterial Network; University of Auckland: Auckland, New Zealand, 2015. [Google Scholar]
- Low, K.; van Loon, R.; Sazonov, I.; Bevan, R.L.T.; Nithiarasu, P. An improved baseline model for a human arterial network to study the impact of aneurysms on pressure-flow waveforms. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 1224–1246. [Google Scholar] [CrossRef] [PubMed]
- Swillens, A.; Lanoye, L.; De Backer, J.; Stergiopulos, N.; Verdonck, P.R.; Vermassen, F.; Segers, P. Effect of an abdominal aortic aneurysm on wave reflection in the aorta. IEEE Trans. Biomed. Eng. 2008, 55, 1602–1611. [Google Scholar] [CrossRef] [PubMed]
- Tong, J.; Cohnert, T.; Holzapfel, G.A. Diameter-related variations of geometrical, mechanical, and mass fraction data in the anterior portion of abdominal aortic aneurysms. Eur. J. Vasc. Endovasc. Surg. 2015, 49, 262–270. [Google Scholar] [CrossRef]
- Martufi, G.; Di Martino, E.S.; Amon, C.H.; Muluk, S.C.; Finol, E.A. Three-dimensional geometrical characterization of abdominal aortic aneurysms: Image-based wall thickness distribution. J. Biomech. Eng. 2009, 131, 061015. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, J.F.; Ruiz, C.; Doblaré, M.; Holzapfel, G.A. Mechanical stresses in abdominal aortic aneurysms influence of diameter, asymmetry, and material anisotropy. J. Biomech. Eng. 2008, 130, 021023. [Google Scholar] [CrossRef]
- Doyle, B.J.; Morris, L.G.; Callanan, A.; Kelly, P.; Vorp, D.A.; McGloughlin, T.M. 3D reconstruction and manufacture of real abdominal aortic aneurysms: From CT scan to silicone model. J. Biomech. Eng. 2008, 130, 034501. [Google Scholar] [CrossRef] [PubMed]
- Shum, J.; Martufi, G.; Di Martino, E.; Washington, C.B.; Grisafi, J.; Muluk, S.C.; Finol, E.A. Quantitative assessment of abdominal aortic aneurysm geometry. Ann. Biomed. Eng. 2011, 39, 277–286. [Google Scholar] [CrossRef]
- Kolipaka, A.; Illapani, V.S.P.; Kenyhercz, W.; Dowell, J.D.; Go, M.R.; Starr, J.E.; Vaccaro, P.S.; White, R.D. Quantification of abdominal aortic aneurysm stiffness using magnetic resonance elastography and its comparison to aneurysm diameter. J. Vasc. Surg. 2016, 64, 966–974. [Google Scholar] [CrossRef] [PubMed]
- Durmus, I.; Kazaz, Z.; Altun, G.; Cansu, A. Augmentation index and aortic pulse wave velocity in patients with abdominal aortic aneurysms. Int. J. Clin. Exp. Med. 2014, 7, 421–425. [Google Scholar]
- Kadoglou, N.P.E.; Papadakis, I.; Moulakakis, K.G.; Ikonomidis, I.; Alepaki, M.; Moustardas, P.; Lampropoulos, S.; Karakitsos, P.; Lekakis, J.; Liapis, C.D. Arterial stiffness and novel biomarkers in patients with abdominal aortic aneurysms. Regul. Pept. 2012, 179, 50–54. [Google Scholar] [CrossRef]
- Kadoglou, N.P.E.; Moulakakis, K.G.; Papadakis, I.; Ikonomidis, I.; Alepaki, M.; Lekakis, J.; Liapis, C.D. Changes in aortic pulse wave velocity of patients undergoing endovascular repair of abdominal aortic aneurysms. J. Endovasc. Ther. 2012, 19, 661–666. [Google Scholar] [CrossRef]
- Länne, T.; Sonesson, B.; Bergqvist, D.; Bengtsson, H.; Gustafsson, D. Diameter and compliance in the male human abdominal aorta: Influence of age and aortic aneurysm. Eur. J. Vasc. Surg. 1992, 6, 178–184. [Google Scholar] [CrossRef]
- Schriefl, A.J.; Zeindlinger, G.; Pierce, D.M.; Regitnig, P.; Holzapfel, G.A. Determination of the layer-specific distributed collagen fibre orientations in human thoracic and abdominal aortas and common iliac arteries. J. R. Soc. Interface 2012, 9, 1275–1286. [Google Scholar] [CrossRef]
- Shum, J.; Dimartino, E.S.; Goldhammer, A.; Goldman, D.H.; Acker, L.C.; Patel, G.; Ng, J.H.; Martufi, G.; Finol, E.A. Semiautomatic vessel wall detection and quantification of wall thickness in computed tomography images of human abdominal aortic aneurysms. Med. Phys. 2010, 37, 638–648. [Google Scholar] [CrossRef]
- Raghavan, M.L.; Kratzberg, J.; de Tolosa, E.M.C.; Hanaoka, M.M.; Walker, P.; da Silva, E.S. Regional distribution of wall thickness and failure properties of human abdominal aortic aneurysm. J. Biomech. 2006, 39, 3010–3016. [Google Scholar] [CrossRef]
- Martufi, G.; Satriano, A.; Moore, R.D.; Vorp, D.A.; Di Martino, E.S. Local quantification of wall thickness and intraluminal thrombus offer insight into the mechanical properties of the aneurysmal aorta. Ann. Biomed. Eng. 2015, 43, 1759–1771. [Google Scholar] [CrossRef] [PubMed]
- Di Martino, E.S.; Bohra, A.; Vande Geest, J.P.; Gupta, N.; Makaroun, M.S.; Vorp, D.A. Biomechanical properties of ruptured versus electively repaired abdominal aortic aneurysm wall tissue. J. Vasc. Surg. 2006, 43, 570–576. [Google Scholar] [CrossRef] [PubMed]
- Shum, J.; Xu, A.; Chatnuntawech, I.; Finol, E.A. A framework for the automatic generation of surface topologies for abdominal aortic aneurysm models. Ann. Biomed. Eng. 2011, 39, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Gaddum, N.R.; Alastruey, J.; Beerbaum, P.; Chowienczyk, P.; Schaeffter, T. A technical assessment of pulse wave velocity algorithms applied to Non-invasive arterial waveforms. Ann. Biomed. Eng. 2013, 41, 2617–2629. [Google Scholar] [CrossRef]
- Segers, P.; Rietzschel, E.R.; De Buyzere, M.L.; De Bacquer, D.; Van Bortel, L.M.; De Backer, G.; Gillebert, T.C.; Verdonck, P.R. Assessment of pressure wave reflection: Getting the timing right! Physiol. Meas. 2007, 28, 1045–1056. [Google Scholar] [CrossRef] [PubMed]
- Westerhof, N.; Sipkema, P.; van den Bos, G.C.; Elzinga, G. Forward and backward waves in the arterial system. Cardiovasc. Res. 1972, 6, 648–656. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A critical review of recurrent neural networks for sequence learning. Comput. Sci. 2015. Available online: http://arxiv.org/abs/1506.00019 (accessed on 4 May 2021).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Chowienczyk, P.; Alastruey, J. Estimating pulse wave velocity from the radial pressure wave using machine learning algorithms. medRxiv 2020. [Google Scholar] [CrossRef]
- Jin, W.; Alastruey, J. Arterial pulse wave propagation across stenoses and aneurysms: Assessment of one-dimensional simulations against three-dimensional simulations and in vitro measurements. J. R. Soc. Interface 2021, 18, 20200881. [Google Scholar] [CrossRef]
- Li, Z.-Y.; U-King-Im, J.; Tang, T.Y.; Soh, E.; See, T.C.; Gillard, J.H. Impact of calcification and intraluminal thrombus on the computed wall stresses of abdominal aortic aneurysm. J. Vasc. Surg. 2008, 47, 928–935. [Google Scholar] [CrossRef]
- Di Martino, E.S.; Vorp, D.A. Effect of variation in intraluminal thrombus constitutive properties on abdominal aortic aneurysm wall stress. Ann. Biomed. Eng. 2003, 31, 804–809. [Google Scholar] [CrossRef]
- Tong, J.; Cohnert, T.; Regitnig, P.; Holzapfel, G.A. Effects of age on the elastic properties of the intraluminal thrombus and the thrombus-covered wall in abdominal aortic aneurysms: Biaxial extension behaviour and material modelling. Eur. J. Vasc. Endovasc. Surg. 2011, 42, 207–219. [Google Scholar] [CrossRef]

| Control (Number) | AAA Patient (Number) | Reference |
|---|---|---|
| 10.0 m/s (20) | 14.8 m/s (18) | [43] |
| 10.03 m/s (42) | 12.99 m/s (108) | [44] |
| 7.97 m/s (31) | 13.11 m/s (48) | [45] |
| 9.33 m/s | 13.63 m/s | Mean value |
| Source | Value | Reference |
|---|---|---|
| Growth ratio of elastic modulus from normal to AAA | ||
| Measured by magnetic resonance elastography | 96.8% | [42] |
| Calculated from the measured pressure and diameter | 49.6% | [46] |
| 73.2% | Mean value | |
| Normal wall thickness | ||
| Derived from clinical measurements | 1.4~1.5 mm | [25] |
| 1.39 mm | [47] | |
| 1.4 mm | Mean value | |
| AAA wall thickness | ||
| Derived from clinical measurements | 2 mm | [37] |
| 1.63 mm | [48] | |
| 1.48 mm | [49] | |
| 2.71 mm | [50] | |
| 2.87 mm | [51] | |
| 1.64 mm | [52] | |
| Used by previous model-based studies | 2 mm | [21,40] |
| 2 mm | Mean value | |
| Parameter | Value |
|---|---|
| Number of LSTM units | 16 |
| Batch size | 32 |
| Epoch number | 256 |
| Optimiser | Adam |
| Cost function | Binary cross-entropy |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Jin, W.; Liang, F.; Alastruey, J. Machine Learning-Based Pulse Wave Analysis for Early Detection of Abdominal Aortic Aneurysms Using In Silico Pulse Waves. Symmetry 2021, 13, 804. https://doi.org/10.3390/sym13050804
Wang T, Jin W, Liang F, Alastruey J. Machine Learning-Based Pulse Wave Analysis for Early Detection of Abdominal Aortic Aneurysms Using In Silico Pulse Waves. Symmetry. 2021; 13(5):804. https://doi.org/10.3390/sym13050804
Chicago/Turabian StyleWang, Tianqi, Weiwei Jin, Fuyou Liang, and Jordi Alastruey. 2021. "Machine Learning-Based Pulse Wave Analysis for Early Detection of Abdominal Aortic Aneurysms Using In Silico Pulse Waves" Symmetry 13, no. 5: 804. https://doi.org/10.3390/sym13050804
APA StyleWang, T., Jin, W., Liang, F., & Alastruey, J. (2021). Machine Learning-Based Pulse Wave Analysis for Early Detection of Abdominal Aortic Aneurysms Using In Silico Pulse Waves. Symmetry, 13(5), 804. https://doi.org/10.3390/sym13050804






