Almost-Minimal-Round BBB-Secure Tweakable Key-Alternating Feistel Block Cipher

Abstract

This paper focuses on designing a tweakable block cipher via by tweaking the Key-Alternating Feistel ($\mathsf{KAF}$ for short) construction. Very recently Yan et al. published a tweakable $\mathsf{KAF}$ construction. It provides a birthday-bound security with 4 rounds and Beyond-Birthday-Bound (BBB for short) security with 10 rounds. Following their work, we further reduce the number of rounds in order to improve the efficiency while preserving the same level of security bound. More specifically, we rigorously prove that 6-round tweakable $\mathsf{KAF}$ cipher is BBB- secure. The main technical contribution is presenting a more refined security proof framework, which makes significant efforts to deal with several subtle and complicated sub-events. Note that Yan et al. showed that 4-round $\mathsf{KAF}$ provides exactly Birthday-Bound security by a concrete attack. Thus, 6 rounds are (almost) minimal rounds to achieve BBB security for tweakable $\mathsf{KAF}$ construction.

1. Introduction

A block cipher, also known as a pseudorandom permutation, which is a pair of algorithms $(E,D)$. A block cipher has two important parameters: block length and key length. If the block length is n bits and the key length is k bits, for a mathematical point of view, the block cipher can be seen as a mapping

$${\{0,1\}}^k\times {\{0,1\}}^n\to {\{0,1\}}^n.$$

E represents a mapping that from the key space and the message space to the message space, and D is the opposite direction of the mapping in E. In addition, we call E is encryption, and D is decryption. The schemes of block cipher are roughly separated into two main classes, which are named Feistel networks and substitution—permutation networks (SPNs).

The tweakable block cipher is formalized by Liskov et al. [1]. It introduces to the block cipher an extra public input parameter tweak. The tweak provides inherent variability for building higher higher-level cryptographic schemes, namely modes of operation. So far, the tweakable block cipher has got received wide applications. Examples include Message Encryption, Message Authentication Code [1,2], and Authenticated Encryption Mode [3,4,5], etc. Now designing secure tweakable block ciphers has become a very important research topic. Cryptographers build tweakable block ciphers either from the scratch [6,7,8], or based on existing cryptographic primitives such as block ciphers or permutations [2,9,10,11]. Among these approaches, one is introducing the tweak to general structures of classical block ciphers, namely the Feistel construction [12] and the Even—Mansour construction [13]. We refer the interested readers to [9,14,15,16,17,18] for tweaking the Even—Mansour construction.

This paper mainly focuses on tweaking the Feistel construction. Since invented by Horst Feistel in 1973 [12], the Feistel construction has been a mainstream class of block ciphers. More specifically, there are several Feistel construction variants, such as Luby—Rackoff [19], Generalized Feistel [20], Key-Alternating Feistel [21], etc. They have been adopted in dedicated block ciphers including international and national standards. In 2007, Goldenberg et al. published the first paper of incorporating tweak to the Feistel constructions [22]. In particular, they paid attention to the Luby—Rackoff ciphers, and XOR tweaks to the dataflow branches. We write such tweak injection as linear tweak injection in this paper. Goldenberg et al. found that 6 rounds and more are secure (against polynomial adversaries). Moreover, they showed that 10 rounds are secure against $2^n$ adversarial queries, that is i.e., fully secure with n as the branch bit size of Luby—Rackoff structure. After that, Mitsuda and Iwata analyzed tweaking Generalized Feistel Structures with similar linear tweak injection [20]. They proved that $2d$ rounds are birthday-bound secure with d as the number of branches of Generalized Feistel Structure. Very recently, Yan et al. published a result of tweaking the Key-Alternating Feistel ($\mathsf{KAF}$) Cipher [23]. They introduced the tweak by mixing round keys, and proved that 4 rounds have a birthday-bound security and 10 rounds enable a beyond-birthday-bound security of roughly $2^{2n/3}$ adversarial queries with n as the branch bit size. We will carry on the research of tweaking the $\mathsf{KAF}$. (It is referred to as Feistel-2 in IACR Tikz Library).

The Feistel network [12] is a popular structure of block ciphers. In the i-th round of the Feistel cipher, the intermediate state of input $x_i=L\Vert R$ is updated by the round function $G_i$, i.e., $L\Vert R\to R\Vert L\oplus G_i(k_i,R)$. After tweaking the generalized Feistel ciphers by Mitsuda and Iwata [20], there is are only a few works about tweaking the Feistel cipher. The most mainstream research is tweaking $\mathsf{KAF}$ ciphers as Yan et al did recently [23]. They introduced the tweak with several round keys by using a universal hash function $H(·)$, that is, $t{k}_i\leftarrow H_{k_i}\left(t\right)$, where $k_i$ is the secret key, t is the tweak. By tweaking $\mathsf{KAF}$ with the i-th round function, the input is updated through

$$m_L\Vert m_R\leftarrow m_R\Vert m_L\oplus F_i(H_{k_i}\left(t\right)\oplus m_R),$$

where $F(·)$ is the ith-round function. Yan et al. presented a 4-round minimized structure with two round keys and a single random function, proved that it achieves Birthday-Bound security. Meanwhile, they presented a 10-round tweakable $\mathsf{KAF}$ ($\mathsf{TKAF}$ for short) construction (depict in Figure 1) that can achieve BBB security. In this work, we aim to optimize Yan et al’s 10-round structure, and adopt other distinct construction of tweakable block ciphers. Then we give the proof that the new construction still meets the BBB security. We compared with Yan et al’s work [23] which lists in Table 1.

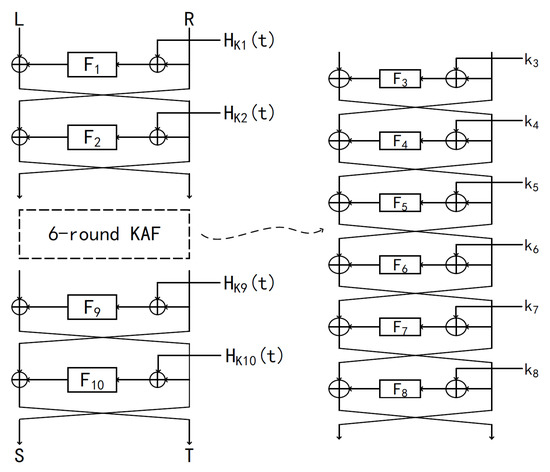
Figure 1. 10-round tweakable Key-Alternating Feistel cipher presented by Yan et al.

Table 1. Comparison with related works.

Key Size	Rounds	Number of Round Functions	Bound	Reference
10n	10	10	2n/3	Yan et al. [23]
6n	6	6	2n/3	Guo et al. [24] (without tweak)
6n	6	6	2n/3	Section 3 (tweaked)

1.1. Our Contributions

In this paper, we present a 6-round $\mathsf{TKAF}$ cipher which meets the BBB security, with tweaking the additional outer four rounds based on based on Guo et al.’s 6-round $\mathsf{KAF}$ [24]. Unlike Yan et al.’s research, we adopt the approach of introducing tweak into the 6-round $\mathsf{KAF}$ directly. By utilizing Guo et al’s proof methodology, we introduce the tweak via using a universal hash function. We prove when the adversary makes distinct queries with different tweaks, due to the uniformity of the mentioned hash function, it still meets BBB security.

1.2. Structure of This Paper

Section 2 is the preliminaries of notations and definitions. Section 3 is the overview of proofs and core contribution. Section 4 is the proof of our conclusion. Section 5 is the future work.

2. Preliminaries

2.1. Notations and General Definitions

Let n denote a positive integer. Then $N=2^n$ and $\mathcal{N}={\{0,1\}}^n$. $\mathcal{F}\left(n\right)$ denotes the set of all functions mapping from $\mathcal{N}$ to $\mathcal{N}$. $\mathcal{P}\left(2n\right)$ denotes the set of all permutations in the range of ${\{0,1\}}^{2n}$. Let $\theta \left(s\right)$ be a random variable relying on one another random variable s. Then we denote by ${\mathbb{E}}_{s\backslash \mathcal{S}}\left[\theta \left(s\right)\right]$ the expectation of $\theta \left(s\right)$ taken over all $s\backslash \mathcal{S}$. For $X,Y\backslash \mathcal{N}$, denote $X\Vert Y$ or simply $XY$ as their concatenation.

2.1.1. Block Cipher

A block cipher is a family of permutations indexed by the secret key. It is denoted as $E:\mathcal{K}\times \mathcal{M}\to \mathcal{C}$, where $\mathcal{K}$ is the key space, $\mathcal{M}$ is the message space, and $\mathcal{C}$ is the ciphertext space. Hence for each $K\backslash \mathcal{K}$, $E(K,·)$ or simply $E_K(·)$ is a permutation from $\mathcal{M}$ to $\mathcal{C}$. In this paper, $\mathcal{M}=\mathcal{C}={\{0,1\}}^{2n}$.

2.1.2. Tweakable Block Cipher

A tweakable block cipher is a family of permutations indexed by the secret key and the public tweak. It is denoted as $\tilde{E}:\mathcal{K}\times \mathcal{T}\times \mathcal{M}\to \mathcal{C}$, where $\mathcal{K}$ is the key space, $\mathcal{T}$ is the tweak space, $\mathcal{M}$ is the message space, and $\mathcal{C}$ is the ciphertext space. Hence for each $K\backslash \mathcal{K}$ and each $T\backslash \mathcal{T}$, $E(K,T,·)$ or simply $E_{K,T}(·)$ is a permutation from $\mathcal{M}$ to $\mathcal{C}$. Similarly, $\mathcal{M}=\mathcal{C}={\{0,1\}}^{2n}$. We denote $\tilde{\Pi }(\mathcal{T},2n)$ as the set of all tweakable permutations with $\mathcal{M}=\mathcal{C}={\{0,1\}}^{2n}$.

2.1.3. Key-Alternating Feistel ($\mathsf{KAF}$) Cipher

A $\mathsf{KAF}$ is a block cipher with $\mathcal{M}=\mathcal{C}={\{0,1\}}^{2n}$. It has an iterative structure. The i-th round function has the form ${\Psi }_{k_i}^{\mathit{F}}(L\Vert R)=(R\Vert L\oplus {\mathit{F}}_i(R\oplus k_i))$, where L and R are the left half and the right half of the inputs respectively, $k_i$ is the i-th secret round key, and ${\mathit{F}}_i$ is the i-th public round function. We denote the r-round $\mathsf{KAF}$ with r public round functions $\mathit{F}=({\mathit{F}}_1,\dots ,{\mathit{F}}_r)$ in $\mathcal{F}\left(n\right)$ and a round-key vector $k=(k_1,\dots ,k_r)$ by

$${\mathsf{KAF}}_k^{\mathit{F}}(L\Vert R)={\Psi }_{k_r}^{{\mathit{F}}_r}\circ \dots \circ {\Psi }_{k_1}^{{\mathit{F}}_1}(L\Vert R).$$

2.1.4. Uniform AXU Hash Functions

A set of hash functions is denoted as $\mathcal{H}:\mathcal{K}\times \mathcal{T}\to \mathcal{N}$. For each key $k\backslash \mathcal{K}$, a keyed hash function $H(k,·)$ or simply $H_k(·)$ maps the tweak space $\mathcal{T}$ to $\mathcal{N}$. $\mathcal{H}$ is said to be uniform hash function if for any $t\backslash \mathcal{T}$ and $y\backslash \mathcal{N}$,

$$Pr\left[k\stackrel{\$}{\leftarrow }\mathcal{K}:H(k,t)=y\right]=2^{-n}.$$

Moreover, it is said to be $ϵ$-almost XOR-universal ($ϵ$-AXU) if for any $t,t^{\prime }\backslash \mathcal{T}$ with $t\ne t^{\prime }$ and any $y\backslash \mathcal{N}$,

$$Pr\left[k\stackrel{\$}{\leftarrow }\mathcal{K}:H_k\left(t\right)\oplus H_k\left(t^{\prime }\right)=y\right]\le ϵ.$$

2.2. Security Definitions

A distinguisher $\mathcal{D}$ can be thought as a fundamental attacker, and it can make queries to one (or more) “oracle” which can be the block ciphers or the random permutations. The advantage of a distinguisher $\mathcal{D}$ in distinguishing two oracles $\mathcal{O}$ and $\mathcal{Q}$ can be defined as:

$$\mathit{Adv}\left(\mathcal{D}\right)=|\mathrm{Pr}\left[{\mathcal{D}}^{\mathcal{O}}\to 1\right]-\mathrm{Pr}\left[{\mathcal{D}}^{\mathcal{Q}}\to 1\right]|.$$

We discuss this under the Random Permutation model. Firstly, we define two worlds–“the real world” and “the ideal world”. When the distinguisher $\mathcal{D}$ interacts with the oracle $(\mathcal{O},\mathit{F})$, the real world means $\mathcal{O}$ is a tweakable block cipher $\tilde{E}(k,·)$, $\mathit{F}=(F_1,\dots ,F_r)$ is a public random function or permutation of $\tilde{E}$, where k is uniformly taken from $\mathcal{K}$. In addition, in the ideal world, $\mathcal{O}$ is a tweakable permutation $\tilde{\Pi }$ and $\mathit{F}=(F_1,\dots ,F_r)$ is a public random function or permutation of $\tilde{\Pi }$. We call $\mathcal{O}$construction oracle and $\mathit{F}$ inner component oracles. The security of a tweakable block cipher is measured by the advantage of the distinguisher $\mathcal{D}$ that distinguishes the two worlds: $(\tilde{E}(k,·),\mathit{F})$ and $(\tilde{\Pi },\mathit{F})$(depict in Figure 2). We write

$$\mathit{Adv}\left(\mathcal{D}\right)=|\mathrm{Pr}\left[{\mathcal{D}}^{\tilde{E}(k,·),\mathit{F}}\to 1\right]-\mathrm{Pr}\left[{\mathcal{D}}^{\tilde{\Pi },\mathit{F}}\to 1\right]|.$$

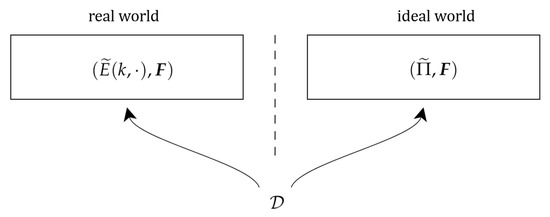
Figure 2. A distinguisher $\mathcal{D}$ distinguish the real world and the ideal world.

Theoretically, we only consider the information-theoretic distinguisher whose computation power is unlimited, i.e., it is determined, and only with limited information, that which means the number of access to the oracle is limited. We assume that the distinguishers do not make redundant queries. We also consider the distinguishers are under the chosen-ciphertext-attack (CCA) model, meanwhile they can choose tweaks, where they have the ability to query all the oracles either forward or backward.

We denote $q_e$ as the quantity of queries to the construction oracle and $q_f$ as the number of queries to each inner component oracle, then the definition of insecurity of the tweakable block cipher $\tilde{E}$ is

$${\mathit{Adv}}_{\tilde{E}}(q_e,q_f)=\underset{\mathcal{D}}{max}\left\{\mathit{Adv}\left(\mathcal{D}\right)\right\}.$$

H-Coefficient Technique

We utilizuse the H-coefficient technique [25,26] to evaluate the upper bound of the advantage of the adversary mentioned above.

Definition 1

(Transcript). A transcript $\tau =({\mathcal{Q}}_E,{\mathcal{Q}}_{\mathit{F}})$ is the response-tuple when the distinguisher $\mathcal{D}$ interacts with its oracle, where ${\mathcal{Q}}_E$ contains the tuples of the form $(t,LR,ST)\backslash \mathcal{T}\times {\{0,1\}}^{2n}\times {\{0,1\}}^{2n}$ which interacts with the construction oracle and ${\mathcal{Q}}_{\mathit{F}}$ contains the tuples $(x,y)$ which interacts with the inner component oracle.

By definition, we can see that $\mathcal{D}$ either makes the direct query $(t,LR)$ to the construction oracle with x to the inner component oracle, receiving answer $ST$ and y, or makes the inverse query $(t,ST)$ to the construction oracle with y to the inner component oracle, receiving answer $LR$ and x. Suppose that $|{\mathcal{Q}}_E|=q_e$, and there are m distinct tweaks in the ${\mathcal{Q}}_E$. We assume there exist $q_i(1\le i\le m)$ distinct queries for the i-th tweak, hence ${\sum }_{i=1}^m{q}_i=q_e$. That means ${\mathcal{Q}}_E=\bigcup {\mathcal{Q}}_{E_i},1\le i\le m$, where ${\mathcal{Q}}_{E_i}$ are the corresponding queries of the i-th tweak. Similarly, we have $|{\mathcal{Q}}_{F_j}|=q_f$ and ${\mathcal{Q}}_{\mathit{F}}=\bigcup {\mathcal{Q}}_{F_j},1\le j\le r$.

We note that all the transcripts of queries are directionless and disordered form, but according to our hypothesis that the distinguisher $\mathcal{D}$ is deterministic. Thus, there is a one-to-one mapping between this statement and the primitive transcript of the interaction of $\mathcal{D}$ with its oracles. Meanwhile, the output of $\mathcal{D}$ is a deterministic function of $\tau$.

In addition, for the function ${\mathit{F}}_j$ and its set of queries ${\mathcal{Q}}_{F_j}$, if for each $(x,y)\backslash {\mathcal{Q}}_{F_j}$, ${\mathit{F}}_j\left(x\right)=y$, we say that ${\mathit{F}}_j$extends${\mathcal{Q}}_{F_j}$, denoted by ${\mathit{F}}_j⊢{\mathcal{Q}}_{F_j}$. Similarly, for the permutation ${\mathit{P}}^{\left(i\right)}$ and its transcript sets ${\mathcal{Q}}_{E_i}$, if for each $(t,LR,ST)\backslash {\mathcal{Q}}_{E_i}$, ${\mathit{P}}^{\left(i\right)}(t,LR)=ST$, we say that ${\mathit{P}}^{\left(i\right)}$ extends ${\mathcal{Q}}_{E_i}$, denoted by ${\mathit{P}}^{\left(i\right)}⊢{\mathcal{Q}}_{E_i}$. With the above definition of “extend”, we can define ${\mathsf{KAF}}_{k^{\left(i\right)}}^{\mathit{F}}⊢{\mathcal{Q}}_{E_i}$. Finally, for ${\mathcal{Q}}_{\mathit{F}}=({\mathcal{Q}}_{F_1},\dots ,{\mathcal{Q}}_{F_t})$ and $\mathit{F}=({\mathit{F}}_1,\dots ,{\mathit{F}}_t)$, if ${\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}\wedge \dots \wedge {\mathit{F}}_t⊢{\mathcal{Q}}_{F_t}$, then we have $\mathit{F}⊢{\mathcal{Q}}_{\mathit{F}}$.

We further define the probability that the interactions of the distinguisher $\mathcal{D}$ with the real world and the ideal world. In addition, we respectively denote them by ${\mathrm{Pr}}_{re}\left(\tau \right)$ and ${\mathrm{Pr}}_{id}\left(\tau \right)$, where $\tau$ is a transcript of these interactions.

With these definitions, we give the core lemma of the H-coefficient technique, and the distinguishing advantage could be inferred by the ratio of ${\mathrm{Pr}}_{re}\left(\tau \right)$ and ${\mathrm{Pr}}_{id}\left(\tau \right)$.

Lemma 1

(From [27]). Assume that there is a function $\phi (q_f,q_e)>0$ such that for every possible transcript τ with $q_e$ and $q_f$ queries of the two types it holds

$$|{\mathrm{Pr}}_{id}\left(\tau \right)-{\mathrm{Pr}}_{re}\left(\tau \right)|\le {\mathrm{Pr}}_{id}\left(\tau \right)·\phi (q_f,q_e),$$

then it holds

$${\mathit{Adv}}_{\mathsf{KAF}}(q_f,q_e)\le \phi (q_f,q_e).$$

According to [27], the upper bound of $|{\mathrm{Pr}}_{id}\left(\tau \right)-{\mathrm{Pr}}_{re}\left(\tau \right)|$ is named “$\phi$-point-wise proximity” of $\tau$, which was raised by Hoang and Tessaro (HT) [27]. We let $\mathcal{K}={\mathcal{K}}_{good}\cup {\mathcal{K}}_{bad}$, where ${\mathcal{K}}_{good}$ and ${\mathcal{K}}_{bad}$ are mutual exclusive subsets. Denote ${\mathrm{Pr}}_{re}(\tau ,k)$ as the probability that $\mathcal{D}$ interacts with the real world, where $k\backslash \mathcal{K}$, and ${\mathrm{Pr}}_{id}(\tau ,k)$ is that $\mathcal{D}$ interacts with the ideal world, where k is a “virtual” key uniformly selected from the key space $\mathcal{K}$. With the above definition, HT provided a lemma to establish point-wise proximity.

Lemma 2

(Lemma 1 of [27]). Fix a transcript τ with ${\mathrm{Pr}}_{id}\left(\tau \right)>0$. Assume that: (i) $\mathrm{Pr}\left[k\backslash {\mathcal{K}}_{bad}\right]\le \delta$, and (ii) there is a function $g:\mathcal{K}\to \left[0,\infty \right)$ such that for all $k\backslash {\mathcal{K}}_{good}$, it holds $\frac{{\mathrm{Pr}}_{re}(\tau ,k)}{{\mathrm{Pr}}_{id}(\tau ,k)}\ge 1-g\left(k\right)$. Then we have

$${\mathrm{Pr}}_{id}\left(\tau \right)-{\mathrm{Pr}}_{re}\left(\tau \right)\le {\mathrm{Pr}}_{id}\left(\tau \right)·(\delta +{\mathbb{E}}_{k\backslash \mathcal{K}}\left[g\left(k\right)\right]).$$

3. Overview

3.1. Beyond Birthday-Bound Security for Six Rounds

In the beginning, we need to guarantee that tweaking the $\mathsf{KAF}$ ciphers does not break its construction, and the influence on efficiency of the scheme execution can not cannot be enormous. For study of the execution efficiency and security, Liskov et al. [1] thought the cost of changing tweaks should be less than that of changing keys. However, the study by Jean et al. [14] showed that the adversary can hardly obtain the key, but has the ability to completely control the tweak.

In this paper, we use a nonlinear compound mode for tweaking the Feistel structure, instead of tweaking dependent or independent keys. As we known, the four rounds of $\mathsf{KAF}$ cipher do not meet BBB security [24], Yan’s [23] work showed that tweaking 10 rounds $\mathsf{KAF}$ cipher can meet BBB security. Our work shows a method for tweaking the $\mathsf{KAF}$ cipher by the nonlinear pattern, and reduces the rounds of the scheme. For requirement of security, we consider to introduce the tweak with the round-key vectors by using a universal hash function.

Firstly, we use the suitable round-key vector which was defined by Guo [24]:

Definition 2

(Suitable Round-Key Vector for 6 Rounds [24]). A round-key vector $k=(k_1,k_2,k_3,k_4,k_5,k_6)$ is suitable if it satisfies the following conditions:

(i) 

$k_1,k_2,k_3,k_4,k_5,k_6$ are uniformly distributed in ${\{0,1\}}^n$;

(ii) 

for $(i,j)\backslash \left\{\right(1,2),(2,3),(4,5),(5,6),(1,6\left)\right\}$, $k_i$ and $k_j$ are independent.

Yan’s [23] work used the minimized 6-round $\mathsf{KAF}$ as a “core”, with additional four more rounds on the first and last sides of the “core”, meanwhile introducing the tweak into these four rounds. They gave a 10-round $\mathsf{TKAF}$ construction with BBB security. In our work, we aim to“tweak” the first and last two rounds of the “core”, and use a universal hash function to merge the tweak into round-key vectors.

Next, we denote this 6-round construction by

$${\mathsf{TKAF}}_k^{\mathit{F}}(t,x)={\Psi }_{k_6,t}^{F_6}\circ {\Psi }_{k_5,t}^{F_5}\circ {\Psi }_{k_4}^{F_4}\circ {\Psi }_{k_3}^{F_3}\circ {\Psi }_{k_2,t}^{F_2}\circ {\Psi }_{k_1,t}^{F_1}\left(x\right),$$

where $\mathit{F}=(F_1,F_2,F_3,F_4,F_5,F_6)$ are random functions, $k=(k_1,k_2,k_3,k_4,k_5,k_6)$ are the corresponding round keys, $t\backslash \mathcal{T}$ is a tweak and $x\backslash {\{0,1\}}^{2n}$ is a message (depict in Figure 3).

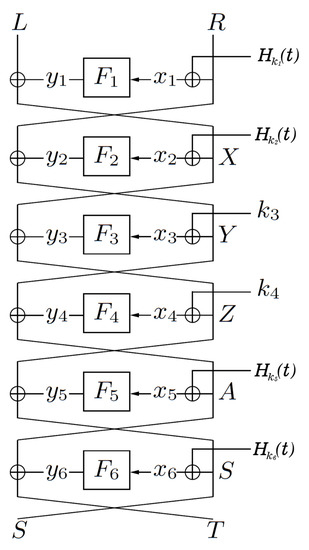
Figure 3. A tweakable Key-Alternating Feistel cipher with 6 rounds.

Finally, we upper- bound the advantage of an adversary to attack this scheme. By utilizing the H-coefficient technique which is in Lemma 2, we firstly upper upper-bound the bad key event $\delta$, then upper- bound the expectation of the function $g\left(k\right)$, which holds $\frac{{\mathrm{Pr}}_{re}(\tau ,k)}{{\mathrm{Pr}}_{id}(\tau ,k)}\ge 1-g\left(k\right)$. By Lemma 1, we could obtain the advantage. Thus, we have this theorem:

Theorem 1.

For the 6-round tweakable $\mathsf{KAF}$ cipher with a suitable round-key vector as specified in Definition 2, it holds

$$\begin{array}{cc}\hfill {\mathit{Adv}}_{\mathsf{TKAF}}(q_f,q_e)& \le (7q_e^3+24q_e^2{q}_f+20q_e{q}_f^2)\frac{1}{N^2}\hfill \\ \hfill & +(4q_e^3+4q_e^2{q}_f+2q_e{q}_f^2+4q_e^2+6q_e{q}_f)\frac{\epsilon }{N}\hfill \\ \hfill & +4q_e^2{q}_f{\epsilon }^2+4q_e^2{\epsilon }^2.\hfill \end{array}$$

(1)

3.2. Core Contribution

In our work, we analyze the influence of tweaking $\mathsf{KAF}$ ciphers on security. We tweak the outer four rounds of Guo et al’s 6-round $\mathsf{KAF}$ and the proof of BBB security is the major research work we have done.

4. Security Proof of Theorem 1

In the following subsections, we present the methodology to prove Theorem 1. We fix a transcript $\tau =({\mathcal{Q}}_E,{\mathcal{Q}}_F)$ with ${\mathcal{Q}}_F=({\mathcal{Q}}_{F_1},{\mathcal{Q}}_{F_2},{\mathcal{Q}}_{F_3},{\mathcal{Q}}_{F_4},{\mathcal{Q}}_{F_5},{\mathcal{Q}}_{F_6})$, where $|{\mathcal{Q}}_E|=q_e$ and $|{\mathcal{Q}}_{F_i}|=q_f,i=1,\dots ,6$. We divide the analysis of this claim into two parts: $\left(i\right)$ define bad key vectors, then $\left(ii\right)$ lower bound the probability ${\mathrm{Pr}}_{re}(\tau ,k)$. We analyze these two parts respectively.

4.1. Bad Key Vectors and Probability

Definition 3

(Bad Key Vectors for 6 rounds). A suitable key vector $k\backslash \mathcal{K}$ is bad, for a transcript $\tau =({\mathcal{Q}}_E,{\mathcal{Q}}_F)$, if one of the follow conditions is met:

• (A-1)there exists $(t,LR,ST)\backslash {\mathcal{Q}}_E$, $(x_1,y_1)\backslash {\mathcal{Q}}_{F_1}$, $(x_6,y_6)\backslash {\mathcal{Q}}_{F_6}$, such that $H_{k_1}\left(t\right)=R\oplus x_1$, $H_{k_6}\left(t\right)=S\oplus x_6$;
• (A-2)there exists $(t,LR,ST)\backslash {\mathcal{Q}}_E$, $(x_1,y_1)\backslash {\mathcal{Q}}_{F_1}$, $(x_2,y_2)\backslash {\mathcal{Q}}_{F_2}$, such that $H_{k_1}\left(t\right)=R\oplus x_1$, $H_{k_2}\left(t\right)=L\oplus y_1\oplus x_2$;
• (A-3)there exists $(t,LR,ST)\backslash {\mathcal{Q}}_E$, $(x_5,y_5)\backslash {\mathcal{Q}}_{F_5}$, $(x_6,y_6)\backslash {\mathcal{Q}}_{F_6}$, such that $H_{k_6}\left(t\right)=S\oplus x_6$, $H_{k_5}\left(t\right)=T\oplus y_6\oplus x_5$.

otherwise, k is good. We denote ${\mathcal{K}}_{bad}$ for the set of bad key vectors, and ${\mathcal{K}}_{good}$ for the good key vectors.

In the beginning, we upper- bound the probability of the bad key vectors. Firstly, we analyze the above three conditions respectively, consider (A-1) first. Since we have the key $k_1$ and $k_6$ picked from the key space $\mathcal{K}$ uniformly and randomly, for the properties of suitable, $k_1$ and $k_6$ are independent of each other (Definition 2). By the uniformity of H, $H_{k_1}$ and $H_{k_6}$ are also independent. Thus Thus, there are $N^2$ possible choices. For $(t,LR,ST)\backslash {\mathcal{Q}}_E$, $(x_1,y_1)\backslash {\mathcal{Q}}_{F_1}$ and $(x_6,y_6)\backslash {\mathcal{Q}}_{F_6}$, we have at most $q_e{q}_f^2$ choices, as $|{\mathcal{Q}}_E|=q_e$, $|Dom{\mathcal{F}}_1|=|Dom{\mathcal{F}}_6|=q_f$, where $Dom\mathcal{F}$ is a set of x that there exists $(x,y)\backslash {\mathcal{Q}}_F$ such that $F\left(x\right)=y$, i.e., $Dom\mathcal{F}\stackrel{def}{=}\{x\backslash {\{0,1\}}^n:\exists (x,y)\backslash {\mathcal{Q}}_F,F\left(x\right)=y\}$. Therefore, the probability of condition (A-1) is at most $\frac{q_e{q}_f^2}{N^2}$.

Similarly, by definition of suitable key vector (Definition 2), it also holds that $(k_1,k_2)$, $(k_5,k_6)$ are independent, and for the uniformity of H, we have $\mathrm{Pr}\left[\left(\mathbf{A-2}\right)\right]=\mathrm{Pr}\left[\left(\mathbf{A-3}\right)\right]\le \frac{q_e{q}_f^2}{N^2}.$

To sum up, we can upper- bound the probability of the bad key vectors with

$$\mathrm{Pr}\left[k\stackrel{\$}{\leftarrow }\mathcal{K}:k\backslash {\mathcal{K}}_{bad}\right]\le \frac{3q_e{q}_f^2}{N^2}.$$

(2)

4.2. Analysis for Good Keys

In the following, we fix the round- key vectors $k\backslash {\mathcal{K}}_{good}$, and aim to lower bound the probability $\mathrm{Pr}\left[\mathit{F}\stackrel{\$}{\leftarrow }{\left(\mathcal{F}\left(n\right)\right)}^6:{\mathsf{TKAF}}_k^{\mathit{F}}⊢{\mathcal{Q}}_E|\mathit{F}⊢{\mathcal{Q}}_F\right]$. By the analytical method of Cogliati et al. [9,15], we divide this proof process into two steps: $\left(i\right)$ upper bounding the probability that a pair of functions $({\mathit{F}}_1,{\mathit{F}}_6)$ satisfies “bad” conditions. By these means, the “good” conditions of the function -pair can transfer the transcripts of the distinguisher on 6 rounds to a special transcripts on 4 rounds, it can be said that we “peel off” the outer two rounds [24]; then $\left(ii\right)$ assuming that $({\mathit{F}}_1,{\mathit{F}}_6)$ is good, by bounding the inner 4 rounds, we will prove the claim of Theorem 1.

Peeling Off the Outer Two Rounds

We pick a pair of round functions $({\mathit{F}}_1,{\mathit{F}}_6)$ such that ${\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}$ and ${\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}$. For each transcript $(t,LR,ST)\backslash {\mathcal{Q}}_E$, denote $X\leftarrow L\oplus {\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)$ and $A\leftarrow T\oplus {\mathit{F}}_6(H_{k_6}\left(t\right)\oplus S)$. From this, we obtain $q_e$ transcripts with the form of $(t,RX,AS)$. For convenience, we denote a new set including all these introduced transcript tuples by ${\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$. Furthermore, we define two subsets of ${\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, the transcripts that collide at the positions of X and A, respectively. Denote them by $\mathcal{ID}\left(X\right)$ and $\mathcal{ID}\left(A\right)$:

$$\begin{array}{cc}\hfill \mathcal{ID}\left(X\right)& =\{(t,RX,AS):(t,RX,AS)\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6),Xisidentical\}\hfill \\ \hfill \mathcal{ID}\left(A\right)& =\{(t,RX,AS):(t,RX,AS)\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6),Aisidentical\}\hfill \end{array}$$

In order to characterize $\tau$, we define four key-dependent quantities:

$$\begin{array}{cc}\hfill n_{\left(1\right)}\left(k\right)& \stackrel{def}{=}\left|\{((t,LR,ST),(x_1,y_1))\backslash {\mathcal{Q}}_E\times {\mathcal{Q}}_{F_1}:H_{k_1}\left(t\right)=R\oplus x_1\}\right|\hfill \\ \hfill n_{\left(6\right)}\left(k\right)& \stackrel{def}{=}\left|\{((t,LR,ST),(x_6,y_6))\backslash {\mathcal{Q}}_E\times {\mathcal{Q}}_{F_6}:H_{k_6}\left(t\right)=S\oplus x_6\}\right|\hfill \\ \hfill n_{(2,3)}\left(k\right)& \stackrel{def}{=}\left|\{((t,LR,ST),(x_2,y_2),(x_3,y_3))\backslash {\mathcal{Q}}_E\times {\mathcal{Q}}_{F_2}\times {\mathcal{Q}}_{F_3}:k_3=R\oplus y_2\oplus x_3\}\right|\hfill \\ \hfill n_{(4,5)}\left(k\right)& \stackrel{def}{=}\left|\{((t,LR,ST),(x_4,y_4),(x_5,y_5))\backslash {\mathcal{Q}}_E\times {\mathcal{Q}}_{F_4}\times {\mathcal{Q}}_{F_5}:k_4=S\oplus y_5\oplus x_4\}\right|\hfill \end{array}$$

Now we define the “bad event” on the pair $({\mathit{F}}_1,{\mathit{F}}_6)$. If the corresponding set ${\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$ of the pair $({\mathit{F}}_1,{\mathit{F}}_6)$ fulfills one of the following “collision” conditions, we say that the predicate is bad, denoted by $\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)$:

• (B-1) there exists $(t,RX,AS)\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, $(x_2,y_2)\backslash {\mathcal{Q}}_{F_2}$, $(x_5,y_5)\backslash {\mathcal{Q}}_{F_5}$, such that $H_{k_2}\left(t\right)=X\oplus x_2$, $H_{k_5}\left(t\right)=A\oplus x_5$;
• (B-2) there exists $(t,RX,AS)\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, $(x_2,y_2)\backslash {\mathcal{Q}}_{F_2}$, $(x_3,y_3)\backslash {\mathcal{Q}}_{F_3}$, such that $H_{k_2}\left(t\right)=X\oplus x_2$, $k_3=R\oplus y_2\oplus x_3$;
• (B-3) there exists $(t,RX,AS)\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, $(x_4,y_4)\backslash {\mathcal{Q}}_{F_4}$, $(x_5,y_5)\backslash {\mathcal{Q}}_{F_5}$, such that $H_{k_5}\left(t\right)=A\oplus x_5$, $k_4=S\oplus y_5\oplus x_4$;
• (B-4) there exist two distinct $(t,RX,AS),(t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, $(x_2,y_2)\backslash {\mathcal{Q}}_{F_2}$, such that $X=X^{\prime }$ and $H_{k_2}\left(t\right)=X\oplus x_2$; or symmetrically two distinct $(t,RX,AS),(t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, $(x_5,y_5)\backslash {\mathcal{Q}}_{F_5}$, such that $A=A^{\prime }$ and $H_{k_5}\left(t\right)=A\oplus x_5$;
• (B-5) there exist two distinct $(t,RX,AS),(t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, $(x_2,y_2)\backslash {\mathcal{Q}}_{F_2}$, such that $A=A^{\prime }$ and $H_{k_2}\left(t\right)=X\oplus x_2$; or symmetrically two distinct $(t,RX,AS),(t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, $(x_5,y_5)\backslash {\mathcal{Q}}_{F_5}$, such that $X=X^{\prime }$ and $H_{k_5}\left(t\right)=A\oplus x_5$;

If the predicate $\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)$ does not hold, then we can deem that $({\mathit{F}}_1,{\mathit{F}}_6)$ is good. Now we bound the probability of $\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)$.

Lemma 3.

It holds

$$\begin{array}{cc}\hfill & \mathrm{Pr}\left[\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)|{\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}\wedge {\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}\right]\hfill \\ \hfill & \le \frac{4q_e^2{q}_f+q_e{q}_f^2}{N^2}+\frac{q_f(n_{\left(1\right)}\left(k\right)+n_{\left(6\right)}\left(k\right))}{N}\hfill \\ \hfill & +\frac{n_{(2,3)}\left(k\right)+n_{(4,5)}\left(k\right)}{N}+4q_e^2{q}_f{\epsilon }^2+q_f\epsilon (n_{\left(1\right)}\left(k\right)+n_{\left(6\right)}\left(k\right)).\hfill \end{array}$$

Proof. 

We prove the above 5 cases of $\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)$ on the condition of ${\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}\wedge {\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}$:

(B-1) For arbitrary $(t,RX,AS)\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, if there exists $(x_2,y_2)\backslash {\mathcal{Q}}_{F_2}$ and $(x_5,y_5)\backslash {\mathcal{Q}}_{F_5}$, such that $H_{k_2}\left(t\right)=X\oplus x_2$ and $H_{k_5}\left(t\right)=A\oplus x_5$. Then for the corresponding $(t,LR,ST)\backslash {\mathcal{Q}}_E$, we have $L\oplus {\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)=H_{k_2}\left(t\right)\oplus x_2$ and $T\oplus {\mathit{F}}_6(H_{k_6}\left(t\right)\oplus S)=H_{k_5}\left(t\right)\oplus x_5$. On account of the uniformity of H, it must hold $H_{k_1}\left(t\right)\oplus R\notin Dom{\mathcal{F}}_1$ (if $H_{k_1}\left(t\right)\oplus R\backslash Dom{\mathcal{F}}_1$ and $H_{k_2}\left(t\right)=X\oplus x_2$, then the condition (A-2) is fulfilled). Similarly, it must be $H_{k_6}\left(t\right)\oplus S\notin Dom{\mathcal{F}}_6$. Thus, on the condition of ${\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}\wedge {\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}$, ${\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)$ and ${\mathit{F}}_6(H_{k_6}\left(t\right)\oplus S)$ keep uniform. SoSo, the probability of both $L\oplus {\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)=H_{k_2}\left(t\right)\oplus x_2$ and $T\oplus {\mathit{F}}_6(H_{k_6}\left(t\right)\oplus S)=H_{k_5}\left(t\right)\oplus x_5$ holding is at most $\frac{1}{N^2}$. AndIn addition, the choices of all 3-tuples $(t,LR,ST)$, $(x_2,y_2)$, $(x_5,y_5)$ do not exceed $q_e{q}_f^2$. Therefore, we have Pr[(B-1)] $\le \frac{q_e{q}_f^2}{N^2}$.

(B-2) and (B-3) We consider (B-2) firstly.

There exists a 3-tuple $((t,LRX,AST),(x_2,y_2),(x_3,y_3))$, such that the number of $k_3=R\oplus y_2\oplus x_3$ is $n_{(2,3)}\left(k\right)$, where $(t,LRX,AST)$ is a joint notation of $(t,LR,ST)$ and its corresponding induced X and A. Moreover, $H_{k_2}\left(t\right)=X\oplus x_2$ means $L\oplus {\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)=H_{k_2}\left(t\right)\oplus x_2$. When $H_{k_1}\left(t\right)\oplus R\backslash Dom{\mathcal{F}}_1$, then it can not cannot hold $L\oplus Img{F}_1(H_{k_1}\left(t\right)\oplus R)=H_{k_2}\left(t\right)\oplus x_2$, otherwise (A-2) is fulfilled. Furthermore Furthermore, when $H_{k_1}\left(t\right)\oplus R\notin Dom{\mathcal{F}}_1$, on the condition of ${\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}$, then ${\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)$ keeps uniform. Meanwhile H also keeps uniform, thus we have the probability of $L\oplus {\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)=H_{k_2}\left(t\right)\oplus x_2$ is at most $\frac{1}{N}$. Therefore, Pr[(B-2)]$\le \frac{n_{(2,3)}\left(k\right)}{N}$. The condition (B-3) is symmetric with (B-2), so with the similar analysis, we have Pr[(B-3)]$\le \frac{n_{(4,5)}\left(k\right)}{N}$.

(B-4) For the given pair of distinct merged transcripts $(t,LRX,AST)$ and $(t^{\prime },L^{\prime }{R}^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime }{T}^{\prime })$ together with $(x_2,y_2)\backslash {\mathcal{Q}}_{F_2}$, we discuss the cases in three conditions:

• Case 1: when $t\ne t^{\prime }$, if it holds $H_{k_1}\left(t\right)\oplus R=H_{k_1}\left(t^{\prime }\right)\oplus R^{\prime }$, i.e., for the $\epsilon$-$AUX$ property of H function, the probability of $H_{k_1}\left(t\right)\oplus H_{k_1}\left(t^{\prime }\right)=R\oplus R^{\prime }$ is at most $\epsilon$. If $H_{k_1}\left(t\right)\oplus R\ne H_{k_1}\left(t^{\prime }\right)\oplus R^{\prime }$, we note that $H_{k_1}\left(t\right)\oplus R\notin Dom{\mathcal{F}}_1$, $H_{k_1}\left(t^{\prime }\right)\oplus R^{\prime }\notin Dom{\mathcal{F}}_1$, otherwise (A-2) is fulfilled. Thus, on the condition of ${\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}$, ${\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)$ and ${\mathit{F}}_1(H_{k_1}\left(t^{\prime }\right)\oplus R^{\prime })$ are independent with each other, also keep uniformly random. Then it holds $\mathrm{Pr}\left[{\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)=L\oplus L^{\prime }\oplus {\mathit{F}}_1(H_{k_1}\left(t^{\prime }\right)\oplus R^{\prime })\right]\le \epsilon +(1-\epsilon )\frac{1}{N}\le \epsilon +\frac{1}{N}$. Therefore, the probability of the collision at the position $H_{k_2}\left(t\right)\oplus X$ and $X=X^{\prime }$ is at most $(\epsilon +\frac{1}{N})\epsilon \le {\epsilon }^2+\frac{1}{N}\epsilon$.
• Case 2: if $t=t^{\prime }$ and $R\ne R^{\prime }$, for $X=X^{\prime }$, the probability of ${\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)\oplus L={\mathit{F}}_1(H_{k_1}\left(t^{\prime }\right)\oplus R^{\prime })\oplus L^{\prime }$ is at most $\frac{1}{N}$. AndIn addition, for $H_{k_2}\left(t\right)=X\oplus x_2$, the probability of $H_{k_2}\left(t\right)={\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)\oplus L\oplus x_2$ is at most $\frac{1}{N}$. For the property of H, we have the probability of the collision at the position X is at most $\frac{1}{N^2}$.
• Case 3: if $t=t^{\prime }$ and $R=R^{\prime }$ but $L\ne L^{\prime }$, it can not cannot be held that $X=X^{\prime }$ and $H_{k_2}\left(t\right)=X\oplus x_2$.

To sum up, the probability of “former” part of (B-4) can not cannot exceed ${\epsilon }^2+\frac{1}{N^2}$, and the analysis of “latter” part is similar to the former part. We consider all possible pairs of transcripts, the quantity of these pairs can not cannot exceed $q_e^2{q}_f$. Therefore, Pr[(B-4)]$\le 2q_e^2{q}_f{\epsilon }^2+\frac{2q_e^2{q}_f}{N^2}$.

(B-5) For the given transcripts $(t,LRX,AST)\ne (t^{*},L^{*}{R}^{*}{X}^{*},A^{*}{S}^{*}{T}^{*})$ and $(x_2,y_2)\backslash {\mathcal{Q}}_{F_2}$, due to the conditions on good key vector, it holds $H_{k_1}\left(t\right)\oplus R\notin Dom{\mathcal{F}}_1$. The same as (B-4), we consider the front part of this condition. According to the state of S, we respectively discuss in three cases:

• Case 1: it holds $H_{k_6}\left(t\right)\oplus S\notin Dom{\mathcal{F}}_6$, then for the distinct $(t,LRX,AST)$ and $(t^{*},L^{*}{R}^{*}{X}^{*},A^{*}{S}^{*}{T}^{*})$, they all have $q_e$ choices.

  -

  If $t\ne t^{*}$, if it holds $H_{k_6}\left(t\right)\oplus S=H_{k_6}\left(t^{*}\right)\oplus S^{*}$, then the probability of $H_{k_6}\left(t\right)\oplus H_{k_6}\left(t^{*}\right)=S\oplus S^{*}$ is at most $\epsilon$;

  -

  If $t\ne t^{*}$, if it holds $H_{k_6}\left(t\right)\oplus S\ne H_{k_6}\left(t^{*}\right)\oplus S^{*}$, then ${\mathit{F}}_6(H_{k_6}\left(t\right)\oplus S)$ and ${\mathit{F}}_6(H_{k_6}$$\left(t^{*}\right)\oplus S^{*})$ are independent and uniformly random. Thus, on the condition of ${\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}$, we have

  $$\mathrm{Pr}\left[T\oplus {\mathit{F}}_6(H_{k_6}\left(t\right)\oplus S)=T^{*}\oplus {\mathit{F}}_6(H_{k_6}\left(t^{*}\right)\oplus S^{*})\right]\le \epsilon +(1-\epsilon )\frac{1}{N}\le \epsilon +\frac{1}{N}.$$

  On the condition of ${\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}$, ${\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)$ is also uniform. Hence, similar with (B-4), we have

  $$\mathrm{Pr}\left[H_{k_2}\left(t\right)\oplus X=H_{k_2}\left(t^{*}\right)\oplus X^{*}\right]\le {\epsilon }^2+\frac{1}{N}\epsilon .$$

  -

  If $t=t^{*}$ but $S\ne S^{*}$, if $A=A^{*}$, then it holds

  $$\mathrm{Pr}\left[{\mathit{F}}_6(H_{k_6}\left(t\right)\oplus S)\oplus T={\mathit{F}}_6(H_{k_6}\left(t^{*}\right)\oplus S^{*})\oplus T^{*}\right]\le \frac{1}{N},$$

  and for $H_{k_2}\left(t\right)=X\oplus x_2$, the probability of $H_{k_2}\left(t\right)={\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)\oplus L\oplus x_2$ is at most $\frac{1}{N}$;

  -

  If $t=t^{*}$ and $S=S^{*}$ but $T\ne T^{*}$, it could not be held that $A=A^{*}$ or $H_{k_2}\left(t\right)=X\oplus x_2$.

  Under the above cases, we have the probability of the collision at the position $H_{k_2}\left(t\right)\oplus X$ and $A=A^{*}$ is at most ${\epsilon }^2+\frac{1}{N^2}$. In addition, for $H_{k_6}\left(t\right)\oplus S\notin Dom{\mathcal{F}}_6$, the probability of (B-5)’s front part is at most $q_e^2{q}_f{\epsilon }^2+\frac{q_e^2{q}_f}{N^2}$.
• Case 2: For $H_{k_6}\left(t\right)\oplus S\backslash Dom{\mathcal{F}}_6$, the choices of $(t,LRX,AST)$ are $n_{\left(6\right)}\left(k\right)$. Similar with Case 1, we have $\mathrm{Pr}\left[L\oplus {\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)\oplus H_{k_2}\left(t\right)\backslash {\mathit{F}}_2\right]\le \frac{q_f}{N}+q_f\epsilon$. Therefore, the probability of holding at least one such transcript $(t,LRX,AST)$ is at most $\frac{q_f·n_{\left(6\right)}\left(k\right)}{N}+q_f{n}_{\left(1\right)}\left(k\right)\epsilon$.

To sum up the above two cases, the probability that the former part of (B-5) holding is at most $q_e^2{q}_f{\epsilon }^2+\frac{q_f·n_{\left(6\right)}\left(k\right)}{N}+\frac{q_e^2{q}_f}{N^2}+q_f{n}_{\left(1\right)}\left(k\right)\epsilon$. Similarly, the latter part of (B-5) is symmetric with the former part. Therefore, we have

$$\mathrm{Pr}\left[\left(\mathbf{B-5}\right)\right]\le 2q_e^2{q}_f{\epsilon }^2+\frac{q_f·(n_{\left(1\right)}\left(k\right)+n_{\left(6\right)}\left(k\right))}{N}+\frac{2q_e^2{q}_f}{N^2}+q_f\epsilon (n_{\left(1\right)}\left(k\right)+n_{\left(6\right)}\left(k\right)).$$

We sum up all the five conditions, it holds

$$\begin{array}{cc}\hfill & \mathrm{Pr}\left[\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)|{\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}\wedge {\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}\right]\hfill \\ \hfill & \le \frac{4q_e^2{q}_f+q_e{q}_f^2}{N^2}+\frac{q_f·(n_{\left(1\right)}\left(k\right)+n_{\left(6\right)}\left(k\right))}{N}\hfill \\ \hfill & +\frac{n_{(2,3)}\left(k\right)+n_{(4,5)}\left(k\right)}{N}+4q_e^2{q}_f{\epsilon }^2+q_f\epsilon (n_{\left(1\right)}\left(k\right)+n_{\left(6\right)}\left(k\right)).\hfill \end{array}$$

Now we prove the Lemma 3. □

4.3. Analysis of the Inner Four Rounds

In the following section, we analyze the inner four rounds of $\mathsf{TKAF}$ which depicts in Figure 4. We denote ${\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$ the set of tuples in the form $(t,RX,AS)$, which is induced by peeling off outer two rounds. Similar with [24], we also write ${\mathit{F}}^{*}=({\mathit{F}}_2,{\mathit{F}}_3,{\mathit{F}}_4,{\mathit{F}}_5)$, further denote

$$\begin{array}{c}\hfill \mathsf{p}(\tau ,{\mathit{F}}_1,{\mathit{F}}_6)=\mathrm{Pr}\left[{\mathit{F}}^{*}\stackrel{\$}{\leftarrow }{\left(\mathcal{F}\left(n\right)\right)}^4:{\mathsf{TKAF}}_k^{{\mathit{F}}^{*}}⊢{\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)|{\mathit{F}}_i⊢{\mathcal{Q}}_{F_i},i=1,2,3,4,5,6\right].\end{array}$$

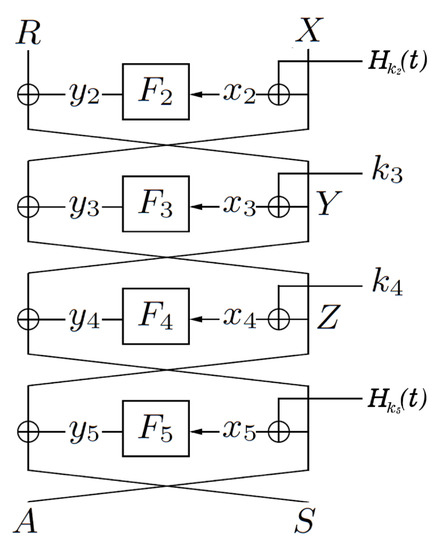
Figure 4. Inner 4 rounds of the tweakable Key-Alternating Feistel cipher.

Lemma 4

(From [24]). Assume that there exists a function $\phi :{\left(\mathcal{F}\left(n\right)\right)}^2\times \mathcal{K}\to \left[0,\infty \right)$ such that for any good $({\mathit{F}}_1,{\mathit{F}}_6)$, it holds

$${\displaystyle \mathsf{p}(\tau ,{\mathit{F}}_1,{\mathit{F}}_6)/\prod _{i=0}^{q_e-1}\left(\frac{1}{N^2-i}\right)\ge 1-\phi ({\mathit{F}}_1,{\mathit{F}}_6,k)}.$$

(3)

Then we have

$$\begin{array}{ccc}\hfill \frac{{\mathrm{Pr}}_{re}(\tau ,k)}{{\mathrm{Pr}}_{id}(\tau ,k)}\ge 1& -\hfill & \hfill \mathrm{Pr}\left[\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)|{\mathit{F}}_1⊢{\mathcal{Q}}_{F_1},{\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}\right]\\ \hfill & -\hfill & \hfill {\mathbb{E}}_{{\mathit{F}}_1,{\mathit{F}}_6}\left[\phi ({\mathit{F}}_1,{\mathit{F}}_6,k)|{\mathit{F}}_1⊢{\mathcal{Q}}_{F_1},{\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}\right].\end{array}$$

Lemma 5.

For any fixed good tuple $({\mathit{F}}_1,{\mathit{F}}_6)$, there exists a function $\phi ({\mathit{F}}_1,{\mathit{F}}_6,k)$ of the function pair and the round- key vector k such that the inequality (3) mentioned in Lemma 4. Then,

$$\begin{array}{cc}\hfill {\mathbb{E}}_{{\mathit{F}}_1,{\mathit{F}}_6,k}\left[\phi ({\mathit{F}}_1,{\mathit{F}}_6,k)\right]& \le 4q_e^2{\epsilon }^2+\frac{7q_e^3+20q_e^2{q}_f+12q_e{q}_f^2}{N^2}\hfill \\ \hfill & +\frac{4q_e^3\epsilon +4q_e^2{q}_f\epsilon +4q_e^2\epsilon +6q_e{q}_f\epsilon }{N}.\hfill \end{array}$$

(4)

Proof. 

Due to the space constraints, the full proof must be deferred to Appendix A. In the following, we only present a proof sketch and the core conclusions. At the beginning of the proof, we define some notations and values in order to present the proof process.

We divide the transcripts in ${\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$ into four sets:

• ${\mathcal{G}}_1=\left\{\right|\mathcal{ID}\left(X\right)|=\left|\mathcal{ID}\left(A\right)\right|=1,and{H}_{k_2}\left(t\right)\oplus X\notin Dom{\mathcal{F}}_2\wedge H_{k_5}\left(t\right)\oplus X\notin Dom{\mathcal{F}}_5\}$;
• ${\mathcal{G}}_2=\{H_{k_2}\left(t\right)\oplus X\backslash Dom{\mathcal{F}}_2\}$;
• ${\mathcal{G}}_3=\{H_{k_5}\left(t\right)\oplus A\backslash Dom{\mathcal{F}}_5\}$;
• ${\mathcal{G}}_4=\left\{\right|\mathcal{ID}\left(X\right)|\ge 2or|\mathcal{ID}\left(A\right)|\ge 2\}$.

Then we denote ${\mathsf{E}}_{{\mathcal{G}}_1}$, ${\mathsf{E}}_{{\mathcal{G}}_2}$, ${\mathsf{E}}_{{\mathcal{G}}_3}$ and ${\mathsf{E}}_{{\mathcal{G}}_4}$ by the events that ${\mathsf{TKAF}}_{H_k\left(t\right)}^{{\mathit{F}}^{*}}⊢{\mathcal{G}}_1,{\mathcal{G}}_2,{\mathcal{G}}_3$ and ${\mathcal{G}}_4$ respectively, and let ${\beta }_1=\left|{\mathcal{G}}_2\right|$, ${\beta }_2=\left|{\mathcal{G}}_3\right|$, ${\beta }_3=\left|{\mathcal{G}}_4\right|$. We list ${\mathcal{G}}_i=\{(t,RX,AS),\dots ,(t,R_{|{\mathcal{G}}_i|}{X}_{|{\mathcal{G}}_i|},A_{|{\mathcal{G}}_i|}{S}_{|{\mathcal{G}}_i|})\}$ with some arbitrary orders. Denote ${\mathsf{E}}_{|{\mathcal{G}}_i|}$ the event that ${\mathsf{TKAF}}_{H_k\left(t\right)}^{{\mathit{F}}^{*}}$ extends the i-th tuple $(t,R_i{X}_i,A_i{S}_i)$. We define four sets of “collision position”:

$$\begin{array}{cc}\hfill Ext{\mathcal{F}}_3^{\left(l\right)}& \stackrel{def}{=}\{x_3:\exists (t,R_i{X}_i,A_i{S}_i)\backslash {\mathcal{G}}_1,i\le l,s.t.x_3=k_3\oplus R_i\oplus {\mathit{F}}_2(H_{k_2}\left(t\right)\oplus X_i)\};\hfill \\ \hfill {\mathcal{G}}_2{\mathcal{F}}_3& \stackrel{def}{=}\{x_3:\exists (t,RX,AS)\backslash {\mathcal{G}}_2,s.t.x_3=k_3\oplus R\oplus Img{F}_2(H_{k_2}\left(t\right)\oplus X)\};\hfill \\ \hfill Ext{\mathcal{F}}_4^{\left(l\right)}& \stackrel{def}{=}\{x_4:\exists (t,R_i{X}_i,A_i{S}_i)\backslash {\mathcal{G}}_1,i\le l,s.t.x_4=k_4\oplus S_i\oplus {\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_i)\};\hfill \\ \hfill {\mathcal{G}}_3{\mathcal{F}}_4& \stackrel{def}{=}\{x_4:\exists (t,RX,AS)\backslash {\mathcal{G}}_3,s.t.x_4=k_4\oplus S\oplus Img{F}_5(H_{k_5}\left(t\right)\oplus A)\}.\hfill \end{array}$$

For convenience, we denote two values $e_3^{\left(l\right)}=|Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3|$, and $e_4^{\left(l\right)}=$$|Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4|$, which are the quantities of choices in the sets. Finally, the function ${\mathsf{Num}}_3^{\left(l\right)}\left(y_3\right)$ is the number of pre-images $y_3$, which belongs to the set $Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}$. That is ${\mathsf{Num}}_3^{\left(l\right)}\left(y_3\right)\stackrel{def}{=}\left|\{x_3\backslash Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}:{\mathit{F}}_3\left(x_3\right)=y_3\}\right|$.

Since we have these definitions mentioned above, we can lower bound

$$\mathsf{p}(\tau ,{\mathit{F}}_1,{\mathit{F}}_6)=\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_1}\wedge {\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}\wedge {\mathsf{E}}_{{\mathcal{G}}_4}|\mathit{F}⊢{\mathcal{Q}}_F\right].$$

Analyzing these four sets in turn. First, we consider $\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_1}|\mathit{F}⊢{\mathcal{Q}}_F\right].$ There are three cases for each transcript $(t,RX,AS)\backslash {\mathcal{G}}_1$:

(i)

The two intermediate values Y and Z derived from ${\mathit{F}}_2$ and ${\mathit{F}}_5$ will not collide with the values that have been queried in the past time. So, the probability of this case is at least

$$\left(1-\frac{q_f+e_3^{(l+1)}+\left|{\mathcal{G}}_2{\mathcal{F}}_3\right|}{N}\right)\left(1-\frac{q_f+e_4^{(l+1)}+\left|{\mathcal{G}}_3{\mathcal{F}}_4\right|}{N}\right)\frac{1}{N^2},$$

(ii)

The intermediate value Y collides with some values of the past queries, but Z is still “free”. So, the probability of this case is at least

$$\begin{array}{c}\hfill \left(\frac{q_f+e_3^{\left(l\right)}}{N}-\frac{{\sum }_{x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4}{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus k_4\oplus x_4)}{N}-\frac{q_f^2}{N^2}-\frac{(2q_f+q_e)(q_f+q_e)}{N^2}\right)\frac{1}{N^2}.\end{array}$$

(iii)

This case is symmetrical to the second one, where Z collides with some past values, but Y is “free”. The probability is at least

$$\left(\frac{q_f+e_4^{\left(l\right)}}{N}-\frac{{\sum }_{x_3\backslash {\mathcal{G}}_2{\mathcal{F}}_3}{\mathsf{Num}}_4^{\left(l\right)}(A_{l+1}\oplus k_3\oplus x_3)}{N}-\frac{(2q_f+q_e)(q_f+q_e)}{N^2}\right)\frac{1}{N^2}.$$

Summing over the above five cases, we have

$$\begin{array}{cc}\hfill {\mathbb{E}}_k\left[\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_1}|\mathit{F}⊢{\mathcal{Q}}_F\right]\right]& \ge (1-\frac{q_e{q}_f^2}{N^2}-\frac{2q_e(2q_f+q_e)(q_f+q_e)}{N^2}\hfill \\ \hfill & -\frac{(q_f+2q_e)({\beta }_1+{\beta }_2)}{N})\frac{1}{N^{2|{\mathcal{G}}_1|}}.\hfill \end{array}$$

Then, we analyze ${\mathsf{E}}_{{\mathcal{G}}_2}$, ${\mathsf{E}}_{{\mathcal{G}}_3}$, and ${\mathsf{E}}_{{\mathcal{G}}_4}$. The events ${\mathsf{E}}_{{\mathcal{G}}_2}$ and ${\mathsf{E}}_{{\mathcal{G}}_3}$ can be considered simultaneously. For the rest events, we need to upper- bound the corresponding “bad” events, then consider the efficiency of introducing tweak. Through this method, we can lower bound these three events. See Appendix A for more details about the proof.

For the proof, we have the results of the following three events:

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}|{\mathsf{E}}_{{\mathcal{G}}_1}\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]& \ge (1-\mathrm{Pr}\left[{\mathsf{Bad}}_1\left({\mathit{F}}_3\right)\right]-\mathrm{Pr}\left[{\mathsf{Bad}}_2\left({\mathit{F}}_4\right)\right])\hfill \\ \hfill & ·\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}|\neg {\mathsf{Bad}}_1\left({\mathit{F}}_3\right)\wedge \neg {\mathsf{Bad}}_2\left({\mathit{F}}_4\right)\right]\hfill \\ \hfill & \ge \left(1-\frac{({\beta }_1+{\beta }_2)(q_f+q_e)}{N}-({\beta }_1+{\beta }_2)\epsilon \right)\hfill \\ \hfill & ·\frac{1}{N^{2\left(\right|{\mathcal{G}}_2|+|{\mathcal{G}}_3\left|\right)}};\hfill \end{array}$$

$$\begin{array}{c}\hfill \mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_4}|{\mathsf{E}}_{{\mathcal{G}}_1}\wedge {\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}\wedge \mathit{F}⊢{\mathcal{G}}_F\right]\ge \left(1-\mathrm{Pr}\left[{\mathsf{Bad}}_3({\mathit{F}}_2,{\mathit{F}}_5)\right]\right)·\frac{1}{N^{2|{\mathcal{G}}_4|}}\\ \hfill \ge \left(1-\frac{2{\beta }_3(q_f+q_e)}{N}-2{\beta }_3\epsilon \right)·\frac{1}{N^{2|{\mathcal{G}}_4|}}.\end{array}$$

Finally, we sum up all four events, i.e.,

$$\begin{array}{cc}\hfill \mathsf{p}(\tau ,{\mathit{F}}_1,{\mathit{F}}_6)& =\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_1}\wedge {\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}\wedge {\mathsf{E}}_{{\mathcal{G}}_4}|\mathit{F}⊢{\mathcal{G}}_F\right]\hfill \\ \hfill & \ge (1-{\theta }_1)(1-{\theta }_2)(1-{\theta }_3)\frac{1}{N^{2\left(\right|{\mathcal{G}}_1|+|{\mathcal{G}}_2|+|{\mathcal{G}}_3|+|{\mathcal{G}}_4\left|\right)}}\hfill \\ \hfill & \ge (1-({\theta }_1+{\theta }_2+{\theta }_3))\frac{1}{N^{2q_e}},\hfill \end{array}$$

where ${\theta }_1$, ${\theta }_2$, ${\theta }_3$ are (A1), (A2) and (A3) respectively, furthermore $|{\mathcal{G}}_1|+|{\mathcal{G}}_2|+|{\mathcal{G}}_3|+|{\mathcal{G}}_4|=q_e$. We note that

$$\begin{array}{c}\hfill \frac{1}{N^{2q_e}}/\prod _{i=0}^{q_e-1}\frac{1}{N^2-i}\ge {(1-\frac{q_e}{N^2})}^{q_e}\ge 1-\frac{q_e^2}{N^2}\ge 1-\frac{q_e^3}{N^2},\end{array}$$

then for (3), we have

$$\begin{array}{cc}\hfill {\mathbb{E}}_k\left[\phi ({\mathit{F}}_1,{\mathit{F}}_6,k)\right]& \le \frac{(3q_e+2q_f)({\beta }_1+{\beta }_2)+2{\beta }_3(q_e+q_f)}{N}\hfill \\ \hfill & +\frac{2q_e(q_e+2q_f)(q_e+q_f)+q_e^3}{N^2}+\frac{q_e{q}_f^2}{N^2}+({\beta }_1+{\beta }_2+2{\beta }_3)\epsilon .\hfill \end{array}$$

We know that ${\beta }_1$, ${\beta }_2$, and ${\beta }_3$ depend on $({\mathit{F}}_1,{\mathit{F}}_6)$. We consider them respectively, focusing on ${\beta }_1$ firstly. For each $(t,RX,AS)\backslash {\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, if $H_{k_1}\left(t\right)\oplus R\backslash Dom{\mathcal{F}}_1$, then it must be $H_{k_2}\left(t\right)\oplus X\notin Dom{\mathcal{F}}_2$ because of ¬(A-2). Thus, on the condition of ${\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}$, ${\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)$ keeps uniform, then we have

$$\mathrm{Pr}\left[H_{k_2}\left(t\right)\oplus L\oplus {\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)\backslash Dom{\mathcal{F}}_2\right]\le \frac{q_f}{N}.$$

Therefore, ${\mathbb{E}}_k\left[{\beta }_1\right]\le \frac{q_e{q}_f}{N}.$ The analysis method of ${\beta }_2$ is symmetric with ${\beta }_1$, by the uniformity of ${\mathit{F}}_6$, we have ${\mathbb{E}}_k\left[{\beta }_2\right]\le \frac{q_e{q}_f}{N}.$

To this end, we consider ${\beta }_3$. For the fixed transcript $(t,LR,ST)$ such that $H_{k_1}\left(t\right)\oplus R\notin Dom{\mathcal{F}}_1$, give a distinct $(t^{\prime },L^{\prime }{R}^{\prime },S^{\prime }{T}^{\prime })$. If $t\ne t^{\prime }$ but $LR=L^{\prime }{R}^{\prime }$, for the uniformity of H, we have

$$\mathrm{Pr}\left[X=X^{\prime }\right]=\mathrm{Pr}\left[L\oplus {\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)=L^{\prime }\oplus {\mathit{F}}_1(H_{k_1}\left(t^{\prime }\right)\oplus R^{\prime })\right]\le \epsilon ;$$

if $t=t^{\prime }$ and $R=R^{\prime }$, then it must be $L\ne L^{\prime }$, thus $X=X^{\prime }$ is impossible; if $t=t^{\prime }$ and $L=L^{\prime }$ but $R\ne R^{\prime }$, on account of $H_{k_1}\left(t\right)\oplus R\notin Dom{\mathcal{F}}_1$, then ${\mathit{F}}_1(H_{k_1}\left(t\right)\oplus R)$ keeps uniformly random conditioned on ${\mathit{F}}_1⊢{\mathcal{Q}}_{F_1}$, therefore $\mathrm{Pr}\left[X=X^{\prime }\right]=\frac{1}{N}$. In addition, the choices of distinct pairs $(t,LR,ST)$ and $(t^{\prime },L^{\prime }{R}^{\prime },S^{\prime }{T}^{\prime })$ are at most $q_e^2$. Thus Thus, we have

$$\begin{array}{c}\hfill {\mathbb{E}}_k\left[\left|\right\{(t,LR,ST):H_{k_1}\left(t\right)\oplus R\notin Dom{\mathcal{F}}_1,and\exists (t^{\prime },L^{\prime }{R}^{\prime },S^{\prime }{T}^{\prime })s.t.X=X^{\prime }\left\}\right|\right]\\ \hfill \le q_e^2\epsilon +q_e^2(1-\epsilon )\frac{1}{N}\le q_e^2\epsilon +\frac{q_e^2}{N}.\end{array}$$

For $H_{k_1}\left(t\right)\oplus R\backslash Dom{\mathcal{F}}_1$, the number of the transcripts $(t,LR,ST)$ which meet the above conditions is $n_{\left(1\right)}\left(k\right)$. We have

$${\mathbb{E}}_k\left[\left|\right\{(t,LR,ST):\exists (t^{\prime },L^{\prime }{R}^{\prime },S^{\prime }{T}^{\prime })s.t.X=X^{\prime }\left\}\right|\right]\le \frac{q_e^2}{N}+q_e^2\epsilon +n_{\left(1\right)}\left(k\right).$$

Symmetrically,

$${\mathbb{E}}_k\left[\left|\right\{(t,LR,ST):\exists (t^{\prime },L^{\prime }{R}^{\prime },S^{\prime }{T}^{\prime })s.t.A=A^{\prime }\left\}\right|\right]\le \frac{q_e^2}{N}+q_e^2\epsilon +n_{\left(6\right)}\left(k\right).$$

Thus, we have

$${\mathbb{E}}_k\left[{\beta }_3\right]\le \frac{2q_e^2}{N}+2q_e^2\epsilon +n_{\left(1\right)}\left(k\right)+n_{\left(6\right)}\left(k\right).$$

Finally, $H_{k_1}\left(t\right)$ and $H_{k_6}\left(t\right)$ are uniform in $2^n$ possible choices,

$${\mathbb{E}}_k\left[n_{\left(1\right)}\left(k\right)\right]={\mathbb{E}}_k\left[n_{\left(6\right)}\left(k\right)\right]=\sum _{(t,LR,ST)\backslash {\mathcal{Q}}_E}\sum _{(x_1,y_1)\backslash {\mathcal{Q}}_{F_1}}\mathrm{Pr}\left[H_{k_1}\left(t\right)=R\oplus x_1\right]\le \frac{q_e{q}_f}{N}.$$

Gathering all the above yields, we have

$$\begin{array}{cc}\hfill {\mathbb{E}}_{{\mathit{F}}_1,{\mathit{F}}_6,k}\left[\phi ({\mathit{F}}_1,{\mathit{F}}_6,k)\right]& \le \frac{6q_e^2{q}_f+4q_e{q}_f^2}{N^2}+\frac{4q_e{(q_e+q_f)}^2}{N^2}\hfill \\ \hfill & +\frac{2q_e(q_e+2q_f)(q_e+q_f)+q_e^3}{N^2}+\frac{q_e{q}_f^2}{N^2}\hfill \\ \hfill & +\frac{4q_e^2(q_e+q_f)\epsilon }{N}+\frac{2q_e{q}_f\epsilon }{N}\hfill \\ \hfill & +\frac{4q_e(q_e+q_f)\epsilon }{N}+4q_e^2{\epsilon }^2\hfill \\ \hfill & =4q_e^2{\epsilon }^2+\frac{7q_e^3+20q_e^2{q}_f+12q_e{q}_f^2}{N^2}\hfill \\ \hfill & +\frac{4q_e^3\epsilon +4q_e^2{q}_f\epsilon +4q_e^2\epsilon +6q_e{q}_f\epsilon }{N},\hfill \end{array}$$

as claimed in (4). □

Now we have Lemma 2, Lemma 4, and (2), we obtain

$$\begin{array}{cc}\hfill \frac{{\mathrm{Pr}}_{re}\left(\tau \right)}{{\mathrm{Pr}}_{id}\left(\tau \right)}\ge 1-(\frac{3q_e{q}_f^2}{N^2}& +{\mathbb{E}}_k\left[\mathrm{Pr}\left[\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)|{\mathit{F}}_1⊢{\mathcal{Q}}_{F_1},{\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}\right]\right]\hfill \\ \hfill & +{\mathbb{E}}_k\left[{\mathbb{E}}_{{\mathit{F}}_1,{\mathit{F}}_6}\left[\phi ({\mathit{F}}_1,{\mathit{F}}_6,k)|{\mathit{F}}_1⊢{\mathcal{Q}}_{F_1},{\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}\right]\right]).\hfill \end{array}$$

For the expectation ${\mathbb{E}}_k\left[\mathrm{Pr}\left[\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)|{\mathit{F}}_1⊢{\mathcal{Q}}_{F_1},{\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}\right]\right]$, we note that $k_3$ and $k_4$ are uniformly picked from $2^n$ possibilities, then

$${\mathbb{E}}_k\left[n_{(2,3)}\left(k\right)\right]={\mathbb{E}}_k\left[n_{(4,5)}\left(k\right)\right]\le \frac{q_e{q}_f^2}{N}.$$

It has been shown that ${\mathbb{E}}_k\left[n_{\left(1\right)}\left(k\right)\right]={\mathbb{E}}_k\left[n_{\left(6\right)}\left(k\right)\right]\le \frac{q_e{q}_f}{N}$. Then Lemma 3 yields

$$\begin{array}{c}\hfill {\mathbb{E}}_k\left[\mathrm{Pr}\left[\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)|{\mathit{F}}_1⊢{\mathcal{Q}}_{F_1},{\mathit{F}}_6⊢{\mathcal{Q}}_{F_6}\right]\right]\\ \hfill \le \frac{4q_e^2{q}_f+5q_e{q}_f^2}{N^2}+\frac{2q_e{q}_f^2\epsilon }{N}+4q_e^2{q}_f{\epsilon }^2.\end{array}$$

From all above, by Lemmas 1 and 2, we have proved the conclusion of Theorem 1.

5. Conclusions and Future Work

This paper presents a result of constructing a tweakable block cipher from the $\mathsf{KAF}$ construction. Our work is based on based on the study by Guo et al. [24], we introduce the tweak into their optimized 6-round scheme $\mathsf{KAF}$ in order to achieve the Beyond Birthday-Bound security. We utilize a universal hash function which is called $\epsilon$-almost XOR-universal hash function, with tweak and round-key vector, we rebuild a new tweakable $\mathsf{KAF}$ scheme $\mathsf{TKAF}$ which meets the security of beyond birthday-bound. Finally Finally, by using the H-coefficient technique [25], we prove the security requirement and obtain a better conclusion with fewer rounds. Our approach is to introduce the tweak into the first and last two rounds of Guo’s 6-round $\mathsf{KAF}$ structure, and utilize the universal hash function as the operation method. Can we introduce the tweak directly into the round function without using the universal hash function, and still meeting the beyond birthday-bound security? Or can we use another linear method to introduce a tweak? We leave these as future work.

Appendix A.1. $\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_1}|\mathit{F}⊢{\mathcal{Q}}_F\right]$

Firstly, we consider the event ${\mathsf{E}}_{{\mathcal{G}}_1}$, i.e., lower bounding $\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_1}|\mathit{F}⊢{\mathcal{Q}}_F\right].$ By the definition, there must be ${\mathsf{E}}_{{\mathcal{G}}_1}={\mathsf{E}}_{|{\mathcal{G}}_1|}\wedge \dots \wedge {\mathsf{E}}_1$. So, Therefore, we consider to lowering bound the probability of ${\mathsf{E}}_{l+1}$ on the condition of ${\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F$.

We note that on the condition of ${\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1$, for arbitrary $x_3\backslash Ext{F}_3^{\left(l\right)}$ and $x_4\backslash Ext{F}_4^{\left(l\right)}$, $F_3\left(x_3\right)$ and $F_4\left(x_4\right)$ will be considered to be “fixed”. For convenience, we denote $x_2^{(l+1)}=H_{k_2}\left(t\right)\oplus X_{l+1}$ and $x_5^{(l+1)}=H_{k_5}\left(t\right)\oplus A_{l+1}$, furthermore denote $Y_{l+1}=R_{l+1}\oplus {\mathit{F}}_2\left(x_2^{(l+1)}\right)$ and $Z_{l+1}=S_{l+1}\oplus {\mathit{F}}_5\left(x_5^{(l+1)}\right)$. Depending on the states of two intermediate values $Y_{l+1}$ and $Z_{l+1}$, we consider the event ${\mathsf{E}}_{l+1}$ in three cases:

• Case 1-no collision: $Y_{l+1}$ and $Z_{l+1}$ satisfy

  $$\begin{array}{c}\hfill k_3\oplus Y_{l+1}\notin Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}\cup {\mathcal{G}}_2{\mathcal{F}}_3\\ \hfill k_4\oplus Z_{l+1}\notin Dom{\mathcal{F}}_4\cup Ext{\mathcal{F}}_4^{\left(l\right)}\cup {\mathcal{G}}_3{\mathcal{F}}_4.\end{array}$$
  It holds ${\mathit{F}}_3(k_3\oplus Y_{l+1})=X_{l+1}\oplus Z_{l+1}$ and ${\mathit{F}}_4(k_4\oplus Z_{l+1})=Y_{l+1}\oplus A_{l+1}$;
• Case 2-left collision: $Y_{l+1}$ satisfies $k_3\oplus Y_{l+1}\backslash Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}$, but $Z_{l+1}$ satisfies $k_4\oplus Z_{l+1}\notin Dom{\mathcal{F}}_4\cup Ext{\mathcal{F}}_4^{\left(l\right)}\cup {\mathcal{G}}_3{\mathcal{F}}_4$. It holds ${\mathit{F}}_4(k_4\oplus Z_{l+1})=Y_{l+1}\oplus A_{l+1}$ and ${\mathit{F}}_5\left(x_5^{(l+1)}\right)=Z_{l+1}\oplus S_{l+1}$;
• Case 3-right collision: $Z_{l+1}$ satisfies $k_4\oplus Z_{l+1}\backslash Dom{\mathcal{F}}_4\cup Ext{\mathcal{F}}_4^{\left(l\right)}$, but $Y_{l+1}$ satisfies $k_3\oplus Y_{l+1}\notin Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}\cup {\mathcal{G}}_2{\mathcal{F}}_3$. It holds ${\mathit{F}}_2\left(x_2^{(l+1)}\right)=Y_{l+1}\oplus R_{l+1}$ and ${\mathit{F}}_3(k_3\oplus Y_{l+1})=Z_{l+1}\oplus X_{l+1}$.

By these, accumulating all probabilities of above three cases, we have

$$\mathrm{Pr}\left[{\mathsf{E}}_{l+1}|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right].$$

Now we consider these three cases respectively.

Appendix A.1.1. Case 1

For $(t,R_{l+1}{X}_{l+1},A_{l+1}{S}_{l+1})\backslash {\mathcal{G}}_1$, by definition, we have $x_2^{(l+1)}=H_{k_2}\left(t\right)\oplus X_{l+1}\notin Dom{\mathcal{F}}_2$. With tuples in ${\mathcal{Q}}_E^{*}({\mathit{F}}_1,{\mathit{F}}_6)$, $X_{l+1}$ does not collide with other corresponding positions since $\left|\mathcal{ID}\right(X_{l+1}\left)\right|=1$. Thus Thus, ${\mathit{F}}_2\left(x_2^{(l+1)}\right)$ remains uniformly random on the condition of ${\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F$. Moreover, $\mathrm{Pr}\left[k_3\oplus Y_{l+1}\backslash Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}\cup {\mathcal{G}}_2{\mathcal{F}}_3\right]\le \frac{q_f+e_3^{(l+1)}+\left|{\mathcal{G}}_2{\mathcal{F}}_3\right|}{N}$. Symmetrically, we have $\mathrm{Pr}\left[k_4\oplus Z_{l+1}\backslash Dom{\mathcal{F}}_4\cup Ext{\mathcal{F}}_4^{\left(l\right)}\cup {\mathcal{G}}_3{\mathcal{F}}_4\right]\le$$\frac{q_f+e_4^{(l+1)}+\left|{\mathcal{G}}_3{\mathcal{F}}_4\right|}{N}$. Then, the probability that these two equations ${\mathit{F}}_3(k_3\oplus Y_{l+1})=X_{l+1}\oplus Z_{l+1}$ and ${\mathit{F}}_4(k_4\oplus Z_{l+1})=Y_{l+1}\oplus A_{l+1}$ are simultaneously fulfilled is $\frac{1}{N^2}$.

From above,

$$\mathrm{Pr}\left[{\mathsf{E}}_{l+1}\wedge \mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}1|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]$$

$$\ge \left(1-\frac{q_f+e_3^{(l+1)}+\left|{\mathcal{G}}_2{\mathcal{F}}_3\right|}{N}\right)\left(1-\frac{q_f+e_4^{(l+1)}+\left|{\mathcal{G}}_3{\mathcal{F}}_4\right|}{N}\right)\frac{1}{N^2}.$$

Appendix A.1.2. Case 2

We consider the opposite case of Case 2, and upper- bound the probability on this condition. Let $\mathsf{pcoll}$ be the probability of the contrary case. We have

$$\begin{array}{c}\hfill \mathsf{pcoll}=\mathrm{Pr}\left[\exists x_3\backslash Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)},\exists x_4\backslash Dom{\mathcal{F}}_4\cup Ext{\mathcal{F}}_4^{\left(l\right)}\cup {\mathcal{G}}_3{\mathcal{F}}_4:\right.\\ \hfill \left.\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right],\end{array}$$

where $\mathsf{Coll}(x_3,x_4)$ stands for the collision event

$$X_{l+1}\oplus y_3=(k_4\oplus x_4)\wedge R_{l+1}\oplus {\mathit{F}}_2\left(x_2^{(l+1)}\right)=k_3\oplus x_3,$$

Then, we consider five subcases of the opposite Case 2 respectively, and upper- bound for each in turn.

• Subcase 2.1:$x_3\backslash Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)},and{x}_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4.$
  For each $x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4$, by definition, we have the number of $x_3\backslash Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}$ which satisfies the collision $X_{l+1}\oplus y_3=k_4\oplus x_4$ is ${\sum }_{x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4}{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus k_4\oplus x_4)$. In addition, similar with Case 1, we can still deem ${\mathit{F}}_2\left(x_2^{(l+1)}\right)$ as uniformly random. Thus, it holds $\mathrm{Pr}\left[{\mathit{F}}_2\left(x_2^{(l+1)}\right)=R_{l+1}\oplus k_3\oplus x_3\right]\le \frac{1}{N}$. Therefore, the upper bound of Subcase 2.1 is

  $$\begin{array}{c}\hfill \sum _{\begin{array}{c}{x}_3\backslash Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}\\ x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\\ \hfill \le \frac{{\displaystyle \sum _{x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4}{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus k_4\oplus x_4)}}{N}.\end{array}$$
• Subcase 2.2:$x_3\backslash Dom{\mathcal{F}}_3,and{x}_4\backslash Dom{\mathcal{F}}_4.$ Define a key-dependent value:

  $$\begin{array}{c}\hfill {\mathsf{Num}}_{3,4}^{+}(k,X)\stackrel{def}{=}\left|\{((x_3,y_3),(x_4,y_4))\backslash {\mathcal{Q}}_{F_3}\times {\mathcal{Q}}_{F_4}:k_4=X\oplus y_3\oplus x_4\}\right|.\end{array}$$
  Then we have the quantity of $(x_3,x_4)$ which satisfies the collision condition $X_{l+1}\oplus y_3=k_4\oplus x_4$ is ${\mathsf{Num}}_{3,4}^{+}(k,X_{l+1})$. Same as Subcase 2.1,

  $$\mathrm{Pr}\left[{\mathit{F}}_2\left(x_2^{(l+1)}\right)=R_{l+1}\oplus k_3\oplus x_3\right]\le \frac{1}{N}.$$
  Thus, we have

  $$\begin{array}{c}\hfill \sum _{\begin{array}{c}{x}_3\backslash Dom{\mathcal{F}}_3\\ x_4\backslash Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\le \frac{{\mathsf{Num}}_{3,4}^{+}(k,X_{l+1})}{N}.\end{array}$$
  It can be seen, $k_4$ is uniform in N values. So, the expectation of ${\mathsf{Num}}_{3,4}^{+}(k,X_{l+1})$ is at most $\frac{q_f^2}{N}$. Thus Thus, the upper bound of the probability on the condition of Subcase 2.2 is at most $\frac{q_f^2}{N^2}$.
• Subcase 2.3:$x_3\backslash Dom{\mathcal{F}}_3,and{x}_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4.$ By definition, we write

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Dom{\mathcal{F}}_3\\ x_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & =\sum _{\begin{array}{c}{x}_3\backslash Dom{\mathcal{F}}_3\\ i=1,\dots ,l\end{array}}\mathsf{sgn}\left(i\right)·\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4^{\left(i\right)})|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right],\hfill \end{array}$$

  where $x_4^{\left(i\right)}=k_4\oplus Z_i$, and for i-th tuple $(t,R_i{X}_i,A_i{S}_i)\backslash {\mathcal{G}}_4$, we have $Z_i=S_i\oplus {\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_i)$. In addition, $\mathsf{sgn}\left(i\right)=1$ if and only if i is the smallest index that satisfies $x_4^{\left(i\right)}\backslash Ext{\mathcal{F}}_4^{\left(i\right)}\setminus Dom{\mathcal{F}}_4$, since $x_4^{\left(i\right)}\notin Ext{\mathcal{F}}_4^{(i-1)}$.
  First, we focus on $\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4^{\left(i\right)})|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]$. Considering the probability on the condition that ${\mathsf{E}}_i$ fits into Case 1,2 and 3. It can be seen that if ${\mathsf{E}}_i$ fits into Case 3, then we have $x_4^{\left(i\right)}\backslash Dom{\mathcal{F}}_4$, it contradicts the Subcase 2.3. Let $y_3=Img{F}_3\left(x_3\right)$, write $Y_i=R_i\oplus {\mathit{F}}_2(H_{k_2}\left(t\right)\oplus X_i)$.

  (i)

  ${\mathsf{E}}_i$ fits into Case 1

  We derive $Z_i$ from $Z_i=S_i\oplus {\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_i)$, and ${\mathit{F}}_5(x_5^{\left(i\right)})$ keeps uniform. Then we have

  $$\begin{array}{cc}\hfill \mathrm{Pr}\left[X_{l+1}\oplus y_3=(k_4\oplus x_4^{\left(i\right)})\right]& =\mathrm{Pr}\left[X_{l+1}\oplus y_3=Z_i\right]\hfill \\ \hfill & =\mathrm{Pr}\left[{\mathit{F}}_5(x_5^{\left(i\right)})=X_{l+1}\oplus y_3\oplus S_i\right]\le \frac{1}{N}.\hfill \end{array}$$

  Furthermore, we have $\mathrm{Pr}\left[{\mathit{F}}_2(x_2^{\left(i\right)})=R_{l+1}\oplus k_3\oplus x_3\right]\le \frac{1}{N}$. Thus

  $$\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4^{\left(i\right)}|{\mathsf{E}}_{i}fitsinto\mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}1\wedge {\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F)\right]\le \frac{1}{N^2}.$$

  (ii)

  ${\mathsf{E}}_i$ fits into Case 2

  Let $x_3^{\left(i\right)}=k_3\oplus Y_i,y_3^{\left(i\right)}={\mathit{F}}_3\left(x_3^{\left(i\right)}\right)$. We have $X_{l+1}\oplus y_3=Z_i=X_i\oplus y_3^{\left(i\right)}$. By definition, the number of choices for such $y_3^{\left(i\right)}$ is ${\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus y_3\oplus X_i)$. Furthermore, for these choices of $y_3^{\left(i\right)}$, the probability of the following two collisions is at most $\frac{1}{N}$, i.e.,

  $$R_i\oplus {\mathit{F}}_2(H_{k_2}\left(t\right)\oplus X_i)=k_3\oplus x_3^{\left(i\right)},R_{l+1}\oplus {\mathit{F}}_2(H_{k_2}\left(t\right)\oplus X_{l+1})=k_3\oplus x_3.$$

  Thus

  $$\begin{array}{c}\hfill \mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4^{\left(i\right)})|{\mathsf{E}}_{i}fitsinto\mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}2\wedge {\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F)\right]\\ \hfill \le \frac{{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus y_3\oplus X_i)}{N^2}.\end{array}$$

  From the above,

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Dom{\mathcal{F}}_3\\ x_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & \le \sum _{x_3\backslash Dom{\mathcal{F}}_3}\sum _{i=,\dots ,l}\mathsf{sgn}\left(i\right)·\frac{{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus y_3\oplus X_i)}{N^2}\hfill \\ \hfill & \le \sum _{x_3\backslash Dom{\mathcal{F}}_3}\frac{q_f+e_3^{\left(l\right)}}{N^2}\le \frac{q_f(q_f+q_e)}{N^2}.\hfill \end{array}$$
• Subcase 2.4:$x_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3,and{x}_4\backslash Dom{\mathcal{F}}_4.$ By definition, we write

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3\\ x_4\backslash Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & =\sum _{\begin{array}{c}i=1,\dots ,l\\ x_4\backslash Dom{\mathcal{F}}_4\end{array}}{\mathsf{sgn}}^{\prime }\left(i\right)·\mathrm{Pr}\left[\mathsf{Coll}(x_3^{\left(i\right)},x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right],\hfill \end{array}$$

  where $x_3^{\left(i\right)}=k_3\oplus Y_i$, and for i-th tuple $(t,R_i{X}_i,A_i{S}_i)\backslash {\mathcal{G}}_4$, we have $Y_i=R_i\oplus {\mathit{F}}_2(H_{k_2}\left(t\right)\oplus X_i)$. In addition, ${\mathsf{sgn}}^{\prime }\left(i\right)=1$ if and only if i is the smallest index that satisfies $x_3^{\left(i\right)}\backslash Ext{\mathcal{F}}_3^{\left(i\right)}\setminus Dom{\mathcal{F}}_3$, since $x_3^{\left(i\right)}\notin Ext{\mathcal{F}}_3^{(i-1)}$.
  First, we focus on $\mathrm{Pr}\left[\mathsf{Coll}(x_3^{\left(i\right)},x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]$. Let $y_4=Img{F}_4\left(x_4\right)$, write $Z_i=S_i\oplus {\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_i)$. That is $y_3^{\left(i\right)}=X_i\oplus Z_i$. Thus, the collision $X_{l+1}\oplus y_3^{\left(i\right)}=(k_4\oplus x_4)$ can be seen as $X_{l+1}\oplus X_i=Z_i\oplus (k_4\oplus x_4)$. Same as Subcase 2.3, we only need to consider two cases on ${\mathsf{E}}_i$.

  (i)

  ${\mathsf{E}}_i$ fits into Case 1

  We know that $Z_i=S_i\oplus {\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_i)$ and ${\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_i)$ keep uniform. Then it holds

  $$\begin{array}{cc}\hfill & \mathrm{Pr}\left[X_{l+1}\oplus X_i=Z_i\oplus (k_4\oplus x_4)\right]\hfill \\ \hfill & =\mathrm{Pr}\left[{\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_i)=S_i\oplus X_{l+1}\oplus X_i\oplus k_4\oplus x_4\right]\le \frac{1}{N}.\hfill \end{array}$$

  Then, we have $\mathrm{Pr}\left[{\mathit{F}}_2(H_{k_2}\left(t\right)\oplus X_{l+1})=R_{l+1}\oplus k_3\oplus x_3^{\left(i\right)}\right]\le \frac{1}{N}$. Thus

  $$\mathrm{Pr}\left[\mathsf{Coll}(x_3^{\left(i\right)},x_4)|{\mathsf{E}}_{i}fitsinto\mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}1\wedge {\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F)\right]\le \frac{1}{N^2}.$$

  (ii)

  ${\mathsf{E}}_i$ fits into Case 3

  Let $x_4^{\left(i\right)}=k_4\oplus Z_i$. We have $X_{l+1}\oplus X_i=x_4^{\left(i\right)}\oplus x_4$ because of $X_{l+1}\oplus X_i=Z_i\oplus k_4\oplus x_4$. We note that if $X_{l+1}$, $x_i$ and $x_4$ are “fixed”, then the possibility of choices of $x_4^{\left(i\right)}$ is at most 1. Therefore, if $Y_{l+1}$ collides with $x_3^{\left(i\right)}$, the following two collisions have to happen:

  $$S_i\oplus {\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_i)=k_4\oplus x_4^{\left(i\right)},R_i\oplus {\mathit{F}}_2(H_{k_2}\left(t\right)\oplus X_{l+1})=k_3\oplus x_3^{\left(i\right)}.$$

  Thus

  $$\begin{array}{c}\hfill \mathrm{Pr}\left[\mathsf{Coll}(x_3^{\left(i\right)},x_4)|{\mathsf{E}}_{i}fitsinto\mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}3\wedge {\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\le \frac{1}{N^2}.\end{array}$$

  According to Subcase 2.3, we have

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3\\ x_4\backslash Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & \le \sum _{i=,\dots ,l;x_4\backslash Dom{\mathcal{F}}_4}{\mathsf{sgn}}^{\prime }\left(i\right)·\frac{1}{N^2}\le \frac{q_f{e}_3^{\left(l\right)}}{N^2}\le \frac{q_f{q}_e}{N^2}.\hfill \end{array}$$
• Subcase 2.5:$x_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3,and{x}_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4.$ By definition, we write

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3\\ x_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & =\sum _{i,j=1,\dots ,l}\mathsf{sgn}\left(i\right)·{\mathsf{sgn}}^{\prime }\left(j\right)·\mathrm{Pr}\left[\mathsf{Coll}(x_3^{\left(i\right)},x_4^{\left(j\right)})|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right],\hfill \end{array}$$

  where $x_3^{\left(i\right)}=k_3\oplus Y_i$, and for i-th tuple $(t,R_i{X}_i,A_i{S}_i)\backslash {\mathcal{G}}_4$, we have $Y_i=R_i\oplus {\mathit{F}}_2(H_{k_2}\left(t\right)\oplus X_i)$. In addition, $\mathsf{sgn}\left(i\right)=1$ if and only if i is the smallest index that satisfies $x_3^{\left(i\right)}\backslash Ext{\mathcal{F}}_3^{\left(i\right)}\setminus Dom{\mathcal{F}}_3$, since $x_3^{\left(i\right)}\notin Ext{\mathcal{F}}_3^{(i-1)}$. In addition, $x_4^{\left(j\right)}=k_4\oplus Z_j$, and for j-th tuple $(t,R_j{X}_j,A_j{S}_j)\backslash {\mathcal{G}}_4$, we have $Z_j=S_j\oplus {\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_j)$. In addition, ${\mathsf{sgn}}^{\prime }\left(j\right)=1$ if and only if j is the smallest index that satisfies $x_4^{\left(j\right)}\backslash Ext{\mathcal{F}}_4^{\left(j\right)}\setminus Dom{\mathcal{F}}_4$, since $x_4^{\left(j\right)}\notin Ext{\mathcal{F}}_4^{(j-1)}$.

  (i)

  When $j>i$, due to $X_{l+1}\oplus y_3^{\left(i\right)}=X_j\oplus y_3^{\left(j\right)}$, according to Subcase 2.3, the number of choices for such $y_3^{\left(i\right)}$ is ${\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus y_3^{\left(i\right)}\oplus X_j)$. Furthermore, for each $(x_3^{\left(i\right)},x_4^{\left(j\right)})$, the upper bound of the probability is $\frac{{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus y_3^{\left(i\right)}\oplus X_j)}{N^2}$.

  (ii)

  When $i>j$, due to $X_{l+1}\oplus X_i=x_4^{\left(i\right)}\oplus x_4^{\left(j\right)}$, according to Subcase 2.4, the upper bound of the probability for each $(x_3^{\left(i\right)},y_3^{\left(j\right)})$ is $\frac{1}{N^2}$.

  To sum up,

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3\\ x_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & \le \sum _{j=1,\dots ,l}\sum _{i=1,\dots ,l}\frac{{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus y_3^{\left(i\right)}\oplus X_j)}{N^2}\hfill \\ \hfill & \le \sum _{j=1,\dots ,l}\frac{q_f+e_3^{\left(l\right)}}{N^2}\le \frac{q_e(q_f+q_e)}{N^2}.\hfill \end{array}$$
• Summing over all five subcases: We have

  $$\begin{array}{c}\hfill {\mathbb{E}}_k\left[\mathsf{pcoll}\right]\le \sum _{x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4}\frac{{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus k_4\oplus x_4)}{N}+\frac{q_f^2}{N^2}+\frac{(2q_f+q_e)(q_f+q_e)}{N^2}.\end{array}$$
  The five cases above are opposite conditions to Case 2. Moreover, if it holds $(t,R_{l+1}{X}_{l+1},$$A_{l+1}{S}_{l+1})\backslash {\mathcal{G}}_1$, then we have $\left(i\right)x_5^{(l+1)}\notin Dom{\mathcal{F}}_5$, $\left(ii\right)|\mathcal{ID}\left(A_{(l+1)}\right)|=1$, that implies the position of $x_5^{(l+1)}$ can be deemed as “new”.
  For these arguments above, we have

  $$\begin{array}{cc}\hfill & {\mathbb{E}}_k\left[\mathrm{Pr}\left[{\mathsf{E}}_{l+1}\wedge \mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}2|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\right]\hfill \\ \hfill & \ge (\frac{q_f+e_3^{\left(l\right)}}{N}-\frac{{\sum }_{x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4}{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus k_4\oplus x_4)}{N}\hfill \\ \hfill & -\frac{q_f^2}{N^2}-\frac{(2q_f+q_e)(q_f+q_e)}{N^2})\frac{1}{N^2}.\hfill \end{array}$$

Appendix A.1.3. Case 3

In this case, if it holds $x_2^{(l+1)}\notin Dom{\mathcal{F}}_2$ and $x_3=k_3\oplus Y_{l+1}\notin Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}\cup {\mathcal{G}}_2{\mathcal{F}}_3$, then we have

$$\begin{array}{cc}\hfill & \mathrm{Pr}\left[\mathsf{TKAF}extends(t,R_{l+1}{X}_{l+1},A_{l+1}{S}_{l+1})\right]\hfill \\ \hfill & =\mathrm{Pr}\left[{\mathit{F}}_2\left(x_2^{(l+1)}\right)=R_{l+1}\oplus Y_{l+1}\wedge {\mathit{F}}_3\left(x_3\right)=X_{l+1}\oplus Z_{l+1}\right]=\frac{1}{N_2}\hfill \end{array}$$

With the similar analysis of Case 2, we denote

$$\begin{array}{c}\hfill \mathsf{pcoll}=\sum _{\begin{array}{c}{x}_3\backslash Dom{\mathcal{F}}_3\cup Ext{\mathcal{F}}_3^{\left(l\right)}\cup {\mathcal{G}}_2{\mathcal{F}}_3\\ x_4\backslash Dom{\mathcal{F}}_4\cup Ext{\mathcal{F}}_4^{\left(l\right)}\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right].\end{array}$$

Also, we consider five subcases in turn.

• Subcase 3.1:$x_3\backslash {\mathcal{G}}_2{\mathcal{F}}_3,and{x}_4\backslash Dom{\mathcal{F}}_4\cup Ext{\mathcal{F}}_4^{\left(l\right)}.$ On this condition, as the constraint $A_{l+1}\oplus y_4=k_3\oplus x_3$, we have

  $$\begin{array}{c}\hfill \sum _{\begin{array}{c}{x}_3\backslash {\mathcal{G}}_2{\mathcal{F}}_3\\ x_4\backslash Dom{\mathcal{F}}_4\cup Ext{\mathcal{F}}_4^{\left(l\right)}\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\\ \hfill \le \frac{{\displaystyle \sum _{x_3\backslash {\mathcal{G}}_2{\mathcal{F}}_3}{\mathsf{Num}}_4^{\left(l\right)}(A_{l+1}\oplus k_3\oplus x_3)}}{N},\end{array}$$

  where ${\mathsf{Num}}_4^{\left(l\right)}\left(y_4\right)=\left|\{x_4\backslash Dom{\mathcal{F}}_4\cup Ext{\mathcal{F}}_4^{\left(i\right)}:{\mathit{F}}_4\left(x_4\right)=y_4\}\right|.$
• Subcase 3.2:$x_3\backslash Dom{\mathcal{F}}_3,and{x}_4\backslash Dom{\mathcal{F}}_4.$ Define a key-dependent value:

  $${\mathsf{Num}}_{3,4}^{-}(k,A)\stackrel{def}{=}\left|\{((x_3,y_3),(x_4,y_4))\backslash {\mathcal{Q}}_{F_3}\times {\mathcal{Q}}_{F_4}:k_3=A\oplus y_4\oplus x_3\}\right|.$$
  On account of the uniformity of $k_3$ in N choices, we have

  $$\begin{array}{c}\hfill {\mathbb{E}}_k\left[\sum _{x_3\backslash Dom{\mathcal{F}}_3,x_4\backslash Dom{\mathcal{F}}_4}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\right]\\ \hfill \le \frac{{\mathbb{E}}_k\left[{\mathsf{Num}}_{3,4}^{-}(k,A_{l+1})\right]}{N}\le \frac{q_f^2}{N^2}.\end{array}$$
• Subcase 3.3:$x_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3,and{x}_4\backslash Dom{\mathcal{F}}_4.$ By definition, we write

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3\\ x_4\backslash Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & =\sum _{\begin{array}{c}i=1,\dots ,l\\ x_4\backslash Dom{\mathcal{F}}_4\end{array}}{\mathsf{sgn}}^{\prime }\left(i\right)·\mathrm{Pr}\left[\mathsf{Coll}(x_3^{\left(i\right)},x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right],\hfill \end{array}$$

  where $x_3^{\left(i\right)}=k_3\oplus Y_i$, and for i-th tuple $(t,R_i{X}_i,A_i{S}_i)\backslash {\mathcal{G}}_4$, we have $Y_i=R_i\oplus {\mathit{F}}_2(H_{k_2}\left(t\right)\oplus X_i)$. In addition, ${\mathsf{sgn}}^{\prime }\left(i\right)=1$ if and only if i is the smallest index that satisfies $x_3^{\left(i\right)}\backslash Ext{\mathcal{F}}_3^{\left(i\right)}\setminus Dom{\mathcal{F}}_3$, since $x_3^{\left(i\right)}\notin Ext{\mathcal{F}}_3^{(i-1)}$. Similar with Subcase 2.3,

  (i)

  ${\mathsf{E}}_i$ fits into Case 1

  We have

  $$\mathrm{Pr}\left[\mathsf{Coll}(x_3^{\left(i\right)},x_4)|{\mathsf{E}}_{i}fitsinto\mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}1\wedge {\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F)\right]\le \frac{1}{N^2}.$$

  (ii)

  ${\mathsf{E}}_i$ fits into Case 3

  We have $A_{l+1}\oplus y_4=A_i\oplus y_4^{\left(i\right)}$. Therefore,

  $$\begin{array}{c}\hfill \mathrm{Pr}\left[\mathsf{Coll}(x_3^{\left(i\right)},x_4)|{\mathsf{E}}_{i}fitsinto\mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}3\wedge {\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F)\right]\\ \hfill \le \frac{{\mathsf{Num}}_4^{\left(l\right)}(A_{l+1}\oplus y_4\oplus A_i)}{N^2}.\end{array}$$

  From above with the similar calculation, we have

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3\\ x_4\backslash Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & \le \sum _{x_4\backslash Dom{\mathcal{F}}_4}\sum _{i=,\dots ,l}{\mathsf{sgn}}^{\prime }\left(i\right)·\frac{{\mathsf{Num}}_4^{\left(l\right)}(A_{l+1}\oplus y_4\oplus A_i)}{N^2}\le \frac{q_f(q_f+q_e)}{N^2}.\hfill \end{array}$$
• Subcase 3.4:$x_3\backslash Dom{\mathcal{F}}_3,and{x}_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4.$ By definition, we write

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Dom{\mathcal{F}}_3\\ x_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & =\sum _{\begin{array}{c}{x}_4\backslash Dom{\mathcal{F}}_4\\ i=1,\dots ,l\end{array}}\mathsf{sgn}\left(i\right)·\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4^{\left(i\right)})|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right],\hfill \end{array}$$
  It also holds $\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4^{\left(i\right)})|{\mathsf{E}}_{i}fitsinto\mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}1\wedge {\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\le \frac{1}{N^2}$. When ${\mathsf{E}}_i$ fits into Case 2, due to $A_{l+1}\oplus A_i=x_3^{\left(i\right)}\oplus x_3$, we have
  $\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4^{\left(i\right)})|{\mathsf{E}}_{i}fitsinto\mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}2\wedge {\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]=\frac{1}{N^2}$.
  Therefore,

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Dom{\mathcal{F}}_3\\ x_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\le \frac{q_f{e}_4^{\left(l\right)}}{N^2}\le \frac{q_f{q}_e}{N^2}.\hfill \end{array}$$
• Subcase 3.5:$x_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3,and{x}_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4.$ Similar to Subcase 2.5, we have

  $$\begin{array}{cc}\hfill & \sum _{\begin{array}{c}{x}_3\backslash Ext{\mathcal{F}}_3^{\left(l\right)}\setminus Dom{\mathcal{F}}_3\\ x_4\backslash Ext{\mathcal{F}}_4^{\left(l\right)}\setminus Dom{\mathcal{F}}_4\end{array}}\mathrm{Pr}\left[\mathsf{Coll}(x_3,x_4)|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\hfill \\ \hfill & \le \sum _{j=1,\dots ,l}\sum _{i=1,\dots ,l}\frac{{\mathsf{Num}}_4^{\left(l\right)}(A_{l+1}\oplus y_4\oplus A_j)}{N^2}\hfill \\ \hfill & \le \sum _{j=1,\dots ,l}\frac{q_f+e_4^{\left(l\right)}}{N^2}\le \frac{q_e(q_f+q_e)}{N^2}.\hfill \end{array}$$
• Summing over all five subcases: We have

  $$\begin{array}{cc}\hfill & {\mathbb{E}}_k\left[\mathrm{Pr}\left[{\mathsf{E}}_{l+1}\wedge \mathrm{C}\mathrm{A}\mathrm{S}\mathrm{E}3|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\right]\hfill \\ \hfill & \ge \left(\frac{q_f+e_4^{\left(l\right)}}{N}-\frac{{\sum }_{x_3\backslash {\mathcal{G}}_2{\mathcal{F}}_3}{\mathsf{Num}}_4^{\left(l\right)}(A_{l+1}\oplus k_3\oplus x_3)}{N}-\frac{(2q_f+q_e)(q_f+q_e)}{N^2}\right)\frac{1}{N^2}.\hfill \end{array}$$

Appendix A.1.4. Conclusions of ${\mathsf{E}}_{{\mathcal{G}}_1}$

Summing over all the three cases:

$$\begin{array}{cc}\hfill & {\mathbb{E}}_k\left[\mathrm{Pr}\left[{\mathsf{E}}_{l+1}|{\mathsf{E}}_l\wedge \dots \wedge {\mathsf{E}}_1\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]\right]\hfill \\ \hfill & \ge (\left(1-\frac{q_f+e_3^{\left(l\right)}+\left|{\mathcal{G}}_2{\mathcal{F}}_3\right|}{N}\right)\left(1-\frac{q_f+e_4^{\left(l\right)}+\left|{\mathcal{G}}_3{\mathcal{F}}_4\right|}{N}\right)\hfill \\ \hfill & +\frac{2q_f+e_3^{\left(l\right)}+e_4^{\left(l\right)}}{N}-\frac{q_f^2}{N^2}-\frac{2(2q_f+q_e)(q_f+q_e)}{N^2}\hfill \\ \hfill & -\frac{1}{N}\sum _{x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4}{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus k_4\oplus x_4)-\frac{1}{N}\sum _{x_3\backslash {\mathcal{G}}_2{\mathcal{F}}_3}{\mathsf{Num}}_4^{\left(l\right)}(A_{l+1}\oplus k_3\oplus x_3))\frac{1}{N^2}.\hfill \end{array}$$

We denote

$$\begin{array}{c}\hfill B_l=\frac{1}{N}\left(\sum _{x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4}{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus k_4\oplus x_4)+\sum _{x_3\backslash {\mathcal{G}}_2{\mathcal{F}}_3}{\mathsf{Num}}_4^{\left(l\right)}(A_{l+1}\oplus k_3\oplus x_3)\right),\end{array}$$

$|{\mathcal{G}}_2{\mathcal{F}}_3|\le |{\mathcal{G}}_2|={\beta }_1$, $|{\mathcal{G}}_3{\mathcal{F}}_4|\le |{\mathcal{G}}_3|={\beta }_2$, and $|{\mathcal{G}}_1|\le q_e$. Then it holds

$$\begin{array}{cc}\hfill & {\mathbb{E}}_k\left[\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_1}|\mathit{F}⊢{\mathcal{Q}}_F\right]\right]\hfill \\ \hfill & {\displaystyle \ge \prod _{l=0}^{|{\mathcal{G}}_1|-1}\left(1-\frac{q_f^2}{N^2}-\frac{2q_e(2q_f+q_e)(q_f+q_e)}{N^2}-\frac{|{\mathcal{G}}_2{\mathcal{F}}_3|+|{\mathcal{G}}_3{\mathcal{F}}_4|}{N}-B_l\right)·\frac{1}{N^{2|{\mathcal{G}}_1|}}}\hfill \\ \hfill & \ge \left(1-\frac{q_e{q}_f^2}{N^2}-\frac{2q_e(2q_f+q_e)(q_f+q_e)}{N^2}-\frac{q_e({\beta }_1+{\beta }_2)}{N}-\sum _{l=0}^{q_e-1}{B}_l\right)·\frac{1}{N^{2|{\mathcal{G}}_1|}}.\hfill \end{array}$$

Secondly, we consider ${\displaystyle \sum _{l=0}^{q_e-1}{B}_l}$. By definition, we have

$$\begin{array}{c}\hfill {\displaystyle \sum _{y_3\backslash {\{0,1\}}^n}{\mathsf{Num}}_3^{\left(l\right)}\left(y_3\right)=q_f+e_3^{\left(l\right)}\le q_f+q_e}\\ \hfill {\displaystyle \sum _{y_4\backslash {\{0,1\}}^n}{\mathsf{Num}}_4^{\left(l\right)}\left(y_4\right)=q_f+e_4^{\left(l\right)}\le q_f+q_e.}\end{array}$$

Thus

$$\begin{array}{c}\hfill {\displaystyle \sum _{l=0}^{q_e-1}\sum _{x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4}{\mathsf{Num}}_3^{\left(l\right)}(X_{l+1}\oplus k_4\oplus x_4)\le \sum _{x_4\backslash {\mathcal{G}}_3{\mathcal{F}}_4}(q_f+q_e)\le (q_f+q_e){\beta }_2.}\end{array}$$

Similarly,

$$\begin{array}{c}\hfill {\displaystyle \sum _{l=0}^{q_e-1}\sum _{x_3\backslash {\mathcal{G}}_2{\mathcal{F}}_3}{\mathsf{Num}}_4^{\left(l\right)}(A_{l+1}\oplus k_3\oplus x_3)\le (q_f+q_e)\left|{\mathcal{G}}_2{\mathcal{F}}_3\right|\le (q_f+q_e){\beta }_1.}\end{array}$$

Finally, we have the upper bound

$$\begin{array}{cc}\hfill {\mathbb{E}}_k\left[\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_1}|\mathit{F}⊢{\mathcal{Q}}_F\right]\right]& \ge (1-\frac{q_e{q}_f^2}{N^2}-\frac{2q_e(2q_f+q_e)(q_f+q_e)}{N^2}\hfill \\ \hfill & -\frac{(q_f+2q_e)({\beta }_1+{\beta }_2)}{N})\frac{1}{N^{2|{\mathcal{G}}_1|}}.\hfill \end{array}$$

(A1)

Appendix A.2. $\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}|{\mathsf{E}}_{{\mathcal{G}}_1}\wedge \mathit{F}⊢{\mathcal{G}}_F\right].$

Next, we analyze the event ${\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}$, we firstly focus on ${\mathsf{E}}_{{\mathcal{G}}_2}$. Define the “bad” event on this condition, we denote by ${\mathsf{Bad}}_1\left({\mathit{F}}_3\right)$: there exists $(t,RX,AS)\backslash {\mathcal{G}}_2$, one of the following conditions is fulfilled:

(i)

$x_4=k_4\oplus X\oplus {\mathit{F}}_3\left(x_3\right)\backslash Dom{\mathcal{F}}_4$, where $x_3=k_3\oplus R\oplus Img{F}_2(H_{k_2}\left(t\right)\oplus X)$;

(ii)

there exists $(t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })\backslash {\mathcal{G}}_2$, such that $X\oplus {\mathit{F}}_3\left(x_3\right)=X^{\prime }\oplus {\mathit{F}}_3\left(x_3^{\prime }\right)$, where $x_3^{\prime }=k_3\oplus R^{\prime }\oplus Img{F}_2(H_{k_2}\left(t^{\prime }\right)\oplus X^{\prime })$;

(iii)

there exists $(t^{*},R^{*}{X}^{*},A^{*}{S}^{*})\backslash {\mathcal{G}}_1\cup {\mathcal{G}}_3$, such that $X\oplus {\mathit{F}}_3\left(x_3\right)=S^{*}\oplus {\mathit{F}}_5(H_{k_5}\left(t^{*}\right)\oplus A^{*})$.

We note that for each $(t,RX,AS)\backslash {\mathcal{G}}_2$, let $x_3=k_3\oplus R\oplus Img{F}_2(H_{k_2}\left(t\right)\oplus X)$, we have $x_3\notin Dom{\mathcal{F}}_3$ (for the condition of $\neg \mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)$) and $x_3\notin Ext{\mathcal{F}}_3^{|{\mathcal{G}}_1|}$ (for the analysis of ${\mathsf{E}}_{{\mathcal{G}}_1}$). Then, on the condition of ${\mathsf{E}}_{{\mathcal{G}}_1}\wedge {\mathit{F}}_3⊢{\mathcal{G}}_{{\mathit{F}}_3}$, the values of function ${\mathit{F}}_3\left(x_3\right)$ keep uniform. Thus, for $(t,RX,AS)$:

(i)

the probability of condition (i) fulfilled is at most $\frac{q_f}{N}$;

(ii)

for each $(t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })\backslash {\mathcal{G}}_2$, if the corresponding $x_3\ne x_3^{\prime }$, we have

$$\mathrm{Pr}\left[X\oplus {\mathit{F}}_3\left(x_3\right)=X^{\prime }\oplus {\mathit{F}}_3\left(x_3^{\prime }\right)\right]\le \frac{1}{N};$$

If the two tuples are distinct, i.e., $(t,RX,AS)\ne (t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })$: (a) $t\ne t^{\prime }$, $X=X^{\prime }$, and $x_3=x_3^{\prime }$, then $\mathrm{Pr}\left[X\oplus {\mathit{F}}_3\left(x_3\right)=X^{\prime }\oplus {\mathit{F}}_3\left(x_3^{\prime }\right)\right]\le \epsilon$; (b) if $t=t^{\prime }$, $X\ne X^{\prime }$, and $x_3=x_3^{\prime }$, then it must be $X\oplus {\mathit{F}}_3\left(x_3\right)\ne X^{\prime }\oplus {\mathit{F}}_3\left(x_3^{\prime }\right)$.

(iii)

for each $(t^{*},R^{*}{X}^{*},A^{*}{S}^{*})\backslash {\mathcal{G}}_1\cup {\mathcal{G}}_3$, we have

$$\mathrm{Pr}\left[X\oplus {\mathit{F}}_3\left(x_3\right)=S^{*}\oplus {\mathit{F}}_5(H_{k_5}\left(t^{*}\right)\oplus A^{*})\right]\le \frac{1}{N}.$$

Summing up the above, we have the probability of ${\mathsf{Bad}}_1\left({\mathit{F}}_3\right)$:

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[{\mathsf{Bad}}_1\left({\mathit{F}}_3\right)|{\mathsf{E}}_{{\mathcal{G}}_1}\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]& \le \frac{|{\mathcal{G}}_2|·(q_f+|{\mathcal{G}}_1|+|{\mathcal{G}}_2|+|{\mathcal{G}}_3\left|\right)}{N}+\left|{\mathcal{G}}_2\right|·\epsilon \hfill \\ \hfill & \le \frac{{\beta }_1(q_f+q_e)}{N}+{\beta }_1·\epsilon .\hfill \end{array}$$

We can see that if ${\mathsf{Bad}}_1\left({\mathit{F}}_3\right)$ does not happen, there are $|{\mathcal{G}}_2|$ values $Z_1,\dots ,Z_{|{\mathcal{G}}_2|}$ in ${\mathcal{G}}_2$ which are distinct (otherwise (ii) is fulfilled). In addition, ${\mathit{F}}_4(k_4\oplus Z_1),\dots ,{\mathit{F}}_4(k_4\oplus Z_{|{\mathcal{G}}_2|})$ are all undetermined (otherwise (i) and (iii) are fulfilled).

Moreover, at the “right” part, there are also $|{\mathcal{G}}_2|$ values $A_1,\dots ,A_{|{\mathcal{G}}_2|}$, such that ${\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_1),\dots ,{\mathit{F}}_5(H_{k_5}\left(t\right)\oplus A_{|}{\mathcal{G}}_2|)$ are also undetermined.

Therefore, the event ${\mathsf{E}}_{{\mathcal{G}}_2}$ is equivalent to ${\mathit{F}}_4$ and ${\mathit{F}}_5$ satisfying $2|{\mathcal{G}}_2|$ new equations, so the probability does not exceed $\frac{1}{N^{2|{\mathcal{G}}_2|}}$.

Similar to the analysis of ${\mathsf{E}}_{{\mathcal{G}}_2}$, we consider the event ${\mathsf{E}}_{{\mathcal{G}}_3}$. Likewise, we define the bad event ${\mathsf{Bad}}_2\left({\mathit{F}}_4\right)$ that there exists $(t,RX,AS)\backslash {\mathcal{G}}_3$, one of the following conditions is fulfilled:

(i)

$x_3=k_3\oplus A\oplus {\mathit{F}}_4\left(x_4\right)\backslash Dom{\mathcal{F}}_3$, where $x_4=k_4\oplus S\oplus Img{F}_5(H_{k_5}\left(t\right)\oplus A)$, the probability is at most $\frac{q_f}{N}$;

(ii)

there exists $(t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })\backslash {\mathcal{G}}_3$, such that $A\oplus {\mathit{F}}_4\left(x_4\right)=A^{\prime }\oplus {\mathit{F}}_4\left(x_4^{\prime }\right)$, where $x_4^{\prime }=k_4\oplus S^{\prime }\oplus Img{F}_5(H_{k_5}\left(t^{\prime }\right)\oplus A^{\prime })$, and the probability is at most $\frac{|{\mathcal{G}}_3|}{N}+\epsilon$;

(iii)

there exists $(t^{*},R^{*}{X}^{*},A^{*}{S}^{*})\backslash {\mathcal{G}}_1\cup {\mathcal{G}}_2$, such that $A\oplus {\mathit{F}}_4\left(x_4\right)=R^{*}\oplus {\mathit{F}}_2(H_{k_2}\left(t^{*}\right)\oplus X^{*})$, and the probability is at most $\frac{|{\mathcal{G}}_1|+|{\mathcal{G}}_2|}{N}$.

Thus, we have the probability of ${\mathsf{Bad}}_2\left({\mathit{F}}_4\right)$:

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[{\mathsf{Bad}}_2\left({\mathit{F}}_4\right)|{\mathsf{E}}_{{\mathcal{G}}_1}\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]& \le \frac{|{\mathcal{G}}_3|·(q_f+|{\mathcal{G}}_1|+|{\mathcal{G}}_2|+|{\mathcal{G}}_3\left|\right)}{N}+\left|{\mathcal{G}}_3\right|·\epsilon \hfill \\ \hfill & \le \frac{{\beta }_2(q_f+q_e)}{N}+{\beta }_2·\epsilon .\hfill \end{array}$$

Same as ${\mathsf{E}}_{{\mathcal{G}}_2}$, the event ${\mathsf{E}}_{{\mathcal{G}}_3}$ is equivalent to ${\mathit{F}}_2$ and ${\mathit{F}}_3$ satisfying $2|{\mathcal{G}}_3|$ new equations.

Therefore, on the condition of ${\mathsf{E}}_{{\mathcal{G}}_1}\wedge \mathit{F}⊢{\mathcal{Q}}_F$, we have

$$\begin{array}{cc}\hfill \mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}|{\mathsf{E}}_{{\mathcal{G}}_1}\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]& \ge (1-\mathrm{Pr}\left[{\mathsf{Bad}}_1\left({\mathit{F}}_3\right)\right]-\mathrm{Pr}\left[{\mathsf{Bad}}_2\left({\mathit{F}}_4\right)\right])\hfill \\ \hfill & ·\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}|\neg {\mathsf{Bad}}_1\left({\mathit{F}}_3\right)\wedge \neg {\mathsf{Bad}}_1\left({\mathit{F}}_4\right)\right]\hfill \\ \hfill & \ge \left(1-\frac{({\beta }_1+{\beta }_2)(q_f+q_e)}{N}-({\beta }_1+{\beta }_2)\epsilon \right)\hfill \\ \hfill & ·\frac{1}{N^{2\left(\right|{\mathcal{G}}_2|+|{\mathcal{G}}_3\left|\right)}}.\hfill \end{array}$$

(A2)

Appendix A.3. $\mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_4}|{\mathsf{E}}_{{\mathcal{G}}_1}\wedge {\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}\wedge \mathit{F}⊢{\mathcal{Q}}_F\right]$

Thirdly, we analyze the event ${\mathsf{E}}_{{\mathcal{G}}_4}$. By definition, for arbitrary $(t,RX,AS)\backslash {\mathcal{G}}_4$, we denote $x_2=H_{k_2}\left(t\right)\oplus X$ and $x_5=H_{k_5}\left(t\right)\oplus A$ such that $x_2\notin Dom{\mathcal{F}}_2$ and $x_5\notin Dom{\mathcal{F}}_5$. Furthermore, on the condition of ${\mathsf{E}}_{{\mathcal{G}}_1}\wedge {\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}$, and the conditions of bad event $\mathsf{Bad}({\mathit{F}}_1,{\mathit{F}}_6)$, the two values of functions ${\mathit{F}}_2\left(x_2\right)$ and ${\mathit{F}}_5\left(x_5\right)$ must be uniform and undetermined.

We also define the bad event ${\mathsf{Bad}}_3({\mathit{F}}_2,{\mathit{F}}_5)$ that there exists $(t,RX,AS)\backslash {\mathcal{G}}_4$, such that $x_2$ and $x_5$ fulfill one of following conditions:

• left part: consider ${\mathit{F}}_2\left(x_2\right)$:

  (i)

  $x_3=k_3\oplus R\oplus {\mathit{F}}_2\left(x_2\right)\backslash Dom{\mathcal{F}}_3$, on account of the randomness of ${\mathit{F}}_2\left(x_2\right)$, for each $(t,RX,AS)\backslash {\mathcal{G}}_4$, the probability of which is at most $\frac{q_f}{N}$;

  (ii)

  there exists $(t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })\backslash {\mathcal{G}}_1\cup {\mathcal{G}}_2\cup {\mathcal{G}}_3$, such that $R\oplus {\mathit{F}}_2\left(x_2\right)=R^{\prime }\oplus {\mathit{F}}_2(H_{k_2}$$\left(t^{\prime }\right)\oplus X^{\prime })$. For distinct two tuples in ${\mathcal{G}}_4$, (a) it might be $t\ne t^{\prime }$, such that Y collides with some “previously-ly determined” $Y^{\prime }$, the probability of which is $\epsilon$; (b) if $t=t^{\prime }$ but $X\ne X^{\prime }$ (it can not cannot be $R=R^{\prime }$), by the randomness of ${\mathit{F}}_2\left(x_2\right)$, for each $(t,RX,AS)\backslash {\mathcal{G}}_4$, the upper bound of the probability is $\frac{|{\mathcal{G}}_1|+|{\mathcal{G}}_2|+|{\mathcal{G}}_3|}{N}+\epsilon \le \frac{q_e}{N}+\epsilon$.

• right part: consider ${\mathit{F}}_5\left(x_5\right)$, similar to the above:

  (i)

  $k_4\oplus S\oplus {\mathit{F}}_5\left(x_5\right)\backslash Dom{\mathcal{F}}_4$, for each $(t,RX,AS)\backslash {\mathcal{G}}_4$, the probability of which is at most $\frac{q_f}{N}$;

  (ii)

  there exists another distinct $(t^{\prime },R^{\prime }{X}^{\prime },A^{\prime }{S}^{\prime })\backslash {\mathcal{G}}_1\cup {\mathcal{G}}_2\cup {\mathcal{G}}_3$, such that $S\oplus {\mathit{F}}_5\left(x_5\right)=S^{\prime }\oplus {\mathit{F}}_5(H_{k_5}\left(t^{\prime }\right)\oplus A^{\prime })$. For each $(t,RX,AS)\backslash {\mathcal{G}}_4$, the upper bound of the probability is $\frac{|{\mathcal{G}}_1|+|{\mathcal{G}}_2|+|{\mathcal{G}}_3|}{N}+\epsilon \le \frac{q_e}{N}+\epsilon$.

Thus, denote $|{\mathcal{G}}_4|={\beta }_3$, we have

$$\begin{array}{c}\hfill \mathrm{Pr}\left[{\mathsf{E}}_{{\mathcal{G}}_4}|{\mathsf{E}}_{{\mathcal{G}}_1}\wedge {\mathsf{E}}_{{\mathcal{G}}_2}\wedge {\mathsf{E}}_{{\mathcal{G}}_3}\wedge \mathit{F}⊢{\mathcal{G}}_F\right]\ge \left(1-\mathrm{Pr}\left[{\mathsf{Bad}}_3({\mathit{F}}_2,{\mathit{F}}_5)\right]\right)·\frac{1}{N^{2|{\mathcal{G}}_4|}}\\ \hfill \ge \left(1-\frac{2{\beta }_3(q_f+q_e)}{N}-2{\beta }_3\epsilon \right)·\frac{1}{N^{2|{\mathcal{G}}_4|}}.\end{array}$$

(A3)