Abstract
In the presence of appropriate non-minimal couplings between a scalar field and the curvature squared Gauss–Bonnet (GB) term, compact objects such as neutron stars and black holes (BHs) can spontaneously scalarize, becoming a preferred vacuum. Such strong gravity phase transitions have attracted considerable attention recently. The non-minimal coupling functions that allow this mechanism are, however, always postulated ad hoc. Here, we point out that families of such functions naturally emerge in the context of Higgs–Chern–Simons gravity models, which are found as dimensionally descents of higher dimensional, purely topological, Chern–Pontryagin non-Abelian densities. As a proof of concept, we study spherically symmetric scalarized BH solutions in a particular Einstein-GB-scalar field model, whose coupling is obtained from this construction, pointing out novel features and caveats thereof. The possibility of vectorization is also discussed, since this construction also originates vector fields non-minimally coupled to the GB invariant.
1. Introduction
The subject of ’spontaneous scalarization’ of asymptotically flat black holes (BHs) has received considerable interest over the last several years. This phenomenon occurs due to non-minimal couplings in the scalar field action, which allows for circumventing well-known no-hair theorems [1].
The typical non-minimal coupling is between a real scalar field and some source term ; it triggers a repulsive gravitational effect, via an effective tachyonic mass for . As a result, the General Relativity (GR) BH solutions are unstable against scalar perturbations in regions where the source term is significant, leading to BH scalar hair growth.
Following [2], let us briefly review this mechanism, restricting to spacetime dimensions. The starting point here is the action for the scalar sector, which has a generic form
with the coupling function, a coupling constant, while the source term generically depends on some extra-matter field(s) and on the metric tensor . The corresponding equation of motion for the scalar field reads
An essential feature of a model allowing for scalarization is the existence of a fundamental solution of the above equation,
providing the ’ground state’ of the scalar model (’Ground state’ is intended to mean an equilibrium solution, which is not necessarily stable). As a result, the usual GR solutions (with ) also solve the considered model (which consists of (1) supplemented with terms for gravity and matter field(s) ), being the fundamental solutions of the model.
Apart from the ground state, the model possesses a second set of solutions, with a nontrivial scalar field—the scalarized BHs. Moreover, usually (there are exceptions for special coupling functions; in some models, the scalarized BHs do not emerge as an instability of the fundamental solutions [3].) they are smoothly connected with the fundamental set, which is approached for . Then, at the linear level, spontaneous scalarization manifests itself as a tachyonic instability triggered by a negative effective mass squared of the scalar field.
Around the ground state, the coupling function possesses the following expression: (with )
Then, the linearized form of Equation (2) (i.e., with a small-) is:
There are time independent solutions (bound states) of the above equation describing scalar clouds: for appropriate choices of the tachyonic condition () can be satisfied for a specific (discrete) set of backgrounds, as specified e.g., by their global charge(s). The onset of the instability is marked by such bound states. The backreacting continuation of the scalar clouds results in scalarized BHs.
Various choices of the source term have been considered in the literature. In the context of this work, of special interest is the case of geometric scalarization, with
the Gauss–Bonnet (GB) invariant, a choice which allows for the scalarization of vacuum Schwarzschild BH (we recall that in this case, with M being the BH mass). This model has been extensively studied, starting with [4,5,6,7], where the first examples of scalarized BHs resulting from this type of mechanism have been reported. Further work includes the study of scalarized BHs in various extensions of the initial framework [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24] and the investigation of solutions’ stability [25,26,27,28]; furthermore, partial analytical results are reported in Refs. [29,30,31,32], while scalarized, rotating BHs are studied in [33,34,35,36,37,38,39].
The explicit form of the coupling function does not appear for be important for the existence of scalarized solutions (although it impacts their properties), as long as the conditions discussed above are satisfied. For example, the results in [4] are found for , while Ref. [5], considers a coupling function .
To the best of our knowledge, a common feature of models allowing for BH scalarization is that the origin of the term in (1), and, in particular, the choice of the coupling function is ad hoc, missing a well motivated origin (The coupling function naturally appears in the string theory context, when including first-order corrections (with the dilaton field). This choice, however, does not allow for BH scalarization, the condition (3) not being satisfied for any finite . Despite this fact, some features found for scalarized BHs occur also in this case, a relevant example being the appearance of repulsive effects for static, spherically symmetric solutions [40]). The main purpose of this work is the study of the basic properties of the BH solutions in a model where the interaction term emerges naturally from a Higgs–Chern–Simons gravity (HCSG), originally proposed in [41,42]. The corresponding expression of the coupling function is
The field here is a Higgs-like scalar field, being a relic of a Yang–Mills (YM) connection in higher dimensions, and approaches a nonzero value at infinity, with two discontinuous vacua at . As we shall see, the expression (7) of the coupling function allows for scalarization of Schwarzschild BHs; the basic properties of the scalarized solutions are rather similar to those in Ref. [4] (where a quadratic coupling function has been employed). However, there are also novel features; an interesting one is that scalarization occurs for both signs of the constant (which is not the case for other models with scalarized static BHs). Another interesting feature is the existence of an extension of the model with a vector field, which allows for vectorization of the generic Einstein-GB-scalar (EGBs) BHs.
This paper is organized as follows: in Section 2, we review the basic features of the model in [41], in particular its derivation starting with a Chern–Pontryagin (CP) density in dimensions. The solutions of the model are reported in Section 3. Both generic configurations (with a value of the scalar field which does not approach asymptotically the ground state) and scalarized BHs are discussed; moreover, a perturbative (analytic) solution is derived in the former case. Working in the probe limit, the solutions of an extension of the original model with an extra-vector field are also reported. We conclude with a summary and a discussion in Section 4.
2. HCS Gravity
The HCSG models in [41,42] are particular examples of gauge theories of gravity, and follow the spirit (and the general framework) in [43,44,45,46,47,48], with the usual identification of the spin-connection and the Riemann curvature with the YM connection and curvature. As a new feature, an extra-Higgs-like scalar and a vector field occur in the four dimensional action for the specific model studied in this work. For completeness, in this section, we briefly review the flavour of the results in Refs. [41,42], which proposes a general framework for the construction of such HCSG models.
The starting point in this construction is the CP density for a YM field in dimensions (),
with F the curvature 2-form. By construction, the CP density can be expressed locally as a total divergence, ().
In the usual approach, a Chern–Simons density is defined as the Dth component of , which results in a YM theory in a odd-dimensional spacetime (At no point is a metric involved in this construction; this is a topological theory). However, the approach in [41,42] (see also the Refs. [49,50] and the Appendix A of Ref. [51]) introduces an extra-step, by considering first the dimensional descent of the CP density (8) to some intermediate dimension , which can be odd or even. As usual with gauge fields, the relics of the gauge connection on the co-dimension(s) are Higgs scalar(s). The remarkable property of the resulting density (dubbed now Higgs-CP density , being given in terms of both the residual gauge field and the Higgs scalar ), is that, like the original CP density, it is also a ,
As with the definition of the usual Chern–Simons densities, the resulting HCS density in dimensions is defined as the dth component of .
For both the Chern–Simons and Higgs–Chern–Simons cases, the final step is the (standard) prescription for the passage to gravity, the spin-connection being identified with the YM connection. In the latter case, this prescription must be extended by the corresponding elements pertaining to the Higgs sector, which generically result in extra frame-vector fields, apart from the scalar field(s) [41,42]. By analogy to the standard Chern–Simons gravities (which exist in odd-dimensions only [52]), the resulting models are dubbed HCSG.
Let us exemplify the generic construction with the simplest two cases, the starting point being the CP densities (8) in dimensions. The case of interest here is , the final Higgs–Chern–Simons being defined in four dimensions, with the following Lagrangians:
these being the 5th components of the corresponding vector in (9). In addition, note that the HCP density leading to is found by considering the reduction of the CP density over a three-dimensional sphere of unit radius. In addition, the gauge group in (10) and (11) is chosen to be while the Higgs field takes its values in the orthogonal complement of in .
After the passage to gravity, the corresponding HCSG Lagrangians read [41]
The scalar ϕ and the ‘frame-vector field‘ Aa are relics of the Higgs scalar (with A2 = AμAμ The density (13) can be cast in a more useful form by dropping a total derivative term, which results in the equivalent expression (Note that ).
Note that a similar construction can also be carried out starting with a CP density in . This results, however, in much more complicated expressions of the corresponding HCSG Lagrangians.
3. The BH Solutions
The Lagrangian of the full model consists of the usual Einstein term for gravity and kinetic term for the scalar field, together with the interaction term (12) or (14).
The solutions of the model with an interaction term (12) (i.e., with a linear coupling function ) have been extensively studied in the literature (For a review of the literature together with an investigation of spinning solutions, see the recent work [53]), starting with Refs. [54,55], falling within the Horndeski class of scalar-tensor theories of gravity [56]. The results in this work show that the term naturally also occurs in this topological construction leading to HCSG models. This model is rather special, the equations of motion being invariant under the transformation (with arbitrary), which leads to a conserved current. The coupling function , however, does not allow for BH scalarization: the condition (3) is not fulfilled.
In this work, we shall focus on the interaction term (14), i.e., with a cubic coupling function as given by (7). As such, the full action of the model reads
where is the standard kinetic term for a vector field (with . Let us remark that the vector field A does not possess the gauge invariance of a Maxwell model.
The corresponding equations of motion are found by varying the action (15) with respect to the metric tensor , scalar field , and vector field . One can easily verify that solves the equations for the vector field. As such, to simplify the study, we shall restrict our study mainly to the scalar-tensor case. Some comments on the general case with can be found at the end of this section.
Setting , the scalar field possess two ground states at . In addition, let us remark that the model is invariant under the transformation
we shall restrict our study to the ground state only. An important physical consequence of the symmetry (16) is that, in contrast to other models in the literature [4,5], the scalarization of Schwarzschild BH occurs for both signs of the coupling constant .
3.1. Einstein-GB-Scalar Field BHs
Restricting our study to spherically symmetric solutions, we consider an ansatz with
This ansatz results in two first order equations for the functions and a second order equation for . There is also an extra second order constraint equation, which is used in practice to monitor the accuracy of the numerical results.
In this work, we shall consider non-extremal (The considered EGBs model is unlikely to possess regular (on and outside a horizon) extremal BH solutions. A clear indication in this direction is the absence of a generalization of the Bertotti–Robinson solution, with a metric (that is, no attractor solutions exist here). However, the situation may change for the model with an extra vector field). BHs only, with a horizon located at . At the horizon, the solution possesses a power series expansion in , that depends only on the parameters , , , and , the first terms being
The coefficient satisfies a second order algebraic equation of the form
where are non-trivial functions of and . Consequently, a real solution of (19) exists only if , a condition which translates into the following inequality:
which implies the existence of a minimal horizon size, determined by and the value of the scalar field at the horizon. As with other EGBs models, a possible interpretation of (20) is that the GB term provides a repulsive contribution, which becomes overwhelming for sufficiently small BHs, and thus prevent the existence of an event horizon.
The approximate form of the solutions in the far field reads
the essential parameters here being M (the ADM mass), and (the scalar ’charge’).
Other physical quantities of interest are found from the horizon data. These are the Hawking temperature, , and the event horizon area, ,
together with the BH entropy, which is the sum of two terms (The expression of the coupling function in (24) is
which guarantees that a scalar field in the ground state provides no contribution to the entropy, . Passing from (7) to (23) is done by adding a (pure topological) GB term to the action (15), which does not contribute to the equations of motion) [57].
In the above relation, is the Ricci scalar of the metric , induced on the spatial sections of the event horizon, H. For the employed ansatz, this results in
On the other hand, the ADM mass M and the scalar ’charge’ are determined by the far field asymptotics (21).
Finally, let us note that the equations of the model are invariant under the transformation
(with an arbitrary constant) such that only quantities invariant under (26) have a physical meaning. For example, one can work with the dimensionless quantities
such that in the GR limit.
3.1.1. Generic Solutions
The solutions of the model fall into two different classes, depending on the asymptotic value of the scalar field being unity or not. In the generic case, the scalar field does approach asymptotically the ground state, .
Let us remark that, for a small enough scalar field, one can construct a perturbative solution as a power series in the dimensionless parameter
Assuming that the horizon is still located at , one considers a generic expansion
the field equations being solved order by order in . The functions , and are polynomials in . The first few terms are simple enough, with
while the terms are too complicated to include here.
We also display the expression of the first few terms for several quantities of interest
with
and
One can verify that this solution provides a reasonable approximation for small and .
Of special interest, however, are the configurations with large values of , which are found numerically, and may form a disconnected branch from that described by the perturbative solution above. In their construction, one starts from the expansion (18) and integrate towards the system of three EGBs equations by using a standard ordinary differential equation solver. In practice, we integrate up to , such that the asymptotic limit (21) is reached with enough accuracy. Given , solutions with the right asymptotics may exist for discrete set of the shooting parameters , indexed by the node number of the scalar field. Here, we shall report the results for the most relevant case of fundamental, nodeless solutions.
Several results in this case are displayed in Figure 1 (left panel), where we show the asymptotic value of the scalar field and mass M of the solutions as a function of the scalar field value at the horizon, . One can see that the solutions exist for a finite range of (located around the ground state ), ending in critical configurations where the condition (20) fails to be satisfied (This last feature cannot be captured within a perturbative approach).
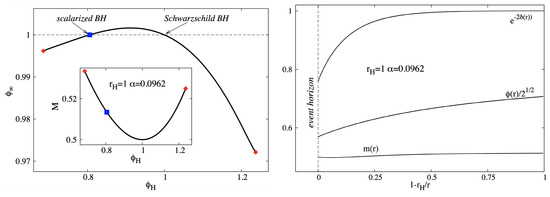
Figure 1.
Left panel: The asymptotic value of the scalar field and the mass M of the solutions are shown as a function of the value of the scalar field at the horizon . The solutions have a fixed value of the horizon radius and of the coupling constant . Right panel: The profile of a typical scalarized solution (marked with a blue square in the left panel and Figure 2) is shown as a function of the compactified coordinate .
3.1.2. Scalarized BHs
As one can see in Figure 1 (left panel), a particular configuration there has , while . This configuration is of special interest, corresponding to a scalarized BH, its profile being displayed in Figure 1 (right panel).
That solution, however, has no special features; similar configurations are found for a range of the parameters . In addition, as with the generic case, only nodeless solutions were studied so far, corresponding to the fundamental states; however, solutions with nodes exist as well, corresponding to excited EGBs configurations.
The basic properties of the scalarized BHs are rather similar to those found in [4] for a quadratic coupling function They can be summarized as follows (see Figure 2). First, these spherically symmetric BHs bifurcate from a special Schwarzschild solution supporting the scalar cloud (i.e., an infinitesimally small scalar field), with . Second, keeping the parameter constant (or, equally, the event horizon radius ), the solutions can be obtained continuously in the parameter space, forming a line, which starts from the smooth GR Schwarzschild limit (), and ends at a limiting solution. Once the limiting configuration is reached, the solutions cease to exist in the parameter space. The existence of the ’critical’ configuration can be understood from the condition (20), with the determinant vanishing at that point. Finally, as with the solutions in Ref. [4], for a given ADM mass, the entropy of the solutions is maximized by the Schwarzschild vacuum BH (although the relative difference is rather small, of order ).
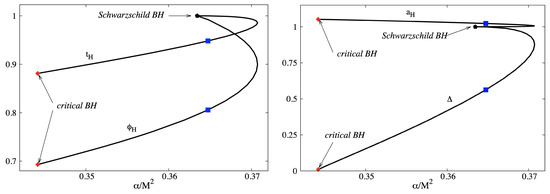
Figure 2.
Several quantities of interest are shown as a function of the ratio for the set of scalarized BHs.
3.2. The Scalar-Vector Model: Perturbative Solutions
The full model (15) contains also a vector field A, which has been consistently set to zero in the above study. The investigation of self-gravitating configurations with is a complicated task, which we do not attempt to address here. Instead, we report the results for a preliminary investigation of scalar-vector solutions in the ’probe limit’, i.e., is for a fixed Schwarzschild BH background, as given by , in the metric ansatz (17). This case is technically much simpler, while the corresponding solutions are likely to capture some of the basic properties of the full model.
Restricting again to the spherically symmetric case, we consider an ansatz with
which can be shown to be consistent. Then, when ignoring the backreaction, the problem reduces to solving the following coupled equations
The approximate form of the solutions close to the horizon reads
where and are arbitrary constants. For large-r, the first terms in a expansion of the solution reads
with , , and free parameters.
Equations (35) are solved numerically, by using the same approach as in the EGBs case. The numerical results indicate the existence, for any , of a continuum of solutions in terms of the constants , which enter the near horizon expansion (36). The asymptotic values of the scalar and vector fields depend of the input parameters , , and (note that, as expected from the structure of the equations, the vector field vanishes identically, when taking ).
Of special interest here are the configurations which approach asymptotically the vector ground state, i.e., with . In Figure 3 (left panel), we display some quantities of interest for a set of such solutions; there, the values of and are fixed, while the parameter is varied (note that we restrict again to the case of nodeless configurations). One can notice that, for a given , the solution with is found for a single value of while . The profile of a typical solution is shown in Figure 3 (right panel).
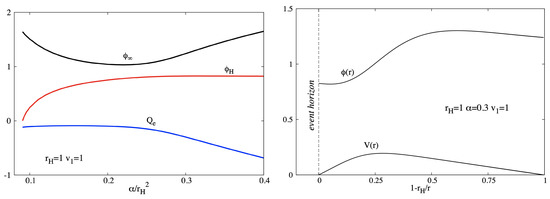
Figure 3.
Left panel: The asymptotic value of the scalar field , the value of the scalar field at the horizon and the charge of the vector field are shown as a function of the ration for solutions of the scalar-vector model in the probe limit. Right panel: The profile of a typical solution of the scalar-vector model in a fixed Schwarzschild BH background is shown as a function of the compactified coordinate . For all solutions, the vector field vanishes both at the horizon and at infinity.
The presence of probe-limit solutions with provides a hint for the existence of vectorized configurations in the full backreacting model. That is, the generic solutions above with may possess generalizations with a nonzero vector field in the bulk, and still approach asymptotically the vector ground state (See the recent work [58] for a study of vectorized BHs together with a review of the literature). We hope to return to the study of these configurations elsewhere.
4. Further Remarks
The main purpose of this work was to point out that families of EGBs models with coupling functions that permit spontaneous scalarization can be motivated by a geometric/topological construction [41,42]. This indicates a more natural embedding for GB spontaneous scalarization models; typically, the necessary coupling is simply postulated ad hoc. Moreover, as a case study, we present a preliminary investigation of the scalarized BH solutions in a particular EGBs model emerging from this sort of construction.
The models discussed herein offer both novel features and challenges. As for the novel features, the corresponding coupling function is a sum of a linear and a cubic term, with the scalar field possessing two disconnected ground states. A consequence of this fact is that the BH scalarization becomes possible for any sign of the coupling constant in front of the GB term (but around a different vacuum for each sign). As for the challenges, the cubic term (or, in general, the highest odd power term) raises the issue of the stability of the model. Moreover, the construction is not complete: it provides the GB term and the non-minimal couplings, but the resulting HCSG term has been added ad hoc to the standard Einstein-scalar field action.
The basic properties of the scalarized BHs constructed herein were found to be rather similar to those in the original work [4], where a quadratic coupling function has been employed. In particular, the scalarized BHs are entropically disfavoured over the Schwarzschild vacuum configuration. Generic solutions (with a scalar field which does not approach asymptotically the ground state) were also studied, and a perturbative solution was reported.
A preliminary investigation of the solutions of the general model in [41] with an extra-vector field has been also considered. Only the probe limit regime of the solutions (i.e., for a fixed Schwarzschild background) has been considered in this case, the results hinting towards the possible existence of ’vectorized’ BHs within the full model.
Author Contributions
The three authors contributed equally to the conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing–original draft preparation, writing–review and editing, visualization, supervision, project administration, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
The work of E.R. is supported by the Center for Research and Development in Mathematics and Applications (CIDMA) through the Portuguese Foundation for Science and Technology (FCT—Fundacao para a Ciência e a Tecnologia), references UIDB/04106/2020 and UIDP/04106/2020, and by national funds (OE), through FCT, I.P., in the scope of the framework contract foreseen in the numbers 4, 5, and 6 of the article 23 of the Decree-Law 57/2016, of 29 August, changed by Law 57/2017, of 19 July. We acknowledge support from the projects PTDC/FIS-OUT/28407/2017, CERN/FIS-PAR/0027/2019, and PTDC/FIS-AST/3041/2020. This work has further been supported by the European Union’s Horizon 2020 research and innovation (RISE) programme H2020-MSCA-RISE-2017 Grant No. FunFiCO-777740. The authors would like to acknowledge networking support by the COST Action CA16104.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Herdeiro, C.A.R.; Radu, E. Asymptotically flat black holes with scalar hair: A review. Int. J. Mod. Phys. D 2015, 24, 1542014. [Google Scholar] [CrossRef]
- Astefanesei, D.; Herdeiro, C.; Oliveira, J.; Radu, E. Higher dimensional black hole scalarization. J. High Energy Phys. 2020, 9, 186. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Herdeiro, C.A.R.; Kunz, J.; Pombo, A.M.; Radu, E. Einstein-Maxwell-scalar black holes: The hot, the cold and the bald. Phys. Lett. B 2020, 806, 135493. [Google Scholar] [CrossRef]
- Silva, H.O.; Sakstein, J.; Gualtieri, L.; Sotiriou, T.P.; Berti, E. Spontaneous scalarization of black holes and compact stars from a Gauss–Bonnet coupling. Phys. Rev. Lett. 2018, 120, 131104. [Google Scholar] [CrossRef] [PubMed]
- Doneva, D.D.; Yazadjiev, S.S. New Gauss–Bonnet black holes with curvature induced scalarization in the extended scalar-tensor theories. Phys. Rev. Lett. 2018, 120, 131103. [Google Scholar] [CrossRef]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss–Bonnet Theories. Phys. Rev. Lett. 2018, 120, 131102. [Google Scholar] [CrossRef] [PubMed]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Black-Hole Solutions with Scalar Hair in Einstein-Scalar-Gauss–Bonnet Theories. Phys. Rev. D 2018, 97, 084037. [Google Scholar] [CrossRef]
- Minamitsuji, M.; Ikeda, T. Scalarized black holes in the presence of the coupling to Gauss–Bonnet gravity. Phys. Rev. D 2019, 99, 044017. [Google Scholar] [CrossRef]
- Brihaye, Y.; Ducobu, L. Hairy black holes, boson stars and non-minimal coupling to curvature invariants. Phys. Rev. B 2019, 795, 135–143. [Google Scholar] [CrossRef]
- Macedo, C.F.B.; Sakstein, J.; Berti, E.; Gualtieri, L.; Silva, H.O.; Sotiriou, T.P. Self-interactions and Spontaneous Black Hole Scalarization. Phys. Rev. D 2019, 99, 104041. [Google Scholar] [CrossRef]
- Doneva, D.D.; Staykov, K.V.; Yazadjiev, S.S. Gauss–Bonnet black holes with a massive scalar field. Phys. Rev. D 2019, 99, 104045. [Google Scholar] [CrossRef]
- Andreou, N.; Franchini, N.; Ventagli, G.; Sotiriou, T.P. Spontaneous scalarization in generalised scalar-tensor theory. Phys. Rev. D 2019, 99, 124022, Erratum in: Phys. Rev. D 2020, 101, 109903. [Google Scholar] [CrossRef]
- Minamitsuji, M.; Ikeda, T. Spontaneous scalarization of black holes in the Horndeski theory. Phys. Rev. D 2019, 99, 104069. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Kahlen, S.; Kunz, J. Critical solutions of scalarized black holes. Symmetry 2020, 12, 2057. [Google Scholar] [CrossRef]
- Guo, H.; Kuang, X.M.; Papantonopoulos, E.; Wang, B. Topology and spacetime structure influences on black hole scalarization. arXiv 2020, arXiv:2012.11844. [Google Scholar]
- Bakopoulos, A.; Kanti, P.; Pappas, N. Large and ultracompact Gauss–Bonnet black holes with a self-interacting scalar field. Phys. Rev. D 2020, 101, 084059. [Google Scholar] [CrossRef]
- Peng, Y. Spontaneous scalarization of Gauss–Bonnet black holes surrounded by massive scalar fields. Phys. Rev. D 2020, 807, 135569. [Google Scholar] [CrossRef]
- Liu, H.S.; Lu, H.; Tang, Z.Y.; Wang, B. Black Hole Scalarization in Gauss–Bonnet Extended Starobinsky Gravity. arXiv 2020, arXiv:2004.14395. [Google Scholar]
- Cardoso, V.; Foschi, A.; Zilhao, M. Collective scalarization or tachyonization: When averaging fails. Phys. Rev. Lett. 2020, 124, 221104. [Google Scholar] [CrossRef] [PubMed]
- Ventagli, G.; Lehébel, A.; Sotiriou, T.P. Onset of spontaneous scalarization in generalized scalar-tensor theories. Phys. Rev. D 2020, 102, 024050. [Google Scholar] [CrossRef]
- Guo, H.; Kiorpelidi, S.; Kuang, X.M.; Papantonopoulos, E.; Wang, B.; Wu, J.P. Spontaneous holographic scalarization of black holes in Einstein-scalar-Gauss–Bonnet theories. Phys. Rev. D 2020, 102, 084029. [Google Scholar] [CrossRef]
- Doneva, D.D.; Staykov, K.V.; Yazadjiev, S.S.; Zheleva, R.Z. Multiscalar Gauss–Bonnet gravity: Hairy black holes and scalarization. Phys. Rev. D 2020, 102, 064042. [Google Scholar] [CrossRef]
- Heydari-Fard, M.; Sepangi, H.R. Thin accretion disk signatures of scalarized black holes in Einstein-scalar-Gauss–Bonnet gravity. arXiv 2020, arXiv:2009.13748. [Google Scholar]
- Bakopoulos, A. Black holes and wormholes in the Einstein-scalar-Gauss–Bonnet generalized theories of gravity. arXiv 2020, arXiv:2010.13189. [Google Scholar]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Radial perturbations of the scalarized Einstein-Gauss–Bonnet black holes. Phys. Rev. D 2008, 98, 084011. [Google Scholar] [CrossRef]
- Silva, H.O.; Macedo, C.F.B.; Sotiriou, T.P.; Gualtieri, L.; Sakstein, J.; Berti, E. Stability of scalarized black hole solutions in scalar-Gauss–Bonnet gravity. Phys. Rev. D 2019, 99, 064011. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Axial perturbations of the scalarized Einstein-Gauss–Bonnet black holes. Phys. Rev. D 2020, 101, 104006. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Polar quasinormal modes of the scalarized Einstein-Gauss–Bonnet black holes. Phys. Rev. D 2020, 102, 024086. [Google Scholar] [CrossRef]
- Hod, S. Spontaneous scalarization of Gauss–Bonnet black holes: Analytic treatment in the linearized regime. Phys. Rev. D 2019, 100, 064039. [Google Scholar] [CrossRef]
- Hod, S. Gauss–Bonnet black holes supporting massive scalar field configurations: The large-mass regime. Eur. Phys. J. C 2019, 79, 966. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Analytical representation for metrics of scalarized Einstein-Maxwell black holes and their shadows. Phys. Rev. D 2019, 100, 044015. [Google Scholar] [CrossRef]
- Hod, S. Onset of spontaneous scalarization in spinning Gauss–Bonnet black holes. Phys. Rev. D 2020, 102, 084060. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E. Spontaneously Scalarized Kerr Black Holes in Extended Scalar-Tensor–Gauss–Bonnet Gravity. Phys. Rev. D 2019, 123, 011101. [Google Scholar] [CrossRef]
- Collodel, L.G.; Kleihaus, B.; Kunz, J.; Berti, E. Spinning and excited black holes in Einstein-scalar-Gauss–Bonnet theory. Class. Quant. Grav. Phys. Rev. D 2020, 37, 075018. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. On the dynamics of the nonrotating and rotating black hole scalarization. arXiv 2021, arXiv:2101.03514. [Google Scholar]
- Dima, A.; Barausse, E.; Franchini, N.; Sotiriou, T.P. Spin-induced black hole spontaneous scalarization. Phys. Rev. D 2020, 125, 231101. [Google Scholar]
- Herdeiro, C.A.R.; Radu, E.; Silva, H.O.; Sotiriou, T.P.; Yunes, N. Spin-induced scalarized black holes. Phys. Rev. Lett. 2021, 126, 011103. [Google Scholar] [CrossRef]
- Berti, E.; Collodel, L.G.; Kleihaus, B.; Kunz, J. Spin-induced black-hole scalarization in Einstein-scalar-Gauss–Bonnet theory. Phys. Rev. Lett. 2021, 126, 011104. [Google Scholar] [CrossRef]
- Doneva, D.D.; Collodel, L.G.; Krüger, C.J.; Yazadjiev, S.S. Black hole scalarization induced by the spin: 2+1 time evolution. Phys. Rev. D 2020, 102, 104027. [Google Scholar] [CrossRef]
- Buonanno, A.; Gasperini, M.; Ungarelli, C. A class of nonsingular gravidilaton backgrounds. Mod. Phys. Lett. A 1997, 12, 1883–1889. [Google Scholar] [CrossRef]
- Tchrakian, D.H. Chern–Simons Gravities (CSG) and Gravitational Chern–Simons (GCS) Densities in All Dimensions. Phys. Atom. Nucl. 2018, 81, 930. [Google Scholar] [CrossRef]
- Radu, E.; Tchrakian, D.H. Gravitational Chern–Simons, and Chern–Simons Gravity in All Dimensions. Phys. Part. Nucl. Lett. 2020, 17, 753–759. [Google Scholar] [CrossRef]
- Utiyama, R. Invariant theoretical interpretation of interaction. Phys. Rev. 1956, 101, 1597–1607. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Lorentz invariance and the gravitational field. J. Math. Phys. 1961, 2, 212–221. [Google Scholar] [CrossRef]
- Witten, E. (2+1)-Dimensional Gravity as an Exactly Soluble System. Nucl. Phys. B 1988, 311, 46. [Google Scholar] [CrossRef]
- Chamseddine, A.H. Topological Gauge Theory of Gravity in Five-dimensions and All Odd Dimensions. Phys. Lett. B 1989, 233, 291. [Google Scholar] [CrossRef]
- Chamseddine, A.H. Topological gravity and supergravity in various dimensions. Nucl. Phys. B 1990, 346, 213. [Google Scholar] [CrossRef]
- Deser, S.; Jackiw, R.; Templeton, S. Topologically Massive Gauge Theories. Ann. Phys. 1982, 140, 372, reprinted in Ann. Phys. 1988, 185, 406; reprinted in Ann. Phys. 2000, 281, 409. [Google Scholar] [CrossRef]
- Tchrakian, T. Notes on Yang–Mills-Higgs monopoles and dyons on Rsup D, and Chern–Simons-Higgs solitons on Rsup D-2: Dimensional reduction of Chern–Pontryagin densities. J. Phys. A 2011, 44, 343001. [Google Scholar] [CrossRef][Green Version]
- Radu, E.; Tchrakian, T. New Chern–Simons densities in both odd and even dimensions. arXiv 2011, arXiv:1101.5068. [Google Scholar]
- Tchrakian, D.H. Higgs-and Skyrme-Chern–Simons densities in all dimensions. J. Phys. A 2015, 48, 375401. [Google Scholar] [CrossRef]
- Tchrakian, D.H. A remark on black holes of Chern–Simons gravities in 2n + 1 dimensions: n = 1, 2, 3. Int. J. Mod. Phys. A 2020, 35, 2050022. [Google Scholar] [CrossRef]
- Delgado, J.F.M.; Herdeiro, C.A.R.; Radu, E. Spinning black holes in shift-symmetric Horndeski theory. J. High Energy Phys. 2020, 4, 180. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Zhou, S.Y. Black hole hair in generalized scalar-tensor gravity. Phys. Rev. Lett. 2014, 112, 251102. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Zhou, S.Y. Black hole hair in generalized scalar-tensor gravity: An explicit example. Phys. Rev. D 2014, 90, 124063. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363. [Google Scholar] [CrossRef]
- Wald, R.M. Black hole entropy is the Noether charge. Phys. Rev. D 1993, 48, 3427. [Google Scholar] [CrossRef] [PubMed]
- Barton, S.; Hartmann, B.; Kleihaus, B.; Kunz, J. Spontaneously vectorized Einstein-Gauss–Bonnet black holes. arXiv 2021, arXiv:2103.0165. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).