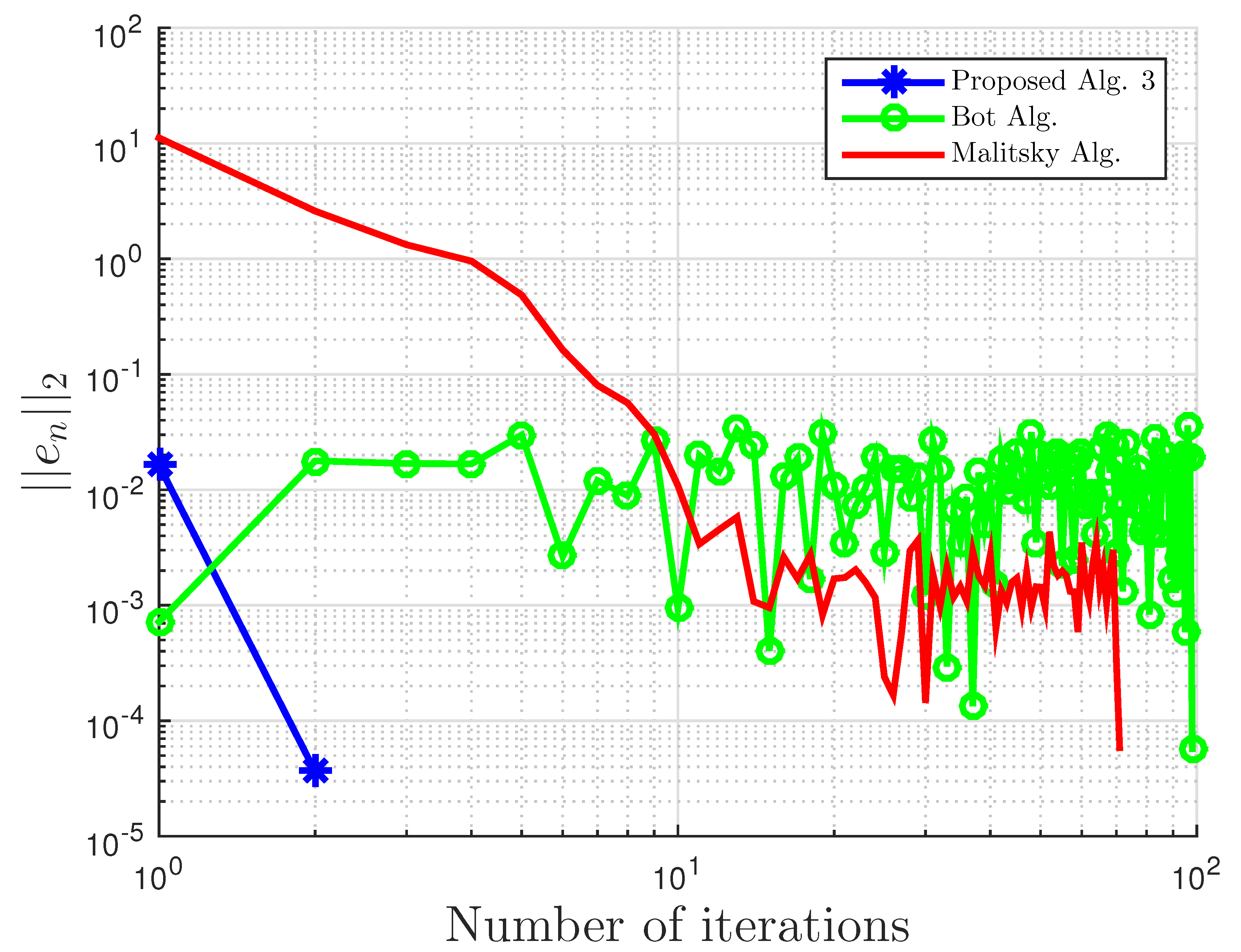
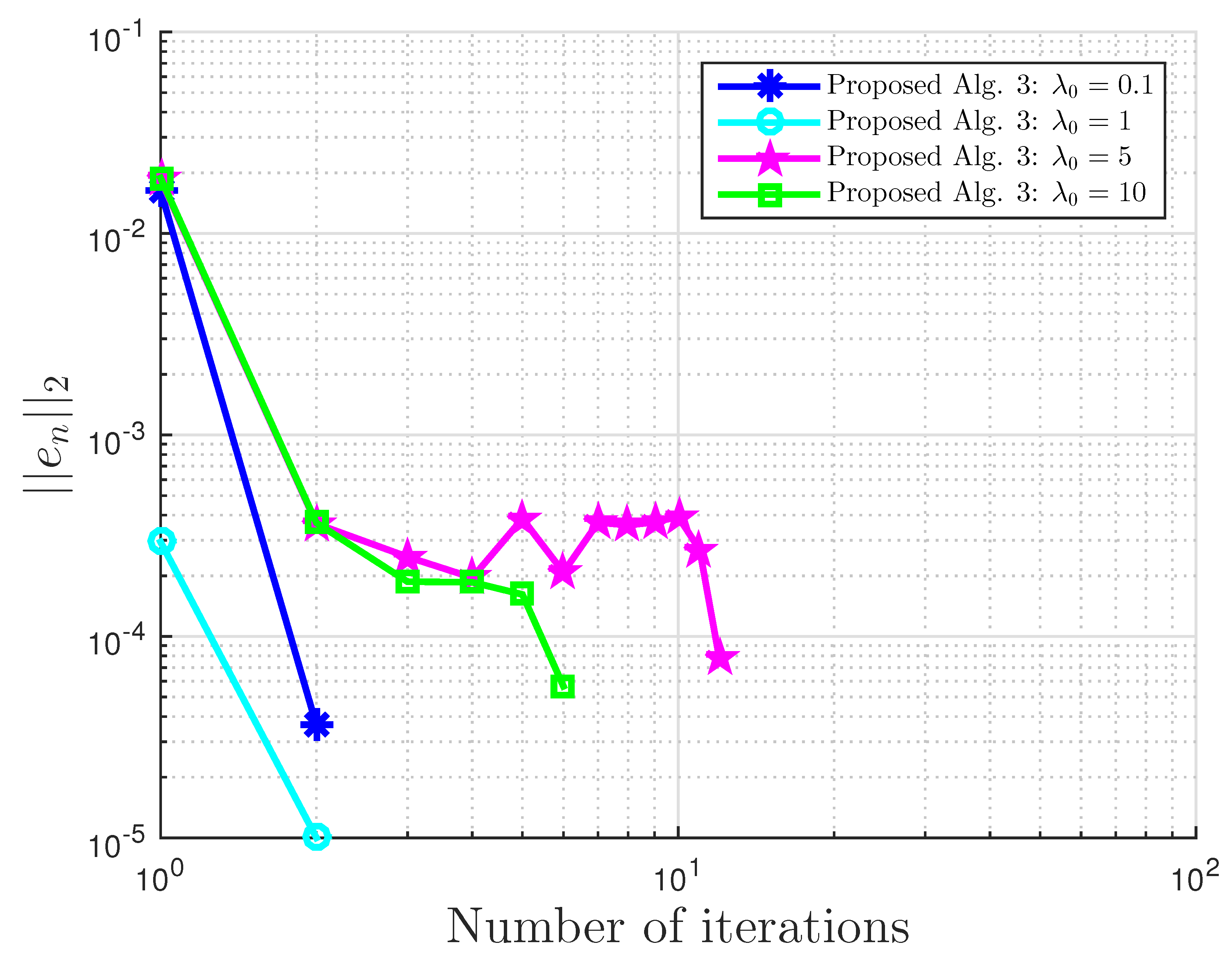
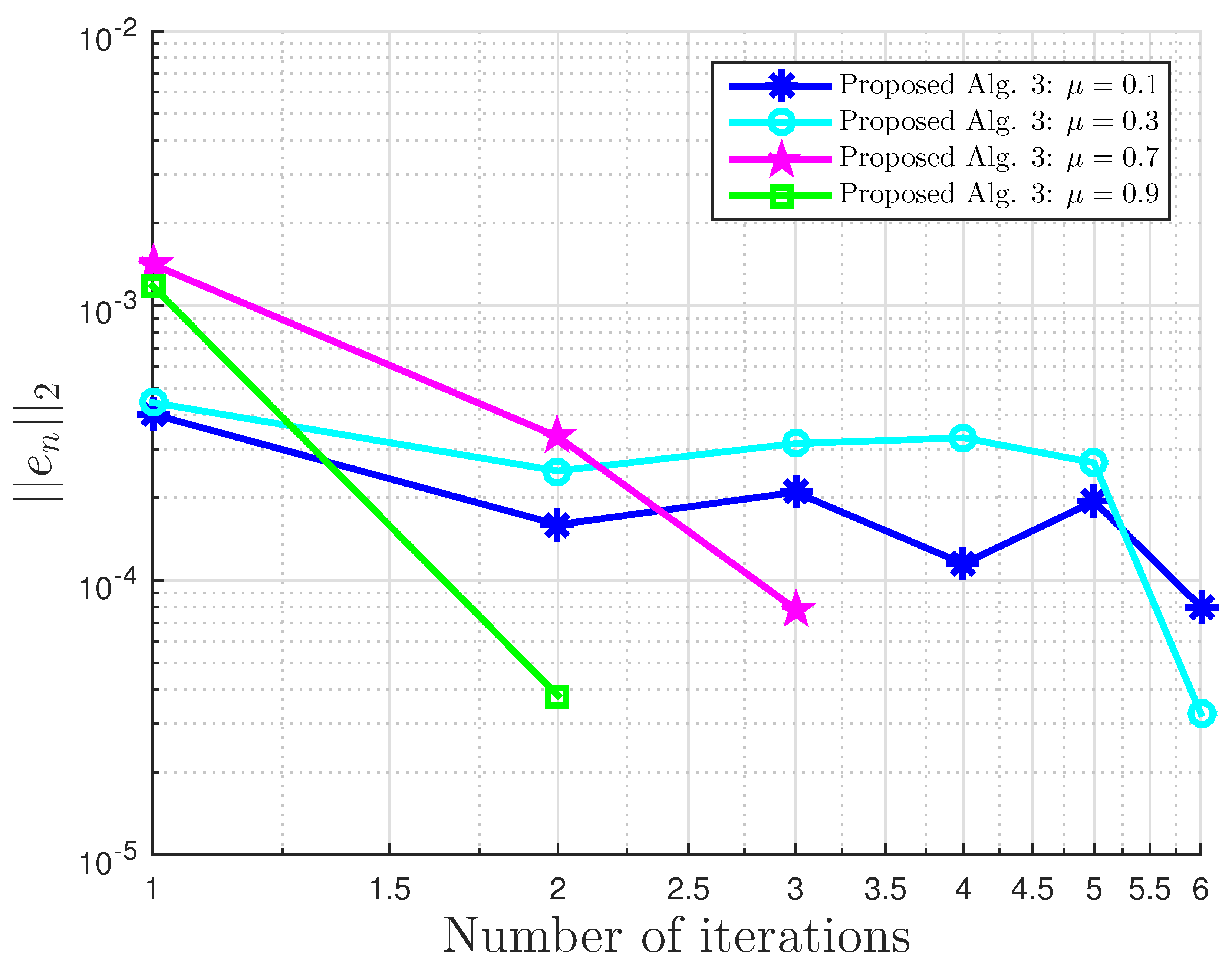
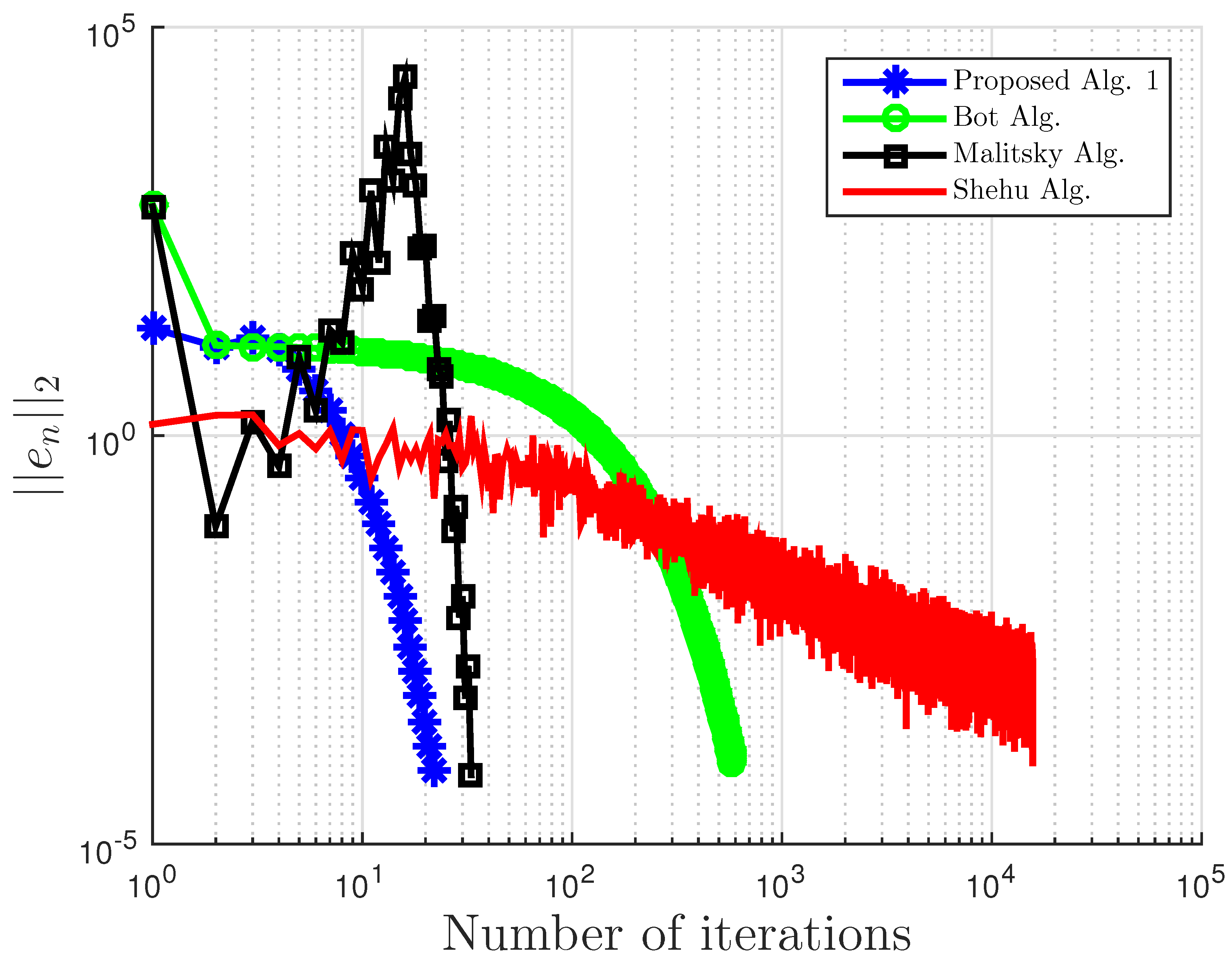
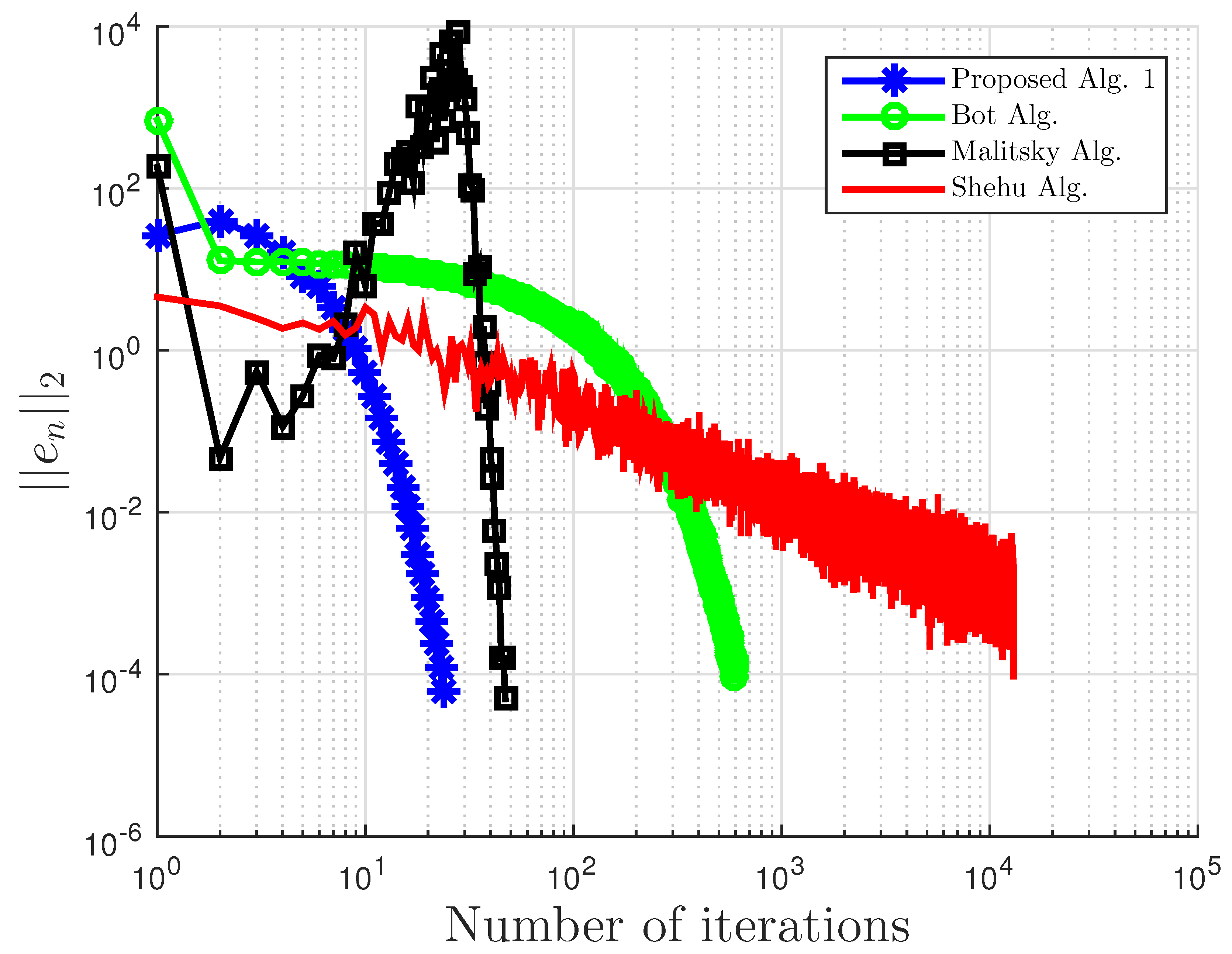
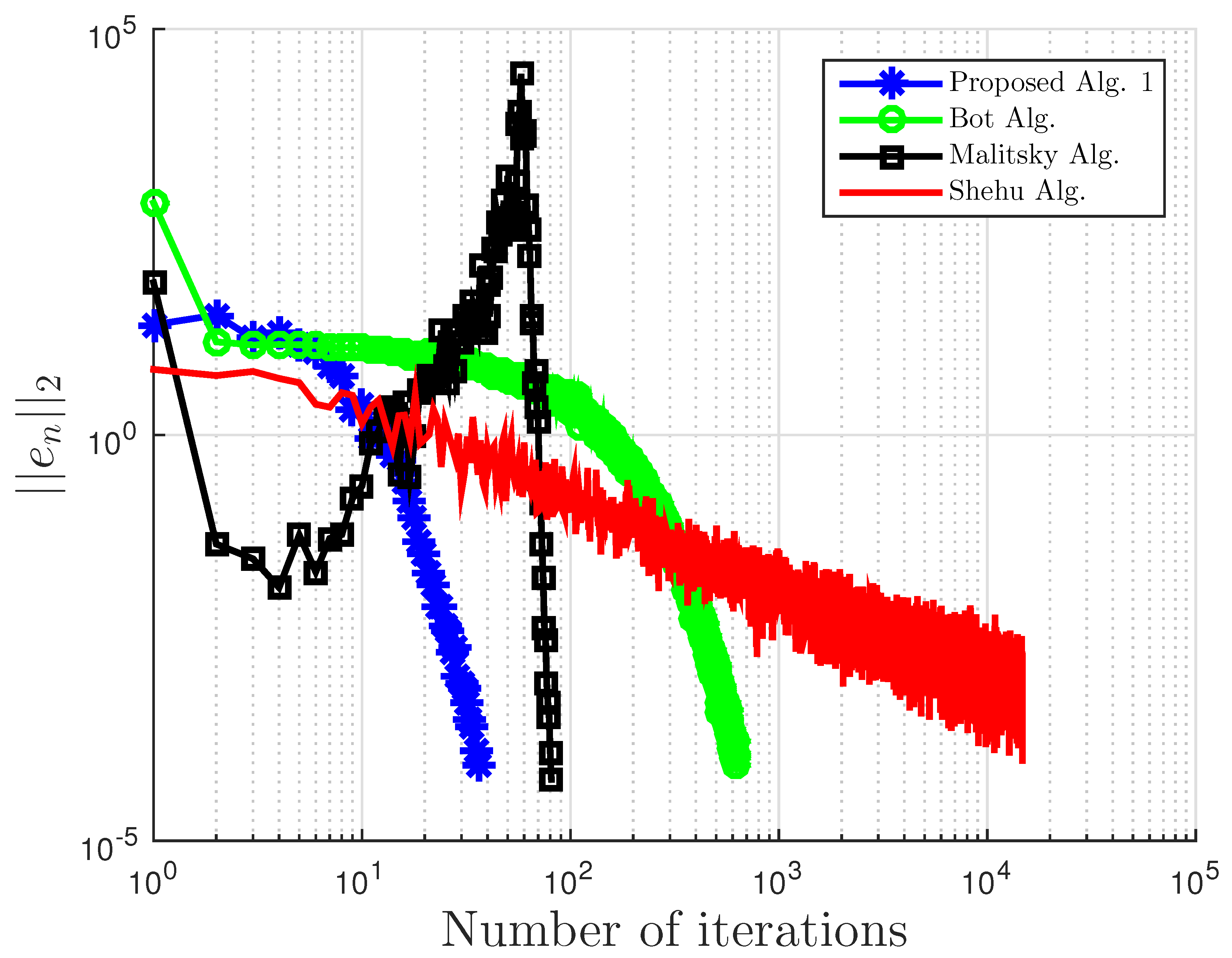
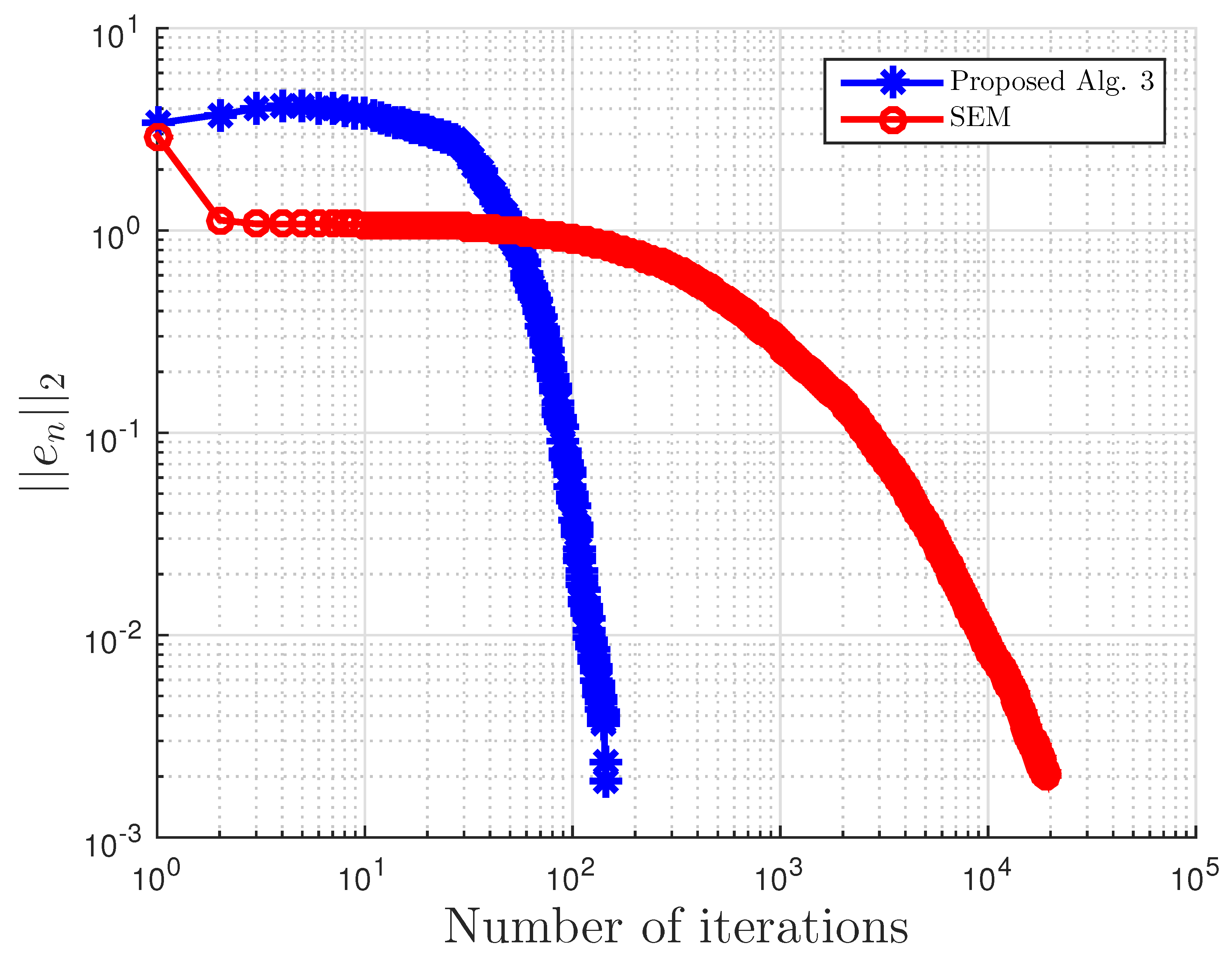
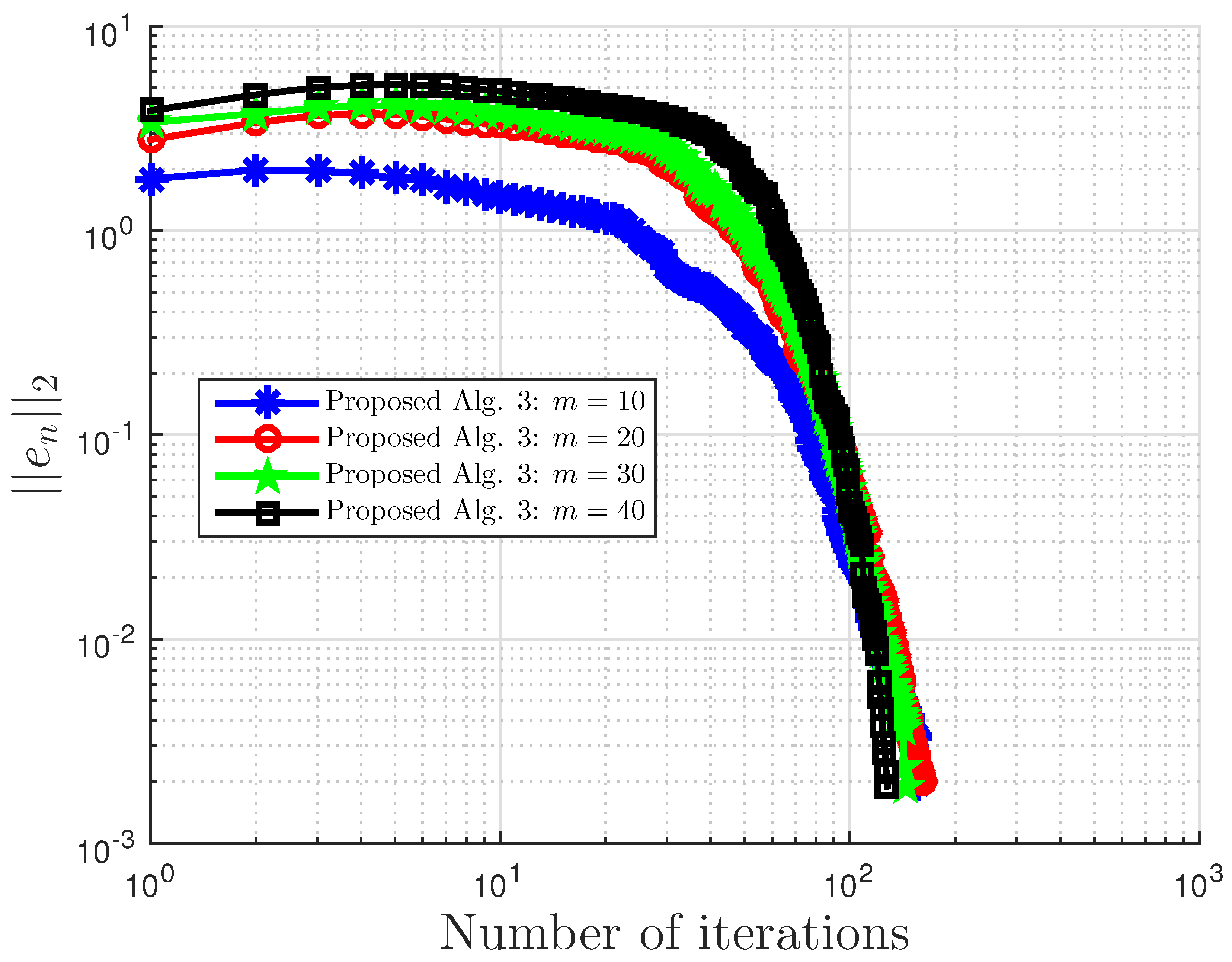
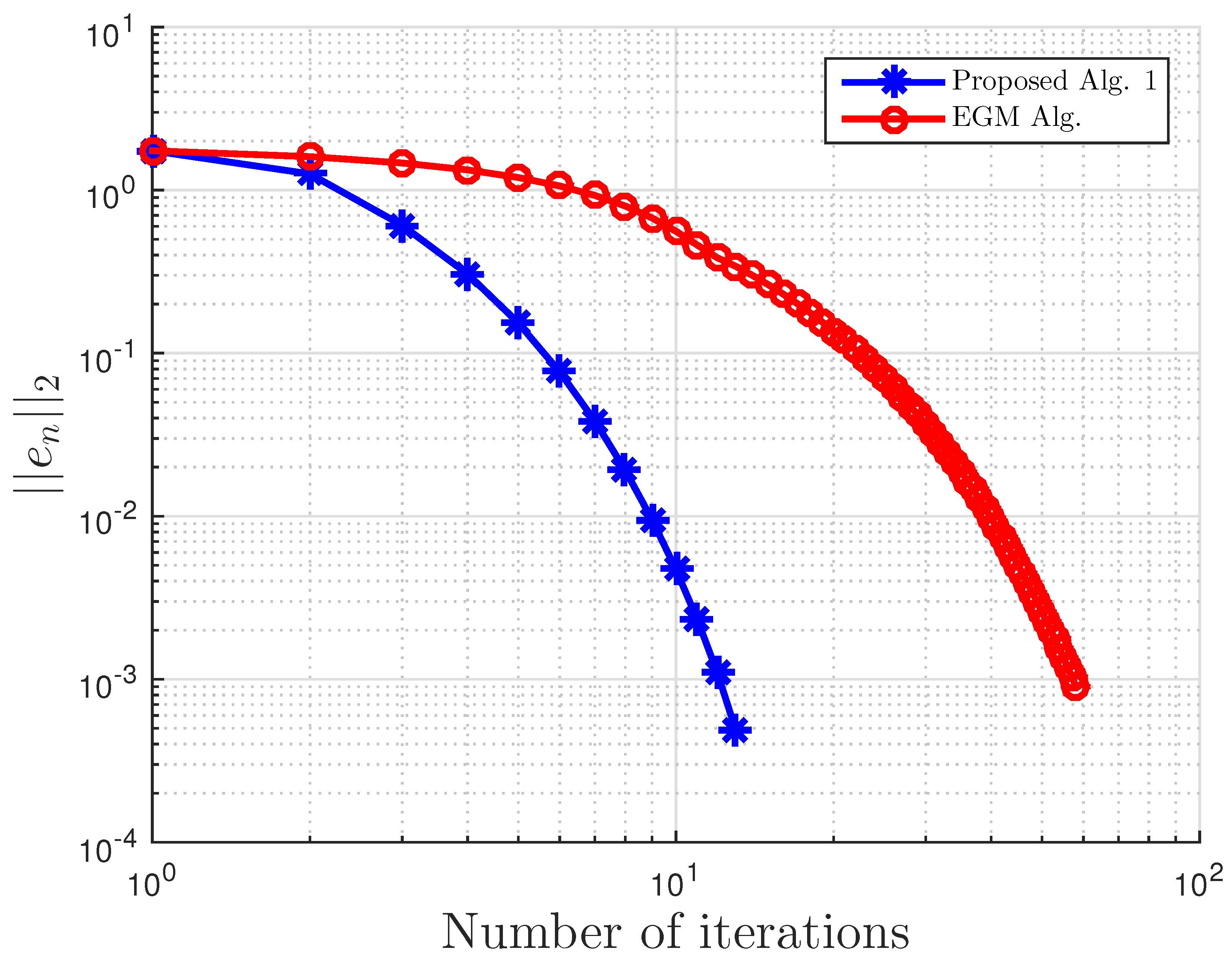
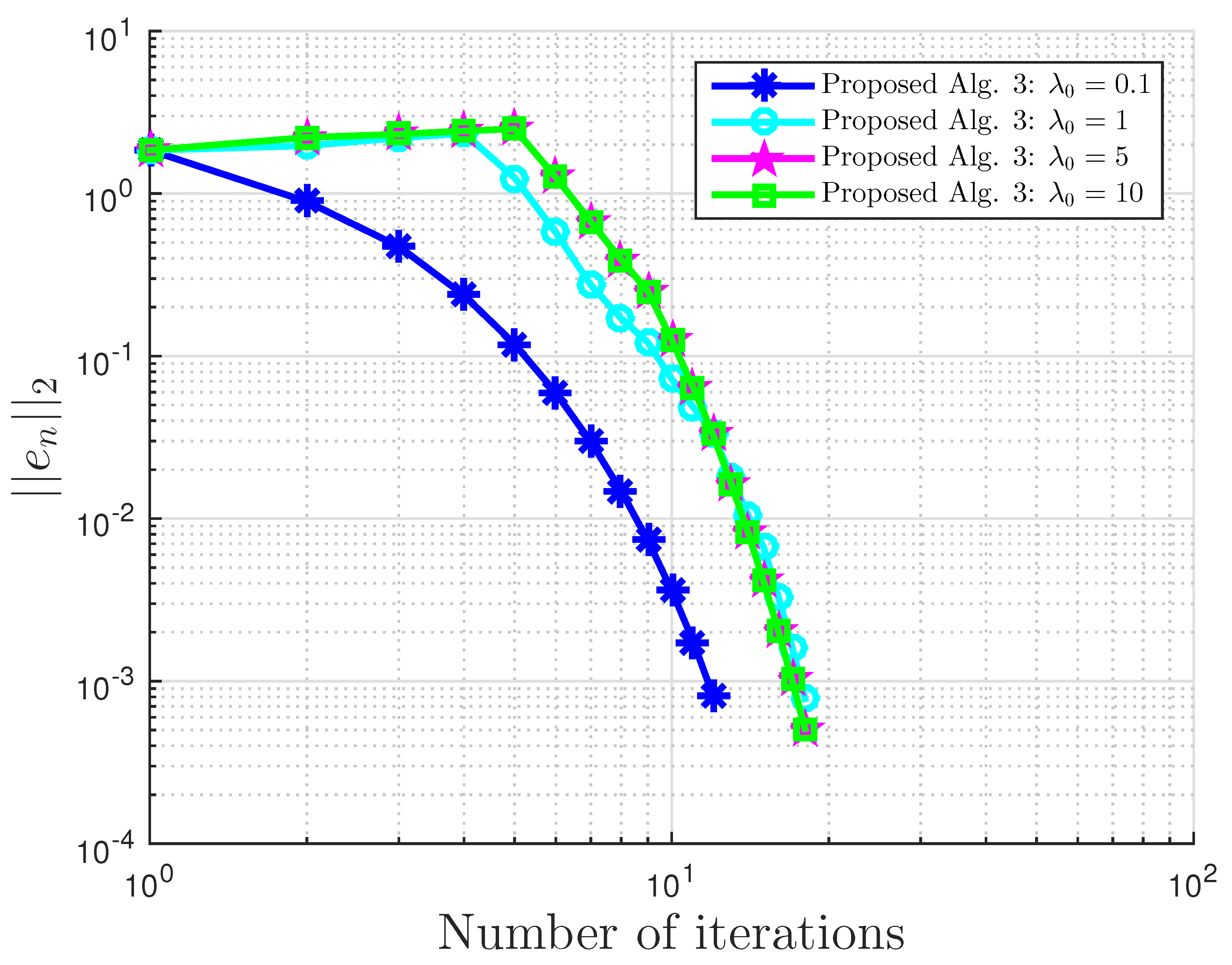
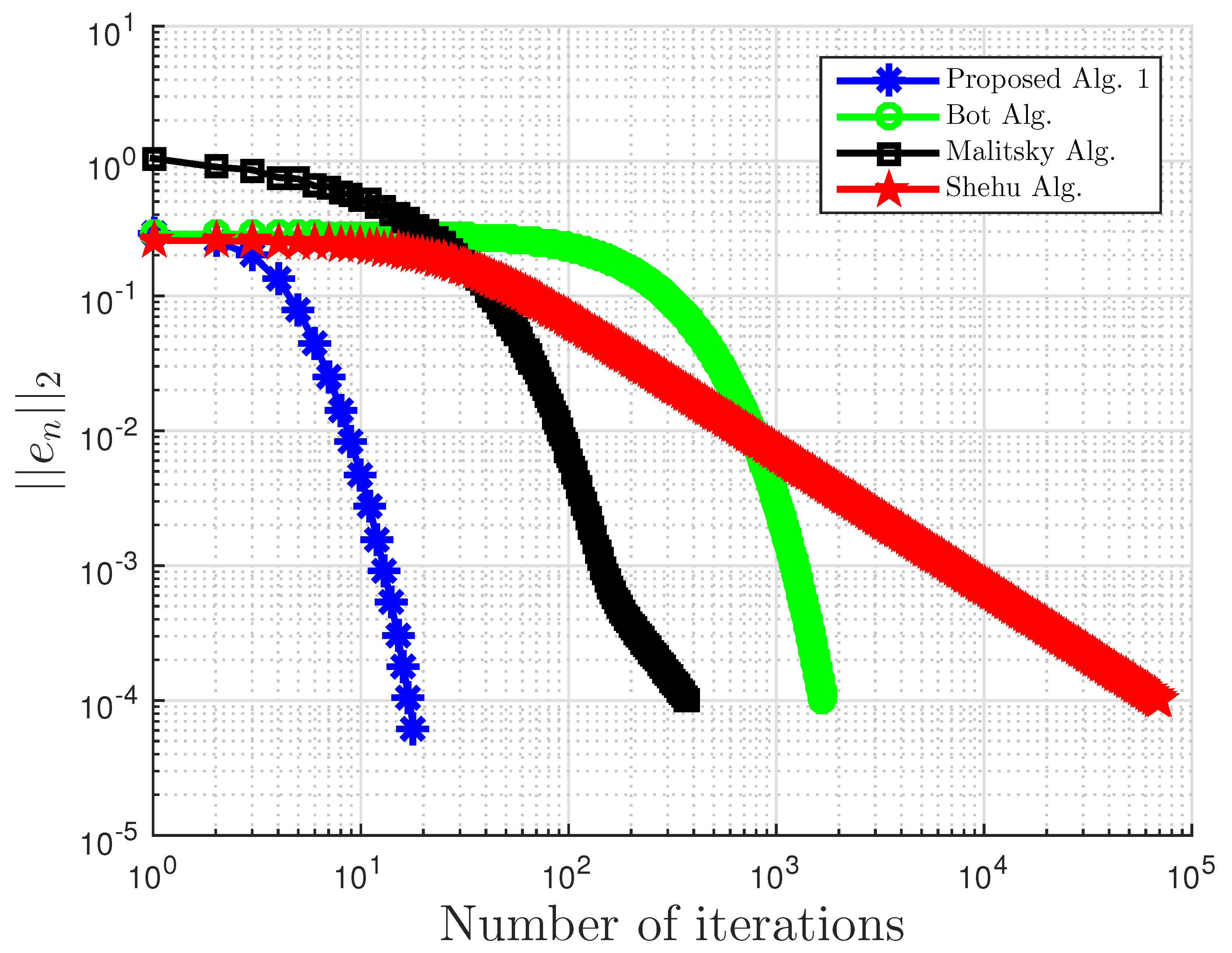
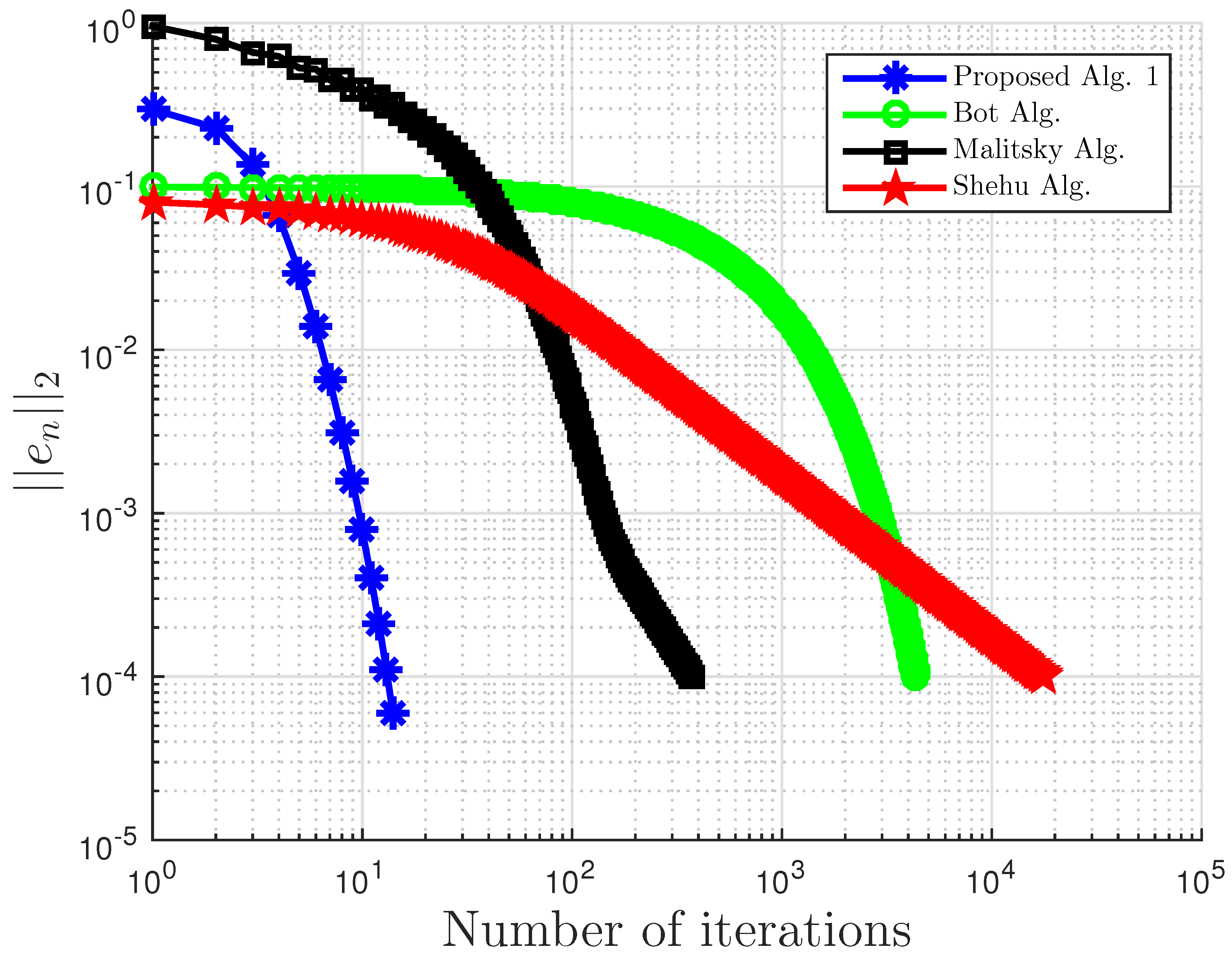
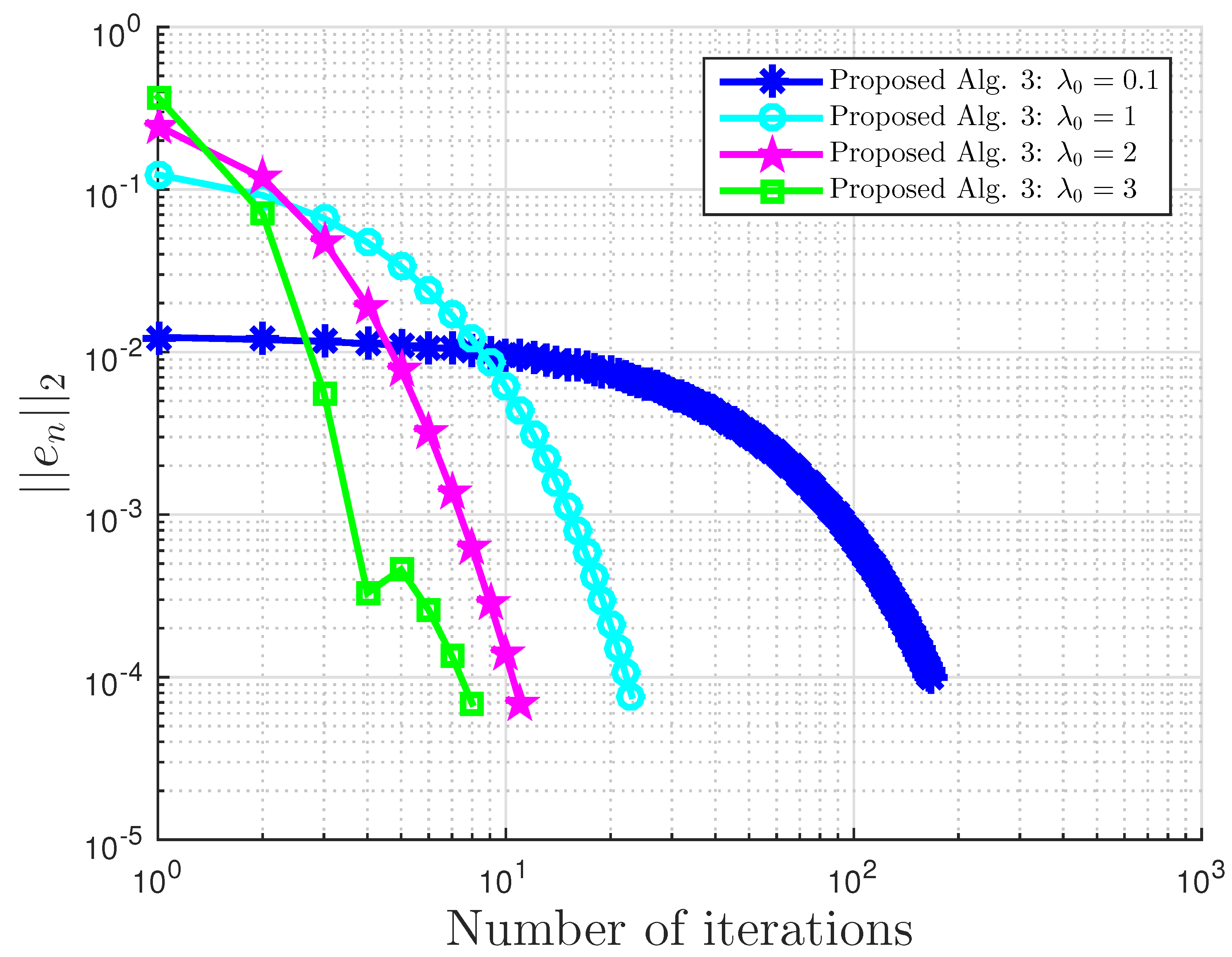
Figure 1.
Example 1: and . Alg., Algorithm.
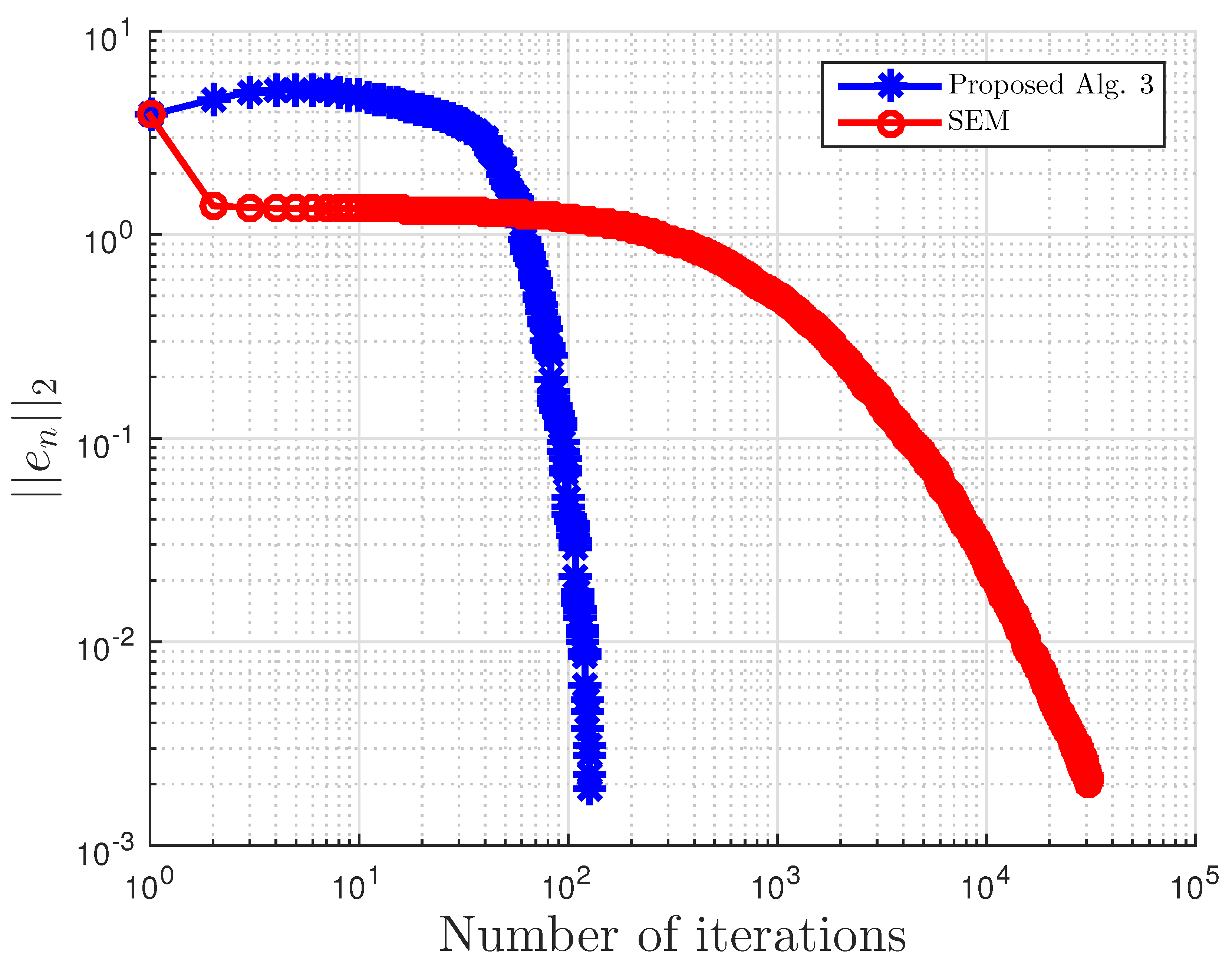
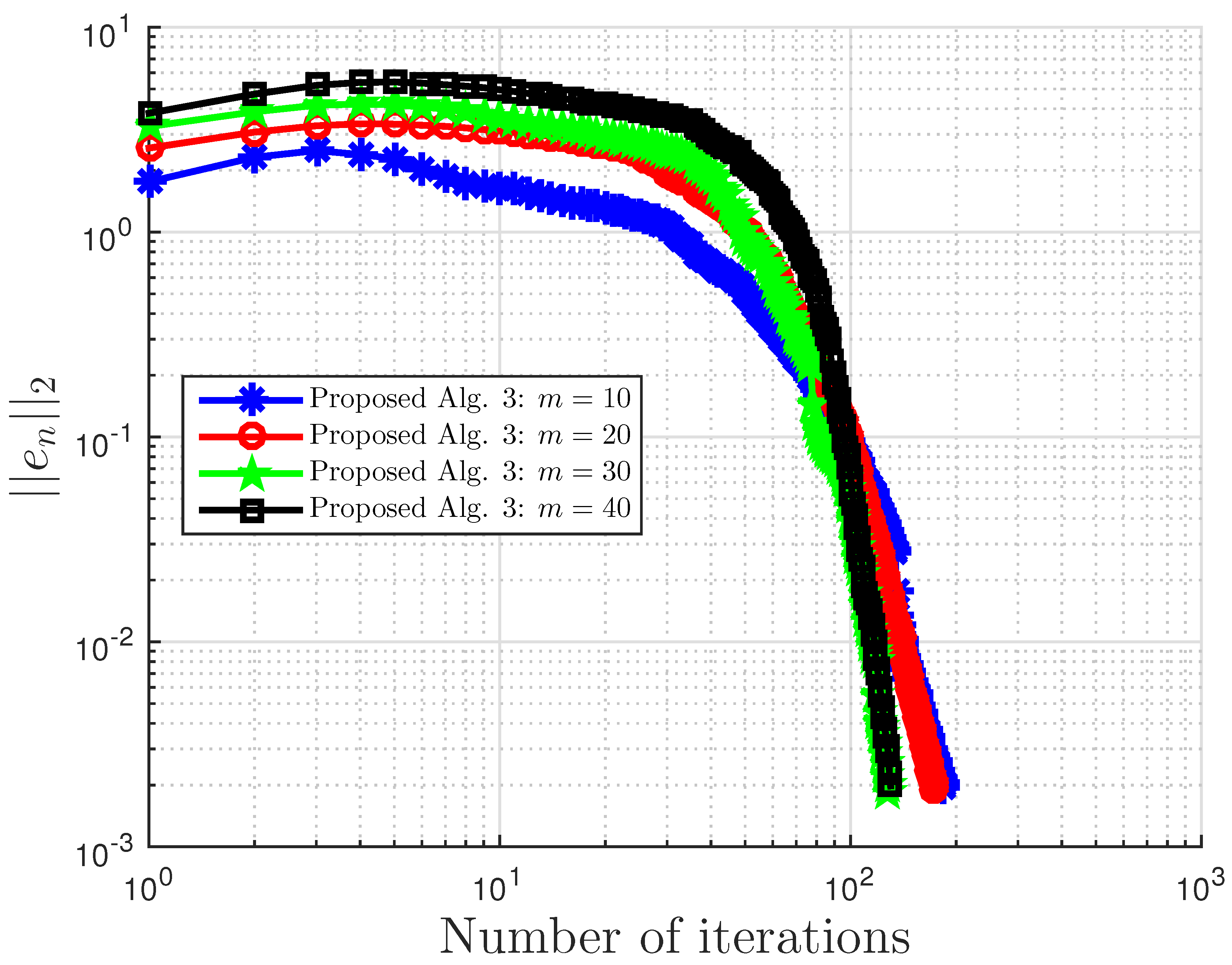
Figure 1.
Example 1: and . Alg., Algorithm.
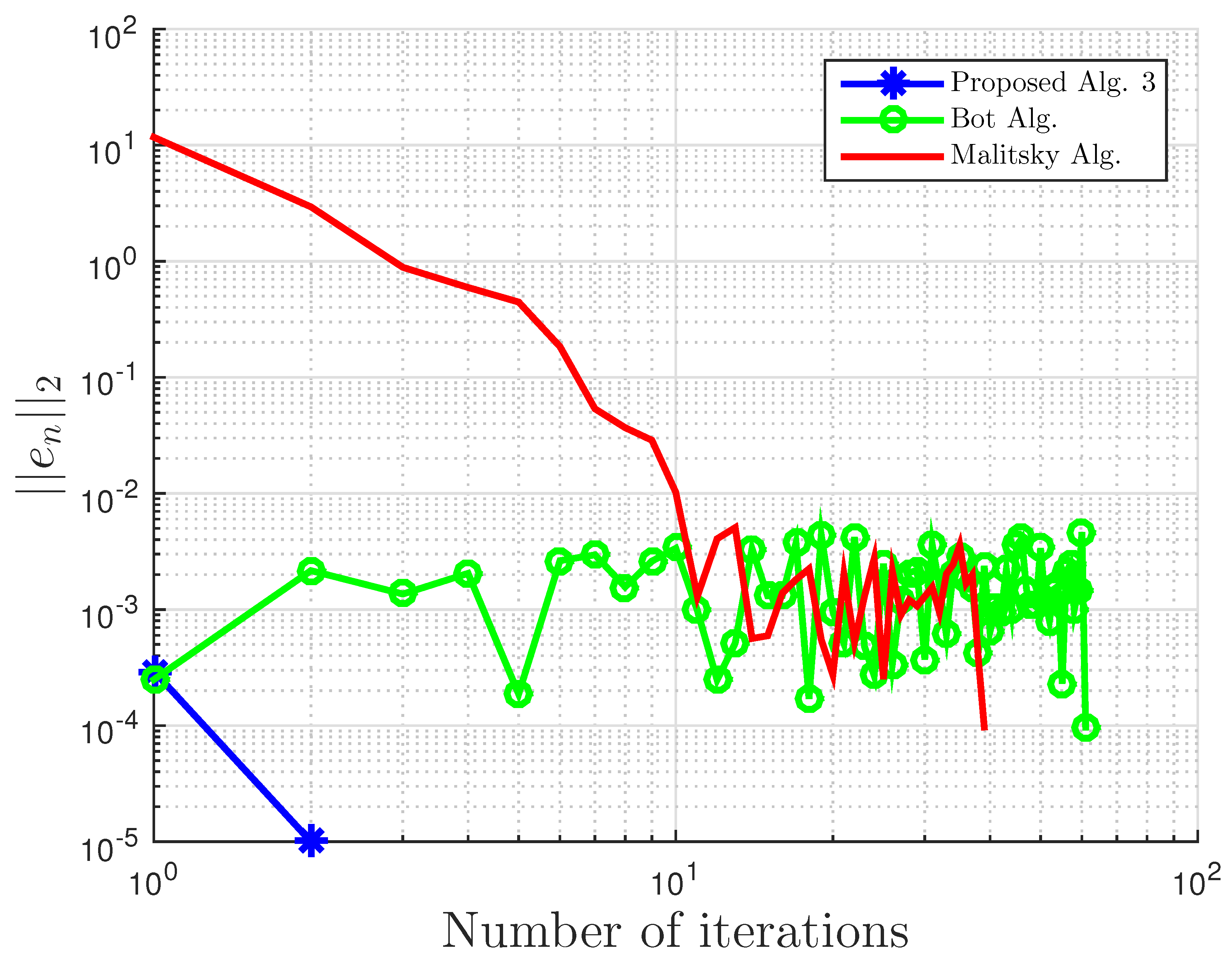
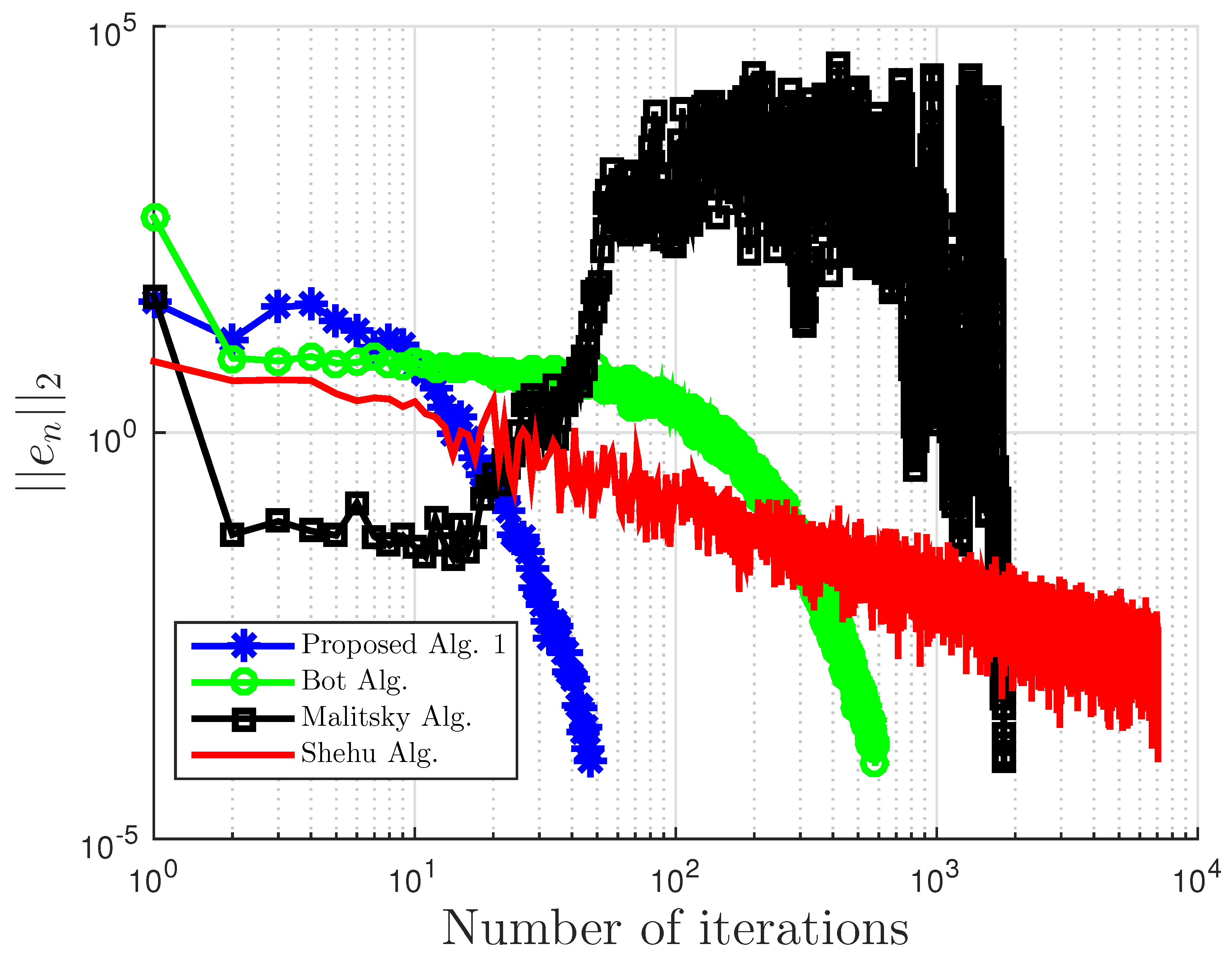
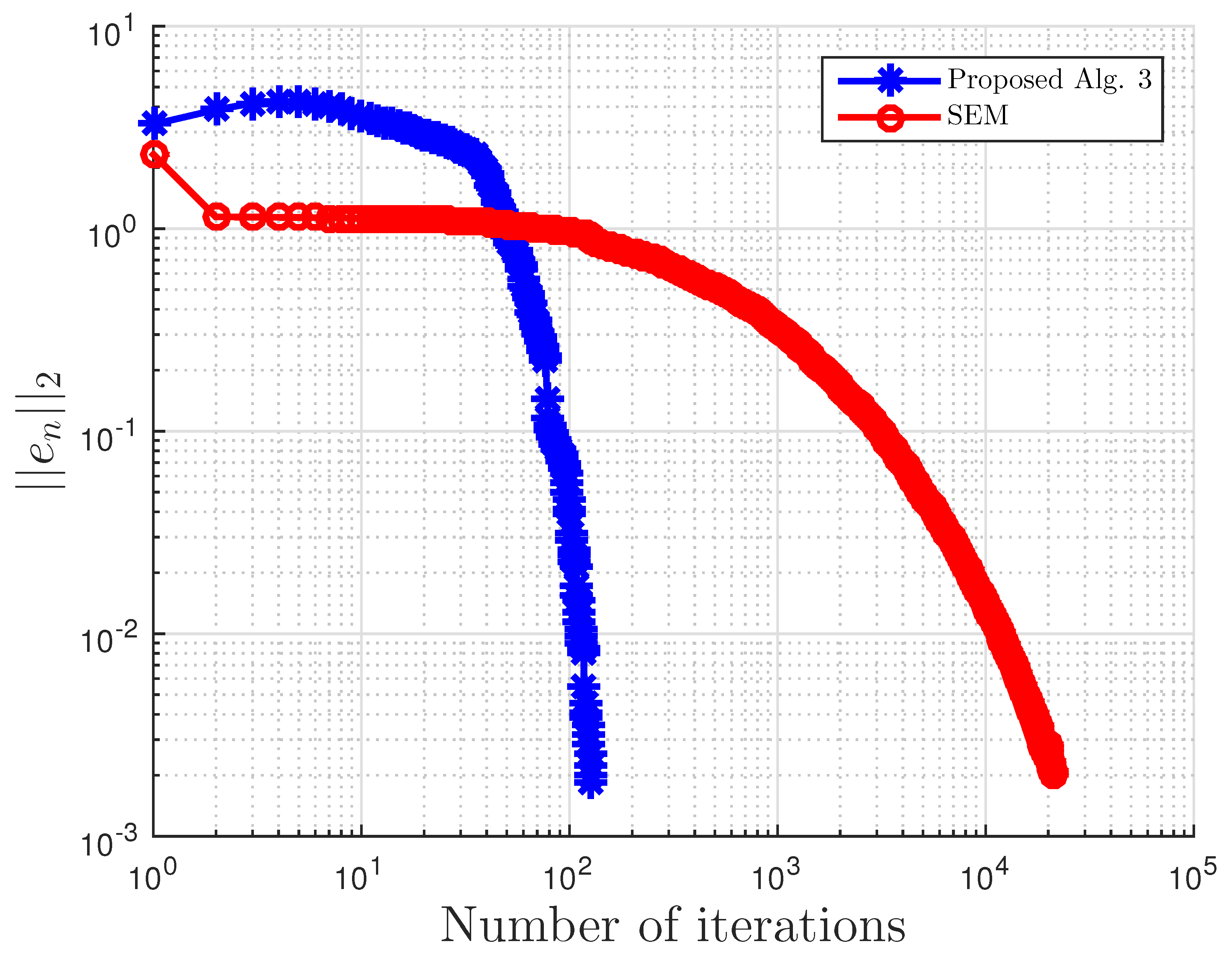
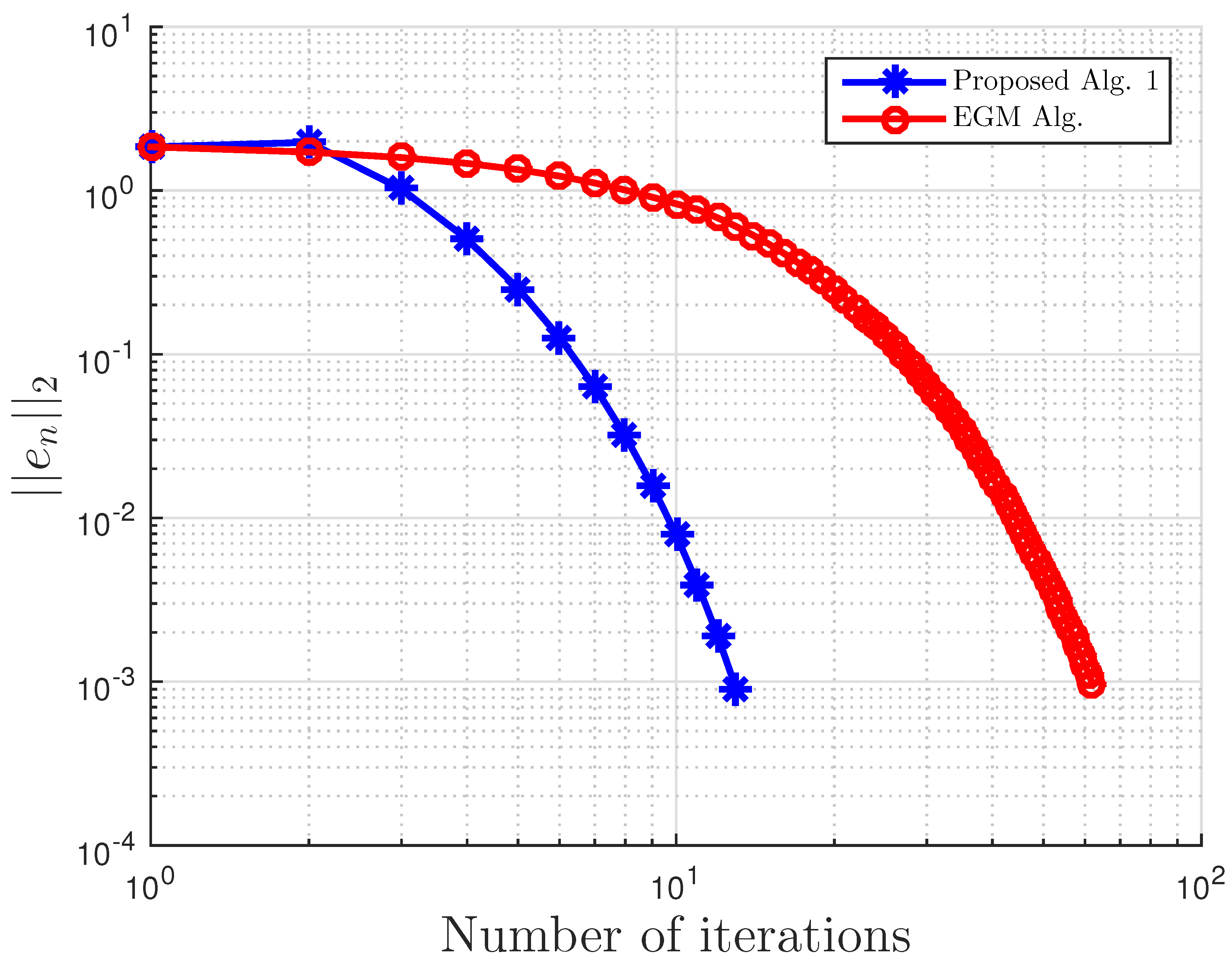
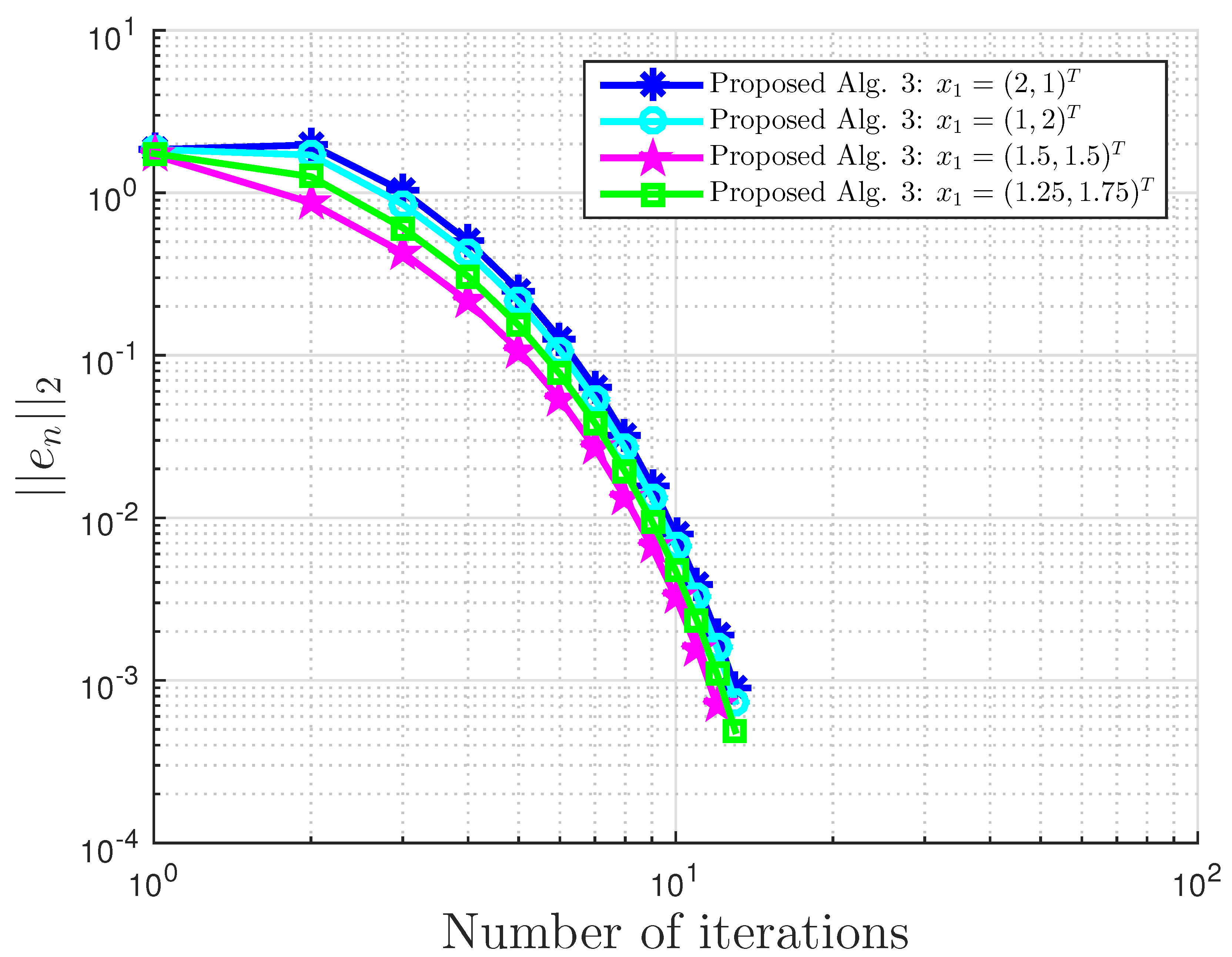
Figure 2.
Example 1: and .
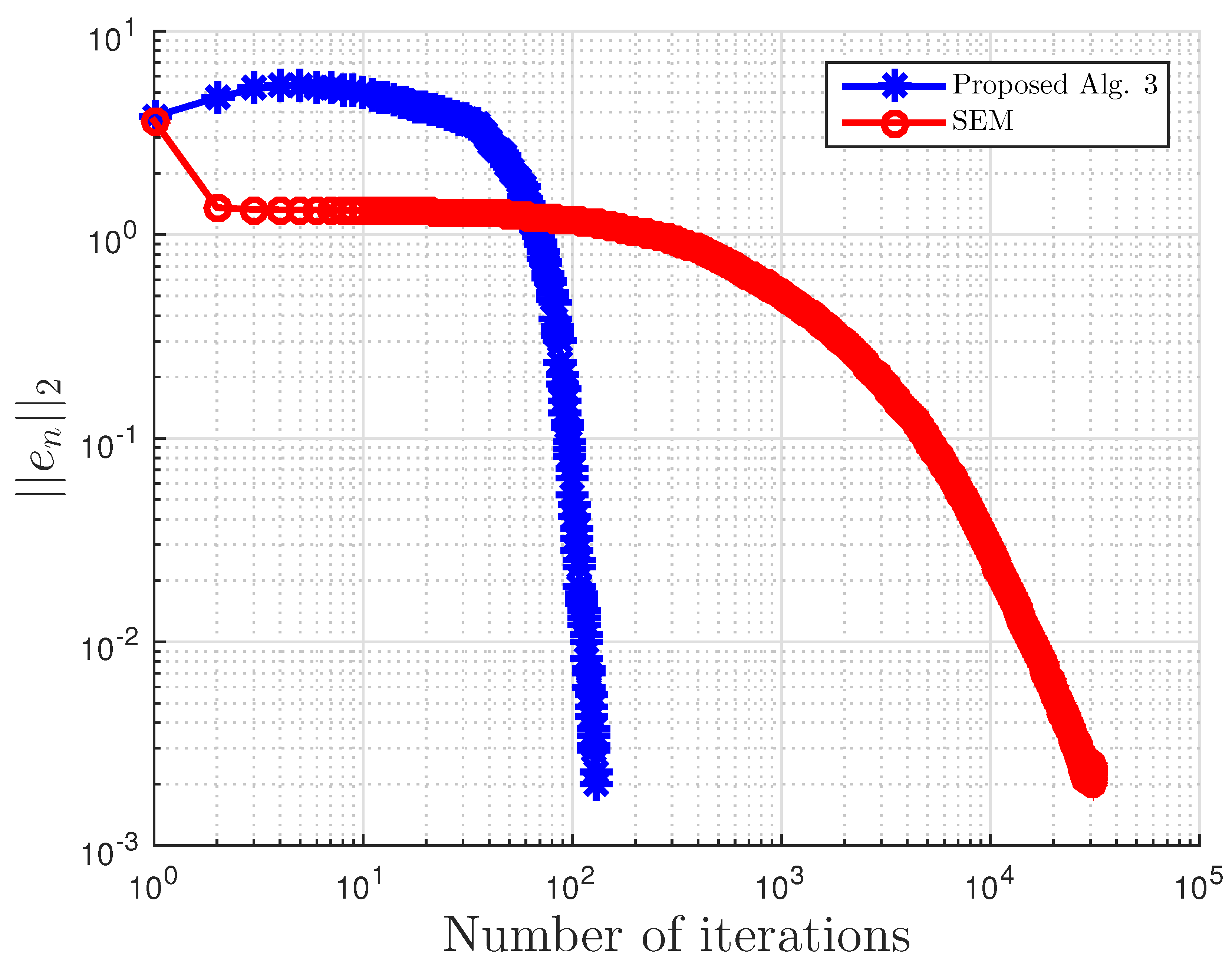
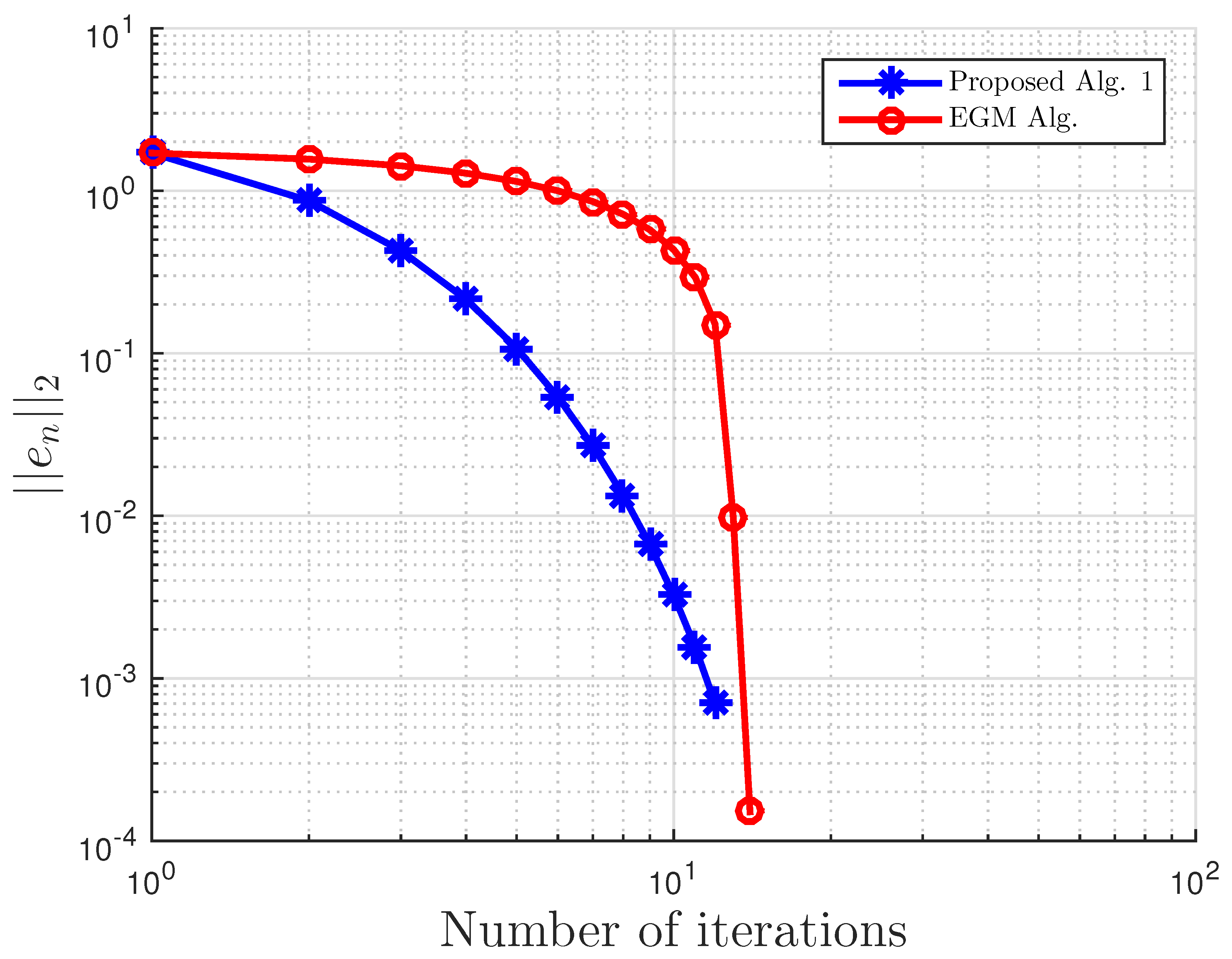
Figure 2.
Example 1: and .
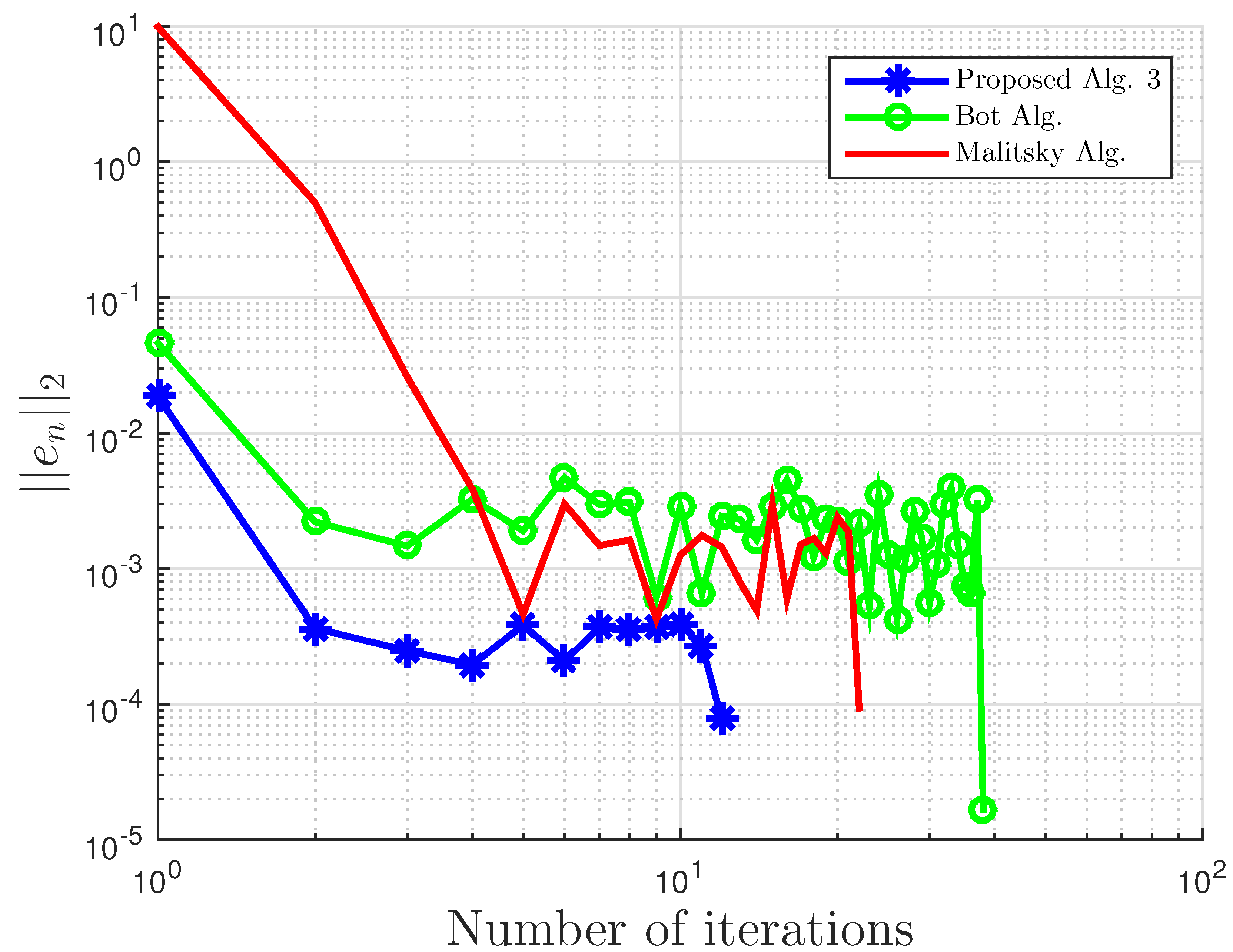
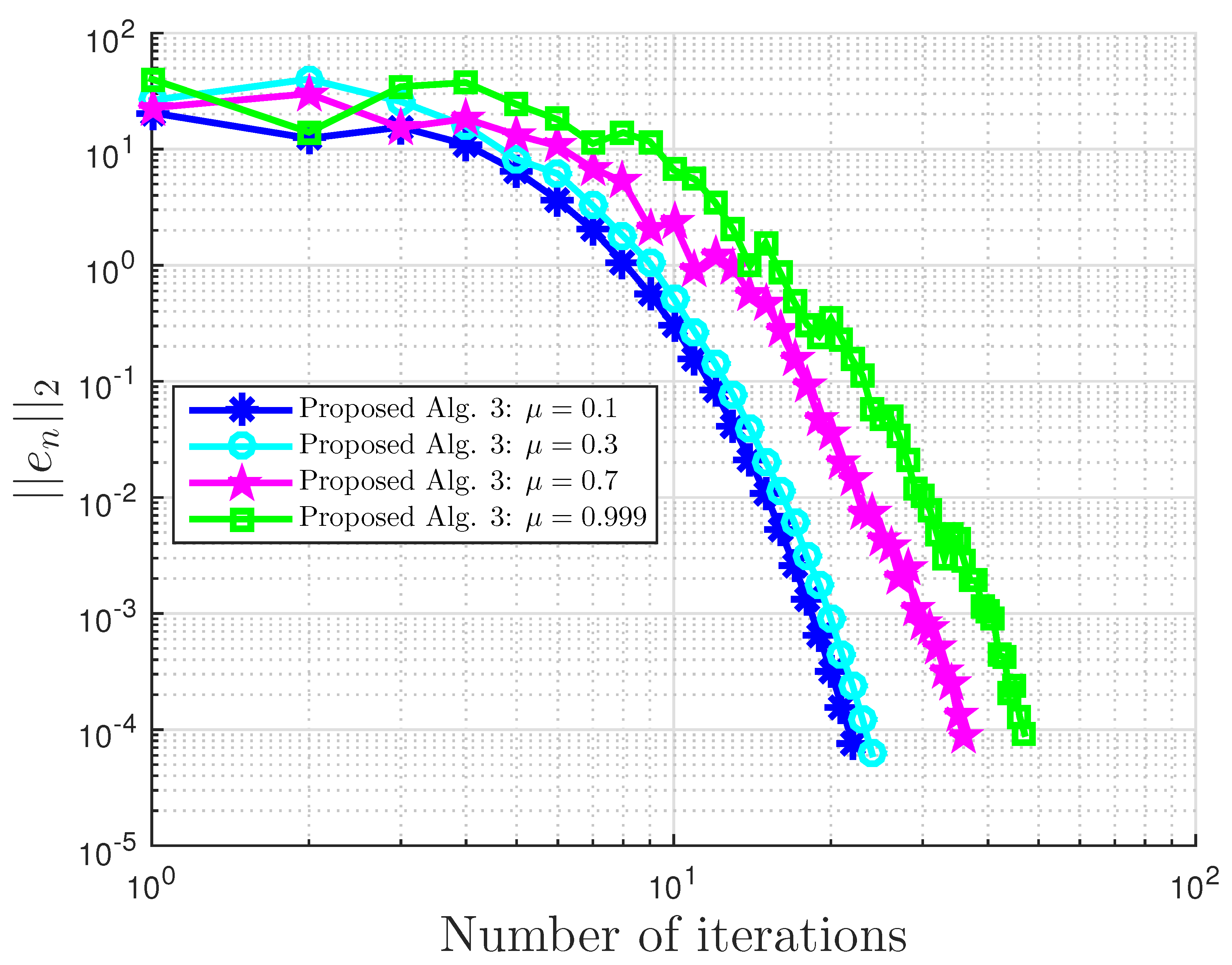
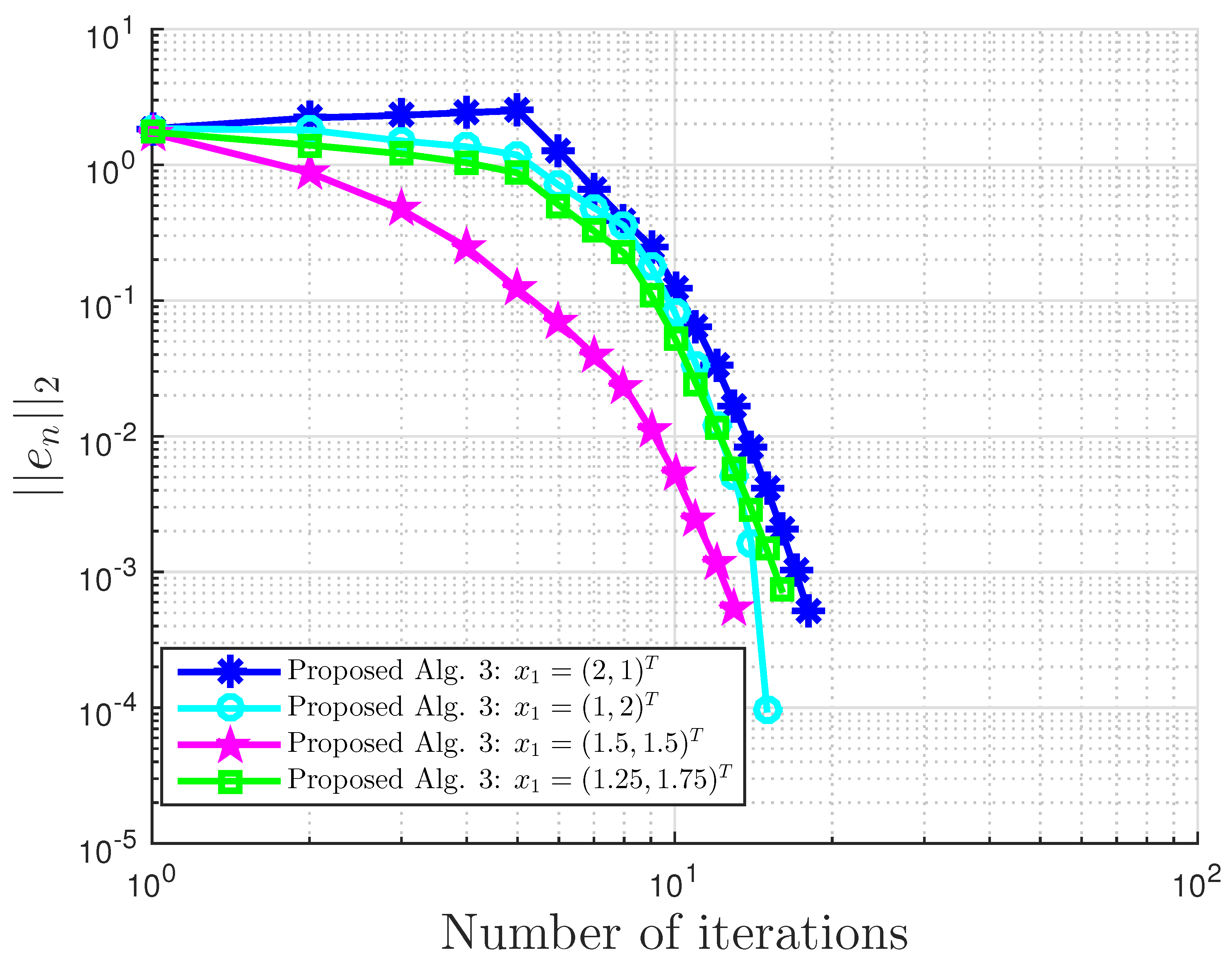
Figure 3.
Example 1: and .
Figure 3.
Example 1: and .
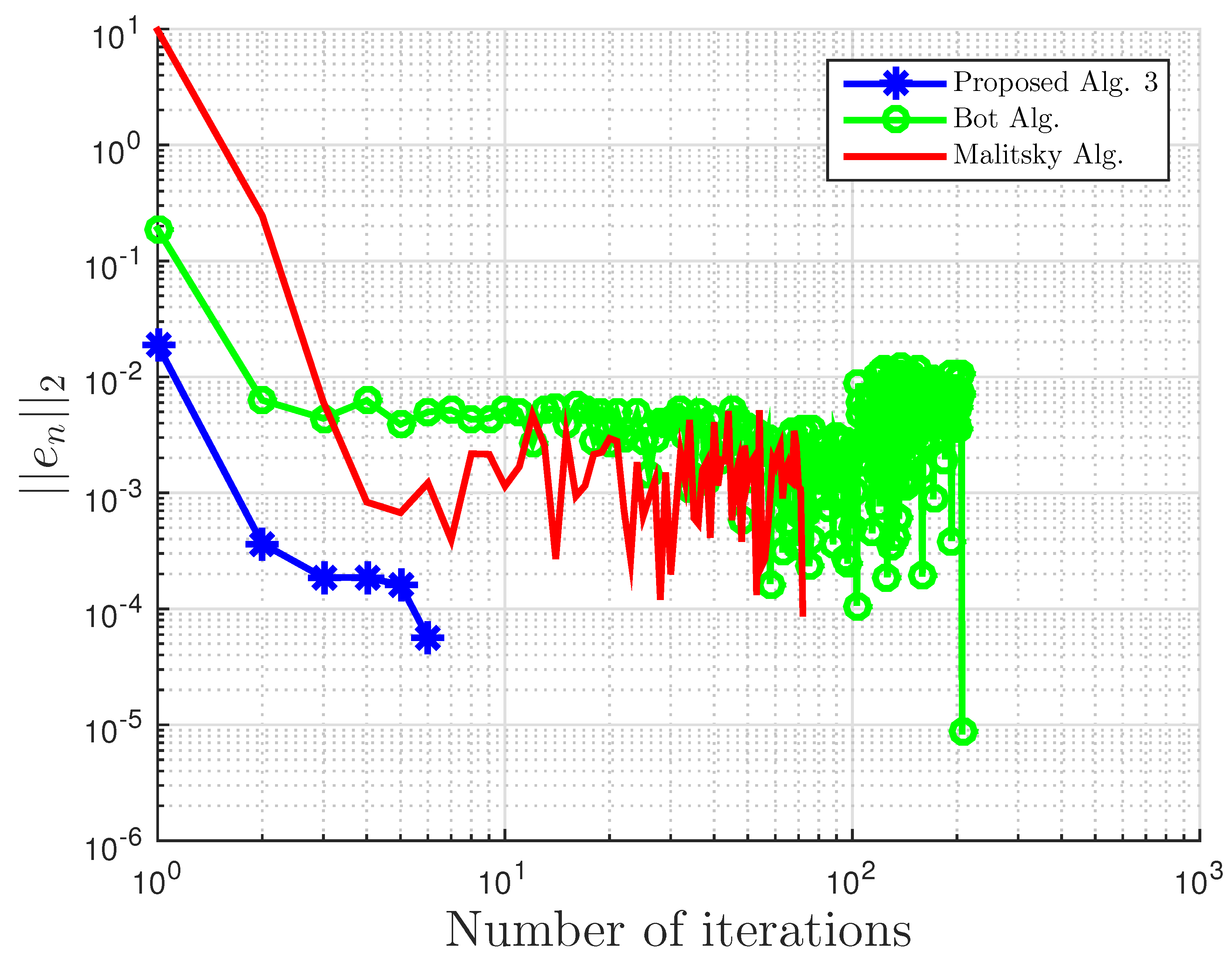
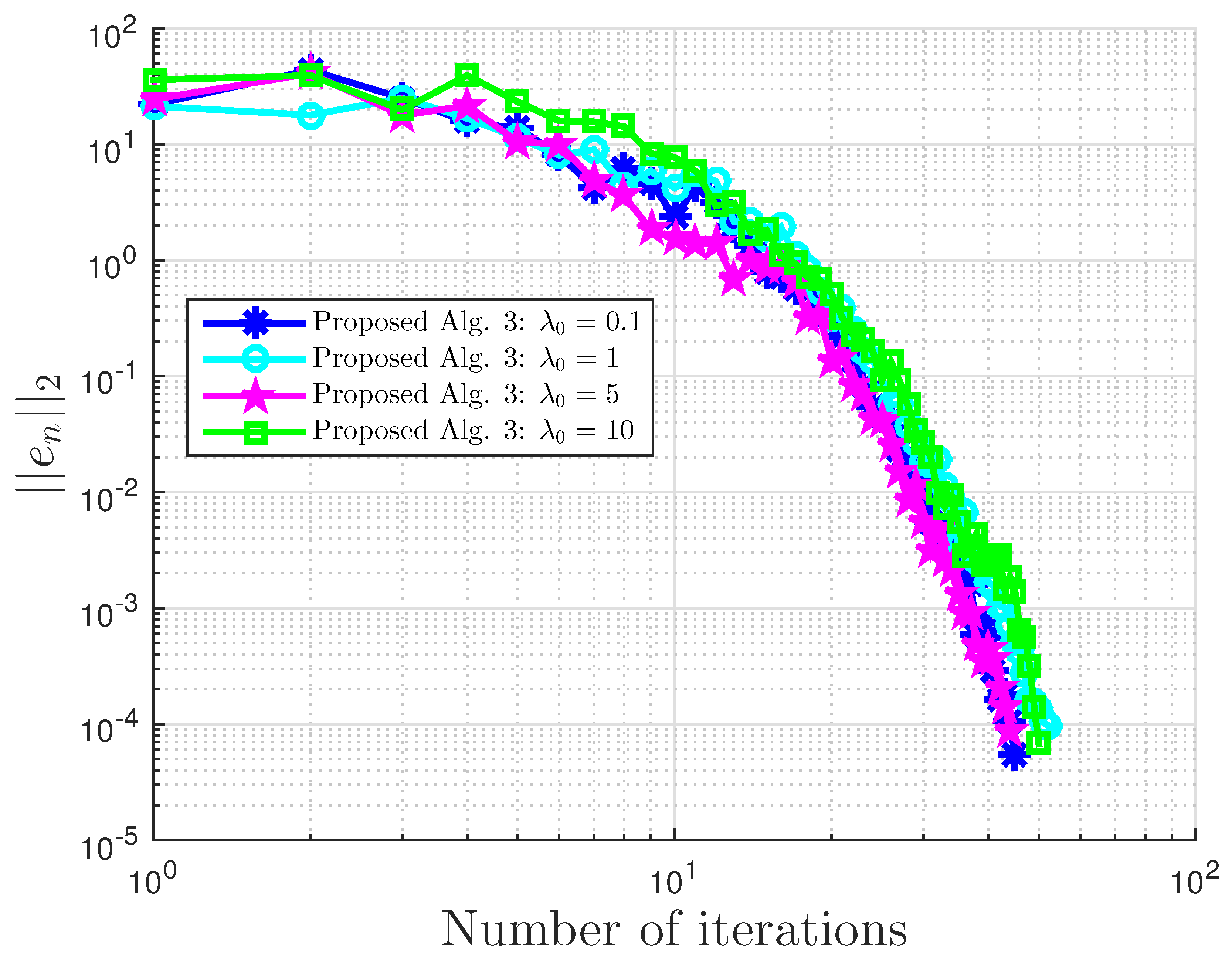
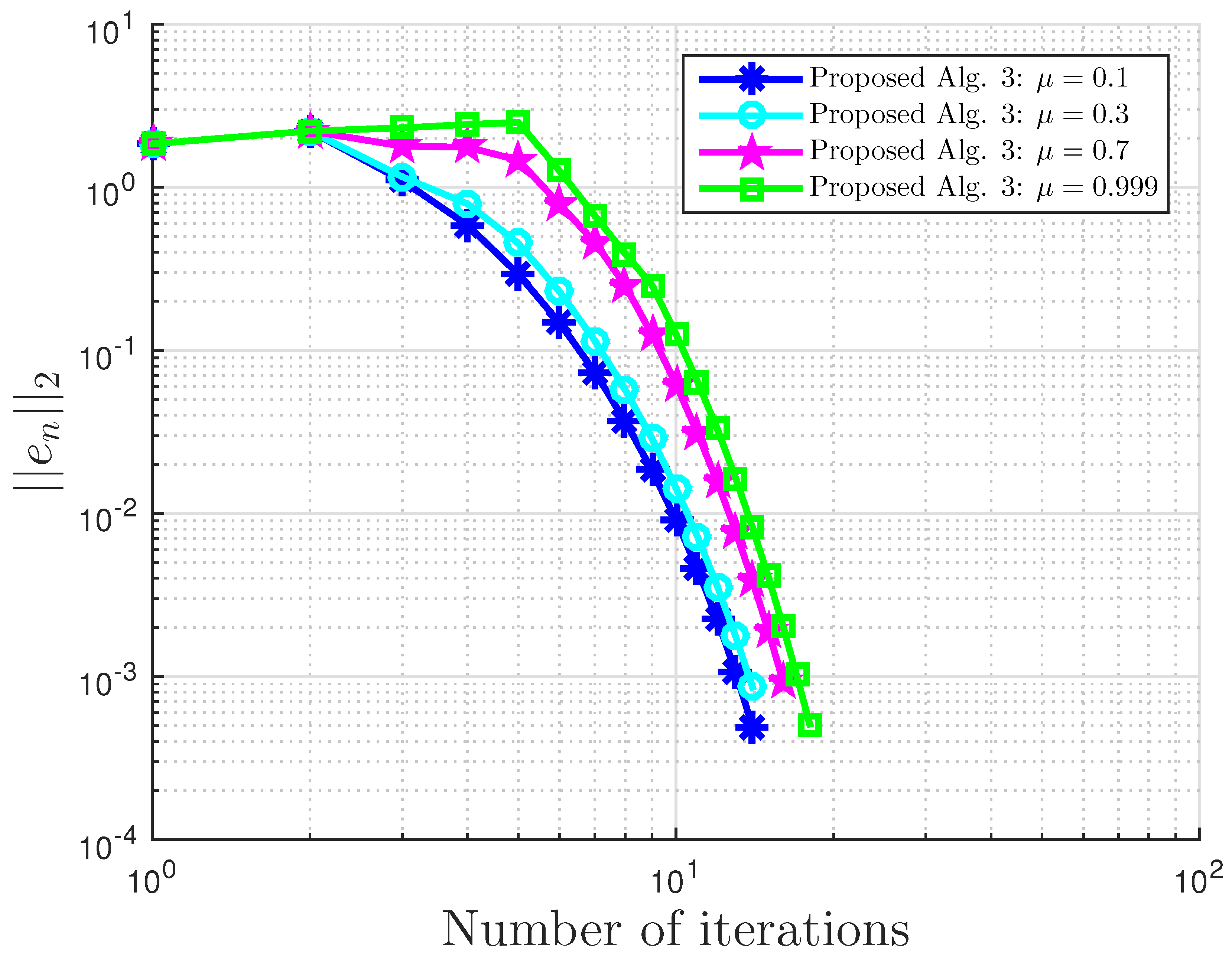
Figure 4.
Example 1: and .
Figure 4.
Example 1: and .
Figure 5.
Example 1: .
Figure 5.
Example 1: .
Figure 6.
Example 1: .
Figure 6.
Example 1: .
Figure 7.
Example 2: and .
Figure 7.
Example 2: and .
Figure 8.
Example 2: and .
Figure 8.
Example 2: and .
Figure 9.
Example 2: and .
Figure 9.
Example 2: and .
Figure 10.
Example 2: and .
Figure 10.
Example 2: and .
Figure 11.
Example 2: .
Figure 11.
Example 2: .
Figure 12.
Example 2: .
Figure 12.
Example 2: .
Figure 13.
Example 3: and .
Figure 13.
Example 3: and .
Figure 14.
Example 3: and .
Figure 14.
Example 3: and .
Figure 15.
Example 3: and .
Figure 15.
Example 3: and .
Figure 16.
Example 3: and .
Figure 16.
Example 3: and .
Figure 17.
Example 3: and .
Figure 17.
Example 3: and .
Figure 18.
Example 3: and .
Figure 18.
Example 3: and .
Figure 19.
Example 3: and .
Figure 19.
Example 3: and .
Figure 20.
Example 3: and .
Figure 20.
Example 3: and .
Figure 21.
Example 3: .
Figure 21.
Example 3: .
Figure 22.
Example 3: .
Figure 22.
Example 3: .
Figure 23.
Example 4: and .
Figure 23.
Example 4: and .
Figure 24.
Example 4: and .
Figure 24.
Example 4: and .
Figure 25.
Example 4: and .
Figure 25.
Example 4: and .
Figure 26.
Example 4: and .
Figure 26.
Example 4: and .
Figure 27.
Example 4: and .
Figure 27.
Example 4: and .
Figure 28.
Example 4: and .
Figure 28.
Example 4: and .
Figure 29.
Example 4: and .
Figure 29.
Example 4: and .
Figure 30.
Example 4: and .
Figure 30.
Example 4: and .
Figure 31.
Example 5: , and .
Figure 31.
Example 5: , and .
Figure 32.
Example 5: , and .
Figure 32.
Example 5: , and .
Figure 33.
Example 5: , and .
Figure 33.
Example 5: , and .
Figure 34.
Example 5: , and .
Figure 34.
Example 5: , and .
Figure 35.
Example 5: .
Figure 35.
Example 5: .
Figure 36.
Example 5: .
Figure 36.
Example 5: .
Table 1.
Example 1 comparison: proposed Algorithm 3, Bot Algorithm 1, and Malitsky Algorithm 2 with .
Table 1.
Example 1 comparison: proposed Algorithm 3, Bot Algorithm 1, and Malitsky Algorithm 2 with .
| | Proposed Algorithm 3 | Bot Algorithm 1 | Malitsky Algorithm 2 |
|---|
| No. of Iter. | CPU Time | No. of Iter. | CPU Time | No. of Iter. | CPU Time |
|---|
| 0.1 | 2 | | 98 | 0.2590 | 71 | 0.1533 |
| 1 | 2 | | 61 | 0.1643 | 39 | 0.0826 |
| 5 | 12 | | 38 | 0.1012 | 22 | 0.0491 |
| 10 | 6 | | 207 | 0.5764 | 72 | 0.1359 |
Table 2.
Example 1: proposed Algorithm 3 with for different values.
Table 2.
Example 1: proposed Algorithm 3 with for different values.
| | | | | |
|---|
| No. of Iter. | 6 | 6 | 3 | 2 |
| CPU Time | | | | |
Table 3.
Example 2 comparison: proposed Algorithm 3, Bot Algorithm 1, Malitsky Algorithm 2, and Shehu Alg. [
37] with
and
.
Table 3.
Example 2 comparison: proposed Algorithm 3, Bot Algorithm 1, Malitsky Algorithm 2, and Shehu Alg. [
37] with
and
.
| | Proposed Algorithm 3 | Bot Algorithm 1 | Malitsky Algorithm 2 | Shehu Alg. [37] |
|---|
| No. of Iter. | CPU Time | No. of Iter. | CPU Time | No. of Iter. | CPU Time | No. of Iter. | CPU Time |
|---|
| 0.1 | 22 | | 582 | 0.1372 | 33 | | 15680 | 8.7073 |
| 0.3 | 24 | | 594 | 0.1440 | 47 | | 13047 | 7.2304 |
| 0.7 | 36 | | 619 | 0.1914 | 81 | | 14736 | 9.8807 |
| 0.999 | 47 | | 581 | 0.3016 | 1809 | 0.7438 | 7048 | 5.4446 |
Table 4.
Example 2: proposed Algorithm 3 with for different values.
Table 4.
Example 2: proposed Algorithm 3 with for different values.
| | | | | |
|---|
| No. of Iter. | 45 | 52 | 44 | 50 |
| CPU Time | | | | |
Table 5.
Comparison of proposed Algorithm 3 and the subgradient-extragradient method (SEM) (
2) for Example 3.
Table 5.
Comparison of proposed Algorithm 3 and the subgradient-extragradient method (SEM) (
2) for Example 3.
| | | | | |
|---|
| Iter. | CPU Time | Iter. | CPU Time | Iter. | CPU Time | Iter. | CPU Time |
|---|
| Proposed Algorithm 3 | 157 | 2.7327 | 162 | 3.9759 | 144 | 4.4950 | 128 | 4.8193 |
| SEM (2) | 3785 | 64.8752 | 13,980 | 243.9019 | 18,994 | 345.3686 | 30,777 | 567.8440 |
| | | | | |
| Iter. | CPU Time | Iter. | CPU Time | Iter. | CPU Time | Iter. | CPU Time |
| Proposed Algorithm 3 | 185 | 4.0691 | 173 | 4.3798 | 128 | 4.8817 | 130 | 6.2658 |
| SEM (2) | 4176 | 77.6893 | 8645 | 150.4267 | 21,262 | 381.0991 | 30,956 | 561.4559 |
Table 6.
Comparison of proposed Algorithm 3 and the extragradient method (EGM) [
16] for Example 4 with
and
.
Table 6.
Comparison of proposed Algorithm 3 and the extragradient method (EGM) [
16] for Example 4 with
and
.
| | Proposed Algorithm 3 | EGM [16] |
|---|
| No. of Iter. | CPU Time | No. of Iter. | CPU Time |
|---|
| 13 | | 62 | |
| 33 | | 62 | |
| 12 | | 14 | |
| 13 | | 58 | |
Table 7.
Proposed Algorithm 3 for Example 4 with and .
Table 7.
Proposed Algorithm 3 for Example 4 with and .
| | Proposed Algorithm 3 |
|---|
| No. of Iter. | CPU Time |
|---|
| 18 | |
| 15 | |
| 13 | |
| 16 | |
Table 8.
Example 4: proposed Algorithm 3 with for different and values.
Table 8.
Example 4: proposed Algorithm 3 with for different and values.
| | |
|---|
| | | | | |
| No. of Iter. | 14 | 14 | 16 | 18 |
| CPU Time | | | | |
| | |
| | | | | |
| No. of Iter. | 12 | 18 | 18 | 18 |
| CPU Time | | | | |
Table 9.
Example 5 comparison: proposed Algorithm 3, Bot Algorithm 1, Malitsky Algorithm 2, and Shehu Alg. [
37] with
and
.
Table 9.
Example 5 comparison: proposed Algorithm 3, Bot Algorithm 1, Malitsky Algorithm 2, and Shehu Alg. [
37] with
and
.
| | Proposed Algorithm 3 | Bot Algorithm 1 | Malitsky Algorithm 2 | Shehu Alg. [37] |
|---|
| Iter. | CPU Time | Iter. | CPU Time | Iter. | CPU Time | Iter. | CPU Time |
|---|
| 23 | | 2159 | 0.23341 | 371 | | 37,135 | 10.8377 |
| 18 | | 1681 | 0.18084 | 374 | | 70,741 | 32.5843 |
| 14 | | 4344 | 0.48573 | 373 | | 17,741 | 5.6272 |
| 43 | | 2774 | 0.29515 | 351 | | 28,758 | 7.3424 |
Table 10.
Example 5: proposed Algorithm 3 with for different and values.
Table 10.
Example 5: proposed Algorithm 3 with for different and values.
| | |
|---|
| | | | | |
| No. of Iter. | 167 | 23 | 11 | 8 |
| CPU Time | | | | |
| | |
| | | | | |
| No. of Iter. | 11 | 11 | 11 | 11 |
| CPU Time | | | | |