Effective Rotor Fault Diagnosis Model Using Multilayer Signal Analysis and Hybrid Genetic Binary Chicken Swarm Optimization
Abstract
1. Introduction
- Proposing a multilayer signal analysis method combining two signal processing methods (LMD and WPD) and PF selection. This technique can reduce the dimension of original data, descend background noise, and extract potential features.
- Proposing a feature selection method using the combination with BCSO and GA and two positions update strategies to enhance global exploration capabilities, improve population diversity, and prevent premature convergence.
- Proposing a rotor bar fault diagnosis model based on multilayer signal analysis, feature selection method, and classification.
2. Multilayer Signal Analysis
2.1. Local Mean Decomposition
- Step 1:
- Find all local extrema of the original signal . Calculate the local mean and local envelope of two successive extrema and by
- Step 2:
- All the local mean and local envelope can be extended by using straight lines extending between successive extrema.
- Step 3:
- Construct local mean function and local envelope function by smoothing the local mean and local envelope using moving averaging method.
- Step 4:
- Subtracting the local mean function from the original signal to obtain a residue signal :
- Step 5:
- Then, the frequency modulated signal can be obtained from and . can be the amplitude demodulated by dividing it by the envelope function.
- Step 6:
- If is a purely frequency modulated signal, then go to Step 7. Otherwise, take as a new signal and repeat Step 1 to 5 until the condition is satisfied.
- Step 7:
- Multiply all the smoothed local envelope functions during iteration to obtain the envelope signal of the first product function .Then, with the envelop function and the final frequency demodulated, the first product function will be generated:
- Step 8:
- Then, treated as the smoothed version of the original data and the procedure is repeated from Step 1 to 7, until is a monotonic function or no more than five oscillations. Finally, can be denoted aswhere is the number of PFs.
2.2. Product Function Selection
2.3. Wavelet Packet Decomposition
2.4. Feature Extraction Process
- Step 1:
- Record vibration signals from test machines.
- Step 2:
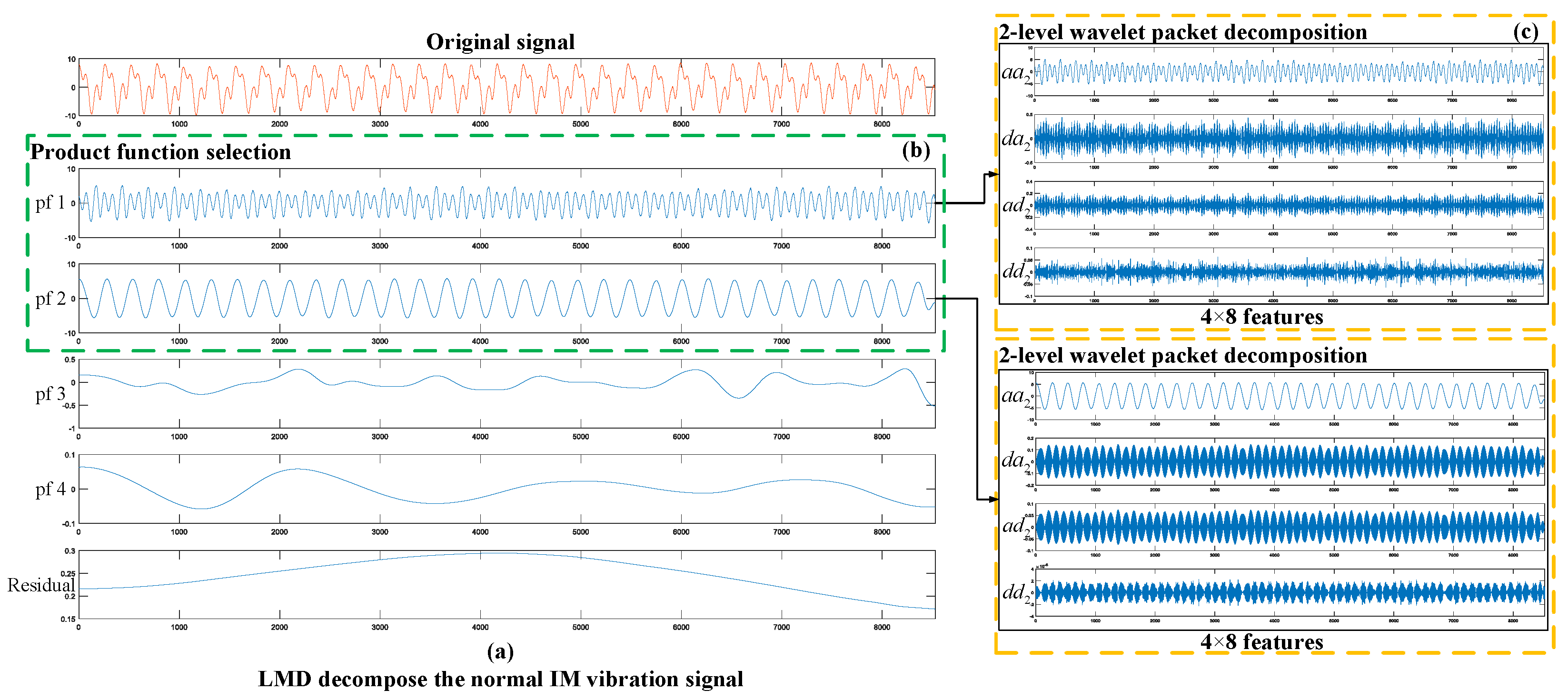
- In the first layer of the multilayer signal analysis, LMD is used to decompose the vibration signals into a set of PFs. Figure 1a illustrates how the LMD decomposes the normal IM vibration signal into four PFs.
- Step 3:
- In the second layer of the multilayer signal analysis, PF selection is used to select the effective components. In this paper, we choose the best two CEV values for the selected PFs into the final layer. Figure 1b illustrates the PF selection method selecting the best two PFs.
- Step 4:
- In the third layer of the multilayer signal analysis, WPD is used to further analyze and denoise the selected PFs. In this paper, two-level WPD is adopted and decomposition construction consists of four wavelet packet coefficients: , , , . The two-level WPD decomposes the selected PFs as shown in Figure 1c.
- Step 5:
- The eight statistical feature parameters are calculated for each wavelet packet coefficient. A total of 64 (2 × 4 × 8) features are extracted from the output decomposition structure of two selected PFs.
3. Hybrid Genetic Binary Chicken Swarm Optimization for Feature Selection
3.1. Binary Chicken Swarm Optimization
- Rooster’s position update equation:where is a Gaussian distribution with a mean of 0 and standard deviation , is a small constant to prevent the denominator being 0. is a rooster’s index, which is selected randomly between 1 and the maximum number of roosters except . and are the fitness values of the ith and kth rooster.
- Hen’s position update equation:Rand is a uniform random number between 0 and 1, is an index of the rooster, which is in the ith hen’s group-mate, is an index of the chicken in all roosters and hens, which is randomly chosen from the swarm, and let .
- Chick’s position update equation:where is an index of the mother hen corresponding to ith chick, FL is a parameter in the range [0.4, 1], which keeps the chick to forage for food around its mother.
3.2. Update the Hen’s Position Based on Levy Flight
3.3. Update the Chick’s Position Based on Inertia Weight
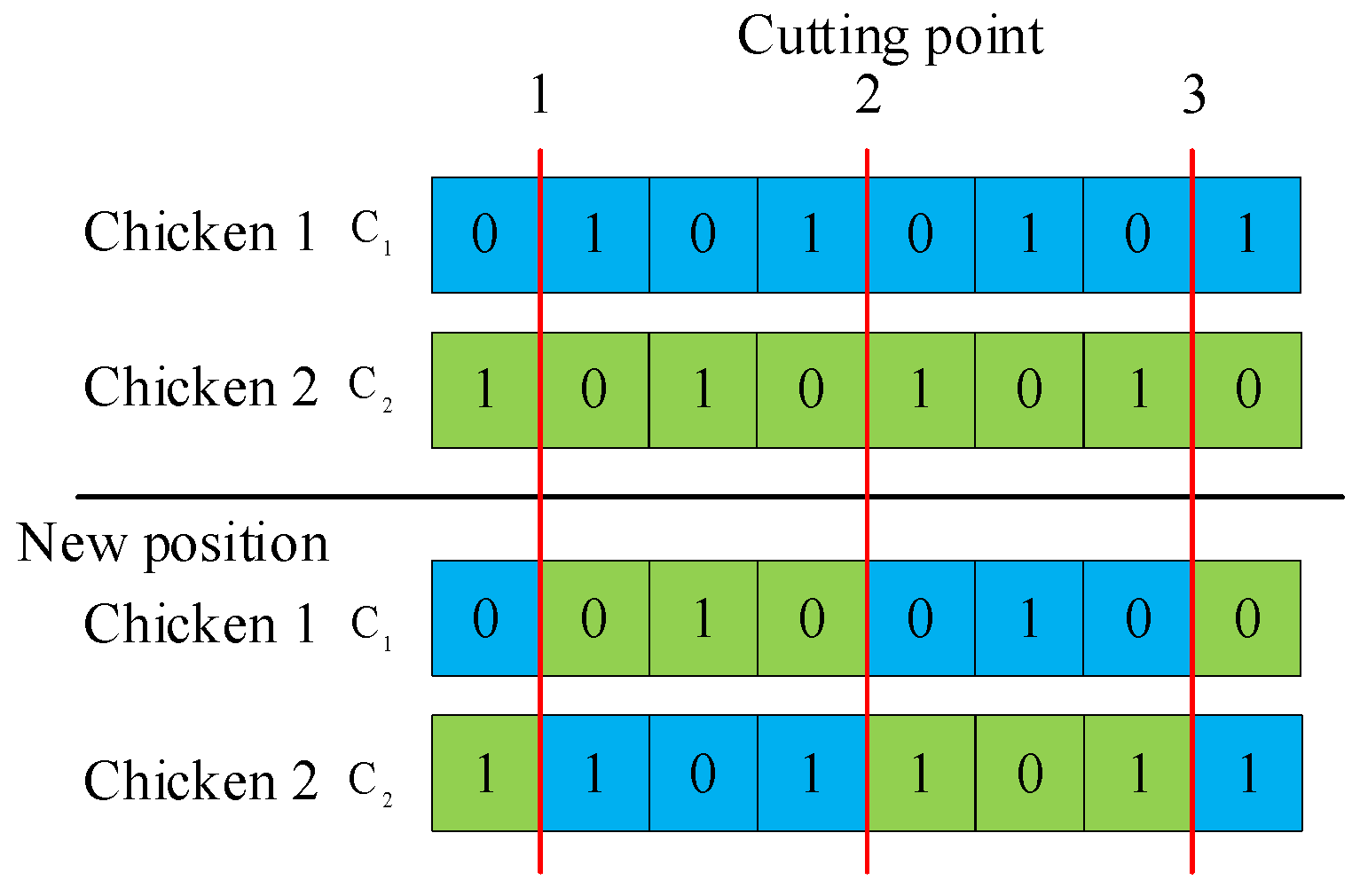
3.4. Update the Chicken’s Position Based on Crossover Operation
- Step 1:
- Randomly selected pairs of solutions carry out the three points crossover operation.
- Step 2:
- Repeat until the new population is formed.
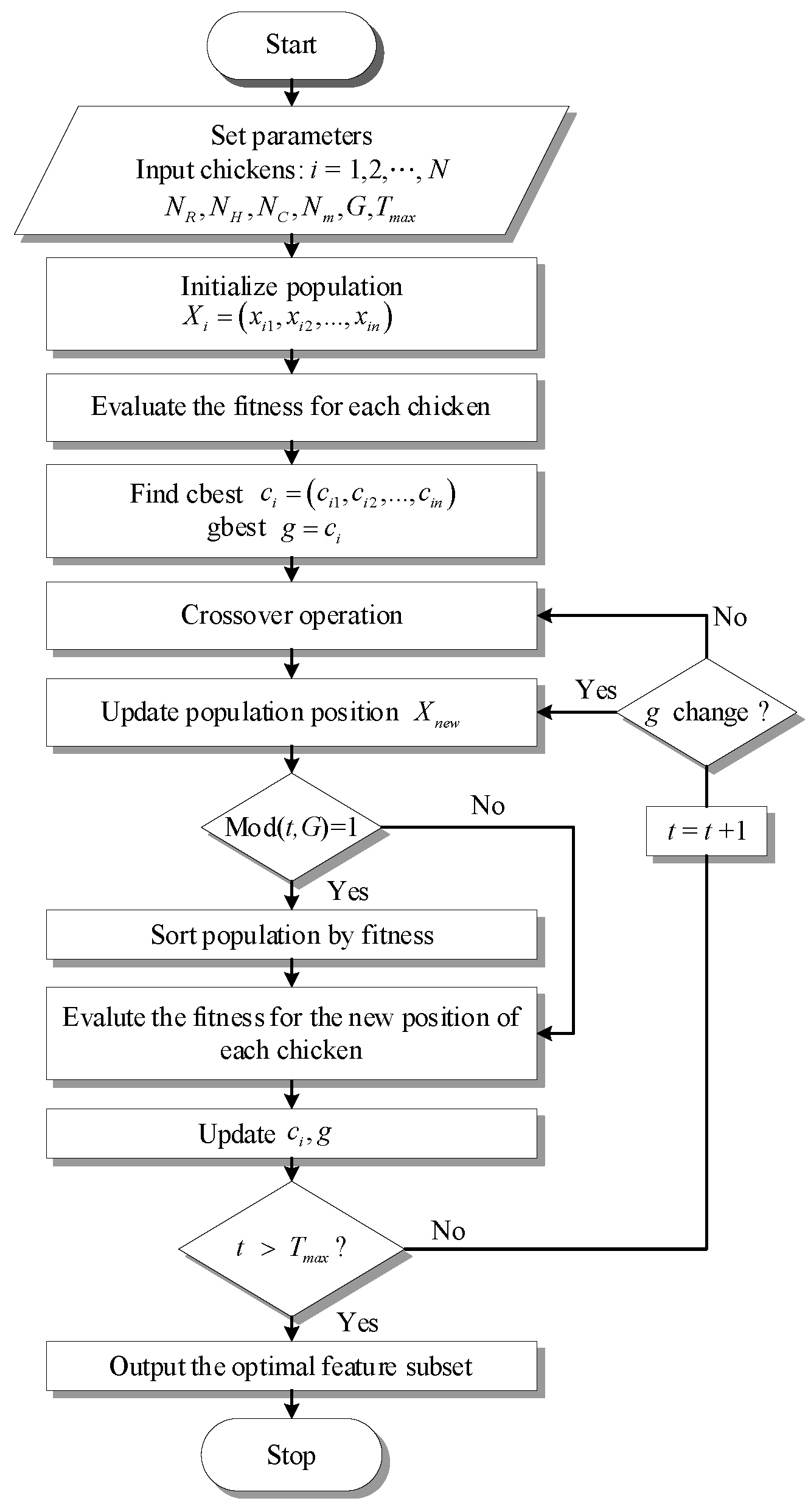
3.5. The Proposed HGBCSO Method
4. Diagnosis Model for Rotor Bar Fault
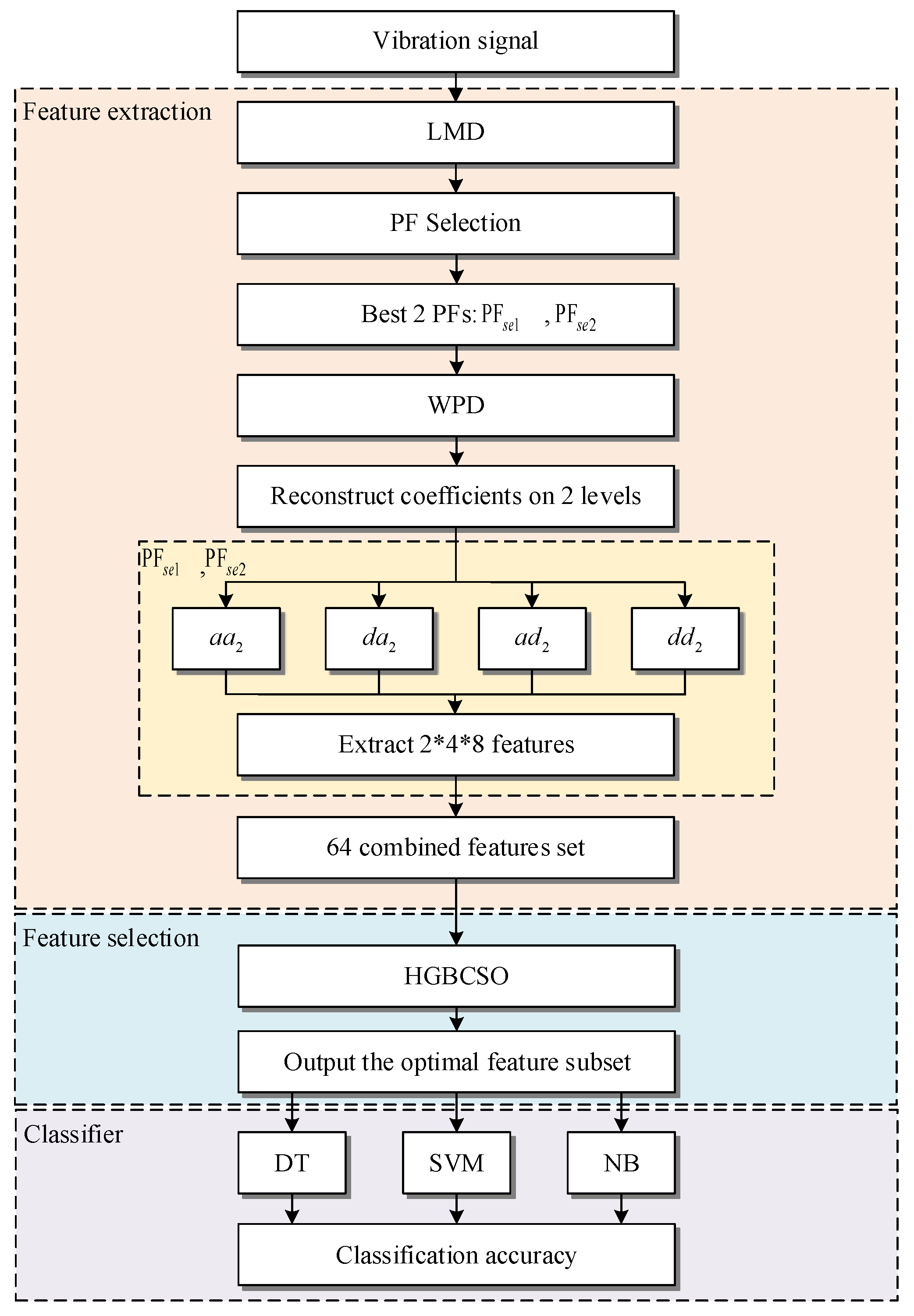
- Stage 1:
- Measuring the vibration signals from the test IM, which are processed by multilayer signal analysis. The first layer is to use LMD to decompose the vibration signals into a set of PFs. The second layer is to use PF selection to select two effective PFs. The third layer is to use WPD to further analyze and denoise the selected PFs. In this model, the wavelet decomposition level is adopted at level 2. The eight statistical feature parameters are calculated for each wavelet packet coefficient. Finally, 64 features are extracted during Stage 1.
- Stage 2:
- Using the proposed method HGBCSO to remove the irrelative features from the feature set, achieving the optimal feature subset. The optimal feature subset will improve the classifier performance of the fault diagnosis model.
- Stage 3:
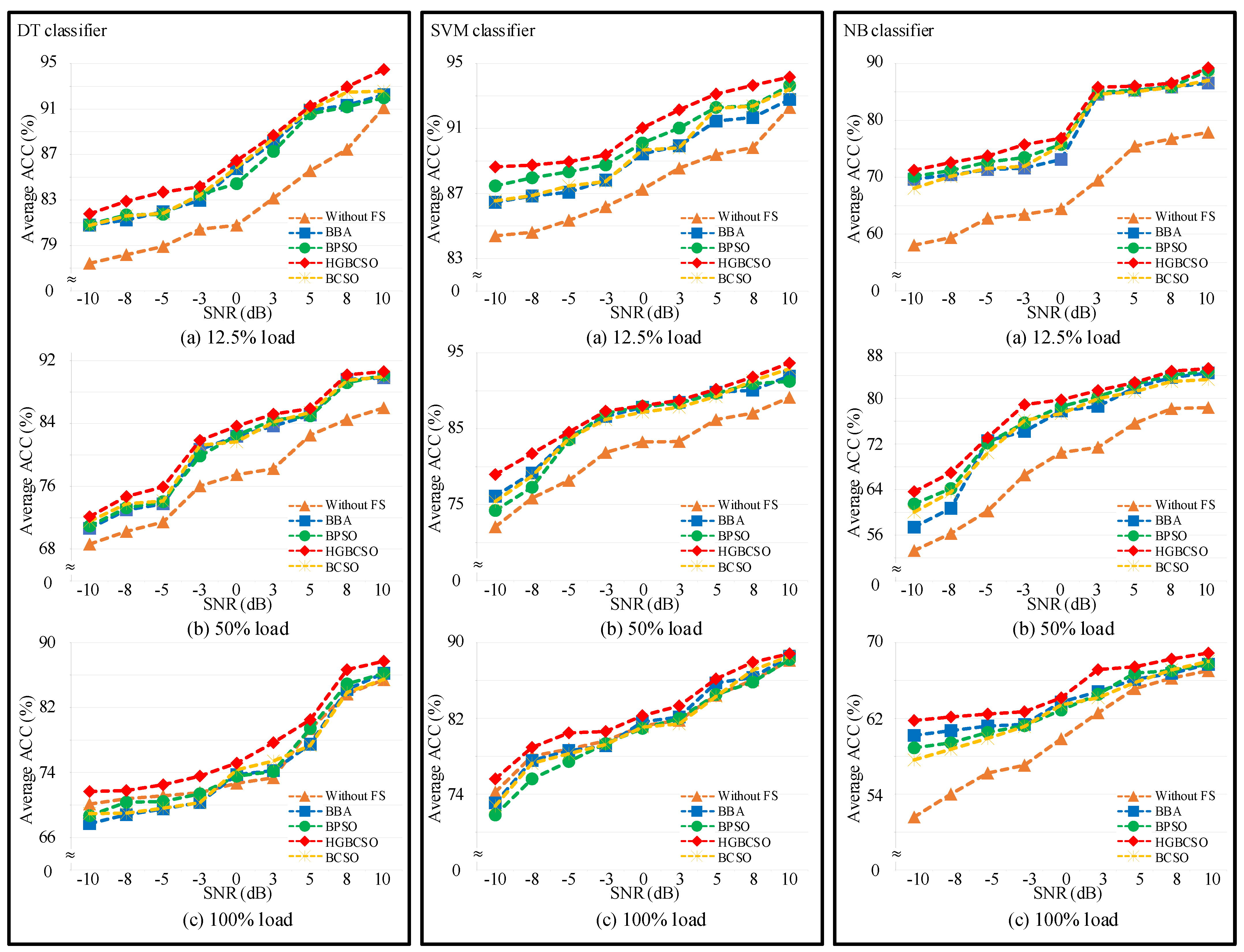
- Three well-known classifiers, including DT, SVM, and NB, are used to classify the optimal feature subset. The ACCs are used to evaluate the robustness of classifiers with rotor bar data to select the best classifier for diagnosing rotor bar faults.
5. Experiment Results
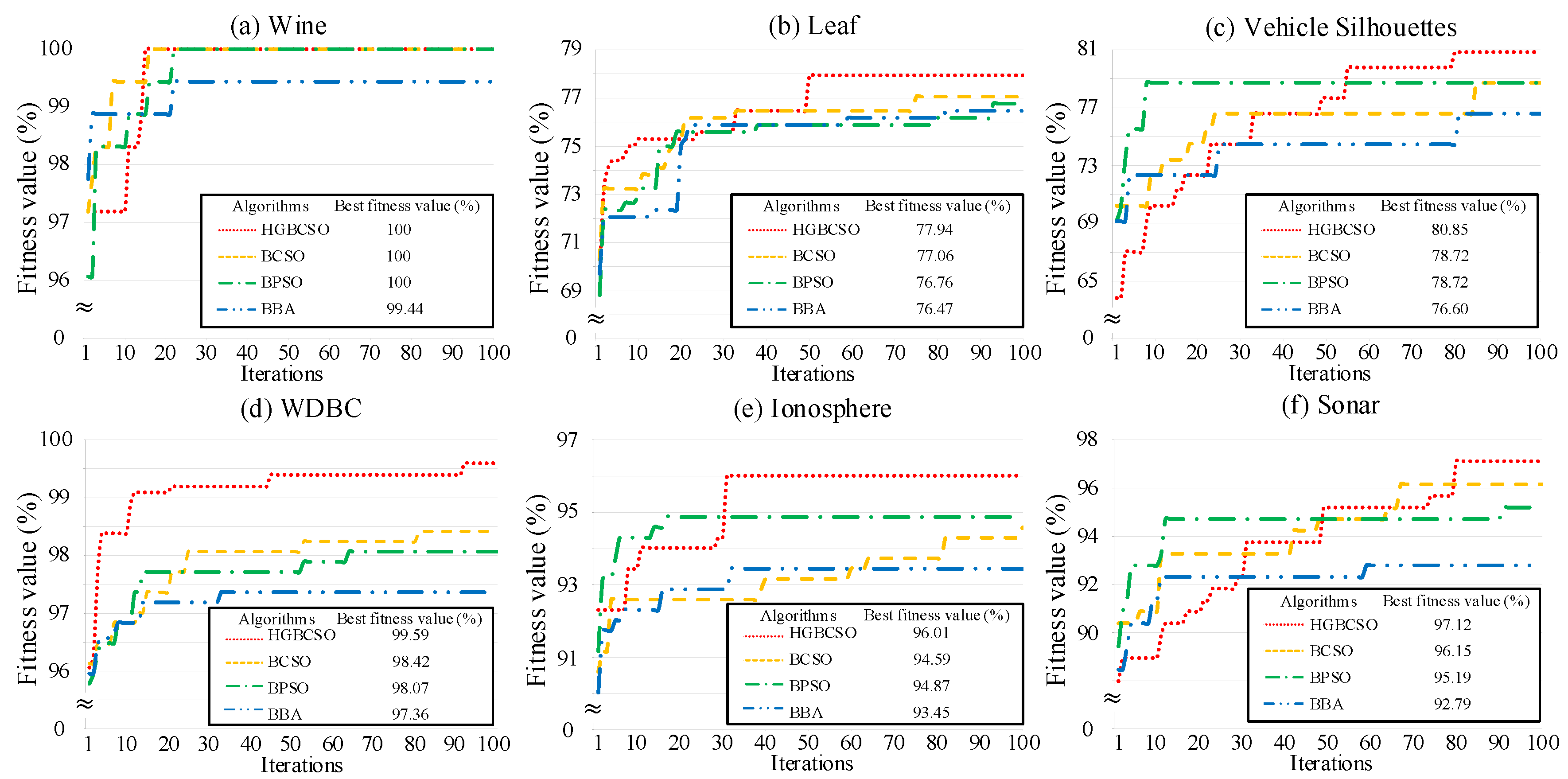
5.1. Case Study 1: UCI Machine Learning Datasets
- Describe of Datasets
- 2.
- Parameter Setting
- 3.
- Experimental Results for UCI Machine Learning Datasets
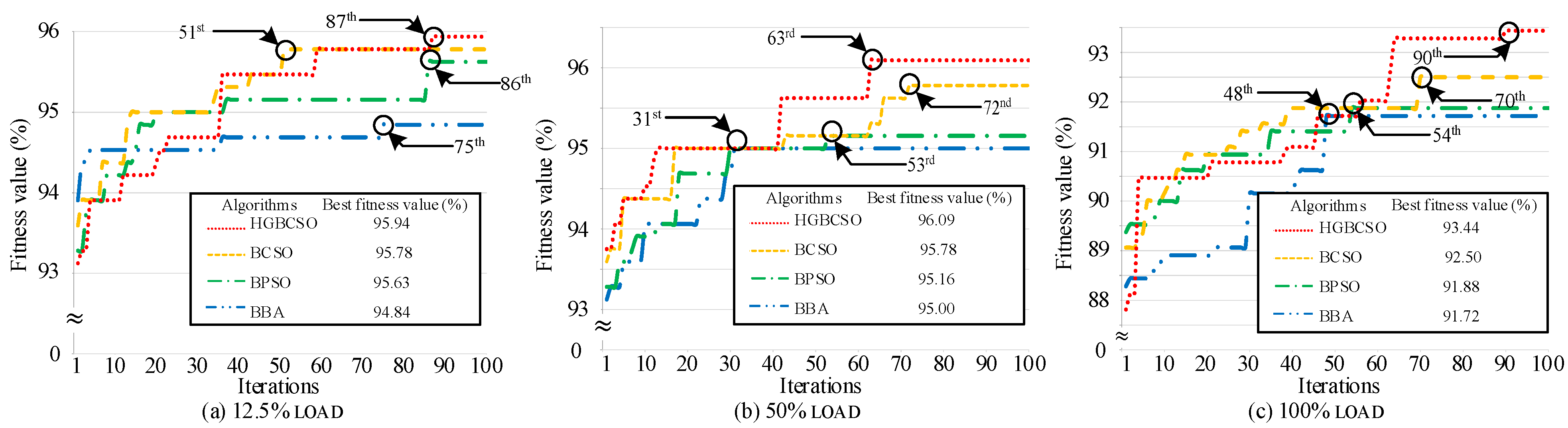
5.2. Case Study 2: Rotor Broken Bar Experimental Database
- Experimental Setup
- 2.
- Experimental Results for Feature Selection
- 3.
- Experimental results for classification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ola, E.H.; Amer, M.; Abdelsalam, A.K.; Williams, B.W. Induction motor broken rotor bar fault detection techniques based on fault signature analysis—A review. Electr. Power Appl. IET 2018, 12, 895–907. [Google Scholar]
- Garcia-Perez, A.; Ibarra-Manzano, O.; Romero-Troncoso, R.J. Analysis of partially broken rotor bar by using a novel empirical mode decomposition method. In Proceedings of the 40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 3403–3408. [Google Scholar]
- Brkovic, A.; Gajic, D.; Gligorijevic, J.; Savic-Gajic, I.; Georgieva, O.; Di Gennaro, S. Early fault detection and diagnosis in bearings for more efficient operation of rotating machinery. Energy 2017, 136, 63–71. [Google Scholar] [CrossRef]
- Gligorijevic, J.; Gajic, D.; Brkovic, A.; Savic-Gajic, I.; Georgieva, O.; Di Gennaro, S. Online condition monitoring of bearings to support total productive maintenance in the packaging materials industry. Sensors 2016, 16, 316. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.-J. Bearing-fault diagnosis using non-local means algorithm and empirical mode decomposition-based feature extraction and two-stage feature selection. IET Sci. Meas. Technol. 2015, 9, 671–680. [Google Scholar] [CrossRef]
- Helmi, H.; Forouzantabar, A. Rolling bearing fault detection of electric motor using time domain and frequency domain features extraction and ANFIS. IET Electr. Power Appl. 2019, 13, 662–669. [Google Scholar] [CrossRef]
- Singh, A.; Grant, B.; DeFour, R.; Sharma, C.; Bahadoorsingh, S. A review of induction motor fault modeling. Electr. Power Syst. Res. 2016, 133, 191–197. [Google Scholar] [CrossRef]
- Delgado-Arredondo, P.A.; Morinigo-Sotelo, D.; Osornio-Rios, R.A.; Avina-Cervantes, J.G.; Rostro-Gonzalez, H.; de Jesus Romero-Troncoso, R. Methodology for fault detection in induction motors via sound and vibration signals. Mech. Syst. Signal Process. 2017, 83, 568–589. [Google Scholar] [CrossRef]
- Yiyuan, G.; Dejie, Y.; Haojiang, W. Fault diagnosis of rolling bearings using weighted horizontal visibility graph and graph Fourier transform. Measurement 2020, 149, 107036. [Google Scholar]
- Fan, H.; Shao, S.; Zhang, X.; Wan, X.; Cao, X.; Ma, H. Intelligent fault diagnosis of rolling bearing using FCM clustering of EMD-PWVD vibration images. IEEE Access 2020, 8, 145194–145206. [Google Scholar] [CrossRef]
- Gao, M.; Yu, G.; Wang, T. Impulsive gear fault diagnosis using adaptive morlet wavelet filter based on alpha-stable distribution and kurtogram. IEEE Access 2019, 7, 72283–72296. [Google Scholar] [CrossRef]
- Pachori, R.B.; Nishad, A. Cross-terms reduction in the Wigner–Ville distribution using tunable-Q wavelet transform. Signal Process. 2016, 120, 288–304. [Google Scholar] [CrossRef]
- Huo, Z.; Zhang, Y.; Francq, P.; Shu, L.; Huang, J. Incipient fault diagnosis of roller bearing using optimized wavelet transform based multi-speed vibration signatures. IEEE Access 2017, 5, 19442–19456. [Google Scholar] [CrossRef]
- Minhas, A.S.; Singh, G.; Singh, J.; Kankar, P.K.; Singh, S. A novel method to classify bearing faults by integrating standard deviation to refined composite multi-scale fuzzy entropy. Measurement 2020, 154, 107441. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Li, P.; Gao, J.; Xu, D.; Wang, C.; Yang, X. Hilbert-Huang transform with adaptive waveform matching extension and its application in power quality disturbance detection for microgrid. J. Mod. Power Syst. Clean Energy 2016, 4, 19–27. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Miao, Q.; Wang, L. An optimized time varying filtering based empirical mode decomposition method with grey wolf optimizer for machinery fault diagnosis. J. Sound Vib. 2018, 418, 55–78. [Google Scholar] [CrossRef]
- Smith, J.S. The local mean decomposition and its application to EEG perception data. J. R. Soc. Inter. 2005, 2, 443–454. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; He, Z.; Zi, Y. A Comparative Study on the Local Mean Decomposition and Empirical Mode Decomposition and Their Applications to Rotating Machinery Health Diagnosis. ASME J. Vib. Acoust. 2010, 132, 021010. [Google Scholar] [CrossRef]
- Cheng, J.; Yang, Y.; Yang, Y. A rotating machinery fault diagnosis method based on local mean decomposition. Dig. Signal Process. 2012, 22, 356–366. [Google Scholar] [CrossRef]
- Guo, W.; Huang, L.; Chen, C.; Zou, H.; Liu, Z. Elimination of end effects in local mean decomposition using spectral coherence and applications for rotating machinery. Dig. Signal Process. 2016, 55, 52–63. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, G.; Liang, L.; Jiang, K. Detection of weak transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis. Mech. Syst. Signal Process. 2015, 54–55, 259–276. [Google Scholar] [CrossRef]
- Shao, R.; Hu, W.; Wang, Y.; Qi, X. The fault feature extraction and classification of gear using principal component analysis and kernel principal component analysis based on the wavelet packet transform. Measurement 2014, 54, 118–132. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, Q.; Wen, J.; Wang, F. Natural gas pipeline small leakage feature extraction and recognition based on LMD envelope spectrum entropy and SVM. Measurement 2014, 55, 434–443. [Google Scholar] [CrossRef]
- Ang, J.C.; Mirzal, A.; Haron, H.; Hamed, H.N.A. Supervised, unsupervised, and semi-supervised feature selection: A review on gene selection. IEEE/ACM Trans. Comput. Biol. Bioinf. 2016, 13, 971–989. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.-B.; Gao, X.Z.; Liu, Y.; Zhang, H. A novel bat algorithm with habitat selection and Doppler effect in echoes for optimization. Expert Syst. Appl. 2015, 42, 6350–6364. [Google Scholar] [CrossRef]
- Karim, A.A.; Isa, N.A.M.; Lim, W.H. Modified particle swarm optimization with effective guides. IEEE Access 2020, 8, 188699–188725. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A new bio-inspired algorithm: Chicken swarm optimization. In Advances in Swarm Intelligence (Lecture Notes in Computer Science); Springer: Cham, Switzerland, 2014; Volume 8794, pp. 86–94. [Google Scholar]
- Liang, X.; Kou, D.; Wen, L. An improved chicken swarm optimization algorithm and its application in robot path planning. IEEE Access 2020, 8, 49543–49550. [Google Scholar] [CrossRef]
- Qu, C.; Zhao, S.; Fu, Y.; He, W. Chicken swarm optimization based on elite opposition-based learning. Math. Probl. Eng. 2017, 2017, 1–20. [Google Scholar] [CrossRef]
- Liang, S.; Fang, Z.; Sun, G.; Liu, Y.; Qu, G.; Zhang, Y. Sidelobe reductions of antenna arrays via an improved chicken swarm optimization approach. IEEE Access 2020, 8, 37664–37683. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Le, T.-A. Optimised approach of feature selection based on genetic and binary state transition algorithm in the classification of bearing fault in BLDC motor. IET Electr. Power Appl. 2020, 14, 2598–2608. [Google Scholar] [CrossRef]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A survey on evolutionary computation approaches to feature selection. IEEE Trans. Evol. Comput. 2016, 20, 606–626. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4108. [Google Scholar]
- Nakamura, R.Y.M.; Pereira, L.A.M.; Rodrigues, D.; Costa, K.A.P.; Papa, J.P.; Yang, X.-S. 9—Binary bat algorithm for feature selection. In Swarm Intelligence and Bio-Inspired Computation; Elsevier: Amsterdam, The Netherlands, 2013; pp. 225–237. [Google Scholar]
- Liu, F.; Yan, X.; Lu, Y. Feature selection for image steganalysis using binary bat algorithm. IEEE Access 2019, 8, 4244–4249. [Google Scholar] [CrossRef]
- Ahmed, K.; Hassanien, A.E.; Bhattacharyya, S. A novel chaotic chicken swarm optimization algorithm for feature selection. In Proceedings of the 3rd International Conference on Research in Computational Intelligence and Communication Networks (ICRCICN), Kolkata, India, 3–5 November 2017; pp. 259–264. [Google Scholar]
- Hafez, A.I.; Zawbaa, H.M.; Emary, E.; Mahmoud, H.A.; Hassanien, A.E. An innovative approach for feature selection based on chicken swarm optimization. In Proceedings of the 7th International Conference of Soft Computing and Pattern Recognition (SoCPaR), Fukuoka, Japan, 13–15 November 2015; pp. 19–24. [Google Scholar]
- Long, J.; Zhang, S.; Li, C. Evolving deep echo state networks for intelligent fault diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 4928–4937. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Le, T.-A. Intelligence bearing fault diagnosis model using multiple feature extraction and binary particle swarm optimization with extended memory. IEEE Access 2020, 8, 198343–198356. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Ficarella, A.; Lay-Ekuakille, A. Cavitation regime detection by LS-SVM and ANN with wavelet decomposition based on pressure sensor signals. IEEE Sens. J. 2015, 15, 5701–5708. [Google Scholar] [CrossRef]
- Sunny; Kumar, V.; Mishra, V.N.; Dwivedi, R.; Das, R.R. Classification and quantification of binary mixtures of gases/odors using thick-film gas sensor array responses. IEEE Sens. J. 2015, 15, 1252–1260. [Google Scholar] [CrossRef]
- Shamshirband, S.; Petković, D.; Javidnia, H.; Gani, A. Sensor data fusion by support vector regression methodology—A comparative study. IEEE Sens. J. 2015, 15, 850–854. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Congedo, P.M.; Malvoni, M.; Laforgia, D. Error analysis of hybrid photovoltaic power forecasting models: A case study of mediterranean climate. Energy Convers. Manag. 2015, 100, 117–130. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Meng, L.; Xiang, J.; Wang, Y.; Jiang, Y.; Gao, H. A hybrid fault diagnosis method using morphological filter–translation invariant wavelet and improved ensemble empirical mode decomposition. Mech. Syst. Signal Process. 2015, 50–51, 101–115. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Lin, J. A new method based on stochastic process models for machine remaining useful life prediction. IEEE Trans. Instrum. Meas. 2016, 65, 2671–2684. [Google Scholar] [CrossRef]
- Xu, F.; Song, X.; Tsui, K.; Yang, F.; Huang, Z. Bearing performance degradation assessment based on ensemble empirical mode decomposition and affinity propagation clustering. IEEE Access 2019, 7, 54623–54637. [Google Scholar] [CrossRef]
- Yu, J.; Lv, J. Weak fault feature extraction of rolling bearings using local mean decomposition-based multilayer hybrid denoising. IEEE Trans. Instrum. Meas. 2017, 66, 3148–3159. [Google Scholar] [CrossRef]
- Xian, G.-M.; Zeng, B.-Q. An intelligent fault diagnosis method based on wavelet packer analysis and hybrid support vector machines. Expert Syst. Appl. 2009, 36, 12131–12136. [Google Scholar] [CrossRef]
- Bansal, J.C.; Singh, P.K.; Saraswat, M.; Verma, A.; Jadon, S.S.; Abraham, A. Inertia weight strategies in particle swarm optimization. In Proceedings of the 2011 IEEE World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, 19–21 October 2011; pp. 633–640. [Google Scholar]
- He, Y.; Hu, M.; Feng, K.; Jiang, Z. An intelligent fault diagnosis scheme using transferred samples for intershaft bearings under variable working conditions. IEEE Access 2020, 8, 203058–203069. [Google Scholar] [CrossRef]
- Van, M.; Kang, H. Wavelet kernel local fisher discriminant analysis with particle swarm optimization algorithm for bearing defect classification. IEEE Trans. Instrum. Meas. 2015, 64, 3588–3600. [Google Scholar] [CrossRef]
- UCI Machine Learning Repository. Available online: http://archive.ics.uci.edu/ml (accessed on 5 September 2020).
- Treml, A.E.; Flauzino, R.A.; Suetake, M.; Maciejewski, N.A.R. Experimental database for detecting and diagnosing rotor broken bar in a three-phase induction motor. IEEE DataPort 2020. [Google Scholar] [CrossRef]
| Feature | Equation |
|---|---|
| (1) Max value | |
| (2) Min value | |
| (3) Root mean square | |
| (4) Mean square error | |
| (5) Standard deviation | |
| (6) Kurtosis | |
| (7) Crest factor | |
| (8) Clearance factor |
| Datasets | Features | Instances | Classes |
|---|---|---|---|
| Wine | 13 | 178 | 3 |
| Leaf | 15 | 340 | 30 |
| Vehicle Silhouettes | 18 | 94 | 4 |
| WDBC | 30 | 569 | 2 |
| Ionosphere | 34 | 351 | 2 |
| Sonar | 60 | 208 | 2 |
| HGBCSO | BCSO | BPSO | BBA |
|---|---|---|---|
| Number of chickens: 10 Number of iterations: 100 Rooster parameter: 0.2 Hen parameter: 0.7 Mother parameter: 0.1 ωmin = 0.4 ωmax = 0.9 | Number of chickens: 10 Number of iterations: 100 Rooster parameter: 0.2 Hen parameter: 0.7 Mother parameter: 0.1 | Number of particles: 10 Number of iterations: 100 c1 = c2 = 2.05 | Number of bats: 10 Number of iterations: 100 Maximum frequency: 2 Minimum frequency: 0 Loudness: 0.9 Pulse rate: 0.9 |
| Datasets | HGBCSO | BCSO | BPSO | BBA | ||||
|---|---|---|---|---|---|---|---|---|
| Avg Fitness Value | Avg No. Fs | Avg Fitness Value | Avg No. Fs | Avg Fitness Value | Avg No. Fs | Avg Fitness Value | Avg No. Fs | |
| Wine | 99.53 | 8.93 | 99.49 | 8.60 | 99.06 | 8.37 | 98.29 | 7.77 |
| Leaf | 76.25 | 10.73 | 76.07 | 10.73 | 75.16 | 10.43 | 72.45 | 9.2 |
| Vehicle Silhouettes | 76.60 | 8.33 | 75.99 | 9.17 | 74.61 | 9.37 | 71.21 | 9.57 |
| WDBC | 99.37 | 16.23 | 97.81 | 16.30 | 97.45 | 15.60 | 96.83 | 15.90 |
| Ionosphere | 94.19 | 13.23 | 93.76 | 14.3 | 93.23 | 14.77 | 91.72 | 15.7 |
| Sonar | 94.37 | 31.07 | 93.53 | 31.13 | 93.33 | 31.43 | 90.51 | 30.43 |
| Algorithms | Avg Fitness Value (%) | Avg No. Fs |
|---|---|---|
| HGBCSO | 95.09 | 31.73 |
| BCSO | 95.05 | 31.97 |
| BPSO | 93.99 | 32.80 |
| BBA | 94.57 | 32.83 |
| Algorithms | Avg Fitness Value (%) | Avg No. Fs |
|---|---|---|
| HGBCSO | 95.22 | 28.6 |
| BCSO | 95.09 | 30.27 |
| BPSO | 94.64 | 33.03 |
| BBA | 94.22 | 32.70 |
| Algorithms | Avg Fitness Value (%) | Avg No. Fs |
|---|---|---|
| HGBCSO | 91.86 | 29.10 |
| BCSO | 91.70 | 30.67 |
| BPSO | 90.83 | 31.50 |
| BBA | 89.85 | 31.57 |
| Algorithms | Features | Feature Indicators (F) |
|---|---|---|
| HGBCSO | 22 | 2, 3, 5, 9, 10, 12, 14, 15, 16, 17, 18, 19, 20, 22, 29, 30, 41, 44, 47, 49, 51, 55. |
| BCSO | 28 | 1, 2, 3, 5, 7, 8, 9, 11, 12, 13, 14, 15, 16, 17, 20, 23, 26, 27, 29, 30, 32, 40, 41, 46, 51, 52, 55, 58. |
| BPSO | 31 | 2, 3, 5, 8, 9, 11, 12, 13, 15, 16, 17, 18, 19, 20, 22, 25, 26, 27, 28, 29, 30, 31, 32, 33, 38, 41, 45, 46, 50, 51, 63. |
| BBA | 32 | 2, 3, 4, 8, 9, 11, 12, 13, 14, 15, 16, 18, 19, 20, 22, 24, 26, 27, 30, 32, 33, 35, 36, 38, 40, 41, 42, 44, 45, 49, 54, 63. |
| Algorithms | Features | Feature Indicators (F) |
|---|---|---|
| HGBCSO | 27 | 1, 5, 6, 7, 9, 10, 11, 12, 13, 14, 19, 20, 21, 22, 24, 25, 26, 28, 31, 33, 36, 39, 40, 42, 48, 53, 61. |
| BCSO | 38 | 1, 3, 4, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 19, 20, 21, 23, 24, 25, 31, 32, 33, 35, 37, 38, 39, 42, 43, 46, 47, 50, 51, 52, 53, 55, 57, 61, 63. |
| BPSO | 30 | 1, 6, 7, 8, 9, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22, 24, 27, 31, 37, 38, 39, 42, 43, 44, 46, 48, 49, 50, 52, 55. |
| BBA | 32 | 1, 3, 4, 7, 8, 9, 10, 11, 12, 13, 14, 16, 18, 20, 22, 25, 27, 29, 31, 34, 35, 36, 38, 39, 40, 45, 48, 51, 54, 56, 58, 60. |
| Algorithms | Features | Feature Indicators (F) |
|---|---|---|
| HGBCSO | 23 | 1, 2, 4, 5, 10, 12, 15, 16, 17, 18, 19, 20, 22, 23, 24, 37, 38, 41, 42, 43, 44, 46, 52. |
| BCSO | 33 | 5, 6, 8, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 22, 23, 24, 25, 27, 32, 33, 37, 40, 41, 43, 44, 45, 49, 51, 52, 53, 56, 61, 63. |
| BPSO | 33 | 3, 5, 6, 8, 9, 10, 11, 12, 14, 16, 17, 19, 20, 21, 22, 23, 25, 27, 28, 36, 37, 42, 44, 47, 49, 50, 52, 53, 54, 55, 59, 61, 63. |
| BBA | 34 | 3, 4, 5, 6, 8, 9, 10, 11, 12, 13, 15, 17, 18, 19, 20, 22, 23, 25, 26, 28, 32, 33, 36, 37, 39, 41, 42, 45, 46, 50, 53, 54, 59, 62. |
| DT | SVM | NB |
|---|---|---|
| Complex tree Split criterion: Gini’s diversity index Surrogate splits: off Max number of splits: 100 | Kernel function: polynomial Polynomial order: 2 Kernel scale: auto Box constraint: 1 | Kernel distributions: normal Support regions: unbounded |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-Y.; Zhuo, G.-L. Effective Rotor Fault Diagnosis Model Using Multilayer Signal Analysis and Hybrid Genetic Binary Chicken Swarm Optimization. Symmetry 2021, 13, 487. https://doi.org/10.3390/sym13030487
Lee C-Y, Zhuo G-L. Effective Rotor Fault Diagnosis Model Using Multilayer Signal Analysis and Hybrid Genetic Binary Chicken Swarm Optimization. Symmetry. 2021; 13(3):487. https://doi.org/10.3390/sym13030487
Chicago/Turabian StyleLee, Chun-Yao, and Guang-Lin Zhuo. 2021. "Effective Rotor Fault Diagnosis Model Using Multilayer Signal Analysis and Hybrid Genetic Binary Chicken Swarm Optimization" Symmetry 13, no. 3: 487. https://doi.org/10.3390/sym13030487
APA StyleLee, C.-Y., & Zhuo, G.-L. (2021). Effective Rotor Fault Diagnosis Model Using Multilayer Signal Analysis and Hybrid Genetic Binary Chicken Swarm Optimization. Symmetry, 13(3), 487. https://doi.org/10.3390/sym13030487







