Abstract
In the field of cognitive science, much research has been conducted on the diverse applications of artificial intelligence (AI). One important area of study is machines imitating human thinking. Although there are various approaches to development of thinking machines, we assume that human thinking is not always optimal in this paper. Sometimes, humans are driven by emotions to make decisions that are not optimal. Recently, deep learning has been dominating most machine learning tasks in AI. In the area of optimal decisions involving AI, many traditional machine learning methods are rapidly being replaced by deep learning. Therefore, because of deep learning, we can expect the faster growth of AI technology such as AlphaGo in optimal decision-making. However, humans sometimes think and act not optimally but emotionally. In this paper, we propose a method for building thinking machines imitating humans using Bayesian decision theory and learning. Bayesian statistics involves a learning process based on prior and posterior aspects. The prior represents an initial belief in a specific domain. This is updated to posterior through the likelihood of observed data. The posterior refers to the updated belief based on observations. When the observed data are newly added, the current posterior is used as a new prior for the updated posterior. Bayesian learning such as this also provides an optimal decision; thus, this is not well-suited to the modeling of thinking machines. Therefore, we study a new Bayesian approach to developing thinking machines using Bayesian decision theory. In our research, we do not use a single optimal value expected by the posterior; instead, we generate random values from the last updated posterior to be used for thinking machines that imitate human thinking.
1. Introduction
Many researchers have discussed whether machines can think like humans [1,2,3,4,5]. At the same time, some studies have been performed on whether machines understand the human mind [5,6,7,8,9]. Turing (1950) was the first scholar to present the possibility of a thinking computer [5]. He proposed the Turing test to determine whether computers can imitate humans [5]. In 2016, AlphaGo defeated Lee Sedol, who is the worldwide Go champion [10]. This represented a meaningful beginning for artificial intelligence (AI) to outperform humans in complex real-world problems [11]. AI is the art of making computers intelligent. In recent decades, AI has seen remarkable progress with the help of a new machine learning algorithm called deep learning. Deep learning provides the dominant performance in most tasks of current connectionist AI [12]. This is a machine learning algorithm that can better describe the information processing structure of the human brain, composed of numerous neurons, by using much more hidden layers than existing neural network algorithms [12]. With the use of deep learning, the pace of AI development is increasing. AI is currently focused on developing technologies that support optimal decision-making, but over time, it is expected to expand to human intelligence beyond optimal decision-making. Consequently, we need research cognitive AI that can interact with humans. Therefore, first of all, we study a method that can model a machine that can imitate human thinking. In various categories of AI, thinking like humans is the cognitive computing approach to making thinking machines because thinking is related to the mind [13,14]. The mind is involved in all parts of human cognition, including spirit, emotion, perception, learning, thought and so on [15]. Since the advent of AI, we have been constantly trying to develop a thinking machine with human emotions [16,17]. Such AI is called the artificial mind (AM) [2,6,8,9,18]. Although there have been several approaches to AM in previous studies, in this paper, we propose a new approach to the implementation of AM for building thinking machines. Unlike classical AI approaches based on symbolic or connectionist concepts, our proposed method does not always make optimal decisions. This is because humans do not always make optimal decisions. Humans sometimes make less-than-optimal decisions. However, it does not deviate significantly from the optimum. Through this behavior, we can build machines that mimic human thinking.
Experts’ opinions on the future of AI are conflicting. Some experts claim that AI destroys humanity, while another expert group argues that human life is dramatically improved with the help of AI. In order to develop AI that facilitates intimacy with humans, we consider implementing a machine that can imitate humans. Thus, we study the development of machines which imitate human thinking. In our research, we use Bayesian learning to build thinking machines which reflect humans. This is because it is possible to use the concepts of prior, likelihood and posterior from Bayesian decision theory and learning to model the human mind [19,20,21]. The prior and likelihood represent human past and present experiences (states), respectively. The posterior, defined as the product of the prior and likelihood, represents the human mind, making the final decision based on past and present states. In order to show the potential of the proposed method for implementation in cognitive AI, we perform simulation studies.
As AI progresses, the asymmetry between humans and AI will increase. Compared to humans, the intelligence of AI is expected to be further strengthened. In order to overcome the asymmetry of intelligence between AI and humans, we study how to build a machine that can imitate humans in this paper. Through this research, we try to demonstrate the symmetry of the intelligence between humans and AI. The remainder of this paper is organized as follows. In Section 2, we deal with the research background related to Bayesian decision theory. The proposed method for building thinking machines similar to humans is described in Section 3. The simulation results to illustrate how the proposed method can be applied in practical areas are shown in Section 4. The final section presents the conclusions of this paper and future research tasks.
2. Review of the Literature
2.1. Bayesian Inference and Learning
In the 1740s, Bayes proposed an approach to making inferences based on conditional probability, called Bayes’ rule [22,23]. When X and are the observed data and parameter of model, Bayesian inference begins based on Bayes’ rule, as shown in Equation (1) [20].
where is the posterior distribution computed with and which are prior and likelihood distributions, respectively. Additionally, is evidence calculated as follows: or for discrete and continuous cases, respectively. This is the sum of all possible values of [19]. Moreover, represents the prior belief of the model parameter and depicts the likelihood of observed data. The posterior distribution is proportional to the product of prior distribution (past) and likelihood function (current). Using this process, we obtain the following updated belief of model parameters [24].
In the Bayesian inferential process shown in Figure 1, the initial belief of the model parameters and the new observed data are multiplied to finally produce the updated belief of the parameters. Because of this learning process, Bayesian inference is a more suitable approach to cognitive AI compared to statistical inference in frequentist or classical machine learning [25]. Bayesian learning has been used in various fields, improving the performance of learning methods. Meng et al. (2020) used Bayesian learning for training neural networks with binary weights [26]. They updated the binary weights by the gradient descent based on Bayesian inference. Liu et al. (2020) studied a method to solve the resolution problem in frequency-difference electrical impedance tomography using multitask structure-aware sparse Bayesian learning by a hierarchical Bayesian framework and modified marginal likelihood maximization [27]. Chen et al. (2020) also applied sparse Bayesian learning to identify structural damage [28]. They proposed a Bayesian learning method consisting of classical Bayesian inference and sparse Bayesian learning for identifying structural damage with sparse characteristics.

Figure 1.
Bayesian inferential process.
2.2. Bayesian Learning for Human Behaviors
In this paper, we consider the Bayesian inference procedure to build a Bayesian learning model for thinking machines. The thinking machine implies both technological and philosophical concepts at the same time [8,9]. Of course, it is difficult to develop thinking machines because it is very difficult to understand the human mind itself. The study of the mind has been carried out through interdisciplinary study involving various fields, such as cognitive science, psychology, brain science, mathematics, statistics, computer science and neuroscience [1]. In many theoretical areas related to the mind, cognitive science plays a key role [1]. Moreover, mind modeling is a very complex and sophisticated type of nonlinear modeling [15,16]. To connect the computer and the mind, Turing (1950) proposed the possibility of thinking machines [5]. In the imitation game, he suggests that the machine can be something which imitates the behavior and mind of humans [5]. Walmsley (2012) showed the merging of human and machine minds. In his paper, he proposed a hypothesis of an extended mind based on cognitive methods and hybrid systems [29]. This is an approach to the technology singularity. The technology singularity was introduced by Kurzweil (2006) and describes the emergence of artificial general intelligence (AGI) [30,31]. Unlike AI, AGI is closely related to the development of thinking computers with general human intellectual abilities. Therefore, AGI is one of the various approaches to machine thinking. In addition, Bayesian learning can be one of the possible approaches to human thinking. Some research related to Bayesian learning for human behaviors has been presented in diverse fields such as human motion and emotion [32,33]. Lee et al. (2019) proposed a Bayesian theory of mind method. This was a framework of nonverbal communication for human–robot interaction using Bayesian learning. Kang and Ren (2016) used a hierarchical Bayesian network model for understanding human emotions. Mousas et al. (2014) showed a method of motion reconstruction using a constrained covariance structure based on principal component analysis and prior distribution [34]. In our research, we develop a model to build thinking machines to imitate the human mind using Bayesian decision theory and learning.
3. Proposed Methodology
We propose a model to build a machine imitating human thinking using Bayesian learning. Though the mind is a unique element that only human beings have, we try to develop a thinking machine similar to humans. The broader the area of the mind, the more difficult the process will be. Thus, we present a model for a limited area. In this paper, we construct a model for machines to imitate human thinking. Turing did not intend to build human intelligence on machines, but instead he wanted to develop a machine that can make humans believe that the computer they are talking to is human. This is Turing’s test [5]. We also study a learning model imitating the human mind to implement the same machine as proposed by Turing. Using our proposed model, we build a machine for AM; that is, our research is related to not AI but AM.
3.1. Bayesian Learning
The proposed machine is updated through learning from continuously observed data. This empirical learning from data provides better performance when combined with Bayesian inference [35]. Thus, we perform empirical Bayesian data analysis and build a model of Bayesian learning for imitating human thinking. In our research, we consider the concepts of prior, likelihood and posterior from Bayesian learning for building thinking machines. The prior represents the belief distribution of initial information. The likelihood function expresses information about the currently observed data, whereas the prior distribution expresses the degree of belief in past data (experiences). The observed data are reflected in the posterior distribution through the likelihood function. The posterior distribution is obtained by Bayes’ rule using prior and likelihood distributions [21]. The notations of the proposed methodology are listed in Table 1.

Table 1.
Notations of proposed methodology.
Based on the notations in Table 1, we show the posterior distribution of parameter θ in Equation (2).
This is the basis of the Bayesian learning process. In the beginning, we select a prior distribution that represents the initial belief about the parameters before new data are observed. Next, we observe new data () and define them by likelihood distribution with current experience. Finally, we update the posterior distribution using prior and likelihood. In the proposed method, we build thinking machines which reflect humans using the updated posterior distribution. is the sum of all values of . This is not dependent on and does not affect the posterior updating. Therefore, we do not consider it in Bayesian learning, as shown in Equation (3).
The posterior distribution is updated by combining the likelihood with the prior. The likelihood function contains the information about on observed data and the prior distribution contains the previous information about . In other words, the posterior distribution is proportional to the product of prior distribution and likelihood function. The thinking process of humans is continuously updated based on repeated learning from data and prior beliefs. Because the goal of our research is to build a Bayesian learning model for imitating the human mind, using Bayesian learning, we make better emotional decisions than previous models for computers that mimic the human mind. We implement the mind in the machine through probability distribution and computation. The machine thinking is not an external feature of the computer but an internal one. Just as humans’ ability to think through learning improves, machines can become increasingly capable of imitating human thinking through learning. Figure 2 illustrates our proposed method.
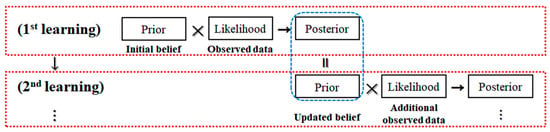
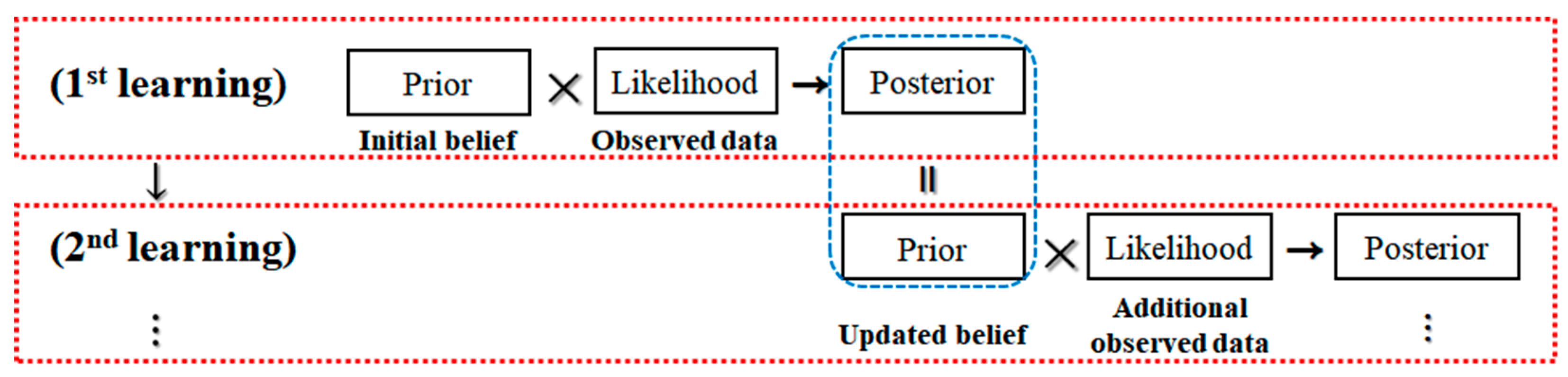
Figure 2.
Proposed Bayesian learning process.
In the first learning stage, we have the initial belief, called prior, and the observed new data, called likelihood. Using the prior and likelihood, we obtain the posterior distribution, and this is our updated belief. At this stage, our decisions are made using this posterior distribution. Next, when new data are added again, new learning is performed again. The previous posterior distribution is used as the current prior distribution and a new likelihood function is generated by new observed data. This results in a new posterior distribution, which becomes the updated belief. Until new data are observed, the thinking machine uses this posterior distribution to make decisions. Through this repeated learning, the machine gradually develops the ability to think like a human. Figure 3 shows the circulating structure of the thinking machine proposed in this paper.
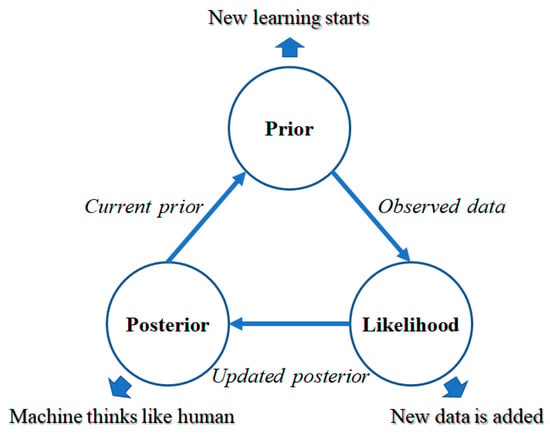
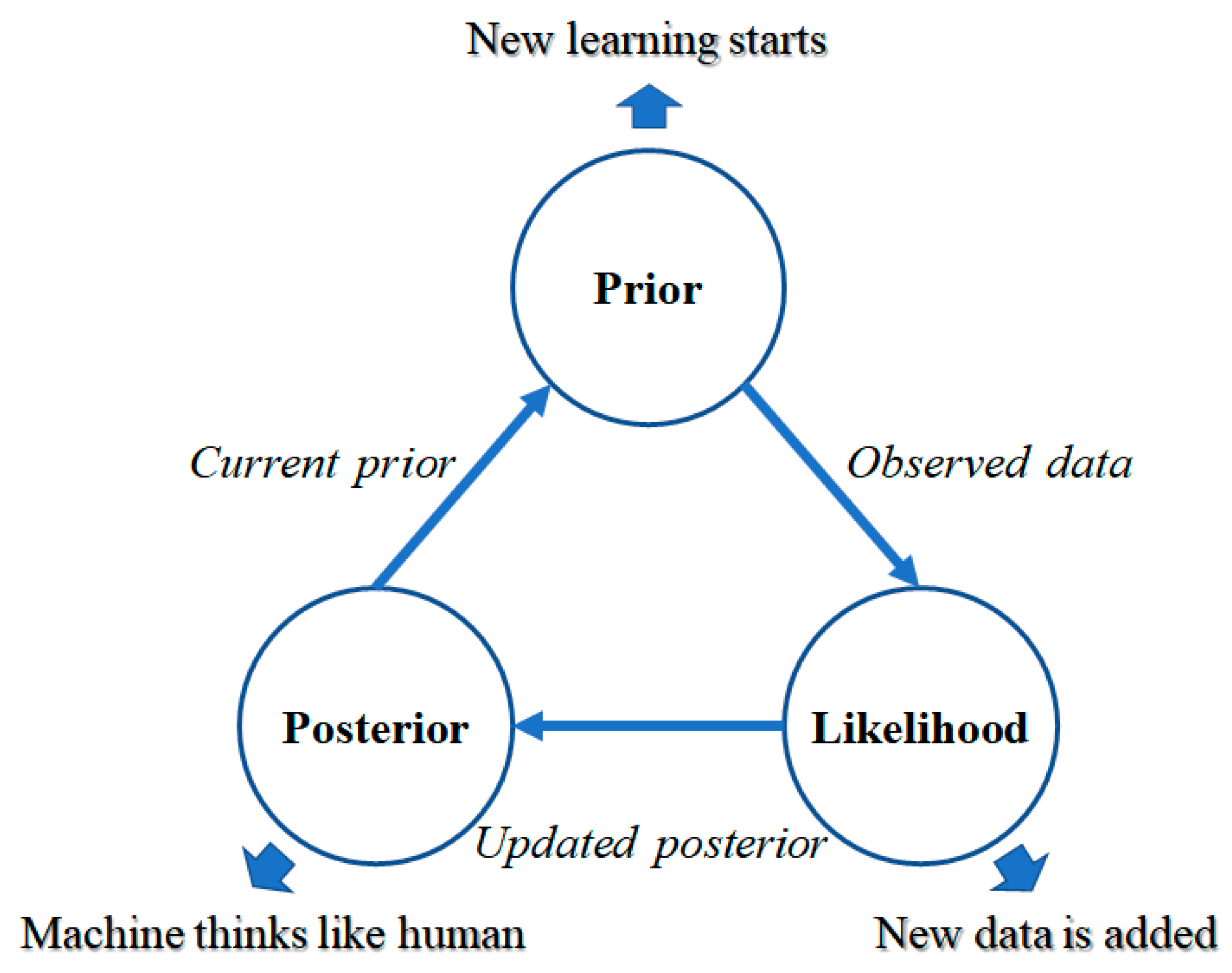
Figure 3.
Thinking machine structure.
In Figure 3, we illustrate the learning structure of the thinking machine. Without adding new data, the machine will think based on the current posterior distribution. However, when new data are added, this posterior distribution is used as the current prior for new learning.
3.2. Bayesian Bootstrap
In this paper, we represent data and belief as as X and θ, respectively. Thus, we express the prior and likelihood as and respectively. In the same way, the posterior distribution is denoted by and the machine’s thinking by . If we assume Gaussian distribution with mean for posterior, the optimal decision by AI always provides a single value based on , but the proposed model generates some random numbers from the posterior distribution . This means that our model provides multiple values for making decisions. In other words, our AM provides various decisions that are not optimal. However, the result is never far from optimal. Most results provided by our model are distributed near optimal values. In addition, human thinking is closer to multi-objective optimization than to single-objective optimization [36]. Therefore, we believe that our model thinks like a human; that is, it imitates human thinking.
The goal of our Bayesian learning is to estimate the unknown parameter μ given on , where is precision represented by the reverse of variance (). We use Bayesian inference to update our posterior associated with values of μ. We select a prior belief for μ and observe data; then, we update the prior to the posterior beliefs. Thus, this posterior distribution for μ (our interesting parameter) represents machine thinking. We also choose normal distribution as the prior distribution for μ in Equation (4).
where and are hyperparameters. We can imitate human thinking and decisions based on the distribution with μ in a given environment. Given the prior belief, and the various outcomes (), we observe experience following normal distribution in Equation (5).
In Equation (5), we obtain the probability based on the likelihood of experience (observed data). This equation can be expressed by using instead of as in Equation (6).
Lastly, we determine posterior distribution using Equations (4) and (6). The posterior distribution unknown is normal distribution in Equation (7).
In general, the optimal decision is performed by the mean value of normal distribution in Equation (7). As long as the parameters of Equation (7) are not changed, the decision is the same every time. However, in this paper, we make the decision using random values generated from the distribution in Equation (7). Assuming that () are random data generated from the normal distribution in Equation (7), the final value to be used for decision-making is estimated in Equation (8).
The expected value of Equation (8) may be changed by random values extracted from the final updated posterior distribution. This means that the variability of E(r) is able to imitate the variability of human thinking. Figure 4 shows a comparison of the decision process between AI and our machines imitating human thinking.
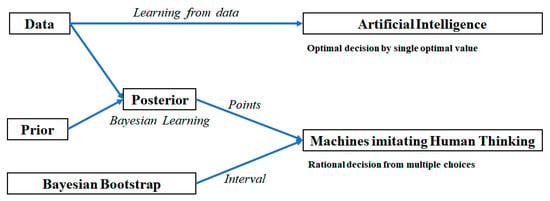
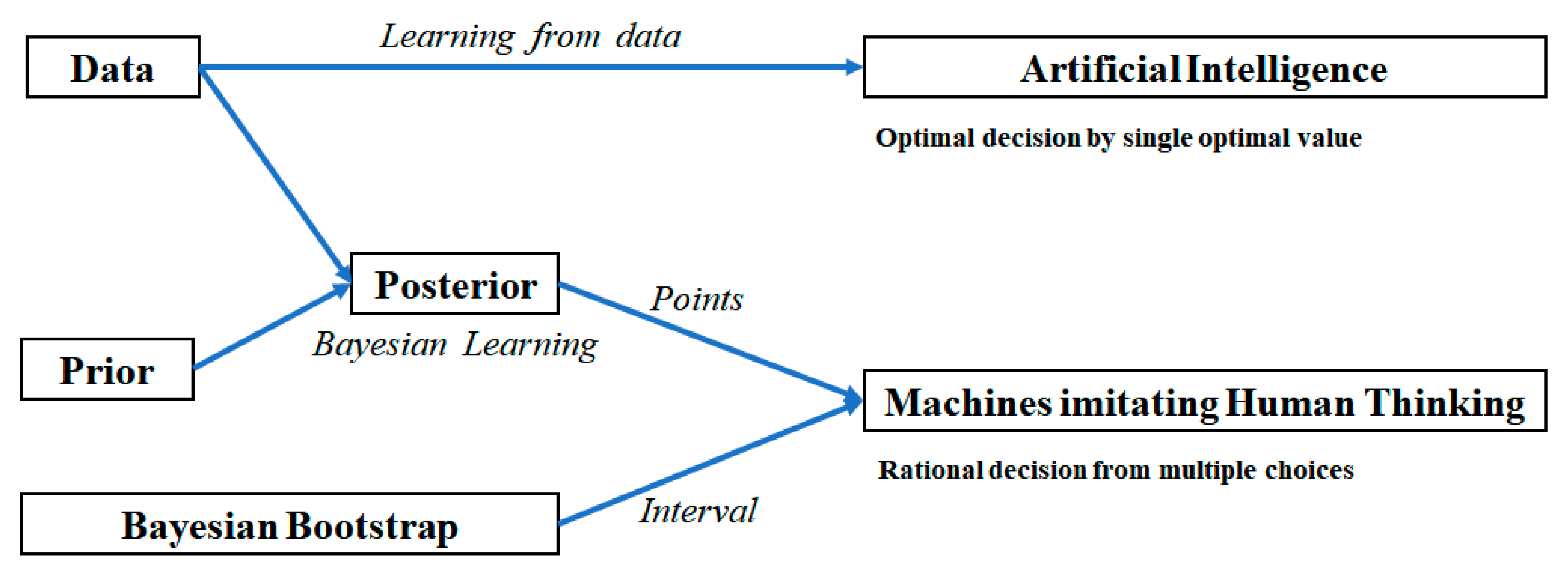
Figure 4.
Decision process of AI and machines which imitate humans.
Using observed data, AI provides optimal decisions using a single optimal value from the results of various machine learning algorithms. On the other hand, the proposed thinking machines carry out rational decision-making via multiple choices from the results of the Bayesian learning model using the final updated posterior computed by multiplying prior and likelihood. We consider another Bayesian decision theory called Bayesian bootstrap. Bootstrap is a method to estimate the sampling distribution of a parameter using the process of taking repeated samples with replacement from a given data sample [37]. Using bootstrap, we can obtain point or interval estimations of model parameters. Bayesian bootstrap is a bootstrap based on Bayesian inference. Bayesian bootstrap performs a simulation of posterior distribution for model parameters [38,39]. Using Bayesian bootstrap, we estimate the interval of parameters for thinking machines. Thus, we have multiple point values from the posterior based on Bayesian decision theory, and an interval from Bayesian bootstrap. Lastly, we construct machines imitating human thinking by combining two results. The purpose of our proposed model is not to support optimal decision-making but to implement machines that can imitate humans who make rational decisions, sometimes not optimal due to emotion. Of course, the model proposed in this paper does not fully implement the human decision-making process, but through the proposed model, we show the beginning of the development of machines that can imitate the human mind.
4. Simulation Study
To illustrate how our research can be applied to develop a machine imitating the human mind, we perform two simulation studies for discrete and continuous cases. The first experiment is the beta-binomial conjugate case for discrete distribution. In the initial learning phase, we assume that 35 successes have been observed in a total of 100 Bernoulli trials. In this case, we consider a binary decision such as to buy or not buy something. In general, from the viewpoint of optimization of AI, the best-quality product will be purchased at the lowest price, but from the viewpoint of AM in this research, our simulation is conducted under the assumption that the product can be purchased through human thinking such as emotion, sometimes without making an optimal decision. Thus, we chose binomial distribution for first experiment, because this is a probability distribution representing binary outcomes based on Bernoulli trials. In this paper, we represent the number of Bernoulli trials and success probability as n and , respectively. In the assumption of this example, represents the probability of buying something. In this case, the likelihood function for observed data is binomial distribution with n = 100 and = 0.35. This is shown in Table 2.

Table 2.
Bayesian learning result: beta-binomial conjugate.
Since the increase in the number of repetitions in our simulation is not significant, we stopped repeated learning at the third phase. In this paper, we stopped at the third step for convenience, but repeated learning is possible up to the nth if new data are observed each time. In Table 2, we define the following distributions for the beta-binomial conjugate.
In Equation (10), the probability of success is distributed to beta distribution with and , which are the parameters to control the shape and position. The posterior distribution is also beta distribution produced by prior and likelihood in Equations (9)–(11). Thus, Table 2 shows the parameter values of prior, likelihood and posterior distributions according to the updated learning phases. In addition, the last column of this table is the expectation of , and this expectation is the optimal value for . In the assumption of this example, means the optimal decision in AI. The posterior distribution is updated step by step as new data are added and learning progresses. Figure 5 shows the structure of posterior distribution at each stage of learning.
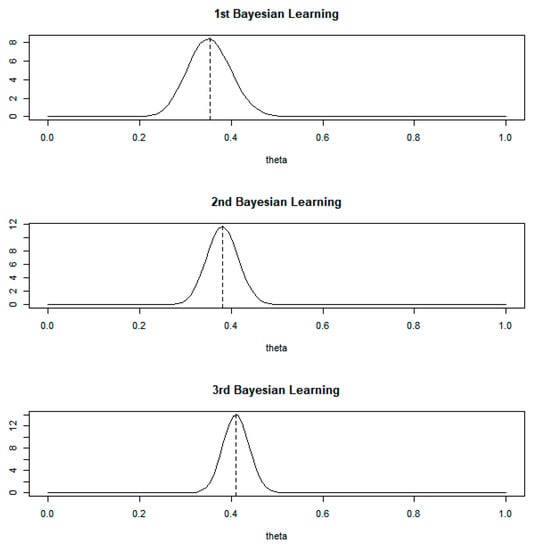
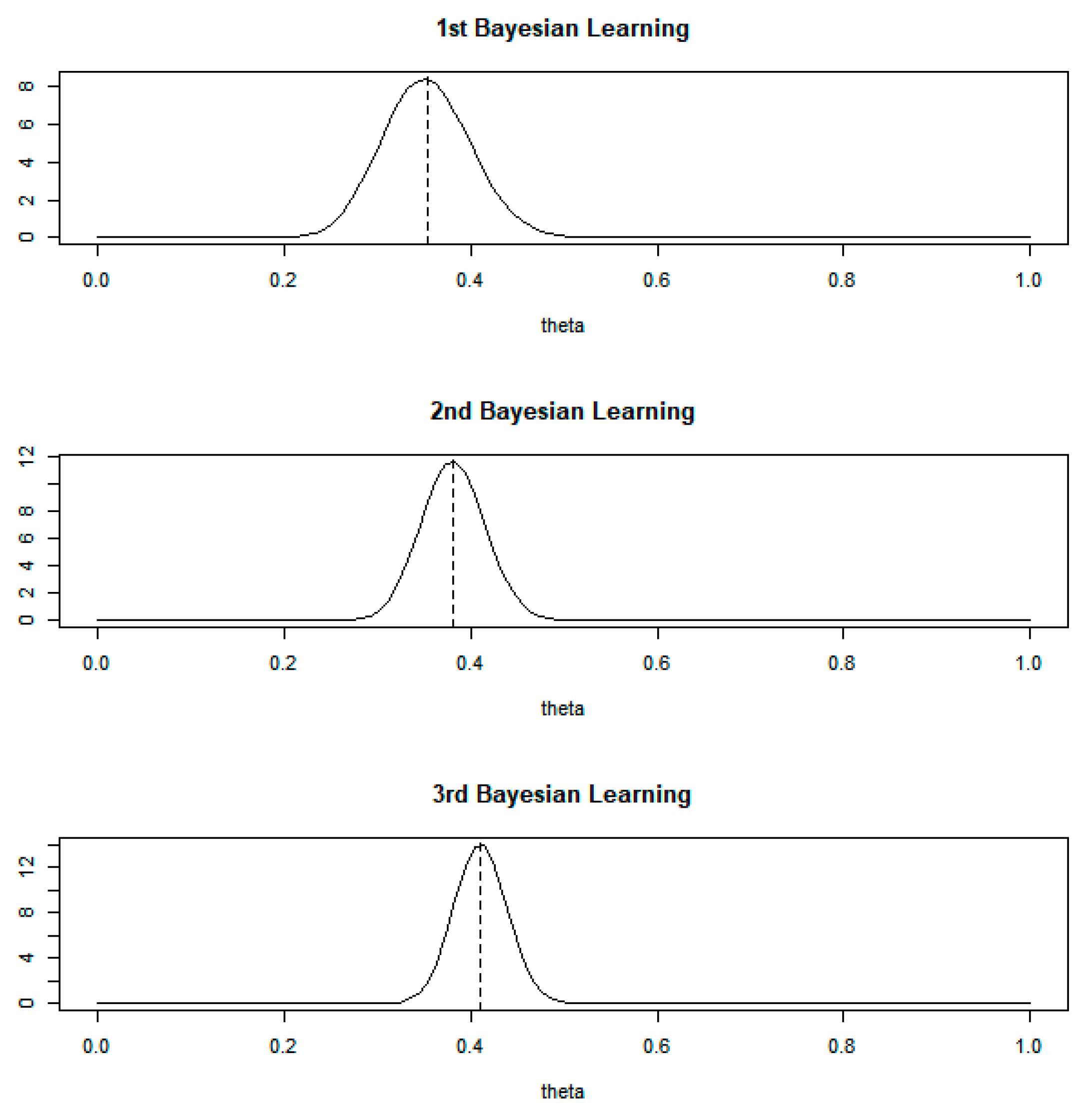
Figure 5.
Posterior of theta: beta-binomial conjugate.
As shown at the top of Figure 5, we can make a decision using the result of the first Bayesian learning process. In general, we performed optimal decision-making using the expectation value (0.3529) from the distribution in the first Bayesian learning process. In the case of thinking machines, we use two approaches, which are multiple points and 95% confidence interval. To provide multiple points for building thinking machines, we generated random numbers from the posterior distribution shown at the top of Figure 5. Moreover, using Bayesian bootstrap, we computed the interval for decision-making in thinking machines. The middle and bottom sections of Figure 5 are also applied in the same way as the upper section. That is, the cases of the second and third Bayesian learning processes are used in the same way as the first Bayesian learning process. Therefore, in this paper, our model provides two results for instead of . We generated random numbers from the posterior distribution from Table 2 and Figure 5. We represent the comparison result of optimal and non-optimal results from the Bayesian learning according to learning phases in Table 3.

Table 3.
Comparison of optimal and non-optimal in beta posterior.
In the third learning phase of Table 3, the optimal provides only one value, namely 0.4106 (), but multiple points provide various results (0.3633, 0.3827, 0.4077, 0.3919, 0.3790). In some cases, we can use the mean value of these five values for decision-making by thinking machines. In addition, we show the 95% confidence interval (0.4094, 0.4133) by Bayesian bootstrap for machines to think like humans. Through these behaviors (values) in our approach, as shown in Table 3, we believe that the machine imitates human thinking.
Next, we carried out a continuous case using a normal–normal conjugate, as shown in Table 4. Compared to binomial distribution, normal distribution can more generally imitate human thinking. This is because normal distribution can model the entire real number.

Table 4.
Bayesian learning result: normal–normal conjugate.
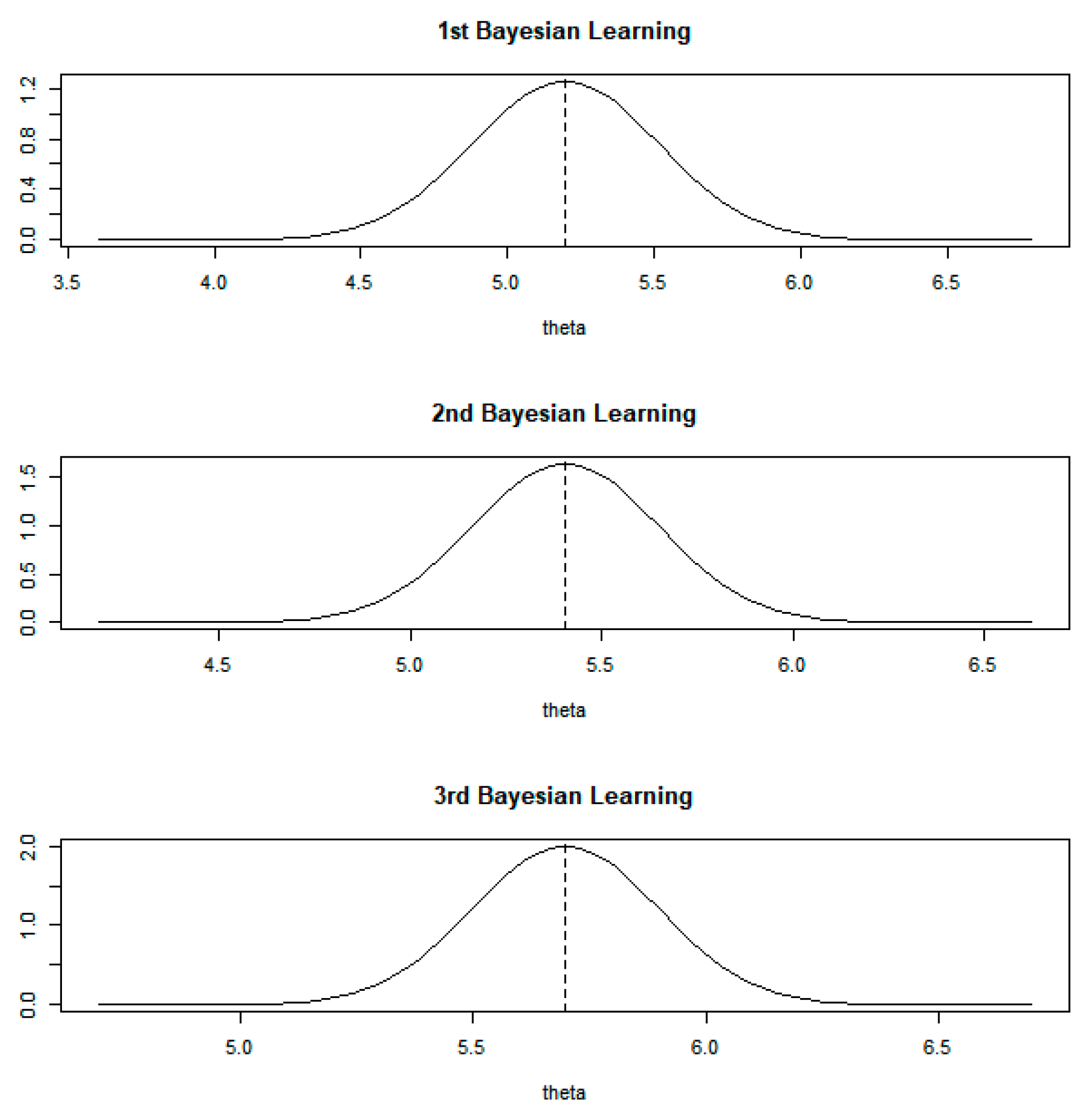
In this case, we used normal distribution for prior, likelihood and posterior. Table 4 shows the optimal values (E(θ)) of three learning phases. Figure 6 illustrates the structures of the posterior distributions that changed according to the Bayesian learning phases.
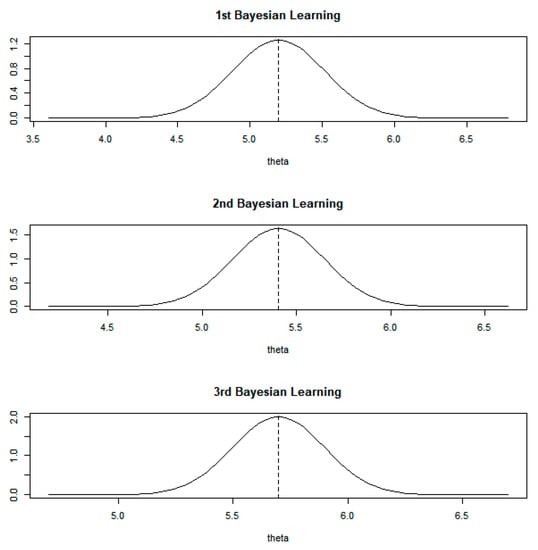
Figure 6.
Posterior of theta: normal–normal conjugate.
As in the case of the beta-binomial conjugate, we can use the results of Bayesian learning given in Figure 6. We also generated random numbers from the posterior distributions and computed the 95% confidence interval to compare the results with the optimal values of given in Table 4. We show the comparison results between optimal, multiple points and interval in Table 5.

Table 5.
Comparison of AI and AM in normal posterior.
We can use the results in the same way as in the case of the beta-binomial conjugate in Table 3. In the third Bayesian learning result, the value for optimal decision-making in the AI approach is 5.6975, which is the expected value of the posterior distribution after the third learning phase. Compared to this, the decision value obtained by the multiple-points approach can be one of the values (5.8345, 6.1208, 5.5106, 5.2896, 5.6123) or the mean of five random values. Furthermore, we calculated the confidence interval using Bayesian bootstrap (5.6860, 5.7129). This result can also be used for decision-making in thinking machines. In our simulation studies, we showed the possibility of Bayesian decision theory and Bayesian bootstrap to develop machines imitating human thinking. The method proposed in this paper is not a perfect way to build a machine that mimics human thinking, but it could represent a new beginning. In this way, our study presents a new approach to cognitive AI after the current optimal AI.
5. Discussion
We undertook the study described in this paper to confirm the possibility of developing a machine capable of imitating human thinking. We are well aware that implementing a machine that can imitate human thinking is a very difficult task. This is because research on human thinking is still being conducted in interdisciplinary fields such as cognitive science, psychology and computer science. Therefore, in this paper, we have not been able to present a perfect methodology for implementing human thinking into machines. In this field, many researchers are still working on different approaches. In this paper, we chose Turing’s imitation method. We have attempted to implement a machine with a degree of difficulty in distinguishing whether a machine is a human or a computer. This paper presents the results of our first attempt.
In this paper, we used simulated data to show how the proposed methodology can be applied to practical problems. We collected the data generated from the probability distributions such as beta, binomial and normal. In the simulation study, we performed posterior updating using the generated datasets and selected a value from the final updated posterior distribution for decision-making. Compared to previous research results, the most important feature of our study is the number of result values that can be provided for decision-making. The existing Bayesian learning provides only one value for decision-making, but the Bayesian learning proposed in this paper can provide multiple values, and since one value can be randomly selected among them, it is possible to overcome deterministic decision-making. In this way, it may be possible to develop machines capable of imitating human thinking. Our research will contribute to the field of AI systems and humanity, such as healthcare robots.
6. Conclusions
To develop a machine that imitates human thinking, we proposed a learning methodology using Bayesian decision theory and Bayesian bootstrap. Through Bayesian learning with prior, likelihood and posterior, we build a posterior distribution to develop thinking machines which reflect humans. Instead of making the optimal decision with a single value, the proposed machine decides by using multiple points, which are random numbers from the posterior distribution after Bayesian learning. In addition, using Bayesian bootstrap, we provided a significance interval of model parameters for machines to imitate human thinking. Therefore, the proposed machine can imitate an emotional decision by selecting one of several possibilities, as humans do. The basic idea of this paper is that thinking machines are possible using Bayesian inference and bootstrap. Of course, it is not possible to build a perfect model of human thinking using the approach proposed in this paper because the modeling of human thinking is a very difficult and complex task. We attempted to build thinking machines to imitate the human mind through Bayesian approaches. This paper represents the results of our first research project for developing a machine that can imitate human thinking. The Bayesian learning and bootstrap proposed in this paper do not fully imitate human thinking. Our research results represent just the beginning of the path to build machines that imitate the human mind. However, from the results of this paper, we can see that the Bayesian learning model could be an effective way to build a machine that imitates human thinking. Thus, based on this paper, we plan to conduct various interdisciplinary studies, such as cognitive AI and cognitive psychology, and Bayesian statistics to develop a machine that can ultimately imitate human thinking.
In our future works, firstly, the data from unstructured sources such as images, voice and video have to be analyzed through new advanced methods. For example, thinking machines have to recognize human facial images for representing interactive feelings. Thus, we will add necessary factors such as the edges of images, allowing the identification of patterns. Next, in convenient Bayesian inference, the prior distribution must be selected as the conjugate prior because of mathematical tractability. To develop a more advanced model for building thinking machines, we have to consider the prior distribution, not conjugate, to build the thinking machines using advanced Bayesian computing based on Markov chain Monte Carlo methods.
We will also conduct research with cognitive AI to implement machines that can imitate human thinking. Thus, we will combine our Bayesian learning approach with the concept of mind from cognitive science as well as cognitive psychology. In addition, we can consider deep learning (DL) algorithms with stochastic gradient descent (SGD). The weights of DL models such as convolution neural networks (CNN) are updated by SGD based on Bayesian learning. In this way, we can implement a more advanced Bayesian learning model imitating human thinking using the mind model of cognitive science and Bayesian DL. We hope to contribute to the development of various AI systems, such as mind, emotion and consciousness.
Author Contributions
S.J. designed this study and built the proposed model. He also performed the case study and illustrated the validity of this research. In addition, he wrote the paper and carried out all the research steps. The author have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bermudez, J.L. Cognitive Science An Introduction to the Science of the Mind, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Duch, W. Towards artificial minds. In Proceedings of the I National Conference on Neural Networks and Applications, Kule, Republic of Botswana, 12–15 April 1994; pp. 17–28. [Google Scholar]
- Hurwitz, J.S.; Kaufman, M.; Bowles, A. Cognitive Computing and Big Data Analysis; Wiley: Indianapolis, India, 2015. [Google Scholar]
- Lake, B.M.; Ullman, T.D.; Tenenbaum, J.B.; Gershman, S.J. Building Machines That Learn and Think Like People. Behav. Brain Sci. 2017, 40, e253. [Google Scholar] [CrossRef] [PubMed]
- Turing, A.M. Computing Machinery and Intelligence. Mind 1950, 49, 433–460. [Google Scholar] [CrossRef]
- Bates, A. Augmented Mind AI, Humans and the Superhuman Revolution; Neocortex Ventures: San Diego, CA, USA, 2019. [Google Scholar]
- Burr, C.; Cristianini, N. Can Machines Read our Minds? Minds Mach. 2019, 29, 461–494. [Google Scholar] [CrossRef]
- Franklin, S.; Wolpert, S.; McKay, S.R.; Christian, W. Artificial minds. Comput. Phys. 1997, 11, 258–259. [Google Scholar] [CrossRef][Green Version]
- Franklin, S. Artificial Minds; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Walsh, T. Machines That Think; Prometheus Books: New York, NY, USA, 2018. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Neisser, U.; Boodoo, G.; Bouchard, T.J., Jr.; Boykin, A.W.; Brody, N.; Ceci, S.J.; Halpern, D.F.; Loehlin, J.C.; Perloff, R.; Sternberg, R.J.; et al. Intelligence: Knowns and unknowns. Am. Psychol. 1996, 51, 77–101. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Pearson: Essex, UK, 2014. [Google Scholar]
- Shi, Z. Mind Computation; World Scientific Publishing: Singapore, 2017. [Google Scholar]
- Minsky, M. The Society of Mind; Simon & Schuster Paperbacks: New York, NY, USA, 1985. [Google Scholar]
- Minsky, M. The Emotion Machine; Simon & Schuster Paperbacks: New York, NY, USA, 2006. [Google Scholar]
- Hoya, T. Artificial Mind System Kernel Memory Approach; Springer: New York, NY, USA, 2005. [Google Scholar]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Kruschke, J.K. Doing Bayesian Data Analysis, 2nd ed.; Elsevier: Waltham, MA, USA, 2015. [Google Scholar]
- Neal, R.M. Bayesian Learning for Neural Networks; Springer: New York, NY, USA, 1996. [Google Scholar]
- McGrayne, S.B. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy; Yale University Press: New Haven, CT, USA, 2011. [Google Scholar]
- Wainer, H.; Savage, S. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines and Emerged Triumphant from Two Centuries of Controversy by Sharon Bertsch McGrayne. J. Educ. Meas. 2012, 49, 214–219. [Google Scholar] [CrossRef]
- Donovan, T.M.; Mickey, R.M. Bayesian Statistics for Beginners; Oxford University Press: Oxford, UK, 2019. [Google Scholar]
- Jun, S. Frequentist and Bayesian Learning Approaches to Artificial Intelligence. Int. J. Fuzzy Logic Intell. Syst. 2016, 16, 111–118. [Google Scholar] [CrossRef][Green Version]
- Meng, X.; Bachmann, R.; Khan, M.E. Training binary neural networks using the Bayesian learning rule. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 12–18 July 2020; pp. 6852–6861. [Google Scholar]
- Liu, S.; Huang, Y.; Wu, H.; Tan, C.; Jia, J. Efficient multitask structure-aware sparse Bayesian learning for frequency-difference electrical impedance tomography. IEEE Trans. Ind. Inform. 2020, 17, 463–472. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, R.; Zheng, J.; Sun, H. Sparse Bayesian learning for structural damage identification. Mech. Syst. Signal Process. 2020, 140, 106689. [Google Scholar] [CrossRef]
- Walmsley, J. Mind and Machine; Palgrave Macmillan: Hampshire, UK, 2012. [Google Scholar]
- Kurzweil, R. The Singularity Is Near When Humans Transcend Biology; Penguin Books: New York, NY, USA, 2006. [Google Scholar]
- Kurzweil, R. How to Create a Mind; Penguin Books: New York, NY, USA, 2013. [Google Scholar]
- Lee, J.J.; Sha, F.; Breazeal, C. A Bayesian Theory of Mind Approach to Nonverbal Communication. In Proceedings of the 14th ACM/IEEE International Conference on Human-Robot Interaction, Daegu, Korea, 11–14 March 2019; pp. 487–496. [Google Scholar]
- Kang, X.; Ren, F. Understanding Blog author’s emotions with hierarchical Bayesian models. In Proceedings of the IEEE 13th International Conference on Networking, Sensing, and Control, Mexico City, Mexico, 28–30 April 2016; pp. 1–6. [Google Scholar]
- Mousas, C.; Newbury, P.; Anagnostopoulos, C.N. Evaluating the covariance matrix constraints for data-driven statistical human motion reconstruction. In Proceedings of the Spring Conference on Computer Graphics, Smolenice, Slovakia, 28–30 May 2014; pp. 99–106. [Google Scholar]
- Casella, G. An introduction to empirical Bayes data analysis. Am. Stat. 1985, 39, 83–87. [Google Scholar]
- Žilinskas, A. On the worst-case optimal multi-objective global optimization. Optim. Lett. 2013, 7, 1921–1928. [Google Scholar] [CrossRef]
- Bruce, P.; Bruce, A.; Gedeck, P. Practical Statistics for Data Scientists; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Rubin, D.B. The Bayesian Bootstrap. Ann. Stat. 1981, 9, 130–134. [Google Scholar] [CrossRef]
- Rohekar, R.Y.; Gurwicz, Y.; Nisimov, S.; Koren, G.; Novik, G. Bayesian Structure Learning by Recursive Bootstrap. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, Canada, 3–8 December 2018; pp. 10546–10556. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).