Plant Age Has a Minor Effect on Non-Destructive Leaf Area Calculations in Moso Bamboo (Phyllostachys edulis)

Abstract

Leaf area is among the most important leaf functional traits, and it determines leaf temperature and alters light harvesting. The calculation of individual leaf area is the basis of calculating the leaf area index (i.e., the total leaf area per unit ground area) that is directly associated with the ability of plants to intercept light for photosynthesis. It is valuable to provide a fast and reliable approach to measuring leaf area. Here, we examined the validity and calculation accuracy of the Montgomery equation (ME), which describes the area of a leaf as a product of leaf length, width and a specific coefficient referred to as the Montgomery parameter, MP. Using ME, we calculated leaf areas of different age groups of bamboo culms. For most broad-leaved plants, leaf area is proportional to the product of leaf length and width, and MP falls within a range of 1/2 to π/4, depending on leaf shape. However, it is unknown whether there is an intra-specific variation in MP resulting from age structure and whether such a variation can significantly reduce the predictability of ME in calculating leaf area. This is relevant as a population of perennial plants usually composes of different age groups. We used Moso bamboos as model as this species is of ecological and economic importance in southern China, and pure stands can cover six to seven plant age groups. We used five age groups of moso bamboo and sampled 260–380 leaves for each group to test whether ME holds true for each group and all groups combined, whether there are significant differences in MP among different age groups, and whether the differences in MP can lead to large prediction errors for leaf area. We observed that for each age group and all groups combined, there were significant proportional relationships between leaf area and the product of leaf length and width. There were small but significant differences in MP among the five age groups (MP values ranged from 0.6738 to 0.7116 for individual plant ages; MP = 0.6936 for all age groups combined), which can be accounted for by the minor intergroup variation of leaf shape (reflected by the leaf width/length ratio). For all age classes, MP estimated for the pooled data resulted in <4% mean absolute percentage error, indicating that the effect of variation in MP among different age groups was small. We conclude that ME can serve as a useful tool for accurate calculations of leaf area in moso bamboo independent of culm age, which is valuable for estimation of leaf area index as well as evaluating the productivity and carbon sequestration capacity of bamboo forests.

1. Introduction

The number of leaves and leaf area are important indices of whole plant carbon capture for plants [1,2,3]. Individual leaf area is affected not only by its spatial position in a plant but also by biological and environmental factors including plant age, competition, temperature, precipitation, etc. [4,5]. Leaf area also reflects the trade-off between the cost and benefit in support economics of plants [6], and it has a scaling relationship with the investments of dry mass needed to construct leaf photosynthetic apparatus, but also with investments to support the leaf in specific position in the canopy [7,8,9]. Saplings usually have a smaller scaling exponent of leaf mass vs. area than adults. This allows younger trees to have larger leaf area and grow faster to accumulate more dry material during the growth season [9,10,11]. The quotient of leaf dry mass and leaf area (LMA) is intimately associated with life forms of plants and climate, especially with precipitation and solar radiation [12,13].

In studies looking at dynamic changes in plant physiological activity and growth through plant ontogeny, leaf area usually needs be continuously measured. Thus, it is important to use a non-destructive approach for regular assessment of change in leaf area. In addition, the calculation of individual leaf area is the basis of total leaf area per plant, and the latter is directly related to the leaf area index (the total area per unit ground area) that is an important plant functional trait [14,15]. The leaf area index has been considered as an indicator of the amount of light interception of plants [16]. Although there exist some complex mathematical models developed for calculation of individual leaf area [17,18,19], application of these is not always practical. In fact, recent studies have demonstrated that a simple equation proposed by Montgomery [20] to describe a proportional relationship between leaf area (A) and the product of leaf length (L) and width (W) of corn (Zea mays), can serve as a general method to estimate leaf area for a large number of broad-leaved plants [21,22,23,24,25,26,27]. Shi et al. [24] found that the proportional equation proposed by Montgomery [20] (referred to further as the Montgomery equation, ME) was valid for calculation of A for a large number of woody plants and herbs belonging to the families Hamamelidaceae, Lauraceae, Magnoliaceae, Oleaceae, Poaceae and Rosaceae. However, the generality of ME for the calculation of A was somewhat uncertain considering that most species used by Shi et al. [24] had non-lobed leaf shapes. Yu et al. [27] choose 15 species of vines with diverse leaf shapes and further tested the validity of ME. With this diverse dataset they confirmed the broad applicability of ME across species with different leaf shapes. In addition, these two studies found that the proportionality coefficients (referred to as the Montgomery parameter, MP) for A vs. LW relationships fell in a narrow range of 1/2 to π/4, i.e., the two ends of this range correspond to triangular and elliptic leaves. On the other hand, use of linear dimensions, L and W for the prediction of A depends on leaf shape, i.e., on the extent of variation in the W/L ratio [28]. Shi et al. [25] choose 101 bamboo species, cultivars, forms and varieties with 90–110 leaves for each taxon to test the influence of the variation in W/L ratio on the goodness of fit of $A\propto L^2$ on a log-log plot. The shape of the leaves of different bamboo taxa is very similar, and the difference in leaf shape has been proved to reflect the variation in W/L ratio [29]. In fact, the shape of bamboo leaves can be described by using a two-parameter polar coordinate equation [3,18,30]. Shi et al. [25] found that the prediction errors in A derived from the relationship $A\propto L^2$ were strongly correlated with the coefficient of variation in the W/L ratio for 101 datasets of bamboo taxa (r = 0.949; p < 0.01). The estimated MP values fell into a range of 0.62 to 0.78. However, the above studies have largely neglected the possible influence of the intraspecific variation in MP on the prediction errors of leaf area using ME.

Natural or semi-natural plant population are composed of individuals of different ages [31]. The age structure of a population can affect the photosynthetic capacity and productivity of forests to a large degree [32,33,34]. If old age groups account for a larger proportion of stand basal area, the productivity of this stand per unit stand leaf area is lower than that of a younger stand with an equivalent leaf area [35]. Also, the culm age has been demonstrated to significantly affect the anatomical characteristics (the length, double-wall thickness and lumen diamater of the fiber) of a bamboo plant [36]. However, whether culm age can affect the shape of bamboo leaves and the measurment of leaf area has not been studied.

Moso bamboo (Phyllostachys edulis (Carriere) J. Houzeau), is a widely distributed early-successional species in subtropical regions of East Asia, especially in China [37]. Moso bamboo is an economically important species with a broad use in landscape, industrial, and daily life [38]. Large areas of moso bamboo forests have contributed greatly to local ecology and economical development in southern China [39,40]. It is economcially and physically feasible to use moso bamboo as a substitute of woody resources due to its excellent bio-mechanical characteristics and fibre properties [39,41,42].

Moso bamboo forests typically consist of several age groups that can be up to 12 to 14 years old [43]. This plant usually forms shoots every second year, but fertilization can result in continuous formation of bamboo shoots [39]. This means that moso bamboo forests can include up to 6–7 age groups. Bamboo leaves are perennial, but their life span has not been studied extensively. Although Shi et al. [25] studied 101 bamboo taxa, the influence of the intra-specific variation in plant age on the calculation accuracy of ME was largely ignored.

In this study, we measured leaf characteristics of bamboo leaves of five age groups to explore: (1) whether ME holds for the leaves of each age group; (2) if ME holds true, whether there are significant differences in the estimated MP values among the five age groups; (3) if the differences of the estimated MP values are significant, whether these differences are large enough to warrant use different MP values to estimate leaf area of plants of different age. Understanding age-specific variation in MP is relevant as in natural conditions, it is often not possible to estimate plant age; however, when the age effects are large, this could result in overly large errors in use of ME for estimation of leaf area.

2. Materials and Methods

2.1. Site Description

The study site is located in Purple Mountain of Nanjing, Jiangsu Province, China (118°49′2″ E, 32°4′17″ N), where moso bamboo plantations date back to 1992. By 2009, due to poor management, including lack of weed removal in the early growth stage, lack of thinning and fertilizer addition, moso bamboo had become ecologically and economically unimportant at the study site. Between 2011–2014, site management was radically changed to improve the mean individual biomass of moso bamboo. The management practices included: (1) regular weed removal in May and July; (2) use of compound fertilizers in June and September, and cake fertilizers in November/December; (3) thinning of bamboo plantations in December of 2012 and 2014 and in January of 2011 and 2013. From 2015 on, new bamboo shoots were not cut off again, and no fertilizers were used. In 2016, moso bamboo forests had grown better, and the mean (±SE) culm diameter at breast height (DBH) was 9.19 ± 1.49 cm, significantly larger than mean DBH in previous years (= 8.5 ± 1.54 cm) (p = 0.0238 < 0.05).

Every year some culms of bamboo shoots were marked by a water-resistant marker at every year, allowing reliable identification of the age of bamboo shoots (see Figure 1 for details). At the time of leaf sampling in early August 2020, there were five age groups of moso bamboo that had grown in 2014, 2015, 2016, 2018 and 2020. Years 2017 and 2019 were left out, because it was difficult to find bamboo culms developed in these years.

2.2. Leaf Collection and Image Processing

We sampled 260–480 leaves from 5–10 individuals for each age group on 3 August 2020. Leaves grown in the lower canopy of each individual were taken randomly from a pool of different-aged leaves to obtain a representative leaf sample for each bamboo age group. For bamboo grown in 2020, all leaves taken were new leaves formed in that year. Fresh leaves were wrapped in wet paper, enclosed in transparent plastic self-sealing bags (28 cm × 20 cm) and transported to the laboratory for the measurements.

The leaves were scanned with an Epson scanner (V550, Epson, Batam, Indonesia) at a 600 dpi resolution. Scanned images were used to measure leaf width (W), length (L), and area (A) using our developed MATLAB (version ≥ 2009a) procedure and R script (based on R version 4.0.2) [30,44,45]. The raw data of leaf area, length, and width of the five groups of moso bamboo can be found in the online Supplementary Table S1.

2.3. Statistical Analyses

We tested the significance of differences in W, L, W/L ratio, and A between the age groups by ANOVA followed by the Tukey’s Honest Significant Difference (HSD) test at 0.05 significant level [46].

The Montgomery equation (ME) was fitted to the data:

$$A=\mathrm{MP}\cdot LW,$$

(1)

where MP denotes the Montgomery parater. To stablilize the variance of the response variable [24,25,27], we used the log-transformation of both sides of Equation (1):

$$\ln (A)=a+\ln (LW),$$

(2)

which can be rewritten as:

$$y=a+x,$$

(3)

where the intercept a is the log-transformation of MP. A least-squares fit to the data was used to estimate the intercept for the data of each age group.

The root-mean-square error (RMSE) was used to measure the goodness of fit for leaf area (A), which equals:

$$\mathrm{RMSE}=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left({\widehat{A}}_i-A_i\right)}^2}}{n}},$$

(4)

where n represents the sample size, i.e., the number of leaves; the subscript i represents the i-th leaf; ${\widehat{A}}_i$ represents the predicted value, and $A_i$ the observed value. In addition, the scaling relationships between L and A, and between W and A were fitted using the log-transformed data to check whether the two one-dimensional leaf measures (L and W) have similar goodness of fit in scaling relationships with A.

$$\ln (A)={\mathsf{\beta }}_1+{\mathsf{\alpha }}_1\ln (L),$$

(5)

$$\ln (A)={\mathsf{\beta }}_2+{\mathsf{\alpha }}_2\ln (W).$$

(6)

Here, ${\mathsf{\alpha }}_1$, ${\mathsf{\alpha }}_2$, ${\mathsf{\beta }}_1$ and ${\mathsf{\beta }}_2$ are the parameters to be fitted. RMSE values were used to compare the two scaling relationships.

To test the significance of the difference between any two groups in the estimated MP values, a bootstrap percentile method was used to calculate the 95% confidence intervals (CI) of the differences between two groups of replicates of MP [47,48]. If CI includes 0, there is no significant difference; alternatively, the MP values are significantly different.

To measure the influence of the intra-specific varition in MP on the calculation error of A, we estimated the mean absolute percentage error (MAPE in %) of n leaves using the fitted MP value:

$$\mathrm{MAPE}=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n\frac{\left|{\widehat{A}}_i-A_i\right|}{A_i}}\times 100\%.$$

(7)

3. Results

Mean leaf width (W), length (L), W/L ratio, and area differed among several plant age groups (Figure 2), but there was no clear relationship with plant age. Group 2014 had the largest leaf width, length, and area, but its mean W/L ratio was lower than that of group 2018. Although group 2016 had the second largest mean leaf width and area and the largest mean leaf length (having no significant difference with that of group 2014), its mean W/L ratio was the second smallest among the five age groups.

The Montgomery equaiton (ME) was confirmed to be valid for each plant age group, and the RMSE values for all the five age groups and all groups combined were all smaller than 0.04 (Figure 3), indicating a good fit for each group and all groups combined. The estimated MP values including the corresponding 95% confidence intervals (CIs) for all groups ranged from 0.67 to 0.72 (Figure 3). The pooled data of the five age groups also showed a good fit (with RMSE = 0.04 and r² = 0.9892). For each group, the RMSE value of ME was lower than that of the scalings of A vs. L and A vs. W (

Table 1. Comparison of the goodness of fit for three models of calculating leaf area.

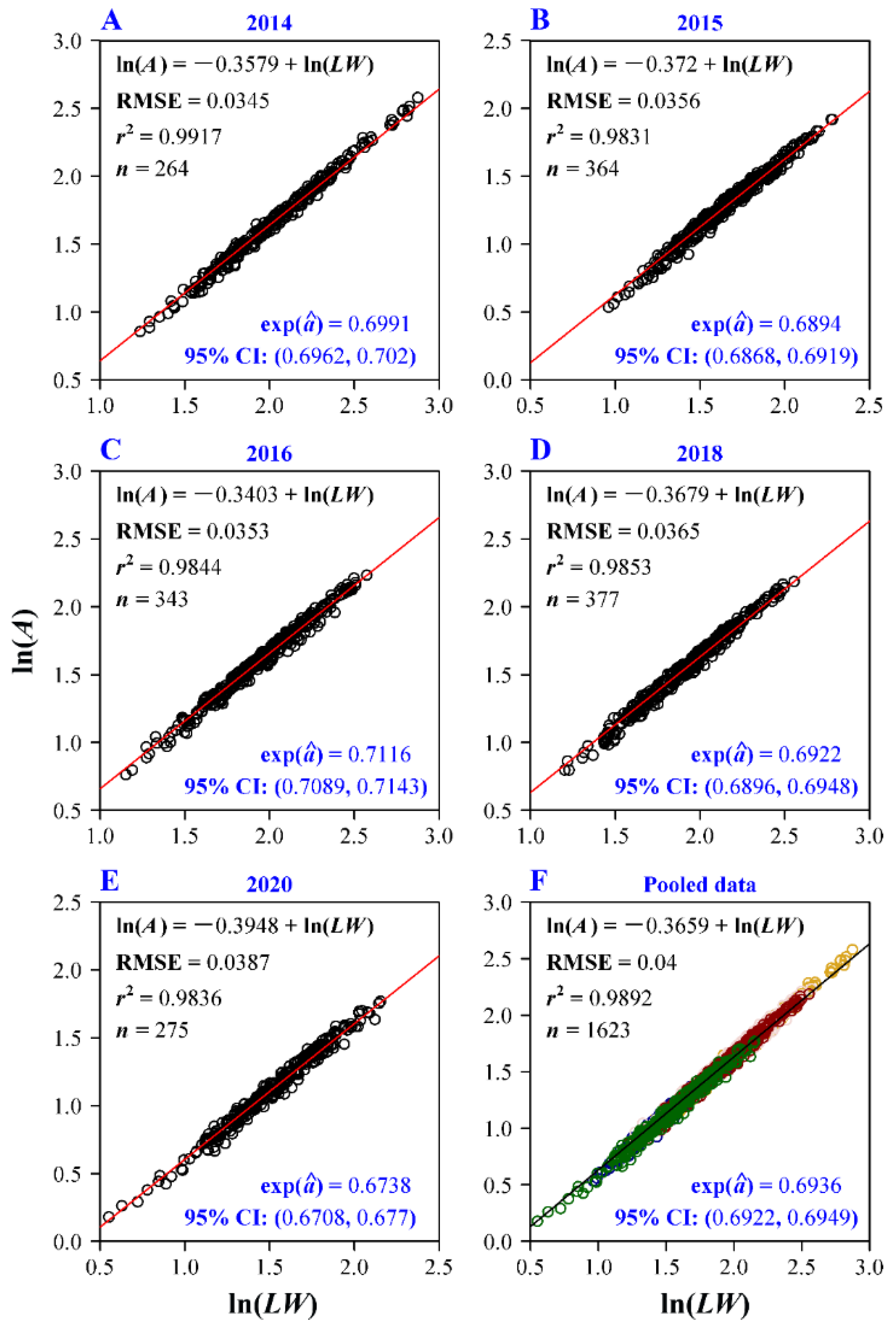
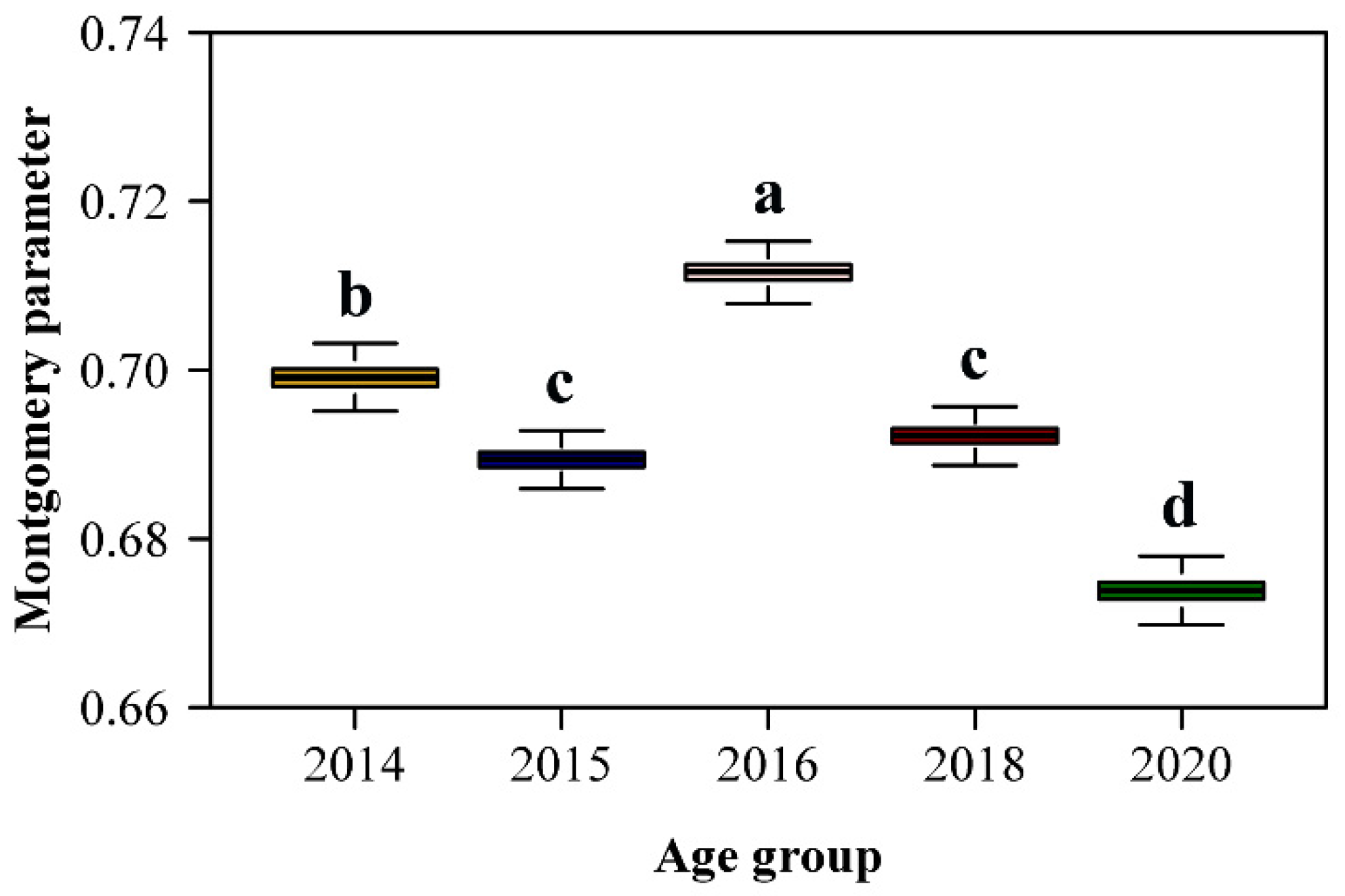
Group	RMSE1	RMSE2	RMSE3
2014	0.0345	0.1709	0.2315
2015	0.0356	0.1413	0.2204
2016	0.0353	0.1602	0.2041
2018	0.0365	0.1359	0.2328
2020	0.0387	0.1114	0.2059

RMSE₁ represents the root-mean-square error using the Montgomery equation; RMSE₂ represents the root-mean-square error using the scaling of leaf area vs. leaf length; RMSE₃ represents the root-mean-square error using the scaling of leaf area vs. leaf width.

). This means that using two linear leaf dimensions, L and W, for calculation of A was superior to the use of only either L or W. The RMSE value of the scaling of A vs. L was smaller than that of A vs. W, indicating that L had a stronger scaling relationship with A than W. This reflects a smaller range of variation in W in different-sized leaves than in L (which were refelcted by the coefficients of variation shown in Figure 2A,B).

Comparison of estimated MP values among plant ages indicated that group 2016 had the largest, and group 2020 the smallest MP (Figure 4). The MP values for 2015 and 2018 groups did not differ. When using the MP value for the pooled data, which was 0.6936, there were small changes in the mean absolute precentage errors (MAPE₂) for groups 2014, 2015 and 2018 compared with the mean absolute precentage errors (MAPE₁) obtained when MP was individually fitted to each plant age group (

Table 2. Mean absolute percentage errors for the calculation of leaf area of moso bamboo.

Group	MAPE1 (%)	MAPE2 (%)
2014	2.78	2.87
2015	2.98	2.94
2016	2.81	3.77
2018	3.04	3.03
2020	3.05	3.88

MAPE₁ represents the mean absolute percentage error using the estimated Montgomery parameter of each group; MAPE₂ represents the mean absolute percentage error using the estimated Montgomery parameter of all groups combined to calculate the leaf area for each group again.

). Large differences among MAPE₂ and MAPE₁ were observed for groups 2016 and 2020, but for both groups MAPE₂ values were smaller than 4%. Given that the MP value based on the pooled data resulted in <4% mean absolute percentage error, reliable leaf area calculation does not require application of separate fiting equations for different plant age groups.

4. Discussion

Previous studies have shown that the prediction accuracy based on the scaling of leaf area (A) vs. leaf width (W) is usually lower than that of A vs. leaf length (L) [24,49]. Our results show that relative to W, L has a stronger scaling relaitionship with A, which is in accordence with those of previous studies (Table 1). The difference in the scaling relationships between two leaf one-dimensional measures and A reflected a difference of the W/L ratio. Leaf shape can be well quantified by its fractal dimension and the W/L ratio, and there was a significant correlation between the two indices [50]. Although leaf shape does not directly determine leaf size, it can largely affect the Montgomery parameter (MP) [27]. This means that the calculation of A largely depends on leaf shape. The leaf shapes of bamboo leaves have been demonstrated to be well described by a two-parameter polar coordinate equation [3,51]. The two parameters in the polar coordinate equation can be re-expressed by L and W, and regardless of the variation in the W/L ratio the theortical A based on that polar coordinate equaiton has been demonstrated to be proporional to the product of L and W, which is exactly the same as the Montgomery equation [30,45]. However, the mean W/L ratios and their extents of variation were not completely proportional (Figure 2C), which resulted in the differences in the estimated MP values (Figure 4).

In our study site, the management patterns of moso bamboo forests were not equal across the different years, which should have influenced the mean individual biomass of moso bamboo. In addition, the individual positions of moso bamboo and inter-annual differences in temperature and precipitation can also cause the differences in the mean individual biomass [52]. Leaf biomass scales with the aboveground biomass of plants [53], which further affects mean leaf size and shape. However, these differences did not lead to large calculation errors of leaf area among different age groups. The estimated MP value for all groups combined was equal to 0.6936 that is approximate to the value 0.696 estimated from pooling the data of the 101 bamboo species, cultivars, forms, and varieties reported in Shi et al. [25]. Thus, we consider that a single MP value exists for calculating leaf area not only for moso bamboo of different ages but also probably for other bamboo species of different ages. At least, the mean absolute percentage errors for leaf area did not exceed 4% for each age group investigated here, using 0.6936 from pooling the data of the five age groups to calculate leaf area for each group. De Swart et al. [23] studied the influence of plant age on the calculation of A based on two leaf one-dimensional measures (i.e., L and W) of Capsicum annuum. They found that ME can fit leaf area well but it cannot account for the changes of leaf shape for the plants of different days after sowing (i.e., different plant ages). They recommend introducing two additional items (W² and W) to ME, i.e., $k_{0}LW+k_{1}W+k_2{W}^2$ where k₀, k₁ and k₂ are constants to be fitted, to render the calculation of A to be independent from plant age. However, the two additional parameters (i.e., k₁ and k₂) only increased r² from 0.993 (ME) to 0.995 (the three-parameter equation). In general, to add one or more additional parameter(s) in a model can increase the goodness of fit, but it also adds the complexity of the model. Their conclusion that the prediction accuracy of ME is dependent of plant age might be problematic, only using the coefficient of determination without considering the trade-off between the goodness of fit and the complexity of a model [54]. Our study showed that the values of mean W do not show a linear increase or decrease or a parabolic change with plant age increasing (Figure 2A). Thus, the parameters k₁ and k₂ proposed by de Swart et al. [23] are meaningless to show the influence of the temporal variation in leaf width on the calculation of A.

5. Conclusions

In summary, we tested whether there is a significant difference in the Montgomery parameter (MP), which is a proportionality coefficient of leaf area vs. the product of leaf length and width, among the five age groups of moso bamboo that grew together at the same site. The differences in MP were significant between groups, but those did not largely increase the prediction errors of leaf area for all age groups. The mean absolute percentage errors of the five age groups were smaller than 4%, when we used the estimate of MP from fitting the pooled data of the five age groups to recalculate leaf area for each group. For all groups, the increased mean absolute percentage errors did not exceed 1% when replacing the MP values from each group with MP from all groups combined. We also compared MP obtained by fitting the pooled data of the five groups of moso bamboo (MP = 0.694) with the value of MP obtained by fitting the pooled data of the 101 bamboo taxa (MP = 0.696, reported in [25]). These two values are very similar and not significantly different. This means that the proportional relationships between leaf area and the product of leaf length and width for bamboo leaves vary little and the differences in the estimated proportionality coefficients can be neglected when calculating the areas of bamboo leaves. However, whether the conclusions apply to the leaves of different geographical populations of the same plant species merits further investigation since there is evidence that climate can significantly influence leaf shape [55].