Abstract
If the isolated system of bosons and fermions was initially in a pure maximally entangled quantum state, then, as a result of decoherence caused by the creation and annihilation of particles, this system not only enters a mixed state but also achieves equilibrium. The time of such a transition does not depend on the size of the system but is determined only by the properties of the particles. This phenomenon allows the problem of the horizon (the homogeneity of the universe) to be solved, since the transition time of different parts of the universe (if they were originally entangled with each other) to equilibrium will not depend on their sizes, and the speed of the interaction may be greater than the speed of light. Based on the decay of entangled states, the problem of the predominance of matter over antimatter in the universe can also be solved.
1. Introduction
Thermalization mechanisms have been studied for many systems, although they remain a subject of discussion (see, for example, [1]). In this case, two stages of this process can be distinguished—decoherence and thermalization. At the first stage, the probabilities of finding particles of the system in one state or another are formed, and at the second stage, the system goes to equilibrium due to diffusion, heat conduction, and other nonequilibrium processes. However, the case when the entire system was initially in a pure quantum state, described by a single wave function, is of interest and should be considered separately. The mechanisms of thermalization of a pure state can be associated with cosmological problems such as the horizon problem, sypersymmetry, and the problem of the predominance of matter over antimatter.
How did the universe come from its original symmetrical state to an asymmetric state?
We show that the assumption that the universe in its early stages was in a pure quantum state allows us to solve these problems.
2. Creation and Annihilation of Particles as a Mechanism of Transition from a Pure Quantum State to a Mixed State
Decoherence, or the measurement process, is considered a mechanism for the transition of a system from a pure state to a mixed one.
Decoherence involves entanglement of the system with particles of the environment, as a result of which the pure state passes to a mixed one. One of the models for decoherence theory is a two-level system (qubit) (see, for example, [2]), where bosonic field modes act as an environment. The Hamiltonian in this model has the form:
where σz is the Pauli spin operator, and gk are coupling constants.
Various scenarios of decoherence of qubits depending on their correlation length are considered in [3]. In particular, for the case where the correlation length is large, the collective interaction of qubits can lead to a significant increase in decoherence.
According to the theory of quantum measurements (see, for example, [4,5,6]), measurement in quantum mechanics consists of two stages. The first stage can be described with sufficient accuracy using the Schrödinger equation. The second stage cannot be described on the basis of this equation, since there occurs the creation or annihilation of particles. On the other hand, if there is no birth (annihilation) of particles, then measurement does not occur at all, and it is impossible to separate the two stages. As shown in [7], the creation of at least one particle separates the linear dynamics of the particle from the actual measurement.
According to the Copenhagen interpretation of quantum mechanics, the measuring instrument is considered macroscopic. This is true for most cases, but, as shown in [8], the assumption of a macroscopicity of the measuring instrument is not mandatory—there may also be a microscopic instrument. However, using such an instrument, a small amount of information can be obtained. In this sense, a macroscopic measuring instrument can be considered a specific set of microscopic instruments.
The most important conclusion is that both the measurement of the particle’s state by a measuring instrument and decoherence of the particle’s state are closely related to the creation (annihilation) of particles.
3. Dynamics of Transition from a Pure State of the System to a Mixed State and Establishment of Equilibrium
Consider a quantum system that is in a pure state
where are the eigenstates of the observed quantity A. As a result of the measurements, the system comes into one of its admissible states, and the probability of finding the observed quantity in a certain state is equal to
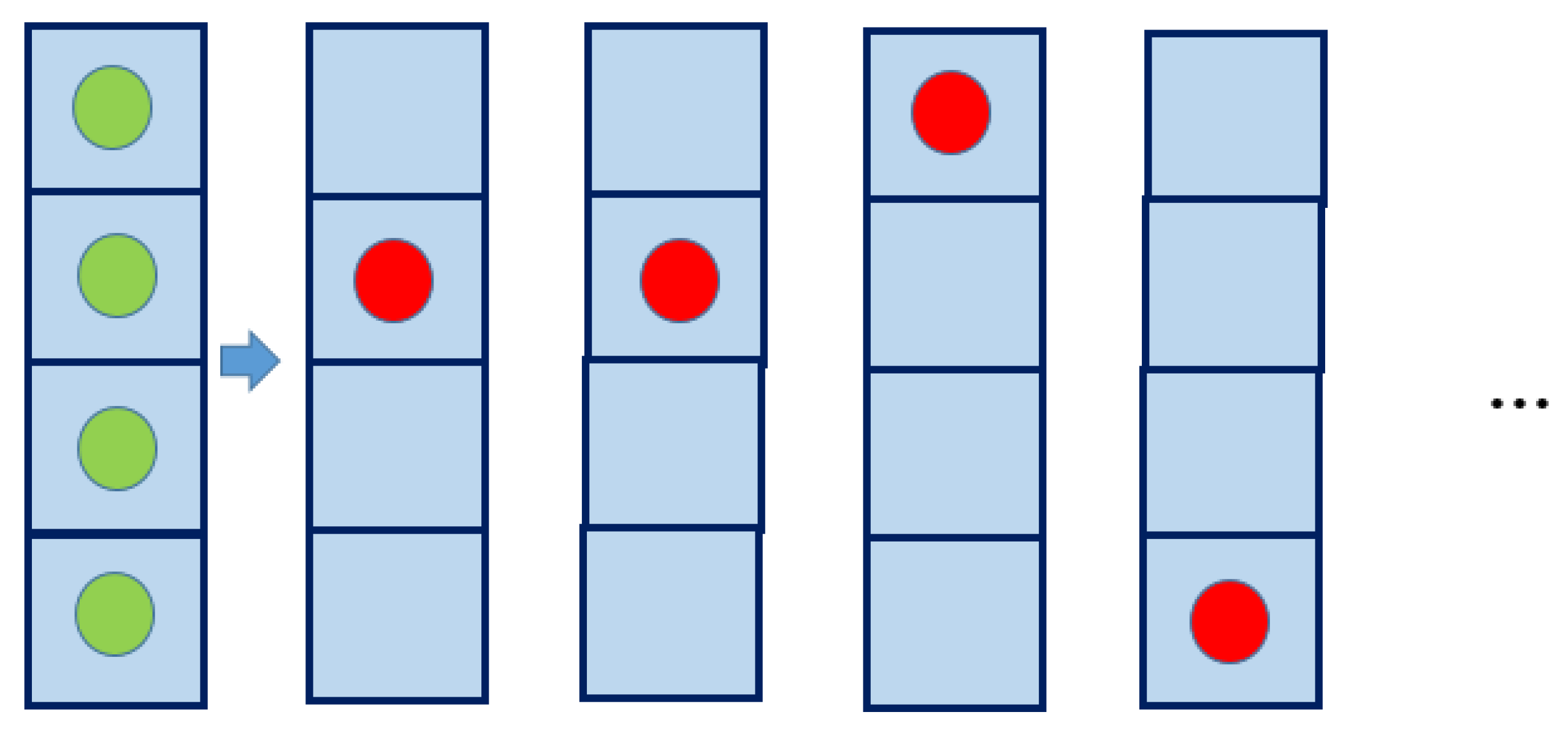
Thus, as a result of repeated measurements, we obtain an ensemble of systems with different configurations (Figure 1).
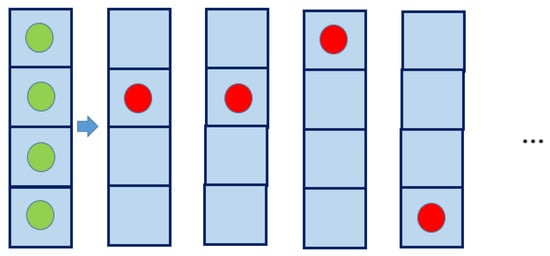
Figure 1.
Ensemble of systems.
In this regard, it is important to consider the frequency interpretation of probability. According to that interpretation [9], we consider a random experiment S and denote the set of the possible results of this experiment as
Consider N implementations of experiment S and write the result xj after each implementation. Then, we get the final sample
In this case, the collective is an endless idealization of this endless sample, for which two Mises principles are true:
- -
- statistical stabilization of the relative frequencies of each characteristic,
- -
- the principle of randomness—the limits of relative frequencies must be stable relative to the rules for choosing a sequence in a collective.
On the other hand, it is obvious that the probability of detecting a system in a certain state as a result of an experiment is proportional to the statistical weight of a given state, i.e., how many ways this state can be realized. Thus, as a result of the measurement, we will more likely get those states of the system that correspond to the largest statistical weight. In a macroscopic system, the maximum statistical weight will correspond to a much greater probability than all other states.
Consider the microcanonical distribution for an isolated system
where En are the permissible energy levels, is the statistical weight, and a is the external parameter. Entropy corresponds to this distribution:
That is, in a stationary state, the system will most likely be in a state with a maximum statistical weight and, therefore, with a maximum entropy corresponding to the microcanonical distribution.
For the realization of some states to be more likely than others, a transition mechanism between states is necessary. Such a mechanism exists in any system (including the ideal one) and represents the creation and annihilation of particles as a result of decoherence of the pure state of the system.
Thus, as a result of measurement (decoherence) of a pure quantum system, we will most likely get the state of the system with maximum entropy. As is known, from the maximum of entropy while maintaining the total energy and the number of particles, one can obtain the Bose and Fermi distributions (see, for example, [10]).
Indeed, let there be Z quantum states. It is necessary to determine the number of ways by which N identical particles can be distributed among these states. The statistical weight of the microstate is for fermions
and bosons
The task is to find the most likely distributions that maximize these expressions. As additional conditions, we choose the following (conservation of the number of particles and energy):
It is easy to show that the statistical weight itself and its logarithm have a maximum in the same point. Therefore, we can write the following from the conditions of its extremum:
Note that the standard derivation of quantum distributions in statistical physics uses the maximum of thermodynamic entropy. In our case, this condition is not used, since there is no thermostat. However, the maximum statistical weight that follows from the decoherence picture discussed above leads to the same results.
Then, we can write for the Lagrange multipliers the following expression:
whence, equating the bracket to zero, it is easy to obtain a distribution for bosons:
and fermions:
In the last formula, we neglected unity compared to .
The average number of particles per quantum state is
From here it is easy to obtain distributions of the Fermi and Bose type:
Thus, even in the absence of a thermostat, equilibrium distributions are established due to the creation and annihilation of particles.
Note that there are two unknown constants in the expressions for the distributions (16, 17). In the presence of thermodynamic equilibrium, these constants are related to temperature and chemical potential. However, if the concept of “thermodynamic equilibrium” is not introduced, then these constants can nevertheless be determined, since the system has conserved (given) quantities: the total number of fermions and the total energy of the system. This means that the concepts of “temperature” and “chemical potential” can be derived from the stationary statistical distribution of particles in a closed system (in the absence of a thermostat).
Note that if the number of bosons is not conserved (photons), then it is impossible to formulate the condition for the conservation of the number of particles (the second condition along with the conservation of the energy of an isolated system). However, in this case, their chemical potential is zero, and the second condition is not necessary to find unknown quantities.
The conclusion made can be extended to nonideal systems in which the creation and annihilation of particles also certainly takes place. Regardless of the type of interaction potential between particles, in the absence of particle creation or annihilation, the evolution of such a system is unitary. Various Hamiltonians of interacting particles in isolated systems are considered, for example, in [11].
Thus, an isolated system of fermions and bosons, which is in a pure state and described by a single wave function, as a result of decoherence (measurement) comes precisely to an equilibrium state with a maximum of entropy. That is, the mixed state in this case simply coincides with the equilibrium state.
We show that the transition of the pure state of a macroscopic system to a mixed one can be used to explain the paradoxes of the homogeneity of the universe and the predominance of matter over antimatter.
4. Mechanism of Thermalization and Solution of the Horizon Problem
Currently, the early stages of the evolution of the universe are modeled both within the framework of inflationary models and using other approaches [12]. To solve such problems as homogeneity, flatness of the universe, and others, an inflationary paradigm has been proposed (see, for example, [13,14,15,16,17]). The disadvantages of inflationary theory include the large number of unknown parameters, as well as the need to go beyond the standard model of elementary particles.
The horizon problem describes the fact that we see isotropy in the temperature of the microwave radiation across the entire sky, but the mechanism that sets the same initial conditions in the remote parts of the universe is unknown.
As alternatives to inflation, one can consider bouncing cosmologies, within which the universe existed before the big bang, and its state after the big bang to one degree or another depends on the state before it [12] and the Penrose conformal cyclic cosmological model [18].
To solve the problems of flatness, uniformity of the universe, and other problems of cosmology, it was assumed in [19] that the universe at the beginning of expansion was in a pure quantum state. Such a statement in relation to the universe requires some auxiliary (albeit natural) assumptions:
- In the early stages, the curvature of the universe is absent, and it itself was in a pure quantum state, characterized by a wave function .
- The pure state of the universe is metastable. As a result of interaction with vacuum fluctuations, after some time τpure, the universe comes into a mixed state.
- In a pure state, the universe is a maximally entangled system of many particles, described by a single wave function.
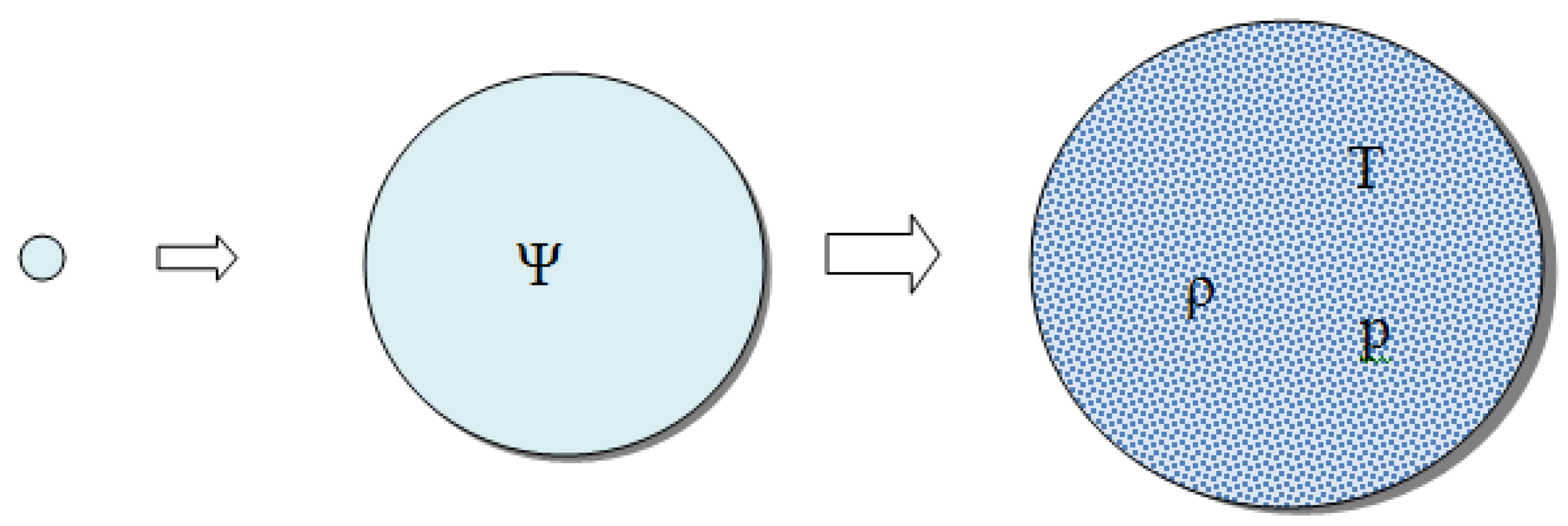
- After the transition of the universe from a pure state to a mixed one as a result of many subsequent births and annihilation of particles, a thermodynamic equilibrium is formed, that is, the universe is thermalized and warmed up (Figure 2).
 Figure 2. Transition of the universe from the pure state to the mixed state.
Figure 2. Transition of the universe from the pure state to the mixed state.
Such a process of expansion of the universe is in many respects similar to the EPR (Einstein-Podolsky-Rosen) experiment, when two particles that were initially in a singlet pure state gradually move away from each other (another variant—two entangled photons move in opposite directions, as in Bohm’s thought experiment). Moreover, such a pair of particles is described by a single wave function. As a result of measuring the parameters of one of the particles, the second particle instantly also goes into a certain state.
Let us consider some basic properties of entangled particles and patterns of decay of entanglement. We list some definitions of entanglement [20]:
Entangled states are such states that cannot be simulated by classical correlations.
Another definition is as follows [21]:
Entanglement implies that the whole system cannot be represented as a product of the subsystems:
One definition is the following [22,23]:
Two identical particles are entangled if their wave functions substantially overlap in the past (time t1), and these particles have hitherto been unitarily removed from each other (without radiation or particle absorption) (time t0 > t1).
This last definition allows a constructive approach to finding systems in which entanglement takes place.
A quantitative characteristic of entanglement is the entropy of partial, reduced density matrices. That is, we are talking about the entanglement of the subsystems among themselves. Entropy, and consequently, the entanglement of a pure system with its environment, is zero. This indicates that fluctuations of individual parts of the system are interconnected. Moreover, the greater the degree of their correlation is, the more random they are separately, since fluctuations in both independently considered parts of the composite system are caused by a single source—purely quantum fluctuations in the composite system.
Another characteristic of entanglement is consistency [24,25]. There are also other quantitative characteristics of entanglement [20].
As shown below, the problem of the temperature matching rate of distant regions of the universe can be solved on the basis of superluminal communication. The problem of superluminal communication has been considered repeatedly and has various aspects.
For example, in experiments with entangled particles [26], it was found that the signal for measuring the state of one particle from an entangled pair propagates at a speed significantly higher than the speed of light.
One argument against spreading information faster than the speed of light is also a possible violation of the second law of thermodynamics [27]. According to the author, if there is no interaction between two entangled particles (for example, in an EPR experiment), when measuring one particle, the state of the second also changes. This change corresponds to an additional decrease in the entropy of an isolated system. Since such processes are prohibited by the second law of thermodynamics, this is considered by a number of authors as a prohibition of superluminal communication. However, this argument implicitly implies that there are thermodynamic parameters in the system, such as entropy, temperature, etc. For a system in a pure state, there is no reason to introduce any thermodynamic parameters; therefore, it is impossible to correctly formulate the second law.
Another manifestation of superluminal communication is Wheeler’s delayed choice experiment. Wheeler’s thought experiment [28] is a variant of an experiment with two slits (there are also other variants of the experiment: photon in an interferometer, quantum circuit, quantum eraser [29]), in which one of the slits can be closed after the photon has passed through both slits but has not yet reached the screen. That is, in fact, the choice of the structure of the system with which the photon interacts is postponed. This experiment is currently being implemented, albeit in a slightly different form [30,31,32,33,34,35]. The main conclusion from the experiment is that wave or partial properties are not realistic properties of a quantum system.
It was shown in [36] that an experiment with Wheeler’s delayed choice on two slits is a natural consequence of the entanglement of a moving photon with gap atoms. The speed of entanglement is not limited by anything, since it is associated with the exchange of virtual particles, which are not subject to the restriction of the speed of light.
Thus, on the basis of experiments, we can conclude that entangled particles can be connected arbitrarily fast (at least, as far as modern measuring instruments can verify this).
Can information be transmitted faster than the speed of light? No-communication theorems that limit the rate of information transfer in an arbitrary quantum system answer this question (see, for example, [37]). However, the speed with which information can be transmitted from one point in the system to another is another question that is not directly related to the speed of decoherence and thermalization. During decoherence, an information channel is not formed, since the interaction is transmitted only in one direction.
Thus, if the scattering particles of the universe were initially entangled with each other, then these particles would simultaneously pass into their ground state (decay), no matter how far apart they are from each other. This means that their further thermalization (associated with the birth and destruction of other particles) will depend on the degree of entanglement of the initial state, but not on the size of the system.
Thus, the problem of the horizon is solved by the fact that entangled particles experience decoherence, regardless of what the distance between them is, even if this distance exceeds the value of ct. Generally, decoherence and thermalization are different processes. That is, a system in a pure state must first come into a mixed state and then relax to equilibrium. However, for an important particular case, when the whole system is in a pure, maximally entangled state, the transition from a pure state to a mixed one in this latter case coincides with thermalization.
Indeed, if the system is in a pure state, it means that it is simultaneously in all its permissible states. That is, it is not in some initial unlikely state from which it would have to come to equilibrium. If it were, for example, in a spatially inhomogeneous state in which the energy of particles at different points is different, then the characteristic relaxation time of such a system to equilibrium would be large—on the order of
where L is the characteristic size of the system, and χ is the thermal diffusivity.
As already shown above, as a result of decoherence (thermalization), the universe will come to its most likely state with a maximum statistical weight, which corresponds to equilibrium.
Thus, decoherence of such an entangled system (universe) will occur relatively quickly, i.e., at a speed independent of its size. It is this property that allows us to solve the horizon problem.
5. Predominance of Matter over Antimatter as a Consequence of Particle Entanglement
At present, matter substantially prevails over antimatter; therefore, this fact needs explanation. Indeed, if in the initial period there was the same amount of matter and antimatter, then two options are possible as a result of annihilation. First, either the one or the other should have overwhelmingly disappeared, turning into radiation. Second, neither matter nor antimatter are completely annihilated; thus, the antimatter must remain somewhere in the universe, along with the matter in the same quantities. Neither the first nor the second options are experimentally observed.
Starting with the work of Sakharov [38], a number of mechanisms for baryogenesis were proposed (see, for example, [39,40,41]), most of which go beyond the standard model and require additional assumptions. The main conditions for baryogenesis (not directly related to the inflationary paradigm) are as follows [42]:
- There must be a physical process that violates the law of conservation of the baryon number.
- There must be a violation of the invariance of C (charge symmetry) and CP (charge conjugation parity symmetry).
- A violation of the state of thermal equilibrium is necessary.
Violation of CP invariance and violation of conservation of baryon and lepton charge have been experimentally discovered [42,43,44,45,46,47,48,49,50]. It remains unclear whether the discovered properties can explain the asymmetry of matter and antimatter observed at the present time. There are also a number of models for symmetry and thermal equilibrium violation [41]).
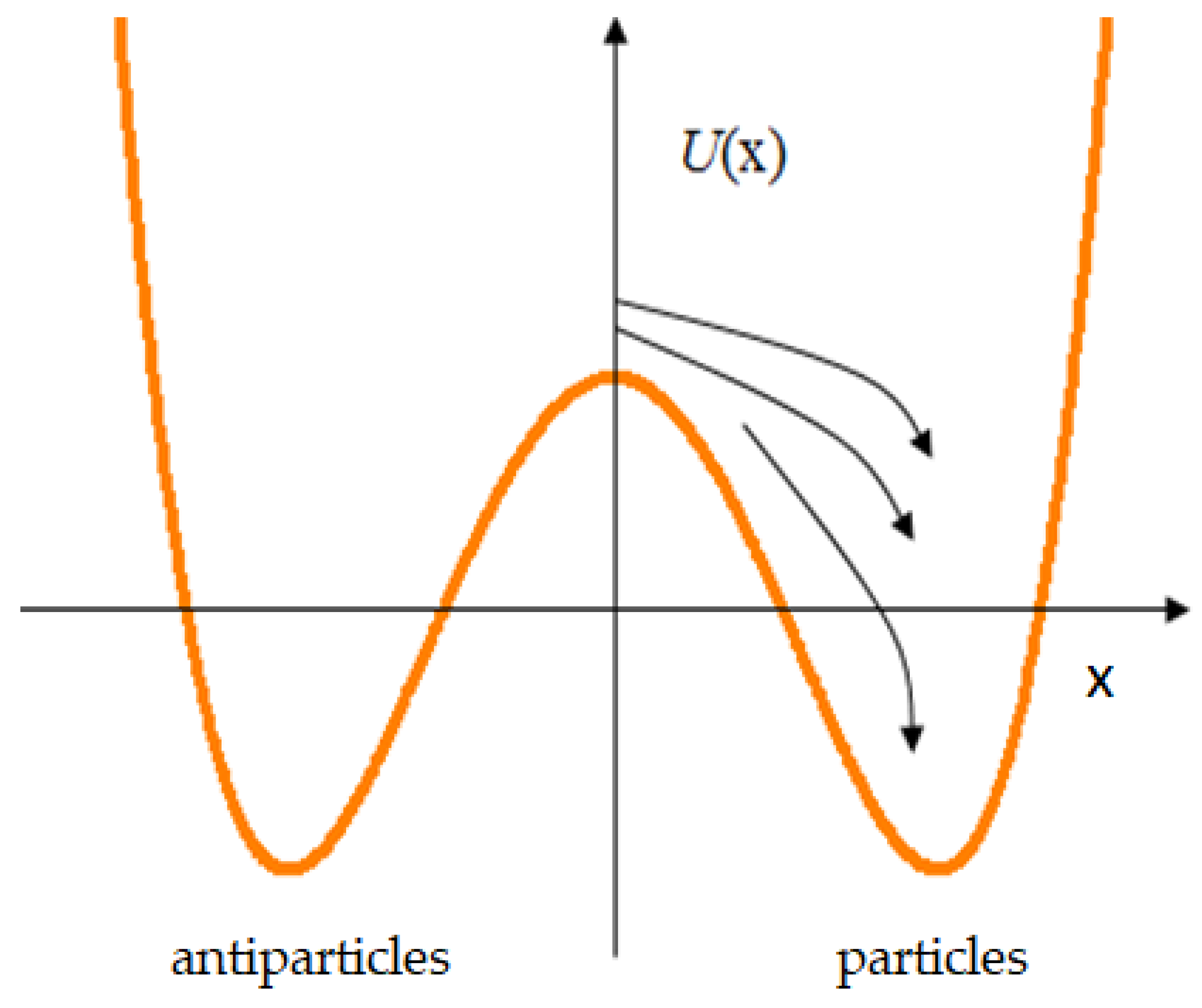
We show that this problem can also be solved on the basis of the decay of the entangled state of an expanding quantum system. Suppose that initial proto-particles (condensate) with equal probability can decay into particles and antiparticles :
Such a situation can, for example, be described using the potential
In the absence of any asymmetry, the birth of a particle or antiparticle in this case is a random process. However, since the particles (from which baryons are subsequently born) are entangled with each other, such a violation will occur immediately in the entire system and not in its individual areas. That is, the resulting fluctuation will be significantly enhanced because of entanglement and will encompass the entire system [19]. Then, there will be either matter or antimatter in the system. If the entanglement between the initial particles is not complete, then the predominance of matter over antimatter will also be incomplete, but sufficient for the formation of baryons. As a result, after annihilation of a part of the matter and antimatter, an excess of one or the other will remain (Figure 3).
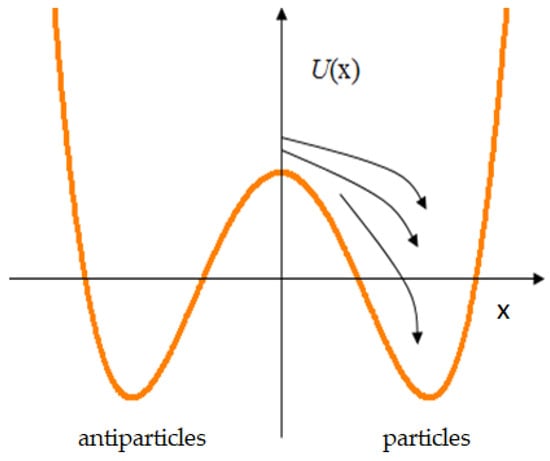
Figure 3.
Decay of a symmetric pure state.
After the decay of the pure state of the universe, the temperature first rises sharply due to decoherence, and then the era of radiation domination begins, during which the temperature begins to decrease. The further evolution of the universe can be described by well-known models, according to which, after this stage (see, for example, [42]), the electroweak interaction is separated from the strong one, and then quarks and known elements are formed.
Consider the annihilation of two types of particles and assume that this is an irreversible process in which particles are converted into radiation. We will also assume that good mixing of particles occurs in the system, i.e., diffusion terms are small. Then, we obtain a system of equations taking into account changes in the scale factor (the characteristic size of the universe):
Denote
as a result, we obtain the system of equations:
According to the notation
subtract the second from the first equation and obtain the solution of the system of equations in the form
If the particle concentrations at the initial moment are equal, then we can make the limit transition in the obtained solutions. Using L’Hopital’s rule for the fraction on the right-hand side for small α, we obtain for this case
Thus, at large times, if the initial concentrations of particles and antiparticles are equal, the concentration of the remaining particles will decrease according to a power law (bearing in mind that in (31) R(t) can have the power form):
This means that after time
a small amount of matter and antimatter will remain, and the universe will consist mainly of radiation.
If the initial concentrations of particles and antiparticles are not equal (which can occur as a result of the decay of a pure state), then after a characteristic time (here we use the Equation (32))
the second component (the one with smaller initial concentration) will disappear, annihilation will stop, and the first component will remain:
In this case, only partial entanglement between the particles of the universe turns out to be quite sufficient.
It can be seen from the obtained expressions that taking into account the expansion of the universe does not qualitatively change the picture of annihilation—in this case, only the time scale changes.
If matter and antimatter do not have time to mix (in this case, diffusion terms will be added to the right particles of the system of Equations (25) and (26)), then somewhere in space there will be significant areas occupied mainly by matter or antimatter. However, the existence of such regions is not confirmed experimentally.
Thus, if at least any significant amount of matter was initially present as “superfluous” in comparison with antimatter, then it will remain in the universe after some time following annihilation and will make up the substance of the universe known today. This excess of matter itself could have arisen as a result of the accidental decay of a pure state simultaneously in the entire universe.
6. Conclusions
An isolated system of bosons and fermions, which has been initially in a pure, maximally entangled quantum state, comes to equilibrium as a result of decoherence caused by the creation and annihilation of particles. The time of such a transition does not depend on the size of the system but is determined only by the properties of the particles and their degree of entanglement. This phenomenon allows us to solve the horizon problem, since the transition time of different parts of the universe to equilibrium will not depend on their sizes, and the transmission rate of the interaction may be greater than the speed of light. This property also allows us to solve the problem of the predominance of matter in the universe, since entanglement can provide the initial predominance of matter (antimatter) in the universe as a whole.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gogolin, C.; Eisert, J. Equilibration, thermalisation, and the emergence of statistical mechanics in closed quantum systems. Rep. Prog. Phys. 2016, 79, 056001. [Google Scholar] [CrossRef]
- Hornberger, K. Entanglement and Decoherence. In Introduction to Decoherence Theory; Buchleitner, A., Viviescas, C., Tiersch, M., Eds.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 768, pp. 221–276. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 2004, 76, 1267. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Balian, R.; Nieuwenhuizen, T.M. Understanding quantum measurement from the solution of dynamical models. Phys. Rep. 2013, 525, 1–166. [Google Scholar] [CrossRef]
- Gurvitz, S. Does the measurement take place when nobody observes it? Fortschr. Phys. 2016, 65, 1600065. [Google Scholar] [CrossRef]
- Melkikh, A.V. Nonlinearity of Quantum Mechanics and Solution of the Problem of Wave Function Collapse. Comm. Theor. Phys. 2015, 64, 47. [Google Scholar] [CrossRef]
- Melkikh, A.V. Quantum information and microscopic measuring instruments. Comm. Theor. Phys. 2019, 72, 015101. [Google Scholar] [CrossRef]
- von Mises, R. The Mathematical Theory of Probability and Statistics; Academic: London, UK, 1964. [Google Scholar]
- Rumer, I.B.; Ryvkin, M.S. Thermodynamics, Statistical Physics and Kinetics; Mir: Moscow, Russia, 1980. [Google Scholar]
- Borgonovi, F.; Izrailev, F.M.; Santos, L.F.; Zelevinsky, V.G. Quantum chaos and thermalization in isolated systems of interacting particles. Phys. Rep. 2016, 626, 1–58. [Google Scholar] [CrossRef]
- Batterfeald, D.; Peter, P. A critical review of classical bouncing cosmologies. Phys. Rep. 2015, 571, 1–66. [Google Scholar] [CrossRef]
- Starobinskii, A.A. A New Type of Isotropic Cosmological Models without Singularity. Phys. Lett. B 1980, 1, 99–102. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D. 1981, 23, 347. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for grand unified theories with radiatively induces symmetry breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. 1982, 108B, 389. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic Inflation Chaotic Inflation. Phys. Lett. B 1983, 129, 177. [Google Scholar] [CrossRef]
- Penrose, R. Cycles of Time, an Extraordinary New View of the Universe; Knopf: New York, NY, USA, 2011. [Google Scholar]
- Melkikh, A.V. A pure quantum universe as an alternative to inflation. International journal of cosmology, astronomy and astrophysics. Int. J. Cosmol. Astron. Astrophys. 2019, 1, 88–93. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Jaeger, G. Entanglement, Information, and the Interpretations of Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Melkikh, A.V. Quantum paradoxes, entanglement and their explanation on the basis of quantization of fields. Modern Phys. Lett. B 2017, 31, 1750007. [Google Scholar] [CrossRef]
- Melkikh, A.V. Quantum system: Wave function, entanglement and the uncertainty principle. Modern Phys. Lett. B 2021. Accepted. [Google Scholar]
- Bennett, C.H.; DiVincenzo, D.P.; Smolin, J.A.; Wootters, W.K. Mixed-state entanglement and quantum error correction. Phys. Rev. A 1996, 54, 3824. [Google Scholar] [CrossRef] [PubMed]
- Hill, S.; Wootters, W.K. Entanglement of a Pair of Quantum Bits. Phys. Rev. Lett. 1997, 78, 5022. [Google Scholar] [CrossRef]
- Salart, D.; Baas, A.; Branciard, C.; Gisin, N.; Zbinden, H. Testing the speed of ‘spooky action at a distance. Nature 2008, 454, 861–864. [Google Scholar] [CrossRef]
- Peacock, K.A.; Hapburn, P.S. Begging the signaling question: Quantum signaling and the dynamics of multiparticle systems. arXiv 1999, arXiv:quant-ph/9906036. [Google Scholar]
- Wheeler, J.A. Mathematical Foundations of Quantum Mechanics; Marlow, A.R., Ed.; Academic: New York, NY, USA, 1978; pp. 9–48. [Google Scholar]
- Ma, X.; Kofler, J.; Zeilinger, A. Delayed-choice gedanken experiments and their realizations. Rev. Mod. Phys. 2016, 88, 015005. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Yu, R.; Kulik, S.P.; Shih, Y.H.; Scully, M. Delayed “choice” quantum eraser. Phys. Rev. Lett. 2000, 84, 1. [Google Scholar] [CrossRef] [PubMed]
- Walborn, S.P.; Terra Cunha, M.O.; Pádua, S.; Monken, C.H. Double-slit quantum eraser. Phys. Rev. A 2002, 65, 0033818. [Google Scholar] [CrossRef]
- Jacques, V.; Wu, E.; Grosshans, F.; Treussart, F.; Grangier, P.; Aspect, A.; Roch, J.F. Experimental Realization of Wheeler’s Delayed-Choice Gedanken Experiment. Science 2007, 315, 966. [Google Scholar] [CrossRef]
- Kaiser, F.; Courdeau, T.; Milman, P.; Ostrowsky, D.B.; Tanzilli, S. Entanglement-Enabled Delayed-Choice Experiment. Science 2012, 338, 637. [Google Scholar] [CrossRef] [PubMed]
- Peruzzo, A.; Shadbolt, P.; Brunner, N.; Popescu, S.; O’Brien, J.L. A Quantum Delayed-Choice Experiment. Science 2012, 338, 634. [Google Scholar] [CrossRef]
- Ma, X.S.; Zotter, S.; Kofler, J.; Ursin, R.; Jennewein, T.; Brunker, C.; Zeilinger, A. Experimental delayed-choice entanglement swapping. Nat. Phys. 2012, 8, 479. [Google Scholar] [CrossRef]
- Melkikh, A.V. Quantum entanglement, Wheeler’s delayed choice experiment and its explanation on the basis of quantization of fields. J. Phys. Conf. Ser. 2017, 880, 012030. [Google Scholar] [CrossRef]
- Peres, A.; Terno, D.R. Quantum information and relativity theory. Rev. Mod. Phys. 2004, 76, 93. [Google Scholar] [CrossRef]
- Sakharov, A.D. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. JETP Lett. 1967, 5, 24. [Google Scholar]
- Kuzmin, V.A.; Rubakov, V.A.; Shaposhnikov, M.E. On anomalous electroweak baryon-number non-conservation in the early universe. Phys. Lett. B 1985, 155, 36–42. [Google Scholar] [CrossRef]
- Dolgov, A.; Silk, J. Baryon isocurvature fluctuations at small scales and baryonic dark matter. Phys. Rev. D 1993, 47, 4244. [Google Scholar] [CrossRef] [PubMed]
- Kusenko, A.; Pearce, L.; Yang, L. Postinflationary Higgs relaxation and the origin of matter-antimatter asymmetry. Phys. Rev. Lett. 2015, 114, 061302. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Trodden, M. Electroweak baryogenesis. Rev. Mod. Phys. 1999, 71, 1463. [Google Scholar] [CrossRef]
- Asaka, T.; Shaposhnikov, M. νMSM, dark matter and baryon asymmetry of the universe. Phys. Lett. B 2005, 620, 17. [Google Scholar] [CrossRef]
- Davidson, S.; Nardi, E.; Nir, Y. Leptogenesis. Phys. Rep. 2008, 466, 105. [Google Scholar] [CrossRef]
- Giovannini, M. Hypermagnetic gyrotropy, inflation, and the baryon asymmetry of the Universe. Phys. Rev. D. 2015, 92, 121301. [Google Scholar] [CrossRef]
- Heeck, J.; Takhistov, V. Inclusive nucleon decay searches as a frontier of baryon number violation. Phys. Rev. D 2020, 101, 015005. [Google Scholar] [CrossRef]
- Drewes, M.; Klaríc, J.; Klose, P. On lepton number violation in heavy neutrino decays at colliders. J. High Energy Phys. 2019, 32. [Google Scholar] [CrossRef]
- LHCb Collaboration. Observation of CP Violation in Charm Decays. Phys. Rev. Lett. 2019, 122, 211803. [Google Scholar] [CrossRef] [PubMed]
- T2K Collaboration. Constraint on the matter–antimatter symmetry-violating phase in neutrino oscillations. Nature 2020, 580, 339–344. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).