Abstract
Recently a non-supersymmetric conformal field theory with an exactly marginal deformation in the large N limit was constructed by Chaudhuri–Choi–Rabinovici. On a non-supersymmetric conformal manifold, the c coefficient of the trace anomaly in four dimensions would generically change. In this model, we, however, find that it does not change in the first non-trivial order given by three-loop diagrams.
Conformal field theories are no longer conformally invariant in curved space-time due to the trace anomaly in even space-time dimensions. They do, however, play a fundamental role in understanding the structure of the energy–momentum tensor and the renormalization group flow.
In four-dimensional conformal field theories, the trace anomaly has the form
and it is known that coefficient a cannot change under exactly marginal deformations, but coefficient c may [1,2,3,4,5,6,7]. However, there has been no explicit field theory example where c changes (except for the effective holographic constructions in [2]). The main obstruction has been that we have no good examples of non-supersymmetric conformal field theories with exactly marginal deformations; in superconformal field theories, while it is easier to realize exactly marginal deformations, c does not change [8].
Recently, Chaudhuri, Choi and Rabinovici have constructed a non-supersymmetric conformal field theory with an exactly marginal deformation in the large N limit [9] (see also [10,11] for other recently constructed examples of non-supersymmetric field theories with exactly marginal deformations in different dimensions than four). This theory may serve as a first non-trivial check if c can really change under exactly marginal deformations. In this short note, we, however, show that it does not change at the first non-trivial order given by three-loop diagrams.
The model (called complex bifundamental model in [9]) is given by four gauge theories with names and , each of which has Dirac fermions in the fundamental representation. We have two complex scalars in the bifundamental representations (under gauge group 1 and ) and (under gauge group 2 and ). The gauge coupling constant for each gauge group is . It has no Yukawa interaction, the absence of which is protected by chiral symmetry, but it has a scalar potential
We take the Veneziano limit of with fixed and consider the limit to make the theory weakly coupled.
In terms of rescaled coupling constants ()
the renormalization group functions in the Veneziano limit are expressed as (no sum over i unless explicitly shown)
The zero of the functions was studied in [9] and they found that there exists a conformal manifold given by
where . From the last line of Equation (5), we see that it has the topology of a circle. As long as is small, we may neglect higher order corrections.
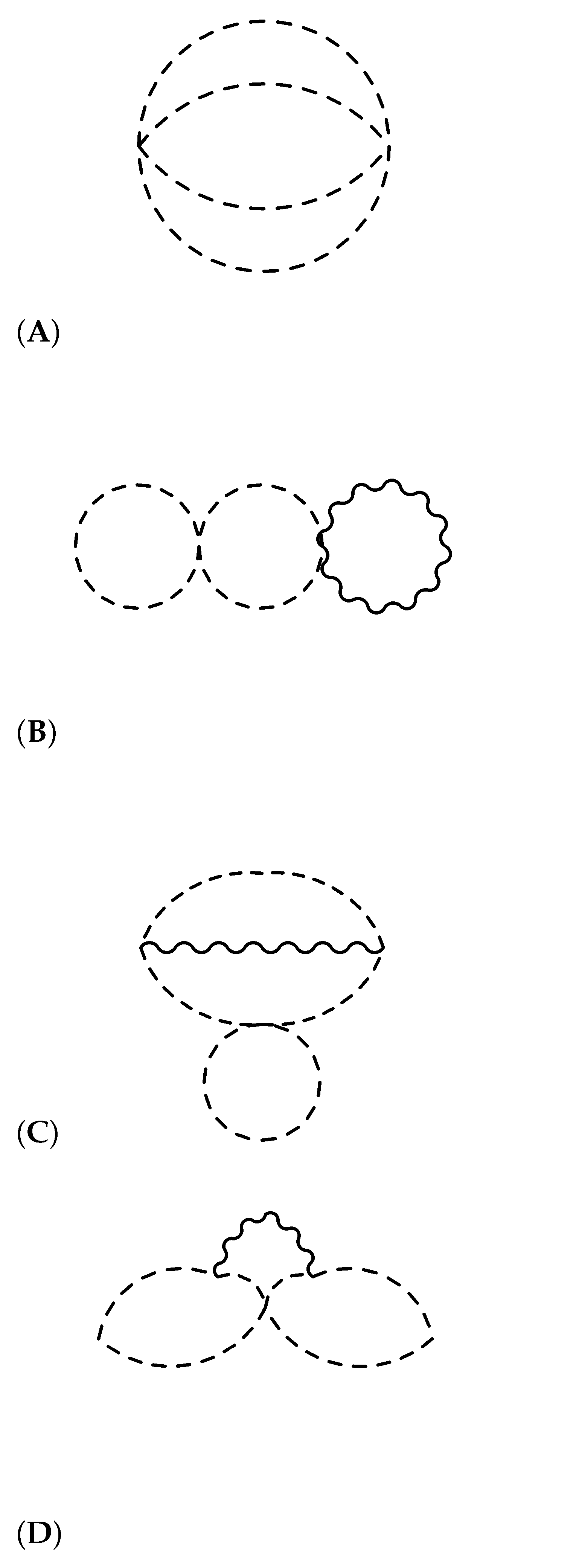
We now ask if the coefficient c in the trace anomaly can change on this conformal manifold. In addition to the coupling constant-independent contributions from the one-loop diagrams (that count a number of fields), the coupling constant-dependent contributions to the trace anomaly that are relevant for us come from the three-loop diagrams shown in Figure 1. The detailed computation for Figure 1A (as well as other two-loop diagrams) can be found in [12,13,14], but we only need the relative coefficient, so we can simply work on combinatorics.
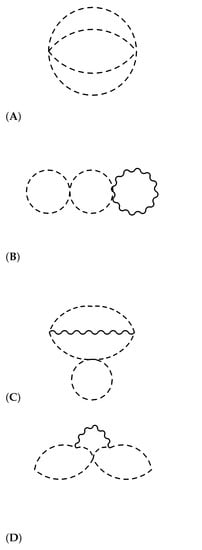
Figure 1.
Three-loop Feynman diagrams that could contribute to c. Wavy lines correspond to gauge fields and dotted lines correspond to scalar fields.
The three-loop Figure 1B–D are not evaluated in the literature, but we see that Figure 1B,C do not contribute to c. This is because the divergence can be simply removed by adding the “mass counter-term”. Figure 1D may contribute in general, but the contributions to c in our theory do not depend on or from the symmetry of the diagrams (It cannot be proportional to because the gauge fields cannot connect and . The relevant diagrams are all symmetric with respect to the exchange of and ).
As for Figure 1A, since the overall contribution to c is known, we can just enumerate diagrams appearing in the Wick contractions of
We see that only planar diagrams will contribute in the Veneziano limit.
Up to an overall proportionality factor, the result in the Veneziano limit is summarized as
on the conformal manifold, where is some numerical constant, which is unimportant for our discussions (A typo in the two-loop gauge contribution [14] that could affect has been corrected in [15]). Since the relative coefficient appearing here coincides with what appears in the last line of Equation (5), we conclude that c does not change on the conformal manifold, although the value itself is perturbatively corrected. We also note that these two- and three-loop diagrams do not change the value of a as anticipated [1,16] (rather trivially without cancellation, unlike c).
The result is surprising in the sense that we generically expect that c would change on a non-supersymmetric conformal manifold. It is an interesting question to see whether the higher loop corrections modify our conclusion. It may be possible to relate the all-loop argument for the existence of the exactly marginal deformation in [9] with the computation of c by closing all the external lines in beta functions to make vacuum diagrams.
Funding
This work is in part supported by JSPS KAKENHI Grant Number 17K14301.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work is in part supported by JSPS KAKENHI Grant Number 17K14301. It is motivated from the online talk by Z. Komargodski at YITP workshop on Strings and Fields 2020, which the author watched on Youtube later.
Conflicts of Interest
The author declares no conflict of interest.
References
- Osborn, H. Weyl consistency conditions and a local renormalization group equation for general renormalizable field theories. Nucl. Phys. B 1991, 363, 486. [Google Scholar] [CrossRef]
- Nakayama, Y. Can we change c in four-dimensional CFTs by exactly marginal deformations? JHEP 2017, 7, 4. [Google Scholar] [CrossRef]
- Meltzer, D.; Perlmutter, E. Beyond a = c: Gravitational couplings to matter and the stress tensor OPE. JHEP 2018, 7, 157. [Google Scholar] [CrossRef]
- Bzowski, A.; McFadden, P.; Skenderis, K. Renormalised CFT 3-point functions of scalars, currents and stress tensors. JHEP 2018, 11, 159. [Google Scholar] [CrossRef]
- Solodukhin, S.N. Logarithmic terms in entropy of Schwarzschild black holes in higher loops. Phys. Lett. B 2020, 802, 135235. [Google Scholar] [CrossRef]
- Niarchos, V.; Papageorgakis, C.; Pomoni, E. Type-B Anomaly Matching and the 6D (2,0) Theory. JHEP 2020, 4, 48. [Google Scholar] [CrossRef]
- Niarchos, V.; Papageorgakis, C.; Pini, A.; Pomoni, E. (Mis-)Matching Type-B Anomalies on the Higgs Branch. arXiv 2020, arXiv:2009.08375. [Google Scholar]
- Anselmi, D.; Freedman, D.Z.; Grisaru, M.T.; Johansen, A.A. Nonperturbative formulas for central functions of supersymmetric gauge theories. Nucl. Phys. B 1998, 526, 543. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Choi, C.; Rabinovici, E. Thermal order in large N conformal gauge theories. arXiv 2020, arXiv:2011.13981. [Google Scholar]
- Chai, N.; Chaudhuri, S.; Choi, C.; Komargodski, Z.; Rabinovici, E.; Smolkin, M. Symmetry Breaking at All Temperatures. Phys. Rev. Lett. 2020, 125, 131603. [Google Scholar] [CrossRef] [PubMed]
- Chai, N.; Chaudhuri, S.; Choi, C.; Komargodski, Z.; Rabinovici, E.; Smolkin, M. Thermal Order in Conformal Theories. Phys. Rev. D 2020, 102, 065014. [Google Scholar] [CrossRef]
- Jack, I.; Osborn, H. Background Field Calculations in Curved Space-time. 1. General Formalism and Application to Scalar Fields. Nucl. Phys. B 1984, 234, 331–364. [Google Scholar] [CrossRef]
- Jack, I. Background Field Calculations in Curved Space-Time. II. Application to a Pure Gauge Theory. Nucl. Phys. B 1984, 234, 365–378. [Google Scholar] [CrossRef]
- Jack, I. Background Field Calculations in Curved Space-Time. 3. Application to a General Gauge Theory Coupled to Fermions and Scalars. Nucl. Phys. B 1985, 253, 323–352. [Google Scholar] [CrossRef]
- Osborn, H.; Stergiou, A. CT for non-unitary CFTs in higher dimensions. JHEP 2016, 6, 79. [Google Scholar] [CrossRef]
- Komargodski, Z.; Schwimmer, A. On Renormalization Group Flows in Four Dimensions. JHEP 2011, 1112, 99. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).