Induced Currents and Aharonov–Bohm Effect in Effective Fermion Models and in Spaces with a Compact Dimension
Abstract
1. Introduction
2. Violation of Chiral Symmetry
3. Model with a Domain Wall
3.1. Dirac Equation in the Model with a Domain Wall
3.2. Vacuum Energy and Induced Current
4. Two-Fermion Model with a Compact Dimension

4.1. Effective Potential of the Model
4.2. Induced Current
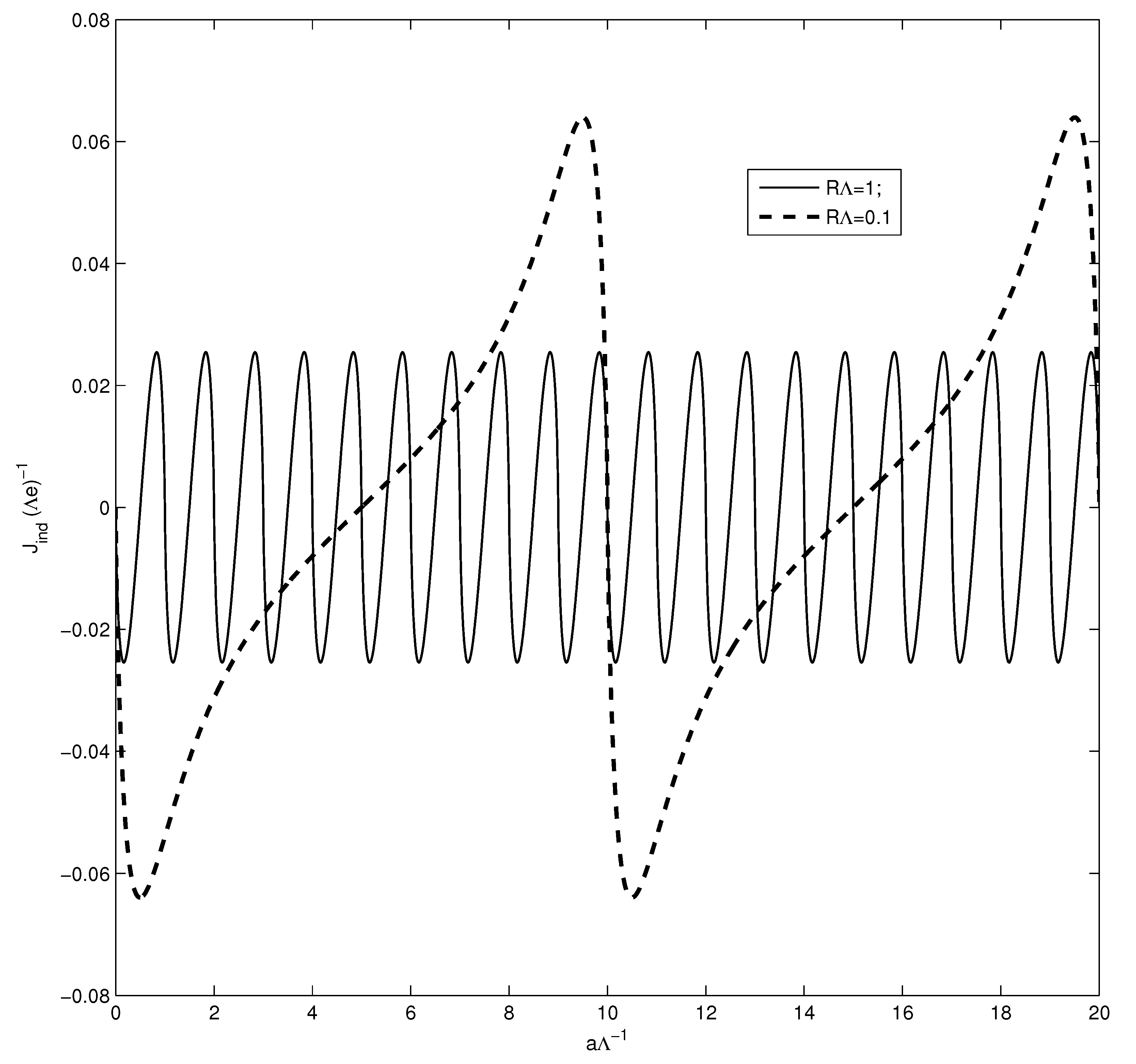
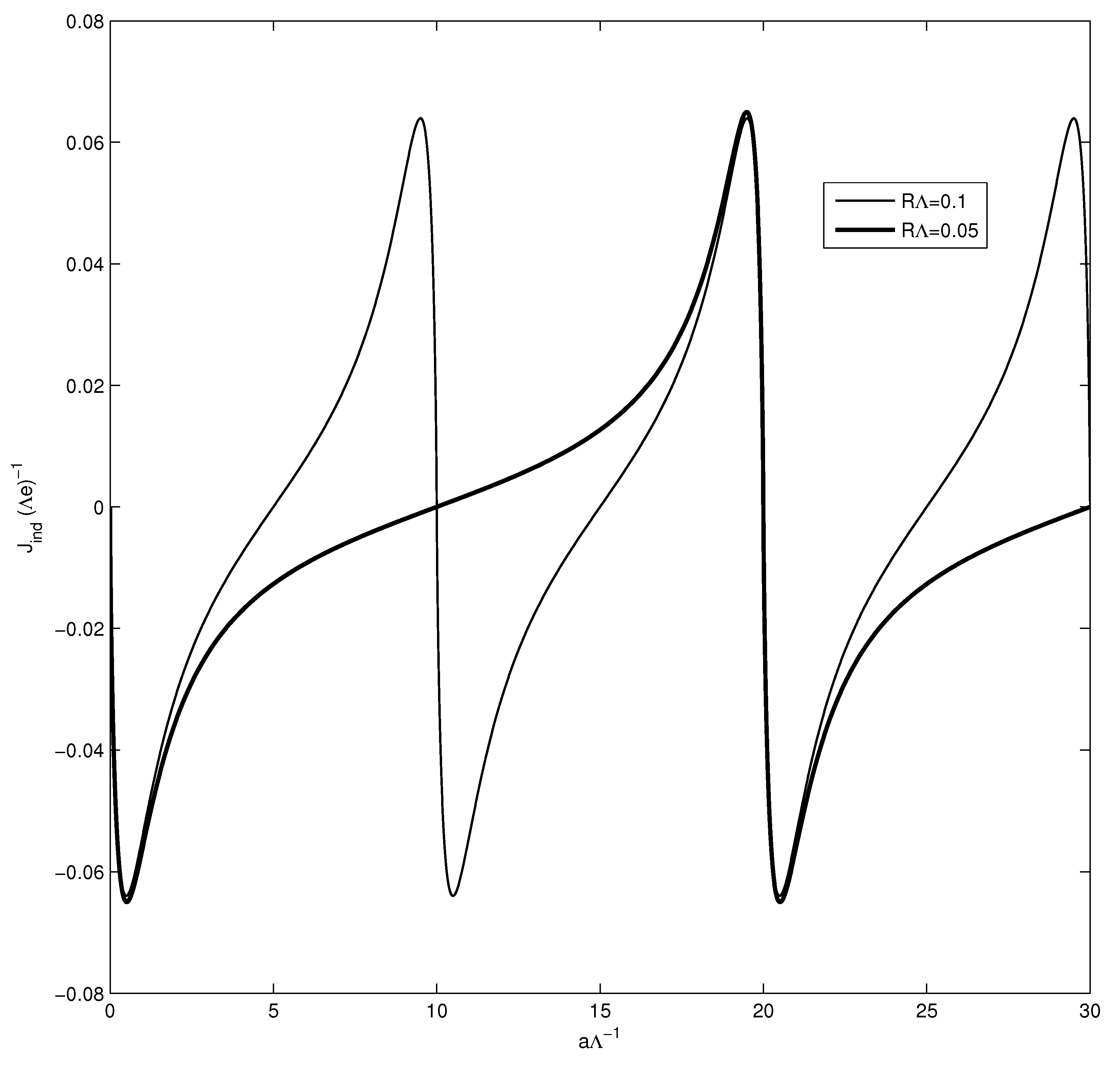
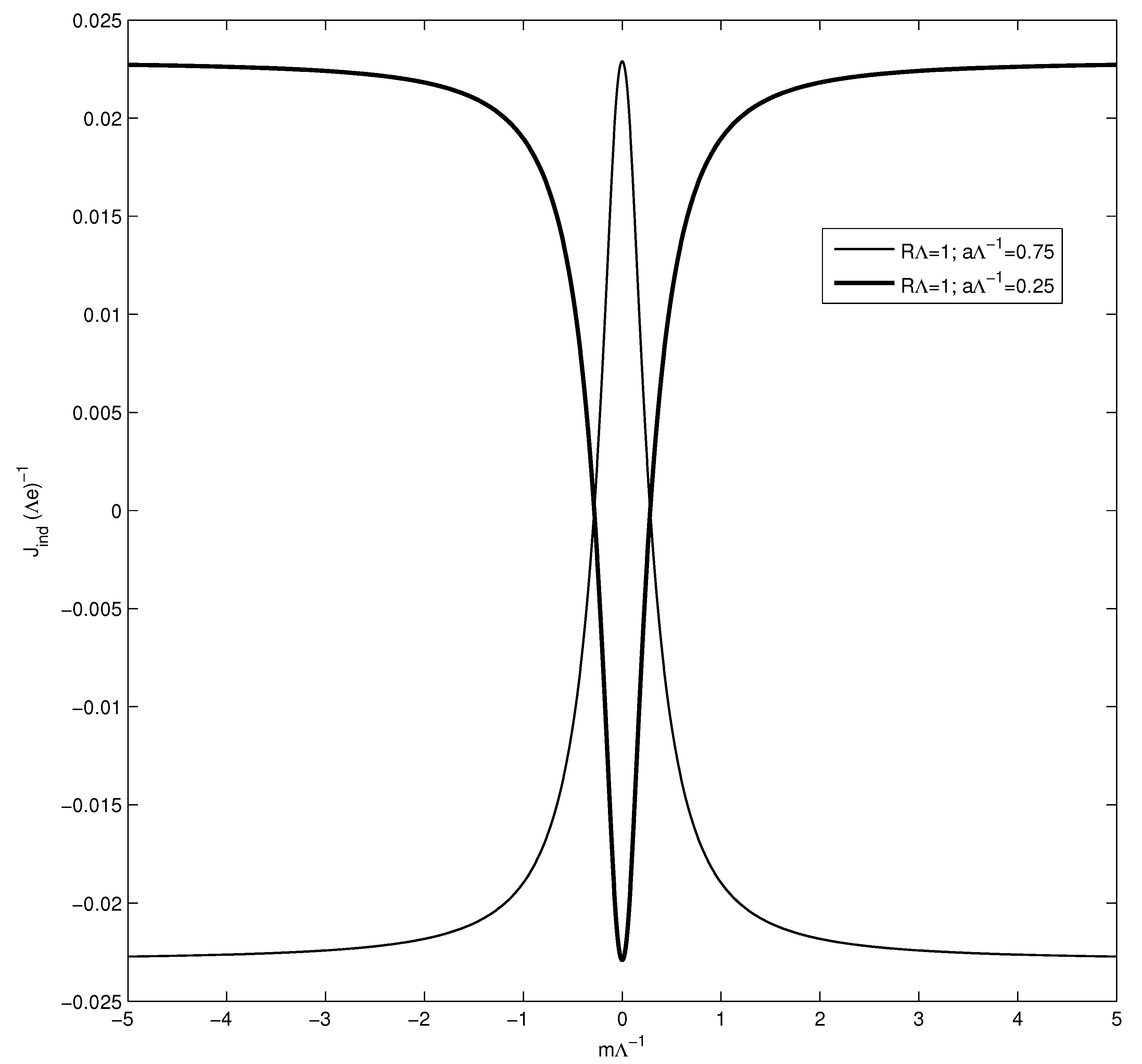
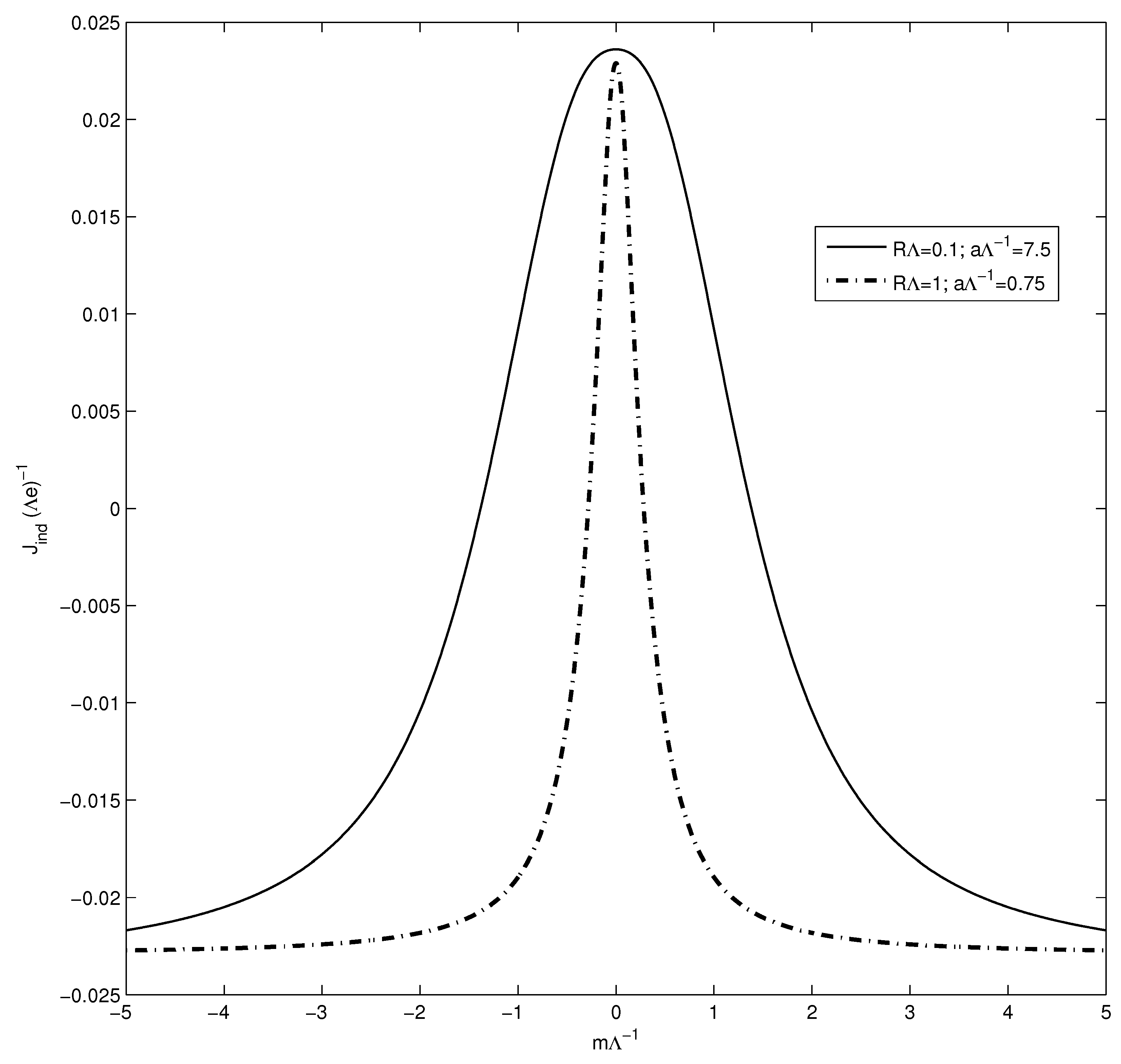
5. Induced Current in a Model with a Compact Dimension
5.1. Model in (4 + 1)-Dimensional Spacetime
5.2. Model in (2 + 1)-Dimensional Spacetime
6. Induced Current in a Planar Model with a Thin Solenoid
7. Summary and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kaluza, T. Unified field theory based on the 5-dimensional relativity. Preuss. Akad. Wiss. Sitzungaber. 1921, 966. [Google Scholar]
- Klein, O. Quantentheorie und fünfdimensionale Relativitätstheorie. Zeitsch. Phys. 1926, 37, 895. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. The Hierarchy Problem and New Dimensions at a Millimeter. Phys. Lett. B 1998, 429, 263. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. Large Mass Hierarchy from a Small Extra Dimension. Phys. Rev. Lett. 1999, 83, 3370. [Google Scholar] [CrossRef]
- Abe, H.; Miguchi, H.; Muta, T. Dynamical fermion masses under the influence of Kaluza-Klein fermions in Randall-Sundrum background. Mod. Phys. Lett. A 2000, 15, 445–454. [Google Scholar] [CrossRef]
- Ebert, D.; Zhukovsky, V.; Tyukov, A.V. Dynamical fermion masses under the influence of Kaluza-Klein fermions and a bulk abelian gauge field. Mod. Phys. Lett. A 2010, 25, 2933–2945. [Google Scholar] [CrossRef]
- Zhukovsky, V.C.; Stepanov, E.A. Effective (2+1)-dimensional field theory of fermions: Fermion mass generation with Kaluza-Klein fermions and gauge field. Phys. Lett. B 2012, 718, 597. [Google Scholar] [CrossRef]
- Hosotani, Y. Dynamical mass generation by compact extra dimensions. Phys. Lett. B. 1983, 126, 309. [Google Scholar] [CrossRef]
- Sundrum, R. Tasi 2004 lectures: To the fifth dimension and back. arXiv 2005, arXiv:0508134v2. [Google Scholar]
- Semenoff, G.W. Condensed-matter simulation of a three-dimensional anomaly. Phys. Rev. Lett. 1984, 53, 2449. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666. [Google Scholar] [CrossRef] [PubMed]
- Katsnelson, M.I. Graphene: Carbon in two dimensions. Mater. Today 2007, 10, 20. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530. [Google Scholar] [CrossRef] [PubMed]
- de Juan, F.; Cortijo, A.; Vozmediano, M.A.H. Charge inhomogeneities due to smooth ripples in graphene sheets. Phys. Rev. B 2007, 76, 165409. [Google Scholar] [CrossRef]
- Gonzalez, J.; Guinea, F.; Vozmediano, M.A.H. The electronic spectrum of fullerenes from the Dirac equation. Nucl. Phys. B 1993, 406, 771. [Google Scholar] [CrossRef]
- Gamayun, A.V.; Gorbar, E.V. Dynamical symmetry breaking on a cylinder in magnetic field. Phys. Lett. B 2005, 610, 74. [Google Scholar] [CrossRef]
- Ebert, D.; Klimenko, K.G.; Kolmakov, P.B.; Zhukovsky, V.C. Phase transitions in hexagonal, graphene-like lattice sheets and nanotubes under the influence of external conditions. Ann. Phys. 2016, 371, 254. [Google Scholar] [CrossRef]
- Ferrer, E.J.; Incera, V.d.; Romeo, A. Photon propagation in space-time with a compactified spatial dimension. Phys. Lett. B 2001, 515, 341. [Google Scholar] [CrossRef]
- Song, D.Y. Four-fermion interaction model on R2 × S1: A dynamical dimensional reduction. Phys. Rev. D 1993, 48, 3925. [Google Scholar] [CrossRef]
- Sitenko, Y.A. Induced vacuum condensates in the background of a singular magnetic vortex in (2 + 1) -dimensional space-time. Phys. Rev. D 1999, 60, 125017. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 1959, 115, 485. [Google Scholar] [CrossRef]
- Caldas, H.; Ramos, R.O. Magnetization of planar four-fermion systems. Phys. Rev. B. 2009, 80, 115428. [Google Scholar] [CrossRef]
- Drut, J.E.; Son, D.T. Renormalization group flow of quartic perturbations in graphene: Strong coupling and large-N limits. Phys. Rev. B 2008, 77, 075115. [Google Scholar] [CrossRef]
- Atiyah, M.; Patodi, V.; Singer, I. Spectral asymmetry and Riemannian geometry. Math. Proc. Camb. Philos. Soc. 1975, 77, 43. [Google Scholar] [CrossRef]
- Jackiw, R.; Milstein, A.I.; Pi, S.-Y.; Terekhov, I.S. Induced Current and Aharonov-Bohm Effect in Graphene. Phys. Rev. B 2009, 80, 033413. [Google Scholar] [CrossRef]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. Chiral magnetic effect. Phys. Rev. D. 2008, 78, 074033. [Google Scholar] [CrossRef]
- Obispo, A.E.; Hott, M. Fractional fermion charges induced by axial-vector and vector gauge potentials and parity anomaly in planar graphenelike structures. Phys. Rev. B. 2014, 89, 165405. [Google Scholar] [CrossRef]
- Basar, G.; Dunne, G.V. The Chiral Magnetic Effect and Axial Anomalies. arXiv 2012, arXiv:1207.499. [Google Scholar]
- Chamon, C.; Hou, C.-Y.; Jackiw, R.; Mudry, C.; Pi, S.-Y.; Schnyder, A.P. Irrational Versus Rational Charge and Statistics in Two-Dimensional Quantum Systems. Phys. Rev. Lett. 2008, 100, 110405. [Google Scholar] [CrossRef]
- Chamon, C.; Hou, C.-Y.; Jackiw, R.; Mudry, C.; Pi, S.-Y.; Semenoff, G. Electron fractionalization for two-dimensional Dirac fermions. Phys. Rev. B 2008, 77, 235431. [Google Scholar] [CrossRef]
- Stepanov, E.A.; Zhukovsky, V.C. Graphene under the influence of Aharonov-Bohm flux and constant magnetic field. Phys. Rev. B 2016, 94, 094101. [Google Scholar] [CrossRef]
- Zhukovsky, V.C.; Stepanov, E.A. Induced current and transmission through the barrier in the four-fermion model in 2 + 1 dimensions. Mosc. Univ. Phys. Bull. 2014, 69, 139. [Google Scholar] [CrossRef]
- Bubnov, A.F.; Gubina, N.V.; Zhukovsky, V.C. Vacuum current induced by an axial-vector condensate and electron anomalous magnetic moment in a magnetic field. Phys. Rev. D 2017, 96, 016011. [Google Scholar] [CrossRef]
- Semenoff, G.W.; Semenoff, V.; Zhou, F. Domain walls in gapped graphene. Phys. Rev. Lett. 2008, 101, 087204. [Google Scholar] [CrossRef]
- Wallace, P.R. The band theory of graphite. Phys. Rev. 1947, 71, 622. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. AC conductivity of graphene: From tight-binding model to 2+ 1-dimensional quantum electrodynamics. Int. J. Mod. Phys. B. 2007, 21, 4611. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Ebert, D.; Zhukovsky, V.C.; Stepanov, E.A. A pseudopotential model for Dirac electrons in graphene with line defects. J. Phys. Condens. Matter 2014, 26, 125502. [Google Scholar] [CrossRef][Green Version]
- Castro Neto, A.H. Selected topics in graphene physics. arXiv 2010, arXiv:1004.3682. [Google Scholar]
- Vozmediano, M.A.H.; Katsnelson, M.I.; Guinea, F. Gauge fields in graphene. Phys. Rep. 2010, 496, 109. [Google Scholar] [CrossRef]
- Jackiw, R. Effects of Dirac’s Negative Energy Sea on Quantum Numbers. arXiv 1999, arXiv:9903255. [Google Scholar]
- Guinea, F.; Horovitz, B.; Le Doussal, P. Gauge field induced by ripples in graphene. Phys. Rev. B 2008, 77, 205421. [Google Scholar] [CrossRef]
- Schön, V.; Thies, M. 2D Model Field Theories at Finite Temperature and Density. arXiv 2000, arXiv:0008175. [Google Scholar]
- Bietenholz, W.; Gfeller, A.; Wiese, U.-J. Dimensional reduction of fermions in brane worlds of the Gross-Neveu model. JHEP 2003, 10, 18. [Google Scholar] [CrossRef]
- Han, T.; Lykken, J.D.; Zhang, R. Kaluza-Klein states from large extra dimensions. Phys. Rev. D 1999, 59, 105006. [Google Scholar] [CrossRef]
- Diakonov, D. Potential Energy of Yang-Mills Vortices in Three and Four Dimensions. Mod. Phys. Lett. A 1999, 14, 1725. [Google Scholar] [CrossRef]
- Haba, N.; Harada, M.; Hosotani, Y.; Kawamura, Y. Dynamical rearrangement of gauge symmetry on the orbifold S1/Z2. Nucl. Phys. B 2003, 657, 169. [Google Scholar] [CrossRef]
- Yu, A.; Brychkov, O.I.; Marichev, A.; Prudnikov, P. Integrals and Series: Volume 1: Elementary Functions; FIZMATLIT: Moscow, Russia, 2003. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products, 7th ed.; Academic Press: Burlington, MA, USA; Elsevier: Burlington, MA, USA, 2007. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhukovsky, V.C. Induced Currents and Aharonov–Bohm Effect in Effective Fermion Models and in Spaces with a Compact Dimension. Symmetry 2021, 13, 210. https://doi.org/10.3390/sym13020210
Zhukovsky VC. Induced Currents and Aharonov–Bohm Effect in Effective Fermion Models and in Spaces with a Compact Dimension. Symmetry. 2021; 13(2):210. https://doi.org/10.3390/sym13020210
Chicago/Turabian StyleZhukovsky, Vladimir Ch. 2021. "Induced Currents and Aharonov–Bohm Effect in Effective Fermion Models and in Spaces with a Compact Dimension" Symmetry 13, no. 2: 210. https://doi.org/10.3390/sym13020210
APA StyleZhukovsky, V. C. (2021). Induced Currents and Aharonov–Bohm Effect in Effective Fermion Models and in Spaces with a Compact Dimension. Symmetry, 13(2), 210. https://doi.org/10.3390/sym13020210




