4D Einstein–Gauss–Bonnet Gravity Coupled with Nonlinear Electrodynamics

Abstract

A new exact spherically symmetric and magnetically charged black hole solution in regularization scheme of Glavan and Lin is obtained. The nonlinear electrodynamics Lagrangian is given by ${\mathcal{L}}_{NED}=-\mathcal{F}/(1+\sqrt[4]{2\beta \mathcal{F}})$, where $\mathcal{F}$ is the field invariant. We study the thermodynamics calculating the Hawking temperature and the heat capacity of the black hole. The phase transitions take place when the Hawking temperature has an extremum and the heat capacity is singular. We demonstrate that black holes are thermodynamically stable in some range of event horizon radii where the heat capacity is positive. The BH shadow radius is calculated and we study its dependance on model parameters.

1. Introduction

The heterotic string theory at the low energy limit gives models of gravity with higher order curvature terms in the action [1,2,3,4,5]. Therefore, it is interesting to investigate a modified Einstein General Relativity (GR) including higher order curvature terms. Probably, such deformed GR can describe gravity in the strong gravity regime where quantum corrections are important. An interesting modified GR with higher order curvature terms is the Lovelock gravity in higher dimensions leading to the second order field equations. The particular case of the Lovelock theory of gravity is the Gauss-Bonnet (GB) gravity resulting to non-trivial dynamics. In four dimensions such model includes the Einstein-Hilbert action and the GB term which is a topological invariant and, as a result, it does not contribute to the gravitational dynamics. But Glavan and Lin [6] shown that if the coupling constant $\alpha$, which can be considered as the inverse of the string tension, is re-scaled by $\alpha /(D-4)$, in the limit $D\to 4$, this scheme yields a non-trivial dynamics without singularities. It was argued, that the model being a classical modified gravity, is free from the Ostrogradsky instability and conserves the number of degrees of freedom. The static spherically symmetric BH solution for the Einstein GB gravity was obtained in [7,8,9] and the authors claimed that the GB term can be considered as a quantum correction to GR. It worth noting that the BH solution within this scheme gives a repulsive gravitational force at short distances. Similar solution was obtained in the gravity theory with quantum corrections [10]. Recently, the regularization scheme of Glavan and Lin attracted extensive attention (see, for example, [11,12,13,14,15,16,17,18,19,20,21,22,23,24]). The BH solutions, within the regularization scheme of [6] with nonlinear electrodynamics (NED), were studied in [25,26,27,28,29,30,31,32,33,34,35].

In [36], it was shown that in a conformally flat metric, only the GB term gives the finiteness of renormalization for a static spherically symmetric ansatz. Thus, the metric obtained is the rigorous solution for quantum gravity corrections and the repulsive nature of gravity at short distances was established. The static BH solution obtained in [36] was recovered and generalized with the inclusion of non-trivial horizon topology in [10]. It should be noted that the regularized GB BH solution also is a solution of the semi-classical Einstein equations with conformal anomaly [37]. We also note that the GB term plays an important role in 4D AdS spacetime within the AdS/CFT correspondence. The topological nature of GB term (a boundary term) in the holographic renormalization leads to the standard thermodynamics for AdS BHs.

Recently, it was argued that the regularization scheme of Glavan and Lin is inconsistent [38,39,40,41,42,43]. In the papers [38,43] the authors note that the GB term in the action leads the contribution to field equations in the form $G_{\mu \nu }=(D-4)A_{\mu \nu }+W_{\mu \nu }$. The first term has a smooth limit for $D\to 4$, and can be renormalised in 4D. But the second term does not have a smooth limit for $D\to 4$ and cannot originate from any action. It was proven in [44] (see also [45]) that the dimensional regularization explored in [6] is justified only for some class of metrics. The authors claim that they constructed the viable theory in 4D.

In this paper we use the naive dimension regularisation proposed in [6] and further investigations are needed to conform the validity of solutions within the well-defined theory of [44,45]. Here, we obtain a BH solution in the framework of EGB action with the action of NED proposed in [46] making use of the regularization scheme of [6]. The model of NED explored is a simple generalisation of linear Maxwell electrodynamics and allows us to get formulas expressed through elementary functions.

The paper is organized as follows: In Section 2, we obtain BH spherically symmetric solutions. It is shown that depending on the model parameters, the metric function can have one (extreme) or two BH horizons or no horizons corresponding to particle-like solution. In Section 3 we calculate the Hawking temperature and the heat capacity. It is demonstrated that the BHs are thermodynamically stable in some range of event horizon radii. In Section 4 we calculated the BH shadow radii within our model. Section 5 is devoted to a conclusion.

2. 4D EGB Model Coupled with NED

The EGB gravity action in D-dimensions coupled to NED is given by [6]

$$I=\int d^{D}x\sqrt{-g}\left[\frac{1}{16\pi G}\left(R+\frac{\alpha }{D-4}{\mathcal{L}}_{GB}\right)+{\mathcal{L}}_{NED}\right],$$

(1)

where $\alpha$ possesses the dimension of (length)${}^2$ and the particular NED Lagrangian, proposed in [46] (For a convenience we substituted $\beta$ in [46] by $2\beta$.), is given by

$${\mathcal{L}}_{NED}=-\frac{\mathcal{F}}{1+\sqrt[4]{2\beta \mathcal{F}}},$$

(2)

where the parameter $\beta$ ($\beta \ge 0$) has the dimension of (length)${}^4$, $\mathcal{F}=(1/4)F_{\mu \nu }{F}^{\mu \nu }=(B^2-E^2)/2$, $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$ is the field tensor. The model of NED (2) is of interest because of its simplicity. The GB Lagrangian reads

$${\mathcal{L}}_{GB}=R^{\mu \nu \alpha \beta }{R}_{\mu \nu \alpha \beta }-4R^{\mu \nu }{R}_{\mu \nu }+R^2.$$

(3)

The variation of action (1) with respect to the metric gives the field equations

$$R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R+\frac{\alpha }{D-4}{H}_{\mu \nu }=-8\pi G{T}_{\mu \nu },$$

(4)

where

$$H_{\mu \nu }=2\left(R{R}_{\mu \nu }-2R_{\mu \alpha }{R}_{\nu }^{\alpha }-2R_{\mu \alpha \nu \beta }{R}^{\alpha \beta }-R_{\mu \alpha \beta \gamma }{R}_{\nu }^{\alpha \beta \gamma }\right)-\frac{1}{2}{\mathcal{L}}_{GB}{g}_{\mu \nu }.$$

(5)

The symmetrical stress-energy tensor of the NED (2) [46] is given by

$$T_{\mu \nu }=-\frac{(4+3\sqrt[4]{2\beta \mathcal{F}})F_{\mu }^{\alpha }{F}_{\nu \alpha }}{4{(1+\sqrt[4]{2\beta \mathcal{F}})}^2}-g_{\mu \nu }{\mathcal{L}}_{NED}.$$

(6)

The GR coupled with NED, having the Maxwell limit $\mathcal{F}\to 0$, does not admit a static, spherically symmetric solution with a regular center and a nonzero electric charge [47]. Thus, to have a regular solution as $r\to 0$ we study a magnetic BH. The magnetic energy density, found from Equation (6), is

$${\rho }_M=T_t^t=\frac{B^2}{2({\beta }^{1/4}\sqrt{B}+1)}=\frac{q_m^2}{2r^3(r+\sqrt{q_m}{\beta }^{1/4})},$$

(7)

where $q_m$ is a magnetic charge, $\mathcal{F}=q_m^2/\left(2r^4\right)$. The $tt$ component of the field Equation (4), at the limit $D\to 4$, gives

$$r(2\alpha f\left(r\right)-r^2-2\alpha )f^{\prime }\left(r\right)-(r^2+\alpha f\left(r\right)-2\alpha )f\left(r\right)+r^2-\alpha =\frac{q_m^{2}rG}{r+\sqrt{q_m}{\beta }^{1/4}},$$

(8)

where we used the regularization scheme of [6]. The static and spherically symmetric line element squared is given by

$$d{s}^2=-f\left(r\right)d{t}^2+\frac{1}{f\left(r\right)}d{r}^2+r^2(d{\vartheta }^2+{sin}^2\vartheta d{\varphi }^2).$$

(9)

The solution to Equation (8) gives the metric function $f\left(r\right)$,

$$f\left(r\right)=1+\frac{r^2}{2\alpha }\left(1-\sqrt{1+\frac{8M\alpha G}{r^3}+\frac{4\alpha q_m^{3/2}G}{{\beta }^{1/4}{r}^3}ln\left(\frac{r}{r+\sqrt[4]{\beta q_m^2}}\right)}\right).$$

(10)

Introducing the dimensionless variable $x=r/\sqrt[4]{\beta q_m^2}$, Equation (10) becomes

$$f\left(x\right)=1+c{x}^2-c\sqrt{x^4+x\left(a+bln\left(\frac{x}{x+1}\right)\right)},$$

(11)

where the dimensionless parameters are

$$a=\frac{8M\alpha G}{{\beta }^{3/4}{q}_m^{3/2}},b=\frac{4\alpha G}{\beta },c=\frac{\sqrt{\beta }{q}_m}{2\alpha },$$

(12)

where $8M\alpha G$ is the constant of integration and M is the BH mass. We have chosen the sign minus in the front of the square root in Equations (10) and (11) to have the stable BH (see [7,8,9]). The solution to Equation (8) at $\beta =0$, making use of the limit $\beta \to 0$ in Equation (8) before the integration, becomes [11] (see also [12])

$$f\left(r\right)=1+\frac{r^2}{2\alpha }\left(1-\sqrt{1+\frac{8M\alpha G}{r^3}-\frac{4\alpha q_m^{2}G}{r^4}}\right).$$

(13)

Note that solution (13) [11,12] is also the exact solution of the well defined theory of [44,45]. It should be stressed that the limit $r\to 0$ in Equation (13) leads to the non-physical complex value of the metric function $f\left(r\right)$. At the same time, the limit $r\to 0$ in Equations (10) and (11) gives the necessary value $f\left(0\right)=1$. The plot of the function (11) is depicted in Figure 1.

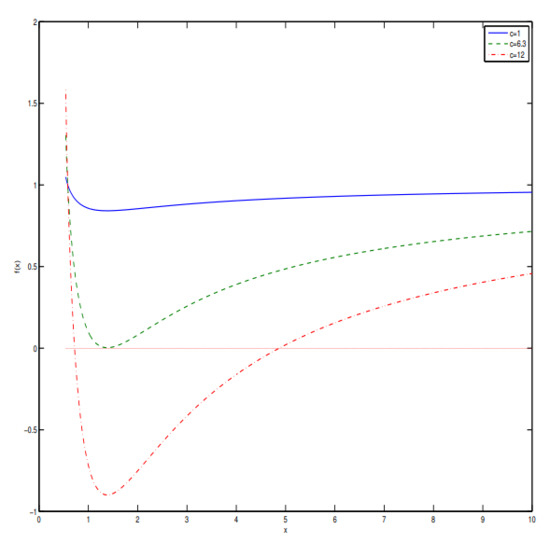
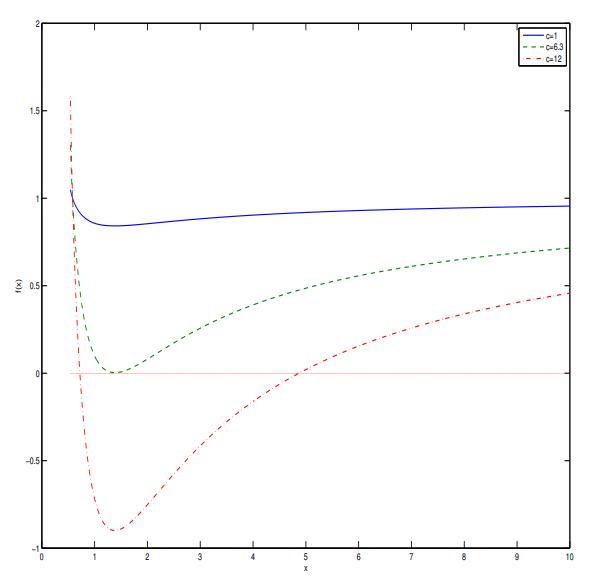
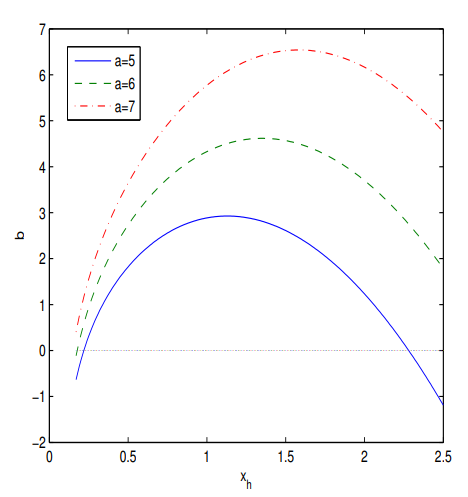
Figure 1. The plot of the function $f\left(x\right)$ for $c=1,6.3,12$ at $a=b=1$.

Figure 1 shows that there can be one extreme horizon or two horizons, or not horizons with the particle-like solution.

3. The BH Thermodynamics

The Hawking temperature is given by

$$T_H\left(r_{+}\right)=\frac{f^{\prime }\left(r_{+}\right)}{4\pi },$$

(14)

where $r_{+}$ is the event horizon radius ($f\left(r_{+}\right)=0$). With the help of Equation (11) ($x_{+}=r_{+}/\sqrt[4]{\beta q_m^2}$) and (14) we find the Hawking temperature

$$T_H\left(x_{+}\right)=\frac{c}{4\pi \sqrt[4]{\beta q_m^2}}\left(2x_{+}-\frac{(4x_{+}^4{c}^2+2c{x}_{+}^2+1)(1+x_{+})+b{c}^2{x}_{+}}{2c{x}_{+}(1+x_{+})(1+c{x}_{+}^2)}\right).$$

(15)

It worth noting that three parameters a, b and c are connected by the equation $f\left(r_{+}\right)=0$. We replaced the parameter a, as a function of b, c and $x_{+}$, into Equation (14). The plot of the dimensionless function $T_H\left(x_{+}\right)\sqrt[4]{\beta q_m^2}$ is given in Figure 2.

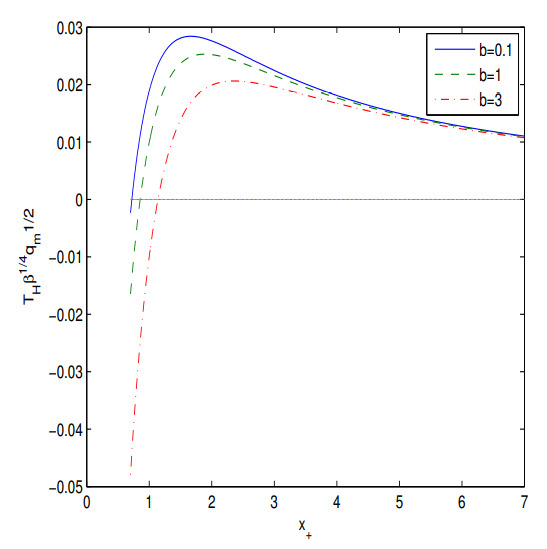
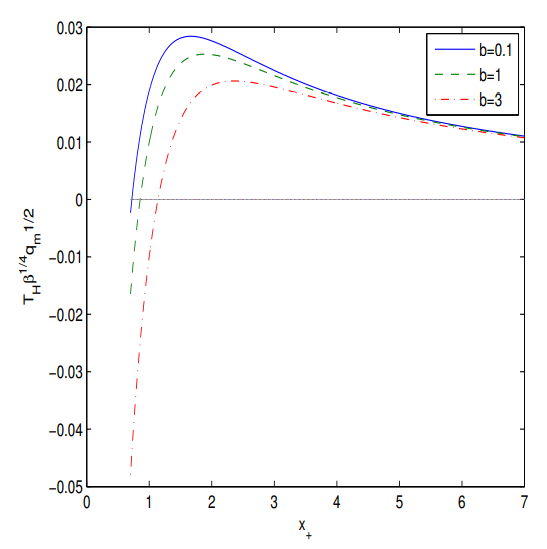
Figure 2. The plot of the function $T_H\left(x_{+}\right)\sqrt[4]{\beta q_m^2}$ for $c=1$ at $b=0.1,1,3$.

According to Figure 2 the Hawking temperature is positive in some range of the event horizon radii $x_{+}$. When the Hawking temperature is negative the BH does not exist. Making use of equation $f\left(x_{+}\right)=0$ we obtain the BH gravitational mass

$$M\left(x_{+}\right)=\frac{{\beta }^{3/4}{q}_m^{3/2}}{8\alpha G}\left(\frac{1+2c{x}_{+}^2}{c^2{x}_{+}}-bln\left(\frac{x_{+}}{x_{+}+1}\right)\right).$$

(16)

The first law of BH thermodynamics is

$$dM\left(x_{+}\right)=T_H\left(x_{+}\right)dS+\varphi dq.$$

(17)

Making use of Equation (17) we find the entropy at the constant charge

$$S=\int \frac{dM\left(x_{+}\right)}{T_H\left(x_{+}\right)}=\int \frac{1}{T_H\left(x_{+}\right)}\frac{\partial M\left(x_{+}\right)}{\partial x_{+}}d{x}_{+}.$$

(18)

With the help of Equation (18) one obtains the heat capacity

$$C_q\left(x_{+}\right)=T_H{\left(\frac{\partial S}{\partial T_H}\right)}_q=\frac{\partial M\left(x_{+}\right)}{\partial T_H\left(x_{+}\right)}=\frac{\partial M\left(x_{+}\right)/\partial x_{+}}{\partial T_H\left(x_{+}\right)/\partial x_{+}}.$$

(19)

From Equations (15) and (16) we find

$$\frac{\partial M\left(x_{+}\right)}{\partial x_{+}}=\frac{{\beta }^{3/4}{q}_m^{3/2}}{8\alpha G}\left(\frac{2c{x}_{+}^2-1}{c^2{x}_{+}^2}-\frac{b}{x_{+}(1+x_{+})}\right),$$

(20)

$$\frac{\partial T_H\left(x_{+}\right)}{\partial x_{+}}=\frac{c}{4\pi \sqrt[4]{\beta q_m^2}}(2-\frac{2c{x}_{+}^2(3+c{x}_{+}^2)}{{(1+c{x}_{+}^2)}^2}$$

$$+\frac{2c{x}_{+}^4+c{x}_{+}^2+1}{2c{x}_{+}^2{(1+c{x}_{+}^2)}^2}+\frac{bc(c{x}_{+}(2+3x_{+})+1)}{2{(1+x_{+})}^2{(1+c{x}_{+}^2)}^2}).$$

(21)

In accordance with Equation (19) the heat capacity has a singularity if the Hawking temperature possesses an extremum, $\partial T_H\left(x_{+}\right)/\partial x_{+}=0$. Taking into account Equations (19)–(21) we plotted the heat capacity (at $b=0.1,1,3$, $c=1$) as a function of the variable $x_{+}$ in Figure 3.

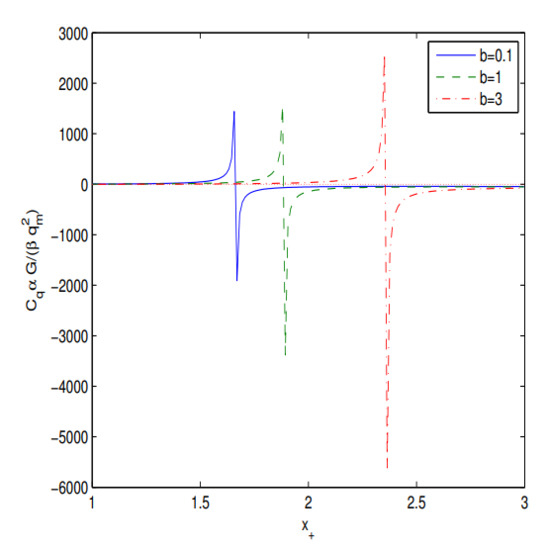
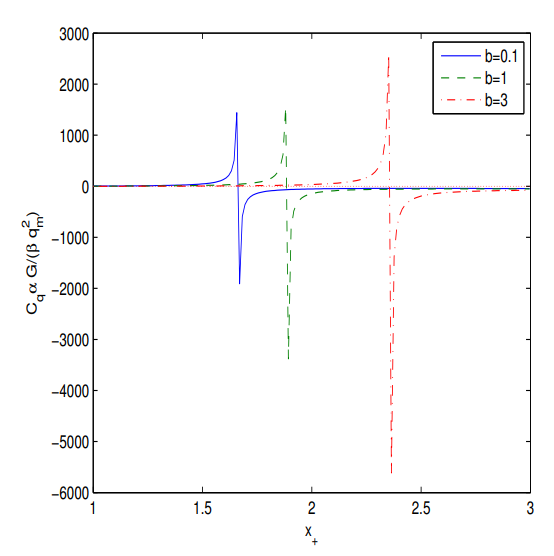
Figure 3. The plot of the function $C_q\left(x_{+}\right)\alpha G/\left(\beta q_m^2\right)$ for $b=0.1,1,3$ at $c=1$.

According to Figure 3 the BH is locally stable in some interval of the horizon radii where the heat capacity is positive. The singularity in the heat capacity occurs in the radii where the Hawking temperature possesses the maximum. In these points the second-order phase transition takes place. We note that the thermodynamic properties of BH in 4D EGB theory were studied in [13,20]. It should be noted that our metric reduces to the metric of [20] in the limit of zero charge and vanishing the cosmological constant (see Equation (13)) and to the metric of [13] at zero charge. It is worth noting that the metric (13) is also exact solution of the well defined theory proposed in [44,45].

4. The Black Hole Shadow

The spherically symmetric BH shadow represents a black circular disk which is due to the gravitational lensing of light. The Event Horizon Telescope collaboration received the first image of the super-massive M87* BH located in the center of the elliptical galaxy Messier 87 [48]. Firstly, the shadow of a neutral Schwarzschild BH, described by the mass and the position of the observer, was studied in [49]. Here, we investigate the BH shadow within action (1) with the regularization scheme of [6]. The Hamiltonian approach for the description of the photon motion in the static spherically symmetric space-time will be employed. We consider the photons moving in the equatorial plane with $\vartheta =\pi /2$. Making use of the Hamilton−Jacobi method for null curves, the photon motion is governed by the equation [50]

$$H=\frac{1}{2}{g}^{\mu \nu }{p}_{\mu }{p}_{\nu }=\frac{1}{2}\left(\frac{L^2}{r^2}-\frac{E^2}{f\left(r\right)}+\frac{{\dot{r}}^2}{f\left(r\right)}\right)=0,$$

(22)

where $p_{\mu }$ is the photon momentum, $\dot{r}=\partial H/\partial p_r$, $E=-p_t$ and $L=p_{\varphi }$ are the energy and angular momentum of the photon (constants of motion). Equation (22) can be written as

$$V+{\dot{r}}^2=0,V=f\left(r\right)\left(\frac{L^2}{r^2}-\frac{E^2}{f\left(r\right)}\right).$$

(23)

The circular orbit radius $r_p$ of the photon can be obtained by solving the equation $V\left(r_p\right)=V^{\prime }{\left(r\right)}_{|r=r_p}=0$, where the prime denotes the derivative with respect to the argument. Thus, we find

$$\xi \equiv \frac{L}{E}=\frac{r_p}{\sqrt{f\left(r_p\right)}},f^{\prime }\left(r_p\right)r_p-2f\left(r_p\right)=0,$$

(24)

where $\xi$ is the impact parameter. We use the numerical method to solve Equation (24) for obtaining the radius of the photon sphere. The shadow radius $r_s$ of the BH observed by a static observer in the position $r_0$ is given by [50]

$$r_s=r_p\sqrt{\frac{f\left(r_0\right)}{f\left(r_p\right)}}.$$

(25)

For a distant observer, $r_0\to \infty$, and we can put $f\left(r_0\right)=1$ in Equation (25) and the impact parameter becomes $\xi =r_s$. The event horizon radius $r_{+}$ is defined by the biggest root of the equation $f\left(r_h\right)=0$. From Equation (11) and $f\left(r_h\right)=0$ we obtain the dependence of the parameters a and b on the horizon radii at $c=1$

$$a=\frac{1+2x_h^2-x_{h}bln(x_h/(x_h+1))}{x_h}c=1,$$

(26)

$$b=\frac{1+2x_h^2-x_{h}a}{x_{h}ln(x_h/(x_h+1))}c=1,$$

(27)

where $x_h=r_h/\sqrt[4]{\beta q_m^2}$. The plots of the functions (26) at $b=1,5,10$ and (27) at $a=5,6,7$ are depicted in Figure 4 and Figure 5, respectively.

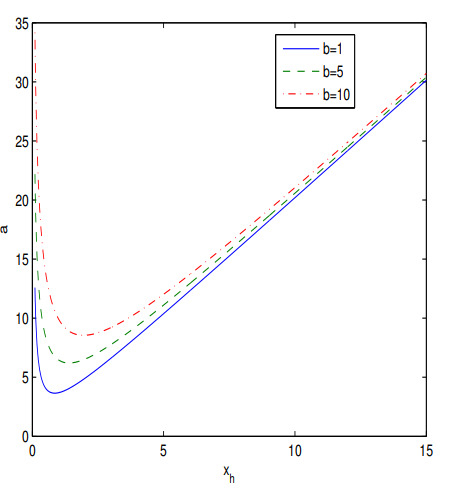
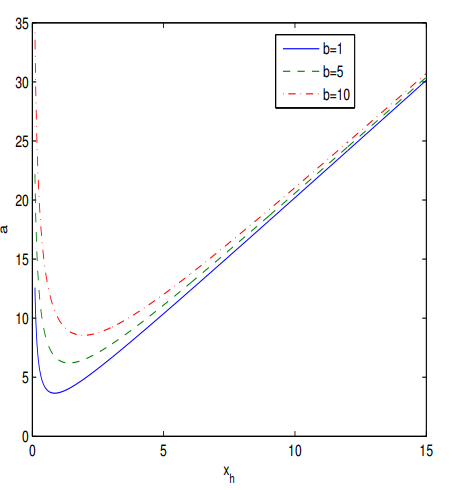
Figure 4. The plot of the function $a\left(x_h\right)$ for $b=1,5,10$ at $c=1$.

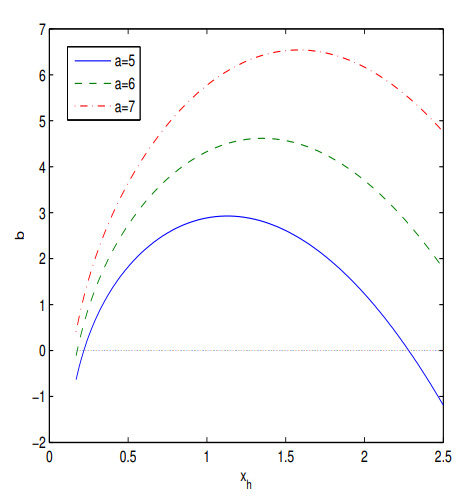
Figure 5. The plot of the function $b\left(x_h\right)$ for $a=5,6,7$ at $c=1$.

Figure 4 shows that when the parameter a increases (at fixed b), the event horizon radius $x_{+}$ (the biggest root of equation $f\left(x_h\right)=0$) increases. According to Figure 5 if the parameter b increases (at fixed a), the event horizon radius decreases.

The shadow radius is formed by the null geodesics around the unstable circular photon orbit. The inner region of shadow is formed by the null geodesics that are captured by BH and they are located inside the event horizon. The photon sphere radii ($x_p$), the event horizon radii ($x_{+}$), and the shadow radii ($x_s$) for some parameters a, b, and c, found from Equations (24) and (25), are presented in Table 1 (in terms of dimensionless variables). The null geodesics radii $x_p$ in Table 1 correspond to the maximum of the potential $V\left(r\right)$ ($V^{″}\le 0$) and they belong to unstable orbits. There are also solutions of Equation (24) with $V^{″}\ge 0$ and the corresponding radii are less than event horizon radii and such geodesics are inside the event horizon.

Table 1. The event horizon, photon sphere and shadow dimensionless radii for $a=5$, $c=1$.

b	1.5	1.7	1.8	2	2.2	2.3	2.4	2.5	2.6
$x_{+}$	1.93	1.87	1.84	1.77	1.69	1.65	1.61	1.56	1.51
$x_p$	3.12	3.05	3.01	2.94	2.86	2.82	2.77	2.73	2.68
$x_s$	5.78	5.70	5.65	5.56	5.47	5.42	5.37	5.32	5.26

In according with Table 1, when increasing the parameter b at fixed a and c, the shadow dimensionless radius $x_s$ decreases. According to Table 1 $x_s>x_{+}$ and, therefore, the BH shadow radius is defined by the radius $r_s=x_s\sqrt[4]{\beta q_m^2}$.

It should be noted that nonlinear interaction of fields within NED results in the self-interaction, and photons propagate along null geodesics of the effective metric [51,52]. But the event horizon radii are still determined by the zeroes of the metric function of (10), $f\left(r_h\right)=0$. As stated in [53], within the current approach the accuracy in the photon sphere radius and impact parameter is not clear.

5. Conclusions

The exact spherically symmetric and magnetically charged BH solution in EGB gravity (with the regularization scheme of [6]) coupled with NED, proposed in [46], was obtained. It was shown that the BH can have two horizons or one extreme horizon, or not horizons corresponding to particle-like solution, depending on the model parameters ($\alpha$, $\beta$, $q_m$ and M). At the limit $r\to 0$, the metric function has the reasonable value $f\left(0\right)=1$ while in the EGB gravity coupled to linear electrodynamics this limit gives the non-physical value of $f\left(0\right)$. The BH Hawking temperature and the heat capacity were calculated. We demonstrated that the phase transitions occur when the heat capacity has the singularity and the Hawking temperature possesses an extremum. The BHs are thermodynamically stable in some range of event horizon radii where the heat capacity is positive. We calculated the BH shadow radii within our model for some model parameters. It is shown that when increasing the parameter b (if a and c are constants) the BH shadow dimensionless radius $x_s$ is decreased.