Abstract
Data imbalance is a thorny issue in machine learning. SMOTE is a famous oversampling method of imbalanced learning. However, it has some disadvantages such as sample overlapping, noise interference, and blindness of neighbor selection. In order to address these problems, we present a new oversampling method, OS-CCD, based on a new concept, the classification contribution degree. The classification contribution degree determines the number of synthetic samples generated by SMOTE for each positive sample. OS-CCD follows the spatial distribution characteristics of original samples on the class boundary, as well as avoids oversampling from noisy points. Experiments on twelve benchmark datasets demonstrate that OS-CCD outperforms six classical oversampling methods in terms of accuracy, F1-score, AUC, and ROC.
1. Introduction
Currently, imbalanced learning for classification problems has attracted more and more attention in machine learning research [1,2]. In the imbalanced datasets, the positive (minority) samples, such as the credit score in the financial sector [3], fault detection in mechanical maintenance [4], abnormal behavior detection in a crowd [5], cancer detection [6], other medical fields [7], etc., play a great role. However, traditional classifiers or learning algorithms attach too much importance to negative (majority) samples [8]. In order to address this problem, many research works have put forward some approaches from two levels, the data level and the algorithm level.
At the algorithm level, ensemble learning has been a hot topic recently. Ensemble learning approaches such as random forest [9], XGboost [10], and AdaBoost [11] build several weak classifiers and then integrate them into a strong classifier based on a voting or averaging operation. This can effectively compensate the drawback of a single classifier on imbalanced datasets to improve the classification precision. At present, there are also many literature works that use deep learning models or algorithms to process the imbalanced datasets, such as CNN [12] and DBN [13]. However, training deep networks generally requires much time consumption.
The data level mainly includes oversampling, undersampling, and hybrid sampling methods. The core idea is to strengthen the importance of the positive samples or reduce the impact of negative samples, so that the positive class has the same importance as the negative class in the classifier training.
Oversampling has been widely used because it retains the original information of the dataset and is easy to operate [14]. For example, CIR [15] synthesizes new positive samples based on calculating the centroid of all attributes of positive samples to create a symmetry between the defect and non-defect records in the imbalanced datasets. FL-NIDS [16] overcomes the imbalanced data problem and is applied to evaluate three benchmark intrusion detection datasets that suffer from imbalanced distributions. OS-ELM [17] uses the oversampling technique when identifying an axle box bearing fault of multiple high-speed electric units.
The synthetic minority over-sampling technique (SMOTE) [18] is a well-known oversampling method. However, SMOTE has three disadvantages: (1) it oversamples uninformative samples [19]; (2) it oversamples noisy samples; and (3) it is difficult to determine the number of nearest neighbors, and there is strong blindness in the selection of nearest neighbors for the synthetic samples.
To address these three problems, many strategies have been presented in literature. Borderline-SMOTE [20] focuses on samples within the selected area to strengthen the class boundary information. RCSMOTE [19] controls the range of synthetic instances. K-means SMOTE [21] combines a clustering algorithm and SMOTE to deal with the overlapped samples of different classes. G-SMOTE [22] generates synthetic samples in a given geometric region. LNSMOTE [23] considers the local neighborhood information of samples. DBSMOTE [24] uses the DBSCAN algorithm, which is based on the density before sampling. Carla Vairetti proposed a method for a high-dimensional dataset [25]. Gaussian-SMOTE [26] is a combination of a Gaussian distribution and SMOTE, based on the probability density of datasets. The above algorithms improve SMOTE to different extents, but they do not extract or make full use of the distribution information of samples, nor do they modify the random choice of the nearest neighbors.
In a binary classification problem, samples that are far away from the class boundary are easily classified. They, especially the noisy samples, generally contribute little to the sampling. Noisy samples produced by statistical errors or other causes often occur in datasets, which may send error messages. Therefore, noisy samples can be regarded as useless information and should be ignored. From this point, we would like to focus on strengthening the information of positive samples near the decision boundary.
In addition, samples often appear in clusters, and the distance between two clusters is much larger than the distance between two samples within one cluster. From this point, we can use cluster methods to extract the density characteristics of the distribution for positive samples as the macro information.
Overall, the boundary information can be regarded as intra-class information, and the distribution features of clusters within one class can be regarded as inter-class information. Motivated by the above discussion, we present a new oversampling method, OS-CCD, based on the concept of the classification contribution degree. The classification contribution degree can not only combine the inter-class information in the dataset with the intra-class information, but also can ignore the useless information.
When using SMOTE, a big problem is determining how many times SMOTE oversamples. There is a much research on this. ADASYN [27] obtains the times of sampling for positive samples with the ratio of negative samples among the K nearest neighbors of positive samples. As a new technique, the classification contribution degree can determine the exact number of the synthetic samples for every positive sample.
In other methods, SMOTE randomly selects one of the nearest neighbors of a positive sample for synthesizing a new sample [28]. With the guidance of the classification contribution degree, we can only select one nearest neighbor, but not a random one. This can highlight the spatial distribution characteristics of the positive class.
The remainder of this paper is organized as follows. Section 2 presents the details of OS-CCD including the definition of the cluster ratio, safe neighborhood, safety degree, and the classification contribution degree. Section 3 demonstrates the experimental process and results. Section 4 concludes the work of this paper.
2. Methodology
2.1. Safe Neighborhood and Classification Contribution Degree
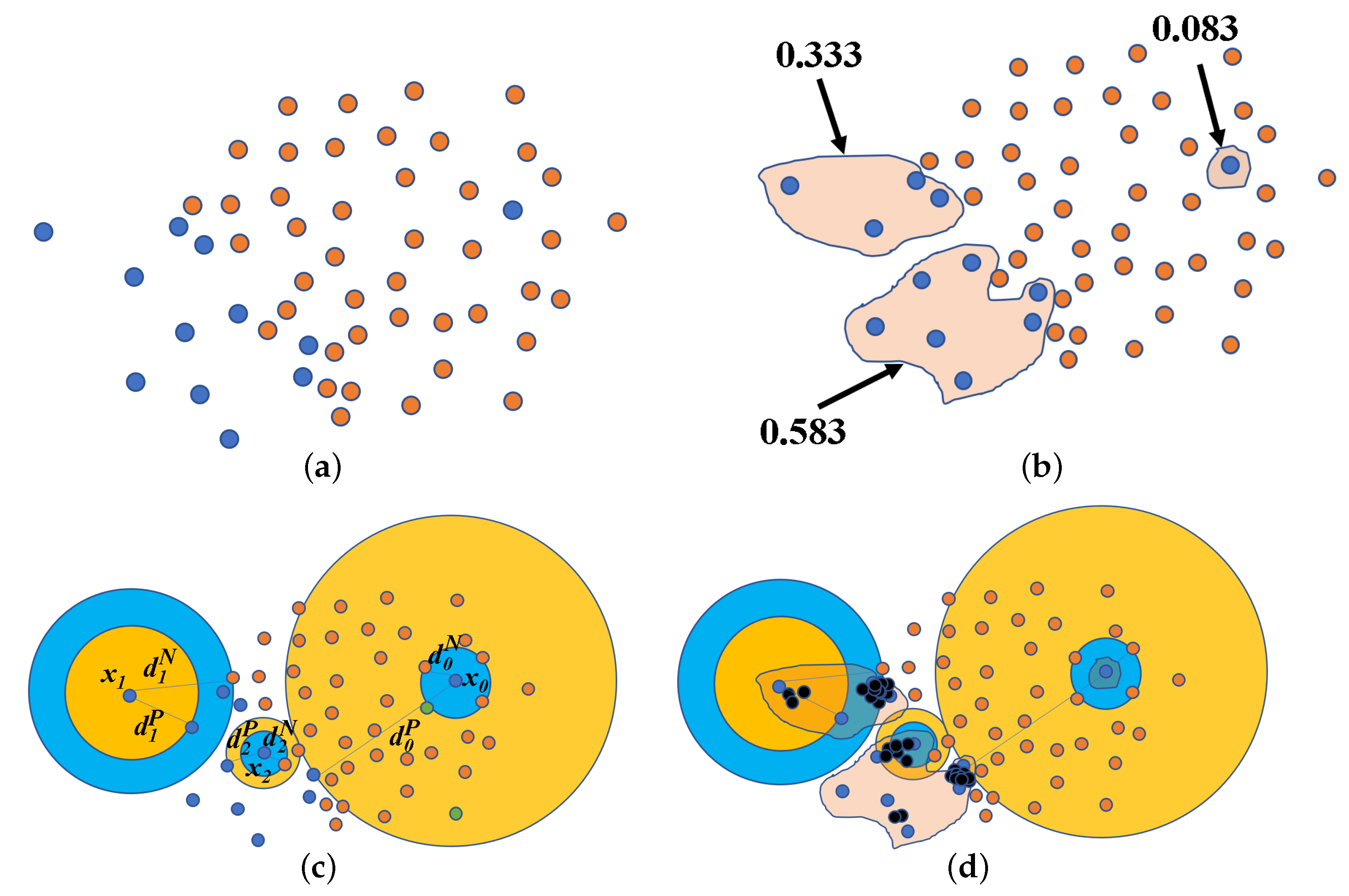
Given an imbalanced dataset, which contains two classes, the positive class P and the negative class N are shown in Figure 1a. To generate new positive samples, we try to extract the category and distribution information contained in P from two directions, the macro distribution characteristics of P and the micro location of each positive sample in the feature space.
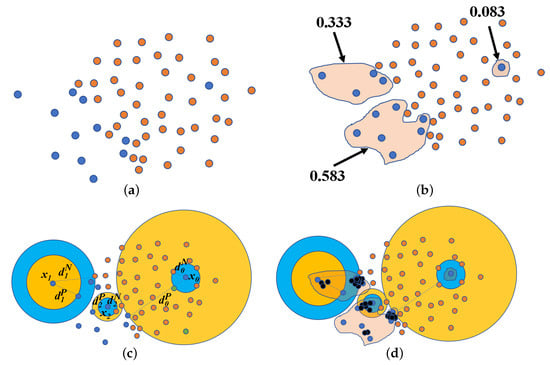
Figure 1.
Diagram of oversampling with OS-classification contribution degree (CCD). (a) The original dataset in the first panel. (b) Positive samples are clustered in the second panel. (c) Type-N and Type-P safe neighborhoods in the third panel. (d) Synthesized samples by OS-CCD in the fourth panel.
The positive samples are scattered in space, and the distance between any two positive samples varies in a large range. Therefore, we first cluster P into K clusters with the k-means algorithm as shown in Figure 1b where . Denote the number of samples in every cluster k as . Generally, different clusters contain different number of samples, which indicates that the distribution of samples in space has density characteristics.
For every cluster, we define a new concept, the cluster ratio , i.e.,
where is the number of samples in P. For example, the cluster ratios of the three clusters shown in Figure 1b are , , and , respectively. can quantitatively reflect the macro distribution characteristics of P.
For each positive sample, its location information generally should be considered relative to other samples including both positive and negative ones. Therefore, nearest neighbors are naturally involved. For every sample of P, we calculate the distance between and its nearest negative sample neighbor. The hypersphere with and being the center and radius, respectively, is called the Type-N safe neighborhood of , and it is shown by the blue disk in Figure 1c. Similarly, we calculate the distance between and its nearest positive sample neighbor. The hypersphere with and being the center and radius, respectively, is called the Type-P safe neighborhood of , and it is shown by the yellow disk in Figure 1c.
If is easily classified correctly, such as in Figure 1c, the union of its Type-N and Type-P safe neighborhoods contains some positive samples, but only one negative sample; if is a noisy point, i.e., it is located in the interior of N, such as in Figure 1c, the union of its two types of safe neighborhoods contains many negative samples, but only one positive sample; If is located near the class boundary, such as in Figure 1c, the union of its two types of safe neighborhoods contains similar numbers of positive and negative samples. Based on this characteristic, we present another definition for every , named the safety degree,
where and are the numbers of positive and negative samples, respectively, contained in the union of the two types of safe neighborhoods of . According to the above analysis, is great if is far away from the class boundary; otherwise, it is close to zero.
Now, we define the classification contribution degree with the cluster ratio and the safety degree for every as follows:
where A is a correction coefficient, which is used to prevent the denominator from being 0. equals the cluster ratio of the cluster k to which belongs.
The classification contribution degree is directly proportional to the cluster ratio and inversely proportional to the degree of safety . It is based on the point that not only easily misclassified samples, but also samples belonging to a cluster containing a large number of elements should play a major role in determining the class boundary. Therefore, the classification contribution degree is a quantitative measurement of the degree to which a sample is the boundary sample. At the same time, it can also identify the noisy point, such as shown in Figure 1c. Its is close to zero from (1) and is large from (2). Therefore, its classification contribution degree is almost zero.
2.2. Oversampling Based on the Classification Contribution Degree
By normalizing the classification contribution degrees as follows:
we can compress the classification contribution degrees within 0–1. With , we can determine a suitable number of synthetic samples for each positive sample as follows:
The sign means the operation of rounding down. If is too small, there are no new samples generated from , such as the noisy point shown in Figure 1c.
The nearest neighbor SMOTE is repeated times to oversample new positive samples as follows:
where is the new synthesized sample, is the nearest positive sample to , and is a random number between .
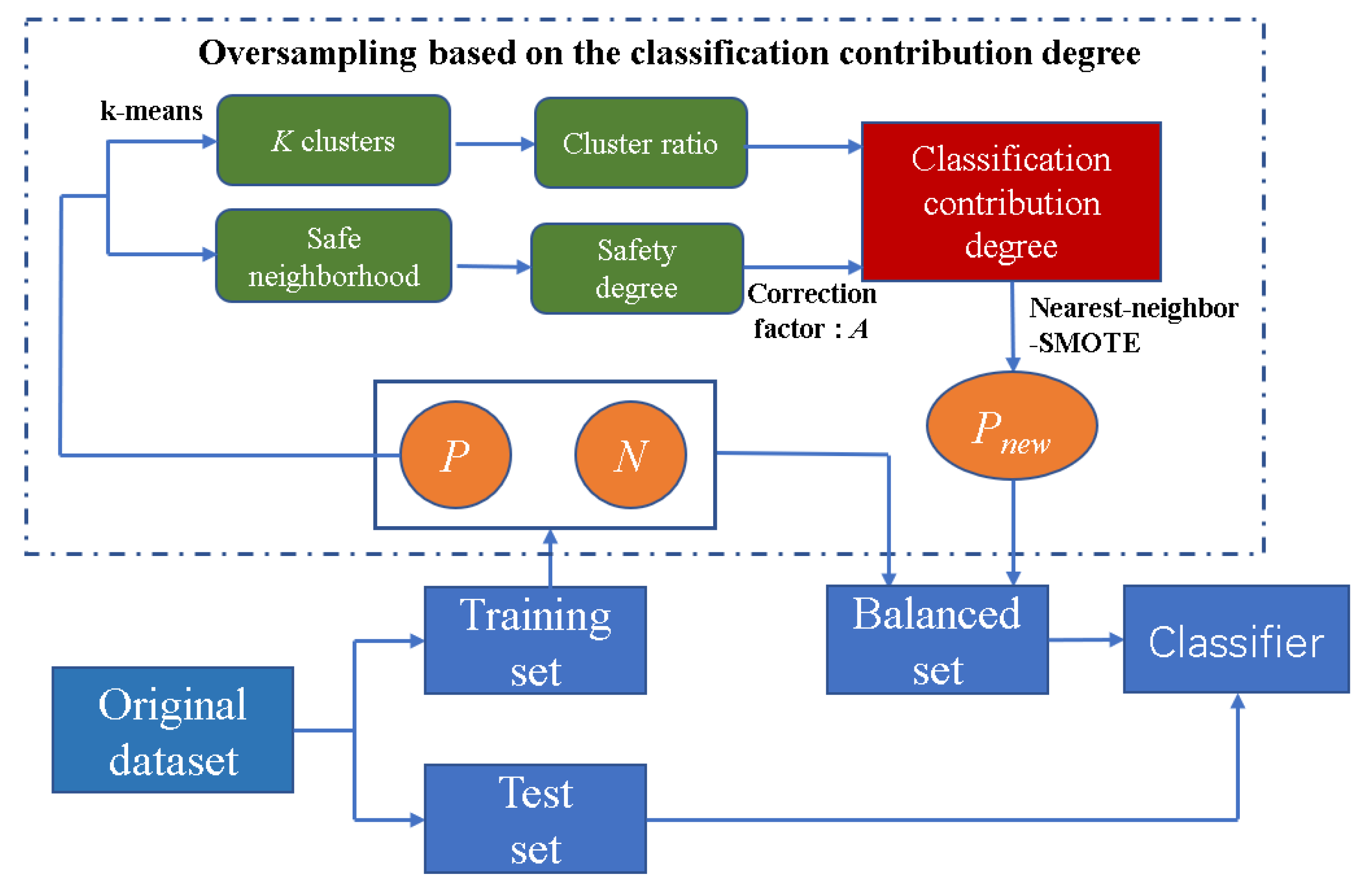
The newly generated samples are shown as the black points in Figure 1d. In particular, for the noisy point as shown in Figure 1c, because the negative samples are farther than the positive samples in the Type-P safe neighborhood, its safety degree is large, leading to a small classification contribution degree. The sampling times are 0 after rounding down in (5), so no samples are generated to avoid noise interference. However, for the easily misclassified positive samples, there are many new samples generated to balance the whole dataset. The flowchart of imbalanced learning with OS-CCD is shown in Figure 2.
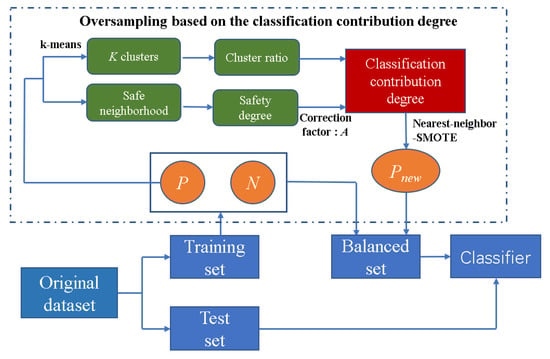
Figure 2.
Flowchart of imbalanced learning with OS-CCD.
3. Results and Discussion
In this section, OS-CCD is compared with six commonly used oversampling methods on twelve benchmark datasets in terms of the accuracy, F1-score, AUC, and ROC. We used the average values of ten independent runs of the fivefold cross-validation performed on 12 datasets to evaluate the oversampling methods.
3.1. Datasets Description and Experimental Evaluation
In this paper, twelve benchmark datasets were collected from the KEEL Tool [29] to verify the effectiveness of our proposed oversampling method. The detailed description of these datasets is shown in Table 1. The imbalance ratio (IR) varies between and . Their sizes vary from 197 to 1484.

Table 1.
Details of the twelve datasets for comparison. IR, imbalance ratio.
To evaluate our method, several evaluation metrics are employed. Accuracy (Acc) [30] is the proportion of correctly classified samples in the whole dataset:
where TP is the number of actual positive samples identified correctly as the positive class, and FN, FP, and TN can be understood similarly. Accuracy has low credibility when dealing with imbalanced data. Therefore, other metrics are also employed. The F1-score [31] is the harmonic average of the precision and recall rate to evaluate the machine learning model in rebalanced data task:
The ROC curve reflects the relationship between the true and false positive rates. AUC [30] is the area under the ROC curve to evaluate the model performance.
3.2. Experimental Method
To test the effectiveness and robustness of OS-CCD, six commonly used classical oversampling methods, random oversampling (RO) [32], SMOTE [18], borderline-SMOTE (BS) [20], k-means SMOTE (KS) [21], NRAS [33], and Gaussian-SMOTE (GS) [34] are used. Including OS-CCD, and the seven oversampling methods are combined with four classifiers, support vector machine (SVM) [35], logistic regression (LR) [36], decision tree (DT) [36], and multi-layer perceptron (MLP) neural network [37]). The 28 approaches are shown in Table 2.

Table 2.
The combination of the 28 approaches of four classifiers and seven oversampling methods.
3.3. Experimental Results
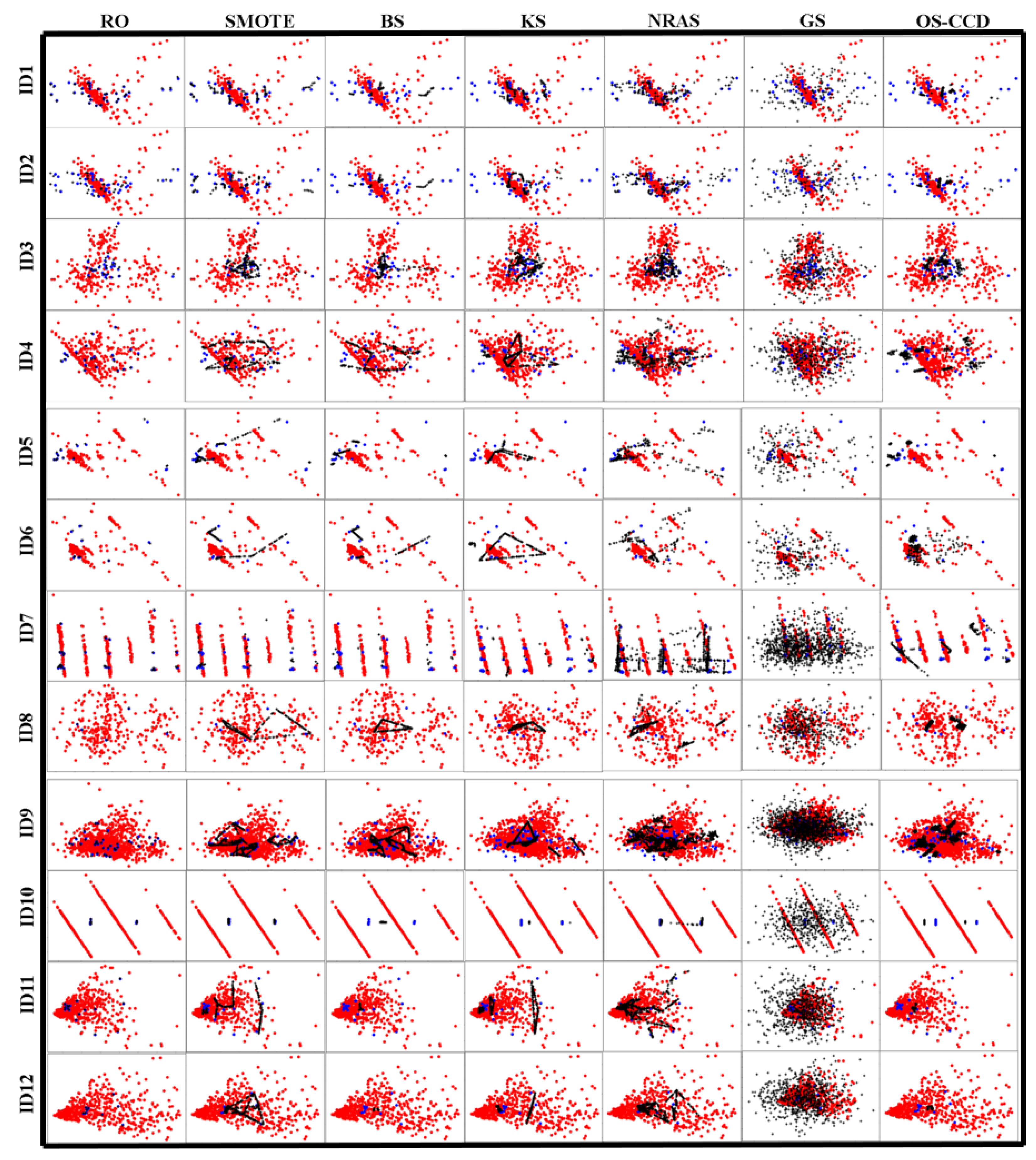
To visualize the sampling results of OS-CCD, we use principal component analysis (PCA) [38] to reduce the dimension of the data and then draw 84 scatter plots for the twelve datasets and seven sampling methods, as shown in Figure 3, where red and blue dots represent the original negative and positive samples, respectively, and black dots represent the newly generated samples.
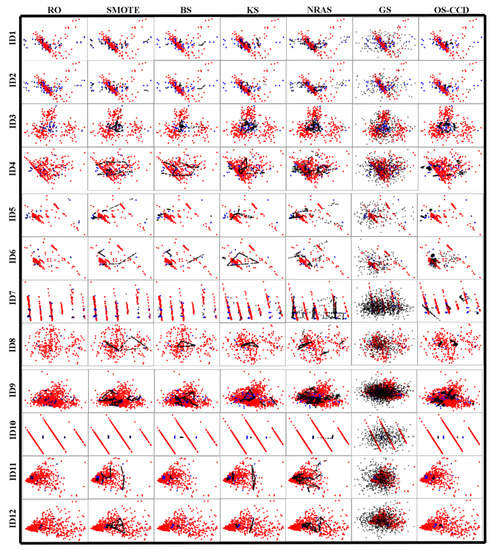
Figure 3.
The oversampling results of the seven methods on the twelve datasets.
As can be seen from Figure 3, the sampling results produced by the seven methods are different on most datasets. On the new-thyroid1 dataset, SMOTE, borderline-SMOTE, NRAS, and Gaussian-SMOTE generate many new positive samples from three loners of the positive class, but OS-CCD only generates a small number of samples from the three. The same thing happens on IDs 2, 4, 5, 7, and 11. This indicates that OS-CCD can oversample a small number of samples in the low-density area of the positive class.
On most datasets, the new samples generated by OS-CCD follow the distribution characteristics of the original positive class. However, borderline-SMOTE, SMOTE and Gaussian-SMOTE generate some samples that overlap with the negative samples, and the random oversampling method only simply replicates every positive sample without regard to other factors.
The remainder of the paper reports the experimental results. The correction coefficient A was one in all experiments, and the cluster number K was set to 3, 4, 4, 4, 3, 4, 12, 3, 4, 2, 6, and 3 for every dataset, respectively, according to the visualization of Figure 3.
Table 3 shows the test classification accuracy comparison of OS-CCD with the other methods. The best values are in bold. It can be seen that the classification performance of OS-CCD outperformed almost all the other oversampling methods on the twelve datasets if the combined classifiers were SVM and MLP. There were only three cases where the values of accuracy produced by OS-CCD were not the highest if the combined classifier was LR, but the accuracies on the three datasets were close to first place. If the combined classifier was DT, there were only three cases where OS-CCD outperformed the other methods. This means that the combination of DT and OS-CCD was not very harmonious.

Table 3.
The classification test Acc (%) of 28 approaches on 12 datasets.
Table 4 shows the test F1-score comparison of OS-CCD with other methods. Similar to the accuracy, SVM and MLP obtained the highest performances on almost all datasets balanced by OS-CCD. Although some values were not number one, they were not far off. The F1-score of LR with OS-CCD on the new-thyroid1 and new-thyroid2 datasets were only less than one percent below the best score. The F1-score of DT with OS-CCD was the highest on only four datasets.

Table 4.
The classification test F1-score (%) of 28 approaches on 12 datasets.
At the same time, the standard deviations of the accuracy and F1-score are also reported in Table 3 and Table 4, respectively. As shown in the tables, the standard deviation of OS-CCD was relatively low, which reflects the stability of our method.
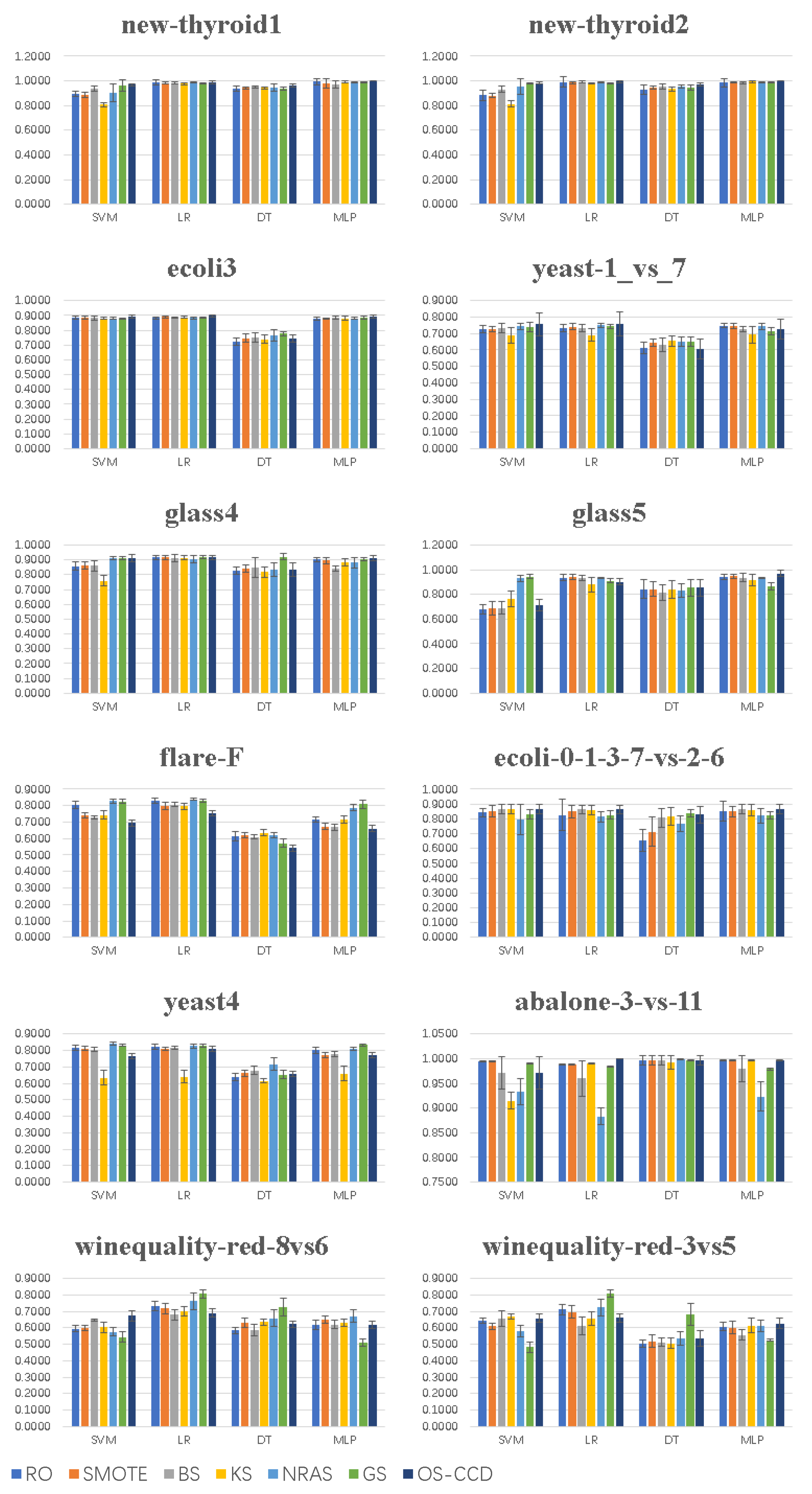
Figure 4 shows the AUC of the 28 approaches on the 12 datasets. It shows that the mean and the standard deviation of the AUC of OS-CCD were better than those of other oversampling methods combined with SVM and MLP on most datasets, except flare-F and yeast4. The reason for this may be that the positive samples of flare-F and yeast4 were so fragmented, as shown in Figure 3, that it was very difficult to determine a suitable number for K in the k-means algorithm. If the combined classifier was DT, OS-CCD could not achieve the best value especially on the last two datasets. The reason for this may be that there were too many isolated noise samples in the two datasets, and OS-CCD could not extract the features of the positive class like GS did.
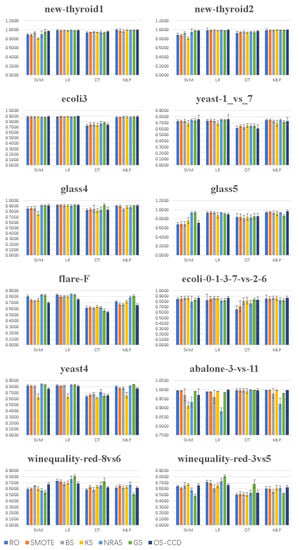
Figure 4.
Histogram of the AUC of the 28 approaches on the 12 datasets.
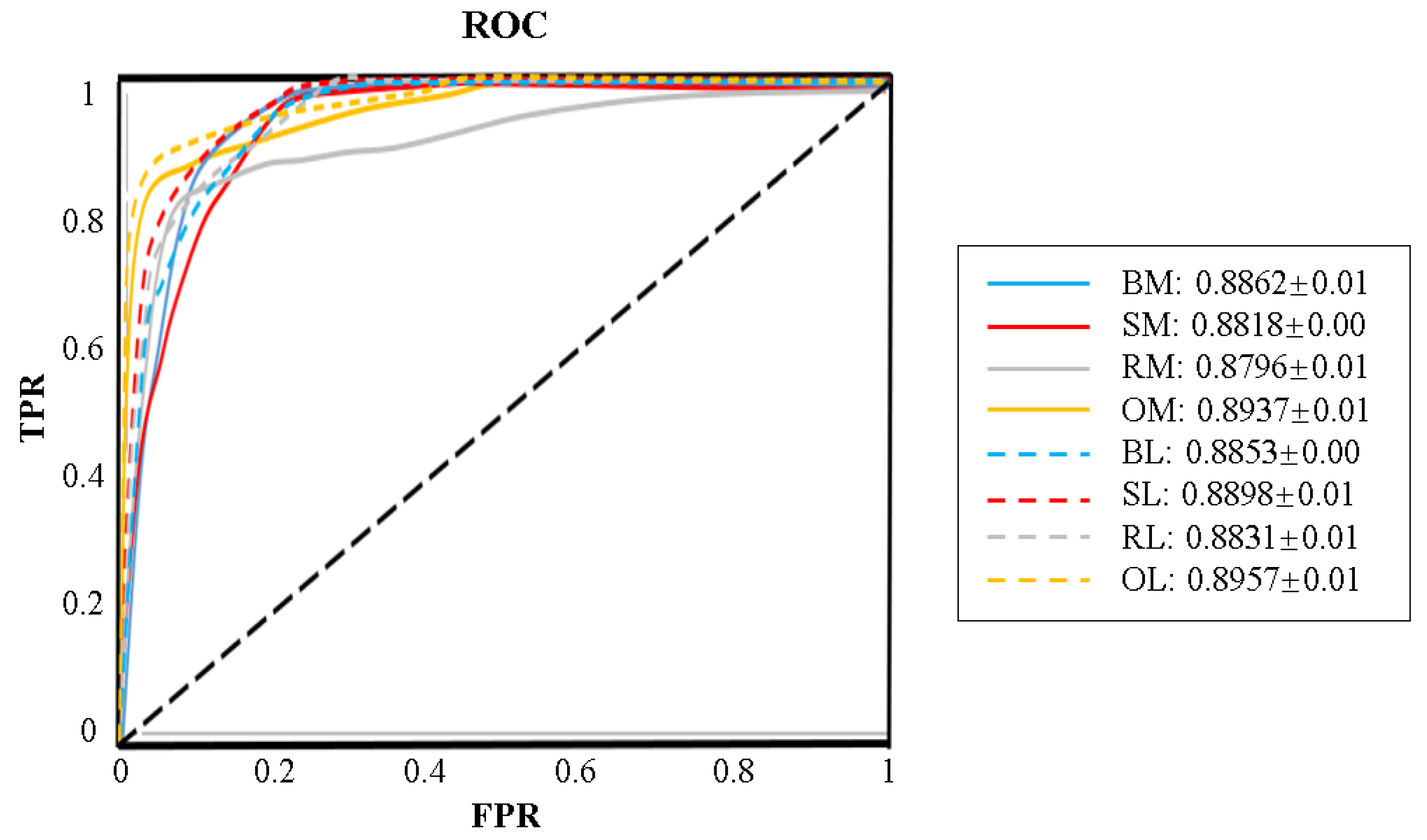
To evaluate the generalization ability of OS-CCD, the ROC curves of MLP and LR with the four oversampling methods are plotted in Figure 5 on the ecoli3 dataset, which contains moderate the data size and imbalance ratio. The black diagonal line represents the random selection. For both MLP and LR, their optimal thresholds combined with OS-CCD are the closest to the upper left corner. This indicates the strong generalization ability of OS-CCD.
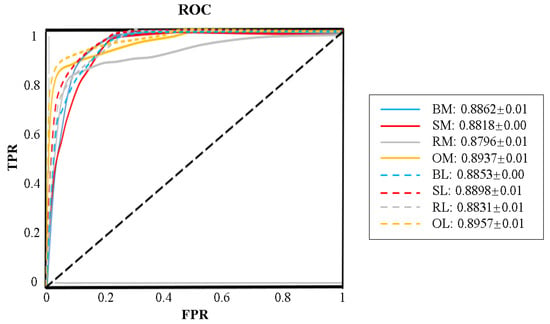
Figure 5.
The ROC on the ecoli3 dataset.
4. Conclusions
In this paper, we present a new oversampling method, OS-CCD, based on a new concept, the classification contribution degree. We first cluster positive samples into K clusters with the k-means algorithm and get the cluster ratio for each positive sample. Secondly, we compute the safety degree based on two types of safe neighborhoods for each possible sample. Then, we present the definition of the classification contribution degree to determine the number of synthetic samples generated by SMOTE from each positive sample. OS-CCD can effectively avoid oversampling from noisy points and can strengthen the boundary information by highlighting the spatial distribution characteristics of the original positive class. High performances of OS-CCD are substantiated in terms of the accuracy, F1-score, AUC, and ROC on twelve commonly used datasets. Further investigations may include the generalization of the classification contribution degree to all samples and the extension of the results to ensemble classifiers.
Author Contributions
Code, writing, original draft, translation, visualization, and formal analysis, Z.J.; discussion of the results, T.P.; supervision and resources, J.Y.; checking the code of this paper, C.Z. All authors read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Key R&D Program of China under Grant 2018AAA0100300 and in part by the National Natural Science Foundation of China under Grant 11201051.
Data Availability Statement
Data available in a publicly accessible repository that does not issue DOIs Publicly available datasets were analyzed in this study. This data can be found here: [http://keel.es].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kovács, G. Smote-variants: A python implementation of 85 minority oversampling techniques. Neurocomputing 2019, 366, 352–354. [Google Scholar] [CrossRef]
- Kovács, G. An empirical comparison and evaluation of minority oversampling techniques on a large number of imbalanced datasets. Appl. Soft Comput. 2019, 83, 105662. [Google Scholar] [CrossRef]
- Brown, I.; Mues, C. An experimental comparison of classification algorithms for imbalanced credit scoring datasets. Expert Syst. Appl. 2012, 39, 3446–3453. [Google Scholar] [CrossRef]
- Samanta, B.; Al-Balushi, K.R.; Al-Araimi, S.A. Artificial neural networks and support vector machines with genetic algorithm for bearing fault detection. Eng. Appl. Artif. Intell. 2003, 16, 657–665. [Google Scholar] [CrossRef]
- Xie, S.; Zhang, X.; Cai, J. Video crowd detection and abnormal behavior model detection based on machine learning method. Neural. Comput. Appl. 2019, 31, 175–184. [Google Scholar] [CrossRef]
- Kalwa, U.; Legner, C.; Kong, T.; Pandey, S. Skin cancer diagnostics with an all-inclusive smartphone application. Symmetry 2019, 11, 790. [Google Scholar] [CrossRef]
- Le, T.; Baik, S.W. A robust framework for self-care problem identification for children with disability. Symmetry 2019, 11, 89. [Google Scholar] [CrossRef]
- Kang, Q.; Fan, Q.W.; Zurada, J.M. Deterministic convergence analysis via smoothing group Lasso regularization and adaptive momentum for Sigma-Pi Sigma neural network. Inf. Sci. 2021, 553, 66–82. [Google Scholar] [CrossRef]
- Díaz-Uriarte, R.; De Andres, S.A. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef]
- Wang, C.; Deng, C.; Wang, S. Imbalance-XGBoost: Leveraging weighted and focal losses for binary label-imbalanced classification with XGBoost. Pattern Recognit. Lett. 2020, 136, 190–197. [Google Scholar] [CrossRef]
- Thanathamathee, P.; Lursinsap, C. Handling imbalanced datasets with synthetic boundary data generation using bootstrap re-sampling and AdaBoost techniques. Pattern Recognit. Lett. 2013, 34, 1339–1347. [Google Scholar] [CrossRef]
- Kvamme, H.; Sellereite, N.; Aas, K.; Sjursen, S. Predicting mortgage default using convolutional neural networks. Expert Syst. Appl. 2018, 102, 207–217. [Google Scholar] [CrossRef]
- Yu, L.; Zhou, R.; Tang, L.; Chen, R. A DBN-based resampling SVM ensemble learning paradigm for credit classification with imbalanced data. Appl. Soft Comput. 2018, 69, 192–202. [Google Scholar] [CrossRef]
- Elreedy, D.; Atiya, A.F. A comprehensive analysis of synthetic minority oversampling technique (SMOTE) for handling class imbalance. Inf. Sci. 2019, 505, 32–64. [Google Scholar] [CrossRef]
- Bejjanki, K.K.; Gyani, J.; Gugulothu, N. Class Imbalance Reduction (CIR): A Novel Approach to Software Defect Prediction in the Presence of Class Imbalance. Symmetry 2020, 12, 407. [Google Scholar] [CrossRef]
- Mulyanto, M.; Faisal, M.; Prakosa, S.W.; Leu, J.-S. Effectiveness of Focal Loss for Minority Classification in Network Intrusion Detection Systems. Symmetry 2021, 13, 4. [Google Scholar] [CrossRef]
- Hao, W.; Liu, F. Imbalanced Data Fault Diagnosis Based on an Evolutionary Online Sequential Extreme Learning Machine. Symmetry 2020, 12, 1204. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Soltanzadeh, P.; Hashemzadeh, M. RCSMOTE: Range-Controlled synthetic minority over-sampling technique for handling the class imbalance problem. Inf. Sci. 2020, 542, 92–111. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced datasets learning. In Proceedings of the International Conference on Intelligent Computing (ICIC), Hefei, China, 23–26 August 2005; pp. 878–887. [Google Scholar]
- Douzas, G.; Bacao, F.; Last, F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F. Geometric SMOTE a geometrically enhanced drop-in replacement for SMOTE. Inf. Sci. 2019, 501, 118–135. [Google Scholar] [CrossRef]
- Maciejewski, T.; Stefanowski, J. Local neighbourhood extension of SMOTE for mining imbalanced data. In Proceedings of the IEEE Symposium on Computational Intelligence and Data Mining (CIDM), Paris, France, 11–15 April 2011; pp. 104–111. [Google Scholar]
- Bunkhumpornpat, C.; Sinapiromsaran, K.; Lursinsap, C. DBSMOTE: Density-based synthetic minority over-sampling technique. Appl. Intell. 2012, 36, 664–684. [Google Scholar] [CrossRef]
- Maldonado, S.; López, J.; Vairetti, C. An alternative SMOTE oversampling strategy for high-dimensional datasets. Appl. Soft Comput. 2019, 76, 380–389. [Google Scholar] [CrossRef]
- Pan, T.; Zhao, J.; Wu, W.; Yang, J. Learning imbalanced datasets based on SMOTE and Gaussian distribution. Inf. Sci. 2020, 512, 1214–1233. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar]
- Fernández, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for learning from imbalanced data: Progress and challenges, marking the 15-year anniversary. J. Artif. Intell. Res. 2018, 61, 863–905. [Google Scholar] [CrossRef]
- Alcalá-Fdez, J.; Fernández, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. Keel data-mining software tool: Data set repository, integration of algorithms and experimental analysis framework. J. Mult-Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Huang, J.; Ling, C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005, 17, 299–310. [Google Scholar] [CrossRef]
- Al-Azani, S.; El-Alfy, E.S.M. Using Word Embedding and Ensemble Learning for Highly Imbalanced Data Sentiment Analysis in Short Arabic Text. In Proceedings of the International Conference on Ambient Systems, Networks and Technologies and International Conference on Sustainable Energy Information Technology (ANT/SEIT), Madeira, Portugal, 16–19 May 2017; pp. 359–366. [Google Scholar]
- Liu, A.; Ghosh, J.; Martin, C.E. Generative Oversampling for Mining Imbalanced Datasets. In Proceedings of the International Conference on Data Mining (DMIN), Las Vegas, NV, USA, 25–28 June 2007; pp. 66–72. [Google Scholar]
- Rivera, W.A. Noise reduction a priori synthetic over-sampling for class imbalanced datasets. Inf. Sci. 2017, 408, 146–161. [Google Scholar] [CrossRef]
- Lee, H.; Kim, J.; Kim, S. Gaussian-Based SMOTE Algorithm for Solving Skewed Class Distributions. Int. J. Fuzzy Log. Intell. Syst. 2017, 17, 229–234. [Google Scholar] [CrossRef]
- Kang, Q.; Shi, L.; Zhou, M.; Wang, X.; Wu, Q.; Wei, Z. A distance-based weighted undersampling scheme for support vector machines and its application to imbalanced classification. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 4152–4165. [Google Scholar] [CrossRef]
- Nie, G.; Rowe, W.; Zhang, L.; Tian, Y.; Shi, Y. Credit card churn forecasting by logistic regression and decision tree. Expert Syst. Appl. 2011, 38, 15273–15285. [Google Scholar] [CrossRef]
- Oh, S.H. Error back-propagation algorithm for classification of imbalanced data. Neurocomputing 2011, 74, 1058–1061. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).