Investigating Human Torso Asymmetries: An Observational Longitudinal Study of Fluctuating and Directional Asymmetry in the Scoliotic Torso

Abstract

The presence of directional and fluctuating asymmetry in adolescent idiopathic scoliosis has not been deeply studied. We aimed to test the presence of both in a scoliosis group and a control group. 24 patients with adolescent idiopathic scoliosis and 24 control subjects were subjected to geometric morphometrics analyses to address our main hypotheses and to make qualitative visualizations of the 3D shape changes in patients with scoliosis. Our results support the hypothesis that both asymmetric traits are present in the scoliosis and control groups, but to a greater degree in patients. A qualitative visualization tool that allows us to measure the impact that directional and fluctuating asymmetry have on the 3D shape of our patients has been developed. Adolescent idiopathic scoliosis is the result of developmental instabilities during growth and the visualization of the 3D shape changes in response to both asymmetric variables has shown different morphological behaviors. Measuring these variables is important, as they can prevent the localization and deformation that is expected to occur during the course of scoliosis in every individual patient and therefore acts as a key clinical finding that may be used in the prognosis of the condition.

1. Introduction

Directional and fluctuating asymmetries have been previously evidenced in the human body. Studies regarding the human crania and face [1,2] or pelvic asymmetries are common [3], but there is a lack of research about their presence in the human torso, specifically in patients with scoliosis. In the 1990s, the theory of idiopathic scoliosis as a result of developmental instability during growth won popularity. Based on the significant presence of directional and fluctuating asymmetries in the torso of patients with idiopathic scoliosis, Goldberg et al. [4,5] gave relevance to the role of both variables in their comprehensive study of the condition. This research line remained latent until the recent appearance of new methodologies applied to the study of the asymmetric properties of the human torso. Specifically, geometric morphometrics (GMM) has been used for decades in other fields of biological research [6] and has recently brought new quantitative and qualitative variables to the study of idiopathic scoliosis [7]. Thus, higher levels of fluctuating asymmetry have been evidenced in other clinical conditions different from scoliosis in the form of positive correlation between asymmetries and symptoms [8]. Furthermore, in a recent study about fluctuating and directional asymmetries using two-dimensional GMM [9], the presence of both types of asymmetry has been revealed in a small group of patients with adolescent idiopathic scoliosis (AIS). However, the absence of a control group, the limited sample size and the two-dimensional approach to a three-dimensional condition such as idiopathic scoliosis led to three major limitations. For this reason, we aimed to test for the presence of both asymmetric traits using three-dimensional data and a control group. Our first hypothesis to be tested is that idiopathic scoliosis is just an increment in the range of variability of the natural asymmetries of the human torso, as was previously suggested in Beyer et al. [10]. In other words, fluctuating and directional asymmetries are expected to be found in control and scoliosis groups, but with significantly higher levels of individual scores among the individuals of the scoliosis group.

In our previous two-dimensional study [9], the individual directional asymmetry score, extracted from a two-dimensional GMM analysis of X-rays of patients with AIS, showed a high predictive power of the Cobb angle (effect size = 0.58). This finding should also hold regarding the three-dimensional aspect of shape and is postulated as our second hypothesis. Due to the greater magnitude of the directional asymmetry effect, the individual directional asymmetry score will be a better predictor of the Cobb angle (measured as effect size) than the individual fluctuating asymmetry score.

In another field of study of scoliosis, Ghaneei et al. [11] found that patients with body mass index (BMI) over 25 reported a greater trend towards underlying trunk deformities, and a strong correlation of BMI with body fat percentage in adolescents has been evidenced. Both BMI and body fat percentage have shown a positive correlation with AIS severity [12]. In this manner, since both factors are possible candidates for representing the nutritional state of a subject, their role in the external environment of the epigenetic theory of “exposome” in patients with AIS needs to be investigated [13]. We aim to study, as the first objective of our research, the correlation of the body fat percentage and the BMI with the Cobb angle and the individual fluctuating asymmetry score as the reference variable of studies regarding developmental instability [6,14]. Thus, the potential role of overweight and/or obesity as a risk factor of AIS will be clarified.

Finally, qualitative variables are basic for the biological comprehension and description of the AIS condition regarding the multiple factors acting all around [7,15]. Particularly, the GMM offers a strong arsenal of visualization tools that clinicians may benefit from. To observe how individual fluctuating and directional asymmetry scores interact with the three-dimensional shape of the torso is our second objective, and the visualization of the shape changes was done to develop a valuable tool for shape prediction models to be used in clinical assessments.

2. Materials and Methods

2.1. Data Acquisition

The sample was composed of 24 adolescents with idiopathic scoliosis and 24 control subjects of the same range of age (10–18) voluntarily recruited after the approval of the Research Ethics Committee (CEIC) of Cantabria, Spain, with approval number 2019.019. A STROBE statement was applied with a compliance of 18/22, and all anthropometric data were collected at the baseline time and six months later by the same researcher, including height, weight and body fat percentage with a body composition monitor, TANITABC-730. BMI was then calculated and used for further analysis, and the Cobb angle was measured three times on different days in tpsDig232 software (http://www.sbmorphometrics.org/soft-dataacq.html, accessed on 24 September 2020), using X-rays available for all patients in the scoliosis group. Cobb angle could not be measured in control subjects due to unavailability of X-rays due to ethical reasons. The intraclass correlation coefficient (ICC) was calculated to assess for the angular measurement reliability.

Torso surface scans of all subjects were done in a standing position with the hands slightly raised over the head following the protocol of González–Ruiz et al. [7]. Then, scans were processed (global registration and fast fusion) in ArtecStudio to obtain 3D meshes at the baseline time and six months after the first scanning process. A loss of five individuals from the AIS group and two individuals from the control group was accounted for in the second measurement due to causes beyond the control of investigators. Finally, the 89 polygon file format files (PLY) with the surface topography of the torsos were post–processed (smoothing and fast mesh simplification) in ArtecStudio software and prepared for the posterior digitization procedure.

Data with a mean and standard deviation of all variables by group and observation are shown in

Table 1. Anthropometric and radiological data of the AIS and control groups classified according to the time of observation (initial or 6 months later).

		AIS Group		Control Group
		Baseline Time (n = 24)	6 Months (n = 19)	Baseline Time (n = 24)	6 Months (n = 22)
Age (years)		12.98 (2.11)	13.26 (2.28)	12.39 (2.46)	13 (2.69)
SEX 1		Male (n = 2) Female (n = 22)	Male (n = 2) Female (n = 17)	Male (n = 13) Female (n = 11)	Male (n = 12) Female (n = 10)
Height (cm)	p-value = 0.85 between groups	158.12 (10.69)	158.43 (11.11)	156.49 (14.68)	159.05 (14.31)
Weight (kg)	p-value = 0.46 between groups	52.83 (10.89)	49.32 (10.41)	48.05 (14.62)	49.53 (12.88)
Body fat (%)	p-value < 0.01 between groups 2	23.98 (6.19)	21.82 (5.89)	17.64 (5.07)	17.46 (5.17)
BMI	p-value = 0.15 between groups	20.41 (2.63)	19.54 (2.31)	19.22 (2.82)	19.19 (2.37)
Cobb angle		23.53 (9.02)	23.36 (10.53)	Data not available due to ethical reasons

¹ All variables except sex are represented by mean (standard deviation). ² Only differences in body fat are observed between groups.

.

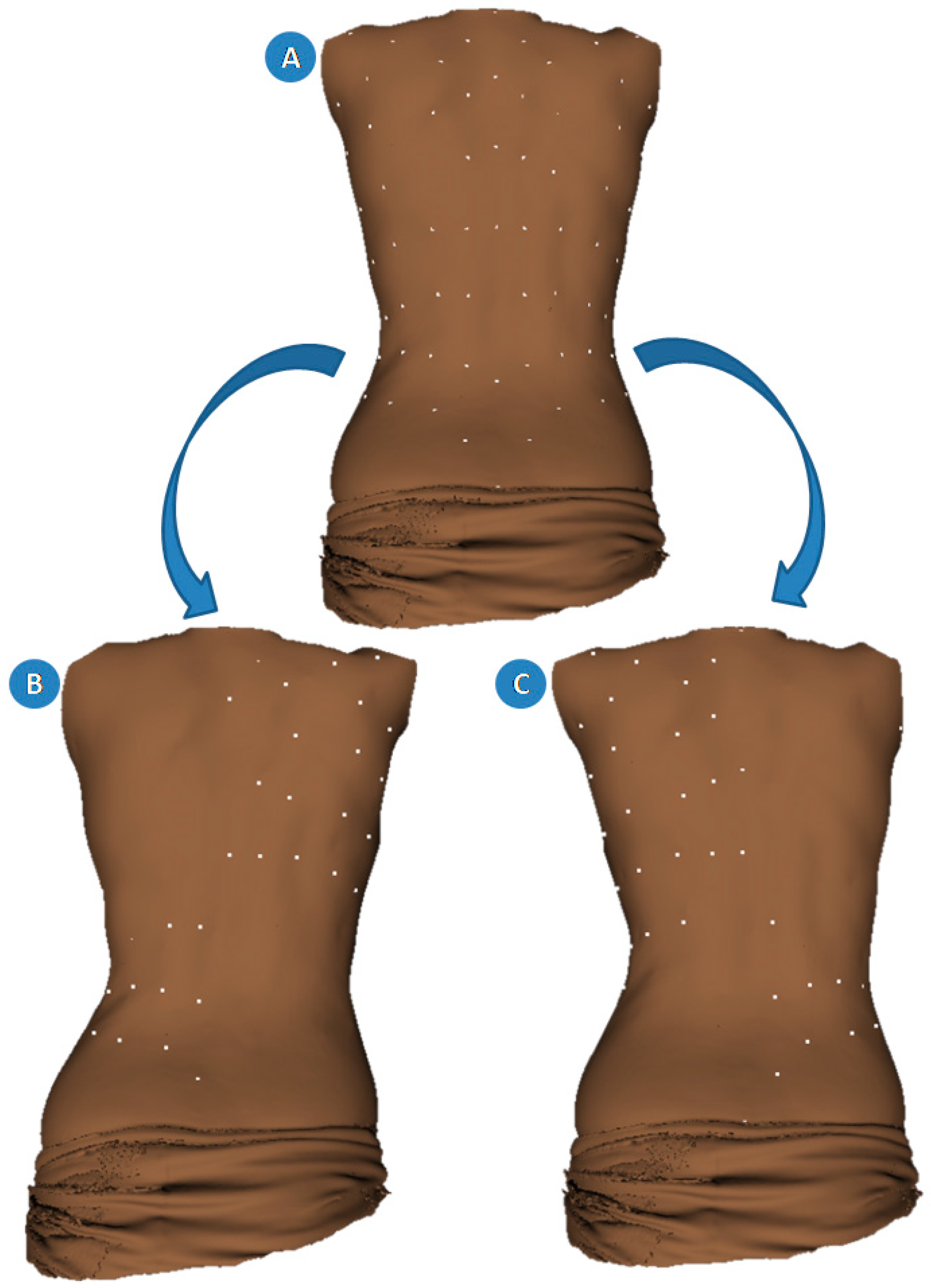
2.2. Geometric Morphometrics

Using the three-dimensional landmarks template described in González–Ruiz et al. [7], we digitized the whole sample twice in Viewbox and subsequently extracted all coordinates from landmarks after the sliding process was done. Two datasets with the coordinates of the first and the second measurements were prepared for further analyses of GMM.

Both coordinate files were introduced in MorphoJ; the median–sagittal landmarks were selected, and the pairing of the bilaterally symmetrical landmarks was done before the Procrustes fit. This reflecting and relabelling analysis revealed the mean asymmetry of shape of the sample [16], which could be considered the expression of the directional asymmetry in the population under study.

Then, the covariance matrix of all individual’s shapes was calculated and, as a result, the symmetric and asymmetric components of the shape were extracted and used to estimate the individual directional asymmetry score following the steps described in González–Ruiz et al. [9]. A Procrustes ANOVA including the whole sample (AIS and controls) was conducted to test for the individual fluctuating asymmetry score and the measurement error. Further analyses regarding hypothesis 1 were carried out using the non–parametric Mann–Whitney U test due to the absence of the normal distribution in the data.

Concerning our second hypothesis, we made a MANOVA of the fluctuating and directional asymmetry score factors as independent variables to test the dependence of the Cobb angle on both factors combined and isolated.

To address the first objective of our study, we made an ordinary least squares regression model with BMI and body fat percentage as independent variables and with the Cobb angle and the individual fluctuating asymmetry score as dependent variables.

Finally, to carry out our second objective, multivariate multiple regressions of the symmetric and asymmetric components of shape were made in MorphoJ on the individual fluctuating and directional asymmetry scores to visualize how shape varies in response to increments of both independent variables. Three-dimensional biological images were shown only for the statistically significant regressions.

We set a significant p-value equal to or less than 0.05 in all regression analyses done to investigate objectives one and two and hypothesis two. The same applied to the Procrustes ANOVA executed to investigate hypothesis one. An effect size (ES) was considered acceptable with R^2 values over 0.25.

3. Results

The ICC for the repeated measures of the Cobb angle was 0.942 with a 95% confidence interval of 0.902–0.968, reflecting excellent reliability according to Koo et al. [17].

3.1. Hypothesis 1

Regarding the non–separated Procrustes ANOVA that included the whole sample, the mean fluctuating asymmetry individual score is significantly higher (p-value < 0.0001) in the AIS group (0.0297 ± 0.0067) than in the control group (0.0233 ± 0.0063), as can be seen in Figure 1. Supplementary analyses for the longitudinal observation and sex effects are shown in Supplementary Tables S1 and S2, respectively. Longitudinal observation does not show significant differences in individual fluctuating asymmetry scores of the sample, while the individual fluctuating asymmetry scores are significantly higher in females than in males. In the case of the individual directional asymmetry score, similar results were obtained. Individual directional asymmetry score is significantly higher (p-value < 0.0001) in AIS (0.0747 ± 0.0141) than in controls (0.0587 ± 0.0124) and in females than in males. The longitudinal observation did not show significant differences in individual directional asymmetry scores. All results regarding the individual directional asymmetry score are shown in Figure 1 and Supplementary Tables S1 and S2. 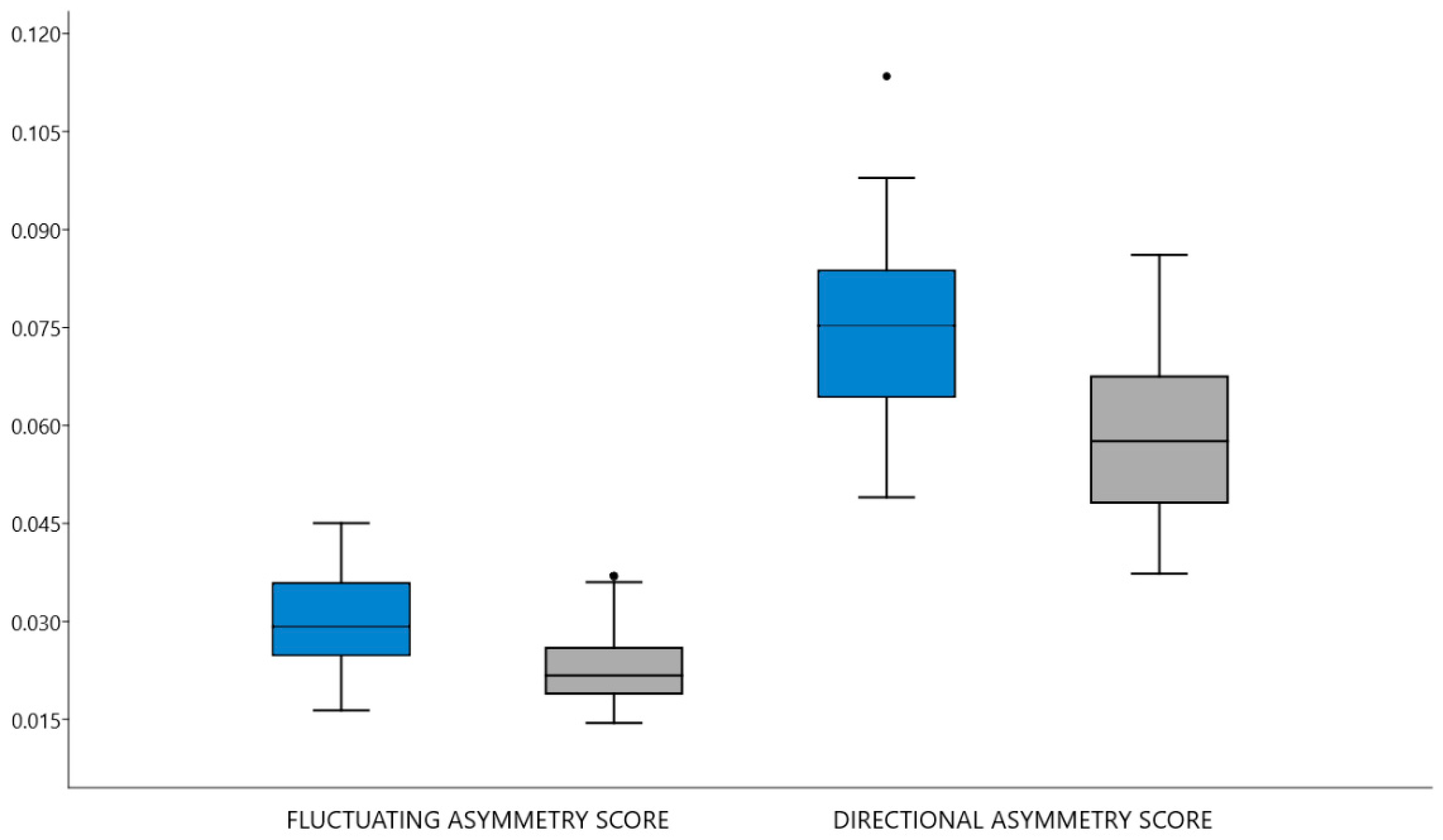In light of these results, we accept hypothesis 1.

3.2. Hypothesis 2

We reject hypothesis 2 because neither the individual directional asymmetry score nor the individual fluctuating asymmetry score are significant determinants of the Cobb angle when used as separate factors, as can be seen in

Table 2. Multivariate multiple linear regression of the individual fluctuating asymmetry and individual directional asymmetry scores on the Cobb angle.

Overall Manova	p–Value	R^2 2
Test on the dependent variable
COBB	0.009 1	0.25
Test on independent variables
DA	0.926	0.16
FA	0.061	0.25

¹ p-value < 0.05 is statistically significant. ² Determination coefficient or effect size.

. Nevertheless, both variables combined showed a significant predictive ability (p-value = 0.009) of the dependent variable with an effect size of 0.25.

3.3. Objective 1

We have observed a significant correlation between the BMI and the Cobb angle (p-value = 0.02; r = 0.41), a fact that was not evidenced between the BMI and the individual fluctuating asymmetry score or between the body fat percentage and both dependent variables (Cobb angle and individual fluctuating asymmetry score). All the results regarding the correlation analyses are shown in

Table 3. The ordinary least squares regressions (OLS) of the BMI and the body fat percentage on the individual fluctuating asymmetry score and the Cobb angle.

	BMI–Cobb Angle	BMI–FA Score	%Body Fat–Cobb Angle	%Body Fat–FA Score
R 3	0.41024	0.30272	0.24722	0.25093
R^2 2	0.16829	0.091639	0.061118	0.062968
p-value	0.0248 1	0.1032	0.1922	0.172

¹p-value < 0.05 is statistically significant. ² Determination coefficient or effect size. ³ Correlation coefficient.

. Additionally, the residuals of the unique significant correlation (BMI–Cobb angle) were plotted to test for normality distribution and validate the results of the analysis. They are represented in Supplementary Figure S1.

3.4. Objective 2

None of the multivariate multiple regressions of the symmetric component of three-dimensional shape on the individual fluctuating and directional asymmetry scores were statistically significant. Only in the group of females with AIS (n = 39) was the multivariate multiple regression of the asymmetric component of the three-dimensional shape on the individual fluctuating and directional asymmetry scores significant (p-value = 0.0026; R^2 = 0.117). Females of the control group (n = 21) and males of both groups (AIS (n = 4) and control (n = 25)) did not show a significant effect of individual fluctuating and directional asymmetry scores on the three-dimensional shape of the torso. For this reason, the shape changes in response to the increments of the individual fluctuating and directional asymmetry scores were strictly represented for females of the AIS group (Figure 2). When the directional asymmetry effect is augmented on the shape visualization (C), right thoracic and left lumbar curves appeared with significant lateral flexion and rotation. In the case of fluctuating asymmetry (B), the observed effect is quite opposite, with less lateral deformity but evidenced rotation at the left side of the thoracic segment and the right side of the lumbar area. Supplementary videos of both effects are available as Supplementary Videos S1 (fluctuating asymmetry effect on the shape) and S2 (directional asymmetry effect on the shape). Additionally, the effect that increments of fluctuating asymmetry and directional asymmetry have on the shape of the torso is specifically represented in Figure 3 and Figure 4, respectively, so they can be used as the clinical prognosis tool that may be discussed deeply in the discussion.

4. Discussion

Our results regarding hypothesis 1 are in agreement with the expected results according to previous studies of idiopathic scoliosis [18]. Taking into account that directional asymmetry is the pattern of difference in the asymmetry of a bilateral trait (in the case of AIS, both sides of the human torso) [19], we expected to find a greater magnitude of this population effect in the group of patients with AIS than in the control group. Directional asymmetry has been extensively related in upper and lower limbs due to occupational or sport activities [20] and its presence in the human torso of healthy subjects has been evidenced before in the spine and pelvis [21]. Thus, the human torso is not perfectly symmetrical, and the presence of directional asymmetry in an asymptomatic grade in the control group was not, therefore, a surprise [22]. Considering that fluctuating asymmetry is the reference variable in studies of developmental instability [6,23], the difference observed between groups may respond to the main role that this instability plays during growth in patients with AIS (even in cases with mild scoliosis) in the acquisition of the asymmetric phenotype [4,5]. Thus, we agree with the theory of AIS being a developmental instability phenomenon during growth, and our results highlighted the ability of GMM methods for measuring asymmetries and their relationship with shape. In fact, to our knowledge, this is the first study to assess individual directional and fluctuating asymmetry scores in the 3D shape of patients with scoliosis. It seems that the presence of fluctuating asymmetry even in mild scoliosis proves that fact, as well as the fact that the magnitude of directional asymmetry is proportional to the severity of the condition, as we have seen in our previous work based on the study of the two-dimensional shape with GMM [9]. In summary, directional and fluctuating asymmetry appear to be intrinsic to human developmental biology, even in control subjects. With this starting point, many clinical conditions (including AIS) have demonstrated the ability to increase the intensity of both traits in patients [8].

Another key point of our results is that both traits are not exclusive for the AIS subjects, but also for the females when compared to males, probably representing a sexual dimorphism trait. Concerning the difference in directional asymmetry between sexes, the low number of males with AIS recruited (n = 2) could have biased the results. Fortunately, the addition of the control group with a better balance between sexes may slightly attenuate this distribution bias in the case of fluctuating asymmetry. It is well-known that the prevalence of AIS among females in adolescence is higher than in males [24], and this is reflected in our results, where the girls showed significantly higher rates of fluctuating asymmetry than the males. Future studies should examine whether fluctuating asymmetry could be linked to one of the multiple etiopathogenic theories that exclusively affect females.

The disagreements about the predictive power of the individual directional asymmetry score (measured as effect size) between our previous two-dimensional GMM research and the outcome of the three-dimensional approach need to be discussed deeply. First of all, the variable to be predicted (Cobb angle) is an angular value measured in an X-ray, which is a two-dimensional projection of the three-dimensional torso of the patient. Then, the two-dimensional individual directional asymmetry score, which reflects the left–right curve direction in the X-ray using all landmark data, is essentially a two-dimensional variable, as the Cobb angle is. Due to the previous reason, the high correlation found in González–Ruiz et al. [9] was not a surprise and made us postulate the same hypothesis in our three-dimensional research. However, the complexity of the three-dimensional shape data made the difference for two main reasons:

-

Our data is limited to the surface of the human torso, and we did not have access to the three-dimensional shape of the spine. It is probable that the measure of the individual directional asymmetry in a dataset of three-dimensional coordinates digitized in each vertebra will show a higher correlation than the surface data did. It is accepted that the concordance between the spine shape and the surface asymmetry of the torso is not accurate enough [25].

-

Additionally, measuring directional asymmetry in a three-dimensional shape will introduce some noise derived from the transversal and sagittal planes, which do not interfere in the two-dimensional approach. To serve as an example, factors such as body fat tissue and breast development in females may confuse the output of three-dimensional directional asymmetry that we have measured in this research [11].

The good news is that, despite the fact that there is not a significant determination of the Cobb angle either from directional asymmetry nor fluctuating asymmetry when separated, both asymmetric features combined have a positive and significant effect on the Cobb angle with an acceptable effect size (0.25). In the future, this could open an opportunity to investigate predictive models of the Cobb angle based on multiple regression analyses to be used in the clinical/medical environment, and that finding may prevent an excess of radiation exposure and its well-known risks, which are associated with the AIS condition [26].

Regarding our first objective of assessment of the correlation between the BMI and the body fat tissue with the Cobb angle and the individual fluctuating asymmetry score, we have found similar results to those of Ghaneei et al. [11]. There was a significant and positive relation of increment of the Cobb angle in response to a BMI increment. Other authors have found an association between both variables and an augmented difficulty in monitoring the three-dimensional shape due to the BMI [27]. What is beyond doubt is that higher levels of BMI and body fat are correlated with curve severity in patients with AIS, despite the fact that this relationship has not been found in our research [12].In the particular case of the correlation between both independent variables (BMI and body fat tissue) and the individual fluctuating asymmetry score, there is a scarcity of literature on the matter. Grivas et al. [28] found a relationship between BMI and trunk asymmetries in a healthy group of adolescents with scoliosis, but the interaction between BMI and fluctuating asymmetry, specifically, has never been studied before. Our explanation for the absence of interaction between both variables is that, in mean terms, our sample has a low BMI. It remains unclear whether, in a sample with a higher prevalence of obesity/overweight among AIS patients, there would be some correlation between fluctuating asymmetry and those particular factors (BMI and body fat tissue).

Concerning the regression analyses of shape changes in response to fluctuating and directional asymmetry effects, only the asymmetric component of shape in females with AIS showed a significant result. It is probable that the reduced sample of males with AIS and the lower amount of fluctuating and directional asymmetry in controls of both sexes explained these results. Finally, from a qualitative perspective of the potential clinical use of three-dimensional GMM, the visualization of the shape changes in response to simulated increments of both asymmetric traits (fluctuating and directional) show two different morphological transformations:

-

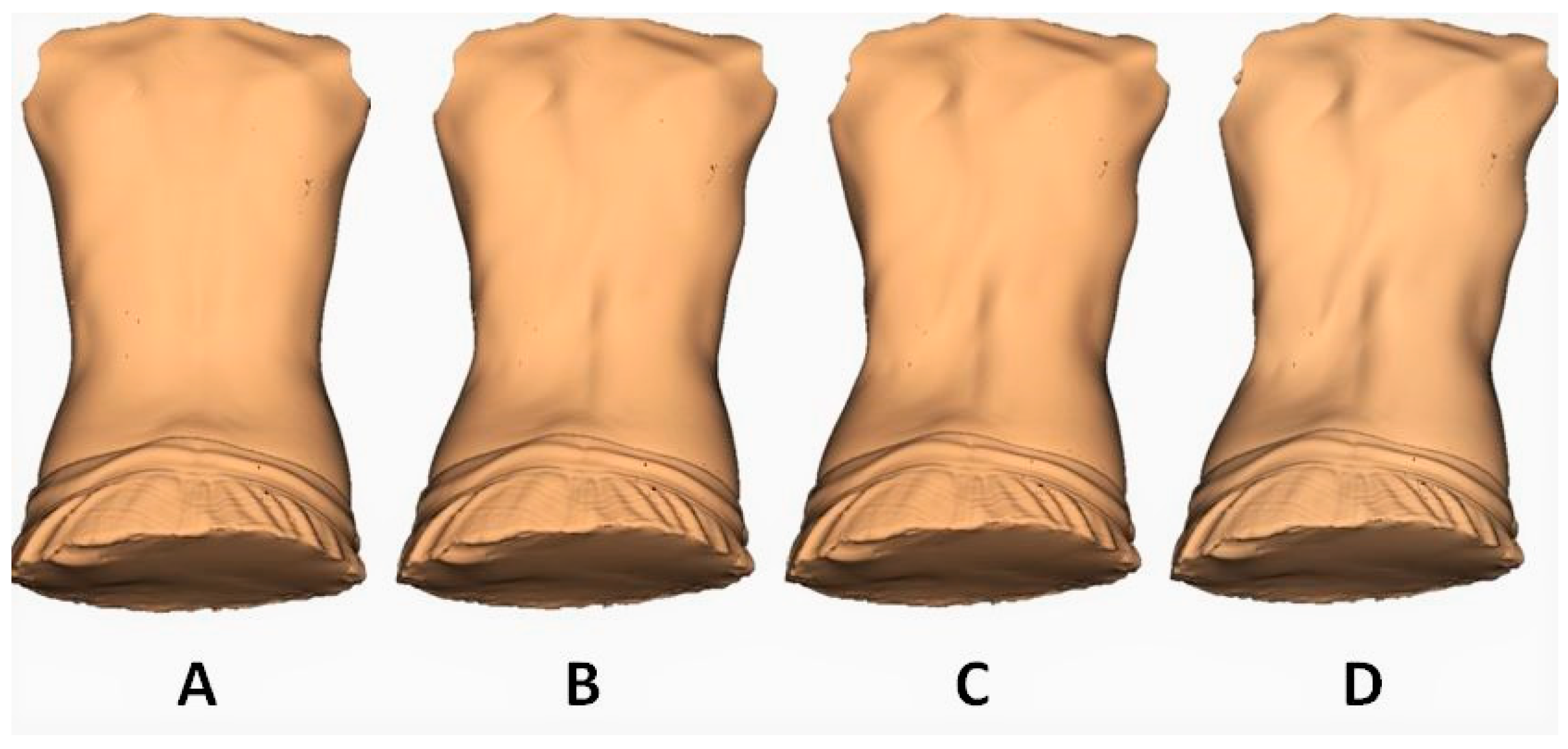
We observed great concordance with our previous two-dimensional GMM findings [9]. The simulated increment of fluctuating asymmetry produced an opposite shape transformation, as can be appreciated in Figure 3 and Supplementary Video S1. In this case, the torso showed a very moderate inclination towards the left side in the thoracic area and towards the right side in the lumbar spine. What is relevant is that the increment of the rotation in both segments was the major trait observed.

-

On the other hand, as we have observed in our previous two-dimensional GMM research [9], the increment of the directional asymmetry effect deforms the torso following the most prevalent pattern described in AIS [18,29]. This increment of the right thoracic and the left lumbar convexities with a lesser effect of rotation in both segments can be observed in Figure 4 and Supplementary Video S2 (right rotation in the thoracic spine and left rotation in the lumbar spine).

How can we interpret these observations? Looking back at the beginning of the introduction section, we find that fluctuating asymmetry is the gold standard in studies of developmental instability [6,30]. Besides, since its presence in AIS subjects in a more significant quantity than in controls has been proven, our argument is that those AIS patients with higher developmental instability suffered during growth present higher levels of fluctuating asymmetry and their scoliosis is characterized by greater deformation in the transversal plane (rotation) rather than in the frontal plane (inclination). This is a major clinical finding, because if we have the opportunity to measure fluctuating and directional asymmetry levels in the first stages of the condition, we will be in the advantageous position of preventing increments in rotation (related to elevated levels of fluctuating asymmetry) or inclination (related to elevated levels of directional asymmetry). One limitation of the clinical application of these analyses is that a minimum sample size is required to obtain the individual variables (20–30 individuals according to Klingenberg [14]) because fluctuating and directional asymmetry are both population-dependent effects. What should be done in the future is the construction of a database with three-dimensional shape information of patients with AIS that will serve as controls for the patient that is being studied individually in the clinical/hospital environment. There is another limitation associated with the development of the methodology described in this paper and its manual procedure. Scanning, digitizing, processing, analyzing and visualizating have been performed manually following a step-by-step path that would take excessive time in the clinical work environment. Efforts must be done in the future to automatize the methodology presented as much as possible and successfully transfer it from virtual morphology labs to hospitals. In this line, machine learning is showing greater results in clinical decisions made for patients with scoliosis [14,31]. Applying all this knowledge to GMM remains to be done in the study of this condition.